Abstract
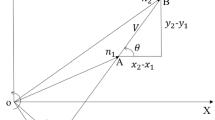
Recent research results suggested a conservative transformation to correct the well-known congruence transformation between Cartesian and joint stiffness matrices of a serial manipulator. This paper utilizes screw geometry to interpret the conservative congruence transformation (CCT). The analysis using screw theory provides better geometric insights into the CCT. The effective geometrical stiffness matrix, due to the change of manipulator geometry under stiffness control in the presence of external force, is confirmed. This paper also points out several erroneous assumptions that may have led to the incorrect formulation of the conventional congruence transformation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Asada H, Slotine JE (1986) Robot analysis and control. John Wiley & Sons, New York.
Ball RS (1986) A treatise on the theory of screws. Cambridge University Press, Cambridge.
Chen SF, Kao I (1999) The conservative congruence transformation of stiffness control in robotic grasping and manipulation. In Proceedings of the 9th International Symposium of Robotics Research, pp 7–14, Snowbird.
Chen SF, Kao I (2000) Conservative congruence transformation for joint and cartesian stiffness matrices of robotic hands and fingers. International Journal of Robotics Research, 19: 835–847.
Hunt KH (1978) Kinematic geometry of mechanisms. Clarendon Press, Oxford.
Kao I, Ngo C (1999) Properties of grasp stiffness matrix and conservative control strategy. International Journal of Robotics Research, 18:159–167.
Mckerrow PJ (1991) Introduction to robotics. Addison-Wesley, New York.
Roth B (1984) Screws, motors, and wrenches that cannot be bought in a hardware store. In Proceedings of the 1st International Symposium of Robotics Research, pp 679–693.
Salisbury JK (1980) Active stiffness control of a manipulator in cartesian coordinates. In Proceedings of the 19th IEEE Conference on Decision and Control, pp 87–97, Albuquerque.
Salisbury JK (1982) Kinematic and force analysis of articulated hands. PhD thesis, Stanford University.
Schilling RJ (1990) Fundamentals of robotics. Prentice-Hall, Upper Saddle River, New Jersey.
Tsai LW (1999) Robot analysis: the mechanics of serial and parallel manipulators. John Wiley & Sons, New York.
Waldron KJ, Wang SL, Bolin SJ (1985) A study of the jacobian matrix of serial manipulators. ASME Journal of Mechanisms, Transmissions, and Automation in Design, 107:230–238.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2003 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Huang, C., Kao, I. (2003). Geometrical Interpretation of the CCT Stiffness Mapping for Serial Manipulators. In: Jarvis, R.A., Zelinsky, A. (eds) Robotics Research. Springer Tracts in Advanced Robotics, vol 6. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-36460-9_28
Download citation
DOI: https://doi.org/10.1007/3-540-36460-9_28
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-00550-6
Online ISBN: 978-3-540-36460-3
eBook Packages: Springer Book Archive