Dynamics of the Judicial Process by Defeater Activation

Abstract

We present a novel activating approach to Argument Theory Change (ATC) for the study of the dynamics of the judicial process. ATC applies belief change concepts to dialectical argumentation for altering trees upon which the semantics for reasoning are defined. The activating approach to ATC considers the incorporation of arguments to define a revision operator for studying how to provoke change to the semantics’ outcome. Our objective is to contribute to the discussion of how to deal with circumstances of the judicial process like hypothetical reasoning for conducting investigations of a legal case, and for handling the dynamics of the judicial process. We finally observe the behavior of our proposal upon the sentences of two different real criminal procedures.

1 Introduction and Motivation

Argumentation provides a theoretic framework for modeling paraconsistent reasoning, a subject of utmost relevance in areas of research like medicine and law. For instance, legal reasoning can be seen as the intellectual process by which judges draw conclusions ensuring the rationality of legal doctrines, legal codes, binding prior decisions like jurisprudence, and the particularities of a deciding case. This definition can be broaden to include the act of making laws. Observe that the evolution of a normative system –for modeling promulgation of laws– would imply the removal/incorporation of norms for ensuring some specific purpose but keeping most conflicts from the original framework unaffected. As an example, we briefly refer to the Argentinean broadcasting media law reformed during 2009. The previous media law, promulgated by the latter de facto regime, empowered the government to regulate the different media allowing total control of news. When democracy was restituted, the regulation of media was extended to private investment groups. As years went by, these groups took over majorities of types of media, conforming monopolies in some cases. This brought excessive power to groups with partial interests, allowing them to manipulate the social opinion about the actual government, and even to condition politicians, thus striking to national sovereignty. Article 161 of the new media law became one of the most controversial points, since it forces monopolistic enterprises to get rid of part of their assets in a maximun period of 1 year. Some enterprises warned that they would be forced to sell off their assets at very low prices. This opposes to article 17 of the National Constitution which speaks about private property rights. Moreover, some members of the Supreme Court think that article 161 recalls the control over the media exercised by totalitarian regimes, which would violate article 1 of the National Constitution. In fact, such situation could evolve to a distrust state on the principle of legal security. Hence, an informal analysis of the case imply working with conflicts among arguments in a sense like: $\langle art~17 \rangle$ counter-argues $\langle art~161 \rangle$, $\langle \langle art~1 \rangle$ and $\langle principle~of~legal~security \rangle \rangle$ counter-argues $\langle art~161 \rangle$, and so on. (The new media law keeps being discussed in Argentina nowadays.) Consequently, the objective of this article is to study the bridge between the dynamics of the legal reasoning and the dynamics of argumentation. To that end, we rely upon abstract argumentation for constructing a theory of argumentation dynamics, and afterwards we study the dynamics of real legal procedures by analyzing the behavior of the theory upon the legal case’s argumentation. However, the arguments that follow from a legal sentence are constructed in an informal manner, since argument mining from legal texts is an independent area that lies beyond the scope of this article.

Argument Theory Change (ATC) [18,19,20] relies upon the theory of belief revision [3, 16] to define models of argumentation change which are devoted to the alteration of dialectical trees pursuing warrant of a particular argument. Dialectical trees are constructed from a graph of arguments where nodes stand for arguments and arcs for the attack relation between pairs of arguments. The root of a dialectical tree is the argument standing for the main issue in dispute of the reasoning process. The dialectical argumentation semantics analyzes the dialectical tree and as a result, the root argument may end up warranted, proposing a reason to believe that the issue in dispute should prevail. This form of argumentation reasoning brings a theoretical perspective that adapts well for modeling the dynamics of the judicial process. The dynamic abstract argumentation framework [21] extends Dung’s framework [14] in order to consider (1) subarguments (internal, necessary parts of an argument that are arguments by themselves), and (2) a set of active arguments (those enabled to be used in the reasoning process). The main contribution provided by ATC is a revision operator that revises a theory by an argument seeking its warrant. For achieving warrant, a revision operator can be defined through deactivation of arguments [20]: the reasoning process disconsiders some arguments for ensuring warrant of the argument at issue. A complementary approach to such revision operation involves only activation of arguments [18]. This approach complements the one based on deactivation because sometimes it is either not feasible to deactivate arguments or the activation of another provokes less change. For instance, studying change in a normative system may imply the derogation of norms through the incorporation of a derogative norm. In this case, the model for derogation is achieved through the activation of an argument standing for a derogative norm in contrast to the proposal of the deactivating approach in which the old norm could only be disconsidered or removed from the system. The activating approach increases the amount of active arguments to achieve warrant. However, since defeaters might be unavailable to be activated, the revision could be not always successful. Moreover, it will be clear that each activation of an argument results in the possible activation of more arguments, thus provoking preexistent arguments to play additional roles.

In this article we present an original model of ATC referred as global activating approach which develops the objective of the activating ATC presented in [18] in a different perspective more related to the deactivating model for logic-based argumentation presented in [19]. The advantage of the global activating model includes reducing the theoretical complexity towards an appropriate axiomatic characterization. Our main objective is to contribute to the discussion of virtues and shortcomings of the activating approach as a theoretical resource for analyzing the current epistemic state of a judicial procedure under the presumption that such a legal practice is dynamic by nature. This means that in order to consider dialectical argumentation as a theoretic model of judicial procedures we necessarily must rely upon a theory with capabilities for handling dynamics of arguments. It is important to mention that we will only concentrate on the particularities related to the argumentation dynamics and not on legal concepts –like burden or standard of proof– related to the specific court to which a judicial procedure corresponds (see [6]). However, in Sect. 3, we analyze the sentences of two different real legal cases: a Supreme Court’s for analyzing the dynamics throughout appellate instances of the judicial process, and secondly, the argumentation related to a process of a criminal court. To that end, we build the corresponding arguments and show that the judicial process, either from the judge’s or from the lawyer’s viewpoint, is dynamic by nature by applying the global model of argumentation dynamics presented here. However, we firstly present the change operation from an abstract perspective (Sect. 2), following a practical take on this matter. There, the usual principles of change from belief revision are considered. The axiomatization of the proposed operator should conform to postulates adapted to dialectical argumentation (see [19]) by following such principles. This part of the work is underway.

2 A Model of Abstract Argumentation Dynamics

2.1 Fundamentals for the Argumentation Framework

Arguments, in the usual sense, are interpreted as a reason for a certain claim from a set of premises. In abstract argumentation [14], these features are abstracted away; hence we will work with arguments as “black boxes of knowledge” which may be divided in several smaller arguments, referred to as subarguments. In the dynamic framework used here we assume a universal set of arguments holding every conceivable argument that could be used by the inference machinery, from which a subset of active arguments can be distinguished. These arguments represent the current state of the world and are the only ones to be considered to compute warrant. Therefore, at a given moment, those arguments that are inactive represent reasons that, though valid, cannot be taken into consideration due to the current context. For instance, the presentation of an appeal outside the acceptable period of time would render this argument inactive. That is, although the appeal constitutes a valid reason, it is incompatible with the current state of the world. A similar concept to inactive arguments is given in [23] to inadmissible arguments. Another configuration for inactiveness can be explained in the context of legal reasoning when some norm can be inferred from multilateral treaties and therefore, although it can be considered to be part of the normative system, its application depends on the decision of the Supreme Court for establishing jurisprudence regarding its applicability. An example in this sense is developed in Sect. 3.1. In this section, we will abstract away from any comprehensive mechanism for activating arguments. Afterwards, the ATC’s activating global model will handle activation of arguments in a proper manner, seeking for a concrete objective. These changes will be performed at a theoretical level, i.e., any inactive argument could be eventually activated. Nonetheless, a practical implementation for legal reasoning should restrict which inactive arguments are currently available to be activated according to interpretation of norms, which lies beyond the scope of this article. The abstract dynamic framework is defined next.

Definition 1

(DAF). A dynamic abstract argumentation framework (DAF) is a tuple ${\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ]}$, where ${\mathbb {U}}$ is a finite set of arguments called universal, ${\mathbb {A}} \subseteq {\mathbb {U}}$ is called the set of active arguments, ${\hookrightarrow } \subseteq {\mathbb {U}} \times {\mathbb {U}}$ denotes the attack relation, and ${\sqsubseteq } \subseteq {\mathbb {U}} \times {\mathbb {U}}$ denotes the subargument relation.

As said before, an argument ${\mathcal {B}} \in {\mathbb {U}}$ may be composed by other arguments. Since an argument is considered a subargument of itself, it holds that ${\mathcal {B}} {\sqsubseteq } {\mathcal {B}}$, and therefore an argument always has at least one subargument. To illustrate the use of arguments and subarguments, consider for instance an argument ${\mathcal {B}}$: “the fact that Steven did not turn in the report indicates that he is irresponsible; since Steven is irresponsible, he should be fired”. There we can identify two subarguments, ${\mathcal {B}} _1$: “failing in turning in reports suggests irresponsibility” and ${\mathcal {B}} _2$: “irresponsible people should be fired”.

The subset of inactive arguments is identified as ${\mathbb {I}} = {\mathbb {U}} \setminus {\mathbb {A}}$. This set contains the remainder of arguments (within the universal set) that is not considered by the argumentative process at a specific moment. The principle characterizing argument activation is:

(Activeness Propagation) ${\mathcal {B}} \in {\mathbb {A}}$ iff ${\mathcal {B}} '\in {\mathbb {A}}$ for any ${\mathcal {B}} '{\sqsubseteq } {\mathcal {B}}$.

A set of active arguments determines that an argument containing them and only them is also active. Furthermore, an argument becoming active makes all of its subarguments to become active. An operator ${\mathrm {C}_{\mathfrak {ap}}}:{\mathcal {P}} ({\mathbb {U}})\rightarrow {\mathcal {P}} ({\mathbb {U}})$ is assumed to implement the closure under activeness propagation. Thus, ${\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ]}$ is closed iff ${\mathbb {A}} ={\mathrm {C}_{\mathfrak {ap}}} ({\mathbb {A}})$. To represent change over the set of active arguments we assume an activation operator ${\oplus }:{\mathcal {P}} ({\mathbb {U}})\times {\mathcal {P}} ({\mathbb {U}})\rightarrow {\mathcal {P}} ({\mathbb {U}})$ such that $\varPsi _1{\oplus } \varPsi _2={\mathrm {C}_{\mathfrak {ap}}} (\varPsi _1\cup \varPsi _2)$, with $\varPsi _1,\varPsi _2\subseteq {\mathbb {U}}$.

Usually, the acceptability analysis over an argumentation framework is made over the graph of arguments implicit from the framework. In this article, we build and evaluate a dialectical tree rooted in the argument under study in order to determine whether it is warranted. This approach allows us to analyze only the relevant portion of the arguments graph since we are evaluating the warrant status of a single argument. A dialectical tree is conformed by a set of argumentation lines; each of which is a non-empty sequence ${\lambda _{}}$ of arguments from a DAF, where each argument in ${\lambda _{}}$ attacks its predecessor in the line. The first argument is called the root, and the last one, the leaf of ${\lambda _{}}$. We refer to a DAF as a dynamic argumentation theory (DAT) if it is closed under activeness propagation and whose argumentation lines are built according to the dialectical constraints (DCs) [15]: different restrictions on the construction of argumentation lines which ensure every line is finally acceptable. We assume DCs to avoid constructing circular argumentation lines. The domain of all acceptable argumentation lines in a DAT ${\mathsf {T}}$, is noted as ${\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}$, while ${\mathfrak {Lines}^{{\mathbb {A}}}_{{\mathsf {T}}}} \subseteq {\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}$ will be the domain enclosing every acceptable line containing only active arguments. The root argument of a line $\lambda$ from a DAT ${\mathsf {T}}$ will be identified through the function ${\mathsf {root}}:{\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}} \rightarrow {\mathbb {U}}$, while the leaf of $\lambda$ through a function ${\mathsf {leaf}}:{\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}} \rightarrow {\mathbb {U}}$. From now on, given a DAT ${\mathsf {T}}$, to refer to an argument ${\mathcal {A}}$ belonging to a line ${\lambda _{}} \in {\mathfrak {Lines}^{{\mathbb {A}}}_{{\mathsf {T}}}}$, we will overload the membership symbol and write “${\mathcal {A}} \in {\lambda _{}}$”, and will refer to $\lambda$ simply as argumentation line (or just line) assuming it is acceptable. Since argumentation lines are an exchange of opposing arguments, conceptually we could think of it as two parties engaged in a discussion: one standing by the root argument and the other arguing against it. Consequently, given a line ${\lambda _{}}$, we identify the set of pro (resp, con) arguments containing all arguments placed on odd (resp, even) positions in $\lambda$, noted as $\lambda ^+$ (resp, $\lambda ^-$).

Definition 2

(Upper Segment). Given a DAT ${\mathsf {T}}$ and a line $\lambda \in {\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}$ such that $\lambda = [{\mathcal {B}} _1,\ldots ,{\mathcal {B}} _n]$, the upper segment of $\lambda$ wrt. ${\mathcal {B}} _i$ $(1\le i\le n)$ is defined as $\lambda ^{\uparrow }_{}[{\small {\mathcal {B}} _{i}}]=[{\mathcal {B}} _1,\ldots , {\mathcal {B}} _{i}]$. The proper upper segment of $\lambda$ wrt. ${\mathcal {B}} _i$ $(i\ne 1)$ is $\lambda ^{\uparrow }_{}({\small {\mathcal {B}} _{i}})=[{\mathcal {B}} _1,\ldots , {\mathcal {B}} _{i-1}]$.

We refer to both proper and non-proper upper segments simply as “upper segment” and either usage will be distinguishable through its notation (round or square brackets respectively). As stated next, the upper segment of an argument in a line constitutes a (non-exhaustive) argumentation line by itself. (Proofs are omitted due to space reasons.)

Proposition 3

For any $\lambda \in {\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}$, if ${\mathcal {B}} \in \lambda$ then $\lambda ^{\uparrow }_{}[{\small {\mathcal {B}}}]\in {\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}$.

As said before, the warrant status of an argument will be determined by analyzing the dialectical tree rooted in it. On the other hand, a dialectical tree rooted in an argument ${\mathcal {A}}$ will be built from a set of argumentation lines rooted in ${\mathcal {A}}$.

Definition 4

(Dialectical Tree). Given a DAT ${\mathsf {T}}$, a dialectical tree ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ rooted in ${\mathcal {A}}$ is built by a set $X\subseteq {\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}$ of lines rooted in ${\mathcal {A}}$, such that an argument ${\mathcal {C}}$ in ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ is: (1) a node iff ${\mathcal {C}} \in \lambda$, for any $\lambda \in X$; (2) a child of a node ${\mathcal {B}}$ in ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ iff ${\mathcal {C}} \in \lambda$, ${\mathcal {B}} \in \lambda '$, for any $\{\lambda ,\lambda '\}\subseteq X$, and $\lambda '^{\uparrow }_{}[{\small {\mathcal {B}}}]=\lambda ^{\uparrow }_{}({\small {\mathcal {C}}})$. A leaf of any line in X is a leaf in ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$.

However, the acceptability of a dialectical tree will depend on the set X of lines used to build such tree. Hence, an acceptable dialectical tree will be constructed from a bundle set ${\mathcal {S}_{{\mathsf {T}}}({\mathcal {A}})}$ which –given a DAT ${\mathsf {T}}$– contains all the acceptable and exhaustive argumentation lines from ${\mathfrak {Lines}^{{\mathbb {A}}}_{{\mathsf {T}}}}$ rooted in ${\mathcal {A}}$. (We refer to a line as exhaustive when no more arguments can be added to it.) Thus, following Definition 4, ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ is acceptable if it is built from a set $X={\mathcal {S}_{{\mathsf {T}}}({\mathcal {A}})}$. The domain of all acceptable dialectical trees from ${\mathsf {T}}$ is noted as $\mathfrak {Trees}_{{\mathsf {T}}}$. We will refer to acceptable dialectical trees simply as dialectical trees (or trees), unless the contrary is explicitly stated. Besides, we will overload the membership symbol and write “${\lambda _{}} \in {\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$” when the line ${\lambda _{}}$ belongs to the bundle set ${\mathcal {S}_{{\mathsf {T}}}({\mathcal {A}})}$ associated to the tree ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})} \in \mathfrak {Trees}_{{\mathsf {T}}}$.

Dialectical trees allow to determine whether the root node of the tree is warranted or not. This evaluation will weigh all the information present in the tree through a marking criterion to evaluate each argument in the tree by assigning them a mark within the domain $\{D,U\}$, where U (resp., D) denotes an undefeated (resp., defeated) argument. We adopt a skeptical marking criterion: (1) all leaves are marked $U$; and (2) every inner node ${\mathcal {B}}$ is marked $U$ iff every child of ${\mathcal {B}}$ is marked $D$, otherwise, ${\mathcal {B}}$ is marked $D$. This marking has been also used to implement DELP  [15], a rule-based argumentation formalism. Using this particular criterion reduces the conceptual complexity of the approach presented here, allowing us to focus exclusively on the change mechanism. Finally, warrant is specified through a marking function ${\mathsf {Mark}}: \mathfrak {Trees}_{{\mathsf {T}}} \rightarrow \{D,U\}$ returning the mark of the root. Thus, given a DAT ${\mathsf {T}}$, an active argument ${\mathcal {A}} \in {\mathbb {A}}$ is warranted iff ${{\mathsf {Mark}} ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})} = U$. Whenever ${\mathcal {A}}$ is warranted, the dialectical tree ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ is called warranting tree; otherwise, it is called non-warranting tree.

The digraph depicted in figure (a) describes a DAT, where triangles are arguments and arcs denote attack. The sets ${\mathbb {A}}$ of active and ${\mathbb {I}}$ of inactive arguments (dashed triangles) compose the universal set ${\mathbb {U}}$. Subarguments were drawninside their superarguments. ${\mathcal {A}}$ ’s superargument is inactive because it contains an inactive subargument. Figure (b) shows a dialectical tree spanning the graph from ${\mathcal {A}}$. Note that inactive arguments are not considered in the tree, which is non-warranting. This status would change by activating, for instance, a defeater for the root’s left defeater.

2.2 A Global Activating Approach

ATC defines a change operator that revises a DAT by an argument, making the necessary modifications to the theory to warrant that argument, by analyzing the dialectical tree rooted in it. The core of the change machinery involves the alteration of some lines in such dialectical tree when it happens to be non-warranting. Therefore, the objective of altering lines is to change the topology of the tree containing them in order to turn it to warranting. Alteration of lines comes from changes applied to the set of active arguments in the theory; that is, arguments cannot be simply removed/added to/from the tree. Hence, since an argument could appear in different positions in several lines in a tree, an alteration of a line could result in collateral alterations of other lines. In this activating approach, by alteration we refer to the addition of an argument (i.e., a defeater) into a line. This may end up extending the line and even incorporating new lines to the domain. Next, we introduce the notion of attacking lines [19]: argumentation lines that are somehow “responsible for a non-warranting dialectical tree”.

Definition 5

(Attacking Line). Given a tree ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$; a line $\lambda \in {\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ is referred as attacking iff every ${\mathcal {B}} \in \lambda ^+$ (resp., ${\mathcal {B}} \in \lambda ^-$) is marked $D$ (resp., $U$).

We refer as attacking set of ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ to the set ${Att({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})} \subseteq {\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}$ containing all the attacking lines from ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$. Note that a tree without attacking lines is warranting.

Theorem 6

A tree ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ is warranting iff ${Att({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})} = \emptyset$.

In order to achieve warrant for an argument ${\mathcal {A}}$, we would need to alter the tree ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ by altering every attacking line in it, with the objective of obtaining a new tree free of attacking lines. The following example shows the importance of identifying the precise argument –in a line to be altered– for which a defeater needs to be activated. Trees are drawn with gray/white triangles denoting defeated/undefeated arguments.

Example 7

Consider a DAT ${\mathsf {T}}$ yielding the tree ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ on the right with lines $\lambda _1=[{\mathcal {A}},{\mathcal {B}} _1,{\mathcal {B}} _3]$ and $\lambda _2=[{\mathcal {A}},{\mathcal {B}} _2,{\mathcal {B}} _4,{\mathcal {B}} _5]$. There is a single attacking line within the attacking set ${Att({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})} = \{\lambda _2\}$. If we activate a defeater for ${\mathcal {B}} _2$ in ${\mathsf {T}}$, we would generate a new line within a new tree having no attacking lines. If we instead add a defeater for ${\mathcal {B}} _5$, the line that was attacking is “extended” and again, in the resulting tree, there would be no attacking lines. On the other hand, if we activate a defeater for ${\mathcal {B}} _4$, we would generate another attacking line.

We call effective alteration to the alteration of an attacking line that turns it to non-attacking. In the ATC deactivating approach, an effective alteration is achieved by deactivating a con argument in the given line, thus truncating the line. Thus, deactivating a con argument in a line leaves a pro argument as the leaf of the new line. However, in the ATC activating approach presented here, the alteration of a given attacking line is done by activating a defeater ${\mathcal {D}}$ for a con argument ${\mathcal {B}}$ in the line. This would imply ${\mathcal {B}}$ to end up marked as defeated since a new line will sprout activating the undefeated argument ${\mathcal {D}}$ as its leaf. Afterwards, the resulting altered line would not be attacking. Note that, any effective alteration of an attacking line has necessarily to be done upon a con argument in the line. To that end, we identify the set of inactive defeaters associated to each argument in order to choose appropriate activations.

Definition 8

(Set of Inactive Defeaters). Given a DAT ${\mathsf {T}} = {\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ]}$, the set of inactive defeaters of an argument ${\mathcal {B}} \in \lambda$, is a function ${\mathsf {idefs}_{{\mathsf {T}}}}:{\mathbb {A}} \times {\mathfrak {Lines}^{{\mathbb {A}}}_{{\mathsf {T}}}} \rightarrow {\mathcal {P}} ({\mathbb {I}})$:

${{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}},\lambda )} = \{{\mathcal {D}} \in {\mathbb {I}}\ |$ exists $\lambda '\in {\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}$ such that ${\mathcal {D}} \in \lambda '$ and $\lambda ^{\uparrow }_{}[{\small {\mathcal {B}}}]=\lambda '^{\uparrow }({\small {\mathcal {D}}})\}$

Each inactive defeater ${\mathcal {D}}$ of ${\mathcal {B}} \in \lambda$ belongs to a line $\lambda '\in {\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}$ which means that $\lambda '$ is acceptable but contains inactive arguments. Requiring $\lambda '^{\uparrow }({\small {\mathcal {D}}})$ to coincide with $\lambda ^{\uparrow }_{}[{\small {\mathcal {B}}}]$ implies not only the segments from the root to ${\mathcal {B}}$ in both $\lambda$ and $\lambda '$ to be equal, but also ${\mathcal {D}} {\hookrightarrow } {\mathcal {B}}$. The following notion allows to anticipate the effect of changes over a DAT ${\mathsf {T}}$ by identifying a hypothetical tree ${\mathcal {H}_{{\mathsf {T}}}({\mathcal {A}},\varPsi )}$, as the tree rooted in ${\mathcal {A}}$ that would result from ${\mathsf {T}}$ by the hypothetical activation of the arguments in a set $\varPsi \subseteq {\mathbb {U}}$. We refer to these trees as hypothetical given that they do not appear within the domain $\mathfrak {Trees}_{{\mathsf {T}}}$.

Definition 9

(Hypothetical Tree). Given a DAT ${\mathsf {T}} = {\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ]}$, ${\mathcal {A}} \in {\mathbb {A}}$, and a set $\varPsi \subseteq {\mathbb {U}}$; the hypothetical tree ${\mathcal {H}_{{\mathsf {T}}}({\mathcal {A}},\varPsi )}$ is the tree built from the set of lines:

$\{\lambda ^{\uparrow }_{}[{\small {\mathcal {B}}}]\ |\ \forall \lambda \in {\mathfrak {Lines}^{{\mathbb {U}}}_{{\mathsf {T}}}}, \forall {\mathcal {C}} \in \lambda ^{\uparrow }_{}[{\small {\mathcal {B}}}]:{\mathcal {C}} \in ({\mathbb {A}} {\oplus } \varPsi )$ holds, where ${{\mathsf {root}}(\lambda )}={\mathcal {A}}$ and either $({{\mathsf {leaf}}(\lambda )}={\mathcal {B}})$ or $(\exists {\mathcal {D}} \in \lambda : \lambda ^{\uparrow }_{}({\small {\mathcal {D}}}) = \lambda ^{\uparrow }_{}[{\small {\mathcal {B}}}]$ and ${\mathcal {D}} \notin ({\mathbb {A}} {\oplus } \varPsi ))\}$

The activation of defeaters may bring new shortcomings towards an effective alteration of lines. The addition of a defeater ${\mathcal {D}}$ in a line ${\lambda _{}}$ provokes a line extension: if ${\mathcal {D}}$ attacks the leaf of ${\lambda _{}}$, the whole line ends up extended; but if ${\mathcal {D}}$ attacks an argument placed strictly above that leaf, a new argumentation line arises by extending an upper segment of ${\lambda _{}}$. The activation of ${\mathcal {D}}$ not only attaches ${\mathcal {D}}$ to ${\lambda _{}}$, but also includes the addition of ${\mathcal {D}}$ ’s (active) defeaters, and these defeaters bring their (active) defeaters, and so on. An entire subtree rooted in ${\mathcal {D}}$ sprouts from the activation of ${\mathcal {D}}$. This subtree could contain arguments that were already active, as well as arguments that are activated by virtue of activeness propagation. For instance, an argumentation line $\lambda =[{\mathcal {A}},{\mathcal {B}} _1,\ldots ,{\mathcal {D}},\ldots ,{\mathcal {B}} _n]$ may have all its arguments active excepting for ${\mathcal {D}}$. Thus, a tree rooted in ${\mathcal {A}}$ would have a line $\lambda ^{\uparrow }_{}({\small {\mathcal {D}}})$. Afterwards, if we activate ${\mathcal {D}}$, the resulting hypothetical tree would have the complete line ${\lambda _{}}$. Hence, an effective alteration in the activating approach requires ensuring that the new line appearing from an alteration ends up as non-attacking, or equivalently, ensuring that the new defeater ${\mathcal {D}}$ ends up undefeated within the resulting tree for ensuring that the selected con argument (attacked by ${\mathcal {D}}$) finally ends up defeated. Moreover, the activation of a defeater may involve activating other argument/s which may extend other argumentation line/s in the evaluated tree. These shortcomings describes different alternatives of what we have called collateral alterations. A fortuitous case results from the collateral alteration of an attacking line which turns the line into non-attacking by chance. However, it may also happen to have a non-attacking line which ends up collaterally altered and turned into attacking, or even to have an effectively altered line which turns into attacking once again due to some collateral alteration occurring above the argument from which the original effective alteration has been done. The following example clarifies this matter.

Example 10

We have two attacking lines ${\lambda _{1}} = [{\mathcal {A}},{\mathcal {B}} _1,{\mathcal {B}} _3,{\mathcal {B}} _5]$ and ${\lambda _{2}} = [{\mathcal {A}},{\mathcal {B}} _2,{\mathcal {B}} _4,{\mathcal {B}} _6]$ from the tree depicted on the right, warranting ${\mathcal {A}}$ implies two effective alterations, one per attacking line. Line $\lambda _1$ can be altered upon ${\mathcal {B}} _5$ by activating a defeater ${\mathcal {D}} _1\in {{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}} _5,{\lambda _{1}})}$. However, assuming that ${\mathcal {C}} _1{\sqsubseteq } {\mathcal {D}} _1$ is also inactive then ${\mathbb {A}} {\oplus } \{{\mathcal {D}} _1\}$ will also activate ${\mathcal {C}} _1$. Afterwards, if it is the case that ${\mathcal {C}} _1{\hookrightarrow } {\mathcal {B}} _4$, then the effective alteration of ${\lambda _{1}}$ produces a collateral alteration over ${\lambda _{2}}$. This situation impose a condition for achieving an effective alteration of ${\lambda _{2}}$. For instance, in figure (a), by activating ${\mathcal {D}} _2\in {{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}} _6,{\lambda _{2}})}$, the line is intended to be altered below a collaterality which will affect the current alteration through the activation of ${\mathcal {D}} _2$, avoiding its effectiveness. The inconvenience is that the collateral alteration extends the segment $\lambda ^{\uparrow }_{2}[{\small {\mathcal {B}} _4}]$, incorporating an attacking line $[{\mathcal {A}},{\mathcal {B}} _2,{\mathcal {B}} _4,{\mathcal {C}} _1]$ to the tree, leaving ineffective the alteration of $\lambda _2$. This shows the importance of avoiding collateral alterations occurring above the specific alteration in the line. In other words, the only safe collateral alterations are those taking place below the selected con argument in the same line. In this case, the alternative will be either to change the alteration of ${\lambda _{1}}$ to avoid the collaterality over ${\lambda _{2}}$, or to change the alteration of ${\lambda _{2}}$ forcing it to occur above the collaterality, i.e., upon the con argument ${\mathcal {B}} _2$. The latter case is illustrated in figure (b). Assuming ${\mathcal {D}} _3\in {{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}} _2,{\lambda _{2}})}$, the resulting tree ends up warranting its root argument ${\mathcal {A}}$, given that all the attacking lines would be effectively altered.

From the example above, if no inactive defeater for a con argument provides an effective alteration then a different con argument should be selected in order to obtain an appropriate inactive defeater for it, ensuring the effective alteration in a different part of the line. Such dynamics allows to overcome from bad collateralitites. The global defeating function triggers a set of inactive defeaters which would effectively alter the necessary lines, controlling collateralities, and ensuring a resulting warranting tree through the analysis over hypothetical trees free of attacking lines. However, when no (appropriate) defeater is available for any con argument in the same line, the revision operation will not succeed, and the global defeating will trigger the empty set.

Definition 11

(Global Defeating). Given a DAT ${\mathsf {T}} = {\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ]}$ and a tree ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})} \in \mathfrak {Trees}_{{\mathsf {T}}}$; the function ${\sigma }:\mathfrak {Trees}_{{\mathsf {T}}}\rightarrow {\mathcal {P}} ({\mathbb {I}})$ is a global defeating function iff it holds:

• 1. ${\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}) = \emptyset$ iff $({Att({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})} =\emptyset$, or there is no non-empty global defeating).

• 2. if ${\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}) \ne \emptyset$ then ${\mathcal {H}_{{\mathsf {T}}}({\mathcal {A}},{\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}))}$ has no attacking lines.

• 3. if ${\mathcal {D}} \in {\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})$ then the following conditions simultaneously hold

  • (a) there is some attacking ${\lambda _{}} \in {\mathcal {H}_{{\mathsf {T}}}({\mathcal {A}},{\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})\setminus \{{\mathcal {D}} \})}$,

  • (b) there is some ${\mathcal {B}} \in \lambda ^{-}$ such that ${\mathcal {D}} \in {{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}},\lambda )}$,

  • (c) for any ${\mathcal {D}} '\in {{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}},\lambda )}$, if ${\mathcal {D}} '{\sqsubseteq } {\mathcal {D}}$ then ${\mathcal {D}} '={\mathcal {D}}$,

  • (d) there is some non-attacking $\lambda '\in {\mathcal {H}_{{\mathsf {T}}}({\mathcal {A}},{\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}))}$ such that $\lambda ^{\uparrow }_{}[{\small {\mathcal {B}}}]=\lambda '^{\uparrow }({\small {\mathcal {D}}})$,

  • (e) if the following conditions simultaneously hold

    • i. there is some $\lambda ''\in {\mathcal {H}_{{\mathsf {T}}}({\mathcal {A}},{\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}))}$,

    • ii. some ${\mathcal {C}} \in {\lambda ''_{}}$ such that ${\mathcal {C}} \not \in {\mathbb {A}} {\oplus } {\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})\setminus \{{\mathcal {D}} \}$,

    • iii. some ${\mathcal {D}} ''\in {\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})$,

    • iv. some $\lambda '''\in {\mathcal {H}_{{\mathsf {T}}}({\mathcal {A}},{\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})\setminus \{{\mathcal {D}} ''\})}$,

    • v. some ${\mathcal {B}} '\in \lambda '''$ such that ${\mathcal {D}} ''\in {{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}} ',\lambda ''')}$, and

    • vi. some ${\mathcal {B}} ''\in \lambda '''$ such that $\lambda '''^{\uparrow }_{}[{\small {\mathcal {B}} ''}]=\lambda ''^{\uparrow }({\small {\mathcal {C}}})$

    then ${\mathcal {B}} '\in \lambda '''^{\uparrow }({\small {\mathcal {B}} ''})$.

The defeating function is the fundamental key of the global activating model, its three conditions are necessary and sufficient for ensuring that it is impossible (resp. of, possible) to turn the non-warranting tree into an altered warranting one, in which case, the function triggers an empty (resp. of, non-empty) set. On the contrary, whenever the original tree is warranting, the defeating function would also trigger an empty-set for ensuring that no unnecessary change will be made. This is controlled by condition (1). Condition (2) states that if the defeating function is non-empty then the activation of the arguments that it maps would result in a tree with no attacking lines. Condition (3) controls the behavior of the function when the revision is possible. It states that the activation of each ${\mathcal {D}} \in {\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})$ alters a specific line that otherwise would be attacking (cond. (3a). The alteration is done over some selected con argument ${\mathcal {B}}$ for which an inactive defeater ${\mathcal {D}}$ is available (cond. 3b), ensuring that ${\mathcal {D}}$ does not contain any strict subargument that would serve for such a purpose (cond. 3c) –this is necessary for avoiding activations that could trigger unnecessary collateralities. Through condition 3d, it is ensured that the alteration is effective. This is done by identifying the new line $\lambda '$ that appears as a result of the alteration of ${\lambda _{}}$. And finally, condition 3e takes care of collateralitites, ensuring that when they occur, they never will take place above the selected argument for altering the line. We will see in detail this case, by referring to Example 10, figure (a): ${\lambda _{}}$ –from Definition 11– is instantiated with ${\lambda _{1}}$, ${\mathcal {D}}$ with ${\mathcal {D}} _1$, ${\mathcal {B}}$ with ${\mathcal {B}} _5$, $\lambda '$ with the alteration of line ${\lambda _{1}}$, i.e., with the extended line $[{\mathcal {A}},{\mathcal {B}} _1,{\mathcal {B}} _3,{\mathcal {B}} _5,{\mathcal {D}} _1]$ (which ends up effectively altered satisfying cond. 3d), $\lambda ''$ with the extended line $[{\mathcal {A}},{\mathcal {B}} _2,{\mathcal {B}} _4,{\mathcal {C}} _1]$ which appears from the collaterality that activates ${\mathcal {C}}$ (instantiated with ${\mathcal {C}} _1$) from the activation of ${\mathcal {D}}$ (instantiated with ${\mathcal {D}} _1$) (cond. 3(e)i and 3(e)ii). Then, ${\mathcal {D}} ''$ is instantiated with ${\mathcal {D}} _2$, $\lambda '''$ with ${\lambda _{2}}$, and ${\mathcal {B}} '$ with ${\mathcal {B}} _6$ which is the con argument that would be defeated by ${\mathcal {D}} ''$ in $\lambda '''$ (cond. 3(e)iii, 3(e)iv, and 3(e)v). Finally, cond. 3(e)vi identifies ${\mathcal {B}} ''$ (instantiated with ${\mathcal {B}} _4$) as the argument that was defeated by the collaterality ${\mathcal {C}}$ (instantiated with ${\mathcal {C}} _1$). This will allow to verify if ${\mathcal {B}} '$ is above ${\mathcal {B}} ''$ in $\lambda '''$, which is violated in Fig. (a) since it would require ${\mathcal {B}} _6$ to be above ${\mathcal {B}} _4$ for ensuring that the alteration of ${\lambda _{2}}$ occurs above the collaterality produced by the alteration of ${\lambda _{1}}$. Observe that the case of Fig. (b) satisfies the conditions of the global defeating function, which will map to aset $\{{\mathcal {D}} _1,{\mathcal {D}} _3\}$. Note that Fig. (1) depicted on the right, shows a special case of that presented in Example 10, Fig. (a), where the bad collaterality is produced by the alteration of the same line. The analysis of Definition 11 can be similarly done, where $\lambda ''$ will coincide with $\lambda '$, ${\mathcal {D}} ''$ with ${\mathcal {D}}$, $\lambda '''$ with $\lambda$, and ${\mathcal {B}} '$ with ${\mathcal {B}}$. On the other hand, the case presented in Fig. (2) shows a different anomaly: the activation of ${\mathcal {D}} _2$ brings its own active defeater ${\mathcal {C}} _2$ to extend the segment $[{\mathcal {A}},{\mathcal {B}} _2]$. In this specific case, the new line $[{\mathcal {A}},{\mathcal {B}} _2,{\mathcal {D}} _2,{\mathcal {C}} _2]$ will be attacking and thus the alteration does not change the mark of the selected con argument ${\mathcal {B}} _2$. This situation will violate condition 3d from Definition 11.

When selecting a con argument from a line $\lambda \in {\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$, a selection criterion could lead the mapping to an argument ${\mathcal {B}} \in \lambda ^-$ by assuming an ordering among arguments. Moreover, deciding among several alternatives for activating inactive defeaters would also require some specific activation criterion which, once again, could be founded upon some ordering among arguments. Both criteria are a necessary condition for determinism. We avoid going further into this subject, abstracting away from specific criteria. Next, we define the condition for a warranting defeating function, as a defeating whose outcome ensures a successful revision. This will depend on the availability of all the necessary inactive defeaters for warranting the tree.

Definition 12

(Warranting Defeating). A defeating function “${\sigma }$” is said to be warranting for ${\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}$ iff $({\sigma } ({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})}) = \emptyset$ iff ${Att({\mathcal {T}_{{\mathsf {T}}}({\mathcal {A}})})} =\emptyset )$.

The activating argument revision is defined upon a warranting defeating. Whenever no such warranting function exists, the revision operation ends up undefined.

Definition 13

(Argument Revision). Given a DAT ${\mathsf {T}} = {\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ]}$ and ${\mathcal {A}} \in {\mathbb {U}}$; the operator “${*}$” stands for an activating argument revision of ${\mathsf {T}}$ by ${\mathcal {A}}$ iff

${\mathsf {T}} {*} {\mathcal {A}} = \langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} '{\oplus } {\sigma } ({\mathcal {T}_{{\mathsf {T}'}}({\mathcal {A}})})]$

where ${\mathsf {T}'} ={\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ']}$ with ${\mathbb {A}} '={\mathbb {A}} {\oplus } \{{\mathcal {A}} \}$, and the global defeating function ${\sigma }$ is warranting for ${\mathcal {T}_{{\mathsf {T}'}}({\mathcal {A}})}$.

Example 14 Consider a DAT ${\mathsf {T}} =\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ]$, where ${\mathbb {A}} =\{{\mathcal {B}} _1,{\mathcal {B}} _2,{\mathcal {B}} _3,{\mathcal {B}} _4,{\mathcal {B}} _5\}$ and ${\hookrightarrow } =\{({\mathcal {B}} _3,{\mathcal {B}} _1),({\mathcal {B}} _4,{\mathcal {B}} _2),({\mathcal {B}} _5,{\mathcal {B}} _4)\}$, and assume we need to revise ${\mathsf {T}}$ by an inactive argument ${\mathcal {A}} \in {\mathbb {I}}$. The revision operator will analyze the construction of a global defeating function upon the DAT ${\mathsf {T}'} =\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} {\oplus } \{{\mathcal {A}} \}]$, whose resulting dialectical tree ${\mathcal {T}_{{\mathsf {T}'}}({\mathcal {A}})}$ coincides with the one depicted in Example 7. Assuming the selection over $\lambda _2 = [{\mathcal {A}},{\mathcal {B}} _2,{\mathcal {B}} _4,{\mathcal {B}} _5]$ is the con argument ${\mathcal {B}} _2$, and${\mathcal {D}} _1\in {{\mathsf {idefs}_{{\mathsf {T}'}}} ({\mathcal {B}} _2,{\lambda _{2}})}$; the mark of ${\mathcal {B}} _2$ turns to $D$. Nonetheless, by assuming ${\mathcal {C}} _1\in {\mathbb {A}} {\oplus } \{{\mathcal {D}} _1\}$ and ${\mathcal {C}} _1{\hookrightarrow } {\mathcal {B}} _3$, line $\lambda _1 = [{\mathcal {A}},{\mathcal {B}} _1,{\mathcal {B}} _3]$ is collaterally altered, and even more, such collateral alteration turns the line to attacking (triggering a new line $\lambda _3=[{\mathcal {A}},{\mathcal {B}} _1,{\mathcal {B}} _3,{\mathcal {C}} _1]$) in the context of the hypothetical tree ${\mathcal {H}_{{\mathsf {T}'}}({\mathcal {A}},\{{\mathcal {D}} _1\})}$. This situation forces the alteration of $\lambda _3$ in order to turn it to non-attacking. Recall that this will require the selection of a con argument placed above the point of the collaterality, i.e., an argument placed above ${\mathcal {C}} _1$. The only alternative is ${\mathcal {B}} _1$. Afterwards, assuming ${\mathcal {D}} _2\in {{\mathsf {idefs}_{{\mathsf {T}'}}} ({\mathcal {B}} _1,{\lambda _{3}})}$, we obtain a hypothetical tree ${\mathcal {H}_{{\mathsf {T}'}}({\mathcal {A}},{\sigma } ({\mathcal {T}_{{\mathsf {T}'}}({\mathcal {A}})}))}$ free of attacking lines, where ${\sigma } ({\mathcal {T}_{{\mathsf {T}'}}({\mathcal {A}})})=\{{\mathcal {D}} _1,{\mathcal {D}} _2\}$. Finally, since ${\sigma }$ is a warranting defeating for ${\mathcal {T}_{{\mathsf {T}'}}({\mathcal {A}})}$, the revision ends up as ${\mathsf {T}} {*} {\mathcal {A}} = \langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} {\oplus } \{{\mathcal {A}},{\mathcal {D}} _1,{\mathcal {D}} _2\}]$.

Theorem 15

If ${\mathsf {T}} {*} {\mathcal {A}}$ relies on a warranting defeating function then ${\mathsf {T}} {*} {\mathcal {A}}$ warrants ${\mathcal {A}}$.

3 Dynamics of Judicial Procedures

3.1 An Example of Dynamics Through Appellate Instances

Under certain circumstances a court can let a criminal defendant off on probation¹. However, this special benefit may not be given to a defendant involved in a gender-based violence case, since probation may end up dismissing the criminal case and thus, no fair nor effective legal procedure would be granted for the woman, contradicting multilateral treaties on the matter like the Vienna Convention on the law of treaties (or Vienna, for short) and the Convention of Belem do Pará on the prevention, punishment, and eradication of violence against women (or BdP, for short). Such exceptional case was not considered by the Argentinean Law until the Supreme Court dictated the definitive sentence on Gongora’s case, on April 23rd, 2013 [11]. In this example, we analyze such a sentence which revoked the prior sentence dictated by the previous appellate instance, referred as Cámara Federal de Casación Penal, from now on, Casación. In short, Casación’s sentence referred to the Penal Code (PC) for conceding the benefit of probation for the case, despite the state of affairs included gender violence evidence as shown in the lowest appellate instance. We will resume the case, by including only the argumentation provided by the Supreme Court, without the specific details of the argumentation given by Casación in the previous appellate instance. We assume ${\mathsf {T}} = {\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ]}$ with arguments ${\mathcal {B}},{\mathcal {B}} _1,{\mathcal {B}} _2,{\mathcal {B}} '$ in ${\mathbb {A}}$, where ${\mathcal {B}} _1{\sqsubseteq } {\mathcal {B}}$ and ${\mathcal {B}} _2{\sqsubseteq } {\mathcal {B}}$, such that:

• ${\mathcal {B}}$: Probation for Gongora is ordered according to arguments ${\mathcal {B}} _1$ and ${\mathcal {B}} _2$.

• ${\mathcal {B}} _1$: Article 76 bis (PC), grants probation for sentences of under 3 years mandatory prison time.

• ${\mathcal {B}} _2$: A mandatory sentence for Gongora’s should not be over 3 years prison time.

• ${\mathcal {B}} '$: Evidence of gender violence.

The argumentation presented through the sentence dictated by the Supreme Court relies mainly upon Vienna and BdP treaties, specifically:

• Article 31(1) (Vienna). “A treaty shall be interpreted in good faith in accordance with the ordinary meaning to be given to the terms of the treaty in their context and in the light of its object and purpose.”

• Article 7.b (BdP). “Apply due diligence to prevent, investigate and impose penalties for violence against women.”

• Article 7.f (BdP). “Establish fair and effective legal procedures for women who have been subjected to violence which include, among others, protective measures, a timely hearing and effective access to such procedures.”

The Supreme Court’s argumentation includes the following arguments:

• ${\mathcal {A}} _1$: Interpreting BdP (due to Vienna, Art. 31(1)) in the light of its objective and purpose (to eradicate violence against women); for gender violence cases, a legal procedure should be ensured (Art. 7.f) without delay (Art. 7.b), discarding any possibility of granting probation.

• ${\mathcal {A}}$: According to ${\mathcal {A}} _1$ and ${\mathcal {B}} '$, probation cannot be granted for Gongora’s.

The consideration of Supreme Court’s arguments can be understood as a dynamic process in which the legal system evolves towards restricting probation grant under the exceptional circumstance of gender violence. We can identify such a dynamic situation by referring to a framework ${\mathsf {T}} {*} {\mathcal {A}}$, whose intermediate stage is defined through a framework ${\mathsf {T}'} = {\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ']}$, where ${\mathbb {A}} '={\mathbb {A}} {\oplus } \{{\mathcal {A}} \}$. Observe that as a consequence, from activeness propagation, ${\mathcal {A}} _1$ ends up contained in ${\mathbb {A}} '$. Note however, that ${\mathcal {A}}$ would not be warranted given that Casación’s sentence (argument ${\mathcal {B}}$) would appear as a counterargument of ${\mathcal {A}}$. At this stage, the theory of ATC, through the evaluation of the dialectical tree ${\mathcal {T}_{{\mathsf {T}'}}({\mathcal {A}})} \in \mathfrak {Trees}_{{\mathsf {T}'}}$ built with the unique argumentation line $\lambda =[{\mathcal {A}},{\mathcal {B}} ]$ (which is an attacking line), is indicating that although argument ${\mathcal {A}}$ is a valid supporter against probation for Gongora’s, we still need to defeat Casación’s previous sentence. Afterwards, the unique selection will be ${\mathcal {B}} \in \lambda ^-$ and therefore, the theory indicates that a defeater ${\mathcal {D}}$, such that ${{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}},\lambda )} \supseteq \{{\mathcal {D}} \}$ (see Definition 8), should be activated looking for a warranting hypothetical tree ${\mathcal {H}_{{\mathsf {T}'}}({\mathcal {A}},\{{\mathcal {D}} \})}$ (see Definition 9). The activation of argument ${\mathcal {D}}$ seems to be identified by the Supreme Court, which develops a second part of the sentence, providing an appropriate justification for their decision exposed through argument ${\mathcal {A}}$. Recall that the activation of ${\mathcal {D}}$ would imply activating each of its subarguments, where ${\mathcal {D}} '{\sqsubseteq } {\mathcal {D}}$, ${\mathcal {D}} _1{\sqsubseteq } {\mathcal {D}} '$, ${\mathcal {D}} _2{\sqsubseteq } {\mathcal {D}} '$, ${\mathcal {A}} _1{\sqsubseteq } {\mathcal {D}} _2$, ${\mathcal {D}} _{2.1}{\sqsubseteq } {\mathcal {D}} _2$, ${\mathcal {D}} _{2.2}{\sqsubseteq } {\mathcal {D}} _2$, and ${\mathcal {D}} '_{2.2}{\sqsubseteq } {\mathcal {D}} _{2.2}$:

• ${\mathcal {D}}$: The application of Art. 76 bis (PC) is restricted under evidence of gender violence.

• ${\mathcal {D}} _1$: Principles of the legal doctrine like law as integrity and coherence posse obligations for considering the complete legal system, including international treaties, and the ability to reinterpret the law in order to avoid contrary decisions.

• ${\mathcal {D}} '_{2.2}$: Article 75(22) (NC) incorporates the international treaties to the constitutional block.

• ${\mathcal {D}} _{2.2}$: From ${\mathcal {D}} '_{2.2}$, both Vienna and BdP have constitutional hierarchy.

• ${\mathcal {D}} _{2.1}$: Art. 31 (NC) establishes the supremacy of the National Constitution.

• ${\mathcal {D}} _2$: From ${\mathcal {D}} _{2.1}$ and ${\mathcal {D}} _{2.2}$, ${\mathcal {A}} _1$ is over Art. 76 bis (PC).

• ${\mathcal {D}} '$: According to ${\mathcal {D}} _1$ and ${\mathcal {D}} _2$, Art. 76 bis (PC) should be reinterpreted in the light of ${\mathcal {A}} _1$.

Finally, ${\mathsf {T}} {*} {\mathcal {A}} =\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} {\oplus } \{{\mathcal {A}},{\mathcal {D}} \}]$ ends up warranting the Supreme Court’s argument ${\mathcal {A}}$ since ${\mathcal {T}_{({\mathsf {T}} {*} {\mathcal {A}})}({\mathcal {A}})}$ is a warranting tree with a unique non-attacking argumentation line $[{\mathcal {A}},{\mathcal {B}},{\mathcal {D}} ]$. From the viewpoint of law, the case is interesting given that argument ${\mathcal {D}}$ can be seen as an instance of creation of law by an administrative operator of the judicial organ, which in the Argentinean Law is an exceptional case normally reserved for the legislature. From a different theoretical perspective, when creation of law is not admitted for judges, argument ${\mathcal {D}}$ can be seen as a case of law discovery, by assuming that the norm was already in the system, but it simply has never been applied before. In this case, the activation of ${\mathcal {D}}$ can be understood as a case of jurisprudence [8].

3.2 An Example of Dynamics on a Criminal Procedure

We analyze a small part of a criminal case sentenced on April, 16th 2007 by the Tribunal en lo Criminal No. 1 (Bahía Blanca) [22]. This was a resonant case due to the great astonishment it caused in society. In short, the prosecutor claims guilt by attempting to prove that Cuchán had killed and burned his girlfriend, Lucy, in a grill at his house, whereas the defense’s case is that the girl died from a cocaine overdose and was afterwards burned by the man in a state of despair. In order to make a practical example, we have extracted a small but representative amount of allegations, i.e., arguments, and organized them within a dialectical tree. The tree’s root is the initial argument posed by the defense, which ends up defeated, and then we will apply ATC’s logical machinery to bring arguments that turn the root argument into a warrant. In this way, ATC proves to be a useful tool to perform hypothetical reasoning. We will assume a DAT ${\mathsf {T}} = {\langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} ]}$, where the set ${\mathbb {U}}$ will include the following arguments:

• ${\mathcal {A}}$: Lucy died of cocaine overdose, so Cuchán did not kill her.

• ${\mathcal B}_1$: Cuchán burned Lucy’s remains; the burning objective was to hide the homicide.

• ${\mathcal B}_2$: According to friends, Lucy never did drugs and she was afraid of cocaine.

• ${\mathcal B}_3$: No traces of violence were found at the crime scene.

• ${\mathcal B}_4$: No records of previous incidents between Cuchán and Lucy implies no motive for a homicide.

• ${\mathcal B}_5$: An overdose might happen the first time a person consumes cocaine.

• ${\mathcal B}_6$: Threads of hair belonging to Lucy were found nearby the crime scene implying violence.

• ${\mathcal B}_7$: Psychological and psychiatric studies discovered Cuchán’s psychopathic features.

• ${\mathcal {D}} _1$: From the autopsy report, no cause of death could be determined.

• ${\mathcal {D}} _2$: If the cause of death cannot be determined, there is no proof for a homicide.

• ${\mathcal {D}} _3$: If the cause of death cannot be determined, there is no proof for an overdose.

• ${\mathcal {D}} _4$: Recorded phone calls suggest Lucy’s friends were threatened to declare in her favor.

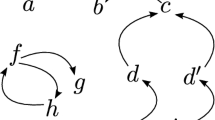
We will assume that every argument is active, except for ${\mathcal {D}} _1$ and ${\mathcal {D}} _4$. Let also consider two more inactive arguments: ${\mathcal {D}}$ and ${\mathcal {D}} '$, where ${\mathcal {D}} _1{\sqsubseteq } {\mathcal {D}}$ and ${\mathcal {D}} _2{\sqsubseteq } {\mathcal {D}}$; ${\mathcal {D}} _1{\sqsubseteq } {\mathcal {D}} '$ and ${\mathcal {D}} _3{\sqsubseteq } {\mathcal {D}} '$. The attack relation among active arguments is depicted on the right. Additionally, we have that ${\mathcal {D}} {\hookrightarrow } {\mathcal {B}} _1$, ${\mathcal {D}} '{\hookrightarrow } {\mathcal {B}} _5$ and ${\mathcal {D}} _4{\hookrightarrow } {\mathcal {B}} _2$. Note that, in each argumentation line, arguments placed at odd positions are those posed by the defense, whereas the ones in even positions correspond to the prosecution. Now suppose the defense accounts with this information –representing the current state of the trial– and wishes to know how to proceed to change the outcome, i.e., which allegations it should present. In order to warrant the defense’s initial argument, we need to effectively alter the attacking lines $\lambda _1 = [{\mathcal {A}},{\mathcal {B}} _1,{\mathcal {B}} _3,{\mathcal {B}} _6]$ and $\lambda _2 = [{\mathcal {A}},{\mathcal {B}} _1,{\mathcal {B}} _4,{\mathcal {B}} _7]$.

We select ${\mathcal {B}} _1$ as the con argument in $\lambda _1$, then, a defeater ${\mathcal {D}} \in {{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}} _1,\lambda _1)}$ appears. The activation of ${\mathcal {D}}$ requires to activate ${\mathcal {D}} _1$ (since ${\mathcal {D}} _2$ is already active). Note that, ${\mathcal {D}}$ itself is interpreted as a collaterally activated defeater for ${\mathcal {B}} _1$ but in $\lambda _2$. Thus, the global defeating function restricts the selection in $\lambda _2$ to occur in the segment $\lambda ^{\uparrow }_{2}[{\small {\mathcal {B}} _1}]$. This will provoke the selection of con arguments in both $\lambda _1$ and $\lambda _2$ to coincide, triggering ${\mathcal {B}} _1$ in both cases. Hence, the activation of ${\mathcal {D}}$ turns both attacking lines into non-attacking, as depicted on the right.

Nonetheless, the revision is not complete, since an undesirable side-effect has occurred: the activation of ${\mathcal {D}} _1$ has also activated argument ${\mathcal {D}} '$, which attacks ${\mathcal {B}} _5$, since it dismisses ${\mathcal {B}} _5$’s overdose hypothesis. This collateral activation is controlled by the global defeating function in its condition 3e. Afterwards, the collateral alteration provokes $\lambda _3$ to turn into a new attacking line $\lambda '=[{\mathcal {A}},{\mathcal {B}} _2,{\mathcal {B}} _5,{\mathcal {D}} ']$ in the context of the hypothetical tree ${\mathcal {H}_{{\mathsf {T}}}({\mathcal {A}},\{{\mathcal {D}} \})}$. From cond. 3a in Definition 11, the new extended line $\lambda '$ is effectively altered through the activation of the inactive defeater ${\mathcal {D}} _4\in {{\mathsf {idefs}_{{\mathsf {T}}}} ({\mathcal {B}} _2,\lambda ')}$ for the selected con argument ${\mathcal {B}} _2$, turning the line into non-attacking. The figure depicted on the right shows that ${\mathcal {A}}$ ends up warranted from the revision operation ${\mathsf {T}}\ {*} {\mathcal {A}} = \langle {\mathbb {U}},{\hookrightarrow },{\sqsubseteq } \rangle [{\mathbb {A}} {\oplus } \{{\mathcal {A}},{\mathcal {D}},{\mathcal {D}} ',{\mathcal {D}} _4\}]$.

4 Conclusions, Related and Future Work

We have presented an approach for studying dynamics of the judicial process through an operator of argument revision which considers activation (incorporation) of arguments. This approach is comprehended within Argument Theory Change [18, 20] and provides another standpoint to change the status of warrant of an argument in dialectical trees. The method is particularly interesting in the context of legal reasoning given that it could bring the theoretical foundations for recommender systems for the study of a legal case prior to the corresponding judicial procedure. This would render different critical points in the legal argumentation of the case for which further investigations could be directed towards discovering implicit norms that have not been applied before (judge’s viewpoint), or towards discovering new pieces of evidence (lawyer’s viewpoint).

Several recent articles (like [5, 7, 9, 10, 12, 13]) deal with the dynamics of arguments. Some consider change by removing attacks between arguments, others by enriching logics with dynamic features. However, our perspective of change pursued here is different: we provoke change upon the morphology of arguments’ graph for studying dynamics. In this sense, [17] is more similar since it studies dynamics upon graphs. However, the main difference is that the argumentation semantics that we follow in this article is necessarily the one derived from dialectical trees, since they probably constitute the most appropriate argumentation model for the analysis of the judicial process.

Regarding future work, the activating approach is the stepping stone towards the definition of a hybrid revision for deciding between the activation or deactivation in order to choose the most appropriate of both. This choice could apply activation in some attacking lines and deactivation in others. From the standpoint of the legal domain, the hybrid method would bring a theoretic model for studying promulgation of laws. A process of promulgation may involve the derogation of invalid norms (by disuse) that break the coherence of the legal ordering when considering the new law. Additionally, it may be the case that some articles of the new law should be modified for avoiding it to be declared inconstitutional due to contradictions –for instance, with some principles of the doctrine. A hybrid operator could model such a situation by activating arguments standing for derogative norms and deactivating arguments standing for conflicting articles of the new law. This would render a recommender system for identifying which previous norms should be derogated and which parts of the new law should be reformulated towards a successful process of promulgation.