Light Structure from Pin Motion: Simple and Accurate Point Light Calibration for Physics-Based Modeling

Abstract

We present a practical method for geometric point light source calibration. Unlike in prior works that use Lambertian spheres, mirror spheres, or mirror planes, our calibration target consists of a Lambertian plane and small shadow casters at unknown positions above the plane. Due to their small size, the casters’ shadows can be localized more precisely than highlights on mirrors. We show that, given shadow observations from a moving calibration target and a fixed camera, the shadow caster positions and the light position or direction can be simultaneously recovered in a structure from motion framework. Our evaluation on simulated and real scenes shows that our method yields light estimates that are stable and more accurate than existing techniques while having a considerably simpler setup and requiring less manual labor.

This project’s source code can be downloaded from: https://github.com/hiroaki-santo/light-structure-from-pin-motion.

1 Introduction

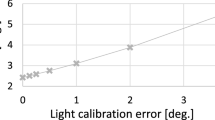
Estimating the position or direction of a light source accurately is essential for many physics-based techniques such as shape from shading, photometric stereo, or reflectance and material estimation. In these, inaccurate light positions immediately cause errors. Figure 1 shows the relation between light calibration error and normal estimation error in a synthetic experiment with directional light, a Lambertian sphere as target object, and a basic photometric stereo method [1, 2]. We can see the importance of accurate light calibration: Working on algorithmic improvements in photometric stereo that squeeze out the last few percent in accuracy is futile if the improvements are overshadowed by the calibration inaccuracy. Despite the importance of accurate light calibration, it remains laborious as researchers have not yet come up with accurate and easy to use techniques.

This paper proposes a method for calibrating both distant and near point lights. We introduce a calibration target, shown in Fig. 2, that can be made from off-the-shelf items for< $ 5 within 1–2 min. Instead of specular highlights on spheres we use a planar board (shadow receiver) and pins (shadow casters) stuck on it that cast small point shadows on the board. Moving the board around in front of a static camera and light source and observing the pin head shadows under various board poses lets us derive the light position/direction.

Fig. 1.

Light calibration error vs. normal error in photometric stereo. Each data point is the mean of 100 runs.

The accuracy with which we can localize the point shadows is the key factor in the overall calibration accuracy. We can control this through the pin head size. Ideally the shadows should be about 1 px wide, but even with off-the-shelf pins we can automatically localize their centers with an accuracy of about 1–2 px (Fig. 3, right), which is in marked contrast to how accurately we can detect specular highlights. Further, since our target is planar, it translates small shadow localization errors only into small light direction errors. This is in contrast to mirror sphere methods where the surface normal, which determines the light reflection angle, changes across the sphere and thus amplifies errors. We will come back to these advantages of our method in Sect. 2.

Fig. 2.

Our calibration board, a camera observing the movement of shadows cast by a point light while the board moves, our algorithm’s workflow, and the estimation result.

Geometrically, point lights are inverse pinhole cameras [3] (see Fig. 4). We can thus build upon past studies on projective geometry. In particular we show that, analogous to structure from motion (SfM) which jointly estimates camera poses and 3D feature positions, we can jointly estimate light position/direction and shadow caster pin positions from moving our calibration target and observing the pin shadows, i.e., we can estimate light (and pin) structure from pin motion.

In this paper we clarify the relationship between our problem and conventional SfM and develop a solution technique for our context. Interestingly, our method’s connection to SfM allows users to place the pins arbitrarily on the board because their positions will be estimated in the calibration process. This means that – in contrast to many previous works – we do not need to carefully manufacture or measure our calibration target. Further, in contrast to some previous methods, we require no hand annotations in the captured imagery. All required information can be inferred automatically with sufficient accuracy.

The primary contributions of our work are twofold. First, it introduces a practical light source calibration method that uses an easy-to-make calibration target. Instead of requiring a carefully designed calibration target, our method only uses needle pins that are stuck at unknown locations on a plane. Second, we show that the calibration of point light source positions/directions can be formulated as a bundle adjustment problem using the observations of cast shadows, and develop a robust solution technique for accurately achieving the calibration.

The benefits from the new calibration target and associated solution method are an extremely simple target construction process (shown in the supplemental video), a calibration process that requires no manual intervention other than moving the board, and improved accuracy compared to prior work.

Fig. 3.

Left and center: Specular highlights on a mirror plane [4] and a mirror sphere. Right: The pin head shadows on our planar board.

2 Related Work

Light source calibration methods can be roughly divided into three categories: (1) estimating light source directions for scenes with a distant point light source, (2) estimating illumination distributions in natural light source environments, and (3) estimating light source positions in scenes with a near point light source.

In the first category, Zhang and Yang [5] (and Wei [6] with a more robust implementation) proposed a method to estimate multiple distant light directions based on a Lambertian sphere’s shadow boundaries and their intensities. Wang and Samaras [7] extended this to objects of arbitrary but known shape, combining information from the object’s shading and the shadows cast on the scene. Zhou and Kambhamettu [8] used stereo images of a reference sphere with specular reflection to estimate light directions. Cao and Shah [9] proposed a method for estimating camera parameters and the light direction from shadows cast by common vertical objects such as walls instead of special, precisely fabricated objects, which can be used for images from less restricted settings.

In the second category, Sato et al. [10, 11] used shadows of an object of known shape to estimate illumination distributions of area lights while being restricted to distant light and having to estimate the shadow receiver’s reflectance.

In the third category, Powell et al. [12] triangulate multiple light positions from highlights on three specular spheres at known positions. Other methods also use reflective spheres [13,14,15,16] or specially designed geometric objects [17,18,19]. In contrast to some of these methods’ simple triangulation schemes, Ackermann et al. [20] model the light estimation as nonlinear least squares minimization of highlight reprojection errors, yielding improved accuracy. Park et al. [21] handle non-isotropic lights and estimate light position and radiant intensity distribution from multi-view imagery of the shading and specular reflections on a plane. Further, some methods are based on planar mirrors [4, 22]. They model the mirror by perspective projection and infer parameters similar to camera calibration.

In highlight-based calibration methods, precisely localizing the light source center’s reflection on the specular surface is problematic in practice: Even with the shortest exposure at which we can still barely detect or annotate other parts of the calibration target (pose detection markers, sphere outline, etc.), the highlight is much bigger than the light source’s image itself (see Fig. 3, left and center). Lens flare, noise, etc. further complicate segmenting the highlight.

Also, since the highlight is generally not a circle but a conic section on a mirror plane or an even more complicated shape on a mirror sphere, the light source center’s image (i.e., the intersection of the mirror and the light cone’s axis) cannot be found by computing the highlight’s centroid, as for example Shen et al. [4] do. We thus argue that it is extremely hard to reliably localize light source centers on specular surfaces with pixel accuracy – even with careful manual annotation. Instead, we employ small cast shadows for stable localization.

Mirror sphere-based calibration methods suffer from the fact that the sphere curvature amplifies highlight localization errors into larger light direction errors because the surface orientation, which determines the reflection angle, differs between erroneous and correct highlight location. Also, the spheres need to be very precise since “even slight geometric inaccuracies on the surface can lead to highlights that are offset by several pixels and markedly influence the stability of the results” (Ackermann et al. [20]). The prices of precise spheres ($\sim$$40 for a high-quality 60 mm bearing ball of which we need 3–8 for accurate calibration) rules out high-accuracy sphere-based calibration for users on a tight budget.

Further, sphere methods typically require annotating the sphere outline in the image which is highly tedious if done accurately, as anyone who has done it can confirm. This is because one has to fit a conic section into the sphere’s image and the sphere’s exact outline is hard to distinguish from the background, especially in dark images, since the sphere also mirrors the background.

The connection between pinhole cameras and point lights has already been shown by others: Hu et al. [3] use it in a theoretical setting similar to ours with point objects and shadows. Each shadow yields a line constraint for the light position and they triangulate multiple such constraints by computing the point closest to all lines. However, they only discuss the idea with geometric sketches.

We push the idea further by deriving mathematical solutions, extending it to distant light, embedding it in an SfM framework [23, 24] that minimizes reprojection error, deriving an initialization for the non-convex minimization, devising a simple calibration target that leverages our method in the real world, and demonstrating our method’s accuracy in simulated and real-world experiments. Given noisy observations, minimizing reprojection error as we do gives better results (see Szeliski [25, Sect. 7.1] or Hartley and Sturm [26]) than the point-closest-to-all-rays triangulation used by Hu et al. [3], Shen and Cheng’s mirror plane method [4], and most sphere methods prior to Ackermann’s [20].

3 Proposed Method

Our method estimates a nearby point light’s position or a distant light’s direction using a simple calibration target consisting of a shadow receiver plane and shadow casters above the plane. Our method automatically achieves the point light source calibration by observing the calibration target multiple times from a fixed viewpoint under a fixed point light source while changing the calibration target’s pose. The positions of the shadow casters on the calibration board are treated unknown, which makes it particularly easy to build the target while the problem remains tractable as we will see later in this section.

To illustrate the relationship between light source, shadow caster, and observed shadow, we begin with the shadow formation model which is connected to perspective camera geometry. We then describe our proposed calibration method that is based on bundle adjustment, as well as its implementation details.

We denote matrices and vectors with bold upper and lower case and the homogeneous representation of $\mathbf {v}$ with $\hat{\mathbf {v}}$. Due to space constraints we show the exact derivations of Eqs. (2), (4), (7), and (9) in the supplemental material.

Fig. 4.

Cameras vs. point lights. Camera matrix projects a scene point to just like light matrix projects to . SfM estimates and from and we estimate and .

3.1 Shadow Formation Model

Let us for now assume that the pose of the shadow receiver plane $\varPi$ is fixed to the world coordinate system’s x-y plane.

Let a nearby point light be located at $\mathbf {l}= \left[ l_x, l_y, l_z\right] ^\top \in \mathbb {R}^3$ in world coordinates. An infinitesimally small caster located at $\mathbf {c}\in \mathbb {R}^3$ in world coordinates casts a shadow on $\varPi$ at $\mathbf {s}\in \mathbb {R}^2$ in $\varPi$’s 2D coordinate system which is $\bar{\mathbf {s}} = \left[ \mathbf {s}^\top , 0\right] ^{\top }$ in world coordinates (because $\varPi$ coincides with the world’s x-y plane). Since $\mathbf {l}$, $\mathbf {c}$ and $\bar{\mathbf {s}}$ are all on one line, the lines $\overline{\mathbf {c}\bar{\mathbf {s}}}$ and $\overline{\mathbf {l}\bar{\mathbf {s}}}$ are parallel:

$$\begin{aligned} (\mathbf {c}-\bar{\mathbf {s}})\times (\mathbf {l}-\bar{\mathbf {s}})=\mathbf {0}. \end{aligned}$$

(1)

From this it follows that the shadow formation can be written as

(2)

As such, point lights and pinhole cameras can be described by similar mathematical models with the following correspondences: (light source $\Leftrightarrow$ camera), (shadow receiver plane $\Leftrightarrow$ image plane), (shadow caster $\Leftrightarrow$ observed point), and (first two matrices of Eq. (2) $\Leftrightarrow$ camera intrinsics and extrinsics), see Fig. 4.

For distant light all light rays in the scene are parallel, is a light direction instead of a position, and the line $\overline{\mathbf {c}\bar{\mathbf {s}}}$ is parallel to $\mathbf {l}$:

$$\begin{aligned} (\mathbf {c}-\bar{\mathbf {s}})\times \mathbf {l}=\mathbf {0}. \end{aligned}$$

(3)

From this follows an expression that resembles orthographic projection:

(4)

3.2 Light Source Calibration as Bundle Adjustment

Our goal is to determine the light source position or direction $\mathbf {l}$ in Eqs. (2) or (4) by observing the shadows cast by unknown casters. A single shadow observation $\mathbf {s}$ does not provide sufficient information to solve this. We thus let the receiver plane undergo multiple poses $\{\left[ \mathbf {R}_i |\mathbf {t}_i \right] \}$. In pose i, the light position $\mathbf {l}_i$ in receiver plane coordinates is related to $\mathbf {l}$ in world coordinates as

With this index i the matrices for nearby and distant light, resp., become

If we use not only multiple poses $\{\left[ \mathbf {R}_i |\mathbf {t}_i \right] \}$ but also multiple shadow casters $\{\mathbf {c}_j\}$ (to increase the calibration accuracy as we show later), we obtain shadows $\{\mathbf {s}_{ij}\}$ for each combination of pose i and caster j. Equations (2) and (4) then become

Assuming that the target poses $\{[\mathbf {R}_i|\mathbf {t}_i]\}$ are known, our goal is to estimate the light position $\mathbf {l}$ in world coordinates and the shadow caster locations $\{\mathbf {c}_j\}$. We formulate this as a least-squares objective function of the reprojection error:

(5)

We solve this nonlinear least-squares problem with Levenberg-Marquardt [27]. For robust estimation we use RANSAC: We repeatedly choose a random observation set, estimate $(\mathbf {l},\mathbf {c}_j,\lambda _{ij})$, and select the estimate with the smallest residual.

Initialization: Equation (5) is non-convex and thus affected by the initialization. To find a good initial guess, we relax our problem into a convex one as follows.

In the near light case, the objective can be written analogous to Eq. (1) as and (using ) rewritten as

(6)

With , , , , and , we obtain the following equation system:

(7)

For distant light the objective is written analogous to Eq. (3) (using $\mathbf {l}_i=\mathbf {R}_i^\top \mathbf {l}$):

$$\begin{aligned} (\mathbf {c}_j - \bar{\mathbf {s}}_{ij})\times \mathbf {R}_i^\top \mathbf {l}= \mathbf {0}. \end{aligned}$$

(8)

Keeping the definitions of $\mathbf {c}_j$, $\bar{\mathbf {s}}_{ij}$, and $\mathbf {R}_i^\top$ from above but setting $\mathbf {l}=\left[ l_x,l_y,1\right] ^\top$ to reduce $\mathbf {l}$ to two degrees of freedom, the system becomes

(9)

To make the estimation of $\varvec{\theta }_j$ robust against outliers, we use $\ell _1$ minimization:

$$\begin{aligned} \varvec{\theta }_j^* = \mathop {\mathrm{argmin}}\limits _{\varvec{\theta }_j} \left\| \mathbf {A}_{ij}\varvec{\theta }_j - \mathbf {b}_{ij}\right\| _1. \end{aligned}$$

(10)

After obtaining $\varvec{\theta }_j^*$ we disregard the second-order variables $l_xc_{j,x}$, etc. – making the problem convex – and use $\mathbf {c}_j^*$ and $\mathbf {l}^*$ as initialization for minimizing Eq. (5).

Minimal Conditions for Initialization: Let $N_p$ and $N_c$ be the number of target poses and casters. For solving Eqs. (7) or (9) we must fulfill

$$\begin{aligned} \underbrace{3N_pN_c}_{\#\text {equations}} \ge \underbrace{12N_c {N_p} +3}_{\#\text {variables}}\,\Leftrightarrow \,N_p\ge 4 + \frac{1}{N_c} \quad \text {or}\quad \underbrace{3N_pN_c}_{\#\text {equations}} \ge \underbrace{9N_c {N_p} +2}_{\#\text {variables}}\,\Leftrightarrow \,N_p\ge 3 + \frac{2}{3N_c}. \end{aligned}$$

Thus, 5 and 4 poses suffice for nearby and distant light, resp., regardless of $N_c$.

3.3 Implementation

To obtain our target’s pose $\{[\mathbf {R}_i|\mathbf {t}_i]\}$, we print ArUco markers [28] on a piece of paper, attach it to the target (see Fig. 2, left), and use OpenCV 3D pose estimation [29]. Our shadow casters are off-the-shelf pins with a length of $\sim$30 mm and a head diameter of $\sim$3 mm, which is big enough to easily detect and small enough to accurately localize them. As mentioned, we can place the pins arbitrarily.

For shadow detection we developed a simple template matching scheme. For the templates we generated synthetic images of shadows consisting of a line with a circle at the end. To deal with varying projective transformations we use 12 rotation angles with 3 scalings each. We match the templates after binarizing the input image to extract shadowed regions more easily. Further we use the color of the pin heads to distinguishing between heads and head shadows.

For Eqs. (5), (7), and (9) we need to assign the same index j to all shadows $\bar{\mathbf {s}}_{ij}$ from the same caster $\mathbf {c}_j$ in different images. Normal SfM solves this correspondence problem using the appearance of feature points. We want our shadows to be very small and can therefore not alter their shape enough to make them clearly distinguishable. Instead, we track them through a video of the calibration process. To facilitate the tracking, we place the pins far apart from each other.

3.4 Estimating Multiple Lights Simultaneously

We can even calibrate multiple lights simultaneously to (a) save time by letting the user capture data for multiple lights in one video and (b) increase the estimation accuracy by constraining each caster’s position by multiple lines from a light through the caster to a shadow (Fig. 5).

Fig. 5.

Two lights casting two shadows per pin.

Above we discussed that tracking helps us find corresponding shadows from the same caster across all images. Multiple lights entail another correspondence problem: finding all shadows from the same light to couple the correct shadows $\bar{\mathbf {s}}_{i,j,k}$ and lights $\mathbf {l}_{i,k}$ in our equations. To solve this we first put each shadow track separately into our algorithm. For each of the $N_l$ lights we get $N_c$ position estimates which vary slightly due to noise. We then cluster the $N_l\times N_c$ estimates into $N_l$ clusters, each corresponding to one light. Finally we solve the bundle adjustment, Eq. (5), with an additional summation over all lights. We initialize Eq. (5) with the mean of the first step’s $N_c$ duplicate estimates.

This solution for the correspondence problem only requires users to provide $N_l$ and in contrast to, e.g., Powell et al.’s [12] ordering constraint it does not fail in certain configurations of camera, lights and target. The clustering might, however, produce wrong clusters if two lights are so close that their clusters overlap, but this may be practically irrelevant since in physics-based modeling two lights need to be far enough apart to give an information gain over one light.

Interestingly, we can even simultaneously calibrate lights whose imagery has not been captured simultaneously. This is possible since applying the board poses transforms all shadow positions – no matter whether they were captured simultaneously or not – into the same coordinate system, namely the target’s.

4 Evaluation

We now assess our method’s accuracy using simulation experiments (Sect. 4.1) and real-world scenes (Sect. 4.2).

4.1 Simulation

We randomly sampled board poses, caster positions and light positions (the latter only for near light conditions) from uniform distributions within the ranges shown in Fig. 6. The casters were randomly placed on a board of size 200 $\times$ 200. For distant light, we sampled the light direction’s polar angle $\theta$ from $\left[ 0^{\circ },45^{\circ }\right]$.

Fig. 6.

Arrows show value ranges for our simulation experiments.

Table 1. Estimation error (mean of ten random trials) in a synthetic, noise-free setting.

We evaluated the absolute/angular error of estimated light positions/directions while varying the distance $t_z$ of the light to the calibration board and the number of casters $N_c$. Table 1 shows that the mean error of each configuration is 14 or more orders of magnitude smaller than the scene extent, confirming that our method solves the joint estimation of light position/direction and shadow caster positions accurately in an ideal setup. In practice, light source estimates will be deteriorated by two main error sources: (1) Shadow localization and (2) the marker-based board pose estimation.

Fig. 7.

Estimation error for synthetic near and distant light with Gaussian noise added to the shadow positions. Each data point is the median of 500 random trials. Top row: $N_p=10$ and $N_c=5$. The noise’s standard deviation $\sigma$ is on the x-axis. Middle row: $N_p=5$ and $N_c$ is on the x-axis. Bottom row: $N_c=5$ and $N_p$ is on the x-axis.

Shadow Localization Errors: To analyze the influence of shadow localization, we perturbed the shadow positions with Gaussian noise. Figure 7 shows the estimation accuracy obtained as solutions from the convex relaxation (Eq. (7) or (9)) compared to the full bundle adjustment (Eq. (5) after initialization with convex relaxation) for near and distant light in various settings. Figure 7’s top row confirms that larger shadow position noise results in larger error and full bundle adjustment mitigates the error compared to solving only the convex relaxation. Increasing the number of casters or board poses makes Eqs. (10) and (5) more overconstrained and should thus reduce the error from noisy shadow locations. Figure 7’s middle and bottom row confirm decreasing errors for larger $N_p$ or $N_c$.

Fig. 8.

Estimation error for synthetic near and distant light with Gaussian noise added to the board orientation (in deg.). Each data point is the median of 500 random trials. Top row: $N_p=10$ and $N_c=5$. The noise’s standard deviation $\sigma$ is on the x-axis. Middle row: $N_p=5$ and $N_c$ is on the x-axis. Bottom row: $N_c=5$ and $N_p$ is on the x-axis.

Board Pose Estimation Errors: To simulate errors in the board pose estimation, we performed an experiment where we added Gaussian noise to the board’s roll, pitch, and yaw. Figure 8’s top row shows that the error is again higher for stronger noise and the bundle adjustment mitigates the error of the convex relaxation. In Fig. 8’s middle and bottom row we increase the number of casters and board poses again. Bundle adjustment and increasing the number of poses reduce the error, but increasing the number of casters does not. However, this is not surprising since adding constraints to our system only helps if the constraints have independent noise. Here, the noises for all shadows $\bar{\mathbf {s}}_{i,j}$ of the same pose i stem from the same pose noise and are thus highly correlated. Therefore, increasing the number of poses is the primary method of error reduction.

Fig. 9.

Our real-world experiment environments. E1 has four LEDs fixed around the camera. In E2 we use a smartphone’s camera and LED. In E3 we observe the board under sun light. E4 has a flashlight fixed about 3 m away from the board.

4.2 Real-World Experiments

We created 4 real-world environments, see Fig. 9. In all experiments we calibrated the intrinsic camera parameters beforehand and removed lens distortions.

Environments E1 and E2 have near light, and E3  and E4  have distant light. In E1 we fixed four LEDs to positions around the camera with a 3D printed frame and calculated the LED’s ground truth locations from the frame geometry. We used a FLIR FL2G-13S2C-C camera with a resolution of $1280\times 960$. In E2  we separately calibrated two smartphones (Sony Xperia XZs and Huawei P9) to potentially open up the path for simple, inexpensive, end user oriented photometric stereo with phones. Both phones have a $1920\times 1080$ px camera and an LED light. We assumed that LED and camera are in a plane (orthogonal to the camera axis and through the optical center) and measured the camera-LED distance to obtain the ground truth. In E3 we placed the board under direct sun light and took datasets at three different times to obtain three light directions. In E4 a flashlight was fixed about 3 m away from the board to approximate distant lighting. In both E3 and E4 we used a Canon EOS 5D Mark IV with a ${35}\,{\mathrm{mm}}$ single-focus lens and a resolution of 6720 $\times$ 4480 and obtained the ground truth light directions from measured shadow caster positions and hand-annotated shadow positions. In E1, E3, and E4 we used the A4-sized calibration board shown in Fig. 2. In E2, since LED and camera are close together, our normal board’s pins occlude the pin shadows in the image as illustrated in Fig. 11(a). We thus used an A6-sized board with four pins with 2 mm heads and brought it close to the camera to effectively increase the baseline (see Fig. 11(b)).

Table 2. Estimation errors in our four real-world scenes.

Table 2 shows the achieved estimation results. The light position errors are $\sim$6.5 mm for E1 and $\sim$2.5 mm for E2 (whose scene extent and target is smaller), the light direction errors are ${\sim }1^{\circ }$, and the caster position errors are $\le$ 2 mm. Figure 10 shows how increasing the number of board poses monotonously decreases the estimation error on two of our real-world scenes.

Fig. 10.

Estimation error for the first light of scene E1 and for scene E4. For each scene we captured 200 images, randomly picked $N_p$ images from these, and estimated the light and caster positions. The gray bars and error bars represent median and interquartile range of 100 random iterations of this procedure.

4.3 Estimating Multiple Lights Simultaneously

Capturing and estimating scene E1’s two top lights simultaneously (reliably detecting shadows of > 2 lights requires a better detector) as described in Sect. 3.4 reduces the mean light and caster position errors from 7.3 and 1.8 mm to 3.5 and 1.5 mm respectively. As mentioned, we can also jointly calibrate lights whose imagery was captured separately. For E1  this decreases errors as shown in Table 3.

Table 3. Average estimation errors (all units in  mm) in scene E1  for 2, 3, and 4 lights captured separately and calibrated separately or simultaneously respectively.

Table 4. Estimation error in scene E1  (averaged over E1’s 4 lights) for Ours  and Shen.

4.4 Comparison with Existing Method

To put our method’s accuracy into perspective, on scenes 2–3 times as big as ours Ackermann et al. [20] achieved accuracies of about 30–70  mm despite also minimizing reprojection error (thus being more accurate than earlier mirror sphere methods based on simpler triangulation schemes [26]) with very careful execution. We believe this is at least partially due to their usage of spheres.

In this section we compare our calibration method – denoted as Ours – with an existing method. Because of Ackermann’s achieved accuracy we ruled out spheres and compared to a reimplementation of a state-of-the-art method based on a planar mirror [4] – denoted as Shen. Their method observes the specular reflection of the point light in the mirror, also models the mirror with perspective projection and infers parameters similar to camera calibration. In our implementation of Shen we again used ArUco markers to obtain the mirrors pose and we annotated the highlight positions manually. For a fair comparison we also annotated the shadow positions for our method manually.

In both methods we observed the target while varying its pose $\sim$500 mm away from the light source. We captured 30 poses for each method and annotated the shadows/reflections. Table 4 shows the estimation error of light source positions for Ours and Shen in scene E1. Ours with hand-annotated shadows as well as detected shadows outperforms Shen with annotated highlights.

5 Discussion

With our noise-free simulation experiments we verified that our formulation is correct and the solution method derives accurate estimates with negligible numerical errors. Thus, the solution quality is rather governed by the inaccuracy of board pose estimation and shadow detection. We showed on synthetic and real-world scenes that even with these inaccuracies our method accurately estimates light source positions/directions with measurements from a sufficient number of shadow casters and board poses, which can easily be collected by moving the proposed calibration target in front of the camera. Further, we showed that we can increase the calibration accuracy by estimating multiple lights simultaneously.

A comparison with a state-of-the-art method based on highlights on a mirror plane showed our method’s superior accuracy. We believe the reason lies in our pin shadows’ accurate localizability. As discussed in Sect. 2, highlights are hard to localize accurately. In contrast, our pin shadows do not “bleed” into their neighborhood and we can easily control their size through the pin head size. If higher localization accuracy is required, one can choose pins smaller than ours.

In contrast to related work, our method requires no tedious, error-prone hand annotations of, e.g., sphere outlines, no precisely fabricated objects such as precise spheres, and no precise measurements of, e.g., sphere positions. Our target’s construction is simple, fast and cheap and most calibration steps (e.g., board pose estimation and shadow detection/matching) run automatically. The only manual interaction – moving the board and recording a video – is simple. To our knowledge no other method combines such simplicity and accuracy.

We want to add a thought on calibration target design: Ackermann [20] pointed out that narrow baseline targets (e.g., Powell’s [12]) have a high light position uncertainty along the light direction. This uncertainty can be decreased by either building a big, static target such as two widely spaced spheres, or by moving the target in the scene as we do. So, again our method is strongly connected to SfM where camera movement is the key to reducing depth uncertainty.

Fig. 11.

With a small camera-to-light baseline the caster may occlude the shadow as seen from the camera (a). To solve this, we use a small caster, bring the board close to the camera (b) and make the board smaller so the camera can capture it fully.

Limitations: One limitation of our method is that it requires the camera to be able to capture sequential images (i.e., a video) for tracking the shadows to solve the shadow correspondence problem. If the casters are sufficiently far apart, a solution would be to cluster the shadows in the board coordinate system. The second limitation are scenes where light and camera are so close together that the caster occludes the image of the shadow (see Fig. 11(a)). This occured in our smartphone environment E2  and the solution is to effectively increase the baseline between camera and light as shown in Fig. 11(b).

Future Work: It may be possible to alleviate the occlusion problem above with a shadow detection that handles partial occlusions. Further, we want to analyze degenerate cases where our equations are rank deficient, e.g., a board with one caster being moved such that its shadow stays on the same spot. Finally, we want to solve the correspondences between shadows from multiple lights (Sect. 4.3) more mathematically principled with equations that describe the co-movement of shadows from one light and multiple casters on a moving plane.