Open Set Learning with Counterfactual Images

Abstract

In open set recognition, a classifier must label instances of known classes while detecting instances of unknown classes not encountered during training. To detect unknown classes while still generalizing to new instances of existing classes, we introduce a dataset augmentation technique that we call counterfactual image generation. Our approach, based on generative adversarial networks, generates examples that are close to training set examples yet do not belong to any training category. By augmenting training with examples generated by this optimization, we can reformulate open set recognition as classification with one additional class, which includes the set of novel and unknown examples. Our approach outperforms existing open set recognition algorithms on a selection of image classification tasks.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In traditional image recognition tasks, all inputs are partitioned into a finite set of known classes, with equivalent training and testing distributions. However, many practical classification tasks may involve testing in the presence of “unknown unknown” classes not encountered during training [1]. We consider the problem of classifying known classes while simultaneously recognizing novel or unknown classes, a situation referred to as open set recognition [2].

A typical deep network trained for a closed-set image classification task uses the softmax function to generate for each input image the probability of classification for each known class. During training, all input examples are assumed to belong to one of K known classes. At test time, the model generates for each input x a probability $P(y_i | x)$ for each known class $y_i$. The highest-probability output class label $y^*$ is selected as $y^* = \arg \max _{y_i} P(y_i | x)$ where P(y|x) is a distribution among known classes such that $\sum _{i=1}^{K} P(y_i|x) = 1$.

In many practical applications, however, the set of known class labels is incomplete, so additional processing is required to distinguish between inputs belonging to the known classes and inputs belonging to the open set of classes not seen in training. The typical method for dealing with unknown classes involves thresholding the output confidence scores of a closed-set classifier. Most commonly, a global threshold $\delta$ is applied to P(y|x) to separate all positive-labeled examples from unknown examples:

(1)

However, this type of global thresholding assumes well calibrated probabilities, and breaks down in many real-world tasks. For example, convolutional network architectures can output incorrect high-confidence predictions when faced with test data from outside the training distribution, as evidenced by work in adversarial example generation [3]. Better methods are needed to facilitate the learning of a decision boundary between the known classes and the unknown open set classes.

Fig. 1.

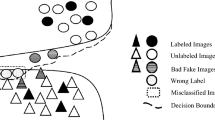
Left: Given known examples (green dots) we generate counterfactual examples for the unknown class (red x). The decision boundary between known and counterfactual unknown examples extends to unknown examples (blue +), similar to the idea that one can train an SVM with only support vectors. Right: Example SVHN known examples and corresponding counterfactual unknown images. (Color figure online)

A number of approaches exist to separate known from unknown data at test time. Some approaches involve learning a feature space through classification of training data, then detecting outliers in that feature space at test time [4, 5]. Other approaches follow the anomaly detection paradigm– where the distribution of training data is modeled without classification, and inputs are compared to that model at test time [6]. Our approach follows another line of research, in which the set of unknown classes is modeled by synthetic data generated from a model trained on the known classes [7].

Figure 1 illustrates our procedure applied to the SVHN dataset, where digits 0 through 4 are known and 5 through 9 are unknown (ie. not included in the training data). We train a generative adversarial network on the set of known classes. Starting from the latent representation of a known example, we apply gradient descent in the latent space to produce a synthetic open set example. The set of synthetic open set examples provide a boundary between known and unknown classes.

Our contributions are the following: (1) We introduce the concept of counterfactual image generation, which aims to generate synthetic images that closely resemble a given real image, but satisfy certain properties, (2) we present a method for training a deep neural network for open set recognition using the output of a generative model, (3) we apply counterfactual image generation, in the latent space learned by a generative adversarial network, to generate synthetic images that resemble known classes images, but belong to the open set; and we show that they are useful for improving open set recognition.

2 Related Work

2.1 Open Set Recognition

A number of models and training procedures have been proposed to make image recognition models robust to the open set of unknown classes. Early work in this area primarily focused on SVM based approaches, such as 1-class SVM [8]. In [9], a novel training scheme is introduced to refine the linear decision boundaries learned by a 1-class or binary SVM to optimize both the empirical and the open set risk. In [4], based on the statistical Extreme Value Theory (EVT), a Weibull distribution is used to model the posterior probability of inclusion for each known class and an example is classified as open class if the probability is below a rejection threshold. In [2], W-SVM is introduced where Weibull distributions are further used to calibrate the scores produced by binary SVMs for open set recognition.

More recently, Bendale et al. explored a similar idea and introduced Weibull-based calibration to augment the softmax layer of a deep network, which they called “OpenMax” [5]. The last layer of the classifier, before the application of the softmax function, is termed the “activation vector”. For each class, a mean activation vector is computed from the set of correctly-classified training examples. Distance to the corresponding mean activation vector is computed for each training example. For each class, a Weibull distribution is fit to the tail of largest distances from the mean activation vector. At test time, the cumulative distribution function of the Weibull distribution fit to distance from the mean is used to compute a probability that any input is an outlier for each class. In this way, a maximum radius is fit around each class in the activation vector feature space, and any activation vectors outside of this radius are detected as open set examples. The OpenMax approach is further developed in [7] and [10].

In [11], a network is trained to minimize the “II-loss”, which encourages separation between classes in a learned representation space. The network can be applied to open set recognition tasks by detecting outliers in the learned feature space as unknown class examples.

2.2 Generative Adversarial Nets

The Generative Adversarial Network was initially developed as an adversarial minimax game in which two neural networks are simultaneously trained: a generator which maps random noise to “fake” generated examples and a discriminator which classifies between“fake” and “real” [12]. Variations of the GAN architecture condition the generator or discriminator on class labels [13], augment the generator with additional loss terms [14], or replace the discriminator’s classification objective with a regression objective as in the Wasserstein critic [15]. The original and primary application of GAN models is the generation of images similar to a training set, and current state-of-the-art GAN models are capable of generating photo-realistic images at high resolution [16].

Generative adversarial nets have been applied to unsupervised representation learning, in which features learned on an unsupervised task transfer usefully to a supervised or semi-supervised task [17, 18]. Architectures that combine generator networks with encoder networks, which invert the function learned by the generator, can be more stable during training and make it possible to distort or adjust real input examples while preserving their realism, which is useful for applications such as style transfer and single-image superresolution [19,20,21,22]. The use of generative adversarial networks for data augmentation has been explored in the context of image classification [23].

2.3 Generative Models for Open Set Recognition

Generative methods have the potential to directly estimate the distribution of observed examples, conditioned on class identity. This makes them potentially useful for open set recognition. A generative adversarial network is used in [6] to compute a measure of probability of inclusion in a known set at test time by mapping input images to points in the latent space of a generator.

Most closely related to our approach, the Generative OpenMax approach uses a conditional generative adversarial network to synthesize mixtures of known classes [7]. Through a rejection sampling process, synthesized images with low probability of inclusion in any known class are selected. These images are included in the training set as examples of the open set class. The Weibull-calibration of OpenMax is then applied to the final layer of a trained classifier. The Generative OpenMax (G-OpenMax) approach effectively detects new and unknown classes in monochrome digit datasets, but does not improve open set classification performance on natural images [7].

Different from G-OpenMax, our work uses an encoder-decoder GAN architecture to generate the synthetic open set examples. This allows the features learned from the known classes to be transfered to modeling new unknown classes. With this architecture, we further define a novel objective for generating synthetic open set examples, which starts from real images of known classes and morphs them based on the GAN model to generate “counterfactual” open set examples.

Fig. 2.

Input examples and corresponding counterfactual images for known classes, generated by optimizing in latent space. Left: SVHN, Right: MNIST

3 Counterfactual Image Generation

In logic, a conditional statement $p \rightarrow q$ is true if the antecedent statement p implies the consequent q. A counterfactual conditional, is a conditional statement in which p is known to be false [24]. It can be interpreted as a what-if statement: if p were true, then q would be true as well. Lewis [24] suggests the following interpretation:

“If kangaroos had no tails, they would topple over” seems to me to mean something like this: in any possible state of affairs in which kangaroos have no tails, and which resembles our actual state of affairs as much as kangaroos having no tails permits it to, the kangaroos topple over.

Motivated by this interpretation, we wish to model possible “states of affairs” and their relationships as vectors in the latent space of a generative adversarial neural network. Concretely, suppose:

• The state of affairs can be encoded as a vector $\mathbf {z \in \mathbf R ^n}$

• The notion of resemblance between two states corresponds to a metric $\mathbf {||z_0 - z^*||}$

• There exists an indicator function $\mathbf {C_p(z)}$ that outputs 1 if p is true given z.

Given an actual state $z_0$ and logical statements p and q, finding the state of affairs in which p is true that resembles $z_0$ as much as possible can be posed as a numerical optimization problem:

We treat $C_p: \mathbf {R}^n \rightarrow \{0, 1\}$ as an indicator function with the value 1 if p is true. Given the optimal $z^*$, the truth value of the original counterfactual conditional can be determined:

For a concrete example, let z be the latent representation of images of digits. Given an image of a random digit and its latent representation $z_0$, our formulation of counterfactual image generation can be used to answer the question “what would this image look like if this were a digit ‘3’?”, where p is “being digit 3”. In Fig. 2, we show images from the known set (left column), and the counterfactual images generated by optimizing them toward other known classes for the SVHN and MNIST datasets. We can see that by starting from different original images, the generated counterfactual images of the same class differ significantly from one another.

Optimization in the latent space is capable of producing examples that lie outside of the distribution of any known class, but nonetheless remain within a larger distribution within pixel space consisting of plausible images (see Fig. 3). The counterfactual image optimization connects to the concept of adversarial image generation explored in [25] and [26]. However, while optimization in pixel space produces adversarial examples, the counterfactual optimization is constrained to a manifold of realistic images learned by the generative model. The combination of diversity and realism makes generated images useful as training examples. In the following section, we show that training on counterfactual images can improve upon existing methods of open set classification.

Fig. 3.

Our model learns to encode training images into a latent space, and decode latent points into realistic images. The space of realistic images includes plausible but non-real examples which we use as training data for the open set of unknown classes.

4 Open Set Image Recognition

In this section, we will first provide an overview of our method for open set recognition, followed by a description of our generative model and the proposed approach for generating counterfactual open set images.

4.1 Overview of the Approach

We assume that a labeled training set X consists of labeled examples of K classes and a test set contains $M > K$ classes, including the known classes in addition to one or more unknown classes. We pose the open set recognition problem as a classification of $K+1$ classes where all instances of the $M-K$ unknown classes must be assigned to the additional class.

We assume the open set classes and the known classes share the same latent space. The essence of our approach is to use the concept of counterfactual image generation to traverse in the latent space, generate synthetic open set examples that are just outside of the known class boundaries, and combine the original training examples of the known classes with the synthetic examples to train a standard classifier of $K+1$ classes. Figure 3 provides a simple illustration of our high level idea.

4.2 The Generative Model

The standard DCGAN training objective penalizes the generation of any image outside of the training distribution, and generators normally suffer from some level of mode collapse.

Inspired by the use of reconstruction losses to regularize the training of generators to avoid mode collapsing in [27] and in [28], we use a training objective based on a combination of adversarial and reconstruction loss.

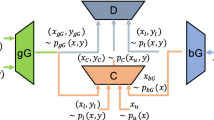
Our encoder-decoder GAN architecture consists of three components: an encoder network E(x), which maps from images to a latent space, a generator network G(z), which maps from latent space back to an image and a discriminator network D that discriminates fake (generated) images from real images.

The encoder and decoder networks are trained jointly as an autoencoder, with the objective to minimize the reconstruction error $||x - G(E(x))||_1$. Simultaneously, the discriminator network D is trained as a Wasserstein critic with gradient penalty. Training proceeds with alternating steps of optimization of the losses $L_D$ and $L_G$, where:

$$\begin{aligned} \mathbf {L_D} = \sum _{x \in \mathbf {X}} D(G(E(x))) - D(x) + P(D) \end{aligned}$$

(2)

$$\begin{aligned} \mathbf {L_G} = \sum _{x \in \mathbf {X}} ||x - G(E(x))||_1 - D(G(E(x))) \end{aligned}$$

(3)

where $P(D) = \lambda (||\nabla _{\hat{x}} D(\hat{x})||_2 - 1)$ is the interpolated gradient penalty term of [29]. Finally, along with the generative model, we also train a simple K-class classifier $C_K$ with cross-entropy loss on the labeled known classes.

4.3 Generating Counterfactual Open Set Examples

Our goal is to use counterfactual image generation to generate synthetic images that closely resemble real examples of known classes but lie on the other side of the true decision boundary between the known classes and the open set. This can be formulated as follows:

where x is the given initial real image.

We do not have a perfect decision function that tests for open set, but we can approximate such a function using the classifier $C_K$ which has learned to differentiate the known classes. We deem an example to belong to the open set if the confidence of the classifier’s output is low. Specifically, we formulate the following objective for counterfactual open set generation:

$$\begin{aligned} z^* = \min _{z} ||z - E(x)||_2^2 + \log \left( 1 + \sum _{i=1}^{K} \exp C_{K}(G(z))_i \right) \end{aligned}$$

(4)

Here $C(G(z))_i$ are the logits of the classifier prediction for the counterfactual image G(z) for class i. The second term of the objective is the negative log-likelihood of the unknown class, assuming the unknown class has a score of zero. By minimizing this term, we aim to simultaneously push the scores of all known classes to be low.

To generate a counterfactual image, we select an input seed image x at random from the training set. We encode the image to a latent point $z = E(x)$, then minimize Eq. (4) through gradient descent for a fixed number of steps to find $z^*$, then decode the latent point to generate the counterfactual image $G(z^*)$. Each counterfactual image $G(z^*)$ is augmented to the dataset with class label $K+1$, indicating the unknown class. After a sufficient number of open set examples have been synthesized, a new classifier $C_{K+1}$ is trained on the augmented dataset.

4.4 Implementation Details

The architecture of our generative model broadly follows [14], with a few differences. Instead of the traditional GAN classification loss, our discriminator is trained as a Wasserstein critic with gradient penalty loss (see Eq. 3) as in [29]. The generator is trained jointly with an encoder E which maps from the input image space to the latent space of the generator, with an effect similar to [19]. The encoder architecture is equivalent to the discriminator, with adjustments to the final layer so that the output matches the dimensionality of the latent space, and no nonlinearity applied.

We additionally include a classifier, both for the baseline method and for our own method after training with generated open set examples. The classifier, both in the K-class and $K+1$ class training settings, has an equivalent architecture to the discriminator and encoder.

In order to easily transfer weights from the K-class to the $K+1$-class classifier, we follow the reparameterization trick from [14] by noting that a softmax layer with K input logits and K output probabilities is over-parameterized. The softmax function is invariant to the addition of any constant to all elements of its input: ie. $\text {softmax}(x) = \text {softmax}(x + C)$. Using this fact, the K-logit classifier can be recast as a $K+1$-class classifier simply by augmenting the K-dimensional vector of logits with an additional constant 0, then applying the softmax function resulting in a $K+1$-dimensional probability distribution.

Our generator network consists of blocks of transposed convolutional layers with stride 2, each block increasing the size of the output feature map by a factor of two. The discriminator, encoder, and classifier all consist of standard blocks of convolutional layers with strided convolutions reducing the size of the feature map after each block. The LeakyReLU nonlinearity is used in all layers, and batch normalization is applied between all internal layers. Dropout is applied at the end of each block in all networks except the generator. A full listing of layers, hyperparameters, and source code is available at https://github.com/lwneal/counterfactual-open-set.

5 Experiments

We evaluate the performance of the open set classifier $C_{K+1}$ by partitioning the classes of labeled datasets into known and unknown sets. At training time, the only input to the network consists of the K known classes. At test time, the network must assign appropriate labels to examples of the known classes and label $K+1$ to examples of the $M-K$ open set classes.

5.1 Datasets

We evaluate open set classification performance using the MNIST, SVHN, CIFAR-10, and Tiny-Imagenet datasets. The MNIST digit dataset consists of ten digit classes, each containing between 6313 and 7877 $28\times 28$ monochrome images in the training fold. We use the labeled subset of the Street View House Numbers dataset [30], consisting of ten digit classes each with between 9981 and 11379 $32 \times 32$ color images. To test on a simple set of non-digit natural images, we apply our method to the CIFAR-10 dataset, consisting of 6000 $32 \times 32$ color images of each of ten natural image categories. The Tiny-Imagenet dataset consists of 200 classes of 500 training and 100 test examples each, drawn from the Imagenet ILSVRC 2012 dataset and downsampled to $32 \times 32$.

Classes within each dataset are partitioned into separate known and unknown sets. Models are trained using examples drawn from the training fold of known classes, and tested using examples from the test fold of both known and unknown classes.

5.2 Metrics

Open set classification performance can be characterized by the overall accuracy or F-score for unknown class detection on a combination of known and unknown data. However, such combined metrics are sensitive not only to the effectiveness of the trained model, but also arbitrary calibration parameters. To disambiguate between model performance and calibration, we measure open set classification performance with two metrics.

Closed Set Accuracy. An open set classifier should remain capable of standard closed-set classification without unreasonably degrading accuracy. To ensure that the open set classifier is still effective when applied to the known subset of classes, we measure classification accuracy of the classifier applied only to the K known classes, with open set detection disabled.

Area Under the ROC Curve for Open Set Detection. In open set classification, it is not known at training time how rare or common examples from the unknown classes will be. For this reason, any approach to open set detection requires an arbitrary threshold or sensitivity to be set, either explicitly or within the training process. The Receiver Operating Characteristic (ROC) curve characterizes the performance of a detector as its sensitivity is varied from zero recall (in this case, no input is labeled as open set) to complete recall (all inputs labeled as open set).

Computing the area under the ROC curve (AUC) provides a calibration-free measure of detection performance, ranging from situations where open set classes are rare to situations in which the majority of input belong to unknown classes. To compute the ROC curve given a trained open set classifier, we vary a threshold $\theta \in [0, 1]$ which is compared to the predicted probability of the open set class $P(y_{K+1} | x) > \theta$ for each input image x.

5.3 Experiments

Open Set Classification. In the Open Set Classification experiment, each dataset is partitioned at random into 6 known and 4 unknown classes. We perform the open set classification experiment with the CIFAR, SVHN, and MNIST datasets, repeated over 5 runs with classes assigned at random to the known or unknown set.

Table 1. Open set classification: area under the ROC curve. Mean and standard deviation of the ROC AUC metric for selected datasets. Results averaged over 5 random partitions of known/open set classes. For all runs, $K=6$ and $M=10$.

Table 2. Closed set accuracy. Classification accuracy among $K=6$ known classes for the open set classifier trained on each dataset. Because softmax thresholding and OpenMax use the same network, classification results are identical.

Extended Open Set Classification. Following [9], we define the openness of a problem based on the number of training and test classes:

$$\begin{aligned} \textit{openness} = 1 - \sqrt{ \frac{K}{M} } \end{aligned}$$

(5)

The previous experiments test the effectiveness of the method where $K=6$ and $M=10$, so the openness score is fixed to $1 - \sqrt{\frac{6}{10}}$. To test the method in a range of greater openness scores, we perform additional experiments using the CIFAR10, CIFAR100, and TinyImagenet datasets.

We train on CIFAR10 as described previously with $K=4$ known classes. At test time, in place of the remaining classes of CIFAR10 we draw 10 unknown classes at random from the more diverse CIFAR100 dataset. To avoid overlap between known and unknown classes, known classes are selected only from non-animal categories and unknown classes are selected from animal categories. The AUC metric for the resulting open set task is reported as CIFAR+10. This experiment is repeated drawing 50 classes from CIFAR100 (CIFAR+50). Finally for the larger TinyImagenet dataset we train with $K=20$ known classes, and test on the full $M=200$ set. Results reported for all methods are averaged among 5 separate samples of known/unknown classes.

Table 3. Extended open set classification: area under the ROC curve. Known vs. unknown class detection for selected datasets. Results averaged over 5 random class partitions.

5.4 Technical Details of Compared Approaches

Our Approach. We begin by training an ordinary K-class classifier $C_K$ with cross-entropy loss on the labeled dataset. Simultaneously, we train the generative model consisting of encoder, generator, and discriminator on the labeled data, following the combined loss described in Sect. 4.

Once the classifier and generative model is fully trained, we apply the counterfactual image generation process. Beginning with encoded training set examples, the counterfactual image generation process finds points in the latent space of the generative model that decode to effective open set examples. For all experiments listed we generate 6400 example images. The original labeled dataset is augmented with the set of all generated images, and all generated images are labeled as open set examples. We initialize the new open-set classifier $C_{K+1}$ with the weights of the baseline $C_K$ classifier.

After training, we use the $C_{K+1}$ classifier directly: unlike the OpenMax methods we do not perform additional outlier detection. For the open set detection task however, we further improve discrimination between known and unknown classes by including a measure of known class certainty. Given an output $P(y_i | x)$ for $i \in [1 ... K+1]$ we recalibrate the probability of open set inclusion as

$$\begin{aligned} P^* = P(y_{K+1}|x) - \max _{i \le K} P(y_{i}|x) \end{aligned}$$

(6)

This modified value $P^*$ is used for evaluation of the AUC metric (Table 3).

Softmax Threshold. We compare our open-set classification approach to a standard confidence-based method for the detection of unknown classes without dataset augmentation. In this method, a classifier network $C_K$ is trained only on known classes and for each input x provides a class prediction P(y|x) for the set of known classes y. For the purpose of open set detection, input images x such that $\max C_K(x) < \theta$ are detected as open set examples.

OpenMax. We implement the Weibull distribution fitting method from [5]. This approach augments the baseline classifier $C_K$ with a new OpenMax layer replacing the softmax at the final layer of the network. First, the baseline network is applied to all inputs in the training set, and a mean activation vector is computed for each class based on the output of the penultimate network layer for all correctly classified examples. Given a mean activation vector for each class $j \in [1 ... K]$, a Weibull distribution with values $(\tau _j, \kappa _j, \lambda _j)$ is fit to the distance from the mean of the set of a number $\eta$ of outlier examples of class j. We perform a grid search for values of $\eta$ used in the FitHigh function, and we find that $\eta =20$ maximizes the AUC metric.

After fitting Weibull distributions for each class, we replace the softmax layer of the baseline classifier with the a new OpenMax layer. The output of the OpenMax layer is a distribution among $K+1$ classes, formed by recalibrating the input logits based on the cumulative distribution function of the Weibull distribution of distance from the mean of activation vectors, such that extreme outliers beyond a certain distance from any class mean are unlikely to be classified as that class.

We make one adjustment to the method as described in [5] to improve performance on the selected datasets. We find that in datasets with a small number of classes (fewer than 1000) the calibration of OpenMax scores using a selected number of top classes $\alpha$ is not required, and we can replace the $\frac{\alpha - i}{\alpha }$ term with a constant 1.

Generative OpenMax. The closest work to ours is the Generative OpenMax method from [7], which uses a conditional GAN that is no longer state-of-the-art. In order to provide a fair comparison with our method, we implemented a variant of Generative OpenMax using our encoder-decoder network instead of a conditional GAN.

Specifically, given the trained GAN and known-class classifier $C_K$, we select random pairs $(x_1, x_2)$ of training examples and encode them into the latent space. We interpolate between the two examples in the latent space as in [7] and apply the generator to the resulting latent point to generate the image:

$$ x_{\text {int}} = G(\theta E(x_1) + (1 - \theta ) E(x_2) ) $$

where $\theta \in [0, 1]$ is drawn from a uniform distribution.

Once the images are generated, we then apply a sample selection process similar to that of [7] to identify a subset of the generated samples to include as open set examples. In particular, we use confidence thresholding – that is, generated examples for which $C_K$’s prediction confidence is less than a fixed threshold $\max _i P(y_i|x_{\text {int}}) < \phi$ are selected for use as open set examples. In all experiments we set $\phi =0.5$.

Once the requisite number of synthetic open set examples have been generated, a new $C_{K+1}$ classifier is trained using the dataset augmented with the generated examples. For all experiments we generate 6,400 synthetic example images. At test time, the Weibull distributions of the OpenMax layer are fit to the penultimate layer activations of $C_{K+1}$ and the OpenMax Weibull calibration process is performed. We report scores for this variant of Generative OpenMax as $\mathbf G-OpenMax ^*$.

5.5 Results

In Table 1, we present the open set detection performance of different approaches on three datasets as measured by the area under the ROC curves. The closed set accuracies are provided in Table 2. From the results we can see that classifiers trained using our method achieve better open set detection performance compared to the baselines and do not lose any accuracy when classifying among known classes.

It is interesting to note that all approaches perform most accurately on the MNIST digit dataset, followed closely by SVHN, with the natural image data of CIFAR and TinyImagenet trailing far behind, indicating that natural images are significantly more challenging for all approaches.

Note in Table 1, our version of the Generative OpenMax outperforms OpenMax on the more constrained digit datasets, but not in the CIFAR image dataset, which includes a wider range of natural image classes that may not be as easily separable as digits. This fits with the intuition given in [7] that generating latent space combinations of digit classes is likely to result in images close to real, but unknown digits. It is possible that combining the features of images of large deformable objects like animals is not as likely to result in realistic classes. However, using the counterfactual optimization, we find that we are able to generate examples that improve open set detection performance without hurting known class classification accuracy.

Fig. 4.

Receiver operating curve plots for open set detection for the SVHN and CIFAR datasets, for $K=6$.

In Fig. 4, we plot the ROC curves for the SVHN and CIFAR datasets. We see that the curve of our method generally lies close to or above all other curves, suggesting a better performance across different sensitivity levels. In contrast, Generative OpenMax performed reasonably well for low false positive rate ranges, but became worse than the non-generative baselines when the false positive rates are high.

6 Conclusions

In this paper we introduce a new method for open set recognition, which uses a generative model to synthesize examples that closely resemble images of known classes but likely belong to the open set.

Our work uses an encoder-decoder model trained with adversarial loss to learn a flexible latent space representation for images. We introduce counterfactual image generation, a technique which we apply to this latent space, which morphs any given real image into a synthetic one that is realistic looking but is classified as an alternative class. We apply counterfactual image generation to the trained GAN model to generate open set training examples, which are used to adapt a classifier to the open set recognition task. On low-resolution image datasets, our approach outperforms previous ones both in the task of detecting known vs. unknown classes and in classification among known classes.

For future work, we are interested in investigating how to best select initial seed examples for generating counterfactual open set images. We will also consider applying counterfactual image generation to data other than still images and increasing the size and resolution of the generative model.