Abstract
In (STOC, 2008), Gentry, Peikert, and Vaikuntanathan proposed the first identity-based encryption (GPV-IBE) scheme based on a post-quantum assumption, namely, the learning with errors (LWE) assumption. Since their proof was only made in the random oracle model (ROM) instead of the quantum random oracle model (QROM), it remained unclear whether the scheme was truly post-quantum or not. In (CRYPTO, 2012), Zhandry developed new techniques to be used in the QROM and proved security of GPV-IBE in the QROM, hence answering in the affirmative that GPV-IBE is indeed post-quantum. However, since the general technique developed by Zhandry incurred a large reduction loss, there was a wide gap between the concrete efficiency and security level provided by GPV-IBE in the ROM and QROM. Furthermore, regardless of being in the ROM or QROM, GPV-IBE is not known to have a tight reduction in the multi-challenge setting. Considering that in the real-world an adversary can obtain many ciphertexts, it is desirable to have a security proof that does not degrade with the number of challenge ciphertext.
In this paper, we provide a much tighter proof for the GPV-IBE in the QROM in the single-challenge setting. In addition, we also show that a slight variant of the GPV-IBE has an almost tight reduction in the multi-challenge setting both in the ROM and QROM, where the reduction loss is independent of the number of challenge ciphertext. Our proof departs from the traditional partitioning technique and resembles the approach used in the public key encryption scheme of Cramer and Shoup (CRYPTO, 1998). Our proof strategy allows the reduction algorithm to program the random oracle the same way for all identities and naturally fits the QROM setting where an adversary may query a superposition of all identities in one random oracle query. Notably, our proofs are much simpler than the one by Zhandry and conceptually much easier to follow for cryptographers not familiar with quantum computation. Although at a high level, the techniques used for the single and multi-challenge setting are similar, the technical details are quite different. For the multi-challenge setting, we rely on the Katz-Wang technique (CCS, 2003) to overcome some obstacles regarding the leftover hash lemma.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Identity-Based Encryption
- Quantum random oracle models
- LWE assumption
- Tight security reduction
- Multi-challenge security
1 Introduction
1.1 Background
Shor [Sho94] in his breakthrough result showed that if a quantum computer is realized, then almost all cryptosystems used in the real world will be broken. Since then, a significant amount of studies have been done in the area of post-quantum cryptography, whose motivation is constructing cryptosystems secure against quantum adversaries. Recently in 2016, the National Institute of Standards and Technology (NIST) initiated the Post-Quantum Cryptography Standardization, and since then post-quantum cryptography has been gathering increasingly more attention.
Random Oracles in Quantum World. In general, security proofs of practical cryptographic schemes are given in the random oracle model (ROM) [BR93], which is an idealized model where a hash function is modeled as a publicly accessible oracle that computes a random function. Boneh et al. [BDF+11] pointed out that the ROM as in the classical setting is not reasonable when considering security against quantum adversaries, since quantum adversaries may compute hash functions over quantum superpositions of many inputs. Considering this fact, as a reasonable model against quantum adversaries, they proposed a new model called the quantum random oracle model (QROM), where a hash function is modeled as a quantumly accessible random oracle. As discussed in [BDF+11], many commonly-used proof techniques in the ROM do not work in the QROM. Therefore even if we have a security proof in the ROM, we often require new techniques to obtain similar results in the QROM.
Identity-Based Encryption in QROM. Identity-Based Encryption (IBE) is a generalization of a public key encryption scheme where the public key of a user can be any arbitrary string such as an e-mail address. The first IBE scheme based on a post-quantum assumption is the one proposed by Gentry et al. (GPV-IBE) [GPV08], which is based on the learning with errors (LWE) assumption [Reg05]. To this date, GPV-IBE is still arguably the most efficient IBE scheme that is based on a hardness assumption that resists quantum attacks. However, since their original security proof was made in the ROM instead of the QROM, it was unclear if we could say the scheme is truly post-quantum. Zhandry [Zha12b] answered this in the affirmative by proving that the GPV-IBE is indeed secure in the QROM under the LWE assumption, hence truly post-quantum, by developing new techniques in the QROM.
Tight Security of GPV-IBE. However, if we consider the tightness of the reduction, the security proof of the GPV-IBE by Zhandry [Zha12b] does not provide a satisfactory security. Specifically, GPV-IBE may be efficient in the ROM, but it is no longer efficient in the QROM. In general, a cryptographic scheme is said to be tightly secure under some assumption if breaking the security of the scheme is as hard as solving the assumption. More precisely, suppose that we proved that if there exists an adversary breaking the security of the scheme with advantage \(\epsilon \) and running time T, we can break the underlying assumption with advantage \(\epsilon '\) and running time \(T'\). We say that the scheme is tightly-secure if we have \(\epsilon '/T'\approx \epsilon /T\). By using this notation, Zhandry gave a reduction from the security of GPV-IBE to the LWE assumption with \(\epsilon '\approx \epsilon ^2/(Q_\mathsf {H}+Q_{\mathsf {ID}})^4\) and \(T'\approx T+(Q_\mathsf {H}+Q_{\mathsf {ID}})^2 \cdot \mathsf {poly}(\lambda )\) where \(Q_\mathsf {H}\) denotes the number of hash queries, \(Q_{\mathsf {ID}}\) denotes the number of secret key queries, \(\lambda \) denotes the security parameter, and \(\mathsf {poly}\) denotes some fixed polynomial. Though the reduction is theoretically interesting, the meaning of the resulting security bound in a realistic setting is unclear. For example, if we want to obtain 128-bit security for the resulting IBE, and say we had \(\epsilon =2^{-128}\), \(Q_\mathsf {H}=2^{100}\), \(Q_{\mathsf {ID}}=2^{20}\), then even if we ignore the blowup for the running time, we would have to start from at least a 656-bit secure LWE assumption, which incurs a significant blowup of the parameters. Indeed, Zhandry left it as an open problem to give a tighter reduction for the GPV-IBE.
Multi-challenge Tightness. The standard security notion of IBE considers the setting where an adversary obtains only one challenge ciphertext. This is because security against adversaries obtaining many challenge ciphertexts can be reduced to the security in the above simplified setting. However, as pointed out by Hofheinz and Jager [HJ12], tightness is not preserved in the above reduction since the security degrades by the number of ciphertexts. Therefore tightly secure IBE in the single-challenge setting does not imply tightly secure IBE in the multi-challenge setting. On the other hand, in the real world, it is natural to assume that an adversary obtains many ciphertexts, and thus tight security in the multi-challenge setting is desirable. However, there is no known security proof for the GPV-IBE or its variant that does not degrade with the number of challenge ciphertexts even in the classical setting.
1.2 Our Contribution
We provide much tighter security proofs for the GPV-IBE in the QROM in the single-challenge setting. Furthermore, we provide a multi-challenge tight variant of GPV-IBE that is secure both in the ROM and QROM. In the following, we describe the tightness of our security proofs by using the same notation as in the previous section.
-
In the single-challenge setting, we give a reduction from the security of GPV-IBE to the LWE assumption with \(\epsilon '\approx \epsilon \) and \(T'= T+(Q_\mathsf {H}+Q_{\mathsf {ID}})^2 \cdot \mathsf {poly}(\lambda )\). If we additionally assume quantumly secure pseudorandom functions (PRFs), then we further obtain a tighter reduction, which gives \(\epsilon '\approx \epsilon \) and \(T'=T+(Q_\mathsf {H}+Q_{\mathsf {ID}}) \cdot \mathsf {poly}(\lambda )\). This is the first security proof for GPV-IBE whose security bound does not degrade with \(Q_{\mathsf {H}}\) or \(Q_{\mathsf {ID}}\) even in the classical setting. We note that the same security bound can be achieved without assuming PRFs in the classical ROM.
-
We give a slight variant of GPV-IBE scheme whose multi-challenge security is reduced to the LWE assumption with \(\epsilon '=\epsilon /\mathsf {poly}(\lambda )\) and \(T'\approx T+(Q_\mathsf {H}+Q_{\mathsf {ID}}+Q_{\mathsf {ch}})^2 \cdot \mathsf {poly}(\lambda )\) where \(Q_{\mathsf {ch}}\) denotes the number of challenge queries. If we additionally assume quantumly secure PRFs, then we further obtain a tighter reduction. Namely, \(\epsilon '\) is the same as the above, and \(T'=T+(Q_\mathsf {H}+Q_{\mathsf {ID}}+Q_{\mathsf {ch}}) \cdot \mathsf {poly}(\lambda )\). This is the first variant of the GPV-IBE scheme whose security bound does not degrade with \(Q_\mathsf {ch}\) even in the classical setting. We note that the same security bound can be achieved without assuming PRFs in the classical ROM.
Moreover, our security proofs are much simpler than the one by Zhandry [Zha12b]. In his work, he introduced new techniques regarding indistinguishability of oracles against quantum adversaries. Though his techniques are general and also useful in other settings (e.g., [Zha12a]), it involves some arguments on quantum computation, and they are hard to follow for cryptographers who are not familiar with quantum computation. On the other hand, our proofs involve a minimal amount of discussions about quantum computation, and our proofs are done almost similar to the counterparts in the classical ROM.
1.3 Technical Overview
GPV-IBE. First, we briefly describe the GPV-IBE [GPV08], which is the main target of this paper. A master public key is a matrix \(\mathbf {A}\in \mathbb {Z}_q^{n\,\times \,m}\) and a master secret key is its trapdoor \(\mathbf {T}_{\mathbf {A}}\in \mathbb {Z}^{m\,\times \,m}\), which enables one to compute a short vector \(\mathbf {e}\in \mathbb {Z}_q^m\) such that \(\mathbf {A}\mathbf {e}= \mathbf {u}\) given an arbitrary vector \(\mathbf {u}\in \mathbb {Z}_q^n\). A private key \(\mathsf {sk}_{\mathsf {ID}}\) for an identity \(\mathsf {ID}\in \mathcal {ID}\) is a short vector \(\mathbf {e}\in \mathbb {Z}_q^m\) such that \(\mathbf {A}\mathbf {e}= \mathbf {u}_{\mathsf {ID}}\) where \(\mathbf {u}_{\mathsf {ID}}=\mathsf {H}(\mathsf {ID})\) for a hash function \(\mathsf {H}:\mathcal {ID}\rightarrow \mathbb {Z}_q^n\), which is modeled as a random oracle. A ciphertext for a message \(\mathsf {M}\in \{0,1\}\) consists of \(c_0 = \mathbf {u}_\mathsf {ID}^\top \mathbf {s}+ x + \mathsf {M}\lfloor q/2 \rceil \) and \(\mathbf {c}_1 = \mathbf {A}^\top \mathbf {s}+ \mathbf {x}\). Here \(\mathbf {s}\) is a uniformly random vector over \(\mathbb {Z}_q^n\) and \(x, \mathbf {x}\) are small “noise” terms where each entries are sampled from some specific Gaussian distribution \(\chi \). Decryption can be done by computing \(w = c_0 - \mathbf {c}_1^\top \mathbf {e}_\mathsf {ID}\in \mathbb {Z}_q\) and deciding if w is closer to 0 or to \(\lfloor q/2 \rceil \) modulo q.
Security Proof in Classical ROM. The above IBE relies its security on the LWE assumption, which informally states the following: given a uniformly random matrix \([\mathbf {A}| \mathbf {u}] \leftarrow \mathbb {Z}_q^{n\,\times \,(m + 1)}\) and some vector \(\mathbf {b}\in \mathbb {Z}_q^{m + 1}\), there is no PPT algorithm that can decide with non-negligible probability whether \(\mathbf {b}\) is of the form \([\mathbf {A}| \mathbf {u}]^\top \mathbf {s}+ \mathbf {x}'\) for some \(\mathbf {s}\leftarrow \mathbb {Z}_q^{n}\) and \(\mathbf {x}' \leftarrow \chi ^{m + 1}\), or a uniformly random vector over \(\mathbb {Z}_q^{m + 1}\), i.e., \(\mathbf {b}\leftarrow \mathbb {Z}_q^{m + 1}\). Below, we briefly recall the original security proof in the classical ROM given by Gentry et al. [GPV08] and see how the random oracle is used by the reduction algorithm. The proof relies on a key lemma which states that we can set \(\mathsf {H}(\mathsf {ID})\) and \(\mathbf {e}\) in the “reverse order” from the real scheme. That is, we can first sample \(\mathbf {e}\) from some distribution and program \(\mathsf {H}(\mathsf {ID}):=\mathbf {A}\mathbf {e}\) so that their distributions are close to uniformly random as in the real scheme. In the security proof, a reduction algorithm guesses \(i\in [Q]\) such that the adversary’s i-th hash query is the challenge identity \(\mathsf {ID}^*\) where Q denotes the number of hash queries made by the adversary. Then for all but the i-th hash query, the reduction algorithm programs \(\mathsf {H}(\mathsf {ID})\) in the above manner, and for the i-th query, it programs the output of \(\mathsf {H}(\mathsf {ID}^*)\) to be the vector \(\mathbf {u}\) contained in the LWE instance that is given as the challenge. Specifically, the reduction algorithm sets the challenge user’s identity vector \(\mathbf {u}_{\mathsf {ID}^*}\) as the random vector \(\mathbf {u}\) contained in the LWE instance. If the guess is correct, then it can embed the LWE instance into the challenge ciphertexts \(c_0^*\) and \(\mathbf {c}_1^*\); in case it is a valid LWE instance, then \((c_0^*, \mathbf {c}_1^*)\) is properly set to \((\mathbf {u}_{\mathsf {ID}^*}^\top \mathbf {s}+ x + \mathsf {M}\lfloor q/2 \rceil , \mathbf {A}^\top \mathbf {s}+ \mathbf {x})\) as in the real scheme. Therefore, the challenge ciphertext can be switched to random due to the LWE assumption. After this switch, \(\mathsf {M}\) is perfectly hidden and thus the security of GPV-IBE is reduced to the LWE assumption. Since the reduction algorithm programs the random oracle in the same way except for the challenge identity, this type of proof methodology is often times referred to as the “all-but-one programming”.
Security Proof in QROM in [Zha12b]. Unfortunately, the above proof cannot be simply extended to a proof in the QROM. The reason is that in the QROM, even a single hash query can be a superposition of all the identities. In such a case, to proceed with the above all-but-one programming approach, the reduction algorithm would have to guess a single identity out of all the possible identities which he hopes that would be used as the challenge identity \(\mathsf {ID}^*\) by the adversary. Obviously, the probability of the reduction algorithm being right is negligible, since the number of possible identities is exponentially large. This is in sharp contrast with the ROM setting, where the reduction algorithm was allowed to guess the single identity out of the polynomially many (classical) random oracle queries made by the adversary. Therefore, the all-but-one programming as in the classical case cannot be used in the quantum case. To overcome this barrier, Zhandry [Zha12b] introduced a useful lemma regarding what he calls the semi-constant distribution. The semi-constant distribution with parameter \(0<p<1\) is a distribution over functions from \(\mathcal {X}\) to \(\mathcal {Y}\) such that a function chosen according to the distribution gives the same fixed value for random p-fraction of all inputs, and behaves as a random function for the rest of the inputs. He proved that a function according to the semi-constant distribution with parameter p and a random function cannot be distinguished by an adversary that makes Q oracle queries with advantage greater than \(\frac{8}{3}Q^4p^2\). In the security proof, the reduction algorithm partitions the set of identities into controlled and uncontrolled sets. The uncontrolled set consists of randomly chosen p-fraction of all identities, and the controlled set is the complement of it. The reduction algorithm embeds an LWE instance into the uncontrolled set, and programs the hash values for the controlled set so that the decryption keys for identities in the controlled set can be extracted efficiently. Then the reduction algorithm works as long as the challenge identity falls inside the uncontrolled set and all identities for secret key queries fall inside the controlled set (otherwise it aborts). By appropriately setting p, we can argue that the probability that the reduction algorithm does not abort is non-negligible, and thus the security proof is completed. Though this technique is very general and useful, a huge reduction loss is inherent as long as we take the above strategy because the reduction algorithm has to abort with high probability. It may be useful to point out for readers who are familiar with IBE schemes in the standard model that the above technique is conceptually very similar to the partitioning technique which is often used in the context of adaptively secure IBE scheme in the standard model [Wat05, ABB10, CHKP10]. The reason why we cannot make the proof tight is exactly the same as that for the counterparts in the standard model.
Our Tight Security Proof in QROM. As discussed above, we cannot obtain a tight reduction as long as we use a partitioning-like technique. Therefore we take a completely different approach, which is rather similar to that used in the public key encryption scheme of Cramer and Shoup [CS98], which has also been applied to the pairing-based IBE construction of Gentry [Gen06]. The idea is that we simulate in a way so that we can create exactly one valid secret key for every identity. Note that this is opposed to the partitioning technique (and the all-but-one programming technique) where the simulator cannot create a secret key for an identity in the uncontrolled set. To create the challenge ciphertext, we use the one secret key we know for that challenge identity. If the adversary can not tell which secret key the ciphertext was created from and if there are potentially many candidates for the secret key, we can take advantage of the entropy of the secret key to statistically hide the message.
In more detail, the main observation is that the secret key \(\mathrm{\mathbf{e}}\), i.e. a short vector \(\mathrm{\mathbf{e}}\) such that \(\mathrm{\mathbf{Ae}} = \mathrm{\mathbf{u}}\), retains plenty of entropy even after fixing the public values \(\mathrm{\mathbf{A}}\) and \(\mathrm{\mathbf{u}}\). Therefore, by programming the hash value \(\mathrm{\mathbf{u}}\) of an identity, we can easily create a situation where the simulator knows exactly one secret key out of the many possible candidates. Furthermore, the simulator knowing a secret key \(\mathrm{\mathbf{e}}_{\mathsf {ID}^*}\) such that \(\mathrm{\mathbf{Ae_{\mathsf {ID}^*}}} = \mathrm{\mathbf{u}}_{\mathsf {ID}^*}\), can simulate the challenge ciphertext by creating \(c_0^* = \mathbf {e}_{\mathsf {ID}^*}^\top \mathbf {c}_1^* + \mathsf {M}\lfloor q/2 \rceil \) and \(\mathbf {c}_1^* = \mathbf {A}^\top \mathbf {s}+ \mathbf {x}\). Here, the key observation is that we no longer require the LWE instance \((\mathbf {u}_{\mathsf {ID}^*}, \mathbf {u}_{\mathsf {ID}^*}^\top \mathbf {s}+ x)\) to simulate the challenge ciphertext. Though the distribution of \(c_0^*\) simulated as above is slightly different from that of the real ciphertext due to the difference in the noise distributions, we ignore it in this overview. In the real proof, we overcome this problem by using the noise rerandomization technique by Katsumata and Yamada [KY16]. Then we use the LWE assumption to switch \(\mathbf {c}_1^*\) to random. Finally, we argue that \(\mathbf {e}_{\mathsf {ID}^*}^\top \mathbf {c}_1^*\) is almost uniform if the min-entropy of \(\mathbf {e}_{\mathsf {ID}^*}\) is high and \(\mathbf {c}_1^*\) is uniformly random due to the leftover hash lemma. Therefore, all information of the message \(\mathsf {M}\) is hidden and thus the proof is completed.
Finally, we observe that the above proof naturally fits in the QROM setting. The crucial difference from the partitioning technique is that in our security proof we program the random oracle in the same way for all identities. Therefore even if an adversary queries a superposition of all identities, the simulator can simply quantumly perform the programming procedure for the superposition. Thus the proof in the classical ROM can be almost automatically converted into the one in the QROM in this case.
Tight Security in Multi-challenge Setting. Unfortunately, the above idea does not extend naturally to the tightly-secure multi-challenge setting. One can always prove security in the multi-challenge setting starting from a scheme that is single-challenge secure via a hybrid argument, however, as mentioned by Hofheinz and Jager [HJ12], this type of reduction does not preserve tightness. A careful reader may think that the above programming technique can be extended to the multi-challenge setting, hence bypassing the hybrid argument. We briefly explain why this is not the case. Informally, in the above proof, the reduction algorithm embeds its given LWE instance \((\mathbf {A}, \mathbf {A}^\top \mathbf {s}+ \mathbf {x})\) into the challenge ciphertext by creating \((c_0^* = \mathbf {e}_{\mathsf {ID}^*}^\top \mathbf {c}_1^* + \mathsf {M}\lfloor q/2 \rceil , \mathbf {c}_1^* = \mathbf {A}^\top \mathbf {s}+ \mathbf {x})\), where \(\mathbf {e}_{\mathsf {ID}^*}\) is the secret key of the challenge user \(\mathbf {u}_{\mathsf {ID}^*}\). Therefore, since the \(\mathbf {c}_1^*\) component of every ciphertext is an LWE instance for the same public matrix \(\mathbf {A}\), to simulate multiple challenge ciphertexts in the above manner, the reduction algorithm must be able to prepare a special type of LWE instance \((\mathbf {A}, \{ \mathbf {A}^\top \mathbf {s}^{(k)} + \mathbf {x}^{(k)} \}_{k \in [N]})\), where \(N = \mathsf {poly}(\lambda )\) is the number of challenge ciphertext queried by the adversary. It can be easily seen that this construction is tightly-secure in the multi-challenge setting with the same efficiency as the single-challenge setting, if we assume that this special type of LWE problem is provided to the reduction algorithm as the challenge. However, unfortunately, we still end up losing a factor of N in the reduction when reducing the standard LWE problem to this special LWE problem. In particular, we only shifted the burden of having to go through the N hybrid arguments to the assumption rather than to the scheme. As one may have noticed, there is a way to bypass the problem of going through the N hybrid arguments by using conventional techniques (See [Reg05, Reg10]) of constructing an unlimited number of fresh LWE instances given a fixed number of LWE instances. However, this techniques requires the noise of the newly created LWE instances to grow proportionally to the number of created instances. In particular, to create the above special LWE instance from a standard LWE instance, we require the size of the noise \(\mathbf {x}^{(k)}\) to grow polynomially with N, where recall that N can be an arbitrary polynomial. Hence, although we can show a tightly secure reduction in the multi-challenge setting, for the concrete parameters of the scheme to be independent of N, we need to assume the super-polynomial LWE assumption to cope with the super-polynomial noise blow up. This is far more inefficient than in the single-challenge setting where we only require a polynomial LWE assumption.
To overcome this problem, we use the “lossy mode” of the LWE problem. It is well known that the secret vector \(\mathbf {s}\) is uniquely defined given an LWE instance \((\mathbf {A}, \mathbf {A}^\top \mathbf {s}+ \mathbf {x})\) for large enough samples. A series of works, e.g., [GKPV10, BKPW12, AKPW13, LSSS17] have observed that if we instead sample \(\mathbf {A}\) from a special distribution that is computationally indistinguishable from the uniform distribution, then \((\mathbf {A}, \mathbf {A}^\top \mathbf {s}+ \mathbf {x})\) leaks almost no information of the secret \(\mathbf {s}\), hence the term “lossy mode”. This idea can be leveraged to prove (almost) tight security of the above single-challenge construction, where the reduction loss is independent of the number of challenge ciphertext. A first attempt of using this idea is as follows: During the security proof of the GPV-IBE, we first change the public matrix \(\mathbf {A}\) to a lossy matrix \(\tilde{\mathbf {A}}\) and generate the secret keys and program the random oracle in the same way as before. To create the challenge ciphertexts, the reduction algorithm honestly samples \(\mathbf {s}^{(k)}\), \(x^{(k)}\), \(\mathbf {x}^{(k)}\) and sets \((c_0^* = \mathbf {u}_{\mathsf {ID}^*}^\top \mathbf {s}^{(k)} + x^{(k)} + \mathsf {M}^{(k)} \lfloor q/2 \rceil , \mathbf {c}_1^* = \mathbf {A}^\top \mathbf {s}^{(k)} + \mathbf {x}^{(k)})\). Now, it may seem that owing to the lossy mode of LWE, we can rely on the entropy of the secret vector \(\mathbf {s}^{(k)}\) to argue that \(c_0^*\) is distributed uniformly random via the leftover hash lemma. The main difference between the previous single-challenge setting is that we can rely on the entropy of the secret vector \(\mathbf {s}^{(k)}\) rather than on the entropy of the secret key \(\mathbf {e}_{\mathsf {ID}^*}\). Since each challenge ciphertext is injected with fresh entropy and we can argue statistically that a single challenge ciphertext is not leaking any information on the message, the reduction loss will be independent of the number of challenge ciphertext query N.
Although the above argument may seem correct at first glance, it incurs a subtle but a fatal flaw, thus bringing us to our proposed construction. The problem of the above argument is how we use the leftover hash lemma. To use the lemma correctly, the vector \(\mathbf {u}_{\mathsf {ID}^*}\) viewed as a hash function is required to be universal. This is true in case \(\mathbf {u}_{\mathsf {ID}^*}\) is set as \(\mathbf {A}\mathbf {e}_{\mathsf {ID}^*}\), where \(\mathbf {A}\leftarrow \mathbb {Z}_q^{n\,\times \,m}\) and \(\mathbf {e}_{\mathsf {ID}^*}\) is sampled from some appropriate distribution. However, this is not true anymore once we change \(\mathbf {A}\) to a lossy matrix \(\tilde{\mathbf {A}}\), since \(\tilde{\mathbf {A}}\) now lives in an exponentially small subset of \(\mathbb {Z}_q^{n\,\times \,m}\), hence, we can no longer rely on the entropy of \(\mathbf {s}^{(k)}\) to statistically hide the message. To overcome this problem, our final idea is to use the Katz-Wang [KW03] technique. Specifically, we slightly alter the encryption algorithm of GPV-IBE to output the following instead:
where \(\mathbf {u}_{\mathsf {ID}|| b} = H(\mathsf {ID}|| b)\) for \(b \in \{ 0, 1 \}\). During the security proof, the reduction algorithm sets \(\mathbf {u}_{\mathsf {ID}|| 0}\) and \(\mathbf {u}_{\mathsf {ID}|| 1}\) so that one of them is uniformly random over \(\mathbb {Z}_q^n\) and the other is constructed as \(\mathbf {A}\mathbf {e}_{\mathsf {ID}}\). Then, for the ciphertext \(c_b\) corresponding to the uniformly random vector \( \mathbf {u}_{\mathsf {ID}|| b}\), we can correctly use the leftover hash lemma to argue that \(c_b\) statistically hides the message \(\mathsf {M}\). By going through one more hybrid argument, we can change both \(c_0, c_1\) into random values that are independent of the message \(\mathsf {M}\). Note that instead of naively using the Katz-Wang technique, by reusing the \(\mathbf {c}_2\) component, the above GPV-IBE variant only requires one additional element in \(\mathbb {Z}_q\) compared to the original GPV-IBE. Furthermore, in the actual construction, we do not require the noise terms \(x_0, x_1\) in \(c_0, c_1\) since we no longer rely on the LWE assumption to change \(c_0, c_1\) into random values. Our construction and security reduction does not depend on the number of challenge ciphertext query N and in particular, can be proven under the polynomial LWE assumption, which is only slightly worse than the single-challenge construction. In addition, due to the same reason as the single-challenge setting, our classical ROM proof can be naturally converted to a QROM proof.
1.4 Discussion
Similar Techniques in Other Works. The idea to simulate GPV-IBE in a way so that we can create exactly one valid secret key for every secret key query is not new. We are aware of few works that are based on this idea. Gentry et al. [GPV08] mentioned that by using this technique, they can prove the security of the GPV-IBE in the standard model based on a non-standard interactive variant of the LWE (I-LWE) assumption which requires a hash function to define. Here since the hash function is given to the adversary, a quantum adversary may query quantum states to the hash functions on its own. Therefore, in addition with the fact that the I-LWE assumption is made in the standard model, the statement made by [GPV08] would hold in the QROM as well. However, they only gave a sketch of the proof, and did not give a formal proof. Alwen et al. [ADN+10] use the idea to construct an identity-based hash proof system (IB-HPS) based on the mechanism of GPV-IBE. We note that they assume the modulus q to be super-polynomial. Outside the context of identity-based primitives, Applebaum et al. [ACPS09] and Bourse et al. [BDPMW16] provide an analysis of rerandomizing LWE samples which can be seen as a refinement of the idea mentioned in [GPV08]. [ACPS09] constructs a KDM-secure cryptosystem based on the LWE problem and [BDPMW16] shows a simple method for constructing circuit private fully homomorphic encryption schemes (FHE) based on the lattice-based FHE scheme of Gentry et al. [GSW13]. Both of their analysis only requires the modulus q to be polynomial. In summary, though similar ideas have been used, all of the previous works are irrelevant to tight security or the security in the QROM.
On Parameter-Tightness of Our Schemes. In the above overview, we focused on the tightness of the security proof. Here, we provide some discussions on how the parameters compare to the original GPV-IBE scheme [GPV08]. For the single challenge setting, our parameters are only a small factor worse than the GPV-IBE scheme. This is because the only difference is using the noise rerandomization technique of [KY16], which only slightly degrades the noise-level.Footnote 1 For the multi-challenge setting, the situation is more different. In this case, the parameters are much worse than the original (single-challenge secure) GPV-IBE scheme. This is because we have to go through the lossy-mode of LWE which requires for larger parameters. The concrete parameters are provided in Sect. 4.2.
Relation to CCA-Secure PKE. By applying the Canetti-Halevi-Katz transformation [CHK04] to our single-challenge-secure IBE scheme, we obtain a public key encryption (PKE) scheme secure against chosen ciphertext attacks (CCA) that is tightly secure in the single-challenge setting under the LWE assumption in the QROM. We note that Saito et al. [SXY18] already proposed such a PKE scheme in the single-challenge setting that is more efficient than the scheme obtained by the above transformation.
On Running Time of Reductions. In the above overview, we ignore the running time of reductions. Though it seems that the above described reductions run in nearly the same time as the adversaries, due to a subtle problem of simulating random oracles against quantum adversaries, there is a significant blowup by a square factor of the number of queries the adversaries make. In the classical ROM, when we simulate a random oracle in security proofs, we usually sample a random function in a lazy manner. That is, whenever an adversary queries a point that has not been queried before, a reduction algorithm samples a fresh randomness and assigns it as a hash value for that point. However, this cannot be done in the QROM because an adversary may query a superposition of all the inputs in a single query. Therefore a reduction algorithm has to somehow commit to the hash values of all inputs at the beginning of the simulation.
Zhandry [Zha12b] proved that an adversary that makes Q queries cannot distinguish a random function and a 2Q-wise independent hash function via quantum oracle accesses. Therefore we can use a 2Q-wise independent hash to simulate a random oracle. However, if we take this method, the simulator has to evaluate a 2Q-wise independent hash function for each hash query, and this is the reason why the running time blowups by \(\varOmega (Q^2)\).
One possible way to avoid this huge blowup is to simulate a random oracle by a PRF secure against quantum accessible adversaries. Since the time needed to evaluate a PRF is some fixed polynomial in the security parameter, the blowup for the running time can be made \(Q\cdot \mathsf {poly}(\lambda )\) which is significantly better than \(\varOmega (Q^2)\). However, in order to use this method, we have to additionally assume the existence of quantumly secure PRFs. Such PRFs can be constructed based on any quantumly-secure one-way function [Zha12a], and thus they exist if the LWE assumption holds against quantum adversaries. However, the reduction for such PRFs are non-tight and thus we cannot rely on them in the context of tight security. Our suggestion is to use a real hash function to implement PRFs and to assume that it is a quantumly secure PRF. We believe this to be a natural assumption if we are willing to idealize a hash function as a random oracle. (See also the discussion in Sect. 2.2.)
1.5 Related Work
Schemes in QROM. Boneh et al. [BDF+11] introduced the QROM, and gave security proofs for the GPV-signature [GPV08] and a hybrid variant of the Bellare-Rogaway encryption [BR93] in the QROM. We note that their security proof for the GPV-signature is tight. Zhandry [Zha12b] proved that GPV-IBE and full-domain hash signatures are secure in the QROM. Targhi and Unruh [TU16] proposed variants of Fujisaki-Okamoto transformation and OAEP that are secure in the QROM. Some researchers studied the security of the Fiat-Shamir transform in the QROM [ARU14, Unr15, Unr17]. Unruh [Unr14b] proposed a revocable quantum timed-release encryption scheme in the QROM. Unruh [Unr14a] proposed a position verification scheme in the QROM. Recently, some researchers studied tight securities in the QROM. Alkim et al. [ABB+17] proved that the signature scheme known as TESLA [BG14] is tightly secure under the LWE assumption. Saito et al. [SXY18] proposed a tightly CCA secure variant of the Bellare-Rogaway encryption. Kiltz et al. [KLS18] gave a tight reduction for the Fiat-Shamir transform in the QROM.
Tightly Secure IBEs. The first tightly secure IBE scheme from lattices in the single challenge setting and in the standard model was proposed by Boyen and Li [BL16]. While the construction is theoretically interesting and elegant, it is very inefficient and requires LWE assumption with super-polynomial approximation factors. As for the construction from bilinear maps, the first tightly secure IBE from standard assumptions in the single challenge setting and in the random oracle model was proposed by Katz and Wang [KW03]. Coron [Cor09] gave a tight reduction for a variant of the original Boneh-Franklin IBE [BF01]. Later, the first realization in the standard model was proposed by Chen and Wee [CW13]. In the subsequent works, it is further extended to the multi-challenge setting [HKS15, AHY15, GDCC16]. They are efficient but are not secure against quantum computers.
2 Preliminaries
Notations. For \(n \in \mathbb {N}\), denote [n] as the set \(\{ 1, \cdots , n \}\). For a finite set S, we let U(S) denote the uniform distribution over S. For a distribution D and integer \(k > 0\), define \((D)^k\) as the distribution \(\prod _{i \in [k]} D\). For a distribution or random variable X we write \(x \leftarrow X\) to denote the operation of sampling a random x according to X. For a set S, we write \(s \leftarrow S\) as a shorthand for \(s \leftarrow U(S)\). Let X and Y be two random variables over some finite set \(S_X, S_Y\), respectively. The statistical distance \(\varDelta (X, Y)\) between X and Y is defined as \(\varDelta (X, Y) = \frac{1}{2} \varSigma _{s \in S_X \cup S_Y} \left| \Pr [X = s] - \Pr [Y = s] \right| \). The min-entropy of a random variable X is defined as \(\mathbf {H}_\infty (X) = -\log (\max _{x} \Pr [X = x])\), where the base of the logarithm is taken to be 2 throughout the paper. For a bit \(b\in \{0,1\}\), \(\bar{b}\) denotes \(1-b\). For sets \(\mathcal X\) and \(\mathcal Y\), \(\mathsf {Func}(\mathcal X,\mathcal Y)\) denotes the set of all functions from \(\mathcal X\) to \(\mathcal Y\). For a vector \(\mathbf {v}\in \mathbb {R}^n\), denote \(||\mathbf {v} ||\) as the standard Euclidean norm. For a matrix \(\mathbf {R}\in \mathbb {R}^{n\,\times \,n}\), denote \(||\mathbf {R} ||\) as the length of the longest column and  as the longest column of the Gram-Schmidt orthogonalization of \(\mathbf {R}\).
as the longest column of the Gram-Schmidt orthogonalization of \(\mathbf {R}\).
2.1 Quantum Computation
We briefly give some backgrounds on quantum computation. We refer to [NC00] for more details. A state  of n qubits is expressed as
of n qubits is expressed as  where \(\{ \alpha _x \}_{x\in \{0,1\}^n}\) is a set of complex numbers such that \(\sum _{x\in \{0,1\}^n}|\alpha _x|^2=1\) and
where \(\{ \alpha _x \}_{x\in \{0,1\}^n}\) is a set of complex numbers such that \(\sum _{x\in \{0,1\}^n}|\alpha _x|^2=1\) and  is an orthonormal basis on \(\mathbb {C}^{2^n}\) (which is called a computational basis). If we measure
is an orthonormal basis on \(\mathbb {C}^{2^n}\) (which is called a computational basis). If we measure  in the computational basis, then the outcome is a classical bit string \(x\in \{0,1\}^n\) with probability \(|\alpha _x|^2\), and the state becomes
in the computational basis, then the outcome is a classical bit string \(x\in \{0,1\}^n\) with probability \(|\alpha _x|^2\), and the state becomes  . An evolution of quantum state can be described by a unitary matrix U, which transforms
. An evolution of quantum state can be described by a unitary matrix U, which transforms  to
to  . A quantum algorithm is composed of quantum evolutions described by unitary matrices and measurements. We also consider a quantum oracle algorithm, which can quantumly access to certain oracles. The running time \(\mathsf {Time}(\mathcal {A})\) of a quantum algorithm \(\mathcal {A}\) is defined to be the number of universal gates (e.g., Hadamard, phase, CNOT, and \(\pi /8\) gates) and measurements required for running \(\mathcal {A}\). (An oracle query is counted as a unit time if \(\mathcal {A}\) is an oracle algorithm.) Any efficient classical computation can be realized by a quantum computation efficiently. That is, for any function f that is classically computable, there exists a unitary matrix \(U_f\) such that
. A quantum algorithm is composed of quantum evolutions described by unitary matrices and measurements. We also consider a quantum oracle algorithm, which can quantumly access to certain oracles. The running time \(\mathsf {Time}(\mathcal {A})\) of a quantum algorithm \(\mathcal {A}\) is defined to be the number of universal gates (e.g., Hadamard, phase, CNOT, and \(\pi /8\) gates) and measurements required for running \(\mathcal {A}\). (An oracle query is counted as a unit time if \(\mathcal {A}\) is an oracle algorithm.) Any efficient classical computation can be realized by a quantum computation efficiently. That is, for any function f that is classically computable, there exists a unitary matrix \(U_f\) such that  , and the number of universal gates to express \(U_f\) is linear in the size of a classical circuit that computes f.
, and the number of universal gates to express \(U_f\) is linear in the size of a classical circuit that computes f.
Quantum Random Oracle Model. Boneh et al. [BDF+11] introduced the quantum random oracle model (QROM), which is an extension of the usual random oracle model to the quantum setting. Roughly speaking, the QROM is an idealized model where a hash function is idealized to be a quantumly accessible oracle that simulates a random function. More precisely, in security proofs in the QROM, a random function \(\mathsf {H}:\mathcal {X}\rightarrow \mathcal {Y}\) is uniformly chosen at the beginning of the experiment, and every entity involved in the system is allowed to access to an oracle that is given  and returns
and returns  . We denote a quantum algorithm \(\mathcal {A}\) that accesses to the oracle defined as above by
. We denote a quantum algorithm \(\mathcal {A}\) that accesses to the oracle defined as above by  . In the QROM, one query to the random oracle is counted as one unit time. As in the classical case, we can implement two random oracles \(\mathsf {H}_0\) and \(\mathsf {H}_1\) from one random oracle \(\mathsf {H}\) by defining \(\mathsf {H}_0(x)\mathrel {\mathop :}=\mathsf {H}(0||x)\) and \(\mathsf {H}_1(x)\mathrel {\mathop :}=\mathsf {H}(1||x)\). More generally, we can implement n random oracles from one random oracle by using \(\lfloor \log n \rfloor \)-bit prefix of an input as index of random oracles.
. In the QROM, one query to the random oracle is counted as one unit time. As in the classical case, we can implement two random oracles \(\mathsf {H}_0\) and \(\mathsf {H}_1\) from one random oracle \(\mathsf {H}\) by defining \(\mathsf {H}_0(x)\mathrel {\mathop :}=\mathsf {H}(0||x)\) and \(\mathsf {H}_1(x)\mathrel {\mathop :}=\mathsf {H}(1||x)\). More generally, we can implement n random oracles from one random oracle by using \(\lfloor \log n \rfloor \)-bit prefix of an input as index of random oracles.
As shown by Zhandry [Zha12b], a quantum random oracle can be simulated by a family of 2Q-wise independent hash functions against an adversary that quantumly accesses to the oracle at most Q times. As a result, he obtained the following lemma.
Lemma 1
([Zha12b, Theorem 6.1]). Any quantum algorithm \(\mathcal {A}\) making quantum queries to random oracles can be efficiently simulated by a quantum algorithm \(\mathcal {B}\), which has the same output distribution, but makes no queries. Especially, if \(\mathcal {A}\) makes at most Q queries to a random oracle \(\mathsf {H}:\{0,1\}^a\rightarrow \{0,1\}^b\), then \(\mathsf {Time}(\mathcal {B})\approx \mathsf {Time}(\mathcal {A})\,+\,Q\cdot T^{2Q\text {-}\mathsf {wise}}_{a,b}\) where \(T^{2Q\text {-}\mathsf {wise}}_{a,b}\) denotes the time to evaluate a 2Q-wise independent hash function from \(\{0,1\}^a\) to \(\{0,1\}^b\).
The following lemma was shown by Boneh et al. [BDF+11]. Roughly speaking, this lemma states that if an oracle outputs independent and almost uniform value for all inputs, then it is indistinguishable from a random oracle even with quantum oracle accesses.
Lemma 2
([BDF+11, Lemma 3]). Let \(\mathcal {A}\) be a quantum algorithm that makes at most Q oracle queries, and \(\mathcal X\) and \(\mathcal Y\) be arrbitrary sets. Let \(\mathcal {H}\) be a distribution over \(\mathsf {Func}(\mathcal X,\mathcal Y)\) such that when we take  , for each \(x\in \mathcal X\), \(\mathsf {H}(x)\) is identically and independently distributed according to a distribution D whose statistical distance is within \(\epsilon \) from uniform. Then for any input z. We have
, for each \(x\in \mathcal X\), \(\mathsf {H}(x)\) is identically and independently distributed according to a distribution D whose statistical distance is within \(\epsilon \) from uniform. Then for any input z. We have

where \(\mathsf {RF}\leftarrow \mathsf {Func}(\mathcal X, \mathcal Y)\) and \(\mathsf {H}\leftarrow \mathcal {H}\).
2.2 Pseudorandom Function
We review the definition of quantum-accessible pseudorandom functions (PRFs) [BDF+11].
Definition 1
(Quantum-accessible PRF). We say that a function \(F{:}\,\mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\) is a quantum-accessible pseudorandom function if for all PPT adversaries \(\mathcal A\), its advantage defined below is negligible:

where \(\mathsf {RF}\leftarrow \mathsf {Func}(\mathcal X, \mathcal Y)\) and \(K\leftarrow \mathcal {K}\).
Zhandry [Zha12a] proved that some known constructions of classical PRFs including the tree-based construction [GGM86] and lattice-based construction [BPR12] are also quantum-accessible PRFs. However, these reductions are non-tight, and thus we cannot rely on these results when aiming for tight security. Fortunately, we can use the following lemma which states that we can use a quantum random oracle as a PRF similarly to the classical case.
Lemma 3
([SXY18, Lemma 2.2]). Let \(\ell \) be an integer. Let \(\mathsf {H}:\{0,1\}^{\ell }\times \mathcal {X}\rightarrow \mathcal {Y}\) and \(\mathsf {H}':\mathcal {X}\rightarrow \mathcal {Y}\) be two independent random functions. If an unbounded time quantum adversary \(\mathcal {A}\) makes a query to \(\mathsf {H}\) at most \(Q_{\mathsf {H}}\) times, then we have

2.3 Identity-Based Encryption
Syntax. We use the standard syntax of IBE [BF01]. Let \(\mathcal {ID}\) be the ID space of the scheme. If a collision resistant hash function \(CRH: \{ 0,1 \}^* \rightarrow \mathcal {ID}\) is available, one can use an arbitrary string as an identity. An IBE scheme is defined by the following four algorithms.
-
\(\mathsf{Setup}(1^\lambda )\rightarrow (\mathsf {mpk}, \mathsf {msk})\): The setup algorithm takes as input a security parameter \(1^\lambda \) and outputs a master public key \(\mathsf {mpk}\) and a master secret key \(\mathsf {msk}\).
-
\(\mathsf{KeyGen}(\mathsf {mpk}, \mathsf {msk}, \mathsf {ID})\rightarrow \mathsf {sk}_\mathsf {ID}\): The key generation algorithm takes as input the master public key \(\mathsf {mpk}\), the master secret key \(\mathsf {msk}\), and an identity \(\mathsf {ID}\in \mathcal {ID}\). It outputs a private key \(\mathsf {sk}_\mathsf {ID}\). We assume that \(\mathsf {ID}\) is implicitly included in \(\mathsf {sk}_\mathsf {ID}\).
-
\(\mathsf{Encrypt} (\mathsf {mpk}, \mathsf {ID}, \mathsf {M})\rightarrow C\): The encryption algorithm takes as input a master public key \(\mathsf {mpk}\), an identity \(\mathsf {ID}\in \mathcal {ID}\), and a message \(\mathsf {M}\). It outputs a ciphertext \(C\).
-
\(\mathsf{Decrypt}(\mathsf {mpk},\mathsf {sk}_\mathsf {ID}, C)\rightarrow \mathsf {M}\ \text { or }\bot \): The decryption algorithm takes as input the master public key \(\mathsf {mpk}\), a private key \(\mathsf {sk}_{\mathsf {ID}}\), and a ciphertext \(C\). It outputs the message \(\mathsf {M}\) or \(\bot \), which means that the ciphertext is not in a valid form.
Correctness. We require correctness of decryption: that is, for all \(\lambda \), all \(\mathsf {ID}\in \mathcal {ID}\), and all \(\mathsf {M}\) in the specified message space,
holds, where the probability is taken over the randomness used in \((\mathsf {mpk},\mathsf {msk})\leftarrow \mathsf {Setup}(1^\lambda )\), \(\mathsf {sk}_\mathsf {ID}\leftarrow \mathsf {KeyGen}(\mathsf {mpk}, \mathsf {msk}, \mathsf {ID})\), and \(\mathsf {Encrypt}(\mathsf {mpk},\mathsf {ID},\mathsf {M})\).
Security. We now define the security for an IBE scheme \(\varPi \). This security notion is defined by the following game between a challenger and an adversary \(\mathcal{A}\). Let \( \mathsf {CTSam}(\cdot )\) be a sampling algorithm that takes as input a master public key of the scheme and outputs an element in the ciphertext space.
- Setup. At the outset of the game, the challenger runs \(\mathsf {Setup}(1^\lambda )\rightarrow (\mathsf {mpk}, \mathsf {msk})\) and gives \(\mathsf {mpk}\) to \(\mathcal{A}\). The challenger also picks a random coin \(\mathsf {coin}\leftarrow \{ 0,1 \}\) and keeps it secretly. After given \(\mathsf {mpk}\), \(\mathcal {A}\) can adaptively make the following two types of queries to the challenger. These queries can be made in any order and arbitrarily many times.
Secret Key Queries. If \(\mathcal {A}\) submits \(\mathsf {ID}\in \mathcal {ID}\) to the challenger, the challenger returns \(\mathsf {sk}_\mathsf {ID}\leftarrow \mathsf {KeyGen}(\mathsf {mpk},\mathsf {msk},\mathsf {ID})\).
Challenge Queries. If \(\mathcal {A}\) submits a message \(\mathsf {M}^*\) and an identity \(\mathsf {ID}^* \in \mathcal {ID}\) to the challenger, the challenger proceeds as follows. If \(\mathsf {coin}= 0\), it runs \(\mathsf {Encrypt}(\mathsf {mpk},\mathsf {ID}^{*},\mathsf {M}^*)\rightarrow C^{*}\) and gives the challenge ciphertext \(C^*\) to \(\mathcal {A}\). If \(\mathsf {coin}= 1\), it chooses the challenge ciphertext \(C^*\) from the distribution \(\mathsf {CTSam}(\mathsf {mpk})\) as  at random and gives it to \(\mathcal {A}\).
at random and gives it to \(\mathcal {A}\).
We prohibit \(\mathcal {A}\) from making a challenge query for an identity \(\mathsf {ID}^*\) such that it has already made a secret key query for the same \(\mathsf {ID}=\mathsf {ID}^*\) and vice versa.
- Guess. Finally, \(\mathcal{A}\) outputs a guess \(\widehat{\mathsf {coin}}\) for \(\mathsf {coin}\). The advantage of \(\mathcal{A}\) is defined as
We say that \(\varPi \) is adaptively-anonymous secure, if there exists efficiently sampleable distribution \(\mathsf {CTSam}(\mathsf {mpk})\) and the advantage of any PPT \(\mathcal {A}\) is negligible in the above game. The term anonymous captures the fact that the ciphertext does not reveal the identity for which it was sent to. (Observe that \(\mathsf {CTSam}(\mathsf {mpk})\) depends on neither of \(\mathsf {ID}^*\) nor \(\mathsf {M}^*\).)
Single Challenge Security. We can also consider a variant of the above security definition where we restrict the adversary to make the challenge query only once during the game. We call this security notion “single challenge adaptive anonymity”, and call the notion without the restriction “multi challenge security”. By a simple hybrid argument, we can show that these definitions are in fact equivalent in the sense that one implies another. However, the proof that the former implies the latter incurs a huge security reduction loss that is linear in the number of challenge queries. Since the focus of this paper is on tight security reductions, we typically differentiate these two notions.
Remark 1
We say that an IBE scheme is stateful if the key generation algorithm has to record all previously issued secret keys, and always outputs the same secret key for the same identity. By the technique by Goldreich [Gol86], a stateful scheme can be converted to a stateless one (in which the key generation algorithm need not remember previous executions) by using PRFs. Since PRFs exist in the QROM without assuming any computational assumption as shown in Lemma 3, if we make the key size of PRFs sufficiently large, this conversion hardly affects the tightness. Therefore in this paper, we concentrate on constructing tightly secure stateful IBE scheme for simplicity.
2.4 Background on Lattices
A (full-rank-integer) m-dimensional lattice \(\varLambda \) in \(\mathbb {Z}^m\) is a set of the form \(\{ \sum _{i \in [m]} x_i \mathbf {b}_i | x_i \in \mathbb {Z} \}\), where \(\mathbf {B}= \{ \mathbf {b}_1, \cdots , \mathbf {b}_m \}\) are m linearly independent vectors in \(\mathbb {Z}^m\). We call \(\mathbf {B}\) the basis of the lattice \(\varLambda \). For any positive integers n, m and \(q\ge 2\), a matrix \(\mathbf {A}\in \mathbb {Z}_q^{n \times m}\) and a vector \(\mathbf {u}\in \mathbb {Z}_q^n\), we define \(\varLambda ^{\perp }(\mathbf {A}) = \{ \mathbf {z}\in \mathbb {Z}^m | \mathbf {A}\mathbf {z}= \mathbf {0}\mod q \},\) and \(\varLambda ^{\perp }_{\mathbf {u}}(\mathbf {A}) = \{ \mathbf {z}\in \mathbb {Z}^m | \mathbf {A}\mathbf {z}= \mathbf {u}\mod q \}.\)
Gaussian Measures. For an m-dimensional lattice \(\varLambda \), the discrete Gaussian distribution over \(\varLambda \) with center \(\mathbf {c}\) and parameter \(\sigma \) is defined as \(D_{\varLambda , \sigma , \mathbf {c}}(\mathbf {x}) = \rho _{\sigma , \mathbf {c}} (\mathbf {x}) / \rho _{\sigma , \mathbf {c}} (\varLambda )\) for all \(\mathbf {x}\in \varLambda \), where \(\rho _{\sigma , \mathbf {c}}(\mathbf {x})\) is a Gaussian function defined as \(\exp (- \pi ||\mathbf {x}-\mathbf {c} ||^2 / \sigma ^2)\) and \(\rho _{\sigma , \mathbf {c}} (\varLambda ) = \sum _{\mathbf {x}\in \varLambda } \rho _{\sigma , \mathbf {c}} (\mathbf {x})\). Further for an m-dimensional shifted lattice \(\varLambda + \mathbf {t}\), we define the Gaussian distribution \(D_{\varLambda + \mathbf {t}, \sigma }\) with parameter \(\sigma \) as the process of adding the vector \(\mathbf {t}\) to a sample from \(D_{\varLambda , \sigma , -\mathbf {t}}\). Finally, we call D a B-bounded distribution, if all the elements in the support of D have absolute value smaller than B.
Discrete Gaussian Lemmas. The following lemmas are used to manipulate and obtain meaningful bounds on discrete Gaussian vectors.
Lemma 4
(Adopted from [GPV08], Lemma 5.2). Let n, m, q be positive integers such that \(m \ge 2n \log q\) and q a prime. Let \(\sigma \) be any positive real such that \(\sigma \ge \sqrt{ n + \log {m} }\). Then for all but \(2^{-\varOmega (n)}\) fraction of \(\mathbf {A}\in \mathbb {Z}_q^{n \times m}\), we have that the distribution of \(\mathbf {u}= \mathbf {A}\mathbf {e}\mod q\) for \(\mathbf {e}\leftarrow D_{\mathbb {Z}^m, \sigma }\) is \(2^{-\varOmega (n)}\)-close to uniform distribution over \(\mathbb {Z}_q^n\). Furthermore, for a fixed \(\mathbf {u}\in \mathbb {Z}_q^n\), the conditional distribution of \(\mathbf {e}\leftarrow D_{\mathbb {Z}^m, \sigma }\), given \(\mathbf {A}\mathbf {e}= \mathbf {u}\mod q\) is \(D_{\varLambda _\mathbf {u}^\bot (\mathbf {A}), \sigma }\).
The following lemma is obtained by combining Lemma 4.4 in [MR07] and Lemma 5.3 in [GPV08].
Lemma 5
([MR07], [GPV08]). Let \(\sigma > 16\sqrt{ \log 2m/\pi } \) and \(\mathbf {u}\) be any vector in \(\mathbb {Z}_q^n\). Then, for all but \(q^{-n}\) fraction of \(\mathbf {A}\in \mathbb {Z}_q^{n \times m}\), we have that

The following lemma can be obtained by a straightforward combination of Lemma 2.6, Lemma 2.10 and Lemma 5.3 in [GPV08] (See also [PR06, Pei07]).
Lemma 6
([PR06, Pei07, GPV08]). Let \(\sigma > 16\sqrt{ \log 2m/\pi } \) and \(\mathbf {u}\) be any vector in \(\mathbb {Z}_q^n\). Then, for all but \(q^{-n}\) fraction of \(\mathbf {A}\in \mathbb {Z}_q^{n\times m}\), we have
The following is a useful lemma used during the security proof. It allows the simulator to create new LWE samples from a given set of LWE samples (i.e., the LWE challenge provided to the simulator) for which it does not know the associating secret vector.Footnote 2 We would like to note that the following lemma is built on top of many previous results [Reg05, Pei10, BLP+13] and is formatted in a specific way to be useful in the security proof for LWE-based cryptosystems.
Lemma 7
(Noise Rerandomization, [KY16], Lemma 1). Let \(q, \ell , m\) be positive integers and r a positive real satisfying \(r > \varOmega (\sqrt{n })\). Let \(\mathbf {b}\in \mathbb {Z}_q^{m}\) be arbitrary and \(\mathbf {z}\) chosen from \(D_{\mathbb {Z}^m, r }\). Then there exists a PPT algorithm \({\mathsf {ReRand}}\) such that for any \(\mathbf {V}\in \mathbb {Z}^{m \times \ell }\) and positive real \(\sigma > s_1(\mathbf {V})\), the output of \({\mathsf {ReRand}}(\mathbf {V}, \mathbf {b}+ \mathbf {z}, r, \sigma )\) is distributed as \(\mathbf {b}' = \mathbf {V}^\top \mathbf {b}+ \mathbf {z}' \in \mathbb {Z}_q^\ell \) where the distribution of \(\mathbf {z}'\) is within \(2^{-\varOmega (n)}\) statistical distance of \(D_{\mathbb {Z}^\ell , 2 r \sigma }\).
Sampling Algorithms. The following lemma states useful algorithms for sampling short vectors from lattices. In particular, the second preimage sampler is the exact gaussian sampler of [BLP+13], Lemma 2.3.
Lemma 8
([GPV08, MP12, BLP+13]) Let \(n, m, q > 0\) be integers with \(m > 3n\lceil \log q \rceil \).
-
\(\mathsf {TrapGen}(1^n, 1^m, q) \rightarrow (\mathbf {A}, \mathbf {T}_\mathbf {A})\): a randomized algorithm that outputs a matrix \(\mathbf {A}\in \mathbb {Z}_q^{n \times m}\) and a full-rank matrix \(\mathbf {T}_\mathbf {A}\in \mathbb {Z}^{m \times m}\), where \(\mathbf {T}_\mathbf {A}\) is a basis for \(\varLambda ^\perp (\mathbf {A})\), the distribution of \(\mathbf {A}\) is \(2^{-\varOmega (n)}\)-close to uniform and
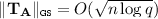 .
. -
\(\mathsf {SamplePre}(\mathrm{\mathbf{A}}, \mathrm{\mathbf{T}}_{\mathrm{\mathbf{A}}}, \mathrm{\mathbf{u}}, \sigma ):\) a randomized algorithm that, given a matrix \(\mathbf {A}\in \mathbb {Z}_q^{n \times m}\), a basis \(\mathbf {T}_\mathbf {A}\in \mathbb {Z}^{m \times m}\) for \(\varLambda ^\bot (\mathbf {A})\), a vector \(\mathbf {u}\in \mathbb {Z}_q^n\) and a Gaussian parameter
 , outputs a vector \(\mathbf {e}\in \mathbb {Z}^m\) sampled from a distribution \(2^{-\varOmega (n)}\)-close to \(D_\mathrm{\Lambda ^{\perp }_{\mathrm{\mathbf{u}}}(\mathrm{\mathbf{A}}), \sigma }\).
, outputs a vector \(\mathbf {e}\in \mathbb {Z}^m\) sampled from a distribution \(2^{-\varOmega (n)}\)-close to \(D_\mathrm{\Lambda ^{\perp }_{\mathrm{\mathbf{u}}}(\mathrm{\mathbf{A}}), \sigma }\). -
\(\mathsf {Sample}\mathbb {Z}(\sigma ):\) a randomized algorithm that, given a Gaussian parameter \(\sigma > 16(\sqrt{\log 2m/\pi })\) , outputs a vector \(\mathbf {e}\in \mathbb {Z}^m\) sampled from a distribution \(2^{-\varOmega (n)}\)-close to \(D_{\mathbb {Z}^m, \sigma }\).
Hardness Assumptions. We define the Learning with Errors (LWE) problem introduced by Regev [Reg05].
Definition 2
(Learning with Errors). For integers \(n = n(\lambda ), m = m(n)\), a prime \(q = q(n) > 2\), an error distribution over \(\chi = \chi (n)\) over \(\mathbb {Z}\), and a PPT algorithm \(\mathcal A\), the advantage for the learning with errors problem \(\mathsf {LWE}_{n, m, q, \chi }\) of \(\mathcal A\) is defined as follows:
where \(\mathbf {A}\leftarrow \mathbb {Z}_q^{n\times m}\), \(\mathbf {s}\leftarrow \mathbb {Z}_q^n\), \(\mathbf {w}\leftarrow \mathbb {Z}_q^m\), \(\mathbf {z}\leftarrow \chi ^m\). We say that the \(\mathsf {LWE}\) assumption holds if \(\mathsf {Adv}_{\mathcal A}^{\mathsf {LWE}_{n, m, q, \chi }}\) is negligible for all PPT \(\mathcal A\).
The (decisional) \(\mathsf {LWE}_{n, m, q, D_{\mathbb {Z}, \alpha q}}\) for \(\alpha q > 2\sqrt{n}\) has been shown by Regev [Reg05] to be as hard as approximating the worst-case \(\mathsf{SIVP}\) and \(\mathsf {GapSVP}\) problems to within \(\tilde{O}(n/\alpha )\) factors in the \(\ell _2\)-norm in the worst case. In the subsequent works, (partial) dequantumization of the reduction were achieved [Pei09, BLP+13].
We also define the LWE assumption against adversaries that can access to a quantum random oracle as is done by Boneh et al. [BDF+11].
Definition 3
(Learning with Errors relative to Quantum Random Oracle). Let n, m, q and \(\chi \) be the same as in Definition 2, and a, b be some positive integers. For a PPT algorithm \(\mathcal A\), the advantage for the learning with errors problem \(\mathsf {LWE}_{n, m, q, \chi }\) of \(\mathcal A\) relative to a quantum random oracle is defined as follows:

where \(\mathbf {A}\leftarrow \mathbb {Z}_q^{n\times m}\), \(\mathbf {s}\leftarrow \mathbb {Z}_q^n\), \(\mathbf {w}\leftarrow \mathbb {Z}_q^m\), \(\mathbf {z}\leftarrow \chi ^m\),  . We say that the \(\mathsf {LWE}\) assumption relative to an (a, b)-quantum random oracle holds if \(\mathsf {Adv}_{\mathcal A,\mathsf {QRO}_{a,b}}^{\mathsf {LWE}_{n, m, q, \chi }}(\lambda )\) is negligible for all PPT \(\mathcal A\).
. We say that the \(\mathsf {LWE}\) assumption relative to an (a, b)-quantum random oracle holds if \(\mathsf {Adv}_{\mathcal A,\mathsf {QRO}_{a,b}}^{\mathsf {LWE}_{n, m, q, \chi }}(\lambda )\) is negligible for all PPT \(\mathcal A\).
It is easy to see that the LWE assumption relative to a quantum random oracle can be reduced to the LWE assumption with a certain loss of the time for the reduction by Lemma 1. Alternatively, if we assume the existence of a quantumly-accessible PRF, then the reduction loss can be made smaller. Namely, we have the following lemmas.
Lemma 9
For any n, m, q, \(\chi \), a, b, and an algorithm \(\mathcal A\) making at most Q oracle queries, there exists an algorithm \(\mathcal B\) such that
and \(\mathsf {Time}(\mathcal {B})\approx \mathsf {Time}(\mathcal {A})+Q\cdot T^{2Q\text {-}\mathsf {wise}}_{a,b}\) where \(T^{2Q\text {-}\mathsf {wise}}_{a,b}\) denotes the time to evaluate a 2Q-wise independent hash function from \(\{0,1\}^a\) to \(\{0,1\}^b\).
Lemma 10
Let \(F:\mathcal {K}\times \{0,1\}^a \rightarrow \{0,1\}^b\) be a quantumly-accessible PRF. For any n, m, q, \(\chi \), a, b and an algorithm \(\mathcal A\) making at most Q oracle queries, there exist algorithms \(\mathcal B\) and \(\mathcal {C}\) such that
and \(\mathsf {Time}(\mathcal {B})\approx \mathsf {Time}(\mathcal {A})+Q\cdot T_{F}\) and \(\mathsf {Time}(\mathcal {C})\approx \mathsf {Time}(\mathcal {A})\) where \(T_{F}\) denotes the time to evaluate F.
In this paper, we give reductions from the security of IBE schemes to the LWE assumption relative to a quantrum random oracle. Given such reductions, we can also reduce them to the LWE assumption or to the LWE assumption plus the security of quantumly-accessible PRFs by Lemma 9 or 10, respectively. The latter is tighter than the former at the cost of assuming the existence of quantumly-accessible PRFs.
Remark 2
A keen reader may wonder why we have to require the extra assumption on the existence of PRFs when we are working in the QROM, since as we mentioned earlier in Sect. 2.2, it seems that we can use a QRO as a PRF. The point here is that during the security reduction, the simulator (which is given the classical LWE instance) must simulate the QRO query to the adversary against the LWE problem relative to a quantum random oracle query, hence, the simulator is not in possession of the QRO. Note that the reason why we are able to use the QRO as a PRF as mentioned in Remark 1 is because the simulator is aiming to reduce the LWE problem relative to a quantum random oracle query to the IBE scheme. Specifically, in this case the simulator can use the QRO provided by its challenge to simulate a PRF.
3 Tightly Secure Single Challenge GPV-IBE
In this section, we show that we can give a tight security proof for the original GPV-IBE [GPV08] in the single-challenge setting if we set the parameters appropriately. Such proofs can be given in both the classical ROM and QROM settings.
3.1 Construction
Let the identity space \(\mathcal {ID}\) of the scheme be \(\mathcal {ID}=\{0,1\}^{\ell _{\mathsf {ID}}}\), where \(\ell _{\mathsf {ID}}(\lambda )\) denotes the identity-length. Let also \(\mathsf {H}: \{0,1\}^{\ell _{\mathsf {ID}}} \rightarrow \mathbb {Z}^n_q\) be a hash function treated as a random oracle during security analysis. The IBE scheme \(\mathsf {GPV}\) is given as follows. For simplicity, we describe the scheme as a stateful one. As remarked in Remark 1, we can make the scheme stateless without any additional assumption in the QROM.
-
Setup\((1^\lambda )\): On input \(1^\lambda \), it first chooses a prime q, positive integers n, m, and Gaussian parameters \(\alpha ', \sigma \), where all these values are implicitly a function of the security parameter \(\lambda \). The precise parameter selection is specified in the following section. It then runs \((\mathbf {A}, \mathbf {T}_\mathbf {A}) \leftarrow \mathsf {TrapGen}(1^n, 1^m, q)\) to generate a matrix \(\mathbf {A}\in \mathbb {Z}_q^{n \times m}\) with a trapdoor \(\mathbf {T}_{\mathbf {A}} \in \mathbb {Z}^{m \times m}\) such that
 . Then it outputs $$\begin{aligned} \mathsf {mpk}= \mathbf {A}\quad \text {and} \quad \mathsf {msk}= \mathbf {T}_{\mathbf {A}} \end{aligned}$$
. Then it outputs $$\begin{aligned} \mathsf {mpk}= \mathbf {A}\quad \text {and} \quad \mathsf {msk}= \mathbf {T}_{\mathbf {A}} \end{aligned}$$ -
KeyGen\(( \mathsf {mpk}, \mathsf {msk}, \mathsf {ID})\): If \(\mathsf {sk}_{\mathsf {ID}}\) is already generated, then this algorithm returns it. Otherwise it computes \(\mathbf {u}_\mathsf {ID}= \mathsf {H}(\mathsf {ID})\) and samples \(\mathbf {e}_\mathsf {ID}\in \mathbb {Z}^{m}\) such that
$$\begin{aligned} \mathbf {A}\mathbf {e}_\mathsf {ID}= \mathbf {u}_{\mathsf {ID}} \mod q \end{aligned}$$using \(\mathbf {e}_\mathsf {ID}\leftarrow \mathsf {SamplePre}(\mathbf {A}, \mathbf {T}_{\mathbf {A}}, \mathbf {u}_\mathsf {ID}, \sigma )\). It returns \(\mathsf {sk}_\mathsf {ID}= \mathbf {e}_\mathsf {ID}\) as the secret key.
-
Enc\((\mathsf {mpk}, \mathsf {ID}, \mathsf {M})\): To encrypt a message \(\mathsf {M}\in \{0,1\}\), it first samples \(\mathrm{\mathbf{s}} \leftarrow \mathbb {Z}^n_q\), \(\mathrm{\mathbf{x}} \leftarrow D_{\mathbb {Z}^m, \alpha ' q}\) and \(x \leftarrow D_{\mathbb {Z}, \alpha ' q}\). Then it sets \(\mathbf {u}_\mathsf {ID}= \mathsf {H}(\mathsf {ID})\) and computes
$$\begin{aligned} c_0 = \mathbf {u}_\mathsf {ID}^\top \mathbf {s}+ x + \mathsf {M}\lfloor q/2 \rceil , \quad \mathbf {c}_1 = \mathbf {A}^\top \mathbf {s}+ \mathbf {x}. \end{aligned}$$Finally, it outputs the ciphertext \(C = (c_0, \mathbf {c}_1) \in \mathbb {Z}_q \times \mathbb {Z}_q^m\).
-
Dec\((\mathsf {mpk}, \mathsf {sk}_\mathsf {ID}, C)\): To decrypt a ciphertext \(C = (c_0, \mathbf {c}_1)\) with a secret key \(\mathsf {sk}_\mathsf {ID}\), it computes \(w = c_0 - \mathbf {c}_1^\top \mathbf {e}_\mathsf {ID}\in \mathbb {Z}_q\) and outputs 0 if w is closer to 0 than to \(\lfloor q/2 \rceil \) modulo q. Otherwise it outputs 1.
3.2 Correctness and Parameter Selection
The following shows correctness of the above IBE scheme.
Lemma 11
(Correctness). Suppose the parameters q, \(\sigma \), and \(\alpha '\) are such that

Let \(\mathrm{\mathbf{e}}_{\mathsf {ID}} \leftarrow \mathsf{KeyGen}(\mathbf {A}, \mathbf {T}_{\mathbf {A}}, {\mathsf {ID}}), C \leftarrow \mathsf{Enc}(\mathbf {A}, {\mathsf {ID}'}, \mathsf {M}\in \{0,1\})\) and \(\mathsf {M}' \leftarrow \mathsf{Dec}(\mathbf {A},\mathrm{\mathbf{e}}_{\mathsf {ID}}, C).\) If \({\mathsf {ID}} = {\mathsf {ID}'}\), then with overwhelming probability we have \(\mathsf {M}' = \mathsf {M}\).
Proof
When the Dec algorithm operates as specified, we have
By Lemma 8 and the condition posed on the choice of \(\sigma \), we have that the distribution of \(\mathbf {e}_\mathsf {ID}\) is \(2^{-\varOmega (n)}\) close to \(D_{\mathrm{\Lambda }_\mathbf {u}^{\perp }(\mathbf {A}),\sigma }\). Therefore, by Lemma 5, we have \(x \le \alpha ' q \sqrt{m}\), \(\Vert \mathbf {x}\Vert \le \alpha ' q \sqrt{m}\), and \(\Vert \mathrm{\mathbf{e}}_{\mathsf {ID}} \Vert \le \sigma \cdot \sqrt{m}\) except for \(2^{-\varOmega (n)}\) probability. Then, the error term is bounded by
Hence, for the error term to have absolute value less than q / 4, it suffices to choose q and \(\alpha '\) as in the statement of the lemma.
Parameter Selection. For the system to satisfy correctness and make the security proof work, we need the following restrictions. Note that we will prove the security of the scheme under the LWE assumption whose noise rate is \(\alpha \), which is lower than \(\alpha '\) that is used in the encryption algorithm.
-
The error term is less than q / 4 (i.e., \(\alpha ' < 1/8m\sigma \) by Lemma 11)
-
TrapGen operates properly (i.e., \(m > 3n\log q\) by Lemma 8)
-
Samplable from \(D_{\mathrm{\Lambda }_\mathbf {u}^{\perp }(\mathbf {A}),\sigma }\) (i.e.,
 by Lemma 8),
by Lemma 8), -
\(\sigma \) is sufficiently large so that we can apply Lemmas 4 and 6 (i.e., \(\sigma > \sqrt{ n + \log {m} }\), \(16\sqrt{ \log 2m/\pi }\)),
-
We can apply Lemma 7 (i.e., \(\alpha ' / 2\alpha > \sqrt{n(\sigma ^2 m+1)}\)),
-
\(\mathsf {LWE}_{n, m, q, D_{\mathbb {Z}, {\alpha q}}}\) is hard (i.e., \(\alpha q > 2\sqrt{n}\)).
To satisfy these requirements, for example, we can set the parameters \(m, q, \sigma , \alpha , \alpha '\) as follows:
where \(\kappa >0\) is a constant that can be set arbitrarily small. To withstand attacks running in time \(2^{\lambda }\), we may set \(n=\tilde{\varOmega }(\lambda )\). In the above, we round up m to the nearest integer and q to the nearest largest prime. We remark that though the above parameter is worse compared to the original GPV-IBE scheme, this is due to our conservative choice of making the statistical error terms appearing in the reduction cost \(2^{-\varOmega (n)}\) rather than the standard negligible notion \(2^{-\omega (\log \lambda )}\). The latter choice of parameters will lead to better parameters, which may be as efficient as the original GPV-IBE.
3.3 Security Proof in QROM
The following theorem addresses the security of \(\mathsf {GPV}\) in the classical ROM setting. Our analysis departs from the original one [GPV08] and as a consequence much tighter. The proof can be found in the full version.
Theorem 1
The IBE scheme \(\mathsf {GPV}\) is adaptively-anonymous single-challenge secure in the random oracle model assuming the hardness of \(\mathsf {LWE}_{n, m, q, D_{\mathbb {Z}, \alpha q}}\). Namely, for any classical adversary \(\mathcal {A}\) making at most \(Q_{\mathsf {H}}\) random oracle queries to \(\mathsf {H}\) and \(Q_{\mathsf {ID}}\) secret key queries, there exists an algorithm \(\mathcal {B}\) such that
and
As we explained in the introduction, our analysis in the ROM can be easily be extended to the QROM setting. We can prove the following theorem that addresses the security of the GPV-IBE scheme in the QROM setting. The analysis here is different from that by Zhandry [Zha12b], who gave the first security proof for the GPV-IBE scheme in the QROM setting and our analysis here is much tighter.
Theorem 2
The IBE scheme \(\mathsf {GPV}\) is adaptively-anonymous single-challenge secure assuming the hardness of \(\mathsf {LWE}_{n, m, q, D_{\mathbb {Z}, \alpha q}}\) in the quantum random oracle model. Namely, for any quantum adversary \(\mathcal {A}\) making at most \(Q_{\mathsf {H}}\) queries to  and \(Q_{\mathsf {ID}}\) secret key queries, there exists a quantum algorithm \(\mathcal {B}\) making \(Q_{\mathsf {H}}+Q_{\mathsf {ID}}\) quantum random oracle queries such that
and \(Q_{\mathsf {ID}}\) secret key queries, there exists a quantum algorithm \(\mathcal {B}\) making \(Q_{\mathsf {H}}+Q_{\mathsf {ID}}\) quantum random oracle queries such that
and
where \(\ell _{r}\) denotes the length of the randomness for \(\mathsf {Sample}\mathbb {Z}\).
Proof
(Proof of Theorem 2 ). Let \(\mathsf {CTSam}(\mathsf {mpk})\) be an algorithm that outputs a random element from \(\mathbb {Z}_q\times \mathbb {Z}_q^{m}\) and \(\mathcal A\) be a quantum adversary that attacks the adaptively-anonymous security of the IBE scheme. Without loss of generality, we can assume that \(\mathcal {A}\) makes secret key queries on the same identity at most once. We show the security of the scheme via the following games. In each game, we define \(X_i\) as the event that the adversary \(\mathcal {A}\) wins in \(\mathsf {Game}_i\).
\(\mathsf {Game}_0{:}\) This is the real security game for the adaptively-anonymous security. At the beginning of the game, the challenger chooses a random function \(\mathsf {H}:\{0,1\}^{\ell _{\mathsf {ID}}}\rightarrow \mathbb {Z}_q^n\). Then it generates  and gives \(\mathbf {A}\) to \(\mathcal {A}\). Then it samples
and gives \(\mathbf {A}\) to \(\mathcal {A}\). Then it samples  and keeps it secret. During the game, \(\mathcal {A}\) may make (quantum) random oracle queries, secret key queries, and a challenge query. These queries are handled as follows:
and keeps it secret. During the game, \(\mathcal {A}\) may make (quantum) random oracle queries, secret key queries, and a challenge query. These queries are handled as follows:
-
When \(\mathcal A\) makes a random oracle query on a quantum state
 , the challenger returns
, the challenger returns  .
. -
When \(\mathcal {A}\) makes a secret key query on \(\mathsf {ID}\), the challenger samples \(\mathbf {e}_\mathsf {ID}= \mathsf {SamplePre}(\mathbf {A},\mathbf {T}_\mathbf {A},\mathbf {u}_{\mathsf {ID}},\sigma )\) and returns \(\mathbf {e}_\mathsf {ID}\) to \(\mathcal {A}\).
-
When \(\mathcal {A}\) makes a challenge query for \(\mathsf {ID}^*\) and a message \(\mathsf {M}^*\), the challenger returns
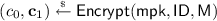 if \(\mathsf {coin}=0\) and
if \(\mathsf {coin}=0\) and  if \(\mathsf {coin}=1\).
if \(\mathsf {coin}=1\).
At the end of the game, \(\mathcal A\) outputs a guess \(\widehat{\mathsf {coin}}\) for \(\mathsf {coin}\). Finally, the challenger outputs \(\widehat{\mathsf {coin}}\). By definition, we have \(\big | \Pr [X_0] - \frac{1}{2} \big | = \big | \Pr [\widehat{\mathsf {coin}}- \mathsf {coin}] - \frac{1}{2} \big | = \mathsf {Adv}^{\mathsf {IBE}}_{\mathcal{A},\mathsf {GPV}}(\lambda ).\)
\(\mathsf {Game}_1{:}\) In this game, we change the way the random oracle \(\mathsf {H}\) is simulated. Namely, the challenger first chooses another random function  . Then we define \(\mathsf {H}(\mathsf {ID})\mathrel {\mathop :}=\mathbf {A}\mathrm{\mathbf{e}}_{\mathsf {ID}}\) where \(\mathbf {e}_{\mathsf {ID}}\mathrel {\mathop :}=\mathsf {Sample}\mathbb {Z}(\sigma ;\widehat{\mathsf {H}}(\mathsf {ID}))\), and use this \(\mathsf {H}\) throughout the game. For any fixed \(\mathsf {ID}\), the distribution of \(\mathsf {H}(\mathsf {ID})\) is identical and its statistical distance from the uniform distribution is \(2^{-\varOmega (n)}\) for all but \(2^{-\varOmega (n)}\) fraction of \(\mathbf {A}\) due to Lemma 4 since we choose \(\sigma > \sqrt{ n+\log m }\). Note that in this game, we only change the distribution of \(\mathbf {u}_\mathsf {ID}\) for each identity, and the way we create secret keys are unchanged. Then due to Lemma 2, we have \(\big | \Pr [X_0] - \Pr [X_1] \big | = 2^{-\varOmega (n)} + 4Q_{\mathsf {H}}^2\sqrt{ 2^{-\varOmega (n)} } = Q^2_{\mathsf {H}} \cdot 2^{-\varOmega (n)} \).
. Then we define \(\mathsf {H}(\mathsf {ID})\mathrel {\mathop :}=\mathbf {A}\mathrm{\mathbf{e}}_{\mathsf {ID}}\) where \(\mathbf {e}_{\mathsf {ID}}\mathrel {\mathop :}=\mathsf {Sample}\mathbb {Z}(\sigma ;\widehat{\mathsf {H}}(\mathsf {ID}))\), and use this \(\mathsf {H}\) throughout the game. For any fixed \(\mathsf {ID}\), the distribution of \(\mathsf {H}(\mathsf {ID})\) is identical and its statistical distance from the uniform distribution is \(2^{-\varOmega (n)}\) for all but \(2^{-\varOmega (n)}\) fraction of \(\mathbf {A}\) due to Lemma 4 since we choose \(\sigma > \sqrt{ n+\log m }\). Note that in this game, we only change the distribution of \(\mathbf {u}_\mathsf {ID}\) for each identity, and the way we create secret keys are unchanged. Then due to Lemma 2, we have \(\big | \Pr [X_0] - \Pr [X_1] \big | = 2^{-\varOmega (n)} + 4Q_{\mathsf {H}}^2\sqrt{ 2^{-\varOmega (n)} } = Q^2_{\mathsf {H}} \cdot 2^{-\varOmega (n)} \).
\(\mathsf {Game}_2{:}\) In this game, we change the way secret key queries are answered. By the end of this game, the challenger will no longer require the trapdoor \(\mathbf {T}_\mathbf {A}\) to generate the secret keys. When \(\mathcal A\) queries a secret key for \(\mathsf {ID}\), the challenger returns \(\mathbf {e}_{\mathsf {ID}}\mathrel {\mathop :}=\mathsf {Sample}\mathbb {Z}(\sigma ;\widehat{\mathsf {H}}(\mathsf {ID}))\). For any fixed \(\mathbf {u}_{\mathsf {ID}}\in \mathbb {Z}_q^n\), let \(\mathbf {e}_{\mathsf {ID},\mathbf {u}_{\mathsf {ID}}}^{(1)} \) and \(\mathbf {e}_{\mathsf {ID},\mathbf {u}_{\mathsf {ID}}}^{(2)} \) be random variables that are distributed according to the distributions of \(\mathbf {e}_{\mathsf {ID}}\) conditioning on \(\mathsf {H}(\mathsf {ID})=\mathbf {u}_{\mathsf {ID}}\) in \(\mathsf {Game}_1\) and \(\mathsf {Game}_2\), respectively. Due to Lemma 8, we have \(\varDelta (\mathbf {e}_{\mathsf {ID},\mathbf {u}_{\mathsf {ID}}}^{(1)},D_\mathrm{\Lambda ^{\perp }_{\mathbf {u}_{\mathsf {ID}}}(\mathrm{\mathbf{A}}), \sigma })\le 2^{ -\varOmega (n) }\). On the other hand, due to Lemma 4, we have \(\varDelta (\mathbf {e}_{\mathsf {ID},\mathbf {u}_{\mathsf {ID}}}^{(2)},D_\mathrm{\Lambda ^{\perp }_{\mathbf {u}_{\mathsf {ID}}}(\mathrm{\mathbf{A}}), \sigma })\le 2^{-\varOmega (n)}\). Since \(\mathcal {A}\) obtains at most \(Q_{\mathsf {ID}}\) user secret keys \(\mathbf {e}_{\mathsf {ID}}\), we have \(\big | \Pr [X_1] - \Pr [X_2] \big | = Q_{\mathsf {ID}}\cdot 2^{-\varOmega (n) }\).
\(\mathsf {Game}_3{:}\) In this game, we change the way the matrix \(\mathbf {A}\) is generated. Concretely, the challenger chooses \(\mathbf {A}\leftarrow \mathbb {Z}_q^{n\times m}\) without generating the associated trapdoor \(\mathbf {T}_{\mathbf {A}}\). By Lemma 8, the distribution of \(\mathbf {A}\) differs at most by \(2^{ -\varOmega (n)}\). Since the challenger can answer all the secret key queries without the trapdoor due to the change we made in the previous game, the view of \(\mathcal {A}\) is altered only by \(2^{ -\varOmega (n)}\). Therefore, we have \(\big | \Pr [X_2] - \Pr [X_3] \big | = 2^{ -\varOmega (n)}.\)
\(\mathsf {Game}_4{:}\) In this game, we change the way the challenge ciphertext is created when \(\mathsf {coin}= 0\). Recall in the previous games when \(\mathsf {coin}= 0\), the challenger created a valid challenge ciphertext as in the real scheme. In this game, to create the challenge ciphertext for identity \(\mathsf {ID}^*\) and message bit \(\mathsf {M}^*\), the challenger first computes \(\mathbf {e}_{\mathsf {ID}^*}\mathrel {\mathop :}=\mathsf {Sample}\mathbb {Z}(\sigma ;\widehat{\mathsf {H}}(\mathsf {ID}^*))\) and \(\mathbf {u}_{\mathsf {ID}^*}\mathrel {\mathop :}=\mathbf {A}\mathbf {e}_{\mathsf {ID}^*}\). Then the challenger picks \(\mathbf {s}\leftarrow \mathbb {Z}_q^n\), \(\bar{\mathbf {x}} \leftarrow D_{\mathbb {Z}^m, {\alpha q}}\) and computes \(\mathbf {v}= \mathbf {A}^\top \mathbf {s}+ \bar{\mathbf {x}} \in \mathbb {Z}_q^m\). It then runs
from Lemma 7, where \(\mathbf {I}_m\) is the identity matrix with size m. Let \(c'_0 \in \mathbb {Z}_q\) denote the first entry of \(\mathbf {c}'\) and \(\mathbf {c}_1 \in \mathbb {Z}_q^m\) denote the remaining entries of \(\mathbf {c}'\). Finally, the challenger outputs the challenge ciphertext as
We now proceed to bound \(| \Pr [X_3] - \Pr [X_4] |\). We apply the noise rerandomization lemma (Lemma 7) with \(\mathbf {V}= [\mathbf {e}_{\mathsf {ID}^*} | \mathbf {I}_m]\), \(\mathbf {b}=\mathbf {A}^\top \mathbf {s}\) and \(\mathbf {z}= \bar{\mathbf {x}}\) to see that the following equation holds:
where \(\mathbf {x}'\) is distributed according to a distribution whose statistical distance is at most \(2^{-\varOmega (n)}\) from \(D_{\mathbb {Z}^{m + 1}, \alpha ' q}\). Here, the last equality follows from \(\mathbf {A}\mathbf {e}_{\mathsf {ID}^*} = \mathbf {u}_{\mathsf {ID}^*}\) and we can appropriately apply the noise rerandomization lemma since we have the following for our parameter selection:
where the second inequality holds with \(1-2^{-\varOmega (n)}\) probability. It therefore follows that the statistical distance between the distributions of the challenge ciphertext in \(\mathsf {Game}_3\) and \(\mathsf {Game}_4\) is at most \(2^{-\varOmega (n)}\). Therefore, we may conclude that \(\big | \Pr [X_3] - \Pr [X_4] \big | = 2^{-\varOmega (n)}.\)
\(\mathsf {Game}_5{:}\) In this game, we further change the way the challenge ciphertext is created when \(\mathsf {coin}= 0\). If \(\mathsf {coin}= 0\), to create the challenge ciphertext the challenger first picks \(\mathbf {b}\leftarrow \mathbb {Z}_q^m\), \(\bar{\mathbf {x}} \leftarrow D_{\mathbb {Z}^m, \alpha q}\) and computes \(\mathbf {v}= \mathbf {b}+ \bar{\mathbf {x}} \in \mathbb {Z}_q^m\). It then runs the \(\mathsf {ReRand}\) algorithm as in \(\mathsf {Game}_4\). Finally, it sets the challenge ciphertext as in Eq. (1). We claim that \(\big | \Pr [X_4] - \Pr [X_5] \big |\) is negligible assuming the hardness of the \(\mathsf {LWE}_{n, m, q, D_{\mathbb {Z}, {\alpha q}}}\) problem relative to a quantum random oracle  . To show this, we use \(\mathcal {A}\) to construct an adversary \(\mathcal {B}\) that breaks the LWE assumption relative to
. To show this, we use \(\mathcal {A}\) to construct an adversary \(\mathcal {B}\) that breaks the LWE assumption relative to  .
.
\(\mathcal {B}\) is given a problem instance of LWE as \((\mathbf {A}, \mathbf {v}= \mathbf {b}+ \bar{\mathbf {x}}) \in \mathbb {Z}_q^{n \times m} \times \mathbb {Z}_q^m\) where \(\bar{\mathbf {x}} \leftarrow D_{\mathbb {Z}^m, \alpha q}\). The task of \(\mathcal {B}\) is to distinguish whether \(\mathbf {b}= \mathbf {A}^\top \mathbf {s}\) for some \(\mathbf {s}\leftarrow \mathbb {Z}_q^n\) or \(\mathbf {b}\leftarrow \mathbb {Z}_q^m\). First, we remark that \(\mathcal {B}\) can simulate the quantum random oracle  for \(\mathcal {A}\) by using its own random oracle
for \(\mathcal {A}\) by using its own random oracle  because \(\mathsf {H}\) is programmed as \(\mathsf {H}(\mathsf {ID})\mathrel {\mathop :}=\mathbf {A}\mathrm{\mathbf{\mathbf {e}}}_{\mathsf {ID}}\) where \(\mathbf {e}_{\mathsf {ID}}\mathrel {\mathop :}=\mathsf {Sample}\mathbb {Z}(\sigma ;\widehat{\mathsf {H}}(\mathsf {ID}))\) by the modification we made in \(\mathsf {Game}_1\). \(\mathcal {B}\) sets the master public key \(\mathsf {mpk}\) to be the LWE matrix \(\mathbf {A}\). Note that unlike the real IBE scheme, \(\mathcal {B}\) does not require the master secret key \(\mathbf {T}_\mathbf {A}\) due to the modification we made in \(\mathsf {Game}_3\). Namely, when \(\mathcal {A}\) queries \(\mathsf {ID}\) for the key oracle, \(\mathcal {B}\) just returns \(\mathbf {e}_{\mathsf {ID}}\mathrel {\mathop :}=\mathsf {Sample}\mathbb {Z}(\sigma ;\widehat{\mathsf {H}}(\mathsf {ID}))\). To generate the challenge ciphertext, \(\mathcal {B}\) first picks \(\mathsf {coin}\leftarrow \{0, 1\}\). If \(\mathsf {coin}= 0\), it generates the challenge ciphertext as in Eq. (1) using \(\mathbf {v}\), and returns it to \(\mathcal {A}\). We emphasize that all \(\mathcal {B}\) needs to do to generate the ciphertext is to run the \(\mathsf {ReRand}\) algorithm, which it can do without the knowledge of the secret randomness \(\mathbf {s}\) and \(\bar{\mathbf {x}}\). If \(\mathsf {coin}= 1\), \(\mathcal {B}\) returns a random ciphertext using \(\mathsf {CTSam}(\mathsf {mpk})\). At the end of the game, \(\mathcal {A}\) outputs \(\widehat{\mathsf {coin}}\). Finally, \(\mathcal {B}\) outputs 1 if \(\widehat{\mathsf {coin}} = \mathsf {coin}\) and 0 otherwise.
because \(\mathsf {H}\) is programmed as \(\mathsf {H}(\mathsf {ID})\mathrel {\mathop :}=\mathbf {A}\mathrm{\mathbf{\mathbf {e}}}_{\mathsf {ID}}\) where \(\mathbf {e}_{\mathsf {ID}}\mathrel {\mathop :}=\mathsf {Sample}\mathbb {Z}(\sigma ;\widehat{\mathsf {H}}(\mathsf {ID}))\) by the modification we made in \(\mathsf {Game}_1\). \(\mathcal {B}\) sets the master public key \(\mathsf {mpk}\) to be the LWE matrix \(\mathbf {A}\). Note that unlike the real IBE scheme, \(\mathcal {B}\) does not require the master secret key \(\mathbf {T}_\mathbf {A}\) due to the modification we made in \(\mathsf {Game}_3\). Namely, when \(\mathcal {A}\) queries \(\mathsf {ID}\) for the key oracle, \(\mathcal {B}\) just returns \(\mathbf {e}_{\mathsf {ID}}\mathrel {\mathop :}=\mathsf {Sample}\mathbb {Z}(\sigma ;\widehat{\mathsf {H}}(\mathsf {ID}))\). To generate the challenge ciphertext, \(\mathcal {B}\) first picks \(\mathsf {coin}\leftarrow \{0, 1\}\). If \(\mathsf {coin}= 0\), it generates the challenge ciphertext as in Eq. (1) using \(\mathbf {v}\), and returns it to \(\mathcal {A}\). We emphasize that all \(\mathcal {B}\) needs to do to generate the ciphertext is to run the \(\mathsf {ReRand}\) algorithm, which it can do without the knowledge of the secret randomness \(\mathbf {s}\) and \(\bar{\mathbf {x}}\). If \(\mathsf {coin}= 1\), \(\mathcal {B}\) returns a random ciphertext using \(\mathsf {CTSam}(\mathsf {mpk})\). At the end of the game, \(\mathcal {A}\) outputs \(\widehat{\mathsf {coin}}\). Finally, \(\mathcal {B}\) outputs 1 if \(\widehat{\mathsf {coin}} = \mathsf {coin}\) and 0 otherwise.
It can be seen that if \(\mathbf {A}, \mathbf {v}\) is a valid LWE sample (i.e., \(\mathbf {v}= \mathbf {A}^\top \mathbf {s}\)), the view of the adversary corresponds to \(\mathsf {Game}_4\). Otherwise (i.e., \(\mathbf {v}\leftarrow \mathbb {Z}_q^m\)), it corresponds to \(\mathsf {Game}_5\). Therefore we have \(\big | \Pr [X_4] - \Pr [X_5] \big | =\mathsf {Adv}_{\mathcal {B},\mathsf {QRO}_{\ell _{\mathsf {ID}},\ell _r}}^{\mathsf {LWE}_{n, m, q, D_{\mathbb {Z}, {\alpha q}}}}(\lambda ) \). As for the running time, we have \(\mathsf {Time}(\mathcal {B})= \mathsf {Time}(\mathcal {A})+(Q_{\mathsf {H}}+Q_{\mathsf {ID}})\cdot \mathsf {poly}(\lambda )\) since all \(\mathcal {B}\) has to do is to run \(\mathcal {A}\) once plus to compute some additional computations that can be done in a fixed polynomial time whenever \(\mathcal {A}\) makes a quantum random oracle or secret key query.
\(\mathsf {Game}_6{:}\) In this game, we further change the way the challenge ciphertext is created. If \(\mathsf {coin}= 0\), to create the challenge ciphertext the challenger first picks \(\mathbf {b}\leftarrow \mathbb {Z}_q^m\), \(\mathbf {x}' \leftarrow D_{\mathbb {Z}^m, \alpha ' q }\) and computes
It then parses \(\mathbf {c}'\) into \(c'_0\) and \(\mathbf {c}_1\) (as in \(\mathsf {Game}_4\)) and sets the challenge ciphertext as Eq. (1). Similarly to the change from \(\mathsf {Game}_3\) to \(\mathsf {Game}_4\), we have \(\big | \Pr [X_5] - \Pr [X_6] \big | = 2^{-\varOmega (n)}\) by Lemma 7.
It remains to show that no adversary has non-negligible chance in winning \(\mathsf {Game}_6\). Notice that when \(\mathsf {coin}=0\), the challenge ciphertext can be written as
where \(x'_0\) is the first entry of \(\mathbf {x}'\) and \(\mathbf {x}'_1\) is the remaining entries. It suffices to show that the joint distribution of \(( \mathbf {b}, \mathbf {e}^\top _{\mathsf {ID}^*} \mathbf {b})\) is statistically close to the uniform distribution over \(\mathbb {Z}_q^m \times \mathbb {Z}_q\), conditioned on \(\mathbf {u}_{\mathsf {ID}^*}\). From the view of \(\mathcal {A}\), \(\mathbf {e}_{\mathsf {ID}^*}\) is distributed as \(D_\mathrm{\Lambda ^{\perp }_{\mathrm{\mathbf{u}}(\mathsf {ID}^*)}(\mathrm{\mathbf{A}}), \sigma }\) because all information of \(\mathbf {e}_{\mathsf {ID}^*}\) revealed to \(\mathcal {A}\) is \(\mathsf {H}(\mathsf {ID}^*)=\mathbf {A}\mathbf {e}_{\mathsf {ID}^*}\) where \(\mathbf {e}_{\mathsf {ID}^*}= \mathsf {Sample}\mathbb {Z}(\sigma ;\widehat{\mathsf {H}}(\mathsf {ID}^*))\) and \(\widehat{\mathsf {H}}(\mathsf {ID}^*)\) is completely random from the view of \(\mathcal {A}\). (Remark that \(\widehat{\mathsf {H}}(\mathsf {ID}^*)\) is used in the game only when \(\mathcal {A}\) queries \(\mathsf {ID}^*\) to the key generation oracle, which is prohibited in the adaptively-anonymous security game.) By Lemma 6, we have
for all but \(2^{-\varOmega (n)}\) fraction of \(\mathbf {A}\). Now we can apply the leftover hash lemma since \(\mathbf {b}\) is distributed uniformly at random over \(\mathbb {Z}_q^m\) and conclude that \(( \mathbf {b}, \mathbf {e}^\top _{\mathsf {ID}^*} \mathbf {b})\) is \(\sqrt{ q/ 2^{m-1}}\)-close to the uniform distribution by the leftover hash lemma. Hence, we have \( \Pr [X_6] \le 2^{-\varOmega (n)} + \sqrt{ q/ 2^{m-1}} < 2^{-\varOmega (n)} \).
Therefore, combining everything together, the theorem is proven.
4 (Almost) Tightly Secure Multi-challenge IBE
In this section, we propose an IBE scheme that is (almost) tightly secure in the multi-challenge setting. The security of the scheme is proven both in the classical ROM and QROM settings. Our construction is obtained by applying the Katz-Wang [KW03] technique to the original GPV-IBE scheme.
4.1 Construction
Let the identity space \(\mathcal {ID}\) of the scheme be \(\mathcal {ID}=\{0,1\}^{\ell _{\mathsf {ID}}}\), where \(\ell _{\mathsf {ID}}(\lambda )\) denotes the identity-length. Let also \(\mathsf {H}: \{0,1\}^{\ell _{\mathsf {ID}}+1} \rightarrow \mathbb {Z}^n_q\) be a hash function treated as a random oracle during the security analysis where \(\ell _{\mathsf {ID}}\) denotes the identity-length. The IBE scheme \(\mathsf {GPV}_{\mathsf {mult}}\) is given as follows. For simplicity, we describe the scheme as a stateful one. As remarked in Remark 1, we can make the scheme stateless without any additional assumption in the QROM.
-
Setup\((1^\lambda )\): On input \(1^\lambda \), it first chooses a prime q, positive integers \(n, m,\gamma \), and Gaussian parameters \(\alpha , \sigma \), where all these values are implicitly a function of the security parameter \(\lambda \). The precise parameter selection is specified in the following section. It then runs \((\mathbf {A}, \mathbf {T}_\mathbf {A}) \leftarrow \mathsf {TrapGen}(1^n, 1^m, q)\) to generate a matrix \(\mathbf {A}\in \mathbb {Z}_q^{n \times m}\) with a trapdoor \(\mathbf {T}_{\mathbf {A}} \in \mathbb {Z}^{m \times m}\) such that
 . Then it outputs $$\begin{aligned} \mathsf {mpk}= \mathbf {A}\quad \text {and} \quad \mathsf {msk}= \mathbf {T}_{\mathbf {A}} \end{aligned}$$
. Then it outputs $$\begin{aligned} \mathsf {mpk}= \mathbf {A}\quad \text {and} \quad \mathsf {msk}= \mathbf {T}_{\mathbf {A}} \end{aligned}$$ -
KeyGen\(( \mathsf {mpk}, \mathsf {msk}, \mathsf {ID})\): If \(\mathsf {sk}_{\mathsf {ID}}\) is already generated, then this algorithm returns it. Otherwise it picks
 , computes \(\mathbf {u}_{\mathsf {ID}\Vert b_\mathsf {ID}} = \mathsf {H}(\mathsf {ID}\Vert b_\mathsf {ID})\), and samples \(\mathbf {e}_{\mathsf {ID}\Vert b_\mathsf {ID}} \in \mathbb {Z}^{m}\) such that $$\begin{aligned} \mathbf {A}\mathbf {e}_{\mathsf {ID}\Vert b_\mathsf {ID}} = \mathbf {u}_{\mathsf {ID}\Vert b_\mathsf {ID}} \mod q \end{aligned}$$
, computes \(\mathbf {u}_{\mathsf {ID}\Vert b_\mathsf {ID}} = \mathsf {H}(\mathsf {ID}\Vert b_\mathsf {ID})\), and samples \(\mathbf {e}_{\mathsf {ID}\Vert b_\mathsf {ID}} \in \mathbb {Z}^{m}\) such that $$\begin{aligned} \mathbf {A}\mathbf {e}_{\mathsf {ID}\Vert b_\mathsf {ID}} = \mathbf {u}_{\mathsf {ID}\Vert b_\mathsf {ID}} \mod q \end{aligned}$$as \(\mathbf {e}_{\mathsf {ID}\Vert b_\mathsf {ID}} \leftarrow \mathsf {SamplePre}(\mathbf {A}, \mathbf {T}_{\mathbf {A}}, \mathbf {u}_{\mathsf {ID}\Vert b_\mathsf {ID}}, \sigma )\). It returns \(\mathsf {sk}_\mathsf {ID}= ( b_\mathsf {ID}, \mathbf {e}_{\mathsf {ID}\Vert b_\mathsf {ID}} )\) as the secret key.
-
Enc\((\mathsf {mpk}, \mathsf {ID}, \mathsf {M})\): To encrypt a message \(\mathsf {M}\in \{0,1\}\), it first samples
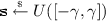 , \(\mathrm{\mathbf{x}} \leftarrow D_{\mathbb {Z}^m, \alpha q}\). Then it computes \(\mathbf {u}_{\mathsf {ID}\Vert 0} = \mathsf {H}(\mathsf {ID}\Vert 0)\) and \(\mathbf {u}_{\mathsf {ID}\Vert 1} = \mathsf {H}(\mathsf {ID}\Vert 1)\) and sets the ciphertext as $$\begin{aligned} c_0 = \mathbf {u}_{\mathsf {ID}\Vert 0}^\top \mathbf {s}+ \mathsf {M}\lfloor q/2 \rceil , \quad c_1 = \mathbf {u}_{\mathsf {ID}\Vert 1}^\top \mathbf {s}+ \mathsf {M}\lfloor q/2 \rceil , \quad \mathbf {c}_2 = \mathbf {A}^\top \mathbf {s}+ \mathbf {x}. \end{aligned}$$
, \(\mathrm{\mathbf{x}} \leftarrow D_{\mathbb {Z}^m, \alpha q}\). Then it computes \(\mathbf {u}_{\mathsf {ID}\Vert 0} = \mathsf {H}(\mathsf {ID}\Vert 0)\) and \(\mathbf {u}_{\mathsf {ID}\Vert 1} = \mathsf {H}(\mathsf {ID}\Vert 1)\) and sets the ciphertext as $$\begin{aligned} c_0 = \mathbf {u}_{\mathsf {ID}\Vert 0}^\top \mathbf {s}+ \mathsf {M}\lfloor q/2 \rceil , \quad c_1 = \mathbf {u}_{\mathsf {ID}\Vert 1}^\top \mathbf {s}+ \mathsf {M}\lfloor q/2 \rceil , \quad \mathbf {c}_2 = \mathbf {A}^\top \mathbf {s}+ \mathbf {x}. \end{aligned}$$Finally, it outputs the ciphertext \(C = (c_0, c_1, \mathbf {c}_2) \in \mathbb {Z}_q \times \mathbb {Z}_q \times \mathbb {Z}_q^m\).
-
Dec\((\mathsf {mpk}, \mathsf {sk}_\mathsf {ID}, C)\): To decrypt a ciphertext \(C = (c_0, c_1, \mathbf {c}_2)\) with a secret key \(\mathsf {sk}_\mathsf {ID}\), it computes \(w = c_{b_\mathsf {ID}} - \mathbf {c}_2^\top \mathbf {e}_{\mathsf {ID}\Vert b_\mathsf {ID}} \in \mathbb {Z}_q\) and outputs 0 if w is closer to 0 than to \(\lfloor q/2 \rceil \) modulo q. Otherwise it outputs 1.
4.2 Correctness and Parameter Selection
The following shows correctness of the above IBE scheme.
Lemma 12
(Correctness). Suppose the parameters q, \(\sigma \), and \(\alpha \) are such that

Let \(\mathrm{\mathbf{e}}_{\mathsf {ID}\Vert b_\mathsf {ID}} \leftarrow \mathsf{KeyGen}(\mathbf {A}, \mathbf {T}_{\mathbf {A}}, {\mathsf {ID}}), C \leftarrow \mathsf{Enc}(\mathbf {A}, {\mathsf {ID}'}, \mathsf {M}\in \{0,1\})\) and \(\mathsf {M}' \leftarrow \mathsf{Dec}(\mathbf {A}, \mathrm{\mathbf{e}}_{\mathsf {ID}\Vert b_\mathsf {ID}}, C).\) If \({\mathsf {ID}} = {\mathsf {ID}'}\), then with overwhelming probability we have \(\mathsf {M}' = \mathsf {M}\).
Proof
When the Dec algorithm operates as specified, we have
By Lemma 8 and the condition posed on the choice of \(\sigma \), we have that the distribution of \(\mathbf {e}_{\mathsf {ID}\Vert b_\mathsf {ID}}\) is \(2^{-\varOmega (n)}\) close to \(D_{\mathrm{\Lambda }_{\mathbf {u}_{\mathsf {ID}\Vert b_\mathsf {ID}}}^{\perp }(\mathbf {A}),\sigma }\). Therefore, by Lemma 5, we have \(\Vert \mathbf {x}\Vert \le \alpha q \sqrt{m}\), and \(\Vert \mathrm{\mathbf{e}}_{\mathsf {ID}\Vert b_\mathsf {ID}} \Vert \le \sigma \cdot \sqrt{m}\) except for \(2^{-\varOmega (n)}\) probability. Then, the error term is bounded by
Hence, for the error term to have absolute value less than q / 4, it suffices to choose q and \(\alpha \) as in the statement of the lemma.
Parameter Selection. For example, we can set the parameters \(\ell , n, m, q, \sigma , \alpha , \beta , \gamma \) as follows:
where \(\kappa >0\) is a constant that can be set arbitrarily small. To withstand attacks running in time \(2^{\lambda }\), we may set \(\ell =\tilde{\varOmega }(\lambda )\). In the above, we round up m to the nearest integer and q to the nearest largest prime. As the case with the single-challenge setting, if we make the more aggressive choice of using the negligible notion \(2^{-\omega (\log \lambda )}\), we will be able to obtain better parameter selections. More detailed discussion on the parameter selection can be found in the full version.
4.3 Security
We can (almost) tightly prove the security of our IBE scheme \(\mathsf {GPV}_{\mathsf {mult}}\) both in the classical ROM and QROM settings. The following theorem addresses the security of \(\mathsf {GPV}_{\mathsf {mult}}\) in the classical ROM setting. The proof of the theorem can be found in the full version.
Theorem 3
The IBE scheme \(\mathsf {GPV}_{\mathsf {mult}}\) is adaptively-anonymous multi-challenge secure assuming the hardness of \(\mathsf {LWE}_{\ell , m, q, \chi }\) in the random oracle model, where \(\chi = D_{\mathbb {Z}, \alpha q}\). Namely, for any classical adversary \(\mathcal {A}\) making at most \(Q_{\mathsf {H}}\) queries to \(\mathsf {H}\), \(Q_{\mathsf {ch}}\) challenge queries, and \(Q_{\mathsf {ID}}\) secret key queries, there exists an algorithm \(\mathcal {B}\) such that
and
As we explained in the introduction, our analysis in the ROM can be easily extended to the QROM setting. We can prove the following theorem that addresses the security of \(\mathsf {GPV}_{\mathsf {mult}}\) in the QROM. The proof can be found in the full version.
Theorem 4
The IBE scheme \(\mathsf {GPV}_{\mathsf {mult}}\) is adaptively-anonymous multi-challenge secure assuming the hardness of \(\mathsf {LWE}_{\ell ,m, q, \chi }\) in the quantum random oracle model, where \(\chi = D_{\mathbb {Z}, \alpha q}\). Namely, for any classical adversary \(\mathcal {A}\) making at most \(Q_{\mathsf {H}}\) quantum random oracle queries, \(Q_{\mathsf {ch}}\) challenge queries, and \(Q_{\mathsf {ID}}\) secret key queries, there exists an algorithm \(\mathcal {B}\) making at most \(3Q_{\mathsf {H}}+2Q_{\mathsf {ID}}+6Q_{\mathsf {ch}}\) quantum random oracle queries such that
and
where \(\ell _{r}\) denotes the length of the randomness for \(\mathsf {Sample}\mathbb {Z}\).
These proofs are similar and obtained by combining the idea of using the lossy mode for LWE with the Katz-Wang technique as we explained in Sect. 1.3. We need some results on randomness extraction and lossy mode LWE during the proof. The details can be found in the full version.
Notes
- 1.
Our parameter selection in the main body may seem much worse compared to GPV-IBE, but this is only because we choose the parameters conservatively. Specifically, we can set the parameters to be only slightly worse than GPV-IBE by setting them less conservatively as in [GPV08]. Please, see end of Sect. 3.2 for more details.
- 2.
Compared to [KY16] our choice of parameter is more conservative since we consider \(2^{-\varOmega (n)}\) statistical distance rather than \(2^{-\omega (\log n)}\).
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_28
Alkim, E., et al.: Revisiting TESLA in the quantum random oracle model. In: Lange, T., Takagi, T. (eds.) PQCrypto 2017. LNCS, vol. 10346, pp. 143–162. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-59879-6_9
Applebaum, B., Cash, D., Peikert, C., Sahai, A.: Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 595–618. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_35
Alwen, J., Dodis, Y., Naor, M., Segev, G., Walfish, S., Wichs, D.: Public-key encryption in the bounded-retrieval model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 113–134. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_6
Attrapadung, N., Hanaoka, G., Yamada, S.: A framework for identity-based encryption with almost tight security. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part I. LNCS, vol. 9452, pp. 521–549. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_22
Alwen, J., Krenn, S., Pietrzak, K., Wichs, D.: Learning with rounding, revisited. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 57–74. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_4
Ambainis, A., Rosmanis, A., Unruh, D.: Quantum attacks on classical proof systems: The hardness of quantum rewinding. In: FOCS, pp. 474–483. IEEE (2014)
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_3
Bourse, F., Del Pino, R., Minelli, M., Wee, H.: FHE circuit privacy almost for free. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part II. LNCS, vol. 9815, pp. 62–89. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_3
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13
Bai, S., Galbraith, S.D.: An improved compression technique for signatures based on learning with errors. In: Benaloh, J. (ed.) CT-RSA 2014. LNCS, vol. 8366, pp. 28–47. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04852-9_2
Bellare, M., Kiltz, E., Peikert, C., Waters, B.: Identity-based (lossy) trapdoor functions and applications. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 228–245. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_15
Boyen, X., Li, Q.: Towards tightly secure lattice short signature and Id-based encryption. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 404–434. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_14
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: STOC, pp. 575–584 (2013)
Banerjee, A., Peikert, C., Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 719–737. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_42
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: CCS, pp. 62–73. ACM (1993)
Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 207–222. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_13
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 523–552. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_27
Coron, J.-S.: A variant of Boneh-Franklin IBE with a tight reduction in the random oracle model. Des. Codes Cryptogr. 50(1), 115–133 (2009)
Cramer, R., Shoup, V.: A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 13–25. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055717
Chen, J., Wee, H.: Fully, (Almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_25
Gong, J., Dong, X., Chen, J., Cao, Z.: Efficient IBE with tight reduction to standard assumption in the multi-challenge setting. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 624–654. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_21
Gentry, C.: Practical identity-based encryption without random oracles. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 445–464. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_27
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Goldwasser, S., Kalai, Y., Peikert, C., Vaikuntanathan, V.: Robustness of the learning with errors assumption. In: ICS, pp. 230–240 (2010)
Goldreich, O.: Two remarks concerning the goldwasser-micali-rivest signature scheme. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 104–110. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_8
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC, pp. 197–206. ACM (2008)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_35
Hofheinz, D., Koch, J., Striecks, C.: Identity-based encryption with (almost) tight security in the multi-instance, multi-ciphertext setting. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 799–822. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_36
Kiltz, E., Lyubashevsky, V., Schaffner, C.: A concrete treatment of fiat-shamir signatures in the quantum random-oracle model. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 552–586. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_18
Katz, J., Wang, N.: Efficiency improvements for signature schemes with tight security reductions. In: Computer and Communications Security, pp. 155–164. ACM (2003)
Katsumata, S., Yamada, S.: Partitioning via non-linear polynomial functions: more compact IBEs from ideal lattices and bilinear maps. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 682–712. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_23
Libert, B., Sakzad, A., Stehlé, D., Steinfeld, R.: All-but-many lossy trapdoor functions and selective opening chosen-ciphertext security from LWE. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part III. LNCS, vol. 10403, pp. 332–364. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_12
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Micciancio, D., Regev, O.: Worst-case to average-case reductions based on gaussian measures. SIAM J. Comput. 37(1), 267–302 (2007)
Nielsen, M.A., Isaac, L.: Quantum Computation and Quantum Information. Cambridge University Press, Chuang (2000)
Peikert, C.: Limits on the hardness of lattice problems in ell \(\_\)p norms. In: Conference on Computational Complexity, pp. 333–346. IEEE (2007)
Peikert, C.: Public-key cryptosystems from the worst-case shortest vector problem. In: STOC, pp. 333–342. ACM (2009)
Peikert, C.: An efficient and parallel gaussian sampler for lattices. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 80–97. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_5
Peikert, C., Rosen, A.: Efficient collision-resistant hashing from worst-case assumptions on cyclic lattices. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 145–166. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_8
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: STOC, pp. 84–93. ACM Press (2005)
Regev, O.: The learning with errors problem. Invited survey in CCC (2010)
Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: FOCS, pp. 124–134. IEEE (1994)
Saito, T., Xagawa, K., Yamakawa, T.: Tightly-secure key-encapsulation mechanism in the quantum random oracle model. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 520–551. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_17
Targhi, E.E., Unruh, D.: Post-quantum security of the fujisaki-okamoto and OAEP transforms. In: Hirt, M., Smith, A. (eds.) TCC 2016, Part II. LNCS, vol. 9986, pp. 192–216. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_8
Unruh, D.: Quantum position verification in the random oracle model. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 1–18. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_1
Unruh, D.: Revocable quantum timed-release encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 129–146. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_8
Unruh, D.: Non-interactive zero-knowledge proofs in the quantum random oracle model. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 755–784. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_25
Unruh, D.: Post-quantum security of fiat-shamir. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part I. LNCS, vol. 10624, pp. 65–95. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_3
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_7
Zhandry, M.: How to construct quantum random functions. In: FOCS, pp. 679–687. IEEE (2012)
Zhandry, M.: Secure identity-based encryption in the quantum random oracle model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 758–775. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_44
Acknowledgement
The first author was partially supported by JST CREST Grant Number JPMJCR1302 and JSPS KAKENHI Grant Number 17J05603. The second author was supported by JST CREST Grant No. JPMJCR1688 and JSPS KAKENHI Grant Number 16K16068.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Katsumata, S., Yamada, S., Yamakawa, T. (2018). Tighter Security Proofs for GPV-IBE in the Quantum Random Oracle Model. In: Peyrin, T., Galbraith, S. (eds) Advances in Cryptology – ASIACRYPT 2018. ASIACRYPT 2018. Lecture Notes in Computer Science(), vol 11273. Springer, Cham. https://doi.org/10.1007/978-3-030-03329-3_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-03329-3_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03328-6
Online ISBN: 978-3-030-03329-3
eBook Packages: Computer ScienceComputer Science (R0)





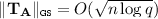 .
. , outputs a vector
, outputs a vector  . Then it outputs
. Then it outputs  by Lemma
by Lemma  , the challenger returns
, the challenger returns  .
.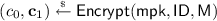 if
if  if
if  . Then it outputs
. Then it outputs  , computes
, computes 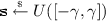 ,
, 