Abstract
We initiate a study of garbled circuits that contain both Boolean and arithmetic gates in secure multiparty computation. In particular, we incorporate the garbling gadgets for arithmetic circuits recently presented by Ball, Malkin, and Rosulek (ACM CCS 2016) into the multiparty garbling paradigm initially introduced by Beaver, Micali, and Rogaway (STOC ’90). This is the first work that studies arithmetic garbled circuits in the multiparty setting. Using mixed Boolean-arithmetic circuits allows more efficient secure computation of functions that naturally combine Boolean and arithmetic computations. Our garbled circuits are secure in the semi-honest model, under the same hardness assumptions as Ball et al., and can be efficiently and securely computed in constant rounds assuming an honest majority.
We first extend free addition and multiplication by a constant to the multiparty setting. We then extend to the multiparty setting efficient garbled multiplication gates. The garbled multiplication gate construction we show was previously achieved only in the two-party setting and assuming a random oracle.
We further present a new garbling technique, and show how this technique can improve efficiency in garbling selector gates. Selector gates compute a simple “if statement” in the arithmetic setting: the gate selects the output value from two input integer values, according to a Boolean selector bit; if the bit is 0 the output equals the first value, and if the bit is 1 the output equals the second value. Using our new technique, we show a new and designated garbled selector gate that reduces by approximately \(33\%\) the evaluation time, for any number of parties, from the best previously known constructions that use existing techniques and are secure based on the same hardness assumptions.
On the downside, we find that testing equality and computing exponentiation by a constant are significantly more complex to garble in the multiparty setting than in the two-party setting.
Research supported by ISF grant 152/17, by the Frankel Center for Computer Science, and by the BGU Cyber Security Research Center.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Garbled circuits are a fundamental cryptographic primitive, introduced by Yao in the 1980s [33]. They are used in one-time programs, key-dependent message security, homomorphic computation, verifiable computation, and more. The original motivation of garbled circuits, and to date still their main use, is for secure computation. The most practical approaches of secure two-party computation are based on garbled circuits.
Since their introduction, garbled circuits have been significantly optimized in a series of works, [5, 21, 25, 26, 29,30,31, 34] being a very partial list. These works reduced the size of the garbled gates and concretely improved the efficiency of garbling protocols. For example, using the free-XOR technique introduced by Kolesnikov and Schneider [25], XOR gates are “for free”, meaning they incur no communication or cryptographic operations.
Due to efficiency reasons, garbled circuits were almost exclusively considered for Boolean circuits. However, there have been a few attempts to efficiently extend the ideas of garbled circuits to arithmetic circuits (in the two-party setting), e.g., [1, 2, 28]. The works of Ball et al. [2] and Malkin et al. [28] showed how to extend free-XOR to free addition and multiplication by a constant. They further showed how to efficiently garble multiplication in \({\mathbb {F}}_p\), for small p. Ball et al. also showed how to efficiently garble exponentiation by a constant. By combining CRT representations in a primorial modulus, Ball et al. showed that the above results extend to efficient garbling of arithmetic circuits over the integers.
Garbled circuits are important also for secure multiparty computation. The multiparty garbling paradigm was introduced by Beaver et al. [4] in the first constant round secure multiparty protocol. The first implementation of secure multiparty computation, FairplayMP [6], followed this multiparty garbling paradigm. Recently, experimental results in [8, 32] suggested that concretely efficient implementations following the multiparty garbling paradigm, such as [8] in the semi-honest model and [22, 32] in the malicious model, are more suited for secure multiparty computations over networks with high latency, such as the internet.
The adversarial model. We assume throughout that the adversary is semi-honest, i.e., follows the protocol but might try to learn private information from the messages it receives. A more realistic adversarial model is the malicious adversary, which can deviate from the protocol arbitrarily. Nevertheless, advances in semi-honest secure computation, and garbled circuits in particular, have often proved to be a significant stepping stone for later advances in the malicious model. Aside from numerous examples in the two-party setting, this was recently demonstrated also in the multiparty setting: the concretely efficient semi-honest protocols of [8] have been efficiently extended to maliciously secure protocols in [22] and [7].
We also assume an honest majority, i.e., the adversary corrupts only a strict minority of the parties. We do so in order to use the efficient constant round protocol for unbounded fan-in multiplication of Bar-Ilan and Beaver [3], which is needed in several of our constructions. Note that this is only needed for gates with mixed Boolean-arithmetic inputs/output. Thus, arithmetic circuits can also be garbled efficiently in the dishonest majority setting, assuming oblivious transfer. Due to space constraints, this is explained in the full version.
The hardness assumption we rely on is the existence of a mixed-modulus circular correlation robust (MMCCR) hash function, introduced by Ball et al. [2]; see Definition 1. The definition of MMCCR hash functions is similar to the definition of circular 2-correlation robust hash functions, introduced by Choi et al. [12] to prove the security of free-XOR [25]. Ball et al. [2] conjecture that one could use AES to construct a MMCCR hash function. Using AES is known to be extremely fast in practice using AES-NI instructions.
Our results and techniques. We study garbled circuits containing both a Boolean part and an arithmetic part in secure multiparty computation. We show both how to compute efficient arithmetic garbled circuits, and also how the Boolean and arithmetic parts of the circuit can efficiently affect each other. This allows for more efficient secure multiparty computation of functions that naturally combine Boolean and arithmetic computations, see our motivating example below.
We begin by extending known results for garbled arithmetic circuits from the two-party setting to the multiparty setting. In the two-party setting, Ball et al. [2] and Malkin et al. [28] showed that the free-XOR idea of Kolesnikov and Schneider [25] can be extended to free addition and multiplication by a constant in \({\mathbb {F}}_p\). We show that these results naturally extend to the multiparty setting. This follows similar lines to the extension of free-XOR to the multiparty setting by Ben-Efraim et al. [8].
We further efficiently extend the half-gates construction of Zahur et al. [34] (which efficiently compute AND gates in the 2-party setting) to efficient multiplication gates in the multiparty setting. There are three challenges we overcome in this extension: (1) Since there is no single garbler, the parties perform the computation using their shares. This requires understanding the values computed in each half gate, which were not explicitly written (only implicitly used) in previous works. (2) Since the evaluating parties also participate in the garbling (and thus have additional knowledge), the output wire’s permutation element and keys are partitioned to avoid revealing secret information. (3) Extending from Boolean to \({\mathbb {F}}_p\) requires extending the technique of [34], by showing that the correct way to look at the solution of [34] is to multiply the external value of one wire with the key of the other. Proving this extended technique based on MMCCR also requires an additional step in the proof that was not needed in previous similar proofs (e.g., in [2, 34]).
Using the half-gate extension, we manage to garble multiplication gates in \({\mathbb {F}}_p\), in the multiparty setting, with only 2p garbled rows. By representing numbers in a primorial modulos and using the Chinese Remainder Theorem, as suggested by Ball et al. [2], we obtain efficient arithmetic computations over the integers. In the two-party setting, efficient garbled multiplication gates were previously suggested by Malkin et al. [28] and by Ball et al. [2], see Table 1.
We then show how the Boolean and arithmetic parts of the circuit efficiently affect each other. In the multiparty setting, this requires a simple primitive that we call a multifield-shared bit, in which the same bit is secret shared in multiple fields of different characteristics. We show an efficient protocol for constructing this primitive in the semi-honest model with an honest majority. Furthermore, we explain that this primitive can be precomputed before the circuit is known.
To show how the Boolean part can efficiently affect the arithmetic part, we look at selector gates, which compute a simple “if statement”: A selector gate has 3 input wires, \(x,y\), and \(w_{0}\). The wires \(x,y\) hold values in \({\mathbb {F}}_p\) and the wire \(w_{0}\) holds a Boolean value representing the selection bit. The output wire \(z\) should equal either \(x\) or \(y\), according to the value of the selection bit. I.e., denote the value on wire \(\omega \) by \(v_{\omega }\), then a selector gate computes the following simple if statement: If (\(v_{w_{0}}==0\)) then \(v_{z}=v_{x}\) else \(v_{z}=v_{y}\).
We show two constructions for garbled selector gates: the first is an extension of known techniques to the multiparty setting, using projection gates from Boolean to \({\mathbb {F}}_p\). To the best of our knowledge, this is the best construction of selector gates using existing techniques that relies only on MMCCR hash functions.Footnote 1 Our second construction is a designated construction, using new techniques described below. This construction reduces the evaluation time by approx. \(33\%\) from the construction using projection gates.
We give an informal overview of the main ideas in the designated selector gate construction: The gate contains two components. Using the first component, the evaluator tries to compute the multiplication between the Boolean value and the values in \({\mathbb {F}}_p\). But since the Boolean value seen by the evaluator is not the real value on the wire, this computation possibly inserts an error. To solve this, the second component is “corrector gates”. The result from the corrector gate is (freely) added in order to correct the values from the first component. However, the (possibly) inserted error depends on the value seen by the evaluator on the Boolean wire. Thus, there are in fact 2 corrector gates, and the evaluator decrypts only one of them, according to the value it sees. This raises a question of security, as a corrupt evaluator can also decrypt the “wrong” corrector gate. This issue is solved by double partitioning of the keys and permutation elements, ensuring the decrypted keys and external values on the “wrong” corrector gate leak no information, even given the correctly decrypted keys and values. To the best of our knowledge, the technique of using a double partition of the keys and permutation elements is new in this setting.
To show how the arithmetic part can affect the Boolean part, we extend to the multiparty setting the construction of Ball et al. [2] of gates that test equality. These equality gates use free subtraction and projection gates. Unfortunately, we find that garbling general projection gates, and garbling equality gates in particular, is significantly more complicated in the multiparty setting. To explain this, we note that the equations for equality gates require exponentiation. In the multiparty setting, the values needed for the offline computation are secret shared, and so this exponentiation is computed using MPC. We optimize these computations using the constant round protocol of [3]. However, this still implies that the offline time for computing equality gates is significantly slower. On the positive side, the size of garbled projection gates and their evaluation time are not affected by this, and therefore the difference in the online phase from the two-party setting is similar to the Boolean case.
A motivating example. Many real-world applications naturally use a mixture of Boolean and arithmetic computations. To illustrate the importance of mixed Boolean-arithmetic circuits, we look at a simple natural problem, the problem of conditional summation. Of course, it is possible to encode the problem as a Boolean circuit or as an arithmetic circuit. However, notice that encoding the conditions in arithmetic 0 / 1 would be very inefficient when the conditions are complex. On the other hand, the summation could be expensive in Boolean, while free in an arithmetic circuit (using free addition). Therefore, a more efficient manner to perform the computation would be to compute the conditions in a Boolean circuit, then use selector gates, and finally compute the summation in an arithmetic circuit. Possibly, the conditions (which are Boolean) could decide multiplication constants instead of only 0, 1, (i.e., weighted conditional summation) in which case multiplication gates are also required.
Comparison with previous works and techniques. Garbled multiplication gates were previously considered in the two-party setting by Malkin et al. [28] and by Ball et al. [2]. In Table 1 we compare our garbled multiplication gates with those of [2] and [28]. We compare only with 2-party garbling protocols, because previous multiparty garbling protocols did not handle arithmetic gates.Footnote 2 For sake of comparison, we also include the values of our garbled multiplication gate in the 2-party setting. The difference is that in the 2-party setting, the number of rows in each half-gate can be reduced by one, using the row reduction technique [29]. Furthermore, in the multiparty setting, each row requires n ciphertexts, and “decrypting” a row requires \(n^2\) decryptions (hash function calls), whereas in the two-party setting each row is a single ciphertext and requires a single decryption.
In Table 2 we compare garbled selector gates using known techniques (projection gates) and the new designated construction.
Other related works. Most protocols for securely computing arithmetic circuits follow the secret-sharing paradigm, e.g., [10, 11, 14,15,16, 23] to name but a few. In the secret-sharing paradigm, the parties share their inputs. Then, for each layer of the circuit, the parties interact in order to compute shares for the next layer. Thus, the number of rounds depends on the depth of the circuit. This could potentially lead to very slow online times when the circuit is very deep and the latency is high (for example over the internet), as demonstrated in [8]. On the other hand, using garbled circuits breaks the dependency of the round complexity on the depth of the underlying circuit. Furthermore, garbled circuits are an important primitive that proved worth investigating even outside the context of secure computation.
Hence, these works in the secret-sharing paradigm are incomparable with our work. In addition, the recent works of Damgård et al. [17] and Keller et al. [24] in the secret-sharing paradigm use gate-scrambling, which shares many ideas with garbling. Advances in garbling techniques could potentially aid these protocols.
Apart from the works of Ball el al. [2] and Malkin et al. [28], another notable work that studied arithmetic garbled circuits in the two-party setting is the work of Applebaum et al. [1]. The main result of [1] relies on LWE and is quite complex. It is unclear if their result can be efficiently extended to the multiparty setting – one of the main difficulties seems to be that their construction requires preprocessing the circuit layer by layer. Thus, it does not seem to naturally lend itself to an efficient constant round multiparty protocol, since a natural protocol for this preprocessing would require rounds corresponding to the depth of the circuit. The secondary result of [1] using CRT has been surpassed by the results of Ball et al. [2].
There have also been several other works that dealt with mixed Boolean-arithmetic computations in secure computation, most notably the ABY framework by Demmler et al. [18]. This work deals with mixed Boolean-arithmetic computations in the 2-party setting by efficiently converting between arithmetic secret-sharing, Boolean secret-sharing (for GMW), and Yao garbled circuits. Their protocol is for 2 parties and not constant round. It is an interesting question if the ABY framework can be extended to the multiparty setting (replacing Yao with a BMR garbled circuit) and, in this case, how it would compare with our constant-round protocol.
Organization. In Sect. 2 we review the basics of multiparty garbling and garbling of arithmetic circuits. In Sects. 3 and 4 we explain how to efficiently garble multiplication gates and selector gates, respectively.Footnote 3 In Sect. 5 we describe our constant-round secure multiparty protocol for mixed Boolean-arithmetic circuits. In Sect. 6 we prove the security of our protocols.
2 Preliminaries
We assume that the reader is familiar with the BGW protocol and its improvement [9, 19]. Sections 2.4 and 4 also use the constant round protocol for unbounded fan-in multiplication of Bar-Ilan and Beaver [3]. This protocol is nicely explained in [13, Sect. 4].
2.1 Security Model
We follow the standard definition of secure multiparty computation for semi-honest adversaries, as it appears in “Foundations of Cryptography” by Oded Goldreich [20].Footnote 4 To prove semi-honest security according to this definition, we present a simulator for the ideal world that receives the output from the trusted party and internally interacts with the real-world adversary. Informally, the protocol is secure if the view of the adversary (input, randomness, messages received) in the ideal world is computationally indistinguishable from the view of the adversary in the real world, given any fixing of the inputs of the honest parties.
2.2 Notation, Conventions, and Security Assumption
We list some of the conventions and notations that we use throughout this paper. We consider a static semi-honest adversary \(\mathcal{A}\) corrupting a strict minority of the parties. The circuit of the function to be computed is denoted by C, and \(g\in C\) denotes both the gate and its index. The set of all wires is denoted by W, and \(\mathcal W\) denotes the wires that are not outputs of “free gates” (e.g., XOR, addition, and multiplication by a constant gates). The respective sets of wires with values in \({\mathbb {F}}_p\) are denoted \(W_p\) and \(\mathcal{W}_p\) respectively. The number of parties in the protocol is n, and \(t=\left\lfloor \frac{n-1}{2} \right\rfloor \) is the bound on the number of corrupt parties. We denote the security parameter by \(\kappa \). For binary fields, the keys are therefore in \({\mathbb {F}}_{2^{\kappa }}\). Notice that for characteristic p fields, keys should be in \({\mathbb {F}}_{p^{\kappa _p}}\), with \(\kappa _p\ge \left\lceil \kappa / \log p \right\rceil \); see also Remark 1. We often abuse notation, writing  .
.
Throughout the paper we have computations in several fields. We often avoid mentioning the field in which the computations are carried out when this can be inferred from the equation. For example, if \(\lambda \in {\mathbb {F}}_p\) and \(\varDelta _p^i\in {\mathbb {F}}_{p^{\kappa }}\) then the multiplication \(\lambda \varDelta _p^i\) is computed in \({\mathbb {F}}_{p^{\kappa }}\). Observe that \({\mathbb {F}}_p\subset {\mathbb {F}}_{p^{\kappa }}\) is a field extension, so this is well defined. We also ensure that the computation is well defined for the shares of \(\lambda \) and \(\varDelta _p^i\); see Remark 1.
We sometimes use vector notation for the keys of the parties. For example, if each party \(P_i\) has a key \(k_{x}^i\in {\mathbb {F}}_{p^{\kappa }}\) then we write  . Addition of vectors and multiplication by a constant are the standard linear algebra operations.
. Addition of vectors and multiplication by a constant are the standard linear algebra operations.
The hardness assumption we rely on, which we define next, is the existence of a mixed-modulus circular correlation robust hash function that we denote by H. This is the exact same assumption used by Ball et al. [2] in the two-party setting. Ball et al. conjectured that it is secure to construct H using AES.
Definition 1
Let H be a hash function, and for each p in some set of primes P let \(\varDelta _{p}\in {\mathbb {F}}_{p^{\kappa }}\). We define an oracle \(\mathcal{O}^{H}_{P}\) that acts as follows:
where \(\rho \in {\mathbb {N}}\), \(p_a,p_b\in P\), \(\gamma \in {\mathbb {F}}_{p_a}\), \(\delta \in {\mathbb {F}}_{p_b}\), \(k\in {\mathbb {F}}_{{p_a}^{\kappa }}\), and the output of H is interpreted as in \({\mathbb {F}}_{{p_b}^{\kappa }}\). Note that \(\gamma \varDelta _{p_a}\) is the inner offset and \(\delta \varDelta _{p_b}\) is the outer offset. Legal queries to the oracle have inputs in the correct domains and satisfy:
-
1.
The oracle is never queried with \(\gamma =0\),
-
2.
For each \(\rho \), all the queries have the same \(p_a,p_b\), and each \(\gamma \in {\mathbb {F}}_{p_a}\setminus 0\) is used in at most one query.
We say that H is mixed-modulus circular correlation robust if for all polynomial time adversaries making only legal queries to the oracle, the oracle \(\mathcal{O}^{H}_{P}\), for random \(\varDelta _p\)s, is indistinguishable from a random function (with the same input/output domains).
We use the shortened notation  (\(\mathcal{F}\) can be thought of as a PRF). In our garbled gates, we use \(\rho =g||j\) (formally, \(\rho =ng+j\)), where g is the index of the gate we garble and \(j\in {[n]}\). In most gates, the key of each party is “encrypted”, using \(\mathcal{F}\), by all parties, see for example Eqs. (2) and (3).Footnote 5 We therefore use the shortened notation
(\(\mathcal{F}\) can be thought of as a PRF). In our garbled gates, we use \(\rho =g||j\) (formally, \(\rho =ng+j\)), where g is the index of the gate we garble and \(j\in {[n]}\). In most gates, the key of each party is “encrypted”, using \(\mathcal{F}\), by all parties, see for example Eqs. (2) and (3).Footnote 5 We therefore use the shortened notation  . The outputs of the \(\mathcal{F}_{k_{x}^i}(g||j)\)’s are, in this case, assumed to be in the same field as \(k_{z}^j\). “Decryption” of the above ciphertext is by subtracting \(\varSigma _{i=1}^{n}\mathcal{F}_{k_{x}^i}(g||j)\).
. The outputs of the \(\mathcal{F}_{k_{x}^i}(g||j)\)’s are, in this case, assumed to be in the same field as \(k_{z}^j\). “Decryption” of the above ciphertext is by subtracting \(\varSigma _{i=1}^{n}\mathcal{F}_{k_{x}^i}(g||j)\).
Remark 1
In our offline protocols, the parties share both “small” field elements \(\lambda \in {\mathbb {F}}_p\) and “large” keys/offsets \(k_{x}^i,\varDelta _p^i\in {\mathbb {F}}_{p^{\kappa }}\), with \(\kappa _p\ge \left\lceil \kappa / \log p \right\rceil \). These are shared using Shamir secret-sharing scheme in fields of characteristic p (to allow linear combinations). Apart from the characteristic, there are three other requirements of the fields in which the elements, keys, and offsets are shared. The first two are always required by Shamir secret-sharing schemes.
-
1.
The field must contain at least \(n+1\) elements.
-
2.
The size of the field is at least the size of the domain of the secret.
-
3.
We need to be able to multiply shares of the field element \(\lambda \in {\mathbb {F}}_p\) with the shares of the offset \(\varDelta _p^i\in {\mathbb {F}}_{p^{\kappa }}\).
In order to satisfy the first requirement, the parties share \(\lambda \) in a field extension \({\mathbb {F}}_{p^{m_p}}\) with \(p^{m_p}>n\). In order to satisfy the second requirement, \(k_{x}^i\) and \(\varDelta _p^i\) are shared in \({\mathbb {F}}_{p^{\kappa }}\), as they cannot be shared in a smaller field. In order to satisfy the third requirement, it must hold also that \(m_p|\kappa _{p}\), so that \({\mathbb {F}}_{p^{m_p}}\subseteq {\mathbb {F}}_{p^{\kappa _p}}\). One way to ensure all the requirements are met is to set \(m_p=\kappa _p=\left\lceil \kappa / \log p \right\rceil \). This is not always the most efficient solution – any implementation should optimize the choice of \(m_p\) and \(\kappa _p\) for each p, in correspondence with the bound on the number of parties, such that they satisfy all the above requirements.
2.3 Multiparty Garbling
In the multiparty setting, the first proposal for constructing a multiparty garbled circuit was given in [4]. We extend a simplified description for the semi-honest model given in [8] to the arithmetic setting (in the field \(\mathbb {F}_p\)), by applying the ideas of [2, 28]. The construction of [8] allows the free-XOR ideas of [25]. In the two-party setting, Malkin et al. [28] and Ball et al. [2] showed that free-XOR extends to free addition, subtraction, and multiplication by a public constant in the field \(\mathbb {F}_p\). As we shall see, this is also the case in the multiparty setting.
The multiparty garbling paradigm consists of two phases. In the first phase, often called the offline or garbling phase, the parties collaboratively construct a garbled circuit. Then, in the second phase, called the online or evaluation phase, the parties exchange masked input values and the corresponding keys. After that, each party (or a designated evaluating party) locally computes the outputs of the function. Our secure computation protocol that follows this paradigm is given in Sect. 5. We next recall the basics of the multiparty garbling paradigm.
Boolean Circuits. For constructing the garbled circuit, each party \(P_i\) chooses, for each wire \(\omega \in \mathcal W\), two random keys, \(k_{\omega ,0}^i\) and \(k_{\omega ,1}^i\). To enable the free-XOR technique [25], the parties need to choose the keys such that \(k_{\omega ,1}^i=k_{\omega ,0}^i\oplus \varDelta ^i\) for some global offset \(\varDelta ^i\).
Each wire \(\omega \) in the circuit is assigned a random secret permutation bit \(\lambda _{\omega }\). This bit masks the real values of the wires during the online phase. For an AND gate with input wires \(x,y\) and output wire \(z\), the garbled gate is the encryptions \(g_{\alpha ,\beta }=\left( g_{\alpha ,\beta }^1 , \dots , g_{\alpha ,\beta }^n\right) \) for \((\alpha ,\beta )\in \{0,1\}^2\), where
Notice that all the values are “encrypted” by all the parties. XOR gates are computed using the free-XOR technique of Kolesnikov and Schneider [25], which was extended to the multiparty setting in [8] – the permutation bit and keys on the output wire are set to be the XOR of those on the input wires; they require no cryptographic operations or communication. For the circuit output wires, the permutation bits are revealed. For input wires of party \(P_i\), the corresponding permutation bits are disclosed to party \(P_i\).
During the evaluation phase, an evaluating party learns at each wire \(\omega \) a bit \(e_{\omega }\), called the external or public value, and the corresponding keys. The keys on the output wire of a garbled gate are recovered by decrypting the row \(g_{e_{x},e_{y}}\) using the keys on the input wires. As was first pointed out in [27], if the evaluating party participates in the garbling (which we generally assume), the external value can be extracted from the decrypted key – an evaluating party \(P_i\) can compare the ith key with the keys it used for the garbling, and thus learn the external value. I.e., if the key is \(k_{z,0}^i\) then \(e_{z}=0\) and if it is \(k_{z,1}^i\) then \(e_{z}=1\).
The external value \(e_{\omega }\) is the XOR of the real value \(v_{\omega }\) with the random permutation bit \(\lambda _{\omega }\). Since the permutation bit is random and secret, the external value reveals nothing about the real value to the evaluating party. The evaluating party uses the external value and keys to continue the evaluation of the proceeding garbled gates. For the output wires of the circuit, the permutation bit values are revealed, and thus the output is learnt by XORing with the external values.
Extension to \({\mathbb {F}}_p\) Arithmetic. The above generalizes naturally to arithmetics in the field \({\mathbb {F}}_p\). We explain this briefly; see [2] for a detailed explanation (in the two-party setting). Instead of each wire having a permutation bit \(\lambda \), now each wire has a random secret permutation field element \(\lambda \in {\mathbb {F}}_p\). The external value on wire \(\omega \) is similarly defined  . The permutation field elements are shared, using a linear secret-sharing scheme, in a field of characteristic p. Furthermore, each party \(P_i\) has a global random secret offset \(\varDelta _p^i\in {\mathbb {F}}_{p^{\kappa }}\). For each wire \(\omega \), each party \(P_i\) has a random key \(k_{\omega }^i\in {\mathbb {F}}_{p^{\kappa }}\). The p keys of each party \(P_i\) that relate to the p possible external values, are set to be
. The permutation field elements are shared, using a linear secret-sharing scheme, in a field of characteristic p. Furthermore, each party \(P_i\) has a global random secret offset \(\varDelta _p^i\in {\mathbb {F}}_{p^{\kappa }}\). For each wire \(\omega \), each party \(P_i\) has a random key \(k_{\omega }^i\in {\mathbb {F}}_{p^{\kappa }}\). The p keys of each party \(P_i\) that relate to the p possible external values, are set to be  for each \(\alpha \in {\mathbb {F}}_p\).Footnote 6
for each \(\alpha \in {\mathbb {F}}_p\).Footnote 6
Thus, addition and subtraction are “free”: The zero keys of the output of an addition/subtraction gate are chosen to be the sum/difference of the keys of the input wires. The permutation field element of the output wire is set to be the sum/difference of the permutation elements of the input wires. Since the keys and permutation elements are shared using a linear secret-sharing scheme in a field of characteristic p, the shares of the addition/subtraction can be computed locally by the parties (by performing local additions on their shares). Similarly, multiplication by a public constant c is also free: if \(c\ne 0\), the zero keys and permutation element of the output wire are set to be the multiplication by c. Again, all the necessary computations can be performed locally by the parties, both at the garbling phase and the evaluation phase. The case of \(c=0\) is dealt using a global 0 wire.
A straightforward method for garbling multiplication gates is to extend Eq. 2 from Boolean to characteristic p. I.e., for a multiplication gate with input wires \(x,y\) and output wire \(z\), the garbled gate is the encryptions
for every \(\alpha ,\beta \in {\mathbb {F}}_p\) and \(j\in {[n]}\). The summations and multiplications in the above equation are carried out in \({\mathbb {F}}_{p^{\kappa }}\). Observe that for this equation to make sense, the output of \(\mathcal{F}^2\) must also be in \({\mathbb {F}}_{p^{\kappa }}\). At the online phase, the evaluator recovers the output keys by decrypting row \((e_x,e_y)\).
The above straightforward method requires \(p^2\) garbled rows. In Sect. 3 we describe a more efficient way to garble multiplication gates in the multiparty setting that requires only 2p garbled rows, by extending the half-gates idea of Zahur et al. [34]. Extension of half-gates to \({\mathbb {F}}_p\) was shown in the two-party setting by Malkin et al. [28], but their techniques are quite different from ours. Also, in the two-party setting, Ball et al. [2] suggested a different solution to garble multiplication gates in O(p) garbled rows. However, their solution relies heavily on projection gates. Unfortunately, projection gates are relatively expensive to garble in the multiparty setting, as we explain in Sect. 2.3.2.
2.3.1 CRT Representation and Application to Arithmetic Garbled Circuits
We briefly explain the idea presented by Ball et al. [2] for constructing efficient arithmetic garbled circuits over the integers; see [2] for a more detailed explanation. The idea is to use the Chinese Remainder Theorem (CRT), along with efficient garbling in the field \({\mathbb {F}}_p\), for small p.
The computations are done in the primorial modulus \(Q_k=2\cdot 3\cdots p_k\), the product of the first k primes. The number of primes k is chosen such that \(Q_k>Z\), where Z is the bound on the possible intemediate values of the computation. Each number is represented by a bundle of wires, one for each of the k primes. We call such a representation a CRT bundle representation. Adding two numbers is free, because the sum can be carried out in each prime separately (and addition in \({\mathbb {F}}_p\) is free), and similarly multiplication by a constant. Multiplication and exponentiation by a constant are also computed separately for each prime. Thus, the total number of computations and garbled rows is the sum of the computations/garbled rows in the different primes. Correctness of computing this way follows from the Chinese Remainder Theorem.
2.3.2 General Projection Gates
One of the main garbling gadgets used by Ball et al. [2] is projection gates. A projection gate is a gate which has one input wire and one output wire. For example, an exponentiation gate that computes \(x\mapsto x^c\), where c is a public constant. In addition to gates \(g:{\mathbb Z}_N\rightarrow {\mathbb Z}_N\), there are also useful projection gates in which the domain of the input wire differs from the domain of the output wire. Ball et al. [2] showed in the two party setting that any projection gate \(g:{\mathbb Z}_{N_1}\rightarrow {\mathbb Z}_{N_2}\) can be garbled using at most \(N_1-1\) garbled rows, where the \(-1\) comes from the row reduction technique [29]. Furthermore, they showed that, in the two-party setting, it is not difficult to compute these garbled projection gates, because the garbler knows all the information for constructing the gate. In particular, the garbler knows all the permutation bits/elements.
In contrast, in the multiparty setting, the parties only hold shares of the permutation bits/elements. Therefore, the garbled gates are computed via an MPC subprotocol with these shares. In general, garbling a projection gate might require computing a very complex equation in MPC. Projection gates in which the output domain differs from the input domain are potentially even more complex.
We discuss three types of projection gates: a projection identity gate from Boolean to \({\mathbb {F}}_p\), an equality testing gate from \({\mathbb {F}}_p\) to Boolean, and an exponentiation by a (public) constant gate from \({\mathbb {F}}_p\) to \({\mathbb {F}}_p\) (the latter two are explained in the full version). The first gate can be computed very efficiently. On the other hand, the equality and exponentiation gates, while significantly more efficient than general projection gates, do still seem to be quite expensive. This is because there are exponentiations in the gate equations, and computing exponentiation in MPC is expensive, even using the protocols suggested in [3] or [13].
On the positive side, the number of garbled rows in our projection gates is only one row more than the respective garbled gates in the two-party construction of [2]. Thus, the size of the garbled projection gates is only slightly more than n times of the respective gate in the two-party setting. Furthermore, at the evaluation phase only a single row is decrypted. Therefore, the online computation is only about \(n^2\) times than the two-party setting. This matches the Boolean case.
2.4 Multifield-Shared Bits
In this section we introduce a new primitive that we use in some of our constructions. Note that garbling multiplication gates does not require this primitive; the primitive is necessary only for garbling mixed Boolean-arithmetic gates. The primitive is a random bit \(b\in \{0,1\}\) that is shared multiple times in different fields, of different characteristics. That is, each party holds multiple shares of the same secret random bit, where each share is in a different field with a different characteristic.
In the semi-honest model with an honest majority, it is quite simple to construct this primitive. First, each party \(P_i\) chooses a random bit \(b_i\). The secret random bit will be \(b=\bigoplus _{i=1}^{n} b_i\). Note that if there is an additional requirement that \(b_{z}=b_{x}\oplus b_{y}\) (as needed in some of our constructions to allow free XOR), then party \(P_i\) sets \((b_{z})_i:=(b_{x})_i\oplus (b_{y})_i\) instead of randomly choosing it – permutation bits/elements are chosen only for the input wires of the circuit and for output wires of garbled gates/components. Next, the parties run protocols to share b in each field; these protocols are run in parallel.
We next explain the bit-sharing protocols. The sharing we describe is of Shamir shares, which is the type of shares used in our constructions. The sharing protocol depends on the characteristic of the field. See Remark 1 regarding the fields in which the shares should be generated.
-
1.
In characteristic 2 fields, each party \(P_i\) shares its bit \(b_i\) amongst all the parties in a \((t+1)\)-out-of-n Shamir sharing. The parties sum (XOR) their received shares to obtain shares of the bit b.
-
2.
In characteristic \(p\ne 2\) fields, each party \(P_i\) shares the value \(b'_i=\left\{ \begin{matrix}-1, &{} b_i=1\\ \ \ 1, &{} b_i=0 \end{matrix}\right. \) amongst all the parties in a \(t+1\)-out-of-n Shamir sharing. Then, the parties use an MPC protocol to compute shares of \(b=\frac{1- \left( \varPi _{i=1}^{n} b'_i\right) }{2}\). This is computed in constant rounds by combining the protocol of Bar-Ilan and Beaver [3] for unbounded fan-in multiplication (to compute shares of \(\varPi _{i=1}^{n} b'_i\)) and then linear operations on the shares (note that 2 is invertible in \({\mathbb {F}}_p\) and the inverse is easily computable).
Observe that b computed in both protocols is the same: \(b=0\) if and only if an even number of \(b_i\)s is 1. This happens if and only if an even number of \(b'_i\)s is \(-1\), which is if and only if \(\varPi _{i=1}^{n} b'_i=1\), so if and only if \(\frac{1-\varPi _{i=1}^{n} b'_i}{2}=0\). The case of \(b=1\) is similar.
Remark 2
In our description of the protocol, we assume the parties know the circuit when computing the multifield-shared bits. However, it is possible to compute all the multifield-shared bits even before the function is known, at almost no extra cost. This is explained in the full version.
3 Multiparty Multiplication Gates
In this section we show how to extend the notion of half-gates, introduced by Zahur et al. [34], to multiplication gates in the multiparty setting. The multiplication gates are in the finite field \(\mathbb {F}_p\) (note that regular half-gates, i.e. AND gates, are multiplication in \({\mathbb {F}}_2\)). The total cost of a multiplication gate in \(\mathbb {F}_p\) will be 2p garbled rows, in comparison with \(p^2\) garbled rows of the naïve construction. In particular, the Boolean AND gate will cost \(4=2*2=2^2\) garbled rows using both the half-gates and the regular construction.
Remark 3
In the two party case, row reduction allows to reduce 2 garbled rows using half-gates, while other methods either allow only a single row reduction or are not compatible with the free-XOR technique. This is the main reason to use half-gates also in the two-party Boolean case. However, no efficient row reduction technique is yet known for the general multiparty case. Therefore, half-gates does not seem to be suitable for the multiparty Boolean case.Footnote 7
Remark 4
In [2], multiplication gates in \({\mathbb {F}}_p\) are constructed differently, mainly using projection gates. As explained, projection gates seem to be considerably more expensive in the multiparty case than in the two-party case. Therefore, multiplication using an extension of the half-gates idea, as explained here, should be preferred in the multiparty setting. In fact, the garbled multiplication gate of [2] require slightly more rows and more decryptions, so possibly using the half-gates extension should be considered also for the two-party setting.
We follow the convention of [34], describing the two half gates as the “Garbler Half Gate” and “Evaluator Half Gate”, because these gates are somewhat similar to the 2-party components of [34]. However, note that in our scenario all parties perform the garbling collaboratively (i.e., there is no single garbler), and each party can perform the evaluation.
Before going into the details of each half-gate, we give an informal overview of the idea. Assume we have a multiplication gate with input wires \(x,y\) and output wire \(z\). During evaluation, the evaluating party learns on the input wires the external values bits \(e_{x}=v_{x}+ \lambda _{x}\) and \(e_{y}=v_{y}+ \lambda _{y}\), where v and \(\lambda \) are the real value and the permutation element on the wires respectively. The evaluating party also learns the keys corresponding to these external values. Using this, the evaluating party should be able to recover the output external value
and corresponding keys.Footnote 8 In the naïve construction, this is done by decrypting the row \((e_{x},e_{y})\), see Sect. 2.3.
In the half-gates construction, the computation is split into two distinct half-gates, each performing a different computation. Informally, the first gate computes \(-\lambda _{y}v_{x}\) and the second half-gate computes \(v_{x}(v_{y}+ \lambda _{y})\). Then, adding the two outputs, which is free, results in \(v_{z}=v_{x}v_{y}\).
To securely compute a multiplication gate using these two half gates in the multiparty setting, two adjustments have to be made. The necessity of these adjustments will become apparent when we discuss security. The first adjustment is that the permutation element on the output wire, \(\lambda _{z}\), must be partitioned \(\lambda _{z} = \widetilde{\lambda _{z}}+ \widehat{\lambda _{z}}\), where \(\widetilde{\lambda _{z}}, \widehat{\lambda _{z}}\in {\mathbb {F}}_p\) are random elements under the constraint that they sum to \(\lambda _{z}\) (which is the random permutation element of the output wire). This is because the outputs of both half gates must be hidden, otherwise information might be leaked on some of the values.Footnote 9
The second adjustment is that the zero keys \(k_{z}^i\) on the output wire also need to be partitioned \(k_{z}^i=\widehat{k_{z}}^i+\widetilde{k}_{z}^i\), where \(\widehat{k_{z}}^i,\widetilde{k}_{z}^i\in {\mathbb {F}}_{p^\kappa }\) are random under the constraint that they sum to \(k_{z}^i\). The main idea of this partition is that the output keys of an honest party \(P_i\) on both half gates do not leak information on the global offset \(\varDelta ^i_p\). The permutation elements and keys \(\widetilde{\lambda _{z}},\widetilde{k}_{z}^i\) are used in the Garbler half gate, and \(\widehat{\lambda _{z}},\widehat{k_{z}}^i\) are used in the Evaluator half gate.
To conclude, informally the half gates construction computes the output using the following equation:

The true construction and resulting equations are more involved, and we next explain them in detail.
3.1 Garbler Half Gate
In the original description of this half gate in [34], the idea is described that the garbler can take advantage that it knows the permutation bit (or color bit in the terminology of [34]). In the multiparty case, no unauthorized subset (i.e., a subset that could be controlled by the adversary) is allowed to know the permutation element on any wire that it should not learn. However, we can use the fact that the permutation elements are secret-shared to do the necessary computations. The computed gate is slightly more complicated than in the two-party case because the garbling parties also participate in the evaluation, and thus have additional information.
As already stated, the garbler half gate should compute the value \(-\lambda _{y}v_{x}+ \widetilde{\lambda _{z}}\). Note that \(v_{x}\) is the real value on the wire \(x\) (in an ungarbled computation) and is therefore never known – neither during garbling nor during the evaluation phase. Thus, we cannot hope to use it directly.
To overcome this, the value is computed using the equation \(-\lambda _{y}v_{x}+ \widetilde{\lambda _{z}}=-\lambda _{y}(v_{x}+ \lambda _{x})+ \lambda _{y}\lambda _{x}+ \widetilde{\lambda _{z}}\). The value \(v_{x}+ \lambda _{x}\) is the external value on wire \(x\) and thus revealed during evaluation. For garbling, the rows are computed for all p values, using the BGW protocol with the shares of permutation bits, and with \(v_{x}+ \lambda _{x}\) treated as a constant (as \(\alpha \) in the \(\alpha \)th row). The final garbled garbler half gate is the set of encryptions
for every \(\alpha \in {\mathbb {F}}_p\) and \(i\in {[n]}\). Note that \(\alpha \) is a constant and all other values are secret-shared. Since the multiplicative depth of this equation is 2, computing this half gate (Eq. (6)) requires two BGW degree-reduction rounds.
To verify that the correct output key is recovered, we observe that if the input external value is \(e_{x}\), then the encryptions \(\tilde{g}_{e_{x}}^i\) are decrypted for all i. Thus, the recovered output keys are
matching the expected value of the keys corresponding to \(-\lambda _{y}v_{x} + \widetilde{\lambda _{z}}\).
3.2 Evaluator Half Gate
As in the two-party case, the main idea of this half gate is that the evaluating party learns at the evaluation phase the external values of the wires, and can use this information for the computation. As we shall see more clearly when we extend the half gates to \(\mathbb {F}_p\), the operation done by the evaluating party is to multiply by this external value.
The evaluator half gate should compute the value \(v_{x}(v_{y}+ \lambda _{y})+ \widehat{\lambda _{z}}\). The value \(v_{y}+ \lambda _{y}\) is the external value \(e_{y}\) on input wire \(y\), and therefore known at evaluation time. On the other hand, the value \(v_{x}\) is the true value on wire \(x\), and thus generally should never be learnt by any subset of parties. Therefore, to compute the gate we use the equation:
The computation of the value \(\lambda _{x}(v_{y}+ \lambda _{y})+ \widehat{\lambda _{z}}\) is similar to the computations in the Garbler Half Gate. Thus, the main addition in this half gate is the computation of the value \((v_{x}+ \lambda _{x})(v_{y}+ \lambda _{y})\). Naïvely, it would seem that this requires \(p^2\) rows in order to garble for each combination of \((v_{x}+\lambda _{x},v_{y}+ \lambda _{y})\in ({\mathbb {F}}_p)^2\). However, in the two party Boolean case, [34] observed that this computation can be obtained practically for free. We first explain the observation of [34], and then extend it to the multiparty \({\mathbb {F}}_p\) case.
In the Boolean case, the external values are \((v_{x}\oplus \lambda _{x})\) and \((v_{y}\oplus \lambda _{y})\). Note first that \((v_{x}\oplus \lambda _{x})(v_{y}\oplus \lambda _{y})\) can be computed at evaluation time as both external values are known. This is still insufficient, because the evaluating party needs to recover some key that corresponds to this value. The “trick” performed by [34] is to XOR with the key on the wire \(x\) if \(v_{y}\oplus \lambda _{y}=1\) and to ignore it if \(v_{y}\oplus \lambda _{y}=0\). We next describe this slightly differently for the \({\mathbb {F}}_p\) case, but the descriptions in fact coincide for \(p=2\).
To extend the technique of [34], during evaluation, each evaluating party multiplies the key on wire \(x\) by the external value \(v_{y}+ \lambda _{y}\) and adds it to the decrypted key. Notice that this completely coincides with the Boolean case when \(p=2\) (since multiplying the key by 0 is the same as ignoring the key). The only subtlety is that now the corresponding multiplication of the zero key must be subtracted from the encrypted key during the garbling. However, the proof for this extended technique is slightly trickier, as we shall see in Sect. 6.
The garbled evaluator half gate is the set of encryptions
for every \(\beta \in {\mathbb {F}}_p\) and \(i\in {[n]}\). Since the multiplicative depth is 1, computing this half gate (Eq. 8) requires one BGW degree-reduction round.
Now during evaluation, the evaluating party multiplies the key on the \(x\) wire by the external value \(e_{y}=v_{y}+\lambda _{y}\). This is then added to the key decrypted at row \(e_{y}\). We next verify that the recovered output keys indeed corresponds to the correct value: the recovered output keys are the sum (for each \(i\in {[n]}\)) of \(e_{y}(k_{x}^i+e_{x}\varDelta _p^i)\) and \(\widehat{k}_{z}^i - e_{y} k_{x}^i+ \left( -e_{y} \lambda _{x} + \widehat{\lambda _{z}}\right) \varDelta _p^i\). Simplifying,
matching the expected key value of \(v_{x}\left( v_{y}+\lambda _{y}\right) + \widehat{\lambda _{z}}\).
3.3 Summing the Two Half Gates
Recall that \(\lambda _{z}=\widetilde{\lambda _{z}}+\widehat{\lambda _{z}}\) and \(k_{z}^i=\widetilde{k}_{z}^i+ \widehat{k}_{z}^i\). At the evaluation phase, once both half gates are evaluated as above, each evaluating party computes for each \(i\in {[n]}\) the output keys of the gate, by summing the two keys it recovered from the two half gates, i.e.,
Next, evaluating party \(P_j\) recovers the external value \(e_{z}=v_{x}v_{y}+\lambda _{z}\), by comparing the recovered key \(k_{z}^j\) with its local keys.
4 Selector Gates
One of the more challenging tasks of performing an arbitrary computation using arithmetic circuits is to perform conditional statements. In this section, we discuss a gate computing a simple if statement. Namely, we build a “selector” gate, which chooses between two input wires in \({\mathbb {F}}_p\), according to a Boolean “selection bit”. I.e., the gate has three input wires \(x,y\), and \(w_{0}\), and an output wire \(z\). The values on the input wires \(x,y\) are from \({\mathbb {F}}_p\) and the value on \(w_{0}\) is the selection bit. The selector gate computes the following if statement: If (\(v_{w_{0}}==0\)) then \(v_{z}=v_{x}\) else \(v_{z}=v_{y}\). Note that by applying this to each wire in the CRT representation, we get a selector gate for integers.
We show two constructions for a selector gate. The first construction is using known techniques. The gate is constructed by first projecting the value of \(w_{0}\) into \({\mathbb {F}}_p\) using a projection gate, and then using a multiplication gate. That is, the gate is computed using the equation:
where \(\varphi \) denotes the projection of the bit into \({\mathbb {F}}_p\). There is one projection and one \({\mathbb {F}}_p\) multiplication in Eq. 9, costing 2 and 2p garbled rows respectively. Thus, a selector gate using the above construction has \(2p+2\) garbled rows. However, note that the evaluator has to decrypt 3 rows using this method: 1 for the projection gate, and 2 for the multiplication gate (1 in each half gate). To the best of our knowledge, this is the best selector gate construction using existing techniques and relying only on the existence of MMCCR PRFs; see Remark 5.
Our second construction will be a new and designated construction of a garbled selector gate. The cost of the designated garbled selector gate will be also \(2p+2\) garbled rows. However, the number of rows the evaluator will have to decrypt will be only 2. Thus, we expect evaluation of this designated selector gate to be approx. \(33\%\) faster.
Remark 5
If \(w_{0}\) is in \({\mathbb {F}}_p\) then a selector gate can be garbled with 2p rows and only 2 decryptions at evaluation (since projection is not needed). However, we argue that it is important to consider the case of Boolean \(w_{0}\) for two reasons: the first is that when computing over the integers using CRT, we would like the same bit to select in all the characteristics. The second is that \(w_{0}\) could be determined by a complex set of conditions, so it would make sense that \(w_{0}\) is the output or intermediate value of a Boolean sub-circuit.
If we do not restrict the security assumption to only MMCCR hash functions, then in the 2-party setting, Ball et al. [2] showed a direct construction of a selector gate that has \(2p-1\) rows and requires only 1 decryption, which can be proved secure based on a random oracle (or possibly also on some extension of Definition 1 to allow correlation and circularity on two input keys). Note that in the 2-party setting, also the new designated construction and the construction using a projection gate have \(2p-1\) rows (this is because row-reduction [29] reduces 1 row from every garbled component). However, they require 2 and 3 decryptions, respectively. Nevertheless, since in the two-party setting this is the only garbled gate which an optimization is known using a stronger assumption, we feel it is important also to optimize constructions that are based only on MMCCR.
4.1 Charateristic 2 to Characteristic p Projection Gates
In this section we explain how to construct a projection gate that maps a bit value on a Boolean wire to the same value on a wire in \({\mathbb {F}}_p\). The projection gate has a single input wire \(w_{0}\) containing a Boolean value, and an output wire \(z\), containing the same value in \({\mathbb {F}}_p\). I.e., if \(v_{w_{0}}=0\) then \(v_{z}=0\) and if \(v_{w_{0}}=1\) then \(v_{z}=1\) (note that \(v_{w_{0}}\in {\mathbb {F}}_2\) and \(v_{z}\in {\mathbb {F}}_p\)). This projection gate is needed if one wishes to multiply the bit value by a value in \({\mathbb {F}}_p\), as in the first selector gate construction described above.
The projection gate takes advantage of the following observation: Suppose that \(v_{w_{0}},\lambda _{w_{0}}\in \{0,1\}\). Then,

where the computations on the left and right are in \({\mathbb {F}}_2\), the computation in middle is in \({\mathbb {F}}_p\), and equality signifies that the value is the same value in \(\{0,1\}\) (whether in \({\mathbb {F}}_2\) or \({\mathbb {F}}_p\)). I.e., if \( v_{w_{0}}= \lambda _{w_{0}}\) then \(v_{w_{0}}-\lambda _{w_{0}} = 0 =v_{w_{0}}\oplus \lambda _{w_{0}}\) and if \(v_{w_{0}}\ne \lambda _{w_{0}}\) then \(v_{w_{0}}+\lambda _{w_{0}} = 1 = v_{w_{0}}\oplus \lambda _{w_{0}}\).
To use Eq. (10), we will assume that \(\lambda _{w_{0}}\) is a multifield-shared bit, shared in both a field of characteristic 2 and a field of characteristic p. Note that although the output value is known to be a bit, it is masked using a random permutation element in \({\mathbb {F}}_p\) to avoid leaking information. Thus, the equation of the gate will be

Hence, the garbled projection gate is the following encryptions for every \(i\in {[n]}\):
As explained in Sect. 2, although \(k_{w_{0},0},k_{w_{0},1}\in {\mathbb {F}}_{2^{\kappa }}\), the output of the PRF in this case is in \({\mathbb {F}}_{p^{\kappa }}\). Assuming we have \(\lambda _{w_{0}}\) as a multifield-shared bit, i.e., the parties already posses Shamir shares of the the bit \(\lambda _{w_{0}}\) in the correct field of characteristic p, Eqs. (12), (13) can be computed using one additional BGW degree-reduction round. Using Eq. (11), it is not difficult to verify that for both values of \(e_{w_{0}}\) the decrypted key corresponds to \(e_{z}\).
4.2 Designated Selector Gate Construction
In this section we explain a designated construction for a selector gate. The gate contains three components. The first component, which we call the chooser partial gate, has 2 garbled rows. The other two components, which we call the corrector partial gates, contain p garbled rows each. Thus, this construction of a selector gate will require \(2p+2\) garbled rows, same as the previous construction. However, this construction requires less decryptions at the evaluation phase, as we explain next.
The main idea we use in our construction can be seen as an extension of the half-gate technique – the evaluating party uses the key of one of the input wires, according to the external value on the selection wire. Furthermore, the evaluating party decodes only one of the two corrector partial gates according to the external value on the selection wire. Therefore, only two rows are decrypted when evaluating the gate (one in the chooser gate and one in the corrector gate), 1 less than the previous construction.
Note that since the external values are known only at the evaluation phase, we cannot prevent a corrupt evaluating party from decrypting also the other corrector partial gate. Thus, we must ensure that the decrypted key from this does not leak any extra information. This is achieved using a double partitioning of the output zero keys and permutation bit. I.e.,
where \(\widehat{\lambda _{z}},\widetilde{\lambda _{z}},\widehat{\widehat{\lambda _{z}}},\widetilde{\widetilde{\lambda _{z}}}\in {\mathbb {F}}_p\) are random such that they satisfy Eq. (14) and likewise \(\widehat{k}_{z}^i,\widetilde{k}_{z}^i,\widehat{\widehat{k}}_{z}^i,\widetilde{\widetilde{k}}_{z}^i\in {\mathbb {F}}_{p^{\kappa }}\) are random such that they satisfy Eq. (15). Note for example that \(\widetilde{\widetilde{\lambda _{z}}}\) is random even given \(\widehat{\lambda _{z}},\widetilde{\lambda _{z}}\). Such observations are crucial for security, as we later explain. Otherwise, a corrupt evaluator could learn secret information by decrypting the “wrong” corrector gate. This idea of double partition of the keys and permutation elements appears to have not been used before in garbled circuits.
4.2.1 Half-Selector Gate
We now show the construction of a half selector gate that receives only two input wires, \(x\) and \(w_{0}\), and outputs either \(x\) or 0 according to \(w_{0}\). This easily extends to a full selector gate, using the equation
I.e., computing the value of \(x-y\) using free subtraction, then using a half-selector, and then freely adding the value of y. It is also possible to construct a full selector gate directly. This is explained in the full version. The construction of the half-selector gate is significantly simpler, but contains most of the main ideas.
Informally, the half-selector gate is computed using the following equation:

This equation works because \(v_{x}(v_{w_{0}}\oplus \lambda _{w_{0}})=\left\{ \begin{matrix} v_{x}v_{w_{0}}-\lambda _{w_{0}}v_{x}&{}\ &{} v_{w_{0}}\oplus \lambda _{w_{0}}=0\\ v_{x}v_{w_{0}}+\lambda _{w_{0}}v_{x}&{}\ &{} v_{w_{0}}\oplus \lambda _{w_{0}}=1, \end{matrix} \right. \) as one can readily verify for the 4 combinations of \(v_{w_{0}},\lambda _{w_{0}}\in \{0,1\}\). Note also that the equations of the chooser gate in the first and second row simplify to \(\widehat{\lambda _{z}}\) and \(v_{x}+\widehat{\widehat{\lambda _{z}}}\) respectively, since the value of \(v_{w_{0}}\oplus \lambda _{w_{0}}\) is already fixed. The reason why we need to use different partitions of \(\lambda _{z}\) in the two rows will become clear when we discuss the corrector partial gates in detail. In short, the reason is to ensure that decrypting the “wrong” corrector gate does not leak any information.
Chooser Partial Gate for Half Selector. The chooser partial gate is somewhat similar to the evaluator half gate. The first garbled row, which is decrypted when \(v_{w_{0}}\oplus \lambda _{w_{0}}=0\), should output a key corresponding to \(v_{x}(v_{w_{0}}\oplus \lambda _{w_{0}})+\widehat{\lambda _{z}}=\widehat{\lambda _{z}}\) if decrypted. The \(\widehat{\lambda _{z}}\) is secret-shared, so this computation is done in a straightforward manner.
The second garbled row is decrypted when \(v_{w_{0}}\oplus \lambda _{w_{0}}=1\), and the output keys should correspond to the value \(v_{x}(v_{w_{0}}\oplus \lambda _{w_{0}})+\widehat{\widehat{\lambda _{z}}}=v_{x}+\widehat{\widehat{\lambda _{z}}}\). Here we use a similar trick as in the evaluator half-gate, i.e., the equation \(v_{x}+\widehat{\widehat{\lambda _{z}}}=(v_{x}+\lambda _{x})-\lambda _{x}+\widehat{\widehat{\lambda _{z}}}\), where for the value \(v_{x}+\lambda _{x}\) the evaluator will add the key on the input wire \(x\), as in the evaluator half gate. To conclude, the chooser partial gate for a half selector gate has the following encryptions for every \(i\in {[n]}\):
At the garbling phase, these equations require one BGW degree-reduction round. At the evaluation phase, if the external value \(e_{w_{0}}\) is 1, the evaluating party also adds the key on wire x after decryption.
We verify that the decrypted keys indeed correspond to the values \(v_{x}(v_{w_{0}}\oplus \lambda _{w_{0}})+\widehat{\lambda _{z}}\) and \(v_{x}(v_{w_{0}}\oplus \lambda _{w_{0}})+\widehat{\widehat{\lambda _{z}}}\):
-
1.
If \(e_{w_{0}}=0\) the decrypted keys are \(\widehat{k}_{z}^i+\widehat{\lambda _{z}}\varDelta _p^i=\widehat{k}_{z,\widehat{\lambda _{z}}}^i=\widehat{k}_{z,v_{x}(v_{w_{0}}\oplus \lambda _{w_{0}})+\widehat{\lambda _{z}}}^i\),
-
2.
If \(e_{w_{0}}=1\) the output is the sum of \(k_{x}^i+e_{x}\varDelta _p^i\) and \(\widehat{\widehat{k}}_{z}^i-k_{x}^i+\left( -\lambda _{x}+\widehat{\widehat{\lambda _{z}}}\right) \varDelta _p^i\). Simplifying:
$$\begin{aligned} \left[ k_{x}^i+e_{x}\varDelta _p^i\right] +\left[ \widehat{\widehat{k}}_{z}^i-k_{x}^i+\left( -\lambda _{x}+\widehat{\widehat{\lambda _{z}}}\right) \varDelta _p^i\right] =\widehat{\widehat{k}}_{z}^i+\left( v_{x}+\widehat{\widehat{\lambda _{z}}}\right) \varDelta _p^i\\=\widehat{\widehat{k}}_{z,v_{x}+\widehat{\widehat{\lambda _{z}}}}^i=\widehat{\widehat{k}}_{z,v_{x}(v_{w_{0}}\oplus \lambda _{w_{0}})+\widehat{\widehat{\lambda _{z}}}}^i. \end{aligned}$$
Corrector Partial Gate for Half Selector. The computation of each corrector partial gate is similar to the garbler half gate. The interesting point is that there are two corrector gates for every selector gate, and only one value is used at evaluation. However, since which of the two is used is known only at the evaluation phase, both corrector gates need to be computed at the garbling phase.
The garbled rows of the first corrector gate, which correspond to the value \(\lambda _{w_{0}}v_{x}+\widetilde{\lambda _{z}}=\lambda _{w_{0}}(v_{x}+\lambda _{x})-\lambda _{w_{0}}\lambda _{x}+\widetilde{\lambda _{z}}\), are the following encryptions for each \(\alpha \in {\mathbb {F}}_p\) and \(i\in {[n]}\):
The garbled rows of the second corrector gate, which correspond to the value \(-\lambda _{w_{0}}v_{x}+\widetilde{\widetilde{\lambda _{z}}}=-\lambda _{w_{0}}(v_{x}+\lambda _{x})+\lambda _{w_{0}}\lambda _{x}+\widetilde{\widetilde{\lambda _{z}}}\), are the following encryptions for each \(\alpha \in {\mathbb {F}}_p\) and \(i\in {[n]}\):
Assuming \(\lambda _{w_{0}}\) is a multifield-shared bit, computing these gates requires two BGW degree-reduction rounds. Verification is slightly tedious and hence omitted.
Combining the above components results in the half-selector gate: At the evaluation phase, an honest evaluating party decrypts the chooser partial gate and only one of the corrector gates, according to the external value on the selector wire \(w_{0}\). By summing the values, the evaluating party recovers the key corresponding to \(v_{x}v_{w_{0}}+\lambda _{z}\).
Observe that the same key is used to decrypt both corrector gates. Thus, a corrupt evaluating party can recover the decrypted keys on both corrector gates, regardless of the external value on wire \(w_{0}\). Therefore, we must ensure that the unused decrypted value does not leak any information. We explain the intuition for the case \(e_{w_{0}}=0\); the case of \(e_{w_{0}}=1\) is similar. Notice that the keys decrypted from the inactive corrector gate are \(\widetilde{\widetilde{k}}_{z}^i+\left( -e_{x}\lambda _{w_{0}}+\lambda _{w_{0}}\lambda _{x}+\widetilde{\widetilde{\lambda _{z}}}\right) \varDelta _p^i\) for \(i\in {[n]}\). There are 2 key observations:
-
Clearly, a corrupt evaluating party \(P_i\) can learn the value \(-e_{x}\lambda _{w_{0}}+\lambda _{w_{0}}\lambda _{x}+\widetilde{\widetilde{\lambda _{z}}}\) by subtracting \(\widetilde{\widetilde{k}}_{z}^i\) and dividing by \(\varDelta _p^i\). Furthermore, \(e_{x}\), \(e_{w_{0}}\), \(\widehat{\lambda _z}\), and \(\lambda _{w_{0}}v_{x}+\widetilde{\lambda _{z}}\) are known to the evaluator from the protocol.Footnote 10 Nevertheless, \(\widetilde{\widetilde{\lambda _{z}}}\in {\mathbb {F}}_p\) is random even given these values. Thus, the value \(-e_{x}\lambda _{w_{0}}+\lambda _{w_{0}}\lambda _{x}+\widetilde{\widetilde{\lambda _{z}}}\) leaks no information on \(\lambda _{w_{0}}\) and \(\lambda _{x}\).
-
A corrupt evaluating party learns \(\widetilde{\widetilde{k}}_{z}^j+\left( -e_{x}\lambda _{w_{0}}+\lambda _{w_{0}}\lambda _{x}+\widetilde{\widetilde{\lambda _{z}}}\right) \varDelta _p^j\) also for every honest party \(P_j\). However, \(\widetilde{\widetilde{k}}_{z}^j\in {\mathbb {F}}_{p^{\kappa }}\) is random even given the keys party \(P_i\) recovers from following the protocol. Thus, this does not leak any information on \(\varDelta _p^j\).
The proof of security in Sect. 6 formalizes the above intuition.
5 Protocol for Secure Computation
In this section we give the details of our secure multiparty computation protocol. The protocol is an extension of the semi-honest BMR protocol, e.g. [8], to the arithmetic case. The details of the garbled gates are explained in Sects. 3 and 4.Footnote 11 The proofs of correctness and security appear at Sect. 6.
The garbling phase of protocols following the multiparty garbling paradigm is often abstracted as a functionality that outputs the garbled circuit and the necessary permutation bits to the respective parties. This functionality, which we term \(F_{GC}\), is described in Fig. 1. We next sketch out a straightforward protocol for securely computing \(F_{GC}\) in constant rounds, using a combination of the BGW protocol [9, 19] and the constant round protocol for unbounded fan-in multiplication of Bar-Ilan and Beaver [3].
-
Step 1, Setup: For each prime p in the primorial modulus, each party \(P_i\) does the following:
-
For each wire \(\omega \in \mathcal{W}_p\) (i.e., input wires of the circuit and output wires of garbled gates/components), randomly chooses a random element \((\lambda _{\omega })_i\in {\mathbb {F}}_p\) and (zero) key \(k_{\omega }^i\in {\mathbb {F}}_{p^{\kappa }}\).Footnote 12 The random permutation element on the wire is
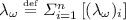 .
. -
In topological order on the circuit, computes \((\lambda _{\omega })_i\) and \(k_{\omega }^i\) for each wire \(\omega \notin \mathcal{W}_p\), by summing/multiplying by a constant (according to gate type), by using \(\lambda _i\) and \(k^i\) on the input wires – see Sect. 2.3 on “free” gates.
-
Each party randomly chooses a random global offset \(\varDelta _p^i\in {\mathbb {F}}_{p^{\kappa }}\).
-
For each garbled component \(g\in C\), compute \(\mathcal{F}_{k_{x,\alpha }^i}(g,j)\) for each \(j\in {[n]}\) and \(\alpha \in {\mathbb {F}}_p\), where p is according to the gate/component type.
-
-
Step 2, Sharing: Each party \(P_i\) shares all the keys, elements, and outputs of \(\mathcal{F}\) in Step 1 using \((t+1)\)-out-of-n Shamir secret-sharing scheme. Multifield-shared bits are also shared using Protocol 2 in Sect. 2.4 for each p. The parties obtain shares of \(\lambda _{\omega }\) for each wire by locally summing their shares of \(\left\{ (\lambda _{\omega })_i \right\} _{i=1}^{n}\).
-
Step 3, Computing the garbled gates: Shares of the garbled rows of each garbled gate/component are computed using their respective equation (e.g., Eqs. 6, 8, 12, 13), where in each equation
-
Addition and multiplication by a constant are computed locally,
-
Multiplication is computed using a BGW degree-reduction round,
-
Exponentiation is computed using the protocol of [3].
More details can be found in the respective section.
-
-
Step 4, Reconstructing the outputs: The parties exchange the shares (of the outputs of \(F_{GC}\)) and reconstruct the outputs of \(F_{GC}\), namely the garbled gates/components and the output permutation elements. Furthermore, each party receives the shares and reconstructs the permutation elements on its input wires.
Remark 6
The above protocol is constant round since all gates are computed in parallel and each step is constant round (Step 1 is local). However, the protocol can be considerably optimized using techniques described in [7], such as share-conversion and masking by additive shares of zeros. Due to space limitations, the optimized protocol is deferred to the full version. An alternative protocol for arithmetic garbled circuits that does not require an honest majority, which is based on oblivious transfer, is also given in the full version.
Next, in Fig. 2 we give the details of our MPC protocol, in the \(F_{GC}\)-hybrid model (i.e., \(F_{GC}\) can be executed securely as a black-box). The protocol is similar to other protocols following the multiparty garbling paradigm, e.g., [8]. The only major difference is the external values are not exclusively Boolean, and the size of the garbled gates/components varies according to the gate type. The evaluation of the various gates (Step 3b in Fig. 2) is explained in the respective section. Correctness and security of the protocol are shown in Sect. 6.
6 Correctness and Security
In this section we state the correctness and security of our protocol. Due to lack of space, we only give sketches of the proofs. The full proof of security, as well as the straightforward proof of Claim 1, will be given in the full version.
Correctness. We briefly explain the correctness of the protocol. To show that the outputs received by the parties in  (Fig. 2) corresponds to the correct output, we show the following statement: for each wire, the evaluating parties recover at evaluation the correct external value \(e_{z}=v_{z}+\lambda _{z}\), and the corresponding keys. For input wires, this statement follows from Step 2. The statement is then proved by induction on the topological ordering of the gates. For output wires of each gate type, this is shown in the respective section. Using the induction argument, the statement holds also for the output wires of the circuit. Thus, in Step 4, the value recovered by the parties at wire \(z\) is \(e_{z}-\lambda _{z}=v_{z}\).
(Fig. 2) corresponds to the correct output, we show the following statement: for each wire, the evaluating parties recover at evaluation the correct external value \(e_{z}=v_{z}+\lambda _{z}\), and the corresponding keys. For input wires, this statement follows from Step 2. The statement is then proved by induction on the topological ordering of the gates. For output wires of each gate type, this is shown in the respective section. Using the induction argument, the statement holds also for the output wires of the circuit. Thus, in Step 4, the value recovered by the parties at wire \(z\) is \(e_{z}-\lambda _{z}=v_{z}\).
Security. We now show the security of our protocol. We assume a semi-honest adversary corrupting a strict minority of the parties. We begin with the following lemma:
Lemma 1
Protocol \(\varPi _{GC}\) securely computes \(F_{GC}\) in the presence of a static semi-honest adversary controlling a strict minority of the parties.
Proof Sketch
Protocol \(\varPi _{GC}\) computes \(F_{GC}\) using only Shamir secret sharing, the BGW protocol, and the constant round protocol for unbounded fan-in multiplication of [3]. These are secure and composable with each other (the protocol of [3] can be based on BGW) in the semi-honest model with an honest majority. The intermediate messages the adversary sees throughout the protocol (Steps 2 and 3) are only Shamir shares, which appear random in the information theoretic sense. Thus, they are easily simulated. The messages of the last round (Step 4) are computed by the simulator using the output (given from the trusted party) and the messages already given to the adversary in previous rounds. \(\square \)
Before stating our main security theorem, we state the following claim that follows from Definition 1:
Claim 1
Let \(B\subset {[n]}\). If H is mixed-modulus circular correlation robust, then for all polynomial time adversaries making only legal queries to the oracle, the oracle

where each \(\mathcal{O}^{H,i}_{P}\) is equal to \(\mathcal{O}^{H}_{P}\) with random and independent \(\varDelta ^i_p\)s for each \(p\in P\) and \(i\in B\), is indistinguishable from a random function (with the same input/output domains).
Claim 1 is proved from Definition 1 by a reduction. The proof is deferred to the full version. Informally, the importance of Claim 1 is to use the claim with B as the set of honest parties, so \(\mathcal{O}^{H,B}_{P}\) mimics “encryption” by all the honest parties. Further, the oracle adds offsets, corresponding to \(\delta _i\varDelta _p^i\)s, to the encrypted keys of the honest parties.
To give some intuition, this allows the distinguisher to change the values to which the encrypted keys correspond to, without knowing the \(\varDelta _p^i\)s. For example, let \(e_{x}\) and \(e_{z}\) be the external values on the input and output wires of the gate. If the distinguisher wants to encrypt row \(e_{x}+1\) with the key corresponding to \(e_{z}+2\), then for the jth part it uses \(\gamma =1\) and \(\delta _i=\left\{ \begin{matrix} 2 &{}\ \ i=j\\ 0 &{}\ \ i\ne j \end{matrix}\right. \) for each \(i\in B\) (the computation of \(\delta _j\) for the evaluator half gate and designated selector gates is slightly more complex, as explained in the proof). This way, the distinguisher only uses the keys \(k_{x,e_{x}}^i,k_{z,e_{z}}^i\) of the honest parties. Next, we state our main security theorem:
Theorem 2
If H is a mixed-modulus correlation robust hash function then Protocol  in Fig. 2 securely computes \(f_{C}\) in the \(F_{GC}\)-hybrid model, in the presence of a static semi-honest adversary.
in Fig. 2 securely computes \(f_{C}\) in the \(F_{GC}\)-hybrid model, in the presence of a static semi-honest adversary.
The proof follows the general ideas used in [12], with the extended assumption. The main difficulty of the proof, on which we focus, is to show how the simulator simulates the output of \(F_{GC}\), and in particular a fake garbled circuit, such that no polynomial time distinguisher can distinguish this fake garbled circuit from a real garbled circuit. To show this, we describe a distinguisher that uses H and legal queries to an oracle \(\mathcal{O}\in \left\{ \mathcal{O}^{H,B}_{P},Rand \right\} \) in order to construct a circuit that distributes either as a real garbled circuit or as a fake garbled circuit, according to the oracle. Thus, distinguishing between the two types of circuits breaks the mixed-modulus correlation robustness of H. See the full version for more details.
There are two main differences from similar proofs: the first appears in multiplication gates, and specifically in the evaluator half gate. The second appears in the designated selector gates. Therefore, we split the proof sketch into two parts. In the first, we give an overview of the general proof structure and ideas, i.e., the construction of the fake circuit by the simulator, and the construction of the circuit by the distinguisher (which distributes as a real or fake circuit according to the oracle). In the second part, we explain the difficulties and necessary changes for evaluator half gates, and give a more detailed explanation on the subtleties of selector gates.
Proof Sketch
Simulator: The simulator chooses a random path on the circuit, i.e., for each wire \(\omega \in \mathcal W\) selects a random external value. For each wire \(\omega \in \mathcal W\) and for each honest party, the simulator chooses random keys corresponding to these external values. Then, the simulator computes the external values and corresponding keys of free gates. Using these values, the simulator computes a single encrypted row for each non-free gate/component – this row corresponds to the external value on the input wire. The other rows are sent as completely random strings (or more precisely as a random vector in \({\mathbb {F}}_{p^{\kappa }}^n\) for the appropriate p). There are slight differences in the designated selector gates, and these are explained later in the proof.
Distinguisher: The distinguisher starts by following the simulator construction for computing the first encrypted row. The other rows are computed differently, by using the oracle. The key observation is that the distinguisher can compute the \(\gamma \)’s it needs to supply the oracle in order to, in the case \(\mathcal{O}=\mathcal{O}^{H,B}_{P}\), encrypt the rows correctly and can compute the \(\delta _i\)’s in order to, if necessary, change the keys of the honest parties that are encrypted in that case.Footnote 13
Computing \(\gamma \) is simply by the difference in the rows – this part is unchanged in the different gate types. Note that this ensures that \(\gamma \ne 0\) and that each \(\gamma \in {\mathbb {F}}_{p_a}\) is used only once for each gate and party index. Thus, the distinguisher makes only legal queries to the oracle.
To compute the \(\delta _i\)’s, the distinguisher uses the inputs to compute the real values on the wires. Using the real and external values, the distinguisher extracts the permutation elements, which are used to compute \(\delta _i\) for each row and each \(i\in B\). In the computation of the \(\delta _i\)’s there are differences and subtleties from similar proofs in both the evaluator half-gate and the designated selector gate, and we address these next.
Evaluator Half Gates: The simulator computes the evaluator half gates exactly the same. I.e., the simulator chooses an “external value” \(\widehat{e}_{z}\) and corresponding random key \(\widehat{k}^i_{z,\widehat{e}_{z}}\). However, note that the “external value” of output wire of the evaluator half gate represents \(\widehat{e}_{z}=v_{x}(v_{y}+ \lambda _{y})+ \widehat{\lambda _{z}}\), but the key \(\widehat{k}^i_{z,\widehat{e}_{z}}\) represents \(\widehat{k}_{z}^i - e_{y} k_{x}^i + \left( -e_{y} \lambda _{x} + \widehat{\lambda _{z}}\right) \varDelta _p^i\). This is because the evaluator should add \(e_{y} k_{x,e_{x}}^i\) after decrypting row \(e_{y}\).
This poses an extra challenge to the distinguisher when trying to compute the other rows, because they require deducting different multiplications of \(k_x^i\), but the distinguisher does not know \(k_x^i\).Footnote 14 However, the distinguisher does know \(k_{x,e_{x}}^i=k_{x}^i+e_{x}\varDelta _p^i\). Therefore, to deduct \(\beta k_{x}^i\), the distinguisher computes \(\beta (k_{x}^i+e_{x}\varDelta _p^i)= \beta k_{x}^i+\beta e_{x}\varDelta _p^i\). Then, this is deducted, and the \(\beta e_{x}\) is aggregated to the computation of the \(\delta _i\) of that row. Thus, the simulator calls the oracle with these aggregated \(\delta _i\)’s. The technical details are given in the full version.
Designated Selector Gates: First note that in the designate selector gates the simulator chooses three random external values and corresponding keys, although one of the corrector gates should not be decrypted. Furthermore, the simulator knows which corrector gate should not be decrypted. Nevertheless, the simulator constructs this gate as usual (one row correctly encrypted, and the other rows are random).
As for the distinguisher, the construction of the two corrector gates is similar to regular gates. The distinguisher builds both corrector gates, despite knowing which one should be decrypted. For the unused row in the chooser gate, the distinguisher uses the technique described for the evaluator half gate.
Conclusion: The proof concludes with the following key observation: If \(\mathcal{O}=Rand\) then the circuit created by the distinguisher distributes as a fake garbled circuit created by the simulator, while if \(\mathcal{O}=\mathcal{O}^{H,B}_{P}\) the circuit distributes as a real garbled circuit, created by a real execution of the protocol. Thus, distinguishing between the two cases breaks the mixed-modulus circular correlation robustness. \(\square \)
At first sight, it might not be obvious where in the proof we required the double partition of the keys and permutation bits. However, a closer inspection shows that by the simulator and distinguisher choosing the external values and keys of the two corrector gates randomly and independently, this fact is implicitly used. Otherwise (without the double partition), in a real garbled circuit the two external values are dependent and similarly the two keys, and would not match the distinguisher’s construction. Furthermore, in a real execution of the protocol, if the \(\lambda \)’s are not double partitioned, by subtraction of the two external values, a corrupt evaluator learns \(2\lambda _{w_{0}}v_x\) (here \(\lambda _{w_{0}}\) is treated as an \({\mathbb {F}}_p\) element), violating security. If the keys are not double partitioned, then a corrupt evaluator can subtract the decrypted keys of an honest party \(P_i\) and recover a multiplication of \(\varDelta _p^i\). Thus, this double partition is crucial.
Notes
- 1.
In the 2-party setting there is a more efficient construction based on stronger assumptions by Ball et al. [2], see Remark 5. Nevertheless, since these stronger assumptions are currently not needed to optimize any other garbled gate, we believe it is of interest also to optimize selector gates which are secure based on MMCCR.
- 2.
- 3.
The garbling of equality testing gates and exponentiation by a public constant are explained in the full version.
- 4.
These security definitions are for the stand-alone model. There appears to be no obstruction to prove also for the stronger UC model, but this has not been done in this work.
- 5.
As we explain later, it is more efficient to garble Boolean gates regularly than using half-gates in the multiparty setting. However, this requires assuming also the existence of a circular two-correlation robust hash function (as defined in [12]), which we denote, using shortened notation, by \(\mathcal{F}^2_{k_1,k_2}\). If we garble AND gates using the half-gates construction in Sect. 3, this extra assumption is not needed.
- 6.
Note that \({\mathbb {F}}_p\subset {\mathbb {F}}_{p^{\kappa }}\) is a field extension so \(\alpha \cdot \varDelta _p^i\) is well defined.
- 7.
Using half gates requires double the amount of decryptions during evaluation and is therefore inferior in this case despite having the same number of garbled rows.
- 8.
As explained in Sect. 2.3, it is enough to learn the keys; the evaluating party learns the external value by comparing with its local key used for the garbling.
- 9.
This is different than the two-party case, where the evaluator half gate can be handled differently, cf. [34].
- 10.
Usually, the permutation bits must remain secret as they hide the value on the wire. However, in this specific case, the value on the wire corresponding to \(v_{x}e_{w_{0}}=0\) is publicly known. Thus, there is no need to hide \(\widehat{\lambda _z}\) in this specific case. However, \(\widehat{\lambda _z}\) is crucial for security, otherwise \(\lambda _z=\widetilde{\lambda _z}\) and this would be insecure when \(e_{w_{0}}=1\).
- 11.
Due to lack of space, some of the constructions are deferred to the full version.
- 12.
In the designated selector gates, this choice is slightly more involved – \(P_i\) randomly chooses \((\widehat{\lambda _{\omega }})_i,(\widehat{\widehat{\lambda _{\omega }}})_i,(\widetilde{\lambda _{\omega }})_i,(\widetilde{\widetilde{\lambda _{\omega }}})_i\) such that \((\widehat{\lambda _{\omega }})_i+(\widetilde{\lambda _{\omega }})_i=(\widehat{\widehat{\lambda _{\omega }}})_i+(\widetilde{\widetilde{\lambda _{\omega }}})_i\). The keys are similarly partitioned; see Sect. 4.
- 13.
All the keys of the corrupt parties are known to the distinguisher. For the honest parties, the distinguisher knows the keys corresponding to the external values (chose them randomly), but does not know the \(\varDelta _p^i\)’s. Therefore, in order to change which value the honest parties’ encrypted keys correspond to, it must use the oracle \(\mathcal{O}^{H,B}_{P}\).
- 14.
The random \(\varDelta _p^i\)s of \(i\in B\) are an internal part of \(\mathcal{O}^{H,B}_{P}\). The \(\varDelta _p^i\)s of the adversary (\(i\notin B\)) are known to both the simulator and the distinguisher.
References
Applebaum, B., Ishai, Y., Kushilevitz, E.: How to garble arithmetic circuits. In: Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, FOCS 2011, pp. 120–129. IEEE Computer Society (2011)
Ball, M., Malkin, T., Rosulek, M.: Garbling gadgets for Boolean and arithmetic circuits. In: Proceedings of the 23rd Conference on Computer and Communications Security, ACM CCS, pp. 565–577 (2016)
Bar-Ilan, J., Beaver, D.: Non-cryptographic fault-tolerant computing in constant number of rounds of interaction. In: PODC (1989)
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols. In: Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing, STOC 1990, pp. 503–513 (1990)
Bellare, M., Hoang, V.T., Keelveedhi, S., Rogaway, P.: Efficient garbling from a fixed-key blockcipher. In: 2013 IEEE Symposium on Security and Privacy, SP 2013, Berkeley, CA, USA, 19–22 May 2013, pp. 478–492 (2013)
Ben-David, A., Nisan, N., Pinkas, B.: FairplayMP: a system for secure multi-party computation. In: Proceedings of the 15th ACM Conference on Computer and Communications Security, ACM CCS, pp. 257–266 (2008)
Ben-Efraim, A., Omri, E.: Concrete efficiency improvements for multiparty garbling with an honest majority. In: Proceedings of the 5th International Conference on Progress in Cryptology, LATINCRYPT (2017, to appear)
Ben-Efraim, A., Lindell, Y., Omri, E.: Optimizing semi-honest secure multiparty computation for the internet. In: Proceedings of the 23rd ACM Conference on Computer and Communications Security, ACM CCS, pp. 578–590 (2016)
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for noncryptographic fault-tolerant distributed computations. In: Proceedings of the 20th ACM Symposium on the Theory of Computing, pp. 1–10 (1988)
Bogdanov, D., Laur, S., Willemson, J.: Sharemind: a framework for fast privacy-preserving computations. In: Jajodia, S., Lopez, J. (eds.) ESORICS 2008. LNCS, vol. 5283, pp. 192–206. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-88313-5_13
Burkhart, M., Strasser, M., Many, D., Dimitropoulos, X.: SEPIA: privacy-preserving aggregation of multi-domain network events and statistics. Network (2010)
Choi, S.G., Katz, J., Kumaresan, R., Zhou, H.-S.: On the security of the “Free-XOR” technique. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 39–53. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_3
Cramer, R., Damgård, I.: Secure distributed linear algebra in a constant number of rounds. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 119–136. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_7
Damgård, I., Geisler, M., Krøigaard, M., Nielsen, J.B.: Asynchronous multiparty computation: theory and implementation. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 160–179. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_10
Damgård, I., Pastro, V., Smart, N.P., Zakarias, S.: Multiparty computation from somewhat homomorphic encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 643–662. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_38
Damgård, I., Keller, M., Larraia, E., Pastro, V., Scholl, P., Smart, N.P.: Practical covertly secure MPC for dishonest majority – or: breaking the SPDZ limits. In: Crampton, J., Jajodia, S., Mayes, K. (eds.) ESORICS 2013. LNCS, vol. 8134, pp. 1–18. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40203-6_1
Damgård, I., Nielsen, J.B., Nielsen, M., Ranellucci, S.: The tinytable protocol for 2-party secure computation, or: gate-scrambling revisited. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 167–187. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_6
Demmler, D., Schneider, T., Zohner, M.: ABY-A framework for efficient mixed-protocol secure two-party computation. In: NDSS (2015)
Gennaro, R., Rabin, M.O., Rabin, T.: Simplified VSS and fast-track multiparty computations with applications to threshold cryptography. In: Proceedings of the Seventeenth Annual ACM Symposium on Principles of Distributed Computing, PODC 1998, pp. 101–111. ACM (1998)
Goldreich, O.: Foundations of Cryptography: Volume 2, Basic Applications. Cambridge University Press, Cambridge (2009)
Gueron, S., Lindell, Y., Nof, A., Pinkas, B.: Fast garbling of circuits under standard assumptions. In: Proceedings of the 22nd ACM Conference on Computer and Communications Security, ACM CCS, pp. 567–578 (2015)
Hazay, C., Scholl, P., Soria-Vazquez, E.: Low cost constant round MPC combining BMR and oblivious transfer. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 598–628. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_21
Keller, M., Orsini, E., Scholl, P.: Mascot: faster malicious arithmetic secure computation with oblivious transfer. In: Proceedings of the 23rd ACM Conference on Computer and Communications Security (ACM CCS), pp. 830–842 (2016)
Keller, M., Orsini, E., Rotaru, D., Scholl, P., Soria-Vazquez, E., Vivek, S.: Faster secure multi-party computation of AES and DES using lookup tables. In: Gollmann, D., Miyaji, A., Kikuchi, H. (eds.) ACNS 2017. LNCS, vol. 10355, pp. 229–249. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61204-1_12
Kolesnikov, V., Schneider, T.: Improved garbled circuit: free XOR gates and applications. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008. LNCS, vol. 5126, pp. 486–498. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70583-3_40
Kreuter, B., Shelat, A., Shen, C.-H.: Billion-gate secure computation with malicious adversaries. In: USENIX Security Symposium, pp. 285–300 (2012)
Lindell, Y., Pinkas, B., Smart, N.P., Yanai, A.: Efficient constant round multi-party computation combining BMR and SPDZ. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 319–338. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_16
Malkin, T., Pastero, V., Shelat, A.: An algebraic approach to garbling. Unpublished manuscript
Naor, M., Pinkas, B., Sumner, R.: Privacy preserving auctions and mechanism design. In: Proceedings of the 1st ACM Conference on Electronic Commerce, EC 1999, pp. 129–139. ACM (1999)
Nielsen, J.B., Orlandi, C.: LEGO for two-party secure computation. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 368–386. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_22
Pinkas, B., Schneider, T., Smart, N.P., Williams, S.C.: Secure two-party computation is practical. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 250–267. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_15
Wang, X., Ranellucci, S., Katz, J.: Global-scale secure multiparty computation. In: Proceedings of the 24th ACM Conference on Computer and Communications Security, ACM CCS, pp. 39–56 (2017)
Yao, A.C.: Protocols for secure computations. In: Proceedings of the 23rd IEEE Symposium on Foundations of Computer Science, pp. 160–164 (1982)
Zahur, S., Rosulek, M., Evans, D.: Two halves make a whole. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 220–250. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_8
Acknowledgements
I would like to thank Amos Beimel, Eran Omri, and Yehuda Lindell for the many ideas and helpful discussions. Special thanks to the anonymous referees for their remarks and suggestions, and to abhi shelat and Mike Rosulek for helping me to better understand their papers.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Ben-Efraim, A. (2018). On Multiparty Garbling of Arithmetic Circuits. In: Peyrin, T., Galbraith, S. (eds) Advances in Cryptology – ASIACRYPT 2018. ASIACRYPT 2018. Lecture Notes in Computer Science(), vol 11274. Springer, Cham. https://doi.org/10.1007/978-3-030-03332-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-03332-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03331-6
Online ISBN: 978-3-030-03332-3
eBook Packages: Computer ScienceComputer Science (R0)





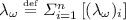 .
.

