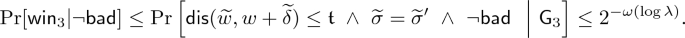Robustly Reusable Fuzzy Extractor from Standard Assumptions

Abstract

A fuzzy extractor (FE) aims at deriving and reproducing (almost) uniform cryptographic keys from noisy non-uniform sources. To reproduce an identical key R from subsequent readings of a noisy source, it is necessary to eliminate the noises from those readings. To this end, a public helper string P, together with the key R, is produced from the first reading of the source during the initial enrollment phase.

In this paper, we consider computational fuzzy extractor. We formalize robustly reusable fuzzy extractor (rrFE) which considers reusability and robustness simultaneously in the Common Reference String (CRS) model. Reusability of rrFE deals with source reuse. It guarantees that the key R output by fuzzy extractor is pseudo-random even if the initial enrollment is applied to the same source several times, generating multiple public helper strings and keys $(P_i,R_i)$. Robustness of rrFE deals with active probabilistic polynomial-time adversaries, who may manipulate the public helper string $P_i$ to affect the reproduction of $R_i$. Any modification of ${P}_i$ by the adversary will be detected by the robustness of rrFE.

• We show how to construct an rrFE from a Symmetric Key Encapsulation Mechanism (SKEM), a Secure Sketch (SS), an Extractor (Ext), and a Lossy Algebraic Filter (LAF). We characterize the key-shift security notion of SKEM and the homomorphic properties of SS, Ext and LAF, which enable our construction of rrFE to achieve both reusability and robustness.

• We present an instantiation of SKEM from the DDH assumption. Combined with the LAF by Hofheinz (EuroCrypt 2013), homomorphic SS and Ext, we obtain the first rrFE based on standard assumptions.

1 Introduction

Uniformly distributed keys are pivots of cryptographic primitives. However, it is not easy for us to create, memorize and safely store random keys. In practice, there are plenty of noisy sources, which possess high entropy and provide similar but not identical reading at each enrollment. Such sources include biometrics like fingerprint, iris, face and voice [9, 17, 19, 20], Physical Unclonable Functions [21, 23] and quantum sources [3, 16]. How to make use of these noisy sources to derive uniform and reproducible keys for cryptographic applications is exactly the concern of Fuzzy Extractors [12].

Fuzzy extractor. A fuzzy extractor ${\mathsf {FE}}$ consists of a pair of algorithms $(\mathsf {Gen},\mathsf {Rep})$. It works as follows. The generation algorithm $\mathsf {Gen}$ takes as input a reading w of some source and outputs a public helper string P and an extracted key R. The reproduction algorithm $\mathsf {Rep}$ takes as input the public helper string P and a reading $w'$ of the same source ($w'$ is a noisy version of w). It reproduces R if w and $w'$ are close enough. The security of fuzzy extractor requires that R is statistically (or computationally) indistinguishable from a uniform one, even conditioned on the public helper string P.

With a fuzzy extractor $\mathsf {FE}$, one may invoke $\mathsf {Gen}$ to generate a random key R and a public helper string P from a noisy source, then he stores the helper string P (publicly), and uses the key R in a cryptographic application. Note that it is not necessary for the user to store R. Whenever key R is needed again, he just re-reads the (noisy) source and invokes $\mathsf {Rep}$ to reproduce R with the help of P.

However, there are two limitations of FE, leading to two issues.

• The extracted key R is (pseudo)random under the assumption that no more than a single extraction is performed on the noisy source by $\mathsf {Gen}$. In reality, biometric information, like fingerprint or iris, is unique and cannot be changed or created. One may hope that the same source is enrolled multiple times by $\mathsf {Gen}$ to generate different keys $R_1, R_2, \ldots , R_\rho$ for different applications. But no security guarantee can be provided for any $R_i$ if $\rho \ge 2$.

• The security notion of FE only considers passive adversary and says nothing about active attacks. If the public helper string P is modified by an active adversary, then the reproduction algorithm $\mathsf {Rep}$ may generate a wrong key $\widetilde{R}$. In this case, one might not realize that $\widetilde{R}$ is a wrong one, and it may lead to unbearable economic loss.

The first issue can be resolved by reusable FE and the second by robust FE.

Reusable Fuzzy Extractor. Reusable Fuzzy Extractor aims to address the first issue. It allows of multiple extractions from the same source, i.e., apply $\mathsf {Gen}$ to correlated readings $w, w_1, \ldots , w_\rho$ of a source to obtain keys and public helper strings (P, R) $\{P_i, R_i\}_{i\in \{1,2,\ldots , \rho \}}$. Define $[\rho ]:=\{1,2,\ldots , \rho \}$. Reusability of FE asks for pseudorandomness of R, even conditioned on $\{P_i, R_i\}_{i\in [\rho ]}$ and P.

The concept of reusable FE was first proposed by Boyen [4], who presented two reusable FE constructions with outsider security and insider security respectively. Outsider security considers the pseudorandomness of R even if the adversary is able to adaptively choose $\delta _i$ and see $P_i$ (but not $R_i$), where $(P_i, R_i)\leftarrow \mathsf {Gen}(w+\delta _i)$. It can be regarded as weak reusability in the sense that the adversary sees only $\{P_i\}_{i\in [\rho ]}$. Insider security is stronger by allowing the adversary to obtain not only $\{P_i\}_{i\in [\rho ]}$ but also $\tilde{R}_i\leftarrow \mathsf {Rep}(\tilde{P}_i, w+\tilde{\delta }_i )$ where $\tilde{P}_i$ and $\tilde{\delta }_i$ are chosen by the adversary. However, the construction for insider security in [4] relies on the random oracle model. Meanwhile, the perturbation $\delta _i$ in the reusable FE constructions [4] is very special and independent of w, no matter for outsider security or insider security. Apon et al. [2] adapted the FE proposed by Fuller et al. [14] to obtain a weakly reusable FE. They also gave a reusable FE based on the LWE assumption. Their security model is similar to [4] but has no special requirements on $\delta _i$ except that $\mathsf {dis}(\delta _i)\le \mathfrak {t}$. However, just like [14] their reusable FE can only tolerate a logarithmic fraction of errors. With the same security model, a reusable FE tolerating linear fraction of errors from the LWE assumption was proposed in [24].

Canetti et al. [6] constructed a reusable FE for Hamming distance. The security model of their reusable FE makes no assumption about how repeating readings are correlated, but their construction only tolerates sub-linear fraction of errors. Moreover, their construction of FE has to rely on a powerful tool named “digital locker”. Up to now, digital locker can only be instantiated with a hash function modeled as random oracle or constructed from the non-standard strong vector DDH assumption. Following the line of constructing reusable FE from digital locker, Alamelou et al. [1] constructed a reusable FE for both the set difference metric and Hamming distance. Their construction tolerates linear fraction of errors but requires that noisy secrets distributions have enough entropy in each symbol of a large alphabet.

Recently, Wen et al. [26] proposed a reusable FE from the DDH assumption which can tolerate linear fraction of errors. But a strong requirement is imposed on the input distribution: any differences between two distinct inputs should not leak too much information of the source w.

As far as we know, the available works on reusable FE follow three lines according to the correlations among source readings $w_i$’s. The first line considers arbitrary correlations among $w_i$’s and has to rely on non-standard assumptions or random oracle. The second line imposes strong requirements on the source, i.e., any differences between two distinct inputs should not leak too much information of the source $w_i$. The third line considers $\delta _i$ ($=w_i-w$) controlled by adversaries. See Fig. 1. The related works are also summarized in Table 1.

Fig. 1.

Related works about reusable FE and robust FE. $\mathsf {H(w_i | w_i-w_j)}$ is the average min-entropy of $\mathsf {w_i}$ conditioned on $\mathsf {w_i-w_j}$.

Robust Fuzzy Extractor. Robust Fuzzy Extractor aims to address the second issue. Robustness of FE requires that any modification of P by an adversary will be detected. Boyen et al. [5] introduced the concept of robust FE, and proposed a general way of converting a FE to a robust one. In their approach, a hash function is employed and modeled as a random oracle. Dodis et al. [10] strengthened robustness to post-application robustness, which guarantees that the FE will detect any modification of P by adversary who also sees R. Later, robust FE was slightly improved in [18]. Nevertheless, it was shown in [13] that in the information theoretic setting, it is impossible to construct a robust FE if the entropy rate of W is less than half in the plain model. Cramer et al. [7] broke this barrier by building a robust FE in the Common Reference String (CRS) model. Recall that CRS can be hardwired or hardcoded into the system so that CRS can be observed but not modified by adversaries. See Fig. 1 and Table 1 for related works of robust FE.

We stress that up to now there is no work ever considering robustness of reusable FE or reusability of robust FE in the standard model, since designing reusable FE or robust FE alone is already an uneasy task.

Table 1. Comparison with known FE schemes. “Robustness?” asks whether the scheme achieves robustness; “Reusability?” asks whether the scheme achieves reusability; “Standard Assumption ?” asks whether the scheme is based on standard assumptions. “Linear Errors?” asks whether the scheme can correct linear fraction of errors. “–” represents the scheme is an information theoretical one.

1.1 Our Contributions

We consider how to construct fuzzy extractors satisfying reusability and robustness simultaneously based on standard assumptions in the CRS model.

• We formalize robustly reusable fuzzy extractor (rrFE) whose security notions include both reusability and post-application robustness in the computational setting.

• We propose a general construction of rrFE from a Symmetric Key Encapsulation Mechanism (SKEM), a Secure Sketch (SS), an Extractor (Ext), and a Lossy Algebraic Filter (LAF) in the CRS model.

  • We characterize the required security notion of SKEM and the homomorphic properties of SS, Ext and LAF, which enable the construction of rrFE to achieve both reusability ad robustness.

  • SKEM is a primitive similar to Key Encapsulation Mechanism (KEM), but the encapsulation and decapsulation make use of the same secret key. We define Key-Shift (KS) security for SKEM, which says that the encapsulated key is pseudorandom, even if the adversary sees multiple encapsulations under shifted secret keys where the shifts are designated by the adversary. We present an instantiation of SKEM and prove its KS-security from the DDH assumption.

• We obtain the first rrFE tolerating linear fraction of errors based on standard assumptions by instantiating SKEM, LAF, SS and Ext. More precisely, SKEM is built from the DDH assumption and LAF by Hofheinz (EuroCrypt 2013) is based on the DLIN assumption.

Our construction is the first FE possessing both reusability and robustness. Meanwhile, our construction is able to tolerate a linear fraction of errors. However, we do not assume arbitrary correlations between different readings of w. Instead, we assume that the shifts between different readings are controlled by the adversary in the security model, just like [2]. Our work can be regarded as a step forward from the the third and fourth branches in Fig. 1.

Table 1 compares our rrFE with the available reusable FE and robust FE.

1.2 Our Approach

Our work stems from the traditional sketch-and-extract paradigm [11] due to Dodis et al. First, we review the traditional sketch-and-extract paradigm [11]. Then we introduce a new primitive called Symmetric Key Encapsulation Mechanism (SKEM) and define for it a so-called Key-Shift security. We also recall the definition of Lossy Algebraic Filter (LAF) introduced by Hofheinz [15]. Equipped with SKEM and LAF, we show how to construct a robustly reusable Fuzzy Extractor (rrFE) from SS, Ext, SKEM and LAF. Finally, we describe the high level idea of why our construction of rrFE achieves both reusability and robustness.

The Sketch-and-Extract Paradigm. In [11], Dodis et al. proposed a paradigm of constructing FE from secure sketch and extractor.

Secure Sketch (SS) is used for removing noises from fuzzy inputs. An SS scheme consists of a pair of algorithms $\mathsf {SS}=$ $(\mathsf {SS{.}Gen}$, $\mathsf {SS{.}Rec})$. Algorithm $\mathsf {SS{.}Gen}$ on input w outputs a sketch s; algorithm $\mathsf {SS{.}Rec}$ on input s and $w'$ recovers w as long as w and $w'$ are close enough. For $\mathsf {SS}$, it is required that W still has enough entropy conditioned on s.

An extractor $\mathsf {Ext}$ distills an almost uniform key R from the non-uniform random variable W of enough entropy, with the help of a random seed $i_{\mathsf {ext}}$.

The sketch-and-extract construction of $\mathsf {FE}=(\mathsf {Gen}, \mathsf {Rep})$ [11] works as follows.

• $\mathsf {Gen}(w, i_{\mathsf {ext}})$: Set $P:=(\mathsf {SS{.}Gen}(w), i_{\mathsf {ext}})$, $R:=\mathsf {Ext}(w, i_{\mathsf {ext}})$. Output (P, R).

• $\mathsf {Rep}(w',P=(s, i_{\mathsf {ext}}))$: Recover $w:=\mathsf {SS{.}Rec}(w',s)$ and output $R:=\mathsf {Ext}(w, i_{\mathsf {ext}})$.

Symmetric Key Encapsulation Mechanism. For reusability, we introduce a technical tool called symmetric key encapsulation mechanism (SKEM). It is similar to Key Encapsulation Mechanism (KEM) [8], except that the encapsulation and decapsulation algorithms share the same secret key sk.

• Encapsulation algorithm $\mathsf {SKEM}{.}\mathsf {Enc}$ takes as input the secret key sk, and outputs a ciphertext c and an encapsulated key $k\in \mathcal {K}$.

• Decapsulation algorithm $\mathsf {SKEM}{.}\mathsf {Dec}$ recovers the key k, on input c and sk.

The requirement for SKEM is key-shift security. That is, $(c,k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(sk)$ is computationally indistinguishable from (c, u), where u is uniformly chosen from $\mathcal {K}$, even if the adversary has an access to a key-shift encapsulation oracle $\mathsf {SKEM}{.}\mathsf {Enc}(sk+\varDelta _i)$, where $\varDelta _i$ is chosen by the adversary adaptively.

Lossy Algebraic Filter. For robustness, we introduce a technical tool named lossy algebraic filter (LAF) by Hofheinz [15]. It is a family of functions indexed by a public key $F_{pk}$ and a tag $\mathsf {tag}$. A tag is lossy, injective or neither. A function from that family takes a vector $X=(X_i)_{i=1}^{\mathfrak {n}}\in \mathbb {Z}_p^{\mathfrak {n}}$ as input. If $\mathsf {tag}$ is an injective tag, then the function $\mathsf {LAF}_{F_{pk},\mathsf {tag}}(\cdot )$ is an injective function. If $\mathsf {tag}$ is lossy, then the function is lossy in the sense that the value only depends on a linear combination of $\sum _{i=1}^{\mathfrak {n}}u_iX_i\in \mathbb {Z}_p$ (instead of the whole X), where the coefficients $\{u_i\}_{i\in [\mathfrak {n}]}$ are independent of the lossy tag and depend only on the public key. In particular, evaluating the same input X under multiple lossy tags with respect to a common public key only reveals the same linear combination $\sum _{i=1}^{\mathfrak {n}}u_iX_i\in \mathbb {Z}_p$, thus leaking at most $\log p$ bits of information about X. It is required that there are many lossy tags and with a trapdoor one can efficiently sample a lossy tag. Additionally, LAF has two more properties named evasiveness and indistinguishability. Evasiveness demands that without the trapdoor, any PPT adversary can hardly find a new non-injective tag even given many lossy tags; indistinguishability demands that it is hard to distinguish lossy tags from random tags for all PPT adversaries.

Our Construction. Our rrFE stems from the basic “sketch-and-extract” FE [11], but an SKEM and an LAF are integrated to this basic FE to achieve reusability and robustness. The construction is shown in Fig. 2.

Fig. 2.

Construction of robustly reusable fuzzy extractor.

In our construction, the reading w of a source plays two roles, one is for extraction(reproduction) of R ($\widetilde{R}$), the other is for authentication (verification). We stress that $\mathsf {LAF}_{F_{pk},\mathsf {tag}}(w)$ can be regarded as a message authentication code (MAC)¹, where w is the authentication key, $\mathsf {tag}$ is the message, and the output of $\mathsf {LAF}$ is just the authenticator $\sigma$.

Below describes how the generation algorithm of our rrFE works.

• The common reference string $\mathsf {crs}$ consists of the public parameter $\mathsf {pp}$ of $\mathsf {SKEM}$, the random seed $i_{\mathsf {ext}}$ of $\mathsf {Ext}$, and the public key $F_{pk}$ of $\mathsf {LAF}$.

• The reading w of a source is fed not only to $\mathsf {SS}$ and $\mathsf {Ext}$, but also to $\mathsf {LAF}$. This results in a sketch s from $\mathsf {SS{.}Gen}$, a secret key sk from $\mathsf {Ext}$, and an authenticator $\sigma$ from $\mathsf {LAF}$.

• We do not take the output sk of $\mathsf {Ext}$ as the final extracted key. Instead, the output sk of $\mathsf {Ext}$ serves as the secret key of $\mathsf {SKEM}{.}\mathsf {Enc}$, which in turn outputs a ciphertext c and an encapsulated key k. This encapsulated key k is served as the final extracted key $R:=k$.

• The evaluation of $\mathsf {LAF}$ on w under tag $\mathsf {tag}=(s,c,t')$ results in an authenticator $\sigma$, where $t'$ is randomly chosen. The public helper string is set as $P:=(s,c, t', \sigma )$.

Given the public helper string $\widetilde{P}=(\widetilde{s}, \widetilde{c}, \widetilde{t'}, \widetilde{\sigma })$ and a reading $w'$, the reproduction algorithm of our rrFE will return the reproduced key $\widetilde{R}:=\mathsf {SKEM}{.}\mathsf {Dec}(\mathsf {Ext}(\widetilde{w}, i_{\mathsf {ext}}), \widetilde{c})$ only if the distance of $\widetilde{w}:= \mathsf {SS{.}Rec}(w',\widetilde{s})$ and $w'$ is no more than a predetermined threshold $\mathfrak {t}$ and the computed authenticator $\widetilde{\sigma }':=\mathsf {LAF}_{F_{pk},( \widetilde{s}, \widetilde{c}, \widetilde{t'})}(\widetilde{w})$ is identical to the authenticator $\widetilde{\sigma }$ contained in $\widetilde{P}$.

Reusability. Reusability says that the extracted key R is pseudorandom even if the PPT adversary knows $P=(s, c, t, \sigma )$ and can adaptively asks the generation oracle with shift $\delta _i$ to get multiple $\{P_i=(s_i,c_i, t_i', \sigma _i),R_i\}_{i\in [\rho ]}$ where $(P_i,R_i)\leftarrow \mathsf {Gen}(w+\delta _i)$.

To achieve reusability, we require that the underlying building blocks $\mathsf {SS}$, $\mathsf {Ext}$ and $\mathsf {LAF}$ are homomorphic and $\mathsf {SKEM}$ is key-shift secure. Recall that $i_{\mathsf {ext}}$ and $F_{pk}$ are parts of $\mathsf {crs}$ so they are independent of each other and distributed as designed. The high level idea of proving reusability is as follows.

• 1. By the homomorphic property of $\mathsf {SS}$, $\mathsf {Ext}$ and $\mathsf {LAF}$, we have

  • $s_i:=\mathsf {SS{.}Gen}(w_i)=\mathsf {SS{.}Gen}(w+\delta _i)=\mathsf {SS{.}Gen}(w)+\mathsf {SS{.}Gen}(\delta _i){=s+\mathsf {SS{.}Gen}(\delta _i)}$;

  • $sk_i=\mathsf {Ext}(w_i, i_{\mathsf {ext}})=\mathsf {Ext}(w+\delta _i,i_{\mathsf {ext}})=\mathsf {Ext}(w, i_{\mathsf {ext}})+\mathsf {Ext}(\delta _i,i_{\mathsf {ext}})=sk+\mathsf {Ext}(\delta _i,i_{\mathsf {ext}})$;

  • $\sigma _i:=\mathsf {LAF}_{F_{pk},\mathsf {tag}_i}(w+\delta _i)=\mathsf {LAF}_{F_{pk},\mathsf {tag}_i}(w)+\mathsf {LAF}_{F_{pk},\mathsf {tag}_i}(\delta _i)=\sigma +\mathsf {LAF}_{F_{pk},\mathsf {tag}_i}(\delta _i)$.

  Observe that the knowledge of $\mathsf {SS{.}Gen}(w), \mathsf {Ext}(w)$ and $\{\mathsf {LAF}_{F_{pk},\mathsf {tag}_i}(w)\}_{i\in [\rho ]}$ suffices for the challenger to simulate the whole view of the adversary in the reusability experiment.

• 2. By the indistinguishability property of $\mathsf {LAF}$, $\{\mathsf {tag}_i\}_{i\in [\rho ]}$ can be replaced with lossy tags. Now the challenger can use $\mathsf {SS{.}Gen}(w), \mathsf {Ext}(w)$ and $\mathcal {S}:=\{\mathsf {LAF}_{F_{pk},\mathsf {tag}}(w) \text { for all lossy tags}\}$ to simulate the view of the adversary.

• 3. By the lossiness of $\mathsf {LAF}$, the information of W leaked by $\mathcal {S}$ is at most $\log p$ bits. By the security of $\mathsf {SS}$, the information of W leaked by $\mathsf {SS{.}Gen}(w)$ is also bounded. Meanwhile, $\mathsf {SS{.}Gen}(w)$ and set $\mathcal {S}$ are independent of $i_{\mathsf {ext}}$ due to the independence between $(W, F_{pk})$ and $i_{\mathsf {ext}}$ (note that the lossy tag space is determined by $F_{pk}$). Consequently, ${sk:=\mathsf {Ext}(w, i_{ext})}$ is almost uniform conditioned on $\mathsf {SS{.}Gen}(w)$ and $\mathcal {S}$.

• 4. Observe that $(c_i, k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(sk_i)$ can be regarded as encapsulations under shifted key $sk_i:=sk+\mathsf {Ext}(\delta _i)$. With a uniform sk (conditioned on $\mathsf {SS{.}Gen}(w)$ and $\mathcal {S}$), the KS-security of SKEM makes sure that $R:=k$ is pseudorandom given P and $\{P_i=(s_i,c_i, t_i', \sigma _i),R_i=k_i\}_{i\in [\rho ]}$, where $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(sk)$.

Robustness. Robustness states that even if the PPT adversary can adaptively asks the generation oracle with shift $\delta _i$ to get $(P_i,R_i)\leftarrow \mathsf {Gen}(w+\delta _i)$, it is still hard to forge a fresh valid $\tilde{P}$.

Following 1, 2 and 3 of the above analysis for reusability, the view of adversary in the robustness experiment can be simulated with the knowledge of $\mathsf {SS{.}Gen}(w)$ and $\mathcal {S}$. Note that the $\mathsf {SS{.}Gen}(w)$ and set $\mathcal {S}$ only leak bounded information of W. Consequently, even if the adversary sees $\{P_i,R_i\}_{i\in [\rho ]}$, there is still enough entropy left in W. By the evasiveness of $\mathsf {LAF}$, the forged tag $\widetilde{\mathsf {tag}}=(\widetilde{s}, \widetilde{c},\widetilde{t'})$ contained in $\widetilde{P}=(\widetilde{s}, \widetilde{c}, \widetilde{t'}, \widetilde{\sigma })$ must be injective, hence $\mathsf {LAF}_{F_{pk},\widetilde{\mathsf {tag}}}(\cdot )$ is an injective function. Consequently, the entropy of W is intactly transferred to $\widetilde{\sigma }':=\mathsf {LAF}_{F_{pk},\widetilde{\mathsf {tag}}}(\widetilde{w})$ and the forged authenticator $\widetilde{\sigma }$ hits the value of $\widetilde{\sigma }'$ with negligible probability.

2 Preliminaries

Let $\lambda$ be the security parameter. We write PPT short for probabilistic polynomial-time. Let $[\rho ]$ denote set $\{1,2\cdots ,\rho \}$. Let $\lceil x\rceil$ denote the smallest integer that is not smaller than x. If X is a distribution, $x\leftarrow X$ denotes sampling x according to distribution X; if X is a set, ${x\leftarrow _{{{\$}}}X}$ denotes choosing x from X uniformly. For a set X, let |X| denote the size of X. Let $\overbrace{xxx}^{y}$ and $\underbrace{xxx}_{y}$ denote $y:=xxx$. For a primitive XX and a security notion YY, by $\mathsf {Exp}_{\text {XX},\mathcal {A}}^{\text {YY}}({\cdot })\Rightarrow 1$, we mean that the security experiment outputs 1 after interacting with an adversary $\mathcal {A}$; by $\mathsf {Adv}_{\text {XX},\mathcal {A}}^{\text {YY}}(1^{\lambda })$, we denote the advantage of a PPT adversary $\mathcal {A}$ and define $\mathsf {Adv}_{\text {XX}}^{\text {YY}}(1^{\lambda }):=\max _{\text {PPT}\mathcal {A}}{\mathsf {Adv}_{\text {XX},\mathcal {A}}^{\text {YY}}(1^{\lambda })}$. Our security proof will proceed by a sequence of games. By $a\overset{\mathsf {G}}{=}b$ we mean that a equals b or is computed as b in game $\mathsf {G}$. By $\mathsf {G}^{\mathcal {A}}\Rightarrow b$, we mean that game $\mathsf {G}$ outputs b after interacting with $\mathcal {A}$.

2.1 Metric Spaces

A metric space is a set $\mathcal {M}$ with a distance function $\mathsf {dis}:\mathcal {M}\times \mathcal {M}\mapsto [0,\infty )$. We usually consider multi-dimensional metric spaces of form $\mathcal {M}=\mathcal {F}^n$ for some alphabet $\mathcal {F}$ (usually a finite filed $\mathbb {F}_p$) equipped with the Hamming distance. For any two element $w, w'\in \mathcal {M}$, the Hamming distance $\mathsf {dis}(w, w')$ is the number of coordinates in which they differ. For an element $w\in \mathcal {M}$, let $\mathsf {dis}(w):=\mathsf {dis}(w,0)$.

2.2 Min-Entropy, Statistical Distance and Extractor

Definition 1

(Min-Entropy). For a random variable X, the min-entropy of X is defined by $H_{\infty }(X)= -\log (\max _x \Pr [X=x])$. The average min-entropy of X given Y is defined by $\widetilde{H}_{\infty }(X|Y)=-\log [\mathbb {E}_{y\leftarrow Y}(\max _x\Pr [X=x|Y=y])]$.

Obviously, for a deterministic function f and a randomized function g with the random coins R independent of X, we have that

$$\begin{aligned}&\widetilde{H}_{\infty }\left( X\mid Y, f(Y)\right) =\widetilde{H}_{\infty }(X\mid Y).\end{aligned}$$

(1)

$$\begin{aligned}&\widetilde{H}_{\infty }(X\mid Y, g(Y,R))=\widetilde{H}_{\infty }(X\mid Y). \end{aligned}$$

(2)

Lemma 1

[11] If Y takes at most $2^{\lambda }$ possible values, then $\widetilde{H}_{\infty }(X\mid Y)\ge \widetilde{H}_{\infty }(X)-\lambda$.

Definition 2

(Statistical Distance). For two random variables X and Y over a set $\mathcal {M}$, the statistical distance of X and Y is given by $\mathbf {SD}(X,Y)=\frac{1}{2}\sum _{w\in \mathcal {M}}|\Pr [X=w]-\Pr [Y=w]|$. If $\mathbf {SD}(X,Y)\le \varepsilon$, X and Y are called $\varepsilon$-statistically indistinguishable, denoted by $X\overset{\varepsilon }{\approx }Y$.

Lemma 2

[22] Let $\mathcal {M}_1$ and $\mathcal {M}_2$ be finite sets, X and Y be random variables over $\mathcal {M}_1$, and $f:\mathcal {M}_1\mapsto \mathcal {M}_2$ be a function. Then $\mathbf {SD}(f(X),f(Y))\le \mathbf {SD}(X,Y)$.

Definition 3

(Average-Case Strong Extractor [11]). We call a function $\mathsf {Ext}:\mathcal {M}\times \mathcal {I}\mapsto \mathcal {SK}$ an average-case $(\mathcal {M},m,\mathcal {SK},\varepsilon )$-strong extractor with seed space $\mathcal {I}$, if for all pairs of random variables (X, Y) such that $X\in \mathcal {M}$ and $\widetilde{H}_{\infty }(X\mid Y)\ge m$, we have

$$\begin{aligned} { (\mathsf {Ext}(X,I),I,Y) \overset{\varepsilon }{\approx } (U,I,Y),} \end{aligned}$$

(3)

where I and U are uniformly distributed over $\mathcal {I}$ and $\mathcal {SK}$, respectively.

2.3 Secure Sketch

Definition 4

(Secure Sketch [11]). An $(m,\hat{m},\mathfrak {t})$-secure sketch (SS) $\mathsf {SS}=(\mathsf {SS{.}Gen},\mathsf {SS{.}Rec})$ for metric space $\mathcal {M}$ with distance function $\mathsf {dis}$, consists of a pair of PPT algorithms and satisfies correctness and security.

• $\mathsf {SS{.}Gen}$ on input $w\in \mathcal {M}$, outputs a sketch s.

• $\mathsf {SS{.}Rec}$ takes as input $w'\in \mathcal {M}$ and a sketch s, and outputs $\tilde{w}$.

Correctness. $\forall w\in \mathcal {M}$, if $\mathsf {dis}(w,w')\le \mathfrak {t}$, then $\mathsf {SS{.}Rec}(w',\mathsf {SS{.}Gen}(w))=w$. Security. For any random variable W over $\mathcal {M}$ with min-entropy m, we have $\widetilde{H}_{\infty }(W\mid {\mathsf {SS{.}Gen}}(W))\ge \hat{m}$.

Lemma 3

[5]. Let $\mathsf {SS}=(\mathsf {SS{.}Gen},\mathsf {SS{.}Rec})$ be an $(m,\hat{m},t)$-SS for $\mathcal {M}$, if $W_0,W_1$ are two random variables over $\mathcal {M}$ satisfying $\mathsf {dis}(W_0,W_1)\le \mathfrak {t}$, then for any variable Y, we have $\widetilde{H}_{\infty }(W_1\mid (\mathsf {SS{.}Gen}(W_0),Y))\ge \widetilde{H}_{\infty }(W_0\mid (\mathsf {SS{.}Gen}(W_0),Y)).$

2.4 Lossy Algebraic Filter

Our construction of robustly reusable fuzzy extractor relies on a technical tool, named lossy algebraic filter which is proposed by Hofheinz [15].

Definition 5

(Lossy Algebraic Filter). An $(l_{\mathsf {LAF}}, \mathfrak {n})$-lossy algebraic filter ${\mathsf {LAF}=(\mathsf {FGen},\mathsf {FEval},\mathsf {FTag} )}$ consists of three PPT algorithms.

• Key generation. $\mathsf {FGen}(1^{\lambda })$ outputs a public key $F_{pk}$ together with a trapdoor $F_{td}$, i.e., $(F_{pk},F_{td})\leftarrow \mathsf {FGen}(1^{\lambda })$. The public key $F_{pk}$ contains an $l_{\mathsf {LAF}}$-bit prime p and defines a tag space $\mathcal {T}_{\mathsf {tag}}=\{0,1\}^*\times \mathcal {T}'$, a lossy tag space $\mathcal {T}_{lossy}\subseteq \mathcal {T}_{\mathsf {tag}}$ and an injective tag space $\mathcal {T}_{inj}\subseteq \mathcal {T}_{\mathsf {tag}}$. A tag $\mathsf {tag}=(t, t')\in \mathcal {T}_{\mathsf {tag}}$ consists of a core tag $t' \in \mathcal {T}'$ and an auxiliary tag $t\in \{0,1\}^*$. $F_{td}$ is a trapdoor that allows of sampling lossy tags.

• Evaluation. $\mathsf {FEval}$ takes as input the public key $F_{pk}$, a tag $\mathsf {tag}=(t, t')$, and $X=(X_i)_{i=1}^{\mathfrak {n}}\in \mathbb {Z}_p^{\mathfrak {n}}$, and outputs $\mathsf {LAF}_{F_{pk},\mathsf {tag}}(X)$, i.e., $\mathsf {LAF}_{F_{pk},\mathsf {tag}}(X)=\mathsf {FEval}(F_{pk},\mathsf {tag},X)$.

• Lossy tag generation. $\mathsf {FTag}$ takes as input the trapdoor $F_{td}$ and an auxiliary tag t, and returns a core tag $t'$, i.e., $t'\leftarrow \mathsf {FTag}(F_{td},t)$, such that $\mathsf {tag}=(t, t')$ is a lossy tag.

We require the following:

• Lossiness. If $\mathsf {tag}\in \mathcal {T}_{inj}$, then the function $\mathsf {LAF}_{F_{pk},\mathsf {tag}}(\cdot )$ is injective. If $\mathsf {tag}\in \mathcal {T}_{lossy}$, then $\mathsf {LAF}_{F_{pk},\mathsf {tag}}(X)$ depends only on $\sum _{i=1}^{\mathfrak {n}}u_i X_i\mod p$ for $u_i\in \mathbb {Z}_p$ that only depends on $F_{pk}$.

• Indistinguishability. For all PPT adversaries, it is hard to distinguish lossy tags from random tags. Formally,

  

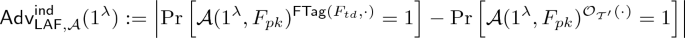
  is negligible for all PPT adversary $\mathcal {A}$, where ${(F_{pk},F_{td})\leftarrow \textsf {FTag}(1^{\lambda })}$ and $\mathcal {O}_{\mathcal {T}'}(\cdot )$ is the oracle that ignores its input and samples a random core tag $t'$.

• Evasiveness. For all PPT adversaries, without the trapdoor, non-injective tags are hard to find, even given multiple lossy tags. More precisely,

  $$\begin{aligned} \mathsf {Adv}_{\mathsf {LAF},\mathcal {A}}^{\mathsf {eva}}(1^{\lambda }):=\Pr \left[ \mathsf {tag}\notin \mathcal {T}_{inj} \mid \mathsf {tag}\leftarrow \mathcal {A}(1^{\lambda }, F_{pk})^{\mathsf {FTag}(F_{td},\cdot )}\right] \end{aligned}$$

  is negligible for all PPT admissible adversary $\mathcal {A}$ where $(F_{pk},F_{td})\leftarrow \mathsf {FGen}(1^{\lambda })$. We call $\mathcal {A}$ is admissible if $\mathcal {A}$ never outputs a tag obtained from its oracle.

Remark 1

If $\mathsf {tag}=(t, t')$, we use $\mathsf {FEval}(F_{pk},t, t' ,X)$ to denote $\mathsf {FEval}(F_{pk},\mathsf {tag},X)$.

Remark 2

Let us consider multiple, say $\mathfrak {m}$, evaluations of $\mathsf {LAF}$ of the same $X=(X_1, X_2, \ldots , X_{\mathfrak {n}})$ under a fixed public key $F_{pk}$ but different tags $(t_j, t_j')$. According to the lossiness property of $\mathsf {LAF}$, each evaluation of $\mathsf {FEval}(F_{pk},t_j, t_j' ,X)$ is completely determined by $\sum _{i=1}^{\mathfrak {n}}u_i X_i$ and $(t_j, t_j')$, so there exists a function f such that $\mathsf {FEval}(F_{pk},t_j, t_j' ,X)=f\left( \sum _{i=1}^{\mathfrak {n}}u_i X_i, (t_j, t_j')\right)$. Suppose that $F_{pk}$ is independent of X. As long as tags $\{(t_j, t_j')\}_{j\in [\mathfrak {m}]}$ are independent of X or are (randomized) functions of $\sum _{i=1}^{\mathfrak {n}}u_i X_i$, we have

(4)

where the last but one step is due to Eq. (2) and the last step is by Lemma 1.

2.5 Homomorphic Properties

We assume that the domains and codomains of Ext, SS and LAF are groups with operation “+” (we abuse “+” for different group operations for simplicity). Now we characterize homomorphic properties of Ext, SS and LAF.

Definition 6

(Homomorphic Average-Case Strong Extractor). An average-case $(\mathcal {M},m,\mathcal {SK},\varepsilon )$-strong extractor $\mathsf {Ext}:\mathcal {M}\times \mathcal {I}\rightarrow \mathcal {SK}$ is homomorphic if for all $w_1,w_2\in \mathcal {M}$, all $i_{\mathsf {ext}}\in \mathcal {I}$, we have $\mathsf {Ext}(w_1+w_2, i_{\mathsf {ext}})=\mathsf {Ext}(w_1, i_{\mathsf {ext}})+\mathsf {Ext}(w_2, i_{\mathsf {ext}}).$

It was shown in [11], universal hash functions are average-case strong extractors. In particular, $\mathsf {Ext}(x,i) :\mathbb {Z}_q^{l+1}\times \mathbb {Z}_q^{l}\rightarrow \mathbb {Z}_q$ defined by

$$\begin{aligned} {\mathsf {Ext}(x,i):=x_0+i_1x_1+\cdots +i_lx_l} \end{aligned}$$

(5)

is an average-case strong $(\mathbb {Z}_q^{l+1}, m, \mathbb {Z}_q,\varepsilon )$-extractor with $\log q\le m+2\log \varepsilon$, as shown in [22]. Obviously, it is homomorphic.

Definition 7

(Homomorphic Secure Sketch). A secure sketch is homomorphic if for all $w_1,w_2\in \mathcal {M}$, $\mathsf {SS{.}Gen}(w_1+w_2)=\mathsf {SS{.}Gen}(w_1)+\mathsf {SS{.}Gen}(w_2)$.

The syndrome-based secure sketch [12] is homomorphic (see the full version [25]).

Definition 8

(Homomorphic Lossy Algebraic Filter). We call an $(l_{\mathsf {LAF}}, \mathfrak {n})$-LAF with domain $\mathbb {Z}_p^{\mathfrak {n}}$ is homomorphic if for all $(F_{pk},F_{td})\leftarrow \mathsf {FGen}(1^{\lambda })$, all $\mathsf {tag}\in \mathcal {T}_{\mathsf {tag}}$ and all $w_1,w_2\in \mathbb {Z}_p^{\mathfrak {n}}$, the following holds $\mathsf {FEval}(F_{pk},\mathsf {tag},w_1+w_2)=\mathsf {FEval}(F_{pk}, \mathsf {tag}, w_1)+\mathsf {FEval}(F_{pk},\mathsf {tag},w_2)$.

The $\mathsf {LAF}$ constructed from the DLIN assumption in [15] is homomorphic. See the full version [25] for the specific construction of homomorphic $\mathsf {LAF}$.

2.6 Decisional Diffie-Hellman Assumption

Definition 9

(Decisional Diffie-Hellman Assumption). The decisional Diffie-Hellman assumption holds w.r.t. a group generation algorithm ${\mathcal {IG}}$, if

is negligible for all PPT adversary $\mathcal {A}$, where $({\mathbb {G}},q,g)\leftarrow {\mathcal {IG}}(1^{\lambda })$, $\mathbb {G}$ is a cyclic group of order q with generator g and ${x,y,z \leftarrow _{{{\$}}}\mathbb {Z}_q}$.

3 Symmetric Key Encapsulate Mechanism

3.1 Definition of SKEM

In this section, we propose a new primitive called symmetric key encapsulate mechanism (SKEM). It is one of the core technical tools in our rrFE.

Definition 10

(Symmetric Key Encapsulate Mechanism). A symmetric key encapsulate mechanism ${\mathsf {SKEM}=(\mathsf {SKEM}{.}\mathsf {Init}, ~\mathsf {SKEM}{.}\mathsf {Enc},~\mathsf {SKEM}{.}\mathsf {Dec})}$ consists of a triple of PPT algorithms.

• $\mathsf {SKEM}{.}\mathsf {Init}$ takes as input the security parameter $1^{\lambda }$ and outputs public parameter $\mathsf {pp}$ which implicitly defines the secret key space $\mathcal {SK}$, encapsulated key space $\mathcal {K}$ and ciphertext space, i.e., $\mathsf {pp}\leftarrow \mathsf {SKEM}{.}\mathsf {Init}(1^{\lambda })$.

• $\mathsf {SKEM}{.}\mathsf {Enc}$ takes as input $\mathsf {pp}$ and the secret key sk, and outputs a ciphertext c and an encapsulated key $k\in \mathcal {K}$, i.e., $(c,k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp},sk)$.

• $\mathsf {SKEM}{.}\mathsf {Dec}$ takes as input $\mathsf {pp}$, the secret key sk and a ciphertext c, and outputs $k\in \mathcal {K}$, i.e., $k\leftarrow \mathsf {SKEM}{.}\mathsf {Dec}(\mathsf {pp}, sk, c)$.

The correctness of $\mathsf {SKEM}$ is that for all $\mathsf {pp}\leftarrow \mathsf {SKEM}{.}\mathsf {Init}(1^{\lambda })$, $sk\in \mathcal {SK}$, $(c,k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk)$, $k'\leftarrow \mathsf {SKEM}{.}\mathsf {Dec}(\mathsf {pp}, sk,c)$, we have $k'=k$.

We require pseudorandomness of the encapsulated key under key-shift attack. Roughly speaking, the encapsulated key is pseudorandom even if the adversary observes multiple encapsulations under shifted secret key where the shift $\varDelta _i$ is designated by the adversary adaptively. The formal definition is given below.

Definition 11

(KS-Security of SKEM). A SKEM $\mathsf {SKEM}=(\mathsf {SKEM}{.}\mathsf {Init}$, $\mathsf {SKEM}{.}\mathsf {Enc},\mathsf {SKEM}{.}\mathsf {Dec})$ is Key-Shift (KS) secure if for all PPT adversary $\mathcal {A}$,

$$\mathsf {Adv}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(1^{\lambda }):=|\Pr [\mathsf {Exp}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(1)\Rightarrow 1]-\Pr [\mathsf {Exp}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(0)\Rightarrow 1]|$$

is negligible. Here $\mathsf {Exp}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(\beta )$, $\beta \in \{0,1\}$, is an experiment played between an adversary $\mathcal {A}$ and a challenger $\mathcal {C}$ as follows.

$\underline{\mathsf {Exp}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(\beta )}{:}$

• $\mathcal {C}$ invokes $\mathsf {pp}\leftarrow \mathsf {SKEM}{.}\mathsf {Init}(1^{\lambda })$, samples ${sk\leftarrow _{{{\$}}}\mathcal {SK}}$ and returns $\mathsf {pp}$ to $\mathcal {A}$.

• Challenge: Challenger $\mathcal {C}$ invokes $(c,k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp},sk)$. If $\beta =0$, it resets k with ${k\leftarrow _{{{\$}}}\mathcal {K}}$. Finally it returns (c, k) to $\mathcal {A}$.

• During the whole experiment, $\mathcal {A}$ may adaptively make encapsulation oracle queries of the following form:

  • $\mathcal {A}$ submits a shift $\varDelta _i\in \mathcal {SK}$ to challenger $\mathcal {C}$.

  • $\mathcal {C}$ invokes $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk+\varDelta _i)$, and returns $(c_i,k_i)$ to $\mathcal {A}$.

• As long as $\mathcal {A}$ outputs a guessing bit $\beta '$, the experiment outputs $\beta '$.

3.2 Construction of Symmetric Key Encapsulate Mechanism

We instantiate a KS-secure SKEM from the DDH assumption, and the construction is given in Fig. 3.

Fig. 3.

Construction of $\mathsf {SKEM}$ with KS-security from the DDH assumption.

Theorem 1

If the DDH assumption holds with respect to $\mathcal {IG}$, then $\mathsf {SKEM}$ constructed in Fig. 3 is KS-secure. More precisely, for any PPT adversary $\mathcal {A}$,

$$\mathsf {Adv}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(1^{\lambda })\le \mathsf {Adv}_{\mathcal {IG}}^{\mathsf {DDH}}(1^{\lambda }).$$

Proof

Suppose that there exists a PPT adversary $\mathcal {A}$ who has advantage $\epsilon$ in the key-shift attack of SKEM in Fig. 3, then we can construct a PPT algorithm $\mathcal {B}$ with the same advantage $\epsilon$ in solving the DDH problem.

Given ${({\mathbb {G}},q,g,g^x,g^y,g^{d})}$, where x, y are uniformly and independently chosen from $\mathbb {Z}_q$, algorithm $\mathcal {B}$ simulates an environment for $\mathcal {A}$ as follows.

• Algorithm $\mathcal {B}$ returns ${\mathsf {pp}=({\mathbb {G}},q,g)}$ to $\mathcal {A}$ and implicitly sets $sk:=x$.

• Algorithm $\mathcal {B}$ returns $(g^y,g^d)$ to $\mathcal {A}$.

• When adversary $\mathcal {A}$ makes an encapsulation query with $\varDelta _i\in \mathbb {Z}_p$, algorithm $\mathcal {B}$ uniformly chooses $y_i\leftarrow \mathbb {Z}_q$ and sets $c_i:=g^{y_i}$, $k_i:=(g^xg^{\varDelta _i})^{y_i}$ and returns $(c_i,k_i)$ to $\mathcal {A}$.

• When adversary $\mathcal {A}$ returns a bit $\beta '$, algorithm $\mathcal {B}$ returns $\beta '$ to its own challenger.

Obviously, $\mathcal {B}$ simulates answers to the encapsulation queries for $\mathcal {A}$ perfectly. For the challenge,

• If $d=xy$, then $\mathcal {B}$ perfectly simulates $\mathsf {Exp}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(1)$ for $\mathcal {A}$.

• If $d=z$, where ${z\leftarrow _{{{\$}}}\mathbb {Z}_q}$, then $\mathcal {B}$ perfectly simulates $\mathsf {Exp}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(0)$ for $\mathcal {A}$.

Consequently,

$$\begin{aligned} {\mathsf {Adv}}_{{\mathcal {IG}},\mathcal {B}}^{\mathsf {DDH}}(1^{\lambda })= & {} \Pr [\mathcal {B}(({\mathbb {G}},q,g),g^x,g^y,g^{xy})=1]-\Pr [\mathcal {B}(({\mathbb {G}},q,g),g^x,g^y,g^{z})=1]\\= & {} |\Pr [\mathsf {Exp}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(1)\Rightarrow 1]-\Pr [\mathsf {Exp}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(0)\Rightarrow 1]| ={\mathsf {Adv}}_{\mathsf {SKEM},\mathcal {A}}^{\mathsf {ks}}(1^{\lambda }). \end{aligned}$$

This completes the proof of Theorem 1.    $\blacksquare$

4 Robustly Reusable Fuzzy Extractor

In this section, we define robustly reusable fuzzy extractor (rrFE) and present a construction of rrFE in the CRS model.

4.1 Definition of Robustly Reusable Fuzzy Extractor

First, we recall the definition of fuzzy extractor presented in [7].

Definition 12

(Fuzzy Extractor). An $(\mathcal {M},m ,\mathcal {R},\mathfrak {t},\varepsilon )$-fuzzy extractor $\mathsf {FE}$ for metric space $\mathcal {M}$ consists of three PPT algorithms $(\mathsf {Init}, \mathsf {Gen}, \mathsf {Rep})$,

• $\mathsf {Init}$ on input security parameter $1^{\lambda }$ outputs common reference string $\mathsf {crs}$, i.e., $\mathsf {crs}\leftarrow \mathsf {Init}(1^{\lambda })$.

• $\mathsf {Gen}$ on input the common reference string $\mathsf {crs}$ and $w\in \mathcal {M}$, outputs a public helper string P and an extracted string $R\in \mathcal {R}$, i.e., $(P,R)\leftarrow \mathsf {Gen}(\mathsf {crs}, w)$.

• $\mathsf {Rep}$ takes as input the common reference string $\mathsf {crs}$, public helper string P and $w'\in \mathcal {M}$, and outputs an extracted string R or $\bot$, i.e., $R/\bot \leftarrow \mathsf {Rep}(\mathsf {crs},P,w')$.

It satisfies the following properties.

• Correctness. If $\mathsf {dis}(w,w')\le \mathfrak {t}$, then for any $\mathsf {crs}\leftarrow \mathsf {Init}(1^{\lambda })$, $(P,R)\leftarrow \mathsf {Gen}(\mathsf {crs}, w)$ and $R'\leftarrow \mathsf {Rep}(\mathsf {crs},P,w')$, it holds that $R'=R$.

• Privacy. For any distribution W over metric space $\mathcal {M}$ with ${H}_{\infty }(W)\ge m$, any PPT adversary $\mathcal {A}$, it holds that

  $$\mathsf {Adv}_{\mathsf {FE},\mathcal {A}}^{\mathsf {ind}}(1^{\lambda }):=|\Pr [\mathcal {A}(\mathsf {crs},P,R)=1]-\Pr [\mathcal {A}(\mathsf {crs},P,U)=1]|\le \varepsilon ,$$

  where $\mathsf {crs}\leftarrow \mathsf {Init}(1^{\lambda })$, $(P,R)\leftarrow \mathsf {Gen}(\mathsf {crs}, W)$ and ${U\leftarrow _{{{\$}}}\mathcal {R}}$.

A fuzzy extractor is reusable if its privacy is retained even if the same noisy source is reused multiple times. We follow the definition of reusability of fuzzy extractor from [2] (which is called “strong reusability” in [2]).

Definition 13

(Reusable Fuzzy Extractor). A fuzzy extractor $\mathsf {rFE}=(\mathsf {Init}$, $\mathsf {Gen}, \mathsf {Rep})$ is an $(\mathcal {M},m ,\mathcal {R}, \mathfrak {t}, \varepsilon _1)$-reusable fuzzy extractor if it is a fuzzy extractor with $\varepsilon _1$-reusability. An $(\mathcal {M},m ,\mathcal {R}, \mathfrak {t},\varepsilon _1)$-fuzzy extractor is $\varepsilon _1$-reusable, if for any distribution W over metric space $\mathcal {M}$ with ${H}_{\infty }(W)\ge m$, for any PPT adversary $\mathcal {A}$, it holds that

$$\mathsf {Adv}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}(1^{\lambda }):=|\Pr [\mathsf {Exp}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}(1)\Rightarrow 1]-\Pr [\mathsf {Exp}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}(0)\Rightarrow 1]|\le \varepsilon _1, $$

where $\mathsf {Exp}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}(\beta )$, $\beta \in \{0,1\}$, describes the reusability experiment played between an adversary $\mathcal {A}$ and a challenger $\mathcal {C}$.

$\underline{\mathsf {Exp}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}(\beta ):}$ // $\beta \in \{0,1\}$

• 1. Challenger $\mathcal {C}$ invokes $\mathsf {crs}\leftarrow \mathsf {Init}(1^{\lambda })$ and returns $\mathsf {crs}$ to $\mathcal {A}$.

• 2. $\mathcal {C}$ samples $w\leftarrow W$ and invokes $(P,R)\leftarrow \mathsf {Gen}(\mathsf {crs},w)$. If $\beta =1$, return (P, R) to $\mathcal {A}$; otherwise, it chooses ${U\leftarrow _{{{\$}}}\mathcal {R}}$ and returns (P, U) to $\mathcal {A}$.

• 3. $\mathcal {A}$ may adaptively make queries of the following form:

  • $\mathcal {A}$ submits a shift $\delta _i\in \mathcal {M}$ satisfying $\mathsf {dis}(\delta _i)\le \mathfrak {t}$ to $\mathcal {C}$.

  • $\mathcal {C}$ invokes $(P_i,R_i)\leftarrow \mathsf {Gen}(\mathsf {crs},w+\delta _i)$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

• 4. As long as $\mathcal {A}$ outputs a guessing bit $\beta '$, the experiment outputs $\beta '$.

Robust fuzzy extractor guarantees that any modification of the public helper string by a PPT adversary will be detected. Now, combining the definition of reusability in [2] and robustness of fuzzy extractor in [7], we give the definition of robustly reusable fuzzy extractor.

Definition 14

(Robustness of Reusable Fuzzy Extractor). Let $\mathsf {rrFE}=(\mathsf {Init}, \mathsf {Gen}, \mathsf {Rep})$ be an $(\mathcal {M},m ,\mathcal {R}, \mathfrak {t},\varepsilon _1)$-reusable fuzzy extractor. We say $\mathsf {rrFE}$ is $\varepsilon _2$-robust if for any distribution W over metric space $\mathcal {M}$ with ${H}_{\infty }(W)\ge m$, for any PPT adversary $\mathcal {A}$, it holds that

$$\mathsf {Adv}_{\mathsf {rrFE},\mathcal {A}}^{\mathsf {rob}}(1^{\lambda }):=\Pr [\mathsf {Exp}_{\mathsf {rrFE},\mathcal {A}}^{\mathsf {rob}}(1^{\lambda })\Rightarrow 1]\le \varepsilon _2,$$

where $\mathsf {Exp}_{\mathsf {rrFE},\mathcal {A}}^{\mathsf {rob}}(1^{\lambda })$ describes the robustness experiment played between an adversary $\mathcal {A}$ and a challenger $\mathcal {C}$.

$\underline{\mathsf {Exp}_{\mathsf {rrFE},\mathcal {A}}^{\mathsf {rob}}(1^{\lambda }){:}}$

• 1. Challenger $\mathcal {C}$ invokes $\mathsf {crs}\leftarrow \mathsf {Init}(1^{\lambda })$, and returns $\mathsf {crs}$ to $\mathcal {A}$.

• 2. $\mathcal {C}$ samples $w\leftarrow W$, invokes $(P,R)\leftarrow \mathsf {Gen}(\mathsf {crs},w)$ and returns (P, R) to $\mathcal {A}$.

• 3. $\mathcal {A}$ may adaptively make queries of the following form:

  • $\mathcal {A}$ submits a shift $\delta _i\in \mathcal {M}$ satisfying $\mathsf {dis}(\delta _i)\le \mathfrak {t}$ to challenger $\mathcal {C}$.

  • $\mathcal {C}$ invokes $(P_i,R_i)\leftarrow \mathsf {Gen}(\mathsf {crs},w+\delta _i)$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

• 4. $\mathcal {A}$ submits its forgery $(\widetilde{P}, \widetilde{\delta })$ to $\mathcal {C}$. $\mathcal {A}$ wins if $\mathsf {dis}(\widetilde{\delta })\le \mathfrak {t}$, $\widetilde{P}$ is fresh (i.e., $\widetilde{P}$ is different from P and those $P_i$) and $\mathsf {Rep}(\mathsf {crs},\widetilde{P},w+\widetilde{\delta })\ne \bot$. The experiment outputs 1 if $\mathcal {A}$ wins and 0 otherwise.

Definition 15

(Robustly Reusable Fuzzy Extractor). An $(\mathcal {M},m ,\mathcal {R}, \mathfrak {t},\varepsilon _1,\varepsilon _2)$-robustly reusable fuzzy extractor (rrFE) is an $(\mathcal {M},m ,\mathcal {R}, \mathfrak {t},\varepsilon _1)$-reusable fuzzy extractor with ${\varepsilon _2}$-robustness.

Remark 3

In the robustness experiment, the adversary submits not only $\widetilde{P}$, but also the shift $\widetilde{\delta }$. In the previous works, such as [8], the authors considered two perturbation styles: (1) the shift is independent of W; (2) the shift can arbitrarily depend on W. In our definition, the shift is controlled by the adversary, and it just sits in the middle of the two styles. The reason we adopt such a definition is to make the perturbation style consistent with that in the reusability experiment.

4.2 Construction of Robustly Reusable Fuzzy Extractor

Figure 4 illustrates our construction of robustly reusable FE $\mathsf {rrFE}=(\mathsf {Init}, \mathsf {Gen}, \mathsf {Rep})$ for metric space $\mathcal {M}$, which makes use of the following building blocks:

• A key-shift secure symmetric key encapsulation mechanism $\mathsf {SKEM}=(\mathsf {SKEM}{.}\mathsf {Init}$, $\mathsf {SKEM}{.}\mathsf {Enc},\mathsf {SKEM}{.}\mathsf {Dec})$. Let its secret key space be $\mathcal {SK}$ and encapsulation key space be $\mathcal {K}$.

• A homomorphic average-case $(\mathcal {M},\hat{m},\mathcal {SK},\varepsilon _{\mathsf {ext}})$-strong extractor $\mathsf {Ext}$.

• A homomorphic $(m-\lceil \log p\rceil , \hat{m},2\mathfrak {t})$-secure sketch $\mathsf {SS}=(\mathsf {SS{.}Gen},\mathsf {SS{.}Rec})$ for metric space $\mathcal {M}$ with $\hat{m}-\lceil \log p\rceil \ge \omega (\log \lambda )$.

• A homomorphic $(l_{\mathsf {LAF}}, \mathfrak {n})$-lossy algebraic filter $\mathsf {LAF}=(\mathsf {FGen},\mathsf {FEval},\mathsf {FTag} )$ with domain $\mathbb {Z}_p^{\mathfrak {n}}$, $l_{\mathsf {LAF}}=\lceil \log p\rceil$, and tag space $\{0,1\}^*\times \mathcal {T}'$. We assume that any $w\in \mathcal {M}$ can be explained as an element in $\mathbb {Z}_p^{\mathfrak {n}}$.

Fig. 4.

Construction of robustly reusable fuzzy extractor $\mathsf {rrFE}$.

The correctness of the fuzzy extractor follows from the correctness of the underlying $\mathsf {SS}$ and $\mathsf {SKEM}$.

Theorem 2

If the underlying $\mathsf {SKEM}$ is key-shift secure with secret key space $\mathcal {SK}$ and encapsulation key space $\mathcal {K}$, $\mathsf {Ext}$ is a homomorphic average-case $(\mathcal {M},\hat{m}$, $\mathcal {SK},\varepsilon _{\mathsf {ext}})$-strong extractor, $\mathsf {SS}$ is a homomorphic $(m-\lceil \log p\rceil , \hat{m},2\mathfrak {t})$-secure sketch for metric space $\mathcal {M}$ with $\hat{m}-\lceil \log p\rceil \ge \omega (\log \lambda )$, and $\mathsf {LAF}$ is a homomorphic $(l_{\mathsf {LAF}}, \mathfrak {n})$-lossy algebraic filter with domain $\mathbb {Z}_p^{\mathfrak {n}}$ and $l_{\mathsf {LAF}}=\lceil \log p\rceil$, and every element in $\mathcal {M}$ can be explained as an element in $\mathbb {Z}_p^{\mathfrak {n}}$, then the fuzzy extractor $\mathsf {rrFE}$ in Fig. 4 is an $(\mathcal {M},m,\mathcal {K},\mathfrak {t}, \varepsilon _1,\varepsilon _2)$-robustly reusable fuzzy extractor, where $\varepsilon _1=2\mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {ind}}(1^{\lambda })+2\varepsilon _{\mathsf {ext}}+ \mathsf {Adv}_{\mathsf {SKEM}}^{\mathsf {ks}}(1^{\lambda })$ and $\varepsilon _2=\mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {ind}}(1^{\lambda })+\varepsilon _{\mathsf {ext}}+\mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {eva}}(1^{\lambda })+2^{-\omega (\log \lambda )}$.

Proof

All we have to do is to show that $\mathsf {rrFE}$ is $\varepsilon _1$-reusable and $\varepsilon _2$-robust, which are proved in Theorems 3 and 4 respectively.

Theorem 3

Given the building blocks specified in Theorem 2, the fuzzy extractor $\mathsf {rrFE}$ in Fig. 4 is $\varepsilon _1$-reusable, where $\varepsilon _1=2\mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {ind}}(1^{\lambda })+2\varepsilon _{\mathsf {ext}}+ \mathsf {Adv}_{\mathsf {SKEM}}^{\mathsf {ks}}(1^{\lambda })$.

Proof

We will prove this theorem by a sequence of games. The changes from Game $\mathsf {G}_{j}$ to Game $\mathsf {G}_{j+1}$ are underlined.

$\mathbf {Game}$ $\mathsf {G}_{0}$: It is exactly experiment $\mathsf {Exp}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}(1)$. More precisely,

• 1. Challenger $\mathcal {C}$ invokes $(F_{pk},F_{td})\leftarrow \mathsf {FGen}(1^{\lambda })$ and $\mathsf {pp}\leftarrow \mathsf {SKEM}{.}\mathsf {Init}(1^{\lambda })$, samples a seed ${i_{\mathsf {ext}}\leftarrow _{{{\$}}}\mathcal {I}}$, sets $\mathsf {crs}=(F_{pk}, i_{\mathsf {ext}},\mathsf {pp})$, and returns $\mathsf {crs}$ to $\mathcal {A}$.

• 2. $\mathcal {C}$ samples $w\leftarrow W$, invokes $s\leftarrow \mathsf {SS{.}Gen}(w)$, $sk \leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$, $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp},sk)$, sets $t:=(s, c)$, samples ${t'\leftarrow _{{{\$}}}\mathcal {T}'}$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}$, $t, t', w)$, sets $P:=(s, c, t', \sigma )$, $R:=k$, and returns (P, R) to $\mathcal {A}$.

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ invokes $s_i\leftarrow \mathsf {SS{.}Gen}(w+\delta _i)$, $sk_i\leftarrow \mathsf {Ext}(w+\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_{i}:=(s_i, c_i)$, samples ${t_{i}'\leftarrow _{{{\$}}}\mathcal {T}'}$, invokes $\sigma _i\leftarrow$ $\mathsf {FEval}$ $(F_{pk},t_i, t_i',w+\delta _i)$, sets $P_i:=(s_i, c_i, t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

• 4. If $\mathcal {A}$ outputs a bit $\beta '$, the game outputs $\beta '$.

Obviously,

$$\begin{aligned} \Pr [\mathsf {Exp}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}(1)\Rightarrow 1]=\Pr [\mathsf {G}_{0}^{\mathcal {A}}\Rightarrow 1]. \end{aligned}$$

(6)

$\mathbf {Game}$ $\mathsf {G}_{1}$: It is the same as $\mathsf {G}_{0}$, except for conceptual changes of generating $(P_i,R_i)$. More precisely,

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ computes $\underline{s_i:=s+\mathsf {SS{.}Gen}(\delta _i)}$, $\underline{sk_i:=sk+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})}$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_{i}:=(s_i,c_i)$, samples $t_{i}'\leftarrow _{{{\$}}}\mathcal {T}'$, computes $\underline{\sigma _i:= \mathsf {FEval}(F_{pk},t_i, t_i', w)+}$ $\underline{\mathsf {FEval}(F_{pk},t_i, t_i', \delta _i)}$, sets $P_i:=(s_i,c_i, t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

Lemma 4

${\Pr [\mathsf {G}_{0}^{\mathcal {A}}\Rightarrow 1]=\Pr [\mathsf {G}_{1}^{\mathcal {A}}\Rightarrow 1].}$

Proof

By the homomorphic property of the deterministic secure sketch, we have:

$$s_i\overset{\mathsf {G}_{0}}{=}\mathsf {SS{.}Gen}(w+\delta _i)=\mathsf {SS{.}Gen}(w)+\mathsf {SS{.}Gen}(\delta _i)=s+\mathsf {SS{.}Gen}(\delta _i)\overset{\mathsf {G}_{1}}{=}s_i.$$

By the homomorphic property of $\mathsf {Ext}$, we have:

$$sk_i\overset{\mathsf {G}_{0}}{=}\mathsf {Ext}(w+\delta _i, i_{\mathsf {ext}})=\mathsf {Ext}(w, i_{\mathsf {ext}})+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})=sk+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})\overset{\mathsf {G}_{1}}{=}sk_i.$$

Similarly, by the homomorphic property of $\mathsf {LAF}$, we have:

$$\sigma _i\overset{\mathsf {G}_{0}}{=}\mathsf {FEval}(F_{pk},t_i, t_i',w+\delta _i)=\mathsf {FEval}(F_{pk},t_i, t_i',w)+\mathsf {FEval}(F_{pk},t_i, t_i',\delta _i)\overset{\mathsf {G}_{1}}{=}\sigma _i.$$

Thus the changes are just conceptual, and Lemma 4 follows.    $\blacksquare$

$\mathbf {Game}$ $\mathsf {G}_{2}$: It is the same as $\mathsf {G}_{1}$, except that the core tags $t', t_i'$ are not uniformly chosen any more. Now they are generated by $\mathsf {FTag}$ in $\mathsf {G}_{2}$. More precisely,

• 2. Challenger $\mathcal {C}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, $sk \leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$, $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk)$, sets $t:=(s, c)$, $\underline{\text {generates}\, t'\, \leftarrow \mathsf {FTag}(F_{td},t)}$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}, t, t', w)$, sets $P:=(s, c, t', \sigma )$, $R:=k$, and returns (P, R) to $\mathcal {A}$.

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $sk_i:=sk+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_{i}:=(s_i,c_i)$, $\underline{\text {generates}\, t_{i}'\leftarrow \mathsf {FTag}(F_{td},t_{i})}$, computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_i,$ $t_i', w)+$ $\mathsf {FEval}(F_{pk},t_i, t_i', \delta _i)$, sets $P_i:=(s_i,c_i, t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

Lemma 5

${|\Pr [\mathsf {G}_{1}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]|\le \mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {ind}}(1^{\lambda })}$.

Proof

Assume there exists a PPT adversary $\mathcal {A}$ such that ${|\Pr [\mathsf {G}_{1}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]|=\epsilon }$. We construct a PPT algorithm $\mathcal {B}$ who, given $F_{pk}$, can distinguish oracle $\mathsf {FTag}(F_{td},\cdot )$ from oracle $\mathcal {O}_{\mathcal {T}'}(\cdot )$ with advantage $\epsilon$. Algorithm $\mathcal {B}$ simulates an environment for $\mathcal {A}$ as follows:

• Given $F_{pk}$, algorithm $\mathcal {B}$ invokes $\mathsf {pp}\leftarrow \mathsf {SKEM}{.}\mathsf {Init}(1^{\lambda })$, samples a seed $i_{\mathsf {ext}}\leftarrow _{{{\$}}}\mathcal {I}$, sets $\mathsf {crs}:=(F_{pk}, i_{\mathsf {ext}},\mathsf {pp})$, and returns $\mathsf {crs}$ to $\mathcal {A}$.

• Algorithm $\mathcal {B}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, $sk \leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$, $(c,k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk)$ and sets $t:=(s,c)$.

  • $\mathcal {B}$ queries its own oracle with $t=(s,c)$, and the oracle replies $\mathcal {B}$ with $t'$.

  After receiving $t'$ from its oracle, $\mathcal {B}$ invokes $\sigma \leftarrow \mathsf {FEval}(F_{pk},t, t', w)$, sets $P:=(t=(s,c),t',\sigma )$, $R:=k$, and returns (P, R) to $\mathcal {A}$.

• Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, algorithm $\mathcal {B}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $sk_i:=sk+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$ and sets $t_{i}=(s_i,c_i)$.

  • $\mathcal {B}$ queries its oracle with $t_i:=(s_i, c_i)$, and the oracle replies $\mathcal {B}$ with $t_{i}'$.

  After receiving $t_{i}'$ from its oracle, $\mathcal {B}$ computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_i, t_i',w)+\mathsf {FEval}$ $(F_{pk},t_i, t_i',\delta _i)$, sets $P_i:=(s_i,c_i,t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

• When $\mathcal {A}$ outputs a bit $\beta '$, algorithm $\mathcal {B}$ returns $\beta '$.

Observe that if the oracle to which $\mathcal {B}$ has access is $\mathsf {FTag}(F_{td},\cdot )$, then $\mathcal {B}$ perfectly simulates $\mathsf {G}_{2}$ for $\mathcal {A}$; otherwise it perfectly simulates $\mathsf {G}_{1}$ for $\mathcal {A}$. Thus

$$\begin{aligned} \mathsf {Adv}_{\mathsf {LAF},\mathcal {B}}^{\mathsf {ind}}(1^{\lambda })=|\Pr [\mathsf {G}_{1}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]|. \end{aligned}$$

This completes the proof of Lemma 5.    $\blacksquare$

$\mathbf {Game}\,{{\mathsf {G}_{3}}}$: It is the same as $\mathsf {G}_{2}$, except that sk is changed to a uniform one. More precisely,

• 2. Challenger $\mathcal {C}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, $\underline{\text {samples}\, \widehat{sk} \leftarrow _{{{\$}}}\mathcal {SK}}$, computes $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, \underline{\widehat{sk}})$, sets $t:=(s, c)$, generates $t' \leftarrow \mathsf {FTag}$ $(F_{td}, t)$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}, t, t', w)$, sets $P:=(s, c, t', \sigma )$, $R:=k$, and returns (P, R) to $\mathcal {A}$.

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $sk_i:=\underline{\widehat{sk}}+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_{i}:=(s_i,c_i)$, generates $t_{i}'\leftarrow \mathsf {FTag}(F_{td},t_{i})$, computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_i$, $t_i', w)+\mathsf {FEval}(F_{pk},t_i, t_i', \delta _i)$, sets $P_i:=(s_i,c_i, t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

Lemma 6

${|\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{3}^{\mathcal {A}}\Rightarrow 1]|\le \varepsilon _{\mathsf {ext}}.}$

Proof

Assume that $\mathcal {A}$ makes $\rho$ queries to the challenger. The only difference between $\mathsf {G}_{2}$ and $\mathsf {G}_{3}$ is that $sk\leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$ in $\mathsf {G}_{2}$ is changed to $\widehat{sk}\leftarrow _{{{\$}}}\mathcal {SK}$ in $\mathsf {G}_{3}$. We will show that the views of adversary $\mathcal {A}$ in $\mathsf {G}_{2}$ and $\mathsf {G}_{3}$ are statistically indistinguishable.

Since $F_{pk}$, $F_{td}$ and $\mathsf {pp}$ are independent of W, we have

$$\begin{aligned} {\widetilde{H}_{\infty }(W \mid (F_{pk}, F_{td}, \mathsf {pp}))=\widetilde{H}_{\infty }(W)\ge {m}.} \end{aligned}$$

(7)

Define $\mathcal {S}: =\{\sigma ~|~ \sigma =\mathsf {FEval}({F_{pk}}, t, t', W) \wedge \mathsf {tag}=(t, t')\in \mathcal {T}_{lossy}\}$, which collects all function values w.r.t. the same W and the same $F_{pk}$ but under all possible lossy tags. By the lossiness of $\mathsf {LAF}$, $\mathcal {S}$ only reveals $\log p$ bits information of W (see Remark 2). According to Lemma 1 and Eq. (7), we have

$$\begin{aligned} {\widetilde{H}_{\infty }(W \mid (F_{pk}, F_{td}, \mathsf {pp},\mathcal {S}))\ge \widetilde{H}_{\infty }(W \mid (F_{pk}, F_{td}, \mathsf {pp}))-\log p \ge m-\log p.} \end{aligned}$$

(8)

Since $\mathsf {SS}$ is a $(m-\log p, \hat{m},2\mathfrak {t})$-secure sketch, we have

$$\widetilde{H}_{\infty }(W \mid (s=\mathsf {SS{.}Gen}(W),\ F_{pk}, F_{td}, \mathsf {pp}, \mathcal {S}))\ge \hat{m}.$$

Define $\textsf {AuxiliaryInput}:=\ \left( s\,=\,\mathsf {SS{.}Gen}(W),\ F_{pk},\ F_{td},\ \mathsf {pp},\ \mathcal {S}\right)$. Obviously $\textsf {AuxiliaryInput}$ is independent of $i_{\mathsf {ext}}$. According to Eq. (3), the average-case $(\mathcal {M},\hat{m},\mathcal {SK},\varepsilon _{\mathsf {ext}})$-strong extractor $\mathsf {Ext}$ implies

$$\begin{aligned} {\Big (~{sk, i_{\mathsf {ext}}, (\underbrace{s=\mathsf {SS{.}Gen}(W), F_{pk}, F_{td}, \mathsf {pp}, \mathcal {S}}_{\textsf {AuxiliaryInput}})}~\Big ) \overset{\varepsilon _{\mathsf {ext}}}{\approx }\Big (~{\widehat{sk}, i_{\mathsf {ext}}, (\underbrace{s=\mathsf {SS{.}Gen}(W), F_{pk}, F_{td}, \mathsf {pp}, \mathcal {S}}_{\textsf {AuxiliaryInput}})}~\Big ), }\end{aligned}$$

(9)

where $sk:=\mathsf {Ext}(W, i_{\mathsf {ext}})$ and $\widehat{sk}\leftarrow _{{{\$}}}\mathcal {SK}$. Since $\mathsf {crs}=(F_{pk}, i_{\mathsf {ext}},\mathsf {pp})$, Eq. (9) implies

$$\begin{aligned} {\Big (~\underbrace{sk, s=\mathsf {SS{.}Gen}(W), \mathsf {crs}, F_{td}, \mathcal {S}}_{\varOmega }~\Big )\overset{\varepsilon _{\mathsf {ext}}}{\approx }\Big (~\underbrace{\widehat{sk},s=\mathsf {SS{.}Gen}(W), \mathsf {crs}, F_{td}, \mathcal {S}}_{\varXi }~\Big ).} \end{aligned}$$

(10)

Let w be a specific value taken by random variable W.

Recall that $P=(s, c, t', \sigma )$ and $R=k$, where $s\leftarrow \mathsf {SS{.}Gen}(w)$, $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, {sk})$, $t:=(s, c)$, $t' \leftarrow \mathsf {FTag}(F_{td},t)$, $\sigma \leftarrow \mathsf {FEval}(F_{pk}, t, t', w)$. Obviously, (P, R) can be regarded as an output of some randomized function on input $\varOmega$.

Define $\widehat{P}:=(s, \widehat{c}, \widehat{t'}, \widehat{\sigma })$ and $\widehat{R}:=\widehat{k}$, where $s\leftarrow \mathsf {SS{.}Gen}(w)$, $(\widehat{c}, \widehat{k})\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}$ $(\mathsf {pp}, \widehat{sk})$, $\widehat{t}=(s, \widehat{c})$, $\widehat{t'} \leftarrow \mathsf {FTag}(F_{td},\widehat{t})$, $\widehat{\sigma }\leftarrow \mathsf {FEval}(F_{pk}, \widehat{t}, \widehat{t'}, w)$. In other words, $(\widehat{P}, \widehat{R})$ is the helper string and the extracted string generated with the random key $\widehat{sk}$. Then $(\widehat{P}, \widehat{R})$ can be regarded as an output of the same randomized function on input $\varXi$ as that for (P, R).

According to Lemma 2, Formula (10) implies

$$\begin{aligned} {\text {in short,}} \qquad \qquad \qquad \qquad \left( \underbrace{\varOmega , P, R}_{\varOmega _0}~\right) \overset{\varepsilon _{\mathsf {ext}}}{\approx }\left( \underbrace{\varXi , \widehat{P}, \widehat{R}}_{\varXi _0} \right) .\qquad \qquad \qquad \end{aligned}$$

(11)

Before $\mathcal {A}$ submits its first query $\delta _1$ in $\mathsf {G}_{2}$, its view is described by $\langle \mathsf {crs}, P,R \rangle$. Obviously, $\delta _1$ can be computed by some randomized function of $\langle \mathsf {crs}, P,R \rangle$ (the function is determined by $\mathcal {A}$’s strategy). Naturally, it can be regarded as an output of some randomized function on input $\varOmega _0$.

Similarly, the first query $\widehat{\delta _1}$ of $\mathcal {A}$ in $\mathsf {G}_{3}$ is determined by the same randomized function of its view $\langle \mathsf {crs}, \widehat{P}, \widehat{R}\rangle$, hence it can also be regarded as an output of the same randomized function of $\varXi _0$.

By Lemma 2 again, Formula (11) implies

$$\begin{aligned} {\Big (~\underbrace{\varOmega , P, R, \delta _1}_{\varOmega _0'}~\Big )\overset{\varepsilon _{\mathsf {ext}}}{\approx }\Big (~\underbrace{\varXi , \widehat{P}, \widehat{R}, \widehat{\delta _1}}_{\varXi _0'}~\Big ).} \end{aligned}$$

(12)

Recall that $P_1:=(s_1,c_1, t_{1}',\sigma _1)$, $R_1:=k_1$, where $s_1=s+\mathsf {SS{.}Gen}(\delta _1)$, $sk_1={{sk}}+\mathsf {Ext}(\delta _1, i_{\mathsf {ext}})$, $(c_1, k_1 )\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_1)$, $t_{1}=(s_1, c_1)$, $t_{1}'\leftarrow \mathsf {FTag}(F_{td},t_{1})$ $\sigma _1= \mathsf {FEval}(F_{pk}, t_{1}, t_{1}', w)+\mathsf {FEval}(F_{pk}, t_{1}, t_{1}', \delta _1)$. Note that $(t_1, t_1')$ is a lossy tag, hence $\mathsf {FEval}(F_{pk}, t_{1}, t_{1}', w)\in \mathcal {S}$. Obviously, $P_1$ and $R_1$ can be determined by some randomized function of $\varOmega _0'$.

Define $\widehat{P_1}:=(\widehat{s_1},\widehat{c_1}, \widehat{t_{1}'},\widehat{\sigma _1})$, $\widehat{R_1}:=\widehat{k_1}$, where $\widehat{s_1}=s+\mathsf {SS{.}Gen}(\widehat{\delta _1})$, $\widehat{sk_1}=\widehat{sk}+\mathsf {Ext}(\widehat{\delta _1}, i_{\mathsf {ext}})$, $(\widehat{c_1}, \widehat{k_1} )\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, \widehat{sk_1})$, $\widehat{t_{1}}=(\widehat{s_1}, \widehat{c_1})$, $\widehat{t_{1}'}\leftarrow \mathsf {FTag}(F_{td},\widehat{t_{1}})$ $\widehat{\sigma _1}= \mathsf {FEval}(F_{pk}, \widehat{t_{1}}, \widehat{t_{1}'}, w)+\mathsf {FEval}(F_{pk}, \widehat{t_{1}}, \widehat{t_{1}'}, \widehat{\delta _1})$. Similarly, $\widehat{P_1}$ and $\widehat{R_1}$ can be determined by the same randomized function of of $\varXi _0'$.

Applying Lemma 2 once more, Formula (12) implies

$$\begin{aligned} {\left( ~\underbrace{\overbrace{\varOmega , P, R, \delta _1}^{\varOmega _0'}, P_1,R_1}_{\varOmega _1}~\right) \overset{\varepsilon _{\mathsf {ext}}}{\approx }\left( ~\underbrace{\overbrace{\varXi , \widehat{P}, \widehat{R}, \widehat{\delta _1}}^{\varXi _0'},\widehat{P_1}, \widehat{R_1}}_{\varXi _1}~\right) .} \end{aligned}$$

(13)

By induction on $i\in [\rho ]$, we have that

$$\begin{aligned} {\left( ~\underbrace{\varOmega , P, R, \{\delta _i, P_i,R_i\}_{i\in [\rho ]}}_{\varOmega _{\rho }}~\right) \overset{\varepsilon _{\mathsf {ext}}}{\approx }\left( ~\underbrace{\varXi , \widehat{P}, \widehat{R}, \{\widehat{\delta _i}, \widehat{P_i}, \widehat{R_i} \}_{i\in [\rho ]}}_{\varXi _{\rho }}~\right) .} \end{aligned}$$

(14)

More precisely,

$$\begin{aligned}&\left( ~\underbrace{\overbrace{sk:=\mathsf {Ext}(W, i_{\mathsf {ext}}), s=\mathsf {SS{.}Gen}(W), \mathsf {crs}, F_{td},\mathcal {S}}^{\varOmega }, P, R, \{\delta _i, P_i,R_i\}_{i\in [\rho ]}}_{\varOmega _{\rho }}~\right) \overset{\varepsilon _{\mathsf {ext}}}{\approx }\nonumber \\&\left( ~\underbrace{\overbrace{sk:=\mathsf {Ext}(W, i_{\mathsf {ext}}), s=\mathsf {SS{.}Gen}(W), \mathsf {crs}, F_{td}, \mathcal {S}}^{\varXi }, \widehat{P}, \widehat{R}, \{\widehat{\delta _i}, \widehat{P_i}, \widehat{R_i} \}_{i\in [\rho ]}}_{\varXi _{\rho }}~\right) . \end{aligned}$$

(15)

$$\begin{aligned} \text {(15) implies} \qquad \qquad \left( ~\underbrace{\mathsf {crs}, P, R, \{\delta _i, P_i,R_i\}_{i\in [\rho ]}}_{\varOmega _{\rho }^*}~\right) \overset{\varepsilon _{\mathsf {ext}}}{\approx }\left( ~\underbrace{\mathsf {crs}, \widehat{P}, \widehat{R}, \{\widehat{\delta _i}, \widehat{P_i}, \widehat{R_i} \}_{i\in [\rho ]}}_{\varXi _{\rho }^*}~\right) . \end{aligned}$$

(16)

Observe that $\varOmega _{\rho }^*$ is just the whole view of $\mathcal {A}$ in $\mathsf {G}_{2}$, and $\varXi _{\rho }^*$ is the whole view of $\mathcal {A}$ in $\mathsf {G}_{3}$. The statistical distance of $\varOmega _{\rho }^*$ and $\varXi _{\rho }^*$ is smaller than $\varepsilon _{\mathsf {ext}}$. As a consequence, we have ${|\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{3}^{\mathcal {A}}\Rightarrow 1]|\le \varepsilon _{\mathsf {ext}}}$.    $\blacksquare$

$\mathbf {Game}$ $\mathsf {G}_{4}$: It is the same as $\mathsf {G}_{3}$, except that R is uniformly chosen from $\mathcal {K}$ instead of being output by $\mathsf {SKEM}$. More precisely,

• 2. Challenger $\mathcal {C}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, samples $\widehat{sk} \leftarrow _{{{\$}}}\mathcal {SK}$, computes $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, {\widehat{sk}})$, sets $t:=(s, c)$, generates $t' \leftarrow \mathsf {FTag}(F_{td},t)$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}, t, t', w)$, sets $P:=(s, c, t', \sigma )$, samples $\underline{R\leftarrow _{{{\$}}}\mathcal {K}}$, and returns (P, R) to $\mathcal {A}$.

Lemma 7

${|\Pr [\mathsf {G}_{3}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{4}^{\mathcal {A}}\Rightarrow 1]| \le \mathsf {Adv}_{\mathsf {SKEM}}^{{\mathsf {ks}}}(1^{\lambda }).}$

Proof

Assume there exists a PPT adversary $\mathcal {A}$ such that $|\Pr [\mathsf {G}_{3}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{4}^{\mathcal {A}}\Rightarrow 1]|=\epsilon$. We construct a PPT algorithm $\mathcal {B}$ who can implement the key-shift attack with the same advantage $\epsilon$. Algorithm $\mathcal {B}$ simulates an environment for $\mathcal {A}$ as follows:

• After receiving $\mathsf {pp}$ from its own challenger, algorithm $\mathcal {B}$ invokes $(F_{pk},F_{td})\leftarrow \mathsf {FGen}(1^{\lambda })$, samples a seed ${i_{\mathsf {ext}}\leftarrow _{{{\$}}}\mathcal {I}}$, sets $\mathsf {crs}=(F_{pk}, i_{\mathsf {ext}},\mathsf {pp})$, and returns $\mathsf {crs}$ to $\mathcal {A}$.

• Algorithm $\mathcal {B}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, asks the challenge oracle of $\mathsf {SKEM}$ to get (c, k). Then $\mathcal {B}$ sets $t:=(s,c)$, generates $t'\leftarrow \mathsf {FTag}(F_{td},t)$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk},t, t', w)$, sets $P:=(t=(s,c), t',\sigma )$, $R:=k$, and returns (P, R) to $\mathcal {A}$.

• Upon receiving a shift $\delta _i\in \mathcal {M}$ queried from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, algorithm $\mathcal {B}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $\varDelta _i:=\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, asks its encapsulation oracle with $\varDelta _i$ to obtain $(c_i,k_i)$, where $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk+\varDelta _i)$. Then $\mathcal {B}$ sets $t_{i}:=(s_i, c_i)$, generates $t_{i}'\leftarrow \mathsf {FTag}(F_{td},t_{i})$, computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_i, t_i',w)+\mathsf {FEval}$ $(F_{pk},t_i, t_i',\delta _i)$, sets $P_i:=(s_i,c_i, t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

• When $\mathcal {A}$ outputs a bit $\beta '$, algorithm $\mathcal {B}$ outputs $\beta '$ to its own challenger.

Note that if (c, k) is generated by $(c,k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(pp,sk)$, then algorithm $\mathcal {B}$ perfectly simulates $\mathsf {G}_{3}$ for $\mathcal {A}$; otherwise k is uniformly chosen from $\mathcal {K}$, then algorithm $\mathcal {B}$ perfectly simulates $\mathsf {G}_{4}$ for $\mathcal {A}$. Hence $\mathcal {B}$ shares exactly the same advantage with $\mathcal {A}$. Thus $\mathsf {Adv}_{\mathsf {SKEM},\mathcal {B}}^{\mathsf {mrka}}(1^{\lambda })=|\Pr [\mathsf {G}_{3}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{4}^{\mathcal {A}}\Rightarrow 1]| \le \mathsf {Adv}_{\mathsf {SKEM}}^{\mathsf {mrka}}(1^{\lambda })$. This completes the proof of Lemma 7.    $\blacksquare$

$\mathbf {Game}$ $\mathsf {G}_{5}$: It is the same as $\mathsf {G}_{4}$, except that the generation of $\widehat{sk}$ is changed back to $sk\leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$. More precisely,

• 2. Challenger $\mathcal {C}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, $\underline{sk\leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})}$, $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, {\underline{sk}})$, sets $t:=(s, c)$, generates $t' \leftarrow \mathsf {FTag}(F_{td},t)$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}, t, t', w)$, sets $P:=(s, c, t', \sigma )$, samples ${R\leftarrow _{{{\$}}}\mathcal {K}}$, and returns (P, R) to $\mathcal {A}$.

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $sk_i:=\underline{{sk}}+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_{i}:=(s_i,c_i)$, generates $t_{i}'\leftarrow \mathsf {FTag}(F_{td},t_{i})$, computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_i,$ $t_i', w)+\mathsf {FEval}(F_{pk},t_i, t_i', \delta _i)$, sets $P_i:=(s_i,c_i, t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

Lemma 8

${|\Pr [\mathsf {G}_{4}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{5}^{\mathcal {A}}\Rightarrow 1]| \le \varepsilon _{\mathsf {ext}}.}$

Proof

The proof is similar to the proof of Lemma 6, since the changes from $\mathsf {G}_{4}$ to $\mathsf {G}_{5}$ is symmetric to that from $\mathsf {G}_{2}$ to $\mathsf {G}_{3}$. We omit the proof here.    $\blacksquare$

$\mathbf {Game}$ $\mathsf {G}_{6}$: It is the same as $\mathsf {G}_{5}$, except that the core tags are changed back to random tags. More precisely,

• 2. $\mathcal {C}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, $sk\leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$, $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, {{sk}})$, sets $t:=(s, c)$, ${\underline{\text {samples}\, t'\,\leftarrow _{{{\$}}}\mathcal {T}'}}$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}$, $t, t', w)$, sets $P:=(s, c, t', \sigma )$, samples ${R\leftarrow _{{{\$}}}\mathcal {K}}$, and returns (P, R) to $\mathcal {A}$.

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, $\mathcal {C}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $sk_i:={{sk}}+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_{i}:=(s_i,c_i)$, ${\underline{\text {samples}\, t_i'\leftarrow _{{{\$}}}\mathcal {T}'}}$, computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_{i},t_{i}', w)+\mathsf {FEval}(F_{pk},t_{i}$, $t_{i}', \delta _i)$, sets $P_i:=(s_i,c_i, t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

Lemma 9

${|\Pr [\mathsf {G}_{5}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{6}^{\mathcal {A}}\Rightarrow 1]| \le \mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {ind}}(1^{\lambda }).}$

Proof

The proof is similar to the proof of Lemma 5, since the changes from $\mathsf {G}_{5}$ to $\mathsf {G}_{6}$ is symmetric to that from $\mathsf {G}_{1}$ to $\mathsf {G}_{2}$. We omit the proof here.    $\blacksquare$

$\mathbf {Game}$ $\mathsf {G}_{7}$: It is the same as $\mathsf {G}_{6}$, except for conceptual changes of generating $(P_i,R_i)$. More precisely,

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ computes $\underline{s_i\leftarrow \mathsf {SS{.}Gen}(w+\delta _i)}$, $\underline{sk_i\leftarrow \mathsf {Ext}(w+\delta _i, i_{\mathsf {ext}})}$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_i:=(s_i, c_i)$, samples ${t_{i}'\leftarrow _{{{\$}}}\mathcal {T}'}$, computes $\underline{\sigma _i\leftarrow \mathsf {FEval}(F_{pk},t_i, t_i', w+\delta _i)}$, sets $P_i:=(s_i, c_i, t_{i}', \sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

Lemma 10

${\Pr [\mathsf {G}_{6}^{\mathcal {A}}\Rightarrow 1]=\Pr [\mathsf {G}_{7}^{\mathcal {A}}\Rightarrow 1].}$

Proof

The proof is identical to the proof of Lemma 4, since the changes from $\mathsf {G}_{6}$ to $\mathsf {G}_{7}$ is symmetric to that from $\mathsf {G}_{0}$ to $\mathsf {G}_{1}$. We omit the proof here.    $\blacksquare$

Note that $\mathsf {G}_{7}$ is identical to experiment $\mathsf {Exp}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}(0)$. Thus

$$\begin{aligned} {\Pr [\mathsf {Exp}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}(0)\Rightarrow 1]=\Pr [\mathsf {G}_{7}\Rightarrow 1].} \end{aligned}$$

(17)

Taking all things together, by Eq. (6), Lemmas 4–10 and Eq. (17), we have that

$$\begin{aligned} {\mathsf {Adv}_{\mathsf {rFE},\mathcal {A}}^{\mathsf {reu}}\le 2\mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {ind}}(1^{\lambda })+2\varepsilon _{\mathsf {ext}}+ \mathsf {Adv}_{\mathsf {SKEM}}^{\mathsf {ks}}(1^{\lambda }).} \end{aligned}$$

This completes the proof of Theorem 3.    $\blacksquare$

Theorem 4

Given the building blocks specified in Theorem 2, the fuzzy extractor $\mathsf {rrFE}$ in Fig. 4 is $\varepsilon _2$-robust, where $\varepsilon _2=\mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {ind}}(1^{\lambda })+\varepsilon _{\mathsf {ext}}+\mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {eva}}(1^{\lambda })+2^{-\omega (\log \lambda )}$.

Proof

Similar to the proof of reusability, we will prove this theorem by a sequence of games again. The changes from Game $\mathsf {G}_{j}$ to adjacent Game $\mathsf {G}_{j+1}$ are underlined. Let $\mathsf {win}_j$ denote the event that adversary $\mathcal {A}$ wins in $\mathsf {G}_{j}$. $\mathsf {G}_{j}$ outputs 1 if $\mathcal {A}$ wins and 0 otherwise. Obviously, ${\Pr [\mathsf {win}_j]=\Pr [\mathsf {G}_{j}^{\mathcal {A}}\Rightarrow 1]}$.

$\mathbf {Game}$ $\mathsf {G}_{0}$: It is identical to the robustness experiment $\mathsf {Exp}_{\mathsf {rrFE},\mathcal {A}}^{\mathsf {rob}}(1^{\lambda })$.

• 1. Challenger $\mathcal {C}$ invokes $(F_{pk},F_{td})\leftarrow \mathsf {FGen}(1^{\lambda })$ and $\mathsf {pp}\leftarrow \mathsf {SKEM}{.}\mathsf {Init}(1^{\lambda })$, samples a seed ${i_{\mathsf {ext}}\leftarrow _{{{\$}}}\mathcal {I}}$, sets $\mathsf {crs}=(F_{pk}, i_{\mathsf {ext}},\mathsf {pp})$, and returns $\mathsf {crs}$ to $\mathcal {A}$.

• 2. Challenger $\mathcal {C}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, $sk \leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$, $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp},sk)$, sets $t:=(s, c)$, samples ${t'\leftarrow _{{{\$}}}\mathcal {T}'}$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}, t, t', w)$, sets $P:=(t=(s, c), t', \sigma )$, $R:=k$, and returns (P, R) to $\mathcal {A}$.

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ computes $s_i\leftarrow \mathsf {SS{.}Gen}(w+\delta _i)$, $sk_i\leftarrow \mathsf {Ext}(w+\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_i:=(s_i, c_i)$, samples ${t_{i}'\leftarrow _{{{\$}}}\mathcal {T}'}$, computes $\sigma _i\leftarrow \mathsf {FEval}(F_{pk},t_i, t_i',w+\delta _i)$, sets $P_i:=(t_i=(s_i, c_i), t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

• 4. $\mathcal {A}$ submits to $\mathcal {C}$ its forgery $(\widetilde{P}, \widetilde{\delta })$ with $\widetilde{P}=(\widetilde{t}=(\widetilde{s},\widetilde{c}),\widetilde{t'},\widetilde{\sigma })$. $\mathcal {A}$ wins if $\mathsf {dis}(\widetilde{\delta })\le \mathfrak {t}$, $\widetilde{P}$ is fresh and $\mathsf {Rep}(\mathsf {crs},\widetilde{P},w+\widetilde{\delta })\ne \bot$. Recall that $\mathsf {Rep}(\mathsf {crs},\widetilde{P},w+\widetilde{\delta })\ne \bot$ if and only if $\mathsf {dis}(\widetilde{w},w+\widetilde{\delta })\le \mathfrak {t}$ and $\widetilde{\sigma }'=\widetilde{\sigma }$ holds, where $\widetilde{w}\leftarrow \mathsf {SS{.}Rec}(w+\widetilde{\delta },\widetilde{s})$ and $\widetilde{\sigma }'\leftarrow \mathsf {FEval}(F_{pk},\widetilde{t}, \widetilde{t'}, \widetilde{w})$. The game outputs 1 if $\mathcal {A}$ wins and 0 otherwise.

Obviously,

$$\begin{aligned} {\Pr [\mathsf {G}_{0}^{\mathcal {A}}\Rightarrow 1]=\Pr [\mathsf {Exp}_{\mathsf {rrFE},\mathcal {A}}^{\mathsf {rob}}(1^{\lambda })\Rightarrow 1].} \end{aligned}$$

(18)

$\mathbf {Game}$ $\mathsf {G}_{1}$: It is the same as $\mathsf {G}_{0}$, except for conceptual changes of generating $(P_i,R_i)$. More precisely,

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ computes $\underline{s_i:=s+\mathsf {SS{.}Gen}(\delta _i)}$, $\underline{sk_i:=sk+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})}$ , $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_i:=(s_i, c_i)$, samples ${t_{i}'\leftarrow _{{{\$}}}\mathcal {T}'}$, computes $\underline{\sigma _i\leftarrow \mathsf {FEval}(F_{pk},t_i, t_i',w)+}$ $\underline{\mathsf {FEval}(F_{pk},t_i, t_i',\delta _i)}$, sets $P_i:=(t_i=(s_i, c_i), t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

Lemma 11

${\Pr [\mathsf {G}_{0}^{\mathcal {A}}\Rightarrow 1]=\Pr [\mathsf {G}_{1}^{\mathcal {A}}\Rightarrow 1].}$

Proof

The changes are just conceptual by the homomorphic properties of $\mathsf {SS}$, $\mathsf {Ext}$, $\mathsf {LAF}$. Similar to the proof of Lemma 4, Lemma 11 follows.    $\blacksquare$

$\mathbf {Game}$ $\mathsf {G}_{2}$: It is the same as $\mathsf {G}_{1}$, except that the core tags $t', t_i'$ are not uniformly chosen any more. Now they are generated by $\mathsf {FTag}$ in $\mathsf {G}_{2}$. More precisely,

• 2. Challenger $\mathcal {C}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, $sk \leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$, $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk)$, sets $t:=(s, c)$, $\underline{\text {generates}\, t'\, \leftarrow \mathsf {FTag}(F_{td},t)}$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}, t, t', w)$, sets $P:=(s, c, t', \sigma )$, $R:=k$, and returns (P, R) to $\mathcal {A}$.

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $sk_i:=sk+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_{i}:=(s_i,c_i)$, $\underline{\text {generates}\, t_{i}'\leftarrow \mathsf {FTag}(F_{td},t_{i})}$, computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_i,$ $t_i', w)+\mathsf {FEval}(F_{pk},t_i, t_i', \delta _i)$, sets $P_i:=(s_i,c_i, t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

Lemma 12

${|\Pr [\mathsf {G}_{1}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]|\le \mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {ind}}(1^{\lambda }).}$

Proof

The proof is similar to that of Lemma 5 (the difference is the output strategy of algorithm $\mathcal {B}$). Assume there exists a PPT adversary $\mathcal {A}$ such that $|\Pr [\mathsf {G}_{1}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]|=\epsilon$. We construct a PPT algorithm $\mathcal {B}$ who, given $F_{pk}$, can distinguish oracle $\mathsf {FTag}(F_{td},\cdot )$ from oracle $\mathcal {O}_{\mathcal {T}'}(\cdot )$ with advantage $\epsilon$. Algorithm $\mathcal {B}$ simulates an environment for $\mathcal {A}$ as follows:

• Given $F_{pk}$, algorithm $\mathcal {B}$ invokes $\mathsf {pp}\leftarrow \mathsf {SKEM}{.}\mathsf {Init}(1^{\lambda })$, samples a seed ${i_{\mathsf {ext}}\leftarrow _{{{\$}}}\mathcal {I}}$, sets $\mathsf {crs}=(F_{pk}, i_{\mathsf {ext}},\mathsf {pp})$, and returns $\mathsf {crs}$ to $\mathcal {A}$.

• Algorithm $\mathcal {B}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, $sk \leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$, $(c,k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk)$, sets $t:=(s,c)$ and queries its oracle with t to obtain $t'$. After receiving $t'$ from its oracle, $\mathcal {B}$ computes $\sigma \leftarrow \mathsf {FEval}(F_{pk},t, t', w)$, sets $P:=(t=(s,c),t',\sigma )$, $R:=k$, and gives (P, R) to $\mathcal {A}$.

• Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, algorithm $\mathcal {B}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $sk_i:=sk+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_{i}:=(s_i,c_i)$ and queries its oracle with $t_{i}$ to obtain $t_{i}'$. After receiving $t_{i}'$ from its oracle, $\mathcal {B}$ computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_i, t_i',w)+\mathsf {FEval}$ $(F_{pk},t_i, t_i',\delta _i)$, sets $P_i:=(s_i,c_i,t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

• When $\mathcal {A}$ submits its forgery $(\widetilde{P}=(\widetilde{s},\widetilde{c},\widetilde{t'},\widetilde{\sigma }), \widetilde{\delta })$, algorithm $\mathcal {B}$ checks whether $\mathcal {A}$ wins. $\mathcal {B}$ returns 1 if $\mathcal {A}$ wins; otherwise, it returns 0.

Recall that $\mathcal {A}$ wins means that conditions $\mathsf {dis}(\widetilde{\delta })\le \mathfrak {t}$, $\widetilde{P}$ is fresh and $\mathsf {Rep}(\mathsf {crs},\widetilde{P},w+\widetilde{\delta })\ne \bot$ are satisfied. These conditions can be efficiently checked by $\mathcal {B}$. Moreover, if the oracle to which $\mathcal {B}$ has access is $\mathsf {FTag}(F_{td},\cdot )$, then $\mathcal {B}$ perfectly simulates $\mathsf {G}_{2}$ for $\mathcal {A}$; otherwise it perfectly simulates $\mathsf {G}_{1}$ for $\mathcal {A}$. Thus

$$ \mathsf {Adv}_{\mathsf {LAF},\mathcal {B}}^{\mathsf {ind}}(1^{\lambda })=\big |\Pr [\mathsf {win}_1]-\Pr [\mathsf {win}_2]\big |=\big |\Pr [\mathsf {G}_{1}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]\big |.$$

This completes the proof of Lemma 12.    $\blacksquare$

$\mathbf {Game}$ $\mathsf {G}_{3}$: It is the same as $\mathsf {G}_{2}$, except that sk is changed to a uniform one. More precisely,

• 2. Challenger $\mathcal {C}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, ${\underline{\text {samples }\widehat{sk} \leftarrow _{{{\$}}}\mathcal {SK}}}$, computes $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, \underline{\widehat{sk}})$, sets $t:=(s, c)$, generates $t' \leftarrow \mathsf {FTag}(F_{td},t)$, computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}, t, t', w)$, sets $P:=(s, c, t', \sigma )$, $R:=k$, and returns (P, R) to $\mathcal {A}$.

• 3. Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, challenger $\mathcal {C}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $sk_i:=\underline{\widehat{sk}}+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$, sets $t_{i}=(s_i,c_i)$, generates $t_{i}'\leftarrow \mathsf {FTag}(F_{td},t_{i})$, computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_i,$ $t_i', w)+\mathsf {FEval}(F_{pk},t_i, t_i', \delta _i)$, sets $P_i:=(s_i,c_i, t_{i}',\sigma _i)$, $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

Lemma 13

${\big |\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{3}^{\mathcal {A}}\Rightarrow 1]\big |\le \varepsilon _{\mathsf {ext}}.}$

Proof

The only difference between $\mathsf {G}_{2}$ and $\mathsf {G}_{3}$ is that $sk\leftarrow \mathsf {Ext}(w, i_{\mathsf {ext}})$ in $\mathsf {G}_{2}$ is changed to ${\widehat{sk}\leftarrow _{{{\$}}}\mathcal {SK}}$ in $\mathsf {G}_{3}$. The proof is exactly the same as that of Lemma 6.

Assume that $\mathcal {A}$ makes $\rho$ queries to the challenger before submitting its forgery $(\widetilde{P},\widetilde{\delta })$. Following similar arguments as those in the proof Lemma 6, we can show that the views of adversary $\mathcal {A}$ before submitting the forgery in $\mathsf {G}_{2}$ and $\mathsf {G}_{3}$ are statistically indistinguishable, i.e.,

$$\begin{aligned} {\Big (~\underbrace{\mathsf {crs}, P, R, \{\delta _i, P_i,R_i\}_{i\in [\rho ]}}_{\varOmega _{\rho }^*}~\Big )\overset{\varepsilon _{\mathsf {ext}}}{\approx }\Big (~\underbrace{\mathsf {crs}, \widehat{P}, \widehat{R}, \{\widehat{\delta _i}, \widehat{P_i}, \widehat{R_i} \}_{i\in [\rho ]}}_{\varXi _{\rho }^*}~\Big ).} \end{aligned}$$

(19)

Here $\varOmega _{\rho }^*$ summerizes the view of $\mathcal {A}$ in $\mathsf {G}_{2}$, and $\varXi _{\rho }^*$ the view of $\mathcal {A}$ in $\mathsf {G}_{3}$ before $\mathcal {A}$ submits its forgery. The statistical distance of $\varOmega _{\rho }^*$ and $\varXi _{\rho }^*$ is smaller than $\varepsilon _{\mathsf {ext}}$. As a consequence,

$$\begin{aligned} {\big |\Pr [\mathsf {win}_2]-\Pr [\mathsf {win}_3]\big | = \big |\Pr [\mathsf {G}_{2}^{\mathcal {A}}\Rightarrow 1]-\Pr [\mathsf {G}_{3}^{\mathcal {A}}\Rightarrow 1] \big |\le \varepsilon _{\mathsf {ext}}}. \end{aligned}$$

   $\blacksquare$

Lemma 14

$\Pr [\mathsf {win}_3]\le \mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {eva}}(1^{\lambda })+2^{-\omega (\log \lambda )}$.

Proof

Let $\mathsf {bad}$ denote the event that $\mathcal {A}$’s forgery $\widetilde{P}=(\widetilde{t}, \widetilde{t'},\widetilde{\sigma })$ contains a non-injective tag, i.e., $(\widetilde{t}, \widetilde{t'})\notin \mathcal {T}_{inj}$. We have

$$\begin{aligned} {\Pr [\mathsf {win}_3]=\Pr [\mathsf {win}_3\wedge \mathsf {bad}]+\Pr [\mathsf {win}_3\wedge \lnot \mathsf {bad}].} \end{aligned}$$

(20)

Thus it suffices to prove the following two claims.

Claim

${\Pr [\mathsf {win}_3\wedge \mathsf {bad}]\le \mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {eva}}(1^{\lambda }).}$

Proof

If there exists a PPT adversary $\mathcal {A}$ whose forgery makes $\mathsf {win}_3\wedge \mathsf {bad}$ happen in $\mathsf {G}_{3}$, we can construct a PPT algorithm $\mathcal {B}$ attacking on $\mathsf {LAF}$’s evasiveness. Given $F_{pk}$ and a lossy tag generation oracle $\mathsf {FTag}(F_{td},\cdot )$, $\mathcal {B}$ aims to output a new lossy tag. To this end, $\mathcal {B}$ simulates $\mathsf {G}_{3}$ for $\mathcal {A}$ as follows:

• After receiving $F_{pk}$ from its own challenger, $\mathcal {B}$ invokes $\mathsf {pp}\leftarrow \mathsf {SKEM}{.}\mathsf {Init}(1^{\lambda })$, samples a seed ${i_{\mathsf {ext}}\leftarrow _{{{\$}}}\mathcal {I}}$, sets $\mathsf {crs}=(F_{pk}, i_{\mathsf {ext}},\mathsf {pp})$, and returns $\mathsf {crs}$ to $\mathcal {A}$.

• $\mathcal {B}$ samples $w\leftarrow W$, computes $s\leftarrow \mathsf {SS{.}Gen}(w)$, samples ${\widehat{sk} \leftarrow _{{{\$}}}\mathcal {SK}}$, computes $(c, k)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, {\widehat{sk}})$, and sets $t:=(s, c)$.

  • $\mathcal {B}$ asks its own lossy tag generation oracle $\mathsf {FTag}(F_{td},\cdot )$ with $t=(s,c)$ and obtains $t'$ from the oracle. Obviously the oracle generates $t'$ by $t' \leftarrow \mathsf {FTag}(F_{td},t)$.

$\mathcal {B}$ computes $\sigma \leftarrow \mathsf {FEval}(F_{pk}, t, t', w)$, sets $P:=(s, c, t', \sigma )$ and $R:=k$, and returns (P, R) to $\mathcal {A}$.

• Upon receiving a shift $\delta _i\in \mathcal {M}$ from $\mathcal {A}$ with $\mathsf {dis}(\delta _i)\le \mathfrak {t}$, $\mathcal {B}$ computes $s_i:=s+\mathsf {SS{.}Gen}(\delta _i)$, $sk_i:={\widehat{sk}}+\mathsf {Ext}(\delta _i, i_{\mathsf {ext}})$, $(c_i,k_i)\leftarrow \mathsf {SKEM}{.}\mathsf {Enc}(\mathsf {pp}, sk_i)$ and sets $t_{i}:=(s_i,c_i)$.

  • $\mathcal {B}$ asks its own lossy tag generation oracle $\mathsf {FTag}(F_{td},\cdot )$ with $t_i=(s_i, c_i)$ and obtains $t_i'$ from the oracle. Obviously the oracle generates $t_i'$ by $t_i' \leftarrow \mathsf {FTag}(F_{td},t_i)$.

$\mathcal {B}$ computes $\sigma _i:= \mathsf {FEval}(F_{pk},t_i, t_i', w)+$ $\mathsf {FEval}(F_{pk},t_i, t_i', \delta _i)$, sets $P_i:=(s_i,c_i$, $t_{i}',\sigma _i)$ and $R_i:=k_i$, and returns $(P_i,R_i)$ to $\mathcal {A}$.

• When $\mathcal {A}$ outputs its forgery $\left( \widetilde{P}=(\widetilde{t}=(\widetilde{s},\widetilde{c}),\widetilde{t'},\widetilde{\sigma }),~\widetilde{\delta }\right)$, $\mathcal {B}$ returns the tag $(\widetilde{t}, \widetilde{t'})$ to it own challenger.

Note that $\mathcal {B}$ perfectly simulates $\mathsf {G}_{3}$ for $\mathcal {A}$, since its oracle generates lossy tags with $\mathsf {FTag}(F_{td},t_i)$.

If event $\mathsf {win}_3\wedge \mathsf {bad}$ occurs, the forged helper string $\widetilde{P}$ must be fresh, i.e., $\widetilde{P}\ne P$ and $\widetilde{P}\ne P_i$ for $i\in [\rho ]$. Define $\mathsf {freshT}$ as the event that the forged tag $(\widetilde{t}, \widetilde{t'})$ is a fresh one, i.e., $(\widetilde{t}, \widetilde{t'})\ne (t, t')$ and $(\widetilde{t}, \widetilde{t'})\ne (t_i, t_i')$ for all $i\in [\rho ]$. Clearly,

$$\begin{aligned} {\Pr [\mathsf {win}_3\wedge \mathsf {bad}]=\Pr [\underbrace{\mathsf {win}_3\wedge \mathsf {bad}\wedge \lnot \mathsf {freshT}}_{\mathsf {Case~ 1}}]+\Pr [\underbrace{\mathsf {win}_3\wedge \mathsf {bad}\wedge \mathsf {freshT}}_{\mathsf {Case~ 2}}].} \end{aligned}$$

(21)

• Case 1. In this case, $\mathsf {freshT}$ does not happen. Then we have $(\widetilde{t}, \widetilde{t'})=(t, t')$ or $(\widetilde{t}, \widetilde{t'})=(t_i, t_i')$ for some $i\in [\rho ]$. With loss of generality, we assume that $(\widetilde{t}, \widetilde{t'})=(t_i, t_i')$. Clearly $\widetilde{t}=t_i$ implies $\widetilde{s}=s_i$. Note that $\mathsf {dis}(\delta _i)\le \mathfrak {t}$ and $\mathsf {dis}(\widetilde{\delta })\le \mathfrak {t}$, thus $\mathsf {dis}(w+\widetilde{\delta },w+\delta _i)\le \mathsf {dis}(w+\widetilde{\delta },w) +\mathsf {dis}( w, w+\delta _i) \le 2\mathfrak {t}$. By the correctness of $(m-\lceil \log p\rceil , \hat{m},2\mathfrak {t})$-secure sketch $\mathsf {SS}$, we have $\widetilde{w}=w+\delta _i$, where $\widetilde{w}\leftarrow \mathsf {SS{.}Rec}(w+\widetilde{\delta },s_i)$ and $s_i\leftarrow \mathsf {SS{.}Gen}(w+\delta _i)$. As a result,

  $$\widetilde{\sigma }'=\mathsf {FEval}(\widetilde{t}, \widetilde{t'},\widetilde{w})=\mathsf {FEval}(t_i, t_i',w+\delta _i)=\sigma _i.$$

  If $\mathsf {win}_3$ occurs, then $\widetilde{\sigma }=\widetilde{\sigma }'$ must hold. This implies $\widetilde{P}=(\widetilde{t}, \widetilde{t'},\widetilde{\sigma })=(t_i, t_i',\sigma _i)=P_i$. This contradicts to the requirement of $\mathsf {win}_3$ that $\widetilde{P}$ is fresh. Thus we have

  $$\begin{aligned} { \Pr [\mathsf {win}_3\wedge \mathsf {bad}\wedge \lnot \mathsf {freshT}]=0.} \end{aligned}$$

  (22)

• Case 2. If both $\mathsf {bad}$ and $\mathsf {freshT}$ occur, then the forged tag $(\widetilde{t}, \widetilde{t'})$ is a fresh non-injective tag. Observe that $\mathcal {B}$ perfectly simulates $\mathsf {G}_{3}$ for $\mathcal {A}$, then $\mathcal {B}$ succeeds in outputting a fresh non-injective tag, as long as $\mathsf {bad}\wedge \mathsf {freshT}$ occurs. Consequently,

  $$\begin{aligned} { \Pr [\mathsf {win}_3\wedge \mathsf {bad}\wedge \mathsf {freshT}]\le \Pr [\mathsf {bad}\wedge \mathsf {freshT}] =\mathsf {Adv}_{\mathsf {LAF},\mathcal {B}}^{\mathsf {eva}}(1^{\lambda }).} \end{aligned}$$

  (23)

Combining (21), (22) and (23) together, we have

$$\begin{aligned} {\Pr [\mathsf {win}_3\wedge \mathsf {bad}]\le \mathsf {Adv}_{\mathsf {LAF},\mathcal {B}}^{\mathsf {eva}}(1^{\lambda }).~~} \end{aligned}$$

   $\blacksquare$

Claim

${\Pr [\mathsf {win}_3|\lnot \mathsf {bad}]\le 2^{-\omega (\log \lambda )}.}$

Proof

In $\mathsf {G}_{3}$, adversary $\mathcal {A}$ interacts with the challenger and presents its forgery $(\widetilde{P}, \widetilde{\delta })$ at the end. Define $\mathcal {A}$’s view before it submits its forgery as

Given the forgery $(\widetilde{P}=(\widetilde{s},\widetilde{c},\widetilde{t'},\widetilde{\sigma }),~\widetilde{\delta })$, $\mathcal {A}$ wins if $\mathsf {Rep}(\mathsf {crs},\widetilde{P},w+\widetilde{\delta })\ne \bot$, $\widetilde{P}$ is fresh and $\mathsf {dis}(\widetilde{\delta })\le \mathfrak {t}$. In the mean time, $\mathsf {Rep}(\mathsf {crs},\widetilde{P},w+\widetilde{\delta })\ne \bot$ if and only if $\mathsf {dis}(\widetilde{w},w+\widetilde{\delta })\le \mathfrak {t}$ and $\widetilde{\sigma }=\widetilde{\sigma }'$ hold, where $\widetilde{w}\leftarrow \mathsf {SS{.}Rec}(w+\widetilde{\delta },\widetilde{s})$ and $\widetilde{\sigma }'\leftarrow \mathsf {FEval}(F_{pk},\tilde{t} ,\tilde{t}', \widetilde{w})$. Therefore,

Now that $\mathsf {bad}$ does not occur, then the tag $\widetilde{\mathsf {tag}}=(\widetilde{t}=(\widetilde{s},\widetilde{c}),\widetilde{ t'})$ contained in $\widetilde{P}$ must be an injective tag. Thus $\mathsf {LAF}_{F_{pk},(t, t')}(\cdot )$ is injective and entropy preserving. This means $\widetilde{\sigma }':=\mathsf {FEval}(F_{pk},\widetilde{t}, \widetilde{t'},\widetilde{W})$ has the same entropy as $\widetilde{W}$. Consequently, it will be hard for adversary $\mathcal {A}$ to forge a valid $\widetilde{\sigma }$ (i.e., $\widetilde{\sigma }=\widetilde{\sigma }'$) if $\widetilde{W}$ has enough min-entropy conditioned on $\mathcal {A}$’s view in $\mathsf {G}_{3}$.

The outline of the proof is as follows.

• First, we prove that if $\mathsf {dis}(\widetilde{w},w+\widetilde{\delta })\le \mathfrak {t}$, then

  $$\begin{aligned} \widetilde{H}_{\infty }(\widetilde{W} \mid \textsf {\fbox {view}}) \ge \widetilde{H}_{\infty }(W \mid \textsf {\fbox {view}}). \end{aligned}$$

  (24)

• Next, we show that

  $$\begin{aligned} \widetilde{H}_{\infty }(W \mid \textsf {\fbox {view}}) \ge \omega (\log \lambda ). \end{aligned}$$

  (25)

• Formulas (24) and (25) give $\widetilde{H}_{\infty }(\widetilde{W} \mid \textsf {\fbox {view}}) \ge \omega (\log \lambda )$.

  If the event $\mathsf {bad}$ does not happen, $(\widetilde{t}, \widetilde{t'})$ must be an injective tag, hence $\mathsf {LAF}_{F_{pk},(\widetilde{t}, \widetilde{t'})}(\cdot )$ is an injective function, and $\widetilde{\sigma }'=\mathsf {FEval}(F_{pk},\widetilde{t}, \widetilde{t'},\widetilde{W})$ preserves the entropy of $\widetilde{W}$. So we have

  

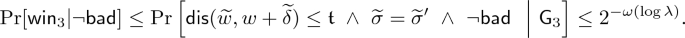
It remains to prove (24) and (25).

• Proof of (24). Define the random variable $\widetilde{W} := \mathsf {SS{.}Rec}(\widetilde{s},W+\widetilde{\delta })$, where W is the random variable in the robustness game. Let $w,\widetilde{w}$ denote the values taken by the random variables $W,\widetilde{W}$, respectively.

  If $\mathcal {A}$ wins, then $\mathsf {dis}(w+\widetilde{\delta },\widetilde{w})\le \mathfrak {t}$. By Lemma 3, we have

  $$\begin{aligned} \widetilde{H}_{\infty }\left( \widetilde{W} \mid \left( \mathsf {SS{.}Gen}(W+\widetilde{\delta }),\textsf {\fbox {view}},\widetilde{\delta }\right) \right) \ge \widetilde{H}_{\infty }\left( {W} +\widetilde{\delta }\mid \left( \mathsf {SS{.}Gen}(W+\widetilde{\delta }),\textsf {\fbox {view}},\widetilde{\delta }\right) \right) . \end{aligned}$$

  (26)

  Note that $\mathsf {SS{.}Gen}(W+\widetilde{\delta })=\mathsf {SS{.}Gen}(W)+\mathsf {SS{.}Gen}(\widetilde{\delta })$. The sketch $s=\mathsf {SS{.}Gen}(W)$ belongs to ${\textsf {\fbox {view}}}$, so $\mathsf {SS{.}Gen}(W+\widetilde{\delta })$ can be computed from $\textsf {\fbox {view}}$ and $\widetilde{\delta }$. As a result, according to Eq. (1),

  $$\begin{aligned} \!\!\widetilde{H}_{\infty }\left( {W} +\widetilde{\delta }\mid \left( \mathsf {SS{.}Gen}(W+\widetilde{\delta }),\textsf {\fbox {view}},\widetilde{\delta }\right) \right) =\widetilde{H}_{\infty }\left( W+\widetilde{\delta } \mid \left( \textsf {\fbox {view}},\widetilde{\delta }\right) \right) .\;\; \end{aligned}$$

  (27)

  Note that $\widetilde{\delta }$ is determined by $\mathcal {A}$ after seeing $\textsf {\fbox {view}}$, therefore, it can be further eliminated from the condition because of Eq. (2), and we have

  $$\begin{aligned} \widetilde{H}_{\infty }\left( W \mid \left( \textsf {\fbox {view}},\widetilde{\delta }\right) \right) =\widetilde{H}_{\infty }\left( W \mid \textsf {\fbox {view}}\right) . \end{aligned}$$

  (28)

  With Eqs. (27) and (28), we have

  $$\begin{aligned} \!\!\widetilde{H}_{\infty }\left( {W} +\widetilde{\delta }\mid \left( \mathsf {SS{.}Gen}(W+\widetilde{\delta }),\textsf {\fbox {view}},\widetilde{\delta }\right) \right) =\widetilde{H}_{\infty }\left( W \mid \textsf {\fbox {view}}\right) .\;\; \end{aligned}$$

  (29)

  Similarly, we have

  $$\begin{aligned} \widetilde{H}_{\infty }\left( \widetilde{W} \mid \left( \mathsf {SS{.}Gen}(W+\widetilde{\delta }),\textsf {\fbox {view}},\widetilde{\delta }\right) \right) = \widetilde{H}_{\infty }\left( \widetilde{W} \mid \textsf {\fbox {view}}\right) . \end{aligned}$$

  (30)

  Combining (26), (29) and (30), we have

  $$\begin{aligned} \widetilde{H}_{\infty }\left( \widetilde{W} \mid \textsf {\fbox {view}}\right) \ge \widetilde{H}_{\infty }\left( W \mid \textsf {\fbox {view}}\right) . \end{aligned}$$

  (31)

• Proof of (25). The general idea of the proof is that we will, step by step, show that the view of adversary can be perfectly simulated by a simulator with $\mathcal {S}$ and s, where $\mathcal {S}: =\{\sigma ~|~ \sigma =\mathsf {FEval}({F_{pk}}, t, t', W) \wedge \mathsf {tag}=(t, t')\in \mathcal {T}_{lossy}\}$ and $s=\mathsf {SS{.}Gen}(W)$. By the lossiness of $\mathsf {LAF}$, the information of W leaked by $\mathcal {S}$ is at most $\log p$ bits. By the fact that $\mathsf {SS}$ is a $(m-\lceil \log p\rceil , \hat{m},2\mathfrak {t})$-secure sketch and the fact that $\hat{m}-\lceil \log p\rceil \ge \omega (\log \lambda )$, we have that ${\widetilde{H}_{\infty }(W \mid \textsf {\fbox {view}}\big )\ge \omega (\log \lambda ).}$ Details can be found in the full version [25].

   $\blacksquare$

Taking all things together, by Eq. (18) and Lemmas 11–14, it follows that

$$\mathsf {Adv}_{\mathsf {rrFE},\mathcal {A}}^{\mathsf {rob}}\le \mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {ind}}(1^{\lambda })+\varepsilon _{\mathsf {ext}}+\mathsf {Adv}_{\mathsf {LAF}}^{\mathsf {eva}}(1^{\lambda })+2^{-\omega (\log \lambda )}.$$

   $\blacksquare$

Corollary 1

If $\mathsf {SS}$ is instantiated by a syndrome-based secure sketch, $\mathsf {Ext}$ is instantiated as Eq. (5), $\mathsf {LAF}$ is instantiated with the scheme in [15], and $\mathsf {SKEM}$ is instantiated with the scheme shown in Fig. 3, then the construction in Fig. 4 results in a robustly reusable fuzzy extractor based on the DLIN assumption and the DDH assumption.

Remark 4

Since there exist efficient linear error correcting codes which can correct linear fraction of errors, the syndrome-based secure sketch is able to correct linear fraction of errors as well, so is our robustly reusable fuzzy extractor.