Abstract
The possibility of basing cryptography on the minimal assumption \(\mathbf{NP }\nsubseteq \mathbf{BPP }\) is at the very heart of complexity-theoretic cryptography. The closest we have gotten so far is lattice-based cryptography whose average-case security is based on the worst-case hardness of approximate shortest vector problems on integer lattices. The state-of-the-art is the construction of a one-way function (and collision-resistant hash function) based on the hardness of the \(\tilde{O}(n)\)-approximate shortest independent vector problem \({\textsf {SIVP}}_{\tilde{O}(n)}\).
Although \({\textsf {SIVP}}\) is NP-hard in its exact version, Guruswami et al. (CCC 2004) showed that \({\textsf {gapSIVP}}_{\sqrt{n/\log n}}\) is in \(\mathbf{NP } \cap \mathbf{coAM }\) and thus unlikely to be \(\mathbf{NP }\)-hard. Indeed, any language that can be reduced to \({\textsf {gapSIVP}}_{\tilde{O}(\sqrt{n})}\) (under general probabilistic polynomial-time adaptive reductions) is in \(\mathbf{AM } \cap \mathbf{coAM }\) by the results of Peikert and Vaikuntanathan (CRYPTO 2008) and Mahmoody and Xiao (CCC 2010). However, none of these results apply to reductions to search problems, still leaving open a ray of hope: can \(\mathbf{NP }\) be reduced to solving search SIVP with approximation factor \(\tilde{O}(n)\)?
We eliminate such possibility, by showing that any language that can be reduced to solving search \({\textsf {SIVP}}\) with any approximation factor \(\lambda (n) = \omega (n\log n)\) lies in AM intersect coAM.
Research supported in part by NSF Grants CNS-1350619 and CNS-1414119..
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
It is a long-standing open question whether cryptography can be based on the minimal assumption that \(\mathbf{NP } \nsubseteq \mathbf{BPP }\). More precisely, one would hope to construct cryptographic primitives such that given a polynomial-time algorithm breaking the security of the primitive, one can efficiently solve \({\textsf {SAT}}\).
The closest we have gotten so far is lattice cryptography. This approach was born out of the breakthrough result of Ajtai [Ajt96], which constructs a one-way function family based on the worst-case hardness of certain lattice problems such as the \(\gamma \)-approximate shortest independent vectors problem (\({\textsf {SIVP}}_\gamma \)), which can be stated as follows: given an n-dimensional lattice, find a set of n linearly independent vectors whose lengthFootnote 1 is at most \(\gamma (n)\) (polynomial in n) times the length of the shortest such vector set. Since the work of Ajtai, the state of the art is a construction of a family of collision resistant hash functions (CRHF) based on the hardness of the shortest independent vectors problem with an approximation factor \(\tilde{O}(n)\) [MR04]. One would hope that this approach is viable for constructing cryptography based on NP-hardness since Blömer and Seifert showed that \({\textsf {SIVP}}_{\gamma }\) is NP-hard for any constant factor [BS99]. Presumably, if one could construct cryptographic primitives based on the hardness of \({\textsf {SIVP}}_{O(1)}\), we would be golden. Alternatively, if one could extend the result of Blömer and Seifert to show the NP-hardness of \({\textsf {SIVP}}_\gamma \) for larger \(\gamma (n)\), we would be closer to the goal of basing cryptography on NP-hardness.
However, there are some negative results when one considers the corresponding gap version of the same lattice problem. The gap problem, denoted by \({\textsf {gapSIVP}}_{\gamma }\), is to estimate the length of the short independent vector set within a factor of \(\gamma (n)\). Peikert and Vaikuntanathan show that \({\textsf {gapSIVP}}_{\omega (\sqrt{n \log n})}\) is in \(\mathbf{SZK }\) [PV08]. Thus there is no Cook reduction from SAT to \({\textsf {gapSIVP}}_{\tilde{O}(\sqrt{n})}\) unless the polynomial hierarchy collapses (as \(\mathbf{BPP }^\mathbf{SZK } \subseteq \mathbf{AM } \cap \mathbf{coAM }\) [MX10]).
Fortunately, the hardness of SIVP is not contradicted by the fact that the gap problem with the same approximation factor is easy. For instance, if one considers any ideal lattice in the field \({\mathbb {Z}}[x]/\langle x^{2^k}+1\rangle \), its successive minima satisfy \(\lambda _1 = \ldots = \lambda _n\), thus \({\textsf {gapSIVP}}_{\sqrt{n}}\) can be trivially solved using Minkowski’s inequality. However, finding a set of short independent vectors in such ideal lattices is still believed to be hard. As none of these negative results apply to reductions to search SIVP, there is still a ray of hope: can \(\mathbf{NP }\) be reduced to solving search SIVP with approximation \(\tilde{O}(n)\)?
Thus, in order to really understand the viability of the approach begun by the work of Ajtai, it seems one must study the search versions of lattice problems. In this work, we relate the hardness of the search version \({\textsf {SIVP}}_{\gamma }\), to the gap version gapSIVP. Informally, we show that if \({\textsf {gapSIVP}}_{\gamma }\) is not hard, neither is \({\textsf {SIVP}}_{\sqrt{n} \cdot \gamma }\).
Main Theorem 1
If \({\textsf {gapSIVP}}_{\gamma } \in \mathbf{SZK}\) and there exists a probabilistic polynomial-time adaptive reduction from a language L to \({\textsf {SIVP}}_{\sqrt{n\log n} \cdot \gamma }\), then \({\textsf {L}} \in \mathbf{AM } \cap \mathbf{coAM }\).
As a quick corollary, combining our result with \({\textsf {gapSIVP}}_{\omega (\sqrt{n\log n})} \in \mathbf{SZK }\) [PV08], any language that can be reduced to \({\textsf {SIVP}}_{\omega (n\log n)}\) lies in AM intersect coAM and thus it is not NP-hard unless the polynomial hierarchy collapses.
Corollary 1.1
If there exists a probabilistic polynomial-time adaptive reduction from a language L to \({\textsf {SIVP}}_{\gamma }\) for any \(\gamma (n) = \omega (n\log n)\), then \({\textsf {L}} \in \mathbf{AM } \cap \mathbf{coAM }\).
1.1 Proof Overview
The first step is to shift from a search problem to a sampling problem. Our goal is to obtain a black-box separation between \({\textsf {SIVP}}_{\gamma }\) and NP-hardness by showing that any language L that can be reduced to \({\textsf {SIVP}}_{\gamma }\) is in AM intersect coAM. Let \(\mathcal R\) be the reduction from L to \({\textsf {SIVP}}_{\gamma }\). We will construct an AM protocol for L using reduction \(\mathcal R\). For a first attempt, the naïve verifier samples a random tape and sends it to the prover. The prover simulates the reduction \(\mathcal R\) and resolves any query to \({\textsf {SIVP}}_\gamma \) using its unbounded computational power. The simulation, including the answers to the reduction’s query to \({\textsf {SIVP}}_\gamma \), is sent to the naïve verifier, so that the verifier can check its correctness. But \({\textsf {SIVP}}_{\gamma }\) is a search problem and there is no unique right answer. The prover has the freedom to decide which answer is chosen upon each query. This freedom allows a malicious prover to fool the naïve verifier. Similar difficulty were faced by Bogdanov and Brzuska, which is resolved by inherently shifting to sampling problems. In order to separate size-verifiable one-way functions from NP-Hardness [BB15], they force the prover to sample a random answer uniformly among all correct ones. Thus the correct answer distribution for each query is unique.
Inspired by the work of Bogdanov and Brzuska, we consider a sampling problem related to \({\textsf {SIVP}}_\gamma \), called the discrete Gaussian distribution. A discrete Gaussian over a lattice is a distribution such that the probability of any vertex \(\mathbf {v}\) is proportional to \(e^{-\pi \Vert \mathbf {v}- \mathbf {c}\Vert ^2 /s^2}\), where \(\mathbf {c}\) is its “center” and parameter s is its “width”. Lemma 4.3 shows that discrete Gaussian sampling is as hard as \({\textsf {SIVP}}_{\gamma }\) in the sense that there is a black-box reduction from \({\textsf {SIVP}}_{\gamma }\) to discrete Gaussian sampling with “width” \(\gamma (n) / \sqrt{n}\). Therefore, if language L can be reduced to \({\textsf {SIVP}}_\gamma \), then it can also be reduced to discrete Gaussian sampling on lattices with “width” \(s \le \lambda _n / \sqrt{n}\).
Lemma 4.3
(Informal). \({\textsf {SIVP}}_{\gamma }\) can be efficiently reduced to discrete Gaussian sampling on lattices with “width” \(\sigma = \frac{\gamma }{\sqrt{n}} \lambda _n\).
Lemma 4.3 is a generalization of [Reg09, Lemma 3.17]. Its proof is quite intuitive. Repeatedly sample from the discrete Gaussian over the same lattice centered at \(\mathbf {0}\). With good probability, the newly sampled vertex is short and is linearly independent from previously sampled verteces.
The next natural question is, which property separates a sampling problem from NP-hardness? Here we introduce the notion of “probability-verifiability”. Informally, a distribution family is probability-verifiable if for any distribution \(\mathcal D\) in this family and for any possible value v, \(\Pr [v \leftarrow \mathcal D]\), the probability that v is sampled from \(\mathcal D\), can be lower bounded within an arbitrarily good precision in AM.
Lemma 4.4
(Informal). If a language \({\textsf {L}}\) can be reduced to a probability-verifiable sampling problem \({\textsf {S}}\), then \({\textsf {L}} \in \mathbf{AM } \cap \mathbf{coAM }\).
Lemma 4.4 is a generalization of [BB15]. Assume language L can be reduced to sampling problem \({\textsf {S}}\). The input of S is interpreted as the description of a distribution, let \(\mathcal P_{\mathsf {pd}}\) denote the distribution specified by input \(\mathsf {pd}\).
Let \(\mathcal R\) be the reduction from L to sampling problem S. On each input x, an execution \(\mathcal R^{{\textsf {S}}}(x)\) is determined by the random tape of reduction \(\mathcal R\), denoted by r, and the answers to the reduction’s queries to S. The transcript is defined as \(\sigma = (r,\mathsf {pd}_1,v_1, \ldots , \mathsf {pd}_T,v_T)\) where \(\mathsf {pd}_t\) is the t-th query to S and \(v_t\) is the corresponding response. Note that \(r,v_1,\ldots ,v_T\) determine the execution, since \(\mathsf {pd}_t\) is determined by \(r,v_1,\ldots ,v_{t-1}\). Then

For simplicity, assume for now that there is an efficient algorithm that computes the probability \(\mathcal P_{\mathsf {pd}}(v)\) given \(\mathsf {pd}\) and value v. This property is stronger than probability-verifiability. Then the probability that \(\mathcal R^{{\textsf {S}}}(x)\) accepts, which equals a sum (Eq. (1)) where each term can be efficient computed, can be lower bounded using the set lower bound protocol of Goldwasser and Sipser [GS86], so \({\textsf {L}}\in \mathbf{AM }\). Symmetrically, \({\textsf {L}}\in \mathbf{coAM }\). The proof of Lemma 4.4 shows the same result from the weaker condition that \({\textsf {S}}\) is probability-verifiable.
There is one last step missing between Lemmas 4.3 and 4.4: Is discrete Gaussian sampling probability-verifiable? What is the smallest factor \(\gamma \) such that discrete Gaussian sampling with “width” \(\le \gamma \lambda _n\) is probability-verifiable? Lemma 4.5 answers this question, and it connects the hardness of discrete Gaussian sampling with the hardness of \({\textsf {gapSIVP}}\).
Lemma 4.5
(Informal). Assume \({\textsf {gapSIVP}}_{\gamma }\) is in SZK. There exists a real valued function \(s(\mathbf {B}) \in [\lambda _n,\tilde{O}(\gamma ) \cdot \lambda _n]\) such that given a lattice basis \(\mathbf {B}\), discrete Gaussian sampling over lattice \(\mathcal L(\mathbf {B})\) with “width” \(s(\mathbf {B})\) is probability-verifiable.
Lemma 4.5 has an easier proof assuming the stronger condition that \({\textsf {gapSIVP}}_{\gamma }\) is in P. If there were some deterministic polynomial time algorithm solving \({\textsf {gapSIVP}}_{\gamma }\), there would exist \(s(\mathbf {B}) \in [\lambda _n(\mathbf {B}), \gamma \lambda _n(\mathbf {B})]\) that can be efficiently computed by binary search. As \(s(\mathbf {B}) \ge \lambda _n(\mathbf {B})\), the verifier can ask the prover to provide a set of n linearly independent vectors \(\mathbf {w}_1,\ldots ,\mathbf {w}_n\) whose length is no longer than \(s(\mathbf {B})\). Given the lattice basis \(\mathbf {B}\) and a set of short linearly independent vectors, there exists an efficient algorithm that samples from the discrete Gaussian with the desired parameter [BLP+13]. When the verifier can sample from a distribution, he can lower bound the probability of each value using the set lower bound protocol [GS86].
This informal proof assumes \({\textsf {gapSIVP}}_{\gamma }\in \mathbf{P }\) in order to compute a function \(s(\mathbf {B})\) that \(s(\mathbf {B}) \approx \lambda _n(\mathbf {B})\). As the verifier only needs to compute such a function \(s(\mathbf {B})\) in an AM protocol, this assumption can be weakened to \({\textsf {gapSIVP}}_{\gamma }\in \mathbf{SZK }\), by combining with Lemma 3.1.
Lemma 3.1
(Informal). Assume \({\textsf {gapSIVP}}_{\gamma }\) is in SZK. There exists a real valued function \(s(\mathbf {B}) \in [\lambda _n,\tilde{O}(\gamma ) \cdot \lambda _n]\) that can be efficiently computed in Arthur-Merlin protocol.
The proof technique of Lemma 3.1 crucially relies on the fact that \({\textsf {gapSIVP}}_{\gamma } \in \mathbf{SZK }\). As a result, we can hardly make use of previous results such as \({\textsf {gapSIVP}}_{\sqrt{n/\log n}} \in \mathbf{NP }\cap \mathbf{coAM }\) [GMR04].
1.2 Related Works
Prior work exploring the problem of basing cryptography on worst-case \(\mathbf{NP }\)-hardness has obtained several negative results for black-box reduction. Brassard [Bra79] first showed that one-way permutations cannot be based on NP-hardness. Goldreich and Goldwasser [GG98] showed that public-key encryption schemes satisfying certain very specific properties cannot be based on NP-hardness. The required properties include the ability to certify an invalid key.
Work of Akavia, Goldreich, Goldwasser and Moshkovitz [AGGM06] and Bogdanov and Brzuska [BB15] showed that a special class of one-way functions called size-verifiable one-way functions cannot be based on \(\mathbf{NP }\)-hardness. A size-verifiable one-way function is one in which the size of the set of pre-images can be efficiently approximated via an \(\mathbf{AM }\) protocol.
Bogdanov and Lee [BL13] showed that homomorphic encryption schemes satisfying a special property cannot be based on \(\mathbf{NP }\)-hardness. The required property is that the homomorphic evaluation produces a ciphertext whose distribution is statistically close to that of a fresh encrypted ciphertext.
Recently, Liu and Vaikuntanathan [LV16] showed that single-server private information retrieval (PIR) schemes cannot be based on NP-hardness.
Several works have also obtained a separation results for restricted types of reductions, most notably non-adaptive reductions which make all oracle queries simultaneously. The work of Feigenbaum and Fortnow [FF91], subsequently strengthened by Bogdanov and Trevisan [BT06], showed that there cannot be a non-adaptive reduction from SAT to the average-case hardness of any problem in \(\mathbf{NP }\), unless the polynomial hierarchy collapses.
On basing lattice problems on NP-hardness, the work of Goldreich and Goldwasser [GG00], subsequently strengthened by Micciancio and Vadhan [MV03], showed that \({\textsf {gapSVP}}_{\sqrt{n/\log n}}\) and \({\textsf {gapCVP}}_{\sqrt{n/\log n}}\) are both contained in \(\mathbf{NP } \cap \mathbf{SZK }\). The shortest vector problem (SVP) and the closest vector problem (CVP), roughly speaking, is the problem of finding the shortest non-zero vector in a lattice or finding the lattice vector that is closest to a given point. The corresponding gap problem \({\textsf {gapSVP}}_\gamma ,{\textsf {gapCVP}}_\gamma \) is to estimate within a factor of \(\gamma (n)\) the length of the shortest non-zero vector or the distance to the closest lattice vector from a given point. The problem gapSVP is connected to gapSIVP via so-called “transference theorems” for lattices [Ban93]. Aharonov and Regev [AR04] explored a slightly looser approximation factor and showed that \({\textsf {gapSVP}}_{\sqrt{n}}\) and \({\textsf {gapCVP}}_{\sqrt{n}}\) are both contained in \(\mathbf{NP } \cap \mathbf{coNP }\).
In prior work on the gap version of the SIVP problem, Guruswami, Micciancio and Regev [GMR04] showed that \({\textsf {gapSIVP}}_{\sqrt{n/\log n}} \in \mathbf{NP } \cap \mathbf{coAM }\). Peikert and Vaikuntanathan [PV08] showed that \({\textsf {gapSIVP}}_{\gamma } \in \mathbf{SZK }\) for any \(\gamma (n) = \omega (\sqrt{n\log n})\). In contrast to these results for promise problems, our work explores the approximate SIVP problem. With an approximation factor \(\gamma (n) = \tilde{O}(n)\), this search problem is the basis of lattice-based collision resistant hash function (CRHF) constructions [Ajt96, MR04]. In particular, Micciancio and Regev constructed CRHF from the worst-case hardness of \({\textsf {SIVP}}_{\gamma (n)}\) for any \(\gamma (n) = \omega (n\log n)\) [MR04]. We separate \({\textsf {SIVP}}_\gamma \) from NP-hardness for the same approximation factor.
2 Preliminaries
Lattice A lattice in \({\mathbb {R}}^n\) is an additive subgroup of \({\mathbb {R}}^n\)
generated by n linearly independent vectors \(\mathbf {b}_1,\ldots ,\mathbf {b}_n \in {\mathbb {R}}^n\). The set of vectors \(\mathbf {b}_1,\ldots ,\mathbf {b}_n\) is called a basis for the lattice. A basis can be represented by matrix \(\mathbf {B}\in {\mathbb {R}}^{n\times n}\) whose columns are the basis vectors. The lattice generated by the columns of \(\mathbf {B}\) is denoted by \(\mathcal L(\mathbf {B})\).
The i-th successive minimum of a lattice \(\mathcal L\), denoted by \(\lambda _i(\mathcal L)\), is defined as the minimum length that \(\mathcal L\) contains i linearly independent vectors of length at most \(\lambda _i(\mathcal L)\). Formally,
where \(r \mathcal B\) is the radius r ball centered at the origin defined as \(r \mathcal B \mathrel {:=}\{\mathbf {x}\in {\mathbb {R}}^n : \Vert \mathbf {x}\Vert _2 \le r\}\). We abuse notations and write \(\lambda _i(\mathbf {B})\) instead of \(\lambda _i(\mathcal L(\mathbf {B}))\).
Shortest Independent Vectors Problem (SIVP). \({\textsf {SIVP}}\) is a computational problem. Given a basis \(\mathbf {B}\) of an n-dimensional lattice, find a set of n linearly independent vectors \(\mathbf {v}_1,\ldots ,\mathbf {v}_n \in \mathcal L(\mathbf {B})\) such that \(\max _i\Vert \mathbf {v}_i\Vert \) is minimized, i.e., \(\Vert \mathbf {v}_i\Vert \le \lambda _n(\mathbf {B})\) for all \(1\le i\le n\).
\({\textsf {SIVP}}_\gamma \) is the approximation version of \({\textsf {SIVP}}\) with factor \(\lambda \). Given a basis \(\mathbf {B}\) of an n-dimensional lattice, find a set of n linearly independent vectors \(\mathbf {v}_1,\ldots ,\mathbf {v}_n \in \mathcal L(\mathbf {B})\) such that \(\Vert \mathbf {v}_i\Vert \le \gamma (n) \cdot \lambda _n(\mathbf {B})\) for all \(1\le i\le n\). The approximation factor \(\gamma \) is typical a polynomial in n.
\({\textsf {gapSIVP}}_\gamma \) is the decision version of \({\textsf {SIVP}}_\gamma \). An input to \({\textsf {gapSIVP}}_\gamma \) is a basis \(\mathbf {B}\) of a n-dimensional lattice and a scalar s. It is a YES instance if \(\lambda _n(\mathbf {B}) \le s\), and is a NO instance if \(\lambda _n(\mathbf {B}) \ge \gamma (n) \cdot s\).
Discrete Gaussian. For any vector \(\mathbf {c}\) and any \(s > 0\), let
be a Gaussian function with mean \(\mathbf {c}\) and width s. Functions are extends to sets in usual way, \(\rho _{\mathbf {c},s}(\mathcal L) = \sum _{\mathbf {v}\in \mathcal L} \rho _{\mathbf {c},s}(\mathbf {v})\). The discrete Gaussian distribution over lattice \(\mathcal L\) with mean \(\mathbf {c}\) and width s, denoted by \(\mathcal N_{\mathcal L, \mathbf {c}, s}\), is defined by
In this work, most discrete Gaussian distributions considered are centered at the origin. Let \(\rho _{s}, \mathcal N_{\mathcal L,s}\) denote \(\rho _{\mathbf {0},s}, \mathcal N_{\mathcal L,\mathbf {0},s}\) respectively.
Lemma 2.1
(Lemma 1.4 in [Ban93]). For each \(a\ge 1\), for any n-dimensional lattice \(\mathcal L\), \(\rho _{as}(\mathcal L) \le a^n \rho _{s}(\mathcal L)\)
Lemma 2.2
(Lemma 1.5 in [Ban93]). For any \(c > 1/\sqrt{2\pi }\), n-dimensional lattice \(\mathcal L\)
where \(C = c \sqrt{2\pi e} \cdot e^{-\pi c^2}\).
Sampling Problems. Besides computational problems and decision problems, we define sampling problems. The input of a sampling problem specifies a distribution, let \(\mathcal P_\mathsf {pd}\) denote the distribution specified by input \(\mathsf {pd}\). The goal is to sample from the distribution \(\mathcal P_\mathsf {pd}\). A probabilistic polynomial-time algorithm \(\mathcal S\) perfectly solves the sampling problem if for any input \(\mathsf {pd}\)
The probability is over the random input tape of \(\mathcal S\). In a more practical definition, \(\mathcal S\) solves the sampling problem if the output distribution of \(\mathcal S(\mathsf {pd})\) is close to \(\mathcal P_\mathsf {pd}\), i.e.
where \(\varDelta _\mathrm{sd}\) denotes the statistical distance.
For example, in this work, discrete Gaussian is considered as a sampling problem. For any function \(s(\cdot )\) mapping lattice bases to positive real numbers, define sampling problem  . The input of
. The input of  is a lattice basis \(\mathbf {B}\). The target output distribution \(\mathcal P_\mathbf {B}\) is the discrete Gaussian distribution \(\mathcal N_{\mathcal L(\mathbf {B}),s(\mathbf {B})}\), where each vector \(v\in \mathcal L(\mathbf {B})\) is sampled with probability
is a lattice basis \(\mathbf {B}\). The target output distribution \(\mathcal P_\mathbf {B}\) is the discrete Gaussian distribution \(\mathcal N_{\mathcal L(\mathbf {B}),s(\mathbf {B})}\), where each vector \(v\in \mathcal L(\mathbf {B})\) is sampled with probability
Probability-Verifiable. A sampling problem is probability-verifiable if there exists an AM protocol to lower bound \(\mathcal P_\mathsf {pd}(v)\) for any \(\mathsf {pd}\) and v. More precisely, there exists a family of error function \(\{\eta _{\mathsf {pd},m}\}\) such that for any \(\mathsf {pd},m\), the error function \(\eta _{\mathsf {pd},m}:\{0,1\}^* \rightarrow [0,+\infty )\) satisfies \(\sum _v \eta _{\mathsf {pd},m}(v) \le \frac{1}{m}\), and the promise problem
-
YES instance: \((\mathsf {pd},v,\hat{p},1^m)\) such that \(\hat{p} = \mathcal P_\mathsf {pd}(v)\)
-
NO instance: \((\mathsf {pd},v,\hat{p},1^m)\) such that \(\hat{p} \ge \mathcal P_\mathsf {pd}(v) + \eta _{\mathsf {pd},m}(v)\)
is in AM.
Sampling Oracles. In order to formalize the (probabilistic) Turing reduction to a sampling problem, we also define sampling oracles, which is a generalization of traditional oracles studied by complexity theorists. Let \(\mathcal S\) be a sampling oracle for a fixed sampling problem. \(\mathcal S\) can be queried on any valid \(\mathsf {pd}\); upon query \(\mathsf {pd}\), sampling oracle \(\mathcal S(\mathsf {pd})\) would always output a fresh sample from distribution \(\mathcal P_\mathsf {pd}\). E.g. if the sampling oracle \(\mathcal S\) is queried for the same \(\mathsf {pd}\) multiple times, it would output i.i.d. samples from distribution \(\mathcal P_\mathsf {pd}\).
A probabilistic Turing reduction from a language \({\textsf {L}}\) to a sampling problem \({\textsf {S}}\) is a probabilistic poly-time oracle Turing machine \(\mathcal R\), such that \(\mathcal R\) can solve \({\textsf {L}}\) given a sampling oracle of \({\textsf {S}}\) in the sense that
If such a reduction exists, we say \({\textsf {L}}\) can be reduced to sampling problem \({\textsf {S}}\), denoted by \({\textsf {L}} \in \mathbf{BPP }^{{\textsf {S}}}\).
Similarly, a computational problem or a search problem can be reduced to a sampling problem \({\textsf {S}}\) if they can be efficiently solved given the sampling oracle of \({\textsf {S}}\).
\({\mathbb {R}}\)-TFAM and \({\mathbb {R}}_\eta \)-TFAM The complexity class \({\mathbb {R}}\)-TFAM is introduced by Mahmoody and Xiao [MX10]. Informally, it’s consist of real-valued functions that can be efficiently computed in AM. A function \(f:\{0,1\}^* \rightarrow {\mathbb {R}}\) is in \({\mathbb {R}}\)-TFAM if the following promise problem is in AM:
-
YES instance: \((x,f(x),1^m)\).
-
NO instance: \((x,y,1^m)\) such that \(|y - f(x)| > \frac{1}{m}\).
The definition of \({\mathbb {R}}\)-TFAM emphasize on the absolute error. The complexity class \({\mathbb {R}}_\eta \)-TFAM is defined to capture those functions that can be efficiently computed in AM with small relative error. A function \(g:\{0,1\}^* \rightarrow {\mathbb {R}}^+\) is in \({\mathbb {R}}_\eta \)-TFAM if the following promise problem is in AM:
-
YES instance: \((x,g(x),1^m)\).
-
NO instance: \((x,y,1^m)\) such that \(|y - g(x)| > \frac{1}{m} \cdot g(x)\).
It follows directly from the definitions that \(g \in {\mathbb {R}}_\eta -\mathbf{TFAM }\) if and only if \(\log g \in {\mathbb {R}}-\mathbf{TFAM }\) for any function \(g:\{0,1\}^* \rightarrow {\mathbb {R}}^+\).
Statistical Zero Knowledge. Statistical zero knowledge (SZK) is the class of decision problems that can be verified by a statistical zero-knowledge proof protocol. Entropy Difference (ED) is a complete problem for SZK [GV99], which is defined as the following: Given two polynomial-size circuits, C and D, let \(\mathcal C\) and \(\mathcal D\) be the distributions of their respective outputs when C, D are fed with uniform random inputs. The problem is to distinguish between
-
YES instance: (C, D) such that \(H(\mathcal C) - H(\mathcal D) \ge 1\);
-
NO instance: (C, D) such that \(H(\mathcal C) - H(\mathcal D) \le - 1\).
Where H is the Shannon entropy. Moreover, the mapping \(H:C \mapsto H(\mathcal C)\) is in \({\mathbb {R}}\)-TFAM.
3 Gap Problems
The lattice problem \({\textsf {gapSIVP}}\) is essentially estimating \(\lambda _n(\mathbf {B})\) given a lattice basis \(\mathbf {B}\). This definition can be generalized to any real valued functions. Define the gap problem of function \(f:\{0,1\}^*\rightarrow {\mathbb {R}}^+\) with gap \(\gamma :\{0,1\}^*\rightarrow [1,+\infty )\), denoted by \({\textsf {gap}}f_{\gamma }\), as the promise problem
-
YES instance: (x, y) such that \(y\le f(x)\);
-
NO instance: (x, y) such that \(y > \gamma (x) \cdot f(x)\).
In this work, estimating \(\lambda _n(\mathbf {B})\) is of critical importance. Its gap problem, \({\textsf {gapSIVP}}_\gamma \), alone is not sufficient for the proof. Instead, a stronger form of approximation is defined. Say \(g:\{0,1\}^*\rightarrow {\mathbb {R}}^+\) is an approximation of function f within factor \(\gamma \) if \(f(x) \le g(x) \le \gamma (x) \cdot f(x)\) for all x. Clearly, computing g is a harder problem than \({\textsf {gap}}f_{\gamma }\), in the sense that there is a trivial reduction from \({\textsf {gap}}f_{\gamma }\) to computing g.
The following Lemma shows a reduction in the other direction: if \({\textsf {gap}}f_{\gamma }\) is in SZK, then there exists an approximation of f within almost the same factor, which can be computed in AM.
Lemma 3.1
For any real valued function \(f:\{0,1\}^*\rightarrow {\mathbb {R}}^+\) and any gap \(\gamma :\{0,1\}^*\rightarrow [1,+\infty )\) that \(\log \gamma (x) \le \mathop {{\text {poly}}}(|x|)\), if \({\textsf {gap}}f_{\gamma } \in \mathbf{SZK }\), then for any constant \(\mu > 1\), there exists \(g:\{0,1\}^*\rightarrow {\mathbb {R}}^+\) such that \(\forall x, g(x) \in [f(x),\mu \gamma (x) f(x)]\) and g is in \({\mathbb {R}}_\eta \)-TFAM.
Lemma 3.1 can be combined with previous results about gapSIVP. Peikert and Vaikuntanathan [PV08] showed that \({\textsf {gapSIVP}}_\gamma \in \mathbf{NISZK } \subseteq \mathbf{SZK }\) for any \(\gamma = \omega (\sqrt{n \log n})\). Thus there exists an approximation of \(\lambda _n\) within a factor \(\tilde{O}(\sqrt{n})\) that can be computed in AM.
Corollary 3.2
For any \(\gamma (n) = \omega (\sqrt{n\log n})\), there exists a function g maps lattice bases to real numbers such that \(g\in {\mathbb {R}}_\eta -\mathbf{TFAM }\) and \(\lambda _n(\mathbf {B}) \le g(\mathbf {B}) < \gamma (n) \cdot \lambda _n(\mathbf {B})\).
Proof (Lemma 3.1)
Entropy Difference (ED) is a complete problem for SZK, so \({\textsf {gap}}f_{\gamma } \in \mathbf{SZK }\) implies the existence of a reduction \((x,y)\mapsto (C_{x,y}, D_{x,y})\) that maps input x together with a real number y to random circuits \(C_{x,y}, D_{x,y}\). Let \(\mathcal C_{x,y}\) and \(\mathcal D_{x,y}\) be the output distributions of \(C_{x,y},D_{x,y}\). The reduction from \({\textsf {gap}}f_{\gamma }\) to ED satisfies the following properties:
-
There is an efficient deterministic algorithm computing \(C_{x,y},D_{x,y}\) given input (x, y).
-
\(H(\mathcal C_{x,y}) - H(\mathcal D_{x,y}) > 2\) for any x, y that \(y\le f(x)\).
-
\(H(\mathcal C_{x,y}) - H(\mathcal D_{x,y}) < -1\) for any x, y that \(y > \gamma (x) \cdot f(x)\).
Define the clamp function
For any fixed constant \(\mu > 1\), define
As \({\text {clamp}}(H(\mathcal C_{x,y})-H(\mathcal D_{x,y})) = 1\) for \(y \le f(x)\),
As \({\text {clamp}}(H(\mathcal C_{x,y})-H(\mathcal D_{x,y})) = 0\) for \(y > \gamma (x) \cdot f(x)\),
In order to complete the proof, we show that g is in \({\mathbb {R}}_\eta \)-TFAM. For any input \(x,\hat{g}\), the prover can prove \(\hat{g} \approx g(x)\) if \(\hat{g} = g(x)\).
Consider the following protocol, \(\varepsilon = 1/\mathop {{\text {poly}}}(m,\ln \gamma )\) will be fixed later.
On any input x, define \(d_i = H(\mathcal C_{x,\mu ^i})-H(\mathcal D_{x,\mu ^i})\). And the honest prover should send \(\hat{d}_i = d_i\). The prover have to prove that \(d_i - \varepsilon< \hat{d}_i < d_i + \varepsilon \). For \(\mu ^i \le f(x)\), \(\hat{d}_i \ge d_i - \varepsilon \ge 1\), then \({\text {clamp}}(\hat{d}_i) = 1 = {\text {clamp}}(d_i)\). For \(\mu ^i \ge \mu \gamma (x) f(x)\), \(\hat{d}_i \le d_i + \varepsilon \le 0\), then \({\text {clamp}}(\hat{d}_i) = 0 = {\text {clamp}}(d_i)\). For \(f(x)< \mu ^i < \mu \gamma (x) f(x)\), \(|{\text {clamp}}(\hat{d}_i) - {\text {clamp}}(d_i)| \le |\hat{d}_i-d_i| < \varepsilon \).

Thus
If \(\varepsilon \) is sufficiently small, \(\hat{g}\) would be close to g(x). To ensure \(|\hat{g} - g(x)| \le \frac{1}{m} g(x)\), it is sufficient to set \(\varepsilon = O(\frac{1}{m(\ln \gamma (x) + 2)})\).
The above “protocol” is not a real protocol, as it requires the prover to send an infinite sequence to the verifier. To compress the proof, the prover need a succinct interactive proof that \(d_j > 1\) for all \(j\le i_L\) and \(d_j < 0\) for all \(j \ge i_H\).
For an index i, if the prover can convince the verifier that \(d_i = H(\mathcal C_{x,\mu ^i})-H(\mathcal D_{x,\mu ^i}) < 2\), the verifier also learns that \(\mu ^i > g(x)\), thus for any \(j \ge i + \lceil \log _\mu \gamma (x) \rceil \), \(\mu ^j > \gamma (x) g(x)\) and \(d_j \le -1\). Similarly, if the prover can convince the verifier that \(d_i = H(\mathcal C_{x,\mu ^i})-H(\mathcal D_{x,\mu ^i}) > -1\) , the verifier also knows that \(d_j \ge 2\) for any \(j \le i - \lceil \log _\mu \gamma (x) \rceil \).
Thus the real AM protocol that proves \(\hat{g} \in (g(x)-\frac{1}{m},g(x)+\frac{1}{m})\) is the following:

\(\square \)
4 Search SIVP and NP-Hardness
Theorem 4.1
For any factor \(\gamma :{\mathbb {N}}\rightarrow \mathbb R\), if \({\textsf {gapSIVP}}_{\gamma } \in \mathbf{SZK }\) and there exists a probabilistic polynomial-time adaptive reduction from a language L to \({\textsf {SIVP}}_{\sqrt{n \ln n} \cdot \gamma }\), then \({\textsf {L}} \in \mathbf{AM } \cap \mathbf{coAM }\).
The smallest factor \(\gamma \) we knows that makes problem \({\textsf {gapSIVP}}_{\gamma }\) be in \(\mathbf{SZK }\) comes from [PV08]: for any factor \(\gamma (n) = \omega (\sqrt{n \log n})\), problem \({\textsf {gapSIVP}}_{\gamma }\) is in SZK.
Corollary 4.2
For any factor \(\gamma (n) = \omega (n \log n)\), if there exists a probabilistic polynomial-time adaptive reduction from a language L to \({\textsf {SIVP}}_{\gamma }\), then \({\textsf {L}} \in \mathbf{AM } \cap \mathbf{coAM }\).
The proof of Theorem 4.1 is the combination of Lemmas 4.3, 4.4 and 4.5. Problem \({\textsf {gapSIVP}}_{\gamma }\) is in \(\mathbf{SZK }\) and there is a reduction from language \({\textsf {L}}\) to search problem \({\textsf {SIVP}}_{\sqrt{n \ln n} \cdot \gamma }\). Lemma 4.3 shows that there is another reduction from \({\textsf {L}}\) to sampling problem  for any s satisfying
for any s satisfying
Lemma 4.5 shows that there exists a function s satisfying (3) such that the sampling problem  is probability-verifiable. Therefore, there exists a reduction from \({\textsf {L}}\) to a probability-verifiable sampling problem. Finally, Lemma 4.4 shows that such a language \({\textsf {L}}\) must live in \(\mathbf{AM } \cap \mathbf{coAM }\).
is probability-verifiable. Therefore, there exists a reduction from \({\textsf {L}}\) to a probability-verifiable sampling problem. Finally, Lemma 4.4 shows that such a language \({\textsf {L}}\) must live in \(\mathbf{AM } \cap \mathbf{coAM }\).
Lemma 4.3
Let \(s(\cdot )\) be a function mapping lattice bases to real numbers, such that \(\forall \mathbf {B}, \lambda _n(\mathbf {B}) \le s(\mathbf {B}) \le \frac{\gamma }{\sqrt{n}} \lambda _n(\mathbf {B})\). Then there exists a probabilistic Turing reduction from \({\textsf {SIVP}}_{\gamma }\) to  .
.
Lemma 4.4
If there exists a probabilistic Turing reduction from a promise problem \({\textsf {L}} = ({\textsf {L}}_Y, {\textsf {L}}_N)\) to probability-verifiable sampling problems, then \({\textsf {L}} \in \mathbf{AM } \cap \mathbf{coAM }\).
Lemma 4.5
For any factor \(\gamma : {\mathbb {N}}\rightarrow \mathbb R\), if \({\textsf {gapSIVP}}_{\gamma (n)/\sqrt{\ln n}} \in \mathbf{SZK }\), then there exists a function \(s(\cdot )\) mapping lattice bases to real numbers, such that \(\forall \mathbf {B}, s(\mathbf {B}) \in [\lambda _n(\mathbf {B}), \gamma (n) \cdot \lambda _n(\mathbf {B})]\) and  is probability-verifiable.
is probability-verifiable.
By combining Lemmas 4.4, 4.5 and [PV08], we can also show that discrete Gaussian sampling with width \(\tilde{O}(\sqrt{n})\cdot \lambda _n\) is not NP-hard unless the polynomial hierarchy collapses.
Theorem 4.6
If there exists a probabilistic Turing reduction from a promise problem \({\textsf {L}}\) to  for \(s(\mathbf {B})=\omega (\sqrt{n} \log n) \cdot \lambda _n(\mathbf {B})\), then \({\textsf {L}} \in \mathbf{AM } \cap \mathbf{coAM }\).
for \(s(\mathbf {B})=\omega (\sqrt{n} \log n) \cdot \lambda _n(\mathbf {B})\), then \({\textsf {L}} \in \mathbf{AM } \cap \mathbf{coAM }\).
4.1 From Search SIVP to Discrete Gaussian Sampling
This section proves Lemma 4.3, which is essentially Lemma 3.17 in Regev’s work [Reg09]. Informally speaking, Regev shows a reduction from \({\textsf {SIVP}}_\gamma \) to  for \(\gamma = \varOmega (\sqrt{n\log n})\); Lemma 4.3 uses similar technique to construct a reduction from \({\textsf {SIVP}}_\gamma \) to
for \(\gamma = \varOmega (\sqrt{n\log n})\); Lemma 4.3 uses similar technique to construct a reduction from \({\textsf {SIVP}}_\gamma \) to  for \(\gamma = \varOmega (\sqrt{n})\).
for \(\gamma = \varOmega (\sqrt{n})\).
The reduction from \({\textsf {SIVP}}_\gamma \) to discrete Gaussian sampling is straightforward: Sample \(n^2\) times from discrete Gaussian distribution of width \(s \in [\lambda _n, \frac{\gamma }{\sqrt{n}} \lambda _n]\). The sampled vectors contain n short, linearly independent vectors with probability exponentially close to 1.
In order to prove Lemma 4.3, we shows that if \(n^2\) vectors are sampled from discrete Gaussian \(\mathcal N_{\mathcal L(\mathbf {B}), s(\mathbf {B})}\), the following two “bad events” occurs with probability exponentially small.
-
One of the sampled vectors is too long, its Euclidean norm is larger than \(\gamma \lambda _n(\mathbf {B})\).
-
The sampled vectors are not full rank.
Lemma 2.2 bounds the probability that an overlong vector is sampled from a discrete Gaussian distribution. Let the constant c in formula (2) equals 1,

As \(\gamma (n) \cdot \lambda _n(\mathbf {B}) \ge \sqrt{n} \cdot s(\mathbf {B})\),

which is exponentially small.
To prove that the \(n^2\) sampled vectors span the whole space, we need a lower bound on the probability a newly sampled vector is linear independent from the previous ones. Lemma 4.7 shows such a lower bound, improves [Reg09, Lemma 3.15] by a factor of \(\sqrt{\ln n}\) (the so-called smoothing parameter).
Lemma 4.7
For any n-dimensional lattice \(\mathcal L\), real number \(s \ge \lambda _n(\mathcal L)\) and for any proper linear subspace \(\mathcal V \subsetneq {\mathbb {R}}^n\), the probability \(\Pr _{\mathbf {v}\leftarrow \mathcal N_{\mathcal L, s}} [\mathbf {v}\not \in \mathcal V]\) is at least 1 / 20.
Proof
By the definition of successive minimum, there exists \(\mathbf {u}\in \mathcal L \setminus \mathcal V\) such that \(\Vert \mathbf {u}\Vert \le \lambda _n(\mathcal L)\). Let \(\mathcal L'\) denote \(\mathcal L \cap \mathcal V\). As \(\mathcal L\) is closed under addition, \(\mathcal L' + \mathbf {u}, \mathcal L' - \mathbf {u}\) are subsets of \(\mathcal L\). Moreover, as \(\mathcal V\) is closed under addition and \(\mathbf {u}\notin \mathcal V\), the sets \(\mathcal L' + \mathbf {u}, \mathcal L', \mathcal L' - \mathbf {u}\) are disjointed.

As \(\Vert \mathbf {u}\Vert \le \lambda _n(\mathcal L) \le s\), for any vector \(\mathbf {v}\)
Thus

\(\square \)
Assume k vectors has been sampled from \(\mathcal N_{\mathcal L(\mathbf {B}), s(\mathbf {B})}\) and their dimension is strictly less than n. By Lemma 4.7, the next n sampled vectors contain a vector linearly independent from the first k with probability exponentially close to 1. By union bound, \(n^2\) samples from \(\mathcal N_{\mathcal L(\mathbf {B}), s(\mathbf {B})}\) contains n linearly independent vectors with probability exponentially close to 1.
4.2 Probability-Verifiable Sampling Problem and NP-hardness
This section proves Lemma 4.4, which is a generalization of [BB15], the proof techniques are similar.
Let \(\mathcal M\) be the reduction from a promise problem \({\textsf {L}}=({\textsf {L}}_Y,{\textsf {L}}_N)\) to \(\mathcal S\). For a given input x, we want to distinguish between \(\Pr [\mathcal M^{\mathcal S}(x) \rightarrow 1] \ge 8/9\) and \(\Pr [\mathcal M^{\mathcal S}(x) \rightarrow 1] \le 1/9\) in AM. Notice that the randomness includes the random tape of \(\mathcal M\) and the randomness \(\mathcal S\) used to answer each query.
A transcript of an execution of \(\mathcal M^{\mathcal S}(x)\) is an tuple \((r,\mathsf {pd}_1,v_1,\mathsf {pd}_2,v_2,\ldots ,\mathsf {pd}_T,v_T)\) consists of the random tape of \(\mathcal M\), all queries to \(\mathcal S\) and the correlated answers. The transcript fully determined the execution \(\mathcal M^{\mathcal S}(x)\), and
In the proof, we construct an AM protocol that estimates this sum.
Proof of Lemma 4.4 . It’s sufficient to show that \({\textsf {L}} = ({\textsf {L}}_Y,{\textsf {L}}_N) \in \mathbf{AM }\). Then the same argument would shows \(\bar{{\textsf {L}}} = ({\textsf {L}}_N, {\textsf {L}}_Y) \in \mathbf{AM }\), which implies \({\textsf {L}} \in \mathbf{coAM }\).
L can be efficiently reduced to a probability-verifiable sampling problem. Let \(\mathcal S\) denote a correlated sampling oracle. The reduction is a probability polynomial-time oracle algorithm \(\mathcal M\) such that
The probability is over the random tape of \(\mathcal M\) and the randomness used by \(\mathcal S\). Without loss of generality, assume there exists \(T = \mathop {{\text {poly}}}(n)\) that \(\mathcal M\) uses T bits of randomness and makes T queries on any input \(x\in \{0,1\}^n\).
Define a transcript of an execution \(\mathcal M^{\mathcal S}(x)\) as a tuple \((r,\mathsf {pd}_1,v_1, \mathsf {pd}_2,v_2, \ldots , \mathsf {pd}_T,v_T)\) where \(r\in \{0,1\}^T\) is the random tape of \(\mathcal M\), \(\mathsf {pd}_t\) is the t-th query to sampling oracle \(\mathcal S\) and \(v_t\) is the t-th sample returned by \(\mathcal S\). The length of \(v_t\) is bounded by some polynomial of n, let \(\ell (n)\) be a polynomial that upper bound \(|v_t|\).
Note that the input, the random tape and oracle’s answers fully determine the reduction. Given the input and random tape, the reduction’s first query is predictable; given the input, random tape and the oracle’s previous answers, the reduction’s next query is predictable. Therefore, we define a transcript \(\sigma = (r,\mathsf {pd}_1,v_1, \mathsf {pd}_2,v_2, \ldots , \mathsf {pd}_T,v_T)\) to be valid, if it’s potentially a transcript of an execution \(\mathcal M^{\mathcal S}(x)\), i.e. if for all \(1\le t\le T\), \(\mathsf {pd}_t\) would the t-th query in execution \(\mathcal M^{\mathcal S}(x)\) when r is the random tape and \(v_1,\ldots ,v_{t-1}\) is the oracle’s previous answers. By this definition, \(\sigma \) is a valid transcript doesn’t implies \(v_t\) has non-zero probability under distribution \(\mathsf {pd}_t\). Let C(x) denote the set of all valid transcripts of \(\mathcal M^{\mathcal S}(x)\).
The transcript also determines the output of the reduction. Define a transcript \(\sigma \) to be accepting, if \(\sigma \) is valid and the corresponding execution \(\mathcal M^{\mathcal S}(x)\) output 1. Let \(C_1(x)\) denote the set of all accepting transcripts of \(\mathcal M^{\mathcal S}(x)\).
Let \(P_x(\sigma )\) denote the probability that \(\sigma \) is the transcript of \(\mathcal M^{\mathcal S}(x)\) when the random tape is uniformly chosen and \(\mathcal S\) is an ideal sampling oracle. Then by chain rule,
for any valid transcript \(\sigma = (r,\mathsf {pd}_1,v_1, \mathsf {pd}_2,v_2, \ldots , \mathsf {pd}_T,v_T)\). For any input x, we know \(C_1(x) \subseteq C(x)\),
by the definition of valid/accepting transcripts. Thus, by condition (4), to distinguish between \(x \in {\textsf {L}}_Y\) and \(x \in {\textsf {L}}_N\), it’s sufficient to distinguish between \(\sum _{\sigma \in C_1(x)} P_x(\sigma ) \ge 8/9\) and \(\sum _{\sigma \in C_1(x)} P_x(\sigma ) \le 1/9\).
Define D(x) as the set of all tuple \((\sigma , k)\) such that \(\sigma = (r,\mathsf {pd}_1,v_1, \mathsf {pd}_2,v_2, \ldots , \mathsf {pd}_T,v_T) \in C_1(x)\), and k is an integer that
where \(K = 10 \cdot 2^{T} \cdot 2^{T(\ell +1)}\). Then the size of D(x) is roughly \(K \cdot \Pr [\mathcal M^{\mathcal S}(x) \rightarrow 1]\) if K is sufficiently large.
The sampling problem is probability-verifiable. By definition, there exists a family of error function \(\{\eta _{\mathsf {pd},m}\}\) such that for any \(\mathsf {pd},m\), the error function \(\eta _{\mathsf {pd},m}:\{0,1\}^* \rightarrow [0,+\infty )\) satisfies \(\sum _v \eta _{\mathsf {pd},m}(v) \le 1\), and the promise problem
-
YES instances: \((\mathsf {pd},v,\hat{p},1^m)\) such that \(\hat{p} = \mathcal P_\mathsf {pd}(v)\)
-
NO instances: \((\mathsf {pd},v,\hat{p},1^m)\) such that \(\hat{p} \ge \mathcal P_\mathsf {pd}(v) + \frac{1}{m} \eta _{\mathsf {pd},m}(v)\)
is in AM. Let ProbLowerBound be the corresponding AM protocol.
Let set \(D'(x)\) consist of all tuple \((\sigma , k)\) such that \(\sigma = (r,\mathsf {pd}_1,v_1, \mathsf {pd}_2,v_2, \ldots , \mathsf {pd}_T,v_T) \in C_1(x)\), and k is an integer that
Here \(K = 10 \cdot 2^{T} \cdot 2^{T(\ell +1)}\) as in the definition of D(x). By definition, \(D(x) \subseteq D'(x)\).
Claim. The promise problem
-
YES instances: \((x,\sigma ,k)\) such that \((\sigma ,k) \in D(x)\)
-
NO instances: \((x,\sigma ,k)\) such that \((\sigma ,k) \notin D'(x)\)
is in AM.
Proof
TranscriptChecking is an AM protocol that solves this promise problem.

For \((\sigma ,k) \in D(x)\), an honest prover could convince the verifier that to accept \((x,\sigma ,k)\).
Any prover, even if it’s malicious, should send \(\hat{p}_t\) such that \(\hat{p}_t \le \mathcal P_{\mathsf {pd}_t}(v_t) + \frac{1}{10T} \eta _{\mathsf {pd}_t,10T}(v_t)\). Otherwise the prover will be caught in ProbLowerBound protocol with overwhelming probability. Thus no prover can make the verifier accept \((x,\sigma ,k)\) with high probability if \((\sigma ,k) \notin D'(x)\). \(\square \)
Claim. The size of D(x) is at least \(\frac{2}{3} K\) if \(x \in {\textsf {L}}_Y\).
Proof
\(x \in {\textsf {L}}_Y\) implies that \(\Pr [\mathcal M^{\mathcal S}(x) \rightarrow 1] \ge \frac{8}{9}\). Thus
\(\square \)
Claim. \(D'(x)\) has size at most \(\frac{1}{3} K\) if \(x \in {\textsf {L}}_N\).
Proof
\(x \in {\textsf {L}}_N\) implies that \(\Pr [\mathcal M^{\mathcal S}(x) \rightarrow 1] \le \frac{1}{9}\).
The second to last inequality symbol relies on the following inequality,
\(\square \)
Combining the claims above, \({\textsf {L}}\) can be reduced to the following promise problem
-
YES instances: x such that \(|D'(x)| \ge |D(x)| \ge \frac{2}{3}K\);
-
NO instances: x such that \(|D(x)| \le |D'(x)| \le \frac{1}{3}K\).
This promise problem can be solved in AM using the set lower bound protocol of Goldwasser and Sipser [GS86]. Thus \({\textsf {L}} \in \mathbf{AM }\).
4.3 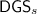 is Probability-Verifiable
is Probability-Verifiable
By Lemma 3.1, for any approximation factor \(\gamma \), if \({\textsf {gapSIVP}}_{\gamma /\mu } \in \mathbf{SZK }\) for any constant \(\mu > 1\), there exists a function g maps lattice bases to real numbers such that g is in \({\mathbb {R}}_\eta \)-TFAM and \(\lambda _n(\mathbf {B}) \le g(\mathbf {B}) < \gamma (n) \lambda _n(\mathbf {B})\).
For any basis \(\mathbf {B}\) and lattice point \(\mathbf {v}\in \mathcal L(\mathbf {B})\), as \(g \in {\mathbb {R}}_\eta -\mathbf{TFAM }\), the verifier can force the prover to provide a sufficiently accurate estimation of \(g(\mathbf {B})\), denoted by \(\hat{g}\). As \(\hat{g} \approx g(\mathbf {B}) \ge \lambda _n(\mathbf {B})\), the verifier can ask the prover to provide a set of linearly independent vectors \({\mathbf W} = (\mathbf {w}_1,\ldots ,\mathbf {w}_n)\) such that \(\Vert {\mathbf W}\Vert \le \hat{g}\). Here the length of a vector set, e.g. \(\Vert \mathbf W\Vert \), is defined as the length of the longest vector in the set.
Given such a short independent vector set \({\mathbf W}\), there exists an efficient algorithm that samples from discrete Gaussian distribution \(\mathcal N_{\mathcal L(\mathbf {B}), \hat{s}}\) such that \(\hat{s} = \varTheta (\sqrt{\log n}) \cdot \hat{g}\) [BLP+13, GPV08]. Moreover, the verifier can estimate the probability that \(\mathbf {v}\) is sampled from \(\mathcal N_{\mathcal L(\mathbf {B}), \hat{s}}\) using the set lower bound protocol.
Let \(s(\mathbf {B}) = \varTheta (\sqrt{\log n}) \cdot g(\mathbf {B})\), then \(\hat{s}\) is a good estimation of \(s(\mathbf {B})\). If the bias between \(\hat{s}\) and \(s(\mathbf {B})\) is sufficiently small, one could expect \(\Pr [\mathbf {v}\leftarrow \mathcal N_{\mathcal L(\mathbf {B}), \hat{s}}] \approx \Pr [\mathbf {v}\leftarrow \mathcal N_{\mathcal L(\mathbf {B}), s(\mathbf {B})}]\).
Proof (Lemma 4.5)
By Lemma 3.1, for sufficiently large n, \({\textsf {gapSIVP}}_{\gamma (n)/\sqrt{\ln n}} \in \mathbf{SZK }\) implies the existence of a function g maps lattice bases to real numbers such that g is in \({\mathbb {R}}_\eta \)-TFAM and \(g(\mathbf {B}) \in [\lambda _n(\mathbf {B}), \gamma (n)/\sqrt{\ln (2n+4)/\pi } \cdot \lambda _n(\mathbf {B})]\). Here \(n\ge 2\) is sufficiently large, as it implies \(\frac{\gamma (n)/\sqrt{\ln (2n+4)/\pi }}{\gamma (n)/\sqrt{\ln n}} \ge 1.01\).
Define \(s(\mathbf {B}) = \sqrt{\ln (2n+4)/\pi } \cdot g(\mathbf {B})\), thus for sufficiently large n
Given any basis \(\mathbf {B}\), vector \(\mathbf {v}\in \mathcal L(\mathbf {B})\) and precision parameter m, the verifier can learn a good estimation on \(g(\mathbf {B})\), denoted by \(\hat{g}\). As \(g(\mathbf {B}) \ge \lambda _n(\mathbf {B})\), the verifier could ask the prover to provide a set of linearly independent vectors of \(\mathcal L(\mathbf {B})\), denoted by \(\mathbf W\), such that \(\Vert \mathbf W\Vert \le \hat{g}\).
Given a set of linearly independent vectors \({\mathbf W}\) that \(\Vert \mathbf W\Vert \le \hat{g}\), there is an efficient algorithm which samples from discrete Gaussian \(\mathcal N_{\mathcal L(\mathbf {B}),\sqrt{\ln (2n+4)/\pi } \cdot \hat{g}}\) [BLP+13]. Let \(\mathcal S\) denote this sampling algorithm. Let \(\hat{s} = \sqrt{\ln (2n+4)/\pi } \cdot \hat{g}\), then \(\hat{s}\) is a good approximation of \(s(\mathbf {B})\). Let r be the random tape in the sampling algorithm \(\mathcal S\), then
We could use the set lower bound protocol to lower bound this probability \(\Pr [\mathbf {v}\leftarrow \mathcal N_{\mathcal L(\mathbf {B}),\hat{s}}]\). Thus the promise problem
-
YES instances: \(({\mathbf W},\mathbf {v},\hat{s}, \hat{p},1^m)\) such that \(\mathbf {v}\in \mathcal L\), \(\Vert \tilde{\mathbf W}\Vert \le \frac{\hat{s}}{\sqrt{\ln (2n+4)/\pi }}\), \(\hat{p} = \Pr [\mathbf {v}\leftarrow \mathcal N_{\mathcal L(\mathbf {B}),\hat{s}}]\)
-
NO instances: \(({\mathbf W},\mathbf {v},\hat{s}, \hat{p},1^m)\) such that \(\hat{p} \ge (1+\frac{1}{m}) \Pr [\mathbf {v}\leftarrow \mathcal N_{\mathcal L(\mathbf {B}),\hat{s}}]\)
is in AM, as it can be solved by protocol ProbLowerBound.

To prove  is probability-verifiable, it is sufficient to show that ProbLowerBound is an AM protocol that estimates the probability \(\Pr [\mathbf {v}\leftarrow \mathcal N_{\mathcal L(\mathbf {B}),\hat{s}}]\) with high accuracy. The estimation error of ProbLowerBound has two sources: (a) the inaccuracy of the set lower bound protocol, which introduce an \(O(\frac{1}{m})\) multiplicative error; and (b) the inaccuracy when estimating \(s(\mathbf {B})\). Let \(\eta _{\mathbf {B}}(\mathbf {v})\) be the estimation error, the error term satisfies
is probability-verifiable, it is sufficient to show that ProbLowerBound is an AM protocol that estimates the probability \(\Pr [\mathbf {v}\leftarrow \mathcal N_{\mathcal L(\mathbf {B}),\hat{s}}]\) with high accuracy. The estimation error of ProbLowerBound has two sources: (a) the inaccuracy of the set lower bound protocol, which introduce an \(O(\frac{1}{m})\) multiplicative error; and (b) the inaccuracy when estimating \(s(\mathbf {B})\). Let \(\eta _{\mathbf {B}}(\mathbf {v})\) be the estimation error, the error term satisfies
To complete the proof, it is sufficient to show that \(\sum _{\mathbf {v}\in \mathcal L(\mathbf {B})}\eta _{\mathbf {B}}(\mathbf {v}) = O(\frac{1}{m})\). By summing (5) over \(\mathbf {v}\in \mathcal L(\mathbf {B})\),
Thus it is sufficient to show
Which is proved as
The last inequality is due to Lemma 2.1. \(\square \)
Notes
- 1.
The length of a vector set is defined as the length of the longest vector in the set.
References
Akavia, A., Goldreich, O., Goldwasser, S., Moshkovitz, D.: On basing one-way functions on NP-hardness. In: Kleinberg, J.M. (ed.) Proceedings of the 38th Annual ACM Symposium on Theory of Computing, 21–23 May 2006, Seattle, WA, USA, pp. 701–710. ACM (2006)
Ajtai, M.: Generating hard instances of lattice problems (extended abstract). In: Miller, G.L. (ed.) Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, 22–24 May 1996, Philadelphia, Pennsylvania, USA, pp. 99–108. ACM (1996)
Aharonov, D., Regev, O.: Lattice problems in NP \(\cap \) coNP. In: Proceedings of 45th Symposium on Foundations of Computer Science, FOCS 2004, 17–19 October 2004, Rome, Italy [DBL04], pp. 362–371 (2004)
Banaszczyk, W.: New bounds in some transference theorems in the geometry of numbers. Math. Ann. 296(1), 625–635 (1993)
Bogdanov, A., Brzuska, C.: On basing size-verifiable one-way functions on NP-hardness. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 1–6. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_1
Bogdanov, A., Lee, C.H.: Limits of provable security for homomorphic encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 111–128. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_7
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) Symposium on Theory of Computing Conference, STOC 2013, 1–4 June 2013, Palo Alto, CA, USA, pp. 575–584. ACM (2013)
Brassard, G.: Relativized cryptography. In: 20th Annual Symposium on Foundations of Computer Science, 29–31 October 1979, San Juan, Puerto Rico, pp. 383–391. IEEE Computer Society (1979)
Blömer, J., Seifert, J.P.: On the complexity of computing short linearly independent vectors and short bases in a lattice. In: Vitter, J.S., Larmore, L.L., Leighton, F.T (eds.) Proceedings of the Thirty-First Annual ACM Symposium on Theory of Computing, 1–4 May 1999, Atlanta, Georgia, USA, pp. 711–720. ACM (1999)
Bogdanov, A., Trevisan, L.: On worst-case to average-case reductions for NP problems. SIAM J. Comput. 36(4), 1119–1159 (2006)
In: Proceedings of 45th Symposium on Foundations of Computer Science, FOCS 2004, 17–19 October 2004, Rome, Italy. IEEE Computer Society (2004)
Feigenbaum, J., Fortnow, L.: On the random-self-reducibility of complete sets. In: Proceedings of the Sixth Annual Structure in Complexity Theory Conference, 30 June–3 July 1991, Chicago, Illinois, USA, pp. 124–132. IEEE Computer Society (1991)
Goldreich, O., Goldwasser, S.: On the possibility of basing cryptography on the assumption that \(P \ne NP\). IACR Cryptol. Eprint Arch. 1998, 5 (1998)
Goldreich, O., Goldwasser, S.: On the limits of nonapproximability of lattice problems. J. Comput. Syst. Sci. 60(3), 540–563 (2000)
Guruswami, V., Micciancio, D., Regev, O.: The complexity of the covering radius problem on lattices and codes. In: 19th Annual IEEE Conference on Computational Complexity, CCC 2004, 21–24 June 2004, Amherst, MA, USA, pp. 161–173. IEEE Computer Society (2004)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Dwork, C. (ed.) Proceedings of the 40th Annual ACM Symposium on Theory of Computing, 17–20 May 2008, Victoria, British Columbia, Canada, pp. 197–206. ACM (2008)
Goldwasser, S., Sipser, M.: Private coins versus public coins in interactive proof systems. In: Proceedings of the Eighteenth Annual ACM Symposium on Theory of Computing, pp. 59–68. ACM (1986)
Goldreich, O., Vadhan, S.: Comparing entropies in statistical zero knowledge with applications to the structure of SZK. In: Proceedings of Fourteenth Annual IEEE Conference on Computational Complexity, pp. 54–73. IEEE (1999)
Liu, T., Vaikuntanathan, V.: On basing private information retrieval on NP-hardness. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 372–386. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_16
Micciancio, D., Regev, O.: Worst-case to average-case reductions based on Gaussian measures. In: Proceedings of 45th Symposium on Foundations of Computer Science, FOCS 2004, 17–19 October 2004, Rome, Italy [DBL04], pp. 372–381 (2014)
Micciancio, D., Vadhan, S.P.: Statistical Zero-knowledge proofs with efficient provers: lattice problems and more. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 282–298. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_17
Mahmoody, M., Xiao, D.: On the power of randomized reductions and the checkability of SAT. In: 2010 IEEE 25th Annual Conference on Computational Complexity (CCC), pp. 64–75. IEEE (2010)
Peikert, C., Vaikuntanathan, V.: Noninteractive statistical zero-knowledge proofs for lattice problems. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 536–553. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_30
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. J. ACM 56(6), 34:1–34:40 (2009)
Acknowledgments
I am grateful to my advisor, Vinod Vaikuntanathan, for getting me started on the topic of NP-hardness and separations. I am indebted to Adam Sealfon, Prashant Nalini Vasudevan, Srinivasan Raghuraman and Akshay Degwekar for their extensive help with the writing of this article. I would like to thank the anonymous reviewers for their careful reading and insightful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Liu, T. (2018). On Basing Search SIVP on NP-Hardness. In: Beimel, A., Dziembowski, S. (eds) Theory of Cryptography. TCC 2018. Lecture Notes in Computer Science(), vol 11239. Springer, Cham. https://doi.org/10.1007/978-3-030-03807-6_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-03807-6_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03806-9
Online ISBN: 978-3-030-03807-6
eBook Packages: Computer ScienceComputer Science (R0)





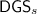 is Probability-Verifiable
is Probability-Verifiable