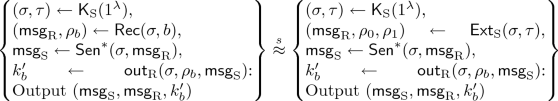Abstract
We continue the study of protocols for secure multiparty computation (MPC) that require only two rounds of interaction. The recent works of Garg and Srinivasan (Eurocrypt 2018) and Benhamouda and Lin (Eurocrypt 2018) essentially settle the question by showing that such protocols are implied by the minimal assumption that a two-round oblivious transfer (OT) protocol exists. However, these protocols inherently make a non-black-box use of the underlying OT protocol, which results in poor concrete efficiency. Moreover, no analogous result was known in the information-theoretic setting, or alternatively based on one-way functions, given an OT correlations setup or an honest majority.
Motivated by these limitations, we study the possibility of obtaining information-theoretic and “black-box” implementations of two-round MPC protocols. We obtain the following results:
-
Two-round MPC from OT correlations. Given an OT correlations setup, we get protocols that make a black-box use of a pseudorandom generator (PRG) and are secure against a malicious adversary corrupting an arbitrary number of parties. For a semi-honest adversary, we get similar information-theoretic protocols for branching programs.
-
New NIOT constructions. Towards realizing OT correlations, we extend the DDH-based non-interactive OT (NIOT) protocol of Bellare and Micali (Crypto’89) to the malicious security model, and present new NIOT constructions from the Quadratic Residuosity Assumption (QRA) and the Learning With Errors (LWE) assumption.
-
Two-round black-box MPC with strong PKI setup. Combining the two previous results, we get two-round MPC protocols that make a black-box use of any DDH-hard or QRA-hard group. The protocols can offer security against a malicious adversary, and require a PKI setup that depends on the number of parties and the size of computation, but not on the inputs or the identities of the participating parties.
-
Two-round honest-majority MPC from secure channels. Given secure point-to-point channels, we get protocols that make a black-box use of a pseudorandom generator (PRG), as well as information-theoretic protocols for branching programs. These protocols can tolerate a semi-honest adversary corrupting a strict minority of the parties, where in the information-theoretic case the complexity is exponential in the number of parties.
S. Garg—Research supported in part from 2017 AFOSR YIP Award, DARPA/ARL SAFEWARE Award W911NF15C0210, AFOSR Award FA9550-15-1-0274, and research grants by the Okawa Foundation, Visa Inc., and Center for Long-Term Cybersecurity (CLTC, UC Berkeley). The views expressed are those of the author and do not reflect the official policy or position of the funding agencies.
Y. Ishai—Supported by ERC grant 742754 (project NTSC), ISF grant 1709/14, NSF-BSF grant 2015782, and a grant from the Ministry of Science and Technology, Israel and Department of Science and Technology, Government of India.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Oblivious Transfer (OT)
- Learning With Errors (LWE)
- Information-theoretic Protocols
- Semi-honest Adversaries
- Garbled Circuit
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
There is an enormous body of work on the round complexity of protocols for secure multiparty computation (MPC). While the feasibility of constant-round MPC has been established a long time ago [Yao86, BB89, BMR90], some of the most basic questions about the exact number of rounds required for MPC remained wide open until recently.
A single round of interaction is clearly insufficient to realize the standard notion of MPC. The focus of this work is on MPC protocols that require only two rounds. Two-round MPC protocols are not only interesting because of the quantitative aspect of minimizing the number of rounds, but also because of the following qualitative advantage. In a two-round MPC protocol, a party can send its first round messages and then go offline until all second-round messages are received and the output can be computed. (In fact, for two-round protocols over insecure channels, the first round messages can be publicly posted.) Moreover, the first round messages can be potentially reused for several computations in which the receiver’s input remains the same. Indeed, in the two-party setting, such two-round protocols are sometimes referred to as “non-interactive secure computation” [IKO+11].
The state of the art on two-round MPC can be briefly summarized as follows. Unless otherwise specified, we restrict our attention to semi-honest adversaries, who may non-adaptively corrupt an arbitrary subset of parties, and allow the protocols to use a common random string.
In the information-theoretic setting, 2-round protocols over secure point-to-point channels are known to exist with \(t<n/3\) corrupted parties [IK00], leaving open the existence of similar protocols with an optimal threshold of \(t<n/2\). These information-theoretic protocols, like all current general constant-round protocols in the information-theoretic setting, have complexity that grows polynomially with n and with the branching program size of the function being computed, and thus can only efficiently apply to rich but limited function classes such as \(\mathsf {NC}^1\), \(\mathsf {NL}\), or other log-space classes.
Settling for computational security, the above information-theoretic protocols imply (via the multi-party garbling technique of [BMR90]) similar protocols for circuits, capturing all polynomial-time computable functions, where the protocols only require a black-box use of any pseudorandom generator (PRG), or equivalently a one-way function. In this setting too, it was open whether the optimalFootnote 1 threshold of \(t<n/2\) can be achieved.
Under stronger cryptographic assumptions, a lot of recent progress has been made on two-round MPC protocols that tolerate an arbitrary number of corrupted parties. The first such protocols required a public-key infrastructure (PKI) setup, where each party can post a public key before its input is known, and were based on the Learning With Errors (LWE) assumption via threshold fully homomorphic encryption [AJW11]. This was followed by protocols without PKI setup, first under indistinguishability obfuscation [GGHR14] or witness encryption [GLS15], and later under LWE via multi-key fully homomorphic encryption [MW16] or spooky encryption [DHRW16]. Using PKI setup, two-round protocols could also be constructed under the Decisional Diffie-Hellman (DDH) assumption via homomorphic secret sharing [BGI17, BGI+18].
In recent works, a new general technique for collapsing rounds via “protocol garbling” [GS17] has been used by Garg and Srinivasan [GS18] and Benhamouda and Lin [BL18] to settle the minimal assumptions required for two-round MPC. These works show that general two-round MPC can be based on any two-round protocol for oblivious transfer (OT) [Rab81, EGL85], namely a protocol allowing a receiver to obtain only one of two bits held by a sender without revealing the identity of the chosen bit. This assumption is clearly necessary, since two-round OT is an instance of two-round general MPC.
Remaining Challenges. Despite apparently settling the problem of two-round MPC, many challenges still remain. First and foremost, the recent OT-based protocols from [GS18, BL18] inherently make a non-black-box use of the underlying OT protocol. This results in poor concrete efficiency, which is unfortunate given the appealing features of two-round MPC discussed above. Second, the recent results leave open the possibility of obtaining information-theoretic security, or alternatively, computational security using symmetric cryptography, in other natural settings. These include protocols for the case of an honest majority (\(t<n/2\)) using secure point-to-point channels,Footnote 2 or alternatively protocols for dishonest majority based on an ideal OT oracle. Finally, the two-round MPC protocols from [GS18, BL18] did not seem to apply to the more general client-server setting, where only clients hold inputs and receive outputs, and communication only involves messages from clients to servers and from servers to clients.Footnote 3
1.1 Our Contribution
In this work we address the above challenges, focusing mainly on the goal of constructing information-theoretic and “black-box” implementations of two-round MPC protocols. We obtain the following results:
Two-Round MPC from OT Correlations. We start by studying two-round MPC using an OT correlations setup, which can be viewed as a minimalFootnote 4 setup for MPC with no honest majority under assumptions that are weaker than OT. An OT correlation setup allows each pair of parties to share many independent instances of correlated randomness where party \(P_i\) gets a pair of random bits (or strings) \((s_0,s_1)\) and party \(P_j\) gets a random bit b and the bit \(s_b\). Using such an OT correlations setup, we get protocols that make a black-box use of a PRG and are secure against either a semi-honestFootnote 5 or malicious adversary corrupting an arbitrary number of parties. For a semi-honest adversary, we get similar information-theoretic protocols for branching programs.
This OT correlation setup can be implemented with good concrete efficiency via OT extension [IKNP03], requiring roughly 128 bits of communication per string-OT. Alternatively, the communication complexity of the setup can be made independent of the circuit size (at a much higher computational cost) by using homomorphic secret sharing based on LWE, DDH, or DCRA [BGI16, DHRW16, FGJI17, BCG+17]. Finally, a fully non-interactive option for implementing the OT correlation setup is discussed next.
New NIOT Constructions. An appealing method of realizing the OT correlation setup is via non-interactive OT (NIOT) [BM90]. An NIOT protocol is the OT analogue of non-interactive key exchange: it allows two parties to obtain a joint OT correlation via a simultaneous message exchange. We present several new constructions of NIOT. First, we extend the DDH-based construction from [BM90] to the malicious security model, improving over an earlier construction based on bilinear maps from [GS17]. Second, we present new NIOT constructions from the Quadratic Residuosity Assumption (QRA) and from LWE.
Two-Round Black-Box MPC with Strong PKI Setup. Combining the protocols based on OT correlations and the NIOT constructions, we get two-round MPC protocols that make a black-box use of any DDH-hard or QRA-hard group. The protocols can offer security against a malicious adversary, and require a strong PKI setup that depends on the number of parties and the size of computation, but not on the inputs or the identity of the participating parties. This is arguably the first “black box” two-round MPC protocol that does not rely on an honest majority or a correlated randomness setup. Our DDH-based protocol can be compared with previous DDH-based two-round MPC protocols from [BGI+18] that require a weaker PKI setup and have better asymptotic communication complexity, but make a non-black-box use of the underlying group except when there are n clients and 2 servers.
Two-Round Honest-Majority MPC from Secure Channels. Given secure point-to-point channels, we get protocols that make a black-box use of a PRG, as well as information-theoretic protocols for branching programs. These protocols can tolerate a semi-honest adversary corrupting a strict minority of the parties, where in the information-theoretic case the complexity of the protocol grows exponentially with the number of parties. Our work leaves open the question of eliminating this slightly super-polynomial dependence as well as the question of obtaining similar results for malicious adversaries. This question has been resolved in the concurrent and independent work of Applebaum, Brakerski and Tsabary [ABT18].
From Standard MPC to Client-Server MPC. Finally, we present a general (non-black-box) transformation that allows converting previous two-round MPC protocols (including the recent OT-based protocols from [GS18, BL18]) to the stronger client-server model. Concretely, we use a PRG to transform any n-party, two-round, MPC protocol with security against semi-honest adversaries corrupting an arbitrary subset of parties to a similar protocol with n clients and m servers, where in the first round each client sends a message to each server and in the second round each server sends a message to each client. The resulting protocol is secure against a semi-honest adversary that corrupts an arbitrary subset of clients and a strict subset of the servers. This setting is particularly appealing when clients would like to be offline except when their input changes or they would like to receive an output.
1.2 Overview of Techniques
In this subsection, we describe the main techniques used to obtain our results.
-
1.
We start with a high-level overview of the OT correlations model and describe the technical challenges in constructing a non-interactive OT protocol.
-
2.
Later, we will show how to use OT correlations to make the compiler of Garg and Srinivasan [GS18] information theoretic. This gives efficient, two-round protocols in the OT correlations model with information theoretic security for branching programs and computational security for circuits making black-box use of a pseudorandom generator.
-
3.
We then explain the main ideas in constructing a two-round, protocol in the honest majority setting with secure point-to-point channels.
OT Correlations Model. The OT correlation is modeled by a two-party ideal functionality. When this functionality is invoked by a (sender, receiver) pair, it samples three bits \((s_0,s_1)\) and b uniformly at random and provides \((s_0,s_1)\) to the sender and \((b,s_b)\) to the receiver. For simplicity, we focus only for the case where sender’s output \((s_0,s_1)\) are bits as there are perfect, round-preserving reductions from bit OT correlations to string OT correlations (refer [BCS96, BCW03]). Given such OT correlations, there is an information theoretic, two-round OT protocol as follows. In the first round, the receiver sends \(u = b \oplus c\) to the sender where c is the choice bit and in the second round, the sender computes \((x_0,x_1) = (m_0 \oplus s_{u},m_1 \oplus s_{1 \oplus u})\) and sends them to the receiver. The receiver outputs \(x_c \oplus r_{b}\).
Bellare-Micali Non-interactive Oblivious Transfer. Bellare and Micali [BM90] gave an efficient, single-round protocol based on Decisional Diffie-Hellman (DDH) assumption [DH76] for computing OT correlations when the adversary corrupting either of the two parties is semi-honest. The protocol is in the common reference string model and is as follows. Let us assume that \(\mathbb {G}\) is a DDH hard group and g is a generator. The CRS is an uniform group element X. The sender chooses \(a \leftarrow \mathbb {Z}^*_{p}\) and sends \(A = g^a\) to the receiver. The receiver chooses a random \(b \leftarrow \mathbb {Z}^*_{p}\) and sends \((B_0,B_1) = (g^b,X/g^b)\) in a randomly permuted order. The sender computes \((B_0^a,B^a_1)\) and outputs it and the receiver computes \(A^b\) and outputs it. The receiver’s choice bit b is statistically hidden from an adversarial sender and the string \(s_{1-b}\) is computationally hidden from the receiver based on the DDH assumption. However, this protocol only works in the semi-honest model as there is no efficient way to extract the receiver’s choice bit or the sender’s correlations. In [GS17], Garg and Srinivasan additionally used Groth-Sahai proofs [GS08] to enable efficient extraction of the correlations from a malicious adversary but this construction relies on bilinear maps.
Our Construction of Non-interactive Oblivious Transfer. Our approach of constructing non-interactive oblivious transfer is via a generalization of the dual-mode framework introduced in the work of Peikert, Vaikuntanathan and Waters [PVW08]. In the dual mode framework, the common reference string can be in one of two indistinguishable modes: namely, the receiver extraction mode or the sender extraction mode. In the receiver extraction mode, the CRS trapdoor enables the simulator to extract the receiver’s correlation b and in the sender extraction mode, the it enables the simulator to extract the sender’s correlation \((s_0,s_1)\) from the malicious party. In either of the two modes, the secrets of the honest party are statistically hidden. We give efficient instantiations of this framework from DDH, Quadratic Residuocity assumption [GM82] and the Learning with Errors assumption [Reg05]. Our DDH and QR based constructions make black-box use of the underlying group. We stress that constructions of dual-mode cryptosystem in [PVW08] do not yield non-interactive oblivious transfer and we need to come up with new constructions. We refer the reader to Sect. 3.1 for the details.
Round-Collapsing Compiler in the OT Correlations Model. Independent works by Benhemouda and Lin [BL18] and Garg and Srinivasan [GS18] gave a “round-collapsing” compiler that takes an arbitrary multi-round MPC protocol and collapses it to two-rounds assuming the existence of a two-round oblivious transfer and garbled circuits. The compiler makes use of the code of the underlying protocol and thus, if the underlying protocol performs cryptographic operations then the resultant two-round protocol makes non-black box use of cryptography. In this work, we will use OT correlations to modify the compiler of [GS18] so that the resulting protocol makes black-box use of cryptography even if the underlying protocol performs cryptographic operations. Let us see how this is done.
We start by observing that OT correlations allow for perfect (resp., statistical) information-theoretic protocols in the presence of an arbitrary number of semi-honest (resp., malicious) corrupted parties. Hence, we will round-collapse, perfectly/statistically secure protocols that are in the OT-hybrid model (e.g., [GMW87, Kil88, IPS08]). We first give a reduction from perfectly/statistically secure protocols in the OT-hybrid model to a perfectly/statistically secure protocols in the OT correlations model. This reduction has a property that all the OT correlations are generated before the actual execution of the protocol and the operations performed in the protocol are information theoretic. Another useful property is that number of OT correlations needed depends only the number of parties and the size of the computation to be performed and in particular, is independent of the actual inputs. At a high level, this reduction relies on the fact that OT correlations can be used to perform information theoretic OTs. Now, given such a protocol in the OT correlations model, we modify the compiler of Garg and Srinivasan to have a pre-processing phase where all the OT correlations needed for the underlying protocol and those consumed by the round-collapsing compiler are generated. Later, these OT correlations are used to perform information theoretic OTs both in the underlying protocol and the round-collapsing compiler. Additionally, we also replace the garbled circuits used in the round-collapsing compiler with a perfectly secure analogue, namely a so-called “decomposable randomized encodings” for low-depth circuits [IK00, AIK04]. With these changes to the [GS18] compiler, we get a perfectly secure two-round protocol in the OT correlations model for constant size functions. Later, we use a result from [BGI+18] to bootstrap this to a perfectly secure, two-round protocol in the OT correlations model for \(\mathsf {NC}^0\) circuits. Two immediate corollaries of this result are a perfectly secure, two-round protocol in the OT correlations model for polynomial sized branching programs and a computationally secure, two-round protocol in the OT correlations model for arbitrary circuits making black-box use of a pseudorandom generator.
Two-Round Protocol in the Honest Majority Setting. To construct a two-round protocol in the plain model (with secure point-to-point channels) when the adversary corrupts a strict minority of the parties, we use the same high level idea of the [GS18] compiler. That is, we take a larger round protocol secure with honest majority and round-collapse it to two-rounds. Two immediate issues arise: (1) The first issue is that the round-collapsing compiler requires the existence of two-round oblivious transfer, (2) the second issue is that round-collapsing compiler could only compress protocols in the presence of a broadcast channels and fails for protocols with secure channels. To address the first issue, we construct a perfectly secure, two-round OT protocol in the presence of honest majority (building on the work of [IKP10]) and to address the second issue, we give a generalization of the [GS18] compiler to compress protocols that may require secure channels. We then use this OT protocol in parallel with the round-collapsing compiler of [GS18] (enhanced to work for protocols with secure channels) to obtain a two-round protocol in the honest majority setting. However, the resulting communication complexity of the protocol grows super-polynomially with the number of parties n. Still, for constant n, the protocol is efficient.
1.3 Organization
In Sect. 2, we will recall some standard definitions about secure computation and tools such as garbled circuits and decomposable randomized encoding. In Sect. 3, we define the OT correlations functionality and give various methods to realize it. In Sect. 4 we give the construction of 2-round semi-honest MPC in the OT correlations hybrid model. We point the reader to the full version of our paper for the other results.
2 Preliminaries
We recall some standard cryptographic definitions in this section. Let \(\lambda \) denote the security parameter. A function \(\mu (\cdot ): \mathbb {N} \rightarrow \mathbb {R}^+\) is said to be negligible if for any polynomial \(\mathsf {poly}(\cdot )\) there exists \(\lambda _0\) such that for all \(\lambda > \lambda _0\) we have \(\mu (\lambda ) < \frac{1}{\mathsf {poly}(\lambda )}\). We will use \(\mathsf {negl}(\cdot )\) to denote an unspecified negligible function and \(\mathsf {poly}(\cdot )\) to denote an unspecified polynomial function.
For a probabilistic algorithm A, we denote A(x; r) to be the output of A on input x with the content of the random tape being r. When r is omitted, A(x) denotes a distribution. For a finite set S, we denote \(x \leftarrow S\) as the process of sampling x uniformly from the set S. We will use PPT to denote Probabilistic Polynomial Time algorithm.
2.1 Decomposable Randomized Encoding
We recall the definitions of randomized encoding [Yao86, IK00, AIK04].
Definition 1
(Randomized Encoding). Let \(f: \{0,1\}^n \rightarrow \{0,1\}^m\) be some function. We say that a function \(\widehat{f} : \{0,1\}^n \times \{0,1\}^\rho \rightarrow \{0,1\}^{m}\) is a perfect randomized encoding of f if for every input \(x \in \{0,1\}\) , the distribution \(\widehat{f}(x;r)\) induced by an uniform choice of \(r{\mathop {\leftarrow }\limits ^{\$}}\{0,1\}^{\rho }\) , encodes the string f(x) in the following sense:
-
Correctness. There exists a decoding algorithm \(\mathsf {Dec}\) such that for every \(x \in \{0,1\}^n\), it holds that:
$$\begin{aligned} \mathop {\Pr }\limits _{r {\mathop {\leftarrow }\limits ^{\$}}\{0,1\}^\rho }[\mathsf {Dec}(\widehat{f}(x;r)) = f(x)] = 1 \end{aligned}$$ -
Privacy: There exists a randomized algorithm S such that for every \(x \in \{0,1\}^n\) and uniformly chosen \(r {\mathop {\leftarrow }\limits ^{\$}}\{0,1\}^\rho \) it holds that
$$\begin{aligned} S(f(x)) \text { is distributed identically to } \widehat{f}(x; r). \end{aligned}$$
Definition 2
(Decomposable Randomized Encoding). We say that \(\widehat{f}(x; r)\) is decomposable if \(\widehat{f}\) can be written as \(\widehat{f}(x; r) = ( \widehat{f}_0(r), \widehat{f}_1(x_1; r), \ldots , \widehat{f}_n(x_n; r))\) where \(\widehat{f}_i\) is chooses between two vectors based on \(x_i\) , i.e., it can be written as \(\mathbf {a}_{i,x_i}\) and \((\mathbf {a}_{i,0},\mathbf {a}_{i,1})\) arbitrarily depend on the randomness r. We will use \(\widehat{f}(;r)\) to denote \((\widehat{f}_0(r), (\mathbf {a}_{1,0},\mathbf {a}_{1,1}), \ldots , (\mathbf {a}_{n,0},\mathbf {a}_{n,1}))\).
We will recall the following two constructions of randomized encoding.
Lemma 1
([Kil88, IK00]). Let \(f : \{0,1\}^n \rightarrow \{0,1\}^m\) be a function computable in \(\mathsf {NC}^0\). Then f has a perfectly secure decomposable randomized encoding \(\widehat{f}\) where the size of the encoding is \(2^{O(d)}(n+m)\) where d is the depth of the circuit.
Lemma 2
([Yao86]). Let \(f: \{0,1\}^n \rightarrow \{0,1\}^m\) be a function computable by an arbitrary circuit. Assuming the existence of one-way functions, f has a computationally secure randomized encoding \(\widehat{f}\).
2.2 Universal Composability Framework
We work in the Universal Composition (UC) framework [Can01] to formalize and analyze the security of our protocols. (Our protocols can also be analyzed in the stand-alone setting, using the composability framework of [Can00], or in other UC-like frameworks, like that of [PW00].) We give the details in the full version. We only focus on static (non-adaptive) adversaries but we note that our perfectly secure protocols are also secure against adaptive adversaries.
3 OT Correlations Functionality
In this section, we define the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality in Fig. 1. Intuitively, the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality obtains a bit b from the receiver and samples two bits \((s_0,s_1)\) randomly from \(\{0,1\}\) and outputs \((s_0,s_1)\) to the sender and \(s_b\) to the receiver.Footnote 6 In the definition, we focus on the case where the sender’s output are just two bits \((s_0,s_1)\) instead of two strings as there are efficient reductions from 1-out-of-2 string OTs to 1-out-of-2 bit OTs using self-intersecting codes or randomness extractors [BCS96, BCW03]. By abusing notation, we will interchangeably use the same functionality to sample two strings instead of two bits.
We first discuss two generic ways from literature for realizing \(\mathcal {F}_{\mathrm {OTCor}}\) functionality and then give two new ways for realizing it.
OT Extension. We first note that any OT protocol can be used to realize \(\mathcal {F}_{\mathrm {OTCor}}\) functionality. A more efficient way would be to use an oblivious transfer extension protocol [Bea96, IKNP03, ALSZ13, ALSZ15, KOS15]. Any OT extension protocol with security against semi-honest/malicious adversaries can be used to realize the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality against semi-honest/malicious adversaries. The only downside of this approach is that it involves multiple rounds of interaction (which is inherent if we want to make black-box use of cryptography [GMMM18]).
Homomorphic Secret Sharing/Threshold FHE. A reusable and a non-interactive approach to realize the weaker formulation wherein the receiver’s choice bit is sampled randomly by the functionality is to use Homomorphic Secret Sharing (HSS) [BGI16, BGI17, BGI+18, BCG+17]. Using Homomorphic Secret Sharing, each party can generate a HSS encoding of a randomly chosen PRG seed and broadcasts this encoding to all other parties. When an OT correlation is to be generated, the parties (using the encodings) locally compute a functionality that expands the receiver’s and the sender’s PRG seed to the required length and samples the prescribed OT correlation from the expanded seeds. At the end of this local computation, the parties hold an additive secret sharing of the OT correlation and the actual correlation can be obtained non-interactively by sending these additive shares to the receiver. This approach is reusable as the encodings just needs to be sent once and can be resused to generate fresh correlations each time.Footnote 7 We also note that we can replace the above homomorphic secret sharing with any threshold FHE construction [MW16, DHRW16, BGG+18]. The downsides of using HSS or threshold FHE is that they make non-black box use of one-way functions in expanding the short seed to a pseudorandom string and they are computationally expensive when compared to the OT extension. Additionally, HSS requires the use of secure channels between every pairs of parties.
In Sect. 3.1, we describe a non-interactive approach to realize \(\mathcal {F}_{\mathrm {OTCor}}\). The advantage of this approach over HSS/threshold-FHE is that it makes black-box use of a groups where either DDH or QR is hard (we also provide an efficient construction from the LWE assumption). However, unlike HSS/threshold-FHE they are not reusable.
3.1 Realizing \(\mathcal {F}_{\mathrm {OTCor}}\): Non-interactive Oblivious Transfer
In this subsection, we define a Non-interactive Oblivious Transfer (NIOT) and show how to realize \(\mathcal {F}_{\mathrm {OTCor}}\) functionality from NIOT.
Definition. A Non-interactive Oblivious Transfer (NIOT) is a tuple of algorithms \((\mathsf {K}_{\text {R}},\mathsf {K}_{\text {S}},\mathsf {Sen},\mathsf {Rec},\mathsf {out}_{\text {S}},\mathsf {out}_{\text {R}})\) having the following syntax, correctness and security guarantees.
-
\(\mathsf {K}_{\text {R}}\) and \(\mathsf {K}_{\text {S}}\) are randomized algorithms that take as input the security parameter (encoded in unary) and output a common random string \(\sigma \) along with some trapdoor information \(\tau \).
-
\(\mathsf {Sen}\) is a randomized algorithm that takes \(\sigma \) as input and outputs \(\mathsf {msg}_{\text {S}}\) along with secret randomness \(\omega \).
-
\(\mathsf {Rec}\) is a randomized algorithm that takes \(\sigma \) and a bit b as input and outputs \(\mathsf {msg}_{\text {R}}\) along with secret randomness \(\rho _b\).
-
\(\mathsf {out}_{\text {S}}\) is a deterministic algorithm that takes as input \(\sigma \), \(\mathsf {msg}_{\text {R}}\) and the secret randomness \(\omega \) and outputs two bits \(k_0,k_1\).
-
\(\mathsf {out}_{\text {R}}\) is a deterministic algorithm that takes as \(\sigma \), \(\mathsf {msg}_{\text {S}}\) and the secret randomness \(\rho _b\) and outputs a bit \(k'_{b}\).
Correctness. We require that for all \(b \in \{0,1\}\),

Security. We require the following security properties to hold.
-
CRS Indistinguishability. We require that
$$\begin{aligned} \left\{ \sigma : (\sigma ,\tau ) \leftarrow \mathsf {K}_{\text {R}}(1^{\lambda }) \right\} {\mathop {\approx }\limits ^{c}}\left\{ \sigma : (\sigma ,\tau ) \leftarrow \mathsf {K}_{\text {S}}(1^{\lambda }) \right\} \end{aligned}$$ -
Sender Security. We require that there exists a PPT a lgorithm \(\mathsf {Ext}_{\text {R}}\) such that for all non-uniform PPT adversarial \(\mathsf {Rec}^*\) the following two distributions are statistically close.

-
Receiver Security. We require that there exists a PPT algrithm \(\mathsf {Ext}_{\text {S}}\) such that for all non-uniform PPT adversarial \(\mathsf {Sen}^*\) and for all \(b \in \{0,1\}\), the following two distributions are statistically close.
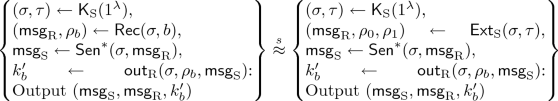
NIOT \(\Rightarrow \varvec{\mathcal {F}}_\mathbf{OTCor}\). In this subsection, we give a realization of the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality from any non-interactive oblivious transfer.
Theorem 1
Assuming the existence of non-interactive oblivious transfer, there is a single round protocol for realizing \(\mathcal {F}_{\mathrm {OTCor}}\) against malicious adversaries in the common reference string model.
Construction. We give a construction realizing the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality in Fig. 2.
Description of the Simulator. We assume that \(\mathcal {A}\) is static and hence the set of honest parties H is known before the execution of the protocol. Recall the properties of \(\mathsf {Ext}_{\text {R}}\) and \(\mathsf {Ext}_{\text {S}}\) from the definition of non-interactive oblivious transfer.
Simulating the CRS. For every \(i \in [n]\),
-
If \(P_i \in H\), sample \((\sigma _{i,j},\tau _{i,j}) \leftarrow \mathsf {K}_{\text {R}}(1^{\lambda })\) for every \(j \in [n] \setminus \{i\}\).
-
If \(P_i \not \in H\), sample \((\sigma _{i,j},\tau _{i,j}) \leftarrow \mathsf {K}_{\text {S}}(1^{\lambda })\) for every \(j \in [n] \setminus \{i\}\).
Publish \(\{\sigma _{i,j}\}_{i,j \in [n]}\) as the common reference string.
Simulating the Interaction with \(\mathcal {Z}\). For every input value for the set of corrupted parties that \(\mathsf {S}\) receives from \(\mathcal {Z}\), \(\mathsf {S}\) writes that value to \(\mathcal {A}\)’s input tape. Similarly, the output of \(\mathcal {A}\) is written as the output on \(\mathsf {S}\)’s output tape.
Simulating the Interaction with \(\mathcal {A}\). For every concurrent interaction with the session identifier sid that \(\mathcal {A}\) may start and for every choice of sender \(P_i\) and the receiver \(P_j\), the simulator does the following:
-
Both \(P_i,P_j \in H\):
-
1.
Compute \((\mathsf {msg}_{\text {S}},\omega ) \leftarrow \mathsf {Sen}(\sigma _{i,j})\) on behalf of \(P_i\) and send \(\mathsf {msg}_{\text {S}}\) to \(P_j\).
-
2.
Sample \(b \leftarrow \{0,1\}\) and compute \((\mathsf {msg}_{\text {R}},\rho _{b}) \leftarrow \mathsf {Rec}(\sigma _{i,j},b)\) on behalf of \(P_j\). Send \(\mathsf {msg}_{\text {R}}\) to \(P_i\).
-
1.
-
\(P_i \in H\) and \(P_j \not \in H\):
-
1.
Compute \((\mathsf {msg}_{\text {S}},\omega ) \leftarrow \mathsf {Sen}(\sigma _{i,j})\) on behalf of \(P_i\) and send \(\mathsf {msg}_{\text {S}}\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) outputs \(\mathsf {msg}_{\text {R}}\).
-
3.
Run \(b' \leftarrow \mathsf {Ext}_{\text {R}}(\sigma _{i,j},\tau _{i,j},\mathsf {msg}_{\text {R}})\).
-
4.
Compute \((s_0,s_1) := \mathsf {out}_{\text {S}}(\sigma _{i,j},\omega ,\mathsf {msg}_{\text {R}})\).
-
5.
Send \(s_{b'}\) to the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality and output whatever \(\mathcal {A}\) outputs.
-
1.
-
\(P_{i} \not \in H\) and \(P_j \in H\):
-
1.
Compute \((\mathsf {msg}_{\text {R}},\rho _0,\rho _1) \leftarrow \text {S}(\sigma _{i,j},\tau _{i,j})\) and send \(\mathsf {msg}_{\text {R}}\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) outputs \(\mathsf {msg}_{\text {S}}\).
-
3.
Compute \(s_b := \mathsf {out}_{\text {R}}(\sigma _{i,j},\rho _b,\mathsf {msg}_{\text {S}})\) for all \(b \in \{0,1\}\).
-
4.
Send \((s_0,s_1)\) to the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality and output whatever \(\mathcal {A}\) outputs.
-
1.
Lemma 3
Assuming the security of non-interactive oblivious transfer, for every \(\mathcal {Z}\) that obeys the rules of interaction for UC security we have \(\textsc {EXEC}_{\mathcal {F},\mathcal {S},\mathcal {Z}}{\mathop {\approx }\limits ^{c}}\textsc {EXEC}_{\pi ,\mathcal {A},\mathcal {Z}}\).
We prove this lemma in the full version.
NIOT from Quadratic Residuocity. In this section we present a construction of non-interactive oblivious transfer from the quadratic residuocity (QR) assumption. We will begin by reviewing the assumption, then describe the construction, and finally prove its correctness and security.
Notations. For a positive integer N, we use \(\mathcal {J}(N)\) to denote the set \(\{x \in \mathbb {Z}/N\mathbb {Z}: \left( \frac{x}{N}\right) =1\}\), where \(\left( \frac{x}{N}\right) \) is the Jacobi symbol of x in \(\mathbb {Z}/N\mathbb {Z}\). We use \(\mathcal {QR}(N)\) to denote the set of quadratic residues in \(\mathcal {J}(N)\). The security of our scheme is based on the following computational assumption.
Definition 3
(Quadratic Residuocity (QR) Assumption [GM82]). Let \(\mathsf {QRgen}(\cdot )\) be a PPT algorithm that generates two equal size primes p, q and \(N=pq\). The following two distributions are computationally indistinguishable:
In the construction and the proof of security, we make use of the notion IBE compatible algorithm proved in [BGH07].
Definition 4
([BGH07]). Let \(\mathcal {Q}\) be a deterministic algorithm that takes as input (N, S, R) where \(N \in \mathbb {Z}^+\) and \(R,S \in \mathbb {Z}/N\mathbb {Z}\). The algorithm outputs two polynomials \(f,g \in \mathbb {Z}/N\mathbb {Z}[x]\). We say that \(\mathcal {Q}\) is IBE-compatible if the following two conditions hold:
-
1.
(Condition 1) If S and R are quadratic residues then f(s)g(r) is a quadratic residue for all square roots r of R and s of S.
-
2.
(Condition 2) If S is a quadratic residue then \(f(s)f(-s)R\) is a quadratic residue for all square roots s of S.
Boneh et al. [BGH07] showed a concrete instantiation of such an IBE-compatible algorithm.
Theorem 2
Assuming the Quadratic Residuocity assumption, there exists a construction of non-interactive oblivious transfer.
The Construction. We give the construction of non-interactive oblivious transfer in Fig. 3.
Correctness. We start with the correctness proof. Notice that if \(b = 0\) then \(\mathsf {msg}_R\) is a quadratic residue and otherwise, \(u \cdot \mathsf {msg}_R\) is a quadratic residue. Let us first consider the case where \(\mathsf {msg}_R\) is a quadratic residue. In that case, Condition 1 in Lemma 4 implies that \(\left( \frac{f(s)}{N}\right) = \left( \frac{g(r)}{N}\right) \). Hence, \(k'_0 = k_0\). A similar argument can be used to show that if \(u \cdot \mathsf {msg}_R\) is a quadratic residue then \(k'_1= k_1\).
CRS Indistinguishability. The CRS indistinguishability property follows directly from quadratic residuocity assumption.
Sender Security. We first give the description of the extractor \(\mathsf {Ext}_{\text {R}}\). On input \(\mathsf {msg}_R\), the extractor uses the trapdoor \(\tau = (p,q)\) to check if \(\mathsf {msg}_R\) is a quadratic residue. It outputs \(b' = 0\) if it is the case and 1 otherwise. We now need to show that \(k_{1-b'}\) is statistically indistinguishable to random and this follows directly from the following lemma given in [BGH07].Footnote 8
Lemma 4
([BGH07]). Let \(N = pq\) be a QR modulus, \(X \in \mathcal {QR}(N)\) and \(R \not \in \mathcal {QR}(N)\). Let x be a random variable uniformly chosen among the four square roots of X. Let f be a polynomial such that \(f(x)f(-x)R\) is a quadratic residue for all four values of x. Then, \(\left( \frac{f(x)}{N}\right) \) is uniformly distributed in \(\{\pm 1\}\).
Proof
Some parts of the proof are taken verbatim from [BGH07]. Let \(x,x'\) be two square-roots of X such that \(x = x' \mod p\) and \(x = -x' \mod q\). Then, the four square roots of X are \(\{\pm x,\pm x'\}\). By definition, we have that \(\left( \frac{f(x)}{p}\right) = \left( \frac{f(x')}{p}\right) \) and \(\left( \frac{f(x')}{q}\right) = \left( \frac{f(-x)}{q}\right) \). Also, from the fact that \(f(x)f(-x)R\) is a quadratic residue, we have that \(\left( \frac{f(x)}{p}\right) \left( \frac{f(-x)}{p}\right) \left( \frac{R}{p}\right) = 1\) and \(\left( \frac{f(x)}{q}\right) \left( \frac{f(-x)}{q}\right) \left( \frac{R}{q}\right) = 1\). Since \(R \not \in \mathcal {QR}(N)\) either \(\left( \frac{R}{p}\right) = -1\) or \(\left( \frac{R}{q}\right) = -1\). We consider two cases:
-
Case-1: \(\left( \frac{R}{q}\right) = -1\). In this case, \(\left( \frac{f(x)}{q}\right) = -\left( \frac{f(-x)}{q}\right) = -\left( \frac{f(x')}{q}\right) \). Thus, \(\left( \frac{f(x)}{N}\right) = -\left( \frac{f(x')}{N}\right) \). Similarly, one can show that \(\left( \frac{f(-x)}{N}\right) = -1\left( \frac{f(-x')}{N}\right) \). Thus, among \(f(x),f(x'),f(-x),f(-x')\), the first two have different Jacobi symbols and the last two have different Jacobi symbols modulo N. Thus, \(\left( \frac{f(x)}{N}\right) \) is uniformly distributed over \(\{\pm 1\}\).
-
Case-2: \(\left( \frac{R}{p}\right) =-1\). In this case, \(\left( \frac{f(x)}{p}\right) = -\left( \frac{f(-x)}{p}\right) = -\left( \frac{f(-x')}{p}\right) \). Thus, \(\left( \frac{f(x)}{N}\right) = -\left( \frac{f(-x')}{N}\right) \). Similarly, one can show that \(\left( \frac{f(x')}{N}\right) = -\left( \frac{f(-x)}{N}\right) \). Thus, among \(f(x),f(-x'),f(-x),f(x')\), the first two have different Jacobi symbols and the last two have different Jacobi symbols modulo N. Thus, \(\left( \frac{f(x)}{N}\right) \) is uniformly distributed over \(\{\pm 1\}\).
Receiver Security. We first give the description of the extractor \(\mathsf {Ext}_{\text {S}}\). On input \(\sigma ,\tau \), it uses \(\tau \) to find the square root \(u'\) of u. It samples a random r and sets \(\mathsf {msg}_R = r^2u\), \(\rho _0 = ru'\) and \(\rho _1 = r\). It is easy to see that this extractor satisfies the receiver security definition.
4 Two-Round Semi-Honest MPC in the \(\mathcal {F}_{\mathrm {OTCor}}\) Model
In this section, we give our construction of two-round MPC against semi-honest adversaries in the \(\mathcal {F}_{\mathrm {OTCor}}\) model when the adversary is allowed to corrupt an arbitrary subset of the parties. The results we obtain against semi-honest adversaries are as follows (all our results are in the \(\mathcal {F}_{\mathrm {OTCor}}\) model):
-
1.
We first give a perfectly secure, two-round protocol for constant-size functionalities.
-
2.
Next, using s result in [BGI+18] and the protocol from Step 1, we will give a protocol with perfectly (resp. statistical) secure, two-round protocol for functionalities with perfect (resp. statistical) randomized encodings with constant degree. Following [AIK04], we will denote the class of functions with perfectly (resp. statistically) secure constant degree randomized encodings as \(\mathsf {PREN}\) (resp. \(\mathsf {SREN}\)). Applebaum et al. [AIK04] showed that some of the natural complexity classes such as \(\mathsf {NC}^1\) and mod-2 branching programs \(\oplus L/\mathsf {poly}\) are contained in \(\mathsf {PREN}\). A complexity class that is in \(\mathsf {SREN}\) but not known to be in \(\mathsf {PREN}\) is \(\mathsf {NL}\).
-
3.
Next, using the result in [BMR90] and the protocol from Step 1, we will give a protocol for all circuits making black-box use of a pseudorandom generator.
4.1 Protocols for Constant-Size Functionalities
For a constant n, let \(f: \{0,1\}^n \rightarrow \{0,1\}\) be a function with constant circuit size.Footnote 9 For each \(i \in [n]\), the party \(P_i\) has input bit \(x_i\) and the parties want to securely compute \(f(x_1,\ldots ,x_n)\).Footnote 10 We give perfectly secure, two-round protocols for computing f both in the dishonest majority setting in the \(\mathcal {F}_{\mathrm {OTCor}}\) hybrid model.
To construct a two-round protocol in the dishonest majority setting, we will use the same high level idea of Garg and Srinivasan [GS18]. To be more precise, we will take an arbitrary round protocol that securely computes the function f and compress it to two-rounds. However, to construct a perfectly secure protocol we will make the following changes to the round-collapsing compiler of [GS18],
-
1.
All the executions of two-round oblivious transfer used by the round-collapsing compiler in [GS18] are replaced with perfectly secure, two-round oblivious transfer from OT correlations.
-
2.
The garbled circuits used in [GS18] compiler are replaced with perfectly secure, decomposable randomized encodings for \(\mathsf {NC}^0\) circuits (cf. Definition 2).
-
3.
The underlying multi-round protocol that we want to round-compress might use cryptographic operations (which is necessary in the dishonest majority setting) and this creates the following two problems: (i) we can no longer argue perfect/statistical security, (ii) a subtle but a more important problem is that the compiler in [GS18] makes use of the code of the underlying protocol and hence if the underlying protocol involves cryptographic operations then the resultant two-round protocol makes non-black box use of cryptographic primitives. To solve the first problem, we will only round-compress perfect/statistical protocols in the OT-hybrid model (e.g., [GMW87, Kil88, IPS08]). Notice that any protocol in the OT-hybrid model can be reduced information theoretically to a protocol in the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality. To make the operations performed by all the parties information theoretic, we will generate OT correlations and make these correlations as part of the party’s input. For example, consider two parties \(P_1\) and \(P_2\) who wish to do an OT in some round of the underlying protocol. Now, \(P_1\) and \(P_2\) will use the OT correlations from their input to perform an information theoretic OT.
The rest of the subsection is organized as follows. We will first recall the notion of conforming protocols from [GS18]. Intuitively, conforming protocols are MPC protocols with some additional structure. [GS18] showed that any MPC protocol can be transformed to a conforming protocol (with some efficiency loss). We give a generalization of the notion of conforming protocols to work in \(\mathcal {F}_{\mathrm {OTCor}}\) model. Then, we will describe our construction of two-round MPC in the \(\mathcal {F}_{\mathrm {OTCor}}\) hybrid model.
Conforming Protocol. We will now recall the notion of conforming protocols from [GS18]. We introduce an additional parameter s such that in each round of the conforming protocol, a single party computes s NAND gates and broadcasts the output of these NAND gates to every party. We note that in the formulation of [GS18], the parameter s was set to 1. We introduce this parameter for better concrete efficiency.
Consider a n-party deterministicFootnote 11 MPC protocol \(\varPhi \) between parties \(P_1, \ldots , P_n\) with inputs \(x_1, \ldots , x_n\), respectively. For each \(i \in [n]\), we let \(x_i \in \{0,1\}^m\) denote the input of party \(P_i\) (\(x_i\)’s also include the randomness used in the protocol and hence they are m bits long). A conforming protocol \(\varPhi \) in the \(\mathcal {F}_{\mathrm {OTCor}}\) is defined by functions \(\mathsf {pre}\), \(\mathsf {post}\), and a OT correlations generation phase and computations steps or what we call actions \(\phi _1,\cdots \phi _T\). The protocol \(\varPhi \) proceeds in four stages: the OT correlations generation phase, the pre-processing stage, the computation stage and the output stage.
-
OT correlations generator: For every instance of the OT to be performed in the protocol, interact with the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality to generate OT correlations.
-
Pre-processing phase: For each \(i \in [n]\), party \(P_i\) computes
$$\begin{aligned} (z_i,v_i) \leftarrow \mathsf {pre}(i,x_i) \end{aligned}$$where \(\mathsf {pre}\) is a randomized algorithm and the input \(x_i\) is now augmented with the OT correlations generated in the previous step. The algorithm \(\mathsf {pre}\) takes as input the index i of the party, its input \(x_i\) and outputs \(z_i \in \{0,1\}^{\ell /n}\) and \(v_i \in \{0,1\}^\ell \) (where \(\ell \) is a parameter of the protocol). Finally, \(P_i\) retains \(v_i\) as the secret information and broadcasts \(z_i\) to every other party. We require that \(v_{i,k} = 0\) for all \(k \in [\ell ]\backslash \left\{ (i-1)\ell /n +1,\ldots , i\ell /n\right\} \).
-
Computation phase: For each \(i \in [n]\), party \(P_i\) sets
$$\begin{aligned} \mathsf {st}_i := (z_1 \Vert \cdots \Vert z_n). \end{aligned}$$Next, for each \(t \in \{1\cdots T\}\) parties proceed as follows:
-
1.
Parse action \( \phi _t\) as \((i,(a_1,b_1,c_1),\ldots ,(a_s,b_s,c_s))\) where \(i \in [n]\) and \(a_j,b_j,c_j \in [\ell ]\) for all \(j \in [s]\).
-
2.
Party \(P_{i}\) computes s \(\mathsf {NAND}\) gates as
$$\begin{aligned} \mathsf {st}_{i,c_j} = \mathsf {NAND}(\mathsf {st}_{i,a_j} \oplus v_{i,a_j} , \mathsf {st}_{i,b_j} \oplus v_{i,b_j}) \oplus v_{i,c_j} \end{aligned}$$for all \(j \in [s]\) and broadcasts \(\{\mathsf {st}_{i,c_j}\}_{j \in [s]}\) to every other party.
-
3.
Every party \(P_k\) for \(k \ne i\) updates \(\mathsf {st}_{k,c_j}\) for all \(j \in [s]\) to the bits received from \(P_i\).
We require that for all \(t, t' \in [T]\) such that \(t \ne t'\), if \(\phi _t = (\cdot ,(\cdot ,\cdot ,c_1),\ldots ,(\cdot ,\cdot ,c_s))\) and \(\phi _{t'} = (\cdot ,(\cdot ,\cdot ,c'_1),\ldots ,(\cdot ,\cdot ,c'_s))\) then \(\{c_j\} \cap \{c'_j\} = \varnothing \). We use \(A_i \subset [T]\) to denote the set of rounds in which the party \(P_i\) sends a message. Namely, \(A_i = \left\{ t \in T\mid \phi _t = (i, (\cdot ,\cdot ,\cdot ),\ldots ,(\cdot ,\cdot ,\cdot ))\right\} .\)
-
1.
-
Output phase: For each \(i \in [n]\), party \(P_i\) outputs \(\mathsf {post}(i,\mathsf {st}_i,v_i)\).
We now show the following lemma which is a generalization of the lemma proved in [GS18].
Lemma 5
For \(s = 1\), any MPC protocol \(\Pi \) in the OT hybrid model can be transformed into a conforming protocol \(\varPhi \) in the \(\mathcal {F}_{\mathrm {OTCor}}\) model while inheriting the correctness and the security of the original protocol. Furthermore, there exists a choice of s such that the number of rounds of the resulting conforming protocol is \(O(n \cdot d_{\max } \cdot r)\) where \(d_{\max }\) is the maximum depth of the boolean circuit computing the next message function of any party and r is the number of rounds of the original protocol \(\Pi \).
We prove the lemma in the full version.
Remark 1
We note that if the i-th party’s output is public then the algorithm \(\mathsf {post}\) need not take \(v_i\) as input.
Compiled Protocol. We describe the compiled protocol in Fig. 4 and give an informal overview below.
Overview. Our construction involves a pre-preprocessing phase followed by the two-rounds of interaction (described in Fig. 4) and a local evaluation phase (described below). In the pre-processing phase, the parties interact with the \(\mathcal {F}_{\mathrm {OTCor}}\) functionality to generate two sets of OT correlations. The first set of OT correlations are generated to execute the two-round oblivious transfer used in the compiler of Garg and Srinivasan [GS18]. The second set of OT correlations are to be hardwired as part of the input in the conforming protocols so that the operations done by each party in the conforming protocol are information theoretic. To obtain perfect security, we also use a decomposable randomized encoding in place of garbled circuits. Apart from these changes, our two-round protocol is exactly same as in [GS18].
Evaluation. To compute the output of the protocol, each party \(P_i\) does the following:
-
1.
For each \(k \in [n]\), let \(\widehat{x}^{k,1}\) be the input encoding received from \(P_k\) at the end of round 2.
-
2.
\(\mathbf{for}\) each t from 1 to T do:
-
(a)
Parse \(\phi _t\) as \((i^*,(a_1,b_1,c_1),\ldots ,(a_s,b_s,c_s))\).
-
(b)
Compute \((\{(\xi _j,\omega _j)\}_{j \in [s]},\widehat{x}^{i^*,t+1}) := \mathsf {Dec}(\widetilde{f}^{i,t},\widehat{x}^{i,t})\).
-
(c)
Set \(\mathsf {st}_{i,c_j} := \xi _j \).
-
(d)
\(\mathbf{for}\) each \(k \ne i^*\) do:
-
i.
Compute \((\{\mathsf {ots}^2_j\}_{j \in [s]},\{{\widehat{x}}^{k,t+1}_{h}\}_{h \in [\ell ] \setminus \{c_j\}_{j \in [s]}}) := \mathsf {Dec}(\widetilde{f}^{i,t},\widehat{x}^{i,t})\).
-
ii.
For every \(j \in [s]\):
-
A.
Parse \(\mathsf {ots}^2_j\) as \((Y_0,Y_1)\) and \(\omega _j\) as \(\{\gamma ^k_j\}_{k \in [n] \setminus \{i^*\}}\).
-
B.
Recover \(\widehat{x}^{k,t+1}_{c_j} := Y_{\xi _j} \oplus \gamma ^k_j\).
-
A.
-
iii.
Set \(\widehat{x}^{k,t+1} := \{\widehat{x}^{k,t+1}_{h}\}_{h \in [\ell ]}\).
-
i.
-
(a)
-
3.
Compute the output as \(\mathsf {post}(i,\mathsf {st}_i,v_i)\).
Asymptotic Cost. Since the function f is constant size, the number of rounds of the underlying protocol and the maximum depth of the next message functions are constant (e.g., if we use [GMW87] as the underlying protocol). As a result of Lemma 5, the number of rounds of the conforming protocol is also a constant since k is a constant. Hence, the asymptotic cost of our protocol is a constant (though concretely it grows as \(2^{O(T)}\) where T is the number of rounds of the conforming protocol).
Security. The only changes that we make when compared to the protocol in [GS18] is that we use information theoretic, two-round oblivious transfer (based on OT correlations) and perfectly secure DRE in place of garbled circuits. We prove the security in the full version.
Theorem 3
For every constant size function f, the protocol in Fig. 4 perfectly computes f against a semi-honest adversaries who might corrupt an arbitrary subset of the parties.
Extensions. We will now describe two-extensions to the protocol in Fig. 4.
-
f need not be known until the second round. We will now describe how to augment the protocol so that the function f to be computed need not be known until the beginning of the second round and only the size of these functions need to be known before the first round. Let us assume for simplicity that, \(|f| = m'\). We define a \((k + m'k)\)-party functionality C that takes \(x_i\) from party \(P_i\) for every \(i \in [k]\) and takes a bit \(y_{i\ell }\) from party \(P_{i\ell }\) for each \(i \in [k]\) and \(\ell \in [m']\) and does the following: it checks if for each \(i,i' \in [n]\) and \(\ell \in [m']\), \(y_{i,\ell } {\mathop {=}\limits ^{?}} y_{i',\ell }\); if yes, it interprets \(y_{1,1},\ldots ,y_{1,m'}\) as the function f and computes an universal circuit \(U(x_1,\ldots ,x_k,f)\) that outputs \(f(x_1,\ldots ,x_k)\). With this functionality, let us now see how to change the two-round protocol so that the parties need not know f until the beginning of the second-round. We will use an underlying conforming protocol that securely computes the constant size circuit C. In the compiled protocol, we will let each party \(P_i\) to additionally emulate the parties \(\{P_{i\ell }\}_{\ell \in [m']}\). To be more precise, in the first round of the protocol, for each \(\ell \in [m']\), the party \(P_i\) sends two first round messages on behalf of party \(P_{i\ell }\); the first message assuming the bit \(y_{i\ell } = 0\) and the second message assuming the bit \(y_{i\ell '} = 1\). In the beginning of the second round, all the parties know the description of the functions f and hence can choose the first round message corresponding to the correct value of \(y_{i\ell }\) and ignore the other message. Based on the chosen messages, the parties generate the second round message in the compiled protocol.
-
Extension to the Client-Server setting. We now describe an extension of our two-round protocol to the client-server setting. In the client server setting, there are n-input clients who holds the inputs, m servers who do not have any input and one output client. The input clients send a single message to each of the m servers and the servers send a single message to the output client and the output client learns the output of the function based on the server’s message. We will assume that any number of clients can be corrupted but there is at least one server who is uncorrupted. We will transform our 2-round protocol in the \(\mathcal {F}_{\mathrm {OTCor}}\) model to one in the client-server model. In the full version, we give a general transformation from any two-round MPC protocol with security against semi-honest adversaries who might corrupt an arbitrary subset of the parties to a protocol in the client-server model. However, this general transformation might make non-black-box use of cryptography but the transformation we give here is specific to protocol in Fig. 4 and is information theoretic.
-
1.
The i-th input client computes the first round message \((z_i, \{\mathsf {ots}^1_{t,j,\alpha ,\beta }\}_{t \in A_i, j \in [s],\alpha ,\beta \in \{0,1\}})\) of our two-round protocol and sends it to each of the servers.
-
2.
In addition to the protocols first round message, the client will generate a randomized encoding of \(\mathsf {NC}^0\) circuits \(\overline{f}^{i,t}\) for every \(t\in [T]\), and sends these randomized encodings along with an additive secret share of the input encoding \((\mathbf {a}^{i,1}_0,\mathbf {a}^{i,1}_1)\) to the servers. Let us now describe the functionality computed by \(\overline{f}^{i,t}\). The functionality takes in the first round messages of all parties and reconstructs \(\mathsf {st}_i\). If \(t \in A_i\), then it computes the same function as that of \(f_{i,t}\) (described in Fig. 4). If \(t \not \in A_i\), it will use \(\mathsf {ots}^1_{t,j,\alpha ,\beta }\) (obtained from the first round messages of the parties) and will generate \(\mathsf {ots}^2_{t,j,\alpha ,\beta }\) exactly as described in the protocol. Then, it computes the same functionality as that of \(f^{i,t}\).
-
3.
The servers on receiving the first round messages from all the input clients, choose the secret share of the input encodings corresponding to the first round messages from all the clients and sends the chosen secret shares to the output client.
-
4.
The output client reconstructs the input encodings from the shares and decodes the randomized encodings exactly as given the evaluation procedure of our two-round protocol to obtain the output.
-
1.
4.2 Protocols for \(\mathsf {PREN}\) and \(\mathsf {SREN}\)
In this subsection, we will use the protocols described in Sect. 4.1 to construct protocols for functions in \(\mathsf {PREN}\) and \(\mathsf {SREN}\). We first define the \(\mathsf {dMULTPlus}\) function below.
We recall the following lemma from [BGI+18].
Lemma 6
([BGI+18]). Let \(g: \{0,1\}^n \rightarrow \{0,1\}\) be a constant degree function i.e., there exists a constant d such that \(g(x_1,\ldots ,x_n) = \sum {a^{\ell }_{i_1\ldots i_d}x_{i_1}x_{i_2}\ldots x_{i_d}}\). There exists a perfectly secure, two-round protocol in the presence of secure channels between every pair of parties for computing g against semi-honest adversary (corrupting an arbitrary subset of parties) in the \(\mathcal {F}_{\mathsf {dMULTPlus}}\) hybrid model. The efficiency of the protocol is \(O(m + n^2)\) where m is the number of monomials in g.
We obtain the following corollary of our Theorem 3.
Corollary 1
There exists a perfectly secure, two-round protocol for realizing \(\mathcal {F}_{\mathsf {dMULTPlus}}\) functionality against semi-honest adversary (corrupting an arbitrary subset of parties) in the \(\mathcal {F}_{\mathrm {OTCor}}\) hybrid model. The efficiency of the protocol is \(2^{\mathsf {poly}(d)}\).
Combining Lemma 6 and Corollary 1 and the observation that \(\mathcal {F}_{\mathrm {OTCor}}\) implies secure channels, we get the following lemma.
Lemma 7
Let \(g: \{0,1\}^n \rightarrow \{0,1\}\) be a constant degree function i.e., there exists a constant d such that \(g(x_1,\ldots ,x_n) = \sum {a^{\ell }_{i_1\ldots i_d}x_{i_1}x_{i_2}\ldots x_{i_d}}\). There exists a perfectly secure, two-round protocol for computing g against semi-honest adversary (corrupting an arbitrary subset of parties) in the \(\mathcal {F}_{\mathrm {OTCor}}\) hybrid model. The efficiency of the protocol is \(O(m + n^2)\) where m is the number of monomials in g.
We now show our main theorem regarding securely computing functions in \(\mathsf {PREN}\) and \(\mathsf {SREN}\).
Theorem 4
Every \(f : \{0,1\}^n \rightarrow \{0,1\}\) in \(\mathsf {PREN}\) (resp. \(\mathsf {SREN}\)) has an efficient, perfectly secure (resp., statistically secure) two-round protocol in the \(\mathcal {F}_{\mathrm {OTCor}}\) model against a semi-honest adversary corrupting an arbitrary subset of parties. The computational cost incurred by each party is \(O(m+n^2)\) where m is the size of the randomized encoding for f.
Proof
Let \(\widehat{f}: \{0,1\}^n \times \{0,1\}^{\rho } \rightarrow \{0,1\}\) be the randomized encoding of the function f. Each party \(P_i\) chooses \(r_i\) uniformly at random from \(\{0,1\}^{\rho }\) and the parties wish to securely compute the functionality \(\widehat{f}(x_1,\ldots ,x_n;r_1 \oplus r_2 \ldots \oplus r_n)\) (i.e., the input of party \(P_i\) is set as \((x_i,r_i)\)).
Let \(\widehat{f}(x_1,\ldots ,x_n;r_1 \oplus r_2 \ldots \oplus r_n) = \sum {a^{\ell }_{i_1i_2\ldots i_d}}v_{i_1}v_{i_2}\ldots v_{i_d}\) where each \(v_{i_d}\) is either some input bit \(x_j\) or a bit of some random string \(r_j\). We will use the protocol from Lemma 7 to securely compute \(\widehat{f}\).
It now follows from the privacy of randomized encodings and the security of the protocol for computing \(\widehat{f}\) the above protocol securely computes f against semi-honest corruptions.
Remark 2
For simplicity, in Theorem 4, we considered a setting where each party holds a single bit as input and the output of the function f is also a single bit. This can be naturally generalized to a setting wherein each party holds a string as input and the number of outputs of the functions is greater than 1.
We obtain the following corollary from Theorem 4.
Corollary 2
There is a perfectly (resp. statistical) secure two-round protocol for branching programs (resp. non-deterministic branching programs) in the \(\mathcal {F}_{\mathrm {OTCor}}\) model against a semi-honest adversary corrupting an arbitrary subset of parties.
4.3 Protocols for Circuits
In this subsection, we will use the protocols described in Sect. 4.1 and make black-box use of a PRG to obtain secure protocols for computing circuits. Without loss of generality, we will restrict ourselves to circuits with fan-in 2 NAND gates. The high level idea is to use the protocol in Sect. 4.1 to compute the BMR garbling of a gate [BMR90]. To obtain the labels for executing the BMR garbled circuit, we run the BMR online phase in parallel.
BMR Garbling. We will now recall the semantics of a BMR garbled gate. The BMR garbling for a NAND gate g that takes wires a and b as input and the output wire is c is a set of values \(\{\widetilde{G}^i_{r_1,r_2}\}_{r_1,r_2 \in \{0,1\}, i \in [n]}\), where
where \(\chi _{r_1,r_2} = \left( (\bigoplus _{i = 1}^{n}{\lambda _{i,a}} \oplus r_1)\cdot (\bigoplus _{i = 1}^{n}{\lambda _{i,b}} \oplus r_2) \oplus 1 \right) \oplus (\bigoplus _{i = 1}^{n}{\lambda _{i,c}})\). Here, F is a PRF, \(k^i_{x,r}\) where \(x \in \{a,b,c,\}\) and \(r \in \{0,1\}\) is a PRF key, \(\lambda _{i,x}\) for \(x \in \{a,b,c,\}\) are bits.Footnote 12 The PRF keys \(k^i_{x,r}\) and the bits \(\lambda _{i,x}\) are chosen by each party before the first round of the protocol.
We notice that each output bit of \(\{\widetilde{G}^i_{r_1,r_2}\}_{r_1,r_2 \in \{0,1\}, i \in [n]}\) is a constant degree (precisely, a degree 3 functionality). We will use the protocol in Lemma 7 to securely compute each output bit of \(\{\widetilde{G}^i_{r_1,r_2}\}_{r_1,r_2 \in \{0,1\}, i \in [n]}\).Footnote 13
Online Phase of BMR. We now describe the two-round BMR online phase.
-
1.
For every wire w, which is the input wire of a party \(P_i\), the other parties \(P_j\) will set \(\lambda _{j,w} = 0\). The party \(P_i\) will compute \(\alpha _w = \lambda _{i,w} \oplus x_w\) and broadcast it to all other parties.
-
2.
For every \(\alpha _w\) obtained, the party \(P_i\) will broadcast \(k^i_{w,\alpha _w}\) to every other party.
Asymptotic Cost. The cost of computing every bit of \(\widetilde{G}^i_{r_1,r_2}\) is \(O(n^2)\) since the number of monomials in \(\widetilde{G}^i_{r_1,r_2}\) is \(O(n^2)\). So the overall complexity of our protocol is \(O(n^3|C|\lambda )\). This gives a factor of n improvement over the cost in [GS18].
Using the above protocol for computing the BMR garbled gate in parallel with the online phase, we obtain the following theorem:
Theorem 5
There is a computationally secure two-round protocol for any circuit C in the \(\mathcal {F}_{\mathrm {OTCor}}\) model against a semi-honest adversary corrupting an arbitrary subset of parties, where the protocol makes a black-box use of a PRG. The computational cost incurred by each party is dominated by \(O(n^3 |C|)\) invocations of a length-doubling PRG.
We the following two corollaries by realizing \(\mathcal {F}_{\mathrm {OTCor}}\) under DDH/QR or LWE in the strong-PKI model.
Corollary 3
(DDH/QR). There is a computationally secure, two-round protocol for any circuit C in the strong-PKI model against a semi-honest adversary corrupting an arbitrary subset of parties, where the protocol makes a black-box use of a PRG and black-box use of a DDH/QR hard group.
Corollary 4
(LWE). Under the LWE assumption, there is a computationally secure, two-round protocol for any circuit C in the strong-PKI model against a semi-honest adversary corrupting an arbitrary subset of parties, where the protocol makes a black-box use of a PRG.
Notes
- 1.
Protocols that offer security with no honest majority imply oblivious transfer. Thus, they provably do not admit a black-box reduction to a PRG [IR89], and a non-black-box reduction would be considered a major breakthrough in cryptography.
- 2.
A recent work of Ananth, Choudhuri, Goel, and Jain [ACGJ18] obtains honest-majority, two-round MPC protocols from one-way functions satisfying the notion of security with abort against malicious adversaries. Our work was done in part following a public announcement of this result.
- 3.
An additional disadvantage of the protocols from [GS18, BL18] compared to most earlier protocols is that their communication complexity is always bigger than the circuit size of the function being computed. However, breaking this circuit size barrier under general assumptions such as OT would require a major breakthrough, regardless of round complexity.
- 4.
- 5.
Our protocol for semi-honest adversaries is expensive but not prohibitively so. With some simple optimizations, the online communication consists of roughly \(1750\cdot n^3\) standard garbled circuits, which is about 135 times the cost of the BMR protocol [BMR90], and the total number of OTs required by the setup is less than 7% of the communication.
- 6.
Here, we let the receiver to choose the bit b and provide as input to the functionality. We can also work with a weaker formulation wherein the functionality can sample a random bit b. However, we chose this formulation as it will lead to concrete improvements in the cost of our two-round MPC protocols.
- 7.
The HSS constructions in [BGI16, BGI17, BGI+18, BCG+17] have a polynomial error probability and this might leak information about the correlations to an adversary. [BCG+17] mentions two ways to prevent such leakages: either bootstrap random pads or use a punctured OT [BGI17]. We refer the reader to [BCG+17] for the details.
- 8.
The lemma in [BGH07] was shown only for \(R \in \mathcal {J}(N)\). We extend it to arbitrary \(R \not \in \mathcal {QR}(N)\).
- 9.
For simplicity, we restrict ourselves to functions that output a single bit. We note that all our results can be generalized to functions with multiple bits with efficiency growing linearly with this number. We also assume that all the parties get the output of this functionality. We can also generalize our result for the case where some specific parties get the output.
- 10.
Again, for simplicity we restrict ourselves to parties with a single input bit and our results naturally generalize to parties with multiple bits as input.
- 11.
Randomized protocols can be handled by including the randomness used by a party as part of its input.
- 12.
For simplicity we consider a PRF. But all our results also work with a length doubling pseudorandom generator.
- 13.
Here, the parties will compute the PRF outputs locally and give these as inputs to the protocol.
References
Applebaum, B., Brakerski, Z., Tsabary, R.: Perfect secure computation in two rounds. To appear in TCC (2018). https://eprint.iacr.org/2018/894
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A.: Round-optimal secure multiparty computation with honest majority. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 395–424. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_14
Applebaum, B., Ishai, Y., Kushilevitz, E.: Cryptography in NC\(^0\). In: 45th FOCS, Rome, Italy, 17–19 October 2004, pp. 166–175. IEEE Computer Society Press (2004)
Asharov, G., Jain, A., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. IACR Cryptology ePrint Archive, p. 613 (2011)
Asharov, G., Lindell, Y., Schneider, T., Zohner, M.: More efficient oblivious transfer and extensions for faster secure computation. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 13, Berlin, Germany, 4–8 November 2013, pp. 535–548. ACM Press (2013)
Asharov, G., Lindell, Y., Schneider, T., Zohner, M.: More efficient oblivious transfer extensions with security for malicious adversaries. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 673–701. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_26
Bar-Ilan, J., Beaver, D.: Non-cryptographic fault-tolerant computing in constant number of rounds of interaction. In: Proceedings of the Eighth Annual ACM Symposium on Principles of Distributed Computing, Edmonton, Alberta, Canada, 14–16 August 1989, pp. 201–209 (1989)
Boyle, E., Couteau, G., Gilboa, N., Ishai, Y., Orrù, M.: Homomorphic secret sharing: Optimizations and applications. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) ACM CCS 17, Dallas, TX, USA, 31 October–2 November 2017, pp. 2105–2122. ACM Press (2017)
Brassard, G., Crépeau, C., Santha, M.: Oblivious transfers and intersecting codes. IEEE Trans. Inf. Theory 42(6), 1769–1780 (1996)
Brassard, G., Crépeau, C., Wolf, S.: Oblivious transfers and privacy amplification. J. Cryptol. 16(4), 219–237 (2003)
Beaver, D.: Correlated pseudorandomness and the complexity of private computations. In: Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, Philadelphia, Pennsylvania, USA, 22–24 May 1996, pp. 479–488 (1996)
Boneh, D., et al.: Threshold cryptosystems from threshold fully homomorphic encryption. To appear in Crypto (2018). https://eprint.iacr.org/2017/956
Boneh, D., Gentry, C., Hamburg, M.: Space-efficient identity based encryption without pairings. In: 48th FOCS, Providence, RI, USA, 20–23 October, pp. 647–657. IEEE Computer Society Press (2007)
Boyle, E., Gilboa, N., Ishai, Y.: Breaking the circuit size barrier for secure computation under DDH. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 509–539. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_19
Boyle, E., Gilboa, N., Ishai, Y.: Group-based secure computation: optimizing rounds, communication, and computation. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 163–193. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_6
Boyle, E., Gilboa, N., Ishai, Y., Lin, H., Tessaro, S.: Foundations of homomorphic secret sharing. In: ITCS 2018, pp. 21:1–21:21, January 2018
Benhamouda, F., Lin, H.: k-round multiparty computation from k-round oblivious transfer via garbled interactive circuits. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 500–532. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_17
Bellare, M., Micali, S.: Non-interactive oblivious transfer and applications. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 547–557. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_48
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols (extended abstract). In: 22nd ACM STOC, Baltimore, MD, USA, 14–16 May, pp. 503–513. ACM Press (1990)
Canetti, R.: Security and composition of multiparty cryptographic protocols. J. Cryptol. 13(1), 143–202 (2000)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, Las Vegas, NV, USA, 14–17 October 2001, pp. 136–145. IEEE Computer Society Press (2001)
Choi, S.G., Elbaz, A., Malkin, T., Yung, M.: Secure multi-party computation minimizing online rounds. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 268–286. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_16
Diffie, W., Hellman, M.E.: New directions in cryptography. IEEE Trans. Inf. Theory 22(6), 644–654 (1976)
Dodis, Y., Halevi, S., Rothblum, R.D., Wichs, D.: Spooky encryption and its applications. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 93–122. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_4
Even, S., Goldreich, O., Lempel, A.: A randomized protocol for signing contracts. Commun. ACM 28(6), 637–647 (1985)
Fazio, N., Gennaro, R., Jafarikhah, T., Skeith, W.E.: Homomorphic secret sharing from paillier encryption. In: Okamoto, T., Yu, Y., Au, M.H., Li, Y. (eds.) ProvSec 2017. LNCS, vol. 10592, pp. 381–399. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68637-0_23
Garg, S., Gentry, C., Halevi, S., Raykova, M.: Two-round secure MPC from indistinguishability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 74–94. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_4
Dov Gordon, S., Liu, F.-H., Shi, E.: Constant-round MPC with fairness and guarantee of output delivery. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 63–82. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_4
Goldwasser, S., Micali, S.: Probabilistic encryption and how to play mental poker keeping secret all partial information. In: 14th ACM STOC, San Francisco, CA, USA, 5–7 May 1982, pp. 365–377. ACM Press (1982)
Garg, S., Mahmoody, M., Masny, D., Meckler, I.: On the round complexity of OT extension. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 545–574. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_19
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: Aho, A. (ed.) 19th ACM STOC, New York City, NY, USA, 25–27 May 1987, pp. 218–229. ACM Press (1987)
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_24
Garg, S., Srinivasan, A.: Garbled protocols and two-round MPC from bilinear maps. In: 58th FOCS, pp. 588–599. IEEE Computer Society Press (2017)
Garg, S., Srinivasan, A.: Two-round multiparty secure computation from minimal assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 468–499. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_16
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: a new representation with applications to round-efficient secure computation. In: 41st FOCS, Redondo Beach, CA, USA, 12–14 November 2000, pp. 294–304. IEEE Computer Society Press (2000)
Ishai, Y., Kushilevitz, E., Meldgaard, S., Orlandi, C., Paskin-Cherniavsky, A.: On the power of correlated randomness in secure computation. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 600–620. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_34
Ishai, Y., Kilian, J., Nissim, K., Petrank, E.: Extending oblivious transfers efficiently. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 145–161. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_9
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Prabhakaran, M., Sahai, A.: Efficient non-interactive secure computation. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 406–425. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_23
Ishai, Y., Kushilevitz, E., Paskin, A.: Secure multiparty computation with minimal interaction. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 577–594. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_31
Ishai, Y., Mittal, M., Ostrovsky, R.: On the message complexity of secure multiparty computation. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 698–711. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_24
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_32
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: Proceedings of the 21st Annual ACM Symposium on Theory of Computing, Seattle, Washigton, USA, 14–17 May 1989, pp. 44–61 (1989)
Kilian, J.: Founding cryptography on oblivious transfer. In: 20th ACM STOC, Chicago, IL, USA, 2–4 May 1988, pp. 20–31. ACM Press (1988)
Keller, M., Orsini, E., Scholl, P.: Actively secure OT extension with optimal overhead. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 724–741. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_35
Mukherjee, P., Wichs, D.: Two round multiparty computation via multi-key FHE. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 735–763. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_26
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Pfitzmann, B., Waidner, M.: Composition and integrity preservation of secure reactive systems. In: Jajodia, S., Samarati, P. (eds.) ACM CCS 2000, Athens, Greece, 1–4 November 2000, pp. 245–254. ACM Press (2000)
Rabin, M.: How to exchange secrets by oblivious transfer. Technical report TR-81, Harvard Aiken Computation Laboratory (1981)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) 37th ACM STOC, Baltimore, MA, USA, 22–24 May 2005, pp. 84–93. ACM Press (2005)
Yao, A.C.-C.: How to generate and exchange secrets (extended abstract). In: 27th FOCS, Toronto, Ontario, Canada, 27–29 October 1986, pp. 162–167. IEEE Computer Society Press (1986)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Garg, S., Ishai, Y., Srinivasan, A. (2018). Two-Round MPC: Information-Theoretic and Black-Box. In: Beimel, A., Dziembowski, S. (eds) Theory of Cryptography. TCC 2018. Lecture Notes in Computer Science(), vol 11239. Springer, Cham. https://doi.org/10.1007/978-3-030-03807-6_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-03807-6_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03806-9
Online ISBN: 978-3-030-03807-6
eBook Packages: Computer ScienceComputer Science (R0)