One-Message Zero Knowledge and Non-malleable Commitments

Abstract

We introduce a new notion of one-message zero-knowledge (1ZK) arguments that satisfy a weak soundness guarantee—the number of false statements that a polynomial-time non-uniform adversary can convince the verifier to accept is not much larger than the size of its non-uniform advice. The zero-knowledge guarantee is given by a simulator that runs in (mildly) super-polynomial time. We construct such 1ZK arguments based on the notion of multi-collision-resistant keyless hash functions, recently introduced by Bitansky, Kalai, and Paneth (STOC 2018). Relying on the constructed 1ZK arguments, subexponentially-secure time-lock puzzles, and other standard assumptions, we construct one-message fully-concurrent non-malleable commitments. This is the first construction that is based on assumptions that do not already incorporate non-malleability, as well as the first based on (subexponentially) falsifiable assumptions.

The full version of this extended abstract can be found on Eprint [BL18].

N. Bitansky—Member of the Check Point Institute of Information Security. Supported by the Alon Young Faculty Fellowship and by Len Blavatnik and the Blavatnik Family foundation.

H. Lin—Supported by NSF grants CNS-1528178, CNS-1514526, CNS-1652849 (CAREER), a Hellman Fellowship, the Defense Advanced Research Projects Agency (DARPA) and Army Research Office (ARO) under Contract No. W911NF-15-C-0236, and a subcontract No. 2017-002 through Galois. The views expressed are those of the authors and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Zero-knowledge proofs [GMR89] are a cornerstone of modern cryptography. Their birth was enabled by introducing two new concepts to classical proofs—interaction and randomness. Indeed, both were shown [GO94] to be essential—for non-trivial languages, zero-knowledge proofs (or their computationally-sound counterparts known as arguments) require a randomized verifier that exchanges at least three messages with the prover. In particular, unlike classical proofs, zero-knowledge proofs cannot be transferred, published, nor stored.

One setting in which this barrier can be circumvented is when a trusted setup (such as a common random string) is available [BFM88]. In the absence of a trusted setup, a natural approach to the problem is to relax the requirements of zero-knowledge protocols. Along this vein, Dwork and Naor [DN07] showed that for witness-indistinguishable (WI) proofs, two messages suffice, and by now, we know how to achieve them with no interaction at all [BOV07, GOS12]. Pass [Pas03] considered a stronger notion—zero-knowledge with a super-polynomial simulator (SPS). Indeed, WI proofs stand at the extreme of this notion, as they admit an exponential-time simulator (that can find a witness for the underlying statement by brute force). In contrast, based on subexponential hardness assumptions, Pass constructed two-message arguments where the zero-knowledge simulator runs in subexponential, or even quasi-polynomial time (without violating the hardness of the underlying language). Such SPS zero-knowledge has proven instrumental for central applications such as concurrent computation [Pas03, PS04, BS05, MMY06, CLP16, GGJS12, GKP17, BGI+17, BGJ+17] and non-malleable commitments [KS17].

While Pass’ proofs break the three-message barrier, they still consist of two messages and do not enjoy the merits of completely non-interactive proofs. Following the introduction of non-interactive WI (NIWI) proofs, Barak and Pass [BP04] investigated the possibility that SPS zero-knowledge can also be made non-interactive (with no trusted setup). They observed that non-interactive proofs (or arguments) that satisfy the usual notion of soundness and have a $T_{\tiny \mathrm {SPS}}$-time simulator are impossible to achieve against non-uniform adversaries, except for languages ${\mathcal {L}}$ decidable in time $T_{\tiny \mathrm {SPS}}$. Indeed, if the simulator cannot decide ${\mathcal {L}}$, there must exist proofs $\pi$ for false statements $x\notin {\mathcal {L}}$, and a non-uniform prover can have such proofs hardwired in its code. Accordingly, Barak and Pass define a notion of SPS zero-knowledge protocols satisfying a weak notion of soundness that only holds against efficient uniform provers. They show how to construct such protocols based on keyless hash functions that are collision-resistant against subexponential uniform adversaries (or more general uniform sampling problems).

This Work: Weak Soundness Against Non-uniform Provers. We introduce a new notion of weak soundness for one-message zero-knowledge (1ZK) that also captures non-uniform adversaries.

The notion is inspired by the notion of multi-collision resistance for keyless hash functions, introduced recently in [BKP18]. Roughly speaking, it requires that an efficient non-uniform adversary cannot do more than hardwire false statements with their accepting proofs in its code. That is, any non-uniform adversary, with description of polynomial size $S$ and arbitrary polynomial running time $T\gg S$, should not be able to find (i.e., output in one shot) more than $K(S)$ false statements $x\notin {\mathcal {L}}$ together with an accepting proof $\pi$, where $K$ is some blowup function (for concreteness, the reader may think of $K(S)=S^2$ throughout this introduction). In other words, false statements with their accepting proofs cannot be significantly compressed.

The zero-knowledge requirement is the same SPS requirement as before—the simulator is allowed to be mildly super-polynomial (and in particular, cannot decide the underlying language ${\mathcal {L}}$). We note that even with such weak soundness, the SPS relaxation is essential—languages ${\mathcal {L}}$ that are hard on average cannot have an efficient simulator.¹

1.1 Results and Discussion

We construct 1ZK arguments satisfying the new notion of weak soundness based on the notion of multi-collision resistance and generalizations thereof. Then, relying on such arguments, we construct one-message (concurrently) non-malleable commitments, which has been a long standing problem. We now elaborate on each of these results.

Constructing 1ZK Arguments. We show how to construct 1ZK arguments from keyless hash functions that satisfy the notion of multi-collision resistance recently introduced in [BKP18]. Such a hash function ${\mathsf {H}}:\{0,1\}^{\lambda }\rightarrow \{0,1\}^{\lambda /2}$ guarantees that no relatively-efficient adversary with non-uniform description of polynomial size $S$ can find more than $K(S)$ collisions in the underlying function.² Here, $K$ is again a fixed polynomial (e.g., quadratic) and relatively-efficient means mildly superpolynomial-time (e.g. quasipolynomial or subexponential).

Theorem 1

(Informal). Assuming multi-collision-resistant keyless hash functions, injective one-way functions, and non-interactive witness-indistinguishable proofs, all subexponentially-secure, there exist 1ZK arguments for NP with weak soundness and a subexponential-time simulator.

As noted in [BKP18], while non-standard, multi-collision resistance is a falsifiable and relatively simple assumption. As candidates they suggest existing keyless hash functions such as SHA, or AES-based hashing, and point out directions for investigating additional candidates. We can, in fact, rely on a more general notion of incompressible problems, for which additional candidates may be found. At high-level, a $(T,K,\varDelta )$-incompressible problem is a collection $\mathcal {W}=\left\{ \mathcal {W}_\lambda \right\} _\lambda$ of efficiently recognizable sets (one set for each security parameter $\lambda$) satisfying the following. On one hand, no $T$-time adversary with non-uniform description of polynomial size $S$ can find more than $K(S)$ solutions $w\in \mathcal {W}_\lambda$. On the other hand, $\mathcal {W}_\lambda$ is relatively dense in $\{0,1\}^{\lambda }$, in the sense that a random $w\leftarrow \{0,1\}^\lambda$ is in $\mathcal {W}_\lambda$ with relatively high probability $\varDelta =2^{-o(\lambda )}$.³ For concreteness, the reader may think of $T= 2^{\lambda ^{.01}}\ll 2^{\lambda ^{.99}} = \varDelta ^{-1}$.

Theorem 2

(Informal). Assuming $(T,K,\varDelta )$-incompressible problems, where $K\ll T\ll \varDelta ^{-1}\ll 2^{\lambda ^{.99}}$, and subexponentially-secure injective one-way functions and non-interactive witness-indistinguishable proofs, there exist 1ZK arguments for NP with $(T,K)$-weak soundness and a $\mathrm {poly}(\varDelta ^{-1})$-time simulator.⁴

We also define and construct, under the same assumptions, a more general notion that we call $\varphi$-tuned 1ZK that admits a more flexible tradeoff between the level of soundness and simulation time, and will be useful when applying these arguments. We defer the details to the technical overview below.

One-Message Non-malleable Commitments. The question of the round complexity of non-malleable commitments [DDN03] has been long pursued. The past two decades have seen impressive progress [Bar02, PR05a, PR05b, LPV08a, LP09, PPV08, PW10, Wee10, Goy11, LP11, GLOV12, GRRV14, GPR16, COSV16, COSV17, Khu17], culminating in two recent constructions of two-message non-malleable commitments [KS17, LPS17] based on subexponential Decision-Diffie-Hellman or Quadratic Residuosity in the first, and subexponential time-lock puzzles [RSW00] in the second (which achieves also full concurrency).

Yet, one-message non-malleable commitments have remained somewhat elusive. So far, they have only been constructed starting from a non-falsifiable assumption that already incorporates non-malleability called adaptive injective one-way functions, against uniform adversaries [LPS17], or for a restricted class of algebraic mauling functions and entropic plaintexts [KY18]. Indeed, one-message non-malleable commitments would give rise to powerful features that cannot be achieved with interaction, such as the ability to publish them on public ledgers, transfer them from one hand to another, or store them for future use.

Relying on 1ZK arguments with weak soundness, we construct one-message fully-concurrent non-malleable commitments against non-uniform adversaries.

Theorem 3

(Informal). Under the same assumptions as in Theorem 2 (or 1), as well as subexponential time-lock puzzles, there exist fully-concurrent one-message non-malleable commitments against all efficient non-uniform adversaries.

We actually prove a more general theorem that transforms commitments satisfying a notion of four-tag non-malleability into full-fledge non-malleable commitments as stated in the above theorem. (More specifically, the former refers to non-malleability w.r.t. four tags, whereas full-fledged non-malleability can handle an exponential number of tags.) Such four-tag (or constant-tag) commitments are constructed in [LPS17] based on sub-exponentially secure time-lock puzzles and injective one-way functions. In addition, we present new candidate four-tag (or constant-tag) non-malleable commitments from a new assumption regarding injective one-way functions that are amenable to hardness amplification, which can replace time-lock puzzles in the above theorem. This yields new candidates from natural one-way functions such as discrete logarithms, RSA, or Rabin. See further details in the technical overview below.

On the Underlying Assumptions. The assumptions that we rely on, most notably incompressible problems, are not standard. Nevertheless, we do find them simple and plausible. Bitansky, Kalai, and Paneth give evidence that multi-collision resistance may hold for existing cryptographic hash functions and in particular does not require any special algebraic structure—they show that this property is satisfied by random oracles, even in the auxiliary-input model [Unr07] (where the adversary may first store arbitrary polynomial information about the oracle).

We also note that all of our assumptions are subexponentially-falsifiable (i.e., falsifiable w.r.t. sub-exponential time adversaries). Here we note that Pass [Pas13] showed that non-malleable commitments in less than three messages cannot be shown secure based on black-box reductions to polynomially-falsifiable assumptions.

A more conservative view of our results would be that to rule out the existence of one-message non-malleable commitments, one must show that incompressible problems do not exist. That is, any efficiently recognizable, somewhat dense, set must have a non-trivial sampler (where by non-trivial we mean that it can output more samples then its non-uniform size). In particular, one would have to show that for any keyless hash function, it is possible to compress collisions. This would also constitute a strong (and non-contrived) separation between random oracles and any keyless hash function.

Using Weak Soundness. Weak soundness is the best one could hope for when considering one-message zero-knowledge without trusted setup and non-uniform cheating provers, but when is it useful? Generally speaking, weak soundness could be leveraged in settings where a prover does not fully determine proven statements, namely, statements have some non-trivial entropy.

This gives some intuition on why weak soundness is useful in our application of non-malleable commitments. Roughly speaking, to maul a commitment c to a value v, the attacker is required to generate a new commitment $c'$ to a related value $v'$, and prove that the new commitment is well-formed. As long as the attacker does not always produce a fixed commitment $c'$, or rather a commitment $c'$ from some fixed polynomial-size set ${\mathcal {Z}}$, proven statements are sufficiently entropic and weak soundness kicks in. In contrast, mauling c into $c'$ from such a set ${\mathcal {Z}}$ would not constitute a meaningful attack—the distribution of the value $v'$ in the commitment $c'$ cannot depend on the committed value v in c, or a reduction that has the set ${\mathcal {Z}}$ hardcoded could break the hiding of c. See more details in the technical overview below.

It is plausible that weak soundness will be found useful in other settings with entropic statements or in different man-in-the-middle attack models.

Robustness Beyond Human Ignorance. When considering the possibility of integrating non-interactive zero-knowledge in real-world systems, the need for a trusted common reference string may present a serious hurdle (certainly in decentralized applications whose essence is to avoid central trust). The system of Barak and Pass [BP04], when instantiated, say, with SHA256, already avoids the need for central trust and suggests a meaningful guarantee of soundness in the face of human ignorance (a term coined by Rogaway [Rog06]). Namely, as long as humanity fails to find collisions in SHA256, it will also fail to find accepting proofs for false statements. However, the moment even a single collision in SHA256 is found, the Barak and Pass system would completely lose soundness—it will be possible to easily prove any false statement.

Our system has a more robust guarantee—finding a few collisions only allows finding a few false statements with accepting proofs, and the mapping from collisions to false statements is deterministic and efficiently computable.

1.2 Technical Overview

We now give an overview of the main ideas and techniques behind our results.

Throughout this overview, it will be convenient to consider a slight variant of incompressible problems requiring that for any efficient adversary ${\mathcal {A}}$ with a non-uniform description of polynomial size $S$, there exists a set ${\mathcal {Z}}$ of size at most $K(S)$, such that ${\mathcal {A}}$ cannot find solutions $w\in \mathcal {W}{\setminus }{\mathcal {Z}}$. In the body, we show that this variant is indeed equivalent to requiring that the adversary fails to find more than $K$ solutions w. We consider a similar variant for the definition of weak soundness, where the adversary cannot output a false statement and accepting proof $(x,\pi )$, except for statements $x$ from some size-$K$ set.

One-Message Zero-Knowledge

The starting point for our construction is the Barak-Pass [BP04] construction against uniform provers. They follow the common [FLS99] paradigm in which the prover provides a WI proof that

“Either $x\in {\mathcal {L}}\,$ or the prover knows some trapdoor”.

The trapdoor should be such that it is too hard for an efficient prover to compute, but only mildly hard, so that a super-polynomial simulator can obtain it relatively fast in time $T_{\tiny \mathrm {td}}\ll 2^{o(|x|)}$. The hardness of obtaining the trapdoor, and the soundness of the proof, guarantee the soundness of the argument, whereas as the WI property, along with the simulator’s ability to find the trapdoor, give rise to SPS simulation. To realize this idea, the prover sends a commitment c and proves that $x\in {\mathcal {L}}$ or c is a commitment to the trapdoor. The commitment is only mildly hard—the committed value could be extracted by brute force in time $T_{\tiny \mathrm {com}}\ll T_{\tiny \mathrm {td}}$, which does not suffice to find the trapdoor. Therefore, violating soundness requires violating the hardness of finding a trapdoor in $T_{\tiny \mathrm {td}}$.

The question is what could be the trapdoor. Focusing on uniform provers, Barak and Pass rely on problems that are hard for uniform algorithms. For instance finding collisions of certain keyless hash functions is conjectured to be hard for uniform algorithms (or more generally, algorithms whose description is smaller than the function’s input), even in time $\mathrm {poly}(T_{\tiny \mathrm {com}})$. This of course miserably fails against non-uniform provers who could simply have such a trapdoor (e.g., a collision) hardwired in their code and use it to cheat.

Leveraging Incompressible Problems. Recall that we are only interested in a weak notion of soundness—we wish to guarantee that there is only a small set of false statements for which the prover may give false proofs (where small is some polynomial $K(S)$ in the prover’s non-uniform description size $S$). A first natural idea is to simply replace the trapdoor problem with an incompressible problem $\mathcal {W}$ (for instance, replace collision-resistance against uniform adversaries with multi-collision resistance against non-uniform ones).

This first attempt, however, fails. The problem is that any single solution in $\mathcal {W}$ allows to efficiently generate accepting proofs for all statements $x$. Thus, a non-uniform attacker with one such hardwired solution, can convince the verifier of accepting any number of false statement, thereby violating the weak soundness requirement. The problem stems from the fact that in such a protocol, the concept of a useful trapdoor is completely detached from the proven statement $x$. We solve this by binding trapdoors and statements, so that, finding accepting proofs for different false statements requires finding different solutions in $\mathcal {W}$. Thus, an attacker who can only find a small set of solutions, can only generate proofs for a small number of corresponding false statements.

More specifically, we aim to achieve two goals. First, every trapdoor $w\in \mathcal {W}$ is associated with a specific statement $x= f(w)$ determined by some efficiently computable function f—this would ensure that the prover could only provide accepting proofs for false statements from a small set $\mathcal {X} = f({\mathcal {Z}})$ determined by the small set ${\mathcal {Z}}$ of trapdoors it may be able to find. Second, we would like to guarantee that for any $x\in {\mathcal {L}}$, the simulator would be able to reverse sample a trapdoor $w\in \mathcal {W}$ such that $x=f(w)$, and it should do so relatively fast.

We achieve the above combinatorial properties as follows. For instances $x$ of size $\ell$, we choose f to be a two-source extractor $\mathsf {2Ext}:\{0,1\}^{n}\times \{0,1\}^{n} \rightarrow \{0,1\}^\ell$, where n is a parameter dictated by the quality of the extractor (in our actual construction $n=4\ell$). We then choose our incompressible problem to be pairs of solutions $\mathcal {W}\times \mathcal {W}\subseteq \{0,1\}^{n}\times \{0,1\}^{n}$ for some underlying incompressible problem $\mathcal {W}$. It is easy to see that the product of incompressible problems is itself an incompressible problem, and so weak soundness is obtained according to the above reasoning. Furthermore, by choosing an appropriate extractor, we can guarantee that as long as $\mathcal {W}$ has density $\varDelta \ge 2^{-o(\ell )}$, for any $x\in \{0,1\}^{\ell }$, it is possible to sample $(w,w')\in \mathcal {W}$ such that $\mathsf {2Ext}(w,w')=x$ in time $O(\varDelta ^{-2})$, as required.

The above is satisfied by any extractor with the following two properties. First, it has an exponentially small error—for independent sources with min-entropy $n - o(\ell )$, the output is ${2^{-\ell -\varOmega (1)}}$-close to uniform. Second, it admits efficient reverse sampling—for any $x$, it is possible to efficiently sample from the uniform distribution on $U_{n}\times U'_{n}$ conditioned on $\mathsf {2Ext}(U,U')=x$. These properties are both satisfied by the classical Hadamard extractor [CG88, Vaz85]. See further details in the full version of this paper.

To recap, the final proof $(c,\pi )$ consists of a commitment c to a string of length 2n, and a NIWI that

Starting from a $(T_{\tiny \mathcal {W}},K,\varDelta )$-incompressible problem, we choose a mildly-hard commitment so that it is extractable in time $T_{\tiny \mathrm {com}}\ll T_{\tiny \mathcal {W}}$. The resulting system is then $(T_{\tiny \mathcal {W}},K)$-weakly-sound and has a $\varDelta ^{-2}$-time simulator. In particular, for the discussed setting of parameters $K\ll T\ll \varDelta ^{-1}\ll 2^{\ell ^{.99}}$, we get a subexponential-time simulator.

$\varphi$-Tuned 1ZK. We also consider a generalization of the 1ZK definition that admits a more flexible soundness vs. simulation-time tradeoff. Specifically, we parameterize our system by a projection function $\varphi (x)$ and obtain the following augmented guarantees:

• Weaker Soundness: we are only guaranteed that the prover produces accepting proofs for false statements $x$ whose projection $\varphi (x)$ is taken from a small set ${\mathcal {Z}}$ (but $x$ itself is not restricted to any small set).

• Faster Simulation: simulation time is only subexponential in $|\varphi (x)|$ and not in $\ell =|x|$. Furthermore, fixing any projection y, there is a corresponding trapdoor state ${{\mathsf {s}}}{{\mathsf {t}}}_y$ that allows simulating any $x\in \varphi ^{-1}(y)$ in polynomial time. A bit more formally, simulation for $x$ can be split into a long preprocessing step ${\mathsf {S}}_{\mathsf {pre}}$, subexponential in $|\varphi (x)|$, that produces ${{\mathsf {s}}}{{\mathsf {t}}}_{\varphi (x)}$, and a short postprocessing step ${\mathsf {S}}_{\mathsf {pos}}$ that takes polynomial time given the trapdoor state ${{\mathsf {s}}}{{\mathsf {t}}}_{\varphi (x)}$.

Note that the above is indeed a generalization of the previous notion when considering the identity as the projection $\varphi$. As we shall see later on, the flexibility of choosing $\varphi$ differently, with the above tradeoff, will be useful in our application to non-malleable commitments. The construction of such $\varphi$-tuned 1ZK is identical to the construction described above only that we require that the trapdoor $(w,w')$ fixes $\varphi (x)$ rather than $x$. See further details in the full version.

One-Message Non-malleable Commitments

We now give an overview of how to use our 1ZK arguments to construct one-message non-malleable commitments. We adopt a standard formulation of non-malleable commitments where players have identities, and the commitment protocol depends on the identity of the committer, which is referred to as the tag of the interaction. Non-malleability [DDN03] ensures that no man-in-the-middle attacker can “maul” a commitment it receives on the left into a commitment of a related value it gives on the right, as long as the tags of the left and right commitments are different. More formally, for any two values u and w, the values the man-in-the-middle commits to after receiving left commitments to u or w, along with the commitments it sees on the left, are indistinguishable. The notion of concurrent non-malleability [DDN03, PR05a] further requires that no attacker can “maul” a set of left commitments into a set of right commitments so that the joint distribution of right committed values depends on the left committed values.

The number $\gamma$ of tags a scheme supports can be viewed as a quantitative measure of how non-malleable it is: A $\gamma$-tag non-malleable commitment gives a family of $\gamma$ commitment schemes—each with a hardwired tag—that are “mutually non-malleable” to each other. Therefore, the fewer tags, the easier it is to construct a corresponding non-malleable commitment. Indeed, as shown by [LPS17], non-interactive non-malleable commitments for a constant number of tags can be constructed from subexponentially-secure injective one-way functions and time-lock puzzles [RSW00]. Full-fledged non-malleable commitments, in contrast, have an exponential number of tags $\gamma = 2^\lambda$. Thus, the main challenge lies in increasing the number of tags from a constant to exponential.

Techniques for amplifying the number of tags have been explored in the literature [DDN03, LP11, KS17, LPS17]. They show that a non-malleable commitment scheme for $\gamma$ tags can be transformed into one for $2^{{\tilde{\varOmega }}(\gamma )}$ tags. Thus, starting from constant-tag non-malleable commitments, applying the transformation iteratively for $O(\log ^*\lambda )$ times yields non-malleable commitments for exponentially many tags. However, all existing tag-amplification techniques crucially rely on interaction—even if the initial constant-tag non-malleable commitments are non-interactive, the transformation increases the message-complexity to at least two. For instance, the tag-amplification technique of Khurana and Sahai makes use of 2-message SPS zero-knowledge arguments. In this work, we show how to replace the 2-message SPS ZK arguments with our 1ZK arguments, which gives a non-interactive tag-amplification technique, and hence non-interactive non-malleable commitments.

Two-Message Tag-Amplification. We start with reviewing the Khurana and Sahai (KS) 2-message tag-amplification technique, which transforms a non-interactive input scheme $\mathsf {iNM}$ for $\gamma$ tags into a 2-message output scheme $\mathsf {oNM}$ for ${\gamma \atopwithdelims (){\gamma /2}} = 2^{\varOmega (\gamma )}$ tags. Each ${\mathsf {tg}'}$ of $\mathsf {oNM}$ consists of a subset of $\gamma /2$ tags ${\mathsf {tg}'}= (\mathsf {tg}_1, \cdots , \mathsf {tg}_{\gamma /2})$ of $\mathsf {iNM}$. To commit to a value v, $\mathsf {oNM}$ computes $\gamma /2$ commitments to v using $\mathsf {iNM}$ with respect to tags $\mathsf {tg}_1, \cdots , \mathsf {tg}_{\gamma /2}$, followed by a 2-message SPS argument that all commitments are consistent. More precisely,

• KS 2-message tag-amplification— $\mathsf {oNM}$ :

• The receiver R sends the first message $\pi _1$ of a 2-message SPS argument.

• To commit to v using ${\mathsf {tg}'}= (\mathsf {tg}_1, \cdots , \mathsf {tg}_{\gamma /2})$, the committer C generates $\{\mathrm {nm}_j \leftarrow \mathsf {iNM}(\mathsf {tg}_j, v)\}_{j \in [\gamma /2]}$ and the second message $\pi _2$ of a 2-message SPS argument that all $\mathsf {iNM}$ commitments commit to the same value. The committed value is defined to be the value committed in $\mathrm {nm}_1$.

To see that $\mathsf {oNM}$ is non-malleable, consider a man-in-the-middle receiving a left commitment using ${\mathsf {tg}'}= (\mathsf {tg}_1, \cdots , \mathsf {tg}_{\gamma /2})$ and giving a right commitment using ${\tilde{\mathsf {tg}}'}= (\tilde{\mathsf {tg}}_1, \cdots , \tilde{\mathsf {tg}}_{\gamma /2})$. If ${\mathsf {tg}'}\ne {\tilde{\mathsf {tg}}'}$, there must exist ${i^\star }$, such that, $\tilde{\mathsf {tg}}_{i^\star }\ne \mathsf {tg}_i$ for all i—the ${i^\star }$’th right $\mathsf {iNM}$ commitment uses a tag different from all left tags.

Then, they reduce the non-malleability of $\mathsf {oNM}$ to the non-malleability of $\mathsf {iNM}$. To do so, they rely on the soundness of the 2-message SPS argument to argue that in left-honest man-in-the-middle executions, the attacker must send consistent $\mathsf {iNM}$ commitments $\{\widetilde{\mathrm {nm}}_j\}$ on the right, or else it would fail in the SPS argument. (Here by left-honest, we mean the proofs on the left are honestly generated and not simulated.) Thus, to show that the right committed values do not change in two left-honest executions with different left committed values u or w, it suffices to show that the value committed in any right $\mathsf {iNM}$ commitment—in particular, the ${i^\star }$’th one $\widetilde{\mathrm {nm}}_{i^\star }$—does not change (in a distinguishable manner). To show this, they gradually simulate components in the left commitment in a sequence of hybrids, while maintaining that ${{\tilde{v}}}_{i^\star }$ committed in $\widetilde{\mathrm {nm}}_{i^\star }$ does not change throughout hybrids.

In the first hybrid, the left SPS argument $(\pi _1, \pi _2)$ is simulated. To ensure that ${{\tilde{v}}}_{i^\star }$ does not change, they rely on complexity leveraging to make simulated proofs “harder to distinguish” than extracting from the commitment $\mathsf {iNM}$; that is, the indistinguishability of SPS simulation holds even when ${{\tilde{v}}}_{i^\star }$ is extracted by brute force. Once the left SPS argument is simulated, the left $\mathsf {iNM}$ commitments are switched to committing to 0 in following hybrids. By the non-malleability of $\mathsf {iNM}$ and the fact that $\widetilde{\mathrm {nm}}_{i^\star }$ uses a tag $\tilde{\mathsf {tg}}_{i^\star }$ different from all left tags, its committed value ${{\tilde{v}}}_{i^\star }$ does not change through these hybrids. Note that this requires the non-malleability of $\mathsf {iNM}$ to hold against $T_{\tiny \mathsf {iNM}}$-time attackers for $T_{\tiny \mathsf {iNM}} \gg T_{\tiny \mathrm {SPS}}$. Using SPS ZK where simulation-time only depends on the underlying security parameter (and not the size of the instance), the above can be satisfied by appropriately choosing the relation between the $\mathsf {iNM}$ security parameter ${n}$ and the SPS security parameter ${\bar{n}}$.

Non-interactive Tag-Amplification. To obtain non-interactive tag-amplification, a natural idea is replacing the 2-message SPS in the KS transformation with our 1ZK argument. However, two challenges arise:

• Challenge 1: Our 1ZK is only weakly sound. Thus, the man-in-the-middle attacker is able to generate an accepting 1ZK argument ${{\tilde{\pi }}}$ even when the right $\mathsf {iNM}$ commitments $\{\widetilde{\mathrm {nm}}_j\}$ are inconsistent (i.e., committing to different values).

• Challenge 2: In our basic 1ZK, the simulation time is subexponential in the length of the statement |x| (and the security parameter). This makes it difficult to guarantee that the simulator cannot break the underling non-malleable commitment, i.e. $T_{\tiny \mathsf {iNM}} \gg T_{\tiny \mathrm {SPS}}$.

  Specifically, the statement x concerns the consistency of $\gamma /2$ $\mathsf {iNM}$ commitments, and thus the simulation time is at least $T_{\tiny \mathrm {SPS}} = 2^{(\gamma \times \ell _{\mathrm {nm}}/2)^\varepsilon }$, where $\ell _{\mathrm {nm}}= \ell _{\mathrm {nm}}({n})$ is the length of $\mathsf {iNM}$ commitments and could scale polynomially with the security parameter ${n}$ of $\mathsf {iNM}$. It could well be that $T_{\tiny \mathsf {iNM}} \ll T_{\tiny \mathrm {SPS}}$.

In a nutshell, to solve the first problem, we rely on the weak soundness of 1ZK to argue that whenever the right $\mathsf {iNM}$ commitments are not consistent (that is, the statement is false), the right commitments are taken from a small “apriori known” set, and their underlying values can be non-uniformly hardcoded into the reduction. To solve the second problem, we make the security of $\mathsf {iNM}$ independent of the simulation time, by introducing an extra commitment under another scheme $\mathsf {Com}$ and using the $\varphi$-tuned version of 1ZK to reduce the simulation time to only depend on the length of commitments in $\mathsf {Com}$, instead of commitments in $\mathsf {iNM}$.

• The Actual Tag-Amplification and Resulting Scheme $\mathsf {oNM}$ :

• To commit to v using ${\mathsf {tg}'}= (\mathsf {tg}_1, \cdots , \mathsf {tg}_{\gamma /2})$, the committer C generates $\underline{c \leftarrow \mathsf {Com}(v)}$, $\{\mathrm {nm}_j \leftarrow \mathsf {iNM}(\mathsf {tg}_j, v)\}_{j \in [\gamma /2]}$, and a 1ZK argument $\pi$ showing that c and all $\mathsf {iNM}$ commitments commit to the same value. The 1ZK statement is given by $x = (c, \mathrm {nm}_1, \cdots , \mathrm {nm}_{\gamma /2})$ and we consider its projection $\varphi (x) = c$ that only fixes the $\mathsf {Com}$ commitment c.

• The committed value is defined to be the value committed in c.

Let us see how the above two problems are resolved.

Resolving Challenge 1: The weak soundness of $\varphi$-tuned 1ZK guarantees that for any attacker ${\mathcal {A}}$ of polynomial size $S$, there is a set ${\mathcal {Z}}$ consisting of a polynomial number $K(S)$ of $\mathsf {Com}$ commitments c (the so called projections) such that ${\mathcal {A}}$ cannot prove a false statement x where the corresponding commitment c is not in ${\mathcal {Z}}$. This means that in left-honest man-in-the-middle executions, one of the following two cases occurs: Either the right $\mathsf {Com}$ commitment ${{\tilde{c}}}$ and the $\mathsf {iNM}$ commitments are all consistent, or the commitment ${{\tilde{c}}}$ belongs to ${\mathcal {Z}}$. In the latter case, the right committed value must belong to the polynomial-sized set $\{{{\tilde{v}}}: {{\tilde{v}}}\text { is the value in }{{\tilde{c}}}\in {\mathcal {Z}}\}$, which can be hardwired non-uniformly into the reduction. In the first case, showing the indistinguishability of the right committed values again reduces to showing that of ${{\tilde{v}}}_{i^\star }$ committed in $\widetilde{\mathrm {nm}}_{i^\star }$.

Resolving Challenge 2: Recall that $\varphi$-tuned 1ZK enjoys a simulation speedup. Specifically, simulation consists of (i) a $2^{|c|^{\delta }}$-time preprocessing phase that depends only on the projection c and computes a trapdoor state ${{\mathsf {s}}}{{\mathsf {t}}}\leftarrow {\mathsf {S}}_{\mathsf {pre}}(c)$, and (ii) a polynomial $\mathrm {poly}(|x|, {\bar{n}})$-time postprocessing phase that generates the simulated proof ${\widehat{\pi }}\leftarrow {\mathsf {S}}_{\mathsf {pos}}(x,{{\mathsf {s}}}{{\mathsf {t}}})$. With this speed-up, let us examine again the sequence of hybrids where the left $\mathsf {Com}$ and $\mathsf {iNM}$ commitments are gradually switched to committing to 0, while the 1ZK argument on the left is simulated. We need to ensure that ${{\tilde{v}}}_{i^\star }$ does not change.

To change the $\mathsf {Com}$ commitment, we require that its hiding holds even in the presence of 1ZK simulation and (brute-force) extraction from ${{\tilde{v}}}_{i^\star }$:

$$\begin{aligned} T_{\tiny \mathsf {Com}} \gg T_{\tiny \mathrm {SPS}} = 2^{|c|^{\delta }} + \mathrm {poly}(|x|, {\bar{n}}) \quad \text { and } \quad T_{\tiny \mathsf {Com}} \gg T_{\tiny \mathsf {iNM.E}} \end{aligned}$$

The latter can be satisfied by setting the security parameter ${\bar{n}}$ of $\mathsf {Com}$ to be sufficiently larger than the security parameter ${n}$ of $\mathsf {iNM}$. The former is more subtle as it requires $\mathsf {Com}$ to be at least $2^{|c|^{\delta }}$-secure, where |c| is the length of $\mathsf {Com}$ commitments. Such a commitment scheme for strings of length $\ell$, can be instantiated by the classical Blum-Micali bit commitment scheme [BM84] (recall that a commitment to b is $f(r), \mathrm {hc}(r)\,\oplus \,b$, where $\mathrm {hc}$ is a hardcore bit of an injective one-way function f), instantiated with any $2^{k^{\rho }}$-hard injective one-way function, and sufficiently large security parameter $k > \varOmega (\ell ^{{\delta }/{\rho }-{\delta }})$.

Next, when changing the left $\mathsf {iNM}$ commitments, we can circumvent the requirement that $T_{\tiny \mathsf {iNM}} \gg T_{\tiny \mathrm {SPS}}$ by leveraging the efficient postprocessing of 1ZK simulation. Recall that given a trapdoor state ${{\mathsf {s}}}{{\mathsf {t}}}\leftarrow {\mathsf {S}}_{\mathsf {pre}}(c)$ that depends only on the projection c, simulating the proof ${\widehat{\pi }}\leftarrow {\mathsf {S}}_{\mathsf {pos}}(x, {{\mathsf {s}}}{{\mathsf {t}}})$ takes only polynomial time. When changing the values committed in left $\mathsf {iNM}$ commitments, the left $\mathsf {Com}$ commitment c is independent—it is by now a commitment to 0. If in two neighboring hybrids, the value ${{\tilde{v}}}_{i^\star }$ on the right changes, there must exist a commitment c (committing to 0) such that conditioned on c occurring in the hybrids the value ${{\tilde{v}}}_{i^\star }$ still changes. With respect to this specific c, 1ZK simulation can now be done in polynomial time, given as non-uniform advice the preprocessed state ${{\mathsf {s}}}{{\mathsf {t}}}\leftarrow {\mathsf {S}}_{\mathsf {pre}}(c)$ depending on c. This suffices for the security reduction, as now, the non-malleability of $\mathsf {iNM}$ is detached from the 1ZK simulation time.

A Subtle Issue. The above description captures the main idea, but misses a subtle issue. Roughly speaking, in order to apply our tag-amplification iteratively, across different iterations, we need to increase the level of security of the $\mathsf {Com}$ schemes used in each iteration. In particular, the security parameter k for the one-way functions underlying $\mathsf {Com}$ needs to grow polynomially in each iteration. If we start with $k> \ell ^{{\delta }/({\rho }-{\delta })} =\ell ^{\varOmega (1)}$, after a super-constant number of iterations (out of the $\log ^*n$ iterations needed), k would grow to be super-polynomial in $\ell$.

To avoid this, we modify the scheme $\mathsf {oNM}$ to have a separate 1ZK argument for each bit commitment $c_j$ (committing to a bit $v_j$ of the committed value), proving that all $\mathsf {iNM}$ commitments are consistent with it, in the sense that, the j’th bit of their committed strings equals to the bit committed in $c_j$. By doing so, $c_j$ only needs to be $2^{|c_j|^{\delta }}$-secure, independent of the length $\ell$ of committed values. Thus, we no longer need to set k to be $k=\ell ^{\varOmega (1)}$, but instead to $k = \ell ^{o(1)}$. Though k still increases through $O(\log ^* n)$ iterations, it is always kept polynomial in $\ell$. See section for a formal description of the final transformation.

Achieving Concurrency. Applying our non-interactive tag amplification to the 4-tag non-malleable commitments of [LPS17] gives a full-fledged non-interactive non-malleable commitment, which however, is only stand-alone (i.e., one-one) but not concurrently non-malleable. This is because the basic commitments of [LPS17] are not concurrently non-malleable.

To obtain concurrent non-malleability, we give another transformation from non-malleable commitments in a restricted concurrent setting, called same-tag concurrency into fully concurrent ones. Roughly speaking, in the same-tag concurrent setting, we require non-malleability to hold with respect to attackers who always use the same tag in all commitments on the right. We observe that the 4-tag commitments of [LPS17] actually are same-tag non-malleable, and our tag amplification preserves this property. Therefore, by applying the same-tag to full-concurrency transformation after tag amplification, we obtain concurrent non-malleability.

Our transformation is inspired by the 2-round non-malleability strengthening transformation in [LPS17], but works in one message and is simpler and more modular; in particular, the transformation of [LPS17] relies directly on time-lock puzzles, whereas we work with any non-malleable commitment satisfying the intermediate notion of same-tag non-malleability.

At a high level, starting from a same-tag non-malleable input scheme $\mathsf {iNM}$, our transformation follows the Naor-Yung paradigm for constructing CCA encryption, producing an output scheme $\mathsf {oNM}$ as follows. $\mathsf {oNM}$ fixes two arbitrary tags $\mathsf {tg}^\star _0, \mathsf {tg}^\star _1$ of $\mathsf {iNM}$ for special use, and commitments are computed using to other tags $\mathsf {tg}\ne \mathsf {tg}^\star _0, \mathsf {tg}^\star _1$.

• The Same-Tag to Fully-Concurrent Transformation and Resulting Scheme $\mathsf {oNM}$ (Simplified):

  • On input v and tag $\mathsf {tg}$, the committer C commits to v using $\mathsf {iNM}$ with the two special tags:

    $$\begin{aligned} \mathrm {nm}_0 \leftarrow \mathsf {iNM}(\mathsf {tg}^\star _0, v) \qquad \mathrm {nm}_1 \leftarrow \mathsf {iNM}(\mathsf {tg}^\star _1, v), \end{aligned}$$

    and proves that both $\mathsf {iNM}$ commitments commit to the same value v. The proof is computed using a simulation-sound variant of our 1ZK argument relative to the tag $\mathsf {tg}$.

To argue the concurrent non-malleability of $\mathsf {oNM}$, it suffices to argue one-many non-malleability [LPV08a] (that is, the man-in-the-middle receives a single commitment on the left and gives many commitments on the right.)

The two commitments of $\mathsf {iNM}$ using special tags $\mathsf {tg}^\star _0$ and $\mathsf {tg}^\star _1$ are the counterparts of the as two public-key encryptions in the Naor-Yung paradigm, and the proof of non-malleability follows similarly to the proof of CCA security. The simulation soundness of 1ZK ensures that the man-in-the-middle attacker can only send consistent $\widetilde{\mathrm {nm}}_{0,j}$ and $\widetilde{\mathrm {nm}}_{1,j}$ in every right commitment j, even when the left 1ZK argument is simulated. Therefore, as the left commitment $\mathrm {nm}_0$ is simulated (by committing to 0), one can argue that the right committed values do not change by showing that values in $\{\widetilde{\mathrm {nm}}_{1,j}\}$ do not change. Similarly, as the left commitment $\mathrm {nm}_1$ is simulated, one can switch to showing that values in $\{\widetilde{\mathrm {nm}}_{0,j}\}$ do not change. Here same-tag non-malleability is essential for arguing that the joint distribution of all right committed values does not change (in a distinguishable manner).

To achieve simulation-soundness, we open the construction of our 1ZK arguments. Recall that these arguments rely on a basic commitment scheme, a NIWI, and an incompressible language. We show that by replacing the basic commitment scheme with a non-malleable one (such as the input scheme $\mathsf {iNM}$), our 1ZK arguments become simulation-sound. For this approach to work, we additionally need “mutual non-malleability” between the commitment in our simulation-sound 1ZK arguments and the $\mathsf {iNM}$ commitments using $\mathsf {tg}^\star _0, \mathsf {tg}^\star _1$. That is, (i) simulating the 1ZK argument on the left does not change the values that the attacker commits to in $\mathsf {iNM}$ commitments $\{\widetilde{\mathrm {nm}}_{0,j}, \widetilde{\mathrm {nm}}_{1,j}\}$ on the right, and (ii) changing the values committed in the $\mathsf {iNM}$ commitments on the left does not allow the attacker to break (weak) soundness on the right. Such “mutual non-malleability” is achieved again relying on the same-tag non-malleability of $\mathsf {iNM}$ and the fact that the $\mathsf {iNM}$ commitments use two special tags $\mathsf {tg}^\star _0, \mathsf {tg}^\star _1$ different from the tags we use for $\mathsf {iNM}$ commitments in 1ZK arguments.

The above discussion is overly-simplified. Indeed, this transformation also has to deal with the challenges presented before in the tag-amplification transformation. They are dealt with using similar techniques. See Sect. ?? for details.

New Candidate Constant-Tag Non-malleable Commitments. As explained above, our transformations start from non-malleable commitments for a constant number of tags, which were previously known based on time-lock puzzles [LPS17]. We also provide new candidate constant-tag non-malleable commitments, based on a new assumption on hardness amplification of (injective) one-way functions.

Known results on hardness amplification have shown ways of strengthening weak one-way functions to strong ones, via direct product lemmas or XOR lemmas. However, these results have a common weakness—hardness does not amplify beyond negligible. Concretely, starting from a function f that is $\delta$-hard against T-time attackers, the k-fold combined function $f'$ is $(\mathrm {poly}(\frac{T'}{T}) + (1-\delta )^k))$-hard for $(T'\ll T)$-time attackers. As the number k of copies increases, the hardness approaches the limit of $\mathrm {poly}(\frac{T'}{T})$.

The work of [DJMW12] showed that this limit is inherent for certain contrived one-way functions, but there is no evidence that this limit should bound natural one-way functions, such as, discrete logarithm, RSA, or Rabin. We put forward the notion of amplifiable one-way functions and hardcore bits: Roughly speaking, we say that a one-way function f is amplifiable, if there is a way to combine (e.g. XOR), say $\ell$, hardcore bits, corresponding to $\ell$ independent images $f(x_1),\dots ,f(x_\ell )$, so that the combined bit is $2^{\ell ^\varepsilon }$-unpredictable; that is, the level of unpredictability increases at least subexponentially as more hardcore bits are combined and beyond the limit $\mathrm {poly}(\frac{T'}{T})$.

We show that amplifiable one-way functions are useful for constructing non-malleable commitments. They essentially allow us to construct commitment schemes $(\mathsf {Com}, \mathsf {Com}')$, such that, $\mathsf {Com}$ is “harder” than $\mathsf {Com}'$ in the time axis—$\mathsf {Com}$ remains hiding in time needed for extracting from $\mathsf {Com}'$, whereas $\mathsf {Com}'$ is “harder” than $\mathsf {Com}$ in the distinguishing axis—the maximum distinguishing advantage of $\mathsf {Com}'$ is smaller than the probability that one can guess a decommitment of $\mathsf {Com}$. As shown in [LPS17], commitments that are harder than each other under different measures are essentially non-malleable. This yields new candidate constant-tag non-malleable commitments with one-way functions that are believed to have amenable hardness amplification behavior, such as, discrete logarithm, RSA, or Rabin.

1.3 Concurrent Work

In concurrent and independent work, Holmgren and Lombardi [HL18] study one-way product functions, which are related to our notion of amplifiable one-way functions. Their notion requires that $\ell$ independent images $f(x_1),\dots ,f(x_\ell )$ cannot be inverted simultaneously by efficient algorithms, except with exponentially small probability in the input size. They show how to use such functions in different parameter regimes to obtain several applications ranging form collision-resistant hashing to correlation intractability (when combined with indistinguishability obfuscation). (The exact inversion probability and choice of $\ell$ depends on the specific application. Most of their applications are in the regime where $\ell$ is small, e.g. constant, and the inversion probability is at most $2^{-n-\omega (\log n)}$.)

While their one-way product functions and our amplifiable one-way functions are very related, there are some notable differences. For once, we make a stronger requirement than the hardness of inversion, namely, the hardness of predicting a combined hardcore bit. (Note that this gap cannot be bridged by the classic Goldreich-Levin theorem, where the adversary’s distinguishing advantage $\varepsilon$ translates to a reduction running in time at least $\mathrm {poly}(\varepsilon ^{-1})$ to invert the underlying function.) On the other hand, since we allow $\ell$ to grow polynomially, our notion could potentially hold for one-way functions where a single copy is only mildly hard to invert, whereas for many of their applications (like collision-resistant hashing), $\ell$ is required to be small, and accordingly the one-way function has to be hard to invert except with exponentially small probability.

Organization. The rest of this extended abstract is organized as follows. In Sect. 2, we give some of the basic definitions used in the paper, including the definition of non-malleable commitments that we achieve. In Sect. 3, we define the notion of incompressible problems. In Sect. 4, we define and construct our new notion of one-message zero knowledge. Our constructions of non-malleable commitments, as well as all proofs, can be found in the full version of the paper.

2 Preliminaries

We rely on the following standard computational concepts:

• We model algorithms as (possibly probabilistic and possibly interactive) Turing machines. A non-uniform algorithm ${\mathsf {M}}$ is given by a family of algorithms ${\mathsf {M}}=\left\{ {\mathsf {M}}_\lambda \right\} _{\lambda \in {\mathbb {N}}}$, where $\lambda$ is a security parameter, and each ${\mathsf {M}}_\lambda$ corresponds to an input size $n(\lambda )$ and has description-size related to $\lambda$.

  • ${\mathsf {M}}$ is $T$-time, if for every $\lambda \in {\mathbb {N}}$, ${\mathsf {M}}_\lambda$ performs at most $T(\lambda )$ steps.

  • ${\mathsf {M}}$ is $S$-size if for every $\lambda \in {\mathbb {N}}$, ${\mathsf {M}}_\lambda$ has description size at most $S(\lambda )$.

  Throughout, we assume w.l.o.g. that the description-size of a non-uniform algorithm is bounded by its running time $S(\lambda ) \le T(\lambda )$ for all $\lambda$. A uniform algorithm ${\mathsf {M}}$ is a special-case of a non-uniform algorithm where for all $\lambda \in {\mathbb {N}}$, ${\mathsf {M}}_\lambda ={\mathsf {M}}$ is a single, constant-size, algorithm. A PPT is a probabilistic polynomial-time uniform algorithm. By default, algorithms in cryptographic schemes are PPTs.

• We model $T$-time adversaries as arbitrary non-uniform $T$-time algorithms ${\mathcal {A}}=\left\{ {\mathcal {A}}_\lambda \right\} _{\lambda \in {\mathbb {N}}}$. Efficient adversaries have polynomial time. Throughout this work, we consider polynomial-size adversaries, and assume w.l.o.g. that their sizes are at least $\lambda$, i.e., $|A_\lambda | \ge \lambda$ (via padding).

• We say that a function $f:{\mathbb {N}}\rightarrow {\mathbb {R}}$ is negligible if for all constants $c > 0$, there exists $N \in {\mathbb {N}}$ such that for all $n > N$, $f(n) < n^{-c}$. We sometimes denote negligible functions by $\mathrm {negl}$.

• We say that a function $f:{\mathbb {N}}\rightarrow {\mathbb {R}}$ is noticeable if there exists a constant $c > 0$ and $N \in {\mathbb {N}}$ such that for all $n > N$, $f(n) \ge n^{-c}$.

• For two functions $T(\lambda ),T'(\lambda )$, we write that $T' \ll T$ if $T' = T^{o(1)}$, when $\lambda \rightarrow \infty$.

In this paper, we will sometimes consider security of primitives against general $\mathrm {poly}(T)$-time adversaries, as illustrated in the definition of $T$-indistinguishability below.

Definition 1

($(T, \mu )$-Indistinguishability). Let ${\mathcal {X}}^{(b)}=\{X^{(b)}_{\lambda }\}_{\lambda \in {\mathbb {N}}}$ for $b \in \{0,1\}$ be two ensembles of random variables indexed by $\lambda \in {\mathbb {N}}$. We say that ${\mathcal {X}}^{(0)}$ and ${\mathcal {X}}^{(1)}$ are $(T,\mu )$-indistinguishable for functions $T,\mu$, if for all $\mathrm {poly}(T)$-time distinguishers ${\mathcal {D}}$, and all large enough $\lambda$,

$$\begin{aligned} \left| \Pr [{\mathcal {D}}(X^{(0)}_\lambda )=1] - \Pr [{\mathcal {D}}(X^{(1)}_\lambda )=1] \right| \le \mu (\lambda )^{\varOmega (1)}. \end{aligned}$$

We say that ${\mathcal {X}}^{(0)}$ and ${\mathcal {X}}^{(1)}$ are $T$-indistinguishable if it is $(T,\mu )$-indistinguishable for some negligible function $\mu$. We say that they are computational indistinguishable if they are $T$-indistinguishable for every polynomial $T$.

We denote the above notions of indistinguishability by ${\mathcal {X}}^{(0)} \thickapprox _{T,\mu } {\mathcal {X}}^{(1)}$, ${\mathcal {X}}^{(0)} \thickapprox _{T} {\mathcal {X}}^{(1)}$, and ${\mathcal {X}}^{(0)} \approx {\mathcal {X}}^{(1)}$, respectively.

2.1 Commitments

We define non-interactive commitments.

Definition 2

(Commitment Scheme). A non-interactive commitment scheme consists of two polynomial-time algorithms $(\mathsf {Com},\mathsf {Open})$, with the following syntax:

• $(c, d)\leftarrow \mathsf {Com}(v, 1^\lambda )$: Given $1^\lambda$ and $v \in \{0,1\}^{*}$, $\mathsf {Com}$ samples a commitment c and a decommitment string d.

• $b = \mathsf {Open}(c, v, d)$: Given a commitment c, value v, and decommitment string d, $\mathsf {Open}$ outputs a bit b, where $b=1$ indicates acceptance. We say that a commitment c is valid, if there exists a decommitment (v, d), such that $\mathsf {Open}(c,v,d) = 1$.

We make the following requirements:

Correctness: For any $\lambda \in {\mathbb {N}}$, $v \in \{0,1\}^*$,

$$\begin{aligned} \Pr [\mathsf {Open}(c, v, d)\ :\ (c,d)\leftarrow \mathsf {Com}(v,1^\lambda ) ] = 1. \end{aligned}$$

Binding: For any string c, values $v,v'$, and decommitment strings $d,d'$,

$$\begin{aligned} \text { if } \mathsf {Open}(c, v,d) = \mathsf {Open}(c, v', d') =1 \text { then } v = v' . \end{aligned}$$

For any polynomial $n=n(\lambda )$,

$$\begin{aligned} \left\{ \mathsf {Com}(v,1^\lambda )\right\} _{\lambda \in {\mathbb {N}}, v, v' \in \{0,1\}^{n\times 2}} \thickapprox _{T} \left\{ \mathsf {Com}(v',1^\lambda )\right\} _{\lambda \in {\mathbb {N}}, v, v' \in \{0,1\}^{n\times 2}} . \end{aligned}$$

Tag-Based Commitments. We consider “tag-based” commitment schemes.

Definition 3

(Tag-based commitment scheme). A commitment scheme $(\mathsf {Com},\mathsf {Open})$ is a tag-based scheme with $t$-bit tags if, in addition to $1^\lambda$, $\mathsf {Com}$ also receive a “tag” (a.k.a. identity) $\mathsf {tg}\in \{0,1\}^{t(\lambda )}$ as input, $c \leftarrow \mathsf {Com}(\mathsf {tg},v,1^\lambda )$. We assume w.l.o.g that commitments generated by $\mathsf {Com}$ contains the tag used for generating them. For any sequence of fixed tags $\mathsf {tg}=\left\{ \mathsf {tg}_\lambda \right\} _\lambda$, the corresponding $(\mathsf {Com}_{\mathsf {tg}},\mathsf {Open}_{\mathsf {tg}})=\left\{ (\mathsf {Com}_{\mathsf {tg}_\lambda },\mathsf {Open}_{\mathsf {tg}_\lambda })\right\} _\lambda$ satisfy correctness, binding, and hiding as defined for plain commitment schemes. By default, a tag-based commitment scheme has $t$-bit tags for some polynomial $t$.

2.2 Non-malleable Commitments

The Man-in-the-Middle (MIM) Execution: Let $\mathsf {NM}= (\mathsf {Com}, \mathsf {Open})$ be a commitment scheme for $t$-bit tags, and ${\mathcal {A}}= \{{\mathcal {A}}_\lambda \}_{\lambda \in {\mathbb {N}}}$ an arbitrary non-uniform adversary. For a security parameter $\lambda$, and $m = m(\lambda )$, ${\mathcal {A}}_\lambda$ on input $1^\lambda$, receives m commitments from an honest committer ${\mathsf {C}}$ to values $v_1, \ldots , v_m \in \{0,1\}^{ \lambda }$, and sends m commitments to ${\mathsf {R}}$ to values $\tilde{v}_1,\ldots ,\tilde{v}_m \in \{0,1\}^{\lambda }$. The commitments received by the adversary are called the left commitments and those sent are called the right commitments. The left and right commitments use $t= t(\lambda )$-bit tags $\mathsf {\mathsf {tg}}_1,\mathsf {\mathsf {tg}}_2,\ldots ,\mathsf {\mathsf {tg}}_m$ and $\mathsf {\tilde{\mathsf {tg}}}_1,\mathsf {\tilde{\mathsf {tg}}}_2,\ldots ,\mathsf {\tilde{\mathsf {tg}}}_m$ chosen adaptively by ${\mathcal {A}}_\lambda$ for each commitment. The values ${{{\tilde{v}}}_j}$ in the j’th right commitment ${\tilde{c}}_j$ is defined as

$$\begin{aligned} {{{\tilde{v}}}_j} = {\left\{ \begin{array}{ll} \bot &{} \text {if } \exists i,\ \mathsf {tg}_i = {\widetilde{\mathsf {tg}}}_j \\ \mathsf {val}({{{\tilde{c}}}_j}) &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$

That is, ${{\tilde{v}}}_j$ is either the unique committed value if the commitment ${{\tilde{c}}}_j$ is valid and uses a tag different from all left tags, or $\bot$ otherwise. (Recall that by binding, ${{\tilde{v}}}_j$ is uniquely defined whenever ${{\tilde{c}}}_j$ is valid.)

We denote by $\mathsf {MIM}^{\mathcal {A}}_{\mathsf {NM}}(v_1,\ldots ,v_m, 1^\lambda )$ the above described man-in-the-middle experiment.

Non-malleability with Respect to Commitment. Let $\mathsf {mim}^{\mathcal {A}}_{\mathsf {NM}}(v_1,\ldots ,v_m, 1^\lambda )$ denote the random variable that describes the view of ${\mathcal {A}}_\lambda$ (consisting of all left commitments) and the values ${{{\tilde{v}}}}_1, \ldots , {{{\tilde{v}}}}_m$ it commits to on the right in the above man-in-the-middle experiment.

Definition 4

(Non-Malleability). A commitment scheme $\mathsf {NM}$ for $t$-bit tags is concurrent $T$-non-malleable if for any non-uniform $\mathrm {poly}(T)$-time adversary ${\mathcal {A}}= \{ {\mathcal {A}}_\lambda \}_{\lambda \in {\mathbb {N}}}$ and for every polynomial $m=m(\lambda )$, it holds that:

$$\begin{aligned}&\qquad \,\,\,\, \left\{ \mathsf {mim}^{\mathcal {A}}_{\mathsf {NM}}(v_1,\ldots ,v_m, 1^\lambda ) \right\} _{\lambda \in {\mathbb {N}}, v_1, \ldots , v_m, v_1', \ldots , v_m'\in \{0,1\}^{\lambda }} \\&\quad \approx _c\ \left\{ \mathsf {mim}^{\mathcal {A}}_{\mathsf {NM}}(v_1',\ldots ,v_m', 1^\lambda ) \right\} _{\lambda \in {\mathbb {N}}, v_1, \ldots , v_m, v_1', \ldots , v_m'\in \{0,1\}^{\lambda }} . \end{aligned}$$

2.3 Non-interactive Witness-Indistinguishable Proofs

We define non-interactive witness-indistinguishable proofs ($\hbox {NIWI}$s).

Definition 5

(NIWI). A non-interactive witness-indistinguishable proof system $({\mathsf {P}},{\mathsf {V}})$ for an NP relation ${\mathcal {R}}(x,w)$ consists of two polynomial-time algorithms:

• $\pi \leftarrow {\mathsf {P}}(x,w,1^\lambda )$: Given an instance x, witness w, and security parameter $1^\lambda$, ${\mathsf {P}}$ produces a proof $\pi$.

• $b={\mathsf {V}}(x,\pi )$: Given a proof $\pi$ for instance $x$, ${\mathsf {V}}$ outputs a bit b, where $b=1$ indicates acceptance.

We make the following requirements:

Completeness: For every $\lambda \in {\mathbb {N}},(x,w) \in {\mathcal {R}}$,

$$\begin{aligned} \mathop {\Pr }\limits _{{\mathsf {P}}}[{\mathsf {V}}(x, \pi ) = 1 : \pi \leftarrow {\mathsf {P}}(x,w,1^\lambda )] = 1. \end{aligned}$$

Soundness: For every $x\notin {\mathcal {L}}({\mathcal {R}})$ and $\pi \in \{0,1\}^*$:

$$\begin{aligned} {\mathsf {V}}(x, \pi ) \ne 1 . \end{aligned}$$

: For any sequence

$$\begin{aligned} {\mathcal {I}}=\left\{ (\lambda ,x,w_0,w_1):\begin{array}{c}\lambda \in {\mathbb {N}},x,w_0,w_1 \in \{0,1\}^{\mathrm {poly}(\lambda )},\\ (x,w_0),(x,w_1)\in {\mathcal {R}}\end{array}\right\} \end{aligned}$$

It holds that

$$\begin{aligned} \left\{ \pi _0 \leftarrow {\mathsf {P}}(x,w_0,1^\lambda )\right\} _{(\lambda ,x,w_0,w_1) \in {\mathcal {I}}} \approx _{T} \left\{ \pi _1 \leftarrow {\mathsf {P}}(x,w_1,1^\lambda )\right\} _{(\lambda ,x,w_0,w_1) \in {\mathcal {I}}}. \end{aligned}$$

Barak, Ong, and Vadhan [BOV07] constructed NIWIs based on NIZK and the worst-case assumption that there exists a problem solvable in deterministic time $2^{O(n)}$ with non-deterministic circuit complexity $2^{\varOmega (n)}$ (or more generally the existence of hitting set generators that fool non-deterministic distinguishers). Groth, Ostrovsky, and Sahai [GOS12] then constructed NIWIs based on standard assumptions on bilinear maps such as the Decision Linear Assumption, the Symmetric External Diffie Hellman assumption, or the Subgroup Decision Assumption. Bitansky and Paneth [BP15] constructed NIWIs from indistinguishability obfuscation and one-way permutations.

2.4 Two-Source Extractors

We rely on the standard notion of two-source extractors.

Definition 6

(Two-Source Extractor). A polynomial-time computable function $\mathsf {2Ext}:\{0,1\}^{n}\times \{0,1\}^{n} \rightarrow \{0,1\}^m$ is a $(k_1,k_2,\varepsilon )$-two-source extractor, if for any two independent sources $X_1,X_2$ with min-entropies at least $k_1$ and $k_2$, respectively, it holds that

$$\begin{aligned} \Vert \mathsf {2Ext}(X_1,X_2) - U_m\Vert _1 \le \varepsilon , \end{aligned}$$

where $U_m$ is the uniform distribution over $\{0,1\}^m$.

We also require efficient reverse sampling, which says that given any y in the image of the extractor $\mathsf {2Ext}$ we can efficiently sample uniformly random and independent sources $X_1$ and $X_2$ conditioned on $\mathsf {2Ext}(X_1,X_2)=y$.

Definition 7

(Efficient Reverse Sampling). A function $\mathsf {2Ext}:\{0,1\}^{n}\times \{0,1\}^{n} \rightarrow \{0,1\}^m$ is efficiently reverse-samplable if there exists a PPT that given $y\in \mathsf {Image}(\mathsf {2Ext})$ outputs a uniformly random pair $x_1,x_2$ such that $\mathsf {2Ext}(x_1,x_2)=y$.

Two source extractors with efficient reverse sampling and an exponentially small error are known based on the Hadamard code over an appropriate field.

3 Incompressible Problems

Following [BKP18], we consider a notion of incompressible problems. Here every security parameter $\lambda$, defines a search problem $\mathcal {W}_\lambda$ with superpolynomially many solutions $w \in \mathcal {W}_\lambda$. Since the problem is fixed, a non-uniform adversary ${\mathcal {A}}=\left\{ {\mathcal {A}}_\lambda \right\}$ may always have hardwired solutions $w\in \mathcal {W}_\lambda$ in its code. We require, however, that it is impossible to significantly compress solutions—an adversary with description size at most $S$ and bounded running time $T$, larger than $S$, should fail to produce more than $S$ solutions (or $K(S)$ solutions for some polynomial blowup function $K(\cdot )$).

Definition 8

(Incompressible Problem). An incompressible problem $\mathcal {W}$ is associated with a polynomial-time verifier algorithm $\mathcal {V}$ and a collection of sets $\left\{ \mathcal {W}_\lambda \right\} _\lambda$, such that $\mathcal {W}_\lambda \subseteq \{0,1\}^{\ell }$ for some polynomial $\ell =\ell (\lambda )$, and for any $w\in \{0,1\}^{\ell }$, $\mathcal {V}(w)=1$ if and only if $w\in \mathcal {W}_\lambda$. For any function $T=T(\lambda )\ge \lambda$ and polynomial $K$, we make the following incompressibility requirement.

(T, K)-Incompressibility: for any non-uniform $\mathrm {poly}(T)$-time, polynomial-size, probabilistic adversary ${\mathcal {A}}= \left\{ {\mathcal {A}}_\lambda \right\}$, there is a negligible function $\mu$, such that for any $\lambda \in {\mathbb {N}}$, letting $K=K(|{\mathcal {A}}_{\lambda }|)$,

We say that $\mathcal {W}$ has density $\varDelta =\varDelta (\lambda )$, if for every sufficiently large $\lambda \in {\mathbb {N}}$, letting $\ell =\ell (\lambda )$, it holds that $|\mathcal {W}_\lambda | \ge \varDelta 2^{\ell }$. We say that $\mathcal {W}$ has subexponential density if it has density $\varDelta = 2^{-\ell ^\varepsilon }$ for some constant $\varepsilon$.

Remark 1

(Parameters). The parameters $T,K,\varDelta$ that we consider will always be such that

$$\begin{aligned} K\le T\ll K\varDelta ^{-1}. \end{aligned}$$

Indeed, when $T<K$ the requirement trivializes and when $T\ge \mathrm {poly}(K\varDelta ^{-1})$ the requirement becomes impossible.

Candidates. Candidates for incompressible problems were introduced in [BKP18]. The problems addressed there come from keyless (shrinking) hash functions where collisions are incompressible in some sense. We can rely on more general incompressible problems, which may give rise to additional candidates. The problems considered in [BKP18] and a discussion of additional possible candidates can be found in the full version of the paper.

4 One-Message Zero Knowledge

In this section, we give a new definition of a one-message zero-knowledge (1ZK) system, and construct such a system based on incompressible problems. The definition relaxes both the zero knowledge requirement and soundness. Here the zero knowledge definition is the standard super-polynomial simulation (SPS) definition [Pas03]. The soundness definition is new and roughly says that a (relatively) efficient adversary of description size $S$ shouldn’t be able to sample more than $S$ (or $K(S)$ for some polynomial blowup $K$) false statements $x$ together with an accepting proof $\pi$. As discussed in the introduction, both of these relaxations are necessary.

We proceed to the formal definition.

Definition 9

(1ZK). A one-message zero-knowledge argument system $({\mathsf {P}},{\mathsf {V}})$ for an NP relation ${\mathcal {R}}(x,w)$ consists of two polynomial-time algorithms:

• $\pi \leftarrow {\mathsf {P}}(x,w,1^\lambda )$: Given an instance x, witness w, and security parameter $1^\lambda$, ${\mathsf {P}}$ produces a proof $\pi$.

• $b={\mathsf {V}}(x,\pi ,1^\lambda )$: Given a proof $\pi$ for instance $x$, ${\mathsf {V}}$ outputs a bit b, where $b=1$ indicates acceptance.

The system is parameterized by functions $T_{\tiny {\mathsf {D}}}(\cdot ),T_{\tiny {\mathsf {S}}}(\cdot ),T_{\tiny {\mathsf {P}}}(\cdot ),K(\cdot )$.

We make the following requirements:

Completeness: For every $\lambda \in {\mathbb {N}},(x,w) \in {\mathcal {R}}$,

$$\begin{aligned} \mathop {\Pr }\limits _{{\mathsf {P}}}[{\mathsf {V}}(x, \pi ,1^\lambda ) = 1 : \pi \leftarrow {\mathsf {P}}(x,w,1^\lambda )] = 1. \end{aligned}$$

: There exists a uniform $\mathrm {poly}(T_{\tiny {\mathsf {S}}})$-time simulator ${\mathsf {S}}$, such that,

$$\begin{aligned} \left\{ \pi \leftarrow {\mathsf {P}}(x,w,1^\lambda )\right\} _{\begin{array}{c} (x ,w) \in {\mathcal {R}}\\ \lambda \in {\mathbb {N}} \end{array}} \approx _{T_{\tiny {\mathsf {D}}}} \left\{ {\widehat{\pi }}\leftarrow {\mathsf {S}}(x,1^\lambda )\right\} _{\begin{array}{c} (x ,w) \in {\mathcal {R}}\\ \lambda \in {\mathbb {N}} \end{array}}. \end{aligned}$$

: For any non-uniform $\mathrm {poly}(T_{\tiny {\mathsf {P}}})$-time, polynomial-size, probabilistic adversary ${\mathcal {A}}=\left\{ {\mathcal {A}}_\lambda \right\} _\lambda$ there exists a negligible $\mu$ and a collection of sets ${\mathcal {Z}}=\left\{ {\mathcal {Z}}_\lambda \right\} _\lambda$, where $|{\mathcal {Z}}_\lambda |\le K(|{\mathcal {A}}_\lambda |)$, such that for any $\lambda \in {\mathbb {N}}$,

$\varphi$-Tuning: Relaxed Soundness and Speeding-up Simulation. We in fact consider a more general definition that allows to get faster simulators on the account of relaxing soundness. Here the argument system is associated with a non-expanding (typically, shrinking) projection function $\varphi (\cdot )$ defined over instances $x$. Soundness is relaxed and guarantees that the adversary could only output accepting pairs $(x,\pi )$ for false statements whose projection $\varphi (x)$ falls in a set of size at most $K(S)$. Simulation is performed in two steps—a first preprocessing step that depends only on $\varphi (x)$, and a postprocessing step that depends on the instance $x$ itself and the state produced in the preprocessing phase. The preprocessing phase takes superpolynomial time, but only depends on $\ell := |\varphi (x)|$ and not on $|x|$; the postprocessing phase takes polynomial time.

Note that the previous basic definition is indeed a special case of this definition by considering the identity projection (in this case the entire simulation is done in the preprocessing phase, and takes superpolynomial time in $|x|$). We gain from this definitions in scenarios where $\varphi :\{0,1\}^{>\ell }\rightarrow \{0,1\}^\ell$ is a shrinking projection—here when $\ell \ll |x|$, simulation can become significantly faster; furthermore, in settings where $\varphi (x)$, and its preprocessing are known ahead of time (but $x$ isn’t), we can get efficient simulation. On the other hand, we will only get the above relaxed soundness guarantee. In our application to non-malleable commitments, relaxed soundness will be enough, and we’ll indeed benefit from the above simulation speedup.

We proceed with the definition.

Definition 10

($\varphi$-tuned 1ZK). A one-message zero-knowledge argument system $({\mathsf {P}},{\mathsf {V}})$ for an NP relation ${\mathcal {R}}(x,w)$ is $\varphi$-tuned for a polynomial-time projection function $\varphi =\left\{ \varphi _\lambda :\{0,1\}^{\ge \ell (\lambda )}\rightarrow \{0,1\}^{\ell (\lambda )}\right\} _\lambda$ if it satisfies:

Simulation Speedup: The system is $(T_{\tiny {\mathsf {D}}},T_{\tiny {\mathsf {S}}})$-zero-knowledge with a uniform simulator ${\mathsf {S}}=({\mathsf {S}}_{\mathsf {pre}},{\mathsf {S}}_{\mathsf {pos}})$ such that ${\mathsf {S}}(x,1^\lambda )$ consists of two phases:

• ${{\mathsf {s}}}{{\mathsf {t}}}\leftarrow {\mathsf {S}}_{\mathsf {pre}}(\varphi _\lambda (x),1^\lambda )$ is a preprocessing phase whose running time $T_{\tiny {\mathsf {S}}_{\mathsf {pre}}}(\ell (\lambda ))$ depends on $\ell (\lambda )=|\varphi _\lambda (x)|$, but not on $|x|$.

• ${\widehat{\pi }}\leftarrow {\mathsf {S}}_{\mathsf {pos}}(x,{{\mathsf {s}}}{{\mathsf {t}}})$ is a postprocessing phase that takes time $\mathrm {poly}(|x|+\lambda )$.

Overall, $T_{\tiny {\mathsf {S}}}(|x|,\lambda ) = \mathrm {poly}(T_{\tiny {\mathsf {S}}_{\mathsf {pre}}}(\ell (\lambda )),|x|)$ depends only polynomially on $|x|$ (and superpolynomially on $|\varphi _\lambda (x)|$).

: For any non-uniform $\mathrm {poly}(T_{\tiny {\mathsf {P}}})$-time, polynomial-size, probabilistic adversary ${\mathcal {A}}=\left\{ {\mathcal {A}}_\lambda \right\} _\lambda$ there exists a negligible $\mu$ and a collection of sets ${\mathcal {Z}}=\left\{ {\mathcal {Z}}_\lambda \right\} _\lambda$, where $|{\mathcal {Z}}_\lambda |\le K(|{\mathcal {A}}_\lambda |)$, such that for any $\lambda \in {\mathbb {N}}$,

4.1 Construction

We now construct a $\varphi$-tuned 1ZK based on incompressible problems and other standard primitives. The parameters of the construction are derived from those of the underlying building blocks, and in particular on the density and incompressability of the incompressible problem.

Building Blocks. In what follows, let $\varphi =\left\{ \varphi _\lambda :\{0,1\}^{\ge \ell (\lambda )}\rightarrow \{0,1\}^{\ell (\lambda )}\right\} _\lambda$ be a polynomial-time projection. Our transformation will make use the following building blocks:

• An incompressible problem $\mathcal {W}=\left\{ \mathcal {W}_\lambda \subseteq \{0,1\}^{4\ell (\lambda )}\right\} _\lambda$ with associated verifier $\mathcal {V}$, density $\varDelta$, and $(T_{\tiny \mathcal {W}},K_{\mathcal {W}})$ incompressability, where $K_{\mathcal {W}} \ll T_{\tiny \mathcal {W}}\ll \Delta ^{-1}$.

• A commitment scheme $(\mathsf {Com},\mathsf {Open})$ that is $T_{\tiny {\mathsf {R}}}$-hiding and $T_{\tiny \mathsf {\mathsf {Com}.E}}$-extractable where $T_{\tiny {\mathsf {R}}}\ll T_{\tiny \mathsf {\mathsf {Com}.E}} \ll T_{\tiny \mathcal {W}}$.

• A $T_{\tiny {\mathsf {D}}}^{\mathsf {niwi}}$-indistinguishable $\hbox {NIWI}$ system for an $\mathbf NP$ language, specified in the construction below.

• A two-source extractor $\mathsf {2Ext}=\left\{ \mathsf {2Ext}:\{0,1\}^{4\ell (\lambda )}\times \{0,1\}^{4\ell (\lambda )}\rightarrow \{0,1\}^{\ell (\lambda )}\right\} _\lambda$ with error $\varepsilon (\lambda ) = 2^{-\ell (\lambda )-2}$ for sources of min-entropies $k_1=k_2 > 4\ell (\lambda )-\log \varDelta ^{-1}$, and efficient reverse sampling.

The Proof System. We now describe the system $({\mathsf {P}},{\mathsf {V}})$ for an NP relation ${\mathcal {R}}$.

• The prover ${\mathsf {P}}(x,w,1^\lambda )$ :

  • Computes a commitment $c \leftarrow \mathsf {Com}(0^{8\ell })$.

  • Computes a NIWI proof $\pi$ for the statement

    

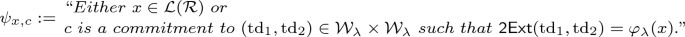
    The prover uses the witness w to compute $\pi$.

  • Overall the proof consists of $(c,\pi )$.

• The verifier ${\mathsf {V}}(x,(c,\pi ),1^\lambda )$ :

  • Applies the NIWI verifier to verify the statement $\psi _{x,c}$.

Theorem 4

The above is a $\varphi$-tuned 1ZK for ${\mathcal {R}}$ that is $(T_{\tiny {\mathsf {S}}},T_{\tiny {\mathsf {D}}})$-zero-knowledge and $(T_{\tiny {\mathsf {P}}},K,\varphi )$-weakly sound for

$$\begin{aligned} T_{\tiny {\mathsf {S}}}= \varDelta ^{-1}, T_{\tiny {\mathsf {D}}}=\min \left\{ T_{\tiny {\mathsf {R}}},T_{\tiny {\mathsf {D}}}^{\mathsf {niwi}}\right\} ,\qquad T_{\tiny {\mathsf {P}}}= T_{\tiny \mathcal {W}}, K= O(K_{\mathcal {W}}). \end{aligned}$$

A Concrete Setting of Parameters. A natural setting of parameters that will be considered throughout this paper is subexponential $\varDelta (\ell ) = 2^{-\ell ^{{\delta }}}$. We can accordingly set $T_{\tiny {\mathsf {R}}}, T_{\tiny \mathsf {\mathsf {Com}.E}}, T_{\tiny \mathcal {W}},T_{\tiny {\mathsf {D}}}^{\mathsf {niwi}}$ to be super-polynomial functions satisfying:

$$\begin{aligned} T_{\tiny {\mathsf {R}}}\ll T_{\tiny \mathsf {\mathsf {Com}.E}} \ll T_{\tiny \mathcal {W}}\ll \varDelta ^{-1} = 2^{{\ell (\lambda )}^{{\delta }}}. \end{aligned}$$

Indeed, the main tradeoff is between the simulation time $T_{\tiny {\mathsf {S}}}$ and the density $\varDelta$ of the incompressible problem $\mathcal {W}$. On one hand, we aim for a short as possible simulation time $T_{\tiny {\mathsf {S}}}\ll 2^{\ell (\lambda )}$.⁵ On the other hand, shorter simulation time requires higher density, which strengthens the corresponding incompressibility assumption. (In terms of existing candidates for incompressible problems based on fixed hash functions, subexponential density corresponds to polynomially-compressing hash functions.)