Towards Tight Security of Cascaded LRW2

Abstract

The Cascaded LRW2 tweakable block cipher was introduced by Landecker et al. at CRYPTO 2012, and proven secure up to $2^{2n/3}$ queries. There has not been any attack on the construction faster than the generic attack in $2^n$ queries. In this work we initiate the quest towards a tight bound. We first present a distinguishing attack in $2n^{1/2}2^{3n/4}$ queries against a generalized version of the scheme. The attack is supported with an experimental verification and a formal success probability analysis. We subsequently discuss non-trivial bottlenecks in proving tight security, most importantly the distinguisher’s freedom in choosing the tweak values. Finally, we prove that if every tweak value occurs at most $2^{n/4}$ times, Cascaded LRW2 is secure up to $2^{3n/4}$ queries.

1 Introduction

A block cipher is a family of permutations that is indexed via a secret key. While block ciphers are omnipresent in cryptographic permutations, they inherently lack flexibility and many applications of block ciphers are either implicitly or explicitly designed from a tweakable block cipher: a function $\widetilde{E}:\mathcal {K}\times \mathcal {T}\times \mathcal {M}\rightarrow \mathcal {M}$ that is a family of permutations indexed by secret key $k\in \mathcal {K}$ and public tweak $t\in \mathcal {T}$. Tweakable block ciphers were formalized by Liskov, Rivest, and Wagner [19] and find a broad range of applications, most notably in the direction of authenticated encryption (such as OCB [15, 32, 33], COPA [1], AEZ [11], and Deoxys [13, 29]) and in XTS disk encryption [9].

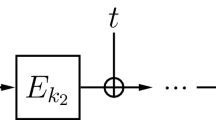
This work centers around a generic tweakable block cipher design that was introduced in Liskov et al.’s original paper [19]. It internally uses a block cipher E, and is defined as follows:

$$\begin{aligned} \mathrm {LRW2}((k,h),t,m)&= E(k,m\oplus h(t))\oplus h(t)\,, \end{aligned}$$

(1)

where k is a block cipher key and h an XOR universal hash function. The construction is strongly related with Rogaway’s $\mathrm {XEX}$ [32] (in turn used in OCB1, OCB2, OCB3, and XTS disk encryption), and extensions by Chakraborty and Sarkar [3], Minematsu [21], and Granger et al. [10]. The $\mathrm {LRW2}$ tweakable block cipher is proven to achieve security up to approximately $2^{n/2}$ queries. This bound is tight: for any two queries $(t,m),(t',m')$ with $m\oplus h(t)=m'\oplus h(t')$, the corresponding ciphertexts satisfy $c\oplus c' = h(t)\oplus h(t') = m\oplus m'$, and such a collision can be found in approximately $2^{n/2}$ queries.

A notable approach towards beyond birthday bound secure tweakable block ciphers is by Landecker et al. [17], who suggested to cascade two independent evaluations of $\mathrm {LRW2}$:

$$\begin{aligned} \mathrm {CLRW2}((k_1,k_2,h_1,h_2),t,m)&= \mathrm {LRW2}((k_2,h_2),t,\mathrm {LRW2}((k_1,h_1),t,m))\,,\\&= E_{k_2}(E_{k_1}(m\oplus h_1(t))\oplus h_1(t)\oplus h_2(t))\oplus h_2(t)\,, \end{aligned}$$

where $k_1,k_2$ are two block cipher keys and $h_1,h_2$ XOR universal hash functions. They proved that this construction is indistinguishable from random up to approximately $2^{2n/3}$ queries. This proof was very technical, and Procter [30] pointed out that it was, in fact, flawed. The proof was subsequently fixed by both Landecker et al. and Procter, but it does not generalize to higher security, either for the construction as is or for a generalization to multiple cascades. So far, there has never been any attack justifying tightness of the bound; the best attack so far is a generic one in $2^n$ queries.

The state of affairs stands in sharp contrast with that of two rounds of Tweakable Even-Mansour, $\mathrm {LRW2}$’s sibling based on public permutations [6]:

$$\begin{aligned} \mathrm {CTEM}((h_1,h_2),t,m)&= p_2(p_1(m\oplus h_1(t))\oplus h_1(t)\oplus h_2(t))\oplus h_2(t)\,, \end{aligned}$$

where $p_1,p_2$ are two permutations and $h_1,h_2$ uniform and XOR universal hash functions. Cogliati et al. [6] proved that $\mathrm {CTEM}$ is indistinguishable from random up to approximately $2^{2n/3}$ queries, and this bound is tight: keeping the tweak constant reduces the scheme to a key alternating cipher for which Bogdanov et al. [2] derived an attack in query complexity approximately $2^{2n/3}$. This attack uses availability of the public permutations and is therefore not applicable to $\mathrm {CLRW2}$.

1.1 Attack on Generalized Cascaded LRW2

We consider a generalized version of Cascaded $\mathrm {LRW2}$, for brevity called “$\mathrm {GCL}$:”

$$\begin{aligned} \mathrm {GCL}^{f_1,f_2,f_3}((k_1,k_2,k_f),t,m)&= E(k_2,E(k_1,m\oplus f_1(t))\oplus f_2(t))\oplus f_3(t)\,, \end{aligned}$$

(2)

where $k_1,k_2$ are two block cipher keys and $k_f$ a key to the masking functions $(f_1,f_2,f_3)$ (for ease of presentation, the key input to the $f_i$’s is left implicit throughout). $\mathrm {GCL}^{f_1,f_2,f_3}$ is depicted in Fig. 1. If $h_1,h_2$ are two XOR universal hash functions, then $\mathrm {GCL}^{h_1,h_1\oplus h_2,h_2}$ matches $\mathrm {CLRW2}$ (where we set $k_f=(h_1,h_2)$).

Fig. 1.

Depiction of $\mathrm {GCL}^{f_1,f_2,f_3}$.

We derive a generic attack against $\mathrm {GCL}^{f_1,f_2,f_3}$ with arbitrary masking in $2n^{1/2}2^{3n/4}$ evaluations. The information-theoretic attack is given in Sect. 3 and relies on a boomerang-style observation on the mode, based on the observation that if there exist four queries where the first and second collide on the input to $E_{k_1}$, the second and third on the output of $E_{k_2}$, and the third and fourth on the input to $E_{k_1}$, then the first and fourth collide at the output of $E_{k_2}$ with probability 1 if the tweak values are selected delicately.

In support of its correctness, the attack is backed up with a formal success probability computation in Sect. 3.3 as well as an implementation in Sect. 3.4. The formal success analysis demonstrates that for $n\ge 27$, the distinguisher’s success probability is at least 1 / 2. The small-scale implementation demonstrates that for $\mathrm {GCL}^{f_1,f_2,f_3}$ based on random permutations on $n=16,20,24$ bits, the special collisions as searched for in the attack indeed appear more often than usual. The gap between the accuracy in n of the experimental verification and the security proof is caused by the fact that some loose probability bounds had to be used in the rather conservative proof.

The attack is independent of the masking functions $f_1,f_2,f_3$. It implies that $\mathrm {GCL}^{f_1,f_2,f_3}$ cannot achieve optimal security, regardless of the choice of masking. The attack particularly applies to $\mathrm {CLRW2}$, therewith improving the best known attack to date.

1.2 Towards Tight Security?

In Sect. 4 we approach the attack from a more theoretical perspective, and describe the main limitations in proving security of $\mathrm {GCL}^{f_1,f_2,f_3}$ beyond $2^{2n/3}$. The quasi-formal discussion relies on equating executions of $\mathrm {GCL}^{f_1,f_2,f_3}$ with a bipartite graph, and by drawing a parallel with Patarin’s mirror theory [20, 22, 26, 28] we indicate various issues in trying to prove security beyond $2^{2n/3}$. The most notable one of these, namely the potential existence of four queries which alternatively collide on the input of $E_{k_1}$ or output of $E_{k_2}$ is precisely the one exploited in our attack in $2n^{1/2}2^{3n/4}$ queries. We also pinpoint where and how the current gap between a security lower bound of $2^{2n/3}$ and an attack upper bound of $2^{3n/4}$ arises. Most importantly, as the distinguisher can freely choose the value of the tweak for every query, it can set a certain distinguishing event with a significant probability.

1.3 Improved Security of Cascaded LRW2 Under Tweak Limits

In Sect. 5 we use these insights obtained in our quest towards tight security. We return to $\mathrm {CLRW2}$, or equivalently $\mathrm {GCL}^{h_1,h_1\oplus h_2,h_2}$, and prove that if (i) $h_1$ and $h_2$ are 4-wise independent XOR universal hash functions and (ii) every tweak value occurs at most $q^{1/3}$ times, where q is the total amount of queries, then Cascaded $\mathrm {LRW2}$ is secure up to $2^{3n/4}$ queries. In Sect. 2.2 we describe two possibilities of designing 4-wise independent XOR universal hash functions. The condition on the occurrence of the tweak seems restrictive, but many modes of operation based on a tweakable block cipher query their primitives for tweaks that are constituted of a nonce or random number concatenated with a counter value [10, 12, 15, 29]: in a nonce-respecting setting, every nonce appears at most $1+q_f$ times, where $q_f$ is the amount of forgery attempts.

The proof relies on Patarin’s mirror theory up to the first recursion, i.e., up to 3n / 4-bit security. It shares ideas with the analysis of Mennink and Neves [20] on Encrypted Davies-Meyer [7], namely that an evaluation (t, m, c) of $\mathrm {CLRW2}$ can be rewritten as a sum of permutations “in the middle.” Adversarial power to choose tweak values, however, precludes optimal security, and security up to $2^{3n/4}$ is the best possible bound.

1.4 Longer Cascades?

Lampe and Seurin [16] suggested the cascade of $\rho \ge 1$ evaluations of $\mathrm {LRW2}$, and proved that for even $\rho$ this construction is secure up to approximately $2^{\rho n/(\rho +2)}$ queries. Lee et al. [18] proved that if the universal hash functions are replaced by random functions, security up to $2^{\rho n/(\rho +1)}$ is achieved. It is generally conjectured that the security of the cascade of $\rho$ $\mathrm {LRW2}$’s is $2^{\rho n/(\rho +1)}$ [16,17,18], but also for this larger cascade, nothing is known on the attack side, besides the trivial attack in $2^n$ queries. Unfortunately, it does not seem possible to generalize the attack of Sect. 3 nor the security proof of Sect. 5 to larger cascades. As before, it is noteworthy that a cascade of $\rho \ge 1$ evaluations of $\mathrm {TEM}$ can be attacked in approximately $2^{\rho n/(\rho +1)}$ queries [2].

2 Preliminaries

For $n\in \mathbb {N}$, $\{0,1\}^{n}$ denotes the set of bit strings of length n, and $\mathsf {perm}(n)$ the set of all permutations on $\{0,1\}^{n}$. Extending notation, for $\kappa \in \mathbb {N}$, we denote by $\mathsf {iperm}(\kappa ,n)$ the set of all “indexed permutations,” families of permutations $p_k\in \mathsf {perm}(n)$, indexed by $k\in \{0,1\}^{\kappa }$. We additionally denote by $\mathsf {iperm}(\kappa ,\tau ,n)$ for $\tau \in \mathbb {N}$ the set of all indexed permutations where the index consists of two elements $(k,t)\in \{0,1\}^{\kappa }\times \{0,1\}^{\tau }$. For $m,n\in \mathbb {N}$ such that $m\ge n$, the falling factorial is defined as $(m)_n=m(m-1)\cdots (m-n+1)=m!/(m-n)!$. For $n\in \mathbb {N}$ and $m\in \{0,\ldots ,2^{n-1}\}$, we denote by $\langle m\rangle _n$ the encoding of m as an n-bit string. If $\mathcal {X}$ is a finite set, $x\xleftarrow {{\scriptscriptstyle \$}}\mathcal {X}$ denotes the event of uniformly randomly drawing x from $\mathcal {X}$.

2.1 Block Ciphers and Tweakable Block Ciphers

A block cipher with key size $\kappa$ and state size n is a function $E\in \mathsf {iperm}(\kappa ,n)$. For fixed key $k\in \{0,1\}^{\kappa }$ we denote $E_k(\cdot )=E(k,\cdot )$, and its inverse is denoted $E_k^{-1}(\cdot )$. A tweakable block cipher with key size $\kappa$, tweak size $\tau$, and state size n is a function $\widetilde{E}\in \mathsf {iperm}(\kappa ,\tau ,n)$. For fixed key $k\in \{0,1\}^{\kappa }$ and $t\in \{0,1\}^{\tau }$ we denote $\widetilde{E}_k(t,\cdot )=\widetilde{E}(k,t,\cdot )$, and its inverse is denoted $\widetilde{E}_k^{-1}(t,\cdot )$.

Let $\kappa ,n\in \mathbb {N}$ and let $E\in \mathsf {iperm}(\kappa ,n)$ be a block cipher. The advantage of a distinguisher $\mathcal {D}$ in breaking the SPRP (strong pseudorandom permutation) security of $E$ is defined as

$$\begin{aligned} \mathbf {Adv}_{E}^{\mathrm {sprp}}(\mathcal {D}) = \mathbf {Pr}\left( \mathcal {D}^{E_k^{\pm }}=1\right) - \mathbf {Pr}\left( \mathcal {D}^{p^{\pm }}=1\right) \,, \end{aligned}$$

(3)

where the probabilities are taken over the random drawing of $k\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa }$, $p\xleftarrow {{\scriptscriptstyle \$}}\mathsf {perm}(n)$, and the randomness used by $\mathcal {D}$. The resources that $\mathcal {D}$ may use are typically expressed in terms of query complexity (to the oracle) and time complexity (for offline computations).

As block ciphers are a special case of tweakable block ciphers with tweak space of size 1 ($\tau =0$), the security definition straightforwardly generalizes to the latter. Let $\kappa ,\tau ,n\in \mathbb {N}$ and let $\widetilde{E}\in \mathsf {iperm}(\kappa ,\tau ,n)$ be a tweakable block cipher. The advantage of a distinguisher $\mathcal {D}$ in breaking the STPRP (strong tweakable pseudorandom permutation) security of $\widetilde{E}$ is defined as

$$\begin{aligned} \mathbf {Adv}_{\widetilde{E}}^{\mathrm {stprp}}(\mathcal {D}) = \mathbf {Pr}\left( \mathcal {D}^{\widetilde{E}_k^{\pm }}=1\right) - \mathbf {Pr}\left( \mathcal {D}^{\widetilde{p}^{\pm }}=1\right) \,, \end{aligned}$$

(4)

where the probabilities are taken over the random drawing of $k\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa }$, $\widetilde{p}\xleftarrow {{\scriptscriptstyle \$}}\mathsf {iperm}(\tau ,n)$, and the randomness used by $\mathcal {D}$. The resources that $\mathcal {D}$ may use are typically bounded as before.

2.2 XOR Universal Hash Functions

We use the notion of $\ell$-wise independent XOR universal hash functions, a slight adaptation of the original definition of Wegman and Carter [34]. For two non-empty sets $\mathcal {X},\mathcal {Y}$, a hash function family $H = \{h:\mathcal {X}\rightarrow \mathcal {Y}\}$ is called $\ell$-wise independent almost XOR universal up to bound $\varepsilon$, denoted $\varepsilon$-AXU$_\ell$, if for any $j\in \{2,\ldots ,\ell \}$, any distinct $x_1,\ldots ,x_j\in \mathcal {X}$ and (not necessarily distinct) $y_2,\ldots ,y_j\in \mathcal {Y}$,

$$\begin{aligned} \mathbf {Pr}\left( h\xleftarrow {{\scriptscriptstyle \$}}H \;:\; h(x_1)\oplus h(x_2)=y_2 \,,\, \ldots \,,\, h(x_1)\oplus h(x_j) = y_j \right) \le \varepsilon ^{j-1}\,. \end{aligned}$$

For $\mathcal {X}=\mathcal {Y}=\{0,1\}^n$, a $2^{-n}$-AXU$_2$ hash function family can be defined using finite field multiplication with respect to some irreducible polynomial to represent the field, i.e., $h(x):= h\otimes x$. It is not $\varepsilon$-AXU$_\ell$ for $\ell >2$. Defining the hash function family as

$$\begin{aligned} \varvec{h}(x) := \bigoplus _{i=1}^{\ell -1} h_i\otimes x^i \end{aligned}$$

for $\varvec{h}=(h_1,\dots ,h_{\ell -1})$ gives a $2^{-n}$-AXU$_\ell$ hash function family for any $\ell \ge 2$. One can alternatively obtain a $(2^n-(\ell -1))^{-1}$-AXU$_\ell$ by defining the hash function family using an ideal cipher or a family of random permutations.

3 Generic Attack

We present a generic attack against $\mathrm {GCL}^{f_1,f_2,f_3}$ in $2n^{1/2}2^{3n/4}$ queries. The attack is generic in nature, it does not exploit any weaknesses in the underlying cipher, and as such we simply assume that $E\xleftarrow {{\scriptscriptstyle \$}}\mathsf {iperm}(\kappa ,n)$ is an ideal cipher. It is fair to assume that the success probability of the attack simply improves if E is less than ideal, except for degenerate cases, e.g., if $E_{k_1}$ and $E_{k_2}$ are almost perfect nonlinear permutations (APNPs, cf., [8, 23, 24]). Throughout the attack, we simply denote $p_1=E_{k_1}$ and $p_2=E_{k_2}$ for brevity.

An informal rationale of our attack is given in Sect. 3.1, and the formal distinguisher in Sect. 3.2. Its advantage is lower bounded in Sect. 3.3, and the analysis is backed up with experimental verification in Sect. 3.4.

3.1 Informal Rationale of Attack

Suppose a distinguisher obtains four queries $(t,m_1,c_1)$, $(t',m_2',c_2')$, $(t,m_3,c_3)$, and $(t',m_4',c_4')$ of $\mathrm {GCL}^{f_1,f_2,f_3}$ such that

$$\begin{aligned} \begin{aligned} m_1 \oplus f_1(t)&= m_2'\oplus f_1(t')\,,\\ c_2'\oplus f_3(t')&= c_3 \oplus f_3(t) \,,\\ m_3 \oplus f_1(t)&= m_4'\oplus f_1(t')\,. \end{aligned}\end{aligned}$$

(5)

In other words, the first and second query collide at the input to $E_{k_1}$, the second and third at the output of $E_{k_2}$, and the third and fourth at the input to $E_{k_1}$. As the four queries are performed using only two tweak values, each occurring twice, we have $f_2(t)\oplus f_2(t')\oplus f_2(t)\oplus f_2(t')=0$, and from a simple inspection of the scheme (see also Fig. 2) one can conclude that, necessarily,

$$\begin{aligned} c_1 \oplus f_3(t)&= c_4'\oplus f_3(t')\,. \end{aligned}$$

(6)

Stated differently, under the assumption that (5) is satisfied, (6) is implied, and therefore the four equations combine to

$$\begin{aligned} m_1 \oplus m_2'&= m_3 \oplus m_4' = f_1(t) \oplus f_1(t')\,,\\ c_2'\oplus c_3&= c_1 \oplus c_4' = f_3(t) \oplus f_3(t')\,. \end{aligned}$$

Unfortunately, the distinguisher does not know $f_1(t)\oplus f_1(t')$ and $f_3(t)\oplus f_3(t')$, but if we ignore these two values in above equations, we obtain

$$\begin{aligned} \begin{aligned} m_1 \oplus m_2'&= m_3 \oplus m_4'\,,\\ c_2'\oplus c_3&= c_1 \oplus c_4'\,, \end{aligned}\end{aligned}$$

(7)

which necessarily holds if $m_1\oplus m_2'=f_1(t)\oplus f_1(t')$ and $c_2'\oplus c_3 = f_3(t)\oplus f_3(t')$, but may hold by accident as well. Stated differently, if for some $d\in \{0,1\}^n$, there are about $2^n$ choices for the four queries such that

$$\begin{aligned} m_1 \oplus m_2' = m_3 \oplus m_4' = d\,, \end{aligned}$$

(8)

the expected number of solutions to (7) is close to 2 if $d=f_1(t)\oplus f_1(t')$ but close to 1 if $d\ne f_1(t)\oplus f_1(t')$. For an ideal permutation, the expected number of solutions is always close to 1 for any $d\in \{0,1\}^n$. By making approximately $2^{3n/4}$ queries, the distinguisher can ensure that there are about $2^n$ solutions to (8) for all d, including $d=f_1(t)\oplus f_1(t')$.

This almost allows for a distinguishing attack, but not quite: as the distinguisher does not actually know $f_1(t)\oplus f_1(t')$, it must simply hope that for some d there is a significant difference, but d may take $2^n$ values and false positives are likely to occur. By extending the number of queries slightly, i.e., by making about $n^{1/2}\cdot 2^{3n/4}$ queries, the case of $f_1(t)\oplus f_1(t')$ will stand out.

We remark that the attack is effectively an XOR subkey recovery attack, as the distinguisher learns $f_1(t)\oplus f_1(t')$ and $f_3(t)\oplus f_3(t')$. In case of Cascaded LRW2, where $f_1=h_1$, $f_2=h_1\oplus h_2$, and $f_3=h_2$ for two XOR universal hash functions $h_1,h_2$, this immediately gives $f_2(t)\oplus f_2(t')$, and potentially more, depending on the specific hash functions.

Fig. 2.

Attack idea: the red (solid) collisions are targeted, the blue (dashed) one is implied by the red ones. (Color figure online)

3.2 Formal Description of Distinguisher

Let $\epsilon =\log _2(n)/2$ (assumed to be integral), and consider the following distinguisher $\mathcal {D}$ making $q=2^{3n/4+\epsilon }$ queries.

• (i) Fix arbitrary distinct $t,t'\in \{0,1\}^{\tau }$;

• (ii) For $i=0,\ldots ,2^{3n/4+\epsilon }-1$, put $m_i=0^{n/4-\epsilon }\Vert \langle i\rangle _{3n/4+\epsilon }$ and query $(t,m_i)$ to obtain $c_i$;

• (iii) For $i=0,\ldots ,2^{3n/4+\epsilon }-1$, put $m'_i=\langle i\rangle _{3n/4+\epsilon }\Vert 0^{n/4-\epsilon }$ and query $(t',m'_i)$ to obtain $c'_i$;

• (iv) For $d\in \{0,1\}^{n}$, define $I_d = \{(i,j) \mid m_i \oplus m'_j = d\}$. Note that $|I_d|=2^{n/2+2\epsilon }$ for all $d\in \{0,1\}^{n}$, and define $q':=2^{n/2+2\epsilon }$;

• (v) For all $d\in \{0,1\}^{n}$ do:

  • Define $N_d=0$;

  • For all distinct $(i,j),(k,l)\in I_d$: if $c_i\oplus c'_l=c'_j\oplus c_k$, put $N_d=N_d+1$;

• (vi) Briefly looking forward, for a random tweakable block cipher we have $\mathbf {Ex}\left( N_d\right) ={q'\atopwithdelims ()2}/(2^n-1)$ for any $d\in \{0,1\}^{n}$, whereas for $\mathrm {GCL}^{f_1,f_2,f_3}$, $\mathbf {Ex}\left( N_{f_1(t)\oplus f_1(t')}\right) \ge 2{q'\atopwithdelims ()2}/2^n$. Inspired by this, define

  $$\begin{aligned} \beta := \frac{3}{2}{q'\atopwithdelims ()2}/2^n\,. \end{aligned}$$

  If there exists a $d\in \{0,1\}^{n}$ such that $N_d\ge \beta$, output 1. Otherwise, output 0.

3.3 Analysis of Distinguisher Advantage

A formal analysis confirms that the distinguisher succeeds with non-negligible probability.

Theorem 1

Let $\kappa ,\tau ,n\in \mathbb {N}$ with $n\ge 16$, let $E\xleftarrow {{\scriptscriptstyle \$}}\mathsf {iperm}(\kappa ,n)$, denote the size of the key space of $(f_1,f_2,f_3)$ by $\kappa _f$, and consider $\mathrm {GCL}^{f_1,f_2,f_3}:\{0,1\}^{2\kappa }\times \{0,1\}^{\kappa _f}\times \{0,1\}^{\tau }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$. Distinguisher $\mathcal {D}$ of Sect. 3.2 with query complexity $2n^{1/2}\cdot 2^{3n/4}$ has advantage

$$\begin{aligned} \mathbf {Adv}_{\mathrm {GCL}^{f_1,f_2,f_3}}^{\mathrm {stprp}}(\mathcal {D}) \ge 1 - \frac{32}{n^2} - \frac{80}{n2^{n/2}} - 5\cdot 2^n\left( \frac{10}{n}\right) ^{3/100\cdot n^2} - \frac{n^{7}}{2^{3n/2}}\,. \end{aligned}$$

(9)

One can verify that the lower bound of (9) is at least 1 / 2 for $n\ge 27$. This theorem is not the core contribution of the article (which is Theorem 2), and its proof is given Appendix A.

Note that the attack is de facto a TPRP-attack, only requiring forward access to the scheme. In addition, it is information-theoretical: the distinguisher’s complexity is solely measured in its number of queries. The offline complexity is around $2^{3n/2}$.

3.4 Experimental Verification

We have implemented the distinguisher of Sect. 3.2 on a small scale, for $n=16,20,24$ and with $p_1,p_2,f_1,f_2,f_3$ instantiated as independent uniform random permutations, noting that a uniform random permutation is a $(2^n-1)^{-1}$-AXU$_2$ hash function (see Sect. 2.2). In each case, two distinct tweaks $t,t'$ are evaluated for $q=2^{3n/4+\epsilon }$ queries, with $\epsilon =0,1,2$ (note that $2\lesssim \log _2(n)/2$ for $n=16,20,24$). The average values $N_d$ for both the real and ideal world and both $d=f_1(t)\oplus f_1(t')$ and random d are summarized in Table 1. The computations confirm soundness of the rationale of Sect. 3.1 and the expected values of Sect. 3.2. In more detail, the expected values given in Sect. 3.2 suggest that $N_d\approx 2^{4\epsilon }$ for $d=f_1(t)\oplus f_1(t')$ in the real world and $N_d\approx 2^{4\epsilon -1}$ in any other case (real or ideal world), and the statistics in Table 1 reasonably accurately match these numbers.

Note that, in particular, for $\epsilon =0$ the value $N_{f_1(t)\oplus f_1(t')}$ already shows a small peak in the real world (for each of $n=16,20,24$), but outliers in $N_d$ for $d\ne f_1(t)\oplus f_1(t')$ are hidden by the statistics. For increasing $\epsilon$, the gap becomes more significant and the success probability increases.

Table 1. Number of elements in $N_d$ for the real and ideal world, for $d=f_1(t)\oplus f_1(t')$ and for random d. For the cases $n=16,20$, the numbers are averaged over 32 attacks; for $n=24$ the numbers are averaged over 8 attacks.

4 Towards Tight Security?

Consider a simplification of $\mathrm {GCL}^{f_1,f_2,f_3}$ with its two block ciphers replaced by random permutations $p_1,p_2$ (this is a typical hybrid argument in security proofs performed at the cost of $2\mathbf {Adv}_{E}^{\mathrm {sprp}}(\mathcal {D}')$ for some distinguisher $\mathcal {D}'$). For simplicity, assume that $f_2$ is injective (the scheme turns out to be significantly weakened if $f_2$ is non-injective). For an evaluation $\mathrm {GCL}^{f_1,f_2,f_3}(t,m)=c$, denote

$$\begin{aligned} x&= p_1(m\oplus f_1(t))\,,\\ y&= p_2^{-1}(c\oplus f_3(t))\,, \end{aligned}$$

in such a way that $x\oplus y = f_2(t)$.

Intuitively, one may think of a proof going “fine” if there is always some randomness available. For example, consider just a single forward query (t, m) to $\mathrm {GCL}^{f_1,f_2,f_3}$. The value $m\oplus f_1(t)$ has never been evaluated by $p_1$, hence the value x will look uniformly randomly drawn from $\{0,1\}^{n}$; the value y satisfies $y=x\oplus f_2(t)$, and also y has never been evaluated by $p_2$ so the value $c\oplus f_3(t)$ is uniformly randomly drawn from $\{0,1\}^{n}$.

A more complicated case appears if there exist two distinct queries $(m_1,t_1)$ and $(m_2,t_2)$ such that $m_1\oplus f_1(t_1)=m_2\oplus f_1(t_2)$. The first query is handled as before, rendering fresh $x_1$ and $c_1\oplus f_3(t_1)$. The second query satisfies $m_1\oplus f_1(t_1)=m_2\oplus f_1(t_2)$, meaning that $x_2=x_1$. However, as the two queries are distinct, this equation implies that $t_1\ne t_2$. As $f_2$ is injective, we subsequently have $f_2(t_1)\ne f_2(t_2)$ and thus $y_2\ne y_1$. The evaluation of $p_2$ on $y_2$ yields a value uniformly drawn from $\{0,1\}^{n}\backslash \{c_1\oplus f_3(t_1)\}$.

Likewise, two queries could also collide at the right side, i.e., $c_1\oplus f_3(t_1)=c_2\oplus f_3(t_2)$. It is unlikely, though, that two queries collide at both the left and right side, at least if $f_1$ and $f_3$ are two randomized functions (as is the case in $\mathrm {CLRW2}$), and we will ignore this case. If more than two queries are involved, one could visualize queries as a bipartite graph ${G}=({U},{V},{E})$. ${U}=\{0,1\}^{n}$ corresponds to the input values to $p_1$, ${V}=\{0,1\}^{n}$ to the output values of $p_2$, and for every query tuple $(t_i,m_i,c_i)$, the edge $(m_i\oplus f_1(t_i),c_i \oplus f_3(t_i))$ with label $f_2(t_i)$ from ${U}$ to ${V}$ is added to ${E}$. An example graph ${G}$ is depicted in Fig. 3.

Fig. 3.

Example of a bipartite graph ${G}$ representing seven evaluations of $\mathrm {GCL}^{f_1,f_2,f_3}$. For brevity, we denote $\bar{m}_i=m_i\oplus f_1(t_i)$ and $\bar{c}_i=c_i\oplus f_3(t_i)$. Graph view rotated for economical reasons.

What the above comprises is an informal introduction to a potential use of Patarin’s mirror theory [20, 22, 26, 28], a powerful approach towards counting the number of solutions to a system of equations of the form $x\oplus y=\lambda$, where $\lambda$ is known. If, in above graph, two queries touch on the left, i.e., $m_1\oplus f_1(t_1)=m_2\oplus f_1(t_2)$, they share the same $x_1=x_2$ but have different $y_1,y_2$.

Unfortunately, the mirror theory does not turn out to be particularly suited here, most importantly as it is tailored towards comparing systems to random functions and we aim to compare our scheme to a family of permutations. Yet, closer inspection of the theory reveals that it puts two conditions on the graph that are “reasonably easily” violated:

• (i) The graph should not contain a path of even length whose labels sum to 0;

• (ii) The graph should not contain a circle.

The first condition prevents that there are two different inputs to $p_1$ with the same output (or two different outputs of $p_2$ with the same input). The second condition prevents that there exists a query with “no randomness.” Both conditions are harmful for any possible even length, in the sense that Patarin’s mirror theorem cannot be applied.

The attack of Sect. 3 relies on the fact that condition (i) can be violated easier than expected. Note that there cannot exist a path of length 2 whose labels sum to 0 (as $f_2$ is injective). A path of length 4 whose labels sum to 0 requires the existence of four queries $(t_1,m_1,c_1),\ldots ,(t_4,m_4,c_4)$ such that

$$\begin{aligned} \begin{aligned} m_1 \oplus f_1(t_1)&= m_2\oplus f_1(t_2)\,,\\ c_2 \oplus f_3(t_2)&= c_3\oplus f_3(t_3)\,,\\ m_3 \oplus f_1(t_3)&= m_4\oplus f_1(t_4)\,,\\ f_2(t_1)\oplus f_2(t_2)\oplus f_2(t_3)\oplus f_2(t_4)&= 0\,. \end{aligned}\end{aligned}$$

(10)

As the four queries are distinct, the path may only appear if $t_1\ne t_2\ne t_3\ne t_4$. However, it may be that $t_1=t_3$ and $t_2=t_4$, and this is how the attack of Sect. 3 exploits a path: in this case, the fourth equation of (10) is satisfied by design and the remaining three can be rewritten as

$$\begin{aligned} \begin{aligned} m_1 \oplus m_2 = m_3\oplus m_4&= f_1(t_1)\oplus f_1(t_2)\,,\\ c_2 \oplus c_3&= f_3(t_1)\oplus f_3(t_2)\,. \end{aligned}\end{aligned}$$

(11)

The attack of Sect. 3 relies on the additional fact that if these conditions are met, then the condition

$$\begin{aligned} c_4 \oplus f_3(t_2)= c_1\oplus f_3(t_1) \end{aligned}$$

(12)

holds with probability 1 in the real world (i.e., there is a circle as depicted in Fig. 4, violating condition (ii)), but with negligible probability in the ideal world. This property (that (11) implies (12)) gives a clean and well-verifiable distinguishing event.

Fig. 4.

A circle in bipartite graph ${G}$ with $f_2(t_1)\oplus f_2(t_2)\oplus f_2(t_3)\oplus f_2(t_4)=0$, as exploited in the attack of Sect. 3. We use the same convention as in Fig. 3.

A distinguisher can choose the $m_i$’s smartly to make sure that $m_1\oplus m_2=m_3\oplus m_4$ is satisfied. Consider a distinguisher that makes queries for at most two tweaks $t,t'$, each queried q times, say for queries $(m_0,c_0),\ldots ,(m_{q-1},c_{q-1})$ and $(m'_0,c'_0),\ldots ,(m'_{q-1},c'_{q-1})$. Inspired by Sect. 3, denote

$$\begin{aligned} I_d = \{ (i,j)\in \{0,\ldots ,q-1\}^2 \mid m_i\oplus m'_j= d \}\,. \end{aligned}$$

The probability that there exist four queries $(i,j)\ne (i',j')$ that comply with the equations of (11), denoted X, is

$$\begin{aligned} \mathbf {Pr}\left( X\right)&= \sum _{d\in \{0,1\}^n} \mathbf {Pr}\left( X \mid f_1(t_1)\oplus f_1(t_2) = d\right) \cdot \mathbf {Pr}\left( f_1(t_1)\oplus f_1(t_2) = d\right) \nonumber \\&\approx \sum _{d\in \{0,1\}^n} \frac{{|I_d|\atopwithdelims ()2}}{2^n}\cdot \mathbf {Pr}\left( f_1(t_1)\oplus f_1(t_2) = d\right) \nonumber \\&\approx \sum _{d\in \{0,1\}^n} \frac{{|I_d|\atopwithdelims ()2}}{2^n}\cdot \frac{1}{2^n}\,, \end{aligned}$$

(13)

where the first approximation assumes independence of events and that the $c_i$’s are generated using a random function (for simplicity of reasoning), and the second approximation assumes that $f_1$ is close to a $2^{-n}$-AXU$_2$ hash function. The two extremes in selecting the $m_i$’s are the following:

• Choose the $m_i$’s and $m'_i$’s such that $|I_d|=q$ for q values of d and $|I_d|=0$ for the remaining $2^n-q$ values. This is achieved by setting $m_i=m'_i=0^{n-\log _2(q)}\Vert \langle i\rangle _{\log _2(q)}$ for $i=0,\ldots ,q-1$. In this case, we obtain for (13):

  $$\begin{aligned} (13) = q \cdot {q\atopwithdelims ()2}/2^{2n} \approx q^3/2^{2n}\,; \end{aligned}$$

• Choose the $m_i$’s and $m'_i$’s such that $|I_d|=q^2/2^n$ for all values of d, i.e., $I_d$ is equally large for all d. This is achieved by setting $m_i=0^{n-\log _2(q)}\Vert \langle i\rangle _{\log _2(q)}$ and $m'_i=\langle i\rangle _{\log _2(q)}\Vert 0^{n-\log _2(q)}$ for $i=0,\ldots ,q-1$ (as in the attack of Sect. 3). In this case, we obtain for (13):

  $$\begin{aligned} (13) = 2^n \cdot {q^2/2^n\atopwithdelims ()2}/2^{2n} \approx q^4/2^{3n}\,. \end{aligned}$$

A security analysis, i.e., an upper bound on the distinguisher’s success probability, would have to take into account any possible distinguisher, and it therefore seems such analysis caps at around $q^3/2^{2n}$. Yet, if the attack of Sect. 3 would have been based on the former strategy instead of the latter, it would have succeeded only if $|I_{f_1(t_1)\oplus f_1(t_2)}|\ne 0$, and the attack should have been evaluated $2^n/q$ times to succeed (resulting in total complexity of about $2^n$). By making $2^{3n/4}$ queries, the distinguisher makes sure that $|I_d|$ is equally large for all d’s and that way spreads its chances, but unfortunately, we see little opportunities in improving the attack.

It is important to remark that the attack of Sect. 3 and the discussion on the distinguishing event (11) consider the case where the distinguisher can choose the tweak values. This implies that an improved security bound can be achieved if the maximum number of queries for each tweak is fixed.

We explicitly remark that this limitation is not a necessary condition. In particular, above reasoning is informal and only included for intuitive reasons, and we cannot draw any formal conclusion from it. However, even for this limited scenario, improved security of $\mathrm {CLRW2}$ is still a non-trivial open problem. We elaborate on the possibility of releasing the tweak usage limitation in Sect. 5.7.

A final condition that the mirror theory puts on the graph, in addition to (i) and (ii) above, is the following:

• (iii) The graph should not contain an excessively large tree.

This is a merely technical requirement to make the proof argument of the mirror theory work, and it is not clear how a violation of condition (iii) may break the scheme. That said, also condition (iii) can be easily violated, depending on the mixing functions in use. For example, if $f_1(t)=f_1\otimes t$ (i.e., the example AXU$_2$ hash function of Sect. 2), a collision of the form

$$\begin{aligned} m_1\oplus f_1(m_1) = m_2\oplus f_1(m_2)\,, \end{aligned}$$

for $m_1,m_2\ne 0$ implies that also

$$\begin{aligned} m_2\oplus f_1(m_2) = m_1^{-1}m_2^2\oplus f_1(m_1^{-1}m_2^2) = \cdots = m_1^{-\lambda }m_2^{\lambda +1}\oplus f_1(m_1^{-\lambda }m_2^{\lambda +1})\,, \end{aligned}$$

for any $\lambda \ge 0$, potentially rendering an excessively large tree. The issue can be resolved by resorting to 4-wise independent XOR universal hash functions (see Sect. 2.2).

5 Improved Security of Cascaded LRW2 Under Tweak Limits

Based on the two conclusions from Sect. 4, we prove that if $h_1$ and $h_2$ are two 4-wise independent XOR universal hash functions and every tweak occurs at most $q^{1/3}$ times, the Cascaded $\mathrm {LRW2}$ construction $\mathrm {GCL}^{h_1,h_1\oplus h_2,h_2}$ of (2) achieves security up to complexity approximately $2^{3n/4}$.

Theorem 2

Let $\kappa ,\tau ,n\in \mathbb {N}$, let $E\in \mathsf {iperm}(\kappa ,n)$, H be an $\varepsilon$-AXU$_4$ hash function family, and consider $\mathrm {GCL}^{h_1,h_1\oplus h_2,h_2}:\{0,1\}^{2\kappa }\times H^2\times \{0,1\}^{\tau }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$. Let $\gamma \in \mathbb {N}$ such that $2\le \gamma \le q/4$ be a threshold. For any distinguisher $\mathcal {D}$ with query complexity at most $q\le 2^n/1600$ that queries each tweak at most $\gamma$ times, there exists a distinguisher $\mathcal {D}'$ that makes at most q queries such that

$$\begin{aligned} \mathbf {Adv}_{\mathrm {GCL}^{h_1,h_1\oplus h_2,h_2}}^{\mathrm {stprp}}(\mathcal {D}) \le 6{q\atopwithdelims ()4}2^n\varepsilon ^4 + {q\atopwithdelims ()2}(2\gamma +1) \varepsilon ^2 + \frac{(\gamma +3)q}{2^n} + 2\mathbf {Adv}_{E}^{\mathrm {sprp}}(\mathcal {D}')\,. \end{aligned}$$

(14)

Putting $\gamma =q^{1/3}$, the bound of (14) yields security up to $q\le 2^{3n/4}$ queries. The limitation $\gamma$ on the number of tweak repeats sounds restrictive, but it is not. In practical applications [10, 12, 29], the tweak is constituted of a random value concatenated with a counter.

The proof of Theorem 2 is based on Patarin’s mirror theory [22, 26, 28], which found popularization in the work of Mennink and Neves on Encrypted Davies-Meyer and its dual [20]. Although the mirror theory is quite simple to understand and apply, its proof is heavy and the recursive argument underneath it is debated by some. In this work, however, we will only use the mirror theory up to 3n / 4-bit security, i.e., rely on the first recursion in the mirror theory proof only.

The security proof is comparable to that of $\mathrm {EDM}$ [20], and in particular also relies on the observation that any evaluation of $c=\mathrm {GCL}^{h_1,h_1\oplus h_2,h_2}(\mathbf{k},t,m)$ for $\mathbf{k}=(k_1,k_2,h_1,h_2)$ can be rewritten as

$$\begin{aligned} E_{k_1}(m\oplus h_1(t)) \oplus E_{k_2}^{-1}(c\oplus h_2(t)) = h_1(t)\oplus h_2(t)\,. \end{aligned}$$

(15)

Differences in the analysis occur due to the possibility of the adversary to choose the tweak and the fact that the tweak occurs in all three parts of the equation (input to $E_{k_1}$, to $E_{k_2}^{-1}$, and in the right hand side $h_1(t)\oplus h_2(t)$). These differences cause that only security up to $2^{3n/4}$ is achievable. However, the differences compared with the analysis in [20] mostly affect description of oracle views and analysis of bad views; the application of the mirror theory is fairly the same. Therefore, we discard much of the details on mirror theory from the proof and include it in Appendix B; the proof is fully intelligible without this appendix.

The proof is given in Sects. 5.1–5.6. We discuss the possibility of releasing the limitation $\gamma$ on the tweak usage in Sect. 5.7.

5.1 H-Coefficient Technique

We will use Patarin’s H-coefficient technique [25, 27], for which we follow the description by Chen and Steinberger [5]. Consider two oracles $\mathcal {O}$ and $\mathcal {P}$ with identical interfaces, and a deterministic distinguisher $\mathcal {D}$ with query complexity q and unbounded computational power that tries to distinguish both oracles. Denote its success probability by $\varDelta _{\mathcal {D}}(\mathcal {O}\,;\, \mathcal {P})$. Let $X_{\mathcal {O}}$ denote the probability distribution of views when $\mathcal {D}$ is interacting with $\mathcal {O}$, and similarly $X_{\mathcal {P}}$ the distribution of views for interaction with $\mathcal {P}$. A view $\nu$ is called “attainable” if $\mathbf {Pr}\left( X_{\mathcal {P}}=\nu \right) >0$, and denote by $\mathcal {V}$ the set of all attainable views. The H-coefficient technique states the following:

Lemma 1

(H-coefficient technique). Let $\mathcal {D}$ be a deterministic distinguisher, and consider a partition $\mathcal {V}= \mathcal {V}_{\mathrm {bad}}\cup \mathcal {V}_{\mathrm {good}}$ of the set of attainable views. Let $\delta ,\epsilon \in [0,1]$ be such that $\mathbf {Pr}\left( X_{\mathcal {P}}\in \mathcal {V}_{\mathrm {bad}}\right) \le \delta$, and $\displaystyle \frac{\mathbf {Pr}\left( X_{\mathcal {O}}=\nu \right) }{\mathbf {Pr}\left( X_{\mathcal {P}}=\nu \right) } \ge 1-\epsilon$ for all $\nu \in \mathcal {V}_{\mathrm {good}}$. Then, the distinguishing advantage satisfies $\varDelta _{\mathcal {D}}(\mathcal {O}\,;\, \mathcal {P}) \le \delta + \epsilon$.

A proof of the technique is given among others in [4, 5, 20].

For view $\nu = \{(x_1,y_1),\ldots ,(x_q,y_q)\}$ consisting of q input/output tuples, an oracle $\mathcal {O}$ is said to extend $\nu$, denoted $\mathcal {O}\vdash \nu$, if $\mathcal {O}(x_i)=y_i$ for all $i=\{1,\ldots ,q\}$.

5.2 General Setting and Views

Let $\widetilde{p}\xleftarrow {{\scriptscriptstyle \$}}\mathsf {iperm}(\tau ,n)$, $\mathbf{k}\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{2\kappa }\times H^2$, and $p_1,p_2\xleftarrow {{\scriptscriptstyle \$}}\mathsf {perm}(n)$. Consider any distinguisher $\mathcal {D}$ whose goal is to distinguish $\mathrm {GCL}^{h_1,h_1\oplus h_2,h_2}_{\mathbf{k}}$ from $\widetilde{p}$.

As a first step, we replace $(E_{k_1},E_{k_2})$ by $(p_1,p_2^{-1})$ at the cost of $2\mathbf {Adv}_{E}^{\mathrm {sprp}}(\mathcal {D}')$, where $\mathcal {D}'$ is some distinguisher with the same query complexity q as $\mathcal {D}$. (Note that we replaced $E_{k_2}$ by the inverse of $p_2$ for simplicity of further analysis.) Denote the resulting scheme with F for brevity; it remains to bound the advantage of $\mathcal {D}$ in distinguishing $\mathcal {O}=F$ (the real world) from $\mathcal {P}=\widetilde{p}$ (the ideal world). As of now, we give the distinguisher unbounded computational power, and its complexity will only be measured by the number of oracle queries it makes. Without loss of generality, we can consider it to be deterministic, and will apply the H-coefficient technique of Lemma 1.

$\mathcal {D}$ makes q construction queries which are recorded in view $\nu '=\{(t_1,m_1,c_1),\ldots ,(t_q,m_q,c_q)\}$. After $\mathcal {D}$’s interaction with its oracle, but before it outputs its decision bit, its oracle will reveal the subkeys $h_1,h_2$. In the real world, these are the XOR universal hash functions used in F, whereas in the ideal world these are dummy functions randomly drawn from H. We denote the complete view by

$$\begin{aligned} \nu =(\nu ',h_1,h_2)\,. \end{aligned}$$

(16)

Without loss of generality, we assume that $\mathcal {D}$ never repeats queries, and hence that $(t_i,m_i)\ne (t_j,m_j)$ and $(t_i,c_i)\ne (t_j,c_j)$ for any $i\ne j$.

5.3 Attainable Index Mappings

In the real world $\mathcal {O}$, each tuple $(t_i,m_i,c_i)\in \nu '$ corresponds to an evaluation of F and satisfies

$$\begin{aligned} p_1(m_i\oplus h_1(t_i)) \oplus p_2(c_i\oplus h_2(t_i)) = h_1(t_i)\oplus h_2(t_i)\,, \end{aligned}$$

where we recall that $E_{k_2}$ was replaced with $p_2^{-1}$. Writing $P_{a_i}:=p_1(m_i\oplus h_1(t_i))$ and $P_{b_i}:=p_2(c_i\oplus h_2(t_i))$, view $\nu$ defines the following q equations:

$$\begin{aligned} \begin{aligned} P_{a_1} \oplus P_{b_1}&= h_1(t_1)\oplus h_2(t_1)\,,\\ P_{a_2} \oplus P_{b_2}&= h_1(t_2)\oplus h_2(t_2)\,,\\ \vdots \!\!\;\qquad&\\ P_{a_q} \oplus P_{b_q}&= h_1(t_q)\oplus h_2(t_q)\,. \end{aligned}\end{aligned}$$

(17)

Here, some of the unknowns may be equal to each other. We have that $P_{a_i}\ne P_{a_j}$ if and only if $m_i\oplus h_1(t_i)\ne m_j\oplus h_1(t_j)$, and $P_{b_i}\ne P_{b_j}$ if and only if $c_i\oplus h_2(t_i)\ne c_j\oplus h_2(t_j)$. No condition a priori holds for $P_{a_i}$ versus $P_{b_j}$, as these are defined by independent permutations. We have

$$\begin{aligned} r = |\{m_i\oplus h_1(t_i) \mid i\in \{1,\ldots ,q\} \}| + |\{c_i\oplus h_2(t_i) \mid i\in \{1,\ldots ,q\} \}| \end{aligned}$$

(18)

unknowns.

5.4 Bad Views

Inspired by the discussion in Sect. 4, we associate a bipartite graph ${G}(\nu )=({U},{V},{E}(\nu ))$ with the view $\nu$. ${U}=\{0,1\}^{n}$ corresponds to the input values to $p_1$, ${V}=\{0,1\}^{n}$ to the output values of $p_2^{-1}$, and for every $(t_i,m_i,c_i)\in \nu '$, the edge $(m_i\oplus h_1(t_i),c_i \oplus h_2(t_i))$ with label $h_1(t_i)\oplus h_2(t_i)$ from ${U}$ to ${V}$ is added to ${E}(\nu )$. The example graph of Fig. 3 still applies, be it with $f_1=h_1$, $f_2=h_1\oplus h_2$, and $f_3=h_2$.

In Sect. 4, we already informally discussed what problems could occur in such a graph, i.e., what properties would make the mirror theory inapplicable: it should not contain a path of even length whose labels sum to 0, a circle, or an excessively large tree. The latter is informal, it is often based on a pre-defined threshold on the maximum size of the tree. As our security analysis will cap on 3n / 4-bit security anyway, we can keep it simple, and put as one of the bad events that ${G}(\nu )$ should not contain a subgraph of $\ge 4$ edges. This would imply the non-existence of an excessively large tree, as well as circles and paths of length $\ge 4$. We still have to rule out the existence of a path of length 2 whose labels sum to 0 and a circle of length 2.

Formally, we say that a view $\nu$ is a bad view if its corresponding tree ${G}(\nu )$ contains

• (i) a path of length 2 whose labels sum to 0;

• (ii) a circle of length 2;

• (iii) a subgraph of $\ge 4$ edges.

5.5 Probability of Bad Views ($\delta$)

By Lemma 1, we have to analyze the probability that a view generated in the ideal world is bad, and the analysis will rely on the fact that $h_1$ and $h_2$ are 4-wise independent universal hash functions. We have

$$\begin{aligned} \mathbf {Pr}\left( X_{\widetilde{p}}\in \mathcal {V}_{\mathrm {bad}}\right) \le \mathbf {Pr}\left( \text {path}\right) + \mathbf {Pr}\left( \text {circle}\right) + \mathbf {Pr}\left( \text {subgraph}\right) \,, \end{aligned}$$

(19)

where the sizes of the path, circle, and subgraph, are left implicit.

(i) a path. Consider any two distinct queries $(t_i,m_i,c_i),(t_j,m_j,c_j)$. They yield a 0-label-sum path if either

$$\begin{aligned} m_i\oplus h_1(t_i)=m_j\oplus h_1(t_j) \text { and } h_1(t_i)\oplus h_2(t_i) = h_1(t_j)\oplus h_2(t_j)\,, \end{aligned}$$

or

$$\begin{aligned} c_i\oplus h_2(t_i)= c_j\oplus h_2(t_j) \text { and } h_1(t_i)\oplus h_2(t_i) = h_1(t_j)\oplus h_2(t_j)\,. \end{aligned}$$

If $t_i=t_j$, then necessarily $m_i\ne m_j$ and $c_i\ne c_j$ (as the two queries are distinct) and the conditions happen with probability 0. Otherwise, as $h_1$ and $h_2$ are $\varepsilon$-AXU$_4$, both conditions happen with probability at most $\varepsilon ^2$. Thus,

$$\begin{aligned} \mathbf {Pr}\left( \text {path}\right) \le 2{q\atopwithdelims ()2}\varepsilon ^2\,. \end{aligned}$$

(20)

(ii) a circle. Consider any two distinct queries $(t_i,m_i,c_i),(t_j,m_j,c_j)$. They yield a circle if

$$\begin{aligned} m_i\oplus h_1(t_i)=m_j\oplus h_1(t_j) \text { and } c_i\oplus h_2(t_i)= c_j\oplus h_2(t_j)\,, \end{aligned}$$

which, as before, happens with probability at most $\varepsilon ^2$. Thus,

$$\begin{aligned} \mathbf {Pr}\left( \text {circle}\right) \le {q\atopwithdelims ()2}\varepsilon ^2\,. \end{aligned}$$

(21)

(iii) a subgraph. Consider any four distinct queries $(t_{i_1},m_{i_1},c_{i_1}),\dots ,$ $(t_{i_4},m_{i_4},c_{i_4})$ to yield a subgraph. We can consider six possible configurations, as described in Fig. 5. In these configurations, only collisions are explicitly indicated; two nodes that are different in the configuration may or may not collide. We treat all configurations independently, where we will rely on the fact that $h_1$ and $h_2$ are $\varepsilon$-AXU$_4$.

Fig. 5.

Possible configurations of subgraphs of 4 edges. Upper shore is ${U}$, lower shore is ${V}$, and labels are omitted for brevity. Two nodes in the same shore may or may not be equal.

• (A) Configuration (A) happens only if

  $$\begin{aligned} m_{i_1}\oplus h_1(t_{i_1}) = m_{i_2}\oplus h_1(t_{i_2}) = m_{i_3}\oplus h_1(t_{i_3}) = m_{i_4}\oplus h_1(t_{i_4})\,. \end{aligned}$$

  If the tweaks are not all distinct, the condition is satisfied with probability 0. On the other hand, if $t_{i_1},t_{i_2},t_{i_3},t_{i_4}$ are all distinct, the condition is satisfied with probability at most $\varepsilon ^3$. There are at most ${q\atopwithdelims ()4}$ possible choices of queries that satisfy this condition on the tweaks;

• (B) Configuration (B) happens only if

  $$\begin{aligned} m_{i_1}\oplus h_1(t_{i_1})&= m_{i_2}\oplus h_1(t_{i_2}) = m_{i_3}\oplus h_1(t_{i_3})\,,\\ c_{i_3}\oplus h_2(t_{i_3})&= c_{i_4}\oplus h_2(t_{i_4})\,. \end{aligned}$$

  Further analysis depends on the values of the tweaks.

  • If $t_{i_1},t_{i_2},t_{i_3},t_{i_4}$ are all distinct, the condition is satisfied with probability at most $\varepsilon ^3$. There are at most ${q\atopwithdelims ()4}$ possible choices of queries that satisfy this condition on the tweaks;

  • If $t_{i_1}=t_{i_2}$, $t_{i_1}=t_{i_3}$, $t_{i_2}=t_{i_3}$, or $t_{i_3}=t_{i_4}$, the condition is satisfied with probability 0;

  • If $t_{i_1}=t_{i_4}$, but $t_{i_1},t_{i_2},t_{i_3}$ are all distinct, the condition is satisfied with probability at most $\varepsilon ^3$. There are at most ${q\atopwithdelims ()3}\cdot (\gamma -1)$ possible choices of queries that satisfy this condition on the tweaks, noting that every tweak occurs at most $\gamma$ times;

  • If $t_{i_2}=t_{i_4}$, but $t_{i_1},t_{i_2},t_{i_3}$ are all distinct, a similar reasoning applies.

  Overall, configuration (B) is satisfied with probability at most

  $$\begin{aligned} \max \left\{ {q\atopwithdelims ()4}\varepsilon ^3 , {q\atopwithdelims ()3}(\gamma -1) \varepsilon ^3 \right\} \le {q\atopwithdelims ()4}\varepsilon ^3\,, \end{aligned}$$

  for $\gamma \le q/4$;

• (C) Configuration (C) happens only if

  $$\begin{aligned} m_{i_1} \oplus h_1(t_{i_1})&= m_{i_2}\oplus h_1(t_{i_2})\,,\\ c_{i_2} \oplus h_2(t_{i_2})&= c_{i_3}\oplus h_2(t_{i_3})\,,\\ m_{i_3} \oplus h_1(t_{i_3})&= m_{i_4}\oplus h_1(t_{i_4})\,. \end{aligned}$$

  Further analysis depends on the values of the tweaks.

  • If $t_{i_1},t_{i_2},t_{i_3},t_{i_4}$ are all distinct, the condition is satisfied with probability at most $2^n\varepsilon ^4$ (obtained by summing over all possible connections between the first and third equation, and then applying the $\varepsilon$-AXU$_4$ bound). There are at most ${q\atopwithdelims ()4}$ possible choices of queries that satisfy this condition on the tweaks;

  • If $t_{i_1}=t_{i_2}$, $t_{i_2}=t_{i_3}$, or $t_{i_3}=t_{i_4}$, the condition is satisfied with probability 0;

  • If $t_{i_1}=t_{i_3}$, but $t_{i_1},t_{i_2},t_{i_4}$ are all distinct, the condition is satisfied with probability at most $\varepsilon ^3$. There are at most ${q\atopwithdelims ()3}\cdot (\gamma -1)$ possible choices of queries that satisfy this condition on the tweaks, noting that every tweak occurs at most $\gamma$ times;

  • If $t_{i_2}=t_{i_4}$, but $t_{i_1},t_{i_2},t_{i_3}$ are all distinct, a similar reasoning applies;

  • If $t_{i_1}=t_{i_4}$, but $t_{i_1},t_{i_2},t_{i_3}$ are all distinct, a similar reasoning applies;

  • If $t_{i_1}=t_{i_3}$ and $t_{i_2}=t_{i_4}$ but $t_{i_1},t_{i_2}$ are distinct, the condition is satisfied with probability at most $\varepsilon ^2$. There are at most ${q\atopwithdelims ()2}\cdot (\gamma -1)$ possible choices of queries that satisfy this condition on the tweaks, noting that every tweak occurs at most $\gamma$ times and that there is at most one option for $(t_{i_4},m_{i_4},c_{i_4})$ once the other three queries are fixed.

  Overall, configuration (C) is satisfied with probability at most

  $$\begin{aligned} \max \left\{ {q\atopwithdelims ()4}2^n\varepsilon ^4 , {q\atopwithdelims ()3}(\gamma -1) \varepsilon ^3 , {q\atopwithdelims ()2}(\gamma -1) \varepsilon ^2 \right\} \le {q\atopwithdelims ()4}2^n\varepsilon ^4 + {q\atopwithdelims ()2}(\gamma -1) \varepsilon ^2\,, \end{aligned}$$

  for $\gamma \le q/4$ and $2^n\varepsilon \ge 1$;

• (D) Configuration (D) is symmetrical to configuration (C);

• (E) Configuration (E) is symmetrical to configuration (B);

• (F) Configuration (F) is symmetrical to configuration (A).

Thus,

$$\begin{aligned} \mathbf {Pr}\left( \text {subgraph}\right)&\le 4{q\atopwithdelims ()4}\varepsilon ^3 + 2{q\atopwithdelims ()4}2^n\varepsilon ^4 + 2{q\atopwithdelims ()2}(\gamma -1) \varepsilon ^2\nonumber \\&\le 6{q\atopwithdelims ()4}2^n\varepsilon ^4 + 2{q\atopwithdelims ()2}(\gamma -1) \varepsilon ^2\,. \end{aligned}$$

(22)

Conclusion for bad events. From (19) and the individual probabilities of (20), (21), and (22), we obtain

$$\begin{aligned} \mathbf {Pr}\left( X_{\widetilde{p}}\in \mathcal {V}_{\mathrm {bad}}\right)&\le 3{q\atopwithdelims ()2}\varepsilon ^2 + 6{q\atopwithdelims ()4}2^n\varepsilon ^4 + 2{q\atopwithdelims ()2}(\gamma -1) \varepsilon ^2\\&\le 6{q\atopwithdelims ()4}2^n\varepsilon ^4 + {q\atopwithdelims ()2}(2\gamma +1) \varepsilon ^2\,, \end{aligned}$$

for $\gamma \ge 2$.

5.6 Ratio for Good Views ($\epsilon$)

Consider a given view $\nu =(\nu ',h_1,h_2)$ where $\nu =\{(t_1,m_1,c_1),\ldots ,(t_q,m_q,c_q)\}$. Define

$$\begin{aligned} r_1&= |\{m_i\oplus h_1(t_i) \mid i\in \{1,\ldots ,q\} \}|\,,\end{aligned}$$

(23)

$$\begin{aligned} r_2&= |\{c_i\oplus h_2(t_i) \mid i\in \{1,\ldots ,q\} \}|\,. \end{aligned}$$

(24)

Note that $r_1+r_2$ is equal to the number of unknowns in the system of equations (see (18)). For any $t\in \{0,1\}^{\tau }$, we denote $u_t=|\{i\in \{1,\ldots ,q\} \mid t_i=t\}|$.

For the ideal world $\widetilde{p}$, we have

$$\begin{aligned} \mathbf {Pr}\left( X_{\widetilde{p}}=\nu \right)&= \mathbf {Pr}\left( \widetilde{p}\xleftarrow {{\scriptscriptstyle \$}}\mathsf {iperm}(\tau ,n) \,:\, \widetilde{p}\vdash \nu '\right) \cdot \mathbf {Pr}\left( (h_1,h_2)=(h'_1,h'_2)\xleftarrow {{\scriptscriptstyle \$}}H^2\right) \nonumber \\&= \frac{1}{\prod _{t\in \{0,1\}^{\tau }}(2^n)_{u_t}}\cdot \frac{1}{|H|^2}\,, \end{aligned}$$

(25)

where for the first probability we use that $\widetilde{p}$ is a family of permutations and for every $t\in \{0,1\}^{\tau }$ the view defines $u_t$ values.

For the real world F, recall that it is built from two permutations $p_1,p_2^{-1}$. We have

$$\begin{aligned} \mathbf {Pr}\left( X_{F}=\nu \right)&= \mathbf {Pr}\left( p_1,p_2^{-1}\xleftarrow {{\scriptscriptstyle \$}}\mathsf {perm}(n) \,:\, F\vdash \nu ' \mid h_1,h_2 \right) \cdot \mathbf {Pr}\left( (h_1,h_2)=(h'_1,h'_2)\xleftarrow {{\scriptscriptstyle \$}}H^2\right) \nonumber \\&= \mathbf {Pr}\left( p_1,p_2^{-1}\xleftarrow {{\scriptscriptstyle \$}}\mathsf {perm}(n) \,:\, F\vdash \nu ' \mid h_1,h_2 \right) \cdot \frac{1}{|H|^2}\,. \end{aligned}$$

(26)

As has become clear from (17), $\nu =(\nu ',h_1,h_2)$ fixes exactly q equations on $r_1$ unknowns for $p_1$ and $r_2$ unknowns for $p_2^{-1}$, where the inputs to $p_1$ and $p_2^{-1}$ are fixed. We rely on the following lemma that is based on Patarin’s mirror theory.

Lemma 2

Consider good view $\nu =(\nu ',h_1,h_2)$ whose system of q equations (17) has no subgraph of $\ge 4$ edges, has no path of length 2 whose labels sum to 0, and no circle of length 2. As long as $5^2\cdot q\le 2^n/64$, the number of solutions to the $r_1+r_2$ unknowns is at least

$$\begin{aligned} \frac{(2^n)_{r_1}(2^n-4)_{r_2}}{2^{nq}}\,. \end{aligned}$$

The proof of Lemma 2 is omitted: it is very similar to the reasoning on $\mathrm {EDM}$ in [20] and follows straightforwardly from Patarin’s mirror theory as reviewed in Appendix B. The side condition $5^2\cdot q\le 2^n/64$ is slightly different from that in [20], as we have adopted the bound from Nachef, Patarin, and Volte [22].

Every such solution defines $r_1$ evaluations of $p_1$, and $r_2$ evaluations of $p_2$, and hence the remaining probability in (26) satisfies

$$\begin{aligned} \mathbf {Pr}\left( p_1,p_2^{-1}\xleftarrow {{\scriptscriptstyle \$}}\mathsf {perm}(n) \,:\, F\vdash \nu ' \mid h_1,h_2 \right) \ge \frac{(2^n)_{r_1}(2^n-4)_{r_2}}{2^{nq}\cdot (2^n)_{r_1}(2^n)_{r_2}}\,. \end{aligned}$$

We obtain for the ratio:

$$\begin{aligned} \frac{\mathbf {Pr}\left( X_{F}=\nu \right) }{\mathbf {Pr}\left( X_{\widetilde{p}}=\nu \right) }&\ge \frac{\prod _{t\in \{0,1\}^{\tau }}(2^n)_{u_t}\cdot |H|^2}{1} \cdot \frac{(2^n)_{r_1}(2^n-4)_{r_2}}{2^{nq}\cdot (2^n)_{r_1}(2^n)_{r_2}\cdot |H|^2}\nonumber \\&= \frac{\prod _{t\in \{0,1\}^{\tau }}(2^n)_{u_t}\cdot (2^n-4)_{r_2}}{2^{nq}\cdot (2^n)_{r_2}}\,. \end{aligned}$$

(27)

Using that for all t, $u_t\le \gamma$, and that $\sum _{t\in \{0,1\}^{\tau }} u_t = q$:

$$\begin{aligned} (27)&\ge \frac{\prod _{t\in \{0,1\}^{\tau }}(2^n-(\gamma -1))^{u_t}\cdot (2^n-4)_{r_2}}{2^{nq}\cdot (2^n)_{r_2}}\nonumber \\&= \left( \frac{2^n-(\gamma -1)}{2^n}\right) ^q\cdot \prod _{i=0}^3 \left( 1 - \frac{r_2}{2^n-i}\right) \,. \end{aligned}$$

(28)

Using that $r_2\le q-1$, and by simple algebra for $q\le 2^n/3$:

$$\begin{aligned} (28)&\ge 1 - \left( \frac{(\gamma -1)q}{2^n} + \frac{q-1}{2^n} + \frac{q-1}{2^n-1} + \frac{q-1}{2^n-2} + \frac{q-1}{2^n-3}\right) \\&\ge 1 - \frac{(\gamma +3)q}{2^n}\,. \end{aligned}$$

We have obtained $\epsilon =\frac{(\gamma +3)q}{2^n}$, provided $5^2\cdot q\le 2^n/64$.

5.7 Releasing Tweak Usage Limitation

The limitation on the tweak usage, namely that the distinguisher can query each tweak at most $\gamma$ times, is used at two places in the proof.

The first place is the last case of configuration (C) in Sect. 5.5, namely the case where $t_{i_1}=t_{i_3}$ and $t_{i_2}=t_{i_4}$. For upper bounding the number of choices for the four queries without relying on parameter $\gamma$, one may take into account that $m_{i_1}\oplus m_{i_2} = m_{i_3}\oplus m_{i_4}$ is necessarily needed. This value needs to be equal to the random value $h_1(t_{i_1})\oplus h_2(t_{i_2})$. However, we see no possibility for deriving a formal bound here.

The second place is in the application of the mirror theory in Sect. 5.6. Our approach to achieve improved 3n / 4-bit security relies on Patarin’s mirror theory, which is specifically developed to work well if a scheme is compared with a random function. Obviously, evaluations of $\mathrm {CLRW2}$ under the same tweak will always give distinct responses. In particular, if a distinguisher uses the same tweak for all queries, all responses will be distinct, and the scheme can be distinguished from a random function with probability about ${q\atopwithdelims ()2}/2^n$. More generally, if every tweak is evaluated at most $\gamma$ times, the scheme can be distinguished from a random function with probability at most around $\gamma q/2^n$. Resolving the $\gamma$ limitation here requires improving Patarin’s mirror theory or employing a different proof technique.

Appendices

A A Proof of Theorem 1

Consider the distinguisher of Sect. 3.2 for any $\epsilon \ge 0$. Its success advantage satisfies

$$\begin{aligned} \mathbf {Adv}_{\mathrm {GCL}^{f_1,f_2,f_3}}^{\mathrm {stprp}}(\mathcal {D})&= \mathbf {Pr}\left( \mathcal {D}^{\mathrm {GCL}^{f_1,f_2,f_3}}=1\right) - \mathbf {Pr}\left( \mathcal {D}^{\widetilde{p}}=1\right) \nonumber \\&= 1 - \mathbf {Pr}\left( \mathcal {D}^{\mathrm {GCL}^{f_1,f_2,f_3}}=0\right) - \mathbf {Pr}\left( \mathcal {D}^{\widetilde{p}}=1\right) \,. \end{aligned}$$

(29)

The derivation relies on the following two lemmas, the proofs of which are in Sects. A.1 and A.2.

Lemma 3

Provided $n\ge 6$, $\mathbf {Pr}\left( \mathcal {D}^{\mathrm {GCL}^{f_1,f_2,f_3}}=0\right) \le \frac{32}{2^{4\epsilon }} + \frac{80}{2^{n/2+2\epsilon }}$.

Lemma 4

For any integral $1\le \alpha \le \sqrt{\beta }-1$, provided $n\ge 16$, $\mathbf {Pr}\left( \mathcal {D}^{\widetilde{p}}=1\right) \le \alpha 2^n\left( \frac{2\alpha }{2^{2\epsilon }}\right) ^{3/(4\alpha ^2)\cdot 2^{4\epsilon }} + \frac{2^{(\alpha +2)2\epsilon }}{2^{(\alpha -2)n/2}}$.

Putting $\epsilon =\log _2(n)/2$, we derive from (29) and Lemmas 3 and 4 that

$$\begin{aligned} \mathbf {Adv}_{\mathrm {GCL}^{f_1,f_2,f_3}}^{\mathrm {stprp}}(\mathcal {D})&\ge 1 - \frac{32}{n^2} - \frac{80}{n2^{n/2}} - \alpha 2^n\left( \frac{2\alpha }{n}\right) ^{3/(4\alpha ^2)\cdot n^2} - \frac{n^{(\alpha +2)}}{2^{(\alpha -2)n/2}}\,, \end{aligned}$$

provided $n\ge 16$, and for any integral $1\le \alpha \le \sqrt{3/8}n-1$. Clearly, the bound is meaningless for $\alpha =1,2$. Computer verification yields optimal choice $\alpha =5$.

1.1 A.1 Proof of Lemma 3

Putting $d^*=f_1(t)\oplus f_1(t')$, we have

$$\begin{aligned} \mathbf {Pr}\left( \mathcal {D}^{\mathrm {GCL}^{f_1,f_2,f_3}}=0\right) = \mathbf {Pr}\left( \forall _{d\in \{0,1\}^{n}} N_d<\beta \right) \le \mathbf {Pr}\left( N_{d^*}<\beta \right) \,. \end{aligned}$$

(30)

Clearly, if $f_2(t)\oplus f_2(t')=0$, then $c_i\oplus c'_j=f_3(t)\oplus f_3(t')$ for all $(i,j)\in I_{d^*}$ and thus $N_{d^*}={q'\atopwithdelims ()2}>\beta$, implying $\mathbf {Pr}\left( N_{d^*}<\beta \right) =0$. Henceforth, assume that $d^{**}:=f_2(t)\oplus f_2(t')\ne 0$.

By Chebychev’s inequality:

$$\begin{aligned} \mathbf {Pr}\left( N_{d^*}<\beta \right)&= \mathbf {Pr}\left( N_{d^*}-\mathbf {Ex}\left( N_{d^*}\right) <\beta - \mathbf {Ex}\left( N_{d^*}\right) \right) \nonumber \\&\le \mathbf {Pr}\left( \big | N_{d^*}-\mathbf {Ex}\left( N_{d^*}\right) \big |\ge \mathbf {Ex}\left( N_{d^*}\right) - \beta \right) \nonumber \\&\le \frac{\mathbf {Var}\left( N_{d^*}\right) }{(\mathbf {Ex}\left( N_{d^*}\right) -\beta )^2}\nonumber \\&= \frac{\mathbf {Ex}\left( \big (N_{d^*}\big )^2\right) - \Big (\mathbf {Ex}\left( N_{d^*}\right) \Big )^2}{(\mathbf {Ex}\left( N_{d^*}\right) -\beta )^2}\,. \end{aligned}$$

(31)

For distinct $(i,j),(k,l)\in I_{d^*}$, define

$$\begin{aligned} N_{d^*}^{(i,j),(k,l)} = {\left\{ \begin{array}{ll} 1 \text {, if } c_i\oplus c'_j=c_k\oplus c'_l\,,\\ 0 \text {, otherwise}\,, \end{array}\right. } \end{aligned}$$

(32)

such that

$$\begin{aligned} N_{d^*} = \sum _{\begin{array}{c} (i,j),(k,l)\in I_{d^*}\\ (i,j)\ne (k,l) \end{array}} N_{d^*}^{(i,j),(k,l)}\,. \end{aligned}$$

(33)

We have

$$\begin{aligned} \mathbf {Ex}\left( N_{d^*}\right)&= \sum _{\begin{array}{c} (i,j),(k,l)\in I_{d^*}\\ (i,j)\ne (k,l) \end{array}} \mathbf {Pr}\left( c_i\oplus c'_j=c_k\oplus c'_l\right) \,, \end{aligned}$$

(34)

and

$$\begin{aligned} \mathbf {Ex}\left( \big (N_{d^*}\big )^2\right)&= \mathbf {Ex}\left( \sum _{\begin{array}{c} (i,j),(k,l)\in I_{d^*}\\ (i,j)\ne (k,l) \end{array}}\sum _{\begin{array}{c} (i',j'),(k',l')\in I_{d^*}\\ (i',j')\ne (k',l') \end{array}} N_{d^*}^{(i,j),(k,l)}N_{d^*}^{(i',j'),(k',l')} \right) \nonumber \\&= \sum _{\begin{array}{c} (i,j),(k,l)\in I_{d^*}\\ (i,j)\ne (k,l) \end{array}}\sum _{\begin{array}{c} (i',j'),(k',l')\in I_{d^*}\\ (i',j')\ne (k',l') \end{array}} \mathbf {Pr}\left( c_i\oplus c'_j=c_k\oplus c'_l\;,\;c_{i'}\oplus c'_{j'}=c_{k'}\oplus c'_{l'} \right) \,. \end{aligned}$$

(35)

Above summation consists of ${q'\atopwithdelims ()2}^2$ terms of independent probabilities, but their values differ depending on overlaps in the two sets $\{(i,j),(k,l)\}$, $\{(i',j'),(k',l')\}$. For any distinct $(i_1,j_1),(i_2,j_2),(i_3,j_3),(i_4,j_4)\in I_{d^*}$, define

$$\begin{aligned} \mathbf {P}_2&:=\mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\right) \,,\\ \mathbf {P}_3&:=\mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}=c_{i_3}\oplus c'_{j_3}\right) \,,\\ \mathbf {P}_4&:=\mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\;,\; c_{i_3}\oplus c'_{j_3}=c_{i_4}\oplus c'_{j_4}\right) \,. \end{aligned}$$

We can observe that the sum in (35) consists of exactly ${q'\atopwithdelims ()2}$ terms satisfying $\big |\{(i,j),(k,l)\}\cup \{(i',j'),(k',l')\}\big | = 2$, in which case the corresponding probability is of the form $\mathbf {P}_2$, exactly ${q'\atopwithdelims ()2}2{q'-2\atopwithdelims ()1}$ terms satisfying $\big |\{(i,j),(k,l)\}\cup \{(i',j'),(k',l')\}\big | = 3$, in which case the corresponding probability is of the form $\mathbf {P}_3$, and exactly ${q'\atopwithdelims ()2}{q'-2\atopwithdelims ()2}$ terms satisfying $\big |\{(i,j),(k,l)\}\cup \{(i',j'),(k',l')\}\big | = 4$, in which case the corresponding probability is of the form $\mathbf {P}_4$. We obtain (using independence of the probabilities)

$$\begin{aligned} \mathbf {Ex}\left( \big (N_{d^*}\big )^2\right)&= {q'\atopwithdelims ()2}\cdot \mathbf {P}_2 + {q'\atopwithdelims ()2}2{q'-2\atopwithdelims ()1}\cdot \mathbf {P}_3 + {q'\atopwithdelims ()2}{q'-2\atopwithdelims ()2}\cdot \mathbf {P}_4\,. \end{aligned}$$

We likewise have $\mathbf {Ex}\left( N_{d^*}\right) = {q'\atopwithdelims ()2}\cdot \mathbf {P}_2$, and using that $\beta = \frac{3}{2}{q'\atopwithdelims ()2}/2^n$, we obtain for (30–31):

$$\begin{aligned} \mathbf {Pr}\left( \mathcal {D}^{\mathrm {GCL}^{f_1,f_2,f_3}}=0\right)&\le \frac{ {q'\atopwithdelims ()2}\cdot \mathbf {P}_2 + {q'\atopwithdelims ()2}2{q'-2\atopwithdelims ()1}\cdot \mathbf {P}_3 + {q'\atopwithdelims ()2}{q'-2\atopwithdelims ()2}\cdot \mathbf {P}_4 - \Big ({q'\atopwithdelims ()2}\cdot \mathbf {P}_2\Big )^2}{({q'\atopwithdelims ()2}\cdot \mathbf {P}_2-\frac{3}{2}{q'\atopwithdelims ()2}/2^n)^2}\nonumber \\&= \frac{ \mathbf {P}_2 + 2{q'-2\atopwithdelims ()1}\cdot \mathbf {P}_3 + {q'-2\atopwithdelims ()2}\cdot \mathbf {P}_4 - {q'\atopwithdelims ()2}\cdot \mathbf {P}_2^2}{{q'\atopwithdelims ()2}(\mathbf {P}_2-\frac{3}{2}/2^n)^2}\,. \end{aligned}$$

(36)

We can derive the following bounds on $\mathbf {P}_2,\mathbf {P}_3,\mathbf {P}_4$.

Claim

Provided $n\ge 6$, $\mathbf {P}_2 \ge 2/2^n$, $\mathbf {P}_3 \le 5/2^{2n}$, and $\mathbf {P}_4 \le \frac{4}{(2^n-6)(2^n-7)}$.

Proof

(proof of claim). Before bounding the probabilities separately, note that in general for any distinct $(i,j),(k,l)\in I_{d^*}$, we have $i\ne k$ and $j\ne l$. Write

$$\begin{aligned} x_{i_1}&= p_1(m_{i_1}\oplus f_1(t))=p_1(m'_{j_1}\oplus f_1(t'))\,,\\ x_{i_2}&= p_1(m_{i_2}\oplus f_1(t))=p_1(m'_{j_2}\oplus f_1(t'))\,,\\ x_{i_3}&= p_1(m_{i_3}\oplus f_1(t))=p_1(m'_{j_3}\oplus f_1(t'))\,,\\ x_{i_4}&= p_1(m_{i_4}\oplus f_1(t))=p_1(m'_{j_4}\oplus f_1(t'))\,, \end{aligned}$$

where we recall that $d^*=f_1(t)\oplus f_1(t')=m_{i_1}\oplus m'_{j_1}=\cdots =m_{i_4}\oplus m'_{j_4}$. Above values $x_{i_1},x_{i_2},x_{i_3},x_{i_4}$ are pairwise distinct as $m_{i_1},m_{i_2},m_{i_3},m_{i_4}$ are pairwise distinct as $i_1,i_2,i_3,i_4$ are. Furthermore, write

$$\begin{aligned} y_{i_1}&= p_2^{-1}(c_{i_1}\oplus f_3(t)) = x_{i_1}\oplus f_2(t)\,,\\ y'_{j_1}&= p_2^{-1}(c'_{j_1}\oplus f_3(t')) = x_{i_1}\oplus f_2(t')\,,\\ y_{i_2}&= p_2^{-1}(c_{i_2}\oplus f_3(t)) = x_{i_2}\oplus f_2(t)\,,\\ y'_{j_2}&= p_2^{-1}(c'_{j_2}\oplus f_3(t')) = x_{i_2}\oplus f_2(t')\,,\\ y_{i_3}&= p_2^{-1}(c_{i_3}\oplus f_3(t)) = x_{i_3}\oplus f_2(t)\,,\\ y'_{j_3}&= p_2^{-1}(c'_{j_3}\oplus f_3(t')) = x_{i_3}\oplus f_2(t')\,,\\ y_{i_4}&= p_2^{-1}(c_{i_4}\oplus f_3(t)) = x_{i_4}\oplus f_2(t)\,,\\ y'_{j_4}&= p_2^{-1}(c'_{j_4}\oplus f_3(t')) = x_{i_4}\oplus f_2(t')\,. \end{aligned}$$

Recall that $d^{**}:=f_2(t)\oplus f_2(t')\ne 0$.

We start with bounding $\mathbf {P}_2$:

$$\begin{aligned} \mathbf {P}_2&= \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\right) \\&= \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2} \mid x_{i_1}\oplus x_{i_2}= d^{**}\right) \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}= d^{**}\right) \\&\;\!+ \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2} \mid x_{i_1}\oplus x_{i_2}\ne d^{**}\right) \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}\ne d^{**}\right) \,. \end{aligned}$$

Given that $x_{i_1}\ne x_{i_2}$, we have

$$\begin{aligned} \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}= d^{**}\right) = \frac{1}{2^n-1}\,. \end{aligned}$$

Conditioned on $x_{i_1}\oplus x_{i_2}= d^{**}$, we have $y_{i_1}=y'_{j_2}$ and $y'_{j_1}=y_{i_2}$, and $c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}$ holds with probability 1. Conditioned on $x_{i_1}\oplus x_{i_2}\ne d^{**}$ and using that $d^{**}\ne 0$, the values $y_{i_1},y'_{j_1},y_{i_2},y'_{j_2}$ are pairwise distinct and

$$\begin{aligned} \mathbf {Pr}\left( p_2(y_{i_1})\oplus p_2(y'_{j_1}) = p_2(y_{i_2})\oplus p_2(y'_{j_2}) \mid x_{i_1}\oplus x_{i_2}\ne d^{**}\right) \le \frac{1}{2^n-3}\,. \end{aligned}$$

We therefore obtain

$$\begin{aligned} \mathbf {P}_2 = \frac{1}{2^n-1} + \frac{1}{2^n-3}\left( 1 - \frac{1}{2^n-1}\right) = \frac{2\cdot 2^n-5}{(2^n-1)(2^n-3)} \ge \frac{2}{2^n}\,. \end{aligned}$$

We next bound $\mathbf {P}_3$:

$$\begin{aligned} \mathbf {P}_3&= \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}=c_{i_3}\oplus c'_{j_3}\right) \\&= \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}=c_{i_3}\oplus c'_{j_3} \mid x_{i_1}\oplus x_{i_2}= d^{**}\right) \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}= d^{**}\right) \\&\;\!+ \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}=c_{i_3}\oplus c'_{j_3} \mid x_{i_1}\oplus x_{i_3}= d^{**}\right) \mathbf {Pr}\left( x_{i_1}\oplus x_{i_3}= d^{**}\right) \\&\;\!+ \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}=c_{i_3}\oplus c'_{j_3} \mid x_{i_2}\oplus x_{i_3}= d^{**}\right) \mathbf {Pr}\left( x_{i_2}\oplus x_{i_3}= d^{**}\right) \\&\;\!+ \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}=c_{i_3}\oplus c'_{j_3} \mid x_{i_1}\oplus x_{i_2},x_{i_1}\oplus x_{i_3},x_{i_2}\oplus x_{i_3}\ne d^{**}\right) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \;\!\!\cdot \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2},x_{i_1}\oplus x_{i_3},x_{i_2}\oplus x_{i_3}\ne d^{**}\right) \,, \end{aligned}$$

using that no two or more of the events “$x_{i_1}\oplus x_{i_2}= d^{**}$,”“$x_{i_1}\oplus x_{i_3}= d^{**}$,” and “$x_{i_2}\oplus x_{i_3}= d^{**}$” can hold simultaneously. Starting with the first line, as before we have

$$\begin{aligned} \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}= d^{**}\right) = \frac{1}{2^n-1}\,. \end{aligned}$$

Conditioned on $x_{i_1}\oplus x_{i_2}= d^{**}$, we have $y_{i_1}=y'_{j_2}$ and $y'_{j_1}=y_{i_2}$, and $c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}$ holds with probability 1. On the other hand, $x_{i_1}\oplus x_{i_3}\ne d^{**}$, and thus, the values $y_{i_1},y'_{j_1},y_{i_3},y'_{j_3}$ are pairwise distinct and

$$\begin{aligned} \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}=c_{i_3}\oplus c'_{j_3} \mid x_{i_1}\oplus x_{i_2}= d^{**}\right) \le \frac{1}{2^n-3} \end{aligned}$$

(we now need to consider an upper bound, as the probability may be 0 if the targeted value is already sampled).

The second and third line go identically. For the fourth line, conditioned on the fact that $x_{i_1}\oplus x_{i_2},x_{i_1}\oplus x_{i_3},x_{i_2}\oplus x_{i_3}\ne d^{**}$ and using that $d^{**}\ne 0$, the values $y_{i_1},y'_{j_1},y_{i_2},y'_{j_2},y_{i_3},y'_{j_3}$ are pairwise distinct and

$$\begin{aligned} \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}=c_{i_3}\oplus c'_{j_3} \mid x_{i_1}\oplus x_{i_2},x_{i_1}\oplus x_{i_3},x_{i_2}\oplus x_{i_3}\ne d^{**}\right) \le \frac{1}{(2^n-4)(2^n-5)}\,. \end{aligned}$$

We therefore obtain

$$\begin{aligned} \mathbf {P}_3 \le \frac{3}{(2^n-1)(2^n-3)} + \frac{1}{(2^n-4)(2^n-5)} \le \frac{4}{(2^n-4)(2^n-5)} \le \frac{5}{2^{2n}}\,, \end{aligned}$$

provided $2^n\ge 45$.

We finally bound $\mathbf {P}_4$:

$$\begin{aligned} \mathbf {P}_4&= \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\;,\; c_{i_3}\oplus c'_{j_3}=c_{i_4}\oplus c'_{j_4}\right) \\&= \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\;,\; c_{i_3}\oplus c'_{j_3}=c_{i_4}\oplus c'_{j_4} \mid x_{i_1}\oplus x_{i_2}= d^{**} \wedge x_{i_3}\oplus x_{i_4}= d^{**}\right) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \!\!\!\cdot \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}= d^{**} \wedge x_{i_3}\oplus x_{i_4}= d^{**}\right) \\&\;\!+ \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\;,\; c_{i_3}\oplus c'_{j_3}=c_{i_4}\oplus c'_{j_4} \mid x_{i_1}\oplus x_{i_2}= d^{**} \wedge x_{i_3}\oplus x_{i_4}\ne d^{**}\right) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \!\!\!\cdot \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}= d^{**} \wedge x_{i_3}\oplus x_{i_4}\ne d^{**}\right) \\&\;\!+ \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\;,\; c_{i_3}\oplus c'_{j_3}=c_{i_4}\oplus c'_{j_4} \mid x_{i_1}\oplus x_{i_2}\ne d^{**} \wedge x_{i_3}\oplus x_{i_4}= d^{**}\right) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \!\!\!\cdot \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}\ne d^{**} \wedge x_{i_3}\oplus x_{i_4}= d^{**}\right) \\&\;\!+ \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\;,\; c_{i_3}\oplus c'_{j_3}=c_{i_4}\oplus c'_{j_4} \mid x_{i_1}\oplus x_{i_2}\ne d^{**} \wedge x_{i_3}\oplus x_{i_4}\ne d^{**}\right) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \!\!\!\cdot \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}\ne d^{**} \wedge x_{i_3}\oplus x_{i_4}\ne d^{**}\right) \,, \end{aligned}$$

For the first line, the event $x_{i_1}\oplus x_{i_2}= d^{**} \wedge x_{i_3}\oplus x_{i_4}= d^{**}$ holds with probability $1/(2^n-2)(2^n-3)$, and conditioned on $x_{i_1}\oplus x_{i_2}= d^{**} \wedge x_{i_3}\oplus x_{i_4}= d^{**}$, the equations $c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}$ and $c_{i_3}\oplus c'_{j_3}=c_{i_4}\oplus c'_{j_4}$ hold with probability 1 (see the analysis of $\mathbf {P}_2$). The second and third line go as in the analysis of $\mathbf {P}_3$, giving

$$\begin{aligned} \mathbf {Pr}\left( x_{i_1}\oplus x_{i_2}= d^{**} \wedge x_{i_3}\oplus x_{i_4}\ne d^{**}\right)&\le \frac{1}{2^n-1}\,, \end{aligned}$$

and

$$\begin{aligned} \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\;,\; c_{i_3}\oplus c'_{j_3}=c_{i_4}\oplus c'_{j_4} \mid x_{i_1}\oplus x_{i_2}= d^{**} \wedge x_{i_3}\oplus x_{i_4}\ne d^{**}\right)&\le \frac{1}{2^n-3}\,. \end{aligned}$$

For the fourth line, conditioned on the fact that $x_{i_1}\oplus x_{i_2}\ne d^{**} \wedge x_{i_3}\oplus x_{i_4}\ne d^{**}$ and using that $d^{**}\ne 0$, the values $y_{i_1},y'_{j_1},y_{i_2},y'_{j_2}$ are pairwise distinct and so are $y_{i_3},y'_{j_3},y_{i_4},y'_{j_4}$, and in addition, $y_{i_1},y_{i_2},y_{i_3},y_{i_4}$ are pairwise distinct and $y'_{j_1},y'_{j_2},y'_{j_3},y'_{j_4}$ are. We obtain

$$\begin{aligned} \mathbf {Pr}\left( c_{i_1}\oplus c'_{j_1}=c_{i_2}\oplus c'_{j_2}\;,\; c_{i_3}\oplus c'_{j_3}=c_{i_4}\oplus c'_{j_4} \mid x_{i_1}\oplus x_{i_2}, x_{i_3}\oplus x_{i_4}\ne d^{**}\right) \le \frac{1}{(2^n-6)(2^n-7)}\,. \end{aligned}$$

We therefore obtain

$$\begin{aligned} \mathbf {P}_4 \le \frac{1}{(2^n-2)(2^n-3)} + \frac{2}{(2^n-1)(2^n-3)} + \frac{1}{(2^n-6)(2^n-7)} \le \frac{4}{(2^n-6)(2^n-7)}\,. \end{aligned}$$

   $\square$

To suit further analysis of (36), we claim that the $\mathbf {P}_4$-term cancels out to the $\mathbf {P}_2^2$-term.

Claim

Provided $6q'\le 2^n$, ${q'-2\atopwithdelims ()2}\cdot \mathbf {P}_4 \le {q'\atopwithdelims ()2}\cdot \mathbf {P}_2^2$.

Proof

(proof of claim). By above claim, $\mathbf {P}_4 \le \frac{4}{(2^n-6)(2^n-7)}$ and $\mathbf {P}_2\ge 2/2^n$, and it remains to prove that

$$\begin{aligned} \frac{(q'-2)(q'-3)}{(2^n-6)(2^n-7)} \le \frac{q'(q'-1)}{2^{2n}}\,. \end{aligned}$$

This in turn follows from the fact that

$$\begin{aligned} \frac{q'-3}{2^n-7} \le \frac{q'-2}{2^n-6} \le \frac{q'-1}{2^n}\,, \end{aligned}$$

as $6q'\le 2^n$.    $\square$

From (36) and the bounds of above two claims, we directly obtain

$$\begin{aligned} \mathbf {Pr}\left( \mathcal {D}^{\mathrm {GCL}^{f_1,f_2,f_3}}=0\right)&{\mathop {\le }\limits ^{a}} \frac{ \mathbf {P}_2 + 2{q'-2\atopwithdelims ()1}\cdot \mathbf {P}_3}{{q'\atopwithdelims ()2}(\mathbf {P}_2-\frac{3}{2}/2^n)^2}\\&{\mathop {\le }\limits ^{b}} \frac{ 2/2^n + 2{q'-2\atopwithdelims ()1}\cdot 5/2^{2n}}{{q'\atopwithdelims ()2}(2/2^n-\frac{3}{2}/2^n)^2}\\&= \frac{ 8\cdot 2^n + 40(q'-2)}{{q'\atopwithdelims ()2}}\\&{\mathop {\le }\limits ^{c}} \frac{32}{2^{4\epsilon }} + \frac{80}{2^{n/2+2\epsilon }}\,, \end{aligned}$$

where ${\mathop {\le }\limits ^{a}}$ holds due to the second claim, ${\mathop {\le }\limits ^{b}}$ holds as $\mathbf {P}_2\ge 2/2^n$ and $\mathbf {P}_3\le 5/2^{2n}$ (note that a lower bound on $\mathbf {P}_2$ suffices for both the numerator and denominator as $A/(A-C) \le B/(B-C)$ for $A\ge B>C>0$), and ${\mathop {\le }\limits ^{c}}$ holds as ${q'\atopwithdelims ()2}\ge (q')^2/4$ and $q'=2^{n/2+2\epsilon }$.

1.2 A.2 Proof of Lemma 4

For any $d\in \{0,1\}^{n}$, recall that $N_d$ counts the number of collisions $c_i\oplus c'_j=c_k\oplus c'_l$ for distinct (i, j), (k, l). There could be multi-collisions; for $\lambda \ge 2$ we say that $(i_1,j_1),\ldots ,(i_\lambda ,j_\lambda )\in I_d$ form a $\lambda$-collision if $c_{i_1}\oplus c'_{j_1}=\dots = c_{i_5}\oplus c'_{j_5}$. Denote by $N_d^\lambda$ the number of $\lambda$-collisions that are not part of a $(\lambda +1)$-collision. Denote by $N_d^{\ge \lambda }$ the number of $\lambda$-collisions (that may be part of a $(\lambda +1)$-collision).

Fix any $1\le \alpha \le \sqrt{\beta }-1$. By basic probability theory,¹

$$\begin{aligned} \mathbf {Pr}\left( \mathcal {D}^{\widetilde{p}}=1\right)&\le \sum _{d\in \{0,1\}^{n}} \mathbf {Pr}\left( N_d\ge \beta \right) \nonumber \\&\le \sum _{d\in \{0,1\}^{n}} \mathbf {Pr}\left( N_d\ge \beta \mid N_d^{\ge \alpha +2}=0\right) + \mathbf {Pr}\left( N_d^{\ge \alpha +2}\ge 1\right) \nonumber \\&\le \sum _{d\in \{0,1\}^{n}} \mathbf {Pr}\left( N_d\ge \beta \mid N_d^{\ge \alpha +2}=0\right) + {q'\atopwithdelims ()\alpha +2}\frac{1}{(2^n)_{\alpha +1}}\,. \end{aligned}$$

(37)

Conditioned on the fact that there is no $(\alpha +2)$-collision, by the pigeonhole principle, $N_d\ge \beta$ only if the number of collisions arising from either 2-collisions, 3-collisions, ..., or $(\alpha +1)$-collisions is at least $\beta /\alpha$. Clearly, a 2-collision contributes 1 to $N_d$, a 3-collision contributes 3 to $N_d$, and generally, an i-collision contributes ${i\atopwithdelims ()2}$ to $N_d$. Therefore, denoting $\mathbf {Pr}^{\star }\!\left( X\right) =\mathbf {Pr}\left( X\;\Big |\; N_d^{\ge \alpha +2}=0\right)$ for brevity,

$$\begin{aligned} \mathbf {Pr}^{\star }\!\left( N_d\ge \beta \right)&\le \sum _{i=2}^{\alpha +1} \mathbf {Pr}^{\star }\!\left( N_d^i\ge \beta /\alpha \right) \nonumber \\&\le \sum _{i=2}^{\alpha +1} {q'\atopwithdelims ()i\cdot \beta /(\alpha {i\atopwithdelims ()2})} \frac{1}{(2^n)_{(i-1)\cdot \beta /(\alpha {i\atopwithdelims ()2})}}\,. \end{aligned}$$

(38)

As $\alpha \le \sqrt{\beta }-1$, we particularly have $(i-1)\cdot \beta /(\alpha {i\atopwithdelims ()2})\ge 2$ for all i, and we obtain

$$\begin{aligned} {q'\atopwithdelims ()i\cdot \beta /(\alpha {i\atopwithdelims ()2})} \frac{1}{(2^n)_{(i-1)\cdot \beta /(\alpha {i\atopwithdelims ()2})}}&{\mathop {\le }\limits ^{a}} \frac{(q')_{(i-1)\cdot \beta /(\alpha {i\atopwithdelims ()2})}\cdot (q'-2)^{\beta /(\alpha {i\atopwithdelims ()2})}}{(2^n)_{(i-1)\cdot \beta /(\alpha {i\atopwithdelims ()2})}} \cdot \left( \frac{e}{i\cdot \beta /(\alpha {i\atopwithdelims ()2})}\right) ^{i\cdot \beta /(\alpha {i\atopwithdelims ()2})}\\&{\mathop {\le }\limits ^{b}} \left( \left( \frac{e\alpha (i-1)}{2}\right) ^i\cdot \frac{(q')^{i-1}(q'-2)}{2^{(i-1)n}} \cdot \frac{1}{\beta ^i}\right) ^{\beta /(\alpha {i\atopwithdelims ()2})}\\&{\mathop {\le }\limits ^{c}} \left( \left( \frac{2e\alpha }{3}\right) ^i\cdot \frac{(i-1)^i}{2^{4\epsilon }(2^{n/2+2\epsilon }-1)^{i-2}}\right) ^{(3\cdot 2^{4\epsilon })/(8\alpha {i\atopwithdelims ()2})}\\&{\mathop {\le }\limits ^{d}} \left( \frac{2\alpha }{2^{2\epsilon }}\right) ^{3/(4\alpha (i-1))\cdot 2^{4\epsilon }}\,, \end{aligned}$$

where ${\mathop {\le }\limits ^{a}}$ holds as ${A\atopwithdelims ()B}\le (A)_B\cdot (e/B)^B$ by Stirling’s approximation, ${\mathop {\le }\limits ^{b}}$ holds as $(A)_{m}/(B)_{m}\le (A/B)^{m}$ if $A\le B$, ${\mathop {\le }\limits ^{c}}$ uses $\beta =\frac{3}{2}{q'\atopwithdelims ()2}/2^n$, $q'(q'-2)\le (q'-1)^2$, and $q'=2^{n/2+2\epsilon }$, and, finally ${\mathop {\le }\limits ^{d}}$ holds as $(i-1)^i\le (2^{n/2-1})^{i-2}$ is satisfied for all i, provided that $n\ge 16$.

We obtain for (38):

$$\begin{aligned} \mathbf {Pr}^{\star }\!\left( N_d\ge \beta \right)&\le \sum _{i=2}^{\alpha +1} \left( \frac{2\alpha }{2^{2\epsilon }}\right) ^{3/(4\alpha (i-1))\cdot 2^{4\epsilon }} \le \alpha \left( \frac{2\alpha }{2^{2\epsilon }}\right) ^{3/(4\alpha ^2)\cdot 2^{4\epsilon }}\,, \end{aligned}$$

and for (37):

$$\begin{aligned} \mathbf {Pr}\left( \mathcal {D}^{\widetilde{p}}=1\right)&\le \alpha 2^n\left( \frac{2\alpha }{2^{2\epsilon }}\right) ^{3/(4\alpha ^2)\cdot 2^{4\epsilon }} + \frac{2^{(\alpha +2)2\epsilon }}{2^{(\alpha -2)n/2}}\,, \end{aligned}$$

again using that $(A)_{m}/(B)_{m}\le (A/B)^{m}$ if $A\le B$. This bound holds for all $1\le \alpha \le \sqrt{\beta }-1$.

B Mirror Theory

We will follow the description of Patarin’s mirror theory [22, 26, 28] by Mennink and Neves [20]. We will restrict ourselves to the simplified setting where the equations are of the form $P_a\oplus P_b=\lambda$, where the $P_a$’s and $P_b$’s come from independent permutations, and we will use the theory for 3n / 4-bit security at most.

1.1 B.1 System of Equations

Consider a system of $q\ge 1$ equations

$$\begin{aligned} \mathcal {E}= \{ P_{\varphi (a_1)}\oplus P_{\varphi (b_1)} = \lambda _1, \cdots , P_{\varphi (a_q)}\oplus P_{\varphi (b_q)} = \lambda _q\} \end{aligned}$$

(39)

over $r\ge 1$ unknowns $\mathcal {P}= \{P_1,\ldots ,P_r\}$, where $\varphi$ is some surjective index mapping

$$\begin{aligned} \varphi : \{a_1,b_1,\ldots ,a_q,b_q\} \rightarrow \{1,\ldots ,r\}\,. \end{aligned}$$

In our work we consider the case that the $P_a$’s and $P_b$’s come from independent permutations, hence $\varphi (a_i)\ne \varphi (b_j)$ for any i, j. We write $\mathcal {I}_1=\{ \varphi (a_i) \mid i\in \{1,\ldots ,q\}\}$ and $\mathcal {I}_2=\{ \varphi (b_i) \mid i\in \{1,\ldots ,q\}\}$, such that $\{1,\ldots ,r\}=\mathcal {I}_1\cup \mathcal {I}_2$ is a partition. For a subset $I\subseteq \{1,\ldots ,q\}$, define the multiset $\mathcal {M}_I$ as

$$\begin{aligned} \mathcal {M}_I = \bigcup _{i\in I}\ \{\varphi (a_i),\varphi (b_i)\}\,. \end{aligned}$$

We give three definitions with respect to the system of equations $\mathcal {E}$.

Definition 1

(circle-freeness). For any $I\subseteq \{1,\ldots ,q\}$, $\mathcal {M}_I$ has an element of odd multiplicity.

Definition 2

($\xi$-block-maximality). There is a partition $\{1,\ldots ,r\} = \mathcal {R}_1\cup \cdots \cup \mathcal {R}_s$ of the r indices, all of size at most $\xi$, such that for any $i\in \{1,\ldots ,q\}$ there is an $\ell \in \{1,\ldots ,s\}$ such that $\{\varphi (a_i),\varphi (b_i)\}\subseteq \mathcal {R}_\ell$.

Definition 3

(non-degeneracy). For any $I\subseteq \{1,\ldots ,q\}$ such that $\mathcal {M}_I$ has exactly two odd multiplicity element from either $\mathcal {I}_1$ or $\mathcal {I}_2$, it satisfies $\bigoplus _{i\in I} \lambda _i \ne 0$.

Circle-freeness implies that there is no linear combination of the equations $\mathcal {E}$ that is independent of the unknowns, $\xi$-block maximality implies that there are not too many unknowns that are jointly related, and non-degeneracy implies that there is no linear combination of the equations $\mathcal {E}$ that implies equality of two distinct unknowns from either $\mathcal {I}_1$ or $\mathcal {I}_2$.

1.2 B.2 Main Result

The main theorem of Patarin’s mirror theory, tailored to the case where we have a partition of the unknowns into two disjoint sets, is given below. We follow [20], with the side condition on $2^n/64$ from [22].

Theorem 3

(mirror theorem). Let $\{1,\ldots ,r\} = \mathcal {I}_1\cup \mathcal {I}_2$ be a partition of the indices. Let $\mathcal {E}$ be a system of equations over the unknowns $\mathcal {P}$ that is (i) circle-free, (ii) $\xi$-block-maximal, and (iii) non-degenerate. Then, as long as $\xi ^2\cdot \max \{|\mathcal {I}_1|,|\mathcal {I}_2|\} \le 2^n/64$, the number of solutions for $\mathcal {P}$ such that $P_i\ne P_j$ for all $i,j\in \mathcal {I}_\ell$ ($\ell =1,2$) is at least

$$\begin{aligned} \frac{\mathrm {NonEq}(\mathcal {I}_1,\mathcal {I}_2;\mathcal {E})}{2^{nq}}\,, \end{aligned}$$

where $\mathrm {NonEq}(\mathcal {I}_1,\mathcal {I}_2;\mathcal {E})$ denotes the number of solutions to $\mathcal {P}$ that satisfy $P_i\ne P_j$ for all $i,j\in \mathcal {I}_\ell$ ($\ell =1,2$) as well as the inequalities imposed by $\mathcal {E}$ (but the equalities themselves released).

A lower bound on the technical quantity $\mathrm {NonEq}(\mathcal {I}_1,\mathcal {I}_2;\mathcal {E})$ can be derived as follows. Every equation $P_{\varphi (a)}\oplus P_{\varphi (b)}=\lambda \ne 0$ in $\mathcal {E}$ imposes $P_{\varphi (a)}\ne P_{\varphi (b)}$. As $\varphi (a)\in \mathcal {I}_1$ and $\varphi (b)\in \mathcal {I}_2$ are in distinct index sets, this inequality $P_{\varphi (a)}\ne P_{\varphi (b)}$ imposes an extra inequality over the ones suggested by $\mathcal {I}_1,\mathcal {I}_2$. An obvious lower bound thus is

$$\begin{aligned} \mathrm {NonEq}(\mathcal {I}_1,\mathcal {I}_2;\mathcal {E}) \ge (2^n)_{|\mathcal {I}_1|}(2^n-(\xi -1))_{|\mathcal {I}_2|}\,, \end{aligned}$$

because every unknown of $\mathcal {I}_2$ is in exactly one block, and connects with at most $\xi -1$ unknowns of $\mathcal {I}_1$ (as the system is $\xi$-block-maximal).