Keywords

1 Introduction

Multiple Instance Learning (MIL) relaxes conditions for data representation. In MIL formalism, objects of interest are described by sets \(\mathcal {B}_1, \mathcal {B}_2, \ldots \) (called bags) consisting of multiple feature vectors of an identical size \(\mathcal {B}=\{ \mathbf {x}_1, \mathbf {x}_2, \ldots \},\; \mathbf {x}\in \mathcal {X}\) (called instances). Each bag is attributed output variable y (e.g. label \(y\in \{0,1\}\) in a binary classification problem). The goal is to infer function \(\mathcal {F}\) from training dataset \(\mathcal {D}=\{(\mathcal {B},y)_1, (\mathcal {B},y)_2, \ldots \}\) that can predict output variables for previously unseen bags \(\mathcal {F}(\mathcal {B})=y\).

This relaxed formalism has received a lot of attention since its first formulation [11]. One of the recent application domains, where MIL formalism seems to fit better than traditional Single Instance Learning (SIL), is network security [20]. For example, in the work [16] dealing with a binary classification of network users as either infected or clean based on monitoring their web requests, the MIL approach enabled to (i) describe the problem more naturally – each user is represented by a bag with instances corresponding to individual requests; representing users with single feature vectors would be too restrictive, since the number of requests can vary from user to user, (ii) save ground truth acquisition costs – security analysts preparing a training dataset did not have to label individual requests as infection-related or benign; it was enough to provide labels on the (higher) user/bag level, resulting in a significantly lower number of items that needed to be annotated, (iii) improve classification performance – a MIL classifier modeling the global contextual information across multiple requests was able to achieve a higher classification precision than a SIL classifier analyzing individual requests one by one.

Although many MIL classifiers have been developed over the years, most of them work well only within their specific application domains and are less effective over a wider range of problems [8] (demonstrated in Sect. 4). A recent survey of MIL classifiers [1] has pointed out that approaches extracting global bag-level information achieve a higher performance in general than their counterparts operating on instance-level trying to infer instance labels from the bag ones (discussed in Sect. 2). Following this observation, we propose a novel bag-level MIL algorithm (Sect. 3) as an extension of traditional single-instance randomized trees [15] to the multiple-instance setting. Ensembles of tree-based learners (e.g. Extremely randomized trees [15] or Breiman’s Random Forests [5]) are known to perform very well across many domains even without a careful hyperparameter tuning [12], which makes a good case for research of a general MIL tree-based model formalism.

2 Related Work

A taxonomy proposed in the review [1] categorizes MIL classifiers into two groups according to the level at which they extract the discriminative information. The first instance-level category considers the discriminative information to lie at the level of individual instances. It is assumed that each instance \(\mathbf {x}\) can be attributed binary label \(y_\mathbf {x}\in \{0,1\}\) and that positive bags contain at least one positive instance \(y_\mathbf {x}=1\). Negative bags are supposed to not contain any positive instance. The instance labels are unknown (even in the training dataset), but are inferred during the learning process. Most algorithms based on this assumption build instance-level classifier \(f(\mathbf {x})=y_\mathbf {x}\) and produce bag labels by a simple aggregation of instance level scores \(\mathcal {F}(\mathcal {B})=\max _{\mathbf {x}\in \mathcal {B}} f(\mathbf {x})\). This category is mostly represented by earlier works, starting with the APR algorithm [11] proposed in 1997. APR (Axis-Parallel Rectangle) algorithm considers all instances in positive bags to be positive and expands/shrinks an hyper-rectangle in the feature space to maximize the number of positive instances falling inside, while minimizing the number of negative ones. MI-SVM [2] initially also assumes that all instances in positive bags are positive, but then maximizes a margin between the positive and negative bags by selecting a single instance to represent each bag. EM-DD [25] uses Expectation-Maximization (EM) algorithm to search for the maximum of diverse density (DD) measure. A location in the feature space has a high DD measure if the number of nearest instances from different positives bags is high and from negative bags low. Other approaches are based e.g. on boosting (MILBoost [23]) or deterministic annealing [14, 17].

The second bag-level category (mostly represented by later works) considers the discriminative information to lie at the level of bags. Representatives of this category do not use the notion of instance labels, which does not reflect the reality in many applications [1], but rather treat bags as whole entities. That is, a bag-level classifier \(\mathcal {F}(\mathcal {B})\) extracts the information from the whole bag to make a decision about the class of \(\mathcal {B}\), instead of aggregating individual instance-level decisions. Bag-level methods are further categorized as either bag-space or embedded-space. Since bags are non-vectorial objects, the bag-space methods define a distance function (or kernel) that can compare any two bags, e.g. \(\mathcal {B}_i\) and \(\mathcal {B}_j\), and plug this function into a distance-based classifier such as k-NN or SVM. Examples of such functions are the minimal Hausdorff distance \(\mathrm {d}(\mathcal {B}_i,\mathcal {B}_j)=\text {argmin}_{\mathbf {x}^i\in \mathcal {B}_i, \mathbf {x}^j\in \mathcal {B}_j} ||\mathbf {x}^i - \mathbf {x}^j ||\) measuring distance between the closest instances or the Earth Movers Distance (EMD) \(\mathrm {d}(\mathcal {B}_i,\mathcal {B}_j)= \frac{\sum _i \sum _j w_{ij} ||\mathbf {x}^i - \mathbf {x}^j ||}{\sum _i \sum _j w_{ij}}\), where weights \(w_{ij}\) are obtained through an optimization process that globally minimizes the distance subject to some constrains, see [24] for details. On the other hand, the embedded-space methods define a transformation mapping bags into single fixed-size vectors, which effectively converts the MIL problem into the standard SIL one. In the work of MI-Kernel [13], each bag is transformed by calculating simple statistics like the maximum, minimum or mean across all feature dimensions and concatenating the results into a single vector. MILES [7] maps each bag into a feature space defined by similarities to instances in the training bags. A sparse 1-norm SVM is then applied to select only the discriminative features (i.e. instances) and construct the classifier. Bag dissimilarity [9], on the other hand, measures similarities to the training bags rather than instances.

Most prior tree-based works fall into the instance-level category. MIForest [17] uses the deterministic annealing approach to uncover the instance labels during the tree growing. MITI [4] introduces a weighted Gini impurity measure and modifies the tree induction procedure to prioritize expansion of nodes with positive instances. MIOForest [21] extends MITI by implementing non-linear splitting rules instead of the traditional axis-orthogonal ones and by optimal combining of individual tree outputs within the forest. To our knowledge, the only tree-based MIL classifier that operates on the level of bags is RELIC [19]. Since we consider RELIC as the closest prior work, we discuss the differences with respect to the proposed solution in detail in Sect. 3.

3 Bag-Level Randomized Trees

The bag-level randomized trees (BLRT) are trained according to the classical top-down greedy procedure for building ensembles of unpruned decision trees. Individual tree learners recursively partition a training dataset by choosing binary splitting rules until pure sample sets are obtained.

The key difference, however, lies in the conditions that are evaluated inside the splitting nodes. While nodes of standard single-instance decision trees (Eq. 1) test only whether feature f of a given sample is greater than certain value v, nodes of the proposed MIL trees also count the number of instances within the sample (i.e. bag) that accomplish the condition. This absolute count is then normalized by bag size \(|\mathcal {B}|\) and compared to value \(r\in [0,1)\) (Eq. 2).

$$\begin{aligned} \mathcal {N}_\text {SIL}(\mathbf {x};f,v) = \left\{ \begin{aligned}&\mathrm {left},&\text {if} \; x_f > v,\\&\mathrm {right},&\text {otherwise}. \end{aligned} \right. \end{aligned}$$
(1)
$$\begin{aligned} \mathcal {N}_\text {MIL}(\mathcal {B};\underbrace{f,v,r}_\varPhi ) = \left\{ \begin{array}{ll} \mathrm {left}, &{} \text {if} \; \left[ \dfrac{1}{|\mathcal {B}|} \sum _{\mathbf {x}\in \mathcal {B}} \mathbbm {1} \left[ x_f> v \right] \right] > r,\\ \mathrm {right}, &{} \text {otherwise}. \end{array} \right. \end{aligned}$$
(2)

Parameter r denotes a relative count of instances \(\mathbf {x}\) inside bag \(\mathcal {B}\) that must satisfy the inner condition \(x_f > v\) to be the whole bag passed to the left branch. It is the only additional parameter that needs to be learned from the training data together with f and v. Symbol \(\mathbbm {1}\) stands for an indicator function that equals one if its argument is true and zero otherwise.

Note that if bags are of size one, nodes \(\mathcal {N}_\text {MIL}\) behave like the traditional \(\mathcal {N}_\text {SIL}\) regardless the value of r parameters. The next special case is when the relative count takes extreme values, i.e. \(r\in \{0,0.\bar{9}\}\)Footnote 1. The proposed algorithm then becomes equivalent to the prior art solution known as RELIC [19]. Under this condition, the splitting rules act as either the universal or the existential quantifier. In particular, bags are tested in two possible ways: if there exists at least one instance that fulfills the inner condition or if the condition is satisfied by all instances. An experiment in Sect. 4 (Fig. 2), however, shows that the ability of the proposed algorithm to test situations also between these two extreme cases is highly beneficial on many datasets.

Search of optimal splitting parameters \(\varPhi ^*=(f,v,r)\) during the tree growth is implemented in a randomized manner. At each node construction, a set of candidate splitting rules \(\mathcal {R}=\{\varPhi _1,\ldots \}\) is generated (based on local training subset \(\mathcal {S}\subseteq \mathcal {D}\)) among which the best one \(\varPhi ^*\) is selected according to a score obtained by an impurity measure such as Information gain [18] or Gini impurity [6]. Specifically, for each feature f out of K randomly selected ones, T values of parameter v are drawn uniformly from interval \([x^{\text {min}}_f,x^{\text {max}}_f)\), where \(x^{\text {min}}_f\) and \(x^{\text {max}}_f\) denote the minimum and the maximum value of feature f across all bags within the local sample set. For each such pair (f, v), other T values of parameter r are generated uniformly from interval [0, 1). In total, there are \(K\times T \times T\) candidate splitting rules at maximumFootnote 2. A detail description of the tree induction procedure is given in Algorithm 1 in the form of pseudo code.

figure a

The above randomized approach is adopted from ExtremelyFootnote 3 randomized trees [15] and generalized to MIL setting by adding the third parameter r (i.e. the relative count). Unlike CART algorithm, used e.g. in Breiman’s Random Forests [5], the randomized search does not require to go over all possible splitting points on selected features, which could be prohibitively expensive in this MIL variant of trees. Furthermore, the explicit randomization in combination with ensemble averaging makes the decision boundary more smooth, resulting in models with better or equal accuracy than that of Random Forests [15].

Algorithm 1 builds M fully grown decision trees. Each tree is trained on the whole sample set rather than a bootstrap replica as realized e.g. in Random Forests. Training on the full original sample set minimizes bias. Variance is reduced by the strong randomization in the splitting parameters combined with the output aggregation across multiple trees. From the computational point of view, the time complexity of the learning procedure is, assuming balanced trees, \(\varTheta (MKT^2 N_I \log N_\mathcal {B})\), where \(N_\mathcal {B}\) and \(N_I\) denote the number of bags and the number of instances within the bags, respectivelyFootnote 4.

In the testing mode, assuming a binary classification problem (i.e. \(y\in \{0,1\}\)), predictions of individual trees are aggregated by a simple arithmetic average to produce final prediction score \(\hat{y}\in [0,1]\).

4 Experiments

The proposed algorithm is evaluated on 29 real-life datasets that are publicly available e.g. on https://doi.org/10.6084/m9.figshare.6633983.v1. The datasets with meta descriptions are listed in Table 1. These classification problems are well known and cover a wide range of conditions in terms of application domains (molecule, scene, image, text, audio spectrogram, etc.), ratios of positive and negative samples (e.g. imbalanced Corel datasets), feature dimensions (from 9 to 6519) and average numbers of bag instances (from 4 to 185). For more details about the datasets we refer the reader to a recent study of MIL datasets [8].

Table 1. Metadata about 29 used datasets together with classification scores and standard deviations presented in percent (AUC \(\times \) 100). Best results are in bold face. Stars denote statistically significant (\(\alpha =0.05\)) differences according to Welch’s t-test.
Full size table

The same collection of datasets was also used in the evaluation of 28 MIL classifiers (including their variants) implemented in the MIL matlab toolbox [22]. The last two columns of Table 1 summarize the results from the evaluation available also through http://homepage.tudelft.nl/n9d04/milweb/. We report only those classifiers that achieved the highest performance by means of AUC metricFootnote 5 at least on one problem. This selection yields to 13 classifiers that are listed in Table 2 together with references to their original papers.

Since an exact experimental protocol is provided as a part of the referenced evaluation, we followed that protocol precisely. For each dataset, the protocol provides indexes of all splits in 5-times repeated 10-fold cross-validation. The material, however, does not specify any approach for hyperparameter optimization. Therefore, we evaluated the proposed model using default parameter settings. We set the number of trees to grow to \(M=500\) that should ensure convergence of the ensemble, the number of randomly selected features at each split to square root of the feature dimension \(K=\sqrt{D}\), which is the default value for tree-based models, and the number of uniformly drawn values of v and r to \(T=8\).

Table 1 summarizes results from the evaluation in terms of average scores and standard deviations. Although among the prior art (28 MIL classifiers) there is no single winning solution and almost each problem is associated with a different classifier, which demonstrates the difficulty and diversity of MIL problems, the proposed model was able to outperform the best prior art algorithm for a given dataset in 17 out of 29 cases. The most significant improvement with respect to the prior art is on the group of image classification problems (Fox, Tiger and Elephant) and on some scene classification problems (Corel Beach and Corel Historical). On the other hand, the proposal is less accurate on text classification problems (NewsgroupsFootnote 6 and Web), Protein and Breast datasets.

From Table 2 showing ranking of algorithms in the evaluation, it can be observed that the second best classifier with the lowest average rank (MI-SVM [2] with Gaussian kernel) ranked first only three times. Overall, the proposed algorithm works very reliably even without any hyperparamter tuning. Indeed, the proposal never ended on any of the last three positions, which is unique among all classifiers. It should be stressed though that not all prior art classifiers were evaluated on all 29 datasets. Column N/A of Table 2 indicates the number of missing evaluations.

Table 2. Number of times that each algorithm obtained each rank in the evaluation.
Full size table

The non-parametric Wilcoxon signed ranks test [10] (testing whether two classifiers have equal performance) confirmed at significance level \(\alpha =0.05\) that the proposed bag-level randomized trees are superior to any other involved method. The test compared pair-wisely the proposal with every prior art method, each time using an intersection of their available datasets. The two most similarly performing methods are mean-inst [13] (p-value 0.037) and MI-SVM [2] with Gaussian kernel (p-value 0.022).

Besides the above evaluation, we also provide comparison to other tree-based MIL algorithms in Table 3, namely RELIC [19], MIOForest [21], MIForest [17], MITI [4] and RF [5]. Except for RELIC, all of them operate on instance-level; labels are assigned to instances and a bag is positive if it contains at least one positive instance. RF represents a naive approach where standard single-instance Random Forests are trained directly on instances that inherited bag labels. Reported classification accuracies in Table 3 are taken from the work of MIOForest [21]. Unfortunately, the classifiers were evaluated only on five pioneering datasets (i.e. Musk1-2 and the image classification problems) and their implementations are not publicly available. As can be seen from Table 3, the proposal clearly outperforms all the prior tree-based MIL solutions on these datasets.

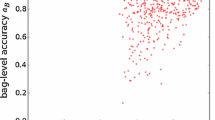
Table 3. Comparison with other tree-based MIL classifiers. Scores refer to accuracy in percent (ACC \(\times \) 100). The prior art results are taken from the work of MIOForest [21].
Full size table

In Fig. 1, we assess various variants of the proposed algorithm. Dots in each subplot represent the 29 datasets. Their (x, y) coordinates are given by AUC scores obtained by the tested variants. If a dot lies on the diagonal (i.e. \(x=y\) line), there is no difference between the two tested variants from that particular dataset perspective. The first two subplots (a-b) illustrate the influence of the ensemble size. It can be observed that it is significantly better to use 100 trees than 10 trees, but building 500 trees usually does not bring any additional performance. Also, according to subplot (c), there is almost no difference between Information gain [18] and Gini impurity measure [6] scoring functions for selecting splitting rules. The next subplot (d) indicates that using higher values (e.g. 16 instead of the default 8) for parameter T (i.e. the number of randomly generated values for parameters v and r at each split) might lead to over-fitting on some datasets. In subplot (e) we tested a variant with an absolute countFootnote 7 instead of the relative one used in Eq. 2. The variant with the absolute count, however, performed significantly worse on the majority of datasets. The last subplot (f) compares the proposed algorithm with its simplified alternative, where traditional Random Forests are trained on a non-optimized bag representation. To do so, all bags \(\{ \mathcal {B}_1, \mathcal {B}_2, \ldots \}\) are transformed into single feature vectors \(\{ \mathbf {b}_1, \mathbf {b}_2, \ldots \}\) of values \(b_\mathcal {B}^{(f,v)} = \frac{1}{|\mathcal {B}|} \sum _{\mathbf {x}\in \mathcal {B}} \mathbbm {1} \left[ x_f > v \right] \), where for each feature f eight equally-spaced values v are generated from interval \([x_f^\text {min}, x_f^\text {max})\) that is estimated beforehand on the whole training sample set. As a result, the non-optimized bag representation is eight times longer than the dimensionality of instances. As can be seen from subplot (f), the Random Forests trained on the non-optimized bag representation are far inferior to the proposed algorithm on all datasets except one. This result highlights the importance to simultaneously optimize the representation parameters with the classification ones as proposed in Sect. 3.

Fig. 1.
figure 1

Pair-wise comparisons of various configurations of the proposed algorithm on the 29 datasets. Subplots (a-b) illustrate the influence of the ensemble size, subplot (c) the impact of selected impurity measure, subplot (d) the effect of parameter T, subplot (c) the performance of the variant with the absolute count and subplot (d) compares the proposed algorithm with RF trained on the non-optimized bag representation.

Full size image
Fig. 2.
figure 2

Histograms of learned values of r parameters (Eq. 2). Datasets from the same source (e.g. Musk1-2, Harddrive1-2 and so forth) usually have very similar distributions that differ from the others.

Full size image

Finally, Fig. 2 shows histograms of learned values of r parameters for some datasets. The first observation is that datasets from the same source (e.g. Fox, Tiger and Elephant) have very similar distributions. This demonstrates that the learned knowledge of randomized trees is not totally random as it might appear to be from the algorithm description. The next observation is that in almost all histograms (except for Mutagenesis problems) one or both extreme values of the parameter (i.e. \(r\in \{0,0.\bar{9}\}\)) are the most frequent ones. As discussed in Sect. 3, the behavior of splitting rules (Eq. 2) with extreme values is approaching to the behavior of the universal or existential quantifier. On Web and Newsgroup datasets, this behavior is even dominant, meaning that the algorithm reduces to the prior art solution RELIC [19]. In the rest cases, however, the added parameter enabled to learn important dataset properties, which is supported by the high level performance reported in this section.

5 Conclusion

In this paper, we have proposed a tree-based algorithm for solving MIL problems called bag-level randomized trees (BLRT)Footnote 8. The algorithm naturally extends traditional single-instance trees, since bags with single instances are processed in the standard single-instance tree way. Multiple instance bags are judged by counting the percent of their instances that accomplish the condition testing whether a feature value is greater than a certain threshold. Judging this percent value is done through an additional parameter that is learned during the tree building process.

Extreme values of the parameter reduce the proposal to the prior art solution RELIC [19]. Unlike other prior art tree-based algorithms, the proposal operates on the bag-level. Ability to analyze global bag-level information is most likely responsible for the superior performance. On the other hand, the algorithm does not identify positive instances within positively classified bags, which can be useful in some applications (e.g. object tracking [3]).

The algorithm falls into the category of embedded-space methods, since the learning procedure can be decoupled into two steps: embedding bags into single feature vectors and training traditional trees on top of the new representation. Features of the new representation then correspond to the counted percent values. The presented single-step approach, however, jointly optimizes the representation and the tree classifier.

As a side effect, the algorithm inherits all desirable properties of tree-based learners. It is assumption-free, scale invariant and robust to noisy and missing features. It can handle both numerical and categorical features. And, it can be easily extended to multi-class and regression problems.