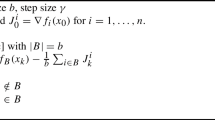MASAGA: A Linearly-Convergent Stochastic First-Order Method for Optimization on Manifolds

Abstract

We consider the stochastic optimization of finite sums over a Riemannian manifold where the functions are smooth and convex. We present MASAGA, an extension of the stochastic average gradient variant SAGA on Riemannian manifolds. SAGA is a variance-reduction technique that typically outperforms methods that rely on expensive full-gradient calculations, such as the stochastic variance-reduced gradient method. We show that MASAGA achieves a linear convergence rate with uniform sampling, and we further show that MASAGA achieves a faster convergence rate with non-uniform sampling. Our experiments show that MASAGA is faster than the recent Riemannian stochastic gradient descent algorithm for the classic problem of finding the leading eigenvector corresponding to the maximum eigenvalue. Code related to this paper is available at: https://github.com/IssamLaradji/MASAGA.

1 Introduction

The most common supervised learning methods in machine learning use empirical risk minimization during the training. The minimization problem can be expressed as minimizing a finite sum of loss functions that are evaluated at a single data sample. We consider the problem of minimizing a finite sum over a Riemannian manifold,

$$ \min _{x\in \mathcal X \subseteq \mathcal {M}} f(x) = \frac{1}{n} \sum _{i=1}^n f_i(x), $$

where $\mathcal X$ is a geodesically convex set in the Riemannian manifold $\mathcal {M}$. Each function $f_i$ is geodesically Lipschitz-smooth and the sum is geodesically strongly-convex over the set $\mathcal {X}$. The learning phase of several machine learning models can be written as an optimization problem of this form. This includes principal component analysis (PCA) [39], dictionary learning [34], Gaussian mixture models (GMM) [10], covariance estimation [36], computing the Riemannian centroid [11], and PageRank algorithm [33].

When $\mathcal {M}\equiv \mathbb R^d$, the problem reduces to convex optimization over a standard Euclidean space. An extensive body of literature studies this problem in deterministic and stochastic settings [5, 22, 23, 28, 29]. It is possible to convert the optimization over a manifold into an optimization in a Euclidean space by adding $x\in \mathcal X$ as an optimization constraint. The problem can then be solved using projected-gradient methods. However, the problem with this approach is that we are not explicitly exploiting the geometrical structure of the manifold. Furthermore, the projection step for the most common non-trivial manifolds used in practice (such as the space of positive-definite matrices) can be quite expensive. Further, a function could be non-convex in the Euclidean space but geodesically convex over an appropriate manifold. These factors can lead to poor performance for algorithms that operate with the Euclidean geometry, but algorithms that use the Riemannian geometry may converge as fast as algorithms for convex optimization in Euclidean spaces.

Stochastic optimization over manifolds and their convergence properties have received significant interest in the recent literature [4, 14, 30, 37, 38]. Bonnabel [4] and Zhang et al. [38] analyze the application of stochastic gradient descent (SGD) for optimization over manifolds. Similar to optimization over Euclidean spaces with SGD, these methods suffer from the aggregating variance problem [40] which leads to sublinear convergence rates.

When optimizing finite sums over Euclidean spaces, variance-reduction techniques have been introduced to reduce the variance in SGD in order to achieve faster convergence rates. The variance-reduction techniques can be categorized into two groups. The first group is memory-based approaches [6, 16, 20, 32] such as the stochastic average gradient (SAG) method and its variant SAGA. Memory-based methods use the memory to store a stale gradient of each $f_i$, and in each iteration they update this “memory” of the gradient of a random $f_i$. The averaged stored value is used as an approximation of the gradient of f.

The second group of variance-reduction methods explored for Euclidean spaces require full gradient calculations and include the stochastic variance-reduced gradient (SVRG) method [12] and its variants [15, 19, 25]. These methods only store the gradient of f, and not the gradient of the individual $f_i$ functions. But, these methods occasionally require evaluating the full gradient of f as part of their gradient approximation and require two gradient evaluations per iteration. Although SVRG often dramatically outperforms the classical gradient descent (GD) and SGD, the extra gradient evaluation typically lead to a slower convergence than memory-based methods. Furthermore, the extra gradient calculations of SVRG can lead to worse performance than the classical SGD during the early iterations where SGD has the most advantage [9]. Thus, when the bottleneck of the process is the gradient computation itself, using memory-based methods like SAGA can improve performance [3, 7]. Furthermore, for several applications it has been shown that the memory requirements can be alleviated by exploiting special structures in the gradients of the $f_i$ [16, 31, 32].

Several recent methods have extended SVRG to optimize the finite sum problem over a Riemannian manifold [14, 30, 37], which we refer to as RSVRG methods. Similar to the case of Euclidean spaces, RSVRG converges linearly for geodesically Lipschitz-smooth and strongly-convex functions. However, these methods also require the extra gradient evaluations associated with the original SVRG method. Thus, they may not perform as well as potential generalizations of memory-based methods like SAGA.

In this work we present MASAGA, a variant of SAGA to optimize finite sums over Riemannian manifolds. Similar to RSVRG, we show that it converges linearly for geodesically strongly-convex functions. We also show that both MASAGA and RSVRG with a non-uniform sampling strategy can converge faster than the uniform sampling scheme used in prior work. Finally, we consider the problem of finding the leading eigenvector, which minimizes a quadratic function over a sphere. We show that MASAGA converges linearly with uniform and non-uniform sampling schemes on this problem. For evaluation, we consider one synthetic and two real datasets. The real datasets are MNIST [17] and the Ocean data [18]. We find the leading eigenvector of each class and visualize the results. On MNIST, the leading eigenvectors resemble the images of each digit class, while for the Ocean dataset we observe that the leading eigenvector represents the background image in the dataset.

In Sect. 2 we present an overview of essential concepts in Riemannian geometry, defining the geodesically convex and smooth function classes following Zhang et al. [38]. We also briefly review the original SAGA algorithm. In Sect. 3, we introduce the MASAGA algorithm and analyze its convergence under both uniform and non-uniform sampling. Finally, in Sect. 4 we empirically verify the theoretical linear convergence results.

2 Preliminaries

In this section we first present a review of Riemannian manifold concepts, however, for a more detailed review we refer the interested reader to the literature [1, 27, 35]. Then, we introduce the class of functions that we optimize over such manifolds. Finally, we briefly review the original SAGA algorithm.

2.1 Riemannian Manifold

A Riemannian manifold is denoted by the pair $(\mathcal {M}, G)$, that consists of a smooth manifold $\mathcal {M}$ over $\mathbb R^d$ and a metric G. At any point x in the manifold $\mathcal {M}$, we define $\mathcal {T_M}(x)$ to be the tangent plane of that point, and G defines an inner product in this plane. Formally, if p and q are two vectors in $\mathcal {T_M}(x)$, then $\left\langle p,q \right\rangle _x = G(p,q)$. Similar to Euclidean space, we can define the norm of a vector and the angle between two vectors using G.

To measure the distance between two points on the manifold, we use the geodesic distance. Geodesics on the manifold generalize the concept of straight lines in Euclidean space. Let us denote a geodesic with $\gamma (t)$ which maps $[0,1] \rightarrow \mathcal {M}$ and is a function with constant gradient,

$$ \frac{d^2}{dt^2} \gamma (t) = 0. $$

To map a point in $\mathcal {T_M}(x)$ to $\mathcal {M}$, we use the exponential function $\mathrm {Exp}_x : \mathcal {T_M}(x) \rightarrow \mathcal {M}$. Specifically, $\mathrm {Exp}_x(p) = z$ means that there is a geodesic curve $\gamma _x^z(t)$ on the manifold that starts from x (so $\gamma _x^z(0)=x$) and ends at z (so $\gamma _x^z(1)=z=\mathrm {Exp}_x(p)$) with a velocity of p ($\frac{d}{dt} \gamma _x^z(0) = p$). When the $\mathrm {Exp}$ function is defined for every point in the manifold, we call the manifold geodesically-complete. For example, the unit sphere in $\mathcal R^n$ is geodesically complete. If there is a unique geodesic curve between any two points in $\mathcal {M}' \in \mathcal {M}$, then the $\mathrm {Exp}_x$ function has an inverse defined by the $\mathrm {Log}_x$ function. Formally the $\mathrm {Log}_x \equiv \mathrm {Exp}_x^{-1}: \mathcal {M}' \rightarrow \mathcal {T_M}(x)$ function maps a point from $\mathcal {M}'$ back into the tangent plane at x. Moreover, the geodesic distance between x and z is the length of the unique shortest path between z and x, which is equal to $\Vert \mathrm {Log}_x(z)\Vert = \Vert \mathrm {Log}_z(x)\Vert$.

Let u and $v \in \mathcal {T_M}(x)$ be linearly independent so they specify a two dimensional subspace $\mathcal S_x \in \mathcal {T_M}(x)$. The exponential map of this subspace, $\mathrm {Exp}_x (\mathcal S_x) = \mathcal {S_M}$, is a two dimensional submanifold in $\mathcal {M}$. The sectional curvature of ${S_M}$ denoted by $\mathrm {K}(\mathcal {S_M},x)$ is defined as a Gauss curvature of ${S_M}$ at x [41]. This sectional curvature helps us in the convergence analysis of the optimization method. We use the following lemma in our analysis to give a trigonometric distance bound.

Lemma 1

(Lemma 5 in [38]). Let a, b, and c be the side lengths of a geodesic triangle in a manifold with sectional curvature lower-bounded by $K_{\mathrm {min}}$. Then

Another important map used in our algorithm is the parallel transport. It transfers a vector from a tangent plane to another tangent plane along a geodesic. This map is denoted by $\varGamma _x^z: \mathcal {T_M}(x) \rightarrow \mathcal {T_M}(z)$, and maps a vector from the tangent plane $\mathcal {T_M}(x)$ to a vector in the tangent plane $\mathcal {T_M}(z)$ while preserving the norm and inner product values.

$$ \left\langle p,q \right\rangle _x = \left\langle \varGamma _x^z(p),\varGamma _x^z(q) \right\rangle _z $$

Grassmann Manifold. Here we review the Grassmann manifold, denoted $\mathrm {Grass}(p,n)$, as a practical Riemannian manifold used in machine learning. Let p and n be positive integers with $p \le n$. $\mathrm {Grass}(p,n)$ contains all matrices in $\mathbb R ^{n \times p }$ with orthonormal columns (the class of orthogonal matrices). By the definition of an orthogonal matrix, if $M \in \mathrm {Grass}(p,n)$ then we have $M^\top M = I$, where $I \in \mathbb R^{p \times p}$ is the identity matrix. Let $q \in \mathcal T_{\mathrm {Grass}(p,n)}(x)$, and $q= U \varSigma V^\top$ be its p-rank singular value decomposition. Then we have:

$$ \mathrm {Exp}_x(tq) = xV \cos (t\varSigma ) V^\top + U \sin (t \varSigma ) V^\top . $$

The parallel transport along a geodesic curve $\gamma (t)$ such that $\gamma (0) = x$ and $\gamma (1) = z$ is defined as:

$$ \varGamma _x^z (tq) = (-xV \sin (t\varSigma ) U^\top + U \cos (t \varSigma ) U^\top + I - UU^\top )q. $$

2.2 Smoothness and Convexity on Manifold

In this section, we define convexity and smoothness of a function over a manifold following Zhang et al. [38]. We call $\mathcal X \in \mathcal {M}$ geodesically convex if for any two points y and z in $\mathcal X$, there is a geodesic $\gamma (t)$ starting from y and ending in z with a curve inside of $\mathcal X$. For simplicity, we drop the subscript in the inner product notation.

Formally, a function $f: \mathcal X \rightarrow \mathbb R$ is called geodesically convex if for any y and z in $\mathcal X$ and the corresponding geodesic $\gamma$, for any $t \in [0,1]$ we have:

$$ f(\gamma (t)) \le (1-t) f(y) + t f(z). $$

Similar to the Euclidean space, if the $\mathrm {Log}$ function is well defined we have the following for convex functions:

$$ f(z) + \left\langle g_z,\mathrm {Log}_z(y) \right\rangle \le f(y), $$

where $g_z$ is a subgradient of f at x. If f is a differentiable function, the Riemannian gradient of f at z is a vector $g_z$ which satisfies $\frac{d}{dt}|_{t=0} f(\mathrm {Exp}_z(tg_z)) = \left\langle g_z,\nabla f(z) \right\rangle _z$, with $\nabla f$ being the gradient of f in $\mathbb R^n$. Furthermore, we say that f is geodesically $\mu$-strongly convex if there is a $\mu > 0$ such that:

$$ f(z) + \left\langle g_z,\mathrm {Log}_z(y) \right\rangle + \frac{\mu }{2} \Vert \mathrm {Log}_z(y)\Vert ^2\le f(y). $$

Let $x^*\in \mathcal X$ be the optimum of f. This implies that there exists a subgradient at $x^*$ with $g_{x^*} =0$ which implies that the following inequalities hold:

$$\begin{aligned}&\Vert \mathrm {Log}_z(x^*)\Vert ^2\le \frac{2}{\mu }(f(z) - f(x^*))\\&\left\langle g_z,\mathrm {Log}_z(x^*) \right\rangle + \frac{\mu }{2} \Vert \mathrm {Log}_z(x^*)\Vert ^2 \le 0 \end{aligned}$$

Finally, an f that is differentiable over $\mathcal {M}$ is said to be a Lipschitz-smooth function with the parameter $L > 0$ if its gradient satisfies the following inequality:

$$ \Vert g_z - \varGamma _{y}^{z}\left[ g_y \right] \Vert \le L \Vert \mathrm {Log}_z(y)\Vert = L\ \mathrm {d}(z,y), $$

where $\mathrm {d}(z,y)$ is the distance between z and y. For a geodesically smooth f the following inequality also holds:

$$ f(y) \le f(z) + \left\langle g_z,\mathrm {Log}_z(y) \right\rangle + \frac{L}{2} \Vert \mathrm {Log}_z(y)\Vert ^2. $$

2.3 SAGA Algorithm

In this section we briefly review the SAGA method [6] and the assumptions associated with it. SAGA assumes f is $\mu$-strongly convex, each $f_i$ is convex, and each gradient $\nabla f_i$ is Lipschitz-continuous with constant L. The method generates a sequence of iterates $x_t$ using the SAGA Algorithm 1 (line 7). In the algorithm, M is the memory used to store stale gradients. During each iteration, SAGA picks one $f_{i_t}$ randomly and evaluates its gradient at the current iterate value, $\nabla f_{i_t}(x_{t})$. Next, it computes $\nu _t$ as the difference between the current $\nabla f_{i_t}(x_{t})$ and the corresponding stale gradient of $f_{i_t}$ stored in the memory plus the average of all stale gradients (line 6). Then it uses this vector $\nu _t$ as an approximation of the full gradient and updates the current iterate similar to the gradient descent update rule. Finally, SAGA updates the stored gradient of $f_{i_t}$ in the memory with the new value of $\nabla f_{i_t}(x_{t})$.

Let $\rho _{\mathrm {saga}} = \frac{\mu }{2(n\mu + L)}$. Defazio et al. [6] show that the iterate value $x_t$ converges to the optimum $x^*$ linearly with a contraction rate $1-\rho _{\mathrm {saga}}$,

$$ \mathbb E_{}\left[ \Vert x_{t}-x^*\Vert ^2 \right] \le (1-\rho _{\mathrm {saga}})^t C, $$

where C is a positive scalar.

3 Optimization on Manifold with SAGA

In this section we introduce the MASAGA algorithm (see Algorithm 2). We make the following assumptions:

• 1. Each $f_i$ is geodesically L-Lipschitz continuous.

• 2. f is geodesically $\mu$-strongly convex.

• 3. f has an optimum in $\mathcal X$, i.e., $x^*\in \mathcal X$.

• 4. The diameter of $\mathcal X$ is bounded above, i.e., $\max _{u,v \in \mathcal X} \mathrm {d}(u,v) \le D$.

• 5. $\mathrm {Log}_x$ is defined when $x \in \mathcal X$.

• 6. The sectional curvature of $\mathcal X$ is bounded, i.e., $K_{\mathrm {min}} \le K_{\mathcal X} \le K_{\mathrm {max}}$.

These assumptions also commonly appear in the previous work [14, 30, 37, 38]. Similar to the previous work [14, 37, 38], we also define the constant $\zeta$ which is essential in our analysis:

$$ \zeta = {\left\{ \begin{array}{ll} \frac{\sqrt{|K_{\mathrm {min}}|}D}{\tanh (\sqrt{|K_{\mathrm {min}}|}D)} &{} \quad \text {if } K_{\mathrm {min}} < 0\\ 1 &{} \quad \text {if } K_{\mathrm {min}} \ge 0 \end{array}\right. } $$

In MASAGA we modify two parts of the original SAGA: (i) since gradients are in different tangent planes, we use parallel transport to map them into the same tangent plane and then do the variance reduction step (line 6 of Algorithm 2), and (ii) we use the $\mathrm {Exp}$ function to map the update step back into the manifold (line 7 of Algorithm 2).

3.1 Convergence Analysis

We analyze the convergence of MASAGA considering the above assumptions and show that it converges linearly. In our analysis, we use the fact that MASAGA’s estimation of the full gradient $\nu _t$ is unbiased (like SAGA), i.e., $\mathbb E_{}\left[ \nu _t\right] = \nabla f(x_{t})$. For simplicity, we use $\nabla f$ to denote the Riemannian gradient instead of $g_x$. We assume that there exists an incremental first-order oracle (IFO) [2] that gets an $i \in \{1,..., n \}$, and an $x \in \mathcal X$, and returns $(f_i(x), \nabla f_i(x)) \in (\mathbb R \times \mathcal {T_M}(x))$.

Theorem 1

If each $f_i$ is geodesically L-smooth and f is geodesically $\mu$-strongly convex over the Riemannian manifold $\mathcal {M}$, the MASAGA algorithm with the constant step size $\eta = \frac{2\mu +\sqrt{\mu ^2-8\rho (1+\alpha ) \zeta L^2} }{4(1+\alpha ) \zeta L^2}$ converges linearly while satisfying the following:

$$ \mathbb E_{}\left[ \mathrm {d}^2( x_{t},x^*)\right] \le (1-\rho )^{t}\varUpsilon ^{0}, $$

where $\rho =\min \{\frac{\mu ^2}{8(1+\alpha ) \zeta L^2}, \frac{1}{n}- \frac{1}{\alpha n}\}$, $\varUpsilon ^0 = 2\alpha \zeta \eta ^2 \sum _{i=1}^n \Vert M^{0}[i]-\varGamma _{x^*}^{x_0}\left[ \nabla f_i(x^*) \right] \Vert ^2 +\mathrm {d}^2( x_0,x^*)$ is a positive scalar, and $\alpha >1$ is a constant.

Proof

Let $\delta _t =\mathrm {d}^2(x_{t},x^*)$. First we find an upper-bound for $\mathbb E_{}\left[ \Vert \nu _t\Vert ^2\right]$.

$$\begin{aligned} \mathbb E_{}\left[ \Vert \nu _t\Vert ^2\right]&= \mathbb E_{}\left[ \Vert \nabla f_{i_t}(x_t)-\varGamma _{x_0}^{x_{t}}\left[ M^{t}[i_t]- \hat{\mu } \right] \Vert ^2\right] \\&=\mathbb E_{}\left[ \Vert \nabla f_{i_t}(x_{t})-\varGamma _{x^*}^{x_{t}}\left[ \nabla f_{i_t}(x^*) \right] -\varGamma _{x_0}^{x_{t}}\left[ M^{t}[i_t]-\varGamma _{x^*}^{x_0}\left[ \nabla f_{i_t}(x^*) \right] - \hat{\mu } \right] \Vert ^2\right] \\&\le 2\mathbb E_{}\left[ \Vert \nabla f_{i_t}(x_{t})-\varGamma _{x^*}^{x_{t}}\left[ \nabla f_{i_t}(x^*) \right] \Vert ^2\right] \\&\quad +\, 2\mathbb E_{}\left[ \Vert \varGamma _{x_0}^{x_{t}}\left[ M^{t}[i_t]-\varGamma _{x^*}^{x_0}\left[ \nabla f_{i_t}(x^*) \right] - \hat{\mu } \right] \Vert ^2\right] \\&\le 2\mathbb E_{}\left[ \Vert \nabla f_{i_t}(x_{t})-\varGamma _{x^*}^{x_{t}}\left[ \nabla f_{i_t}(x^*) \right] \Vert ^2\right] \\&\quad +\, 2\mathbb E_{}\left[ \Vert M^{t}[i_t]-\varGamma _{x^*}^{x_0}\left[ \nabla f_{i_t}(x^*) \right] \Vert ^2\right] \\&\le 2 L^2 \delta _t + 2\mathbb E_{}\left[ \Vert M^{t}[i_t]-\varGamma _{x^*}^{x_0}\left[ \nabla f_{i_t}(x^*) \right] \Vert ^2\right] \end{aligned}$$

The first inequality is due to $(a+b)^2 \le 2 a^2+ 2 b^2$ and the second one is from the variance upper-bound inequality, i.e., $\mathbb E_{}\left[ x^2 - \mathbb E_{}\left[ x\right] ^2\right] \le \mathbb E_{}\left[ x^2 \right]$. The last inequality comes from the geodesic Lipschitz smoothness of each $f_i$. Note that the expectation is taken with respect to $i_t$.

$$\begin{aligned} \mathbb E_{}\left[ \delta _{t+1}\right]&\le \mathbb E_{}\left[ \delta _t - 2\left\langle \nu _t,\mathrm {Exp}_{x_{t}}^{-1}(-x^*) \right\rangle +\zeta \eta ^2\Vert \nu _t\Vert ^2\right] \\&= \delta _t - 2\eta \left\langle \nabla f(x_{t}),\mathrm {Exp}_{x_{t}}^{-1}(-x^*) \right\rangle +\zeta \eta ^2\mathbb E_{}\left[ \Vert \nu _t\Vert ^2\right] \\&\le \delta _t - \eta \mu \delta _t +\zeta \eta ^2\mathbb E_{}\left[ \Vert \nu _t\Vert ^2\right] \\&\le (1-\mu \eta )\delta _t + \zeta \eta ^2\left[ 2L^2 \delta _t + 2\mathbb E_{}\left[ \Vert M^{t}[i_t]-\varGamma _{x^*}^{x_0}\left[ \nabla f_{i_t}(x^*) \right] \Vert ^2\right] \right] \\&= (1-\mu \eta + 2\zeta L^2\eta ^2 )\delta _t + 2\zeta \eta ^2 \varPsi _t \end{aligned}$$

The first inequality is due to the trigonometric distance bound, the second one is due to the strong convexity of f, and the last one is due to the upper-bound of $\nu _t$. $\varPsi _t$ is defined as follows:

$$ \varPsi _t = \frac{1}{n}\sum _{i=1}^n \Vert M^{t}[i]-\varGamma _{x^*}^{x_0}\left[ \nabla f_i(x^*) \right] \Vert ^2. $$

We define the Lyaponov function

$$ \varUpsilon ^{t}= \delta _t+ c\,\varPsi _t $$

for some $c > 0$. Note that $\varUpsilon ^{t} \ge 0$, since both $\delta _t$ and $\varPsi _t$ are positive or zero. Next we find an upper-bound for $\mathbb E_{}\left[ \varPsi _{t+1}\right]$.

$$\begin{aligned} \mathbb E_{}\left[ \varPsi _{t+1}\right]&= \frac{1}{n}(\frac{1}{n}\sum _{i=1}^n \Vert \nabla f_i(x_{t})-\varGamma _{x^*}^{x_{t}}\left[ \nabla f_i(x^*) \right] \Vert ^2 )\\&\quad +\, (1-\frac{1}{n})(\frac{1}{n}\sum _{i=1}^n \Vert M^{t}[i]-\varGamma _{x^*}^{x_0}\left[ \nabla f_i(x^*) \right] \Vert ^2)\\&= \frac{1}{n}(\frac{1}{n}\sum _{i=1}^n \Vert \nabla f_i(x_{t})-\varGamma _{x^*}^{x_{t}}\left[ \nabla f_i(x^*) \right] \Vert ^2 )+ (1-\frac{1}{n}) \varPsi _t\\&\le \frac{L^2}{n} \delta _t + (1-\frac{1}{n}) \varPsi _t\\ \end{aligned}$$

The inequality is due to the geodesic Lipschitz smoothness of $f_i$. Then, for some positive $\rho \le 1$ we have the following inequality:

$$\begin{aligned} \mathbb E_{}\left[ \varUpsilon ^{t+1}\right] -(1-\rho )\varUpsilon ^{t}&\le (1-\mu \eta + 2\zeta L^2\eta ^2 - (1-\rho ) + \frac{cL^2}{n} )\delta _t \nonumber \\&+\, ( 2\zeta \eta ^2 - c(1-\rho ) + c(1-\frac{1}{n}) )\varPsi _t. \end{aligned}$$

(1)

In the right hand side of Inequality 1, $\delta _t$ and $\varPsi _t$ are positive by construction. If the coefficients of $\delta _t$ and $\varPsi _t$ in the right hand side of the Inequality 1 are negative, we would have $\mathbb E_{}\left[ \varUpsilon ^{t+1}\right] \le (1-\rho )\varUpsilon ^{t}$. More precisely, we require

$$\begin{aligned}&2\zeta \eta ^2 - c(1-\rho ) + c(1-\frac{1}{n}) \le 0 \end{aligned}$$

(2)

$$\begin{aligned}&1-\mu \eta + 2\zeta L^2\eta ^2 - (1-\rho ) + \frac{cL^2}{n} \le 0 \end{aligned}$$

(3)

To satisfy Inequality 2 we require $\rho \le \frac{1}{n} - \frac{ 2\zeta \eta ^2 }{c}$. If we set $c=2\alpha n \zeta \eta ^2$ for some $\alpha > 1$, then $\rho \le \frac{1}{n}- \frac{1}{\alpha n }$, which satisfies our requirement. If we replace the value of c in Inequality 3, we will get:

$$\begin{aligned}&\rho -\mu \eta +2\zeta L^2\eta ^2 + 2\alpha \zeta L^2\eta ^2 \le 0\\&\eta \in (\eta ^- = \frac{2\mu -\sqrt{\mu ^2-8\rho (1+\alpha ) \zeta L^2} }{4(1+\alpha ) \zeta L^2}, \eta ^+ =\frac{2\mu +\sqrt{\mu ^2-8\rho (1+\alpha ) \zeta L^2} }{4(1+\alpha ) \zeta L^2} )\\ \end{aligned}$$

To ensure the term under the square root is positive, we also need $\rho < \frac{\mu ^2}{8(1+\alpha ) \zeta L^2}$. Finally, if we set $\rho = \min \{\frac{\mu ^2}{8(1+\alpha ) \zeta L^2}, \frac{1}{n}- \frac{1}{\alpha n}\}$ and $\eta = \eta ^+$, then we have:

$$ \mathbb E_{}\left[ \varUpsilon ^{t+1}\right] \le (1-\rho )^{t+1}\varUpsilon ^{0}, $$

where $\varUpsilon ^{0}$ is a scalar. Since $\varPsi _t > 0$ and $\mathbb E_{}\left[ \delta _{t+1}\right] \le \mathbb E_{}\left[ \varUpsilon ^{t+1}\right]$, we get the required bound:

$$ \mathbb E_{}\left[ \delta _{t+1}\right] \le (1-\rho )^{t+1}\varUpsilon ^{0}. $$

Corollary 1

Let $\beta = \frac{n\mu ^2}{8\zeta L^2}$, and $\bar{\alpha } = \beta + \sqrt{\frac{\beta ^2}{4} + 1} > 1$. If we set $\alpha = \bar{\alpha }$ then we will have $\rho =\frac{\mu ^2}{8(1+\bar{\alpha }) \zeta L^2} = \frac{1}{n}- \frac{1}{\bar{\alpha } n}$. Furthermore, to reach an $\epsilon$ accuracy, i.e., $\mathbb E_{}\left[ \mathrm {d}^2( x_T,x^*)\right] < \epsilon$, we require that the total number of MASAGA (Algorithm 2) iteration T satisfy the following inequality:

$$\begin{aligned} T \ge (\frac{8 (1+ \bar{\alpha })\zeta L^2}{\mu ^2}) \log (\frac{1}{\epsilon }). \end{aligned}$$

(4)

Note that this bound is similar to the bound of Zhang et al. [37]. To make it clear, notice that $\bar{\alpha } \le 2\beta + 1$. Therefore, if we plug this upper-bound into Inequality 4 we get

$$ T = \mathcal O (\frac{(2\beta + 2)\zeta L^2}{\mu ^2}) \log (\frac{1}{\epsilon })= \mathcal O (\frac{n\mu ^2}{8\zeta L^2} \frac{\zeta L^2}{\mu ^2}+\frac{\zeta L^2}{\mu ^2}) \log (\frac{1}{\epsilon }) = \mathcal O (n+\frac{\zeta L^2}{\mu ^2}) \log (\frac{1}{\epsilon }). $$

The $\frac{L^2}{\mu ^2}$ term in the above bound is the squared condition number that could be prohibitively large in machine learning applications. In contrast, the original SAGA and SVRG algorithms only depend on $\frac{L}{\mu }$ on convex function within linear spaces. In the next section, we improve upon this bound through non-uniform sampling techniques.

3.2 MASAGA with Non-uniform Sampling

Using non-uniform sampling for stochastic optimization in Euclidean spaces can help stochastic optimization methods achieve a faster convergence rate [9, 21, 31]. In this section, we assume that each $f_i$ has its own geodesically $L_i$-Lipschitz smoothness as opposed to a single geodesic Lipschitz smoothness $L = \max \{L_i\}$. Now, instead of uniformly sampling $f_i$, we sample $f_i$ with probability $\frac{L_i}{n\bar{L}}$, where $\bar{L} = \frac{1}{n} \sum _{i=1}^n L_i$. In machine learning applications, we often have $\bar{L} \ll L$. Using this non-uniform sampling scheme, the iteration update is set to

$$ x_{t+1}=\mathrm {Exp}_{x_{t}}^{}(-\eta ( \frac{\bar{L}}{L_{i_t}} \nu _t)), $$

which keeps the search direction unbiased, i.e., $\mathbb E_{}\left[ \frac{\bar{L}}{L_{i_{t}}}\nu _t\right] = \nabla f(x_{t})$. The following theorem shows the convergence of the new method.

Theorem 2

If $f_i$ is geodesically $L_i$-smooth and f is geodesically $\mu$-strongly convex over the manifold $\mathcal {M}$, the MASAGA algorithm with the defined non-uniform sampling scheme and the constant step size $\eta = \frac{2\mu +\sqrt{\mu ^2-8\rho (\bar{L}+\alpha L ) \frac{\zeta }{\gamma }\bar{L}} }{4(\bar{L}+\alpha L ) \frac{\zeta }{\gamma }\bar{L}}$ converges linearly as follows:

$$ \mathbb E_{}\left[ \mathrm {d}^2( x_{t},x^*)\right] \le (1-\rho )^{t}\varUpsilon ^{0}, $$

where $\rho = \min \{ \frac{\gamma \mu ^2}{8(1+\alpha ) \zeta L \bar{L}}, \frac{\gamma }{n}- \frac{\gamma }{\alpha n} \}$, $\gamma = \frac{\min \{L_i\}}{\bar{L}}$, $L = \max \{L_i\}$, $\bar{L} = \frac{1}{n} \sum _{i=1}^n L_i$, and $\alpha >1$ is a constant, and $\varUpsilon ^0 = \frac{2\alpha \zeta \eta ^2}{\gamma } \sum _{i=1}^n \frac{\bar{L}}{L_{i_{}}}\Vert M^{0}[i]-\varGamma _{x^*}^{x_0}\left[ \nabla f_i(x^*) \right] \Vert ^2 +\mathrm {d}^2( x_0,x^*)$ are positive scalars.

Proof of the above theorem could be found in the supplementary material.

Corollary 2

Let $\beta = \frac{n\mu ^2}{8\zeta L\bar{L}}$, and $\bar{\alpha } = \beta + \sqrt{\frac{\beta ^2}{4} + 1} > 1$. If we set $\alpha = \bar{\alpha }$ then we have $\rho =\frac{\gamma \mu ^2}{8(1+\bar{\alpha }) \zeta L\bar{L}} = \frac{\gamma }{n}- \frac{\gamma }{\bar{\alpha } n}$. Now, to reach an $\epsilon$ accuracy, i.e., $\mathbb E_{}\left[ \mathrm {d}^2( x_T,x^*)\right] < \epsilon$, we require:

$$\begin{aligned} T = \mathcal O (n + \frac{\zeta L\bar{L}}{\gamma \mu ^2}) \log (\frac{1}{\epsilon }), \end{aligned}$$

(5)

where T is the number of the necessary iterations.

Observe that the number of iterations T in Equality 5 depends on $\bar{L} L$ instead of $L^2$. When $\bar{L} \ll L$, the difference could be significant. Thus, MASAGA with non-uniform sampling could achieve an $\epsilon$ accuracy faster than MASAGA with uniform sampling.

Similarly we can use the same sampling scheme for the RSVRG algorithm [37] and improve its convergence. Specifically, if we change the update rule of Algorithm 1 of Zhang et al. [37] to

$$ x_{t+1}^{s+1}=\mathrm {Exp}_{x_{t}^{s+1}}{-\eta ( \frac{\bar{L}}{L_{i_t}} \nu _t^{s+1})}, $$

then Theorem 1 and Corollary 1 of Zhang et al. [37] will change to the following ones.

Theorem 3

(Theorem 1 of [37] with non-uniform sampling). If we use non-uniform sampling in Algorithm 1 of RSVRG [37] and run it with the option I as described in the work, and let

$$ \alpha = \frac{3\zeta \eta \bar{L}^2}{\mu - 2\zeta \eta \bar{L}^2} + \frac{(1+4\zeta \eta ^2 - 2\eta \mu )^m( \mu - 5 \zeta \eta \bar{L}^2)}{\mu - 2\zeta \eta \bar{L}^2} < 1, $$

where m is the number of the inner loop iterations, then through S iterations of the outer loop, we have

$$ \mathbb E_{}\left[ \mathrm {d}^2( \tilde{x}^S,x^*)\right] \le (\alpha )^{S} \mathrm {d}^2( \tilde{x}^0,x^*) $$

The above theorem can be proved through a simple modification to the proof of Theorem 1 in RSVRG [37].

Corollary 3

(Corollary 1 of [37] with non-uniform sampling). With non-uniform sampling in Algorithm 1 of RSVRG, after $\mathcal O (n + \frac{\zeta \bar{L}^2}{\gamma \mu ^2}) \log (\frac{1}{\epsilon })$ IFO calls, the output $x_a$ satisfies

$$ \mathbb E_{}\left[ f(x_a) - f(x^*) \right] \le \epsilon . $$

Note that through the non-uniform sampling scheme we improved the RSVRG [37] convergence by replacing the $L^2$ term with a smaller $\bar{L}^2$ term.

4 Experiments: Computing the Leading Eigenvector

Computing the leading eigenvector is important in many real-world applications. It is widely used in social networks, computer networks, and metabolic networks for community detection and characterization [24]. It can be used to extract a feature that “best” represents the dataset [8] to aid in tasks such as classification, regression, and background subtraction. Furthermore, it is used in the PageRank algorithms which requires computing the principal eigenvector of the matrix describing the hyperlinks in the web [13]. These datasets can be huge (the web has more than three billion pages [13]). Therefore, speeding up the leading eigenvector computation will have a significant impact on many applications.

We evaluate the convergence of MASAGA on the problem of computing the leading eigenvalue on several datasets. The problem is written as follows:

$$\begin{aligned} \min _{\{x \; | \; x^\top {}x=1\}} f(x) = -\frac{1}{n}x^\top \left( \sum _{i=1}^n z_iz_i^\top \right) x, \end{aligned}$$

(6)

which is a non-convex objective in the Euclidean space $\mathbb {R}^d$, but a (strongly-) convex objective over the Riemannian manifold. Therefore, MASAGA can achieve a linear convergence rate on this problem. We apply our algorithm on the following datasets:

• Synthetic. We generate Z as a $1000 \times 100$ matrix where each entry is sampled uniformly from (0, 1). To diversify the Lipschitz constants of the individual $z_i$’s, we multiply each $z_i$ with an integer obtained uniformly between 1 and 100.

• MNIST [17]. We randomly pick 10, 000 examples corresponding to digits 0–9 resulting in a matrix $Z \in \mathbb {R}^{10,000 \times 784}$.

• Ocean. We use the ocean video sequence data found in the UCSD background subtraction dataset [18]. It consists of 176 frames, each resized to a $94 \times 58$ image.

We compare MASAGA against RSGD [37] and RSVRG [4]. For solving geodesically smooth convex functions on the Riemannian manifold, RSGD and RSVRG achieve sublinear and linear convergence rates respectively. Since the manifold for Eq. 6 is that of a sphere, we have the following functions:

$$\begin{aligned} \begin{aligned}&P_X(H)=H - \text {trace}(X^\top {}H)X,&\nabla _r f(X) = P_X(\nabla f(X)),\\&\mathrm {Exp}_X(U)=\cos (||U||)X+ \frac{\sin (||U||)}{||U||}U,&\varGamma _y^x(U) = P_y(U), \end{aligned} \end{aligned}$$

(7)

where P corresponds to the tangent space projection function, $\nabla _r f$ the Riemannian gradient function, $\mathrm {Exp}$ the exponential map function, and $\varGamma$ the transport function. We evaluate the progress of our algorithms at each epoch t by computing the relative error between the objective value and the optimum as $\frac{f(x^t)-f^*}{|f^*|}$. We have made the code available at https://github.com/IssamLaradji/MASAGA.

Fig. 1.

Comparison of MASAGA (ours), RSVRG, and RSGD for computing the leading eigenvector. The suffix (U) represents uniform sampling and (NU) the non-uniform sampling variant.

Fig. 2.

The obtained leading eigenvectors of all MNIST digits.

For each algorithm, a grid-search over the learning rates $\{10^{-1},$ $10^{-2},..., 10^{-9}\}$ is performed and plot the results of the algorithm with the best performance in Fig. 1. This plot shows that MASAGA is consistently faster than RSGD and RSVRG in the first few epochs. While it is expected that MASAGA beats RSGD since it has a better convergence rate, the reason MASAGA can outperform RSVRG is that RSVRG needs to occasionally re-compute the full gradient. Further, at each iteration MASAGA requires a single gradient evaluation instead of the two evaluations required by RSVRG. We see in Fig. 1 that non-uniform (NU) sampling often leads to faster progress than uniform (U) sampling, which is consistent with the theoretical analysis. In the NU sampling case, we sample a vector $z_i$ based on its Lipschitz constant $L_i = ||z_i||^2$. Note that for problems where $L_i$ is not known or costly to compute, we can estimate it by using Algorithm 2 of Schmidt et al. [31].

Figures 2 and 3 show the leading eigenvectors obtained for the MNIST dataset. We run MASAGA on 10,000 images of the MNIST dataset and plot its solution in Fig. 2. We see that the exact solution is similar to the solution obtained by MASAGA, which represent the most common strokes among the MNIST digits. Furthermore, we ran MASAGA on 500 images for digits 1–6 independently and plot its solution for each class in Fig. 3. Since most digits of the same class have similar shapes and are fairly centered, it is expected that the leading eigenvector would be similar to one of the digits in the dataset.

Fig. 3.

The obtained leading eigenvectors of the MNIST digits 1–6.

Fig. 4.

The obtained leading eigenvectors of the ocean dataset after 20 iterations.

Figure 4 shows qualitative results comparing MASAGA, RSVRG, and RSGD. We run each algorithm for 20 iterations and plot the results. MASAGA’s and RSVRG’s results are visually similar to the exact solution. However, the RSGD result is visually different than the exact solution (the difference is in the center-left of the two images).

5 Conclusion

We introduced MASAGA which is a stochastic variance-reduced optimization algorithm for Riemannian manifolds. We analyzed the algorithm and showed that it converges linearly when the objective function is geodesically Lipschitz-smooth and strongly convex. We also showed that using non-uniform sampling improves the convergence speed of both MASAGA and RSVRG algorithms. Finally, we evaluated our method on a synthetic dataset and two real datasets where we empirically observed linear convergence. The empirical results show that MASAGA outperforms RSGD and is faster than RSVRG in the early iterations. For future work, we plan to extend MASAGA by deriving convergence rates for the non-convex case of geodesic objective functions. We also plan to explore accelerated variance-reduction methods and block coordinate descent based methods [26] for Riemannian optimization. Another potential future work of interest is a study of relationships between the condition number of a function within the Euclidean space and its corresponding condition number within a Riemannian manifold, and the effects of sectional curvature on it.