Abstract
In this paper, we propose a variational Bayesian algorithm for mixture models that can deal with censored data, which is the data under the situation that the exact value is known only when the value is within a certain range and otherwise only partial information is available. The proposed algorithm can be applied to any mixture model whose component distribution belongs to exponential family; it is a natural generalization of the variational Bayes that deals with “standard” samples whose values are known. We confirm the effectiveness of the proposed algorithm by experiments on synthetic and real world data.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Censoring is the situation that the exact value is known only when the value is within a certain range and otherwise only partial information is available [1]. It is quite common such as data about lifetimes, for example, human life span, mechanical failure [2], active period of smartphone apps [3] and users’ contract periods of telecommunication and e-commerce service [4, 5]. Most observation periods are limited and many samples may not expire within the period. Therefore, their true lifetimes are unknown and they become censored samples (Fig. 1a). Obviously, methods that can handle censored data are essential in fields such as insurance design, facility maintenance and marketing.
One promising approach for dealing with censored data is to adapt mixture models since the probability density underlying censored data often exhibits multimodality. For example, the distribution of machine failure is formed by initial failures and aging failures. For the estimation of mixture models from “standard” data (all samples of which have known values), variational Bayes (VB) [6] is a commonly used algorithm. However, VB for mixture models using censored data has received little attention in the literature.
In this study, we propose the VB algorithm that can deal with Censored data for Mixture models (VBCM). VBCM estimates the variational distribution of parameters and that of two types of latent variables that are indicative of the cluster assignments and the (unobserved) values of censored samples. It is shown that the update equations in VBCM use the expectation of sufficient statistics w.r.t. truncated distribution and cumulative density function, neither of which appear in the standard VB (VB with “standard” data). We also confirm that VBCM, inheriting a property from VB, the quantity used for model selection is analytically tractable and yields predictive distributions in analytic form. We derive the VBCM algorithm for (i) Gaussian mixture models (GMM) and more general (ii) mixture models whose components belong to the exponential family (EFM). VBCM can be seen as the generalization of VB since, if there are no censored samples, it reduces to VB.
We further extend the derived VBCM algorithm to develop a stochastic algorithm. As stated above, the update equation includes expected sufficient statistics; by replacing these with stochastically computed values clearly turns VBCM into a stochastic algorithm. By combining with the existing stochastic VB approach [7,8,9], we develop a stochastic VBCM, which can be seen, theoretically, as a natural gradient algorithm [10].
We conduct experiments on both synthetic and real data. The results show the superiority of the proposed algorithm in over existing VB and EM based algorithms where test log-likelihood is used as the performance metric.
The contributions of this paper are summarized below:
-
We develop VBCM, a VB algorithm that can deal with censored data for mixture models. We also show that the objective of VBCM, which can be used for model selection, is analytically tractable and its predictive distribution have analytic form.
-
We extend VBCM to the stochastic algorithm. It is theoretically proven that the algorithm is a (stochastic) natural gradient algorithm.
-
We confirm the effectiveness of the proposed VBCM algorithm by numerical experiments using both synthetic data and real data.
The rest of this paper is organized as follows. In Sect. 2, we introduce related works. Mixture models and the generative process of censored data are illustrated in Sect. 3. Section 4 presents the proposed VBCM algorithm for GMM and its extension to EFM and to a stochastic algorithm is provided in Sect. 5. Section 6 is devoted to the experimental evaluation and Sect. 7 concludes the paper.
2 Related Works
Researchers continue to develop new algorithms for survival analysis based on promising machine learning algorithms. For example, Pölsterl et al. extend the support vector machine for censored data [11] and Fernandez et al. propose a method based on Gaussian processes [12]. Our study follows this context and we consider how to extend VB for analyzing censored data.
To model censored data, we introduce latent variables to handle the values of censored samples. The idea is not new as is shown by Dempster’s paper [13]. Starting with mixture models that process censored data, one more latent variable indicating cluster assignment is used to develop the expectation-maximization algorithm called EMCM [14, 15]. We use these latent variables to develop a new VB algorithm with Censored data for Mixture models (VBCM).
We also derive stochastic algorithm variant of VBCM; it stochastically computes expected sufficient statistics, an necessary step for parameter update in VBCM. Stochastic algorithms are also an active research topic in machine learning and stochastic VB algorithms have been published e.g., [7, 9]. The above papers use the term “stochastic” to indicate mainly the use of parts of stochastically selected/generated training data. We follow this concept in developing a stochastic VBCM.
3 Mixture Models for Censored Data
3.1 Data Description
Here, we describe censored data. We explain using failure data shown in Fig. 1a since the data is the representative of censored data. Let N be the number of devices. For each device, its installation time is known. The failure time of a device is exactly known if it fails within the known observation period. If the device is alive at the end of the period, we know only that its failure time exceeds the end of period. Similarly, if the device is already broken at the beginning of the period, we know only its failure time precedes the beginning. We call the devices whose failure time is exactly observed as observed samples and the devices whose failure time is not exactly observed as censored samples.
We consider that the censored data is to be processed so that we can predict lifetime (time to failure), as shown in Fig. 1b. We denote the range of the observation period, where the lifetime of the i-th device is exactly observed, as \(C_i = (C^L_i, C^R_i)\). This definition covers the setting that the period length depends on a device unlike Fig. 1a. We also denote the lifetime of the i-th observed sample (device) as \(x_i\). Let \(w_i=(w_{io}, w_{i\ell }, w_{ig})\) be the indicator variable which is set to \(w_i=(1,0,0)\) if the lifetime of the i-th device is observed, \(w_{i}=(0,1,0)\) if it precedes \(C^L_i\), and \(w_{i}=(0,0,1)\) if it is exceeds \(C^R_i\). Then, the observed variables are \(W=\{w_i\}^N_{i=1}, X=\{ x_i \}_{i \in \mathcal {I}_o}\), where \(\mathcal {I}_o\) is the set of observed samples. Similarly, we define the set of samples whose values precede (exceed) \(C^L_i\) \((C^R_i)\) as \(\mathcal {I}_{\ell }\) \((\mathcal {I}_{g})\). Note that target of this study is not limited to lifetime estimation and includes any type of problem wherein the data contains censored samples.
3.2 Models
We use mixture models to estimate the distribution underlying the censored data. The probability density function (PDF) of mixture models is defined as the linear summation of component distribution f,
where K is the number of components and \(\varTheta \) represents the model parameters. \(\varvec{\pi }= \{\pi _1, \cdots , \pi _K\}\) and \(\varvec{\varphi } = \{\varphi _1, \cdots , \varphi _K\}\) represent the k-th component’s mixing ratio and parameters, respectively. Examples of component f are (i) Gaussian distribution, \(f_G\) and, more generally, (ii) a distribution belonging to the exponential family, \(f_E\), whose PDFs are defined as
where \(\mu _k\) and \(\lambda _k\) are the mean and precision, and \(\eta _k\) is the natural parameter. T(x) is sufficient statistics and \(A(\eta _k)\) is the log-normalizer. The exponential family includes various type of distributions such as exponential distribution and Poisson distribution:
By assigning specific values to T(x) and \(A(\eta _k)\), the above densities are represented by Eq. (3) (See Table 1). We call the mixture models whose components are Gaussian and exponential family the Gaussian mixture models (GMM) and exponential family mixtures (EFM), respectively. Our notation f is the component distribution without distinction as to which distribution is adopted. We also denote the cumulative density function (CDF) of f as F:
The generative process of censored data using mixture models consists of 5 steps. At first, parameters \(\varTheta = \{ \varvec{\pi }, \varvec{\varphi } \}\) follow prior distribution \(P(\varTheta )=P(\varvec{\pi })P(\varvec{\varphi })\). \(P(\varvec{\pi })\) is the Dirichlet distribution
and \(P(\varvec{\varphi })\) is a conjugate prior of component distribution. It is the Gaussian-gamma distribution when the component distribution is Gaussian:
The conjugate prior for exponential family distribution exists and is defined as
where the normalizer \(\mathcal {Z}(\xi _0, \nu _0)\) is defined depending on the component distribution used (See Table 1). It follows that the prior for GMM is \(P(\varvec{\pi })P(\varvec{\mu }, \varvec{\lambda })\) and for EFM is \(P(\varvec{\pi })P(\varvec{\eta })\). Note that \(\alpha _0, \mu _0, \tau _0, a_0, b_0, \xi _0, \nu _0\) are the hyperparametersFootnote 1.
In the second step, for each i-th sample, latent variable \(z_i = \{z_{i1}, \cdots , z_{iK}\}\) which indicates the belonging componentFootnote 2, follows a multinomial distribution:
The third step is to generate observed variable \(w_i\), which indicates an exact value is observed or is less/larger than \(C_i^L\)/\(C_i^R\). Variable \(w_i\) follows a multinomial distribution whose parameters are defined from the CDF of component distribution since e.g., \(F(C_i^L|\varphi _k)\) is the probability that random variable following \(f(\cdot | \varphi _k)\) takes a value less than \(C_i^L\) (See Fig. 3):

In the final step, if \(w_{io} = 1\), observed variable \(x_i \in (C_i^L, C_i^R)\) follows truncated component distribution:
where truncated distribution \(f_{tr}(x| \varphi , a, b)\) is defined as the distribution whose PDF is given by:
Note that, if f is Gaussian, then \(f_{tr}(x| \varphi , a, b)\) is the truncated Gaussian distribution \(\mathcal {TN}(x| \mu , \sigma ^2, a, b)\) (See Fig. 2). When \(w_{i\ell }=1\) or \(w_{ig}=1\), latent variable \(y_i\) also follows a truncated distribution as follows:
Repeating the above procedure for all i generates X, W, Z, Y. The distributions used for generating X, W, Y are illustrated in Fig. 3. Using Eqs. (6)–(15), the joint probability of the variables and the parameters is given by

where dependency on \(\varvec{C}_i\) is omitted. Figure 4 shows a graphical model. In the experiments, we also use the following likelihood of observed variables:

4 Proposed Variational Bayes
4.1 General Formulation and Derivation for GMM
Variational Bayes (VB) is a method that estimates variational distribution \(q(\varvec{\pi }, \varvec{\varphi }, Z, Y)\), which approximates a posterior of parameters and latent variables [6, 16]. VB needs to decide the factorization form of the variational distribution. Our VB algorithm considers the distribution in which each parameter is independent of the latent variables but Y and Z are dependent: \(q(\varvec{\pi }, \varvec{\varphi }, Z, Y) = q(\varvec{\pi })q(\varvec{\varphi })q(Y, Z)\). This factorization form yields a tractable algorithm. Under the above factorization form, a variational distribution can be estimated by maximizing the functional \(\mathcal {L}\), which is defined as
We detail this functional in Sect. 4.2. From the optimality condition inherent in the variational method, the variational distribution that maximizes \(\mathcal {L}\) must satisfy \(q(\varvec{\pi }) \propto \exp \left( \mathbb {E}_{q(\varvec{\varphi })q(Y, Z) } \left[ \log P(X, W, Y, Z, \theta ) \right] \right) \), \(q(\varvec{\varphi } ) \propto \exp \bigl ( \mathbb {E}_{q(\varvec{\pi })q(Y, Z)} \bigl [ \log \) \(P(X, W, Y, Z, \theta ) \bigr ] \bigr )\) and \(q(Y,Z) \propto \exp \left( \mathbb {E}_{q(\varvec{\pi })q(\varvec{\varphi })} \left[ \log P(X, W, Y, Z, \theta ) \right] \right) \).
For the Gaussian mixture models (GMM), \(q(\varvec{\pi }), q(\varvec{\mu }, \varvec{\lambda }), q(Y, Z)\) follow Dirichlet, Gaussian-gamma and mixture of truncated Gaussian, respectively:
where \(\bar{z}_{ik}=s_{ik}\), \(\bar{\lambda }_k = a_k / b_k\), \(\mathbb {E}_q [\log \pi _k]=\psi (\alpha _k) - \psi (\sum _{k'}\alpha _{k'})\), \(\mathbb {E}_q [\log \lambda _k]=\psi (a_k) - \log (b_k)\) and \(\psi (\cdot )\) is the digamma function. Moreover, \(\bar{y}^{\ell }_{ik}, \bar{y}^{g}_{ik}, \bar{y}^{\ell (2)}_{ik}, \bar{y}^{g(2)}_{ik}\) are the moments of truncated Gaussian distribution:
The above terms are derived using the mean and variance of truncated Gaussian distribution \(\mathcal {TN}(x | \mu , \sigma ^2, a, b)\) [17]:
where \(\alpha = \frac{a-\mu }{\sigma }\), \(\beta = \frac{b-\mu }{\sigma }\) and, \(\phi \) and \(\varPhi \) is the PDF and CDF of standard normal.
VBCM for GMM repeats the above parameter update following Eqs. (19)–(27). Algorithm 1 shows a pseudo code. The objective \(\mathcal {L}\) monotonically increases with the updates and the algorithm converges to (local) minima.
There are two main differences from standard VB and VBCM: (i) Use of CDF in updating q(Y, Z) in Eq. (26). (ii) Use of the moments of truncated distribution in Eqs. (28)–(31). Both differences are needed to deal with censored samples. We emphasize that, if the data contains no censored samples, VBCM reduces to VB. Therefore, VBCM can be seen as the generalized form of VB.

4.2 Evidence Lower Bound and Model Selection
The objective functional used in VBCM (and thus VB) is an important quantity since it can be used for model selection, i.e., determination of the number of components, K. Because the functional is a lower bound of (logarithm of) Evidence, It can be seen as quantifying the goodness of the model [18]. Although Evidence is not analytically tractable, the functional for VB, which is referred to as Evidence Lower BOund (ELBO), is analytically tractable in many cases.
Also, we show that ELBO, which is defined as Eq. (18), is analytically tractable for VBCM. By expanding the term \(\log P(X,W, Y, Z | \varTheta )\) and \(\log q(Y, Z)\), ELBO is written as
Since the final term \(\mathbb {E}_{q}[\log P(\varTheta ) - \log q(\varvec{\pi })q(\varvec{\varphi })]\) has analytic form, ELBO for VBCM is an analytically tractable quantity. In the experiments, we use ELBO in model selection.
4.3 Predictive Distribution
VB, and also VBCM, estimates the variational distribution of the parameter \(q(\varTheta )=q(\varvec{\pi })q(\varvec{\varphi })\), in other words, the parameter uncertainty is estimated. Such uncertainty is used for prediction following the Bayesian approach by using predictive distribution, which is defined as
This distribution differs from the model distribution in general. When the model is GMM, the predictive distribution is the mixture of Student-t’s distribution [19]:
where \(\mathrm {St}\) is the PDF of Student-t’s distribution:
As shown in Fig. 2, Student-t’s distribution has, compared to Gaussian distributions, a long tail, and converges to Gaussian in the limit \(\nu \rightarrow \infty \). Therefore, when the number of samples belonging to a component, \(N_k\), is small, which means \(2a_k\) is small, the component distribution has a long tail reflecting parameter uncertainty; it converges to Gaussian as \(N_k\) goes to infinity. Note that this property does not hold in the non-Bayesian approach using plug-in distribution
In the experiments we use the above predictive distributions for evaluation.
5 Extensions
5.1 Generalization for Exponential Family Mixtures (EFM)
In this section, we generalize the algorithm presented in the previous section. Here, we first show the VB algorithm for any mixture model whose component belongs to the exponential family. Following the previous section, the variational distributions of EFM \(q(\varvec{\pi })\), \(q(\varvec{\eta })\), and q(Y, Z) are given by Dirichlet, conjugate posterior and mixture of truncated exponential family distribution, respectively.
where \(\bar{\eta }_k\) and \(\mathbb {E}_q [ A(\eta _k)]\) for exponential/Poisson distribution is shown in Table 1. \(\bar{T}^{\ell }_{ik}, \bar{T}^{g}_{ik}\) is the expectation of sufficient statistics w.r.t. truncated exponential family:
Similar to GMM, (i) CDF is used in Eq. (41) and (ii) expectation of sufficient statistics w.r.t. truncated distribution is used in Eq. (43). VBCM for EFM is the algorithm that performs iterative updating following Eqs. (37)–(42). It is guaranteed that objective \(\mathcal {L}\) increases monotonically and converges.
We used the analytic form of the moments of truncated distribution in GMM (Eqs. (28)–(31)). However, truncated distributions are not well supported in popular statistical librariesFootnote 3 and it is desirable to develop a general algorithm that can be easily applied to any (exponential family) mixture model. Therefore, we investigate the approach that eliminates the need to know its analytic form in the next subsection.
5.2 Stochastic Algorithm
The key idea that permits VBCM to be used without demanding the analytic form of the expectation of sufficient statistics w.r.t. truncated distribution is to use stochastic sampling such as importance sampling [20]. This approach yields the VBCM stochastic algorithm, called here stochastic VBCM (SVBCM). Developing the stochastic VB algorithm itself is a important topic [7,8,9]. The term “stochastic” mainly means, in existing studies, that parameter update uses a part of stochastically selected/generated training data; its use makes the algorithm more flexible. Therefore, we develop SVBCM which combine the existing approach with stochastic computation of the expectation of sufficient statistics.

The proposed SVBCM algorithm is described in Algorithm 2. The algorithm considers that, each (algorithmic) time step t, sees the arrival of new data \((x_t, w_t)\). The new data may be observed samples or censored samples. When the new data arrive, the parameters of \(q(z_t)\), \(s_t\), is computed and sample \(\tilde{z}_t\) using \(q(z_t)\). If the new data are observed samples, \(\tilde{T}_{tk}\) is set to \(T(x_t)\) and otherwise \(\tilde{T}_{tk}\) is set to the value approximating \(\bar{T}^{\ell }_{tk}\) or \(\bar{T}^{g}_{tk}\) which is computed using any sampling scheme such as importance sampling. Next, we compute temporal parameters \(\tilde{\alpha }, \tilde{\xi }, \tilde{\nu }\). These are interpreted as those computed using Eqs. (37), (38) if all training data are new data, i.e., \(x_i=x_t, w_i=w_t\) \((\forall i)\). Finally, the parameters of \(q(\pi )\), \(q(\eta )\) are updated by taking the weighted average of \(\tilde{\alpha }, \tilde{\xi }, \tilde{\nu }\) and the current parameter. The weight \(\rho _t\) has the role of controlling learning speed. Following [8], we use \(\rho _t = (\varsigma +t)^{-\kappa }\) in the experiments, where \(\varsigma \ge 0\), and \(\kappa \in (0.5,1)\) are the control parameters.
Algorithm 2 is valid in the mini-batch setting where multiple data \(\{(x_t, w_t)\}^{S}_{t=1}\) arrive at once by modifying the update of temporal parameter as follows: \( \tilde{\alpha }_k = \alpha _0 + (N/S) \sum _{t} \tilde{z}_{tk}, \tilde{\xi }_{k} = \xi _0 + (N/S) \sum _{t} \tilde{z}_{tk}\tilde{T}_{tk}, \tilde{\nu }_k=\nu _0 + (N/S) \sum _{t} \tilde{z}_{tk} \), where S is the mini-batch size. If \(S=N\) and \(\rho _t=1.0~(\forall t)\) the algorithm is almost equivalent to the batch algorithm.
The update of variational distribution \(q(\pi )\), \(q(\eta )\) at final step of the algorithm can be seen as the natural gradient [10] of per-sample ELBO \(\mathcal {L}^{per}(x_t, w_t)\):
Note that summation over samples equals ELBO, \(\sum \nolimits ^N_{i=1}\mathcal {L}^{per}(x_i, w_i) = \mathcal {L}\).
Theorem 1
The update of stochastic VBCM is the (stochastic) natural gradient of per-sample ELBO \(\mathcal {L}^{per}(x_t, w_t)\).
Proof. We use the relationFootnote 4 \(\bar{\eta } = -\frac{\partial }{\partial \xi } \log \mathcal {Z}(\xi , \nu )\), \(\mathbb {E}_{q(\eta )}[A(\eta )] = \frac{\partial }{\partial \nu } \log \mathcal {Z}(\xi , \nu )\). Since \(\frac{\partial \log F(C| \eta )}{\partial \eta } = \frac{1}{F(C| \eta )} \int ^C_{-\infty }\frac{\partial f(x| \eta )}{\partial \eta } dx = \mathbb {E}_{f_{tr}(x|\eta , -\infty , C)}[T(x)] - \mathbb {E}_{f(x|\eta )}[T(x)]\), the partial derivative of \(\mathcal {L}\) w.r.t. \(\xi _k\) and \(\nu _k\) are written as
It follows that the update for \(\xi _k, \eta _k\) is the stochastic natural gradient of \(\mathcal {L}^{per}\):

The proof of \(\alpha _k\) is analogous. \(\square \)
Therefore, SVBCM can estimate variational distributions efficiently.
5.3 Predictive Distribution
The predictive distribution of EFM is shown at the end of this section. It is known the predictive distribution Eq. (33) for EFM is given by
where \(\mathcal {Z}\) is the normalizer of conjugate prior (Table 1). When the models are EMM/PMM, whose components are exponential/Poisson distribution, the above predictive distribution is the mixture of gamma-gamma/negative binomial distribution (e.g., [21]),
where \(\mathrm {GG}\) and \(\mathrm {NB}\) is the PDF of the gamma-gamma distribution and negative binomial distribution, respectivelyFootnote 5. The above predictive distributions are used in the experimentsFootnote 6.
6 Experiments
6.1 Setting
This section confirms the properties and predictive performance of VBCM.
Synthetic Data: We prepared three synthetic data set, gmm, emm and pmm, using manually made true distributions, GMM, EMM and PMM. We set the true number of components to \(K^*=2\) and set the true mixing ratio to \(\pi ^*=(1/2,1/2)\). The true component parameters were set to \((\mu _1, \mu _2)=(-3.0,3.0)\), \((\lambda _1, \lambda _2)=(1.0,1.0)\) for gmm, \((\lambda _1, \lambda _2)=(0.3,3.0)\) for emm, and \((\lambda _1, \lambda _2)=(1.0,5.0)\) for pmm, respectively. We randomly generated 10 pairs of training and test data using the true distributions. The thresholds used in censoring gmm, emm and pmm were set to \((C^L_i, C^R_i)=(-4.0, 4.0)\), \((-\infty , 4.0)\) and \((-\infty , 6.0)\) for all i, respectively. The number of samples in each test data was 10000.
Real Survival Data: We also used two publicity available survival data sets, Rossi et al. [22]’s criminal recidivism data (rossi) and north central cancer treatment group (NCCTG)’s lung cancer data (ncctg)Footnote 7. rossi is data pertaining to 432 convicts who were released from Maryland state prisons in the 1970s and who were followed for one year after release. The data contains the week of first arrest after release or censoring and we used the week information as the observed variable. ncctg is the survival data of patients with advanced lung cancer in NCCTG and we used the survival time information. rossi and ncctg contain, approximately, 74% and 28% censored samples, respectively. We standardized the data and prepared five data sets by dividing the data into five, using 80% of the data as training and the remaining 20% as test.
Baseline: We compare VBCM with three existing algorithms, EM, VB and EMCM. EM and VB use observed samples and do not use censored samples. EMCM is the EM algorithm that can use censored samples for learning mixture models [14, 15]. We applied all algorithms with GMM to gmm, rossi and ncctg, with EMM to emm, and with PMM to pmm. We used the predictive distribution described by Eq. (33) for VB and VBCM and Eq. (36) for EM and EMCM.
Evaluation Metric: To evaluate predictive performance, we use the test log likelihood metric (larger values are better). Since test data contains censored data, based on Eq. (17), test log-likelihood is defined as

where \(\{x^{te}_{i}\}^{N_{te}}_{i=1}, \{w^{te}_i\}^{N_{te}}_{i=1}\) is the test data and \(N_{te}\) is the number of test data.
6.2 Result
Algorithm Behavior: Figure 5(a)(b) shows the convergence behavior of ELBO. It is confirmed that the VBCM converges within 20 iterations and stochastic algorithm (SVBCM) with mini-batch size \(S=10, 20\) also converges to the nearly optimal resultFootnote 8. These indicate the effectiveness of VBCM and SVBCM as a estimation algorithm for mixture models. Figure 5(c) shows that ELBO is maximized when K corresponds to the true \(K=K^*=2\). This indicates the validity of ELBO as a model selection criterion.
Behavior of VBCM for gmm (\(N=100, K=5\)). The convergence behaviors of (a) VBCM and (b) stochastic VBCM (SVBCM) with different runs are shown. (c) ELBO at converged parameter in each VBCM run for various K. Symbols “ ” are plotted with small horizontal perturbations to avoid overlap and the blue line connects maximum values. ELBO is maximized when K is equals to the true value \(K=K^*=2\).
” are plotted with small horizontal perturbations to avoid overlap and the blue line connects maximum values. ELBO is maximized when K is equals to the true value \(K=K^*=2\).
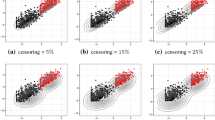
Synthetic Data Result: Figure 6 (a)(b)(c) shows the predictive performance for synthetic data. VBCM outperforms the existing algorithms. More precisely, the performance of VBCM is much better than VB and EM. This implies that the use of censored samples strengthens the superiority of VBCM. This is also confirmed by Fig. 7. Figure 7a shows that VB yielded components whose mean was nearer to the origin than the true value while VBCM predictions were close to the true distributions. This occurs because VB ignores the censored samples. Comparing VBCM with EMCM, VBCM is superior when the number of training data is small. This seems to be caused by using the Bayesian approach for making predictions; it integrates parameter uncertainty.
Real Survival Data Result: Figures 6(d)(e) show the predictive performance with real survival data. Similar to the synthetic data result, VBCM outperforms the existing algorithms. Since rossi contains more censored samples than ncctg, VBCM and EMCM attain better performance with rossi than VB or EM. The difference is small in ncctg and the performances of VBCM and VB are comparable when the number of training data (ratio) is small; VBCM and EMCM have comparable performance when the number of training data is large. These results imply that VBCM inherits the good points of VB and EMCM.
7 Conclusion
In this study, we proposed VBCM, a generalized VB algorithm that can well handle censored data using mixture models. The proposed algorithm can be applied to any mixture model whose component distribution belongs to exponential family and experiments on three synthetic data and two real data sets confirmed its effectiveness. Promising future work is to extend VBCM to support Dirichlet process mixture models [23].
Notes
- 1.
We set
 ,
, 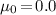 ,
,  ,
,  ,
, 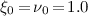 in the experiments.
in the experiments. - 2.
If the i-th sample belongs to the k-th component, \(z_{ik}=1\) and \(z_{ik'}=0\) for all \(k'\ne k\).
- 3.
For example, scipy.stats in python only supports truncated normal distribution and truncated exponential distribution.
- 4.
Derived from \(\mathcal {Z}(\xi , \nu )\) is a normalizer, \(\mathcal {Z}(\xi , \nu )^{} = \bigl ( \int \exp \{ \eta \xi - \nu A(\eta ) \} d \eta \bigr )^{-1}\).
- 5.
\(\mathrm {GG}(x|a,r,b) = \frac{r^a}{\varGamma (a)} \frac{\varGamma (a+b)}{\varGamma (b)} \frac{x^{b-1}}{(r+x)^{(a+b)}}\), \(\mathrm {NB}(k|r,p)= \frac{\varGamma (k+r)}{k!\varGamma (r)} p^k (1-p)^r\).
- 6.
We found that gamma-gamma distributions are not implemented in standard statistical libraries and so the experiment uses the plug-in distribution \(f(x|\bar{\eta }_k)\) as the component of predictive distribution of EMM.
- 7.
Available at e.g., R survival package and python lifeline package.
- 8.
The other control parameters were \(\varsigma _0= 10.0, \kappa =0.6\). The stochastic algorithm uses randomly chosen training data repeatedly.
References
Kleinbaum, D.G., Klein, M.: Survival Analysis, vol. 3. Springer, New York (2010)
Park, C.: Parameter estimation from load-sharing system data using the expectation–maximization algorithm. IIE Trans. 45(2), 147–163 (2013)
Jung, E.Y., Baek, C., Lee, J.D.: Product survival analysis for the app store. Mark. Lett. 23(4), 929–941 (2012)
Lu, J.: Predicting customer churn in the telecommunications industry—an application of survival analysis modeling using SAS. SAS User Group International (SUGI27) Online Proceedings, pp. 114–27 (2002)
Nagano, S., Ichikawa, Y., Takaya, N., Uchiyama, T., Abe, M.: Nonparametric hierarchal Bayesian modeling in non-contractual heterogeneous survival data. In: KDD, pp. 668–676 (2013)
Attias, H.: Inferring parameters and structure of latent variable models by variational Bayes. In: UAI, pp. 21–30 (1999)
Sato, M.A.: Online model selection based on the variational Bayes. Neural Comput. 13(7), 1649–1681 (2001)
Hoffman, M., Bach, F.R., Blei, D.M.: Online learning for latent dirichlet allocation. In: NIPS, pp. 856–864 (2010)
Hoffman, M.D., Blei, D.M., Wang, C., Paisley, J.: Stochastic variational inference. J. Mach. Learn. Res. 14(1), 1303–1347 (2013)
Amari, S.I.: Natural gradient works efficiently in learning. Neural Comput. 10(2), 251–276 (1998)
Pölsterl, S., Navab, N., Katouzian, A.: Fast training of support vector machines for survival analysis. In: Appice, A., Rodrigues, P.P., Santos Costa, V., Gama, J., Jorge, A., Soares, C. (eds.) ECML PKDD 2015. LNCS (LNAI), vol. 9285, pp. 243–259. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-23525-7_15
Fernández, T., Rivera, N., Teh, Y.W.: Gaussian processes for survival analysis. In: NIPS, pp. 5021–5029 (2016)
Dempster, A.P., Laird, N.M., Rubin, D.B.: Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 39(1), 1–38 (1977)
Chauveau, D.: A stochastic EM algorithm for mixtures with censored data. J. Stat. Plan. Inference 46(1), 1–25 (1995)
Lee, G., Scott, C.: EM algorithms for multivariate gaussian mixture models with truncated and censored data. Comput. Stat. Data Anal. 56(9), 2816–2829 (2012)
Jordan, M.I., Ghahramani, Z., Jaakkola, T.S., Saul, L.K.: An introduction to variational methods for graphical models. Mach. Learn. 37(2), 183–233 (1999)
Johnson, N., Kotz, S., Balakrishnan, N.: Continuous Univariate Probability Distributions, vol. 1. Wiley, Hoboken (1994)
MacKay, D.J.: Information Theory, Inference and Learning Algorithms. Cambridge University Press, Cambridge (2003)
Murphy, K.P.: Conjugate Bayesian analysis of the univariate Gaussian: a tutorial (2007). http://www.cs.ubc.ca/~murphyk/Papers/bayesGauss.pdf
Bishop, C.M.: Pattern Recognition and Machine Learning. Springer, New York (2006)
Bernardo, J.M., Smith, A.F.: Bayesian Theory, vol. 405. Wiley, Hoboken (2009)
Rossi, P.H., Berk, R.A., Lenihan, K.J.: Money, Work, and Crime: Experimental Evidence. Academic Press, Cambridge (1980)
Blei, D.M., Jordan, M.I.: Variational inference for dirichlet process mixtures. Bayesian Anal. 1(1), 121–143 (2006)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Kohjima, M., Matsubayashi, T., Toda, H. (2019). Variational Bayes for Mixture Models with Censored Data. In: Berlingerio, M., Bonchi, F., Gärtner, T., Hurley, N., Ifrim, G. (eds) Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2018. Lecture Notes in Computer Science(), vol 11052. Springer, Cham. https://doi.org/10.1007/978-3-030-10928-8_36
Download citation
DOI: https://doi.org/10.1007/978-3-030-10928-8_36
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-10927-1
Online ISBN: 978-3-030-10928-8
eBook Packages: Computer ScienceComputer Science (R0)











 ,
, 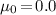 ,
,  ,
,  ,
, 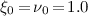 in the experiments.
in the experiments.