Abstract
We present a criterion for the arithmetic discrete hyperplane  to be facet connected when \(\theta \) is the connecting thickness
to be facet connected when \(\theta \) is the connecting thickness  . We encode the shift \(\mu \) in a numeration system associated with the normal vector
. We encode the shift \(\mu \) in a numeration system associated with the normal vector  and we describe an incremental construction of the plane based on this encoding. We deduce a connectedness criterion and we show that when the Fully Subtractive algorithm applied to
and we describe an incremental construction of the plane based on this encoding. We deduce a connectedness criterion and we show that when the Fully Subtractive algorithm applied to  has a periodic behaviour, the encodings of shifts \(\mu \) for which the plane is connected may be recognised by a finite state automaton.
has a periodic behaviour, the encodings of shifts \(\mu \) for which the plane is connected may be recognised by a finite state automaton.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Discrete hyperplane
- Connectedness
- Connecting thickness
- Fully subtractive algorithm
- Numeration system
- Finite state automaton
1 Introduction
The arithmetic discrete hyperplane with normal vector  , shift \(\mu \in \mathbb {R}\) and thickness \(\theta \in \mathbb {R}\), is the set of points in \(\mathbb {Z}^d\) defined by
, shift \(\mu \in \mathbb {R}\) and thickness \(\theta \in \mathbb {R}\), is the set of points in \(\mathbb {Z}^d\) defined by

where \(\langle \cdot , \cdot \rangle \) denotes the usual scalar product on \(\mathbb {R}^d\) [1, 9].
For \(\kappa \) in \(\{0,\dots ,d-1\}\), two points  and
and  in \(\mathbb {Z}^d\) are \(\kappa \)-neighbours if and only if
in \(\mathbb {Z}^d\) are \(\kappa \)-neighbours if and only if  and
and  . In particular,
. In particular,  and
and  are \((d-1)\)-neighbours if and only if
are \((d-1)\)-neighbours if and only if  for some i, where
for some i, where  is the canonical basis of \(\mathbb {R}^d\). A set \(S \subset \mathbb {Z}^d\) is \(\kappa \)-connected if and only if for all
is the canonical basis of \(\mathbb {R}^d\). A set \(S \subset \mathbb {Z}^d\) is \(\kappa \)-connected if and only if for all  and
and  in S, there exists a path
in S, there exists a path  in S where
in S where  and
and  are \(\kappa \)-neighbours for all \(i=1,\dots ,n-1\).
are \(\kappa \)-neighbours for all \(i=1,\dots ,n-1\).
Many works have been devoted to determining the conditions under which the hyperplane  is \(\kappa \)-connected, see [3,4,5, 7] among others. The set of thicknesses \(\theta \) for which
is \(\kappa \)-connected, see [3,4,5, 7] among others. The set of thicknesses \(\theta \) for which  is non-empty and \(\kappa \)-connected is a right unbounded interval of \(\mathbb {R}^+\) the lower bound of which, denoted by
is non-empty and \(\kappa \)-connected is a right unbounded interval of \(\mathbb {R}^+\) the lower bound of which, denoted by  , is called the \(\kappa \)-connecting thickness of
, is called the \(\kappa \)-connecting thickness of  with shift \(\mu \). In this work, we consider only the \((d-1)\)-connectedness which is the only case where a general algorithm is known to compute the \(\kappa \)-connecting thickness. We shall therefore drop the subscript \(\kappa \) in all denotations and speak of connectedness and connecting thickness.
with shift \(\mu \). In this work, we consider only the \((d-1)\)-connectedness which is the only case where a general algorithm is known to compute the \(\kappa \)-connecting thickness. We shall therefore drop the subscript \(\kappa \) in all denotations and speak of connectedness and connecting thickness.
By definition of  ,
,  is empty or disconnected for all
is empty or disconnected for all  and is non-empty and connected for all
and is non-empty and connected for all  . The question which arises naturally is whether
. The question which arises naturally is whether  is connected or not. In [5], we showed that
is connected or not. In [5], we showed that  is almost always disconnected, excepted when
is almost always disconnected, excepted when  belongs to some specific set which was proven to be Lebesgue negligible by Kraaikamp and Meester [8]. In this case,
belongs to some specific set which was proven to be Lebesgue negligible by Kraaikamp and Meester [8]. In this case,  which does not actually depend on \(\mu \) and will therefore be denoted simply by
which does not actually depend on \(\mu \) and will therefore be denoted simply by  . We showed that for such vectors,
. We showed that for such vectors,  may be connected or not, depending on the value of \(\mu \). In particular,
may be connected or not, depending on the value of \(\mu \). In particular,  is always connected while
is always connected while  is always disconnected.
is always disconnected.
In the present work, we investigate the general case where \(\mu \) is arbitrary. We first set our main definitions and recall how the connecting thickness  may be computed by means of the Fully Subtractive algorithm. Then we introduce a numeration system associated with the normal vector
may be computed by means of the Fully Subtractive algorithm. Then we introduce a numeration system associated with the normal vector  , in which the shift \(\mu \) may be encoded as an infinite sequence in \(\{0,1\}^\omega \). Based on this encoding, we describe an incremental construction of
, in which the shift \(\mu \) may be encoded as an infinite sequence in \(\{0,1\}^\omega \). Based on this encoding, we describe an incremental construction of  and we show that, provided that the encoding of \(\mu \) has some property called bi-admissibility, we actually construct the connected component of
and we show that, provided that the encoding of \(\mu \) has some property called bi-admissibility, we actually construct the connected component of  in
in  . We first give a purely geometrical connectedness criterion based on a particular projection of a connected component of
. We first give a purely geometrical connectedness criterion based on a particular projection of a connected component of  . Then we investigate specific patterns occurring in the encoding of \(\mu \) and we introduce the notion of minimal interior patterns which allows us to deduce a more operational connectedness criterion. Finally, we study the case where the Fully Subtractive algorithm applied to the normal vector
. Then we investigate specific patterns occurring in the encoding of \(\mu \) and we introduce the notion of minimal interior patterns which allows us to deduce a more operational connectedness criterion. Finally, we study the case where the Fully Subtractive algorithm applied to the normal vector  has a periodic behaviour. We show that in this case, the language of encodings of shifts \(\mu \) for which
has a periodic behaviour. We show that in this case, the language of encodings of shifts \(\mu \) for which  is connected is a regular language which may therefore be recognised by a finite state automaton.
is connected is a regular language which may therefore be recognised by a finite state automaton.
2 Preliminaries
The \((d-1)\)-connecting thickness may be computed by means of the Fully Subtractive algorithm as follows. Let  be the vector \((1,\dots ,1)\). For each \(k \in \{1,\dots ,d\}\), we define \(\gamma _k\) as
be the vector \((1,\dots ,1)\). For each \(k \in \{1,\dots ,d\}\), we define \(\gamma _k\) as

Given a vector  , the algorithm computes a sequence of pairs
, the algorithm computes a sequence of pairs  where
where  . For all \(n\ge 1\), if
. For all \(n\ge 1\), if  has at least two components and no component is 0 then
has at least two components and no component is 0 then  where \(\delta _n\) is the index of a minimal coordinate of
where \(\delta _n\) is the index of a minimal coordinate of  . If some component becomes 0 in the process, it is simply erased and we continue with
. If some component becomes 0 in the process, it is simply erased and we continue with  . If
. If  has only one component left, the algorithm stops. This sequence has the property that for all \(n\ge 1\),
has only one component left, the algorithm stops. This sequence has the property that for all \(n\ge 1\),  is non-empty and connected if and only if
is non-empty and connected if and only if  is non-empty and connected [4, 5].
is non-empty and connected [4, 5].
If the process terminates with  , which happens if and only if
, which happens if and only if  for some integral vector
for some integral vector  [5], then
[5], then  . Otherwise,
. Otherwise,  converges to
converges to  and
and  which does not depend on \(\mu \) and will therefore be denoted simply by
which does not depend on \(\mu \) and will therefore be denoted simply by  .
.
The set \(\mathcal {K}_d\) is defined as the set of vectors  such that the Fully Subtractive algorithm erases no component and
such that the Fully Subtractive algorithm erases no component and  for all \(n\ge 1\). If
for all \(n\ge 1\). If  then
then  and
and  . We proved in [5] that
. We proved in [5] that  may be connected only if for some \(n \ge 1\),
may be connected only if for some \(n \ge 1\),  belongs to some \(\mathcal {K}_{d'}\), in which case,
belongs to some \(\mathcal {K}_{d'}\), in which case,  for all \(m\ge n\). Kraaikamp and Meester proved in [8] that \(\mathcal {K}_d\) is Lebesgue negligible when \(d\ge 3\).
for all \(m\ge n\). Kraaikamp and Meester proved in [8] that \(\mathcal {K}_d\) is Lebesgue negligible when \(d\ge 3\).
From now on,  is a vector in \(\mathcal {K}_d\) with \(d \ge 3\) and
is a vector in \(\mathcal {K}_d\) with \(d \ge 3\) and  .
.
Given the sequence of vectors  computed by the Fully Subtractive algorithm, we define the directive sequence \(\Delta = (\delta _n)_{n\ge 1}\) where \(\delta _n\) is the index of the minimal component of
computed by the Fully Subtractive algorithm, we define the directive sequence \(\Delta = (\delta _n)_{n\ge 1}\) where \(\delta _n\) is the index of the minimal component of  . This minimal component is unique since otherwise
. This minimal component is unique since otherwise  would have a zero component, which is impossible by definition of \(\mathcal {K}_d\). The sequence \(\Delta \) is therefore well defined. For all \(n\ge 1\) we set \(\Delta ^n = \delta _n\delta _{n+1}\dots \) and
would have a zero component, which is impossible by definition of \(\mathcal {K}_d\). The sequence \(\Delta \) is therefore well defined. For all \(n\ge 1\) we set \(\Delta ^n = \delta _n\delta _{n+1}\dots \) and  .
.
To each vector  in \(\mathcal {K}_d\) is associated a unique sequence \(\Delta \) which has the property that each \(k \in \{1,\dots ,d\}\) occurs infinitely many times in \(\Delta \). Conversely, each sequence \(\Delta \in \{1,\dots ,d\}^\omega \) in which each \(k\in \{1,\dots ,d\}\) occurs infinitely many times is associated with a unique direction in \(\mathcal {K}_d\), which means that the vector
in \(\mathcal {K}_d\) is associated a unique sequence \(\Delta \) which has the property that each \(k \in \{1,\dots ,d\}\) occurs infinitely many times in \(\Delta \). Conversely, each sequence \(\Delta \in \{1,\dots ,d\}^\omega \) in which each \(k\in \{1,\dots ,d\}\) occurs infinitely many times is associated with a unique direction in \(\mathcal {K}_d\), which means that the vector  is determined by \(\Delta \) up to a multiplicative factor [5, 6].
is determined by \(\Delta \) up to a multiplicative factor [5, 6].
For all \(n\ge 1\), we set  and
and  where
where  is the transpose of \(\gamma _i\). We have
is the transpose of \(\gamma _i\). We have  and for all \(n\ge 1\), \(\Omega ^n=\sum _{i\ge n}\theta _i\). In particular, \(\Omega = \Omega ^1 = \sum _{i\ge 1} \theta _i\).
and for all \(n\ge 1\), \(\Omega ^n=\sum _{i\ge n}\theta _i\). In particular, \(\Omega = \Omega ^1 = \sum _{i\ge 1} \theta _i\).
We denote by \(\mathbb {Z}^\omega \) the set of sequences of integers and by \(\mathbb {Z}^\star 0^\omega \) the set of sequences with finitely many non-zero terms. The length of \(\sigma \in \mathbb {Z}^\omega \), denoted by \(|\sigma |\), is the smallest index \(n\ge 0\) such that \(\forall m>n,\ \sigma _m=0\). If no such index exists then \(|\sigma |=+\infty \). If \(\sigma \) is a finite sequence then \(|\sigma |\) denotes its natural length. We define the mappings \(\psi ^\Delta \) on \(\mathbb {Z}^\star 0^\omega \) by \(\psi ^\Delta (\sigma ) = \sum _n \sigma _n\,T^\Delta _n\) and  on \(\mathbb {Z}^\omega \) by
on \(\mathbb {Z}^\omega \) by  when this sum converges. It is in particular the case when \(\sigma \) is bounded. Given \(\sigma \in \{0,1\}^\omega \) we denote by \(\widetilde{\sigma }\) the sequence obtained by replacing zeros with ones and ones with zeros in \(\sigma \). We have
when this sum converges. It is in particular the case when \(\sigma \) is bounded. Given \(\sigma \in \{0,1\}^\omega \) we denote by \(\widetilde{\sigma }\) the sequence obtained by replacing zeros with ones and ones with zeros in \(\sigma \). We have  . When \(\sigma \in \mathbb {Z}^\star 0^\omega \), we have
. When \(\sigma \in \mathbb {Z}^\star 0^\omega \), we have  . These definitions are naturally extended to the case where \(\sigma \in \mathbb {Z}^\star \) by \(\psi ^\Delta (\sigma ) = \psi ^\Delta (\sigma 0^\omega )\) and
. These definitions are naturally extended to the case where \(\sigma \in \mathbb {Z}^\star \) by \(\psi ^\Delta (\sigma ) = \psi ^\Delta (\sigma 0^\omega )\) and  .
.
If \(\xi ^{\Delta ,k}_n\) is the index of the \(n^{\mathrm {th}}\) occurrence of k in \(\Delta \), we recall [5, 6] that for all \(k\in \{1,\dots ,d\}\) and for all \(n\ge 1\), we have
In the sequel, we symmetrise our problem by studying the connectedness of  so that
so that  . We have
. We have  if and only if there exists
if and only if there exists  such that
such that  . In this case, we have
. In this case, we have  which is disconnected when \(d\ge 3\) [5]. In all other cases,
which is disconnected when \(d\ge 3\) [5]. In all other cases,  is connected if and only if
is connected if and only if  is.
is.
We may also reduce the study to the case where \(\mu \in [0;\Omega ]\). Indeed, if \(q=\left\lfloor {\mu /v_1}\right\rfloor \) and \(\mu '=\mu -q\,v_1\), then  , and
, and  . Thus
. Thus  is a translate of
is a translate of  by an integral vector and is connected if and only if
by an integral vector and is connected if and only if  is.
is.
3 \(\Delta \)-Numeration System
We showed in [5] that  , meaning that
, meaning that  . We now extend this result.
. We now extend this result.
Theorem 1

To prove this theorem, we need a technical lemma.
Lemma 2
-
1.
\(2 \theta _1 < \Omega \).
-
2.
If \(d \ge 3\), \(j < n\) and \(\delta _j \ne \delta _n\), then \(\theta _j + \sum _{i=1}^n \theta _i > \Omega \).
-
3.
If \(d\ge 3\) and
 then \(v_i+v_j > \Omega \) for all \(i \ne j\).
then \(v_i+v_j > \Omega \) for all \(i \ne j\).
Proof of Theorem 1. The inclusion  is obvious since for all \(\sigma \in \{0,1\}^\omega \), we have
is obvious since for all \(\sigma \in \{0,1\}^\omega \), we have  .
.
Now let \(x \in [0;\Omega ]\), \(r_1 = x\) and for all \(n \ge 1\), \(r_{n+1} = r_n - \sigma _n\,\theta _n\) where \(\sigma _n = 1\) if \(r_n \ge \theta _n\) and \(\sigma _n=0\) otherwise. Then we have \(x = \sum _{k<n} \sigma _k\,\theta _k + r_n\) and \(r_n \in [0;\Omega ^{n}]\) for all n. Indeed, we obviously have \(r_n \ge 0\) for all n. By hypothesis, we have \(r_1 = x \in [0;\Omega ^{1}] = [0;\Omega ]\). Now, for \(n\ge 1\), assume that \(r_n \le \Omega ^{n}\) and let us show that \(r_{n+1} \le \Omega ^{n+1}\). If \(r_n < \theta _n\) then \(\sigma _n=0\) and \(r_{n+1} = r_n < \theta _n\). By Lemma 2 applied to  we get \(2\,\theta _n < \Omega ^{n}\) and thus \(\theta _n < \Omega ^{n}-\theta _n = \Omega ^{n+1}\). If \(r_n \ge \theta _n\), then \(\sigma _n=1\) and \(r_{n+1} = r_n-\theta _n \le \Omega ^{n}-\theta _n = \Omega ^{n+1}\).
we get \(2\,\theta _n < \Omega ^{n}\) and thus \(\theta _n < \Omega ^{n}-\theta _n = \Omega ^{n+1}\). If \(r_n \ge \theta _n\), then \(\sigma _n=1\) and \(r_{n+1} = r_n-\theta _n \le \Omega ^{n}-\theta _n = \Omega ^{n+1}\).
Since  and
and  , we have \(\lim _{n\rightarrow \infty } r_n = 0\) hence \(\lim _{n\rightarrow \infty } \sum _{k<n} \sigma _k\,\theta _k = \sum _{n\ge 1} \sigma _n\,\theta _n = x\). Then we have \(\sigma = (\sigma _n)_{n\ge 1} \in \{0,1\}^\omega \) and
, we have \(\lim _{n\rightarrow \infty } r_n = 0\) hence \(\lim _{n\rightarrow \infty } \sum _{k<n} \sigma _k\,\theta _k = \sum _{n\ge 1} \sigma _n\,\theta _n = x\). Then we have \(\sigma = (\sigma _n)_{n\ge 1} \in \{0,1\}^\omega \) and  . \(\square \)
. \(\square \)
The sequence \((\theta _n)_{n\ge 1}\) may be seen as the basis of a numeration system in which we can encode any \(\mu \in [0;\Omega ]\) as a sequence \(\overline{\mu }\in \{0,1\}^\omega \). Note that by considering a bi-infinite sequence \(\Delta \), we would define a full numeration system in which any non negative real number may be encoded as \(\sigma .\sigma '\) with \(\sigma \in \{0,1\}^\star \) and \(\sigma ' \in \{0,1\}^\omega \).
Definition 3
(\(\Delta \)-admissible sequence)
-
A sequence \(\sigma \in \{0,1\}^\omega \) is \(\Delta \)-admissible iff there does not exist \(k\in \{1,\dots ,d\}\) and an index \(n_0\) such that \(\sigma _n=0 \iff \delta _n = k\) for all \(n\ge n_0\).
-
A sequence \(\sigma \in \{0,1\}^\omega \) is \(\Delta \)-bi-admissible iff \(\sigma \) and \(\widetilde{\sigma }\) are \(\Delta \)-admissible.
-
If there exist k and \(n_0\) such that \(\sigma _n=0 \iff \delta _n = k\) for all \(n\ge n_0\), then k is unique. In this case, we say that \(\sigma \) is \(\Delta \)-non-admissible of type k.
A \(\Delta \)-non-admissible sequence is analogous to the writing \(1=0.9999\dots \) in the classical numeration system in base 10. For instance, if \(\Delta =(12213)^\omega \) then \(\sigma = 11001(01101)^\omega \) is \(\Delta \)-non-admissible of type 1. We have actually  . This principle is general: for all \(\Delta \)-non-admissible sequence \(\sigma \), a finite sequence \(\sigma '\) exists such that
. This principle is general: for all \(\Delta \)-non-admissible sequence \(\sigma \), a finite sequence \(\sigma '\) exists such that  .
.
Proposition 4
Let \(\sigma \in \{0,1\}^\omega \) be a \(\Delta \)-non-admissible sequence of type k, \(n_0\) such that \(\delta _{n_0}=k\) and \(\sigma _n = 0 \iff \delta _n = k\) for all \(n\ge n_0\). Then  .
.
Proof
For all \(n\ge 0\), let \(\zeta _n = \xi ^{\Delta ,k}_n\). Let \(r_0\) be such that \(n_0 = \zeta _{r_0}\) and for all \(r\ge r_0\), let \(\sigma ^{r} = \sigma _1\dots \sigma _{\zeta _r-1}1\). We have \(\sigma ^{r_0} = \sigma _1\dots \sigma _{n_0-1}1\) and by Eq. 2, for all \(r\ge r_0\),  . Then
. Then

and since  and
and  , we get the result at the limit. \(\square \)
, we get the result at the limit. \(\square \)
If a sequence \(\sigma \) is not \(\Delta \)-bi-admissible then, by applying this transformation to either \(\sigma \) or \(\widetilde{\sigma }\), we get in all cases a \(\Delta \)-bi-admissible sequence. Hence the corollary:
Corollary 5
For all \(\sigma \in \{0,1\}^\omega \), there exists a \(\Delta \)-bi-admissible sequence \(\sigma '\) such that  .
.
Definition 6
(\(\Delta \)-normalised sequence). A sequence \(\sigma \in \{0,1\}^\omega \) is \(\Delta \)-normalised if and only if it is \(\Delta \)-admissible and it does not contain a sub-sequence \(01^{k}\) with \(k\ge 1\) at a position i such that \(\delta _i=\delta _{i+k}\).
Proposition 7
For all \(\mu \in [0;\Omega ]\), there exists a unique \(\Delta \)-normalised sequence \(\sigma \in \{0,1\}^\omega \) such that  .
.
Definition 8
(\(\Delta \)-normal form). Given a sequence \(\sigma \in \mathbb {N}^\omega \) such that  , the unique \(\Delta \)-normalised sequence \(\sigma ' \in \{0,1\}^\omega \) such that
, the unique \(\Delta \)-normalised sequence \(\sigma ' \in \{0,1\}^\omega \) such that  is called the \(\Delta \)-normal form of \(\sigma \) and is denoted by \(\sigma \mathord \Downarrow ^\Delta \).
is called the \(\Delta \)-normal form of \(\sigma \) and is denoted by \(\sigma \mathord \Downarrow ^\Delta \).
Note that given a sequence \(\sigma \), there does not always exist a sequence \(\sigma '\) which is both \(\Delta \)-bi-admissible and \(\Delta \)-normalised and such that  . For instance, if \(\Delta =(123)^\omega \) then \(\sigma = (100)^\omega \) is \(\Delta \)-normalised but not \(\Delta \)-bi-admissible because \(\widetilde{\sigma } = (011)^\omega \) is not \(\Delta \)-admissible. Since the \(\Delta \)-normal form is unique, there is no \(\Delta \)-normalised and \(\Delta \)-bi-admissible sequence \(\sigma '\) such that
. For instance, if \(\Delta =(123)^\omega \) then \(\sigma = (100)^\omega \) is \(\Delta \)-normalised but not \(\Delta \)-bi-admissible because \(\widetilde{\sigma } = (011)^\omega \) is not \(\Delta \)-admissible. Since the \(\Delta \)-normal form is unique, there is no \(\Delta \)-normalised and \(\Delta \)-bi-admissible sequence \(\sigma '\) such that  .
.
4 Incremental Construction of 
In [5] and [6], we presented an incremental construction of  when \(\mu =0\). We now extend this construction to the case where \(\mu \) is arbitrary.
when \(\mu =0\). We now extend this construction to the case where \(\mu \) is arbitrary.
As said before, we may always reduce the study of the connectedness of  to the case where \(\mu \in [0;\Omega ]\). Then there exists a sequence \(\overline{\mu }= (\mu _i)_{i \ge 1} \in \{0,1\}^\omega \) such that
to the case where \(\mu \in [0;\Omega ]\). Then there exists a sequence \(\overline{\mu }= (\mu _i)_{i \ge 1} \in \{0,1\}^\omega \) such that  . We define the sequence \((\mathcal {S}^{\Delta ,\overline{\mu }}_n)_{n\ge 0}\) of subsets of \(\mathbb {Z}^d\) by
. We define the sequence \((\mathcal {S}^{\Delta ,\overline{\mu }}_n)_{n\ge 0}\) of subsets of \(\mathbb {Z}^d\) by  and for all \(n\ge 1\),
and for all \(n\ge 1\),

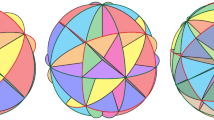
For example, let  where \(\alpha \in [0;1]\) and \(\alpha +\alpha ^2+\alpha ^3=1\). We have \(\Delta =(123)^\omega \). The picture below shows \(\mathcal {S}^{\Delta ,\overline{\mu }}_{12}\) for \(\overline{\mu }=(01)^\omega \) and \(\overline{\mu }=(011001)^\omega \). We have
where \(\alpha \in [0;1]\) and \(\alpha +\alpha ^2+\alpha ^3=1\). We have \(\Delta =(123)^\omega \). The picture below shows \(\mathcal {S}^{\Delta ,\overline{\mu }}_{12}\) for \(\overline{\mu }=(01)^\omega \) and \(\overline{\mu }=(011001)^\omega \). We have  and
and  . We shall see in Sect. 6 that
. We shall see in Sect. 6 that  is connected in the first case and disconnected in the second case.
is connected in the first case and disconnected in the second case.

We observe that the geometry of \(\mathcal {S}^{\Delta ,\overline{\mu }}_{n}\) does not seem to depend on \(\overline{\mu }\). Only the position with respect to the origin changes. Indeed, we have

Where \(\mathcal {S}^\Delta _n\) stands for \(\mathcal {S}^{\Delta ,0^\omega }_n\). For all \(\overline{\mu }\in \{0,1\}^\omega \) and all \(n \ge 0\), \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) is a translate of \(\mathcal {S}^\Delta _n\) by an integral vector, and therefore inherits topological properties of \(\mathcal {S}^\Delta _n\), especially the fact that \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) is symmetric, connected and circuit-free [5, 6].
Let \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) be the limit of the sequence \((\mathcal {S}^{\Delta ,\overline{\mu }}_n)_{n\ge 0}\). We have

and as an immediate corollary, we get that for all \(\overline{\mu }\in \{0,1\}^\omega \), \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) is connected and circuit-free.
When \(\mu =0\), we have  [5]. The next theorem establishes the relationship between \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) and
[5]. The next theorem establishes the relationship between \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) and  .
.
Theorem 9
If \(d\ge 3\), \(\overline{\mu }\in \{0,1\}^\omega \) is a \(\Delta \)-bi-admissible sequence and  , then \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) is the connected component of
, then \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) is the connected component of  in
in  .
.
Proof
(sketch). We observe that by hypothesis, we have \(\mu \in \left[ 0;\Omega \right] \) and thus  . Then we prove that any neighbour in
. Then we prove that any neighbour in  of a point
of a point  belongs to \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \). Let \(\Sigma ^{\overline{\mu }} = (\{0,1\}^\omega - \overline{\mu }) \cap \{-1,0,1\}^\star 0^\omega \), i.e. the set of sequences \(\sigma \in \{-1,0,1\}^\star 0^\omega \) such that \(\sigma +\overline{\mu }\in \{0,1\}^\omega \). We have \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty = \psi ^\Delta (\Sigma ^{\overline{\mu }})\). We consider a sequence \(\sigma \in \Sigma ^{\overline{\mu }}\) such that
belongs to \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \). Let \(\Sigma ^{\overline{\mu }} = (\{0,1\}^\omega - \overline{\mu }) \cap \{-1,0,1\}^\star 0^\omega \), i.e. the set of sequences \(\sigma \in \{-1,0,1\}^\star 0^\omega \) such that \(\sigma +\overline{\mu }\in \{0,1\}^\omega \). We have \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty = \psi ^\Delta (\Sigma ^{\overline{\mu }})\). We consider a sequence \(\sigma \in \Sigma ^{\overline{\mu }}\) such that  and we assume
and we assume  . Then we exhibit a sequence \(\tau \in \Sigma ^{\overline{\mu }}\) such that
. Then we exhibit a sequence \(\tau \in \Sigma ^{\overline{\mu }}\) such that  . \(\square \)
. \(\square \)
The fact that \(\overline{\mu }\) is \(\Delta \)-bi-admissible is crucial in the theorem above. Let us consider for instance \(\Delta =(123)^\omega \) and \(\overline{\mu }= (011)^\omega \). This sequence is \(\Delta \)-non-admissible of type 1 since for \(n\ge 1\), we have \(\mu _n=0 \iff \delta _n=1\). We have  and
and  hence
hence  . In this case,
. In this case,  which is connected and is therefore equal to the connected component of
which is connected and is therefore equal to the connected component of  . However, we may show that
. However, we may show that  where
where  is the connected component of
is the connected component of  in
in  which is disconnected. Similarly, \(\overline{\mu }= (100)^\omega \) is \(\Delta \)-admissible but not \(\Delta \)-bi-admissible since \(\widetilde{\overline{\mu }} = (011)^\omega \) which is not \(\Delta \)-admissible. In this case,
which is disconnected. Similarly, \(\overline{\mu }= (100)^\omega \) is \(\Delta \)-admissible but not \(\Delta \)-bi-admissible since \(\widetilde{\overline{\mu }} = (011)^\omega \) which is not \(\Delta \)-admissible. In this case,  and we have
and we have  which is connected. But
which is connected. But  .
.
Proposition 10
If \(\overline{\mu }\) is a \(\Delta \)-non-admissible sequence of type k and \(\overline{\mu }'\) is a \(\Delta \)-admissible sequence such that \(|\overline{\mu }'| < +\infty \) and  , then
, then  where
where  is the connected component of
is the connected component of  in
in  .
.
When  is disconnected, the incremental construction builds only
is disconnected, the incremental construction builds only  , the connected component of
, the connected component of  in
in  . We may build the other connected components of
. We may build the other connected components of  as follows. Given a point
as follows. Given a point  , we have
, we have  . Since
. Since  , we have
, we have  and there exists a \(\Delta \)-bi-admissible encoding \(\overline{\mu }'\) of
and there exists a \(\Delta \)-bi-admissible encoding \(\overline{\mu }'\) of  . Then \(\mathcal {S}^{\Delta ,\overline{\mu }'}_\infty \) is the connected component of
. Then \(\mathcal {S}^{\Delta ,\overline{\mu }'}_\infty \) is the connected component of  in
in  which means that
which means that  is the connected component of
is the connected component of  in
in  . This way, we may build all the connected components provided that we know a starting point in each of them.
. This way, we may build all the connected components provided that we know a starting point in each of them.  may even be built directly by initialising the construction with
may even be built directly by initialising the construction with  instead of
instead of  . Note that initialising the construction with
. Note that initialising the construction with  without considering \(\overline{\mu }'\) does not give the result. It would build
without considering \(\overline{\mu }'\) does not give the result. It would build  which is different from
which is different from  .
.
For instance, let us consider a vector  the directive sequence of which is \(\Delta =(1213)^\omega \), \(\overline{\mu }=(1000)^\omega \) which is \(\Delta \)-bi-admissible and
the directive sequence of which is \(\Delta =(1213)^\omega \), \(\overline{\mu }=(1000)^\omega \) which is \(\Delta \)-bi-admissible and  . Then
. Then  has two connected components. The point
has two connected components. The point  belongs to
belongs to  and a \(\Delta \)-bi-admissible encoding of
and a \(\Delta \)-bi-admissible encoding of  is \(\overline{\mu }'=(0011)^\omega \). Figure 1 shows
is \(\overline{\mu }'=(0011)^\omega \). Figure 1 shows  and
and  .
.
5 Connectedness Criterion
Let \(\mathcal {B}\) be the closed ball \([-\frac{1}{2},+\frac{1}{2}]^d\),  the vector \((1,\dots ,1)\) and
the vector \((1,\dots ,1)\) and  the orthogonal projection on the plane
the orthogonal projection on the plane  . By a slight abuse of notation, for any set \(S\subset \mathbb {R}^d\), we denote by
. By a slight abuse of notation, for any set \(S\subset \mathbb {R}^d\), we denote by  and
and  the interior and the boundary of
the interior and the boundary of  in
in  .
.
Theorem 11
Let  , \(\mu \in \left[ 0,\Omega \right] \) and
, \(\mu \in \left[ 0,\Omega \right] \) and  the connected component of
the connected component of  in
in  . Then
. Then  is connected if and only if
is connected if and only if  is empty.
is empty.
The proof of this theorem requires two additional lemmas.
Lemma 12
For all  , we have
, we have  .
.
Lemma 13
Let  such that
such that  and
and  . Then
. Then  .
.
Proof of Theorem 11. We first note that  since \(\mu \in \left[ 0,\Omega \right] \) and thus
since \(\mu \in \left[ 0,\Omega \right] \) and thus  . Since
. Since  , the discrete plane
, the discrete plane  is \((d-1)\)-separating [1] which implies
is \((d-1)\)-separating [1] which implies  and therefore
and therefore  . If
. If  is connected then
is connected then  hence
hence  . Its boundary in
. Its boundary in  is therefore empty.
is therefore empty.
Assume now that  is disconnected and let
is disconnected and let  . Then
. Then  contains no point of the form
contains no point of the form  . Indeed, if
. Indeed, if  belongs to
belongs to  then it is connected to
then it is connected to  in
in  and cannot belong to
and cannot belong to  . But these points are the only
. But these points are the only  which could belong to
which could belong to  such that
such that  . We deduce that
. We deduce that  is disjoint from
is disjoint from  which therefore has a non-empty boundary in
which therefore has a non-empty boundary in  . \(\square \)
. \(\square \)
Definition 14
(Interior and border of \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\)). Let  :
:
-
 is interior in \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) if and only if
is interior in \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) if and only if  is contained in
is contained in  ;
; -
 is on the border of \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) if and only if it is not interior in \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\).
is on the border of \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) if and only if it is not interior in \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\).
We saw earlier that \(\mathcal {S}^{\Delta ,\overline{\mu }}_n = \mathcal {S}^\Delta _n - \psi ^\Delta (\mu _1\dots \mu _n)\). Thus a point  is interior in \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) if and only if
is interior in \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) if and only if  is interior in \(\mathcal {S}^\Delta _n\). Therefore we shall mainly study \(\mathcal {S}^\Delta _n\). All results will apply immediately to \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) by translation.
is interior in \(\mathcal {S}^\Delta _n\). Therefore we shall mainly study \(\mathcal {S}^\Delta _n\). All results will apply immediately to \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\) by translation.
Proposition 15
Let \(\sigma \in \{0,1\}^n\) such that \(\psi ^\Delta (\sigma )\) is interior in \(\mathcal {S}^\Delta _n\).
-
For all \(\sigma ' \in \{0,1\}^\star \), \(\psi ^\Delta (\sigma \sigma ')\) is interior in \(\mathcal {S}^\Delta _{n+|\sigma '|}\).
-
For all \(\Delta _0 \in \{0,\dots ,d\}^\star \) and all \(\sigma _0 \in \{0,1\}^{|\Delta _0|}\), \(\psi ^{\Delta _0\Delta }(\sigma _0\sigma )\) is interior in \(\mathcal {S}^{\Delta _0\Delta }_{|\Delta _0|+n}\).
Again, we need two technical lemmas.
Lemma 16
Let  be the 0-neighbourhood of
be the 0-neighbourhood of  in \(\mathbb {Z}^d\). A point
in \(\mathbb {Z}^d\). A point  is interior in \(\mathcal {S}^\Delta _n\) if and only if for all
is interior in \(\mathcal {S}^\Delta _n\) if and only if for all  such that
such that  , and all i, j such that \(i\ne j\), \(y_i \le 0\) and \(y_j \ge 0\), \(\mathcal {S}^\Delta _n\) contains at least one point in
, and all i, j such that \(i\ne j\), \(y_i \le 0\) and \(y_j \ge 0\), \(\mathcal {S}^\Delta _n\) contains at least one point in  .
.
Lemma 17
Let \(\Delta =\delta _1\dots \delta _{n_0} \in \{1,\dots ,d\}^{n_0}\), \(\Delta ' \in \{1,\dots ,d\}^\omega \) and  where
where  is the transpose of \(\gamma \). For all \(n\ge 0\), we have
is the transpose of \(\gamma \). For all \(n\ge 0\), we have
The picture below shows an example of this composition.

Proof of Proposition 15 (sketch). The first point is obvious since \(\mathcal {S}^\Delta _n \subset \mathcal {S}^\Delta _m\) for all \(n\le m\).
We prove the second point for \(|\Delta _0|=1\), i.e. \(\Delta _0 = \delta \in \{1,\dots ,d\}\), and \(\sigma _0 = \varepsilon \in \{0,1\}\). The general result follows by induction. We consider more generally a set \(\mathcal {S}\) having the property of Lemma 12. Using Lemmas 16 and 17, we determine that we have to prove that if  is interior in \(\mathcal {S}\), then for all
is interior in \(\mathcal {S}\), then for all  such that
such that  , and all i, j such that \(i\ne j\), \(y_i \le 0\) and \(y_j \ge 0\), \(\mathcal {S}\) contains at least one point in
, and all i, j such that \(i\ne j\), \(y_i \le 0\) and \(y_j \ge 0\), \(\mathcal {S}\) contains at least one point in

We consider 18 cases according to the respective values of \(\varepsilon \), i, j and \(y_\delta \). \(\square \)
Lemma 16 allows us to determine whether a point  is interior in \(\mathcal {S}^\Delta _n\) by looking only at its 0-neighbourhood. Using this lemma we may compute all possible configurations in which
is interior in \(\mathcal {S}^\Delta _n\) by looking only at its 0-neighbourhood. Using this lemma we may compute all possible configurations in which  is interior. These are subsets of the 0-neighbourhood of
is interior. These are subsets of the 0-neighbourhood of  which satisfy the conditions of the lemma. By Lemma 12, we may restrict this neighbourhood to the points
which satisfy the conditions of the lemma. By Lemma 12, we may restrict this neighbourhood to the points  such that
such that  . We may also keep only the configurations which are minimal with respect to inclusion. Then
. We may also keep only the configurations which are minimal with respect to inclusion. Then  is interior in \(\mathcal {S}^\Delta _n\) if and only if its 0-neighbourhood in \(\mathcal {S}^\Delta _n\) contains one of these minimal configurations.
is interior in \(\mathcal {S}^\Delta _n\) if and only if its 0-neighbourhood in \(\mathcal {S}^\Delta _n\) contains one of these minimal configurations.
We find 64 minimal configurations in dimension 3 and 1498 in dimension 4. If we consider only configurations which appear in planes the coordinates of the normal vector of which are sorted in ascending order, we find, in dimension 3, the 21 minimal configurations shown below. Other minimal configurations are obtained by permuting the coordinates.

Lemma 18
If for all n,  is at bounded distance of the border of \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\), then there exists \(n_0\) such that
is at bounded distance of the border of \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\), then there exists \(n_0\) such that  is on the border of \(\mathcal {S}^{\Delta ^{n_0},\overline{\mu }^{n_0}}_n\) for all n, where \(\overline{\mu }^{n_0}\) denotes the sequence \((\mu _n)_{n\ge n0}\).
is on the border of \(\mathcal {S}^{\Delta ^{n_0},\overline{\mu }^{n_0}}_n\) for all n, where \(\overline{\mu }^{n_0}\) denotes the sequence \((\mu _n)_{n\ge n0}\).
Proof
Since  is at bounded distance of the border of \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\), \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) has a non-empty border.
is at bounded distance of the border of \(\mathcal {S}^{\Delta ,\overline{\mu }}_n\), \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) has a non-empty border.
If  is on the border of \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) then we may take \(n_0=1\). Otherwise, let m be such that
is on the border of \(\mathcal {S}^{\Delta ,\overline{\mu }}_\infty \) then we may take \(n_0=1\). Otherwise, let m be such that  is interior in \(\mathcal {S}^{\Delta ,\overline{\mu }}_m\) or equivalently, \(\psi ^\Delta (\mu _1\dots \mu _m)\) is interior in \(\mathcal {S}^\Delta _m\). For all \(k\ge 0\), we have \(\mathcal {S}^\Delta _{m+k} = \mathcal {S}^{\delta _1\dots \delta _m}_m+ \varGamma ^{\delta _1\dots \delta _m}(\mathcal {S}^{\Delta ^{m+1}}_k)\). The distance from \(\psi ^{\Delta ^{m+1}}(\mu _{m+1}\dots \mu _{m+k})\) to the border of \(\mathcal {S}^{\Delta ^{m+1}}_k\) is strictly less than the distance from \(\psi ^\Delta (\mu _1\dots \mu _{m+k})\) to the border of \(\mathcal {S}^{\Delta }_{m+k}\). By repeating this operation, we find eventually \(n_0\) such that the distance from \(\psi ^{\Delta ^{n_0}}(\overline{\mu }^{n_0})\) to the border of \(\mathcal {S}^{\Delta ^{n_0}}_{k}\) is zero for all \(k \ge 0\). This means that \(\psi ^{\Delta ^{n_0}}(\overline{\mu }^{n_0})\) is on the border of \(\mathcal {S}^{\Delta ^{n_0}}_{k}\), or equivalently
is interior in \(\mathcal {S}^{\Delta ,\overline{\mu }}_m\) or equivalently, \(\psi ^\Delta (\mu _1\dots \mu _m)\) is interior in \(\mathcal {S}^\Delta _m\). For all \(k\ge 0\), we have \(\mathcal {S}^\Delta _{m+k} = \mathcal {S}^{\delta _1\dots \delta _m}_m+ \varGamma ^{\delta _1\dots \delta _m}(\mathcal {S}^{\Delta ^{m+1}}_k)\). The distance from \(\psi ^{\Delta ^{m+1}}(\mu _{m+1}\dots \mu _{m+k})\) to the border of \(\mathcal {S}^{\Delta ^{m+1}}_k\) is strictly less than the distance from \(\psi ^\Delta (\mu _1\dots \mu _{m+k})\) to the border of \(\mathcal {S}^{\Delta }_{m+k}\). By repeating this operation, we find eventually \(n_0\) such that the distance from \(\psi ^{\Delta ^{n_0}}(\overline{\mu }^{n_0})\) to the border of \(\mathcal {S}^{\Delta ^{n_0}}_{k}\) is zero for all \(k \ge 0\). This means that \(\psi ^{\Delta ^{n_0}}(\overline{\mu }^{n_0})\) is on the border of \(\mathcal {S}^{\Delta ^{n_0}}_{k}\), or equivalently  is on the border of \(\mathcal {S}^{\Delta ^{n_0},\overline{\mu }^{n_0}}_{k}\). \(\square \)
is on the border of \(\mathcal {S}^{\Delta ^{n_0},\overline{\mu }^{n_0}}_{k}\). \(\square \)
Proposition 19
Let \(\mu \in [0;\Omega ]\) and \(\overline{\mu }\in \{0,1\}^\omega \) a \(\Delta \)-bi-admissible sequence such that  . Then
. Then  is connected if and only if for all \(m\ge 1\), there exists \(n\ge m\) such that \(\psi ^{\Delta ^{m}}(\mu _m\cdots \mu _n)\) is interior in \(\mathcal {S}_{n-m+1}^{\Delta ^{m}}\).
is connected if and only if for all \(m\ge 1\), there exists \(n\ge m\) such that \(\psi ^{\Delta ^{m}}(\mu _m\cdots \mu _n)\) is interior in \(\mathcal {S}_{n-m+1}^{\Delta ^{m}}\).
Since each point in \(\mathcal {S}^\Delta _n\) may be coded by a word in \(\{0,1\}^n\), we consider the language of words which code interior points. We define the language \(\mathcal {L}^{\Delta }\) as the set of words \(\sigma \in \{0,1\}^\star \) such that \(\psi ^\Delta (\sigma )\) is interior in \(\mathcal {S}^\Delta _{|\sigma |}\) and for all  , we define the language
, we define the language  as
as

Intuitively,  is the set of codes of points
is the set of codes of points  such that
such that  and
and  belong to the same \(\mathcal {S}^\Delta _n\), i.e.
belong to the same \(\mathcal {S}^\Delta _n\), i.e.  .
.
Lemma 20
For all  :
:
-
1.
 ;
; -
2.
 is non-empty if and only if
is non-empty if and only if 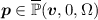 or
or 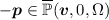 .
.
The language \(\mathcal {L}^\Delta \) may then be defined from the minimal interior configurations we defined earlier. If \(\mathcal {C}\) is the set of these minimal configurations, then

We saw that if \(\psi ^\Delta (\mu _1\dots \mu _n)\) is interior in \(\mathcal {S}^\Delta _n\), then \(\psi ^\Delta (\mu _1\dots \mu _m)\) is interior in \(\mathcal {S}^\Delta _m\) for all \(m\ge n\). Then there exists a minimal index \(n_1\) such that \(\psi ^\Delta (\mu _1\dots \mu _{n_1})\) is interior in \(\mathcal {S}^\Delta _{n_1}\), meaning that \(\psi ^\Delta (\mu _1\dots \mu _{n_1-1})\) is on the border of \(\mathcal {S}^\Delta _{n_1-1}\). Similarly, there exists a maximal index \(n_0\) such that \(\psi ^{\Delta ^{n_0}}(\mu _{n_0}\dots \mu _{n_1})\) is interior in \(\mathcal {S}^{\Delta ^{n_0}}_{n_1-n_0+1}\), which means that \(\psi ^{\Delta ^{n_0+1}}(\mu _{n_0+1}\dots \mu _{n_1})\) is on the border of \(\mathcal {S}^{\Delta ^{n_0+1}}_{n_1-n_0}\). Thus the pair \((\delta _{n_0}\dots \delta _{n_1},\mu _{n_0}\dots \mu _{n_1})\) is a minimal interior pattern. For all \(\Delta '\) and all \(\overline{\mu }'\), if there exists an index i such that \(\delta '_i\dots \delta '_{i+n_1-n_0} = \delta _{n_0}\dots \delta _{n_1}\) and \(\mu '_i\dots \mu '_{i+n_1-n_0}=\mu _{n_0}\dots \mu _{n_1}\), then \(\psi ^{\Delta '}(\mu '_1\dots \mu '_m)\) is interior in \(\mathcal {S}^{\Delta '}_m\) for all \(m \ge i+n_1-n_0\).
Definition 21
(Interior Patterns)
-
A pattern is an element of \(\cup _{n\ge 0} (\{1,\dots ,d\}^n \times \{0,1\}^n)\).
-
A pattern \((\delta _1\dots \delta _n,\sigma _1\dots \sigma _n)\) is interior if and only if \(\psi ^{\delta _1\dots \delta _n}(\sigma _1\dots \sigma _n)\) is interior in \(\mathcal {S}^{\delta _1\dots \delta _n}_n\).
-
An interior pattern \((\delta _1\dots \delta _n,\sigma _1\dots \sigma _n)\) is minimal if and only if neither \((\delta _2\dots \delta _n,\sigma _2\dots \sigma _n)\) nor \((\delta _1\dots \delta _{n-1},\sigma _1\dots \sigma _{n-1})\) is interior.
We set \(\mathcal {L}^\Delta _n = \mathcal {L}^{\Delta ^n}\) and
where \(\overline{\mathcal {L}}= \{0,1\}^\star \setminus \mathcal {L}\).
\(\mathcal {M}^\Delta _n\) is the set of words \(\sigma \in \{0,1\}^\star \) such that \((\delta _n\dots \delta _{n+|\sigma |-1},\sigma )\) is a minimal interior pattern. Thus the set of all minimal interior patterns which may appear in \((\Delta ,\overline{\mu })\) is
and the set of all minimal interior patterns is
Theorem 22
Let \(\mu \in [0;\Omega ]\) and \(\overline{\mu }\) a \(\Delta \)-bi-admissible encoding of \(\mu \). Then  is connected if and only if \((\Delta ,\overline{\mu })\) contains infinitely many minimal interior patterns.
is connected if and only if \((\Delta ,\overline{\mu })\) contains infinitely many minimal interior patterns.
6 The Periodic Case
We consider now the specific case where \(\Delta \) is periodic, that is \(\Delta =(\delta _1\dots \delta _p)^\omega \) for some \(p\ge 1\) and \(\{\delta _1,\dots ,\delta _p\}=\{1,\dots ,d\}\). This means that after p application of the Fully Subtractive algorithm to the normal vector  , we obtain a vector
, we obtain a vector  which is proportional to
which is proportional to  . In other words,
. In other words,  for some
for some  . The value \(\beta \) is the inverse of the Pisot eigenvalue of \(\gamma _{\delta _1}^{-1}\dots \gamma _{\delta _p}^{-1}\) which was proven to be Pisot in [2].
. The value \(\beta \) is the inverse of the Pisot eigenvalue of \(\gamma _{\delta _1}^{-1}\dots \gamma _{\delta _p}^{-1}\) which was proven to be Pisot in [2].
For each  , there exists \(\pi \in \{0,1\}^\star \) such that
, there exists \(\pi \in \{0,1\}^\star \) such that  . The language
. The language  is obviously recognised by the infinite automaton which contains for each word \(\sigma \in \{0,1\}^\star \) a state labelled with \(\sigma \) and for each \(\alpha \in \{0,1\}\) the transition
is obviously recognised by the infinite automaton which contains for each word \(\sigma \in \{0,1\}^\star \) a state labelled with \(\sigma \) and for each \(\alpha \in \{0,1\}\) the transition  . A state is final if and only if
. A state is final if and only if  and \(|(\sigma +\pi )\mathord \Downarrow ^\Delta 0^\omega | \le |\sigma |\). When \(\Delta \) is periodic, this infinite automaton is actually equivalent to a finite one, which means that
and \(|(\sigma +\pi )\mathord \Downarrow ^\Delta 0^\omega | \le |\sigma |\). When \(\Delta \) is periodic, this infinite automaton is actually equivalent to a finite one, which means that  is a regular language.
is a regular language.
Theorem 23
If \(\Delta \) is periodic then  is a regular language for all
is a regular language for all  .
.
Proof
(sketch). We saw that  is non-empty if and only if
is non-empty if and only if  or
or  and
and  . We have obviously
. We have obviously  . It is therefore sufficient to prove the result when
. It is therefore sufficient to prove the result when  . A word \(\sigma \in \{0,1\}^\star \) belongs to
. A word \(\sigma \in \{0,1\}^\star \) belongs to  if and only if \(\psi ^\Delta (\sigma +\pi )\) belongs to \(\mathcal {S}^\Delta _{|\sigma |}\), i.e. if and only if
if and only if \(\psi ^\Delta (\sigma +\pi )\) belongs to \(\mathcal {S}^\Delta _{|\sigma |}\), i.e. if and only if  and \(|(\sigma +\pi )\mathord \Downarrow ^\Delta 0^\omega | \le |\sigma |\).
and \(|(\sigma +\pi )\mathord \Downarrow ^\Delta 0^\omega | \le |\sigma |\).
We consider an incremental construction of the automaton in which states are labelled with triples \((\sigma ,k,n) \in \{0,1\}^\star \times (\mathbb {N}\setminus \{0\}) \times (\mathbb {N}\setminus \{0\})\). The initial state is \((\pi \mathord \Downarrow ^\Delta ,1,1)\) and we add two special states: a final state \(\top \) and a trap state \(\bot \) with the transitions  and
and  . For each state \((\sigma ,k,n)\) and each \(\alpha \in \{0,1\}\) we have a transition
. For each state \((\sigma ,k,n)\) and each \(\alpha \in \{0,1\}\) we have a transition  where ‘
where ‘ ’ is a function which simplifies states. If
’ is a function which simplifies states. If  then
then  . If
. If  and \(|(\sigma +0^{k-1}1)\mathord \Downarrow ^{\Delta ^n}0^\omega | \le k\) then
and \(|(\sigma +0^{k-1}1)\mathord \Downarrow ^{\Delta ^n}0^\omega | \le k\) then  . In all other cases, the simplification of \((\sigma ,k,n)\) consists in removing from \(\sigma \mathord \Downarrow ^{\Delta ^n}\) a useless prefix of size \(\ell \): if \(\sigma \mathord \Downarrow ^{\Delta ^n} = \tau _1\dots \tau _\ell \sigma '\), then the result of the simplification is \((\sigma ',k-\ell ,1+(n+\ell -1)\bmod p)\). Intuitively, a prefix is useless if it does not actually participate in the computation of the \(\Delta ^n\)-normal form of \(\sigma +0^{k-1}\mu \), i.e. for all \(\mu \in \{0,1\}^\star \),
. In all other cases, the simplification of \((\sigma ,k,n)\) consists in removing from \(\sigma \mathord \Downarrow ^{\Delta ^n}\) a useless prefix of size \(\ell \): if \(\sigma \mathord \Downarrow ^{\Delta ^n} = \tau _1\dots \tau _\ell \sigma '\), then the result of the simplification is \((\sigma ',k-\ell ,1+(n+\ell -1)\bmod p)\). Intuitively, a prefix is useless if it does not actually participate in the computation of the \(\Delta ^n\)-normal form of \(\sigma +0^{k-1}\mu \), i.e. for all \(\mu \in \{0,1\}^\star \),

which may be tested in finite time. We first show that k is bounded by \(p+2\). Then, from Lemma 17 we have \(\mathcal {S}^\Delta _{p+n} =\mathcal {S}^{\delta _1\dots \delta _p}_p+\varGamma ^{\delta _1\dots \delta _p}(\mathcal {S}^\Delta _n)\) where \(\varGamma ^{\delta _1\dots \delta _p}\) is the inverse of a Pisot operator [2]. Using this decomposition, we are able to prove that \(2\mathcal {S}^\Delta _m \cap \mathcal {S}^\Delta _\infty \subset \mathcal {S}^\Delta _{m+r}\) for some fixed r. We deduce that after m steps of the construction of the automaton, \(|(\sigma +\pi )\mathord \Downarrow ^\Delta 0^\omega |\) has not grown more than r. Using the fact that k is bounded, we deduce that after simplification, the length of \(\sigma \) is also bounded. Since \(\Delta \) is periodic, we may replace n with \(1+(n-1) \bmod p\) which is also bounded. Therefore, the automaton has only finitely many states. \(\square \)
From this theorem, we deduce that \(\mathcal {L}^\Delta _n\) and \(\mathcal {M}^\Delta _n\) are regular languages for all n and may therefore be recognised by finite state automata. In particular, the words \(\sigma \) such that \(\psi ^\Delta (\sigma )\) is interior in \(\mathcal {S}^\Delta _{|\sigma |}\) are recognised by a finite state automaton. Since \(\Delta \) is periodic, the sequences \((\mathcal {L}^\Delta _n)_{n\ge 1}\) and \((\mathcal {M}^\Delta _n)_{n\ge 1}\) are also periodic and their periods divide the period of \(\Delta \).
For example, if  , where \(\alpha \in [0;1]\) and \(\alpha +\alpha ^2+\alpha ^3=1\), then \(\Delta = (123)^\omega \) and we find for all n, \(\mathcal {M}^\Delta _n = \mathcal {M}\cup \widetilde{\mathcal {M}}\) where
, where \(\alpha \in [0;1]\) and \(\alpha +\alpha ^2+\alpha ^3=1\), then \(\Delta = (123)^\omega \) and we find for all n, \(\mathcal {M}^\Delta _n = \mathcal {M}\cup \widetilde{\mathcal {M}}\) where
As announced in the example under Sect. 4, we deduce that  is connected when
is connected when  and disconnected when
and disconnected when  .
.
If we take  , where \(\alpha \in [0;1]\) and \(\alpha ^3-\alpha ^2-3\,\alpha +1=0\), then \(\Delta =(1213)^\omega \). We find for all \(n\ge 0\), \(\mathcal {M}^\Delta _{2\,n+1} = \emptyset \) and \(\mathcal {M}^\Delta _{2\,n+2} = \mathcal {M}\cup \widetilde{\mathcal {M}}\) where
, where \(\alpha \in [0;1]\) and \(\alpha ^3-\alpha ^2-3\,\alpha +1=0\), then \(\Delta =(1213)^\omega \). We find for all \(n\ge 0\), \(\mathcal {M}^\Delta _{2\,n+1} = \emptyset \) and \(\mathcal {M}^\Delta _{2\,n+2} = \mathcal {M}\cup \widetilde{\mathcal {M}}\) where
In order for  to be disconnected, \(\overline{\mu }\) must have a suffix which avoids completely the minimal interior patterns. As stated by the next theorem, this happens almost never which means that
to be disconnected, \(\overline{\mu }\) must have a suffix which avoids completely the minimal interior patterns. As stated by the next theorem, this happens almost never which means that  is actually almost always connected.
is actually almost always connected.
Theorem 24
The set  is Lebesgue negligible.
is Lebesgue negligible.
References
Andrès, E., Acharya, R., Sibata, C.: Discrete analytical hyperplanes. CVGIP: Graph. Model Image Process. 59(5), 302–309 (1997)
Avila, A., Delecroix, V.: Some monoids of Pisot matrices, preprint (2015). https://arxiv.org/abs/1506.03692
Brimkov, V.E., Barneva, R.P.: Connectivity of discrete planes. Theor. Comput. Sci. 319(1–3), 203–227 (2004). https://doi.org/10.1016/j.tcs.2004.02.015
Domenjoud, E., Jamet, D., Toutant, J.-L.: On the connecting thickness of arithmetical discrete planes. In: Brlek, S., Reutenauer, C., Provençal, X. (eds.) DGCI 2009. LNCS, vol. 5810, pp. 362–372. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04397-0_31
Domenjoud, E., Provençal, X., Vuillon, L.: Facet connectedness of discrete hyperplanes with zero intercept: the general case. In: Barcucci, E., Frosini, A., Rinaldi, S. (eds.) DGCI 2014. LNCS, vol. 8668, pp. 1–12. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-09955-2_1
Domenjoud, E., Vuillon, L.: Geometric palindromic closures. Uniform Distribution Theory 7(2), 109–140 (2012). https://math.boku.ac.at/udt/vol07/no2/06DomVuillon13-12.pdf
Jamet, D., Toutant, J.L.: Minimal arithmetic thickness connecting discrete planes. Discrete Appl. Math. 157(3), 500–509 (2009). https://doi.org/10.1016/j.dam.2008.05.027
Kraaikamp, C., Meester, R.: Ergodic properties of a dynamical system arising from percolation theory. Ergodic Theory Dyn. Syst. 15(04), 653–661 (1995). https://doi.org/10.1017/S0143385700008592
Réveillès, J.P.: Géométrie discrète, calcul en nombres entiers et algorithmique. Thèse d’état, Université Louis Pasteur, Strasbourg, France (1991)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Domenjoud, E., Laboureix, B., Vuillon, L. (2019). Facet Connectedness of Arithmetic Discrete Hyperplanes with Non-Zero Shift. In: Couprie, M., Cousty, J., Kenmochi, Y., Mustafa, N. (eds) Discrete Geometry for Computer Imagery. DGCI 2019. Lecture Notes in Computer Science(), vol 11414. Springer, Cham. https://doi.org/10.1007/978-3-030-14085-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-14085-4_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-14084-7
Online ISBN: 978-3-030-14085-4
eBook Packages: Computer ScienceComputer Science (R0)




 then
then 

 when
when  is interior in
is interior in  is contained in
is contained in  ;
; is on the border of
is on the border of  ;
; is non-empty if and only if
is non-empty if and only if 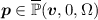 or
or 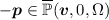 .
.