Abstract
We give an efficient decision procedure that, on input two (acyclic) expressions making arbitrary use of common cryptographic primitives (namely, encryption and pseudorandom generators), determines (in polynomial time) if the two expressions produce computationally indistinguishable distributions for any cryptographic instantiation satisfying the standard security notions of pseudorandomness and indistinguishability under chosen plaintext attack. The procedure works by mapping each expression to a symbolic pattern that captures, in a fully abstract way, the information revealed by the expression to a computationally bounded observer. Our main result shows that if two expressions are mapped to different symbolic patterns, then there are secure pseudorandom generators and encryption schemes for which the two distributions can be distinguished with overwhelming advantage. At the same time if any two (acyclic) expressions are mapped to the same pattern, then the associated distributions are indistinguishable.
Research supported in part by NSF under grant CNS-1528068. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
For example, \(\mathbb {G}_0(k)\) gives partial information about k because it allows to distinguish k from any other key \(k'\) chosen independently at random: all that the distinguisher has to do is to compute \(\mathbb {G}_0(k')\) and compare the result to \(\mathbb {G}_0(k)\).
- 2.
For cyclic expressions, i.e., expressions containing encryption cycles, our soundness theorem still holds, but with respect to a slightly stronger “co-inductive” adversarial model based on greatest fixed point computations [26].
- 3.
Active attacks against pseudorandom generators may be considered in the context of leakage resilient cryptography, fault injection analysis, and other side-channel attacks, which are certainly interesting, but also much more specialized models than those considered in this paper.
- 4.
We do not assume any specific property about \(\pi \), other than invertibility and efficiency, i.e., \(\pi (w_1,w_2)\) should be computable in polynomial (typically linear) time, and the substrings \(w_1\) and \(w_2\) can be uniquely recovered from \(\pi (w_1,w_2)\), also in polynomial time. In particular, \(\pi (w_1,w_2)\) is not just the string concatenation operation \(w_1;w_2\) (which is not invertible), and the strings \(\pi (w_1,w_2)\) and \(\pi (w_2,w_1)\) may have different length. For example, \(\pi (w_1,w_2)\) could be the string concatenation of a prefix-free encoding of \(w_1\), followed by \(w_2\).
- 5.
All that the distinguisher has to do, on input a pair of keys \((\sigma _0,\sigma _1)\), is to compute \(\mathcal {G}_0(\sigma _1)\) and check if the result equals \(\sigma _0\).
- 6.
The Hasse diagram of a partial order relation \(\preceq \) is the graph associated to the transitive reduction of \(\preceq \), i.e., the smallest relation R such that \(\preceq \) is the symmetric transitive closure of R.
- 7.
Notice that by (7), the functions \(\mathtt {proj}(\cdot ,S)\) and \(\mathtt {proj}(\cdot ,T)\) commute, i.e., \(\mathtt {proj}(\mathtt {proj}(e,S),T) = \mathtt {proj}(\mathtt {proj}(e,T),S)\) for any expression e. Indeed, for example, if \(S = \{k_1\}\), \(T = \{k_2\}\) and
 , then
, then  ,
,  , and
, and 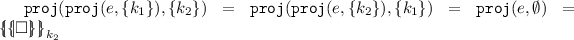 .
. - 8.
By symmetry, and the final application of \(\mathbb {G}\) in the definition of \(\mathbf {rec}\), keys recoverable from partial information of type \(\mathbf {keys}(e) \cap \mathbb {G}^+(\mathbf {keys}(e))\) are also captured implicitly by the this definition, simply by swapping the role of the two keys.
- 9.
As we will see, the key recovery map \(\mathbb {F}_e\) is monotone, i.e., if \(S \subseteq S'\), then \(\mathbb {F}_e(S) \subseteq \mathbb {F}_e(S')\), for any two sets of keys \(S,S'\). Therefore, \(\mathbb {F}_e\) defines a monotonically increasing sequence of known sets of keys \(S_0 \subset S_1\subset S_2 \subset \ldots S_n = S_{n+1}\) and the set of keys recoverable by the adversary \(S_n = \text{ fix }(\mathbb {F}_e)\) is precisely the least fixed point of \(\mathbb {F}_e\), i.e., the smallest set S such that \(\mathbb {F}_e(S) = S\).
References
Abadi, M., Gordon, A.: A calculus for cryptogaphic protocols: the spi calculus. Inf. Comput. 148(1), 1–70 (1999). https://doi.org/10.1006/inco.1998.2740
Abadi, M., Jürjens, J.: Formal eavesdropping and its computational interpretation. In: Kobayashi, N., Pierce, B.C. (eds.) TACS 2001. LNCS, vol. 2215, pp. 82–94. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45500-0_4
Abadi, M., Rogaway, P.: Reconciling two views of cryptography (the computational soundness of formal encryption). J. Cryptol. 15(2), 103–127 (2002). https://doi.org/10.1007/s00145-007-0203-0
Abadi, M., Warinschi, B.: Security analysis of cryptographycally controlledaccess to XML documents. J. ACM 55(2), 1–29 (2008). https://doi.org/10.1145/1346330.1346331. Prelim. version in PODS’05
Backes, M., Pfitzmann, B.: Symmetric encryption in a simulatable Dolev-Yao style cryptographic library. In: CSFW 2004, pp. 204–218. IEEE (2004). https://doi.org/10.1109/CSFW.2004.20
Backes, M., Pfitzmann, B., Waidner, M.: Symmetric authentication in a simulatable Dolev-Yao-style cryptographic library. Int. J. Inf. Secur. 4(3), 135–154 (2005). https://doi.org/10.1007/s10207-004-0056-6
Bellare, M., Miner, S.K.: A forward-secure digital signature scheme. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 431–448. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_28
Böhl, F., Cortier, V., Warinschi, B.: Deduction soundness: prove one, get five for free. In: CCS 2013, pp. 1261–1272. ACM (2013). https://doi.org/10.1145/2508859.2516711
Burrows, M., Abadi, M., Needham, R.M.: A logic of authentication. ACM Trans. Comput. Syst. 8(1), 18–36 (1990). https://doi.org/10.1145/77648.77649
Canetti, R., Garay, J., Itkis, G., Micciancio, D., Naor, M., Pinkas, B.: Multicast security: a taxonomy and some efficient constructions. In: INFOCOM 1999, pp. 708–716 (1999). https://doi.org/10.1109/INFCOM.1999.751457
Comon-Lundh, H., Cortier, V.: Computational soundness of observational equivalence. In: CCS 2008, pp. 109–118. ACM (2008). https://doi.org/10.1145/1455770.1455786
Cortier, V., Warinschi, B.: A composable computational soundness notion. In: CCS 2011, pp. 63–74. ACM (2011). https://doi.org/10.1145/2046707.2046717
Dolev, D., Yao, A.: On the security of public key protocols. IEEE Trans. Inf. Theory 29(2), 198–208 (1983). https://doi.org/10.1109/TIT.1983.1056650
Horvitz, O., Gligor, V.: Weak key authenticity and the computational completeness of formal encryption. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 530–547. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_31
Goldreich, O.: Foundations of Cryptography, Volume I - Basic Tools. Cambridge Unievrsity Press, Cambridge (2001)
Goldreich, O.: Foundation of Cryptography, Volume II - Basic Applications. Cambridge Unievrsity Press, Cambridge (2004)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986). https://doi.org/10.1145/6490.6503
Goldwasser, S., Micali, S.: Probabilistic encryption. J. Comput. Syst. Si. 28(2), 270–299 (1984). https://doi.org/10.1016/0022-0000(84)90070-9
Hajiabadi, M., Kapron, B.M.: Computational soundness of coinductive symbolic security under active attacks. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 539–558. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_30
Katz, J., Lindell, Y.: Introduction to Modern Cryptography (Cryptography and Network Security Series). Chapman & Hall/CRC, Boca Raton (2007)
Kemmerer, R.A., Meadows, C.A., Millen, J.K.: Three system for cryptographic protocol analysis. J. Cryptology 7(2), 79–130 (1994). https://doi.org/10.1007/BF00197942
Laud, P.: Encryption cycles and two views of cryptography. In: NORDSEC 2002, pp. 85–100. No. 2002:31 in Karlstad University Studies (2002)
Laud, P., Corin, R.: Sound computational interpretation of formal encryption with composed keys. In: Lim, J.-I., Lee, D.-H. (eds.) ICISC 2003. LNCS, vol. 2971, pp. 55–66. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24691-6_5
Li, B., Micciancio, D.: Symbolic security of garbled circuits. In: Computer Security Foundations Symposium - CSF 2018, pp. 147–161. IEEE (2018). https://doi.org/10.1109/CSF.2018.00018
Malkin, T., Micciancio, D., Miner, S.: Efficient generic forward-secure signatures with an unbounded number of time periods. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 400–417. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_27
Micciancio, D.: Computational soundness, co-induction, and encryption cycles. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 362–380. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_19
Micciancio, D.: Symbolic encryption with pseudorandom keys. Report 2009/249, IACR ePrint archive (2018). https://eprint.iacr.org/2009/249. version 201800223:160820
Micciancio, D., Panjwani, S.: Adaptive security of symbolic encryption. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 169–187. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_10
Micciancio, D., Panjwani, S.: Corrupting one vs. corrupting many: the case of broadcast and multicast encryption. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006. LNCS, vol. 4052, pp. 70–82. Springer, Heidelberg (2006). https://doi.org/10.1007/11787006_7
Micciancio, D., Panjwani, S.: Optimal communication complexity of generic multicast key distribution. IEEE/ACM Trans. Network. 16(4), 803–813 (2008). https://doi.org/10.1109/TNET.2007.905593
Micciancio, D., Warinschi, B.: Completeness theorems for the Abadi-Rogaway logic of encrypted expressions. J. Comput. Secur. 12(1), 99–129 (2004). https://doi.org/10.3233/JCS-2004-12105
Micciancio, D., Warinschi, B.: Soundness of formal encryption in the presence of active adversaries. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 133–151. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_8
Millen, J.K., Clark, S.C., Freedman, S.B.: The Interrogator: protocol security analysis. IEEE Trans. Softw. Eng. SE–13(2), 274–288 (1987). https://doi.org/10.1109/TSE.1987.233151
Paulson, L.C.: The inductive approach to verifying cryptographic protocols. J. Comput. Secur. 6(1–2), 85–128 (1998). https://doi.org/10.3233/JCS-1998-61-205
Yao, A.C.: Protocols for secure computations (extended abstract). In: FOCS 1982, pp. 160–164 (1982). https://doi.org/10.1109/SFCS.1982.38
Acknowledgments
The author thanks the anonymous Eurocrypt 2019 referees for their useful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Micciancio, D. (2019). Symbolic Encryption with Pseudorandom Keys. In: Ishai, Y., Rijmen, V. (eds) Advances in Cryptology – EUROCRYPT 2019. EUROCRYPT 2019. Lecture Notes in Computer Science(), vol 11478. Springer, Cham. https://doi.org/10.1007/978-3-030-17659-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-17659-4_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17658-7
Online ISBN: 978-3-030-17659-4
eBook Packages: Computer ScienceComputer Science (R0)


 , then
, then  ,
,  , and
, and 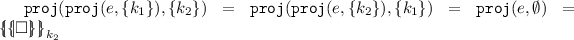 .
.