Abstract
A joining implication is a restricted form of an implication where it is explicitly specified which attributes may occur in the premise and in the conclusion, respectively. A technique for sound and complete axiomatization of joining implications valid in a given formal context is provided. In particular, a canonical base for the joining implications valid in a given formal context is proposed, which enjoys the property of being of minimal cardinality among all such bases. Background knowledge in form of a set of valid joining implications can be incorporated. Furthermore, an application to inductive learning in a Horn description logic is proposed, that is, a procedure for sound and complete axiomatization of \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions from a given interpretation is developed. A complexity analysis shows that this procedure runs in deterministic exponential time.
1 Introduction
Formal Concept Analysis (abbrv. FCA) [10] is subfield of lattice theory that allows to analyze data-sets that can be represented as formal contexts. Put simply, such a formal context binds a set of objects to a set of attributes by specifying which objects have which attributes. There are two major techniques that can be applied in various ways for purposes of data mining, machine learning, knowledge management, knowledge visualization, etc. On the one hand, it is possible to describe the hierarchical structure of such a data-set in form of a formal concept lattice [10]. On the other hand, the theory of implications (dependencies between attributes) valid in a given formal context can be axiomatized in a sound and complete manner by the so-called canonical base [11], which furthermore contains a minimal number of implications w.r.t. the properties of soundness and completeness. So far, some variations of the canonical base have been developed, e.g., incorporation of valid background knowledge [29], constraining premises and conclusions in implications by some closure operator [3], and incorporation of arbitrary background knowledge [22], among others. The canonical base in its default form as well as its variations can be be computed by the algorithm NextClosures [17, 22] in a highly parallel way such the necessary computation time is almost inverse linear proportional to the number of available CPU cores.
Description Logic (abbrv. DL) [2] belongs to the field of knowledge representation and reasoning. DL researchers have developed a large family of logic-based languages, so-called description logics (abbrv. DLs). These logics allow their users to explicitly represent knowledge as ontologies, which are finite sets of (human- and machine-readable) axioms, and provide them with automated inference services to derive implicit knowledge. The landscape of decidability and computational complexity of common reasoning tasks for various description logics has been explored in large parts: there is always a trade-off between expressibility and reasoning costs. It is therefore not surprising that DLs are nowadays applied in a large variety of domains [2]: agriculture, astronomy, biology, defense, education, energy management, geography, geoscience, medicine, oceanography, and oil and gas. Furthermore, the most notable success of DLs is that these constitute the logical underpinning of the Web Ontology Language (abbrv. OWL) [13] in the Semantic Web.
Within this document, we propose the new notion of so-called joining implications in FCA. More specifically, we assume that there are two distinct sets of attributes: the first one containing the attributes that may occur in premises of implications, while conclusions must only contain attributes from the second set. A canonical base for the joining implications valid in a given formal context is developed and it is proven that it has minimal cardinality among all such bases. Then, an application to inductive learning in a Horn description logic [24] is provided. Roughly speaking, such a Horn DL is obtained from some DL by disallowing any disjunctions. Reasoning procedures can then work deterministically, i.e., reasoning by case is not required [14]. Hornness is not a new notion: Horn clauses in first-order logic are disjunctions of an arbitrary number of negated atomic formulae and at most one non-negated atomic formula. It is easy to see that such Horn clauses have an implicative character, since \(\lnot \phi _1\vee \ldots \vee \lnot \phi _n\vee \psi \) is equivalent to \(\phi _1\wedge \ldots \phi _n\rightarrow \psi \). A logic program is a set of Horn clauses, and a Datalog program is a function-free logic program [7]. All commonly known Horn description logics can be translated into Datalog—more specifically, each \({\mathsf {Horn\text {-}}}\mathcal {DL} \)
 can be translated into some Datalog program
can be translated into some Datalog program
 such that, for each simple ABox
such that, for each simple ABox
 , the ontology
, the ontology  is satisfiable if, and only if, the Datalog programm
is satisfiable if, and only if, the Datalog programm  is satisfiable. For deeper insights please consider [12, 15, 24]. The most important advantage of Horn fragments is that these often have a significantly lower computational complexity. Using the canonical base of joining implications, we show how the \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions valid in a given interpretation can be axiomatized. This continues a line of research that combines FCA and DL for the sake of inductive learning, cf. [4, 5, 9, 18, 19, 21, 27] just to name a few.
is satisfiable. For deeper insights please consider [12, 15, 24]. The most important advantage of Horn fragments is that these often have a significantly lower computational complexity. Using the canonical base of joining implications, we show how the \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions valid in a given interpretation can be axiomatized. This continues a line of research that combines FCA and DL for the sake of inductive learning, cf. [4, 5, 9, 18, 19, 21, 27] just to name a few.
Due to space constraints some technical lemmas and some proofs have been moved to a technical report [20].
2 Joining Implications in Formal Contexts
Throughout this section, assume that  is some formal context, that is, G is a set of objects, M is a set of attributes, and \(I\subseteq G\times M\) is an incidence relation. If \((g,m)\in I\), then we say that g has m. It is well-known that the two mappings
is some formal context, that is, G is a set of objects, M is a set of attributes, and \(I\subseteq G\times M\) is an incidence relation. If \((g,m)\in I\), then we say that g has m. It is well-known that the two mappings  and
and  defined below constitute a Galois connection, cf. [10].
defined below constitute a Galois connection, cf. [10].

In particular, this means that the following statements hold true for any sets \(A,C\subseteq G\) and \(B,D\subseteq M\).

An implication over M is a term \(X\rightarrow Y\) where \(X,Y\subseteq M\). It is valid in
 if \(X^I\subseteq Y^I\) is satisfied, i.e., if each object that has all attributes in X also has all attributes in Y, and we shall then write
if \(X^I\subseteq Y^I\) is satisfied, i.e., if each object that has all attributes in X also has all attributes in Y, and we shall then write  . A model of \(X\rightarrow Y\) is a set \(U\subseteq M\) such that \(X\subseteq U\) implies \(Y\subseteq U\), denoted as \(U\models X\rightarrow Y\). An implication set
. A model of \(X\rightarrow Y\) is a set \(U\subseteq M\) such that \(X\subseteq U\) implies \(Y\subseteq U\), denoted as \(U\models X\rightarrow Y\). An implication set
 entails an implication \(X\rightarrow Y\) if any model of
entails an implication \(X\rightarrow Y\) if any model of
 , i.e., any set that is a model of all implications in
, i.e., any set that is a model of all implications in
 , is also a model of \(X\rightarrow Y\), and we denote this by
, is also a model of \(X\rightarrow Y\), and we denote this by  .
.
We are now interested in a restricted form of implications. In particular, we restrict the sets of attributes that may occur in the premise X and in the conclusion Y, respectively, of every implication \(X\rightarrow Y\). Thus, let further  be a set of premise attributes and let
be a set of premise attributes and let  be a set of conclusion attributes such that
be a set of conclusion attributes such that  holds true. For each
holds true. For each  , we define the subcontext
, we define the subcontext  where
where  . Furthermore, we may also write
. Furthermore, we may also write  instead of
instead of  for subsets \(X\subseteq G\) or
for subsets \(X\subseteq G\) or  . Please note that then each pair
. Please note that then each pair  is a Galois connection between
is a Galois connection between  and
and  , that is, similar statements like above are valid.
, that is, similar statements like above are valid.
Definition 1
A joining implication from  to
to  , or simply
, or simply  -implication, is an expression \(X\rightarrow Y\) where
-implication, is an expression \(X\rightarrow Y\) where  and
and  . It is valid in
. It is valid in
 , written
, written  , if
, if  holds true.
holds true.
Example
Consider the formal context  in Fig. 1. It considers six persons as objects and their symptoms and illnesses as attributes. Furthermore, we regard the symptoms as premise attributes and the illnesses as conclusion attributes. Note that, in general, it is not required that the sets
in Fig. 1. It considers six persons as objects and their symptoms and illnesses as attributes. Furthermore, we regard the symptoms as premise attributes and the illnesses as conclusion attributes. Note that, in general, it is not required that the sets  and
and  form a partition of the attribute set. For other use cases both could overlap, one could be contained in the other, or their union could be a strict subset of the whole attribute set. The concept lattice is displayed in Fig. 2.Footnote 1
form a partition of the attribute set. For other use cases both could overlap, one could be contained in the other, or their union could be a strict subset of the whole attribute set. The concept lattice is displayed in Fig. 2.Footnote 1
The expression  is no
is no
 , since the attribute \(\textsf {Cold}\) must not occur in a premise and, likewise, the attribute \(\textsf {Chills}\) must not occur in a conclusion. The expression
, since the attribute \(\textsf {Cold}\) must not occur in a premise and, likewise, the attribute \(\textsf {Chills}\) must not occur in a conclusion. The expression  is a well-formed joining implication and it is valid in
is a well-formed joining implication and it is valid in  , since
, since  is a subset of
is a subset of  . Furthermore, the expression
. Furthermore, the expression  is a well-formed joining implication as well, but it is not valid in
is a well-formed joining implication as well, but it is not valid in  , as
, as  is not a subset of
is not a subset of  .
.
In the following, we shall characterize the set of all joining implications valid in
 . Of course, the
. Of course, the
 set
set

contains only valid
 and further entails any valid
and further entails any valid
 , since
, since  is equivalent to
is equivalent to  and so
and so  .
.
Remark that a closure operator on M is some mapping  with the following properties for all subsets \(X,Y\subseteq M\).
with the following properties for all subsets \(X,Y\subseteq M\).

It is easy to verify that, for each Galois connection (f, g), the compositions \(f\circ g\) and \(g\circ f\) are closure operators. It is well-known that each implication set
 induces a corresponding closure operator
induces a corresponding closure operator  such that the models of
such that the models of
 are exactly the closures of
are exactly the closures of  , cf. [10, 22]: for each \(U\subseteq M\), the closure
, cf. [10, 22]: for each \(U\subseteq M\), the closure  is the smallest superset of U such that
is the smallest superset of U such that  implies
implies  for any implication \(X\rightarrow Y\) in
for any implication \(X\rightarrow Y\) in
 . In particular, we can readily verify the following.
. In particular, we can readily verify the following.

For the above joining implication set, we easily get that  satisfies
satisfies

for any \(X\subseteq M\).
An implication \(X\rightarrow Y\) is valid in a closure operator \(\phi \), written \(\phi \models X\rightarrow Y\), if \(Y\subseteq \phi (X)\) holds true, cf. [17]. Please note that this coincides with the notion of validity in a formal context
 if we consider the closure operator
if we consider the closure operator  and, likewise, entailment by an implication set
and, likewise, entailment by an implication set
 is the same as validity in
is the same as validity in  . Now consider an implication set
. Now consider an implication set
 . We say that
. We say that
 is sound for \(\phi \) if
is sound for \(\phi \) if  holds true, that is, if \(\phi \models X\rightarrow Y\) is satisfied for each implication
holds true, that is, if \(\phi \models X\rightarrow Y\) is satisfied for each implication  . Furthermore,
. Furthermore,
 is complete for \(\phi \) if, for any implication \(X\rightarrow Y\), it holds true that \(\phi \models X\rightarrow Y\) implies
is complete for \(\phi \) if, for any implication \(X\rightarrow Y\), it holds true that \(\phi \models X\rightarrow Y\) implies  .
.
Definition 2
An implication set is join-sound or  -sound if it is sound for
-sound if it is sound for  , and it is join-complete or
, and it is join-complete or  -complete if it is complete for
-complete if it is complete for  . Fix some
. Fix some
 implication set
implication set
 . A
. A
 set is called joining implication base or
set is called joining implication base or
 -implication base relative to
-implication base relative to
 if it is
if it is
 and its union with
and its union with
 is
is
 .
.
Obviously, the above  is a joining implication base relative to \(\emptyset \).
is a joining implication base relative to \(\emptyset \).
Further fix some implication set
 as well as a closure operator \(\phi \) such that
as well as a closure operator \(\phi \) such that  . Now remark that a pseudo-closure of \(\phi \) relative to
. Now remark that a pseudo-closure of \(\phi \) relative to
 is a set \(P\subseteq M\) such that \(P\ne \phi (P)\) and
is a set \(P\subseteq M\) such that \(P\ne \phi (P)\) and  (i.e.,
(i.e.,  ) hold true and \(Q\subsetneq P\) implies \(\phi (Q)\subseteq P\) for each pseudo-closure Q of \(\phi \) relative to
) hold true and \(Q\subsetneq P\) implies \(\phi (Q)\subseteq P\) for each pseudo-closure Q of \(\phi \) relative to
 . We shall denote the set of all pseudo-closures of \(\phi \) relative to
. We shall denote the set of all pseudo-closures of \(\phi \) relative to
 as
as  . Then, the canonical implication base of \(\phi \) relative to
. Then, the canonical implication base of \(\phi \) relative to
 is defined as
is defined as  , and it is sound for \(\phi \) and is further complete for \(\phi \) relative to
, and it is sound for \(\phi \) and is further complete for \(\phi \) relative to
 , i.e., \(\phi \models X\rightarrow Y\) if, and only if,
, i.e., \(\phi \models X\rightarrow Y\) if, and only if,  for each implication \(X\rightarrow Y\), cf. [11, 17, 29]. It is easy to see that we can replace each implication \(P\rightarrow \phi (P)\) by \(P\rightarrow \phi (P)\setminus P\) to get an equivalent implication set.
for each implication \(X\rightarrow Y\), cf. [11, 17, 29]. It is easy to see that we can replace each implication \(P\rightarrow \phi (P)\) by \(P\rightarrow \phi (P)\setminus P\) to get an equivalent implication set.
Our aim for the sequel of this section is to find a canonical representation of the valid joining implications of some formal context, i.e., we shall provide a joining implication base that has minimal cardinality among all joining implication bases. For this purpose, we consider the canonical implication base of the above closure operator  and show how we can modify it to get a canonical joining implication base. We start with showing that we can rewrite any join-sound and join-complete implication set into a joining implication base in a certain normal form. For the remainder of this section, fix some arbitrary join-sound joining implication set
and show how we can modify it to get a canonical joining implication base. We start with showing that we can rewrite any join-sound and join-complete implication set into a joining implication base in a certain normal form. For the remainder of this section, fix some arbitrary join-sound joining implication set
 that is used as background knowledge.
that is used as background knowledge.
Lemma 3
Fix some join-sound implication set
 over M. Further assume that
over M. Further assume that  is join-complete, and define the following set of joining implications.
is join-complete, and define the following set of joining implications.

Then,  is a joining implication base relative to
is a joining implication base relative to
 .
.
Proof
Since  obviously holds true, we know that
obviously holds true, we know that  is join-sound. For join-completeness we show that
is join-sound. For join-completeness we show that  . Thus, consider some
. Thus, consider some  . As
. As  is join-complete, it must hold true that
is join-complete, it must hold true that  , that is, there are implications \(X_1\rightarrow Y_1\), \(\ldots \), \(X_n\rightarrow Y_n\) in
, that is, there are implications \(X_1\rightarrow Y_1\), \(\ldots \), \(X_n\rightarrow Y_n\) in  such that the following statements are satisfied.
such that the following statements are satisfied.

Let  and
and  . Since
. Since
 is join-sound, we have
is join-sound, we have  for each index \(k\in L\). Define
for each index \(k\in L\). Define  . An induction on
. An induction on  shows the following.
shows the following.

Of course,  is satisfied for any index \(k\in L\). We conclude that
is satisfied for any index \(k\in L\). We conclude that  entails
entails  and we are done. \(\square \)
and we are done. \(\square \)
The transformation from Lemma 3 can now immediately be applied to the canonical implication base of the closure operator  to obtain a joining implication base, which we call canonical. This is due to fact that, by definition,
to obtain a joining implication base, which we call canonical. This is due to fact that, by definition,  is both
is both
 and
and
 .
.
Proposition 4
The following is a joining implication base relative to
 and is called canonical joining implication base or canonical
and is called canonical joining implication base or canonical
 -implication base of
-implication base of
 relative to
relative to
 .
.

Proof
Remark that  holds true and, consequently, the canonical implication base for
holds true and, consequently, the canonical implication base for  relative to
relative to
 evaluates to
evaluates to

We already know that  is join-sound and its union with
is join-sound and its union with
 is join-complete. Since
is join-complete. Since  holds true, an application of Lemma 3 shows that
holds true, an application of Lemma 3 shows that  is indeed a joining implication base relative to
is indeed a joining implication base relative to
 . \(\square \)
. \(\square \)
Example
We continue with investigating our exemplary formal context  . In order to compute the canonical joining implication base of it (relative to \(\emptyset \)), we first need to construct the canonical base of the closure operator
. In order to compute the canonical joining implication base of it (relative to \(\emptyset \)), we first need to construct the canonical base of the closure operator  .Footnote 2
.Footnote 2

Now applying the transformation from Lemma 3 yields the following set of joining implications, which is the canonical joining implication base. In particular, only the fourth implication is altered.

The canonical base of  , which coincides with the canonical base of the induced closure operator
, which coincides with the canonical base of the induced closure operator  , is as follows. Note that it is sound and complete for all implications valid in
, is as follows. Note that it is sound and complete for all implications valid in  , i.e., no constraints on premises and conclusions are imposed.
, i.e., no constraints on premises and conclusions are imposed.

If we apply the transformation from Lemma 3 to  , then we obtain the following set of joining implications. Obviously, it is not complete, since it does not entail the valid joining implication
, then we obtain the following set of joining implications. Obviously, it is not complete, since it does not entail the valid joining implication  .
.

We close this section with two further important properties of the canonical joining implication base. On the one hand, we shall show that it has minimal cardinality among all joining implication bases or, more generally, even among all join-sound, join-complete implication bases. On the other hand, we investigate the computational complexity of actually computing the canonical joining implication base.
Proposition 5
The canonical joining implication base  has minimal cardinality among all implication sets that are join-sound and have a union with
has minimal cardinality among all implication sets that are join-sound and have a union with
 that is join-complete.
that is join-complete.
Proof
Consider some implication set
 such that
such that  is join-sound and join-complete. According to Lemma 3, we can assume that—without loss of generality—
is join-sound and join-complete. According to Lemma 3, we can assume that—without loss of generality— holds true. In particular, note that
holds true. In particular, note that  is always true.
is always true.
Join-soundness and join-completeness of  yield that
yield that  and
and  are equivalent. It is well-known [11, 29] that
are equivalent. It is well-known [11, 29] that  has minimal cardinality among all implication bases for
has minimal cardinality among all implication bases for  relative to
relative to
 , and so it follows that
, and so it follows that  .
.
Clearly, the choice  implies
implies  . It is further apparent that
. It is further apparent that  holds true and we infer that, in particular,
holds true and we infer that, in particular,  and
and  must contain the same number of implications. \(\square \)
must contain the same number of implications. \(\square \)
The next proposition shows that computing the canonical joining implication base is not more expensive than computing the canonical implication base where no constraints on the premises and conclusions must be satisfied. It uses the fact that canonical implication bases of closure operators can be computed using the algorithm NextClosures [17].
Proposition 6
The canonical joining implication base can be computed in exponential time, and there exist formal contexts for which the canonical joining implication base cannot be encoded in polynomial space.
Proof
The canonical implication base of the closure operator  relative to some background implication set
relative to some background implication set
 can be computed in exponential time by means of the algorithm NextClosures, cf. [5, 17], which is easy to verify. The transformation of
can be computed in exponential time by means of the algorithm NextClosures, cf. [5, 17], which is easy to verify. The transformation of  into
into  as described in Lemma 3 can be done in polynomial time.
as described in Lemma 3 can be done in polynomial time.
Kuznetsov and Obiedkov have shown in [26, Theorem 4.1] that the number of implications in the canonical implication base  of a formal context
of a formal context  can be exponential in
can be exponential in  . Clearly, if we let
. Clearly, if we let  and set both
and set both  and
and  to M, then
to M, then  and
and  coincide. \(\square \)
coincide. \(\square \)
We have seen in the running example that the canonical
 base can be used to characterize implications between symptoms and diagnoses/illnesses. A further applications is, for instance, formal contexts encoding observations between attributes satisfied yesterday and today, i.e., we could construct the canonical base of
base can be used to characterize implications between symptoms and diagnoses/illnesses. A further applications is, for instance, formal contexts encoding observations between attributes satisfied yesterday and today, i.e., we could construct the canonical base of
 and then use it as a forecast stating which combinations of attributes being satisfied today would imply which combinations of attributes being satisfied tomorrow. In general, we could think of the premise attributes as observable attributes and the conclusion attributes as goal/decision attributes. By constructing the canonical
and then use it as a forecast stating which combinations of attributes being satisfied today would imply which combinations of attributes being satisfied tomorrow. In general, we could think of the premise attributes as observable attributes and the conclusion attributes as goal/decision attributes. By constructing the canonical
 base from some formal context in which the goal/decision attributes have been manually assessed, we would obtain a set of rules with which we could analyze new data sets for which only the observable attributes are specified.
base from some formal context in which the goal/decision attributes have been manually assessed, we would obtain a set of rules with which we could analyze new data sets for which only the observable attributes are specified.
3 The Description Logic \({\mathsf {Horn\text {-}}}\mathcal {M} \)
A Horn description logic [12, 15, 24] is some description logic that, basically, does not allow for any usage of disjunction. While Hornness decreases expressiveness, it often also significantly lowers the computational complexity of some common reasoning tasks, e.g., instance checking or query answering. These are, thus, of importance in practical applications where computation times and costs must not be too high.
In the sequel of this section, we introduce the description logic \({\mathsf {Horn\text {-}}}\mathcal {M} \), which is the Horn variant of  [18]. Restrictions are imposed on concept inclusions only and, generally speaking, premises must always be
[18]. Restrictions are imposed on concept inclusions only and, generally speaking, premises must always be  concept descriptions while conclusions may be arbitrary
concept descriptions while conclusions may be arbitrary  concept descriptions, that is, \(\mathcal {M} \) concept descriptions except that in unqualified smaller-than restrictions
concept descriptions, that is, \(\mathcal {M} \) concept descriptions except that in unqualified smaller-than restrictions  only the case \(n=1\) is allowed. More specifically, a \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion is an expression \(C\sqsubseteq D\) where the concept descriptions C and D are built by means of the following grammar. Beforehand, fix some signature \(\varSigma \), which is a disjoint union of a set
only the case \(n=1\) is allowed. More specifically, a \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion is an expression \(C\sqsubseteq D\) where the concept descriptions C and D are built by means of the following grammar. Beforehand, fix some signature \(\varSigma \), which is a disjoint union of a set
 of individual names, a set
of individual names, a set
 of concept names, and a set
of concept names, and a set
 of role names. In the below grammar, A can be replaced by an arbitrary concept name from
of role names. In the below grammar, A can be replaced by an arbitrary concept name from
 and, likewise, r can be replaced by an arbitrary role name from
and, likewise, r can be replaced by an arbitrary role name from
 .
.

As usual, we denote by \(\mathcal {DL} (\varSigma )\) the set of all \(\mathcal {DL}\) concept descriptions over \(\varSigma \) for each description logic \(\mathcal {DL}\). The role depth  of a concept description E is the maximal number of nestings of restrictions within E.Footnote 3 We then further denote by \(\mathcal {DL} _d(\varSigma )\) the set of all \(\mathcal {DL}\) concept descriptions over \(\varSigma \) with a role depth not greater than d. Note that the above syntactic characterization follows easily from the results in [12, 15, 24]. A finite set of concept inclusions is called terminological box (abbrv. TBox).
of a concept description E is the maximal number of nestings of restrictions within E.Footnote 3 We then further denote by \(\mathcal {DL} _d(\varSigma )\) the set of all \(\mathcal {DL}\) concept descriptions over \(\varSigma \) with a role depth not greater than d. Note that the above syntactic characterization follows easily from the results in [12, 15, 24]. A finite set of concept inclusions is called terminological box (abbrv. TBox).
As it has already been pointed out in [15], the following properties can be expressed in a sufficiently strong Horn DL, e.g., in \({\mathsf {Horn\text {-}}}\mathcal {M} \).
-
Inclusion of Simple Concepts. \(A\sqsubseteq B\) states that each individual being A is also B.
-
Concept Disjointness. \(A\sqcap B\sqsubseteq \bot \) states that there are no individuals that are both A and B.
-
Domain Restrictions.
 states that each individual having an r-successor must be an A.
states that each individual having an r-successor must be an A. -
Range Restrictions.
 states that each individual being an r-successor must be an A.
states that each individual being an r-successor must be an A. -
Functionality Restrictions.
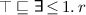 states that each individual has at most one r-successor.
states that each individual has at most one r-successor. -
Participation Constraints.
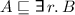 states that each individual that is an A has an r-successor that is a B.
states that each individual that is an A has an r-successor that is a B.
A concept assertion is an expression  where a is an individual name from
where a is an individual name from
 and E is some concept description, and further a role assertion is an expression
and E is some concept description, and further a role assertion is an expression  where
where  and r is some role name from
and r is some role name from
 . A finite set of concept and role assertions is called assertional box (abbrv. ABox). The union of a terminological and an assertional box yields an ontology. We often call the assertional part of an ontology the data and the terminological part of an ontology the schema. If a question of the form
. A finite set of concept and role assertions is called assertional box (abbrv. ABox). The union of a terminological and an assertional box yields an ontology. We often call the assertional part of an ontology the data and the terminological part of an ontology the schema. If a question of the form  is to be decided, then we also call the axiom \(\alpha \) the query.
is to be decided, then we also call the axiom \(\alpha \) the query.
An interpretation
 is a pair
is a pair  consisting of a non-empty set
consisting of a non-empty set  of objects, called domain, and an extension mapping
of objects, called domain, and an extension mapping  such that
such that  for
for  ,
,  for each
for each  , and
, and  for each
for each  . The extension mapping is then extended to all concept descriptions in the following recursive manner; the names of these concept descriptions are shown in the right column.
. The extension mapping is then extended to all concept descriptions in the following recursive manner; the names of these concept descriptions are shown in the right column.

Now a concept inclusion \(C\sqsubseteq D\) is valid in
 if
if  holds true, written
holds true, written  . A concept assertion
. A concept assertion  is valid in
is valid in
 if
if  is satisfied, and we shall denote this as
is satisfied, and we shall denote this as  . Likewise, a role assertion
. Likewise, a role assertion  is valid in
is valid in
 if
if  holds true, and we symbolize this as
holds true, and we symbolize this as  . If
. If
 is an ontology, then
is an ontology, then
 is a model of
is a model of
 if
if  holds true for each axiom
holds true for each axiom  , and we shall denote this as
, and we shall denote this as  . Furthermore, an ontology
. Furthermore, an ontology  entails another ontology
entails another ontology  , written
, written  , if each model of
, if each model of  is a model of
is a model of  too. In case
too. In case  for some single axiom \(\alpha \), we shall omit set parenthesis and simply write
for some single axiom \(\alpha \), we shall omit set parenthesis and simply write  . Note that, if \(x\mathrel {*}y\) is an axiom and
. Note that, if \(x\mathrel {*}y\) is an axiom and
 is either an interpretation or an ontology, then we sometimes write
is either an interpretation or an ontology, then we sometimes write  instead of
instead of  .
.
There are several standard reasoning tasks as follows.
-
Knowledge Base Consistency. Given an ontology
 , is there a model of
, is there a model of
 ?
? -
Concept Satisfiability. Given a concept description E and an ontology
 , is there a model of
, is there a model of
 in which E has a non-empty extension?
in which E has a non-empty extension? -
Concept Subsumption. Given two concept descriptions C and D and an ontology
 , does
, does
 entail \(C\sqsubseteq D\)?
entail \(C\sqsubseteq D\)? -
Instance Checking. Given an individual a, a concept description E, and an ontology
 , does
, does
 entail
entail  ?
?
There are two approaches to determining the computational complexity of the above tasks.
-
Combined Complexity. This is the default. Necessary time and space for solving the reasoning problem is measured as a function in the size of the whole input. For instance, if
 is to be decided, then time and space requirements are measured as a function of
is to be decided, then time and space requirements are measured as a function of  .
. -
Data Complexity. Determining data complexity is more meaningful for practical purposes, as in most cases the size of the stored data easily outgrows the size of the schema and query. In particular, time and space needed for solving the reasoning problem is measured as a function in the size of the ABox only. If, e.g.,
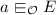 is to be decided where
is to be decided where
 is the union of an ABox
is the union of an ABox
 and some TBox
and some TBox
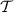 , then necessary time and space is only measured as a function of
, then necessary time and space is only measured as a function of 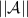 .
.
So far, the computational complexity of reasoning in \(\mathcal {M}\) and its sibling \({\mathsf {Horn\text {-}}}\mathcal {M} \) has not been determined and, thus, we shall catch up on this here. Since for a large variety of description logics complexity results have been obtained, we can immediately find the following results for \(\mathcal {M}^{-}\)  , the sublogic of \(\mathcal {M}\) in which we disallow existential self-restrictions
, the sublogic of \(\mathcal {M}\) in which we disallow existential self-restrictions  . Note that we always consider the case of a general TBox, i.e., where no restrictions are imposed on the concept inclusions (except those possibly implied by Hornness).
. Note that we always consider the case of a general TBox, i.e., where no restrictions are imposed on the concept inclusions (except those possibly implied by Hornness).
-
Concept subsumption in \(\mathcal {M}^{-}\) is
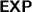 -complete (combined complexity). Since \(\mathcal {M}^{-}\) is a sublogic of \(\mathcal {SHIQ}\) and concept subsumption in \(\mathcal {SHIQ}\) is in
-complete (combined complexity). Since \(\mathcal {M}^{-}\) is a sublogic of \(\mathcal {SHIQ}\) and concept subsumption in \(\mathcal {SHIQ}\) is in
 [28, 30], it follows that concept subsumption in \(\mathcal {M}^{-}\) is in
[28, 30], it follows that concept subsumption in \(\mathcal {M}^{-}\) is in
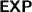 as well. Furthermore, \(\mathcal {FL}_{0} \) is a sublogic of \(\mathcal {M}^{-}\) in which concept subsumption is
as well. Furthermore, \(\mathcal {FL}_{0} \) is a sublogic of \(\mathcal {M}^{-}\) in which concept subsumption is
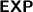 -hard [1]. We conclude that concept subsumption in \(\mathcal {M}^{-}\) must be
-hard [1]. We conclude that concept subsumption in \(\mathcal {M}^{-}\) must be
 -hard too.
-hard too. -
Concept subsumption in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is
 -complete (combined complexity). \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is a sublogic of \({\mathsf {Horn\text {-}}}\mathcal {SHIQ} \) and for the latter concept subsumption is known to be in
-complete (combined complexity). \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is a sublogic of \({\mathsf {Horn\text {-}}}\mathcal {SHIQ} \) and for the latter concept subsumption is known to be in
 [24]. Thus, concept subsumption in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is also in
[24]. Thus, concept subsumption in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is also in
 . Since \(\mathcal {ELF}\) is a sublogic of \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) in which concept subsumption is
. Since \(\mathcal {ELF}\) is a sublogic of \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) in which concept subsumption is
 -hard [1], we infer that the same problem in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) must be
-hard [1], we infer that the same problem in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) must be
 -hard too.
-hard too. -
Instance checking in \(\mathcal {M}^{-}\) is
 -complete (data complexity). Instance checking in \(\mathcal {SHIQ}\) is in
-complete (data complexity). Instance checking in \(\mathcal {SHIQ}\) is in
 (data complexity) [14] and since \(\mathcal {M}^{-}\) is a sublogic of \(\mathcal {SHIQ}\), it follows that instance checking in \(\mathcal {M}^{-}\) is also in
(data complexity) [14] and since \(\mathcal {M}^{-}\) is a sublogic of \(\mathcal {SHIQ}\), it follows that instance checking in \(\mathcal {M}^{-}\) is also in
 (data complexity). Furthermore, \(\mathcal {EL}^{kf}\) is a sublogic of \(\mathcal {M}^{-}\) in which instance checking is
(data complexity). Furthermore, \(\mathcal {EL}^{kf}\) is a sublogic of \(\mathcal {M}^{-}\) in which instance checking is
 -hard (data complexity) [23], and this result immediately transfers to \(\mathcal {M}^{-}\).
-hard (data complexity) [23], and this result immediately transfers to \(\mathcal {M}^{-}\). -
Instance checking in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is
 -complete (data complexity). As instance checking in \({\mathsf {Horn\text {-}}}\mathcal {SHIQ} \) is in
-complete (data complexity). As instance checking in \({\mathsf {Horn\text {-}}}\mathcal {SHIQ} \) is in  (data complexity) [14] and \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is a sublogic of \({\mathsf {Horn\text {-}}}\mathcal {SHIQ} \), we conclude that the similar problem in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is in
(data complexity) [14] and \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is a sublogic of \({\mathsf {Horn\text {-}}}\mathcal {SHIQ} \), we conclude that the similar problem in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is in  (data complexity) as well. Furthermore, \(\mathcal {EL}\) is a sublogic of \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) and instance checking in \(\mathcal {EL}\) is
(data complexity) as well. Furthermore, \(\mathcal {EL}\) is a sublogic of \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) and instance checking in \(\mathcal {EL}\) is 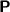 -hard (data complexity) [6]. Consequently, instance checking in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is
-hard (data complexity) [6]. Consequently, instance checking in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is  -hard as well.
-hard as well.
We see that terminological reasoning in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) is not cheaper than in \(\mathcal {M}^{-}\), but that assertional reasoning with knowledge bases containing both a schema (TBox) and data (ABox) is considerably cheaper in \({\mathsf {Horn\text {-}}}\mathcal {M}^{-} \) than in \(\mathcal {M}^{-}\) if we only take into account the size of the ABox (data complexity), unless  . It is obvious that the hardness results transfer from \(\mathcal {M}^{-}\) to \(\mathcal {M}\) and accordingly for the Horn variants. Furthermore, since \(\mathcal {M}\) and \({\mathsf {Horn\text {-}}}\mathcal {M} \) can each be seen as a sublogic of \(\mu \mathcal {ALCQ} \) in which concept subsumption is
. It is obvious that the hardness results transfer from \(\mathcal {M}^{-}\) to \(\mathcal {M}\) and accordingly for the Horn variants. Furthermore, since \(\mathcal {M}\) and \({\mathsf {Horn\text {-}}}\mathcal {M} \) can each be seen as a sublogic of \(\mu \mathcal {ALCQ} \) in which concept subsumption is
 -complete [8, 25], we can infer that concept subsumption in \(\mathcal {M}\) as well as in \({\mathsf {Horn\text {-}}}\mathcal {M} \) is
-complete [8, 25], we can infer that concept subsumption in \(\mathcal {M}\) as well as in \({\mathsf {Horn\text {-}}}\mathcal {M} \) is
 -complete (combined complexity) as well. Unfortunately, the author cannot provide sharp upper bounds for the data complexity of instance checking in \(\mathcal {M}\) and \({\mathsf {Horn\text {-}}}\mathcal {M} \). If one takes a closer look on the proofs in [15], one could get the impression that it might suffice to include the case
-complete (combined complexity) as well. Unfortunately, the author cannot provide sharp upper bounds for the data complexity of instance checking in \(\mathcal {M}\) and \({\mathsf {Horn\text {-}}}\mathcal {M} \). If one takes a closer look on the proofs in [15], one could get the impression that it might suffice to include the case  for the translation of concept descriptions into first-order logic. While the author conjectures that this extended translation allows for obtaining the same complexity results, it is necessary to check whether all later steps in the proof indeed work as before.
for the translation of concept descriptions into first-order logic. While the author conjectures that this extended translation allows for obtaining the same complexity results, it is necessary to check whether all later steps in the proof indeed work as before.
Henceforth, it makes sense to use a \({\mathsf {Horn\text {-}}}\mathcal {M} \) TBox as the schema for ontology-based data access (abbrv. OBDA) applications. This motivates the development of a procedure that can learn \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions from observations in form of an interpretation.
The next section makes use of the notion of a model-based most specific concept description, which we shall define now. Fix some description logic \(\mathcal {DL}\), an interpretation
 , a subset
, a subset  , as well as some role-depth bound
, as well as some role-depth bound  . The model-based most specific concept description (abbrv. MMSC) of X in
. The model-based most specific concept description (abbrv. MMSC) of X in
 is then some \(\mathcal {DL}\) concept description E that satisfies the following conditions.
is then some \(\mathcal {DL}\) concept description E that satisfies the following conditions.
-
1.
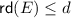
-
2.

-
3.
 implies \(E\sqsubseteq _\emptyset F\) for each \(\mathcal {DL}\) concept description F where
implies \(E\sqsubseteq _\emptyset F\) for each \(\mathcal {DL}\) concept description F where  .
.
Since MMSCs are unique up to equivalence, we shall denote these as  . In [18] the author has shown how MMSCs can be computed in the description logic \(\mathcal {M}\). For any sublogic of \(\mathcal {M}\), the computation method can suitably be adapted by simply ignoring unsupported concept constructors.
. In [18] the author has shown how MMSCs can be computed in the description logic \(\mathcal {M}\). For any sublogic of \(\mathcal {M}\), the computation method can suitably be adapted by simply ignoring unsupported concept constructors.
It is easy to see that this MMSC mapping  is the adjoint of the extension mapping
is the adjoint of the extension mapping  , that is, the pair of both constitutes a galois connection just like it is the case for the pair of derivation operators \(\cdot ^I\) induced by a formal context. This implies that the following statements hold true, where X and Y are arbitrary subsets of the domain
, that is, the pair of both constitutes a galois connection just like it is the case for the pair of derivation operators \(\cdot ^I\) induced by a formal context. This implies that the following statements hold true, where X and Y are arbitrary subsets of the domain  , and E and F are any \(\mathcal {DL}\) concept descriptions with a role depth of at most d.
, and E and F are any \(\mathcal {DL}\) concept descriptions with a role depth of at most d.

Compared to the FCA setting, we have replaced intent descriptions using sets of attributes by intent descriptions using \(\mathcal {DL}\) concept descriptions.
4 Inductive Learning in \({\mathsf {Horn\text {-}}}\mathcal {M} \)
Now fix some finitely representable interpretation
 over a signature \(\varSigma \), and further let
over a signature \(\varSigma \), and further let  be a role-depth bound. Similarly to [5, 9, 18], we define the induced formal context
be a role-depth bound. Similarly to [5, 9, 18], we define the induced formal context  where
where  , the premise attribute set is defined by
, the premise attribute set is defined by

while the conclusion attribute set is given as

and \((\delta ,C)\in I\) if  . Our interest is to axiomatize the \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions valid in
. Our interest is to axiomatize the \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions valid in
 . Of course, it holds true that
. Of course, it holds true that  is a \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion for each subset
is a \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion for each subset  and each subset
and each subset  . As in [5, 9, 18], such a concept inclusion is valid in
. As in [5, 9, 18], such a concept inclusion is valid in
 if, and only if, the joining implication
if, and only if, the joining implication  is valid in the induced formal context
is valid in the induced formal context  . As we are only interested in axiomatizing these concept inclusions that are valid in
. As we are only interested in axiomatizing these concept inclusions that are valid in
 and are no tautologies, we define the following joining implication set that we shall use as background knowledge on the FCA side.
and are no tautologies, we define the following joining implication set that we shall use as background knowledge on the FCA side.

We will see at the end of this section that the model-based most specific concept descriptions  can have an exponential size w.r.t.
can have an exponential size w.r.t.  and d in \(\mathcal {M}^{\mathord {\le }1}\). Since the problem of deciding subsumption in \({\mathsf {Horn\text {-}}}\mathcal {M} \) is
and d in \(\mathcal {M}^{\mathord {\le }1}\). Since the problem of deciding subsumption in \({\mathsf {Horn\text {-}}}\mathcal {M} \) is
 -complete, we infer that a naïve approach of computing
-complete, we infer that a naïve approach of computing
 needs double exponential time. However, a more sophisticated analysis yields that most concept inclusions cannot be valid. In particular, a concept description from
needs double exponential time. However, a more sophisticated analysis yields that most concept inclusions cannot be valid. In particular, a concept description from  only contains concept names and existential (self-)restrictions and, thus, these can never be subsumed (w.r.t. \(\emptyset \)) by a concept description from
only contains concept names and existential (self-)restrictions and, thus, these can never be subsumed (w.r.t. \(\emptyset \)) by a concept description from  containing a negated concept name, a local functionality restriction, a qualified at-least restriction where \(n>1\), or a value restriction. Thus, we conclude from the characterization in [18, Section 8] that
containing a negated concept name, a local functionality restriction, a qualified at-least restriction where \(n>1\), or a value restriction. Thus, we conclude from the characterization in [18, Section 8] that
 does not contain any implication
does not contain any implication  or
or  except for the trivial cases where
except for the trivial cases where  (only for the second form), and it can hence be computed in single exponential time. Even in the case where the tautological TBox
(only for the second form), and it can hence be computed in single exponential time. Even in the case where the tautological TBox
 is not that simple, e.g., for another description logic where subsumption is also
is not that simple, e.g., for another description logic where subsumption is also
 -complete and model-based most specific concept descriptions can have exponential sizes, we could also dispense with the expensive computation of
-complete and model-based most specific concept descriptions can have exponential sizes, we could also dispense with the expensive computation of
 , since the canonical base can then still be computed in single exponential time with the only drawback that it could contain tautologies.
, since the canonical base can then still be computed in single exponential time with the only drawback that it could contain tautologies.
In the remainder of this section, we show how the techniques from Sect. 2 can be applied to axiomatize \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions valid in
 . Note that the proofs are suitable adaptations of those for the \({\mathcal {EL}}^{\!\bot } \) case [5] or of those for the \(\mathcal {M}\) case [18]. We first show that the TBox consisting of the concept inclusions
. Note that the proofs are suitable adaptations of those for the \({\mathcal {EL}}^{\!\bot } \) case [5] or of those for the \(\mathcal {M}\) case [18]. We first show that the TBox consisting of the concept inclusions  for all
for all  concept descriptions C with a role depth not exceeding d is sound and complete. As a further step, we prove by means of structural induction that also the TBox containing the concept inclusions
concept descriptions C with a role depth not exceeding d is sound and complete. As a further step, we prove by means of structural induction that also the TBox containing the concept inclusions  where
where
 is a subset of
is a subset of  is sound and complete. Furthermore, when computing the MMSC of a conjunction
is sound and complete. Furthermore, when computing the MMSC of a conjunction  where
where  we do not have to do this on the DL side, which is expensive, but it suffices to compute the result
we do not have to do this on the DL side, which is expensive, but it suffices to compute the result  on the FCA side by applying the derivation operators
on the FCA side by applying the derivation operators  and
and  . The conjunction
. The conjunction  is then (equivalent to) the MMSC in the DL \(\mathcal {M}^{\mathord {\le }1}\). The proofs for the three aforementioned statements can be found in the technical report [20].
is then (equivalent to) the MMSC in the DL \(\mathcal {M}^{\mathord {\le }1}\). The proofs for the three aforementioned statements can be found in the technical report [20].
The main result for inductive learning of \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions is as follows. It states that (the premises of) each
 base of the induced context
base of the induced context  give rise to a base of \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions for
give rise to a base of \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions for
 .
.
Proposition 7
If
 is a joining implication base for
is a joining implication base for  relative to
relative to
 , then the following TBox is sound and complete for the \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions that are valid in
, then the following TBox is sound and complete for the \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions that are valid in  and have role depths not exceeding d.
and have role depths not exceeding d.

Instantiating the previous proposition with the canonical
 base now yields the following corollary.
base now yields the following corollary.
Corollary 8
The following \({\mathsf {Horn\text {-}}}\mathcal {M} \) TBox, called canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base for
 and d, is sound and complete for the \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions that are valid in
and d, is sound and complete for the \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions that are valid in
 and have role depths at most d.
and have role depths at most d.

The closure operator  is defined by
is defined by  .
.
In the sequel of this section, we investigate the computational complexity of computing the canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base. As it turns out, the complexity is the same as for computing the canonical
 base—both can be obtained in exponential time. Afterwards, we investigate whether we can show that the canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base has minimal cardinality.
base—both can be obtained in exponential time. Afterwards, we investigate whether we can show that the canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base has minimal cardinality.
Proposition 9
The canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base for a finitely representable interpretation
 and role depth bound \(d\ge 1\) can be computed in exponential time with respect to d and the cardinality of the domain
and role depth bound \(d\ge 1\) can be computed in exponential time with respect to d and the cardinality of the domain  , and further there exist finitely representable interpretations
, and further there exist finitely representable interpretations
 for which the canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base cannot be encoded in polynomial space.
for which the canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base cannot be encoded in polynomial space.
Note that in order to save space for representing the model-based most specific concept descriptions, we could also represent them in the form  where
where  is the model-based most specific concept description without any bound on the role depth and
is the model-based most specific concept description without any bound on the role depth and  denotes the unraveling of some concept description E (formulated in a DL with greatest fixed-point semantics) up to role depth d. In general, these unbounded MMSCs
denotes the unraveling of some concept description E (formulated in a DL with greatest fixed-point semantics) up to role depth d. In general, these unbounded MMSCs  only exist in extensions of the considered DL with greatest fixed-point semantics. The advantage is that then the size of
only exist in extensions of the considered DL with greatest fixed-point semantics. The advantage is that then the size of  is exponential only in
is exponential only in  but not in d.
but not in d.
The author conjectures that, for each finitely representable interpretation
 , the canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base
, the canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base  has minimal cardinality among all \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion bases for
has minimal cardinality among all \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion bases for
 and d. However, it is not immediately possible to suitably adapt the minimality proof for the \(\mathcal {EL}\) case described in [5, 9], since not all notions from \(\mathcal {EL}\) are available in more expressive description logics. The crucial point is that we need the validity of the following claim, which resembles [9, Lemma 5.16] or [5, Lemma A.9], respectively, for our case of \({\mathsf {Horn\text {-}}}\mathcal {M} \).
and d. However, it is not immediately possible to suitably adapt the minimality proof for the \(\mathcal {EL}\) case described in [5, 9], since not all notions from \(\mathcal {EL}\) are available in more expressive description logics. The crucial point is that we need the validity of the following claim, which resembles [9, Lemma 5.16] or [5, Lemma A.9], respectively, for our case of \({\mathsf {Horn\text {-}}}\mathcal {M} \).
Claim
Fix some \({\mathsf {Horn\text {-}}}\mathcal {M} \) TBox  in which all occurring concept descriptions have role depths not exceeding d. Further assume that
in which all occurring concept descriptions have role depths not exceeding d. Further assume that
 is a finitely representable model of
is a finitely representable model of
 such that, for each subconcept
such that, for each subconcept  of C, the filler X is (equivalent to) some model-based most specific concept description of
of C, the filler X is (equivalent to) some model-based most specific concept description of
 in the description logic
in the description logic  ; more specifically, we assume that
; more specifically, we assume that  is satisfied for each
is satisfied for each  . If \(C\not \sqsubseteq _\emptyset D\) and
. If \(C\not \sqsubseteq _\emptyset D\) and  , then \(C\sqsubseteq _\emptyset E\) and \(C\not \sqsubseteq _\emptyset F\) holds true for some concept inclusion \(E\sqsubseteq F\) contained in
, then \(C\sqsubseteq _\emptyset E\) and \(C\not \sqsubseteq _\emptyset F\) holds true for some concept inclusion \(E\sqsubseteq F\) contained in
 .
.
However, the author has just developed a computation procedure for so-called most specific consequences, cf. [19, 21, Definition 3], in a description logic that is more expressive than \({\mathcal {EL}}^{\!\bot } \). A proof of the above claim can then be obtained as a by-product. This will be subject of a future publication.
5 Conclusion
In Formal Concept Analysis, a restricted form of implications has been introduced: so-called joining implications. From the underlying attribute set M two subsets  and
and  are declared, and then only those implications are considered in which the premises only contain attributes from
are declared, and then only those implications are considered in which the premises only contain attributes from  and in which the conclusions only contain attributes from
and in which the conclusions only contain attributes from  . A canonical base for the joining implications valid in some given formal context has been devised, and it has been proven that it has minimal cardinality and can be computed in deterministic exponential time.
. A canonical base for the joining implications valid in some given formal context has been devised, and it has been proven that it has minimal cardinality and can be computed in deterministic exponential time.
The former results have then been applied to the problem of inductive learning in the Horn description logic \({\mathsf {Horn\text {-}}}\mathcal {M} \). More specifically, we have proposed a canonical base for the \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusions valid in a given interpretation. While the author conjectures that it has minimal cardinality, it has been demonstrated that it can be computed in deterministic exponential time.
Future research could deliver the proof for the claimed minimality of the canonical \({\mathsf {Horn\text {-}}}\mathcal {M} \) concept inclusion base, or could investigate means that allow for the integration of existing knowledge to make incremental learning possible. The author believes that both tasks can be tackled as soon as computation procedures for most specific consequences in \({\mathsf {Horn\text {-}}}\mathcal {M} \) are available. This will be subject of future publications.
Eventually, the author wants to point out that incremental learning from a sequence of interpretations [19, 21, Section 8.4 for the \({\mathcal {EL}}^{\!\bot } \) case] is probably more practical than model exploration or ABox exploration [9], since new observations that could show invalidity of concept inclusions are not requested from the expert at a certain time point, but are rather processed upon availability (“push instead of pull”). However, completeness of the eventual result for the considered domain of interest is only achieved if all typical individuals occur in the sequence at some time point.
Notes
- 1.
We have not introduced the notion of a concept lattice here, since it is not needed for our purposes; the interested reader is rather referred to [10].
- 2.
- 3.
Formally, the role depth is recursively defined as follows:
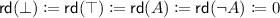 , and
, and 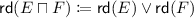 , and
, and 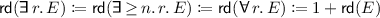 , and
, and  .
.
References
Baader, F., Brandt, S., Lutz, C.: Pushing the \(\cal{EL}\) envelope. In: Kaelbling, L.P., Saffiotti, A. (eds.) IJCAI-05, Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence, Edinburgh, Scotland, UK, July 30–August 5 2005, pp. 364–369. Professional Book Center (2005)
Baader, F., Horrocks, I., Lutz, C., Sattler, U.: An Introduction to Description Logic. Cambridge University Press, New York (2017)
Belohlávek, R., Vychodil, V.: Closure-based constraints in formal concept analysis. Discrete Appl. Math. 161(13–14), 1894–1911 (2013)
Borchmann, D.: Learning terminological knowledge with high confidence from erroneous data. Doctoral thesis, Technische Universität Dresden, Dresden, Germany (2014)
Borchmann, D., Distel, F., Kriegel, F.: Axiomatisation of general concept inclusions from finite interpretations. J. Appl. Non-Class. Logics 26(1), 1–46 (2016)
Calvanese, D., De Giacomo, G., Lembo, D., Lenzerini, M., Rosati, R.: Data complexity of query answering in description logics. In: Doherty, P., Mylopoulos, J., Welty, C.A. (eds.) Proceedings, Tenth International Conference on Principles of Knowledge Representation and Reasoning, Lake District of the United Kingdom, 2–5 June 2006, pp. 260–270. AAAI Press (2006)
Dantsin, E., Eiter, T., Gottlob, G., Voronkov, A.: Complexity and expressive power of logic programming. ACM Comput. Surv. 33(3), 374–425 (2001)
De Giacomo, G., Lenzerini, M.: A uniform framework for concept definitions in description logics. J. Artif. Intell. Res. 6, 87–110 (1997)
Distel, F.: Learning description logic knowledge bases from data using methods from formal concept analysis. Doctoral thesis, Technische Universität Dresden, Dresden, Germany (2011)
Ganter, B., Wille, R.: Formal Concept Analysis: Mathematical Foundations. Springer, Heidelberg (1999). https://doi.org/10.1007/978-3-642-59830-2
Guigues, J.L., Duquenne, V.: Famille minimale d’implications informatives résultant d’un tableau de données binaires. Mathématiques et Sciences Humaines 95, 5–18 (1986)
Hernich, A., Lutz, C., Papacchini, F., Wolter, F.: Horn-Rewritability vs. PTime query evaluation in ontology-mediated querying. In: Lang, J. (ed.) Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI 2018, Stockholm, Sweden, 13–19 July 2018, pp. 1861–1867. ijcai.org (2018)
Hitzler, P., Krötzsch, M., Rudolph, S.: Foundations of Semantic Web Technologies. Chapman and Hall/CRC Press, Boca Raton (2010)
Hustadt, U., Motik, B., Sattler, U.: Data complexity of reasoning in very expressive description logics. In: Kaelbling, L.P., Saffiotti, A. (eds.) IJCAI-05, Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence, Edinburgh, Scotland, UK, July 30 - August 5 2005, pp. 466–471. Professional Book Center (2005)
Hustadt, U., Motik, B., Sattler, U.: Reasoning in description logics by a reduction to disjunctive datalog. J. Autom. Reason. 39(3), 351–384 (2007)
Kriegel, F.: Concept Explorer FX (2010–2019), Software for Formal Concept Analysis with Description Logic Extensions. https://github.com/francesco-kriegel/conexp-fx
Kriegel, F.: NextClosures with constraints. In: Huchard, M., Kuznetsov, S. (eds.) Proceedings of the Thirteenth International Conference on Concept Lattices and Their Applications, Moscow, Russia, 18–22 July 2016. CEUR Workshop Proceedings, vol. 1624, pp. 231–243. CEUR-WS.org (2016)
Kriegel, F.: Acquisition of terminological knowledge from social networks in description logic. In: Missaoui, R., Kuznetsov, S.O., Obiedkov, S. (eds.) Formal Concept Analysis of Social Networks. LNSN, pp. 97–142. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-64167-6_5
Kriegel, F.: Most specific consequences in the description logic \(\cal{EL}\). LTCS-Report 18–11, Chair of Automata Theory, Institute of Theoretical Computer Science, Technische Universität Dresden, Dresden, Germany (2018, accepted for publication in Discrete Applied Mathematics). https://tu-dresden.de/inf/lat/reports#Kr-LTCS-18-11
Kriegel, F.: Joining implications in formal contexts and inductive learning in a horn description logic (Extended Version). LTCS-Report 19–02, Chair of Automata Theory, Institute of Theoretical Computer Science, Technische Universität Dresden, Dresden, Germany (2019). https://tu-dresden.de/inf/lat/reports#Kr-LTCS-19-02
Kriegel, F.: Most specific consequences in the description logic \(\cal{EL}\). Discrete Applied Mathematics (2019). https://doi.org/10.1016/j.dam.2019.01.029
Kriegel, F., Borchmann, D.: NextClosures: parallel computation of the canonical base with background knowledge. Int. J. Gen. Syst. 46(5), 490–510 (2017)
Krisnadhi, A., Lutz, C.: Data complexity in the \(\cal{EL}\) family of description logics. In: Dershowitz, N., Voronkov, A. (eds.) LPAR 2007. LNCS (LNAI), vol. 4790, pp. 333–347. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75560-9_25
Krötzsch, M., Rudolph, S., Hitzler, P.: Complexities of horn description logics. ACM Trans. Comput. Logic 14(1), 2:1–2:36 (2013)
Kupferman, O., Sattler, U., Vardi, M.Y.: The complexity of the graded \({\mu }\)-Calculus. In: Voronkov, A. (ed.) CADE 2002. LNCS (LNAI), vol. 2392, pp. 423–437. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45620-1_34
Kuznetsov, S.O., Obiedkov, S.A.: Some decision and counting problems of the Duquenne-Guigues basis of implications. Discrete Appl. Math. 156(11), 1994–2003 (2008)
Rudolph, S.: Relational exploration: combining description logics and formal concept analysis for knowledge specification. Doctoral thesis, Technische Universität Dresden, Dresden, Germany (2006)
Schild, K.: A correspondence theory for terminological logics: preliminary report. In: Mylopoulos, J., Reiter, R. (eds.) Proceedings of the 12th International Joint Conference on Artificial Intelligence, Sydney, Australia, 24–30 August 1991, pp. 466–471. Morgan Kaufmann (1991)
Stumme, G.: Attribute exploration with background implications and exceptions. In: Bock, H.H., Polasek, W. (eds.) Studies in Classification, Data Analysis, and Knowledge Organization, pp. 457–469. Springer, Heidelberg (1996). https://doi.org/10.1007/978-3-642-80098-6_39
Tobies, S.: Complexity results and practical algorithms for logics in knowledge representation. Doctoral thesis, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany (2001)
Acknowledgments
The author gratefully thanks Sebastian Rudolph for the very idea of learning in Horn description logics as well as for a helpful discussion on basics of Horn description logics. The author further thanks the reviewers for their constructive remarks.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Kriegel, F. (2019). Joining Implications in Formal Contexts and Inductive Learning in a Horn Description Logic. In: Cristea, D., Le Ber, F., Sertkaya, B. (eds) Formal Concept Analysis. ICFCA 2019. Lecture Notes in Computer Science(), vol 11511. Springer, Cham. https://doi.org/10.1007/978-3-030-21462-3_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-21462-3_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-21461-6
Online ISBN: 978-3-030-21462-3
eBook Packages: Computer ScienceComputer Science (R0)



 .
.
 .
. states that each individual having an r-successor must be an A.
states that each individual having an r-successor must be an A. states that each individual being an r-successor must be an A.
states that each individual being an r-successor must be an A.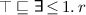 states that each individual has at most one r-successor.
states that each individual has at most one r-successor.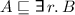 states that each individual that is an A has an r-successor that is a B.
states that each individual that is an A has an r-successor that is a B. , is there a model of
, is there a model of
 ?
? , is there a model of
, is there a model of
 in which E has a non-empty extension?
in which E has a non-empty extension? , does
, does
 entail
entail  , does
, does
 entail
entail  ?
? is to be decided, then time and space requirements are measured as a function of
is to be decided, then time and space requirements are measured as a function of  .
.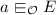 is to be decided where
is to be decided where
 is the union of an ABox
is the union of an ABox
 and some TBox
and some TBox
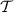 , then necessary time and space is only measured as a function of
, then necessary time and space is only measured as a function of 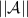 .
.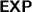 -complete (combined complexity). Since
-complete (combined complexity). Since  [
[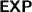 as well. Furthermore,
as well. Furthermore, 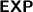 -hard [
-hard [ -hard too.
-hard too. -complete (combined complexity).
-complete (combined complexity).  [
[ . Since
. Since  -hard [
-hard [ -hard too.
-hard too. -complete (data complexity). Instance checking in
-complete (data complexity). Instance checking in  (data complexity) [
(data complexity) [ (data complexity). Furthermore,
(data complexity). Furthermore,  -hard (data complexity) [
-hard (data complexity) [ -complete (data complexity). As instance checking in
-complete (data complexity). As instance checking in  (data complexity) [
(data complexity) [ (data complexity) as well. Furthermore,
(data complexity) as well. Furthermore, 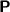 -hard (data complexity) [
-hard (data complexity) [ -hard as well.
-hard as well.

 implies
implies  .
. , and
, and 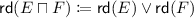 , and
, and 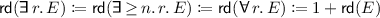 , and
, and  .
.