Abstract
This paper gives a formal definition of the protocol specification language Scribble. In collaboration with industry, Scribble has been developed as an engineering incarnation of the formal multiparty session types. In its ten years of development, Scribble has been applied and extended in manyfold ways as to verify and ensure correctness of concurrent and distributed systems, e.g. type checking, runtime monitoring, code generation, and synthesis. This paper introduces a core version of Scribble, Featherweight Scribble. We define the semantics of Scribble by translation to communicating automata and show a behavioural-preserving encoding of Scribble protocols to multiparty session type.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsReferences
Behavioural Types: From Theory to Tools. River Publishers, Delft (2017)
Bocchi, L., Lange, J., Yoshida, N.: Meeting deadlines together. In: 26th International Conference on Concurrency Theory. LIPIcs, vol. 42, pp. 283–296. Schloss Dagstuhl (2015)
Bocchi, L., Yang, W., Yoshida, N.: Timed multiparty session types. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 419–434. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44584-6_29
Brand, D., Zafiropulo, P.: On communicating finite-state machines. J. ACM 30(2), 323–342 (1983)
Castro, D., Hu, R., Jongmans, S.-S., Ng, N., Yoshida, N.: Distributed programming using role parametric session types in go. In: 46th ACM SIGPLAN Symposium on Principles of Programming Languages, pp. 1–30. ACM (2019)
W3C WS-CDL. http://www.w3.org/2002/ws/chor/
Coppo, M., Dezani-Ciancaglini, M., Padovani, L., Yoshida, N.: A gentle introduction to multiparty asynchronous session types. In: Bernardo, M., Johnsen, E.B. (eds.) SFM 2015. LNCS, vol. 9104, pp. 146–178. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-18941-3_4
De Nicola, R., Ferrari, G., Pugliese, R.: Klaim: a kernel language for agents interaction and mobility. IEEE Trans. Softw. Eng. 24, 315–330 (1998)
Demangeon, R., Honda, K., Raymond, H., Neykova, R., Yoshida, N.: Practical interruptible conversations: distributed dynamic verification with multiparty session types and Python. FMSD 46(3), 197–225 (2015)
Deniélou, P.-M., Yoshida, N.: Multiparty session types meet communicating automata. In: Seidl, H. (ed.) ESOP 2012. LNCS, vol. 7211, pp. 194–213. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28869-2_10
Deniélou, P.-M., Yoshida, N.: Multiparty compatibility in communicating automata: characterisation and synthesis of global session types. In: Fomin, F.V., Freivalds, R., Kwiatkowska, M., Peleg, D. (eds.) ICALP 2013. LNCS, vol. 7966, pp. 174–186. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39212-2_18
Honda, K., et al.: Structuring communication with session types. In: Agha, G., et al. (eds.) Concurrent Objects and Beyond. LNCS, vol. 8665, pp. 105–127. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44471-9_5
Honda, K., Mukhamedov, A., Brown, G., Chen, T.-C., Yoshida, N.: Scribbling Interactions with a Formal Foundation. In: Natarajan, R., Ojo, A. (eds.) ICDCIT 2011. LNCS, vol. 6536, pp. 55–75. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19056-8_4
Honda, K., Vasconcelos, V.T., Kubo, M.: Language primitives and type discipline for structured communication-based programming. In: Hankin, C. (ed.) ESOP 1998. LNCS, vol. 1381, pp. 122–138. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0053567
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. In: POPL 2008, pp. 273–284. ACM (2008)
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. JACM 63, 1–67 (2016)
Hu, R., Neykova, R., Yoshida, N., Demangeon, R., Honda, K.: Practical interruptible conversations. In: Legay, A., Bensalem, S. (eds.) RV 2013. LNCS, vol. 8174, pp. 130–148. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40787-1_8
Hu, R., Yoshida, N.: Hybrid session verification through endpoint API generation. In: Stevens, P., Wąsowski, A. (eds.) FASE 2016. LNCS, vol. 9633, pp. 401–418. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49665-7_24
Hu, R., Yoshida, N.: Explicit connection actions in multiparty session types. In: Huisman, M., Rubin, J. (eds.) FASE 2017. LNCS, vol. 10202, pp. 116–133. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54494-5_7
Lange, J., Tuosto, E.: Yoshida, N.: From communicating machines to graphical choreographies. In: POPL, pp. 221–232. ACM (2015)
Neykova, R., Bocchi, L., Yoshida, N.: Timed runtime monitoring for multiparty conversations. FAOC 29, 877–910 (2017)
Neykova, R., Hu, R., Yoshida, N., Abdeljallal, F.: A session type provider: compile-time API generation for distributed protocols with interaction refinements in F#. In: 27th International Conference on Compiler Construction, pp. 128–138. ACM (2018)
Neykova, R., Yoshida, N.: Let it recover: multiparty protocol-induced recovery. In: CC. ACM (2017, to appear)
Ng, N., de Figueiredo Coutinho, J.G., Yoshida, N.: Protocols by default. In: Franke, B. (ed.) CC 2015. LNCS, vol. 9031, pp. 212–232. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46663-6_11
Scalas, A., Dardha, O., Hu, R., Yoshida, N.: A linear decomposition of multiparty sessions for safe distributed programming. In: 31st European Conference on Object-Oriented Programming. LIPIcs, vol. 74, pp. 24:1–24:31. Schloss Dagstuhl (2017)
Scribble Project.. http://www.scribble.org
Takeuchi, K., Honda, K., Kubo, M.: An interaction-based language and its typing system. In: Halatsis, C., Maritsas, D., Philokyprou, G., Theodoridis, S. (eds.) PARLE 1994. LNCS, vol. 817, pp. 398–413. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58184-7_118
Yoshida, N., Hu, R., Neykova, R., Ng, N.: The scribble protocol language. In: Abadi, M., Lluch Lafuente, A. (eds.) TGC 2013. LNCS, vol. 8358, pp. 22–41. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-05119-2_3
Acknowledgments
We thank the reviewers for their comments. This work is par- tially supported by EPSRC projects EP/K034413/1, EP/K011715/1, EP/L00058X/1, EP/N027833/1 and EP/N028201/1. The first author was supported by an EPSRC Doctoral Prize Fellowship.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Scribble Normal Form
Proposition 4.6 (SNF Translation): Let  be a Scribble local protocol, then
be a Scribble local protocol, then  .
.
Proof. First we consider  . The proof is mechanical and is done by induction on the transition rules applied for closed terms of
. The proof is mechanical and is done by induction on the transition rules applied for closed terms of  .
.
-
1.
(base case) If
 then both
then both  and
and  produce an empty set of traces and no rules can be applied.
produce an empty set of traces and no rules can be applied. -
2.
(inductive case) if
 then
then 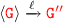 such that
such that  .
.-
(a)
if

 can do \({\mathtt {A}}{\mathtt {B}}!\texttt {msg}\) or \(\ell \) by \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) or \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\) respectively.
can do \({\mathtt {A}}{\mathtt {B}}!\texttt {msg}\) or \(\ell \) by \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) or \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\) respectively.Then
 follows by the induction hypothesis (IH) and by the definition of encoding
follows by the induction hypothesis (IH) and by the definition of encoding -
(b)


By

By IH
 s.t
s.t 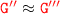
By Lemma 4.5

Thus,
 s.t
s.t 
By

By Lemma 4.5

-
(c)

From
 with
with 
From IH
 s.t
s.t 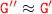 From
From  it follows that
it follows that s.t
s.t 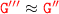
From \({\scriptstyle \lfloor {\textsc {choice}}\rfloor }\) it follows

-
(a)
Now we consider  . The proof is by induction on the definition of encoding of closed terms of
. The proof is by induction on the definition of encoding of closed terms of  .
.
-
1.
(base case) If
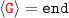 then both
then both  and
and  produce an empty set of traces and no rules can be applied.
produce an empty set of traces and no rules can be applied. -
2.
(inductive case) if
 then
then  such that
such that  .
.-
(a)
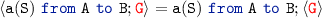
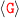 can do
can do  or \(\ell \) by
or \(\ell \) by  or
or 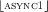 respectively.
respectively.Then
 follows by the IH and by the definition of encoding
follows by the IH and by the definition of encoding -
(b)

From IH:

Thus, if

then
 s.t
s.t 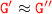
From
 rule:
rule: 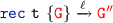
-
(c)
 =
=  From
From  with
with 
By Lemma 4.5
 it follows that
it follows that s.t
s.t 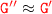
From IH it follows that
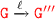 s.t
s.t  .
.
-
(a)
B From Global Protocols to Global Types
Proposition 4.8 (Correspondence of Global Protocols and Global Types): Let  be a Scribble global protocol, then
be a Scribble global protocol, then  .
.
Proof. First, we consider  . The proof is done by induction (on the depth of the tree) on the transition rule applied.
. The proof is done by induction (on the depth of the tree) on the transition rule applied.
-
1.
(Base case) If
 then both
then both  and
and  produce an empty set of traces.
produce an empty set of traces. -
2.
(Inductive case) if
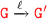 and we have to prove that
and we have to prove that  .
.
-
if
 then we either have a send action by \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) or \(\ell \) transition by \({\scriptstyle \lfloor {\textsc {ASYNC1}}\rfloor }\)
then we either have a send action by \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) or \(\ell \) transition by \({\scriptstyle \lfloor {\textsc {ASYNC1}}\rfloor }\)-

By (1)
 and
and(2)
 and
and(3)
 :
: 
we have

-
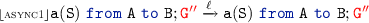
By (1)
 and
and 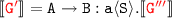 By (2)
By (2)  , which follows from the premise
, which follows from the premise  of the \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\) and by IH and (3)
of the \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\) and by IH and (3)  , which follows from the premise of \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\):
, which follows from the premise of \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\):we can apply the \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }_{MPST}\) rule:

-
-
if
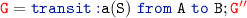
We proceed as in the above case. We either have a receive action by the rule \({\scriptstyle \lfloor {\textsc {recv}}\rfloor }\) or \(\ell \) transition by the rule \({\scriptstyle \lfloor {\textsc {async2}}\rfloor }\).
-
 where
where 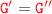
By (1)
 and
and  and
and(3) \({\scriptstyle \lfloor {\textsc {branch}}\rfloor }_{MPST}\):

therefore

-
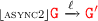 where
where 
By (1)
 and
and  By (2)
By (2)  , which follows from the premises
, which follows from the premises  of the \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\) and by the induction hypothesis and
of the \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\) and by the induction hypothesis and(3) \({\mathtt {A}}, {\mathtt {B}} \not \in subj(\ell )\), which follows from the premise of \({\scriptstyle \lfloor {\textsc {async2}}\rfloor }\):
we can apply the \({\scriptstyle \lfloor {\textsc {async2}}\rfloor }_{MPST}\) rule:

-
-
if

By \({\scriptstyle \lfloor {\textsc {choice}}\rfloor }\) we have
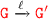 where by the rule premise we have for
where by the rule premise we have for  that
that which brings us back to the first case.
which brings us back to the first case. -
if
 the thesis directly follows by induction since
the thesis directly follows by induction since(1) by
 where
where 
(2)

By


(3) From IH,
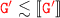 and therefore
and therefore 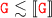
Now we consider  .
.
The proof is done by induction on transition rules applied to the encoding of  .
.
-
1.
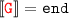 then both
then both  and
and  then no rules can be applied.
then no rules can be applied. -
2.
if
 , then we either have a send action by \({\scriptstyle \lfloor {\textsc {select}}\rfloor }_{MPST}\) or \(\ell \) transition by \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\).
, then we either have a send action by \({\scriptstyle \lfloor {\textsc {select}}\rfloor }_{MPST}\) or \(\ell \) transition by \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\).-

By
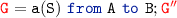 and
and  and
and  it follows that
it follows that 
-
 where
where and
and 
By (1) the rule premise
 and by (2) IH it follows that
and by (2) IH it follows that  .
.Given also that \({\mathtt {A}}, {\mathtt {B}} \not \in subj(\ell )\), we can apply \({\scriptstyle \lfloor {\textsc {async1}}\rfloor }\). Thus,

-
-
3.
if

Then by \({\scriptstyle \lfloor {\textsc {choice}}\rfloor }\) we have that
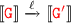 when
when  for \(i \in I\).
for \(i \in I\).Thus, we have to prove that
if
 then
then  , which follows from a).
, which follows from a). -
4.
if
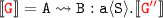
 can do a receive action by \({\scriptstyle \lfloor {\textsc {branch}}\rfloor }_{MPST}\) or \(\ell \) transition by \({\scriptstyle \lfloor {\textsc {async2}}\rfloor }\).
can do a receive action by \({\scriptstyle \lfloor {\textsc {branch}}\rfloor }_{MPST}\) or \(\ell \) transition by \({\scriptstyle \lfloor {\textsc {async2}}\rfloor }\).-
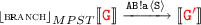
By
 and
and and
and 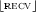 it follows that
it follows that 
-
 where
where and
and 
By (1) the rule premise
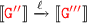 and by (2) IH it follows that
and by (2) IH it follows that  .
.Given also that \({\mathtt {A}}, {\mathtt {B}} \not \in subj(\ell )\), we can apply \({\scriptstyle \lfloor {\textsc {async2}}\rfloor }\). Thus,

-
-
5.
if
 the thesis directly follows by induction.
the thesis directly follows by induction.
C From Local Protocols to Local Types
Proposition 4.12 (Correspondence of Local Protocols and Local Types): Let  be a Scribble local protocol, then
be a Scribble local protocol, then  .
.
Proof.
First, we consider  .
.
The proof is done by induction (on the depth of the tree) on the transition rule applied.
-
1.
(Base case) If
 then both
then both  and
and  produce an empty set of traces.
produce an empty set of traces. -
2.
(Inductive case)
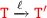 and we have to prove that
and we have to prove that  . We proceed by case analysis on the structure of
. We proceed by case analysis on the structure of 
-
(a)
if
 by \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\)
by \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) by \({\scriptstyle \lfloor {\textsc {LSel}}\rfloor }\)
by \({\scriptstyle \lfloor {\textsc {LSel}}\rfloor }\) -
(b)
if
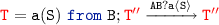 by
by 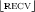
 by \({\scriptstyle \lfloor {\textsc {LBra}}\rfloor }\)
by \({\scriptstyle \lfloor {\textsc {LBra}}\rfloor }\) -
(c)
if

Depending on the structure of
 , this case folds back to previous cases a) and b).
, this case folds back to previous cases a) and b).if
 then
then 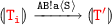 by
by 
if
 then
then  by \({\scriptstyle \lfloor {\textsc {LBra}}\rfloor }\)
by \({\scriptstyle \lfloor {\textsc {LBra}}\rfloor }\) -
(d)
if
 the thesis directly follows by induction.
the thesis directly follows by induction.
-
(a)
Now we consider  .
.
The proof is done by induction on transition rules applied to the encoding.
-
1.
(Base case) If
 then both
then both  and
and  produce an empty set of traces.
produce an empty set of traces. -
2.
(Inductive case)
 and we have to prove that
and we have to prove that  . We proceed by case analysis on the structure of
. We proceed by case analysis on the structure of 
-
if

 by \({\scriptstyle \lfloor {\textsc {LSel}}\rfloor }\)
by \({\scriptstyle \lfloor {\textsc {LSel}}\rfloor }\) by \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\)
by \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) -
if

 by \({\scriptstyle \lfloor {\textsc {Lbra}}\rfloor }\)
by \({\scriptstyle \lfloor {\textsc {Lbra}}\rfloor }\) by \({\scriptstyle \lfloor {\textsc {recv}}\rfloor }\)
by \({\scriptstyle \lfloor {\textsc {recv}}\rfloor }\) -
if
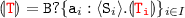

By \({\scriptstyle \lfloor {\textsc {recv}}\rfloor }\) and the structure of
 we have that
we have that  and therefore we can apply \({\scriptstyle \lfloor {\textsc {choice}}\rfloor }\)
and therefore we can apply \({\scriptstyle \lfloor {\textsc {choice}}\rfloor }\)Thus,

-
if
 the case is analogical to the previous one.
the case is analogical to the previous one. -
if
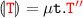 the thesis directly follows by induction.
the thesis directly follows by induction.
Proposition 4.13 (Correspondence of Configurations): Let  be a configuration of Scribble local protocols, then
be a configuration of Scribble local protocols, then  .
.
Proof. The proof is by induction on the number of transition steps.
Inductive hypothesis: 
Now we want to prove that if  then
then

We do a case analysis on the transition label \(\ell \):
(1) if \(\ell = {\mathtt {A}}{\mathtt {B}} ! \mathtt {a}\langle \mathtt {S}\rangle \)
By  and Proposition 4.12 it follows:
and Proposition 4.12 it follows: 
By definition of configuration of local protocols:
 .
.
(2) if \(\ell = {\mathtt {A}}{\mathtt {B}} ? \mathtt {a}\langle \mathtt {S}\rangle \)
By 
By definition of configuration of local protocols:
\(w'_{{\mathtt {A}}{\mathtt {B}}}=w_{{\mathtt {A}}{\mathtt {B}}}\cdot \mathtt {a}(\mathtt {\mathtt {S}})\wedge (\Rightarrow w_{ij}=w'_{ij})_{ij\not = {\mathtt {A}}{\mathtt {B}}} \)
In (1) and (2) we have by definition that  , which by the inductive hypothesis implies that
, which by the inductive hypothesis implies that 
Then by the definition of configuration of local protocols (from (1) and (2)) it follows that  .
.
D From Sribble to CFSM
Lemma 5.5 (Soundness of the translation). Given a local protocol  , then
, then  .
.
Proof. In the proof we assume  . Also we assume
. Also we assume  . When
. When  the lemma is trivially true since
the lemma is trivially true since  produces an empty set of traces,
produces an empty set of traces,  is an empty relation and \(q_0\), the initial state, is also a final state.
is an empty relation and \(q_0\), the initial state, is also a final state.
First, we consider  . Next we prove that if
. Next we prove that if  then
then  such that
such that  and
and  , and
, and  .
.
The proof is by induction on the transition relation for local types. In all cases we assume that  .
.
-
\({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) if the reduction is by \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) we have
 .
.Thus,
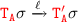 where \(\ell = \texttt {msg}!{\mathtt {A}}{\mathtt {B}}\).
where \(\ell = \texttt {msg}!{\mathtt {A}}{\mathtt {B}}\).Since
 we proceed by case analysis on
we proceed by case analysis on  .
.Case 1:

By Definition 5.2(1-2) and
 .
.Case 2:
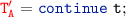
We have that
 , where
, where  .
.By \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) we have
 .
.By Definition 5.2(1-1) and
 it follows that
it follows that with
with 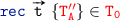 .
.By Lemma 5.4 we have
 and we conclude the case.
and we conclude the case. -
\({\scriptstyle \lfloor {\textsc {recv}}\rfloor }\) is similar to Case \({\scriptstyle \lfloor {\textsc {send}}\rfloor }\) and thus we omit.
-
\({\scriptstyle \lfloor {\textsc {choice}}\rfloor }\) if the reduction is by \({\scriptstyle \lfloor {\textsc {choice}}\rfloor }\) we have
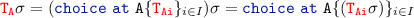 .
.Case 1: if
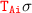 has the shape
has the shape 
then we have
 for some \(j \in I\) with \(\ell = \texttt {msg}_j!{\mathtt {A}}{\mathtt {B}}\).
for some \(j \in I\) with \(\ell = \texttt {msg}_j!{\mathtt {A}}{\mathtt {B}}\).Since
 =
=  , we proceed by case analysis on
, we proceed by case analysis on  .
.Case 1.1:

By Definition 5.2(3-a-2) and
 =
= 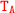 we have
we have  .
.Case 1.2:

-
(1*)
We have that
 , where
, where  .
. -
(2*)
By \({\scriptstyle \lfloor {\textsc {choice}}\rfloor }\) we have
 .
.By Definition 5.2(3-a-2) and

with
 .
.By Lemma 5.4 we have
 .
.
Applying the IH to (1*) and (2*) we conclude the case.
Case 2: if
 has the shape
has the shape 
this case is similar to Case 1 and thus we omit.
Note that since the normal form of local types does not allow for unguarded choice, hence, all possible transitions of
 are the transitions from Case 1 and Case 2.
are the transitions from Case 1 and Case 2. -
(1*)
-
\({\scriptstyle \lfloor {\textsc {rec}}\rfloor }\) if the reduction is by \({\scriptstyle \lfloor {\textsc {rec}}\rfloor }\) we have then

 . We note that
. We note that  does not contain the term
does not contain the term  since unguarded recursive variables are not allowed. Hence,
since unguarded recursive variables are not allowed. Hence,  is either send, receive or choice and by IH and
is either send, receive or choice and by IH and  ,
, 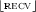 ,
,  we conclude this case.
we conclude this case.
We next consider  . We prove that given a local protocol
. We prove that given a local protocol  if
if  then
then  s.t.
s.t.  and
and  and
and  with
with  . We proceed by case analysis on the transitions in \(\delta \).
. We proceed by case analysis on the transitions in \(\delta \).
Case 1:  and \(\ell = \texttt {msg}?{\mathtt {A}}{\mathtt {B}}\).
and \(\ell = \texttt {msg}?{\mathtt {A}}{\mathtt {B}}\).
Then  and we have by
and we have by  .
.
Case 1.1: if 
The hypothesis follows from  .
.
Case 1.2: if 
By Definition 5.2  .
.
By Definition 5.3 and Lemma 5.4 we have  .
.
From IH and  we conclude the case.
we conclude the case.
Case 2:  and \(\ell = \texttt {msg}!{\mathtt {A}}{\mathtt {B}}\).
and \(\ell = \texttt {msg}!{\mathtt {A}}{\mathtt {B}}\).
Proceeds in a similar way as Case 2 and thus we omit.
Case 3:

Then we have by \({\scriptstyle \lfloor {\textsc {choice}}\rfloor }\)
 for some \(j \in I\).
for some \(j \in I\).
Case 3.1: if 
From IH and  we conclude the case.
we conclude the case.
Case 3.2: if 
By Definition 5.2 
By Definition 5.3 and Lemma 5.4 we have  s.t.
s.t.  .
.
We have that  , hence we conclude the case.
, hence we conclude the case.
Case 4:

Proceeds in a similar way as Case 3 and thus we omit.
Case 5:

Note that the  is either message send or message receive. Hence, By applying the IH and Case 1, 2 we conclude the case.
is either message send or message receive. Hence, By applying the IH and Case 1, 2 we conclude the case.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Neykova, R., Yoshida, N. (2019). Featherweight Scribble. In: Boreale, M., Corradini, F., Loreti, M., Pugliese, R. (eds) Models, Languages, and Tools for Concurrent and Distributed Programming. Lecture Notes in Computer Science(), vol 11665. Springer, Cham. https://doi.org/10.1007/978-3-030-21485-2_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-21485-2_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-21484-5
Online ISBN: 978-3-030-21485-2
eBook Packages: Computer ScienceComputer Science (R0)


 then both
then both  and
and  produce an empty set of traces and no rules can be applied.
produce an empty set of traces and no rules can be applied. then
then 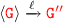 such that
such that  .
.
 can do
can do  follows by the induction hypothesis (IH) and by the definition of encoding
follows by the induction hypothesis (IH) and by the definition of encoding


 s.t
s.t 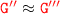

 s.t
s.t 



 with
with 
 s.t
s.t 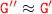 From
From  it follows that
it follows that s.t
s.t 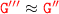

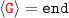 then both
then both  and
and  produce an empty set of traces and no rules can be applied.
produce an empty set of traces and no rules can be applied. then
then  such that
such that  .
.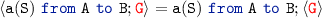
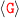 can do
can do  or
or  or
or 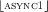 respectively.
respectively. follows by the IH and by the definition of encoding
follows by the IH and by the definition of encoding


 s.t
s.t 
 rule:
rule: 
 =
=  From
From  with
with 
 it follows that
it follows that s.t
s.t 
 s.t
s.t  .
. then both
then both  and
and  produce an empty set of traces.
produce an empty set of traces.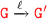 and we have to prove that
and we have to prove that  .
. then we either have a send action by
then we either have a send action by 
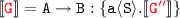 and
and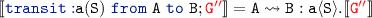 and
and :
: 

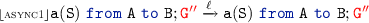
 and
and 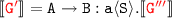 By (2)
By (2)  , which follows from the premise
, which follows from the premise  of the
of the  , which follows from the premise of
, which follows from the premise of 
 where
where 
 and
and  and
and

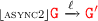 where
where 
 and
and  By (2)
By (2)  , which follows from the premises
, which follows from the premises  of the
of the 

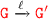 where by the rule premise we have for
where by the rule premise we have for  that
that which brings us back to the first case.
which brings us back to the first case. the thesis directly follows by induction since
the thesis directly follows by induction since where
where 



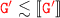 and therefore
and therefore 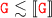
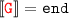 then both
then both  and
and  then no rules can be applied.
then no rules can be applied. , then we either have a send action by
, then we either have a send action by 
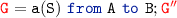 and
and  and
and  it follows that
it follows that 
 where
where and
and 
 and by (2) IH it follows that
and by (2) IH it follows that  .
.

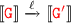 when
when  for
for  then
then  , which follows from a).
, which follows from a).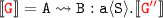
 can do a receive action by
can do a receive action by 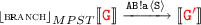
 and
and and
and 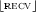 it follows that
it follows that 
 where
where and
and 
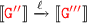 and by (2) IH it follows that
and by (2) IH it follows that  .
.
 the thesis directly follows by induction.
the thesis directly follows by induction. then both
then both  and
and  produce an empty set of traces.
produce an empty set of traces.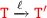 and we have to prove that
and we have to prove that  . We proceed by case analysis on the structure of
. We proceed by case analysis on the structure of 
 by
by  by
by 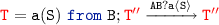 by
by 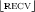
 by
by 
 , this case folds back to previous cases a) and b).
, this case folds back to previous cases a) and b). then
then 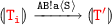 by
by 
 then
then  by
by  the thesis directly follows by induction.
the thesis directly follows by induction. then both
then both  and
and  produce an empty set of traces.
produce an empty set of traces. and we have to prove that
and we have to prove that  . We proceed by case analysis on the structure of
. We proceed by case analysis on the structure of 

 by
by  by
by 
 by
by  by
by 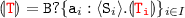

 we have that
we have that  and therefore we can apply
and therefore we can apply 
 the case is analogical to the previous one.
the case is analogical to the previous one.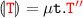 the thesis directly follows by induction.
the thesis directly follows by induction. .
.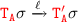 where
where  we proceed by case analysis on
we proceed by case analysis on  .
.
 .
.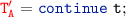
 , where
, where  .
. .
. it follows that
it follows that with
with 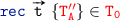 .
. and we conclude the case.
and we conclude the case.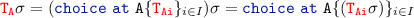 .
.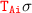 has the shape
has the shape 
 for some
for some  =
=  , we proceed by case analysis on
, we proceed by case analysis on  .
.
 =
= 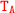 we have
we have  .
.
 , where
, where  .
. .
.
 .
. .
. has the shape
has the shape 
 are the transitions from Case 1 and Case 2.
are the transitions from Case 1 and Case 2.
 . We note that
. We note that  does not contain the term
does not contain the term  since unguarded recursive variables are not allowed. Hence,
since unguarded recursive variables are not allowed. Hence,  is either send, receive or choice and by IH and
is either send, receive or choice and by IH and  ,
, 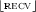 ,
,  we conclude this case.
we conclude this case.