Surface Prediction for Spatial Augmented Reality Using Cubature Kalman Filtering

Abstract

Projection mapping onto non-rigid deformable objects requires highly accurate tracking of its surface position. Traditional methods of using measured deformations of the surface can be inadequate due to potential sources of time delay, such as projector lag. Previous work done by Gomes et al. [3] demonstrated a novel approach for predicting the motion of a non-rigid surface to assist in the compensation of any delays. This paper improves upon the extended Kalman filter algorithm, presented by Gomes et al., by introducing a higher order approximation using the cubature Kalman filter. This algorithm is verified using an experimental setup where an image is projected onto a deformable surface being disturbed by a “random” force. The results show a marked improvement over the extended Kalman filter. The error results demonstrate that the cubature Kalman filter can be applied to situations with low measurement capture rates as well as higher levels of occlusion.

1 Introduction

Spatial augmented reality (SAR) is the use of projection technology for the purpose of transforming any object into a display surface. This, currently, is most often used by the entertainment industry to project large, sometimes user interactive, scenes onto walls or other rigid surfaces such as tables and buildings. Projection mapping onto non-rigid surfaces could be very useful in the entertainment and fashion industries, and the field of surgical training. Current rigid mapping algorithms, however, would not be able to function if significant deformations were to alter the surface, such as those involved with textiles, leading to a lack of realism and immersion. Current methods to solve this problem [7, 10, 11] involve the real-time tracking of surface geometry and projecting a warped image onto the measured surface. However, for quickly changing surfaces there is no mention of how well these techniques perform. If a surface being tracked is moving quickly the image processing and surface tracking time required may cause delays that lead to image distortions. Other solutions [6] that have been shown to work for high speed deformations rely on highly customised and expensive projector and tracking systems. Other issues that arise due to the nature of this problem include inherent system time delays for real time purposes as well as occlusions. Projectors are notorious for having slow response times, also called input lag, which along with algorithm processing times can be a large damper on any real time effects. Occlusions occur when an object being tracked is blocked from observation and so can no longer be measured. A common occurrence when tracking non-rigid surfaces is self-occlusion where by the object itself prevents it from being fully measured. A prediction scheme can be used to approximate the position of the surface at some future time, which can smooth the overall experience. The goal of this paper is to improve upon the extended Kalman filter (EKF) algorithm presented by Gomes et al. [3] by implementing a cubature Kalman filer (CKF) process. This paper does not cover any image warping or projection techniques as it is assumed standard techniques will be used for projection. This paper is organized as follows: Sect. 2 discusses the modelling of the non-rigid surface, Sect. 3 introduces the EKF and CKF prediction based surface tracking algorithms, Sect. 4 provides a description of the experimental procedure for real-time application of the algorithm, Sect. 5 presents the results of the experiment, and Sect. 6 lists conclusions and future work.

2 System Model

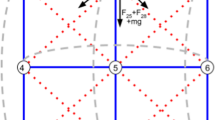
The CKF algorithm requires a physically accurate deformable model that will describes the motion of the surface being tracked. Several different deformable models have been studied in the field of computer graphics ranging from aesthetically pleasing to physically accurate. This paper uses the mass-spring system used by Gomes [4] due to its simplicity, speed, and ease of construction. The mass-spring model was first developed by Provot [9], it uses an interconnection of point masses (nodes), springs, and dampers to represent a surface. Each point mass is connected to all adjacent nodes with structural springs (or dampers), diagonal nodes with shear springs (or dampers) and nodes that are two steps away with flexion springs (or dampers), as shown in Fig. 1. This allows each point mass to be connected from between 3 to 12 other nodes.

Fig. 1.

Connection of point masses with structural springs (blue), shear springs (red dashed), and flexion springs (grey dashed) (Color figure online)

The dynamics of the system can be written in the state space form:

$$\begin{aligned} x[k+1]=f(x[k],u[k]), \end{aligned}$$

(1)

$$\begin{aligned} y[k]=Cx[k], \end{aligned}$$

(2)

where x[k] is the state vector containing the position and velocity information of each node at time-step k, f(x, u) contains the nonlinear dynamics of the system and u[k] is a vector of input forces. The matrix C in Eq. (2) selects only the position states from the state vector to be the output of the model.

To account for errors between the model and the real-life plant, a random process w[k], with covariance $Q_k$, is added to the state equation (1) and a random process v[k], with covariance $R_k$, is added to the output equation (2). The state and output equations now become:

$$\begin{aligned} x[k+1]=f(x[k],u[k])+w[k], \end{aligned}$$

(3)

$$\begin{aligned} y[k]=Cx[k]+v[k]. \end{aligned}$$

(4)

As stated in [3], the inner dynamics of the model are linear, however, the geometry of the model causes nonlinearities (similar to those of a pendulum). These nonlinearities require linearization to be used with the EKF estimation algorithm previously presented, discussed further in Sect. 3. Using the first order Taylor series expansion for linearization, the dynamics are converted to the simpler form of:

$$\begin{aligned} x[k+1]=Fx[k]+Bu[k]+w[k], \end{aligned}$$

(5)

where F is the Jacobian matrix of f(x, u) with respect to x and B is a matrix that selects the inputs related to the velocity states.

With the dynamics of the surface defined in a state space form, the model can easily be implemented into estimation filters; one of which will be used in the algorithm described in the next section.

3 Prediction Algorithm

A common technique to predict states of a nonlinear dynamic system is the EKF algorithm [1]. The EKF is a extension of the standard Kalman filter, which is an algorithm that uses measured outputs of a system to make state estimates, which are essentially the best guess of the internal behaviour of the system. The Kalman filter can be used to find state estimates when measurements are corrupted with noise or when the system is not modelled perfectly, but can also be used as an algorithm for predicting what the state value will be. The standard Kalman filter produces the optimal estimate of a system under the condition that the dynamics of system are linear and any measurement or modelling error is normally distributed. The EKF extends the Kalman filter to systems that have nonlinear dynamics, in a very straightforward way. The EKF takes the nonlinear model, finds the closest linear model of the system each time a prediction is needed, and uses the standard Kalman filter algorithm to predict the states. Since the dynamics of the mass-spring system are nonlinear, the EKF is a suitable choice for predicting the motion of a non-rigid surface. However, since the EKF uses the linearized model, Eq. (5), to update the estimates of the system, it only provides a first-order approximation of system states. As a result, the EKF may only give a “near-optimal” estimate of the system. There are other filtering techniques that provide a solution to the state estimates of a system which may be more accurate than the EKF. In this paper, the Cubature Kalman filter will be used instead of the EKF to predict the position and velocity of non-rigid surfaces.

To develop a more accurate way of predicting the states of a nonlinear system, one can take advantage of the “nice” properties of Gaussian distributions. Since it is assumed that the nonlinear mass-spring system is modelled with error that is normally distributed, these properties can be exploited. It is well known that the best state prediction, $x_{k|k-1}$, of a dynamic system is given by a conditional expectation [2]. Furthermore, when the source of noise in the model is normally distributed, the state prediction can be written as an integral of the nonlinear model f(x, u) and of the Gaussian density function. Since this integral may be difficult to solve, it can be approximated as

$$\begin{aligned} x_{k|k-1}\approx \sum _{i=1}^m\omega _if(\zeta _{i}) \end{aligned}$$

(6)

where $\omega _i$ are weights and $\zeta _{i}$ are sample points which are chosen in a specific manner. This method of approximation is called a Gaussian quadrature rule for solving the conditional expectation of a normally distributed random variable [2]. As already stated, the standard way of solving for a conditional expectation is to solve a complicated integral equation (which may not have a closed form solution). A Gaussian quadrature rule allows for a computationally less intensive approximation of the conditional expectation. The difficult part of finding an accurate approximation, as given in Eq. (6), is solving for the weights $\omega _{i}$ and sample points $\zeta _{i}$. There may be many combinations weights and sample points that give a “somewhat” accurate solution of the state prediction. The Cubature Kalman filter (CKF) is a one of many approaches to finding weights and sample points that are “optimal” in a certain sense [2]. In fact, the CKF provides a solution for the state prediction that is more accurate (third order approximation of the true solution) than the solution given by the EKF (first order approximation). The CKF uses what are called cubature rules to solve for the weights and sample points; the mathematics of which are beyond the scope of this paper. The weights and sample points given by the cubature rules can be found by

$$\begin{aligned} \omega _{i}=1/m,\quad i=1,2,\ldots m \end{aligned}$$

(7)

and

$$\begin{aligned} \zeta _i=\sqrt{\frac{m}{2}}\{\mathbf {1}\}_i,\quad i=1,2,\ldots m \end{aligned}$$

(8)

where $m=2n$, n is the number of states of the system, and $\{\mathbf {1}\}_i$ is the $i^\text {th}$ element of the set of all n-dimensional unit axis vectors. Figure 2 provides a simple illustration of how the sample points of the CKF allows it to be a more accurate prediction algorithm than the EKF. Solving the cubature rules is only a small portion of the entire CKF algorithm which is very simply depicted in Fig. 3.

Fig. 2.

Visualisation of the EKF and CKF algorithms propagation accuracy when compared to a true sampling technique

Figure 3 shows a simple flow chart of the CKF algorithm where the function f(x, u) describes the dynamics of mass-spring model and the plant is the real-life system on which measurements are made. At each prediction time-step, $T_m$, the most recent estimate of the non-rigid surface, $x_{k-1|k-1}$ is offset by each sample point $\zeta _i$ for $i=1,\ldots 2n$ multiplied by the square root of the most recent covariance matrix $P^{1/2}_{k-1|k-1}$ to create a set of 2n vectors. Each of these 2n offset estimate vectors are passed through the mass-spring model, Eq. (1), and are then averaged to create a prediction of the plant’s position and velocity $x_{k|k-1}$. This prediction is used as the best “guess” of what the surface will look like one time-step into the future. The covariance matrix of each of the 2n offset vectors are sent through a simple linear transformation and are averaged to create the predicted state covariance matrix $P_{k|k-1}$. The state covariance matrix gives a description of how correlated the states of the system are to one another at each iteration of the algorithm. This entire step is known as the prediction step of the CKF. After a new measurement, y, is made from the real-world system, the state prediction $x_{k|k-1}$ is now offset by the same sample points $\zeta _i$ for $i=1,\ldots 2n$ multiplied by the square root of the predicted covariance matrix $P^{1/2}_{k|k-1}$, is averaged again, and is subtracted from the measurement y. This “error” is then combined with the state prediction $x_{k|k-1}$ and predicted covariance matrix $P_{k|k-1}$ to produce the “near-optimal” state estimate $x_{k|k}$ and estimated state covariance $P_{k|k}$. This part of the algorithm is called the update step of the CKF. The state estimate will then be used to create a new prediction for the next time-step, and the algorithm repeats itself. An issue that can arise when measuring the position of a surface is the occlusion of markers. If only measurement data was used to determine the surface geometry, losing vision of a marker would make the projection nearly impossible. However, using this prediction algorithm, the lost marker’s position can be approximated using the prediction step of the CKF, which is a very close estimate of the true position of the marker. This allows occlusion compensation to be nearly free, provided the markers are not covered for an extended period of time.

When running the CKF algorithm for SAR applications, a projector needs to project images on the predicted surface. This can pose issues as the projector takes a certain amount of time to receive and process images from a computer and an additional amount of time to draw a frame. It is well known that projectors suffer from delays when processing images and these delays usually range from 20 ms to 100 ms depending on the type of projector [5]. This delay, $T_d$, is troublesome when using the CKF for surface prediction in real-time. Since an image needs to be sent to the projector $T_d$ seconds in advance to be projected at the correct time, the CKF needs to predict the geometry of the surface $T_d$ seconds in the future at each predict step. Now, since measurements are received every $T_m$ seconds, the CKF can only update the state estimate every $T_m$ seconds. An issue arises when the delay time $T_d$ and measurement time $T_m$ do not match (i.e. are vastly different). The time of the current state prediction and the time at which the measurement is made will never be the same. This means the traditional CKF algorithm will not work, as the prediction and measurement times need to line up. To fix this issue, a further prediction, using numerical integration, is made to align the time of the current state prediction with the current measurement. At this stage, a new estimate can be made using the regular CKF algorithm.

When compensating for the delay caused by the drawing of a frame, it is imperative to consider the speed at which the surface is moving compared to the drawing rate. Surfaces that move quickly with respect to the drawing rate of the projector may incur additional image distortion because the projector is still drawing an “old” image. To compensate for the effects of surface movement during the drawing of frames, an inter-frame prediction (IFP) method is used, as proposed in [3]. Considering that the update rate of the CKF is $T_m$ seconds, if the cloth’s position changes significantly during inter-sample periods, there may be significant error between the prediction and the actual position of the cloth when a new measurement is made. To compensate for this, an interpolation approach is used. As the cloth is moving, the CKF solves for an estimate of the velocity states, and using a first-order approximation, the inter-sample position of every node is calculated. This estimation is based on the assumption that drawing horizontally is instantaneous.

Fig. 3.

Block diagram of the CKF algorithm with the mass-spring model

Using the state prediction ${x}_{k|k-1}$, which was solved with Eq. (1) and the corresponding time-step, $n\varDelta T$, where n is the row number and the time-step $\varDelta T$ is defined by

$$\begin{aligned} \varDelta T=\frac{1}{\text {frame rate}\times (\#\text {rows}-1)}, \end{aligned}$$

(9)

the inter-frame prediction can be computed. First the state prediction vector is split into a position prediction vector ${p}_{k|k-1}$ and a velocity prediction vector ${v}_{k|k-1}$. The position predictions are then reordered, such that the elements are ordered based on their horizontal position with respect to the projector. More specifically, the first i elements of the position vector would contain the positional information of the first horizontal row of nodes with respect to the projector, the next j elements would contain the positional information of the second horizontal row of nodes with respect to the projector, and so on (Fig. 4).

Fig. 4.

Orientation of cloth with respect to projector for inter-frame prediction

After reordering the states, the predictions are passed through the state transition function f(x, u), described by Eq. (1). This returns the derivative of the position state predictions, and as a result, the velocities to obtain the next position vector. The velocity vector is then multiplied by a matrix describing the time at which each row of the object is predicted. The result is added to the position estimates to obtain the inter-frame position predictions ${p}_{k|k-1}'$. At a time $t_0$, when the system receives a measurement from the cameras, the current prediction at $t_0$ is combined with the measurement to produce the new estimate. This is done using the aforementioned Kalman update step. Since the time between measurements, $T_m$, is quite large, the IFP algorithm is run at a time-step of $\varDelta T$ to counteract the effects of surface motion while drawing. When each new estimate is calculated, every $T_m$ seconds, the Kalman predict step of the CKF is run to create a prediction $T_d$ seconds into the future. This is done to have a prediction of the surface when the projector is ready to draw a frame. This new Kalman prediction replaces the prediction from the IFP algorithm, and the whole sequence repeats itself until termination. The entire CKF-IFP algorithm, compensating for projector delay, is shown in Fig. 5.

Fig. 5.

Timing diagram of CKF-IFP algorithm. $\varDelta T$ is the IFP time-step, $T_m$ is the measurement time, and $T_d$ is the delay time.

4 Experimental Setup

Validation of the algorithm proposed in Sect. 3 will be performed using the experimental procedure proposed in [3]. The goal of the experiment is to show the effectiveness of using the CKF-IFP algorithm when compared to projecting with the EKF-IFP procedure. This will be done by projecting an image onto a perturbed surface, and using subjective measures to determine whether using the CKF-IFP algorithm is superior to using the EKF-IFP. To maintain consistency with previous measures a towel is chosen to be the surface for the experiment as it is very deformable and sensitive to external forces. Positional data of the surface of the towel is required for the prediction algorithms to function. Several choices of data capture systems can be considered, such as image processing techniques or 3D scanning systems; however, this experiment uses an infrared motion capture system for added position accuracy. The NaturalPoint OptiTrack system [8] is an infra-red (IR) camera-based motion capture system that provides positional data, both translational and rotational, within millimeter precision. For this experiment, a three camera configuration is used to measure the position of 12.7 mm diameter infra-red markers. The markers are placed on the towel to match the initial positions of the mass nodes in the model. Specifically, 20 markers are placed on the towel corresponding to a $5 \times 4$ node mass-spring system used to model the system. The towel is hung vertically, just as it would be on a standard towel rack, such that all the IR markers are visible to the cameras. An Epson VS240 short-throw projector is placed directly in front of the towel, and below the cameras as to not interfere with the cameras’ view. Figure 6 shows the complete experimental setup.

Fig. 6.

Photo of experimental setup with three motion capture cameras, a projector and a towel being projected onto.

Before the CKF-IFP algorithm in Sect. 3 can be used the mass-spring model parameters need to be chosen so that the simulated deformable model has similar characteristics to the real-life system. Using visual inspection, mass values of 0.025 kg for each node, spring constant values of $300\frac{\mathrm{N}}{\mathrm{m}}$, and damper values of $0.08\frac{\text {N}\cdot \text {s}}{\text {m}}$ for each spring and damper connection are chosen. Errors in parameter choice are considered to be process noise and lumped into the w[k] term and will be handled by the CKF. The initial position states of the mass-spring model are set to be equal to the position of the IR markers on the towel and the velocity states are set to 0, as the towel is at rest. Since the initial states of the mass-spring model match the initial conditions of the real-life surface, the initial state covariance matrix is set to the zero matrix, as there is no uncertainty between the initial state and the true position of the surface. The measurement noise covariance matrix $R_k$ is set so that the variance of each position state is 0.01 mm$^2$, and the covariance between any two position states is 0 mm$^2$ (considered independent). These values of variance are chosen based on the error specifications given by the OptiTrack system. The model noise covariance matrix $Q_k$ is chosen to be an identity matrix, as 1 m can easily be assumed to be an extreme upper bound for the uncertainty in node position.

Before the experiment can be run the system needs to be properly calibrated. A still image is projected onto the towel when it is at rest, as seen in Fig. 6. The projection parameters are then adjusted so that the computer knows where the projector is relative to the surface. Finally, the timing parameters $T_m$ and $T_d$ are tuned so that the speed of motion of the model matches that of the towel. After the system adequately matches the mass-spring model to the towel, a rotating fan is placed behind the towel to create a “random” motion on the surface. This is done to test the robustness of the prediction algorithms under conditions of randomness. Additionally, the delay time-step is set to 30 ms and the rate at which the measurement are sampled is varied between 100 fps (10 ms) and 50 fps (20 ms). This is done to verify the usefulness of the algorithms on systems where data is less easily available as well its ability to deal with occlusions, as occlusions lead to fewer measurements being made available. The results of the projection method are visually inspected and predictions of the surface position states are stored to be compared to the real-world values offline.

5 Results

The effectiveness of the CKF-IFP algorithm presented in Sect. 3 is evaluated on the experimental setup described in Sect. 4, qualitative and quantitative methods are used. Qualitatively, the results of the both the EKF and CKF prediction algorithms are visually compared to each other. When the image is projected onto a flat surface (the towel at rest), both projection methods produce the exact same results. However, once the towel is disturbed by the fan, there is a noticed difference. Both algorithms perform better than no algorithm running, however, the CKF-IFP method produces slightly more true-to-life results when compared to the EKF-IFP, this is especially true with the lower 50 fps measurement sample rate. When comparing static compensation of the algorithms, both the CKF and EKF algorithms perform identically to that stated in [3] and far outperform the standard, sans algorithm, projection method, as shown in Fig. 7. In the three orientations shown in Fig. 7 the CKF and EKF algorithms both compensate identically since the towel being stationary means their solutions converge. However, the uncompensated projection produces clipped and undesirable results. Specifically, the uncompensated projection method displays parts of the image past the towel, onto the wall, while the prediction algorithms “paints” the image on the towel.

Fig. 7.

Visual comparison of standard projection and prediction algorithms on static deformations

Fig. 8.

Mean error graph display the average error between measured and predicted node positions over time with a 100 fps measurement sample rate.

Fig. 9.

Mean error graph display the average error between measured and predicted node positions over time with a 50 fps measurement sample rate.

Quantitatively, the success of the CKF-IFP algorithm is evaluated using the mean error between the measured position of the markers and the predicted position of the mass nodes. At every measurement time-step, the difference between measured position of node and the predicted position of the node are squared and then averaged. The mean error is defined as

$$\begin{aligned} E[k]=\frac{1}{N}\sum _{k=1}^N\Vert y[k]-Cx_{k|k-1}\Vert \end{aligned}$$

(10)

where N is the total number of nodes (20 in this case), y[k] as defined in Eq. (2) is the output vector, and $x_{k|k-1}$ is the state prediction vector. Figure 8 shows the mean error (ME) between measured and predicted node positions over a 10 s window for both the CKF and EKF algorithms with a measurement sample rate of 100fps. It can be seen that after every large input (strong gust from the fan), the ME for both algorithms increases drastically. This is due to the non-anticipatory behaviour of real systems. After this peak in error, the ME exponentially decreases to a point where there is almost no difference between predictions and measurements. The mean error for the CKF and EKF peak at roughly 1.6 mm and 2.9 mm, respectively, when the towel is most affected by the input force, and 0.5 mm and 0.8 mm when the towel comes back to rest. These effects are even more pronounced when the measurement sampling rate is reduced to 50 fps as shown in Fig. 9. The maximum ME for the CKF and EKF in this case goes up to roughly 2.3 mm and 5.3 mm, respectively while the ME at rest is 0.6 mm for both cases. This demonstrates that CKF performs significantly better than the EKF, especially in the 50 fps measurement sample rate case. The implications of this result are that the CKF would be better suited for applications with slower measurement rates as well as in systems with higher occlusion occurrences.

6 Conclusion

This paper implements an improvement to the EKF techniques for predicting the motion of non-rigid surfaces for image projection specified by Gomes et al. [3]. The CKF based algorithm, named the CKF-IFP algorithm, predicts the position of a non-rigid surface by using a set of sample points to improve the accuracy of Kalman filter when applied to highly nonlinear models. The algorithm is shown to handle the delays often associated with projectors as well as handle brief occlusions of the surface far better than its EKF counterpart. Using a mass-spring system to model the dynamics of a towel, the CKF-IFP algorithm was able to improve on the position prediction of the nodes with errors ranging between 2.3 mm and less than 0.5 mm on average. The CKF-IFP algorithm was shown to outperform the EKF-IFP algorithm even when tested with a worse measurement sample rate than its counterpart. These results were observed when the non-rigid surface was being perturbed by random forces. Projection using the CKF-IFP algorithm created a more realistic and useful experience when compared to the EKF-IFP and so should be able to expand on its practical uses.

6.1 Future Work

As the mass, spring and damper parameters for the model were chosen quite arbitrarily, finding parameters that match the surface material properties would allow for more robust prediction. Future work will include using machine learning techniques for parameter identification. Additional future work includes using less obstructive motion capturing systems since the marker based motion capture system is quite expensive and sensitive to environmental conditions. A more cost-effective camera based system, combined with computer vision techniques, can instead be used to capture the position of surfaces in real-time. Although this will likely cause an increase in sensor noise in the system, the prediction algorithm should be able to compensate for the additional measurement error.

Additional work to improve the performance of the algorithm includes the distribution of the nodes on the objects surface as well as taking advantage of having access to the makeup of the surface. It is of great interest to analyse the effects of distributing the nodal masses on the mass-spring system in a way that is more optimal. Namely, to take advantage of the fact that, in the case of a hanging towel, the nodes at the top of the towel move far less than those at the bottom. Taking this information into account it would be possible to better distribute the nodal masses to improve the simulation accuracy of the areas of higher error. Additionally, by having access to the material of the non-rigid surface, it would be possible to make a surface out of interconnected masses and springs. This would allow our model of the system to be nearly perfect, instead of an approximation of the true physical system. If the model is nearly identical to the real system it would allow for far greater accuracy in prediction.