A Fast kNN-Based Approach for Time Sensitive Anomaly Detection over Data Streams

Abstract

Anomaly detection is an important data mining method aiming to discover outliers that show significant diversion from their expected behavior. A widely used criteria for determining outliers is based on the number of their neighboring elements, which are referred to as Nearest Neighbors (NN). Existing kNN-based Anomaly Detection (kNN-AD) algorithms cannot detect streaming outliers, which present time sensitive abnormal behavior characteristics in different time intervals. In this paper, we propose a fast kNN-based approach for Time Sensitive Anomaly Detection (kNN-TSAD), which can find outliers that present different behavior characteristics, including normal and abnormal characteristics, within different time intervals. The core idea of our proposal is that we combine the model of sliding window with Locality Sensitive Hashing (LSH) to monitor streaming elements distribution as well as the number of their Nearest Neighbors as time progresses. We use an $\epsilon$-approximation scheme to implement the model of sliding window to compute Nearest Neighbors on the fly. We conduct widely experiments to examine our approach for time sensitive anomaly detection using three real-world data sets. The results show that our approach can achieve significant improvement on recall and precision for anomaly detection within different time intervals. Especially, our approach achieves two orders of magnitude improvement on time consumption for streaming anomaly detection, when compared with traditional kNN-based anomaly detection algorithms, such as exact-Storm, approx-Storm, MCOD etc, while it only uses 10% of memory consumption.

This work was supported by the National Key Research and Development Program of China (2016YFB0801305).

1 Introduction

Anomaly (a.k.a. outlier) detection [4] is an important data mining method in applications, such as DDoS detection [12] and medical health monitoring [23]. The task is to identify instances or patterns that do not conform to their expected behaviors [9]. Anomaly detection over data streams is a popular topic in computational science because of its inherent vagueness in definition of outliers, like how to define regular behavior, to what degree an outlier needs to be inconsistent with the regular behaviors when confronting the one-pass and infinite high-speed data streams [21].

Anomaly detection can be classified into supervised [20] and unsupervised [16] in principle. Supervised scenarios are not appropriate for data steams processing due to lack of label information about outliers for one-pass streaming elements. Unsupervised anomaly detection does not require any label information and it is appropriate for data steams processing. Currently, unsupervised anomaly detection methods over data streams can be classified into three categories: (1) Statistical based, (2) Clustering based, and (3) k Nearest Neighbors (kNN) based [22].

kNN-based approaches have drawn the most attention of researchers to find anomalies over data streams. kNN-based approaches assume that the proximity of outliers to their nearest neighbors deviates significantly from the proximity of normal data to their neighbors. Given a dataset D and a threshold k, if data point x has less than k neighbors in D, x is marked as outlier. This kind of approaches have gained popularity as they are easy to implement on the fly. However, current kNN-based anomaly detection method cannot detect outliers with time sensitive abnormal distribution. For example, in DDoS applications, like port scanning, SATAN scanning or IP half-way scanning, attackers send scanning packets in different time intervals and this kind of pre-attack cannot be detected by current kNN-based methods [24, 26].

We briefly describe challenges of anomaly detection over data streams, which are addressed in our work:

• (1) Abnormal distribution detection. When detecting outliers, kNN-based methods only focus on whether the NN number reaches the threshold but do not care the changes of NN number with time. However, there may be some cases where the NN number is normal but the distribution is significantly uneven during a time period. This kind of anomaly cannot be detected by only counting NN, so that we need time sensitive anomaly detection algorithm.

• (2) Concept drift. Most existing data stream anomaly detection techniques ignore one important aspect of stream data: arrival of novel anomalies. In dynamically changing and non-stationary environments, the data distribution can change over time yielding the phenomenon of concept drift [13]. Concept drift is aware of different time intervals, but traditional anomaly detection techniques don’t take time into consideration, and as a result many novel anomalies cannot be detected.

• (3) Real-time requirements. Streaming applications require fast-response and real-time processing from volumes of high-speed and multidimensional dynamic streaming data over time. However, storing all the streaming data requires unbearably large memory so that it is necessary to reduce memory requirements. Additionally, algorithms communicating with DRAM (main memory) are just too slow for the speed at which the data is generated. Ideally, we need ultra-low memory anomaly detection algorithms that can entirely sit in the cache which can be around 2–10 times faster than accessing main memory [11].

The contributions of this paper are as follows:

• (1) We propose a kNN-based approach kNN-TSAD for Time Sensitive Anomaly Detection, which combines an $\epsilon$-approximation scheme Deterministic Waves (DW) with LSH to monitor streaming elements distribution as well as the number of their Nearest Neighbors as time progresses. We use LSH to count NN number without massive calculation of distances between data points. We use DW to monitor distribution of streaming elements during different time intervals. Thus, our anomaly detection method is time sensitive.

• (2) The time and space efficiency of our approach is very high and it well meets the real-time requirements. We combine DW with LSH by the way that every item of the hash array is implemented as a DW window and data update can be very efficient and cost very low. Furthermore, we use LSH to search NN which does not need massive range queries and distance calculation, and it does not need to store neighbor information for every element.

• (3) We provide a comparison of our algorithm with other five traditional kNN-based algorithms based on three real-world datasets. Our experiment shows that kNN-TSAD is two orders of magnitude faster than other algorithms but only uses 10% of memory consumption. Moreover the recall and precision of kNN-TSAD are higher than others over datasets with abnormal distribution.

2 Preliminaries

In the section, we first give the problem definition, and then we will introduce the LSH structure, SRP and the DW model used in this paper.

2.1 Problem Definition

In this paper, we take data distribution into account and we detect kNN-based outliers as well as outliers with abnormal distribution. We give the definition of kNN-based time sensitive outlier in the data streams in Definition 1. The used notation is summarized in Table 1.

Table 1. Frequently used notations.

Definition 1

(kNN-based Time Sensitive Outlier in Data Streams). Given a data stream DS, the current window W, a point $x_{t}$ in DS and two threshold parameters $\alpha$ and $\beta$, we aim to decide whether $x_{t}$ is an outlier or not. We denote the answer by $NN(x_{t}, W)$ and $V(x_{t}, W)$. Formally, if $NN(x_{t}, W) < \alpha \mu$ or $V(x_{t}, W)>\beta \delta$, $x_{t}$ is an outlier, otherwise not.

2.2 Locality Sensitive Hashing

Locality Sensitive Hashing (LSH) is a popular sublinear time algorithm for efficient approximate nearest neighbors search. LSH leverages a family of functions where each function hashes the points in such a way that under the hash mapping, similar points have a high probability of getting the same hash value so that to be mapped into the same bucket. The probability of collision for an LSH hash function is proportional to the similarity distance between the two data vectors, that is $Pr[h(x) = h(y)] \propto sim(x,y)$.

Definition 2

(LSH Family). A family $\mathcal {H}$ is called $(S_{0},cS_{0},u_{1},u_{2})-sensitive$ if for any two data points x,y $\in \mathbb {R}^{d}$ and h chosen uniformly from $\mathcal {H}$ satisfies the following:

• (1) If $sim(x,y)\ge S_{0}$ then $Pr[h(x) = h(y)]\ge u_{1}$.

• (2) If $sim(x,y)\le cS_{0}$ then $Pr[h(x) = h(y)]\le u_{2}$.

2.3 Signed Random Projections

Usually, the family of hash functions of LSH are generated from random projections, the intuition is that points that are nearby in the space will also be nearby in all projections [10, 15]. Given a vector x, it utilizes a random vector w with each component generated from i.i.d. normal (i.e., $w_{i}\sim N(0,1)$), and only stores the sign of the projection. We define a hash function $h_{w}(x)$ as follows:

$$\begin{aligned} h_{w}(x) = sign(w^{T}x) \end{aligned}$$

(1)

And corresponding to this vector w we define the projection function as follows:

$$\begin{aligned} sign(w^{T}x)= {\left\{ \begin{array}{ll} 0&{} w^{T}x\ge 0\\ 1&{} w^{T}x<0 \end{array}\right. } \end{aligned}$$

(2)

For vectors x and w, the probability $Pr[h(x)=h(w)]=1-\frac{\theta (x, w)}{\pi }$.

2.4 Deterministic Waves

Deterministic Waves [14] is a $\epsilon$-approximation scheme for the Basic Counting problem for any sliding window up to a prespecified maximum window size W. The most important thing that distinguishes DW from other sliding-window models is that, for the sum of integers in [0, 1, ..., R] it improves the per-item processing time from O(1) amortized ($O(\log N)$ worst case) to O(1) worst case. The space complexity of DW is $O(\frac{1}{\epsilon }\log ^{2}(\epsilon W))$.

Consider a data stream of integers and a desired positive $\epsilon <1$. The algorithm maintains two counters: pos, which is the current length of the stream, and rank, which is the current integers sum in the stream. The procedure of estimating the sum of integers in a window of size $n\le W$ is as follows. Let $s = max(0, pos-n+1)$, we estimate the sum of integers in stream positions [s, pos]. The steps are:

• (1) Let $p_{1}$ be the maximum position stored in the wave that is less than s, and $p_{2}$ be the minimum position stored in the wave that is greater than or equal to s. (If no such $p_{2}$ exists, return $\hat{x}:=0$ as the exact answer.) v is the integer value at $p_{2}$. Let $r_{1}$ and $r_{2}$ be the rank of $p_{1}$ and $p_{2}$ respectively.

• (2) Return $\hat{x}$ := $rank - \frac{r_{1}+r_{2}-v}{2}$.

3 kNN-TSAD Algorithm

In this section we first walk through an overview of the framework, and then describe the procedure in detail.

Fig. 1.

Framework overview of kNN-TSAD.

3.1 Overview of the Framework

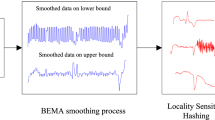
Our kNN-TSAD algorithm combines the functionality of LSH and sliding windows which supports time-based sliding windows queries, so that it can be used for compactly summarizing high-speed and multidimensional streams over sliding windows. It replaces every item of the LSH array with sliding window structures (i.e., DW windows) covering the last W time units of data streams. Figure 1 illustrates the overview of our proposed framework. $DW\_W$ is a two-dimensional LSH array of L rows and $2^{K}$ columns. K and L are pre-specified hyper-parameters. $H_{i}, i\in {0,1, \ldots ,L-1}$ are a group of hash functions, and results of $H_{i}$ are corresponding to the ith row of $DW\_W$. Every item of the LSH array is a DW window. There are two main phases of our kNN-TSAD algorithm.

Insert Phase. The framework performs inserting a data point as follows:

• (1) The nearest neighbors are searched by applying LSH on the data point.

• (2) The data point is inserted into corresponding neighbourhoods which are implemented as DW windows, and expired data are deleted from DW windows.

• (3) The global mean count and the mean variance of active sliding window are updated.

Query Phase. The framework performs an anomaly query as follows:

• (1) NN number of current data point and variance of current window are calculated.

• (2) NN number and variance of the current data point are compared with mean values, and then an anomaly decision result is given.

3.2 Nearest Neighbors Searching

In kNN-based methods for anomaly detection, NN searching is the most important part. Existing methods search neighbors by computing distances of every two data points, and then compare to a distance threshold. This process is quite time consuming. Instead, utilization of LSH can significantly reduce time overhead and improve efficiency of NN searching.

Fig. 2.

An example of NN searching using LSH.

Fig. 3.

An example of time sensitive monitoring.

We randomly generate $K\times L$ vectors $w_{ij}, i\in {0,1, \ldots ,L-1}, j\in {0,1, ,K-1},$ with each component generated from i.i.d. normal (i.e., $w_{ij}\sim N(0,1)$). Then using these random vectors we define $K\times L$ independent signed random projections $h_{ij}, i\in {0,1,\ldots ,L-1}, j\in {0,1,\ldots ,K-1}$, given in Eqs. 1 and 2 and each of them gives one-bit output. So that we can finally generate L K-bit hash functions $H_{i}(x) = [h_{i1}(x);h_{i2}(x);...;h_{iK}(x)], i\in {0,1,\ldots ,L-1}$, which respectively correspond to the indexes in L rows of hash array $DW\_W$. Final NN number of a data point x is the average of all $H_{i}(x)$. By this way the collision probability is significantly reduced from $p=1-\frac{\theta (x, y)}{\pi }$ to $p=Pr[H(x)= H(y)]=p^{K}$, if and only if $h_{j}(x)=h_{j}(y)$ for all $j\in {0,1,\ldots ,K-1}$, $H(x)= H(y)$. Figure 2 shows an example of NN searching process of a data point.

3.3 Time Sensitive Monitoring

To monitor the sliding windows in more detail, we preset a time interval whose length is $\frac{1}{w}$ of the window size. Utilizing the recorded position queue in the DW model, we calculate the average counts of each time interval based on different time range within the sliding window and then work out their variance. The variance will significantly deviate from average level if distribution of data in current sliding window is abnormal.

We have illustrated the procedure of estimating the count of DW in Sect. 2.4, we use the same method to calculate the count of every time interval. Let $tw_{i}, i\in {0,1,\ldots ,w-1}$ be the left bound of every time interval, and $tw_{0}$ be the left bound time of the sliding window. Let $p_{i1}$ be the maximum position stored in the wave that is before $tw_{i}$, and $p_{i2}$ be the minimum position stored in the wave that is after or at $tw_{i}$. Let $r_{i1}$ and $r_{i2}$ be the counts of $p_{i1}$ and $p_{i2}$ respectively. So that $r_{i}$ := $\frac{r_{i1}+r_{i2}-1}{2}$, $i\in {0,1,\ldots ,w-1}$, and rank is the current exact count. Then we use different time range to compute average count of each time interval $cs_{i}$ and $cs_{i} = \frac{rank - r_{i}}{w-i}$. For example, as shown in Fig. 3, $p_{11}$ is the maximum position before $tw_{1}$ and $p_{12}$ is the minimum position after $tw_{1}$. Counts of the two positions are 16 and 24 respectively, so that we estimate the count at $tw_{1}$ which is $r_{1} = \frac{16+24-1}{2} = 20$. The current count rank is 50, thus $cs_{1} = \frac{rank - r_{1}}{2} = 15$, $cs_{0} = \frac{rank - r_{0}}{3} = 16$ and $cs_{2} =\frac{rank - r_{2}}{1} = 16$. Finally we get $\bar{cs}$ = $\frac{15+16+16}{3}=15$, and then the current variance $\sigma ^{2}=2$.

3.4 Efficient Update

Updating operation of our algorithm is to straightforward increment (or decrement) the counters when a data point is added (or removed). We only need to add or delete data points in the corresponding DW window and update the global mean values $\mu$ and the mean variance $DW\_W[i][H_{i}(x)]{.}\delta$ of current sliding window. This operation does not need lots of distance computation to update neighbor information like traditional kNN-based algorithms.

As a new data point $x_{t}\in DS$ arrives, we add it to the DW window at corresponding index $H_{i}(x)$ of each row so that every DW window keeps the number of hits to this particular window. We get the neighbors count c of $x_{t},$ $c = \frac{1}{L}\sum _{i=0}^{L-1}DW\_W[i][H_{i}(x)]$. Then we calculate average count of every time interval $cs_{j},j\in [0,w-1]$ so as to calculate the variance $\sigma ^{2}$. We compute the mean count $\mu$,

$$\begin{aligned} \mu = \frac{1}{n+1}\left( n\mu +\frac{1}{L}\sum _{i=0}^{L-1}DW\_W\left[ H_{i}(x)\right] \right) \end{aligned}$$

(3)

and the mean variance $DW\_W[i][H_{i}(x)]{.}\delta$ of past part of $DW\_W[i][H_{i}(x)]$,

$$\begin{aligned} DW\_W[i][H_{i}(x)]{.}\delta = \frac{DW\_W[i][H_{i}(x)]{.}count\times DW\_W[i][H_{i}(x)]{.}\delta +\sigma ^{2}}{DW\_W[i][H_{i}(x)]{.}count+1}. \end{aligned}$$

(4)

Deviation from the mean values indicate anomaly. It turns out that we can dynamically update the mean values $\mu$ and $DW\_W[i][H_{i}(x)]{.}\delta$ on the fly, as we observe new coming data.

3.5 Anomaly Detection

Our algorithm serves for data streams which are high-speed and one-pass. We use two types of queries to accurately conduct anomaly detection.

• (1) kNN-based anomaly detection queries. kNN-based anomaly detection is a global procedure. A global mean count $\mu$ is calculated to get the threshold $\alpha \mu$. In inserting phase we compute current count and compare with the threshold, and if a DW window satisfies $c < \alpha \mu$, all data in that window are marked as outliers. The process is shown in Algorithm 1.

• (2) Distribution anomaly detecion queries. Distribution anomaly detection is a local procedure. Every DW window keeps a mean variance $DW\_W[i][H_{i}(x)]{.}\delta$, and with it we get a threshold $\beta DW\_W[i][H_{i}(x)]{.}\delta$ of every DW window. In inserting phase we compute current variance $\sigma ^{2}$ and compare with the threshold, if a DW window satisfies $\sigma ^{2} > \beta DW\_W[i][H_{i}(x)]{.}\delta$, there exists a distribution anomaly. The process is shown in Algorithm 2.

3.6 Complexity Analysis

Time Complexity: For a new coming data point, we need to compute KL hashes, Lw DW counts and a variance. For random projections based LSH, signed random projection is a special case. We can calculate KL LSH hashes of the data vector, with dimensions d, in time $O(d\log d + KL)$. Using DW model, each item is processed in O(1) worst case. At each time instant, it can provide an estimate in O(1) time. Finding the time division nodes needs to traverse the position queue of DW, the time is $O(\frac{1}{\epsilon }(\log (\epsilon W)))$, thus the total time we need is $O(d\log d + \frac{1}{\epsilon }(\log (\epsilon W))$.

Space Complexity: It is presented in [14] that an $\epsilon$-approximation DW window for basic counting uses only $O(\frac{1}{\epsilon }\log ^{2}(\epsilon W))$ memory bits of workspace, and here we need $2^{K}\times L$ DW windows in the two-dimensional array. K and L are preset constant parameters, and in all our experiments we use $K = 15$ and $L = 50$ for all the three datasets. However, it is unlikely that the DW windows will get too many hits, the number of hits of all our experiments is no more than 3000. Therefore, with these small constant values, the memory cost is extremely low, and the required memory is $O(\frac{1}{\epsilon }\log ^{2}(\epsilon W))$.

Fig. 4.

Time comparison.

Fig. 5.

Memory comparison.

4 Experimental Evaluation

4.1 Datasets

We choose the following three real-world and synthetic datasets for our evaluation: (1) TAO, (2) Statlog Shuttle and (3) KDD-Cup99 HTTP. The first dataset contains 575,648 records with 3 attributes. It is available at Tropical Atmosphere Ocean project [3]. The second dataset shuttle dataset [2] describes radiator positions in a NASA space shuttle with 9 attributes. It was designed for supervised anomaly detection. In the original datasets, about 20% of the data are regarded as anomaly. The third dataset is KDD-Cup99 HTTP [1]. KDD-Cup99 HTTP dataset is the largest benchmark for unsupervised anomaly detection evaluation. It contains simulated normal and attack traffic on an IP level in a computer network environment in order to test intrusion detection systems. We use HTTP traffic only and also limit DoS traffic from the dataset. We sample part of it and the features of “protocol” and “port” information is removed. There are totally 395,423 instances with 6,315 labeled anomalies.

4.2 Experimental Methodology

Our experiments are conducted in a 3.30 GHz core Windows machine with 8 GB of RAM. Experiments focus on four aspects: (1) time efficiency; (2) memory consumption; (3) recall and precision; (4) time sensitivity property. We use five kNN-based anomaly detection algorithms to compare with our proposal. We summarize the time and space complexities of each algorithm and provide comparison in Table 2. S denotes the slide size which characterizes the speed of the data stream, k is the neighbor count threshold, and $\eta$ denotes the fraction of the window stored in micro-clusters in the MCOD algorithm. For fair evaluation and reproducibility, we implement all the algorithms in Java.

Table 2. Comparison of kNN-based anomaly detection algorithms.

As shown in Fig. 4, when W increases, the CPU time for each algorithm increases as well, due to a larger number of data points to be processed in every window. We can see among the six algorithms kNN-TSAD is consistently efficient. The reason is that adding and removing data points in kNN-TSAD are very efficient as well as neighbor searching. It does not need to carry out range queries and calculate distances to update neighbor information like other kNN-based algorithms, thus kNN-TSAD saves much time.

Figure 5 reports the memory consumption of the evaluated algorithms when varying the window size W. The memory requirement increases with W consistently across different datasets. The five traditional methods store neighborhood information for every data point in current window, which requires large amount of memory. However, every item of the kNN-TSAD array (i.e. every DW window) is a neighborhood with no need to extra store neighborhood information. Thus kNN-TSAD consumes much less memory compared with other methods.

Fig. 6.

Recall comparison.

Fig. 7.

Precision comparison.

Exact-Storm, AbstractC, MCOD and Thresh_LEAP calculate all the neighbours to decide whether a data point is an outlier. They only differ in neighborhood searching and storing, such that they get almost the same anomaly detection result. So in terms of recall and precision we solely need to test on one of them, we choose MCOD. Approx-Storm adapts exact-Storm with two approximations to reduce the number of data points and the space for neighbor stored in each window. We plot the recall and precision of kNN-TSAD, MCOD and approx-Storm to make a comparison (see Figs. 6 and 7). We can see approx-Storm gets the lowest recall and precision of the three. MCOD calculate exact number of neighbors of every data points so that it gives the highest recall and precision. kNN-TSAD is between the other two algorithms on dataset Shuttle and KDD-Cup99. But on dataset TAO, as seen in Figs. 6(a) and 7(a), kNN-TSAD gets the best anomaly detection result. This is because that part of abnormal data in the TAO dataset appears in a concentrated way during a period of time. In this case the number of neighbors exceeds the threshold due to high frequency. kNN-TSAD divides the sliding window into several time intervals and calculates the variance of their counts to monitor count distribution. Figure 8 shows the variation of variance over the time period when outliers appear. Obviously between 3900 s and 6000 s, the variance experienced a process of sharp increase and decrease indicating that there appears an anomaly. However this cannot be detected by other kNN-based algorithms, and this is why kNN-TSAD get the highest recall and precision over TAO.

To summarize, kNN-TSAD provides the highest performance over dataset TAO whose anomaly detection depends on the data distribution, and this indicates the time sensitive property of our approach. Moreover, kNN-TSAD cost the least time and space over all datasets compared with other algorithms and shows its excellent time and space efficiency. LSH and DW introduce calculation error to the algorithm, so that the recall and precision are slightly lower than MCOD which count exact NN number. But when compared with the approximate method Approx-Storm, the recall and precision are significantly higher.

5 Related Work

Anomaly detection has been studied for years in the communities of multidimensional data sets [5] and the metric spaces [25]. Usually, similarity is used to decide whether an object is an outlier or not. Extensively, the problem of anomaly detection has been studied by the statistics community [17], where the objects are modeled as a distribution, and outliers are those whose deviation from this distribution is more than others. However, for high-dimensional data, statistical techniques fail to model the distribution accurately. Additionally, for large databases these techniques fail to scale well either.

Fig. 8.

Variation of variance over time.

The problem of anomaly detection has been also addressed by data mining communities. Techniques that focus on identifying Nearest Neighbors-based patterns are popular in data mining and other related communities. k Nearest Neighbors-based outliers were first introduced by Knorr and Ng [18]. Given parameters k and R, an object is marked an outlier if there are less than k objects in the input data set lying within distance R from it. However, this algorithm operates in a static fashion. This means that if there happen some changes in the data, the algorithm must be executed from scratch, leading to performance degradation while updating frequently. For example in the streaming case, where objects arrive in a streaming fashion [7].

In [6], an exact algorithm exact-Storm was proposed to efficiently detect outliers over data streams. It stores up to k preceding neighbors and the number of succeeding neighbors of x. x is an outlier if x has less than k neighbors. An approximate algorithm approx-Storm is derived from the former one. Up to $\rho W$ $(0<\rho <1)$ safe inliers are preserved for each window, and it only store the ratio between the number of x’s preceding neighbors which are safe inliers and the number of safe inliers in the window. Such it can estimate the number of x’s neighbours. Kontaki et al. [19] proposed the MCOD algorithm which aims to reduce the number of distance computations. MCOD stores the neighboring data points in micro-clusters, and a micro-cluster is composed of no less than $k + 1$ data points. Some data points may not fall into any micro-clusters, if they have less than k neighbors, they are outliers. Cao et al. [8] proposed a framework named LEAP which encompasses two general optimization principles. First, the “minimal probing” principle uses a lightweight probing operation to gather minimal yet sufficient evidence for outlier detection. Second, the “lifespan-aware prioritization” principle leverages the temporal relationships among stream data points to prioritize the processing order among them during the probing process. Yang et al. [27] proposed an algorithm Abstract-C which maintains a compact summary of the neighbourships, namely the count of the neighbors for each data point. Instead of storing a list of preceding neighbors or number of succeeding neighbors for each data point x, a sequence is used to store the number of neighbors in every window that x participates in.

kNN-based anomaly detection methods rely on neighbors search to decide whether a data point is an outlier. And neighbors searching relies on calculating the similarity between data points which is time consuming. In this paper, we use LSH to measure similarity between data points. Data points with high similarity are more likely to enter the same buckets after hashing. There is no need to calculate the similarity of every two data points.

6 Conclusion

Anomaly detection applications need to provide real-time monitoring and the capability of detecting anomalies over continuous data streams using limited resources. In this paper, we leverage the features of LSH and DW and propose a kNN-based time sensitive anomaly detection approach kNN-TSAD over data streams. Our approach can detect abnormal data distribution over different time intervals which cannot be found by traditional kNN-based methods. Moreover, our approach demonstrates high time and space efficiency for solving the problem of data stream processing. However, we can see from the experiments that the recall and precision of our approach are slightly lower than exact algorithms in some cases. In the future, we plan to design a more efficient monitoring strategy to improve and optimize our approach to get higher recall and precision.