Keywords

1 Introduction

Modern aerospace and nanotechnologies are in need of the improved computational methods and mathematical models of gas flow in a wide range of Mach and Knudsen numbers. One of the areas to which the present paper belongs is related to the development of hybrid or composed flow models. These models involve the combined use of the methods of molecular kinetic theory and continuum mechanics.

A number of models suggest the separation of the computational domain of geometric space into hydrodynamic and kinetic subdomains, for example [1,2,3]. In the hydrodynamic subdomain, the Navier – Stokes equations are used; in the kinetic one, the model BGK kinetic equation with a certain numerical implementation, or statistical models, are used.

The models of [4, 5] distinguish hydrodynamic and kinetic subdomains in the space of velocities: hydrodynamic for “slow” molecules and kinetic for “fast” molecules. In the subdomain of “slow” molecules, the Euler or Navier-Stokes models are used, and for fast molecules the BGK equation.

The BGK model was obtained for the weight function (the velocity distribution function of molecules) of a monatomic gas. Its collision integral corresponds to a gas with a Prandtl number \( Pr = 1 \) [6]. Thus, this model implies some hypothetical gas. The continuous transition from this model to hydrodynamics is very difficult without the use of artificial smoothing procedures [1].

The model [7] in the kinetic subdomain of the geometric space uses the S-model [6], which distinguishes it favorably from the models cited above. Prandtl number of the S-model is \( Pr = 2/3 \), which corresponds to monatomic gas. When calculating the flow near a rough surface, satisfactory results were obtained even in the transition region of the flow. The limitation of this model lies in the fact that the consistency of the kinetic and hydrodynamic description exists only for monatomic gases.

The present work has as its goal the development of a hybrid model of the flow of polyatomic gases. The Navier-Stokes-Fourier model (NSF) [8] is composed with the model kinetic equation of polyatomic gases (MKE) [9]. The NSF model is a rigorous first approximation of the system of moment equations for polyatomic gases [10]. When obtaining this approximation, nonequilibrium quantities (stress deviator, heat fluxes, difference of translational and rotational temperatures) in their moment equations were set so small that their second and higher degrees can be neglected. Flows that satisfy the conditions of the first approximation will be called weakly nonequilibrium.

The relaxation terms of MKE are obtained using the polyatomic gas system used in the development of the NSF model. The coefficient of bulk viscosity of the NSF model is presented in such a way that this model is the first approximation in the above sense of the MKE model. Thus, both composable models are based on a single physical model.

Section 2 provides basic assumptions and notations used in the paper. Section 3 provides a general description of the hybrid model. Section 4 provides the method of composing the kinetic and hydrodynamic models. Section 5 discusses a particular case of using the model to describe the profile of a plane shock wave.

2 Basic Assumptions and Notations

We consider the flow of monocomponent perfect gases. All expressions are written for polyatomic gases. In the case of monatomic gases, the expressions remain valid after obvious transformations.

The index writing of tensor expressions is used. A repeated Greek index indicates a summation from 1 to 3. The velocity space integral is denoted by \( \int { \ldots \;d{\mathbf{c}}} \equiv \int\limits_{ - \infty }^{ + \infty } {dc_{1} } \int\limits_{ - \infty }^{ + \infty } {dc_{2} } \int\limits_{ - \infty }^{ + \infty } { \ldots \;dc_{3} } \) (Table 1).

Table 1. The notations used
Full size table

In considered models the following is accepted: \( Pr = {{4\gamma } \mathord{\left/ {\vphantom {{4\gamma } {\left( {9\gamma - 5} \right)}}} \right. \kern-0pt} {\left( {9\gamma - 5} \right)}} \).

3 Hybrid Model

3.1 Hydrodynamic Model

The NSF model, which differs from the traditional system of conservation equations in the Navier-Stokes approximation by the presence of the coefficient of bulk viscosity in the equations of nonequilibrium stress, is considered as a hydrodynamic model. In terms of [8], the system of equations of this model has the following form:

$$ \left\{ {\begin{array}{*{20}l} {\frac{\partial \rho }{\partial t} + \frac{{\partial \rho u_{\alpha } }}{{\partial x_{\alpha } }} = 0} \hfill \\ {\frac{{\partial u_{i} }}{\partial t} + u_{\alpha } \frac{{\partial u_{i} }}{{\partial x_{\alpha } }} + \frac{1}{\rho }\frac{{\partial P_{i\alpha } }}{{\partial x_{\alpha } }} = 0\quad \quad i = 1,\;2,\;3} \hfill \\ {\frac{\partial T}{\partial t} + u_{\alpha } \frac{\partial T}{{\partial x_{\alpha } }} + \left( {\gamma - 1} \right)\frac{{P_{\alpha \beta } }}{\rho }\frac{{\partial u_{\alpha } }}{{\partial x_{\beta } }} + \frac{1}{{c_{v} \rho }}\frac{{\partial q_{\alpha } }}{{\partial x_{\alpha } }} = 0} \hfill \\ \end{array} } \right. $$
(1)

where

\( P_{ij} = \delta_{ij} R\rho T - \mu \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) + \delta_{ij} \frac{2}{3}\left( {1 - \frac{5 - 3\gamma }{2}Z} \right)\mu \frac{{\partial u_{\alpha } }}{{\partial x_{\alpha } }} \), \( q_{i} = - \frac{{c_{p} }}{\Pr }\mu \frac{\partial T}{{\partial x_{i} }} \).

The viscosity coefficient \( \mu \) and the parameter \( Z \) are determined by the dependencies which are used in the MKE model [9], but with preservation of the order of approximation of the NSF model, i.e.\( \mu = \mu \left( {T_{t} = T} \right) \), \( Z = Z\left( {T_{t} /T_{r} = 1} \right) \).

3.2 Kinetic Model

As a kinetic model of the flow, the MKE model [9] is used, built for a single-particle weight function, the phase space of which is supplemented by the energy of rotational degrees of freedom \( \varepsilon \): \( f\left( {t,\;{\mathbf{x}},\;{\varvec{\upxi}},\;\varepsilon } \right) \). After reducing the dimension of the weight function, the kinetic equations of the model take the form:

$$ \frac{\partial }{\partial t}\left| {\begin{array}{*{20}c} {f_{t} } \\ {f_{r} } \\ \end{array} } \right| + \xi_{\alpha } \frac{\partial }{{\partial x_{\alpha } }}\left| {\begin{array}{*{20}c} {f_{t} } \\ {f_{r} } \\ \end{array} } \right| = \frac{p}{\mu }\left| {\begin{array}{*{20}c} {f_{t}^{ + } - f_{t} } \\ {f_{r}^{ + } - f_{r} } \\ \end{array} } \right| $$
(2)

where

$$ f_{t} = \int {fd\varepsilon } ,f_{r} = \int {\varepsilon fd\varepsilon } , $$
$$ f_{t}^{ + } = \frac{n}{{\left( {2\pi RT_{t}^{ + } } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}\exp \left( { - \frac{{c^{2} }}{{2RT_{t}^{ + } }}} \right)\left( {1 + \frac{{\phi_{\alpha }^{{}} c_{\alpha } }}{{3\rho \left( {RT_{t}^{ + } } \right)^{2} }}\left( {\frac{{c^{2} }}{{5RT_{t}^{ + } }} - 1} \right)} \right) $$
$$ f_{r}^{ + } = \frac{5 - 3\gamma }{{2\left( {\gamma - 1} \right)}}kT_{r}^{ + } f_{t}^{ + } ,T_{t}^{ + } = T + 0.5\left( {5 - 3\gamma } \right)\left( {1 - {1 \mathord{\left/ {\vphantom {1 {\rm Z}}} \right. \kern-0pt} {\rm Z}}} \right)\left( {T_{t} - T_{r} } \right) $$
$$ T_{r}^{ + } = T - 1.5\left( {\gamma - 1} \right)\left( {1 - {1 \mathord{\left/ {\vphantom {1 {\rm Z}}} \right. \kern-0pt} {\rm Z}}} \right)\left( {T_{t} - T_{r} } \right),T_{t} = \left( {3Rn} \right)^{ - 1} \int {c^{2} f_{t} d{\mathbf{c}}} ,\phi_{i} = 0.5m_{0} \int {c_{i} c^{2} f_{t} d{\mathbf{c}}} $$
$$ T_{r} = 2\left( {\gamma - 1} \right)\left( {\left( {5 - 3\gamma } \right)R\rho } \right)^{ - 1} \int {f_{r} d{\mathbf{c}}} ,\phi_{i} = 0.5m_{0} \int {c_{i} c^{2} f_{t} d{\mathbf{c}}} , $$

The viscosity coefficient \( \mu = \mu \left( {T_{t} } \right) \) and the parameter \( Z = Z\left( {T_{t} ,T_{r} } \right) \) showing the amount of intermolecular collisions per one inelastic collision are considered as free parameters of the model.

The remaining moments of the weight function required for the hybrid model are defined as:

$$ n = \int {f_{t} d{\mathbf{c}}} , $$
(3)
$$ u_{i} = n^{ - 1} \int {\xi_{i} f_{t} d{\mathbf{c}}} , $$
(4)
$$ P_{ij} = m_{0} \int {c_{i} c_{j} f_{t} d{\mathbf{c}}} , $$
(5)
$$ \omega_{i} = \int {c_{i} f_{r} d{\mathbf{c}}} . $$
(6)

In [9], the results of calculations using MKE were compared with the well-studied R-model [11, 12] and experimental data [13, 14]. We obtained a satisfactory agreement between the calculated profile of a plane hypersonic shock wave and experimental data even for such a “thin” parameter as the temperature of the rotational degrees of freedom. In the test calculations of this work, the MKE model that is not composed with the hydrodynamic model is considered as a reference.

It should be noted that the models are well consistent, since the NSF model is a strong first approximation of the kinetic model.

4 The Method of Composing Kinetic and Hydrodynamic Models

One of the applications of the hybrid model involves the application of the kinetic model in strongly nonequilibrium domains of the flow field and the hydrodynamic model in other domains.

Another application relates to weakly nonequilibrium flows near active (gas-absorbing or gas-emitting) surfaces. In this case, the kinetic model is necessary only for the formation of boundary conditions on the surface. In Fig. 1, the schemes of the computational domain for both cases are presented: variants A and B, respectively. The vertical line on variant B denotes a streamlined surface.

Fig. 1.
figure 1

Schemes of computational domains. A – flow region that does not interact with a solid surface, B – near-wall flow region, ○ – nodes of the hydrodynamic model, + – nodes of the kinetic model, ● – models joining nodes

Full size image

Without loss of generality, we consider a one-dimensional stationary flow field with a geometrical coordinate \( x_{i} \equiv x \), and a velocity coordinate corresponding to it. It is supposed that a finite-difference method is used for a numerical solution. Derivatives in system (1) are approximated by central differences on three nodes, in system (2) by one-sided differences upstream, also on three nodes. Note that the direction of flow in the kinetic equations is determined by the direction of the molecular velocity. In this case, it is a speed \( \xi_{x} \) that has two opposite directions: \( \xi_{x} > 0 \) and \( \xi_{x} < 0 \). Consequently, there are two multidirectional difference schemes. Such a discrete analogue of the computational domain will later be used for numerical tests.

In both variants on Fig. 1, the computational domain is shown twice, separately for the hydrodynamic (open circles) and kinetic (crosses) models. In option A, the solution area of the hydrodynamic solution is divided into two subdomains. The boundary conditions of the left subdomain are formed in the node (the joining node), indicated by a black dot and belonging to the area of the kinetic solution. For the selected differential template, one node is sufficient. Values \( \rho \), \( u_{x} \), \( T \) in this node are defined as the moments of the weight function calculated in the kinetic domain. Similar is the solution in the right subdomain of the hydrodynamic solution. When describing a flow in the near-wall region, one hydrodynamic subdomain is sufficient. In variant A, a kinetic subdomain is located between the hydrodynamic subdomain and the wall (not shown in Fig. 2).

Fig. 2.
figure 2

The referenced temperature profiles in a plane shock wave of a diatomic gas. \( M_{\infty } = 1.55. \) The solid line is the hybrid model; fine dotted line is model MKE; large dotted line is NSF model; vertical dash-dotted lines are the boundaries of the kinetic subdomain of the hybrid model

Full size image

The boundary conditions of the kinetic solution are formed in the nodes of the hydrodynamic domain (black circles): two nodes in each hydrodynamic subdomain for the corresponding (\( \xi_{x} > 0 \) or \( \xi_{x} < 0 \)) difference patterns. Since the hydrodynamic model is less informative than the kinetic model, an approximating weight function is used to reconstruct the weight function in the nodes. In the case of a near-wall flow, the weight function is determined in the node boundary with the wall, which is determined by the law of interaction of molecules with a solid surface.

Taking into account the order of approximation of the hydrodynamic model, as an approximating weight function, it is advisable to take the expansion of the equilibrium, Maxwell function. Such an expansion is used in a number of works, for example [7], for monatomic gases. In the case of polyatomic gas for functions \( f_{At} \) и \( f_{Ar} \) similar expansions lead to the expressions [9]:

$$ f_{At}^{{}} = f_{M}^{{}} \left( {1 + \frac{1}{{\rho \left( {RT_{t}^{{}} } \right)^{2} }}\left( {\frac{1}{2}p_{\alpha \beta }^{{}} c_{\alpha } c_{\beta } + \phi_{\alpha }^{{}} \left( {\frac{{c^{2} }}{{5RT_{t}^{{}} }} - 1} \right)c_{\alpha } } \right)} \right) , $$
(7)
$$ f_{Ar}^{{}} = kT_{r}^{{}} \left( {\frac{5 - 3\gamma }{{2\left( {\gamma - 1} \right)}}f_{At}^{{}} + f_{M}^{{}} \frac{{\omega_{\alpha } c_{\alpha } }}{{\rho R^{2} T_{t}^{{}} T_{r}^{{}} }}} \right), $$
(8)
$$ f_{M}^{{}} = \frac{n}{{\left( {2\pi RT_{t}^{{}} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}\exp \left( { - \frac{{c^{2} }}{{2RT_{t}^{{}} }}} \right) $$
(9)

The macroparameters of these expressions are determined by the hydrodynamic model and are considered in the appropriate approximation:

$$ \begin{aligned} T_{r} = T,p_{ij} = - \mu \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) & + \delta_{ij} \frac{2}{3}\left( {1 - \frac{5 - 3\gamma }{2}Z} \right)\mu \frac{{\partial u_{\alpha } }}{{\partial x_{\alpha } }}\varphi = - \frac{15}{4}R\mu \frac{\partial T}{{\partial x_{i} }}, \\ & \omega_{i} = - \frac{5 - 3\gamma }{{2\left( {\gamma - 1} \right)}}R\mu \frac{\partial T}{{\partial x_{i} }} \\ \end{aligned} $$
(10)

Variant B in Fig. 1 assumes a solution of the NSF model in the entire near-wall computational region. This allows to build computational grids with hydrodynamic steps, which is fundamentally important for small Kn. The grid of the kinetic solution with a step of the order of the mean free path of the molecules is constructed within the last, near-wall step of the hydrodynamic grid. Macroparameters, \( \rho \), \( u_{x} \), \( T \) in the kinetic model joining nodes are obtained by interpolating the hydrodynamic solution. In this case, the role of the kinetic model is reduced only to the formation of boundary conditions on a solid surface for the hydrodynamic model.

After calculating the weight function of molecules moving to the surface, the weight function of the reflected molecules is restored at the boundary node. For this, any law of interaction of molecules with the surface can be used. For example, for chemo or cryosorbing surfaces, the diffuse reflection law can be used, taking into account the mass absorption coefficient [15].

At the next stage, the weight function of the reflected molecules is calculated and macroparameters are calculated in the kinetic domain. For the general, hydrodynamic solution, only the boundary node macroparameters are used. The kinetic model is used only to form the boundary conditions of the hydrodynamic model.

Variant B was considered in [16] for the Couette flow. It is shown that the solution is smooth in a wide range of Knudsen and Mach numbers and agrees well with the “pure” kinetic solution. In this work, in connection with its orientation, the near-wall flows were not considered.

5 Numerical Tests. The Problem of the Structure of the Shockwave

The problem is solved in a stationary formulation and is formulated as follows. On the boundaries of the computational domain, the Rankine-Hugoniot conditions are set. The size of the computational domain is about one hundred of free paths of the molecule in the undisturbed flow:

$$ \lambda_{\infty } = 3.2\mu_{\infty } \left( {2\pi RT_{\infty } } \right)^{ - 1/2} /\rho_{\infty } $$
(11)

The system of equations of the MKE model is transformed as follows:

$$ \xi_{x} \frac{\partial }{\partial x}\left| {\begin{array}{*{20}c} {f_{t} } \\ {f_{r} } \\ \end{array} } \right| = \frac{p}{\mu }\left| {\begin{array}{*{20}c} {f_{t}^{ + } - f_{t} } \\ {f_{r}^{ + } - f_{r} } \\ \end{array} } \right| . $$
(12)

The transformation of the functions and parameters entering into (12) is obvious.

The system of equations of the NSF model for this problem:

$$ \left\{ {\begin{array}{*{20}l} {\rho u_{x} = \rho_{\infty } u_{x\infty } } \hfill \\ {\rho u_{x} {{\partial u_{x} } \mathord{\left/ {\vphantom {{\partial u_{x} } {\partial x}}} \right. \kern-0pt} {\partial x}} + {{\partial P_{xx} } \mathord{\left/ {\vphantom {{\partial P_{xx} } {\partial x_{x} }}} \right. \kern-0pt} {\partial x_{x} }} = 0} \hfill \\ {\rho u_{x} {{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0pt} {\partial x}} + \left( {\gamma - 1} \right)P_{xx} {{\partial u_{x} } \mathord{\left/ {\vphantom {{\partial u_{x} } {\partial x_{x} }}} \right. \kern-0pt} {\partial x_{x} }} + c_{v}^{ - 1} {{\partial q_{x} } \mathord{\left/ {\vphantom {{\partial q_{x} } {\partial x}}} \right. \kern-0pt} {\partial x}} = 0} \hfill \\ \end{array} } \right. $$
(13)

In all calculations, approximations of the viscosity coefficient were taken as \( \mu = \mu \left( {T_{t}^{s} } \right) \) for the kinetic model and \( \mu = \mu \left( {T_{{}}^{s} } \right) \) for the hydrodynamic one. The power s was chosen from considerations of the best coincidence of the density profile with the experimental profiles of [13, 14]. The parameter \( Z \) approximations for various flow regimes are taken from [9, 12, 17]. Difference schemes are as described in Sect. 4, variant A. The grid pitch was \( \approx 0. 1\lambda_{\infty } \).

To solve the system of hydrodynamic equations, we used the stationary Thomas method (sweep method) on a three-diagonal matrix. For the kinetic equations, a stationary solution method was also used with differences up the molecular flow.

The calculated shock wave profiles of the hybrid model were compared with the shock wave profiles of the MKE and NSF models. Calculations showed that the greatest disarrangement between the shock wave profiles of the hybrid model and the MKE model takes place on the temperature profiles. Density and group velocity profiles agreed much better. In the following, only temperature profiles referenced to a single segment \( T^{*} \) will be considered.

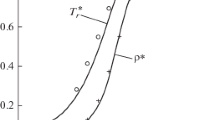
In the region of moderate Mach numbers, the hybrid model produced smooth temperature profiles, although in the kinetic solution subdomain, some difference was observed from the temperature profiles of the MKE model. Figure 2 shows temperature profiles for \( {\text{M}}_{\infty } = 1.55 \).

The size of the kinetic subdomain of the hybrid model was \( 7.8\lambda_{\infty } \). The joining nodes of the models were in the high gradient subdomain. With an increase in the size of the kinetic subdomain, the corresponding temperature profile became closer to the temperature profile of the MKE model. Analysis of the second temperature derivatives at the joining nodes did not reveal a discontinuity of the first derivatives, that is, a break in the graph.

This type of solution was observed until \( {\text{M}}_{\infty } \approx 2 \). For larger Mach numbers, even for sufficiently large sizes of the kinetic subdomain (\( 20 \div 30\;\lambda_{\infty } \)), a discontinuity of derivatives appeared at its boundary nodes. At the same time, the temperature profile of the kinetic region of the hybrid model came close to the temperature profile of the MKE model.

Figure 3 shows the temperature profiles in the case of hypersonic flow. In the left boundary node of the kinetic subdomain of the hybrid model, a pronounced discontinuity of the derivatives is observed. The size of the kinetic subdomain of the hybrid model is \( 17.2\;\lambda_{\infty } \). The temperature profile of the kinetic subdomain of the hybrid model almost coincides with the temperature profile of the MKE. If a smooth solution in the field of moderate Mach numbers was quite expected, then the indicated coincidence of temperature profiles seems to be quite paradoxical.

Fig. 3.
figure 3

Same as Fig. 2, \( M_{\infty } = 7 \)

Full size image

Another characteristic feature of the hybrid model is that throughout the computational domain, including the derivative discontinuity node, the conservation laws are fulfilled up to the error of numerical integration of the weight function over the velocity space.

This feature of the hybrid model is related to the fact that the components of its NSF and MKE models require the exact fulfillment of the conservation laws, and the non-equilibrium parameters of the NSF model are determined only in the first approximation.

From Fig. 3 it also follows that despite the discontinuity of the derivative in the boundary node of the kinetic subdomain, the hybrid model can significantly improve the hydrodynamic solution.

A quantitative estimate of the maximum relative error in calculating the temperature depending on the size of the kinetic region of the combined model is shown in Fig. 4. This data allows one to select a compromise solution in terms of accuracy and efficiency. As mentioned above, the largest relative error in the calculation of a plane shock wave was observed on the temperature profile.

Fig. 4.
figure 4

Maximum relative error of temperature calculation depending on the length of the kinetic subdomain of the hybrid model

Full size image

6 Conclusion

With regard to the presented hybrid model, we note the following. The results of this work, together with the results of [16], show that the combination of hydrodynamic and kinetic models of flow can be quite successful if both models are based on the same physical model.

By analogy with the proposed model, a hybrid model can be constructed in which the moment equations of any arbitrarily high order are used to hydrodynamically describe the flow. This removes the question of setting boundary conditions on a solid surface. For all moments included in the system of differential equations, Dirichlet boundary conditions hold.

Additional research requires the development of an algorithm to isolate highly non-equilibrium domains in a flow field, for example, the selection of a shock wave front. The upper estimate of the size of the kinetic subdomain of the model in the case of shock waves can serve as data for a plane shock wave presented in Fig. 4.

According to the authors, the important result of the research is a model effect obtained for highly non-equilibrium flows. It has been established that with a small flow nonequilibrium, including the joining region, the kinetic subdomain of the combined model differs, albeit insignificantly, from the subdomain of the “pure” kinetic model. In the case of crosslinking of models in the subdomain of high nonequilibrium and the presence, as a consequence, of a rupture of the derivatives of hydrodynamic parameters, the kinetic subdomain practically coincided with the “pure” kinetic solution.

In the stitching region of the NSF and MKE models, the boundary conditions of these models are formed. The rupture of the derivatives, which clearly contradicts the physical nature of the flow, “reformulates” the boundary conditions of the MKE model. In this case, the solution in the kinetic region of the hybrid model is in better agreement with the molecular kinetic theory.

The authors of this work could not explain the reasons for such a paradoxical behavior of the hybrid model. Authors will be grateful for useful comments.

This work was conducted with the financial support of the Ministry of Education and Science of the Russian Federation, project №9.7170.2017/8.9.