Abstract
Nets are generalisations of sequences involving possibly uncountable index sets; this notion was introduced about a century ago by Moore and Smith, together with the generalisation to nets of various basic theorems of analysis due to Bolzano-Weierstrass, Dini, Arzelà, and others. This paper deals with the Reverse Mathematics study of theorems about nets indexed by subsets of Baire space, i.e. part of third-order arithmetic. Perhaps surprisingly, over Kohlenbach’s base theory of higher-order Reverse Mathematics, the Bolzano-Weierstrass theorem for nets and the unit interval implies the Heine-Borel theorem for uncountable covers. Hence, the former theorem is extremely hard to prove (in terms of the usual hierarchy of comprehension axioms), but also unifies the concepts of sequential and open-cover compactness. Similarly, Dini’s theorem for nets is equivalent to the uncountable Heine-Borel theorem.
This research was supported by the John Templeton Foundation grant a new dawn of intuitionism with ID 60842. Opinions expressed in this paper do not necessarily reflect those of the John Templeton Foundation. I thank Thomas Streicher and Anil Nerode for their valuable advice. Finally, I thank the three referees for their valuable suggestions that have significantly improved the paper.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
To be absolutely clear, variables (of any finite type) are allowed in quantifier-free formulas of the language
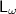 : only quantifiers are banned.
: only quantifiers are banned. - 2.
Simpson mentions in [42] the caveat that e.g.
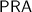 and
and
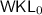 have the same first-order strength, but the latter is strictly stronger than the former.
have the same first-order strength, but the latter is strictly stronger than the former. - 3.
References
Aliprantis, C.D., Border, K.C.: Infinite Dimensional Analysis: A Hitchhiker’s Guide, 3rd edn. Springer, Berlin (2006). https://doi.org/10.1007/3-540-29587-9
Avigad, J., Feferman, S.: Gödel’s functional (“Dialectica”) interpretation. In: Handbook of Proof Theory. Stud. Logic Found. Math. 137, 1998, pp. 337–405
Bartle, R.G.: Nets and filters in topology. Am. Math. Mon. 62, 551–557 (1955)
Bartle, R.G.: On compactness in functional analysis. Trans. Am. Math. Soc. 79, 35–57 (1955)
Benacerraf, P., Putnam, H.: Philosophy of Mathematics: Selected Readings, 2nd edn. Cambridge University Press, Cambridge (1984)
Bernays, P.: Sur le Platonisme Dans les Mathématiques. L’EnseignementMathématique 34, 52–69 (1935)
Berger, J., Schuster, P.: Dini’s theorem in the light of reverse mathematics. In: Lindström, S., Palmgren, E., Segerberg, K., Stoltenberg-Hansen, V. (eds.) Logicism, Intuitionism, and Formalism. Synthese Library, vol. 341, pp. 153–166. Springer, Dordrecht (2009). https://doi.org/10.1007/978-1-4020-8926-8_7
Brace, W.J.: Almost uniform convergence. Portugal. Math. 14, 99–104 (1956)
Burgess, P.J.: Fixing Frege: Princeton Monographs in Philosophy. Princeton University Press, Princeton (2005)
Cousin, P.: Sur les fonctions de n variables complexes. Acta Math. 19, 1–61 (1895)
Friedman, H.: Some systems of second order arithmetic and their use. In: Proceedings of the International Congress of Mathematicians (Vancouver, B.C. 1974), vol. 1, pp. 235–242 (1975)
Friedman, H.M.: Systems of second order arithmetic with restricted induction, I & II (Abstracts). J. Symb. Log. 41, 557–559 (1976)
Friedman, H.M.: Interpretations, according to Tarski. In: The Nineteenth Annual Tarski Lectures on Interpretations of Set Theory in Discrete Mathematics and Informal Thinking, vol. 1, pp. 42 (2007). http://u.osu.edu/friedman.8/files/2014/01/Tarski1052407-13do0b2.pdf
Gandy, R.: General recursive functionals of finite type and hierarchies of functions. Ann. Fac. Sci. Univ. Clermont-Ferrand 35, 5–24 (1967)
Hirschfeldt, D.R.: Slicing the Truth. Lecture Notes Series, vol. 28, Institute for Mathematical Sciences, National University of Singapore, World Scientific Publishing (2015)
Hunter, J.: Higher-order reverse topology, ProQuest LLC, Ann Arbor, MI. Ph.D. thesis - The University of Wisconsin - Madison (2008)
Kelley, J.L.: General Topology: Graduate Texts in Mathematics, vol. 27. Springer, New York (1975). Reprint of the 1955 edition
Koellner, P.: Large Cardinals and Determinacy, The Stanford Encyclopedia of Philosophy (2014). https://plato.stanford.edu/archives/spr2014/entries/large-cardinals-determinacy/
Kohlenbach, U.: Foundational and mathematical uses of higher types. In: Reflections on the Foundations of Mathematics 2002. Lecture Notes in Logic, vol. 15, ASL 2002, pp. 92–116 (2002)
Kohlenbach, U.: Higher order reverse mathematics. In: Reverse Mathematics 2001. Lecture Notes in Logic, vol. 21, ASL 2005, pp. 281-295 (2005)
Kupka, I.: A generalised uniform convergence and Dini’s theorem. N. Z. J. Math. 27(1), 67–72 (1998)
Medvedev, F.A.: Scenes from the History of Real Functions. Science Networks. Historical Studies, vol. 7. Birkhäuser Verlag, Basel (1991). https://doi.org/10.1007/978-3-0348-8660-4
Montalbán, A., Shore, R.A.: The limits of determinacy in secondorder arithmetic. Proc. Lond. Math. Soc. 104(2), 223–252 (2012)
Moore, E.H.: On a form of general analysis with application to linear differential and integral equations. Atti IV Cong. Inter. Mat. (Roma 1908) 2, 98–114 (1909)
Moore, E.H.: Introduction to a Form of General Analysis. Yale University Press (1910)
Moore, E.H.: Definition of limit in general integral analysis. Proc. Natl. Acad. Sci. U. S. A. 1(12), 628–632 (1915)
Moore, E.H., Smith, H.L.: A general theory of limits. Am. J. Math. 44(2), 102–121 (1922)
Muldowney, P.: A General Theory of Integration in Function Spaces, Including Wiener and Feynman Integration, vol. 153. Longman Scientific & Technical/Wiley, Harlow (1987)
Mummert, C., Simpson, S.G.: Reverse mathematics and \({\Pi }_{2}^{1}\) comprehension. Bull. Symb. Log. 11(4), 526–533 (2005)
Mummert, C.: On the reverse mathematics of general topology, ProQuest LLC, Ann Arbor, MI. Ph.D. thesis - The Pennsylvania State University (2005)
Mummert, C.: Reverse mathematics of MF spaces. J. Math. Log. 6(2), 203–232 (2006)
Naimpally, S.A., Peters, J.F.: Preservation of continuity. Sci. Math. Jpn. 76(2), 305–311 (2013)
Normann, D., Sanders, S.: Nonstandard analysis, computability theory, and their connections. arXiv:abs/1702.06556 (2017)
Normann, D., Sanders, S.: The strength of compactness in computability theory and nonstandard analysis. arXiv:1801.08172 (2018)
Normann, D., Sanders, S.: On the mathematical and foundational significance of the uncountable. J. Math. Log. (2018). https://doi.org/10.1142/S0219061319500016
Normann, D., Sanders, S.: Pincherle’s theorem in Reverse Mathematics and computability theory. arXiv:1808.09783 (2018)
Reed, M., Simon, B.: Analysis of Operators. Methods of Modern Mathematical Physics, vol. 4. Academic Press, Cambridge (1978)
Sakamoto, N., Yamazaki, T.: Uniform versions of some axioms of second order arithmetic. MLQ Math. Log. Q. 50(6), 587–593 (2004)
Sanders, S.: Splittings and disjunctions in reverse mathematics. NDJFL, p. 18. arXiv:1805.11342 (2018)
Simpson, S.G. (ed.): Reverse Mathematics 2001. Lecture Notes in Logic, vol. 21, ASL, La Jolla, CA (2005)
Simpson, S.G.: Subsystems of Second Order Arithmetic. Perspectives in Logic, 2nd edn. Cambridge University Press, Cambridge (2009)
Simpson, S.G.: The Gödel Hierarchy and Reverse Mathematics. Kurt Gödel. Essays for his centennial, pp. 109–127 (2010)
Stillwell, J.: Reverse Mathematics, Proofs from the Inside Out. Princeton University Press, Princeton (2018)
Swartz, C.: Introduction to Gauge Integrals, World Scientific (2001)
Timofte, V., Timofte, A.: Generalized Dini theorems for nets of functions on arbitrary sets. Positivity 20(1), 171–185 (2016)
Toma, V.: Strong convergence and Dini theorems for non-uniform spaces. Ann. Math. Blaise Pascal 4(2), 97–102 (1997)
Troelstra, A.S.: Meta Mathematical Investigation of Intuitionistic Arithmetic and Analysis. Lecture Notes in Mathematics, vol. 344. Springer, Berlin (1973). https://doi.org/10.1007/BFb0066739
Wang, H.: Eighty years of foundational studies. Dialectica 12, 466–497 (1958)
Wolk, E.S.: Continuous convergence in partially ordered sets. Gen. Topol. Appl. 5(3), 221–234 (1975)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Sanders, S. (2019). Nets and Reverse Mathematics. In: Manea, F., Martin, B., Paulusma, D., Primiero, G. (eds) Computing with Foresight and Industry. CiE 2019. Lecture Notes in Computer Science(), vol 11558. Springer, Cham. https://doi.org/10.1007/978-3-030-22996-2_22
Download citation
DOI: https://doi.org/10.1007/978-3-030-22996-2_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-22995-5
Online ISBN: 978-3-030-22996-2
eBook Packages: Computer ScienceComputer Science (R0)


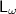 : only quantifiers are banned.
: only quantifiers are banned.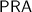 and
and
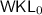 have the same first-order strength, but the latter is strictly stronger than the former.
have the same first-order strength, but the latter is strictly stronger than the former. and [
and [