Abstract
We firstly define an improved version of the spiking neuron model with dendrites introduced in [8] and we focus here on the fundamental mathematical properties of the framework. Our main result is that, under few simplifications with respect to biology, dendrites can be simply abstracted by delays. Technically, we define a method allowing to reduce neuron shapes and we prove that reduced forms define equivalence classes of dendritic structures sharing the same input/output spiking behaviour. Finally, delays by themselves appear to be a simple and efficient way to perform an abstract dendritic integration into spiking neurons without explicit dendritic trees. This overcomes an explicit morphology representation and allows exploring many equivalent configurations via a single simplified model structure.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsReferences
Brette, R., Gerstner, W.: Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 94(5), 3637–3642 (2005)
Buchera, D., Goaillard, J.M.: Beyond faithful conduction: short-term dynamics, neuromodulation, and long-term regulation of spike propagation in the axon. Prog. Neurobiol. 94(4), 307–346 (2011)
Byrne, J.H., Roberts, J.L.: From Molecules to Networks. Academic Press, Cambridge (2004)
Dayan, P., Abbott, L.F.: Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Massachusetts Institute of Technology Press, Cambridge (2001)
Debanne, D.: Information processing in the axon. Nat. Rev. Neurosci. 5, 304–316 (2004)
Gerstner, W., Naud, R.: How good are neuron models? Science 326(5951), 379–380 (2009)
Gorski, T., Veltz, R., Galtier, M., Fragnaud, H., Telenczuk, B., Destexhe, A.: Inverse correlation processing by neurons with active dendrites. bioRxiv, Forthcoming (2017)
Guinaudeau, O., Bernot, G., Muzy, A., Gaffé, D., Grammont, F.: Computer-aided formal proofs about dendritic integration within a neuron. In: BIOINFORMATICS 2018–9th International Conference on Bioinformatics Models, Methods and Algorithms (2018)
Guinaudeau, O., Bernot, G., Muzy, A., Grammont, F.: Abstraction of the structure and dynamics of the biological neuron for a formal study of the dendritic integration. In: Advances in Systems and Synthetic Biology (2017)
Häusser, M., Mel, B.: Dendrites: bug or feature? Curr. Opin. Neurobiol. 13(3), 372–383 (2003)
Huguenard, J.R.: Reliability of axonal propagation: the spike doesn’t stop here. Proc. Natl. Acad. Sci. 97(17), 9349–9350 (2000)
Izhikevich, E.M.: Polychronization: computation with spikes. Neural Comput. 18(2), 245–282 (2006)
Lapicque, L.: Recherches quatitatives sur l’excitation electrique des nerfs traitee comme polarisation. J. Physiol. Pathol. Gen. 9, 620–635 (1907)
Maass, W., Schnitger, G., Sontag, E.D.: On the computational power of sigmoid versus Boolean threshold circuits. In: Proceedings of the 32nd Annual Symposium on Foundations of Computer Science, pp. 767–776. IEEE (1991)
Maass, W.: Networks of spiking neurons: the third generation of neural network models. Neural Netw. 10(9), 1659–1671 (1997)
Maass, W.: On the relevance of time in neural computation and learning. Theoret. Comput. Sci. 261(1), 157–178 (2001)
McCulloch, W.S., Pitts, W.: A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5(4), 115–133 (1943)
Mel, B.W.: Information processing in dendritic trees. Neural Comput. 6(6), 1031–1085 (1994)
Paulus, W., Rothwell, J.C.: Membrane resistance and shunting inhibition: where biophysics meets satate dependent human neurophysiology. J. Physiol. 594(10), 2719–2728 (2016)
Rall, W.: Branching dendritic trees and motoneuron membrane resistivity. Exp. Neurol. 1(5), 491–527 (1959)
Rall, W.: Theory of physiological properties of dendrites. Ann. N. Y. Acad. Sci. 96(1), 1071–1092 (1962)
Segev, I., London, M.: Untangling dendrites with quantitative models. Science 290(5492), 744–750 (2000)
Stern, E.A., Jaeger, D., Wilson, C.J.: Membrane potential synchrony of simultaneously recorded striatal spiny neurons in vivo. Nature 394(6692), 475–478 (1998)
Stuart, G., Spruston, N., Häusser, M.: Dendrites. Oxford University Press, Oxford (2016)
Thorpe, S., Imbert, M.: Biological constraints on connectionist modelling. In: Connectionism in Perspective, pp. 63–92 (1989)
Thorpe, S., Delorme, A., Van Rullen, R.: Spike-based strategies for rapid processing. Neural Netw. 14(6), 715–725 (2001)
Van Rullen, R., Thorpe, S.J.: Rate coding versus temporal order coding: what the retinal ganglion cells tell the visual cortex. Neural Comput. 13(6), 1255–1283 (2001)
Williams, S.R., Stuart, G.J.: Dependence of EPSP efficacy on synapse location in neocortical pyramidal neurons. Science 295(5561), 1907–1910 (2002)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Appendices
A Appendices
1.1 A.1 Induction Lemmas and Proofs
Lemma 4
[Interval Induction Principle]. Let \(\psi \) be a property on positive real numbers, we define the interval induction principle as follows: If there exists an increasing sequence  of positive real numbers such that \(t_0=0\) and \(\lim \limits _{n \rightarrow +\infty } t_i = + \infty \), and such that
of positive real numbers such that \(t_0=0\) and \(\lim \limits _{n \rightarrow +\infty } t_i = + \infty \), and such that  , then
, then  .
.
Proof. Let us prove by induction on i that  , \(\forall t \in [0,t_i[\), \(\psi (t)\) is satisfied.
, \(\forall t \in [0,t_i[\), \(\psi (t)\) is satisfied.
-
If \(i=0\) then \([0,t_0[=\emptyset \) so \(\forall t \in [0,t_0[\), \(\psi (t)\) is satisfied.
-
If \(\forall t \in [0, t_i[\), \(\psi (t)\) is satisfied, then from the induction principle of the lemma, \(\forall t \in [t_i, t_{i+1}[\), \(\psi (t)\) is satisfied. Therefore, considering the union of the two intervals, it comes \(\forall t \in [0, t_{i+1}[\), \(\psi (t)\) is satisfied.
So for any  , there exists i such that \(t_i>t\) because \(\lim \limits _{i \rightarrow +\infty } t_i = + \infty \) and therefore, \(\psi (t)\) is satisfied because \(t \in [0, t_i[\). \(\square \)
, there exists i such that \(t_i>t\) because \(\lim \limits _{i \rightarrow +\infty } t_i = + \infty \) and therefore, \(\psi (t)\) is satisfied because \(t \in [0, t_i[\). \(\square \)
Lemma 5
[Archimedean Induction Principle]. Let \(\psi \) be a property on positive real numbers, we define the archimedean induction principle as follows: If there exists  such that
such that  , then
, then  .
.
Proof. Because  is archimedean, it is sufficient to apply Lemma 4 with \(t_i=i \times a\).
is archimedean, it is sufficient to apply Lemma 4 with \(t_i=i \times a\).
1.2 A.2 Proof of Theorem 1
Given a neuron N, let \(\partial ^0=(\{\eta _s^0\}_{s \in Sy(N)}\), \(\{\eta _c^0\}_{c \in Co(N)})\) be an initial dendritic state of N in continuity with an input signal I. There exists a unique family  such that for all
such that for all  and for all \(\varepsilon \in [0, inf(\{\varDelta _c~|~c \in Co(N)\})]\): \(\partial ^{t+\varepsilon }=\varepsilon \)-shift\(^I(\partial ^t)\).
and for all \(\varepsilon \in [0, inf(\{\varDelta _c~|~c \in Co(N)\})]\): \(\partial ^{t+\varepsilon }=\varepsilon \)-shift\(^I(\partial ^t)\).
Proof. The uniqueness of the family \(\{\partial ^t\}\) was already proved in the body of this paper. Let us prove the existence of the family  \(\{\eta _c^t\}_{c \in Co(N)})\). It is equivalent to prove that for any \(t_0\) the definition of \(\partial ^{t_0}\) does not depend on its decomposition. Therefore, assuming \(t_0=t_1+\varepsilon _1=t_2+\varepsilon _2\), one must have \({\varepsilon _2}\)-shift\(^I(\partial ^{t_2}) = {\varepsilon _1}\)-shift\(^I(\partial ^{t_1})\).
\(\{\eta _c^t\}_{c \in Co(N)})\). It is equivalent to prove that for any \(t_0\) the definition of \(\partial ^{t_0}\) does not depend on its decomposition. Therefore, assuming \(t_0=t_1+\varepsilon _1=t_2+\varepsilon _2\), one must have \({\varepsilon _2}\)-shift\(^I(\partial ^{t_2}) = {\varepsilon _1}\)-shift\(^I(\partial ^{t_1})\).
One can always assume that \(t_1<t_2\) and hence \(t_2=t_1+\varepsilon _0\) where \(\varepsilon _0>0\). We note  , the \(\varepsilon _1\)-extension of \(\{\partial ^t\}\).
, the \(\varepsilon _1\)-extension of \(\{\partial ^t\}\).
-
1.
\(\partial ^{t_0}\) as the \(\varepsilon _1\)-shift of \(\partial ^{t_1}\):
-
(a)
For all synapse \(s \in Sy(N)\): \(\eta _s^{t_0}=\eta _s^{t_1+\varepsilon _1}=\overline{\eta }_s^{t_1}(\varepsilon _1)\).
-
(b)
For all compartment \(c \in Co(N)\):
-
i.
\(\forall \delta \in [0, \varDelta _c - \varepsilon _1]\), \(\eta _c^{t_0}(\delta )=\eta _c^{t_1+\varepsilon _1}(\delta )=\eta _c^{t_1}(\delta +\varepsilon _1)\);
-
ii.
\(\forall \delta \!\in \! [\varDelta _c - \varepsilon _1, \varDelta _c]\), \(\eta _c^{t_0}(\delta )\,{=}\,\eta _c^{t_1+\varepsilon _1}(\delta )\,{=}\,\left( \sum \limits _{x \in Pred_N(c)}\overline{\eta }_{x}^{t_1}(\delta -\varDelta _c+\varepsilon _1) \right) \times \alpha _{c}\).
-
i.
-
(a)
-
2.
\(\partial ^{t_0}\) as the \(\varepsilon _2\)-shift of \(\partial ^{t_2}\):
-
(a)
For all synapse \(s \in Sy(N)\): \(\eta _s^{t_0}=\eta _s^{t_2+\varepsilon _2}=\overline{\eta }_s^{t_2}(\varepsilon _2)=\overline{\eta }_s^{t_1+\varepsilon _0} (\varepsilon _2) = \overline{\eta }_s^{t_1} (\varepsilon _2+\varepsilon _0) = \overline{\eta }^{t_1}_s(\varepsilon _1)\) which is equal to \(\eta _s^{t_1+\varepsilon _1}\) (computed in 1. (a)). This proves that the definition of \(\eta _s^{t_0}\) does not depend on its decomposition.
-
(b)
For all compartment \(c \in Co(N)\), one has to consider 3 cases, the union of which covers all the interval \([0,\varDelta _c]\).
-
i.
If \(\delta \in [0,\varDelta _c - \varepsilon _1]\) then a fortiori \(\delta \in [0,\varDelta _c - \varepsilon _2]\) because \(\varepsilon _2 < \varepsilon _1\). So: \(\eta _c^{t_0}(\delta )=\eta _c^{t_2+\varepsilon _2}(\delta )=\eta _c^{t_2}(\delta +\varepsilon _2).\) Moreover, \(\delta +\varepsilon _2 \leqslant \varDelta _c - \varepsilon _0\) as \(\delta \leqslant \varDelta _c-(\varepsilon _0+\varepsilon _2) = \varDelta _c - \varepsilon _1\). So: \(\eta _c^{t_2}(\delta +\varepsilon _2) = \eta _c^{t_1+\varepsilon _0} (\delta +\varepsilon _2) = \eta _c^{t_1} (\delta -\varepsilon _2+\varepsilon _0) = \eta ^{t_1}_c(\delta +\varepsilon _1)\) which is equal to \(\eta _c^{t_1+\varepsilon _1}(\delta )\) from 1(b).
-
ii.
If \(\delta \in [\varDelta _c - \varepsilon _1, \varDelta _c - \varepsilon _2]\) then a fortiori \(\delta \in [0,\varDelta _c - \varepsilon _2]\) because \(\varepsilon _1 < \varDelta _c\). So: \(\eta _c^{t_0}(\delta )=\eta _c^{t_2+\varepsilon _2}(\delta )=\eta _c^{t_2}(\delta +\varepsilon _2).\) Moreover, \(\delta +\varepsilon _2 \in [\varDelta _c - \varepsilon _0, \varDelta _c]\) as \(\varDelta _c - \varepsilon _1 + \varepsilon _2 = \varDelta _c - (\varepsilon _1 - \varepsilon _2) = \varDelta _c - \varepsilon _0\). So:
$$\begin{aligned}\eta _c^{t_2}(\delta +\varepsilon _2)&= \eta _c^{t_1+\varepsilon _0} (\delta +\varepsilon _2) = \left( \sum \limits _{x \in Pred_N(c)} \overline{\eta }_{x}^{t_1}(\delta +\varepsilon _2-\varDelta _c+\varepsilon _0) \right) ~\times ~\alpha _{c}\\&= \left( \sum \limits _{x \in Pred_N(c)} \overline{\eta }_{x}^{t_1}(\delta -\varDelta _c+\varepsilon _1) \right) \times \alpha _{c}\end{aligned}$$which is equal to \(\eta _c^{t_1+\varepsilon _1}(t)\) from 1(b).
-
iii.
If \(\delta \in [\varDelta _c - \varepsilon _2, \varDelta _c]\) then: \(\eta _c^{t_2+\varepsilon _2}(\delta )=\left( \sum \limits _{x \in Pred_N(c)} \overline{\eta }_{x}^{t_2}(\delta -\varDelta _c+\varepsilon _2) \right) \times \alpha _{c}\). Moreover, since \(\delta \in [\varDelta _c - \varepsilon _2, \varDelta _c]\), \((\delta -\varDelta _c+\varepsilon _2) \in [0,\varepsilon _2] \subset [0, \varDelta _c - \varepsilon _0]\) because \(\varepsilon _1 = \varepsilon _2 + \varepsilon _0 \leqslant \varDelta _c\) and hence \(\varepsilon _2<\varDelta _c - \varepsilon _0\). Therefore \(\overline{\eta }_{x}^{t_2}(\delta -\varDelta _c+\varepsilon _2) = \overline{\eta }_{x}^{t_1+\varepsilon _0}(\delta -\varDelta _c+\varepsilon _2) =\overline{\eta }_{x}^{t_1}(\delta -\varDelta _c+\varepsilon _2+\varepsilon _0) = \overline{\eta }_{x}^{t_1}(\delta -\varDelta _c+\varepsilon _1)\). It comes: \(\eta _c^{t_2+\varepsilon _2}(\delta )= \left( \sum \limits _{x \in Pred_N(c)} \overline{\eta }_{x}^{t_1}(\delta -\varDelta _c+\varepsilon _1) \right) \times \alpha _{c}\) which is equal to \(\eta _c^{t_1+\varepsilon _1}(\delta )\) from 1(b).
Thus, \(\forall \delta \in [0,\varDelta _c]\), \(\eta _c^{t_0}\) as the \(\varepsilon _2\)-shift of \(\eta _c^{t_2}\) (computed in 2.) is equal to \(\eta _c^{t_0}\) as the \(\varepsilon _1\)-shift of \(\eta _c^{t_1}\) (computed in 1.) which proves that the definition of \(\eta _c^{t_0}\) does not depend on its decomposition. \(\square \)
-
i.
-
(a)
1.3 A.3 Proof of Lemma 1
Given a soma \(\triangledown = (\beta , \gamma )\) there exists a unique family of functions  indexed by the set of continuous functions
indexed by the set of continuous functions  , such that for any couple \((e^0, p^0) \in Nominal(\beta )\), \(P_F\) satisfies:
, such that for any couple \((e^0, p^0) \in Nominal(\beta )\), \(P_F\) satisfies:
-
\(P_F(e^0,p^0,0)=p^0\);
-
For all
 the right derivative \(\frac{dP_F(e^0,p^0,t)}{dt}\) exists and is equal to \(F(t)-\gamma .P_F(e^0,p^0,t)\); Moreover for all
the right derivative \(\frac{dP_F(e^0,p^0,t)}{dt}\) exists and is equal to \(F(t)-\gamma .P_F(e^0,p^0,t)\); Moreover for all 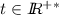 ,
,  exists and: If \((t+e^0, \ell ) \in Nominal(\beta )\) then \(P_F(e^0,p^0,t)\) is differentiable, therefore \(P_F(e^0,p^0,t) = \ell \); Otherwise, for any \(h \geqslant t\), \(P_F(e^0,p^0,h)=P_G(0,\ell -p^\beta ,h-t)\) where G is defined by:
exists and: If \((t+e^0, \ell ) \in Nominal(\beta )\) then \(P_F(e^0,p^0,t)\) is differentiable, therefore \(P_F(e^0,p^0,t) = \ell \); Otherwise, for any \(h \geqslant t\), \(P_F(e^0,p^0,h)=P_G(0,\ell -p^\beta ,h-t)\) where G is defined by:  .
.
Proof. We need to prove the existence of a unique function \(P_F(e^0,p^0,t)\). Let us consider the strictly increasing sequence of positive real numbers \(t_0...t_n...\) built as follows:
Basic Case:
-
From the Cauchy-Lipschitz theorem (also known as Picard-Lindelöf), there exists a unique function f(t) such that \(f'(t)=g(t,f(t)) = F(t)-\gamma . f(t)\) and \(f(0) = p^0\) because:
-
g is uniformly Lipschitz continuous in f, meaning that the Lipschitz constant (k) is not dependent of t so \(\forall t, \exists k \in R^{*+}\) such that \(|g(t,x)-g(t,y)| \leqslant k |x-y|\) meaning \(|(F(t)-\gamma .x)-(F(t)-\gamma .y)| \leqslant k |x-y|\) meaning \(\gamma |y-x| \leqslant k |x-y|\) which is obvious for \(k = \gamma \);
-
g is continuous in t because F is continuous in t.
-
-
Let \(t_0\) be the smallest
 such that \((e^0+t,f(t)) \notin Nominal(\beta )\) then \(t_0>0\) because \((e^0,f(0))=(e^0,p^0) \in Nominal(\beta )\). If \(t_0 =+\infty \) then the lemma is proven. Otherwise, \(P_F(e^0,p^0,t_0)=P_G(0,p_1,0)\). Therefore, there exists a unique function \(P_F(e^0,p^0,t)\) on the interval \([0,t_0]\) and since it is differentiable, \(\lim \limits _{h \rightarrow t^-} (P_F(e^0,p^0,h))\) exists on \(]0,t_0]\).
such that \((e^0+t,f(t)) \notin Nominal(\beta )\) then \(t_0>0\) because \((e^0,f(0))=(e^0,p^0) \in Nominal(\beta )\). If \(t_0 =+\infty \) then the lemma is proven. Otherwise, \(P_F(e^0,p^0,t_0)=P_G(0,p_1,0)\). Therefore, there exists a unique function \(P_F(e^0,p^0,t)\) on the interval \([0,t_0]\) and since it is differentiable, \(\lim \limits _{h \rightarrow t^-} (P_F(e^0,p^0,h))\) exists on \(]0,t_0]\).
Induction Step:
-
Inductively, assume that the existence of a unique function \(P_F(e^0,p^0,t)\) is proved on an interval \([0,t_i]\) where
 and \(P_F(e^0,p^0,t_i)=P_{G_i}(0,p_i,0)\) where \(G_i(u)=F(u+t_i)\). Let \(\varDelta t\) be the smallest
and \(P_F(e^0,p^0,t_i)=P_{G_i}(0,p_i,0)\) where \(G_i(u)=F(u+t_i)\). Let \(\varDelta t\) be the smallest  such that \((e^0+\varDelta t,f(t)) \notin Nominal(\beta )\). If \(\varDelta t =+\infty \) then the lemma is proven. Otherwise, let \(t_{i+1} = t_i + \varDelta t\), we have proven that there exists a unique function \(P_F(e^0,p^0,t)\) on the interval \([0,t_{i+1}]\) and since it is differentiable on \([t_i,t_{i+1}]\), \(\lim \limits _{h \rightarrow t^-} (P_F(e^0,p^0,h))\) exists on this interval and therefore it exists on \([0,t_{i+1}]\).
such that \((e^0+\varDelta t,f(t)) \notin Nominal(\beta )\). If \(\varDelta t =+\infty \) then the lemma is proven. Otherwise, let \(t_{i+1} = t_i + \varDelta t\), we have proven that there exists a unique function \(P_F(e^0,p^0,t)\) on the interval \([0,t_{i+1}]\) and since it is differentiable on \([t_i,t_{i+1}]\), \(\lim \limits _{h \rightarrow t^-} (P_F(e^0,p^0,h))\) exists on this interval and therefore it exists on \([0,t_{i+1}]\). -
Finally for any i, \(\varDelta t\) is greater than \(e_\beta \) and consequently the sequence of \(t_i\) diverges towards \(+ \infty \) which proves the lemma, according to Lemma 4. \(\square \)
1.4 A.4 Proof of Commutativity Lemma 2
Given a neuron N, let \(\partial =(\{\eta _s\}_{s \in Sy(\mathbb {P}(N))},\{\eta _c\}_{c \in Co(\mathbb {P}(N))})\) be a dendritic state of \(\mathbb {P}(N)\) in continuity with an input signal I and let  such that \(\varepsilon \leqslant inf(\{\varDelta _c~|~c \in Co(N)\})\). For any \(c_s \in Co(\mathbb {P}(N))\) we have: \(\varepsilon \)-shift\(^{I_{|_s}}(\overleftarrow{\mathbb {P}_N}(\{\eta _c\},c_s)) = \overleftarrow{\mathbb {P}_N}(\varepsilon \)-shift\(^{I_{|_s}}(\{\eta _c\}),c_s)\).
such that \(\varepsilon \leqslant inf(\{\varDelta _c~|~c \in Co(N)\})\). For any \(c_s \in Co(\mathbb {P}(N))\) we have: \(\varepsilon \)-shift\(^{I_{|_s}}(\overleftarrow{\mathbb {P}_N}(\{\eta _c\},c_s)) = \overleftarrow{\mathbb {P}_N}(\varepsilon \)-shift\(^{I_{|_s}}(\{\eta _c\}),c_s)\).
Proof. We need to prove \(\varepsilon \)-shift\(^{I_{|_s}}(\overleftarrow{\mathbb {P}_N}(\{\eta _c\},c_s)) = \overleftarrow{\mathbb {P}_N}(\varepsilon \)-shift\(^{I_{|_s}}(\{\eta _c\}),c_s)\). Let us note:
-
1.
\(\overleftarrow{\mathbb {P}_N}(\{\eta _c\},c_s)=\overleftarrow{\eta }_c=\{\overleftarrow{\eta }_c\}_{c \in Co(N)}\)
-
2.
\(\varepsilon \)-shift\(^{I_{|_s}}(\{\overleftarrow{\eta }_c\})=\overleftarrow{\eta }_c^\varepsilon =\{\overleftarrow{\eta }_c^\varepsilon \}_{c \in Co(N)}\)
-
3.
\(\varepsilon \)-shift\(^{I_{|_s}}(\{\eta _c\})=\eta _{c_s}^\varepsilon =\{\eta _{c_s}^\varepsilon \}_{c_s \in Co(\mathbb {P}(N)}\)
-
4.
\(\overleftarrow{\mathbb {P}_N}(\{\eta _c^\varepsilon \},c_s)=\overleftarrow{\eta _c^\varepsilon }=\{\overleftarrow{\eta _c^\varepsilon }\}_{c \in Co(N)}\)
We then need to prove \(\forall c \in Co(N)\), \(\overleftarrow{\eta }_{c}^\varepsilon =\overleftarrow{\eta _{c}^\varepsilon }\). For simplicity, we note \(\eta _s(x) = \overline{\eta }_s(x)\) since we only consider \(\varepsilon \)-extended synaptic states in this proof.
-
1.
From Definition 14:
-
(a)
If \(c \notin Path_N(s{\rightarrow }\triangledown )\) then \(\forall \delta \in [0,\varDelta _c]\), \(\overleftarrow{\eta }_c(\delta )=0\);
-
(b)
If \(c \in Path_N(s{\rightarrow }\triangledown )\), there exists i such that \(c=c_i\) with \(Path_N(s{\rightarrow }\triangledown )=c_1,...,c_i,...,c_n\).
Therefore, \(\forall \delta \in [0,\varDelta _c]\), \(\overleftarrow{\eta }_c(\delta )=\eta _{c_s}\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta \right) /\varPi _N^{c_{i+1}{\rightarrow }c_n}\).
-
(a)
-
2.
From Definition 10:
-
(a)
If \(c \notin Path_N(s{\rightarrow }\triangledown )\):
-
i.
If \(\delta \in [0,\varDelta _c - \varepsilon ]\), \(\overleftarrow{\eta }_c^\varepsilon (\delta ) = \overleftarrow{\eta }_c(\delta +\varepsilon ) = 0\) (because of 1. (a)).
-
ii.
If \(\delta \in [\varDelta _c - \varepsilon , \varDelta _c]\), \(\overleftarrow{\eta }_c^\varepsilon (\delta )=\left( \sum \limits _{x \in Pred_N(c)} \overleftarrow{\eta }_{x}(\delta -\varDelta _c+\varepsilon ) \right) \times \alpha _{c}\).
For each \(x \in CoPred_N(c)\), since \(c \notin Path_N(s{\rightarrow }\triangledown )\) then \(x \notin Path_N(s{\rightarrow }\triangledown )\) and therefore \(\overleftarrow{\eta }_{x}=0\) (because of 1. (a)). Moreover, for each \(x \in SyPred_N(c)\) and considering \(I_{|_s}\), \(\overleftarrow{\eta }_x=0\) because \(\forall x \in SyPred_N(c)\), x is different from s as \(c \notin Path_N(s{\rightarrow }\triangledown )\). We thus have \(\overleftarrow{\eta }_c^\varepsilon (\delta )=0\).
-
i.
-
(b)
If \(c \in Path_N(s{\rightarrow }\triangledown )\):
-
i.
If \(\delta \in [0,\varDelta _c - \varepsilon ]\), \(\overleftarrow{\eta }_c^\varepsilon (\delta ) = \overleftarrow{\eta }_c(\delta +\varepsilon ) = \eta _{c_s}\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta +\varepsilon \right) /\varPi _N^{c_{i+1}{\rightarrow }c_n}\) (because of 1. (b)).
-
ii.
If \(\delta \in [\varDelta _c - \varepsilon , \varDelta _c]\), \(\overleftarrow{\eta }_c^\varepsilon (\delta )=\left( \sum \limits _{x \in Pred_N(c)}\overleftarrow{\eta }_{x}(\delta -\varDelta _c+\varepsilon ) \right) \times \alpha _{c}\).
Since c has only one predecessor compartment \(x \in Path_N(s{\rightarrow }\triangledown )\) (potentially having \(\overleftarrow{\eta }_{x} \ne 0\)), we have \(CoPred_N(c)=\{c_{i-1}\}\) (except \(CoPred_N(c)=\varnothing \) if \(c_i=c_1\)). Moreover, \(SyPred_N(c)=\{s\}\) if \(c_i = c_1\) while if \(c_i \ne c_1\) for each \(x \in SyPred_N(c)\), \(\overleftarrow{\eta }_x=0\) (considering \(I_{|_s}\)). Therefore:
-
A.
if \(c_i \ne c_1\), \(\overleftarrow{\eta }_c^\varepsilon (\delta )=\overleftarrow{\eta }_{c_{i-1}}(\delta -\varDelta _c+\varepsilon )\times \alpha _c\). From 1. (b), \(\overleftarrow{\eta }_{c_{i-1}}(\delta )=\eta _{c_s}\left( \varSigma _N^{c_{i}{\rightarrow }c_n}+\delta \right) /\varPi _N^{c_{i}{\rightarrow }c_n}\).
Therefore, \(\overleftarrow{\eta }_c^\varepsilon (\delta )=\left( \eta _{c_s}\left( \varSigma _N^{c_{i}{\rightarrow }c_n}+\delta -\varDelta _c+\varepsilon \right) /\varPi _N^{c_{i}{\rightarrow }c_n}\right) \times \alpha _c =\eta _{c_s}\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta +\varepsilon \right) /\varPi _N^{c_{i+1}{\rightarrow }c_n}\).
-
B.
if \(c_i = c_1\), \(\overleftarrow{\eta }_c^\varepsilon (\delta )=(\overleftarrow{\eta }_{s}(\delta -\varDelta _c+\varepsilon ))\times \alpha _c\) and from the remark of Definition 14, \(\overleftarrow{\eta }_c^\varepsilon (\delta )=(\eta _{s}(\delta -\varDelta _c+\varepsilon ))\times \alpha _c\).
-
A.
-
i.
-
(a)
-
3.
From Definition 10:
-
(a)
if \(\delta \in [0,\varDelta _{c_s} - \varepsilon ]\), \(\eta _{c_s}^\varepsilon (\delta )=\eta _{c_s}(\delta +\varepsilon )\).
-
(b)
if \(\delta \in [\varDelta _{c_s} - \varepsilon , \varDelta _{c_s}]\), \(\eta _{c_s}^\varepsilon (\delta )=\left( \sum \limits _{x \in Pred_N(c_s)} \eta _{x}(\delta -\varDelta _{c_s}+\varepsilon ) \right) \times \alpha _{c}\).
Since \(c_s \in Co(\mathbb {P}(N))\), \(CoPred_N(c_s)=\varnothing \) and \(SyPred_N(c_s)=\{s\}\). Therefore, \(\eta _{c_s}^\varepsilon (\delta )=(\eta _{s}(\delta -\varDelta _{c_s}+\varepsilon ))\times \alpha _{c}\).
-
(a)
-
4.
Lastly, from Definition 14:
-
(a)
If \(c \notin Path_N(s{\rightarrow }\triangledown )\) then \(\forall \delta \in [0,\varDelta _c]\), \(\overleftarrow{v_c^\varepsilon }(\delta )=0\) which is equal to \(\overleftarrow{\eta }_c^\varepsilon (\delta )\) (computed in 2. (a)).
-
(b)
If \(c \in Path_N(s{\rightarrow }\triangledown )\), there exists i such that \(c=c_i\) and \(Path_N(s{\rightarrow }\triangledown )=c_1,...,c_i,...,c_n\). Therefore, \(\forall \delta \in [0,\varDelta _c]\), \(\overleftarrow{\eta _c^\varepsilon }(\delta )=\eta _{c_s}^\varepsilon \left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta \right) /\varPi _N^{c_{i+1}{\rightarrow }c_n}\). Since \(\eta _{c_s}^\varepsilon =\varepsilon \)-shift\(^{I_{|_s}}(\eta _{c_s})\), we have:
-
i.
If \(\delta \in [0,\varDelta _c-\varepsilon ]\) then \(\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta \right) \in [0,\varDelta _{c_s}-\varepsilon ]\) therefore, \(\eta _{c_s}^\varepsilon \left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta \right) =\eta _{c_s}\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta +\varepsilon \right) \) and hence, \(\overleftarrow{\eta _c^\varepsilon }(\delta )=\eta _{c_s}\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta +\varepsilon \right) / \varPi _N^{c_{i+1}{\rightarrow }c_n}\) which is equal to \(\overleftarrow{\eta }_c^\varepsilon (\delta )\) (computed in 2. (b) i.).
-
ii.
If \(\delta \in [\varDelta _c-\varepsilon , \varDelta _c]\) then:
-
A.
If \(c_i \ne c_1\), \(\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta \right) \in [0,\varDelta _{c_s}-\varepsilon ]\) therefore, \(\eta _{c_s}^\varepsilon \left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta \right) =\eta _{c_s}\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta +\varepsilon \right) \) and hence, \(\overleftarrow{\eta _c^\varepsilon }(\delta )=\eta _{c_s}\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta +\varepsilon \right) / \varPi _N^{c_{i+1}{\rightarrow }c_n}\) which is equal to \(\overleftarrow{\eta }_c^\varepsilon (\delta )\) (computed in 2. (b) ii. A.).
-
B.
If \(c_i\, {=}\, c_1\), \(\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta \right) \!\in \! [\varDelta _{c_s}-\varepsilon , \varDelta _{c_s}]\) thus, \(\eta _{c_s}^\varepsilon \left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta \right) =\left( \sum \limits _{x \in Pred_N(c_s)} \eta _{x}\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta -\varDelta _{c_s}+\varepsilon \right) \right) ~\times ~\alpha _{c_s}\) and hence \(\overleftarrow{\eta _c^\varepsilon }(\delta )=\left( \eta _{s}\left( \varSigma _N^{c_{i+1}{\rightarrow }c_n}+\delta -\varDelta _{c_s}+\varepsilon \right) \times \alpha _{c_s}\right) /\varPi _N^{c_{i+1}{\rightarrow }c_n}\) (because \(CoPred_N(c_s)=\varnothing \) and \(SyPred_N(c_s)=\{s\}\)). Since \(c_i=c_1\), \(\varSigma _N^{c_{i+1}{\rightarrow }c_n}=\varDelta _{c_s}-\varDelta _{c_1}\) therefore \(\overleftarrow{\eta _c^\varepsilon }(\delta )=\left( \eta _{s}(\delta -\varDelta _{c_1}+\varepsilon )\right. \left. \times \alpha _{c_s}\right) / \varPi _N^{c_{i+1}{\rightarrow }c_n}\) and hence \(\overleftarrow{\eta _c^\varepsilon }(\delta )=\left( \eta _{s}(\delta -\varDelta _{c_1}+\varepsilon )\right) \times \alpha _{c_1}\) which is equal to \(\overleftarrow{\eta }_c^\varepsilon (\delta )\) (computed in 2. (b) ii. B.).
-
A.
-
i.
-
(a)
This concludes the proof. In 4., we had to consider two cases (a) and (b). The case (a) was directly solved whereas the case (b) was divided in two sub-cases i. and ii. The case i. was directly solved whereas the case ii. was divided in two sub-sub-cases A. and B. which were both solved. So, owing to this decomposition, the lemma is proved for all the possible conditions. \(\square \)
1.5 A.5 Proof of Commutativity Lemma 3
Given a neuron N, let \(\partial =(\{\eta _s\}_{s \in Sy(N)},\{\eta _c\}_{c \in Co(N)})\) and \(\partial '=(\{\eta '_s\}_{s \in Sy(N)}\), \(\{\eta '_c\}_{c \in Co(N)})\) be two dendritic states of N in continuity with an input signal I. Let A and \(A'\) be two disjoint subsets of Sy(N) such that \(A \cup A' = Sy(N)\) and let  such that \(\varepsilon \leqslant inf(\{\varDelta _c~|~c \in Co(N)\})\).
such that \(\varepsilon \leqslant inf(\{\varDelta _c~|~c \in Co(N)\})\).
We have: \(\varepsilon \)-shift\(^I(\{\eta _c\}+\{\eta '_c\})=\varepsilon \)-shift\(^{I_{|_A}}(\{\eta _c\}) +\varepsilon \)-shift\(^{I_{|_{A'}}}(\{\eta '_c\})\).
Proof. According to Definition 10, for any \(c \in Co(N)\), we note \(\eta ''_c=\eta _c+\eta '_c\).
-
1.
Let us consider \(\varepsilon \)-shift\(^I(\{\eta _c\}+\{\eta '_c\})\):
-
If \(\delta \in [0, \varDelta _c - \varepsilon ]\), \(\varepsilon \)-shift\(^I(\eta _c+\eta _c')(\delta )=\varepsilon \)-shift\(^I(\eta _c'')(\delta )=\eta _c''(\delta +\varepsilon )=(\eta _c+\eta _c')(\delta +\varepsilon )=\eta _c(\delta +\varepsilon )+\eta _c'(\delta +\varepsilon )\).
-
If \(\delta \in [\varDelta _c - \varepsilon , \varDelta _c]\), \(\varepsilon \)-shift\(^I(\eta _c+\eta _c')(\delta )=\varepsilon \)-shift\(^I(\eta _c'')(\delta )\)
\(=(\sum \limits _{x \in Pred_N(c)} (\overline{\eta }''_{x}(\delta -\varDelta _{c}+\varepsilon )) )~\times ~\alpha _{c}\)
\(=(\sum \limits _{x \in Pred_N(c)} ((\overline{\eta }_{x}+\overline{\eta }'_{x})(\delta -\varDelta _{c}+\varepsilon )) )~\times ~\alpha _{c} \)
\(= (\sum \limits _{x \in Pred_N(c)} (\overline{\eta }_{x}(\delta -\varDelta _{c}+\varepsilon ) + \overline{\eta }'_{x}(\delta -\varDelta _{c}+\varepsilon )) )~\times ~\alpha _{c}\)
-
-
2.
Let us consider \(\varepsilon \)-shift\(^{I_{|_A}}(\{\eta _c\}) +\varepsilon \)-shift\(^{I_{|_{A'}}}(\{\eta '_c\})\):
-
If \(\delta \in [0, \varDelta _c - \varepsilon ]\), \(\varepsilon \)-shift\(^{I_{|_A}}(\eta _c) +\varepsilon \)-shift\(^{I_{|_{A'}}}(\eta _c')=\eta _c(\delta +\varepsilon )+\eta _c'(\delta +\varepsilon )\).
-
If \(\delta \in [\varDelta _c - \varepsilon , \varDelta _c]\), \(\varepsilon \)-shift\(^{I_{|_A}}(\eta _c) +\varepsilon \)-shift\(^{I_{|_{A'}}}(\eta _c')\)
\(=(\sum \limits _{c' \in CoPred_N(c)} \overline{\eta }_{c'}(\delta -\varDelta _{c}+\varepsilon ) + \sum \limits _{s \in SyPred_N(c) \cap s \in A} \overline{\eta }_{s}(\delta -\varDelta _{c}+\varepsilon ) ) \times \alpha _{c} \)
\(+ (\sum \limits _{c' \in CoPred_N(c)} \overline{\eta }'_{c'}(\delta -\varDelta _{c}+\varepsilon ) + \sum \limits _{s \in SyPred_N(c) \cap s \in A'} \overline{\eta }_{s}(\delta -\varDelta _{c}+\varepsilon ) ) \times \alpha _{c} \)
\(= (\sum \limits _{c' \in CoPred_N(c)} \overline{\eta }_{c'}(\delta -\varDelta _{c}+\varepsilon ) + \sum \limits _{s \in SyPred_N(c) \cap s \in A} \overline{\eta }_{s}(\delta -\varDelta _{c}+\varepsilon ) \)
\(+ \sum \limits _{c' \in CoPred_N(c)} \overline{\eta }'_{c'}(\delta -\varDelta _{c}+\varepsilon ) + \sum \limits _{s \in SyPred_N(c) \cap s \in A'} \overline{\eta }_{s}(\delta -\varDelta _{c}+\varepsilon ) )~\times ~\alpha _{c} \)
\(= (\sum \limits _{c' \in CoPred_N(c)} (\overline{\eta }_{c'}(\delta -\varDelta _{c}+\varepsilon ) + \overline{\eta }'_{c'}(\delta -\varDelta _{c}+\varepsilon )) \)
\(+ \sum \limits _{s \in SyPred_N(c)} \overline{\eta }_{s}(\delta -\varDelta _{c}+\varepsilon ) ) \times \alpha _{c}\)
\(= (\sum \limits _{x \in Pred_N(c)} (\overline{\eta }_{x}(\delta -\varDelta _{c}+\varepsilon ) + \overline{\eta }'_{x}(\delta -\varDelta _{c}+\varepsilon )) )~\times ~\alpha _{c}\).
-
Thus, \(\varepsilon \)-shift\(^{I_{|_A}}(\{\eta _c\}) +\varepsilon \)-shift\(^{I_{|_{A'}}}(\{\eta '_c\}) = \varepsilon \)-shift\(^I(\{\eta _c\}+\{\eta '_c\})\) as the formulas obtained in 1. and 2. are the same. \(\square \)
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Guinaudeau, O., Bernot, G., Muzy, A., Gaffé, D., Grammont, F. (2019). Formal Neuron Models: Delays Offer a Simplified Dendritic Integration for Free. In: Cliquet Jr., A., et al. Biomedical Engineering Systems and Technologies. BIOSTEC 2018. Communications in Computer and Information Science, vol 1024. Springer, Cham. https://doi.org/10.1007/978-3-030-29196-9_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-29196-9_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29195-2
Online ISBN: 978-3-030-29196-9
eBook Packages: Computer ScienceComputer Science (R0)


 the right derivative
the right derivative 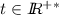 ,
,  exists and: If
exists and: If  .
. such that
such that  and
and  such that
such that