Towards Efficient Pairwise Ranking for Service Using Multidimensional Classification

Abstract

With the growing popularity of services which meet the divergent requirements from users, service selection and recommendation have drawn significant attention in services computing community. Service ranking is the most important part in service selection and recommendation. Although there have been several existing approaches of service ranking which is basically rating-based, suffering from the heterogeneity of ranking criteria from users. Moreover, the efficiency of such comparison-based approaches is the bottleneck in reality. To attack these challenges, an efficient pairwise ranking scheme with multidimensional classification is proposed in this paper, which also fully considers the context information of service and users. Furthermore, the scheme is able to mitigate data sparsity of users similarity matrix and improve accuracy. Next, we introduce a random walk model for ranking formulation, and propose a Markov chain based approach to obtain the global ranking. Finally, the efficacy of our approach is validated by experiments adopting the real-world YELP dataset.

1 Introduction

Nowadays, with the rapid development of service-oriented architecture (SOA), an increasing amount of functionally similar service have been published on the Internet, which makes the selection of suitable service a complex task. To achieve this goal, recommendation techniques have been applied to help users satisfy their needs and preferences. Recommendation systems are all over e-commerce system, social network, advertising recommendation, search engine, etc. To satisfy user requirements, Quality-of-service (QoS) criteria are considered as one of the most important factors in the field of service recommendation. Furthermore, the importance of service recommendation is the selection of service. Since users may have different needs and preferences in various contexts, (e.g. users’ favorite service may change over time and place.) the selection of suitable service for users is still a challenging problem.

In most recommendation processes, users indicate their preferences for the service through rating. Typically, the utility function is estimated based on prior user ratings, which is applied to predict the service relevant to the specified user [2], then the top-k services are picked out and recommended to the user. So the ranking method shows its importance. However, in many real world applications, it is quite difficult to aggregate the ratings from multiple users, since different users may have different criteria with can be closely correlated with their preferences, and thus “the trust level” of service ratings from different users should be considered very carefully in service raking.

The variety of context information should also be taken into account when service ranking. There are several factors that need to be considered, such as functionality, location, constraints, price, performance, availability, etc., making the service ranking be a very complex multidimensional mathematical problem. With the growing number of the dimension, the search space to solve the problems grows exponentially. Therefore, the efficiency problem in service ranking, which seeks to solve the problem with acceptably low complexity, is another challenge for researchers.

In this paper, a context-based multidimensional classification model is presented, enhancing the high-efficiency and accuracy of ranking. The multidimensional property can be formulated as the process of service ranking. Firstly, we classify users and obtain the context-based service of the nearest neighbors of the users, and then a pairwise comparison method is applied within the ranking process. Comparisons between of service are formulated as the stochastic process of random walk, and thus, ranking results can be obtained by rated the steady-state probabilities of the underlying Markov chain.

The main contributions of our work are listed as below. Firstly, a context-based multidimensional classification method is presented, which is quite helpful for improving the accuracy of ranking aggregation as well as dramatically reducing the computational complexity. Secondly, we apply the pairwise comparison model to ranking aggregation, which is robust to the variety of ranking criteria and preferences from different users. Finally, we conduct experiments based on real-world large-scale service rating data to empirically validate the effectiveness and efficiency of our approach.

The remainder of this paper is organized as follows. Section 2 presents the basic concepts and the related work used. In Sect. 3, we propose a pairwise ranking method with multidimensional classification, and its properties and capabilities are discussed. In Sect. 4, we implement our approach and conduct real-data-based experiments to demonstrate its accuracy and efficacy. Finally, we conclude this paper in Sect. 5.

2 Related Work

2.1 Existing Problems

The algorithms about ranking can also be divided into two categories: ranking with implicit feedback (PRIF) [6,7,8,9] and ranking with explicit feedback (PREF) [13, 14]. The main algorithm of PREF is Collaborative Filtering [1, 3, 5], and the foremost of PRIF is Bayesian Personalized Ranking (BPR) [16], which converts the OCCF problem into a ranking problem.

One of the most successful technologies for recommendation systems called Collaborative Filtering, has been developed and improved over the past decades, and several relevant algorithms were designed and delivered for conduct service ranking. For example, Shi et al. [14] proposed Extended Collaborative Less-Is-More Filtering (xCLiMF) model, which could be seen as a generalization of the CLiMF method. The key idea of the xCLiMF algorithm is that it builds a model by optimizing Expected Reciprocal Rank, an evaluation metric that generalizes Reciprocal Rank (RR) in order to incorporate user’ explicit feedback.

The above implicit feedback model based on ranking learning is mostly based on the two-dimensional matrix of user services, without considering the context information, such as time and place. For example, the location information that a user interacts with the system when looking for a restaurant is important contextual information. Adomavicius and Tuzhilin et al. [2] pointed out earlier that integrating context information into the ranking would be conducive to improving the accuracy of ranking, and proposed the widely cited concept of “context-aware recommendation system”. In the field of context-aware, different scholars have proposed various solutions, such as context pre-filtering, context post-filtering, TimeSVD, tensor decomposition model [4, 9], etc. The first two methods are hybrid methods based on collaborative filtering, whose drawback is that it may cause loss of information. The latter two are model-based methods, which lead to executable algorithms with high time complexity and do not develop.

In our paper, we study the problem from a totally different angle of classification. We focus on its implicit context information and rating, and group into different classes.

2.2 Collaborative Filtering

Now, we introduce traditional collaborative filtering and classification algorithm.

Most collaborative filtering system apply the user-based technique, also called user to user approach. Collaborative filtering systems predict a user interest in new service based on the recommendations of other users with similar interests. Instead of performing content indexing or content analysis, collaborative filtering systems entirely depend on interest rankings from members of a participating community.

In the user-based approach [13], a number of users are selected based on their similarity to the active users. A prediction for the active users is made by calculating a weight average of the ratings of the selected users. The similar formula is expressed by $sim(a,u)=\cos (\varvec{a},\varvec{u})$, where $a$ and $u$ are two users. Therefore, a prediction for the rating assigned by user $a$, who is computed as follows: $P(a_i)=\bar{r_a}+k\sum _{u=1}^N(r_{u,i}-\bar{r_a})\times sim(a,u)$, where $k=\frac{1}{\sum _{u\in \hat{S}}\times \mid sim(a,u)\mid )}$, $\hat{S}$ is the similar set of current user $a$, and $\bar{r_a}$ and $\bar{r_u }$ are the average ratings of user $a$ and user $u$ respectively. Note that if no one has rated service $i$, the prediction is equal to the average of all the ratings that user $a$ has made.

2.3 Classification

Early research work on clustering usually assumed that there was one true clustering of data. However, complex data are typically multifaceted and can be meaningfully clustered in many different ways. Clustering algorithms [10, 11] usually employ a distance metric based (e.g., Euclidean) similarity measure in order to partition the database such that data points in the same partition are more similar than points in different partitions.

Two main of the challenges in cluster analysis are: first to select an appropriate measure of similarity to define clusters, and second to specify the optimal number of clusters in the data set. In this direction, clustering algorithms have been developed which prove to perform very satisfactorily in clustering and finding the number of clusters [9, 10]. The present work, a clustering algorithm which tackles these two important problems and is able to partition a data set and the optimal number of clusters existing in the data set.

In this paper, we present our clustering approach that is based on hierarchical clustering. We firstly introduce the concepts used in the classification as follows.

• (1) Neighbors: Two similar users are called neighbors. In other words, we set user $a$ and user $u$ be neighbors if their similarity greater than a threshold value $\theta$. Let $SIM(a,u)$ be a similarity function that is closeness between the pair of users $a$ and $u$. Function value is between 0 and 1, with larger values indicating that the users are more similar. To sum up, given a threshold $\theta$ between 0 and 1, a pair of users $a$, $u$ are defined to be neighbors if the following holds: $SIM(a,u)\ge \theta$.

• (2) Link: Let us define $link(a,u)$ to be the number of common neighbors between $a$ and $u$. If $link(a,u)$ is large, then it is more probable that $a$ and $u$ belong to the same classification. Therefore, we use link to merge users into a single cluster. The link-based approach adopts a global approach to the clustering problem and it is very robust.

• (3) Criterion Function: Since we are interested in each cluster to have a high degree of connectivity, we would like to maximize the sum of $link(a,u)$ for data point pairs $a$, $u$ belonging to a single cluster, at the same time, minimize the sum of $link(a,u)$ for $a$, $u$ in different clusters. This leads us to the criterion function that we would like to maximize for the $k$ clusters. We’ll discuss this issue in detail at Sect. 3.

3 Multidimensional Classification Model

The multidimensional classification problem is a generalization of the recently-popularized task of multi-label classification, where each data instance is associated with multiple class variables. In this section, we describe classification model based on multidimensional similarity and ranking.

3.1 Classification

Multiple classification brings an ability to view a type from more than one perspective. Users have many influencing factors and preferences when rating, such as time, place, weather, etc. Generally, users preferences are represented by users explicit ratings or implicit context information. In this section, we consider the perspective of ratings as dimensions.

We let $D_1,D_2,... D_n$ be dimensions, each dimension $D_i$ being an perspective of a rating $R_{u,i}$, for example, ratings that a user provided for same service are two dimensions in March 2019 and February 2019.

Then, we define the multidimensional space for these dimensions as a cartesian product $Space=D_1 \times D_2 \times ...\times D_n$. Therefore, the user preference for the service should be combined with the ratings and dimensional space, shown as Eq. (1).

$$\begin{aligned} D_1\,\times \,D_2\,\times \,...\,\times \,D_n \rightarrow Ratings \end{aligned}$$

(1)

For example, there is a three-dimensional space $Space= Service\quad demand \times Date \times Place$, the ratings given by users can be seen as a 3*3 matrix in three dimensions, of course the matrix is sparse. In this paper, we set up a matrix of user to service supporting user preference, $A=[r_{u,s}]_{m*n}$, where $r_{u,s}$ is the rating of service $s$ assigned by user $u$, $m$ is the number of users, and $n$ is the number of service. The matrix of User-Service is illustrated by Fig. 1, and $r_{u,i}$ is defined as,

$$\begin{aligned} r_{u,i}= \left\{ \begin{aligned} r&, \quad r \in [1,5],if\quad ratings\quad exit \\ 0&,\quad otherwise \end{aligned} \right. \end{aligned}$$

(2)

Fig. 1.

User-Service matrix

In the above example, the rating in 3-dimensional space $Space=Service\quad demand \times Date \times Place$, is denoted as $r^{|S|\times |D|\times |P|}_{u,s}$, where $S$ represents the service demand dimension, $D$ represents the date dimension, and $P$ represents the place dimension.

In this paper, $r_{u,s}^{|S|}$ can be represented as a vector $\varvec{S}=<\varvec{s_1},\varvec{s_2},...\varvec{s_n}>$, where each vector represents a user demand dimensional attribute $r_{u,s}^{|D|}$ can be represented as a vector $\varvec{D}=<\varvec{d_1},\varvec{d_2},...\varvec{d_m}>$, where each vector represents service dimensional attribute and similarly $r_{u,s}^{|P|}$ can be represented as a vector $\varvec{P}=<\varvec{p_1},\varvec{p_t},...\varvec{p_n}>$. 3-dimensional rating can be supposed to product of 3 vectors. The extension of the multidimensional profiling approaches proposed in this section to N-dimensional data is straightforward.

Similar procedure can generate a matrix with a given factor number $\varvec{k}=<\varvec{k_1},\varvec{k_2},...,\varvec{k_i},...\varvec{k_n}>$ for the user-service matrix, where $\varvec{k_i}$ is a vector in $i$ dimension and $n$ is the number of dimensions.

The profiles of a user $u$ and a service $s$ in latent factor spaces are represented as follows,

$$\begin{aligned} \begin{aligned} \varvec{k}&=\prod _{i=1}^n \varvec{k_i}, 0\le |\varvec{k_i}| \le |1| \end{aligned} \end{aligned}$$

(3)

The profiles created by the N-dimensional vector can essentially preserve the multidimensional semantic relations in the data. Thus, the value of matrix $r_{u,s}^{|K|}$ is defined as,

$$\begin{aligned} r_{u,s}^{|K|}=\left\{ \begin{aligned} r.\varvec{k}&,\quad r \in [1,5], if \quad ratings\quad exit \\ 0&,\quad otherwise \end{aligned} \right. \end{aligned}$$

(4)

Next, we present an improved collaborative algorithm integrated with the multidimensional approach proposed and classifying users according to the method. Traditionally, collaborative systems try to predict the rating of a service based on users’ history data. It works by finding users with similar preference and recommending similar services to users.

The standard collaborative algorithm [2] works with the following procedure: First, formulate user rating into user-service matrix, differently, user rating in our approach are created by the multidimensional method. Second, generate user neighborhoods based on a predefined similarity measurement between any two users, such as Jaccard similarity or Cosine similarity. In our approach, the cosine similarity algorithm is adopted to calculate users similarity according to the rating in different dimension.

$$\begin{aligned} \begin{aligned} sim(a,u)=\cos {(\varvec{a},\varvec{u})}=\frac{\varvec{a} \cdot \varvec{u}}{|\varvec{a}|_2 * |\varvec{u}|_2} \\ =\frac{\sum _{s\in S_{au}}r_{a,s} r_{u,s}}{\sqrt{\sum _{s\in S_{au}}r_{a,s}^2 }\sqrt{\sum _{s\in S_{au}}r_{u,s}^2 }} \end{aligned} \end{aligned}$$

(5)

The Eq. (5) calculates similarity between two users $a$ and $u$, where $S_{a,u}$ represents service sets that have been rated by both user $a$ and $u$.

We compute a user final similarity based on their preferences combined Eq. (5). Each rating has a corresponding dimension. The dimension $D_i$ determines the similarity between users. The final similarity of users is calculated jointly by different dimensions. Suppose the rating under the multi-dimension $D_i, {i \in [0,n]}$ of service $s$ assigned by user $u$ is $r_{u,s}^{\sum _{i=1}^n|D_i|}$. We take the dimensional variable as the vector of the User-Service matrix, then the similarity between different dimension $D_i$ can be calculated by Eq. (6).

$$\begin{aligned} \begin{aligned} sim(a,u)=\frac{\sum _{s\in S_{au}}(r_{a,s}^{\sum _{i=1}^n|D_i|} r_{u,s}^{\sum _{i=1}^n|D_i|})}{\sqrt{\sum _{s\in S_{au}}r_{a,s}^2 }\sqrt{\sum _{s\in S_{au}}r_{u,s}^2 }} \end{aligned}\end{aligned}$$

(6)

The user similarity is classified by agglomerative clustering method that we assign each user to its own cluster. The rationale for the above criterion formula $E_l$ is as follows,

$$\begin{aligned} \begin{aligned} E_l=\sum _{i=1}^k n_i \cdot \sum _{a,u\in N}\frac{link(a,u)}{n_i^{1+2f(\theta )}} \end{aligned}\end{aligned}$$

(7)

where $N$ denotes user sets. The concept of $link$ has been discussed in Sect. 2. It may seem that since one of our goals was to sums up the $links$ between pairs of users $a$ and $u$ in the same cluster and maximize $link(a,u)$. However, it may not be easy to determine an accurate value for function $f(\theta )=\frac{1-\theta }{1+\theta }$. We select the optimal $\theta$ according to the OSTU. The optimal $\theta$ is the minimum number of links between the final clusters and the maximum number of links within clusters.

Next, the best clustering of users were those that resulted in the highest values for the criterion function. Since our goal is to find a clustering that maximizes the criterion function, we use a measure similar to the criterion function in order to determine the best pair of clusters to merge at each step of clustering algorithm.

Then, we define the goodness measure $g(a,u)$ for merging $a$, $u$ as follows,

$$\begin{aligned} \begin{aligned} g(a,u)=\frac{link(N_a,N_u)}{(n_a+n_j)^{1+2f(\theta )}-n_a^{1+2f(\theta )}-n_u^{1+2f(\theta )}} \end{aligned} \end{aligned}$$

(8)

$link(N_a,N_u)$ is the number of neigbours about two user sets $N_a$ and $N_u$, $n_a$ and $n_u$ are the numbers of the two user sets. The pair of clusters for which the above goodness measure is maximum is the best pair of clusters to be merged at any given step. In general, it is a good candidate for merging.

3.2 Comparison-Based Ranking

Ammar and Shah [15] have brought to the fore the problem of comparison-based ranking. They presented detailed mathematical models of ranking from the entropy point of view. In this paper, we study the problem from other point of view of ranking based on multidimensional classification. Comparing on ranking and rating, ranking has better evaluation accuracy and efficiency.

In order to obtain service ranking, we select some users to rate the service, and we use a comparative ranking model to focus on the final ranking. This paper adopts a model obtain the users ranking of service evaluation based on Markov decision processes.

The pairwise comparison model reflects the relationship between different services. In this section, we sort the user ratings for the services, and compare in pair all user ratings, and finally obtain a comparison matrix, defined as a comparison matrix as follows,

$$\begin{aligned} \begin{aligned} B=[P_{ij}]_{n*n},i \in n \end{aligned}\end{aligned}$$

(9)

Here, $P_{ij}$ is the frequency of service $i$ being rated higher than service $j$ in all user ratings. We let $P_{ij}^l$ denote the outcome of the l-th comparison of the pair $i$ and $j$, such that $P_{ij}^{l}=1$ if service $j$ is preferred over (ranked higher) than $j$ and 0 otherwise.

$$\begin{aligned} P_{ij}^l=\left\{ \begin{aligned} 1,with\quad probability \quad \frac{P_{ji}}{P_{ij}+P_{ji}} \\ 0,with \quad probability \quad \frac{P_{ij}}{P_{ij}+P_{ji}} \end{aligned} \right. \end{aligned}$$

(10)

As Eq. (10) shows, if $P_{ij}^l=1$ which represents the service $i$ is ranked higher than service $j$ for most users, Therefore, it is more likely to recommend service $i$ to users when there is no other factors to consider.

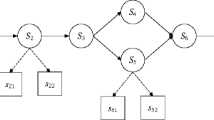
The relationship between the services can be denoted as a directed graph $G=(V,E)$, where $V$ represents the set of services used to be ranked, and $E$ represents the weight of compared services in pairs.

Here, the transmission from service $i$ to service $j$ can be denoted as $(i,j,q_{ij})$. $q_{ij}$ indicates the probability service $i$ is ranked higher than $j$, which can be obtain by the fraction of times that service $i$ ranks higher than service $j$ when compared. Therefore we can obtain the value of $q_{ij}$ by the following equation,

$$\begin{aligned} \begin{aligned} q_{ij}=\frac{1}{k}\sum _{l=1}^k P_{ij}^l \end{aligned}\end{aligned}$$

(11)

where $k$ is the number of comparisons between $i$ and $j$. We let $q_{ij}=q_{ji}=0$ if the pair has not been compared.

In this model, each comparision can be denoted by a random walk process, and we propose a Markov model-based approach to derive the service ranking. With the random walk model, in order to obtain the service ranking, the random walk can be regarded as a discrete-time Markov chain (DTMC) [12].

We solve this Markov chain in the following step. First, we use $\pi =[\pi _1,\pi _2,...\pi _n]$ represent the steady-state probabilities in DTMC, which have the relationship as $\sum _{i=1}^n\pi _i=1$. Therefore, the steady-state probabilities can be obtained from the following equations,

$$\begin{aligned} \left\{ \begin{aligned} \pi \cdot p&=\pi \\ \sum _{i=1}^n\pi _i&=1 \end{aligned} \right. \end{aligned}$$

(12)

4 Evaluation

4.1 Data Set

We select Yelp Open Dataset in Dataset Challenge to implement experiment. The dataset itself contains almost 5 million reviews from over 1.1 million users on over 150,000 businesses from 12 metropolitan areas.

In this section, due to the huge amount of data, we select four cities to implement experiment, i.e., Gastonia, Mississauga, Henderson, and Toronto, the numbers of services in cities are 500, 2000, 3000, 20000.

For example, in Gastonia, we calculate users similarity based on multidimensional classification model. Then, we mark neighbors and $link$ (that the number of common neighbors between two users), and perform clustering method based on users similarity and Criterion Function (7,8). Next, we divide users of Gastonia into 6 groups according our classification method (Eq. (1)). In the next process, we establish a Markov chain based on rated for each classification group to obtain the business ranking. When recommending service to users, we determine users’ groups at first, and then recommend top service by ranking.

4.2 Evaluation Index

To verify the effectiveness of our algorithm, three methods are used as contrast experiments: collaborative filtering (CF), direct pairwise ranking (PR), pairwise ranking after classification (CR). Comparing a traditional CF (Eq. (5)) to a direct pairwise ranking, one can see that the effect of multidimensional classification model on improving ranking accuracy. In many scenarios, users pay more attention to the services with higher rankings, we selected an index kendall tau distance for evaluating the quality of ranking.

The Kendall tau rank distance is a metric that counts the number of pairwise disagreements between two ranking lists. The larger the distance, the more dissimilar the two lists are. In this section, we use the concept of Kendall tau distance to verify the error rate of our ranking. The Kendall tau distance between two lists $\tau _1$ and $\tau _2$ is computed by,

$$\begin{aligned} K(\tau _1,\tau _2)=\sum _{i,j\in P}\bar{K_{i,j}}(\tau _1,\tau _2) \end{aligned}$$

(13)

where $P$ is the set of unordered pairs of distinct elements in $\tau _1$ and $\tau _2$, $K_{i,j}$ $(\tau _1,\tau _2 )=0$ if $i$ and $j$ are in the same order in $\tau _1$ and $\tau _2$, $K_{i,j} (\tau _1,\tau _2 )=1$ if $i$ and $j$ are in the inverted order in $\tau _1$ and $\tau _2$. For example, the Kendall tau distance between $\{0, 3, 1, 6, 2, 5, 4\}$ and $\{1, 0, 3, 6, 4, 2, 5\}$ is 4.

Next, we define error rate as follows,

$$\begin{aligned} Error\quad rate=\frac{K(\tau _1,\tau _2)}{N_S} \end{aligned}$$

(14)

where $N_S$ is the total number of pairs of services.

4.3 Experimental Results

The Ranking Performance: For a user, we calculate the error rate between service ranking and the real ranking by Kendall tau distance.

For example, the error rate is calculated with a random selected 9 users in Gastonia (the number of services is 500) as shown Fig. 2. Obviously, compared with other methods, our method (CR) has high classification accuracy and its error probability is less. Compared with CF, CR decreases the error average rate by 0.37% for each user. It seems that the sample size is in Fig. 3, where reason is that Gastonia is a small-scale city, and the improvement is not so significant too small to be making accurate classification.

In Fig. 3, we prove the impact of different number of services on error rate through experiment data. It turns out that the average error rate decreases with the increase of the number of service all of three methods, but obviously CR has more dependent on the number of services. Large-scale service sets are more friendly to classification results and lower error rates. When the number of services rises from 500 to 20000, compared with CF, CR decreases the error rate average by 1.27%.

Fig. 2.

The error rate of 9 users in Gastonia.

Fig. 3.

The average error rate of CF and CR.

Matrix Density: In the experiment, the compare matrix (Eq. (9)) we obtained is sparse in the ranking, but the density of sparse matrix has increased after classification. Experimental results show, the density of sparse matrix increased from 0.032% to 0.05% in Gastonia developing 0.5-fold. As shown in the Fig. 4, the density matrix of CF and PR does not change as the number of services increases, but there is an incremental gradient in density by CR method and large-scale services having a larger increase. It turns out that reduce the sparsity of the matrix by classification and reduce the computational complexity.

Time Complexity: It is assumed that there are $n$ services rated by $m$ users. During the procedures of computing similarity and partial ranking, each two services need to be compared in our approach, so the computational complexity is $O(|N_{S_u}|^2)$, where the $N_{S_u}$ represents the number of ranked services by user $u$. The iterative algorithm is adopted in our algorithm, whose computational complexity is $O(n^2)$.

In multidimensional classification model, the time complexity of classification becomes $O(nlogn)$ on average, and that is $O(n^2*logn)$ in the worst case. Along with ranking process, we has total time complexity of $O(nlogn+w^2 )$, where $w$ is the number of services in a group. The run-time efficiency comparison between the two methods is shown in the Fig. 5.

Fig. 4.

Matrix density.

Fig. 5.

Time complexity.

5 Conclusions

In this paper, we study the fundamental ranking problem in service recommendation from a pairwise comparison viewpoint. Random walk model is applied to formulate the comparisons among the rating data collected from multiple users, and Markov chains are used for ranking aggregation and calculation. A multidimensional classification approach is designed according to user data (e.g., time, place, weather, etc.) and is combined with the comparison-based model. With the classification technique, the ranking calculation can be personalized and its accuracy can be significantly enhanced. Also, since the data can be classified into multiple small groups, the computational workload and the sparse in matrix can be dramatically reduced. Finally, we adopt real-world dataset collected by Yelp and demonstrate the efficacy of our approach empirically. This work is expected to provide a computationally efficient methodology of service ranking for personalized recommendation. We believe that, with the rapid development of classification models and data analytics techniques, there will be several avenues for our future work to further improve the accuracy and performance of the service ranking approaches.