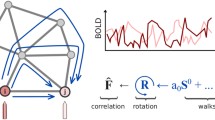
Abstract
Analysis of dynamic functional connectivity allows for studying the time variant behavior of brain connectivity during specific tasks or at rest. There is, however, a debate around the significance of studies analyzing the dynamic connectivity, as it is usually estimated using short subsequences of the entire time-series. Therefore, a question that naturally arises is whether the dynamic connectivity information is robust enough to compare connectivity matrices. In this paper we investigate the importance of the choice of metric on the space of graphs to answer this question, using a dataset of twins under the assumption that twins connectivity is more similar than in any other pair of unrelated subjects. Specifically, the problem was formulated as a classification task between twin and non-twin pairs. The approach described in the paper relies on geodesic clustering of dynamic connectivity matrices to find a subset of brain states, which were then used to encode the pairwise connectivity similarities between subjects. Experiments were performed to compare the use of Euclidean distance in a vectorial space and a geodesic distance in the Riemannian space of symmetric positive definite matrices. We showed that the geodesic distance provided a better classification of twins subjects, suggesting this use of this distance can robustly compare dynamic connectivity matrices.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Dynamic functional connectivity
- Geodesic clustering
- Connectomes
- Task-based fMRI
- SVM
- Symmetric positive definite matrices
1 Introduction
Connectomics is a relatively recent field of research in neuroimaging, which allows neuroscientists to inspect the association between different regions in the brain. Analysis of functional connectivity (FC) using time series extracted from functional magnetic resonance imaging (fMRI) has allowed new advances in the understanding of the connectivity organization of the human brain. In recent decades, FC has been widely used to examine the functional organization of brain network in many psychiatric and neurodegenerative diseases. In most cases, FC is defined as temporal covariance or correlation of BOLD activity between different brain regions [1]. Dynamic functional connectivity (DFC) is a new approach allowing studying how brain connectivity is modulated in time. Analysis of DFC is usually based on the study of a time series of connectivity matrices obtained with a sliding window approach, in which the overall time-series signal is divided into overlapping segments, which are used to estimate the time-dependent correlation/covariance of brain activity [2, 3]. Recent studies suggest that uncontrolled but reoccurring patterns of brain connectivity among intrinsic network can be captured during task or rest by examining the dynamic behavior of FC [2, 4]
Many methods have been proposed to examine DFC. In [5, 6] authors proposed an approach based on singular value decomposition and dictionary learning to investigate the DFC patterns. In [5], estimation of eigen-connectivity and extraction of its temporal weights has been proposed. Clustering of DFC matrices with k-means and independent component analysis have been proposed in [2] suggesting that clusters are brain states representing specific patterns of brain connectivity. In [7], a framework similar to [2] using temporal independent component analysis (TICA) instead of clustering is proposed to compute the states, which are maximally mutually temporally independent. Moreover, as suggested by [8, 9] states can also be computed by clustering dynamically derived graph metrics or some higher-level information e.g. computing similarity vectors between different independent vector analysis (IVA) components [10] instead of DFC matrices.
Almost all MRI studies on DFC are based on resting state fMRI. In this paper, on the contrary, we have investigated task-based fMRI, which encourages the identification of integration mechanism between specific task-related brain regions and is useful to identify task-related networks in brain connectivity [11, 12]. Specifically, we used a task-based fMRI dataset acquired on twins [13], to investigate the effect of genetic heritability on the dynamics of functional brain networks. The main purpose of this study is to evaluate if there are DFC patterns shared among twins, allowing discriminating twin pairs from unrelated pairs. In our previous study [13], we have shown that differentiation between two groups was measurable when using the graph Laplacian representation of non-dynamic FC matrices, which transforms the representation of data into the smoothed space of positive semi-definite matrices [14]. A Fréchet metric on this space was then used to measure the similarity between networks [13]. In [15] we have further extended the use of graph Laplacian and Fréchet metric to classify between MZ & DZ twin pairs using DFC matrices. To this aim we computed the distance between each pair of DFC matrices and the vector representation of the sequence of distances was then used by a linear SVM for classification.
In this paper, we want to investigate the DFC analysis exploiting the concept of brain states. To perform this investigation, we exploited the similarity of DFC patterns associated with the brain states of the two groups (twins and non-twins). To this aim, we clustered the DFC matrices into reference states and then we used a compact representation to perform a classification.
Some recent approaches suggest similar FC analysis, e.g., in [16] SVMs were used to discriminate traumatic brain injury after encoding DFC with k-means clustering. Similarly, in [17] enhanced FC variability was used to classify autism spectrum disorder from healthy controls. All above methods, exploiting clustering to generate a set of reference states, are based on similarities computed in a vectorial space. Using metrics on the vectorial space – like the Euclidean distance frequently used in k-means – is sub-optimal [15]. We know however, that FC matrices can be managed to form a manifold of positive definite matrices, and a more appropriate choice of similarity is to use a geodesic metric defined on the smooth manifold. Therefore, in our approach we used a geodesic metric both to cluster the matrices with k-means and to extract the features to be used by the classifier.
We made some experiments both using the Euclidean metric in a vectorial space and a geodesic metric (Log Euclidean distance) on the Riemannian space of symmetric positive definite matrices. The results suggest that using a proper geodesic distance is much more valuable in describing the similarity between graphs, allowing a better clustering of graphs and, for our specific task, resulting in a much higher classification accuracy when compared to a method based on simple Euclidean distance.
In the following Sect. 2 we will describe the data and the processing methods used to estimate the DFC with graphical LASSO, to cluster the graphs using geodesic metric within k-means, and to encode the subject pairs building the features with the geodesic metric. In Sect. 3 we will provide the results of all experiments, and a brief discussion with some concluding remarks will be given in Sect. 4.
2 Materials and Methods
2.1 Data Acquisition and Pre-processing
A total of 26 subjects, corresponding to 13 twin pairs (7 monozygotic, 6 dizygotic,) were recruited from the population-based Italian Twin Registry. fMRI data was acquired on a 3-Tesla MR imaging unit Siemens Allegra system (Siemens, Erlangen, Germany) with a standard head coil. T2*-weighted images were acquired using a gradient-echo EPI-BOLD pulse sequence (TR: 2000 ms; TE: 30 ms; flip angle 75°; FOV: 92 × 192; 31 axial slices; thickness: 3 mm; in-plane: 3 mm2; matrix: 64 × 64). High-resolution MPRAGE T1-weighted structural images were acquired in the same session (TR: 2300 ms; TE: 3.93 ms; flip angle 12°; FOV: 256 × 256; 160 axial slices; slice thickness: 1 mm; matrix 256 × 256). In our experiment, fMRI data were collected with right and left hand consecutively in two separate scans by using traditional Poffenberger paradigm [18], the task protocol was well synchronized for all subjects, allowing the comparison of BOLD signal across different subjects. fMRI pre-processing was done including realignment, time slice correction, motion correction and normalization. Mean time-series of each region, defined using the Automated Anatomical Labeling atlas [19] (90 ROI Cerebrum only), were then extracted from processed fMRI. For further details of the processing pipeline refers to [13].
2.2 Dynamic Functional Connectivity Estimation
Given N the number of regions in the atlas (in our case AAL is made by \( N = 90 \)) we estimated the \( N \times N \) covariance matrices \( \sum_{i} \left( w \right) \), for all subject \( i = 1\, \ldots \,M \), (M is total number of subjects) and for all sliding windows \( w = 1\, \ldots \,W \) over the fMRI time-series (W is the total number of windows). In our experiments we used a sliding window of size \( \Delta t = 30 \) TR (60 s) and a step size of 4 TR (8 s) [14]. This resulted in \( W = 83 \) DFC matrices \( \sum_{i} \) describing the modulation of connectivity along the entire recorded sequence. Due to the relatively small windows size, the estimation of the covariance matrices might be unstable and heavily affected by the limited amount of information. To overcome this issue a more robust estimate of the covariance with small data can be obtained from the estimate of a sparse version of the inverse of the covariance matrix \( \sum_{i}^{ - 1} \left( w \right) \) [20,21,22]. This sparse precision matrix can be obtained regularizing the estimated parameters with the graphical LASSO as described in [23]. This method has proven to be very effective when there are limited number of observations at each node [2, 24], such as in our case where we have small intervals of fMRI scan.
The covariance matrices are always guaranteed to be symmetric positive semi-definite, however, in real applications they are frequently also symmetric positive definite (SPD). If some matrices are not SPD we can apply a small regularization \( (\sum_{i} = \sum_{i} +\uplambda{\text{I}}) \) making them SPD. In this way they form a Riemannian manifold of SPD matrices [24] which enable us to analyze the DFC matrices on the manifold instead of using the vector space [13, 25]. To take full advantage of the manifold structure of SPD matrices, it is essential to consider a geodesic distance, which measure the shortest path between two points (two matrices in our case) along the smooth and curved manifold [13]. There are some possible alternative geodesic distances on the Riemannian manifold of SPD matrices [25, 26], we decided to adopt the Log-Euclidean distance, which is simple, and fast to compute:
where \( \sum_{i} \sum_{j} \) are two DFC matrices.
As described in our previous work [13], there is no effect of task (left and right hand) between the two groups. So, for each subject we averaged the DFC matrices across tasks by using geodesic mean (see Eq. 2) [27] so that the geometric nature of matrices is maintained.
2.3 Dynamic States and Geodesic Clustering Analysis
In order to define a set of states describing intrinsic brain network patterns, we have used geodesic k-means clustering on SPD matrices [28] to associate a state to each cluster. To initialize the cluster centroids, we first selected a set of exemplar matrices [2] from the data (8 matrices per subject in our case) maximizing the distance from the rest of the exemplars of the same subject. The geodesic k-means was then applied on the set of exemplars to obtain the initial centroids, which were then refined running again the geodesic k-means on all DFC matrices of all subjects. In order to run the geodesic k-means, we used the Log-Euclidean distance [25] as defined in Eq. (1) for which the mean of multiple covariance matrices can be computed in a closed form:
In order to choose the optimal number K of clusters we used two criteria. The first criterion was based on the minimization of the Sum of Squared Error (SSE):
where \( \Sigma \) is a DFC matrix associated to cluster Ci and mi is the corresponding centroid.
The second criterion was based on the necessity of having in any cluster some matrices for all subjects, due to the encoding framework explained below. We, therefore, computed the SSE by using Eq. (3) ranging over a number of clusters \( \left( {K = 2\, \ldots \,10} \right) \). In our case the best solution fulfilling with the two criteria resulted to be with \( {\text{K}} = 2 \). This result also supports the hypothesis that in a task-based fMRI there appears at least two macro states, one is a task-related state and the second one is a no-task state.
2.4 Feature Extraction and Classification
The working hypothesis is that dynamic connectivity between twin pairs would be more similar than between un-related pairs, and based on this we can classify pairs either as twins or as unrelated. Therefore, we need to encode the subject’s similarity taking into account the brain state. To this aim, subjects’ representatives were computed for all clusters. More specifically, the subset of all DFC matrices of a subject associated to a cluster were averaged with a geodesic mean creating a subject representative for that cluster. In this way, a subject has a representative for each cluster.
At this point, we could compute the features characterizing the similarity between the subjects. For each pair of subjects we measured the inter-subject geodesic distance between the two subject representatives of each cluster. In addition, we computed the geodesic distance of each subject representative from the cluster centroids. Therefore, for each pair of subjects (twins or unrelated) there are 3 distances per cluster (features) and in our experiments the data representation included a total of 6 features because we have K = 2 clusters.
In our data set, we have 13 twin pairs, corresponding to 26 subjects that can be recombined to form 312 unrelated pairs. In short, we have a dataset composed of 13 samples from the twin’s class and 312 samples from the unrelated class. Due to the high unbalanced dataset, we opted to use the weighted SVM [29] with three cross-fold validation. To this aim, we divided our data into 3 chunks randomly selecting the samples while maintaining the proportion between the classes (each fold was composed by 104 samples from the unrelated pairs and 4 from twin’s pairs). For statistical purpose, we repeated 100 times this cross-validation procedure with the randomized selection of folds. We evaluated the results in terms of average accuracy, precision, recall, F1 score and confusion matrix.
In all our experiments, all distances between graphs and means of graphs were computed using the Log-Euclidean distance Eq. (1) and the corresponding geodesic mean Eq. (2) respectively. However, for the sake of comparison we performed identical experiments using the Euclidean distance and the corresponding Euclidian mean.
3 Results
Figure 1 shows the results of classification with the weighted SVM when using the Log-Euclidean distance (blue bars) and the Euclidean distance (red bars). It can be observed that using the geodesic metric to describe the data considerably boosts the performance during classification, i.e., during the exploitation of the encodings. In particular, the accuracy with “geodesic encoding”, 87.21%, is much higher than the “Euclidean encoding” accuracy, 66.35%. Similar differences can be observed for the precision (88.35% versus 67.42%) and F1 score (92.92% versus 79.14%). Higher and similar recall for both metrics could be due to the higher unbalance in the classes. The embed table in Fig. 1 summarizes these results.
The mean confusion matrix for both distance metrics is given in Table 1. It can be observed that when using geodesic distance during the data encoding the rate of correctly classified pairs is much better than using Euclidean distance. These results strongly support the fact that the use of Euclidean metric on symmetric positive definite matrices is suboptimal. Hence, a better way to compare and process the undirected weighted graphs described by SPD is to use a geodesic distance on the Riemannian space.
4 Discussion and Conclusion
In this paper, we have presented a novel computational framework, which allows distinguishing between twins and unrelated pairs of subjects using their dynamic functional brain connectivity. To this aim, we designed a specific encoding of graphs into subjects’ similarities, exploiting the concept of geodesic metric on the Riemannian manifold of SPD matrices.
In particular, for the encoding of data we derived a subject-wise graph similarity representation exploiting a geodesic k-means clustering. Indeed, the algorithm uses the Log-Euclidean metric on the space of functional brain graphs. Once the clusters were generated, the Log-Euclidean metric was also used to calculate the similarity of two subjects in terms of distance between subjects and distance from cluster centroid. These distances were used as features for the data representation. Due to the highly unbalanced dataset to solve the classification task we used the weighted SVM.
In order to evaluate whether, beyond having a good estimation of covariance matrices, it is important to use metrics working on the space of data, we made an identical experiment using the Euclidean distance in place of the geodesic distance. The results of our study clearly demonstrate that use of Euclidean distance is not the best choice, as it is not properly managing the complex structure of graphs, indeed the classification performance is boosted when using the geodesic distance.
This study also reveals that a careful encoding of the dynamic functional connectivity allows a clear distinction of twin pairs from non-twin pairs.
References
Friston, K.J., Frith, C.D., Liddle, P.F., Frackowiak, R.S.J.: Functional connectivity: the principal-component analysis of large (PET) data sets. J. Cereb. Blood Flow Metab. 13, 5 (1993). https://doi.org/10.1038/jcbfm.1993.4
Allen, E.A., Damaraju, E., Plis, S.M., Erhardt, E.B., Eichele, T., Calhoun, V.D.: Tracking whole-brain connectivity dynamics in the resting state. Cereb. Cortex 24(3), 663–676 (2014)
Chang, C., Liu, Z., Chen, M.C., Liu, X., Duyn, J.H.: EEG correlates of time-varying BOLD functional connectivity. NeuroImage 72(15), 227–236 (2013)
Sakoǧlu, Ü., Pearlson, G.D., Kiehl, K.A., Wang, Y.M., Michael, A.M., Calhoun, V.D.: A method for evaluating dynamic functional network connectivity and task-modulation: application to schizophrenia. MAGMA 23, 351–366 (2010). https://doi.org/10.1007/s10334-010-0197-8
Leonardi, N., et al.: Principal components of functional connectivity: a new approach to study dynamic brain connectivity during rest. NeuroImage 83, 937–950 (2013)
Leonardi, N., Shirer, W., Greicius, M., Van De Ville, D.: Disentangling dynamic networks: separated and joint expressions of functional connectivity patterns in time. Hum. Brain Mapp. 35(12), 5984–5995 (2014)
Yaesoubi, M., Miller, R.L., Calhoun, V.D.: Mutually temporally independent connectivity patterns: a new framework to study the dynamics of brain connectivity at rest with application to explain group difference based on gender. NeuroImage 107, 85–94 (2015)
Li, X., et al.: Dynamic functional connectomics signatures for characterization and differentiation of PTSD patients. Hum. Brain Mapp. 35, 1761–1778 (2014)
Chiang, S., et al.: Time-dependence of graph theory metrics in functional connectivity analysis. NeuroImage 125, 601–615 (2016)
Ma, S., Calhoun, V.D., Phlypo, R., Adal, T.: Dynamic changes of spatial functional network connectivity in healthy individuals and schizophrenia patients using independent vector analysis. NeuroImage 90, 196–206 (2014)
Varoquaux, G., Craddock, R.C.: Learning and comparing functional connectomes across subjects. NeuroImage 80, 405–415 (2013)
Richiardi, J., Eryilmaz, H.I., Schwartz, S., Vuilleumier, P.: Decoding brain states from fMRI connectivity graphs. NeuroImage 56(2), 616–626 (2011)
Yamin, A., et al.: Comparison of brain connectomes using geodesic distance on manifold: a twin’s study. In: International Symposium on Biomedical Imaging 2019, Venice, 8–11 April 2019
Li, K., Guo, L., Nie, J., Li, G., Liu, T.: Review of methods for functional brain connectivity detection using fMRI. Comput. Med. Imaging Graph. 33(2), 131–139 (2009)
Yamin, A., et al.: Investigating the impact of genetic background on brain dynamic functional connectivity through machine learning: a twins study. In: IEEE-EMBS International Conference on Biomedical and Health Informatics, Chicago, IL, USA, 19–22 May 2019
Victor, M.V., Andrew, R.M., Kent, A.K., Vince, D.C.: Dynamic functional network connectivity discriminates mild traumatic brain injury through machine learning. Neuroimage: Clin. 19, 30–37 (2018)
Tejwani, R., Liska, A., You, H.: Autism Classification Using Brain Functional Connectivity Dynamics and Machine Learning (2019). https://arxiv.org/pdf/1712.08041.pdf
Poffenberger, A.T.: Reaction Time to Retinal Stimulation, with Special Reference to the Time Lost in Conduction Through Nerve Centers. The Science Press, New York (1912)
Tzourio-Mazoyer, N., et al.: Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289 (2002)
Marrelec, G., et al.: Partial correlation for functional brain interactivity investigation in functional MRI. Neuroimage 32, 228–237 (2006)
Varoquaux, G., Gramfort, A., Poline, J.B., Thirion, B., Zemel, R, Shawe-Taylor, J.: Brain covariance selection: better individual functional connectivity models using population prior. In: Advances in Neural Information Processing Systems, Vancouver, Canada (2010)
Smith, S.M., et al.: Network modelling methods for FMRI. Neuroimage 54, 875–891 (2011)
Friedman, J., Hastie, T., Tibshirani, R.: Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9(3), 432–441 (2008). https://doi.org/10.1093/biostatistics/kxm045
Rashid, B., Damaraju, E., Pearlson, G.D., Calhoun, V.D.: Dynamic connectivity states estimated from resting fMRI identify differences among Schizophrenia, bipolar disorder, and healthy control subjects. Front. Hum. Neurosci. 8, 897 (2014). https://doi.org/10.3389/fnhum.2014.00897
Dodero, L., Minh, H.Q., Biagio, M.S., Murino, V., Sona, D.: Kernel-based classification for brain connectivity graphs on the Riemannian manifold of positive definite matrices. In: ISBI 2015, 16–19 April 2015
Dodero, L., Sambataro, F., Murino, V., Sona, D.: Kernel-based analysis of functional brain connectivity on Grassmann manifold. In: Navab, N., Hornegger, J., Wells, W., Frangi, A. (eds.) MICCAI 2015. LNCS, vol. 9351, pp. 604–611. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24574-4_72
Dryden, I.L., Koloydenko, A., Zhou, D.: Non-Euclidean statistics for covariance matrices, with applications to diffusion tensor imaging. Ann. Appl. Stat. 3(3), 1102–1123 (2009)
Lee, H., Ahn, H.-J., Kim, K.-R., Kim, P., Koo, J.-Y.: Geodesic clustering for covariance matrices. Commun. Stat. Appl. Methods 22, 321–331 (2015). https://doi.org/10.5351/CSAM.2015.22.4.321
Yang, X., Song, Q., Cao, A.: Weighted support vector machine for data classification. In: Proceedings of 2005 IEEE International Joint Conference on Neural Networks, Montreal, Quebec, vol. 2, pp. 859–864 (2005). https://doi.org/10.1109/IJCNN.2005.1555965
Acknowledgement
The authors acknowledge Cigdem Beyan and Muhammad Shahid for the helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Yamin, A. et al. (2019). Analysis of Dynamic Brain Connectivity Through Geodesic Clustering. In: Ricci, E., Rota Bulò, S., Snoek, C., Lanz, O., Messelodi, S., Sebe, N. (eds) Image Analysis and Processing – ICIAP 2019. ICIAP 2019. Lecture Notes in Computer Science(), vol 11752. Springer, Cham. https://doi.org/10.1007/978-3-030-30645-8_58
Download citation
DOI: https://doi.org/10.1007/978-3-030-30645-8_58
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-30644-1
Online ISBN: 978-3-030-30645-8
eBook Packages: Computer ScienceComputer Science (R0)