Abstract
Regular expressions can be visualized using railroad or syntax diagrams. The construction does not depend on fancy artistic skills. Rather, a diagram can be systematically constructed through simple, local transformations due to Manna. We argue that the result can be seen as a nondeterministic finite automaton with  -transitions. Despite its simplicity, the construction has a number of pleasing characteristics: the number of states and the number of edges is linear in the size of the regular expression; due to sharing of sub-automata and auto-merging of states the resulting automaton is often surprisingly small. The proof of correctness relies on the notion of a subfactor. In fact, Antimirov’s subfactors (partial derivatives) appear as target states of non-
-transitions. Despite its simplicity, the construction has a number of pleasing characteristics: the number of states and the number of edges is linear in the size of the regular expression; due to sharing of sub-automata and auto-merging of states the resulting automaton is often surprisingly small. The proof of correctness relies on the notion of a subfactor. In fact, Antimirov’s subfactors (partial derivatives) appear as target states of non- -transitions, suggesting a smooth path to nondeterministic finite automata without
-transitions, suggesting a smooth path to nondeterministic finite automata without  -transitions. Antimirov’s subfactors, in turn, provide a fine-grained analysis of Brzozowski’s factors (derivatives), suggesting a smooth path to deterministic finite automata. We believe that this makes a good story line for introducing regular expressions and automata.
-transitions. Antimirov’s subfactors, in turn, provide a fine-grained analysis of Brzozowski’s factors (derivatives), suggesting a smooth path to deterministic finite automata. We believe that this makes a good story line for introducing regular expressions and automata.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Actually, Conway’s axiomatization is incomplete as pointed out by Abramsky and Vickers [1]: only if the axiom \(\sum \{a\}=a\) is added, his \(\mathbf S \)-algebras are equivalent to regular algebras.
- 2.
A regular algebra is really a blend of a complete join-semilattice and a monoid. It is a standard result of lattice theory that a complete join-semilattice is a complete lattice. However, a complete join-semilattice homomorphism is not necessarily a complete lattice homomorphism, as there is no guarantee that it also preserves meets.
- 3.
Backhouse uses the terms matrix and graph interchangeably.
- 4.
Backhouse’s definition is actually more general: a matrix is given by a function
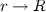 where
where  is a fixed relation, the dimension of the matrix. This allows him to distinguish between non-existent edges and edges that are labelled with 0.
is a fixed relation, the dimension of the matrix. This allows him to distinguish between non-existent edges and edges that are labelled with 0. - 5.
We use “correctness” and “completeness” only in this very narrow sense.
References
Abramsky, S., Vickers, S.: Quantales, observational logic and process semantics. Math. Struct. Comput. Sci. 3(2), 161–227 (1993). https://doi.org/10.1017/S0960129500000189
Aho, A.V., Lam, M.S., Sethi, R., Ullman, J.D.: Compilers: Principles, Techniques, & Tools, 2nd edn. Pearson Addison-Wesley, Boston (2007)
Antimirov, V.: Partial derivatives of regular expressions and finite automaton constructions. Theor. Comput. Sci. 155(2), 291–319 (1996). https://doi.org/10.1016/0304-3975(95)00182-4. http://www.sciencedirect.com/science/article/pii/0304397595001824
Backhouse, R.: Regular algebra applied to language problems. J. Logic Algebraic Program. 66(2), 71–111 (2006). https://doi.org/10.1016/j.jlap.2005.04.008. http://www.sciencedirect.com/science/article/pii/S1567832605000329
Broda, S., Machiavelo, A., Moreira, N., Reis, R.: On the average state complexity of partial derivative automata: an analytic combinatorics approach. Int. J. Found. Comput. Sci. 22(07), 1593–1606 (2011). https://doi.org/10.1142/S0129054111008908
Brzozowski, J.A.: Derivatives of regular expressions. J. ACM 11(4), 481–494 (1964). https://doi.org/10.1145/321239.321249. http://doi.acm.org/10.1145/321239.321249
Champarnaud, J.M., Ziadi, D.: From Mirkin’s prebases to Antimirov’s word partial derivatives. Fundam. Inf. 45(3), 195–205 (2001)
Conway, J.H.: Regular Algebra and Finite Machines. Chapman and Hall, London (1971)
Jensen, K., Wirth, N.: Pascal: User Manual and Report, 2nd edn. Springer, Heidelberg (1978)
Kleene, S.C.: Representation of events in nerve nets and finite automata. Technical report, RM-704, U.S. Air Force, Project RAND, Research Memorandum, December 1951
Mac Lane, S.: Categories for the Working Mathematician. Graduate Texts in Mathematics, 2nd edn. Springer, Heidelberg (1998)
Manna, Z.: Introduction to Mathematical Theory of Computation. McGraw-Hill Book Company, New York (1974)
McNaughton, R., Yamada, H.: Regular expressions and state graphs for automata. IRE Trans. Electron. Comput. EC-9(1), 39–47 (1960). https://doi.org/10.1109/TEC.1960.5221603
Mirkin, B.G.: An algorithm for constructing a base in a language of regular expressions. Eng. Cybern. 5, 110–116 (1966)
Rabin, M.O., Scott, D.: Finite automata and their decision problems. IBM J. Res. Dev. 3(2), 114–125 (1959). https://doi.org/10.1147/rd.32.0114
Thompson, K.: Programming techniques: Regular expression search algorithm. Commun. ACM 11(6), 419–422 (1968). https://doi.org/10.1145/363347.363387. http://doi.acm.org/10.1145/363347.363387
Acknowledgements
A big thank you is due to Bernhard Möller for pointing me to Manna’s textbook on the “Mathematical Theory of Computation” [12]. Thanks are also due to Clare Martin and Sebastian Schweizer for proof-reading a preliminary version of the manuscript. The TikZ diagrams for Thompson’s construction, see Fig. 5, are due to Ian McLoughlin, who kindly granted permission to use them. As always, the anonymous referees of MPC provided detailed feedback, suggesting numerous improvements regarding presentation and organization of the material. In response to their comments I moved the section on “Railroad Diagrams” to the front and I clarified Antimirov’s contribution. Finally, I owe a particular debt of gratitude to Roland Backhouse, who provided numerous comments, pointing out, in particular, the relevance of Conway’s work. The paragraph on “linear mechanisms” was added in response to his suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Hinze, R. (2019). Self-certifying Railroad Diagrams. In: Hutton, G. (eds) Mathematics of Program Construction. MPC 2019. Lecture Notes in Computer Science(), vol 11825. Springer, Cham. https://doi.org/10.1007/978-3-030-33636-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-33636-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-33635-6
Online ISBN: 978-3-030-33636-3
eBook Packages: Computer ScienceComputer Science (R0)


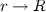 where
where  is a fixed relation, the dimension of the matrix. This allows him to distinguish between non-existent edges and edges that are labelled with 0.
is a fixed relation, the dimension of the matrix. This allows him to distinguish between non-existent edges and edges that are labelled with 0.