Keywords

1 Introduction

Data representation methods have been widely applied to various fields in pattern recognition and machine learning [1,2,3]. Over the past few decades, matrix factorization methods have become one of the most popular data representation techniques due to its efficiency and effectiveness. Many classical matrix factorization techniques, such as Singular Value Decomposition (SVD) [4], Principal Component Analysis (PCA) [5], Nonnegative Matrix Factorization (NMF) [6] and Concept Factorization (CF) [7], have shown the encouraging performances in image classification, object tracking, document clustering, etc. [8, 9].

NMF has aroused increasing interests due to its physical and theoretical interpretations. NMF naturally leads to a part-based representation of data by imposing the nonnegative constraint on both coefficient and basis matrices. The basic idea behind NMF is to seek two nonnegative matrices to approximate the original data matrix. However, NMF cannot deal with the data matrix containing with some negative elements due to the noise or outlier. Therefore, Xu et al. [7] proposed a variation of NMF, called Concept Factorization (CF), for document clustering. Different from the NMF methods, CF can deal with the data matrix mixed with nonnegative elements. In order to discover the local geometric structure of data, Cai et al. [10] proposed a Locally Consistent Concept Factorization (LCCF) method for data representation. It models the manifold structure of data using the graph regularizer. Shu et al. [11] proposed a Local Learning Concept Factorization (LLCF) method to learn the discriminant structure and the local geometric structure, simultaneously, by adding the local learning regularization term into the model of CF. Motivated by the deep learning, Li et al. [12] proposed a multilayer concept factorization method to discover the structure information hidden in data using the multilayer framework. Pei et al. [13] developed a CF with adaptive neighbors method for clustering. The idea of this proposed method is to integrate an ANs regularizer into the CF decomposition. However, the aforementioned methods cannot update dynamically the optimal graph model, which is used to explore the intrinsic geometric manifold structure of data in matrix decomposition.

To solve this issue, we propose a novel method named as Concept Factorization with Optimal Graph Learning (CF_OGL) in this paper. Specifically, we impose a rank constraint on the Laplacian matrix of the initially given graph, and then iteratively update it. Therefore, the learned graph has exactly c connected components, whose structure is beneficial to the clustering applications. Then the learned graph regularizer is used to constrain the model of the concept factorization method, and thus the geometric structure of data can be better preserved in low dimensional feature space. Extensive experimental results on three datasets demonstrate that our proposed CF_OGL method outperforms other state-of-the-art methods in clustering.

This paper is organized as follows: We briefly describe both CF and LCCF algorithms in Sect. 2. In Sect. 3, we introduce our proposed CF_OGL algorithm and then derive its updating rules. In Sect. 4, we carry out some experiments to investigate the proposed CF_OGL algorithm. Finally, conclusions are drawn in Sect. 5.

2 The Relative Work

In this section, the models of both CF and LCCF are briefly presented.

2.1 CF

Concept factorization is a popular matrix factorization technique to deal with high dimensional data. Given a data matrix \(X=[x_1, x_2, ..., x_n] \in {R^{m \times n}}\), \(x_i\) denotes a m-dimensional vector. In CF, the entire data points are used to lineally represent each underlying concept, and all the concepts seek to lineally approximate to each data point, simultaneously. Therefore, we can give the objective function of CF as

$$\begin{aligned} X = XU{V^T} \end{aligned}$$
(1)

where \( U \in {R^{n \times k}}\) and \( V \in {R^{n \times k}}\). Using the Euclidean distance metric to measure the reconstruction error, its minimization problem can be given as follows:

$$\begin{aligned} \begin{array}{c} \mathop {\min }\limits _{U, V} \left\| {X - XU{V^T}} \right\| _F^2 \\ s.t. U \ge 0, V \ge 0 \\ \end{array} \end{aligned}$$
(2)

where \({\left\| \cdot \right\| _F}\) denotes the matrix Frobenius norm. Using the multiplicative updating algorithm, we derive the updating rules of Eq. (2) as follows:

$$\begin{aligned} \begin{array}{c} u_{ij}^{t + 1} \leftarrow u_{ij}^t\frac{{{{({{KV}})}_{ij}}}}{{{{({{KU}}{{{V}}^T}{{V}})}_{ij}}}}\\ v_{ij}^{t + 1} \leftarrow v_{ij}^t\frac{{{{({{KW}})}_{ij}}}}{{{{({{V}}{{{W}}^T}{{KW}})}_{ij}}}} \\ \end{array} \end{aligned}$$
(3)

where \({{K}} = {{{X}}^T}{{X}}\). To deal with the nonlinear data, CF is easily kernelized using kernel trick.

2.2 LCCF

Traditional CF method fails to consider the manifold structure information of data. To solve this issue, Cai et al. [10] proposed the LCCF method, which models the manifold structure embedded in data using the fixed graph model. Therefore, the objective function of LCCF can be given as follow:

$$\begin{aligned} \begin{array}{c} \mathop {\min }\limits _{U, V} \left\| {X -XU{V^T}} \right\| _F^2 + \lambda tr({V^T}LV)\\ s.t. U \ge 0, V \ge 0 \\ \end{array} \end{aligned}$$
(4)

where \(\lambda \) stands for a balance parameter, and tr(.) denotes the trace of a matrix. D is a diagonal matrix, \({D_{ii}} = \sum \nolimits _S {{W_{ij}}}\), \(L = D - W\). Similarly, we derive the updating rules of Eq. (4) as follows:

$$\begin{aligned} \begin{array}{c} u_{ij}^{t + 1} \leftarrow u_{ij}^t\frac{{{{({{KV}})}_{ij}}}}{{{{({{KU}}{{{V}}^T}{{V}})}_{ij}}}}\\ v_{ij}^{t + 1} \leftarrow v_{ij}^t\frac{{{{({{KW+\lambda WV}})}_{ij}}}}{{{{({{V}}{{{W}}^T}{{KW+\lambda DV}})}_{ij}}}}\\ \end{array} \end{aligned}$$
(5)

According to the rules (5), we can achieve a local minimum of Eq. (4).

3 The Proposed Method

3.1 Motivation

Traditional CF methods cannot effectively explore the intrinsic geometric manifold structure embedded in high dimensional data using the fixed graph model. By addint the rank constraint into the Laplacian matrix of the initially given graph, we learn an optimal graph model with exactly c connected components. In CF_AGL, the learned graph regularizer is further constructed, and then imposed on the model of CF. Therefore, our proposed method explores the semantic information hidden in high dimensional data effectively.

3.2 Constrained Laplacian Rank (CLR)

A graph learning method, called Constrained Laplacian Rank (CLR), was proposed to explore the intrinsic geometric structure of data, whose goal is to learn an optimal graph model [14]. Therefore, the CLR method is formulated by the following optimization problem:

$$\begin{aligned} {\ J_{CLR}={\min _{\sum \nolimits _j {{a_{ij}} = 1}, {a_{ij}} \ge 0, rank({L_Q}) = n - k}} \left\| {Q - W} \right\| _F^2} \end{aligned}$$
(6)

where \(L_Q\) stands for the Laplacian matrix of the matrix Q. Denote \({\sigma _i}({L_Q})\) as the i-th smallest eigenvalue of \(L_A\). It is worth noting that \({\sigma _i}({L_Q}) > 0\) because of its positive semidefinition. Therefore, Eq. (6) can be reformulated as the following problem for a large enough value of \({\sigma _i}\):

$$\begin{aligned} {J_{CLR}} = \mathop {\min }\limits _{\sum \nolimits _j {{q_{ij}} = 1}, {q_{ij}} \ge 0} \left\| {Q - W} \right\| _F^2 + 2\lambda \sum \limits _{i = 1}^k {{\sigma _i}({L_Q})} \end{aligned}$$
(7)

According to the Ky Fans Theorem, we have the following equivalent definition as

$$\begin{aligned} {\sum \limits _{i = 1}^k {{\sigma _i}({L_Q})} = \mathop {\min }\limits _{F \in {^{n \times k}},{F^T}F = I} Tr({F^T}{L_Q}F)} \end{aligned}$$
(8)

Therefore, we can further rewrite the problem (7) as follows:

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _Q \left\| {Q - W} \right\| _F^2 + \lambda Tr(F{L_Q}{F^T}) \\ s.t.\,F{F^T} = I, Q1 = 1, Q \ge 0, Q \in {R^{n \times n}}\\ \end{array} \end{aligned}$$
(9)

3.3 Our Proposed Method

By integrating the learned graph regularization term into the model of CF, the objective function of our proposed CF_OGL method can given as follows:

$$\begin{aligned} \begin{array}{c} \mathop {\min }\limits _{Q, U, V} (\left\| {Q - W} \right\| _F^2 + \beta Tr(F{L_Q}{F^T}) + \lambda Tr(V{L_Q}{V^T})\\ +\,\mu \left\| {X - XU{V^T}} \right\| ) \\ s.t.F{F^T} = I, V \ge 0, U \ge 0, Q1 = 1, Q \ge 0, Q \in {R^{n \times n}}\\ \end{array} \end{aligned}$$
(10)

It is impractical to find the global optimal solution of problem (10) because it is not a convex problem in U, V and A together. Fortunately, we can achieve a local solution by optimizing the variables alternatively. Therefore, the optimization scheme of our proposed CF_OGL method mainly consists of two parts:

Fixing Q and F, Update U and V. By fixing the variables A and F, the Eq. (10) can be rewritten as the following problem:

$$\begin{aligned} \begin{array}{c} \mathop {\min }\limits _{U, V} (\lambda Tr(V{L_Q}{V^T}) + \mu \left\| {X - XU{V^T}} \right\| ) \\ s.t.{V{V^T} = I, Q \ge 0, U \ge 0} \\ \end{array} \end{aligned}$$
(11)

Similarly, it is easy to derive the updating rules of problem (10) as follows:

$$\begin{aligned} \begin{array}{c} u_{ij}^{t + 1} \leftarrow u_{ij}^t\frac{{{{({{KV}})}_{ij}}}}{{{{({{KU}}{{{V}}^T}{{V}})}_{ij}}}}\\ \end{array} \end{aligned}$$
(12)
$$\begin{aligned} \begin{array}{c} v_{ij}^{t + 1} \leftarrow v_{ij}^t\frac{{{{({{KW+\lambda WV}})}_{ij}}}}{{{{({{V}}{{{W}}^T}{{KW+\lambda DV}})}_{ij}}}} \\ \end{array} \end{aligned}$$
(13)

Fixing U and V, Update Q and F. By fixing U and V, we can rewrite the Eq. (10) as the following optimization problem:

$$\begin{aligned} \begin{array}{c} \mathop {\min }\limits _{Q,U,V} (\left\| {Q - W} \right\| _F^2 + \beta Tr(F{L_Q}{F^T})) \mathrm{{ }}\\ s.t. F{F^T} = I, Q1 = 1,Q \ge 0,Q \in {R^{n \times n}}\\ \end{array} \end{aligned}$$
(14)

(A) When Q is fixed, the Eq. (14) becomes

$$\begin{aligned} \begin{array}{c} \mathop {\min }\limits _{F{F^T} = I} (\beta Tr(F{L_Q}{F^T})) \mathrm{{ }}\\ \end{array} \end{aligned}$$
(15)

It is easy to know that the solution scheme of F can be converted into solving the k smallest eigenvalues problem of \(L_Q\).

(B) When F is fixed, the problem (14) becomes the following optimization problem:

$$\begin{aligned} \begin{array}{c} \mathop {\min \sum \limits _{i,j = 1} {{{\left( {{q_{i,j}} - {w_{i,j}}} \right) }^2}} + \frac{\beta }{2}}\limits \sum \limits _{i,j = 1} {\left\| {{f_i} - {f_j}} \right\| _2^2{q_{i,j}}} \\ \mathrm{{ }}s.t.\sum \nolimits _j {{q_{ij}}} = 1,{q_{ij}} \ge 0 \\ \end{array} \end{aligned}$$
(16)

For each row \({w_i}\), we have the vector form as

$$\begin{aligned} \begin{array}{c} \mathop {\min }\limits _{{q_i} \ge 0,{q_i}1 = 1} \left\| {{q_i} - ({w_i}}-\frac{\beta }{2}d_i^T) \right\| _2^2 \end{array} \end{aligned}$$
(17)

where \(d_{ij}={\left\| {{f_i} - {f_j}} \right\| _2^2}\). The problem (17) can be solved by the optimization algorithm proposed in [14].

figure a

4 Experimental Results

In this section, we carry out some experiments to investigate the proposed CF_OGL method on the Yale, ORL and FERET datasets. To demonstrate its effectiveness, the proposed CF_OGL method is compared with several state-of-the-art methods, such as K-means, PCA, NMF, CF and LCCF. Two well accepted measurements, such as accuracy (AC) and normalized mutual information (NMI), are used as metrics to quantify the performance of data representation in clustering.

4.1 Yale Face Dataset

The Yale face dataset includes a total of 165 face images from 15 individuals. In each experiment, the P categories images were randomly sampled from the Yale dataset to evaluate the performances of all methods. We run all methods ten times for each value of P, and recorded their average results. The results of all methods on the Yale dataset are shown in Table 1. We can clearly see that our proposed CF_OGL method outperforms other state-of-the-art methods regardless of the choices of P. Specifically, the average AC and NMI of the proposed CF_OGL method are 3.7% and 5.1% higher than those of LCCF, respectively. The main reason is that our propose CF_OGL method can learn an optimal graph structure, which can significantly improve the clustering performance than LCCF.

Fig. 1.
figure 1

Some samples from the Yale dataset

Full size image
Table 1. The clustering performances on the Yale face dataset
Full size table

4.2 ORL Face Dataset

The ORL face dataset contrains 400 face images from 40 distinct subjects. For some subjects, the face images were taken at different times, varying the lighting and facial expressions. In this experiment, we adopted the above similar experimental scheme to investigate the effectiveness of our proposed CF_OGL method. Table 2 provides the clustering results of six methods on the ORL face dataset. It can be observed that CF_OGL can achieve the best performance among all the compared methods. The main reason is that our proposed CF_OGL method can learn the optimal graph and thus effectively preserve the intrinsic geometric structure of data. Therefore, it outperforms other state-of-the-art methods on this dataset (Figs. 1 and 2).

Fig. 2.
figure 2

Some samples from the ORL dataset

Full size image
Table 2. The clustering performances on the ORL face dataset
Full size table
Fig. 3.
figure 3

Some samples from the FERET dataset

Full size image
Fig. 4.
figure 4

Performances of all methods versus different vaules of the parameter \(\lambda \)

Full size image
Fig. 5.
figure 5

Performances of all methods versus different vaules of the parameter \(\beta \)

Full size image

4.3 FERET Face Dataset

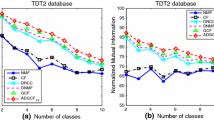
The FERET face database contains 200 different individuals with about 7 face samples for each individual. Here, we randomly chose P categories samples from the FERET dataset, and mixed them as the experimental subset for clustering. All methods were run ten times, and then their average performances were recorded as the final results. The clustering performances for each method on the FERET dataset are summarized in Table 3. It is easy to find that the average performance of our proposed CF_OGL method has certain advantage compared with other methods in clustering (Fig. 3).

Table 3. The clustering performances on the FERET face dataset
Full size table

4.4 The Analysis of the Parameters

In our proposed CF_OGL, the parameters \(\beta \), \(\lambda \) and \(\mu \) have an effect on the clustering performance. Specifically, we randomly chose 10, 20, 80 categories samples as the dataset to carry out the experiments. However, the parameter selection of the proposed CF_OGL method is still an open problem. Therefore, we determine the parameters by grid search at first and then change them within certain ranges. Here, we only investigate the parameters \(\beta \) and \(\lambda \). The Figs. 4 and 5 show the performances of all methods varied with different values of \(\beta \) and \(\lambda \) on three datasets, respectively. It is clear to see that our proposed method can achieve a relative stable performance in a large range.

5 Conclusion

In this paper, a novel matrix factorization technique, called Concept Factorization with adaptive graph learning (CF_OGL), is proposed for data representation. In order to learn an optimal graph, we impose a rank constraint on the Laplacian matrix of the initially given graph. Then the learned graph regularizer is integrated into the model of CF. Therefore, our proposed CF_OGL method effectively exploits the geometric manifold structure embedded in high dimensional data. Experimental results have shown that the proposed CF_OGL algorithm achieves better performance in comparison with other state-of-the-art algorithms.