Dynamic Multi-label Learning with Multiple New Labels

Abstract

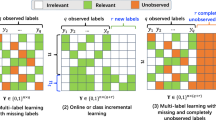
In a traditional multi-label learning task, an instance or object often has multiple labels. Previous works assume that the class labels are always fixed, i.e, the class labels in the test set are the same as that in the training set. Different from previous methods, we study a new problem setting where multiple new labels emerge in a dynamic environment. In this paper, we decompose the multiple labels pool to adjust the dynamic environment. The proposed method has several functions: classify instances on currently known labels, detect the emergence of several new labels then separate them using clustering, and construct a new classifier for each new label that works collaboratively with the classifier for known labels. Experimental results on publicly available data sets demonstrate that our method achieves superior performance, compared with the state-of-the-arts.

1 Introduction

In the traditional supervised learning, only one label is often to be predicted for each instance [10, 13]. However, in many practical application, one instance might be associated with multiple labels simultaneously. For example, an image may be complicated and contain multiple topics [1, 18]; in the document classification tasks, an article may be related to several semantic labels [14]; in the gene function prediction and classification tasks, a gene may have multiple isolated functions [3, 16].

In recent years, some methods have been proposed to process such data and achieve great performance [2, 5, 7, 18]. For example, multi-instance multi-label learning (MIML) [2] is a recent proposed framework for training multiple labels model for already known labels and has some variant adopting algorithms based on that [4, 6]. The algorithms mentioned above ignore a fact that data stream might emerge some unseen new labels. To solve this problem with the situation of streaming data, there exist some experimental methods being proposed to revise a pre-trained model as the new labels emerging by multiple iterations, such as Multi-Label Learning with Emerging New Labels (MuENL) [8]. However, this kind of method is only able to deal with one single new label in one iteration. In other words, when the test data contain multiple new labels in one iteration, this method will take the multiple new labels as just one new label. This will lead to degenerating performance.

To meet the above challenge, we propose a novel multi-label learning method which can handle multiple new labels emerging in one iteration. In order to make the proposed method better adopt to the complicated environment, we integrate some features into the algorithm [8], which can achieve significant improvement. With the dynamic multi-label learning setting, we assume that objects arrive in a data stream, and no ground truths for class labels are available in the test data stream at all times, except for the initial training data set. Our method consists of four components: (1) A linear classifier is constructed to optimize both the pairwise label ranking loss and the classification loss on the known labels; (2) a new outlier detector based on both initial and test data stream are constructed; (3) the cluster for the emerging new labels are found based on the Density-based spatial clustering of applications with noise (DBSCAN) [9]; (4) a classifier updating procedure can incorporate new labels to produce a robust classifier. This can tolerate detection errors for the future data stream which contains the same new label, and then remodel the detector for each new label identified.

The rest of the paper is organized as follows: The Sect. 2 describes some related work about the multi-label learning, incremental learning, and outlier detection. Section 3 introduces the problem formation and the details of our algorithm. Section 4 describe the experiments, followed by the conclusion in Sect. 5.

2 Related Work

In this section we review some related works of our proposed method, which mainly include multi-label learning, incremental learning and outlier detection, successively.

Multi-label classification is a special case of the typical classification problem where one instance may be associated with multiple labels. The multi-label classification problem has been a question of great interest in a wide range of real-world applications in recent years, such as image annotation [15], text classification [17, 18], and so on. Formally, multi-label classification can be thought as a generalization of multi-class classification. For given input space $\mathbf {X} = \{\varvec{x}_1, \varvec{x}_2, \cdots , \varvec{x}_n\}$, the classification is aim to predict $\hat{\varvec{y}} \in 2^{\mathbf {L}}$ where $2^{\mathbf {L}}$ is a powerset of label set $\mathbf {L}$, so that each predicted output is a subset to the label set. The common techniques to perform multi-label learning are problem transformation methods and adapted algorithms [20]. The problem transformation methods try to transform the origin problem into multiple traditional single-label classification problems (including binary-class and multi-class), then apply off-the-shelf algorithms to the transformed equivalent problem set. For example, Binary Relevance (BR) [19] is the most common technique which simply decomposes multi-label task into multiple binary classification independently, each of which is to predict single label in label set. Due to the neglect of labels correlations, BR has been criticized for poor performance [20, 21]. There are many researches that take the label correlation into account [22, 23].

Furthermore, the methods mentioned above all assume that class label numbers are in a fixed count, thus, they cannot not be applied to our problem setting. To fit with the dynamic multi-label learning setting, one may use incremental learning to cope with potential infinite data stream. The goal of incremental learning is for the learning model to learn new data without forgetting its existing knowledge, i.e., without re-training from scratch. One common approach to perform incremental learning is batch-incremental learning [12, 24]. When new arrived data filled up a batch with enough amount of data, the system will sufficient to train/update a good performing classifier by exploited such batch of data. Moreover, in real-world dynamic scenario, new unknown labels may emerge with the stream of data. Learning new labels from data stream is a kind of incremental learning is called class-incremental learning (C-IL) [25]. Here our multi-label learning setting with emerging new labels is the combination of batch-incremental learning and class incremental learning.

In multi-instance multi-label learning case, a new label may co-occur with known labels which makes it difficult to separate instances with new labels only from instances with known labels only. Besides, to train new effective classifiers for new labels, one need filter out the uninformative data whose labels are all known. The straightforward strategy to handle such data selection problem is design a detection to determine whether observed instance has new unknown labels. Zhu et al. proposed MuENL [8] approach to address above challenges by taking both feature and label spaces into account. As for the detection solution for new unknown label, MuENL regards it as an outlier detection problem. The batch to train classifiers for new unknown labels in MuENL only select from the data whose features deviate from the general data sets as the new label data samples. It is worth mentioned that MuENL only constructs one classifier for one batch of observed instance to predict one new label or one meta-label [26] that encapsulates a subset of labels.

3 The MuPND Approach

The challenge here is to study a robust classifier for multi-labels containing both new and old labels. Furthermore, we also integrate the DBSCAN algorithm to address the awkward problems when there are multi-new labels erupting concurrently in just one iteration. We call our method proposed in this paper MuPND.

3.1 Problem Formulation

Our approach and experiment are based on a open dynamic multi-learning setting, we have an initial labeled training data set, and then the unlabeled test data come successively in a data stream fashion. Suppose the $\mathcal {X}$ denote the input feature space, and we define the $X_{0}=\left[ \varvec{x}_{-n+1}, \cdots , \varvec{x}_{-1}, \varvec{x}_{0}\right] ^{\top } \subseteq \mathcal {X}$ as the observed initial data set in the training process. Then the unlabeled test data stream contains an instance $\varvec{x}_{t}$ which probably has a new label at the time t. Let $X_{t}, t \in \{1,2, \cdots , T\}$ be the accessible data trunk at time t.

We denote $\varvec{c}_{0}=\{1,2, \cdots , \ell \}$ as the already known labels in the initial training data set. And the number in the vector $\varvec{c}$ represents the index of the labels set. At the time t, the original $\varvec{c}_0$ is being updated to $\varvec{c}_t$ and initial $\ell$ is being updated to $\ell ^{'}$, the $\ell ^{'}$ represents the maximum numbers of labels set. That is, at the time t, supposing we have detected $n (n\ge 0)$ new labels, the label collection will be enlarged with n new labels, $\ell ^{\prime }=\ell +n : \varvec{c}_{t}=\varvec{c}_{t-1} \cup \left\{ \ell ^{\prime }\right\}$. Let $Y_{0}=\left[ \varvec{y}_{-n+1}, \cdots , \varvec{y}_{-1}, \varvec{y}_{0}\right] \in \{-1,1\}^{\ell \times n}$ be the initial label matrix of $X_{0}$, and $\varvec{y}_{t}= \left[ y_{t, 1}, \cdots , y_{t, \ell }\right]$ represents the label vector of the test data $\varvec{x}_t$ at the time t. The $y_{t, j}$ has two opposite values:$\{-1,1\}$. If $\varvec{x}_t$ contains the j-th label, the $y_{t, j}$ should be 1, otherwise $y_{t, j}$ should be ${-1}$.

Theorem 1

Given the initial $X_0$ and $Y_0$, our goal is to find a function set $\mathcal {H}_{t}=\left[ h_{t, 1}, h_{t, 2}, \cdots , h_{t, \ell }\right]$, where $h_{i,j}$ has two opposite values $\{-1,1\}^{\ell }$ represents whether owns j-th class label, $j \in \{1,2, \cdots , \ell \},$ at time $t \in \{1,2, \cdots , T\}$. And for each $\varvec{x}_{t}$, we output $\hat{\varvec{y}}_{t}=\mathcal {H}_{t}\left( \varvec{x}_{t}\right)$ as the predicted label vector.

3.2 The Algorithm

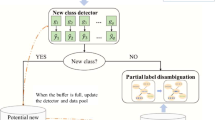
We assume that the ground truth is not available throughout the entire test data stream. The problems needed to be solved in new multi-labels learning mainly lie in two aspects. The first one is to construct a detector to identify new labels. The Second one is to take multiple new labels apart if they erupt in one iteration, that is, when we might need to update the model for multiple labels concurrently. Otherwise, there is a considerably great chance that we might mistakenly train one weight vector for multiple new labels.

And we approach this problems mentioned above by using the following two core technologies. (i) Firstly, we use a extended isolation forest called MuENLForest [8] which will generate a outlier detector $\mathcal {D}_{t}\left( \varvec{x}_{t}\right)$ based on the previous training data and label attributes. If the output of $\mathcal {D}_{t}\left( \varvec{x}_{t}\right) = 1$, then it indicates that the current $\varvec{x}_t$ contains a new label. Otherwise, if the output is -1, it indicates there is no new label in $\varvec{x}_t$. (ii) Secondly, we adopt the Density-based spatial clustering of applications with noise (DBSCAN) to the buffer container when it reaches the pre-set maximum. That is, for the data with new labels in the container, we cluster them into several groups, and each group maps to one new label. Finally, when the cluster procedure finishes, we execute the classifier model updating process step by step, and each step depended on the previous step in order to get a more robust model: $\mathcal {H}_{t}=\left[ h_{t, 1}, h_{t, 2}, \cdots , h_{t, \ell }\right]$ $\rightarrow$ $\mathcal {H}^{'}_{t}=\left[ h_{t, 1}, h_{t, 2}, \cdots , h_{t, \ell }, \mathcal {D}_{t}\right]$.

Algorithm 1 summarizes the MuPND method. It has four components: (i) the multi-label classifier for $\mathcal {H}_{0}$. (ii) MuENLForest detector $\mathcal {D}_{t}$. (iii) DBSCAN explicitly decomposes the multiple new labels lying in the buffer pool into n new labels. (iv) update the model $\mathcal {H}_{t} \rightarrow \mathcal {H}_{t+n}$. One point we need to declare is that the weight sampling vector are used to reduce the probability of previous instances being selected during the construction of MuENLForest, and give a preference to recent instances. Therefore we let the $\varvec{s}$ being multiplied by a decay factor 0.8.

The Linear Multi-label Classifier. Formally, given an instance $\varvec{x}$, we define the linear classifier on label i as

$$\begin{aligned} h_{i}(\varvec{x})={\text {sign}}\left( \varvec{w}_{i}^{\top } \varvec{x}+b_{i}\right) \end{aligned}$$

(1)

While we minimize the misclassification loss and the pairwise label ranking loss in order to obtain the overall performance. The convex optimization for each $\varvec{w}_i$ can be written as

$$\begin{aligned} \begin{array}{c}{\min \limits _{w_{i}, b_{i}, \xi , \zeta } \frac{1}{2}\left\| \varvec{w}_{i}\right\| ^{2}+C_{1} \sum \nolimits _{k=1}^{n} \xi _{k}+C_{2} \sum \nolimits _{j=1}^{\ell } \sum \nolimits _{k=1}^{n} \zeta _{j, k}} \\ { \text{ s.t. } \quad y_{i, k} f_{i, k} \ge 1-\xi _{k}} \\ {\varDelta _{j, k}\left( f_{i, k}-f_{j, k}\right) \ge 1-\zeta _{j, k}} \\ {\xi _{k} \ge 0, \zeta _{j, k} \ge 0} \\ {j \in \{1,2, \cdots , \ell \}, k \in \{1,2, \cdots , n\}}\end{array} \end{aligned}$$

(2)

In details, $\varDelta _{j, k}=y_{i, k}-y_{j, k}, f_{i, k}=\varvec{w}_{i}^{\top } \varvec{x}_{k}+b_{i}$, and $C_{1}, C_{2}$ are two parameters to trade off. To simplify the calculative process, we replace the $b_i$ by adding an attribute value 1 at the end of $\varvec{x}_k$, then $f_{i, k}=\varvec{w}_{i}^{\top }\left[ \varvec{x}_{k} ; 1\right]$. Equation (2) can be rewritten as

$$\begin{aligned} \begin{array}{l}{\min \limits _{\varvec{w}_{i}} \sum \nolimits _{j=1}^{\ell } \sum \nolimits _{k=1}^{n}\left[ 1-\left( y_{i, k}-y_{j, k}\right) \left( f_{i, k}-f_{j, k}\right) \right] _{+}} \\ {\quad +\lambda _{1} \sum \nolimits _{k=1}^{n}\left[ 1-y_{i, k} f_{i, k}\right] _{+}+\frac{\lambda _{2}}{2}\left\| \varvec{w}_{i}\right\| ^{2}}\end{array} \end{aligned}$$

(3)

MuENLForest for New Label Detection. Here, we suppose the new label appears when an instance has an unseen co-occurrence feature or label. There are some previous work that have already done a nice job, such as the isolation forest (iForest) [11]. However, the traditional iForest only considers the input feature space, and employs the average path length calculated by the test instance traverses over all trees as the anomaly score. And whether the instance contains a new label depends on whether it locates in a spare region. Since instances with new labels may share the same dense region of instances with some common known labels. Therefore, we adopt an extended iForest called MuENLForest [8] as our new label detector, which captures the characteristics in both the feature space and the label patterns.

We can briefly describe the construction of MuENLForest in following procedures: MuENLForest consists of g MuENLTree; and each MuENLTree is built using a random subset of $\left( X_{t}, \mathcal {H}_{t}\left( X_{t}\right) \right)$ of size $\psi$ (pre-set constant value) using sampling weight $\varvec{s}_t$. And the novel part of the MuENLForest is that a covering ball is being attached at each leaf node of the tree. The following part gives a detail about how the covering ball functions in the outlier detection.

Theorem 2

MuENLTree is a binary tree consists of internal nodes and leaf nodes. Let $\varvec{a}=\left[ \varvec{x}, \mathcal {H}_{t}(\varvec{x})\right]$ denote the training sample with predictive values. Each internal node is being split into two son nodes by the test: $\left\| \varvec{a}^{\varvec{q}}-\varvec{p}_{1}\right\| \le \left\| \varvec{a}^{\varvec{q}}-\varvec{p}_{2}\right\|$, where $\varvec{p}_{1}$ and $\varvec{p}_{2}$ are two cluster center both having $\varvec{q}$ attributes and $\varvec{a^q}$ is the $\varvec{q}$ projection of $\varvec{a}$. Each leaf node has a ball covering S satisfying radius r = $\max _{\varvec{x} \in S}\Vert \varvec{a}-\varvec{m}\Vert$, where $\varvec{m}={\text {mean}}(S)$.

As a result, for those instances which contain the similar features and attributes, they will locate on the same leaf node. After we have constructed the MuENLForest, that is $\mathcal {D}_{t}(\cdot )$, we are ready to predict the new label. If $\mathcal {D}_{t}\left( \varvec{x}_{t}\right) =1$, it indicates the instance $\varvec{x}_{t}$ contains a new label. Otherwise, if $\mathcal {D}_{t}\left( \varvec{x}_{t}\right) =-1$, it does not have a new label. More specifically, if the instance falls on the same leaf node but outside the covering ball, it suggests that the instance has some attributes different from others. Therefore, the instance holds a new label in a considerably high probability.

DBSCAN to Decompose the Buffer Pool. Every time, when the new labels Buffer pool reaches the BUFFER${\_}$MAX${\_}$SIZE, the traditional approaches will regard all the instances in the Buffer Pool have a common new label. Under the real circumstance, we might meet the situation that the instances in one Buffer Pool will contain multiple labels in one iteration. That is, for example, Buffer pool contains BUFFER${\_}$MAX${\_}$SIZE instances emerging with $n (n> 1)$ new labels. Such behaviors that mistakenly training one model for multiple new labels can be avoided by applying the DBSCAN algorithms. Generally, the DBSCAN decomposes the Buffer container into n central clusters, which can improve the robust of the classifier for multiple new labels. The following part gives details how the DBSCAN functions and being integrated with the decomposition process.

The DBSCAN is a density-based clustering non-parametric algorithm, which can describe the closeness of sample distribution. In this paper, we assume that instances with the same new label will locate in the same cluster. Therefore, different clusters will represent the different labels. It makes sense, because we have already illustrated that among the MuENLForest leaf nodes, those instances with new labels are determined by their distance away from the normal instances as mentioned in the above section.

There is one other thing worth noting is that we need to update the classifier of new label located in each cluster dependently. That is, supposing we have trained the classifier for the i-th label, the next step for us to train the classifier for the $i+1$-th label are based on the i-th label classifier.

Multi-label Classifier Update. Finally, once the DBSCAN has completed the decomposition process for multiple new labels, we can update the multi-label classifier. The update process includes the construction for new labels, and update of the existing model for known labels. Here we adopt a previous method [9], that is to introduce a latent variable which estimates the true label assignment of each instance in $\mathcal {X}_{t}$, where a predicted label by the detector is the initial value of the latent variable. Then the optimization process simultaneously learns this latent label assignment and the classifier which best fits the data. In this way, the learned classifier is more tolerant to the errors of the detector. The solution can be formulated as the following:

Suppose there are n clusters collected in the buffer pool, and $X_{B,i}$ represents collection of instances containing i-th new labels. $X_{U}$ is the set of instances with (predicted) known labels only, where $X_{U}=X_{t} \backslash X_{B}$ and $X_{B}= \left[ X_{B,1},X_{B,2},\dots ,X_{B,n}\right]$. Let $\varvec{p}=\left[ p_{1}, p_{2}, \cdots , p_{m}\right] ^{\top }$ be the unknown assignment of the new label of the $X_{t,i}=\left[ X_{B,i} ; X_{U}\right]$ where m is the number of instances in $\left[ X_{B,i} ; X_{U}\right]$; and $p_{k}=1$ if $\varvec{x}_{k} \in \left[ X_{B,i} ; X_{U}\right]$; $p_{k}=0$ otherwise.

Different from Eq. (3), we replace $y_{i, k}$ with $2 p_{k}-1$. As a result, the optimization problem of building classifier $\varvec{w}_{a}$ and learning $\varvec{p}$ for the new label $\ell$ is cast as follows:

$$\begin{aligned} \begin{aligned} \min _{\varvec{w}_{a}, p}&\sum _{j=1}^{\ell } \sum _{k=1}^{m}\left[ 1-\left( 2 p_{k}-1-y_{j, k}\right) \left( f_{\ell , k}-f_{j, k}\right) \right] _{+} \\+\lambda _{1}&\sum _{k=1}^{m}\left[ 1-\left( 2 p_{k}-1\right) f_{\ell , k}\right] _{+}+\frac{\lambda _{2}}{2}\left\| \varvec{w}_{a}\right\| ^{2}+\frac{\lambda _{3}}{2}\Vert \varvec{p}\Vert ^{2} \\ \text{ s.t. } p_{k}&\in \{0,1\}, k \in \{1,2, \cdots , m\} \end{aligned} \end{aligned}$$

(4)

Since above equation is a NP-hard problem. Therefore, we relax the constraint from $p_{k} \in \{0,1\}$ to $p_{k} \in [0,1]$, then optimize $\varvec{p}$ and $\varvec{w}_a$ alternately. That is, we can do the optimization in Eqs. (5) and (6).

$$\begin{aligned} \begin{aligned} \min _{\varvec{p}}&\sum _{j=1}^{\ell } \sum _{k=1}^{m}\left[ 1-\left( 2 p_{k}-1-y_{j, k}\right) \left( f_{\ell , k}-f_{j, k}\right) \right] _{+} \\ {}&+\lambda _{1} \sum _{k=1}^{m}\left[ 1-\left( 2 p_{k}-1\right) f_{\ell , k}\right] _{+}+\frac{\lambda _{3}}{2}\Vert \varvec{p}\Vert ^{2} \\ \text{ s.t. } p_{k}&\in [0,1], k \in \{1,2, \cdots , m\} \end{aligned} \end{aligned}$$

(5)

After we have solve the Eqs. (5) and (6) using the subgradient of the objective function. Then we project $\varvec{p}$ to $[0,1] : \varvec{p} \leftarrow \min \left( \mathbf {1},[\varvec{p}]_{+}\right)$ to satisfy the box constraint.

$$\begin{aligned} \begin{aligned} \min _{\varvec{w}_{a}}&\sum _{j=1}^{\ell } \sum _{k=1}^{m}\left[ 1-\left( 2 p_{k}-1-y_{j, k}\right) \left( f_{\ell , k}-f_{j, k}\right) \right] _{+} \\ {}&+\lambda _{1} \sum _{k=1}^{m}\left[ 1-\left( 2 p_{k}-1\right) f_{\ell , k}\right] _{+}+\frac{\lambda _{2}}{2}\left\| \varvec{w}_{a}\right\| ^{2} \end{aligned} \end{aligned}$$

(6)

4 Experiments

4.1 Experiment on Yeast Data Set

To evaluate the performance of MuPND approach, we use the yeast data set. We divide the data set into two parts, the first one is initial training data set with already known class labels, and the second one is unlabeled instances. To ensure that the emerging order of the test data in second part has no effects on the result, we shuffle the data stream randomly. Table 1 shows the details about our experiment data information. As shown in the Table 1, there are 1313 instances with known labels in the initial training data set and 402 unlabeled instances as test data stream.

Table 1. Yeast data set information

Firstly, as illustrated above in the Algorithm section, we get a initial classifier and outlier detection forest by training the fist part of data. After the training process has already completed, we adjust the BUFFER$\_$MAX$\_$SIZE to a enough big integer to simulate the situation that we might meet multiple new labels in one iteration. In our experiment using yeast data set, 3 new labels (A to C) are emerging in one buffer pool, that is one iteration. Then we apply the DBSCAN to split the buffer pool into three groups which represent 3 new labels. Table 2 shows the parameters used in the MuPND, including the MinPts and radius parameter of DBSCAN used in the experiment.

Table 2. Parameters used in MuPND

4.2 Experiment Result

When DBSCAN finishes the cluster tasks, we update the classifier separately and dependently for each new label. To be more specifically, firstly we train a new classifier for new label, supposedly A, and then append the weight vector $\varvec{w}_a$ to the previous Model. Once we get a new Model for new label A, then we need to retrain the detection forest using the predicted values by new Model. That is, every time we update Model, we will use the Model from previous step. After each updating the label classifier for one new label, we evaluate the performance of the classifier. The experiment results are shown in the Table 3. We evaluate the average precision.

On the same data set, we conducted experiments with the method proposed in this paper and the MuENL method respectively. The experiment data are shown below. Through this comparative experiment, we can see that in general, the algorithm in this paper can achieve better performance in Average Precision.

Table 3. Average precision

5 Conclusions

The paper proposes a dynamic multi-label learning method for handling with multiple new labels. The core idea of decomposing the new label pool into multiple new labels separately has enabled the whole problem to be solved satisfactorily. The public data set demonstrate that the performance, especially average precision, get improved by our method. In the future, we will try to optimize other loss functions, such as ranking loss and hamming loss.