A Novel Hybrid Genetic Algorithm for the Two-Stage Transportation Problem with Fixed Charges Associated to the Routes

Abstract

This paper concerns the two-stage transportation problem with fixed charges associated to the routes and proposes an efficient hybrid metaheuristic for distribution optimization. Our proposed hybrid algorithm incorporates a linear programming optimization problem into a genetic algorithm. Computational experiments were performed on a recent set of benchmark instances available from literature. The achieved computational results prove that our proposed solution approach is highly competitive in comparison with the existing approaches from the literature.

1 Introduction

This work deals with a variant of the transportation problem, namely the fixed-charges transportation problem in a two-stage supply chain network consisting of a set of manufacturers, a set of distribution centers (DC’s) and a set of customers, whose scope is to identify and select the manufacturers and the distribution centers fulfilling the demands of the customers under minimal costs. The main characteristic of the two-stage fixed-charges transportation problem (TSFCTP) is that a fixed charge is associated with each route that may be opened in addition to the variable transportation cost which is proportional to the amount of goods shipped.

The fixed-charges transportation problem (FCTP) generalizes the classical transportation problem and it was introduced by Balinski [1]. Guisewite and Pardalos [6] showed that the fixed-charges transportation problem is NP-hard. For more information on the FCTP, including a review of exact and heuristic algorithms developed for solving the problem, we refer to Buson et al. [2]. For a review on the variants of the fixed-charges transportation problem and related problems to the investigated TSFCTP, we refer to Cosma et al. [4] and Pop et al. [9].

The existing literature regarding the two-stage transportation problem with fixed-charges associated to the routes is rather scarce. The form investigated in our paper was introduced by Jawahar and Balaji [7]. They described a mathematical model of the transportation problem as a mixed integer linear programming, a heuristic approach based on genetic algorithm (GA) with a specific coding scheme suitable for two-stage transportation problems, as well as a set of 20 benchmark instances of various sizes and capacities. Their obtained computational results have been compared to lower bounds and approximate solutions obtained by relaxing the integrality constraints. Raj and Rajendran [10] proposed two scenarios of the two-stage transportation problem: the first one, called Scenario 1, considers fixed charges associated to the routes in addition to unit transportation costs and unlimited capacities of the DCs, while the second one, called Scenario 2, considers the opening costs of the DCs in addition to unit transportation costs. In the case of Scenario 1, which coincides with the form considered in our paper, they described a two-stage genetic algorithm in order to solve the problem. They also proposed a solution representation that allows a single-stage genetic algorithm to solve it. The major feature of these GA’s is a compact representation of the chromosomes based on permutations. Pop et al. [8] proposed a hybrid algorithm that combines a steady-state genetic algorithm with a local search procedure for solving the problem. Recently, Calvete et al. [3] described a matheuristic approach for the problem that incorporates an optimization problem within an evolutionary algorithm and proposed a set of 20 larger randomly generated instances and Cosma et al. [5] developed an efficient multi-start Iterated Local Search procedure for the total distribution costs minimization of the TSFCTP, which constructs an initial solution, uses a local search procedure to increase the exploration, a perturbation mechanism and a neighborhood operator in order to diversify the search.

Our novel solution approach has some important and original features that differentiate it from the existing ones from the literature. We used an integer chromosome representation in which the genes have integer values that represent estimates of the number of units to be transported on each transportation link of the model. For an efficient exploration of the solutions space and in order to avoid evolution stalling due to local minima, several chromosome populations have been created, evolving separately to different offspring, which are finally merged into the populations.

We organized the remainder of the paper as follows: in Sect. 2, we give some notations and definitions related to the two-stage transportation problem with fixed-charges associated to the routes that will be used throughout the paper and we also present a mixed integer formulation of the problem. The novel solution approach for solving the considered transportation problem is described in Sect. 3 and some preliminary computational experiments and the achieved results are presented and analyzed in Sect. 4. Finally, we conclude our work and discuss our plans for future work in Sect. 5.

2 Definition of the Two-Stage Fixed-Charges Transportation Problem

In order to define the considered two-stage fixed-charges transportation problem, we start by defining the related sets, decision variables and parameters:

p	the number of manufacturers and i is the manufacturer identifier;
q	the number of distribution centers (DCs) and j is the DC identifier;
r	the number of customers and k is the customer identifier;
$S_i$	the capacity of manufacturer i;
$D_k$	the demand of customer k;
$f_{ij}$	the fixed charge for the link from manufacturer i to DC j
$g_{jk}$	the fixed charge for the link from DC j to customer k;
$b_{ij}$	the unit cost of transportation from manufacturer i to DC j;
$c_{jk}$	the unit cost of transportation from DC j to customer k.
$x_{ij}$	the number of units transported from manufacturer i to DC j,
$y_{jk}$	the number of units transported from DC j to customer k,
$z_{ij}$	is 1 if the route from manufacturer i to DC j is used and 0 otherwise,
$w_{jk}$	is 1 if the route from DC j to customer k is used and 0 otherwise

Given a set of p manufacturers, a set of q distribution centers (DC’s) and a set of r customers with the following properties:

• 1. Each manufacturer may ship to any of the q DCs at a transportation cost $b_{ij}$ per unit from manufacturer i, where $i \in \{1,...,p\}$, to DC j, where $j\in \{1,...,q\}$, plus a fixed charge $f_{ij}$ for operating corresponding the route.

• 2. Each DC may ship to any of the r customers at a transportation cost $c_{jk}$ per unit from DC j, where $j\in \{1,...,q\}$, to customer k, where $k\in \{1,...,r\}$, plus a fixed charge $g_{jk}$ for operating the corresponding route.

• 3. Each manufacturer $i \in \{1,...,p\}$ has $S_i$ units of supply and each customer $k\in \{1,...,r\}$ has a given demand $D_k$.

The aim of the two-stage fixed-charges transportation problem is to determine the routes to be opened and corresponding shipment quantities on these routes, such that the customer demands are fulfilled, all shipment constraints are satisfied, and the total distribution costs are minimized.

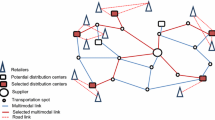
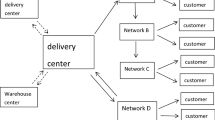
An illustration of the investigated TSFCTP is presented in the next figure (Fig. 1).

Fig. 1.

Illustration of the two-stage fixed-charges transportation problem

The TSFCTP can be modeled as the following mixed integer problem described by Raj and Rajendran [10]:

$$\begin{aligned}&\min \;\; Z\;=&\sum _{i=1}^{p}\sum _{j=1}^{q}(b_{ij}x_{ij}+f_{ij}z_{ij})+ \sum _{j=1}^{q}\sum _{k=1}^{r}(c_{jk}y_{jk}+g_{jk}w_{jk}) \end{aligned}$$

(1)

$$\begin{aligned}&s.t.&\sum _{j=1}^{q}x_{ij}\le S_i, \; \qquad \qquad \forall \; i\in \{1,...,p\} \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{j=1}^{q}y_{jk}= D_k, \;\;\; \qquad \quad \forall \; k\in \{1,...,r\} \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{i=1}^{p}x_{ij} = \sum _{k=1}^{r}y_{jk}, \; \qquad \forall \; j\in \{1,...,q\} \end{aligned}$$

(4)

$$\begin{aligned}&x_{ij}\ge 0, \ \qquad \qquad \qquad \, \forall \; i\in \{1,...,p\}, \; \forall \; j\in \{1,...,q\} \end{aligned}$$

(5)

$$\begin{aligned}&y_{jk}\ge 0, \ \qquad \qquad \qquad \, \forall \; j\in \{1,...,q\}, \forall \; k\in \{1,...,r\} \end{aligned}$$

(6)

$$\begin{aligned}&z_{ij} = \left\{ \begin{array}{ll} 1,\; x_{ij}>0\\ 0,\; x_{ij}=0 \end{array} \right. \, \;\;\;\; \forall \; i\in \{1,...,p\}, \; \forall \; j\in \{1,...,q\} \end{aligned}$$

(7)

$$\begin{aligned}&w_{jk} = \left\{ \begin{array}{ll} 1,\; y_{jk}>0\\ 0,\; y_{jk}=0 \end{array} \right. \, \;\;\; \forall \; j\in \{1,...,q\}, \; \forall \; k\in \{1,...,r\} \end{aligned}$$

(8)

The objective function minimizes the total distribution cost: the fixed charges and the transportation per-unit costs. Constraints (2) guarantee that the quantity shipped out from each manufacturer does not exceed the available capacity, constraints (3) guarantee that the total shipment received from DCs by each customer is equal to its demand and constraints (4) are the flow conservation conditions and they guarantee that the units received by a DC from manufacturers are equal to the units shipped from the DCs to the customers. The last four constraints ensure the integrality and non-negativity of the decision variables.

The considered two-stage transportation problem with fixed charges associated to the routes is a NP-hard optimization problem because it extends the fixed-charges transportation problem, which have been shown to be NP-hard by Guisewite and Pardalos [6]. That is why in order to tackle the two-stage transportation problem with fixed charges associated to the routes, we proposed an efficient hybrid genetic algorithm.

3 Description of the Hybrid Metaheuristic Algorithm

Our proposed hybrid metaheuristic approach consists of a genetic algorithm (GA) whose operation is based on solving a set of linear optimization problems.

GAs are search heuristic methods inspired from the theory of natural evolution. They can deliver good solutions efficiently, making them attractive for solving difficult optimization problems.

One of the most important elements of a GA is the chromosome representation scheme. In our genetic algorithm, each chromosome contains $p\times q + q\times r$ genes, that represent the transportation links in the distribution system. There are $p\times q$ links from the p manufacturers to the q DCs, and $q\times r$ links from the q DCs to the r customers. The value of each gene represents an estimate of the number of units transported along the corresponding transportation link, in the optimal solution of the TSFCTP. The gene corresponding to the link from manufacturer i to DC j is denoted $\tilde{x}_{ij}$, and the gene corresponding to the link from DC j to customer k is denoted $\tilde{y}_{jk}$. The genes are used to estimate the total cost for transporting one unit on the corresponding link, so that it includes the correct fraction of the fixed charge required for opening that link. These estimated costs denoted $\tilde{b}_{ij}$ and $\tilde{c}_{jk}$ are computed according to relations (9) and (10), where $\tilde{b}_{ij}$ correspond to the links from manufacturers to DCs and $\tilde{c}_{jk}$ correspond to the links from DCs to customers.

$$\begin{aligned} \tilde{b}_{ij} = \left\{ \begin{array}{ll} b_{ij}+\displaystyle \frac{f_{ij}}{\tilde{x}_{ij}}, \;\;\;\; \text{ if } \; \tilde{x}_{ij}>0\\ b_{ij}+f_{ij}, \;\;\;\;\; \text{ if } \; \tilde{x}_{ij}=0 \end{array} \right. \end{aligned}$$

(9)

$$\begin{aligned} \tilde{c}_{jk} = \left\{ \begin{array}{ll} c_{jk}+\displaystyle \frac{g_{jk}}{\tilde{y}_{jk}}, \;\;\; \;\text{ if } \; \tilde{y}_{jk}>0\\ c_{jk}+g_{jk}, \;\;\;\;\; \text{ if } \; \tilde{y}_{jk}=0 \end{array} \right. \end{aligned}$$

(10)

The value of the genes that form the initial population chromosomes are chosen randomly. However, it is improbable that the random estimates will be close to reality. For improving the quality of the chromosomes, we developed a simple algorithm called Estimates Correction, that will be used also for improving each new chromosome created by the crossover operator.

For defining the Estimates Correction algorithm, we consider the following linear optimization problem:

$$\begin{aligned}&\min \ \sum _{i=1}^{p}\sum _{j=1}^{q}\tilde{b}_{ij}x_{ij}+ \sum _{j=1}^{q}\sum _{k=1}^{r}\tilde{c}_{jk}y_{jk} \\&s.t. \ \ (2), \,(3), \,(4), \,(5), \,(6) \nonumber \end{aligned}$$

(11)

where $\tilde{b}_{ij}$ and $\tilde{c}_{jk}$ are the total unit transportation cost estimates, calculated according to (9) and (10).

This is a well-known optimization problem, namely the Minimum Cost Flow Problem, for which there are several algorithms that solve it efficiently. For the results presented in this paper, we used the Network Simplex algorithm.

The Estimates Optimization algorithm works as follows:

Step 1 initializes the total cost of distribution $\tilde{Z}$. The linear optimization problem (11) is optimally solved in step 2. The amounts $x_{ij}$ and $y_{jk}$ determined in step 2 are used in step 3 to calculate the total cost Z of the TSFCTP. Steps 2 and 3 may repeat because of the loop created by the jump in step 11, but there is no guarantee that the solutions will always be improved. The decision to stop or continue the algorithm is taken in step 4. The algorithm is stopped if the last iteration worsened the solution, or the resulting chromosome is a duplicate. Two chromosomes are considered identical, if the corresponding linear optimization problems (11) have identical solutions, even if the $\tilde{x}_{ij}$ and $\tilde{y}_{jk}$ estimates are different. The last saved chromosome represents the result of the algorithm. If step 7 is reached, it means that the last iteration improved the TSFCTP solution. In this case, the chromosome is saved, the $\tilde{x}_{ij}$ and $\tilde{y}_{jk}$ estimates are updated in step 10, and the algorithm continues with a jump to step 2.

The operating principle of our genetic optimization algorithm is shown in Fig. 2.

Fig. 2.

The operating principle of our genetic optimization algorithm

The process of evolution for a chromosome population is presented in Algorithm 2.

The selection operator chooses two parent chromosomes p1 and p2 from the current population, for mating. The two parents are chosen using the tournament selection strategy (lines 3, 4). The number of participants in each tournament is randomly selected between 2 and 10.

The crossover operator combines the genes of the two parents, to form the chromosome of the offspring (line 5). The genes of the offspring are taken either from p1 or p2 with equal probabilities. This results in an offspring carrying equal genetic information from both parents.

Each new chromosome can suffer a mutation, with 0.01 probability. The mutation operator chooses randomly a client k, and clears all the estimates for its links $\tilde{y}_{jk}$. Then maximum 5 DCs are randomly chosen and the estimates of their links to client k are replaced with random values in the interval $[0,D_k]$. Next a DC j is randomly chosen and all the estimates for the links from j to the manufacturers $\tilde{x}_{ij}$ are cleared. Then maximum 5 manufacturers are randomly chosen and their estimates for the links to DC j are replaced with random values in the interval $[0,S_i]$.

The resulting offspring is passed through the Estimates Correction algorithm, that also evaluates its fitness value Z. If the offspring has better fitness than the last individual in the current population, then the crossover and eventual mutation are considered successful, and the individual is retained. Unfit chromosomes are destroyed immediately.

The internal loop (lines 2–6) of the Genetic Evolution algorithm performs at least 3N crossover operations for each new generation. If those operations fail to create at least 2N new fit chromosomes, then the number of crossover operations is increased to maximum 10N, or until 2N fit chromosomes are created.

The Admission operation in line 7 of the Genetic Evolution algorithm takes some of the chromosomes in the current population and offspring to form the new population, hopping that it will be better than the previous one. The age of each chromosome is incremented when it is passed from the old into the new population. The following rules have been applied to create the new population:

• The maximum age of chromosomes was limited to 3 generations. Older chromosomes are not allowed into the new population.

• The first 2/3N chromosomes in the new population are composed of the fittest chromosomes from the old population and offspring. At most, half of these chromosomes may originate from the old population.

• The remaining 1/3N chromosomes are randomly chosen from the rest of the old population and offspring.

The main loop of the Genetic Evolution algorithm ends when the best chromosome is no longer improved in the last three consecutive generations. This chromosome could represent the optimal solution to the TSFCTP, but usually for complex problems it is only a local minimum.

Our main optimization procedure is presented in Algorithm 3.

The initial population is composed of $N=\displaystyle min(\frac{pq+qr}{5},500)$ randomly generated chromosomes. The $\tilde{x}_{ij}$ estimates are chosen randomly from the interval $[0,S_i]$, and the $\tilde{y}_{jk}$ estimates are chosen randomly from the interval $[0,D_k]$. Each random chromosome in the initial population is passed through the Estimates Correction algorithm.

The chromosome population is improved by calling the Genetic Evolution procedure. This procedure ends when the optimal solution of TSFCTP is found or is reached in a local minimum. The population thus obtained represents a new breed of chromosomes, the evolution of which is stopped, because any subsequent gains would appear far too slow.

The main loop of the algorithm (lines 3 14) creates new breeds of chromosomes that are merged together using hybrid selection and the crossover operator, for the best possible coverage of the solutions space. The loop ends when the running time limit of the algorithm is exceeded. Each breed evolution starts with a population of random chromosomes.

The Loop on lines 7 11 creates a new chromosome population by merging two different breeds. The selection process organizes one tournament in each of the two breeds that are merged together Thus each offspring will contain genetic information from both breeds. In the merging operation, a minimum of 5N crossover operations are performed, that result in at least 4N new fit chromosomes. If this is not possible, then the number of crossover operations is extended up to a maximum of 15N.

The Hybrid Admission operation performed at the end of the loop, creates a new population, taking chromosomes from the two merged populations and their offspring, based on the rules described above. The newly created population follows the normal process of evolution.

4 Computational Results

In order to analyze the performance of our proposed algorithm, we tested it on a set of benchmark instances that was proposed by Calvete et al. [3]. We performed 5 independent runs for each instance, as there were performed by Calvete et al. [3].

The computational results obtained by our proposed solution approach in comparison to the matheuristic approach proposed by Calvete et al. [3] are presented in Table 1. The first column in Table 1 gives the number of the instance and the second one provides its size. The next two columns contain the optimal solution obtained by CPLEX when it is available and the corresponding time. The running time of CPLEX was limited to 3600 s. The instances for which CPLEX could not find the optimal solution within the running time, are marked with an asterisk. The last columns provide the results reported by Calvete et al. [3] and our achieved results. The following information is provided: the minimum and maximum objective function values obtained in the five runs of each instance ($Z_{min}$, and $Z_{max}$), the average gap and the average time spent by the algorithms for finding the best solution. The gap was calculated as proposed by Calvete et al. [3]: $gap = 100\times (Z-Z_{min})/Z_{min}$, where Z is the average of the solutions objective value.

The computational times are reported in seconds. The results written in bold represent cases for which the best results have been achieved either by CPLEX, or using the mat heuristic proposed by Calvete et al. [3], or by our novel solution approach.

Table 1. Computational results achieved by our proposed soft computing approach compared to existing methods

Regarding the computational times, it is difficult to make a fair comparison between algorithms, because they did not run on the same computer and they were implemented in different programming languages. In order to be able to make an objective comparison, we will analyze the processing power of the computers that ran the two algorithms, and the efficiencies of the programming languages used for their implementation.

The matheuristic algorithm proposed by Calvete et al. [3] has been run on an Intel Pentium D CPU at 3.0 GHz having 3.2 GB of RAM, while our algorithm on an Intel Core i5-4590 processor at 3.3 GHz with 4GB of RAM. The single thread ratings of the two processors can be found in [12] and we observed that our processor runs 3.03 times faster. As regards the programming languages, we used Java, while the algorithm proposed by Calvete et al. [3] was programmed in C++. A comparison between the two programming languages in terms of efficiency can be found in [11]. The time factor for C++: 1, the time factor for Java 64 bit: 5.8. Therefore, our programming language is 5.8 times slower. In consequence, we considered that the greater speed of the Core i5 processor roughly compensates the slowness of the Java programming language. Because the ratings are always approximate, we did not use any scaling factor. The running times reported in Table 1 are the times measured during the experiments.

Analyzing the computational results reported in Table 1, we can observe that the algorithm developed by Calvete et al. [3] provided the optimal solutions in 10 out of 20 instances and our proposed solution approach obtained the optimal solutions for all the instances for which CPLEX delivered the optimal solution.

Our algorithm provided the optimal solution in all the five runs in less than 1 s for the first ten instances and within 15.3 s in the case of instance 11 and within 299.2 s in the case of instance 13. We should point out that in the case of instance 12, the solution reported by Calvete et al. [3] as to be obtained by CPLEX is wrong. We obtained a different solution using CPLEX which is displayed in Table 1.

In the case of instances 14 and 16, our algorithm provided in all the five runs better solutions compared to the ones delivered by CPLEX within 3600 s and Calvete et al. [3]. For 6 out of 20 instances our proposed approach does not provide the same solution in all the five runs, but we can remark that the gap ranges between 0.0003 and 0.103, fact that proves the stability of our proposed solution approach. Instance 17 is the only one for which the algorithm developed by Calvete et al. [3] delivered a better value of the minimum objective function ($Z_{min}$) than our proposed algorithm, but our maximum objective value function ($Z_{max}$) is better.

Overall, the comparison between our proposed solution approach and the algorithm of Calvete et al. [3] can be summarized as follows:

Our algorithm provided the best maximum objective value function ($Z_{max}$) and the best gap for each of the 20 instances and our algorithm provided the best minimum objective function ($Z_{min}$) for each of the instances, with only one exception: instance 17, for which our solution is 0.009% weaker. The computation times of our algorithm are better for 10 out of 20 instances. Our algorithm needed longer computation times for some instances, but that is explicable because our algorithm found better solutions for those instances.

Compared with CPLEX, our algorithm found better solutions or the same solutions for 18 out of 20 instances. The exceptions are instances 17 and 19, for which our solutions are 0.009% respectively 0.016% weaker. Our algorithm performs faster than CPLEX for all the instances.

5 Conclusions

In this paper, we described a novel hybrid genetic algorithm for solving the two-stage transportation problem with fixed charges associated to the routes. Our method incorporates a linear programming optimization procedure within the framework of a genetic algorithm. Some important features of our proposed algorithm are: the use of an efficient representation in which the chromosomes are generated in two stages, the use of several chromosome populations that are created and that evolve separately to different offspring, which are finally merged into the populations, giving us the possibility to explore other parts of the solutions space and escaping from local optima.

We evaluated the performance of the proposed solution approach on a set of benchmark instances recently proposed by Calvete et al. [3]. The computational results that we achieved, prove the efficiency of our proposed solution approach in yielding high quality solutions within reasonable running times, besides its superiority against other existing competing methods from the literature.

In future, we plan to improve the developed hybrid genetic algorithm by combining with local search methods and to evaluate the generality and scalability of the proposed solution approach by testing it on larger instances.