1 Introduction

The problem of multi-view learning is studied extensively in the literature and its merits has been demonstrated in extracting richer representation from available multiple views at the training time (Chaudhuri et al. 2009; Hardoon et al. 2004; Foster et al. 2008). To capture nonlinearity in the model, one can either use kernel methods or follow the recent growing path of the deep neural network (DNN). Both of these methods have been explored in the literature and researchers proposed some advanced two-view models (Hardoon et al. 2004; Bach and Jordan 2003; Andrew et al. 2013). Kernel based methods, such as KCCA (Hardoon et al. 2004), require large memory to store a massive amount of training data to use at the test time. To overcome this issue and improve the kernel based method in terms of memory and speed, some kernel approximation techniques based on random sampling of training data are proposed in Williams and Seeger (2001) and Lopez-Paz et al. (2014). On the other hand, the main advantage of the DNN over kernel based method is that, its parametric model can be better trained with larger amount of data using the fast stochastic optimization techniques.

The proposed deep two-view methods can be mainly categorized in two groups. On one hand, there are models inspired by auto-encoder, e.g. split autoencoder (SplitAE) of Ngiam et al. (2011), in which the deep autoencoders are trained so that the reconstruction error of both views are minimized. In this methods, the encoding network of both view are shared while each view has its own (split) decoder network. On the other hand, another pathway is based on canonical correlation analysis (CCA), such as deep CCA (DCCA) method (Andrew et al. 2013) that extends the linear single layer CCA to deep CCA in which the model parameters are estimated to maximize the cross correlation between the projection of both views.

To combine the benefits of both deep auto-encoder (AE) and CCA for multi-view datasets and hence enhance learned representation, the idea of deep CCA-Auto encoder (DCCAE) is proposed in Wang et al. (2015b). This method tries to optimize the following objective function that is combination of reconstruction errors of two autoencoders and the canonical correlation between the learned bottleneck features (the output of the deep encoders)

$$\begin{aligned} \min _{W_f,W_g, W_p, W_q, U, V} ~~&-{\textstyle \frac{1}{T}} \mathop {\mathrm {tr}}\mathbf {U}^T f(\mathbf {X}) g(\mathbf {Y})^T \mathbf {V}\nonumber \\&+{\textstyle \frac{\lambda }{T}}\sum _{i=1}^{T} \left( \Vert \mathbf {x}_i - p( f(\mathbf {x}_i)) \Vert ^2 +\Vert \mathbf {y}_{i} - q( g(\mathbf {y}_i)) \Vert ^2 \right) \nonumber \\ \text {s.t. }&{\textstyle \frac{1}{T}} \mathbf {U}^T f(\mathbf {X}) f(\mathbf {X})^T \mathbf {U}= \mathbf {I}\nonumber \\&{\textstyle \frac{1}{T}} \mathbf {V}^T g(\mathbf {Y}) g(\mathbf {Y})^T \mathbf {V}= \mathbf {I}\nonumber \\&u_i^T f(\mathbf {X}) g(\mathbf {Y})^T v_j = 0 \quad \text { for } i \ne j \end{aligned}$$
(1)

Here, the functions \(\{f, g, p, q\}\) are flexible nonlinear mappings modeled by neural networks that are parameterized by the set of learnable parameters \(\{W_f,W_g, W_p, W_q\}\). \(\lambda > 0\) is a trade-off parameter that controls the reconstruction error and canonical correlation between the projected views in the objective function (1). In this equation, CCA term tries to maximize the mutual information between the projected views, \(f(\mathbf {x}_i)\) and \(g(\mathbf {y}_i)\), and AE loss tries to minimize the reconstruction error between views and their projections. This approach was shown to outperform DCCA and SplitAE for classification and clustering tasks in two-view application (Wang et al. 2015b).

On the other hand, DCCAE has some drawbacks that limits its applications. Its main drawbacks are two folds. First, the objective function and the constraints couples all the training samples through the (cross-)covariance terms, this will block the stochastic optimization method (e.g. SGD) to be applied here in its standard form. Nevertheless, it was shown in Wang et al. (2015a) that if the mini-batch size is large enough the stochastic gradient can approximate the true gradient but still this requires very large mini-batch sizes which imposes heavy computational complexity on the training algorithm. Second, it does not estimate the hidden state and a model that can generate the second view based on the observation from the primary (first) view. In addition, the empirical studies showed that the canonical term of the objective function (1) dominates in practice and hence the objective is less sensitive to the reconstruction error; this in turn result in the trained autoencoders that don’t reconstruct the views very well while mainly trying to learn projected mapping \( \mathbf {U}^T f(\mathbf {X}), ~ \mathbf {V}^T f(\mathbf {Y}) \) that are maximally correlated.

Wang et al. (2015b) also proposed a modification of their DCCAE method, in which the constraints are relaxed so that the feature dimensions are no longer required to be uncorrelated, the objective of this method, also called as correlated autoencoder (CorrAE), is formulated as

$$\begin{aligned} \min _{W_f,W_g, W_p, W_q, U, V} ~~&-{\textstyle \frac{1}{T}} \mathop {\mathrm {tr}}\mathbf {U}^T f(\mathbf {X}) g(\mathbf {Y})^T \mathbf {V}\nonumber \\&+{\textstyle \frac{\lambda }{T}}\sum _{i=1}^{T} \left( \Vert \mathbf {x}_i - p( f(\mathbf {x}_i)) \Vert ^2 +\Vert \mathbf {y}_{i} - q( g(\mathbf {y}_i)) \Vert ^2 \right) \nonumber \\ \text {s.t. }&{\textstyle \frac{1}{T}} \mathbf {u}_i^T f(\mathbf {X}) f(\mathbf {X})^T \mathbf {u}_i = {\textstyle \frac{1}{T}} \mathbf {v}_i^T g(\mathbf {Y}) g(\mathbf {Y})^T \mathbf {v}_i = 1. \end{aligned}$$
(2)

This variation of the deep multi-view model is designed to examine the importance of the correlation among the learned feature dimensions by comparing its performance with that of the original DCCAE method in some learning tasks.

Deep Generative Multi-view (DGMV) Model: On the other hand, it was shown by White et al. (2012) and Yu et al. (2014) that simple linear CCA can be expressed as a linear generative two-view form where the views are generated as perturbed linear model of the latent representation \(\varvec{\phi }_i\) as

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {x}_i = \mathbf {C}\varvec{\phi }_i+ \epsilon _i, \\ \mathbf {y}_i = \mathbf {E}\varvec{\phi }_i+ \nu _i \end{array}\right. } \end{aligned}$$
(3)

where the perturbation terms are Gaussian independent and identically distributed (i.i.d.) vectors \(\epsilon \sim \mathcal {N} (0 , {\varvec{\varSigma }}_{\epsilon })\) and \(\nu \sim \mathcal {N} (0 , {\varvec{\varSigma }}_{\nu })\). This model makes the latent representation explicit and its joint model parameter estimation and latent variable inference can be expressed as a regularized loss objective function that can be reformulated as a convex optimization problem. We can generalize (3) to nonlinear model resulting in the deep nonlinear generative multi-view model

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {x}_i = p(\varvec{\phi }_i)+ \epsilon _i, \\ \mathbf {y}_i = q(\varvec{\phi }_i)+ \nu _i \end{array}\right. } \end{aligned}$$
(4)

where the generative mappings \( p(\varvec{\phi }_i),~ q(\varvec{\phi }_i)\) can be modeled by deep neural networks parameterized by \(W_p, W_q\). Therefore, given the shared latent representation \( \varvec{\phi }_i \), two views can be generated by a non-linear mapping plus independent Gaussian noises hence one can formulate the following regularized loss objective function

$$\begin{aligned} \min _{W_p, W_q, \varPhi } ~~ \frac{1}{T} \sum _{i=1}^{T} \left( \Vert x_i - p( \phi _i) \Vert ^2 +\Vert y_{i} - q( \phi _i) \Vert ^2 \right) + \mathcal {R} ( \varPhi ), \end{aligned}$$
(5)

In this work, we tackle this deep multi-view subspace learning problem by introducing auto-encoders as inference model.

2 Problem Definition

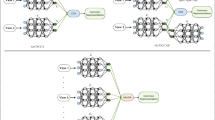
As explained in the previous section, we prefer a deep multi-view network that offers a model to explicitly infer the shared latent source that generates both views and can predict the second view based on the available primary view at the test time. To this end, we introduce two auto-encoder networks with encoder (recognition) networks f(),  g() that provide latent projected views, \(f_{\mathbf {x}_i} = f(\mathbf {x}_i)\) and \(g_{\mathbf {y}_i} = g(\mathbf {y}_i)\), and the decoder (reconstruction) networks \(p(\phi _i),~ q(\phi _i)\) that reconstruct each view based on the latent representation. The encoders and decoders can be modeled by deep neural networks with learnable parameter matrices \(\{\mathbf {W}_f,\mathbf {W}_g, \mathbf {W}_p, \mathbf {W}_q\}\) that correspond to each deep model function. Inspired by the generative interpretation of linear CCA (3), we add a generative linear two-view layer, on top of auto-encoder in the latent space, in order to obtain a shared latent representation \( \varvec{\phi }_i \) for the pair of encoded projected \(\{f_{\mathbf {x}_i}, ~g_{\mathbf {y}_i}\}\). Since the auto-encoders reconstruct each individual view, the latent variable \( \varvec{\phi }_i \) indeed provides a shared underlying representation of both views in a deep nonlinear form. In the other words, the deep generative two-view network (DGMV) can be expressed mathematically as the following pairs of models

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {x}_i = p(f_{\mathbf {x}_i})+ \epsilon _i, \\ \mathbf {y}_i = q(g_{\mathbf {y}_i})+ \nu _i \end{array}\right. } , \nonumber \\ {\left\{ \begin{array}{ll} f_{\mathbf {x}_i} = \mathbf {C}\varvec{\phi }_i+ \epsilon '_i, \\ g_{\mathbf {y}_i} = \mathbf {E}\varvec{\phi }_i+ \nu '_i \end{array}\right. } \end{aligned}$$
(6)

where \(\mathbf {C}, \mathbf {E}\) are the factor loading matrices (matrices of basis) for each view and the latent representations vectors \( \varvec{\phi }_i \) are stacked in the matrix \(\varPhi \). Figure 1 depicts the graphical representation of this model. Consequently, the deep multi-view subspace learning problem can be formulated by the following combined regularized objective function

$$\begin{aligned}&\min _{\mathbf {W}_f, \mathbf {W}_g, \mathbf {W}_p, \mathbf {W}_q, \mathbf {C}, \mathbf {E}, \varPhi } ~~ \underbrace{{\textstyle \frac{\lambda }{T}}\sum _{i=1}^{T} \Vert \mathbf {x}_i - p( f(\mathbf {x}_i)) \Vert ^2 + \Vert \mathbf {y}_i -q( g(\mathbf {y}_i)) \Vert ^2 }_\text {autoencoder objective terms} \nonumber \\&+ \underbrace{{\textstyle \frac{1}{T}} \sum _{i=1}^{T} \mathcal {L}_1\left( \mathbf {C}\phi _i; f(\mathbf {x}_i) \right) + \mathcal {L}_2\left( \mathbf {E}\phi _i; g(\mathbf {y}_i) \right) + \lambda _r \sum _{j=1}^{K} \mathcal {R}_1 ( \varPhi _{j:}) \mathcal {R}_2 ( \mathbf {C}_{:j} ,\mathbf {E}_{:j})}_\text {linear two-view objective terms} \nonumber \\ \end{aligned}$$
(7)

Here, \(\{\mathcal {L}_1,~ \mathcal {L}_2\}\) are the loss functions that measure the divergences between the latent projected views \(\{f_{\mathbf {x}_i}, y_{\mathbf {y}_i}\}\) and their corresponding factorized estimates \( \{\mathbf {C}\varvec{\phi }_i, \mathbf {E}\varvec{\phi }_i\}\). These losses are assumed to be convex in their first arguments, where different noise assumptions result different loss functions, for instance the i.i.d. Gaussian noise assumption amounts to \(\ell _2\) losses. The regularizer terms, \(\mathcal {R}_1 ( \varPhi _{j:}), \mathcal {R}_2 ( \mathbf {C}_{:j} ,\mathbf {E}_{:j})\), capture special structures on the factors loading matrices and the latent features which are controlled by constant factor \(\lambda _r\). On the other hands, the loss functions that measure the fitness error between each view and its reconstruction by the auto-encoder are modeled by \(\ell _2\) losses. Minimizing these loss terms results the latent projections that best reconstruct each view. The parameter \(\lambda > 0\) balances the trade-off between the auto-encoder loss and the linear two-view loss.

Fig. 1.
figure 1

Graphical representation of the deep generative two-view model.

Full size image

2.1 Deep Multi-view with Conditionally Independent Views

One important assumption in multi-view learning is that the views are conditionally independent given the shared latent representation (Yu et al. 2014). This property is crucial in some applications aiming to recover a natural latent representation. As explained in White et al. (2012), this property can be encouraged by selecting regularizer terms of the form \(\mathcal {R}_2 ( \mathbf {C}_{:j} ,\mathbf {E}_{:j})=\max \{ \Vert \mathbf {C}_{:j}\Vert _2 ,\Vert \mathbf {E}_{:j}\Vert _2 \}\) in the optimization objective (7). Using this regularizer, the basis of reconstruction models of each view are individually constrained and don’t compete against each other to obtain their own share in reconstructing the views \(\mathbf {x}_i ,~ \mathbf {y}_i\), so this regularizer better respects the conditional independence of the views. Here, we select \(\mathcal {R}_1 ( \varPhi _{j:}) = \Vert \varPhi _{j:} \Vert _2 \) to encourage row-wise sparsity which, in turn, results in low-rank representation. Subsequently, the two-view objective terms in Eq. (7) can be reformulated as a convex optimization problem in the parameters of linear two-view model, \( \{\mathbf {C}, \mathbf {E}, \varvec{\varPhi }\} \) (White et al. 2012; Yu et al. 2014). Although, the combined objective function of the deep generative model (7) is not convex in the parameters of deep networks, we found this convex reformulation of the linear two-view layer to be beneficial for the training of deep two-view model and final latent variable in practice.

2.2 Advantages of the Proposed Model

  • As mentioned above, the proposed method provide a model for inferring the hidden representation underlying both views and subsequently predicting the second view based on the available primary view at the test time. This is in contrast to CCA-based methods, such as DCCAE, that don’t directly offer a model for generating samples from the latent variable so it is difficult to reconstruct one view based on the other one (Wang et al. 2015b).

  • In addition, as opposed to CCA-based methods that require sufficiently large batch size in order to estimate the whitening matrices in the constraints and the gradients, the average loss function (empirical risk) in (7) exhibits the standard summation form that enables random sampling for stochastic gradient calculation therefore the stochastic optimization algorithms can be readily employed here to optimize for deep network parameters.

  • In contrast to the DCCAE that is limited to standard CCA formulation on the projected views, our proposed model is more flexible to include different types of losses for the two-view objective formulation to capture different properties of latent variables and hence is able to learn more complex models.

  • Also, dissimilar to CCA based methods that are limited to two views, this generative model can be naturally extended to datasets with more than two views available at the training (Guo 2013), so it can better integrate different information related to the same source to enhance representation learning.

  • Additionally, it is expected that the reconstruction losses are more involved in deep generative multi-view training compared to DCCAE since all the objective terms in (7) has the form of losses. So, one might expect that other forms of losses can be replaced for the \(\ell _2\) of reconstruction error in the objective function (7) to improve reconstruction ability of the model; the property that doesn’t seem practical in the DCCAE as its CCA term tends to dominate in practice while ignoring the reconstruction terms which in turn results in poor reconstructed views. This property will be investigated in the experimental studies in Sect. 3.

  • Similar to the deep variational CCA model (Wang et al. 2016), we can introduce private variables that capture view-specific structures in the datasets and disentangle the underlying shared and private information in each view.

The combination of the aforementioned advantages, make the proposed deep generative two-view model a powerful and flexible candidate in multi-view settings with different downstream goals such as classification, subspace clustering, speech recognition and word pair semantic similarity. In the following section we empirically study the performance of the proposed method.

3 Experiments

Experimental Design. For the experiments, we used the two-view noisy digits datasets of Wang et al. (2015b) created based on MNIST dataset that consists of grayscale digit images of size \(28 \times 28\) pixels. To synthesize the views, the pixel values are scaled to range [0, 1]. The first view of the dataset is generated by rotating each image at angles randomly sampled from uniform distribution \(\mathcal {U}(-\pi /4,\pi /4)\) and the second view is selected from a different image of the same identity as in the first view and a random uniform noise is added, then the final value is truncated to remain in range [0, 1]. Following this procedure, both views are just sharing the same identity (label) of the digit but not the style of the handwriting as they are based on arbitrary images in the same class. The training set is divided into training/validation subsets of length 50K/10K and the performance is measured on the 10K images in the test set. This noisy MNIST two-view dataset was used in Wang et al. (2015b) to evaluate the performance of the multi-view model.

Table 1. Classification error of different multi-view learning algorithms on a two-view data set generated based on the MNIST digit images. The results of DGMV method are averaged over 3 rials. The performance of the DGMV is compared against the following benchmark methods: Linear CCA: linear single layer CCA, SplitAE: split autoencoder with Sigmoid gates (Ngiam et al. 2011), DCCA: deep CCA with Sigmoid gates (Andrew et al. 2013), Randomized KCCA: randomized kernel CCA approximation with Gaussian RBF kernels and random Fourier features (Lopez-Paz et al. 2014), CorrAE: deep correlated auto-encoder with Sigmoid gates (2) (Wang et al. 2015b), DistAE: deep minimum-distance auto-encoder with Sigmoid gates (Wang et al. 2015b), DCCAE: deep CCA-Auto encoder with Sigmoid gates (1) (Wang et al. 2015b), VCCA: deep variational CCA with ReLU gates (Wang et al. 2016), VCCA-private: deep variational CCA with an extra pair of latent variables for modeling the private information within each view. ReLU gates are used as the nonlinearities in all the networks (Wang et al. 2016), the performance results of the benchmark methods are from Wang et al. (2015b, 2016).
Full size table

To make a fair comparison, we used neural network architecture for the auto-encoders with the same capacity as the one used in Wang et al. (2015b). Accordingly, for the deep network models, the encoding networks are composed of three fully-connected nonlinear layers of size 1024 units and the last linear layer of size K where K is the dimensionality of the final mapping of the encoding network. The decoding networks consist of three fully-connected layers of 1024 nonlinear units with final layer of size 784 that reconstruct the original images. Sigmoid function is used as the nonlinearity in the deep auto-encoders. Here, we used sigmoid gate function for all the hidden units of the deep networks. In order to prevent over-fitting, we also applied stochastic drop-out to all the layers as regularization techniques.

In the experiments, the downstream task is classification and the misclassification rate is measured as the performance metric. For that goal, the one-versus-one linear SVM classification algorithm is applied on the shared latent representation \(\varvec{\phi }\) of the proposed models or the projected mappings of the CCA based methods. It is worth emphasizing that the proposed DGMV model is able to infer the shared underlying representation of both views based on both encoding projections \(\{f_{\mathbf {x}_i}, ~g_{\mathbf {y}_i}\}\). The shared latent representation is not naturally available in the CCA-based methods which are only able to construct the projection of each individual view. To tune the parameters of the SVM algorithm, cross-validation procedure is employed selecting the best performing model, averaged over 3 trials, on the validation set and the final classification error is evaluated on the test set. For the proposed deep multi-view models, we used the \(\ell _2\) loss function for both \(\mathcal {L}_1, \mathcal {L}_2\) in the objective function (7). To train the deep generative multi-view (DGMV) model, the stochastic gradient descent is used for learning the parameters of the deep networks and accelerated proximal gradient descent (Karami et al. 2017) is employed for optimization of the latent two-view model while we alternatively switch between training of latent multi-view model and the deep AEs after each epoch of training while keeping the other set fixed. Furthermore, we practically found that the convex reformulation of the linear two-view model results in better performance than non-convex optimization algorithm for the training of the latent two-view model and inference of shared latent variable. Similar to Wang et al. (2015b), deep auto-encoders are pre-trained using the layer-wise training method of restricted Boltzmann machines (RBMs) (Hinton and Salakhutdinov 2006). The parameters of each algorithm are tuned through cross validation with grid search.

Fig. 2.
figure 2

(a) Running time of different learning algorithms over the rounds (epochs) of SGD optimization, (b) histogram of one dimensions of the primary projected view \(f(x_i)\) of DCCAE and (c) histogram of one dimensions of the primary projected view \(f(x_i)\) of DGMV.

Full size image

Classification performance of different methods are presented in Table 1 in bit error rate where the best dimensionality of latent variable for each method is reported in parenthesis. The results highlight that DGMV outperform the available methods in terms of the classification performance. In CCA based methods, the dimensionality of the projected latent variable, K, is selected from the set \(\{5, 10, 20, 30, 50\}\) in Wang et al. (2015b) and the best results are achieved by \(K=10\) while in our experiments we found that DGMV can benefit from larger projected latent variable size and it achieves better performance with larger K.

In order to evaluate the learning behavior of the methods, we also compare the running time of different learning algorithms in CPU seconds over the rounds (epochs) of optimization in Fig. 2(a). To make a fair comparison, all experiments were rerun on the same machine using Matlab. Comparing the computation times, we can see that the training of the proposed DGMV methods is faster than DCCAE and while the running time of DCCA is shorter per epoch but it needs more epochs of training (50 epochs versus 14 epochs used for DCCAE and deep two-view models) until it converge to a reasonable result.

Moreover, the histograms of projected view, depicted in Fig. 2(b) and (c), confirm that the outputs of the encoders in DCCAE are not Gaussian distributed while CCA is known to work well in the Gaussian setting while on the other hand, the histograms of projected view of deep generative multi-view model in Fig. 2(c) shows that its distribution is approximately Gaussian.

Fig. 3.
figure 3

Reconstruction fitness of both views for different learning algorithms over the rounds (epochs) of optimization.

Full size image

3.1 Reconstruction Performance

To examine the sample generation behavior of the proposed method, the reconstruction performance of the proposed methods is also evaluated and compared against that of DCCAE. First, the reconstruction error of each view is evaluated for different methods with latent variable dimensionality of \(K=10\). As the validation fitness over the course of training in Fig. 3 illustrates, DGMV tends to decrease the reconstruction errors of both views as the training algorithm progresses while DCCAE leads to increased reconstruction error to achieve smaller canonical correlation among the projected views. This empirical study shows that DCCAE sacrifices the reconstruction ability and focuses on canonical correlation term in order to achieve good discrimination performance while accurate reconstruction of input signal is highly desirable in practice.

Fig. 4.
figure 4

(a) Samples of the training dataset in the first views and their reconstructed images generated by autoencoder network of view 1 (AE1) depicted in columns 1 and 2, respectively. (b) Samples of the training dataset in the first views and their reconstructed images generated by autoencoder network of view 2 (AE2) depicted n columns 1 and 2, respectively. (c) Column 3 is the predicted images of the second view based on the samples from the first (primary) view of the test dataset in column 1. The second column shows the observed noisy samples of the second view.

Full size image

Also to illustrate the reconstruction capability of the proposed method, some training samples of digits in both views and their reconstructed images are depicted in Figs. 4(a) and (b) each reconstruction image is generated by its own autoencoder network. Figure 4(c) depicts the predicted images of the second view based on the 1st view using the combined network: 1st encoder (f()) \(\rightarrow \) latent linear multi-view on the encoded projections \(\rightarrow \) 2nd decoder (q()). Here, the network is trained with latent variable dimensionality of \(K = 70\). These figures shows the reconstruction capability of DGMV method where the generated samples in the input space can denoise the noisy observation, the ability that was missing in DCCA and DCCAE. More specifically, one can observe from Fig. 4(c) that the rotations of images in the first view are eliminated from the generated images in the second view and a prototypical image of same digit is reconstructed by feeding a sample from that digit class to the network. This observation, which is also reported in Wang et al. (2016) for variational CCA (VCCA) model, can be justified by the fact that the 2nd view only contains the class information of the 1st view but not its style and the rotation so the trained autoencoder of the second view (AE2) will ignore the style information of the 1st view. More generated samples from different experimental setup can be found in Appendix A.1.

4 Conclusion and Discussion

In this work, a new deep generative multi-view model is proposed that extends the linear generative interpretation of classical CCA to a nonlinear deep architecture. The proposed deep multi-view network provides a model for inferring the hidden representation underlying both views that subsequently provides better class separation and also reconstruction. Furthermore, training of the model parameters enjoys the stochastic optimization algorithms that provide fast and efficient learning. This deep network can generate samples in the input space, so it can be employed to reconstruct one view based on available primary view at the test time. In addition to its denoising capability, this method also showed the potential to suppress more complex forms of distortion, such as random rotation, from the signal. While CCA based methods achieve good discrimination performance at the expense of sacrificing the reconstruction error, the proposed method offers both class separation and sample generation in a more flexible way.