A Logic of Knowledge and Belief Based on Abstract Arguments

Abstract

We introduce a logic of knowledge and belief in a framework in which belief has a standard KD45 characterization and knowledge undergoes the classical tripartite analysis that knowledge is justified true belief, which has a natural link to the studies of logics of evidence and justification. The characterization of knowledge is based on a flexible model that avoids unwanted properties concerned with the problem of logical omniscience. We axiomatize the logic, prove its soundness and completeness, and then extend the logic to a multi-agent setting. We also compare our framework with existing logics of knowledge and belief.

Funding support by the National Social Science Foundation of China (Grant No. 16CZX048, 18ZDA290).

1 Introduction

Modern studies in epistemic logic and doxastic logic was initiated in [26, 46] and later examined extensively in [20, 33]. Most variants of epistemic and doxastic logics do not mix the two notions. Although there are traditions characterizing both knowledge and belief in one framework (say, [29, 38]), this has received far less attention compared with the efforts made in either side.

For the literature on the logics of both knowledge and belief, and in particular of the relationship between them, there are various approaches that can largely be classified into two categories: those treating both knowledge and belief as primitive concepts, and those where knowledge or belief is a derived concept. We will look more into this in Sect. 5, but just to mention here approaches based on the famous tripartite definition of knowledge dating back to Plato, that knowledge is “justified true belief” (though Gettier [23] argues this is insufficient), which falls into the second category (see, e.g., [32] for an implementation in logic). Our work lies in this category as well.

We study knowledge and belief in the field of modal logic. We interpret belief using a primitive KD45 relation (a binary relation that is serial, transitive and Euclidean), and interpret knowledge as a true belief which has an appropriate argument, in the sense that all of the basic facts in the argument are beliefs. This clearly relates to the work on logical approaches in the justification of knowledge [10, 40], in particular, the fruitful direction of justification logic [3, 4, 21], which will be discussed in Sect. 5.

The application of justification logic in the discipline of epistemic logic [6, 7] connects to the problem of logical omniscience. In normal modal systems, all logical validities are necessarily true, since the technical characterization in a normal epistemic logic makes it true that the modal box operator is closed under logical consequence. This becomes a problem when the modal box is used to express knowing and believing in epistemic and doxastic logics. Classical modal systems, such as those between S4 and S5 which are typically used to characterize knowledge and those like KD45 and K45 for belief, all have the problem of logical omniscience. This problem has been recognized already in [26, p. 31], and we refer to [36, 37] for more details. One of the main solutions to this problem was to view knowledge or belief defined in this way to be implicit or potential (or more generally, some concept that is not knowledge or belief, but closely related), that one can only obtain in an ideal case, such as having an extreme power of reasoning. Only when the one is aware of the implicit knowledge or belief, it becomes explicit. This tradition has attracted a lot of attention since the seminal work on the logic of (un)awareness [19].

There have been solutions to the problem of logical omniscience without using the notion of awareness, since very early [16, 27] to very new attempts [11, 18]. For example, [45] introduces a logic of knowledge that does not have the problem by means of treating “knowing p” requiring the truth of p and the truth of its “epistemic counterparts”. This has a close relationship to our model, and will be discussed in Sect. 5. Our framework avoids the problem of logical omniscience for knowledge, due to a similar style of construction.

The paper is presented in this way. We first introduce a logic of knowledge and belief called LKB in the next section. An axiomatization of LKB is introduced in Sect. 3, and we show its soundness and completeness there. In Sect. 4 we extend LKB to characterize multiple agents. We discussed related work in Sect. 5 and conclude in Sect. 6.

2 The Logic LKB

In this section we introduce a logic LKB for reasoning about knowledge and belief in a framework based on abstract justification. We first introduce the language of LKB, called $\mathcal {L}$ here. We assume a countably infinite set P of propositional variables.

Definition 1 (languages)

The language $\mathcal {L}$ for LKB is given by the following grammar rule:

$$\begin{aligned} \varphi \;{:}{:}\!= p \mid \lnot \varphi \mid (\varphi \wedge \varphi ) \mid B \varphi \mid K \varphi , \end{aligned}$$

where $p \in P$. Moreover, let $\mathcal {PL}$ be the language of propositional logic, i.e., the sublanguage of $\mathcal {L}$ without the operators B and K.

$B \varphi$ and $K \varphi$ are read as “the agent believes $\varphi$” and “the agent knows $\varphi$”, respectively. For simplicity, here we focus on a single-agent system. We shall study a multi-agent extension in Sect. 4. Other propositional connectives are defined by usual abbreviations.

Now we introduce the formal models for LKB.

Definition 2 (models)

A model is a quadruple $M = ( W, R, S, V )$ such that:

• W is a non-empty set of (possible) worlds (or states),

• $R \subseteq W \times W$ is a binary relation that is serial, transitive and Euclidean,

• $S:W \rightarrow \wp (\wp (\wp (W)))$ is an argumentation function, and

• $V: P \rightarrow \wp (W)$ is a valuation that assigns every propositional variable a set of possible worlds.

As usual, M, together with a state w of it, forms a pointed model (M, w).

In the above definition, it is clear that (W, R, V) forms a standard Kripke model, more precisely, a KD45 model, as the relation R is serial, transitive and Euclidean. This follows the classical way of modeling belief [20, 33]. What deserves extra explanation is the argumentation function S, which maps a state to a set of sets of sets of states. This has a flavor of neighborhood semantics [15]. Intuitively, a set of states will be used to stand for the states where a formula is true. A set of formulas is understood as a argument (or proof). Hence S will be used in an interpretation to link a state to a set of arguments, which will play an important role in the interpretation of knowledge.

Let us first introduce the formal semantics.

Definition 3 (satisfaction)

Given a model $M = (W, R, S, V)$ and a world $w \in W$, that a formula $\alpha$ is satisfied (or true) in the pointed model (M, w) (notation: $M,w\models \alpha$) is inductively defined as follows:

$$\begin{array}{lll} M,w \models p &{} \text { iff } &{} w \in V(p) \\ M,w \models \lnot \varphi &{} \text { iff } &{} \text {not}\ M,w \models \varphi \\ M,w \models (\varphi \wedge \psi ) &{} \text { iff} &{} M,w \models \varphi \text { and } M,w \models \psi \\ M,w \models B \varphi &{} \text { iff } &{} \text {for all }u\in W\text {, if } wRu \text { then } M,u \models \varphi \\ M,w \models K \varphi &{} \text { iff } &{} M,w \models \varphi \text { and there exists }X \in S(w) \text { such that: }[\![\varphi ]\!]_{M} \in X \\ &{}&{} \text {and for all }\psi \in \mathcal {PL} \cup \{\varphi \}\text { , if }[\![\psi ]\!]_{M} \in X \text { then } M,w \models B \psi \\ \end{array}$$

where ${[\![\varphi ]\!]}_{M} = \{ x \in W \mid M,x \models \varphi \}$ denotes the truth set of $\varphi$ in M (similarly for the truth set of $\psi$). We omit the subscript M when it is clear from the context.

A formula $\varphi$ is called valid, denoted $\models \varphi$, if for all pointed models (M, w), $M,w \models \varphi$; otherwise it is called invalid. For any set $\varGamma$ of formulas, we say $\varphi$ is a semantic consequence of $\varGamma$, denoted $\varGamma \models \varphi$, if every pointed model (M, w) that satisfies all formulas of $\varGamma$ also satisfies $\varphi$.

The interpretation of $K\varphi$ follows the tripartite definition of knowledge, that knowledge is “justified true belief”, as it can be easily observed from the interpretation that the truth of $K\varphi$ implies the truth of $\varphi$ and $B\varphi$, and that there is an argument for $\varphi$.

More precisely, $K\varphi$ is true, if $\varphi$ is true and there is an appropriate argument of it, in the sense that all propositional formulas following that argument, together with $\varphi$ itself, must be believed to be true. In short, an argument comprises the truth sets of its consequences, and an appropriate argument is one such that the consequences are beliefs. A technical issue here is that we could not enforce the belief of all formulas in an argument, or otherwise the inductive definition contains a vicious circle. A typical solution is to consider only simpler formulas (say, according to modal depths), but to make it simple in this paper we consider only propositional formulas and the relevant formula $\varphi$. This does get an intuitive explanation: beliefs and disbeliefs are not so important for an argument compared to basic facts. We give an example below to make the above clearer.

Example 1

Consider an agent who believes that the number 47 is a prime and all her argument for this is that 47 is not divisible by 7. We may all agree that the agent does not know that 47 is a prime since the composite 8 is also not divisible by 7 and the agent’s belief happens to be true.

Let p denote the proposition “47 is a prime” and q “8 is a prime”, respectively. In the above setting, we see that the agent proposes an argument/reason for p, i.e., every number not divisible by 7 is a prime. In addition to p, the argument leads to other consequences including q. In the formal semantics the argument is represented by some $X\in S(w)$ which comprises the truth sets of its consequences (i.e., the truth sets of p and q).¹

This scenario can be modeled in our framework by a model $M = (W, R, S, V)$ with $W = \{w\}$, $R = \{(w,w)\}$, $S(w) = \{\{\{w\}, \emptyset \}\}$, $V (p) = \{w\}$ and $V (q) = \emptyset$. Note that S(w) here consists of a unique argument, i.e., $X = \{{[\![p]\!]}, {[\![q]\!]}\} = \{\{w\},\emptyset \}$. The frame (W, R) on which M is based is typically represented by the following diagram:

It is not hard to verify that $M,w \models B p$ and $M,w\models p$. Now one can see that $M,w \not \models Kp$: the two consequences of the unique argument X, i.e., p and q, are not all beliefs, for $M,w\not \models B q$.

Two immediate notes are:

• 1. We have chosen to model arguments in a semantic way, i.e., truth sets of consequences are used in the interpretation of arguments. We could have used a syntactical method to interpret an argument as a set of formulas (consequences of the argument). A benefit of the latter is to give us a weaker logic that lacks the rule of the replacements of equivalents. We on the other hand tend to admit this rule (see Proposition 1).

• 2. The interpretation of the knowledge operator includes an $\exists \forall$ type of identification of the appropriate arguments, which may lead to undecidability. A natural constraint can be enforced on the argumentation function S so that there is only a finite number of possible arguments in each state. For simplicity we do not carry out the constraint in this paper.

We list some (in)validities of the logic regarding the characterization of knowledge, including those for characterizing that knowledge is true belief.

Proposition 1 (LKB knowledge)

The following properties hold for all formulas $\varphi$ and $\psi$:

• 1. (verity) $\models K \varphi \rightarrow \varphi$

• 2. (being belief) $\models K \varphi \rightarrow B \varphi$

• 3. (replacement of equivalents) if $\models \varphi \leftrightarrow \psi$ then $\models K \varphi \leftrightarrow K \psi$

The following hold for some formulas $\varphi$ and $\psi$:

• 1. (lack of distribution over implication) $\not \models K(\varphi \rightarrow \psi )\rightarrow (K\varphi \rightarrow K\psi )$

• 2. (lack of positive introspection) $\not \models K\varphi \rightarrow KK\varphi$

• 3. (lack of negative introspection) $\not \models \lnot K\varphi \rightarrow K\lnot K\varphi$

• 4. (lack of generalization) Even if $\models \varphi$, it is not necessarily $\models K\varphi$

• 5. Even if $\models \varphi \rightarrow \psi$, it is not necessarily $\models K\varphi \rightarrow K\psi$.

Proof

The first two clauses can be seen easily from the definitions.

• 3. Assume $\models \varphi \leftrightarrow \psi$. Let $M = (W, R, S, V)$ be a model and $w \in W$. We need to show that $M, w \models K \varphi \leftrightarrow K \psi$, namely $M, w \models K \varphi$ if and only if $M, w \models K \psi$. Without loss of generality, suppose $M,w \models K \varphi$, and it suffices to show that $M,w\models K\psi$. By definition $M,w \models \varphi$ and there is an appropriate argument X for $\varphi$, in the sense that $X \in S(w)$ and $[\![\varphi ]\!] \in X$ and $\forall \chi \in \mathcal {PL} \cup \{\varphi \} : [\![\chi ]\!] \in X \Rightarrow M,w \models B \chi$. By the assumption we have $[\![ \varphi ]\!] = [\![ \psi ]\!]$. Moreover, $\models B\varphi \leftrightarrow B\psi$ (B is a standard KD45 modal operator). Therefore X is also appropriate for $\psi$. This shows $M,w\models K\psi$, and thus $M, w \models K \varphi \leftrightarrow K \psi$.

• 4. We give a countermodel. Consider the model $M_1=(W_1,R_1,S_1,V_1)$ such that $W_1=\{w,u,v \}$, $R_1=\{(w,w),(u,u),(v,v)\}$, with $(W_1, R_1)$ illustrated below:

  

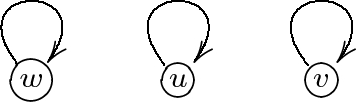
  and $V_1(p)=\{w\}$, $V_1(q)=\{w,v\}$, $S_1(w) = \{ \{\{w,u,v\}\}, \{\{w\}\} \}$ and $S_1(u) = S_1(v) = \emptyset$.

We have $M_1, w \models K(p \rightarrow q)$, because (1) $M_1,w \models p \rightarrow q$ and (2) $\{\{w,u,v\}\}$ is an appropriate argument since $[\![ p \rightarrow q ]\!]_{M_1} = \{w, u, v\} \in \{\{w,u,v\}\}$ and $M_1, w\models B\psi$ for any $\psi \in \mathcal {PL} \cup \{(p\rightarrow q)\}$ (for $\{x\in W_1 \mid wRx\}\subseteq \{w,u,v\}$). Similarly, we have $M_1, w \models Kp$, but $M_1, w \not \models Kq$. So, $M_1, w \not \models K(p \rightarrow q) \rightarrow (Kp \rightarrow Kq)$.

• 5. consider a countermodel $M_2=\{W_2,R_2,S_2,V_2\}$ with $(W_2,R_2)$ illustrated below:

  

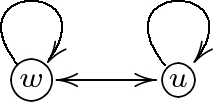
  $S(w) = \{\{\{ w,u \}\}\}$, $S(u) = \emptyset$, and $V(p)=\{w,u\}$. We have $M_2,w \models Kp$ and $M_2, u \not \models Kp$. Thus $M_2, w \not \models BKp$. Since $\models KKp \rightarrow BKp$, $M_2,w \not \models KKp$.

• 6. Consider a countermodel $M_3=\{W_3,R_3,S_3,V_3\}$ with $W_3,R_3$ illustrated below:

  

  $S(w) = \emptyset$ and $V{p}=\emptyset$. We have $M_3,w \models \lnot Kp$ but $M_3,w \not \models K\lnot K p$.

• 7. The model $M_3$ introduced in clause 6 is a suitable countermodel, since

  $\models \lnot (p \wedge \lnot p)$ and $M_3, w \not \models K \lnot (p \wedge \lnot p)$.

• 8. It is clear that $\models p\rightarrow (p\vee q)$. Using the model $M_1$ in clause 4, we can show that $M_1, w \models Kp$. We can also show that $M_1, w \not \models K(p \vee q)$. Therefore $\not \models Kp \rightarrow K(p \vee q)$.

Remark 1

The lack of generalization and distribution over implication for knowledge is what we would like to see, for these are direct causes of the problem of logical omniscience. The reader may instead want to have the principles of positive and negative introspection. Here we presented a logic without these principles mainly for the purpose of pursuing a simple and flexible framework. If one would like to enforce, for example, positive introspection, it can be done by adding the following constraint on the argumentation function S in a model: for all worlds w, for all $X \in S(w)$,

• 1. for all formulas $\varphi$, if ${[\![\varphi ]\!]}\in X$ then ${[\![K\varphi ]\!]}\in X$, and

• 2. for all worlds u such that wRu, if $X \in S(w)$, then $X\in S(u)$.

Remark 2

The semantics we introduced for LKB still has the problem of logical omniscience for the belief operator. We choose to do so mainly to keep the interpretation simple. Our framework extends easily if we adopt a weaker interpretation for the belief operator that does not involve the problem.

Moreover, the weak logic LKB does not enforce some relationships between knowledge and belief either. For example, positive and negative introspection ($B\varphi \rightarrow KB\varphi$, $\lnot B\varphi \rightarrow K\lnot B\varphi$, $K\varphi \rightarrow BK\varphi$ and $\lnot K\varphi \rightarrow B\lnot K\varphi$) are not valid.

3 Axiomatization

In this section we introduce a sound and complete axiomatization of the logic LKB, i.e., LKB, which is given in Fig. 1. The axioms PC, K, D, 4, 5 and the rules N and MP form an axiomatization of the standard KD45 logic of belief. There are a few more axioms and rules for the characterization of knowledge.

The soundness of LKB is not hard to verify. All the axioms are valid, and the rules preserve validity, some of which are shown in Proposition 1. As for the completeness, we prove by the canonical model method, and this will be our main task for the rest of this section.

We refer to a modal logic textbook (say, [12]) for the definitions of proof, deduction and a (maximal) consistent set of formulas in an axiomatization. A well-known Lindenbaum’s Lemma claims that any consistent set of formulas is a subset of a maximal consistent set of formulas, which also holds for LKB.

Fig. 1.

The axiomatization LKB

As a notational convention, the set of all maximal consistent sets of $\mathcal {L}$ formulas is denoted MCS. Moreover, we shall write $[\![\varphi ]\!]^c$ for the set of all maximal consistent sets of formulas containing $\varphi$, i.e., $[\![\varphi ]\!]^c = \{\varGamma \in MCS \mid \varphi \in \varGamma \}$.

We first introduce some properties of maximal consistent sets of formulas.

Lemma 1

Let $\varGamma \in MCS$. The following hold:

• 1. $\varGamma$ is closed under modus ponens, i.e., if $\varphi , (\varphi \rightarrow \psi ) \in \varGamma$, then $\psi \in \varGamma$;

• 2. For all formulas $\varphi$, either $\varphi \in \varGamma$ or $\lnot \varphi \in \varGamma$, but not both;

• 3. $[\![\varphi ]\!]^c = [\![\psi ]\!]^c$ if and only if $\varphi \leftrightarrow \psi$ is a LKB theorem.

Proof

The first two clauses can be shown in the same way as in the literature. Now for the third:

From left to right. Suppose $\nvdash _\mathbf{LKB } \varphi \leftrightarrow \psi$, then $\{\varphi , \lnot \psi \}$ or $\{\lnot \varphi , \psi \}$ is consistent. Without loss of generality, we consider the first case, i.e., $\{\varphi , \lnot \psi \}$ is consistent. Then there is $\varDelta \in MCS$ such that $\{\varphi , \lnot \psi \}\subseteq \varDelta$. By the second clause of this lemma, $\psi \notin \varDelta$, which implies that $[\![\varphi ]\!]^c \ne [\![\psi ]\!]^c$, as is to be shown.

From right to left. Suppose $[\![\varphi ]\!]^c\ne [\![\psi ]\!]^c$ and $\vdash _\mathbf{LKB } \varphi \leftrightarrow \psi$. Without loss of generality, consider the case when there exists $\varDelta \in MCS$ such that $\varphi \in \varDelta$ and $\psi \notin \varDelta$. It follows that $\nvdash _\mathbf{LKB } \varphi \leftrightarrow \psi$, for otherwise there is a violation of the first and second clauses of this lemma.

Definition 4 (canonical model)

The canonical model for LKB is the structure $M^c = (W^c, R^c, S^c, V^c)$ where:

• $W^c=MCS$, i.e., the set of all maximal consistent sets of formulas;

• $R^c$ is binary relation on $W^c$ defined by: $(w,u) \in R^c$ iff for all formula $\varphi$, if $B \varphi \in w$ then $\varphi \in u$;

• $S^c: W^c \rightarrow \wp (\wp (\wp (W^c)))$ is such that $S^c(w)=\{ \{[\![\varphi ]\!]^c\} \mid K\varphi \in w\}$;

• $V^c$ is the valuation defined by: $V^c (p) = {[\![p]\!]}^c$ for all $p\in P$.

It is easy to see that $M^c=(W^c, R^c, V^c)$ forms the canonical model for the standard KD45 logic. Since LKB includes an axiomatization of KD45 as a subsystem, we can use the classical method to show that $R^c$ is serial, transitive and Euclidean (cf., say, [12]). Moreover, $S^c$ matches the type of an argumentation function. It is not hard to verify that the canonical model is a model of LKB.

Lemma 2 (truth)

For any formula $\varphi \in \mathcal {L}$ and any $w\in MCS$:

$$\begin{aligned} \mathcal {M}^c, w \models \varphi \quad \text {iff}\quad \varphi \in w \end{aligned}$$

Proof

First of all, we can define the modal degree of any formula $\varphi \in \mathcal {L}$, notation $d(\varphi )$, as follows:

$$\begin{array}{rcl} d(p) &{}=&{} 0 \\ d(\lnot \varphi ) &{}=&{} d(\varphi ) \\ d((\varphi \wedge \psi )) &{}=&{} \max (d(\varphi ), d(\psi )) \\ d(B \varphi ) &{}=&{} d(\varphi ) + 1 \\ d(K \varphi ) &{}=&{} d(\varphi ) + 1. \end{array}$$

Our proof is carried out by nested induction on $d(\varphi )$ and within that on the structure of $\varphi$. The case $d(\varphi ) = 0$ is trivial. Suppose for every $\varphi$ such that $d(\varphi ) \le n$: $\mathcal {M}^c, w \models \varphi \Leftrightarrow \varphi \in w$. We are going to show that the same holds for all $\varphi$ such that $d(\varphi ) \le n+1$. The only interesting case is the inductive step for $K \varphi$:

From left to right. Suppose $K \varphi \notin w$. We claim that $\{ [\![\varphi ]\!]^c \} \notin S^c(w)$. Suppose not, there must be a $\psi$ such that $K\psi \in w$ and $[\![ \psi ]\!]^c = [\![ \varphi ]\!]^c$. This implies that $\vdash _\mathbf{LKB } \varphi \leftrightarrow \psi$ by Lemma 1(3). Therefore $\vdash _\mathbf{LKB } K\varphi \leftrightarrow K\psi$ by rule the RE. But $K\varphi \notin w$, this contradicts the fact that w is closed under modus ponens. Thus $\{ [\![ \varphi ]\!]^c \} \notin S^c(w)$. Since $d(\varphi ) < d(K \varphi )$, by the induction hypothesis, $[\![ \varphi ]\!] = [\![ \varphi ]\!]^c$, therefore $\{ [\![ \varphi ]\!] \} \notin S^c(w)$, and so $\mathcal {M}^c, w \nvDash K\varphi$.

From right to left. We need to show that: (1) $\mathcal {M}^c,w \models \varphi$ and (2) there is X in $S^c (w)$ such that $[\![ \varphi ]\!] \in X$ and $\forall \psi \in \mathcal {PL} \cup \{\varphi \} : [\![ \psi ]\!] \in X \Rightarrow \mathcal {M}^c, w \models B \psi$. For (1), from $\vdash K\varphi \rightarrow \varphi$ it follows that $\varphi \in w$. Since $d(\varphi ) < d(K \varphi )$, $\mathcal {M}^c,w \models \varphi$ by the induction hypothesis. For (2), since $K\varphi \in w$, $\{ [\![\varphi ]\!]^c \} \in S^c(w)$. We claim that $\{ [\![\varphi ]\!]^c \}$ is the suitable X. Firstly, by the induction hypothesis, $[\![ \varphi ]\!] = [\![\varphi ]\!]^c$, so $[\![ \varphi ]\!] \in \{ [\![\varphi ]\!]^c \}$. Secondly, for each $\psi \in \mathcal {PL} \cup \{\varphi \}$, $[\![ \psi ]\!] = [\![\psi ]\!]^c$ by the induction hypothesis. If $[\![ \psi ]\!] \in \{ [\![\varphi ]\!]^c \}$, it must be that $[\![\psi ]\!]^c = {[\![\psi ]\!]} = [\![\varphi ]\!]^c$. By Lemma 1(3), it follows that $\vdash _\mathbf{LKB } \varphi \leftrightarrow \psi$. Since $K \varphi \in w$ and $\vdash _\mathbf{LKB } K\varphi \rightarrow B\varphi$, $B\varphi \in w$. Therefore $B\psi \in w$. So it suffices to show that $\mathcal {M}^c, w \models B\psi$, which is a standard result for a normal modal logic. Therefore, $\mathcal {M}^c, w \models K\varphi$.

With the above lemma, a standard argument leads us to the following theorem.

Theorem 1 (soundness and completeness)

For any formula $\varphi$ and any set $\varGamma$ of formulas, $\varGamma \vdash _\mathbf{LKB } \varphi$ if and only if $\varGamma \models \varphi$.

4 Extending to Multiple Agents

In this section we study the extension of LKB to allow multiple agents. Let A be a finite set of agents. It is natural to introduce the following multi-agent language:

Definition 5

(language $\mathcal {L}^m$). The language $\mathcal {L}^m$ is given as follows:

$$\begin{aligned} \varphi \;{:}{:}\!= p \mid \lnot \varphi \mid (\varphi \wedge \varphi ) \mid B_a \varphi \mid K_a\varphi , \end{aligned}$$

where $p\in P$ is a propositional variable and $a\in A$.

To make a difference, we shall call the multi-agent extension of LKB the logic LKB$^m$. Definitions of the semantics can also be extended naturally from the single-agent case.

Definition 6

(LKB$^m$ models). An LKB$^m$ model (or simply, a model, when there is no confusion in the context) is a tuple $M = ( W, R, S, V )$ such that:

• W is a non-empty set of worlds;

• $R: A\rightarrow \wp (W \times W)$ assigns every agent a serial, transitive and Euclidean relation on W; for convenience, we write $R_a$ for R(a) for any $a\in A$;

• $S:W \rightarrow \wp (\wp (\wp (W)))$ is an argumentation function; and

• $V: P \rightarrow \wp (W)$ is a valuation that assigns every propositional variable a set of possible worlds.

As usual, M, together with a state w of it, forms a pointed model (M, w).

Definition 7

(LKB$^m$ satisfaction). Given an LKB$^m$ model $M = (W, R, S, V)$ and a world $w \in W$, that a formula $\alpha$ is satisfied in the pointed model (M, w) (notation: $M,w\models \alpha$) is defined as follows:

$$\begin{array}{lll} M,w \models p &{} \text { iff } &{} w \in V(p) \\ M,w \models \lnot \varphi &{} \text { iff } &{} \text {not}\ M,w \models \varphi \\ M,w \models (\varphi \wedge \psi ) &{} \text { iff} &{} M,w \models \varphi \text { and } M,w \models \psi \\ M,w \models B_a \varphi &{} \text { iff } &{} \text {for all } u\in W \text {, if }wR_au \text { then }M,u \models \varphi \\ M,w \models K_a \varphi &{} \text { iff } &{} M,w \models \varphi \text { and there exists }X \in S(w) \text { such that: }{[\![\varphi ]\!]} \in X \\ &{}&{} \text {and for all } \psi \in \mathcal {PL} \cup \{\varphi \} \text { , if } {[\![\psi ]\!]} \in X \text { then } M,w \models B_a \psi \text { .}\\ \end{array}$$

Conventions are made as in Definition 3.

The extension goes smoothly by equipping the knowledge and belief operators, together with their semantic counterparts, for all the agents. In fact, we can carry out in the same way to reach an axiomatization for the multi-agent logic. The axiomatization LKBm given in Fig. 2 is a sound and complete axiomatization of the logic LKB$^m$.

Fig. 2.

The axiomatization LKBm

Theorem 2

(LKBm soundness and completeness). For any $\mathcal {L}^m$ formula $\varphi$ and any set $\varGamma$ of $\mathcal {L}^m$ formulas, $\varGamma \vdash _\mathbf{LKBm } \varphi$ if and only if $\varGamma \models \varphi$.

Proof

The theorem can be shown in very much the same way as for LKB.

Remark 3 (global vs. local argumentation functions)

In the definition of a model for the multi-agent logic, we kept the argumentation function S the same as in a model for the single-agent logic. One may argue that we also have a reason to introduce an argumentation function for each agent:

$$\begin{aligned} S:A\rightarrow W\rightarrow \wp (\wp (\wp (W))). \end{aligned}$$

Both options have an explanation.

For what we defined above, for an agent to achieve knowledge, an argument must be global, in the sense that it works as well for all other agents. What this represents is more like a mathematical proof which does not easily get refused by others. Yet a local argumentation function allows an agent to have its own argument for something, even though others may disagree. This is perhaps more like an argument in daily life.

Our framework allows the flexibility of making a distinction between global and local argumentation, which we expect a good impact on the approaches to reasoning about different levels of knowledge.

That said, we do not introduce a logic for knowledge based on local argumentation. One of the main difficulties is to understand what higher-order knowledge means in this case. For example, a formula $K_a K_b \varphi$ requires that agent a has an argument for $K_b\varphi$, which in turn requires that agent b has an argument for $\varphi$. But do we assume there is information adopt in common by both agents, say some simple tautologies? How can these be characterized? We leave such questions for future work.

5 Related Work

In this section we compare our work with existing literature. As already mentioned in the introduction, there have been a great amount of work in the area of logics of knowledge, belief and their relationships, which connects to the research on the concepts of proof, evidence and justification, and the logics of them.

Of special relevance is Williamson’s work on knowledge and evidence [43, 44]. In a later development [45], he introduces a logic of knowledge which is capable of solving the problem of logical omniscience, based on the idea that “knowing p requires safety from the falsity of p and of its epistemic counterparts.” Formally, a model is a structure (W, R, V), where R consists of triples $\langle w, w^{*}, f \rangle$ in which w and $w^{*}$ are worlds, and f is a function mapping a formula in w to a counterpart formula of it in $w^{*}$ which may endure extra constraints. Knowledge is interpreted in a way that:

$$\begin{aligned} w \models K\varphi \text { iff for all } \langle w, w^{*}, f \rangle \in R, w^{*} \models f(\varphi ). \end{aligned}$$

By an epistemic counterpart, he refers to a belief that is alike in various epistemically relevant respects, such as how they are formed, which circumstance they are formed in, etc. Our framework, though technically quite different, are conceptually close to this type of modeling.

Justification logics [3, 4, 21] are a family of modal logics with the modalities replaced with justification terms, inspired by the logic of proofs [1, 2] where a justification of a formula is largely a deductive proof of it, or more precisely, a “proof polynomial” that encodes a proof. Fitting [21] adapted Artemov’s framework using a semantic solution that can be traced back to [34]. An evidence function $\mathcal {E}$ is added to a standard Kripke model, making a quadruple $(W,R,\mathcal {E},V)$. The function $\mathcal {E}$ assigns an evidence set of formulas to each proof polynomial t at each world w that consists of everything t justifies at w. The interpretation looks as follows:

$$\begin{aligned} M,w \models t:\varphi \quad \text {iff}\quad \varphi \in \mathcal {E}(w,t) \text { and for all } u, \text { if } wRu \text { then } M,u \models \varphi \text {.} \end{aligned}$$

Along the line of [21], Artemov and Nogina [6, 7] introduced justification into the framework of epistemic logic. A model there is a quintuple $(W,R,R^e,\mathcal {E},V)$ where (W, R, V) is a standard Kripke model with the binary relation R used for interpreting potential knowledge in the standard way. $\mathcal {E}$ is an evidence function as in [21], together with an extra relation $R^e$, the justification of a formula $\varphi$ is interpreted as follows:

$$\begin{aligned} w \models t:\varphi \quad \text {iff}\quad \varphi \in \mathcal {E}(w,t) \text { and for all }u \text {, if } w R^e u \text { then }M,u\models \varphi \end{aligned}$$

This is used to model a type of explicit knowledge. We need to point out here that the concept of justification has been brought into the field of epistemic logic already in [10].

Although epistemic justifications are mainly used to characterize only the notion of knowledge, the differences in the interpretation of implicit and explicit knowledge has a technical similarity to that of belief and knowledge in this paper. This similarity is even more obvious when implicit/potential knowledge is regarded as belief.

Now we move on the literature on logics with both knowledge and belief, in particular the relationship between them. These can be classified into two categories:

• (i) those taking both knowledge and belief as primitive and focus on the interaction properties between the two notions;

• (ii) those in which knowledge or belief is not a primitive, but a derived notion from the other or some notions different from the two.

In the first category, various axioms that hold for knowledge and/or belief have been discussed already in [26]. The JTB definition of knowledge (“justified true belief”) has been implemented in epistemic logic in [32]. In [29], a combined system of knowledge and belief was introduced based on Kripke semantics (the notions of common knowledge and belief are also studied there). In their models, two accessibility relations are used to represent epistemic uncertainty and doxastic uncertainty, respectively. The logic in [29] has some interesting validities characterizing the relationship between knowledge and belief. For example, for all agents a and formulas $\varphi$, the following are valid:

And $B_a\varphi \rightarrow B_a K_a\varphi$ is invalid there. Some of these principles, together with others (such that $B\varphi \leftrightarrow \lnot K\lnot K \varphi$), were examined in [38] and followed by [28]. Also based on [38], recently [8, 9] introduced a logic of knowledge and belief using a topological style of semantics. Different logics were introduced for reasoning about knowledge and belief in a combined way in [41, 42]. More sophisticated constructions are used there, which goes further away from the topic here. In [30], formulas of the forms $K\varphi$, $C^{\varphi } \psi$ and $B^{\varphi } \psi$ are taken to be primitive, which are interpreted as “the agent knows $\varphi$”, “the agent is certain of $\psi$ under the evidence $\varphi$” and “the agent believes $\psi$ under the evidence $\varphi$”, respectively. Then $B\varphi$ (“$\varphi$ is believed”) is defined as $B^{\top } \varphi$.

In the second category, besides the well-known JTB analysis of knowledge using belief and many work in this strand (see, e.g., [31, 39, 44]), there are also approaches defining belief out of knowledge. For example, [22] defines belief in terms of knowledge and plausibility: an agent believes $\varphi$ if he knows that $\varphi$ is more plausible than $\lnot \varphi$. [13] defines belief in a similar fashion. It’s worth noting that, though from a very different motivation, their models have a flavor of neighborhood semantics which is similar to ours (we use a neighborhood function that selects the truth set of not mere a single formula). In [35], Moses and Shoham suggest that belief be viewed as defeasible knowledge. In particular, they come up with a definition of belief to be knowledge-relative-to-assumptions, and make a connection to the notion of nonmonotonicity.

6 Conclusion

In this paper we introduced a logic of knowledge and belief in which we provided with an alternative implementation of the tripartite analysis of knowledge (knowledge = justified true belief). Our work has a conceptual link to the research on justification logic, bringing a formal notion of justification into the definition of knowledge, yet different in that justification is used in forming knowledge out of true belief, instead of forming explicit knowledge out of implicit knowledge. Our model is a combination of standard KD45 model for belief with an argumentation function for knowledge that is of a flavor of the neighborhood semantics.

We introduced a sound and completeness axiomatization for our logic, and extended it to model multiple agents. In the multi-agent setting, we had two options, to model global or local arguments. We studied a logic of global arguments, and leave that of local ones for future work. As the reader may observe, our logic characterizes a weak notion of knowledge, without the problem of logical omniscience, but also lacking properties such as positive and negative introspection ($K\varphi \rightarrow KK\varphi$ and $\lnot K\varphi \rightarrow K\lnot K\varphi$) as well as the principle for the interaction between belief and knowledge (e.g. $B\varphi \rightarrow KB\varphi$). The model we propose is capable of modeling these principles by imposing further constraints (see Remark 1 for an example). We leave this also for future work.

One of the requirements of a formula to be knowledge is to have an argument for it. Occasionally we used other words, such as “proof”, “justification”, “evidence”, etc., in place of “argument”, though we do not in fact impose any structures of the argument – it is simply treated as a set of formulas. This is one of the reasons we call it “abstract argument” as in the title. Our work, however, does not have a direct link to the study of formal argumentation, in particular that of abstract argumentation framework [17]. We are interested in achieving a connection to that, perhaps by means of bringing an argumentation framework into the interpretation of knowledge, so that only the accepted ones are counted as arguments.

Also interesting to look into are the group notions of knowledge and belief. It is a natural task to study the extensions of our logic by incorporating common and distributed knowledge/belief. We are interested in comparing these with the logic of knowledge and belief presented in [29], and also extensions of justification logic with common knowledge [5, 14] and distributed knowledge [24, 25]. Other interesting tasks include modeling dynamics in our framework.