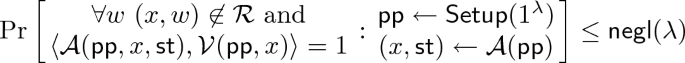Transparent SNARKs from DARK Compilers

Abstract

We construct a new polynomial commitment scheme for univariate and multivariate polynomials over finite fields, with logarithmic size evaluation proofs and verification time, measured in the number of coefficients of the polynomial. The underlying technique is a Diophantine Argument of Knowledge (DARK), leveraging integer representations of polynomials and groups of unknown order. Security is shown from the strong RSA and the adaptive root assumptions. Moreover, the scheme does not require a trusted setup if instantiated with class groups. We apply this new cryptographic compiler to a restricted class of algebraic linear IOPs, which we call Polynomial IOPs, to obtain doubly-efficient public-coin interactive arguments of knowledge for any NP relation with succinct communication. With linear preprocessing, the online verifier’s work is logarithmic in the circuit complexity of the relation.

There are many existing examples of Polynomial IOPs (PIOPs) dating back to the first PCP (BFLS, STOC’91). We present a generic compilation of any PIOP using our DARK polynomial commitment scheme. In particular, compiling the PIOP from PLONK (GWC, ePrint’19), an improvement on Sonic (MBKM, CCS’19), yields a public-coin interactive argument with quasi-linear preprocessing, quasi-linear (online) prover time, logarithmic communication, and logarithmic (online) verification time in the circuit size. Applying Fiat-Shamir results in a SNARK, which we call .

Supersonic is also concretely efficient with 10 KB proofs and under 100 ms verification time for circuits with 1 million gates (estimated for 120-bit security). Most importantly, this SNARK is transparent: it does not require a trusted setup. We obtain zk-SNARKs by applying a hiding variant of our polynomial commitment scheme with zero-knowledge evaluations. Supersonic is the first complete zk-SNARK system that has both a practical prover time as well as asymptotically logarithmic proof size and verification time. The full version of the paper is available online [19].

1 Introduction

In recent years, there has been a surge of industry interest in verifiable outsourced computation [52] (such as trustless cloud computing) as well as zero-knowledge proofs. In particular, blockchains use efficient zero-knowledge proofs as a solution for balancing privacy and publicly-verifiable integrity: examples include anonymous transactions in ZCash [5, 37] and verifying Ethereum smart contracts over private inputs [27]. In these applications, zero-knowledge proofs are posted to the blockchain ledger as a part of transactions and nodes must verify many proofs in the span of a short period of time. Therefore, succinctness and fast verification are necessary properties for the deployment of such proof systems. Verifiable computation is also being explored as a scaling solution for blockhain transactions [20], and even as a way to entirely eliminate the need for maintaining historical blockchain data [40].

Following this pragmatic interest, there has also been a surge of research focused on obtaining proof systems with better concrete efficiency characteristics: succinctness (the proof size is sublinear in the original computation length T), non-interactivity (the proof is a single message), prover-scalability (proof generation time scales linearly or quasi-linearly in T), and verifier-scalability (verification time is sublinear in T). Proof systems that achieve all of these properties for general NP statements are called SNARGs (“succinct non-interactive arguments”). The proof is called an argument when it is only sound assuming the prover is computationally bounded, i.e., computationally sound as opposed to statistically sound. Succinct statistically sound proofs are unlikely to exist [32].

Currently, there are numerous constructions that achieve different tradeoffs between proof size, proof time, and verification time, but also under different trust models as well as cryptographic assumptions. Some constructions also achieve better efficiency by relying on a preprocessing model in which a one-time expensive setup procedure is performed in order to generate a compact verification key $\textsf {{VK}}$, which is later used to verify proof instances efficiently. Somewhat unfortunately, the best performing proof systems to date (considering proof size and verification time) require a trusted preprocessing. These are the pairing-based SNARKs extending from GGPR [6, 9, 31, 35, 47], which have been implemented in numerous libraries [6, 16], and even deployed in live systems such as the ZCash [1] cryptocurrency. The trusted setup can be performed via multi-party computation (MPC) by a committee of parties, such that trust in only one of the parties is sufficient. This has been done on two occasions for the ZCash blockchain, involving elaborate “ceremonies” to engender public trust in the process [54].

A proof system is called transparent if it does not involve any trusted setup. Recent progress has yielded transparent proof systems for special types of computations: zk-STARKs [4] generate zero-knowledge proofs of size $O(\log ^2 T)$ for a uniform computation¹, and the GKR protocol produces interactive proofs with communication $O(d \log T)$ for computations expressed as low-depth circuits of total size T and depth d [33]. In both cases, non-interactivity can be achieved in the random oracle model with the Fiat-Shamir heuristic [21, 28]. These transparent proof systems perform significantly worse than SNARKs based on preprocessing. For computations expressed as an arithmetic circuit of 1-million gates, STARKs [4] report a proof size of 600 KB, whereas preprocessing SNARKs achieve 200 bytes [35]. Bulletproofs [13, 18] is a transparent zero-knowledge proof system whose proofs are much smaller than those of STARK, but these proofs have a verification time that scales linearly in the size of the circuit; for an arithmetic circuit of one million gates the verification time is close to 1 min, more than 1,000 times more expensive than verifying a STARK proof for the same computation.

Another thread of research has produced proof systems that remove trust from the circuit preprocessing step, and instead have a universal (trusted) setup: a one-time trusted setup that can be reused for any computation [30, 43, 55]. All of these systems build SNARKs by combining an underlying reduction of circuit satisfiability to probabilistic testing of polynomials (with degree at most linear in the circuit size) together with polynomial commitment schemes. In a polynomial commitment scheme, a prover commits to a $\mu$-variate polynomial f over $\mathbb {F}$ of total degree at most d with a message that is much smaller than sending all the coefficients of f. The prover can later produce a non-interactive argument that $f(z) = y$ for arbitrary $z \in \mathbb {F}^\mu$ and $y \in \mathbb {F}$. The trusted portion of the universal SNARK is entirely confined to the polynomial commitment scheme’s setup. These constructions use variants of the Kate et al. commitment scheme for univariate polynomials [39], which requires a trusted setup.

1.1 Summary of Contributions

Following the observations of the recent universal SNARK constructions [30, 43, 55], SNARKs can be built from polynomial commitment schemes where all the trust is confined to the setup of the commitment scheme. The main technical contribution of our work is thus a new polynomial commitment scheme without trusted setup (i.e., a transparent polynomial commitment scheme), which we can use to construct transparent SNARKs. The observation that transparent polynomial commitments imply transparent SNARKs was also implicit in the recent works that build transparent SNARKs from multi-round classical PCPs, and specifically interactive oracle proofs of proximity (IOPPs) [3]. As a secondary contribution, we present a framework that unifies all existing approaches to constructing SNARKs from polynomial commitments using the language of interactive oracle proofs (IOPs) [7, 45]. We view polynomial commitment schemes as a compiler for Polynomial IOPs, and re-characterize the results of prior works as providing a variety of Polynomial IOPs for NP.

New polynomial commitment scheme. We construct a new polynomial commitment scheme for $\mu$-multivariate polynomials of total degree d with optional zero-knowledge arguments of knowledge for correct evaluation that have $O(\mu \log d)$ size proofs and are verifiable in $O(\mu \log d)$ time. The commitment scheme requires a group of unknown order: two candidate instantiations are RSA groups and class groups of an imaginary quadratic order. Using RSA groups, we can apply the scheme to obtain universal preprocessing SNARKs with constant-size setup parameters, as opposed to the linear-size parameters from previous attempts. Using class groups, we can remove the trusted setup from trusted-setup SNARKs altogether, thereby making them transparent. Our polynomial commitment scheme leverages the power of integer commitments and Diophantine Arguments of Knowledge [42]; accordingly, we classify this tool (and others of its kind) as a DARK proof system.

Polynomial IOP formalism. All SNARK constructions can be viewed as combining an underlying information-theoretic statistically-sound protocol with a “cryptographic compiler” that transforms the underlying protocol into a succinct argument at the cost of computational soundness. We define a Polynomial IOP as a refinement of algebraic linear IOPs [9, 11, 38], where in each round of interaction the prover provides the verifier with oracle access to a multivariate polynomial function of bounded degree. The verifier may then query this oracle to evaluate the polynomial on arbitrary points of its choice. The existing universal and transparent SNARK constructions provide a variety of statistically-sound Polynomial IOPs for circuit satisfiability (or RAM programs, in the case of STARKs); these are then cryptographically compiled using some form of a polynomial commitment, typically using Merkle trees or pairing groups.

The precise definition of Polynomial IOPs as a central and standalone notion raises the question about its exact relation to other IOP notions. We present a univariate Polynomial IOP for extracting an indicated coefficient of a polynomial. Furthermore, we present a univariate Polynomial IOP for proving that the inner product between the coefficient vectors of two polynomials equals a given value. This proof system is of independent interest. Together with an offline pre-processing phase during which the correctness of a multivariate polynomial is ascertained, these two tools enable us to show that any algebraic linear IOP can be realized with a multivariate Polynomial IOP.

Polynomial IOP compiler. We present a generic compilation of any public-coin Polynomial IOP into a doubly-efficient public-coin interactive argument of knowledge using an abstract polynomial commitment scheme. We prove that if the commitment scheme’s evaluation protocol has witness-extended emulation, then the compiled interactive argument has this knowledge property as well. If the commitment scheme is hiding and the evaluation is honest-verifier zero knowledge (HVZK), then the compiled interactive argument is HVZK as well. Finally, public-coin interactive arguments may be cryptographically compiled into SNARKs using the Fiat-Shamir heuristic.

New SNARK without trusted setup. The main practical outcome of this work is a new transparent proof system ($\textsf {{Supersonic}}$) for computations represented as arbitrary arithmetic circuits, obtained by cryptographically compiling the Polynomial IOPs underlying Sonic [43], PLONK [30], and Marlin [22] using the DARK polynomial commitment scheme. $\textsf {{Supersonic}}$ improves the proof size by an order of magnitude over STARKs without compromising on verification time. For one million gates, $\textsf {{Supersonic}}$’s proofs are just 7.8 KB and take around 75 ms to verify. Using the notation $O_\lambda (\cdot )$ to hide multiplicative factors dependent on the security parameter $\lambda$, STARKs have size and verification complexity $O_\lambda (\log ^2 T)$ whereas $\textsf {{Supersonic}}$ has size and verification complexity $O_\lambda (\log T)$. (The additional multiplicative factors dependent on $\lambda$ are actually better for $\textsf {{Supersonic}}$ as well.) As a caveat, while the prover time in $\textsf {{Supersonic}}$ is asymptotically on par with STARKs (i.e., quasilinear in T), the concrete efficiency is much worse due to the use of heavy-weight “crypto operations” over 1200 bit class group elements in contrast to the light-weight FFTs and hash functions in STARKs. Furthermore, $\textsf {{Supersonic}}$ is not quantum-secure due to its reliance on groups of unknown order, whereas STARKs are a candidate quantum-secure SNARK.

1.2 Related Work

Arguments based on hidden order groups. Fujisaki and Okamoto [29] proposed homomorphic integer commitment schemes based on the RSA group. They also provide protocols to prove that a list of committed integers satisfy modular polynomial equations as opening a commitment bit by bit. Damgård and Fujisaki [25] patched the soundness proof of that protocol and were the first to suggest using class groups of an imaginary quadratic order as a candidate group of unknown order. Lipmaa drew the link between zero-knowledge proofs constructed from integer commitment schemes and Diophantine complexity [42], coining the term Diophantine Arguments of Knowledge. Recently, Couteau et al. study protocols derived from integer commitments specifically in the RSA group to reduce the security assumptions needed; in the process they develop proofs for polynomial evaluation modulo a prime $\pi$ that is not initially known to the verifier, in addition to a proof showing that an integer X lies in the range [a, b] by showing that $1+4(X-a)(b-X)$ decomposes as the sum of 3 squares [24].

Pietrzak [44] developed an efficient proof of repeated squaring, i.e., proving that $x^{2^T} = y$ with $O(\log T)$ proof size and verification time in order to build a conceptually simple verifiable delay function [10] based on the RSW time-lock puzzle [46]. Wesolowski [53] improves on this result by proposing a single-round protocol to prove correct repeated squaring in groups of unknown order with a constant size proof. Boneh et al. [12] observe that this protocol generalizes to arbitrary exponents (PoE) and develop a proof of knowledge of an integer exponent (PoKE), as well as a zero-knowledge variant. They use both PoE and PoKE to construct efficient accumulators and vector commitment schemes.

Transparent polynomial commitments. Whaby et al. constructed a transparent polynomial commitment scheme [51] for multilinear polynomials by combining a matrix commitment of Bootle et al. [14] with the inner-product argument of Bünz et al. [18]. For polynomials of degree d it has commitments of size $O(\sqrt{d})$ and evaluation arguments with $O(\sqrt{d})$ communication. Recently, Vlasov and Panarin [50], concurrently with Zhang et al. [56], show how to build a transparent polynomial commitment based on FRI (Fast Reed Solomon IOPP) [3]. The scheme has $O(\lambda )$ size commitments and evaluation arguments with $O(k \cdot \log ^2 d)$ communication for repetition parameter k.

Polynomial IOP formalism. In concurrent work Chiesa et al. [22] introduce an information theoretic framework called algebraic holographic proofs (AHP). They also show that with a polynomial commitment scheme an AHP can be compiled to a preprocessing SNARK. The AHP framework is essentially equivalent to our Polynomial IOP framework. In other concurrent work, Chiesa, Ojha, and Spooner show interesting connections between algebraic holographic proofs and recursive proof composition. In the same work, the authors develop an AHP-based transparent SNARK called Fractal [23].

2 Technical Overview

This technical overview provides an informal description of our key technical contribution: a polynomial commitment scheme with logarithmic evaluation proofs and verification time. The commitment scheme relies on four separate tools.

• 1. Integer encoding of polynomials. Given a univariate polynomial $f(X)\in \mathbb {Z}_p[X]$ the prover first encodes the polynomial as an integer. Interpreting the coefficients of f(X) as integers in² [0, p), define $\hat{f}(X)$ to be the integer polynomial with these coefficients. The prover computes $\hat{f}(q)\in \mathbb {Z}$ for some large integer $q\ge p$. This is an injective map from polynomials with bounded coefficients to integers and is also decodable: the coefficients of f(q) can be recovered from the base-q expansion of $\hat{f}(q)$. For example, suppose that $f(X)=2X^3+3X^2+4X+1 \in \mathbb {Z}_5[X]$ and $q=10$. Then the integer $\hat{f}(10)=2341$ encodes the polynomial f(X) because its coefficients appear in the decimal expansion of $\hat{f}(10)$.

  Note that this encoding is also additively homomorphic, assuming that q is sufficiently large. For example, let $g(X)=4X^3\,+\,1X^2\,+\,3$ such that $\hat{g}(10)=4103$. Then $\hat{f}(10)+\hat{g}(10)=6444=(\hat{g}+\hat{f})(10)$. The more homomorphic operations we want to permit, the larger q needs to be. The encoding additionally permits multiplication by polynomials ($\hat{f}(q)\cdot q^k$ is equal to the encoding of $f(X)\cdot X^k$).

• 2. Succint integer commitments. The integer $x \leftarrow \hat{f}(q)$ encoding a degree d polynomial f(X) lies between $q^d$ and $q^{d+1}$; in other words, its size is $(d+1) \log _2 q$ bits. The prover commits to x using a succinct integer commitment scheme that is additively homomorphic. Specifically, we use exponentiation in a group $\mathbb {G}$ of unknown order: the commitment is the single group element $\mathsf {g}^x$ for a base element $\mathsf {g} \in \mathbb {G}$ specified in the setup. (Note that if the order n of $\mathbb {G}$ is known then this is not an integer commitment; $\mathsf {g}^x$ could be opened to any integer $x' \equiv x \bmod n$.)

• 3. Evaluation protocol. The evaluation protocol is an interactive argument to convince a verifier that $\mathsf {C}$ is an integer commitment to $\hat{f}(q)$ such that $f(z) = y$ at a provided point $z \in \mathbb {Z}_p$. The protocol must be evaluation binding: it should be infeasible for the prover to succeed in arguing that $f(z) = y$ and $f(z) = y'$ for $y \ne y'$. The protocol should also be an argument of knowledge, which informally means that any prover who succeeds at any point x must “know” the coefficients of the committed f. As a warmup, we first describe how a prover can efficiently convince a verifier that $\mathsf {C}$ is a commitment to an integer polynomial of degree at most d with bounded coefficients. Assume for now that $d=2^k-1$. The protocol uses a recursive divide-and-combine strategy. In each step we split f(X) into two degree $d'=\lfloor \frac{d}{2}\rfloor$ polynomials $f_L(X)$ and $f_R(X)$. The left half $f_L(X)$ contains the first $d'+1$ coefficients of f(X) and the right half $f_R(X)$ the second, such that $f(X)=f_L(X)+X^{d'+1}f_R(X)$. The prover now commits to $f_L$ and $f_R$ by computing $\mathsf {C}_L\leftarrow \mathsf {g}^{\hat{f}_L(q)}$ and $\mathsf {C}_R\leftarrow \mathsf {g}^{\hat{f}_R(q)}$. The verifier checks the consistency of these commitments by testing $\mathsf {C}_L\mathsf {C}_R^{q^{d'+1}}=\mathsf {C}$. The verifier then samples random $\alpha \in \mathbb {Z}_p$ and computes $\mathsf {C}'\leftarrow \mathsf {C}_L^{\alpha }\mathsf {C}_R$, which is an integer commitment to $\alpha \hat{f}_L(q) + \hat{f}_R(q)$. The prover and verifier recurse on the statement that $\mathsf {C}'$ is a commitment to a polynomial of degree at most $d'$, thus halving the “size” of the statement. After $\log _2(d+1)$ rounds, the commitment $\mathsf {C}'$ exchanged between prover and verifier is a commitment to a polynomial of degree 0, i.e., to a scalar $c \in \mathbb {Z}_p$. So $\mathsf {C}'$ is of the form $\mathsf {g}^{\hat{c}}$ where $\hat{c}$ is some integer congruent to c modulo p. The prover sends $\hat{c}$ to the verifier directly. The verifier checks that $\mathsf {g}^{\hat{c}} = \mathsf {C}'$ and also that $\hat{c} < q$.³

  To also show that $f(z) = y$ at a provided point z, the prover additionally sends $y_L=f_L(z)\bmod p$ and $y_R=f_R(z)\bmod p$ in each round. The verifier checks consistency with the claim, i.e., that $y_L+z^{d'+1}y_R=y$, and also computes $y' \leftarrow \alpha y_L+y_R\bmod p$ to proceed to the next round. (The recursive claim is that $\mathsf {C}'$ commits to $f'$ such that $f'(z) = y' \bmod p$.) In the final round of recursion, the value of the constant polynomial in z is the constant itself. So in addition to testing $\mathsf {C} = \mathsf {g}^{\hat{c}}$ and $\hat{c} < q$, the verifier also checks that $\hat{c} \equiv y \bmod p$.

• 4. Outsourcing exponentiation for efficiency. The evaluation protocol requires communicating only 2 group elements and 2 field elements per round. However, the verifier needs to check that $\mathsf {C}_L\mathsf {C}_R^{(q^{d'+1})}=\mathsf {C}$, and naïvely performing the exponentiation requires $\varOmega (d \cdot \log q)$ work. To reduce this workload, we employ a recent technique for proofs of exponentiation (PoE) in groups of unknown order due to Wesolowski [53] in which the prover computes this exponentiation and the verifier verifies it in essentially constant time. This outsourcing reduces the total verifier time (i.e., of the entire protocol) to a quantity that is logarithmic in d.

3 Preliminaries

3.1 Assumptions

The cryptographic compilers make extensive use of groups of unknown order, i.e., groups for which the order cannot be computed efficiently. Concretely, we require groups for which two specific hardness assumptions hold. First the Strong RSA Assumption [2] which roughly states that it is hard to take arbitrary roots of random elements. Secondly, the much newer Adaptive Root Assumption [53] which is the dual of the Strong RSA Assumption and states that it is hard to take random roots of arbitrary group elements. Both of these assumptions hold in generic groups of unknown order [12, 26].

The r-strong RSA assumption as presented below is a parameterization on the Strong RSA assumption. For $r=1$, our definition is identical to the standard Strong RSA Assumption. Higher values of r allows the adversary to take certain roots efficiently. For $r=2$, the adversary is efficiently able to take square roots. In class groups of imaginary quadratic order taking square roots is easy. In rth order class groups taking rth roots is easy.

Assumption 1

(r-Strong RSA Assumption). The r-Strong RSA Assumption states that an efficient adversary cannot compute $\ell$th roots for a given random group element, if $\ell$ not a power of r. Specifically, it holds for $\textit{GGen}$ if for any probabilistic polynomial time adversary $\mathcal {A}$:

Assumption 2

(Adaptive Root Assumption). The Adaptive Root Assumption holds for $\textit{GGen}$ if there is no efficient adversary $(\mathcal {A}_0,\mathcal {A}_1)$ that succeeds in the following task. First, $\mathcal {A}_0$ outputs an element $\mathsf {w} \in \mathbb {G}$ and some $\textsf {st}$. Then, a random prime $\ell$ in $\textsf {Primes}(\lambda )$ is chosen and $\mathcal {A}_1(\ell ,\textsf {st})$ outputs $\mathsf {w}^{1/\ell } \in \mathbb {G}$. For all efficient $(\mathcal {A}_0,\mathcal {A}_1)$:

Groups of unknown order. We consider two candidate groups of unknown order. Both have their own upsides and downsides.

RSA Group. In the multiplicative group $\mathbb {Z}_n^*$ of integers modulo a product $n=p\cdot q$ of large primes p and q, computing the order of the group is as hard as factoring n. The Adaptive Root Assumption does not hold for $\mathbb {Z}_n^*$ because $-1 \in \mathbb {Z}_n^*$ can be easily computed and has order two. This can be resolved though by working instead in the quotient group $\mathbb {Z}_n^* / \langle -1\rangle \cong \mathrm {QR}_n$. The downside of using an RSA group, or more precisely, the group of quadratic residues modulo an RSA modulus, is that this modulus cannot be generated in a publicly verifiable way without exposing the order, and thus requires a trusted setup.

Class Group. The class group of an imaginary quadratic order is defined as the quotient group of fractional ideals by principal ideals of an order of a number field $\mathbb {Q}(\sqrt{\varDelta })$, with ideal multiplication. A class group $\mathcal {C}\ell (\varDelta )$ is fully defined by its discriminant $\varDelta$, which needs to satisfy only public constraints such as $\varDelta \equiv 1 \bmod 4$ and $-\varDelta$ must be prime. As a result, $\varDelta$ can be generated from public coins, thus obviating the need for a trusted setup. A group element can be represented by two integers strictly smaller (in absolute value) than $-\varDelta$, which in turn is on the same order of magnitude as RSA group elements for a similar security level. We refer the reader to Buchmann and Hamdy’s survey [17] and Straka’s accessible blog post [49] for more details.

Working in $\mathcal {C}\ell (\varDelta )$ does present an important difficulty: there is an efficient algorithm due to Gauss to compute square roots of arbitrary elements [15], and by repetition, arbitrary power of two roots. As a result, such class groups cannot be used to commit to integers but rather to dyadic rationals, which are rational numbers whose denominator is a power of two. Additionally, the standard Strong RSA Assumption is broken if computing square roots is easy. We therefore give a weakening of the Strong RSA assumption, called 2-Strong-RSA assumption, which is believed to still hold even if computing square roots is easy. The 2-Strong-RSA assumption assumes that computing non square roots is hard.

3.2 Interactive Arguments of Knowledge

Interactive arguments are interactive proofs [34] in which security holds only against a computationally bounded prover. In an interactive argument of knowledge for a relation $\mathcal {R}$, the prover convinces the verifier that it “knows” a witness w for a statement x such that $(x, w) \in \mathcal {R}$. In this paper, knowledge means that the argument has witness-extended emulation.

Definition 1

(Interactive Argument). Let $(\mathcal {P}, \mathcal {V})$ denote a pair of PPT interactive algorithms and $\textsf {{Setup}}$ denote a non-interactive setup algorithm that outputs public parameters $\textsf {pp}$ given a security parameter. Both $\mathcal {P}$ and $\mathcal {V}$ have access to $\textsf {pp}$. Let $\langle \mathcal {P} (\textsf {pp}, x, w), \mathcal {V} (\textsf {pp}, x) \rangle$ denote the output of V on input x after its interaction with P, who has witness w. The triple $(\textsf {{Setup}}, \mathcal {P}, \mathcal {V})$ is called an argument for relation $\mathcal {R}$ if for all non-uniform PPT adversaries $\mathcal {A}$ the following properties hold:

•   Perfect Completeness.

  $$ \Pr \left[ \begin{array}{c} (x, w) \not \in \mathcal {R} \ \text {or} \\ \ \langle \mathcal {P} (\textsf {pp}, x, w), \mathcal {V} (\textsf {pp}, x) \rangle = 1 \\ \end{array}: \begin{array}{c} \textsf {pp} \leftarrow \textsf {{Setup}}(1^\lambda ) \\ (x, w) \leftarrow \mathcal {A}(\textsf {pp}) \\ \end{array} \right] = 1 $$

•   Computational soundness.

  

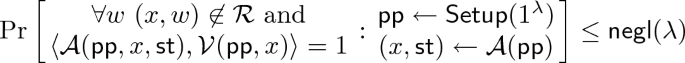
Definition 2

(Witness-extended emulation [36, 41]). Given a public-coin interactive argument tuple $(\textsf {Setup}, \mathcal {P}, \mathcal {V})$ and arbitrary prover algorithm $\mathcal {P} ^*$, let $\textsf {Record}(\mathcal {P} ^*, \textsf {pp}, x, \mathsf {st})$ denote the message transcript between $\mathcal {P} ^*$ and $\mathcal {V}$ on shared input x, initial prover state $\mathsf {st}$, and $\textsf {pp}$ generated by $\textsf {Setup}$. Furthermore, let $\mathcal {E} ^{\textsf {Record}(\mathcal {P} ^*, \textsf {pp}, x, \mathsf {st})}$ denote an machine $\mathcal {E}$ with a transcript oracle for this interaction that can be rewound to any round and run again on fresh verifier randomness. The tuple $(\textsf {Setup}, \mathcal {P}, \mathcal {V})$ has witness-extended emulation if for every deterministic polynomial time $\mathcal {P} ^*$ there exists an expected polynomial time emulator $\mathcal {E}$ such that for all non-uniform polynomial time adversaries $\mathcal {A}$ the following condition holds:

3.3 Commitment Schemes

In defining the syntax of the various protocols, we use the following convention with respect to public values (known to both the prover and the verifier) and secret ones (known only to the prover). In any list of arguments or returned tuple (a, b, c; d, e) those variables listed before the semicolon are public, and those variables listed after it are secret. When there is no secret information, the semicolon is omitted.

Definition 3

(Commitment scheme). A commitment scheme $\varGamma$ is a tuple $\varGamma = (\textsf {{Setup}}, \textsf {{Commit}}, \textsf {{Open}})$ of PPT algorithms where:

• $\textsf {{Setup}}(1^\lambda ) \rightarrow \textsf {pp}$ generates public parameters $\textsf {pp}$;

• $\textsf {{Commit}}(\textsf {pp}; x) \rightarrow (c; r)$ takes a secret message x and outputs a public commitment c and (optionally) a secret opening hint r (which might or might not be the randomness used in the computation).

• $\textsf {{Open}}(\textsf {pp}, c, x, r) \rightarrow b \in \{0, 1\}$ verifies the opening of commitment c to the message x provided with the opening hint r.

A commitment scheme $\varGamma$ is binding if for all PPT adversaries $\mathcal {A}$:

We now extend the syntax to polynomial commitment schemes. The following definition generalizes that of Kate et al. [39] to allow interactive evaluation proofs. It also stipulates that the polynomial’s degree be an argument to the protocol, contrary to Kate et al. where the degree is known and fixed.

Definition 4

(Polynomial commitment). A polynomial commitment scheme is a tuple of protocols $\varGamma = (\textsf {{Setup}}, \textsf {{Commit}}, \textsf {{Open}}, \textsf {{Eval}})$ where $(\textsf {{Setup}}, \textsf {{Commit}}, \textsf {{Open}})$ is a binding commitment scheme for a message space R[X] of polynomials over some ring R, and

• $\textsf {{Eval}}(\textsf {pp}, c, z, y, d, \mu ; f(X)) \rightarrow b \in \{0, 1\}$ is an interactive public-coin protocol between a PPT prover $\mathcal {P}$ and verifier $\mathcal {V}$. Both $\mathcal {P}$ and $\mathcal {V}$ have as input a commitment c, points $z, y \in R$, and a degree d. The prover additionally knows the opening of c to a secret polynomial $f(X) \in R[X]$ with $\deg (f(X)) \le d$. The protocol convinces the verifier that $f(z) = y$. In a multivariate extension of polynomial commitments, the input $\mu > 1$ indicates the number of variables in the committed polynomial and $z \in R^\mu$.

A polynomial commitment scheme is correct if an honest committer can successfully convince the verifier of any evaluation. Specifically, if the prover is honest then for all polynomials $f(X) \in R[X]$ and all points $z \in R$,

Knowledge soundness. Any successful prover in the $\textsf {{Eval}}$ protocol must know a polynomial f(X) such that $f(z) = y$ and c is a commitment to f(X). More formally, since $\textsf {{Eval}}$ is a public-coin interactive argument we define this knowledge property as a special case of witness-extended emulation (Definition 2).

Define the following NP relation given $\textsf {pp} \leftarrow \textsf {{Setup}}(1^\lambda )$:

$$ \mathcal {R_\textsf {Eval}}(\textsf {pp}) = \left\{ \langle (c, z, y, d), (f(X), r) \rangle : \begin{array}{l} f \in R[X] \ \text {and} \ \deg (f(X)) \le d \ \text {and} \ f(z) = y \\ \text {and} \ \textsf {{Open}}(\textsf {pp}, c, f(X), r) = 1 \\ \end{array} \right\} $$

The correctness definition above implies that if $\varGamma = (\textsf {{Setup}}, \textsf {{Commit}}, \textsf {{Open}}, \textsf {{Eval}})$ is correct then $\textsf {{Eval}}$ is a correct interactive argument for $\mathcal {R}_\textsf {Eval}(\textsf {pp})$, with overwhelming probability over the randomness of $\textsf {{Setup}}$. We say that $\varGamma$ has witness-extended emulation if $\textsf {{Eval}}$ has witness-extended emulation as an interactive argument for $\mathcal {R}_\textsf {Eval}(\textsf {pp})$.

3.4 Proofs of Exponentiation

Wesolowski [53] introduced a simple yet powerful proof of correct exponentiation (“$\mathsf {PoE}$”) in groups of unknown order. A prover can efficiently convince a verifier that a large exponentiation in such a group was done correctly. For instance, the prover wishes to convince the verifier that $\mathsf {w} = \mathsf {u}^x$ for known group elements $\mathsf {u}, \mathsf {w} \in \mathbb {G}$ and exponent $x \in \mathbb {Z}$, and the verifier wants to verify this with much less work than performing the exponentiation. To do this, the verifier samples a large enough prime $\ell$ at random and the prover provides him with $\mathsf {Q} \leftarrow \mathsf {u}^q$ where $q = \lfloor \frac{x}{\ell } \rfloor$. The verifier then simply computes the remainder $r \leftarrow (x \mod \ell )$ and checks that $\mathsf {Q}^\ell \mathsf {u}^r = \mathsf {w}$. The protocol is an argument for the relation $\mathcal {R}_\mathsf {PoE} = \left\{ \langle (\mathsf {u}, \mathsf {w}, x), \varnothing \rangle \ : \ \mathsf {u}^x = \mathsf {w} \right\}$. The proof verification uses just $O(\lambda )$ group operations. When x is $x=q^d$ the verifier can compute $r\leftarrow x \bmod \ell$ using just $\log (d) \ell$-bit multiplications.

Lemma 1

( PoE soundness [53]).   PoE is an argument system for Relation $\mathcal {R}_\textsf {PoE}$ with negligible soundness error, assuming the Adaptive Root Assumption (Assumption 2) holds for $\textit{GGen}$.

4 Polynomial Commitments from Groups of Unknown Order

4.1 Information-Theoretic Abstraction

Before we present our concrete polynomial commitment scheme based on groups of unknown order, we present the underlying information theoretic protocol that abstracts the concrete cryptographic instantiations. The purpose of this abstraction is two-fold: first, it provides an intuitive stepping stone from which presenting and studying the concrete cryptographic protocol is easier; and second, it opens the door to alternative cryptographic instantiations that provide the same interface but based on alternative hardness assumptions.

Let $[\![ * ]\!] : \mathbb {Z}_p[X] \rightarrow \mathbb {S}$ be a homomorphic commitment function that sends polynomials over a prime field to elements of some set $\mathbb {S}$. Moreover, let $\mathbb {S}$ be equipped with operations $* + * : \mathbb {S} \times \mathbb {S} \rightarrow \mathbb {S}$ and $* \cdot * : \mathbb {Z}_p[X] \times \mathbb {S} \rightarrow \mathbb {S}$ that accommodate two homomorphisms for $[\![ * ]\!]$:

• a linear homomorphism: $a \cdot [\![f(X)]\!] + b \cdot [\![g(X)]\!] = [\![af(X) + bg(X)]\!]$

• a monomial homomorphism: $X^d \cdot [\![f(X)]\!] = [\![X^d f(X)]\!]$.

For now, assume both prover and verifier have oracle access to the function $[\![*]\!]$ and to the operations $* \cdot *$ and $* + *$. (Later on, we will instantiate this commitment function using groups of unknown order and an encoding of polynomials as integers.)

The core idea of the evaluation protocol is to reduce the statement that is being proved from one about a polynomial f(X) of degree d and its evaluation $y = f(z)$, to one about a polynomial $f'(X)$ of degree $d'=\lfloor \frac{d}{2}\rfloor$ and its evaluation $y' = f'(z)$. For simplicity, assume that $d+1$ is a power of 2. The prover splits f(X) into $f_L(X)$ and $f_R(X)$ such that $f(X) = f_L(X) + X^{d'+1} f_R(X)$ and such that both halves have degree at most $d'$. The prover obtains a random challenge $\alpha \in \mathbb {Z}_p$ from the verifier and proceeds to prove that $f'(X)=\alpha \cdot f_L(X) + f_R(X)$ has degree $d'$ and that $f'(z) = y' = \alpha y_L + y_R$ with $y_L = f_L(z)$ and $y_R = f_R(z)$.

The proof repeats this reduction by using $f'(X),z,y'$ and $d'$ as the input to the next recursion step. In the final step, $f(X) = f$ is a constant and the verifier checks that $f=y$.

The commitment function binds the prover to one particular polynomial for every commitment held by the verifier. In particular, at the start of every recursion step, the verifier is in possession of a commitment $[\![f(X)]\!]$ to f(X). The prover provides commitments $[\![f_L(X)]\!]$ and $[\![f_R(X)]\!]$, and the verifier checks their soundness homomorphically by testing $[\![f(X)]\!] = [\![f_L(X)]\!] + X^{d'+1} \! \cdot \! [\![f_R(X)]\!]$. From these commitments, the verifier can also compute the commitment to $f'(X)$ homomorphically, via $[\![f'(X)]\!] = \alpha \! \cdot \! [\![f_L(X)]\!] + [\![f_R(X)]\!]$. In the last step, the verifier checks that the constant polynomial f matches the commitment by computing $[\![f]\!]$ outright.

4.2 Integer Polynomial Encoding

We propose using integer commitments in a group of unknown order as a concrete instantiation of the homomorphic commitment scheme required for the abstract protocol presented in Sect. 4.1. At the heart of our protocol is thus an encoding of integer polynomials with bounded coefficients as integers, which also has homomorphic properties. Any commitment scheme which is homomorphic over integer polynomials is automatically homomorphic over $\mathbb {Z}_p[X]$ polynomials as well (by reducing integer polynomials modulo p). Polynomials over $\mathbb {Z}_p[X]$ can be lifted to integer polynomials in a canonical way by choosing representatives in [0, p). Therefore, from here on we will focus on building a homomorphic integer encoding of integer polynomials, and how to combine this with a homomorphic integer commitment scheme.

Strawman encoding. In order to encode integer polynomials over an odd prime field $\mathbb {F}_p$, we first lift them to the ring of polynomials over the integers by choosing representatives in [0, p). In the technical overview (Sect. 2) we noted that a polynomial $f \in \mathbb {Z}[X]$ with positive coefficients bounded by q can be encoded as the integer f(q). The coefficients of f can be recovered via the base q decomposition of f(q). This encoding is an injective mapping from polynomials in $\mathbb {Z}[X]$ of degree at most d with positive coefficients less than q to the set $[0, q^{d+1})$. The encoding is also partially homomorphic. If f is encoded as f(q) and g is encoded as g(q) where coefficients of both g, f are less than q/2, then the base-q decomposition of $f(q) + g(q)$ gives back the polynomial $f + g$. By choosing a sufficiently large $q \gg p$ it is possible to perform several levels of homomorphic operations on encodings.

What goes wrong? Unfortunately, this simple encoding scheme does not quite work yet for the protocol outlined in Sect. 2. The homomorphic consistency checks ensure that if $[\![f_L(X)]\!]$ is a homomorphic integer commitment to the encoding of $f_L \in \mathbb {Z}[X]$, $[\![f_R(X)]\!]$ is a homomorphic integer commitment to the encoding of $f_R \in \mathbb {Z}[X]$, and both $f_L, f_R$ are polynomials with q/2-bounded coefficients, then $[\![f(X)]\!]$ is an integer commitment to the encoding of $f_L + X^{d'}f_R$. (Moreover, if $f_L(z) = y_L \bmod p$ and $f_R(z) = y_R \bmod p$ then $f(z) = y_L + z^{d'} y_R \bmod p$).

However, the validity of $[\![f_L(X)]\!]$ and $[\![f_R(X)]\!]$ are never checked directly. The verifier only sees the opening of the commitment at the bottom level of recursion. If the intermediate encodings use integer polynomials with coefficients larger than q/2 the homomorphism is not preserved. Furthermore, even if $[\![f(X)]\!]$ is a commitment to $f^*(q)$ with positive q-bounded coefficients, an adversarial prover could find an integer polynomial $g^*$ that does not have positive q-bounded coefficients such that $g^*(q) = f^*(q)$ and $g^* \not \equiv f^* \bmod p$ (i.e, $g^*$ with coefficients greater than q or negative coefficients). The prover could then commit to $g^*_L(q)$ and $g^*_R(q)$, and recurse on $\alpha g^*_L(q) + g^*_R(q)$ instead of $\alpha f^*_L(q) + f^*_R(q)$. This would be non-binding. (For example $f^*(X)= q-1$ and $g^*(X)=X-1$, or $f^*(X) = q +1$ and $g^*(X) = X + 1$).

Inferring coefficient bounds. So what can the verifier infer from the opened commitment $[\![f']\!]$ at the bottom level of recursion? The opened commitment is an integer $f' = \alpha f_L + f_R$. From $f'$, the verifier can infer a bound on the absolute value of the coefficients of the integer polynomial $f(X) = f_L + X f_R$, given that $f_L$ and $f_R$ were already committed in the second to last round. The bound holds with overwhelming probability over the randomness of $\alpha \in [0,p)$. This is reasoned as follows: if $f'_0 \leftarrow \alpha _0 f_L + f_R$ and $f'_1 \leftarrow \alpha _1 f_L + f_R$ such that $\max (|f'_0|, |f'_1|) < q / (2p)$ for some distinct $\alpha _0 \ne \alpha _1$, then $|f_L| \le |f'_1 - f'_0| < q / p$ and $|f_R| \le |\alpha _0 f'_1 - \alpha _1 f'_0| < q/2$. If no such pair exists, i.e. the bound only holds for a unique $\alpha$, then there is a negligibly small probability 1/p that $f'$ would have passed the bound check.

What about negative coefficients? As shown above, the verifier can infer a bound on the absolute values of $f_L$ and $f_R$, but still cannot infer that $f_L$ and $f_R$ are both positive integers. Moreover, if $f_R > 0$ and $f_L < 0$, then it is still possible that $f_L + q f_R > 0$, and thus that there is a distinct $g \ne f$ with q-bounded positive coefficients such that $g(q) = f(q)$. For example, say $f_R = q/2$ and $f_L = -1$ then $f_L + q f_R = q^2/2 - 1$, and $\alpha f_L + f_R = q/2 - \alpha > 0$ for every $\alpha \in [0,p)$. Yet, also $q^2/2 - 1 = g(q)$ for $g(X) = (q/2 - 1)X + q-1$.

Ensuring injectivity. How can we ensure the encoding scheme is injective over polynomials with either positive/negative coefficients bounded in absolute value? Fortunately, it is a fact that if $|f_L| < q/2$ and $|f_R| < q/2$ then at least one coefficient of g must be larger than q/2. In other words, if the prover had committed instead to $f^*_L$ and $f^*_R$ such that $g(X) = f^*_L + Xf^*_R$ then the verifier could reject the opening of $\alpha \hat{f}^*_L + \hat{f}^*_R$ with overwhelming probability based on its size.

More generally, for every integer z in the range $B = (-\frac{q^{d+1}}{2}, \frac{q^{d+1}}{2})$ there is a unique degree (at most) d integer polynomial h(X) with coefficients whose absolute values are bounded by q/2 such that $h(q) = z$. We prove this elementary fact below and show how the coefficients of h can be recovered efficiently from z (Fact 1). If the prover is committed to h(q) at level i of the protocol, there is a unique pair of integers polynomial $h_L$ and $h_R$ with coefficients of absolute value bounded by q/2 such that $h_L(q) + q^{\frac{d+1}{2}} h_R(q) = h(q)$, and if the prover recurses on any other $h_L^*$ and $h_R^*$ with larger coefficients then the verifier’s bound check at the bottom level of recursion will fail with overwhelming probability.

Final Encoding scheme. Let $\mathbb {Z}(b):=\{x \in \mathbb {Z}: \vert x \vert \le b\}$ denote the set of integers with absolute value less than or equal to b. Define $\mathbb {Z}(b)[X] := \{f \in \mathbb {Z}[X]: ||f||_\infty \le b\}$, the set of integer polynomials with coefficients from $\mathbb {Z}(b)$. (For a polynomial $g \in \mathbb {Z}[X]$ the norm $||g||_\infty$ is the maximum over the absolute values of all individual coefficients of g.)

• Encoding. For any integer q, the function $\mathsf {Enc} : \mathbb {Z}(b)[X] \rightarrow \mathbb {Z}$ maps $h(X) \mapsto h(q)$. A polynomial $f(X) \in \mathbb {Z}_p[X]$ is first mapped to $\mathbb {Z}(p/2)[X]$ by replacing each coefficient of f with its unique integer representative from $(-p/2,p/2)$ of the same equivalence class modulo p.

• Decoding. Decoding works as follows. Define the partial sum $S_k := \sum _{i=0}^k f_i q^i$ with $S_{-1} := 0$. Assuming $|f_i| < q/2$ for all i, observe that for any partial sum $S_k$ we have $|S_k|<\frac{q^{k+1}}{2}$. Therefore, when $S_k < 0$ then $S_k \bmod q^{k+1} > q^{k+1}/2$ and when $S_k \ge 0$ then $S_k \bmod q^{k+1} < q^{k+1}/2$. This leads to a decoding strategy for recovering $S_k$ from $y \in \mathbb {Z}$. The decode algorithm sets $S_k$ to $y \bmod q^{k+1}$ if this value is less than $q^{k+1}/2$ and to $q^{k+1}- (y \bmod q^{k+1})$ otherwise. Two consecutive partial sums yield a coefficient of f(X): $f_k = \frac{S_{k} - S_{k-1}}{q^{k}} \in \mathbb {Z}(b)$. These operations give rise to the following algorithm.

Fact 1

Let q be an odd integer. For any z in the range $B = (-\frac{q^{d+1}}{2}, \frac{q^{d+1}}{2})$ there is a unique degree (at most) d integer polynomial h(X) in $\mathbb {Z}(\frac{q-1}{2})[X]$ such that $h(q) = z$.

4.3 Concrete Polynomial Commitment Scheme

We now instantiate the abstract homomorphic commitment function $[\![ * ]\!]$. To this end we sample a group of unknown order $\mathbb {G}$, and sample a random element $\mathsf {g}$ from this group. Lift the field polynomial $f(X)\in \mathbb {Z}_p[X]$ to an integer polynomial with bounded coefficients, i.e., $\hat{f}(X)\in \mathbb {Z}(\frac{p-1}{2})[X]$ such that $\hat{f}(X)\bmod p=f(x)$. We encode $\hat{f}(X)$ as an integer by evaluating it at a “large enough” integer q. Finally we use exponentiation in $\mathbb {G}$ to commit to the integer. Therefore, $[\![f(X)]\!]$, corresponds to $\mathsf {g}^{\hat{f}(q)}$. This commitment function inherits the homomorphic properties of the integer encoding for a limited number of additions and multiplications-by-constant. The monomial homomorphism for $X^d$ is achieved by raising the group element to the power $q^{d}$. To maintain consistency between the prover’s witness polynomials and the verifier’s commitments, the prover operates on polynomials with integer coefficients $\hat{f}(X), \hat{g}(X)$, etc., without ever reducing them modulo p.

The $\textsf {{Setup}}, \textsf {{Commit}}$ and $\textsf {{Open}}$ functionalities are presented formally below. Note that the scheme is parameterized by p and q.

• $\textsf {{Setup}}(1^\lambda ):$ Sample $\mathbb {G}\overset{\$}{\leftarrow }\textit{GGen}(\lambda )$ and $\mathsf {g} \overset{\$}{\leftarrow }\mathbb {G}$. Return $\textsf {pp} = (\lambda ,\mathbb {G},\mathsf {g}, q)$.

• $\textsf {{Commit}}(\textsf {pp};f(X) \in \mathbb {Z}_p[X]):$ Compute $\mathsf {C} \leftarrow \mathsf {g}^{\hat{f}(q)}$ and return $(\mathsf {C};\hat{f}(X))$.

• $\textsf {{Open}}(\textsf {pp},\mathsf {C}, f(X), \hat{f}(X)):$ Check that $\hat{f}(X)\in \mathbb {Z}(q/2)[X]$ and $\mathsf {g}^{\hat{f}(q)} = \mathsf {C}$ and $f(X) = \hat{f}(X) \bmod p$.

Evaluation protocol. Using the cryptographic compilation of the information theoretic protocol we get an $\textsf {{Eval}}$ protocol with logarithmic communication. In every round, however, the verifier needs to check consistency between $[\![f_L(X)]\!],[\![f_R(X)]\!]$ and $[\![f(X)]\!]$. This is done by checking that $\mathsf {C}_L \cdot \mathsf {C}_R^{q^{d'+1}}=\mathsf {C}$. This naive check is highly inefficient as the exponent $q^{d'+1}$ has O(d) bits. To resolve this inefficiency, we utilize a proof of exponentiation (PoE) [44, 53] to outsource the computation to the prover. The PoE protocol is an argument that a large exponentiation in a group of unknown order was performed correctly. Wesolowski’s PoE [53] is public coin, has constant communication and verification time, and is thus particularly well-suited here.

We now specify subtleties that were previously glossed over. First, we handle the case where $d+1$ is not a power of 2. Whenever $d+1$ is odd in the recursion, the polynomial is shifted by one degree—specifically, $f'(X) = X f(X)$ and the protocol proceeds to prove that $f'(X)$ has degree bounded by $d' = d+1$ and evaluates to $y' = zy$ at z. The verifier obtains the matching commitment $\mathsf {C}'\leftarrow \mathsf {C}^q$.

Second, the coefficients of f(X) grow by a factor of $\frac{p+1}{2}$ in every recursion step, but eventually the transmitted constant f has to be tested against some bound because if it is too large it should be rejected. However, the function interface provides no option to specify the allowable size of coefficients. We therefore define and use a subroutine $\textsf {{EvalBounded}}$, which takes an additional argument b and which proves, in addition to what $\textsf {{Eval}}$ proves, that all coefficients $f_i$ of f(X) satisfy $|f_i| \le b$. Importantly, b grows by a factor for $\frac{p+1}{2}$ in every recursion step. This subroutine is also useful if commitments were homomorphically combined prior to the execution of $\textsf {{EvalBounded}}$. The growth of these coefficients determines a lower bound on q: q should be significantly larger than b. Exactly which factor constitutes “significantly” is determined by the knowledge-soundness proof.

In the final round we check that the constant f satisfies $|f|\le b$ and the protocol’s correctness is guaranteed if $b = \frac{p-1}{2}(\frac{p+1}{2})^{\lceil \log _2(d+1)\rceil }$. However, q needs to be even larger than this value in order for extraction to work (and hence, for the proof of witness-extended emulation to go through). In RSA groups, where computing square roots is hard, we need $q>p^{2\log (d+1)+1}$; whereas in class groups where computing square roots is easy, we need $p^{3\log (d+1)+1}$. When this condition is satisfied, we can prove that the original committed polynomial has coefficients smaller than $\frac{q}{2}$. To avoid presenting two algorithms whose only difference is the one constant, we capture this constant explicitly in the variable $\varvec{\varsigma }_{p,d}$ and set its value depending on the context: We now present the full, formal $\textsf {{Eval}}$ protocol below.

4.4 Security Analysis

Lemma 2

The polynomial commitment scheme is binding for polynomials in $\mathbb {Z}(b)[X]$ for $b<q/2$ if either the Adaptive Root Assumption or the Strong RSA Assumption hold.

Lemma 3

The polynomial commitment scheme is correct for polynomials in $\mathbb {Z}_p[X]$ of degree at most d if $q> p^{\lceil \log _2(d+1)\rceil +1}$.

All security proofs are in the full version of this paper [19, §A.1–§A.2]. Next is the main security theorem, which states that the evaluation protocol has witness-extended emulation. We start with a high-level intuitive overview where we also identify potential obstacles.

Proof idea. The goal is to construct an extractor by recursively computing f(X) from $f'(X)$. In the final round the verifier receives f such that $|f| \le b$, and therefore the extractor possesses this constant polynomial as well. Working backwards from here, the extractor uses rewinding in every step to find $f_L(X)$ and $f_R(X)$ and thereby finds $f(X) = f_L(X) + X^{d'+1}f_R(X)$. Specifically, in each round the extractor has $f'(X)=\alpha f_L(X)+ f_R(X)$. Suppose the extractor also possesses $f''(X)=\alpha ' f_L(X)+ f_R(X)$. From $f'(X)$, $f''(X)$, $\alpha$ and $\alpha '$ it is easy to compute $f_L(X)$ and $f_R(X)$. The extractor then computes $f(X)=f_L(X)+X^{d'+1} f_R(X)$. A careful analysis shows that if the coefficients of $f'(X)$ are bounded by b then $f_L(X)$ and $f_R(X)$ must have coefficients bounded by $b \cdot p$ in absolute value. Using a similar analysis we can show that $f(z)\bmod p=y$ for the extracted polynomial f(X).

This argument shows that there is an extractor algorithm $\mathcal {X}$ capable of extracting the witness f(X) from a binary tree of accepting transcripts. Moreover, a tree-finding algorithm $\mathcal {T}$ can output such a tree by repeatedly rewinding the prover, running it with fresh verifier randomness each time, and recording the resulting transcripts. As a result, the Generalized Forking Lemma [14] applies and establishes that the protocol has witness-extended emulation.

The full proof takes into account the cryptographic compilation of the protocol using the integer encoding and the commitment scheme based on groups of unknown order. Additionally the full proof will need to support dyadic rationals because taking square roots is easy in class groups.

Theorem 1

The polynomial commitment scheme for polynomials in $\mathbb {Z}_p[X]$ of degree at most $d=\mathsf {poly}({\lambda })$, instantiated using $q>p^{2\lceil \log _2(d+1)\rceil +1}$ and $\textit{GGen}$, has witness extended emulation (Definition 2) if the Adaptive Root Assumption and the Strong RSA Assumption hold for $\textit{GGen}$.

Theorem 2

Let $\textit{GGen}$ generate groups $\mathbb {G}$ of unknown order such that the order of $\mathbb {G}$ is odd, and such there exists a PPT algorithm for taking square roots in $\mathbb {G}$. The polynomial commitment scheme for polynomials in $\mathbb {Z}_p[X]$ of degree at most $d=\mathsf {poly}({\lambda })$, instantiated using $q>p^{3\lceil \log _2(d+1)\rceil +1}$ and $\textit{GGen}$, has witness extended emulation (Definition 2) if the Adaptive Root Assumption and the 2-Strong RSA Assumption hold for $\textit{GGen}$.

The proof of Theorem 2 is nearly identical to the proof of Theorem 1 but the extracted polynomials are polynomials over the dyadic rationals and not over the integers. This requires the bound on q to be larger by a factor of $p^{\log (d+1)}$. Both proofs are presented in the full version of this paper [19, §A.3–§A.4].

4.5 Optimizations and Extensions

Out of space constraints, a number of interesting but non-essential sections are omitted. The full version of this paper [19] presents a range of optimizations for greater prover and verifier efficiency and smaller proof size. It also shows how to achieve extend the commitment to multivariate polynomials and shows how to make the commitment hiding with a ZK evaluation protocol.

4.6 Comparison

In Table 1 we give a comparison between different polynomial commitment schemes in the literature. In particular, we evaluate the size of the reference string ($|\textsf {pp}|$), the prover and verifier time, as well as the size of the evaluation proof ($|\pi |$). Column 2 indicates whether the setup is transparent, i.e., whether the reference string is structured. The symbol $\mathbb {G}_U$ denotes a group of unknown order, $\mathbb {G}_{B}$ a group with a bilinear map (pairing), and $\mathbb {G}_{P}$ a group with prime (and known) order. Furthermore, $\textsf {EXP}$ refers to exponentiation of a $\lambda$ bit number in these groups, and $\mathsf {H}$ is either the size of a hash output, or the time it takes to compute a hash, depending on context.

Note that even when precise factors are given, the numbers should be interpreted as estimates. For example we chose to not display smaller order terms. Note also that the prover time for the group based schemes could be brought down by a log factor when using multi-exponentiation techniques.

Table 1. Comparison table between different polynomial commitment schemes for an $\mu$-variate polynomial of degree d.

5 Transparent SNARKs via Polynomial IOPs

5.1 Algebraic Linear IOPs

An interactive oracle proof (IOP) [7, 45] is a multi-round interactive PCP: in each round of an IOP the verifier sends a message to the prover and the prover responds with a polynomial length proof, which the verifier can query via random access. A t-round $\ell$-query IOP has t rounds of interaction in which the verifier makes exactly $\ell$ queries in each round. Linear IOPs [11] are defined analogously except that in each round the prover sends a linear PCP [38], in which the prover sends a single proof vector $\varvec{\pi } \in \mathbb {F}^m$ and the verifier makes linear queries to $\pi$. Specifically, the PCP gives the verifier access to an oracle that receives queries of the form $\mathbf {q} \in \mathbb {F}^m$ and returns the inner product $\langle \varvec{\pi }, \mathbf {q} \rangle$.

Bitansky et al. [9] defined a linear PCP to be of degree $(d_Q, d_V)$ if there is an explicit circuit of degree $d_Q$ that derives the query vector from the verifier’s random coins, and an explicit circuit of degree $d_V$ that computes the verifier’s decision from the query responses. In a multi-query PCP, $d_Q$ refers to the maximum degree over all the independent circuits computing each query. Bitansky et al. called the linear PCP algebraic for a security parameter $\lambda$ if it has degree $(\mathsf {poly}({\lambda }), \mathsf {poly}({\lambda }))$. The popular linear PCP based on Quadratic Arithmetic Programs (QAPs) implicit in the GGPR protocol [31] and follow-up works is an algebraic linear PCP with $d_Q \in O(m)$ and $d_V = 2$, where m is the size of the witness.

For the purposes of the present work, we are only interested in the algebraic nature of the query circuit and not the verifier’s decision circuit. Of particular interest are linear PCPs where each query-and-response interaction corresponds to the evaluation of a fixed $\mu$-variate degree d polynomial at a query point in $\mathbb {F}^\mu$. This description is equivalent to saying that the PCP is a vector of length $m = {d + \mu \atopwithdelims ()\mu }$ and the query circuit is the vector of all $\mu$-variate monomials of degree at most d (in some canonical order) evaluated at a point in $\mathbb {F}^\mu$. We call this a $(\mu , d)$ Polynomial PCP and define Polynomial IOPs analogously. As we will explain, we are interested in Polynomial PCPs where $\mu \ll m$ because we can cryptographically compile them into succinct arguments using polynomial commitments, in the same way that Merkle trees are used to compile classical (point) IOPs.

In general, evaluating the query circuit for a linear PCP requires $\varOmega (m)$ work. However, a general “bootstrapping” technique can reduce the work for the verifier: the prover expands the verifier’s random coins into a full query vector, and then provides the verifier with a second PCP demonstrating that this expansion was computed correctly. It may also help to allow the verifier to perform O(m) work in a one-time preprocessing stage (for instance, to check the correctness of a PCP oracle), enabling it to perform sublinear “online” work when verifying arbitrary PCPs later. We call this a preprocessing IOP. In fact, we will see that any t-round $(\mu , d)$ algebraic linear IOP can be transformed into a $(t+1)$-round Polynomial IOP in which the verifier preprocesses $(\mu , d)$ Polynomial PCPs, at most one for each distinct query.

We recall the formal definition of public-coin linear IOPs as well an algebraic linear IOPs. Since we are not interested in the algebraic nature of the decision algorithm, we omit specifying the decision polynomial. From here onwards we use algebraic linear IOP as shorthand for algebraic query linear IOP.

Definition 5

(Public-coin linear IOP). Let $\mathcal {R}$ be a binary relation and $\mathbb {F}$ a finite field. A t-round $\ell$-query public-coin linear IOP for $\mathcal {R}$ over $\mathbb {F}$ with soundness error $\epsilon$ and knowledge error $\delta$ and query length $\mathbf {m} = (m_1,...,m_t)$ consists of two stateful PPT algorithms, the prover $\mathcal {P}$, and the verifier $\mathcal {V} = (\mathcal {Q}, \mathcal {D})$, where the verifier consists in turn of a public deterministic query generator $\mathcal {Q}$ and a decision algorithm $\mathcal {D}$, that satisfy the following requirements:

Protocol syntax. For each ith round there is a prover state $\textsf {st}^\mathcal {P} _i$ and a verifier state $\textsf {st}^\mathcal {V} _i$. For any common input x and $\mathcal {R}$ witness w, at round 0 the states are $\textsf {st}^\mathcal {P} _0 = (x, w)$ and $\textsf {st}^\mathcal {V} _0 = x$. In the ith round (starting at $i = 1$) the prover outputs a single⁴ proof oracle $\mathcal {P} (\textsf {st}^\mathcal {P} _{i-1}) \rightarrow \varvec{\pi }_i \in \mathbb {F}^{m_i}$. The verifier samples public random coins $coins _i \overset{\$}{\leftarrow }\{0,1\}^*$ and the query generator computes a query matrix from the verifier state and these coins: $\mathcal {Q} (\textsf {st}^\mathcal {V} _{i-1}, coins _i) \rightarrow \mathbf {Q}_i \in \mathbb {F}^{m_i \times \ell }$. The verifier obtains the linear oracle response vector $\varvec{\pi }_i^\top \mathbf {Q}_i = \mathbf {a}_i \in \mathbb {F}^{1 \times \ell }$. The updated prover state is $\textsf {st}^\mathcal {P} _i \leftarrow (\textsf {st}^\mathcal {P} _{i-1}, \mathbf {Q}_i)$ and verifier state is $\textsf {st}^\mathcal {V} _i \leftarrow (\textsf {st}^\mathcal {V} _{i-1}, coins _i, \mathbf {a}_i)$ Finally, $\mathcal {D}(\textsf {st}^\mathcal {V} _t)$ returns 1 or 0.

(Querying prior round oracles: The syntax can be naturally extended so that in the ith round the verifier may query any oracle, whether sent in the ith round or earlier.)

Argument of Knowledge. As a proof system, $(\mathcal {P}, \mathcal {V})$ satisfies perfect completeness, soundness with respect to the relation $\mathcal {R}$ and with soundness error $\epsilon$, and witness-extended emulation with respect $\mathcal {R}$ with knowledge error $\delta$.

Furthermore, a linear IOP is stateless if for each $i \in [t]$, $\mathcal {Q} (\textsf {st}^\mathcal {V} _{i-1},$ $coins _i) = \mathcal {Q} (i, coins _i)$. It has algebraic queries if, additionally, for each $i \in [t]$, the map decomposes into two maps, , where $\varvec{\varSigma }_i \in \mathbb {F}^{\mu _i \times \ell }$ is a matrix of $\mu _i < m_i$ rows and $\ell$ and $\mathcal {Q} _1(i, \cdot )$ is described by $\ell \mu _i$-variate polynomial functions of degree at most $d = \mathsf {poly}({\lambda })$: $\varvec{p}_1, \ldots , \varvec{p}_\ell : \mathbb {F}^{\mu _i} \rightarrow \mathbb {F}^{m_i}$ such that for all $k \in [\ell ]$, $\varvec{p}_k(\varvec{\sigma }_{i,k}) = \mathbf {q}_{i,k}$, where $\varvec{\sigma }_{i,k}$ and $\mathbf {q}_{i,k}$ denote the kth column of $\varvec{\varSigma }_i$ and $\mathbf {Q}_i$, respectively.

We note that the separation into two maps subtly relaxes the definition of Bitansky et al. [9], which instead requires that $\mathbf {Q}_i$ be determined via $\varvec{p}_1, \ldots , \varvec{p}_\ell$ evaluated at a random $\varvec{r} \overset{\$}{\leftarrow }\mathbb {F}^{\mu _i}$. The [9] definition corresponds to the special case that $\mathcal {Q} _0(i, \cdot )$ samples a random element of $\mathbb {F}^{\mu _i}$ based on $\textit{coins}_i$. The point is that $\mathcal {Q} _0$ can also do other computations that do not necessarily sample $\varvec{r}$ uniformly, or even output a matrix rather than a vector. The separation into two steps is only meaningful when $\mu _i$ is smaller than $m_i$. The significance to SNARK constructions is that the query can be represented compactly as $\varvec{\varSigma }_i$, and the prover will take advantage of the algebraic map $\mathcal {Q} _1(i, \cdot )$ to demonstrate that $\varvec{\varSigma }_i$ was expanded correctly into $\mathbf {Q}_i$ and applied to the proof oracle $\pi _i$. We first present a standalone definition of Polynomial IOPs, and then explain how it is a special case of Algebraic Linear IOPs.

Definition 6

(Public coin Polynomial IOP). Let $\mathcal {R}$ be a binary relation and $\mathbb {F}$ a finite field. Let $\mathbf {X} = (X_1, \ldots , X_\mu )$ be a vector of $\mu$ indeterminates. A $(\mu , d)$ Polynomial IOP for $\mathcal {R}$ over $\mathbb {F}$ with soundness error $\epsilon$ and knowledge error $\delta$ consists of two stateful PPT algorithms, the prover $\mathcal {P}$, and the verifier $\mathcal {V}$, that satisfy the following requirements:

Protocol syntax. For each ith round there is a prover state $\textsf {st}^\mathcal {P} _i$ and a verifier state $\textsf {st}^\mathcal {V} _i$. For any common input x and $\mathcal {R}$ witness w, at round 0 the states are $\textsf {st}^\mathcal {P} _0 = (x, w)$ and $\textsf {st}^\mathcal {V} _0 = x$. In the ith round (starting at $i = 1$) the prover outputs a single proof oracle $\mathcal {P} (\textsf {st}^\mathcal {P} _{i-1}) \rightarrow \pi _i$, which is a polynomial $\pi _i(\mathbf {X}) \in \mathbb {F}[\mathbf {X}]$. The verifier deterministically computes the query matrix $\varvec{\varSigma }_i \in \mathbb {F}^{\mu \times \ell }$ from its state and a string of public random bits $coins _i \overset{\$}{\leftarrow }\{0,1\}^*$, i.e, $\mathcal {V} (\mathsf {st}^\mathcal {V} _{i-1}, coins _i) \rightarrow \varvec{\varSigma }_i$. This query matrix is interpreted as a list of $\ell$ points in $\mathbb {F}^\mu$ denoted $(\varvec{\sigma }_{i,1}, \ldots , \varvec{\sigma }_{i, \ell })$. The oracle $\pi _i$ is queried on all points in this list, producing the response vector $(\pi _i(\varvec{\sigma }_{i,1}), \ldots , \pi _\ell (\varvec{\sigma }_{i, \ell })) = \mathbf {a}_i \in \mathbb {F}^{1 \times \ell }$. The updated prover state is $\textsf {st}^\mathcal {P} _i \leftarrow (\textsf {st}^\mathcal {P} _{i-1}, \varvec{\varSigma }_i)$ and verifier state is $\textsf {st}^\mathcal {V} _i \leftarrow (\textsf {st}^\mathcal {V} _{i-1}, \varvec{\varSigma }_i, \mathbf {a}_i)$. Finally, $\mathcal {V} (\textsf {st}^\mathcal {V} _t)$ returns 1 or 0.

(Extensions: multiple and prior round oracles; various arity. The syntax can be naturally extended such that multiple oracles are sent in the ith round; that the verifier may query oracles sent in the ith round or earlier; or that some of the oracles are polynomials in fewer variables than $\mu$.)

Argument of Knowledge. As a proof system, $(\mathcal {P}, \mathcal {V})$ satisfies perfect completeness, soundness with respect to the relation $\mathcal {R}$ and with soundness error $\epsilon$, and witness-extended emulation with respect $\mathcal {R}$ with knowledge error $\delta$.

Furthermore, a Polynomial IOP is stateless if for each $i \in [t]$, $\mathcal {V}(\mathsf {st}^\mathcal {V} _{i-1}, coins _i) = \mathcal {V}(i, coins _i)$.

Polynomial IOPs as a subclass of Algebraic Linear IOPs. In a Polynomial IOP, the two-step map is a special case of the two-step map in an algebraic linear IOP. Here $\mathbf {M} : \mathbb {F}^{\mu } \rightarrow \mathbb {F}^{m}$ represents the vector of monomials of degree at most d (in some canonical order) and the map associated with $\mathbf {M}$ is evaluation. Note that there are $m = {\mu + d \atopwithdelims ()d}$ such monomials. Furthermore, for any $\mathbf {q}_{i,k}$, the inner product $\varvec{\pi }_i^\mathsf {T} \mathbf {q}_{i,k}$ corresponds to the evaluation at $\varvec{\sigma }_{i,k}$ of the polynomial $\pi _i(\mathbf {X}) \in \mathbb {F}[\mathbf {X}]$, whose coefficient vector (in the same canonical monomial order) is equal to $\varvec{\pi }_i$.

5.2 Polynomial IOP Reductions

In this section we show that one can construct any algebraic linear IOP from a (multivariate) Polynomial IOP. This construction rests on two tools for univariate Polynomial IOPs. These tools are treated explicitly in the full version of this paper [19]. They can be realized with a small constant number of evaluations.

• Coefficient queries. The verifier verifies that an indicated coefficient of a polynomial oracle has a given value.

• Inner products. The verifier verifies that the inner product of the coefficient vectors of two polynomial oracles equals a given value.

Reducing algebraic linear IOPs to polynomial IOPs.

Theorem 3

Any public-coin t-round stateless algebraic linear IOP can be implemented with a $t+1$-round Polynomial IOP with preprocessing. Suppose the original $\ell$-query IOP is $(\mu ,d)$ algebraic with query length $(m_1,...,m_t)$ then the resulting Polynomial IOP has for each $i \in [t]$: $2\ell$ degree $m_i$ univariate polynomial oracles, $\ell$ pre-processed multivariate oracles of degree d and $\mu +1$ variables, $\ell$ degree $2m_i$ univariate polynomial oracles and $2\ell$ degree $2m_i$ univariate polynomial oracles. There is exactly one query to each oracle on a random point in $\mathbb {F}$. The soundness loss of the transformation is ${\mathsf {negl}}(\lambda )$ for a sufficiently large field (i.e., whose cardinality is exponential in $\lambda$).

We formally prove Theorem 3 in the full version of this paper [19]. Here we present the transformation without proof.

By definition of a $(\mu , d)$ algebraic linear IOP, in each ith round of the IOP there are $\ell$ query generation functions $\varvec{p}_{i,1},\ldots ,\varvec{p}_{i,\ell }: \mathbb {F}^\mu \rightarrow \mathbb {F}^{m_i}$, where each $\varvec{p}_{i,k}$ is a vector whose jth component is a $\mu$-variate degree-d polynomial $p_{i,k,j}$. These polynomials are applied to a seed matrix $\varvec{\sigma }_{i,k} \in \mathbb {F}^\mu$ (which is identifiable with or derived from the verifier’s ith round public-coin randomness $coins _i$); this evaluation produces $\varvec{p}_{i,k}(\varvec{\sigma }_{i,k}) = \mathbf {q}_{i,k} \in \mathbb {F}^{m_i}$ for all $k \in [\ell ]$. The vectors $\mathbf {q}_{i,k}$ are the columns of the query matrix $\mathbf {Q}_i \in \mathbb {F}^{m_i \times \ell }$.

Preprocessed oracles. For each round i of the original algebraic linear IOP, the prover and verifier preprocess $(\mu +1)$-variate degree-d polynomial oracles. For each $k \in [\ell ]$, the vector of polynomials $\varvec{p}_{i,k} = (p_{i,k,1},\ldots ,p_{i,k, m_i}) \in (\mathbb {F}[\mathbf {X}])^{m_i}$ with $\mathbf {X} = (X_1,\ldots ,X_\mu )$ is encoded as a single polynomial in $\mu + 1$ variables as follows. Introduce a new indeterminate Z, and then define $\tilde{P}_{i,k}(\mathbf {X}, Z) := \sum _{j=1}^{m_i} p_{i,k,j}(\mathbf {X}) Z^j \in \mathbb {F}[\mathbf {X},Z]$. The prover and verifier establish the oracle $\tilde{P}_{i,k}$, meaning that the verifier queries this oracle on enough points to be reassured that it is correct everywhere.

The transformed IOP. The original algebraic linear IOP is modified as follows.

• Wherever the original IOP prover sends an oracle $\varvec{\pi }_i$ of length $m_i$, the new prover sends a degree $m_i - 1$ univariate polynomial oracle $f_{\pi _i}$ whose coefficient vector is the reverse of $\varvec{\pi }_i$.

• Wherever the original IOP verifier makes $\ell$ queries within a round to a particular proof oracle $\varvec{\pi }_i$, where queries are defined by query matrix $\mathbf {Q}_i \in \mathbb {F}^{m_i \times \ell }$, consisting of column query vectors $(\mathbf {q}_{i,1},...,\mathbf {q}_{i,\ell })$, the new prover and verifier engage in the following interactive subprotocol for each $k \in [\ell ]$ in order to replace the kth linear query $\langle \varvec{\pi }_i, \mathbf {q}_{i,k} \rangle$:

  • Verifier: Run the original IOP verifier to get the public coin seed matrix $\varvec{\varSigma }_i$ and send it to the prover.

  • Prover: Derive the query matrix $\mathbf {Q}_i$ from $\varvec{\varSigma }_i$ using the polynomials $\varvec{p}_{i,1}, \ldots , \varvec{p}_{i, \ell }$. Send an oracle for the polynomial $F_{i,k}$ whose coefficient vector is $\mathbf {q}_{i,k}$.

  • Verifier: Sample uniform random $\beta \overset{\$}{\leftarrow }\mathbb {F}$ and query both $F_{i,k}$ and $\tilde{P}_{i,k}$ (the kth preprocessed oracle for round i) at $\beta$ in order to check that $F_{i,k} (\beta ) = \tilde{P}_{i,k}(\varvec{\sigma }_{i,k}, \beta )$. If the check fails, abort and output 0.

  • Prover: Compute $a_{i,k} = \langle \varvec{\pi }, \mathbf {q}_{i,k} \rangle$ and send $a_{i,k}$ to the verifier.

  • The prover and verifier run the inner product Polynomial IOP on the oracles $F_{i,k}$ and $f_{\pi _i}$ to convince the verifier that $a_{i,k} = \langle \mathbf {q}_{i,k}, \varvec{\pi }_i \rangle$. If the inner product subprotocol fails the verifier aborts and outputs 0.

If all substeps succeed, then the verifier obtains correct output of each oracle query; in other words, the responses are identical in the new and original IOP. These outputs are passed to the original verifier decision algorithm, which outputs 0 or 1.

5.3 Compiling Polynomial IOPs

Let $\varGamma = (\textsf {{Setup}}, \textsf {{Commit}}, \textsf {{Open}}, \textsf {{Eval}})$ be a multivariate polynomial commitment scheme. Given any t-round Polynomial IOP for $\mathcal {R}$ over $\mathbb {F}$, we construct an interactive protocol $\varPi = (\textsf {{Setup}}, \mathcal {P}, \mathcal {V})$ as follows. For clarity in our explanation, $\varPi$ consists of t outer rounds corresponding to the original IOP rounds and subrounds where subprotocols may add additional rounds of interaction between outer rounds.

• $\textsf {{Setup}}$: Run $\textsf {pp} \leftarrow \textsf {{Setup}}(1^\lambda )$

• In any round where the IOP prover sends a $(\mu , d)$ polynomial proof oracle $\varvec{\pi }: \mathbb {F}^\mu \rightarrow \mathbb {F}$, in the corresponding outer round of $\varPi$, $\mathcal {P}$ sends the commitment $c_{\varvec{\pi }} \leftarrow \textsf {{Commit}}(\textsf {pp}; \varvec{\pi })$

• In any round where the IOP verifier makes an evaluation query $\mathbf {z}$ to a $(\mu , d)$ polynomial proof oracle $\varvec{\pi }$, in the corresponding outer round of $\varPi$, insert an interactive execution of $\textsf {{Eval}}(\textsf {pp}, c_\pi , \mathbf {z}, y, \mu , d; \varvec{\pi })$ between $\mathcal {P}$ and $\mathcal {V}$, where $\varvec{\pi }(\mathbf {z}) = y$.

If $\mathcal {V}$ does not abort in any of these subprotocols, then it receives a simulated IOP transcript of oracle queries and responses. It runs the IOP verifier decision algorithm on this transcript and outputs the result.

Theorem 4

If the polynomial commitment scheme $\varGamma$ has witness-extended emulation, and if the t-round Polynomial IOP for $\mathcal {R}$ has negligible knowledge error, then $\varPi$ is a public-coin interactive argument for $\mathcal {R}$ that has witness-extended emulation.

5.4 Concrete Instantiations

Several proof systems use Polynomial IOPs and our compiler can be applied to them. We present PLONK [30] here and discuss several other proof systems [4, 22, 31, 43, 48] in the full version [19].

Theorem 6 provides the main theoretical result of this work, tying together the new DARK polynomial commitment scheme (Theorem 1), the compilation of Polynomial IOPs into SNARKs with preprocessing using polynomial commitments (Theorem 4), and a concrete univariate Polynomial IOPs. To enable this tie-up, we re-characterize the result of PLONK in terms of Polynomial IOPs, making use of the coefficient query technique (Sect. 5.2) as necessary.

Theorem 5

( PLONK, [30]). There is a 3-round HVZK Polynomial IOP with preprocessing for any NP relation $\mathcal {R}$ (with arithmetic complexity n) that makes 12 queries overall to 12 univariate degree n polynomial oracles. The total number of distinct query points is 2. The preprocessing verifier does O(n) work to check 7 of the univariate degree n polynomials.

Combining the $\textsf {{PLONK}}$ Polynomial IOP with the new transparent polynomial compiler of Sect. 4 gives the following result. Analogous results are obtained by using Sonic [43] or Marlin [22] instead.

Theorem 6

(New Transparent zk-SNARK). There exists an $O(\log n)$-round public-coin interactive argument of knowledge for any NP relation with arithmetic complexity n that has $O(\log n)$ communication, $O(\log n)$ “online” verification, quasilinear prover time, and a preprocessing step that is verifiable in quasilinear time. The argument of knowledge has witness-extended emulation assuming it is instantiated with a group $\mathbb {G}$ for which the Strong RSA Assumption, and the Adaptive Root Assumption hold.

6 Evaluation

We now evaluate Supersonic, the trustless-setup SNARK built on the Polynomial IOPs underlying Sonic [43], PLONK [30], and Marlin [22] and compiled using our DARK polynomial commitment scheme. The commitment scheme has several useful batching properties. It is possible to evaluate k polynomials of degree at most d using only 2 group elements and $(k+1)$ field elements. To take advantage of this we delay the evaluation until the last step of the protocol. We present the proof size for both the compilation of Sonic, PLONK and Marlin in Table 2. We use 1600 bits as the size of class group elements and $\lambda =120$. The security of 1600 bit class groups is believed to be equivalent to 3048bit RSA groups and have 120 bits of security [8, 17]. This leads to proof sizes of 16.5 KB for Sonic, 10.1 KB using PLONK and 12.3 KB using Marlin for circuits with $n = 2^{20}$ (one million) gates. Using 3048-bit RSA groups the proof sizes becomes 18.4 KB for the compilation of PLONK. If 100 bits of security suffice then a 1200 bit class group can be used and the compiled PLONK proofs are 7.8 KB for the same setting. In a 2048-bit RSA group this becomes 12.7 KB.

The comparison between the Polynomial IOPs is slightly misleading because n represents different indicators of complexity. Nevertheless this calculation shows that there are Polynomial IOPs that can be compiled using the DARK polynomial commitment scheme to SNARKs of roughly 10 KB in size. These numbers stand in contrast to STARKs which achieve proofs of 600 KB for computation of similar complexity [4]. We compare Supersonic to different other proof systems in Table 3. Supersonic is the only proof system with efficient verifier time, small proof sizes that does not require a trusted setup. Using 10 $\upmu$s per group operation⁵, this gives a verification time of around 72 ms.

Table 2. Proof size for $\textsf {{Supersonic}}$. Column 2 says how many polynomials are committed to in the SRS (offline oracles) and how many are sent by the prover (online oracles). Column 3 states the number of distinct evaluation points. The proof size calculation uses $|\mathbb {Z}_p|=120$ and $|\mathbb {G}|=1600$ for $n=2^{20}$ gates.

Table 3. Comparison table between different succinct arguments. In column order we compare on transparent setup, CRS size, prover and verifier time, asymptotic proof size and concrete proof for an NP relation with arithmetic complexity $2^{20}$. Even when precise factors are given the numbers should be seen as estimates. For example, we chose to not display smaller order terms. The symbol $\mathbb {G}_U$ denotes an element in group of unknown order, $\mathbb {G}_{B}$ one in a group with a bilinear map (pairing), $\mathbb {G}_{P}$ one in a prime order group with known order. Furthermore, $\textsf {EXP}$ refers to exponentiation of $\lambda$-bit numbers in these groups, and $\mathsf {H}$ is either the size of a hash output or the time it takes to compute a hash. The prover time for the group based schemes can be brought down by a log factor when using multi-exponentiation techniques.

7 Conclusion

In this work we presented the DARK compiler: a polynomial commitment scheme from falsifiable assumptions in groups of unknown order with evaluation proofs that can be verified in logarithmic time. We also presented Polynomial IOPs, a unifying information-theoretical framework underlying the information theoretic foundation of several recent SNARK constructions. Polynomial IOPs can be compiled into a concrete SNARK using a polynomial commitment scheme and the Fiat-Shamir transform. We showed that applying the DARK compiler to recent Polynomial IOPs yields the first trustless SNARKs (i.e., with a transparent untrusted setup) that have practical proof sizes and verification times. In particular, this is the first trustless/transparent SNARK construction that has asymptotically logarithmic verification time (ignoring the $\lambda$-dependent factors, which are comparable to $\lambda$-dependent factors in prior works). Finally, unlike all known SNARKs in bilinear groups, the construction does not require knowledge of exponent assumptions. Several important open questions remain:

• Our polynomial commitment scheme has prover time linear in the total number of coefficients, even for zero coefficients. Consequently for a sparse bivariate polynomial of degree d in each variable the prover time is quadratic in d. A sparse polynomial commitment scheme would directly enable an efficient compilation of simple information theoretic protocols such as QAPs.

• Asymptotically, Supersonic’s prover time is on par with pairing-based SNARK constructions, however, a concrete implementation and performance comparison remains open.

• This work further motivates the study of class groups and groups of unknown order. In particular we rely on a recently introduced Adaptive Root Assumption.

• Our polynomial commitment scheme uses a simple underlying information theoretic protocol that could be compiled using a (partially) homomorphic commitment scheme over polynomials, or even another type of integer homomorphic commitment scheme. This leaves open whether there are different ways of instantiating our DARK compiler under different cryptographic assumptions.