Impossibility Results for Lattice-Based Functional Encryption Schemes

Abstract

Functional Encryption denotes a form of encryption where a master secret key-holder can control which functions a user can evaluate on encrypted data. Learning With Errors (LWE) (Regev, STOC’05) is known to be a useful cryptographic hardness assumption which implies strong primitives such as, for example, fully homomorphic encryption (Brakerski-Vaikuntanathan, FOCS’11) and lockable obfuscation (Goyal et al., Wichs et al., FOCS’17). Despite its stre ngth, however, there is just a limited number of functional encryption schemes which can be based on LWE. In fact, there are functional encryption schemes which can be achieved by using pairings but for which no secure instantiations from lattice-based assumptions are known: function-hiding inner product encryption (Lin, Baltico et al., CRYPTO’17) and compact quadratic functional encryption (Abdalla et al., CRYPTO’18). This raises the question whether there are some mathematical barriers which hinder us from realizing function-hiding and compact functional encryption schemes from lattice-based assumptions as LWE.

To study this problem, we prove an impossibility result for function-hiding functional encryption schemes which meet some algebraic restrictions at ciphertext encryption and decryption. Those restrictions are met by a lot of attribute-based, identity-based and functional encryption schemes whose security stems from LWE. Therefore, we see our results as important indications why it is hard to construct new functional encryption schemes from LWE and which mathematical restrictions have to be overcome to construct secure lattice-based functional encryption schemes for new functionalities.

A. Ünal—The author is supported by ERC Project 724307 ‘PREP-CRYPTO’.

Work done while the author was working at Karlsruhe Institute of Technology.

1 Introduction

Functional Encryption (FE) schemes are special encryption schemes in which the holder of a master secret key can issue secret keys for specific functions to users. By knowing a secret key for a function f and a ciphertext for a message x, an adversary shall learn nothing more of x than f(x). FE schemes have proven to be extremely versatile. Not only does their notion generalize other forms of encryption like Attribute-Based (ABE) or Identity-Based Encryption (IBE), but also do we know that compact single-key FE and linearly compact FE for cubic polynomials together with plausible assumptions imply indistinguishability obfuscation [10, 14, 29].

Function-Hiding Functional Encryption (FHFE) schemes are an even stronger subclass of FE where we demand that an adversary – given a secret key for a function f and a ciphertext for a message x – learns nothing about f and x except of f(x); i.e., the secret keys now hide the functions they are supposed to evaluate.

We know that FE schemes with a bounded number of secret keys, an adversary may learn, are already achievable from minimal assumptions [11]. However, if we try to achieve security for an unbounded number of secret keys, then we are left with (function-hiding) inner-product encryption, linearly compact quadratic FE and FE schemes for constant-degree polynomials which are yielded by relinearizing. Of course, there are special cases of FE like attribute-based and identity-based encryption schemes. In those schemes, a ciphertext is accompanied with a non-hidden attribute or identity and decryption is successful iff the attribute/identity matches the policy of the secret key. However, the main focus in this work are FE schemes, since we are interested in schemes which perform various computations on hidden inputs. We stress here that for linearly compact quadratic FE and function-hiding inner-product FE there are just pairing-based constructions known so far [3, 12, 13, 21, 28].

Learning With Errors (LWE) [30] is a well-established hardness assumption. It states that it is hard to solve a system of linear equations over a modulus q, if the solution has sufficient entropy, the coefficients of the equations are chosen uniformly random from $\mathbb {Z}_q$ and one column of the presented system has been perturbed by a small noise-vector whose entries are sampled from a suitable error-distribution. Because of its strong homomorphic properties, there are fully homomorphic encryption schemes and lockable obfuscation schemes whose security can be proven solely under LWE [17, 24, 32]. Up to now, it is not possible to construct those schemes from other standard assumptions. Intuitively, one would assume that its homomorphic properties imply a lot of different FE schemes. But as we have stressed, the most complex already existing FE schemes cannot be replicated by lattice-based constructions. In fact, inner product encryption is the only FE scheme whose security can be based on LWE (again, putting ABE and IBE aside). Because of the aforementioned amply homomorphic properties of LWE, this is very surprising and leads us to the following question:

We show that there are two properties, both very common under LWE-based FE schemes, which make it impossible for a function-hiding inner-product encryption scheme to be secure. The first property lies in the decryption algorithms of LWE-based encryption schemes: If we take a close look at the pairing-based schemes, we see that decryption is always complex, for it involves computing discrete logarithms of the target group of the pairing. On the other hand, a lot of LWE-based IBE and FE schemes have simple decryption algorithms [2, 4, 6, 7, 16, 19]. In most cases, for moduli $q> p > 1$, a secret key ${{\,\mathrm{\textsf {sk}}\,}}$ in such a scheme usually determines a multivariate polynomial $g_{{{\,\mathrm{\textsf {sk}}\,}}}(Y_1,\ldots , Y_s)$ of constant total degree, while the ciphertext is a vector ${{\,\mathrm{\textsf {ct}}\,}}\in \mathbb {Z}_q^s$. At decryption, the polynomial is evaluated at the ciphertext which yields a value $g_{{{\,\mathrm{\textsf {sk}}\,}}}({{\,\mathrm{\textsf {ct}}\,}}) \in \mathbb {Z}_q$; this value will be rounded to the nearest number of $\mathbb {Z}_p$, i.e., it will be divided by $\left\lfloor {q}/{p}\right\rfloor$ and then rounded to the nearest integer in $\{0,\ldots , p-1\}$. In full detail, this means

$$\begin{aligned} {{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {sk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}) = \left\lceil \frac{g_{{{\,\mathrm{\textsf {sk}}\,}}}({{\,\mathrm{\textsf {ct}}\,}})}{\left\lfloor {q}/{p}\right\rfloor }\right\rfloor . \end{aligned}$$

We believe that this property already suffices to render a FHFE scheme insecure. Therefore, we state here the following conjecture:

Conjecture 1

Let ${{\,\mathrm{\textsf {FE}}\,}}= ({{\,\mathrm{\textsf {Setup}}\,}}, {{\,\mathrm{\textsf {KeyGen}}\,}}, {{\,\mathrm{\textsf {Enc}}\,}}, {{\,\mathrm{\textsf {Dec}}\,}})$ be a correct private-key functional encryption scheme for computing inner-products of vectors in $\mathbb {Z}_p^n$. If there is a constant $d' \in \mathbb {N}$ and a polynomial s in the security parameter, s.t.

• each ciphertext ${{\,\mathrm{\textsf {ct}}\,}}$ sampled by ${{\,\mathrm{\textsf {Enc}}\,}}$ is a vector in $\mathbb {Z}_q^s$,

• each secret key ${{\,\mathrm{\textsf {sk}}\,}}$ sampled by ${{\,\mathrm{\textsf {KeyGen}}\,}}$ is a multivariate polynomial in $\mathbb {Z}_q[Y_1,\ldots , Y_s]$ of total degree $\le d'$

• and the decryption algorithm works by

  $$\begin{aligned} {{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {sk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}) = \left\lceil \frac{{{\,\mathrm{\textsf {sk}}\,}}({{\,\mathrm{\textsf {ct}}\,}})}{\left\lfloor {q}/{p}\right\rfloor }\right\rfloor , \end{aligned}$$

then ${{\,\mathrm{\textsf {FE}}\,}}$ cannot be function-hiding secure for an unbounded number of secret keys.

We leave it as an open question to prove or refute Conjecture 1. Instead, we prove in this work a weaker version of the above statement. If we are to take a closer look at the aforementioned IBE and FE schemes and some ABE schemes [15, 23], we can distinguish an additional property which seems to be common for some LWE-based schemes. They tend to have very algebraic encryption algorithms. Take, for example, a closer look at ciphertext encryption in the LWE-based inner-product encryption schemes of Agrawal et al. [7]. For an input vector $x \in \{0,\ldots , p\,-\,1\}^l$ and two publicly known matrices $A\in \mathbb {Z}^{m\times n}_q,U\in \mathbb {Z}^{l\times n}_q$, ciphertexts are generated by sampling a uniformly random vector $s\leftarrow \mathbb {Z}^n_q$, two gaussian noise vectors ${e_0\leftarrow \mathcal {D}_{\mathbb {Z}^m,\alpha q}}, {e_1 \leftarrow \mathcal {D}_{\mathbb {Z}^l,\alpha q}}$ and outputting ${{\,\mathrm{\textsf {ct}}\,}}= {(As +e_0, Us + e_1 + b \cdot x)}$ where b is either $\left\lfloor q/K\right\rfloor$ or $p^{k-1}$. Note that we can distinguish two parts in this encryption algorithm: a very complex offline part, where $m+l$ multivariate degree-1 polynomials $g_1(X),\ldots , g_m(X), h_1(X), \ldots , h_l(X)$ are sampled by only knowing the public key (A, U, p, q, K) and without looking at the input x:

$$\begin{aligned} g_i(X_1,\ldots , X_l)&= \langle a_i ~ | ~ s\rangle +e_{0,i},\\ h_i(X_1,\ldots , X_l)&= \langle u_i ~ | ~ s\rangle +e_{1,i} + \left\lfloor q/K\right\rfloor \cdot X_i. \end{aligned}$$

And, a simple online part which just consists of inserting x in the polynomials sampled before and outputting the ciphertext ${{\,\mathrm{\textsf {ct}}\,}}= (g_1(x),\ldots , g_m(x),$ $h_1(x), \ldots , h_l(x))$. This distinction in a complex offline and a simple online part can be seen in the other aforementioned schemes, too. Therefore, we extract it as an additional characteristic of some LWE-based schemes and make it more precise in the following:

We say ${{\,\mathrm{\textsf {Enc}}\,}}$ is an encryption algorithm of depth d over $\mathbb {Z}_q$, if there is a ppt algorithm ${{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}$, s.t. we have for each master secret key ${{\,\mathrm{\textsf {msk}}\,}}$ and input $x\in \mathbb {Z}_p^n$:

$$\begin{aligned} {{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, x) =&\left\{ \right. \nonumber \\&~~~~ (r_1,\ldots , r_s) \leftarrow {{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}({{\,\mathrm{\textsf {msk}}\,}}) \end{aligned}$$

(1)

$$\begin{aligned}&~~~~ \textsf {return }(r_1(x), \ldots , r_s(x)) \\&\left. \right\} \nonumber \end{aligned}$$

(2)

where we demand that each $r_i$ is a multivariate polynomial in $\mathbb {Z}_q[X_1,\ldots , X_n]$ of total degree $\le d$. We will call line (1) the offline part and line (2) the online part of ${{\,\mathrm{\textsf {Enc}}\,}}$. Indeed, with this additional property we can prove an FHFE scheme to be insecure.

1.1 Contribution

For moduli $q= q(\lambda )>p = p(\lambda )$ such that q is prime, $\frac{q}{p}$ is polynomially bounded and p is not bounded by a constant, we prove the following:

Theorem 1

(Informal Main Theorem). Assume that the prerequisites of Conjecture 1 hold and that additionally ${{\,\mathrm{\textsf {Enc}}\,}}$ is of depth d over $\mathbb {Z}_q$ for some constant $d \in \mathbb {N}$.

Then, ${{\,\mathrm{\textsf {FE}}\,}}$ cannot be function-hiding secure for an unbounded number of secret keys.

To be more precise, we give a bound of the maximum number of secret keys which can be issued to an adversary before he can break ${{\,\mathrm{\textsf {FE}}\,}}$ (Corollary 4). On a very high level, our proof idea is to use the algebraic structure of the composition ${{\,\mathrm{\textsf {Dec}}\,}}\circ {{\,\mathrm{\textsf {Enc}}\,}}$. By doing so, we show that the decryption noises are generated in a very algebraic way, are small and contain information about the encrypted ciphertexts. Therefore, we can prove Theorem 1 by analysing them.

As an additional result, we show that private-key encryption schemes where the encryption algorithms are of constant depth and the ciphertext vectors are short enough cannot be secure (Theorem 5 and Corollary 3). This result does not depend on the decryption algorithms of the private-key encryption schemes.

Generality of Our Results. We note here that there are a lot of LWE-based ABE schemes whose decryption algorithms are too complex to be subsumed by the equation ${{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {sk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}) = \left\lceil {{{\,\mathrm{\textsf {sk}}\,}}({{\,\mathrm{\textsf {ct}}\,}})}/{\left\lfloor {q}/{p}\right\rfloor }\right\rfloor$. This is because they allow policy-predicates which cannot be computed by constant-depth circuits. Since the policy-predicate needs to be computed at decryption, their decryption algorithms must be at least as complicated as the most complex policy-predicate they allow. However, the aforementioned ABE schemes in [15, 23] have decryption algorithms that become simple enough to fit the equation ${{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {sk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}) = \left\lceil {g_{{{\,\mathrm{\textsf {sk}}\,}}}({{\,\mathrm{\textsf {ct}}\,}})}/{\left\lfloor {q}/{p}\right\rfloor }\right\rfloor$, if we restrict the policy-circuits in those schemes to be of constant depth and if attributes and policy match at decryption.

Two-Input Quadratic Functional Encryption. We can derive from Theorem 1 an impossibility result for 2-input quadratic FE schemes. A 2-input quadratic FE scheme evaluates functions with two distinguished inputs and has a left and a right encryption algorithm. To decrypt a value f(x, y), one needs a secret key for f, a left ciphertext for x and a right ciphertext for y. Since such a scheme contains a secret key for the quadratic function $f(x,y) = \langle x ~ | ~ y\rangle$, it can emulate a function-hiding inner-product encryption scheme, even if it is only single-key secure.

Corollary 1

Let $2{{\,\mathrm{\textsf {FE}}\,}}= ({{\,\mathrm{\textsf {Setup}}\,}}, {{\,\mathrm{\textsf {KeyGen}}\,}}, {{\,\mathrm{\textsf {Enc}}\,}}^R, {{\,\mathrm{\textsf {Enc}}\,}}^L, {{\,\mathrm{\textsf {Dec}}\,}})$ be a correct private-key 2-input functional encryption scheme for quadratic functions $f : \mathbb {Z}_p^n \times \mathbb {Z}_p^n \overset{}{\rightarrow } \mathbb {Z}_p$. If there are $s \in {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )$ and a constant $d' \in \mathbb {N}$, s.t.

• ${{\,\mathrm{\textsf {Enc}}\,}}^L$ is of constant depth d over $\mathbb {Z}_q$,

• each ciphertext ${{\,\mathrm{\textsf {ct}}\,}}^L$ sampled by ${{\,\mathrm{\textsf {Enc}}\,}}^L$ is a vector in $\mathbb {Z}_q^s$,

• each pair of a secret key ${{\,\mathrm{\textsf {sk}}\,}}$ and a right ciphertext ${{\,\mathrm{\textsf {ct}}\,}}^R$ determines a multivariate polynomial $g_{{{\,\mathrm{\textsf {sk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}^R}\in \mathbb {Z}_q[X_1,\ldots , X_s]$ of total degree $\le d'$ s.t. the decryption algorithm works by

  $$\begin{aligned} {{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {sk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}^L, {{\,\mathrm{\textsf {ct}}\,}}^R) = \left\lceil \frac{g_{{{\,\mathrm{\textsf {sk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}^R}({{\,\mathrm{\textsf {ct}}\,}})}{\left\lfloor {q}/{p}\right\rfloor }\right\rfloor , \end{aligned}$$

then $2{{\,\mathrm{\textsf {FE}}\,}}$ cannot be single-key secure.

1.2 Interpretation and Open Problems

To prove Theorem 1, we assume that the exterior modulus q of the FHFE scheme ${{\,\mathrm{\textsf {FE}}\,}}$ is prime. Furthermore, we need that the fraction q/p is bounded by a polynomial in the security parameter $\lambda$ and that the interior modulus p is for almost all $\lambda$ greater than some constant which depends on the depth of ${{\,\mathrm{\textsf {FE}}\,}}$. Note that q/p is usually a bound for the error noise used in LWE-based schemes. Since LWE is assumed to be hard, even if its modulus q is a prime and the deviation of its error noise is bounded by a polynomial in $\lambda$, we do not think that those requirements are big restrictions for our results.

We see the results in this paper as a useful argument in understanding the difficulties in constructing LWE-based function-hiding functional encryption schemes. An even more useful argument would be to close the gap and prove Conjecture 1. Because of Theorem 1, to prove our conjecture, it now suffices to transform a function-hiding inner-product encryption scheme which is correct and secure and fulfils the requirements of the conjecture to one that fulfils the requirements of Theorem 1. In other words, it suffices to take an FHFE scheme which already decrypts in an LWE-like manner and simplify its encryption algorithm to one of constant depth which stays secure and correct.

Another way to extend the results here is to prove Theorem 1 for encryption algorithms where, in the online part, one first computes a bit-decomposition $G^{-1}(x)$ of an input vector x and then applies the polynomials sampled in the offline part to $G^{-1}(x)$. A lot of the techniques here would not be suitable for this task; indeed, one would need to develop more advanced techniques to show this.

1.3 Related Work

The idea of decomposing encryption algorithms into simple online and complex offline parts has already been studied with the purpose of finding FE schemes with practical usages (we cite [8, 26] as examples). However, to the best of our knowledge, this is the first work where the online/offline structure of encryption has been used to prove an impossibility result.

Ananth and Vaikuntanathan showed that FE for P/poly with a bounded number of secret keys can already be achieved from minimal assumptions, i.e. public-key encryption in the asymmetric setting and one-way functions in the symmetric setting [11]. The ciphertexts in their schemes are growing linearly with the number of secret keys which can be handed out to an adversary. It is presumably hard to improve their result, since we know that a bounded FE scheme with sufficiently compact ciphertexts would already imply indistinguishability obfuscation [10, 14].

As mentioned, it is hard to construct FE schemes for stronger functionalities. In recent years, researchers circumvented this problem and looked at novel FE schemes with additional properties: Abdalla, Chotard and other researchers constructed multi-input and decentralized multi-client inner-product encryption schemes [1, 3, 5, 20]. Those are inner-product encryption schemes where a function has multiple inputs and to decrypt one needs a secret key and multiple suitable ciphertexts. In the decentralized schemes, one gets rid of the master secret key holder. Jain et al. introduced the notion of 3-restricted FE [9, 27], which can be understood as cubic FE where a ciphertext just hides two out of three factors.

1.4 Technical Overview

To prove Theorem 1, we need to show the existence of a selective adversary who wins the function-hiding IND-CPA game against the function-hiding inner-product encryption scheme ${{\,\mathrm{\textsf {FE}}\,}}$. In this game, the adversary submits an unbounded number of inputs $x_i^0$ and functions $f_j^0$ for world 0 and an unbounded number of inputs $x_i^1$ and functions $f_j^1$ for world 1. Then, the challenger draws a random bit $b \leftarrow \{0,1\}$ and sends the corresponding ciphertexts and secret keys of world b to the adversary. The adversary wins, if he guesses b correctly and if the submitted inputs and functions would not tell him trivially in which world he lives, i.e., if we have for all i and j

$$\begin{aligned} f_j^0(x_i^0) = f_j^1(x_i^1). \end{aligned}$$

We do not directly construct an adversary to break ${{\,\mathrm{\textsf {FE}}\,}}$. Instead, we show how an adversary can reduce the problem of breaking ${{\,\mathrm{\textsf {FE}}\,}}$ to the problem of breaking other encryption schemes with additional properties. To do so, we apply multiple transformations to ${{\,\mathrm{\textsf {FE}}\,}}$. Eventually, we end with a private-key encryption scheme whose ciphertexts are short integer vectors and whose encryption algorithm is of constant depth. Then, we construct a simple adversary who can break such encryption schemes.

To make our argument go through, we need the transformations to preserve the security and correctness of the transformed schemes. It is easy to see that security is preserved, since we ensure that all changes to ${{\,\mathrm{\textsf {FE}}\,}}$ can be computed by an adversary while he plays the above security game against ${{\,\mathrm{\textsf {FE}}\,}}$. On the other hand, we can not always guarantee that our transformations preserve correctness. In fact, one transformation step applied to ${{\,\mathrm{\textsf {FE}}\,}}$ changes it in such a way that decryption succeeds only in a non-negligible number of cases. Furthermore, it is important that at each time we have an encryption algorithm of constant depth. This means, each transformation step either changes the encryption algorithm without changing its depth or at most changes its depth to another constant value.

Our proof consists of three major steps:

• (1) We first change ${{\,\mathrm{\textsf {FE}}\,}}$ s.t. all ciphertexts have short entries relative to the modulus q. To do this, the adversary queries a lot of secret keys for the zero-function and learns, by doing so, the structure of the space of secret keys. Then, he can exchange a ciphertext with a vector of decryption noises. Those noises have to be short, because otherwise they would make a correct decryption impossible. On the other hand, however, we show that those noises contain enough information about the original ciphertext to make decryption possible in a non-negligible number of cases. Therefore, we can assume ${{\,\mathrm{\textsf {FE}}\,}}$ to have short ciphertexts. Then, we use a straightforward transformation to convert ${{\,\mathrm{\textsf {FE}}\,}}$ to a private-key encryption scheme ${{\,\mathrm{\textsf {SKE}}\,}}_q$ whose ciphertexts are short relative to q and whose encryption algorithm is of constant depth over $\mathbb {Z}_q$.

• (2) Since the encryption algorithm of ${{\,\mathrm{\textsf {SKE}}\,}}_q$ is of constant depth, ${{\,\mathrm{\textsf {SKE}}\,}}_q$ encrypts a number x by sampling some polynomials, evaluating those polynomials at x and reducing the result modulo q. To analyse the ciphertexts of ${{\,\mathrm{\textsf {SKE}}\,}}_q$, we need to get rid of the arithmetic overflows in the online part of its encryption algorithm. We observe that, if r(X) is a polynomial with small coefficients, then, for some small x values, r(x) does not change when we reduce it modulo q. Furthermore, we know the ciphertexts of ${{\,\mathrm{\textsf {SKE}}\,}}_q$ to be short relative to q. By using this fact, we can apply simple changes to the encryption algorithm of ${{\,\mathrm{\textsf {SKE}}\,}}_q$ to ensure that the polynomials sampled by its offline algorithm have very small coefficients. By doing so, we can change ${{\,\mathrm{\textsf {SKE}}\,}}_q$ to a private-key encryption scheme ${{\,\mathrm{\textsf {SKE}}\,}}$ of constant depth whose ciphertext vectors are sufficiently short and where no arithmetic overflows do occur in the online part of its encryption algorithm.

• (3) In ${{\,\mathrm{\textsf {SKE}}\,}}$, a message x gets encrypted by sampling random integer polynomials $r_1,\ldots , r_m$ of constant degree and computing $(r_1(x),\ldots , r_m(x))$ as ciphertext without any arithmetic overflows. Intuitively, such a scheme should not be secure and, indeed, we show that such a scheme can only be secure, if its ciphertexts do not contain any information about the encrypted messages. But this makes decryption impossible. Since we showed that a correct and secure FHFE scheme ${{\,\mathrm{\textsf {FE}}\,}}$ can be transformed into a secure private-key encryption scheme whose ciphertexts contain a non-negligible amount of information, it follows that ${{\,\mathrm{\textsf {FE}}\,}}$ could not be secure and correct in the first place.

We now take a closer look at the techniques used in each step.

Replacing Ciphertexts with Decryption Noise. We describe here how to make the ciphertexts of ${{\,\mathrm{\textsf {FE}}\,}}$ short. For simplicity, let us assume that we have already relinearized ciphertexts and secret keys, i.e. decryption works by

$$\begin{aligned} {{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {sk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}) = \left\lceil \frac{{\langle {{\,\mathrm{\textsf {sk}}\,}} ~ | ~ {{\,\mathrm{\textsf {ct}}\,}}\rangle }}{\left\lfloor q/p\right\rfloor }\right\rfloor . \end{aligned}$$

Query a lot of secret keys $v_1,\ldots , v_m\leftarrow {{\,\mathrm{\textsf {KeyGen}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, 0)$ for the zero-function and draw a ciphertext ${{\,\mathrm{\textsf {ct}}\,}}_x$ for an arbitrary input $x \in \mathbb {Z}_p^n$. Each $v_i$ must decrypt ${{\,\mathrm{\textsf {ct}}\,}}_x$ to zero, since this is the value of the zero-function applied to x. Because of decryption correctness of ${{\,\mathrm{\textsf {FE}}\,}}$, we can therefore assume that we have for each $v_i$

$$\begin{aligned} \left| \langle v_i ~ | ~ {{\,\mathrm{\textsf {ct}}\,}}_x\rangle \right| \le \left\lfloor \frac{q}{p}\right\rfloor . \end{aligned}$$

Otherwise, ${\langle v_i ~ | ~ {{\,\mathrm{\textsf {ct}}\,}}_x\rangle }/{\left\lfloor {q}/{p}\right\rfloor }$ would not round to zero. We can now exchange ${{\,\mathrm{\textsf {ct}}\,}}_x$ with the following new ciphertext for x:

$$\begin{aligned} {{\,\mathrm{\textsf {ct}}\,}}_x' = (\langle v_1 ~ | ~ {{\,\mathrm{\textsf {ct}}\,}}_x\rangle , \ldots , \langle v_m ~ | ~ {{\,\mathrm{\textsf {ct}}\,}}_x\rangle ). \end{aligned}$$

This ciphertext just consists of noise values which are generated when decrypting ${{\,\mathrm{\textsf {ct}}\,}}_x$ with secret keys for the zero-function. Therefore, each entry of ${{\,\mathrm{\textsf {ct}}\,}}_x'$ is bounded by $\left\lfloor {q}/{p}\right\rfloor$. The question remains, how much information about x is left in ${{\,\mathrm{\textsf {ct}}\,}}_x'$ and if it is even possible to recover f(x) from ${{\,\mathrm{\textsf {ct}}\,}}_x'$ and ${{\,\mathrm{\textsf {sk}}\,}}_f$. We show that in a non-negligible number of cases a successful decryption is still possible. That is because of the function-hiding property of ${{\,\mathrm{\textsf {FE}}\,}}$ which vaguely implies that a secret key for f has to lie in ${{\,\mathrm{{\textsf {span}}}\,}}_{\mathbb {Z}_q}\{v_1,\ldots , v_m\}$ with non-negligible probability.

Getting Rid of Arithmetic Overflows. The key observation in step (2) is that, if we evaluate a polynomial of degree d with small coefficients at a small input, reducing the result modulo q will not change its value. However, the polynomials $r_1(X),\ldots , r_m(X)$ sampled in the offline part of the encryption algorithm of ${{\,\mathrm{\textsf {SKE}}\,}}_q$ do not necessarily have small coefficients. We only know them to have small output values. We prove that there is a constant c, s.t. each $c\cdot r_i$ has sufficiently small coefficients modulo q. The existence of c can be shown by using a quasi-inverse¹ of the Vandermonde matrix V for the tuple $(0,1,\ldots , d)$, that is an integer matrix whose product with V equals a scaled identity matrix.

By simply multiplying ciphertexts of ${{\,\mathrm{\textsf {SKE}}\,}}_q$ with c, we can make them behave like they were outputted from an encryption algorithm of constant depth where no arithmetic overflows do occur in its online part. Therefore, we can transform ${{\,\mathrm{\textsf {SKE}}\,}}_q$ into ${{\,\mathrm{\textsf {SKE}}\,}}$.

Quasi-inverses of Vandermonde have been recently used by Esgin et al. to extract witnesses out of many polynomial relations [22]. However, in this work, we use a different quasi-inverse than them, which yields better bounds for our results.

Statistically Distinguishing Random Polynomials. We describe here, how our adversary breaks ${{\,\mathrm{\textsf {SKE}}\,}}$ in step (3). It suffices to look at the j-th coordinate of a ciphertext of ${{\,\mathrm{\textsf {SKE}}\,}}$. At input x, the j-th coordinate is computed by sampling a random polynomial $r_j(X)$ of constant degree d in the offline part and evaluating it at x. Our adversary works by guessing one $x\ne 0$ and comparing and . We show, if for each x the means and do not differ by a non-negligible amount, then $r_j(X)$ is of degree at most $d-1$ with overwhelming probability. By inductively using hybrids, one can see that $r_j(X)$ must be of degree 0, i.e. constant, with overwhelming probability. But, if $r_j(X)$ is constant, the value $r_j(x)$ does not carry any information about x. Therefore, if the ciphertexts of ${{\,\mathrm{\textsf {SKE}}\,}}$ contain a non-negligible amount of information about the encrypted messages, it follows that there must be some j and $x\ne 0$ s.t. our adversary can successfully distinguish and and, therefore, successfully distinguish ciphertexts for 0 from ciphertexts for x.

1.5 Organization of This Work

We first introduce some preliminaries in Sect. 2 and some important definitions and concepts in Sect. 3. Then, in Sect. 4, we give an adversary who breaks private-key encryption schemes of constant depth which do not make use of arithmetic overflows. In Sect. 5, we then derive an impossibility result for private-key encryption schemes of constant depth with short ciphertexts over $\mathbb {Z}_q$ by transforming them to schemes we broke in the preceding section. Finally, in Sect. 6, we show the impossibility of LWE-like FHFE schemes with simple online/offline encryption by transforming them to schemes of the preceding section.

Due to lack of space, we have ot omit the proofs of some lemmas. The reader can find those proofs in the full version of this paper [31].

2 Preliminaries

For $n \in \mathbb {N}= \{1,2,3,\ldots \}$, set $[n] := \left\{ 1,\ldots , n\right\}$. We define two sets of functions:

For functions $f,g : \mathbb {N}\overset{}{\rightarrow } \mathbb {R}$, we write $f(\lambda ) \ge g(\lambda ) - {{\,\mathrm{{\textsf {negl}}}\,}}(\lambda )$, if there is an $\varepsilon \in {{\,\mathrm{{\textsf {negl}}}\,}}(\lambda )$ s.t. we have $f(\lambda ) \ge g(\lambda ) - \varepsilon (\lambda )$ for all $\lambda$.

For $x \in \mathbb {R}$, we define the following roundings: $\left\lfloor x\right\rfloor := \max \left\{ z\in \mathbb {Z} ~ | ~ z\le x\right\}$, ${\left\lceil x\right\rceil := \min \left\{ z\in \mathbb {Z} ~ | ~ z\ge x\right\} }$ and ${\left\lceil x\right\rfloor := \max \left\{ z\in \mathbb {Z} ~ | ~ ~2\cdot \left| x-z\right| \le 1\right\} }$.

For two discrete distributions $\mathcal {D}_1, \mathcal {D}_2$ over a set X we define the statistical distance of $(\mathcal {D}_1, \mathcal {D}_2)$ by $\varDelta (\mathcal {D}_1, \mathcal {D}_2) := \frac{1}{2} \sum _{x \in X} \left| \mathcal {D}_1(x) - \mathcal {D}_2(x)\right|$.

2.1 Statistical Preliminaries

Theorem 2

(Hoeffding’s Inequality). Let $n \in \mathbb {N}$ and $B,t \ge 0$. For n independent random variables $X_1,\ldots , X_n$ with $\left| X_i\right| \le B$, we have

Corollary 2

Let $\mathcal {D}$ be a memoryless source that outputs real numbers which are bounded by $B\ge 0$. Let $r \in \mathbb {N}$ and set $n = 2r^3$. Let $\mu$ be the mean of $\mathcal {D}$ and let $E_n$ be the random variable which is sampled by n-fold querying $\mathcal {D}$, summing its outputs and dividing this sum by n. Then, we have

$$\begin{aligned} \Pr \left[ \left| E_n- \mu \right| \le \frac{ B}{r} \right] \ge 1 - 2e^{-r}. \end{aligned}$$

2.2 Algebraic Preliminaries

Theorem 3

Let $f(X) = \sum _{i = 0}^d a_i X^i$ be a polynomial of degree d over $\mathbb {R}$. Then

$$\begin{aligned} d! \cdot a_d=\sum _{k = 0}^d (-1)^{d - k}\left( {\begin{array}{c}d\\ k\end{array}}\right) f(k). \end{aligned}$$

This theorem can be proven by using discrete derivatives. For example, a proof can be deduced by trick 2 of [25], Section 5.3. Alternatively, the reader can find a full proof in [31].

Now, let $q \in \mathbb {N}$ be a modulus.

Definition 1

For $a \in \mathbb {Z}$, we define the absolute value modulo q by

$$\begin{aligned} \left| a \bmod q\right| := \min _{z\in q\mathbb {Z}} \left| a + z\right| \in \left\{ 0,\ldots , \left\lfloor \frac{q}{2}\right\rfloor \right\} . \end{aligned}$$

Lemma 1

• (a) For $a \in \mathbb {Z}$, we have $\left| a \bmod q\right| = 0 \Leftrightarrow a \in q\mathbb {Z}$.

• (b) For $a_1,\ldots , a_n \in \mathbb {Z}$, we have $\left| \sum _{i = 1}^n a_i \bmod q \right| \le \sum _{i = 1}^n \left| a_i \bmod q\right|$.

• (c) For $a, z \in \mathbb {Z}$, we have $\left| z \cdot a \bmod q\right| \le \left| z\right| \cdot \left| a \bmod q\right|$.

2.3 Learning Theory-Preliminaries

In this subsection, we study the problem of learning vector subspaces. Let $\mathbb {F}$ be an arbitrary field.

Lemma 2

Let $s \in \mathbb {N}_0 = \{0,1,2, \ldots \}$ and let $\mathcal {D}$ be a discrete distribution over $\mathbb {F}^s$. For $m\in \mathbb {N}$, we have

$$\begin{aligned} \mathop {\Pr }\limits _{v_1,\ldots , v_{m} \leftarrow \mathcal {D}} \left[ v_{m} \in {\mathsf{span}}_\mathbb {F}\left\{ v_1,\ldots , v_{m-1}\right\} \right] \ge 1 - \frac{s}{m}. \end{aligned}$$

Proof

Let $m > s$ and fix $v_1,\ldots , v_{m} \in {{\,\mathrm{{\textsf {supp}}}\,}}(\mathcal {D})$. Denote by $S^m$ the group of permutations of the set [m] and by $T \subset S^m$ the subgroup of order m which is generated by the cyclic rotation $(123\ldots m)$. For $\tau \in T$ set $V_\tau := {{\,\mathrm{{\textsf {span}}}\,}}_\mathbb {F}\left\{ v_{\tau (1)}, \ldots , v_{\tau (m-1)}\right\}$. Since each $v_i$ is an s-dimensional vector, we have

$$\begin{aligned} m - s \le&\#\left\{ j\in [m] ~ | ~ v_j \in {{\,\mathrm{{\textsf {span}}}\,}}_\mathbb {F}\left\{ v_i ~|~ i \in [m] \setminus \{j\} \right\} \right\} = \#\left\{ \tau \in T ~ | ~ v_{\tau (m)} \in V_\tau \right\} . \end{aligned}$$

Therefore, for each fixed choice $v_1,\ldots , v_{m} \in {{\,\mathrm{{\textsf {supp}}}\,}}(\mathcal {D})$ we have

$$\begin{aligned} \Pr _{\tau \leftarrow T}\left[ v_{\tau (m)} \in V_\tau \right] \ge \frac{m-s}{m}. \end{aligned}$$

Since the vectors $v_1,\ldots , v_{m}$ are identically and independently distributed, we furthermore have

Combining both things, we get

   $\square$

Theorem 4

Let $s \in \mathbb {N}_0$ and let $\mathcal {D}$ be a discrete distribution over $\mathbb {F}^s$. Then, there exists an algorithm which makes s queries to $\mathcal {D}$ and $O(s^3)$-fold use of the four basic arithmetic operations in $\mathbb {F}$ to compute a number $k \le s$, a matrix $B \in \mathbb {F}^{s\times k}$ which consists of k samples of $\mathcal {D}$ and a second matrix $B^+ \in \mathbb {F}^{k\times s}$ s.t. with $V := B \cdot \mathbb {F}^k$

• (a) we have $B^+\cdot B = 1_{k\times k}$,

• (b) $B\cdot B^+$ is the identity on V, i.e., for all $v \in V$, we have $B\cdot B^+\cdot v = v$,

• (c) a certain proportion of the samples of $\mathcal {D}$ lies in V, i.e. $\Pr _{v\leftarrow \mathcal {D}}\left[ v \in V\right] \ge \frac{1}{s}$.

3 Definitions

In this section, we give basic definitions and state elementary lemmas for this work.

3.1 Functional Encryption

Throughout this work, let $\lambda$ denote the security parameter. Let $(F_\lambda )_\lambda$ be a family of function descriptions with a family of domains $(X_\lambda )_\lambda$ and codomains $(Y_\lambda )_{\lambda }$. We tacitly assume in the following that the size of each $f \in F_\lambda , x \in X_\lambda$ and $y \in Y_\lambda$ is bounded by a polynomial in $\lambda$, that we can efficiently sample uniformly random elements of those families and that there is a deterministic polytime evaluation algorithm which on input $(f,x) \in F_\lambda \times X_\lambda$ outputs the correct value $y \in Y_\lambda$. We denote the output of this algorithm by f(x).

Definition 2

A functional encryption scheme ${{\,\mathrm{\textsf {FE}}\,}}= ({{\,\mathrm{\textsf {Setup}}\,}}, {{\,\mathrm{\textsf {KeyGen}}\,}},$${{\,\mathrm{\textsf {Enc}}\,}}, {{\,\mathrm{\textsf {Dec}}\,}})$ for the family $(F_\lambda )_\lambda$ is a quadruple of four ppt algorithms where

${{\,\mathrm{\textsf {Setup}}\,}}(1^\lambda )$:

on input $1^\lambda$ generates a master secret key ${{\,\mathrm{\textsf {msk}}\,}}$,

${{\,\mathrm{\textsf {KeyGen}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, f)$:

on input ${{\,\mathrm{\textsf {msk}}\,}}$ and a function $f \in F_\lambda$ generates a secret key ${{\,\mathrm{\textsf {sk}}\,}}_f$,

${{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, x)$:

on input ${{\,\mathrm{\textsf {msk}}\,}}$ and an input value $x \in X_\lambda$ generates a ciphertext ${{\,\mathrm{\textsf {ct}}\,}}_x$,

${{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {sk}}\,}}_f, {{\,\mathrm{\textsf {ct}}\,}}_x)$:

on input a secret key ${{\,\mathrm{\textsf {sk}}\,}}_f$ and a ciphertext ${{\,\mathrm{\textsf {ct}}\,}}_x$ outputs a value $y \in Y_\lambda$.

We call ${{\,\mathrm{\textsf {FE}}\,}}$ correct, if we have for each samplable² $(f_\lambda )_\lambda \in (F_\lambda )_\lambda$ an $\varepsilon \in {{\,\mathrm{{\textsf {negl}}}\,}}(\lambda )$, s.t. it holds for all $(x_\lambda )_\lambda \in (X_\lambda )_\lambda$

We call ${{\,\mathrm{\textsf {FE}}\,}}$ better than guessing (by $\frac{1}{r}$), if there exists a polynomial $r \in {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )$ s.t. we have for each $(x_\lambda )_\lambda \in (X_\lambda )_\lambda$ and each samplable $(f_\lambda )_\lambda \in (F_\lambda )_\lambda$

We call ${{\,\mathrm{\textsf {FE}}\,}}$ useless, if we have for each polynomial $r \in {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )$

While being correct is a common requirement for encryption schemes, being useless implies that a successful decryption is almost impossible, since the ciphertexts contain nearly no information. Being better than guessing, however, implies that in some cases the ciphertexts and secret keys contain enough information for a successful decryption. Now, one would assume that a scheme cannot be useless and better than guessing at the same time and, indeed, we have the following lemma:

Lemma 3

Let $\# Y_\lambda \ge 2$ for all $\lambda$ and let $(F_\lambda )_\lambda$ contain a samplable $(f_\lambda )_\lambda$ s.t. each $f_\lambda$ is surjective. Then, we have:

• (a) If ${{\,\mathrm{\textsf {FE}}\,}}$ is correct, it is better than guessing.

• (b) If ${{\,\mathrm{\textsf {FE}}\,}}$ is useless, it is not better than guessing.

3.2 Encryption Algorithms

Now, let R be a ring with an associated valuation $\left| \cdot \right| _R : R \overset{}{\rightarrow } \mathbb {N}_0$. In this work, we always assume $R = \mathbb {Z}$ or $R = \mathbb {Z}_q$ for a prime $q = q(\lambda )$. In the first case $\left| \cdot \right| _\mathbb {Z}= \left| \cdot \right|$ is the archimedean absolute value. In the latter case $\left| \cdot \right| _{\mathbb {Z}_q} = \left| \cdot \bmod q\right|$ is the absolute value modulo q we defined in Definition 1.

Furthermore, let $X_\lambda = \{0,\ldots , N\}^n$ now consist of n-dimensional vectors for a polynomial $n = n(\lambda ) \in {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )$ and some $N = N(\lambda )$.

Definition 3

We say the scheme ${{\,\mathrm{\textsf {FE}}\,}}$ or rather its encryption algorithm ${{\,\mathrm{\textsf {Enc}}\,}}$ is of length s over R, if the output of ${{\,\mathrm{\textsf {Enc}}\,}}$ is always an element of $R^s$. Furthermore, we say in this case that ${{\,\mathrm{\textsf {Enc}}\,}}$ is of

• (a) width B, if the infinity-norm of almost all ciphertexts is bounded by B. I.e., there is an $\varepsilon \in {{\,\mathrm{{\textsf {negl}}}\,}}(\lambda )$, s.t. we have for each $(x_\lambda )_\lambda \in (X_\lambda )_\lambda$

  

• (b) depth d, if ${{\,\mathrm{\textsf {Enc}}\,}}$ consists of two parts: an offline part – a ppt algorithm ${{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}$ which on input ${{\,\mathrm{\textsf {msk}}\,}}$ generates s polynomials over $R[X_1,\ldots , X_n]$ of total degree $\le d$ – and an online part which generates a ciphertext by evaluating the polynomials sampled by ${{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}$ at the input x. I.e., ${{\,\mathrm{\textsf {Enc}}\,}}$ works as follows

  $$\begin{aligned} \begin{aligned}&{{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, x): \\ \hline&(p_1,\ldots , p_s) \leftarrow {{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}({{\,\mathrm{\textsf {msk}}\,}}) \\&{{\,\mathrm{\textsf {ct}}\,}}_x := (p_1(x), \ldots , p_s(x)) \\&\textsf {return }{{\,\mathrm{\textsf {ct}}\,}}_x \\ \hline \end{aligned} \end{aligned}$$

where we demand that each $p_i$ is a polynomial of total degree $\le d$ over R.

3.3 Security Notions

In this work, we study the notion of selective and function-hiding IND-CPA security where the adversary is allowed to submit a priori multiple challenge inputs $(x_i^0,x_i^1)$ and a bounded number of challenge functions $(f_j^0,f_j^1)$. To be feasible, the adversary must ensure that the output values $f_j^b(x_i^b)$ do not already tell him, if he lives in world 0 or world 1, i.e. he must ensure $f_j^0(x_i^0) = f_j^1(x_i^1)$. The challenger will send the adversary the ciphertexts and secret keys for one random bit $b \leftarrow \{0,1\}$. To win, the adversary has to guess the bit b.

Definition 4

Let ${{\,\mathrm{\textsf {FE}}\,}}= ({{\,\mathrm{\textsf {Setup}}\,}}, {{\,\mathrm{\textsf {KeyGen}}\,}}, {{\,\mathrm{\textsf {Enc}}\,}}, {{\,\mathrm{\textsf {Dec}}\,}})$ be a functional encryption scheme for the family $(F_\lambda )_\lambda$ and let $m \in {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )$. We say that ${{\,\mathrm{\textsf {FE}}\,}}$ is selectively m -bounded function-hiding IND-CPA secure (m -fh-IND-CPA secure), if each ppt adversary $\mathcal {A}$ has a negligible advantage in winning the following game:

• Step 1: The adversary $\mathcal {A}$ submits two lists³ of possible inputs $(x^0_i)_{i = 1}^n, (x^1_i)_{i = 1}^n$ and two lists of possible functions $(f^0_j)_{j = 1}^m, (f^1_j)_{j = 1}^m$ to the challenger $\mathcal {C}$.

• Step 2: The challenger $\mathcal {C}$ generates a master secret key ${{\,\mathrm{\textsf {msk}}\,}}\leftarrow {{\,\mathrm{\textsf {Setup}}\,}}(1^\lambda )$ and draws a secret bit $b \leftarrow \{0,1\}$. Then, $\mathcal {C}$ computes ${{\,\mathrm{\textsf {ct}}\,}}_{x_i^b} := {{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, x_i^b)$ for each $i = 1,\ldots , n$, ${{\,\mathrm{\textsf {sk}}\,}}_{f_j^b} := {{\,\mathrm{\textsf {KeyGen}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, f_j^b)$ for each $j = 1,\ldots , m$ and sends the lists $({{\,\mathrm{\textsf {ct}}\,}}_{x_i^b})_{i = 1}^n$ and $({{\,\mathrm{\textsf {sk}}\,}}_{f_j^b})_{j = 1}^m$ to $\mathcal {A}$.

• Step 3: The adversary $\mathcal {A}$ guesses b.

The adversary wins the above game, if he guesses b correctly, and, if we have $f_j^0(x_i^0) = f_j^1(x_i^1)$ for all $i = 1,\ldots ,n$ and $j = 1,\ldots , m$. The advantage of $\mathcal {A}$ is defined by

$$\begin{aligned} {{\,\mathrm{\textsf {Adv}}\,}}(\mathcal {A}) := 2 \Pr [\mathcal {A}\text { wins}] - 1 = \Pr [\mathcal {A}\text { wins}~|~ b = 0] + \Pr [\mathcal {A}\text { wins}~|~ b = 1] - 1. \end{aligned}$$

We call ${{\,\mathrm{\textsf {FE}}\,}}$ selectively unbounded function-hiding IND-CPA secure

(fh-IND-CPA secure), if ${{\,\mathrm{\textsf {FE}}\,}}$ is m-fh-IND-CPA secure for each polynomial

${m \in {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )}$, and we call ${{\,\mathrm{\textsf {FE}}\,}}$ selectively IND-CPA secure

(IND-CPA secure), if ${{\,\mathrm{\textsf {FE}}\,}}$ is 0-fh-IND-CPA secure.

3.4 Private-Key Encryption

We define private-key encryption schemes as a special case of functional encryption schemes:

Definition 5

A private-key encryption scheme is a functional encryption scheme ${{\,\mathrm{\textsf {SKE}}\,}}= ({{\,\mathrm{\textsf {Setup}}\,}}, {{\,\mathrm{\textsf {KeyGen}}\,}}, {{\,\mathrm{\textsf {Enc}}\,}}, {{\,\mathrm{\textsf {Dec}}\,}})$ for a function family $(F_\lambda )_\lambda$ where each $F_\lambda$ only contains the identity function $\mathrm {Id} : X_\lambda \overset{}{\rightarrow } X_\lambda$.

When discussing private-key encryption schemes we sometimes omit ${{\,\mathrm{\textsf {KeyGen}}\,}}$ from the header of the scheme and write ${{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, \cdot )$ instead of ${{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {KeyGen}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, \mathrm {Id}), \cdot )$. Note that we call ${{\,\mathrm{\textsf {SKE}}\,}}$ IND-CPA secure, if it is selectively 0-bounded function-hiding IND-CPA secure in the sense of Definition 4. This differs from the usual security notion in literature, where the adversary is usually allowed to submit only one pair of challenge messages and can inquire ciphertexts adaptively. However, by using a hybrid argument, one can show that the security loss which occurs by allowing multiple challenge messages is polynomially bounded. If we consider message spaces of superpoly size, then we can construct private-key encryption schemes which are selectively, but not adaptively, secure. Therefore, the security notion for ${{\,\mathrm{\textsf {SKE}}\,}}$ we use here is weaker than the usual one in literature.

3.5 Transformations

Definition 6

Let ${{\,\mathrm{\textsf {FE}}\,}}= ({{\,\mathrm{\textsf {Setup}}\,}}, {{\,\mathrm{\textsf {KeyGen}}\,}}, {{\,\mathrm{\textsf {Enc}}\,}}, {{\,\mathrm{\textsf {Dec}}\,}})$, ${{\,\mathrm{\textsf {FE}}\,}}'= ({{\,\mathrm{\textsf {Setup}}\,}}', {{\,\mathrm{\textsf {KeyGen}}\,}}',$${{\,\mathrm{\textsf {Enc}}\,}}', {{\,\mathrm{\textsf {Dec}}\,}}')$ be two functional encryption schemes for the same functionality. We say that ${{\,\mathrm{\textsf {FE}}\,}}$ is virtually ${{\,\mathrm{\textsf {FE}}\,}}'$, if ${{\,\mathrm{\textsf {Setup}}\,}}= {{\,\mathrm{\textsf {Setup}}\,}}'$, ${{\,\mathrm{\textsf {KeyGen}}\,}}= {{\,\mathrm{\textsf {KeyGen}}\,}}'$, ${{\,\mathrm{\textsf {Dec}}\,}}= {{\,\mathrm{\textsf {Dec}}\,}}'$ and there is an $\varepsilon \in \mathsf{negl}(\lambda )$, s.t. for all sequences $(x_\lambda )_\lambda \in (X_\lambda )_\lambda$ the statistical distance between the following two distributions is bounded from above by $\varepsilon$:

$$\begin{aligned}&\left\{ ({{\,\mathrm{\textsf {msk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}_x) ~ | ~ {{\,\mathrm{\textsf {msk}}\,}}\leftarrow {{\,\mathrm{\textsf {Setup}}\,}}(1^\lambda ), {{\,\mathrm{\textsf {ct}}\,}}_x \leftarrow {{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, x_\lambda )\right\} ,\\&\left\{ ({{\,\mathrm{\textsf {msk}}\,}},{{\,\mathrm{\textsf {ct}}\,}}_x') ~ | ~ {{\,\mathrm{\textsf {msk}}\,}}\leftarrow {{\,\mathrm{\textsf {Setup}}\,}}(1^\lambda ), {{\,\mathrm{\textsf {ct}}\,}}_x' \leftarrow {{\,\mathrm{\textsf {Enc}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}, x_\lambda )\right\} . \end{aligned}$$

Now, let ${{\,\mathrm{\textsf {FE}}\,}}$ be a functional encryption scheme for functions $(F_\lambda )$ with inputs $(X_\lambda )$ and let ${{\,\mathrm{\textsf {FE}}\,}}$ be one for functions $(F_\lambda ')$ with inputs $(X_\lambda ')$. We say there is an adversarial transformation from ${{\,\mathrm{\textsf {FE}}\,}}$ to ${{\,\mathrm{\textsf {FE}}\,}}'$, if there are ppt algorithms $\mathcal {T}_{{{\,\mathrm{\textsf {ct}}\,}}}, \mathcal {T}_{{{\,\mathrm{\textsf {sk}}\,}}}, \mathcal {T}_F,\mathcal {T}_X$ s.t. we have the following equalities of distributions for all ${x' \in X_\lambda '}$, $f' \in F'_\lambda$, ${{\,\mathrm{\textsf {msk}}\,}}\in {{\,\mathrm{{\textsf {supp}}}\,}}({{\,\mathrm{\textsf {Setup}}\,}})$:

$$\begin{aligned} {{\,\mathrm{\textsf {Setup}}\,}}'(1^\lambda )&= {{\,\mathrm{\textsf {Setup}}\,}}(1^\lambda ),\\ {{\,\mathrm{\textsf {Enc}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}, x')&= \mathcal {T}_{{{\,\mathrm{\textsf {ct}}\,}}}({{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, \mathcal {T}_X(x'))),\\ {{\,\mathrm{\textsf {KeyGen}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}, f')&= \mathcal {T}_{{{\,\mathrm{\textsf {sk}}\,}}}({{\,\mathrm{\textsf {KeyGen}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, \mathcal {T}_F(f'))). \end{aligned}$$

If $(F_\lambda ) = (F'_\lambda )$, then we always assume $\mathcal {T}_F = \mathrm {Id}_{F_\lambda }$ and $\mathcal {T}_X = \mathrm {Id}_{X_\lambda }$.

Let $k\in \mathbb {N}$ be constant and let $({{\,\mathrm{\textsf {FE}}\,}}^i)_{i = 1}^k$ be a sequence of functional encryption schemes. We say there is a virtual adversarial transformation from ${{\,\mathrm{\textsf {FE}}\,}}^1$ to ${{\,\mathrm{\textsf {FE}}\,}}^k$, if, for each $i = 1,\ldots , k-1$, ${{\,\mathrm{\textsf {FE}}\,}}^i$ is virtually ${{\,\mathrm{\textsf {FE}}\,}}^{i+1}$ or there is an adversarial transformation from ${{\,\mathrm{\textsf {FE}}\,}}^i$ to ${{\,\mathrm{\textsf {FE}}\,}}^{i+1}$.

We can now observe the following facts:

Lemma 4

• (a) If ${{\,\mathrm{\textsf {FE}}\,}}$ is virtually ${{\,\mathrm{\textsf {FE}}\,}}'$, then ${{\,\mathrm{\textsf {FE}}\,}}$ is m-fh-IND-CPA secure, correct, better than guessing resp. useless iff ${{\,\mathrm{\textsf {FE}}\,}}'$ is so.

• (b) If ${{\,\mathrm{\textsf {FE}}\,}}$ is m-fh-IND-CPA secure and there is an adversarial transformation from ${{\,\mathrm{\textsf {FE}}\,}}$ to ${{\,\mathrm{\textsf {FE}}\,}}'$, then ${{\,\mathrm{\textsf {FE}}\,}}'$ is m-fh-IND-CPA secure.

At some points, we want to ensure that an encryption algorithm ${{\,\mathrm{\textsf {Enc}}\,}}$ of width B never outputs a ciphertext whose largest entry is not bounded by B. We can ensure such a behaviour by replacing each ciphertext of ${{\,\mathrm{\textsf {Enc}}\,}}$ which is too big with the zero vector. It is clear that this change just has a statistically negligible impact on a scheme. One can even ensure that by doing so we do not harm the depth of ${{\,\mathrm{\textsf {Enc}}\,}}$:

Lemma 5

For $n = 1$, let ${{\,\mathrm{\textsf {FE}}\,}}$ be of length s, width B and depth d over R. If d is constant and B is polynomial, then ${{\,\mathrm{\textsf {FE}}\,}}$ is virtually a scheme ${{\,\mathrm{\textsf {FE}}\,}}' = ({{\,\mathrm{\textsf {Setup}}\,}}', {{\,\mathrm{\textsf {KeyGen}}\,}}', {{\,\mathrm{\textsf {Enc}}\,}}', {{\,\mathrm{\textsf {Dec}}\,}}')$ of length s and depth d over R where we have ${{{\,\mathrm{\textsf {Enc}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}', x) \in \{-B, \ldots , B\}^s}$ for all $\lambda$, $x \in X_\lambda$ and ${{{\,\mathrm{\textsf {msk}}\,}}' \in \mathsf{supp}({{\,\mathrm{\textsf {Setup}}\,}}'(1^\lambda ))}$.

4 Online/Offline Encryption Without Overflows

In this section, we show that private-key encryption schemes of polynomial width that are better than guessing cannot be IND-CPA secure, if their encryption algorithms have a very simple online part in which no arithmetical overflows do occur.

Theorem 5

Let $d \in \mathbb {N}$ be constant, $N\ge 2d$ and let ${{\,\mathrm{\textsf {SKE}}\,}}$ be a private-key encryption scheme of depth d and width $B \in \mathsf{poly}(\lambda )$ with message space $X_\lambda = \{0,\ldots , N\}$ over $\mathbb {Z}$.

If ${{\,\mathrm{\textsf {SKE}}\,}}$ is selectively IND-CPA secure, then ${{\,\mathrm{\textsf {SKE}}\,}}$ is useless.

Proof

(Theorem 5 Part 1). Let ${{\,\mathrm{\textsf {SKE}}\,}}$ be an IND-CPA secure scheme of length s, depth d and width B over $\mathbb {Z}$ for messages $X_\lambda = \{0,\ldots , N\}$. If we define ${{\,\mathrm{\textsf {SKE}}\,}}' = ({{\,\mathrm{\textsf {Setup}}\,}}', {{\,\mathrm{\textsf {Enc}}\,}}', {{\,\mathrm{\textsf {Dec}}\,}}')$ like in Lemma 5, then ${{\,\mathrm{\textsf {SKE}}\,}}$ is virtually ${{\,\mathrm{\textsf {SKE}}\,}}'$. In particular, ${{\,\mathrm{\textsf {SKE}}\,}}'$ is of the same length and depth and is secure and useless iff ${{\,\mathrm{\textsf {SKE}}\,}}$ is so. Furthermore, ${{\,\mathrm{\textsf {SKE}}\,}}'$ is now strictly of width B, i.e., it never outputs a ciphertext outside of $\{-B, \ldots , B\}^s$. It now suffices to prove that ${{\,\mathrm{\textsf {SKE}}\,}}'$ is useless. $\blacksquare$

To prove Theorem 5, we define an adversary which we will show to have a non-negligible advantage against ${{\,\mathrm{\textsf {SKE}}\,}}'$, if ${{\,\mathrm{\textsf {SKE}}\,}}'$ is not useless.

Definition 7

Let $r \in {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )$, $N \ge 2d$ and $s \ge 1$. Set $m = 2r^3$.

We define the following selective adversary $\mathcal {A}$ which plays the IND-CPA security-game in Definition 4 with the scheme ${{\,\mathrm{\textsf {SKE}}\,}}'$:

• Step 1: The adversary $\mathcal {A}$ draws $y \leftarrow [2d]$ and then, for $b = 0,1$, submits the following two lists of 3m messages each:

  

  He submits two empty lists of possible functions.

• Step 2: The adversary $\mathcal {A}$ receives a list of ciphertexts $({{\,\mathrm{\textsf {ct}}\,}}_{x_i^b}')_{i = 1}^{3m}$. Let ${{\,\mathrm{\textsf {ct}}\,}}_{x_i^b,j}'$ denote the j-th entry of ${{\,\mathrm{\textsf {ct}}\,}}_{x_i^b}'$. For $k = 0,1,2$ and $j = 1,\ldots , s$ he computes the arithmetical means

  $$\begin{aligned} c_{k, j} := \frac{1}{m}\sum _{i = 1 + km}^{(k+1)m} ({{\,\mathrm{\textsf {ct}}\,}}_{x_i^b,j}')^2 \end{aligned}$$

• Step 3: If there is a j s.t. $\left| c_{2,j} - c_{1,j} \right| > 2\frac{B}{r}$, the adversary outputs 0. Otherwise, if there is a j s.t. $\left| c_{0,j} - c_{1,j} \right| > 2\frac{B}{r}$, he outputs 1. If none of the above requirements should be met, then the adversary outputs a random bit ${b' \leftarrow \{0,1\}}$.

The following lemma shows in which cases $\mathcal {A}$ has a non-negligible advantage.

Lemma 6

Let $r \in \mathsf{poly}(\lambda )$ s.t. $r \ge \lambda$. For a fixed ${{\,\mathrm{\textsf {msk}}\,}}'$, set ${{\,\mathrm{\textsf {CT}}\,}}_{y}' = {{\,\mathrm{\textsf {Enc}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}', y)$. The adversary in Definition 7 has a non-negligible advantage in the selective IND-CPA game against ${{\,\mathrm{\textsf {SKE}}\,}}'$, if the following probability is non-negligible

Proof

Fix for this proof a master secret key ${{\,\mathrm{\textsf {msk}}\,}}' \in {{\,\mathrm{{\textsf {supp}}}\,}}({{\,\mathrm{\textsf {Setup}}\,}}'(1^\lambda ))$ and denote by ${{{\,\mathrm{\textsf {CT}}\,}}_{y}'}^2$ the distribution of drawing ${{\,\mathrm{\textsf {ct}}\,}}'_y \leftarrow {{\,\mathrm{\textsf {Enc}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}', y)$ and squaring all its entries. In step 2, $\mathcal {A}$ approximates the means of ${{{\,\mathrm{\textsf {CT}}\,}}_{0}'}^2, {{{\,\mathrm{\textsf {CT}}\,}}_{b\cdot y}'}^2$ and ${{{\,\mathrm{\textsf {CT}}\,}}_{y}'}^2$. By $\mathrm {\textsf {Bounded}}$ we denote the event that for each $k = 0,1,2$ the distance between $c_k$ and its mean is at most B/r, i.e. the event Bounded holds iff

Since ${{\,\mathrm{\textsf {Enc}}\,}}'$ always outputs values bounded by B, we have, according to Corollary 2, that the probability that event $\mathrm {\textsf {Bounded}}$ will occur is at least $(1 - 2e^{-r})^{3s} \ge 1 - 6se^{-r}$. Therefore, for each fixed ${{\,\mathrm{\textsf {msk}}\,}}'$, it follows

Similarly, for each fixed ${{\,\mathrm{\textsf {msk}}\,}}' \in {{\,\mathrm{{\textsf {supp}}}\,}}({{\,\mathrm{\textsf {Setup}}\,}}'(1^\lambda ))$, we get .

Now, assume additionally for ${{\,\mathrm{\textsf {msk}}\,}}'$ that the following event $\mathrm {\textsf {Seperated}}$ does hold

Let y denote the value drawn by $\mathcal {A}$ in step 1. If $\mathrm {\textsf {Seperated}}$ holds for ${{\,\mathrm{\textsf {msk}}\,}}'$, then

Similarly, we get . Therefore, for ${{\,\mathrm{\textsf {msk}}\,}}'\leftarrow {{\,\mathrm{\textsf {Setup}}\,}}'(1^\lambda )$, we get now

Now, if we set $\varepsilon := \Pr \left[ \mathrm {\textsf {Seperated}}\right]$, we have

Since our lemma requires $\varepsilon$ to be non-negligible and $r \ge \lambda$, it follows that $\mathcal {A}$ has a non-negligible advantage.   $\square$

To conclude the proof of Theorem 5, we need to show that the prerequisites of Lemma 6 do occur, if ${{\,\mathrm{\textsf {SKE}}\,}}'$ is not useless. In fact, we show a purely mathematical statement in the following which implies the uselessness of ${{\,\mathrm{\textsf {SKE}}\,}}'$, if the prerequisites of Lemma 6 are not met. Our statement says that for a distribution of polynomials the means of the squared outputs of the polynomials for $x = 0,\ldots , 2d$ need to be widespread, because, otherwise, it is very unlikely for the sampled polynomials to be non-constant. If the polynomials sampled by ${{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}'({{\,\mathrm{\textsf {msk}}\,}}')$ are with overwhelming probability constant, then, of course, the sampled ciphertexts do not carry any information about the encrypted input x.

Lemma 7

Let $\mathcal {D}$ be a distribution over integer polynomials of degree $d>0$. If there is a function $\varepsilon = \varepsilon (\lambda )$ s.t. for all $x \in \{1,\ldots , 2d\}$ we have

then it follows

Proof

For $p \leftarrow \mathcal {D}$, we set $f(X) := p(X)^2 - p(0)^2$. Then, f is a random integer polynomial of degree 2d. If we have $p(X) = \sum _{i = 0}^da_iX^i$, then the leading coefficient of f is $a_{d}^2$. Now, by Theorem 3, it follows

$$\begin{aligned} (2d)! \cdot a_{d}^2 = \sum _{i = 0}^{2d}(-1)^{2d - i} \left( {\begin{array}{c}2d\\ i\end{array}}\right) f(i). \end{aligned}$$

Hence

If we draw $p(X) = \sum _{i = 0}^da_iX^i\leftarrow \mathcal {D}$, it follows

   $\square$

Lemma 7 already implies that the offline algorithm of an IND-CPA secure encryption scheme of depth d and polynomial width will – with overwhelming probability – sample polynomials of degree $d-1$. In the following theorem, we generalize this observation for arbitrary degrees $d-k$.

Theorem 6

Let $\mathcal {D}$ be a distribution over integer polynomials of degree d. If there are functions $\varepsilon =\varepsilon (\lambda )$ and $B = B(\lambda )$ s.t. for all $x \in \{1,\ldots , 2d\}$ and $p \in \mathsf{supp}(\mathcal {D})$ we have

then we have for all $k = 0,\ldots , d$

Theorem 6 is proven by using induction over k where the base case and the induction step both follow by Lemma 7. Since its proof is very technical, we omit it here. We can now finish the proof of Theorem 5.

Proof

(Theorem 5 Part 2). Let $\mathcal {A}$ be the adversary in Definition 7. For $\mathcal {A}$ to have negligible advantage against ${{\,\mathrm{\textsf {SKE}}\,}}'$, according to Lemma 6, it is necessary to have for all $r= 4r'B \in {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )$

where we take the probability over ${{\,\mathrm{\textsf {msk}}\,}}' \leftarrow {{\,\mathrm{\textsf {Setup}}\,}}'(1^\lambda )$. But now, by Theorem 6, we have for each $r \in (2 + 2B^2)^d \cdot {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )$

Therefore, the uselessness of ${{\,\mathrm{\textsf {SKE}}\,}}'$ and, in particular, the uselessness of ${{\,\mathrm{\textsf {SKE}}\,}}$ follow.    $\square$

5 Online/Offline Encryption with Short Ciphertexts

In Sect. 4, we showed that encryption schemes of constant depth and polynomial width without arithmetic overflows cannot be secure. In this section, we show the same result for encryption schemes of constant depth and polynomial width which may make use of arithmetic overflows but have short ciphertexts. We do so by transforming such schemes to encryption schemes without arithmetic overflows. I.e., if the ciphertexts are of short width, we can transform their encryption algorithm to one of constant depth over $\mathbb {Z}$ by using a simple multiplication trick. As before, throughout this section, let $\lambda$ denote the security parameter and let $B = B(\lambda ), d = d(\lambda )$ and $N = N(\lambda )$ be arbitrary variables depending on $\lambda$. Let $s \in {{\,\mathrm{{\textsf {poly}}}\,}}(\lambda )$. Additionally, introduce a modulus variable $q = q(\lambda )$. We prove in this section the following theorem:

Theorem 7

Let q be a prime, $N\ge d+1$ and let ${{\,\mathrm{\textsf {SKE}}\,}}_q$ be a private-key encryption scheme of depth d and width B over $\mathbb {Z}_q$ for messages $X_\lambda = \{0,\ldots , N\}$ s.t.

$$\begin{aligned} 2(d + 1)^2 \cdot (d!)^3 \cdot d^d \cdot N^d \cdot B \le q -1. \end{aligned}$$

If ${{\,\mathrm{\textsf {SKE}}\,}}_q$ is selectively IND-CPA secure, then there exists a virtual adversarial transformation to an encryption scheme ${{\,\mathrm{\textsf {SKE}}\,}}$ of depth d and width $(d!)^2 B$ over $\mathbb {Z}$ for messages $X_\lambda = \{0,\ldots , N\}$ which preserves selective IND-CPA security and – in both directions – correctness, being better than guessing and uselessness.

Theorems 7 and 5 imply together the following impossibility result:

Corollary 3

Let q be a prime and let ${{\,\mathrm{\textsf {SKE}}\,}}_q$ be a private-key encryption scheme of depth d and width B for messages $x = 0,\ldots , N$ over $\mathbb {Z}_q$ s.t. $N \ge 2d$ and

$$\begin{aligned} 2(d + 1)^2 \cdot (d!)^3 \cdot d^d \cdot N^d \cdot B \le q -1. \end{aligned}$$

If ${{\,\mathrm{\textsf {SKE}}\,}}_q$ is selectively IND-CPA secure, $B \in \mathsf{poly}(\lambda )$ and $d \in \mathbb {N}$ constant, then ${{\,\mathrm{\textsf {SKE}}\,}}_q$ is useless.

Proof

Because of Theorem 7, there is an IND-CPA secure private-key encryption scheme ${{\,\mathrm{\textsf {SKE}}\,}}$ over $\mathbb {Z}$ of polynomial width $(d!)^2B$ and constant depth $d \in \mathbb {N}$ for messages $X_\lambda = \{0,\ldots , N\}$ which is useless iff ${{\,\mathrm{\textsf {SKE}}\,}}_q$ is useless. Since $N\ge 2d$, ${{\,\mathrm{\textsf {SKE}}\,}}$ is useless according to Theorem 5.    $\square$

To prove Theorem 7, let $q>2$ be a prime and define a map $\iota : \mathbb {Z}_q \overset{}{\rightarrow }$

$\{-\frac{q-1}{2}, \ldots , 0, \ldots , \frac{q-1}{2}\} \subset \mathbb {Z}$ by setting for all $a \in \mathbb {Z}_q$

$$\begin{aligned} \iota (a \bmod q) := a + zq ~~~~\text { for }z \in \mathbb {Z}\text { s.t. } \left| a + zq\right| = \left| a \bmod q\right| . \end{aligned}$$

Then, $\iota$ preserves absolute values and we have

$$\begin{aligned} \iota (a \bmod q) \bmod q = a \bmod q. \end{aligned}$$

One first idea for proving Theorem 7 could be to just apply $\iota$ component-wise to each ciphertext, i.e. treat each ciphertext modulo q as it would be an integer vector. Technically, we would replace ${{\,\mathrm{\textsf {Enc}}\,}}$ by $\iota \circ {{\,\mathrm{\textsf {Enc}}\,}}$. While $\iota \circ {{\,\mathrm{\textsf {Enc}}\,}}$ would be indeed of length s and width B over $\mathbb {Z}$, it is not clear, if it would be of depth d over $\mathbb {Z}$. To make this precise, for $p \in \mathbb {Z}_q[X]$, we denote by $I(p\bmod q)$ the coefficient-wise application of $\iota$, i.e.

$$\begin{aligned} I\left( \sum _{i = 0}^d a_i X^i \bmod q \right) := \sum _{i = 0}^d \iota (a_i \bmod q) X^i. \end{aligned}$$

Then, we have the equation $I(p \bmod q) \bmod q = p \bmod q$ again. Now, for $\iota \circ {{\,\mathrm{\textsf {Enc}}\,}}$ to be of depth d over $\mathbb {Z}$, we would need a suitable offline algorithm. We could, for example, take $I\circ {{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}$ as candidate. If p is a polynomial over $\mathbb {Z}_q$ sampled by ${{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}$, we would then need the following kind of equality for all $x \in X_\lambda$

$$\begin{aligned} \iota (p(x)\bmod q) = I(p \bmod q) (x). \end{aligned}$$

(3)

While Eq. (3) holds for polynomials p with small coefficients, it does not hold in general. Therefore, we need to apply minor changes to the polynomials sampled by ${{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}$ as we will see later. To this end, consider the Vandermonde matrix for the tuple $(0,1,\ldots , d)$

$$\begin{aligned} V:= ((i - 1)^{j - 1})_{i,j= 1,\ldots , d+1} =\left( \begin{matrix} 1 &{} 0 &{} 0 &{} \ldots &{} 0\\ 1 &{} 1 &{} 1 &{} \ldots &{} 1\\ 1 &{} 2 &{} 4 &{} \ldots &{} 2^d\\ \vdots &{} &{} &{} &{} \vdots \\ 1 &{} d &{} d^2 &{} \ldots &{} d^d \end{matrix} \right) \in \mathbb {Z}^{(d+1) \times (d+1)}. \end{aligned}$$

We can deduce the coefficients of a polynomial by applying $V^{-1}$ to its output values. However, $V^{-1}$ has very large entries modulo q, therefore we use the following integer quasi-inverse W with bounded entries.

Lemma 8

There exists an integer matrix $W\in \mathbb {Z}^{(d+1)\times (d +1)}$ whose entries are bounded by $(d!)^3d^d$, s.t. $V\cdot W = W\cdot V = (d!)^2\cdot \mathrm {Id}_{(d+1)\times (d +1)}$.

Lemma 9

Let $q > 2$ be a prime, set $c = (d!)^2$ and let $p \in \mathbb {Z}_q[X]$ be a polynomial of degree d. Furthermore, let $N \ge d + 1$. If we have for all $x = 0,\ldots , d$

$$\begin{aligned} \left| p(x) \bmod q\right| \le \frac{q - 1}{ 2(d + 1)^2 \cdot (d!)^3 \cdot d^d \cdot N^d }, \end{aligned}$$

then we have for all $x = 0,\ldots , N$

$$\begin{aligned} I ( c \cdot p \bmod q)(x) = \iota ( c\cdot p(x) \bmod q). \end{aligned}$$

Proof

It is clear that we have for any integer polynomial p and any $x \in \mathbb {Z}$

$$\begin{aligned} I ( c \cdot p \bmod q)(x) \bmod q = c \cdot p(x) \bmod q = \iota ( c\cdot p(x) \bmod q) \bmod q. \end{aligned}$$

Therefore, in our case, it suffices to show that the absolute value of ${I ( c \cdot p \bmod q)(x)}$ is bounded by $\frac{q - 1}{2}$, since $\iota ( c\cdot p(x) \bmod q)$ is a value of $\{-\frac{q-1}{2}, \ldots , \frac{q-1}{2}\}$ which differs from $I ( c \cdot p \bmod q)(x)$ only by a value in $q \mathbb {Z}$.

Let $p(X) = \sum _{i = 0}^d a_i X^i \in \mathbb {Z}_q[X]$ and set $a = (a_0,\ldots , a_d) \in \mathbb {Z}_q^{d+1}$ to be the column vector of $p's$ coefficients. Then, we have

$$ V\cdot a \bmod q = \left( \begin{matrix} 1 &{} 0 &{} 0 &{} \ldots &{} 0\\ 1 &{} 1 &{} 1 &{} \ldots &{} 1\\ 1 &{} 2 &{} 4 &{} \ldots &{} 2^d\\ \vdots &{} &{} &{} &{} \vdots \\ 1 &{} d &{} d^2 &{} \ldots &{} d^d \end{matrix} \right) \cdot \left( \begin{matrix} a_0\\ a_1\\ a_2\\ \vdots \\ a_d \end{matrix} \right) \bmod q = \left( \begin{matrix} p(0)\\ p(1)\\ p(2)\\ \vdots \\ p(d) \end{matrix} \right) \bmod q.$$

Let $W = (w_{i,j})_{i,j} \in \mathbb {Z}^{(d+1)\times (d+ 1)}$ be the quasi-inverse of V from Lemma 8. Since $WVa = c a \mod q$, we have for each $a_i$

$$\begin{aligned} c \cdot a_i \bmod q = \sum _{i = 0}^d w_{i,j} p(j) \bmod q. \end{aligned}$$

In particular, we have now

$$\begin{aligned} \left| c \cdot a_i \bmod q\right| = \left| \sum _{i = 0}^d w_{i,j} p(j) \bmod q\right| \le \sum _{i = 0}^d \left| w_{i,j}\right| \cdot \left| p(j) \bmod q\right| . \end{aligned}$$

Set

$$\begin{aligned} B := \max _{x = 0,\ldots d} \left| p(x) \bmod q\right| \le \frac{q - 1}{ 2(d + 1)^2 \cdot (d!)^3 \cdot d^d \cdot N^d }. \end{aligned}$$

Since each $\left| w_{i,j}\right|$ is bounded by $(d!)^3d^d$ and each $\left| p(j) \bmod q\right|$ is bounded by B, we get

$$\begin{aligned} \left| c \cdot a_i \bmod q\right| \le \sum _{i = 0}^d \left| w_{i,j}\right| \cdot \left| p(j) \bmod q\right| \le \sum _{i = 0}^d(d!)^3d^dB = (d + 1)(d!)^3d^dB . \end{aligned}$$

Therefore, we have for all $x = 0,\ldots , N$

$$\begin{aligned}&\left| I ( c \cdot p \bmod q)(x)\right| \\ =&\left| \sum _{i = 0}^d \iota \left( c \cdot a_i \bmod q\right) x^i\right| \le \sum _{i = 0}^d \left| \iota \left( c \cdot a_i \bmod q\right) x^i\right| \\ \le&\sum _{i = 0}^d \left| \iota \left( c \cdot a_i \bmod q\right) \right| \cdot \left| x^i\right| \le \sum _{i = 0}^d(d + 1)(d!)^3d^dB\cdot \left| x\right| ^i\\ \le&(d + 1)(d!)^3d^dB\cdot \left( \sum _{i = 0}^dN^i\right) \le (d + 1)(d!)^3d^dB \cdot (d+1)N^d \le \frac{q - 1}{2}. \end{aligned}$$

Ergo, the claim follows.    $\square$

Proof

(Theorem 7). Because of Lemma 5, we can – by using the same argument we used in the first part of the proof of Theorem 5 – w.l.o.g. assume that the encryption algorithm of ${{\,\mathrm{\textsf {SKE}}\,}}_q = ({{\,\mathrm{\textsf {Setup}}\,}}_q, {{\,\mathrm{\textsf {Enc}}\,}}_q, {{\,\mathrm{\textsf {Dec}}\,}}_q)$ never outputs a ciphertext whose entries modulo q are not bounded by B. Set

$$\begin{aligned} c:= (d!)^2 \in \mathbb {Z},~~~ h := c^{-1} \bmod q \in \mathbb {Z}_q \end{aligned}$$

and define a scheme ${{\,\mathrm{\textsf {SKE}}\,}}= ({{\,\mathrm{\textsf {Setup}}\,}}, {{\,\mathrm{\textsf {Enc}}\,}}, {{\,\mathrm{\textsf {Dec}}\,}})$ over $\mathbb {Z}$ by applying the following adversarial transformation to ${{\,\mathrm{\textsf {SKE}}\,}}_q$:

$$\begin{aligned} {{\,\mathrm{\textsf {Setup}}\,}}(1^\lambda ) :=&{{\,\mathrm{\textsf {Setup}}\,}}_q(1^\lambda ),\\ {{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}},x) :=\,&\iota (c \cdot {{\,\mathrm{\textsf {Enc}}\,}}_q({{\,\mathrm{\textsf {msk}}\,}},x) \bmod q),\\ {{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}) :=&{{\,\mathrm{\textsf {Dec}}\,}}_q({{\,\mathrm{\textsf {msk}}\,}}, (h\cdot {{\,\mathrm{\textsf {ct}}\,}}\bmod ~q) ). \end{aligned}$$

It is clear that ${{\,\mathrm{\textsf {SKE}}\,}}_q$ is correct, better than guessing (resp. useless) iff ${{\,\mathrm{\textsf {SKE}}\,}}$ is correct, better than guessing (resp. useless), since we have

$$\begin{aligned} \left( h\cdot (\iota (c \cdot {{\,\mathrm{\textsf {ct}}\,}}\bmod ~q)) \bmod q\right) = (h\cdot (c \cdot {{\,\mathrm{\textsf {ct}}\,}}) \bmod q) = {{\,\mathrm{\textsf {ct}}\,}}\bmod ~q. \end{aligned}$$

Since ${{\,\mathrm{\textsf {SKE}}\,}}_q$ is IND-CPA secure and the above transformations are adversarial, ${{\,\mathrm{\textsf {SKE}}\,}}$ is IND-CPA secure.

It remains to show that ${{\,\mathrm{\textsf {Enc}}\,}}$ is an encryption algorithm of depth d and width cB over $\mathbb {Z}$. Now, for each $({{\,\mathrm{\textsf {ct}}\,}}_1,\ldots , {{\,\mathrm{\textsf {ct}}\,}}_s)\leftarrow {{\,\mathrm{\textsf {Enc}}\,}}_q({{\,\mathrm{\textsf {msk}}\,}}, x)$, we have

$$\begin{aligned} \left| \iota (c \cdot {{\,\mathrm{\textsf {ct}}\,}}_j \bmod ~q)\right| = \left| c \cdot {{\,\mathrm{\textsf {ct}}\,}}_j \bmod ~q\right| \le c \cdot \left| {{\,\mathrm{\textsf {ct}}\,}}_j \bmod ~q\right| \le cB, \end{aligned}$$

therefore ${{\,\mathrm{\textsf {Enc}}\,}}$ is of width cB over $\mathbb {Z}$. To show that ${{\,\mathrm{\textsf {Enc}}\,}}$ is of depth d we have to give a feasible offline algorithm ${{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}$ for ${{\,\mathrm{\textsf {Enc}}\,}}= \iota (c \cdot {{\,\mathrm{\textsf {Enc}}\,}}_q)$. This is done by setting

$$\begin{aligned} {{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}({{\,\mathrm{\textsf {msk}}\,}}) := I( c \cdot {{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}, q}({{\,\mathrm{\textsf {msk}}\,}}) \bmod q). \end{aligned}$$

Let $x \in \{0,\ldots , N\}$. If we fix the randomness r of ${{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, x, r)$ and set $(p_1, \ldots , p_s) = {{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline},q}({{\,\mathrm{\textsf {msk}}\,}},r)$ and $(p_1', \ldots , p_s') = {{\,\mathrm{\textsf {Enc}}\,}}_{\mathrm {offline}}({{\,\mathrm{\textsf {msk}}\,}},r)$, then

$$\begin{aligned}&{{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, x, r) = \iota (c \cdot {{\,\mathrm{\textsf {Enc}}\,}}_q({{\,\mathrm{\textsf {msk}}\,}},x,r) \bmod q) \\ =\,&(\iota (c \cdot p_1(x) \bmod q), \ldots , \iota (c \cdot p_s(x) \bmod q))\\ {\mathop {=}\limits ^{(*)}}\,&(I(c \cdot p_1 \bmod q)(x), \ldots , I(c \cdot p_s \bmod q)(x)) =( p_1'(x), \ldots , p_s' (x)), \end{aligned}$$

where eq. $(*)$ follows from Lemma 9. Therefore, ${{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}, x)$ is of depth d.    $\square$

6 Lattice-Based Function-Hiding Functional Encryption

In this section, let $n(\lambda ) \ge 1$ be a polynomial in $\lambda$ and let $q(\lambda ) > p(\lambda ) \ge N(\lambda )\ge 1$. Further, let $X_\lambda = \{0,\ldots , p\}^n$, $Y_\lambda = \{0,\ldots , p\}$ and let $(F_\lambda )_\lambda$ be a function family which contains (besides other functions) the zero-function $0 \in F_\lambda$ – which maps each $x \in X_\lambda$ to zero – and the projection $\pi _1 \in F_\lambda$ – which maps each $x \in X_\lambda$ to its first coordinate.

Let ${{\,\mathrm{\textsf {FE}}\,}}= ({{\,\mathrm{\textsf {Setup}}\,}}, {{\,\mathrm{\textsf {KeyGen}}\,}}, {{\,\mathrm{\textsf {Enc}}\,}}, {{\,\mathrm{\textsf {Dec}}\,}})$ be a functional encryption scheme for $(F_\lambda )_\lambda$ of depth $d_1$ and length s over $\mathbb {Z}_q$ and let $d_2 \in \mathbb {N}$ be a constant s.t. each secret key ${{\,\mathrm{\textsf {sk}}\,}}\in {{\,\mathrm{{\textsf {supp}}}\,}}({{\,\mathrm{\textsf {KeyGen}}\,}})$ is a polynomial in $\mathbb {Z}_q[X_1,\ldots , X_s]$ of total degree $\le d_2$ with

$$\begin{aligned} {{\,\mathrm{\textsf {Dec}}\,}}({{\,\mathrm{\textsf {sk}}\,}}, {{\,\mathrm{\textsf {ct}}\,}}) = \left\lceil { {{\,\mathrm{\textsf {sk}}\,}}({{\,\mathrm{\textsf {ct}}\,}}) }/{\left\lfloor q/p\right\rfloor }\right\rfloor . \end{aligned}$$

Finally, set $m = \left( {\begin{array}{c}s +d_2 \\ d_2\end{array}}\right)$. We prove in this section the following theorem:

Theorem 8

If q is a prime and ${{\,\mathrm{\textsf {FE}}\,}}$ is selectively ${(m + 1)}$-bounded function-hiding IND-CPA secure and correct, then there exists an adversarial transformation from ${{\,\mathrm{\textsf {FE}}\,}}$ to a private-key encryption scheme of depth $d:=d_1 \cdot d_2$, width $\left\lfloor {q}/{p}\right\rfloor$ and length m over $\mathbb {Z}_q$ for messages $x = 0,\ldots , N$ which is selectively IND-CPA secure and better than guessing.

Corollary 4

(Impossibility Result). Assume that q is a prime, $d_1$ is constant and $\frac{q}{p}$ is bounded by a polynomial in $\lambda$ and that for almost all $\lambda \in \mathbb {N}$ we have

$$\begin{aligned} p(\lambda )\ge (d+ 1)^2 \cdot 2^{d+1} \cdot (d!)^3 \cdot d^{2d}. \end{aligned}$$

Then, ${{\,\mathrm{\textsf {FE}}\,}}$ cannot be both selectively $(m+1)$-bounded function-hiding IND-CPA secure and correct.

Proof

Assume that ${{\,\mathrm{\textsf {FE}}\,}}$ is both and set $N = 2d$. Because of Theorem 8, we can transform ${{\,\mathrm{\textsf {FE}}\,}}$ to a private-key encryption scheme over $\mathbb {Z}_q$ with depth d and width $B:=\left\lfloor {q}/{p}\right\rfloor$ for messages $X'_\lambda = \{0,\ldots , 2d\}$ which is IND-CPA secure and better than guessing. Then, we have

$$\begin{aligned} B=\left\lfloor \frac{q}{p}\right\rfloor \le \frac{q - 1}{p} \le \frac{q - 1}{2(d+ 1)^2 \cdot (d!)^3 \cdot d^{d} \cdot \left( 2d\right) ^d}. \end{aligned}$$

Now, according to Corollary 3, this encryption scheme must be useless and therefore cannot be better than guessing. In particular, ${{\,\mathrm{\textsf {FE}}\,}}$ cannot be correct.    $\square$

We prove Theorem 8 by applying adversially three transformations to ${{\,\mathrm{\textsf {FE}}\,}}$. First, we relinearize the ciphertexts and secret keys s.t. decryption becomes evaluating a scalar product, dividing by $\left\lfloor q/p\right\rfloor$ and rounding down. Second, we draw m secret keys $v_1,\ldots , v_m \leftarrow {{\,\mathrm{\textsf {KeyGen}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}, 0)$ for the zero-function and replace a ciphertext ${{\,\mathrm{\textsf {ct}}\,}}'$ with a vector of decryption noises $\langle {{\,\mathrm{\textsf {ct}}\,}}' ~ | ~ v_i\rangle$. Because of decryption correctness, each noise value must be small; therefore, we get a new ciphertext of small width. By using sufficiently many secret keys, we can ensure that the new ciphertext contains enough information s.t. the probability of a correct decryption becomes high enough. We will not always be able to decrypt correctly, but we show that we are still better than guessing by $\frac{1}{m}$. In fact, this is implied by Lemma 10 which states that a secret key of a non-zero function must sufficiently resemble a secret key of the zero-function. As a last step, we convert the current FE scheme into a private-key encryption scheme for messages $x \in \{0,\ldots , N\}$ which is better than guessing and of small width over $\mathbb {Z}_q$. Since all transformations can be applied by an adversary, the scheme stays IND-CPA secure (however, we lose some security in the second transformation step, since we have to ask for m secret keys). If we started with a FE scheme of constant depth, then the final scheme will also be of constant depth.

Proof

(Theorem 8 Step 1). As a first step, we relinearize the ciphertexts and secret keys of ${{\,\mathrm{\textsf {FE}}\,}}$. Note that each polynomial ${{\,\mathrm{\textsf {sk}}\,}}\in \mathbb {Z}_q[X_1,\ldots , X_s]$ of total degree $\le d_2$ can be written as a vector of its coefficients. This yields a linear transformation

$$\begin{aligned} \varPhi : \left\{ {{\,\mathrm{\textsf {sk}}\,}}\in \mathbb {Z}_q[X_1,\ldots , X_s] ~|~ \deg {{\,\mathrm{\textsf {sk}}\,}}\le d_2 \right\} \overset{}{\longrightarrow } \mathbb {Z}_q^{\left( {\begin{array}{c}s+d_2\\ d_2\end{array}}\right) }. \end{aligned}$$

On the other hand, there is a polynomial map ${\varPhi ^+ : \mathbb {Z}_q^s\overset{}{\longrightarrow } \mathbb {Z}_q^{m}}$ of degree $d_2$ which maps each vector to a vector of different products of its entries s.t. we have for all ${{\,\mathrm{\textsf {sk}}\,}}\in \mathbb {Z}_q[X_1,\ldots , X_s]$ of total degree $\le d_2$ and all ${{\,\mathrm{\textsf {ct}}\,}}\in \mathbb {Z}_q^s$

$$\begin{aligned} {{\,\mathrm{\textsf {sk}}\,}}({{\,\mathrm{\textsf {ct}}\,}}) = \langle \varPhi \left( {{\,\mathrm{\textsf {sk}}\,}}\right) ~ | ~ \varPhi ^+\left( {{\,\mathrm{\textsf {ct}}\,}}\right) \rangle . \end{aligned}$$

(4)

Now, we define a new scheme ${{\,\mathrm{\textsf {FE}}\,}}' = ({{\,\mathrm{\textsf {Setup}}\,}}', {{\,\mathrm{\textsf {KeyGen}}\,}}', {{\,\mathrm{\textsf {Enc}}\,}}', {{\,\mathrm{\textsf {Dec}}\,}}')$ by setting

$$\begin{aligned} {{\,\mathrm{\textsf {Setup}}\,}}'(1^\lambda )&:={{\,\mathrm{\textsf {Setup}}\,}}(1^\lambda ),&{{\,\mathrm{\textsf {KeyGen}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}', f)&:= \varPhi \left( {{\,\mathrm{\textsf {KeyGen}}\,}}({{\,\mathrm{\textsf {msk}}\,}}', f)\right) ,\\ {{\,\mathrm{\textsf {Enc}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}', x)&:= \varPhi ^+\left( {{\,\mathrm{\textsf {Enc}}\,}}({{\,\mathrm{\textsf {msk}}\,}}', x) \right) ,&{{\,\mathrm{\textsf {Dec}}\,}}'({{\,\mathrm{\textsf {sk}}\,}}', {{\,\mathrm{\textsf {ct}}\,}}')&:= \left\lceil { \langle {{\,\mathrm{\textsf {sk}}\,}}' ~ | ~ {{\,\mathrm{\textsf {ct}}\,}}'\rangle }/{\left\lfloor q/p\right\rfloor }\right\rfloor . \end{aligned}$$

Applying $\varPhi$ and $\varPhi ^+$ together forms an adversarial transformation, therefore ${{\,\mathrm{\textsf {FE}}\,}}'$ is $(m+1)$-fh-IND-CPA secure. Because of Eq. (4), ${{\,\mathrm{\textsf {FE}}\,}}'$ is correct. Further, ${{\,\mathrm{\textsf {Enc}}\,}}'$ is of depth $d:= d_1\cdot d_2$ and its outputs are vectors of length $m = \left( {\begin{array}{c}s + d_2\\ d_2\end{array}}\right)$.    $\blacksquare$

Lemma 10

For each sampleable ${(f_\lambda )_\lambda \in (F_\lambda )_\lambda }$ there is an $\varepsilon \in {{\,\mathrm{{\textsf {negl}}}\,}}(\lambda )$ s.t.

Proof

Lemma 2 states

Consider an adversary $\mathcal {A}$ who plays the IND-CPA game from Definition 4 against ${{\,\mathrm{\textsf {FE}}\,}}'$ and works as follows:

• Step 1: For $b=0,1$ and $i = 1,\ldots , m+1$, the adversary sets

  

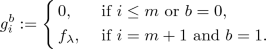
  and submits two empty lists of possible inputs and two lists of possible functions $(g^0_i)_{i = 1}^{m+1}, (g^1_i)_{i = 1}^{m+1}$.

• Step 2: After receiving $({{\,\mathrm{\textsf {sk}}\,}}_{g^b_i}')_{i = 1}^{m+1}$, $\mathcal {A}$ computes ${V:= {{\,\mathrm{{\textsf {span}}}\,}}_{\mathbb {Z}_q}\left\{ {{\,\mathrm{\textsf {sk}}\,}}_{g^b_1}',\ldots , {{\,\mathrm{\textsf {sk}}\,}}_{g^b_{m}}'\right\} }$.

• Step 3: The adversary outputs 0, if ${{\,\mathrm{\textsf {sk}}\,}}_{g^b_{m+1}}' \in V$, and 1 otherwise.

If we set

then we can compute the advantage of $\mathcal {A}$ by

$$\begin{aligned} \varepsilon :=&\Pr [\mathcal {A}\text { wins}~|~ b = 0] + \Pr [\mathcal {A}\text { wins}~|~ b = 1] - 1= P_1 + (1 - P_2) - 1 = P_1 - P_2. \end{aligned}$$

$\varepsilon$ is negligible, since ${{\,\mathrm{\textsf {FE}}\,}}'$ is $(m+1)$-fh-IND-CPA secure. Therefore

$$\begin{aligned} P_2 = P_1 - \varepsilon (\lambda ) \ge \frac{1}{m+1} - \varepsilon (\lambda ). \end{aligned}$$

   $\square$

Proof

(Theorem 8 Step 2). Let ${{\,\mathrm{\textsf {FE}}\,}}' = ({{\,\mathrm{\textsf {Setup}}\,}}', {{\,\mathrm{\textsf {KeyGen}}\,}}', {{\,\mathrm{\textsf {Enc}}\,}}', {{\,\mathrm{\textsf {Dec}}\,}}')$ be a correct and $(m+1)$-fh-IND-CPA secure functional encryption scheme where ${{\,\mathrm{\textsf {Enc}}\,}}'$ is of depth d and length m over $\mathbb {Z}_q$. Let furthermore ${{\,\mathrm{\textsf {Dec}}\,}}'$ be computed by

$$ {{\,\mathrm{\textsf {Dec}}\,}}'({{\,\mathrm{\textsf {sk}}\,}}', {{\,\mathrm{\textsf {ct}}\,}}') = \left\lceil { {\langle {{\,\mathrm{\textsf {sk}}\,}}' ~ | ~ {{\,\mathrm{\textsf {ct}}\,}}'\rangle }/{\left\lfloor q/p\right\rfloor } }\right\rfloor . $$

We now adversarially transform ${{\,\mathrm{\textsf {FE}}\,}}'$ to a functional encryption scheme ${{\,\mathrm{\textsf {FE}}\,}}''$ for the same functionality which is 1-fh-IND-CPA secure, better than guessing and whose encryption algorithm has depth d, width $\left\lfloor {q}/{p}\right\rfloor$ and length m over $\mathbb {Z}_q$.

In the IND-CPA game against ${{\,\mathrm{\textsf {FE}}\,}}'$, our adversary first queries m secret keys $v_1,\ldots , v_{m}\leftarrow {{\,\mathrm{\textsf {KeyGen}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}', 0)$ for the zero function and then makes use of the algorithm $\mathcal {B}$ described in Theorem 4 to compute $V,A,A^+ \leftarrow \mathcal {B}(v_1,\ldots , v_{m})$ s.t. $V = {{\,\mathrm{{\textsf {span}}}\,}}_{\mathbb {Z}_q}\{ v_1,\ldots , v_{m} \}$ and $A \in \mathbb {Z}_q^{m\times k}, A^+ \in \mathbb {Z}_q^{k\times m}$ are matrices with

$$\begin{aligned} V = A \cdot \mathbb {Z}_q^k ~~\text { and }~~ A \cdot A^+ v = v \text { for all }v \in V. \end{aligned}$$

After our adversary queried m secret keys, ${{\,\mathrm{\textsf {FE}}\,}}'$ remains 1-fh-IND-CPA secure. However, by doing so, the adversary gained the additional data $V,A,A^+$ with which he can transform ${{\,\mathrm{\textsf {FE}}\,}}'$ to ${{\,\mathrm{\textsf {FE}}\,}}'' = ({{\,\mathrm{\textsf {Setup}}\,}}'', {{\,\mathrm{\textsf {KeyGen}}\,}}'', {{\,\mathrm{\textsf {Enc}}\,}}'', {{\,\mathrm{\textsf {Dec}}\,}}'')$ by setting:

$$\begin{aligned}&{{\,\mathrm{\textsf {Setup}}\,}}''(1^\lambda ):= {{\,\mathrm{\textsf {Setup}}\,}}'(1^\lambda )&{{\,\mathrm{\textsf {Enc}}\,}}''({{\,\mathrm{\textsf {msk}}\,}}'', x) := A^T \cdot {{\,\mathrm{\textsf {Enc}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}'', x)\\[2mm]&\begin{aligned}&{{\,\mathrm{\textsf {KeyGen}}\,}}''({{\,\mathrm{\textsf {msk}}\,}}'', f):\\\hline&{{\,\mathrm{\textsf {sk}}\,}}_f' \leftarrow {{\,\mathrm{\textsf {KeyGen}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}', f)\\&{{\,\mathrm{{\textsf {if}}}\,}}\ {{\,\mathrm{\textsf {sk}}\,}}_f' \in V\\&~~~~ {{\,\mathrm{\textsf {sk}}\,}}_f'' := A^+ \cdot {{\,\mathrm{\textsf {sk}}\,}}_f'\\&{{\,\mathrm{{\textsf {else}}}\,}}\\&~~~~ {{\,\mathrm{\textsf {sk}}\,}}_f'' := \bot \\&{{\,\mathrm{{\textsf {return}}}\,}}\ {{\,\mathrm{\textsf {sk}}\,}}_f''\\\hline \end{aligned}&\begin{aligned}&{{\,\mathrm{\textsf {Dec}}\,}}''({{\,\mathrm{\textsf {sk}}\,}}'', {{\,\mathrm{\textsf {ct}}\,}}''):\\\hline&{{\,\mathrm{{\textsf {if}}}\,}}\ {{\,\mathrm{\textsf {sk}}\,}}'' = \bot \\&~~~~ y \leftarrow \{0,\ldots , p\}\\&{{\,\mathrm{{\textsf {else}}}\,}}\\&~~~~ y \leftarrow {{\,\mathrm{\textsf {Dec}}\,}}'({{\,\mathrm{\textsf {sk}}\,}}'', {{\,\mathrm{\textsf {ct}}\,}}'')\\&{{\,\mathrm{{\textsf {return}}}\,}}\ y\\\hline \\ \end{aligned} \end{aligned}$$

${{\,\mathrm{\textsf {FE}}\,}}''$ has the following properties:

Security: The above changes can be applied by an adversary while he plays the IND-CPA game from Definition 4. Therefore, ${{\,\mathrm{\textsf {FE}}\,}}''$ is 1-fh-IND-CPA secure, since our adversary has to query m secret keys for the zero function which does not leak any information about encrypted messages.

Depth and Length: Since the transformation of the encryption algorithm is done by multiplication with the matrix $A^T\in \mathbb {Z}_q^{k\times m}$, the depth of the encryption algorithm does not change. Furthermore, ${{\,\mathrm{\textsf {Enc}}\,}}''$ is of length⁴ $k \le m$ over $\mathbb {Z}_q$.

Width: We have to show that ${{\,\mathrm{\textsf {Enc}}\,}}''$ is of width $\left\lfloor {q}/{p}\right\rfloor$. To this end, let $(x_\lambda )_\lambda \in (X_\lambda )_\lambda$, draw ${{\,\mathrm{\textsf {msk}}\,}}'' \leftarrow {{\,\mathrm{\textsf {Setup}}\,}}''(1^\lambda )$, ${{\,\mathrm{\textsf {ct}}\,}}''\leftarrow {{\,\mathrm{\textsf {Enc}}\,}}''({{\,\mathrm{\textsf {msk}}\,}}'', x_\lambda )$ and fix a component ${{\,\mathrm{\textsf {ct}}\,}}_i''$ of ${{\,\mathrm{\textsf {ct}}\,}}'' = ({{\,\mathrm{\textsf {ct}}\,}}_1'',\ldots , {{\,\mathrm{\textsf {ct}}\,}}_k'') \in \mathbb {Z}_q^k$. Note that the columns of the matrix $A = (v_{j_1}|\ldots | v_{j_k})$ are some of the vectors $v_1,\ldots , v_{m} \leftarrow {{\,\mathrm{\textsf {KeyGen}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}', 0)$ according to Theorem 4. Since ${{\,\mathrm{\textsf {ct}}\,}}'' = A^T{{\,\mathrm{\textsf {ct}}\,}}'$ for some ${{\,\mathrm{\textsf {ct}}\,}}' \leftarrow {{\,\mathrm{\textsf {Enc}}\,}}'({{\,\mathrm{\textsf {msk}}\,}}', x_\lambda )$, there is, because of the correctness of ${{\,\mathrm{\textsf {FE}}\,}}'$, an $\varepsilon _0 \in {{\,\mathrm{{\textsf {negl}}}\,}}(\lambda )$ s.t. for all $(x_\lambda )_\lambda \in (X_\lambda )_\lambda$

where in the first three terms we take the randomness over the computation of ${{\,\mathrm{\textsf {msk}}\,}}''$ and ${{\,\mathrm{\textsf {ct}}\,}}''$. Therefore, ${{\,\mathrm{\textsf {Enc}}\,}}''$ is of width $\left\lfloor {q}/{p}\right\rfloor$.

Better than Guessing: It remains to show that ${{\,\mathrm{\textsf {FE}}\,}}''$ is better than guessing. Fix $(x_\lambda )_\lambda \in (X_\lambda )_\lambda$ and a samplable $(f_\lambda )_\lambda \in (F_\lambda )_\lambda$ and draw ${{{\,\mathrm{\textsf {msk}}\,}}'' \leftarrow {{\,\mathrm{\textsf {Setup}}\,}}''(1^\lambda )}$, ${{{\,\mathrm{\textsf {sk}}\,}}_f'' \leftarrow {{\,\mathrm{\textsf {KeyGen}}\,}}''({{\,\mathrm{\textsf {msk}}\,}}'', f_\lambda )}$, ${{{\,\mathrm{\textsf {ct}}\,}}_x'' \leftarrow {{\,\mathrm{\textsf {Enc}}\,}}''({{\,\mathrm{\textsf {msk}}\,}}'', x_\lambda )}$. Then, we have

Now, we have ${{\,\mathrm{\textsf {sk}}\,}}_f'' \ne \bot$ iff ${{\,\mathrm{\textsf {sk}}\,}}_f' \in V$. Because of Lemma 10, the probability for this is at least $\frac{1}{m+1} - \varepsilon _1$ for some $\varepsilon _1 \in {{\,\mathrm{{\textsf {negl}}}\,}}(\lambda )$. If ${{\,\mathrm{\textsf {sk}}\,}}_f' \in V$, we have

$$\begin{aligned} {{\,\mathrm{\textsf {Dec}}\,}}''({{\,\mathrm{\textsf {sk}}\,}}_f'', {{\,\mathrm{\textsf {ct}}\,}}_x'') =&{{\,\mathrm{\textsf {Dec}}\,}}'({{\,\mathrm{\textsf {sk}}\,}}_f'', {{\,\mathrm{\textsf {ct}}\,}}_x'') = \left\lceil \frac{ \langle {{\,\mathrm{\textsf {sk}}\,}}_f'' ~ | ~ {{\,\mathrm{\textsf {ct}}\,}}_x''\rangle }{\left\lfloor q / p\right\rfloor }\right\rfloor = \left\lceil \frac{ \langle A^+{{\,\mathrm{\textsf {sk}}\,}}_f' ~ | ~ A^T{{\,\mathrm{\textsf {ct}}\,}}_x'\rangle }{\left\lfloor q / p\right\rfloor }\right\rfloor \\ =&\left\lceil \frac{ \langle AA^+{{\,\mathrm{\textsf {sk}}\,}}_f' ~ | ~ {{\,\mathrm{\textsf {ct}}\,}}_x'\rangle }{\left\lfloor q / p\right\rfloor }\right\rfloor = {{\,\mathrm{\textsf {Dec}}\,}}'({{\,\mathrm{\textsf {sk}}\,}}_f', {{\,\mathrm{\textsf {ct}}\,}}_x'). \end{aligned}$$

The last term equals $f_{\lambda }(x_\lambda )$ with probability at least $1 - \varepsilon _2$ for some ${\varepsilon _2 \in {{\,\mathrm{{\textsf {negl}}}\,}}(\lambda )}$. Now, let $\lambda$ be big enough s.t. $1 - \varepsilon _2(\lambda ) \ge \frac{1}{p(\lambda )+1}$, then

(5)

Therefore, ${{\,\mathrm{\textsf {FE}}\,}}''$ is better than guessing by $\frac{p}{(m+1)(p+1)}$.    $\blacksquare$

Since $(F_\lambda )_\lambda$ contains the projection onto the first coordinate, there is a straightforward way to adversially transform ${{\,\mathrm{\textsf {FE}}\,}}''$ to a private encryption scheme over $\mathbb {Z}_q$ with width $\left\lfloor {q}/{p}\right\rfloor$ and depth d which is better than guessing and selectively IND-CPA secure. For this purpose set $\widetilde{X}_\lambda = \{0,\ldots , N(\lambda )\}$.

Proof

(Theorem 8 Step 3). Let ${{\,\mathrm{\textsf {FE}}\,}}'' = ({{\,\mathrm{\textsf {Setup}}\,}}'', {{\,\mathrm{\textsf {KeyGen}}\,}}'', {{\,\mathrm{\textsf {Enc}}\,}}'', {{\,\mathrm{\textsf {Dec}}\,}}'')$ be the functional encryption scheme of the preceding step. Then, ${{\,\mathrm{\textsf {FE}}\,}}''$ is 1-fh-IND-CPA secure, better than guessing and of depth d and width $B := \left\lfloor {q}/{p}\right\rfloor$ over $\mathbb {Z}_q$. Additionally, ${{\,\mathrm{\textsf {FE}}\,}}''$ has the special property that for all samplable $(f_\lambda )_\lambda$ there is an $\varepsilon \in {{\,\mathrm{{\textsf {negl}}}\,}}(\lambda )$, s.t. we have for all $(x_\lambda )_\lambda$

We adversarially transform ${{\,\mathrm{\textsf {FE}}\,}}''$ to a private-key encryption scheme ${{\,\mathrm{\textsf {SKE}}\,}}''' = ({{\,\mathrm{\textsf {Setup}}\,}}''', {{\,\mathrm{\textsf {Enc}}\,}}''', {{\,\mathrm{\textsf {KeyGen}}\,}}''', {{\,\mathrm{\textsf {Dec}}\,}}''')$ of depth d and width B over $\mathbb {Z}_q$ for the message space $\widetilde{X}_\lambda$ which is IND-CPA secure and better than guessing. For this end set:

$$\begin{aligned}&\begin{aligned} {{\,\mathrm{\textsf {Setup}}\,}}'''(1^\lambda )&:= {{\,\mathrm{\textsf {Setup}}\,}}''(1^\lambda ) \\ {{\,\mathrm{\textsf {Enc}}\,}}'''({{\,\mathrm{\textsf {msk}}\,}}''', x)&:= {{\,\mathrm{\textsf {Enc}}\,}}''({{\,\mathrm{\textsf {msk}}\,}}''', (x, 0\ldots , 0))\\ {{\,\mathrm{\textsf {KeyGen}}\,}}'''({{\,\mathrm{\textsf {msk}}\,}}''', \mathrm {Id}_{\widetilde{X}_\lambda })&:= {{\,\mathrm{\textsf {KeyGen}}\,}}''({{\,\mathrm{\textsf {msk}}\,}}''', \pi _1)\\&\\&\\&\\ \end{aligned}&\begin{aligned}&{{\,\mathrm{\textsf {Dec}}\,}}'''({{\,\mathrm{\textsf {sk}}\,}}''', {{\,\mathrm{\textsf {ct}}\,}}'''):\\\hline&{{\,\mathrm{{\textsf {if}}}\,}}\ {{\,\mathrm{\textsf {sk}}\,}}''' = \bot \\&~~~~ y \leftarrow \{0,\ldots , N\}\\&{{\,\mathrm{{\textsf {else}}}\,}}\\&~~~~ y \leftarrow {{\,\mathrm{\textsf {Dec}}\,}}''({{\,\mathrm{\textsf {sk}}\,}}''', {{\,\mathrm{\textsf {ct}}\,}}''')\\&{{\,\mathrm{{\textsf {return}}}\,}}\ y\\\hline \end{aligned} \end{aligned}$$

Note that this adversarial transformation is the only one in this work, where we have two functional encryption schemes for different functionalities. Now, ${{\,\mathrm{\textsf {SKE}}\,}}'''$ is IND-CPA secure, because ${{\,\mathrm{\textsf {FE}}\,}}''$ is 1-fh-IND-CPA secure (in fact, ${{\,\mathrm{\textsf {FE}}\,}}''$ being 0-fh-IND-CPA secure would already suffice). ${{\,\mathrm{\textsf {Enc}}\,}}'''$ is of depth d and width B over $\mathbb {Z}_q$, since ${{\,\mathrm{\textsf {Enc}}\,}}''$ is so. The computations marked by the number (5) in the preceding transformation step show – mutatis mutandis – that ${{\,\mathrm{\textsf {SKE}}\,}}'''$ is better than guessing by $\frac{N}{(m+1)\cdot (N+1)}$.    $\square$