Abstract
We present the first maliciously secure protocol for succinct non-interactive secure two-party computation (SNISC): Each player sends just a single message whose length is (essentially) independent of the running time of the function to be computed. The protocol does not require any trusted setup, satisfies superpolynomial-time simulation-based security (SPS), and is based on (subexponential) security of the Learning With Errors (LWE) assumption. We do not rely on SNARKs or “knowledge of exponent”-type assumptions.
Since the protocol is non-interactive, the relaxation to SPS security is needed, as standard polynomial-time simulation is impossible; however, a slight variant of our main protocol yields a SNISC with polynomial-time simulation in the CRS model.
R. Pass—Supported in part by NSF Award SATC-1704788, NSF Award RI-1703846, and AFOSR Award FA9550-18-1-0267. This research is based upon work supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via 2019-19-020700006. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of ODNI, IARPA, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for governmental purposes notwithstanding any copyright annotation therein.
A. Polychroniadou—This paper was prepared in part for information purposes by the Artificial Intelligence Research group of JPMorgan Chase & Co and its affiliates (“JP Morgan”), and is not a product of the Research Department of JP Morgan. JP Morgan makes no representation and warranty whatsoever and disclaims all liability, for the completeness, accuracy or reliability of the information contained herein. This document is not intended as investment research or investment advice, or a recommendation, offer or solicitation for the purchase or sale of any security, financial instrument, financial product or service, or to be used in any way for evaluating the merits of participating in any transaction, and shall not constitute a solicitation under any jurisdiction or to any person, if such solicitation under such jurisdiction or to such person would be unlawful. © 2020 JPMorgan Chase & Co. All rights reserved.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Protocols for secure two-party computation (2PC) allow two parties to compute any function (f) of their private inputs (x and y) without revealing anything more than the output f(x, y) of the function. Since their introduction by Yao [42] and Goldreich, Micali and Wigderson [22], they have become one of the most central tools in modern cryptography. In this work, our focus is on 2PC in a setting with a non-interactivity requirement: each player sends just a single message. The first player—typically referred to as the receiver (or R)—computes some message \(m_1\) based on its input x and sends \(m_1\) to the second player. The second player—referred to as the sender (S)—next computes a response \(m_2\) (based on its input y and the message \(m_1\) it received) and sends it back to the receiver. Upon receiving the response \(m_2\), the receiver can finally compute and output f(x, y). (Note that in such a non-interactive scenario, it is essential that only the receiver obtains the output—in other words, that the functionality is “one-sided”; otherwise, since the protocol only has two rounds, the sender will be able to compute the output given only \(m_1\), meaning that it could obtain \(f(x,y^*)\) on any number of inputs \(y^*\) of its choice.)
SNISC: Succinct Non-interactive Secure Computation. As far as we know, this notion of non-interactive 2PC was first formally studied in [30] under the name non-interactive secure computation (NISC); however, informal versions of it became popular in connection with Gentry’s breakthrough result on fully homomorphic encryption (FHE) [21]. One of the original applications of FHE was the private outsourcing of some computation to a remote party: for instance, consider a scenario where a client (the receiver) has some secret input x and wishes a powerful server (the sender) to compute some potentially time-consuming function f on x (and potentially another input y belonging to the server). Using FHE, the client/receiver simply lets \(m_1\) be an FHE encryption of x; the server/sender can next use homomorphic evaluation to obtain an encryption \(m_2\) of f(x, y) to send back, which can be decrypted by the client/receiver. Indeed, an FHE scheme not only directly yields a NISC, but it also yields a succinct NISC (SNISC)—where both the communication complexity of the protocol and the running time of an honest receiver are “essentially” independent of the running time of f. More formally, we define a SNISC as a NISC where the communication complexity and receiver running time depend only on the length of the inputs and outputs, and polylogarithmically on the running time of the function f to be computed (where we assume that f is given as a Turing machine).
The problem with this folklore approach towards “private outsourcing” or succinct NISC is that using FHE alone only satisfies semi-honest security, as opposed to fully malicious security. For instance, a malicious sender could decide to compute any other function of its choice instead of the correct f! Of course, we could always extend the protocol using ZK-SNARKs (succinct non-interactive arguments of knowledge) [6, 8, 20, 27, 32] to prove correctness of the messages \(m_1\) and \(m_2\), but doing so comes at a cost. First, we now need to assume some trusted setup, such as a common reference string (CRS). Additionally, all known constructions of SNARKs are based on knowledge- or extractability-type assumptions, which in general are known to be problematic with respect to arbitrary auxiliary input [7, 9].Footnote 1 Thus, the question as to whether succinct non-interactive secure computation with malicious security is possible in the plain model remains open:
Does there exist a succinct non-interactive secure computation protocol without any trusted setup (and without using extractability assumptions)?
NISC protocols in models with trusted setup have been extensively studied. There exist known constructions of NISC in the OT-hybrid model [30], in the CRS model based on cut-and-choose [1, 33], assuming tamper-proof stateful [26] and stateless [4, 29] hardware tokens, and in the global random oracle model [15]. As far as we know, none of the above protocols are succinct.
The plain model, however, presents additional issues: Goldreich-Oren’s [23] classic impossibility result for two-round zero-knowledge proofs immediately shows that even a non-succinct (let alone succinct) NISC with malicious security cannot satisfy the standard polynomial-time simulation-based notion of security.Footnote 2 Thus, to get any NISC, let alone a succinct one, we need to use some relaxed notion of simulatability for the definition of secure computation. Superpolynomial-time simulation-based security (SPS) [36, 38] has emerged as the standard relaxation of simulation-based security: under SPS security, the attacker is restricted to be a non-uniform polynomial time algorithm, but the simulator (in the definition of secure computation) is allowed to run in (slightly) superpolynomial time (e.g., in quasi-polynomial time). Non-succinct NISC protocols with SPS simulation are known under various standard assumptions [3, 36, 41]. Most notably, the work of [3] constructs a maliciously secure (non-succinct) NISC with quasi-polynomial simulation in the plain model which can securely compute any functionality based on the subexponential security of various standard hardness assumptions; we return to this result in more detail later on. However, all previous works only construct NISC protocols that are non-succinct.
Towards achieving succinctness for NISC, a very recent work by Brakerski and Kalai [13] takes us a step on the way: they focus on a notion of “private delegation” where the receiver’s/client’s input x is publicly known (and thus does not need to be kept hidden) but the input y of the sender/server is considered private. The authors present a delegation protocol that achieves witness indistinguishability (WI) for the sender—as shown in [36], WI is a strict relaxation of SPS security.Footnote 3 While their protocol achieves the desired notion of succinctness, it still falls short of the goal of producing a succinct NISC protocol due to the fact that its only considers privacy for one of the players (namely, the sender); this significantly simplifies the problem. Additionally, their notion of privacy (witness indistinguishability) is also weaker than what we are aiming to achieve (i.e., simulation-based SPS security).
1.1 Our Results
In this work, we provide an affirmative answer to the above question, presenting the first SNISC for general functionalities. Our protocol is in the plain model (i.e., no trusted setup), and we do not rely on any extractability-based assumptions.
Theorem 1 (Informally stated)
Assuming subexponential security of the LWE assumption, there exists a maliciously SPS-secure SNISC for any efficient functionality. Furthermore, the simulator of the protocol runs in quasi-polynomial time.
Our protocol relies on three primitives:
-
A (leveled) FHE scheme [21] with quasi-polynomial security. For our purposes, we additionally require the FHE to satisfy perfect correctness. Such schemes can be based on the (quasi-polynomial security of the) LWE (Learning With Errors) assumption [40], as shown in [11, 24].
-
A (non-private) delegation scheme for polynomial time computations with quasi-polynomial security. For our purpose, we require a scheme that satisfies perfect completeness and allows the sender to adaptively choose the functionality (i.e., we need what is referred to as an “adaptive delegation scheme”). Such schemes can in fact be based on the above notion of quasi-polynomial FHE, and hence in turn on the quasi-polynomial security of the LWE assumption [12].
-
A (non-succinct) SPS-secure NISC for general functionalities f with a quasi-polynomial simulator. Such a scheme exists based on the existence of a subexponentially-secure “weak oblivious transfer” protocolFootnote 4 [3]Footnote 5; this in turn can be based on the subexponential security of any one of the DDH [35], Quadratic Residuosity, or \(N^\text {th}\) Residuosity [28] assumptions, or (as shown in [10]) on subexponential security of the LWE assumption.
More precisely, if the underlying NISC protocol has a \(T(n) \cdot \textsf {poly}(n)\)-time simulator, and if all the other primitives are secure against \(T(n) \cdot \textsf {poly}(n)\) time attackers, the final protocol is secure and has a \(T(n) \cdot \textsf {poly}(n)\)-time simulator:
Theorem 2 (Informally stated)
Assuming the existence of a T(n)-time simulatable NISC protocol, a subexponentially sound adaptive delegation scheme for polynomial-time computations with perfect completeness, and a subexponentially secure leveled FHE scheme with perfect correctness, there exists \(T(n) \cdot \textsf {poly}(n)\)-time simulatable SNISC for any efficient functionality.
As a corollary, we can directly instantiate our protocol using a NISC with polynomial-time simulation in the CRS model based on a two-round universally composable OT protocol (in the CRS model), which [37] shows can be based on the polynomial security of LWE. Hence:
Corollary 1 (Informally stated)
Assuming the polynomial security of the LWE assumption, there exists a maliciously-secure SNISC (with a polynomial-time simulator) in the CRS model for any efficient functionality.
We defer the proof of this corollary to the full version of our paper [34].
1.2 Technical Overview
At a high level, our approach begins with the semi-honestly secure approach of using FHE (which we detailed in the introduction) and attempts to compile it to become secure with respect to malicious attackers. Instead of using ZK-SNARKs (which rely on non-standard assumptions and trusted setup), we will instead use an adaptive delegation scheme and a non-succinct NISC. For our approach to work, we will strongly rely on perfect correctness/completeness properties of both the FHE and the delegation scheme; as far as we know, perfect correctness of these types of primitives has not previously been used to enable applications (where the goal itself isn’t perfect correctness).Footnote 6 Despite this, though, recent constructions (or slight variants) of both FHE and delegation protocols fortunately do provide these guarantees.
Adaptive Delegation: A Starting Point. To explain the approach, we shall start from a (flawed) candidate which simply combines an FHE scheme and an adaptive delegation scheme. In an adaptive delegation scheme (as given in [12]), a verifier generates a public/secret key-pair  and sends
and sends  to the prover. The prover next picks some statement \(\tilde{x}\) and function g, computes the output \(\tilde{y} = g(\tilde{x})\), and produces a “short” proof \(\pi \) of the validity of the statement that \(\tilde{y} = g(\tilde{x})\). The prover finally sends \((\tilde{x},g, \tilde{y},\pi )\) to the verifier, who can use its secret key
to the prover. The prover next picks some statement \(\tilde{x}\) and function g, computes the output \(\tilde{y} = g(\tilde{x})\), and produces a “short” proof \(\pi \) of the validity of the statement that \(\tilde{y} = g(\tilde{x})\). The prover finally sends \((\tilde{x},g, \tilde{y},\pi )\) to the verifier, who can use its secret key  to check the validity of the proof. We will rely on an adaptive delegation scheme satisfying perfect completeness—that is, for all public keys in the range of the key generation algorithm, the prover can convince the verifier with probability 1.
to check the validity of the proof. We will rely on an adaptive delegation scheme satisfying perfect completeness—that is, for all public keys in the range of the key generation algorithm, the prover can convince the verifier with probability 1.
The candidate SNISC leverages delegation to “outsource” the computation of the homomorphic evaluation to the sender: specifically, the receiver first generates a public/secret key-pair  for the FHE, encrypts its input x using the FHE (obtaining a ciphertext \(\mathsf {ct}_x\)), generates a public/secret key pair
for the FHE, encrypts its input x using the FHE (obtaining a ciphertext \(\mathsf {ct}_x\)), generates a public/secret key pair  for the delegation scheme, and finally sends
for the delegation scheme, and finally sends  to the sender. The sender in turn encrypts its input y, obtaining a ciphertext \(\mathsf {ct}_y\); next, it lets g be the function for homomorphically evaluating f on two ciphertexts, computes \(g(\mathsf {ct}_x,\mathsf {ct}_y)\) (i.e., homomorphically evaluates f on \(\mathsf {ct}_x\) and \(\mathsf {ct}_y\)) to obtain a ciphertext \(\mathsf {ct}_\mathsf {out}\), and computes a delegation proof \(\pi \) (with respect to
to the sender. The sender in turn encrypts its input y, obtaining a ciphertext \(\mathsf {ct}_y\); next, it lets g be the function for homomorphically evaluating f on two ciphertexts, computes \(g(\mathsf {ct}_x,\mathsf {ct}_y)\) (i.e., homomorphically evaluates f on \(\mathsf {ct}_x\) and \(\mathsf {ct}_y\)) to obtain a ciphertext \(\mathsf {ct}_\mathsf {out}\), and computes a delegation proof \(\pi \) (with respect to  ) of the validity of the computation of g. Finally, the sender sends \((\mathsf {ct}_y,\mathsf {ct}_\mathsf {out}, \pi )\) to the receiver, who verifies the proof and, if the proof is accepting, decrypts \(\mathsf {ct}_\mathsf {out}\) and outputs it.
) of the validity of the computation of g. Finally, the sender sends \((\mathsf {ct}_y,\mathsf {ct}_\mathsf {out}, \pi )\) to the receiver, who verifies the proof and, if the proof is accepting, decrypts \(\mathsf {ct}_\mathsf {out}\) and outputs it.
Intuitively, this approach hides the input x of the receiver, but clearly fails to hide the input y of the sender, as the receiver can simply decrypt \(\mathsf {ct}_y\) to obtain y. So, rather than providing \(\mathsf {ct}_y\) and \(\pi \) in the clear (as even just the proof \(\pi \) could leak things about \(\mathsf {ct}_y\)), we instead use the (non-succinct) NISC to run the verification procedure of the delegation scheme. That is, we can add to the protocol a NISC instance where the receiver inputs  , the sender inputs \(\mathsf {ct}_x, \mathsf {ct}_y,\mathsf {ct}_\mathsf {out}, \pi \), and the functionality runs the verification algorithm for the delegation scheme, outputting either \(\bot \) if verification fails or, otherwise, \(\mathsf {ct}_\mathsf {out}\) (which can be decrypted by the receiver).
, the sender inputs \(\mathsf {ct}_x, \mathsf {ct}_y,\mathsf {ct}_\mathsf {out}, \pi \), and the functionality runs the verification algorithm for the delegation scheme, outputting either \(\bot \) if verification fails or, otherwise, \(\mathsf {ct}_\mathsf {out}\) (which can be decrypted by the receiver).
Input Independence: Leveraging Perfect Correctness of FHE. The above approach intuitively hides the inputs of both players, and also ensures that the function is computed correctly. But there are many problems with it. For instance, while it guarantees that the sender does not learn the receiver’s input x, it does not guarantee “input independence”, or that the sender’s input does not depend on the receiver’s somehow: for instance, the sender can easily maul \(\mathsf {ct}_x\) into, say, an encryption \(\mathsf {ct}_y\) of \(x+1\) and use that as its input. On a more technical level, simulation-based security requires the simulator to be able to extract the inputs of malicious players, but it is not clear how this can be done here—in fact, a simulator cannot extract the sender’s input y due to the above malleability attack.
To overcome this issue, we again leverage the non-succinct NISC to enable extractability: we add x and the randomness, \(r_x\), needed to generate \(\mathsf {ct}_x\) as an input from the receiver, and we add \(\mathsf {ct}_x\) (i.e., the ciphertext obtained from the receiver), y, and the randomness needed to generate \(\mathsf {ct}_y\) as input from the sender. The functionality additionally checks that the ciphertexts \(\mathsf {ct}_x, \mathsf {ct}_y\) respectively are valid encryptions of the inputs x, y using the given randomness. (It is actually essential that the sender includes the ciphertext \(\mathsf {ct}_x\) from the receiver as part of its input, as opposed to having the receiver input it, as otherwise we could not guarantee that the receiver is sending the same ciphertext to the sender as it is inputting to the NISC). If we have perfect correctness for the underlying FHE scheme with respect to the public-keys selected by the receiver, this approach guarantees that we can correctly extract the inputs of the players. The reason that we need perfect correctness is that the NISC only guarantees that the ciphertexts have been honestly generated using some randomness, but we have no guarantees that the randomness is honestly generated. Perfect correctness ensures that all randomness is “good” and will result in a “well-formed” ciphertext on which homomorphic computation, and subsequently decryption, will always lead to the correct output.
Dealing with a Malicious Receiver: Interactive Witness Encryption and Perfectly Correct Delegation. While the above protocol suffices to deal with a malicious sender (although, as we shall discuss later on, even this is not trivial due to the potential for “spooky interactions” [17]), it still does not allow us to deal with a malicious receiver. The problem is that the receiver could send invalid public keys, either for the FHE or for the delegation scheme. For instance, if the public key for the FHE is invalid, perfect correctness may no longer hold, and we may not be able to extract a correct input for the receiver. Likewise, if the public key for the delegation scheme is invalid, we will not be able to determine whether the verification algorithm of the delegation scheme will be accepting, and thus cannot carry out a simulation. Typically, dealing with a malicious receiver would require adding a zero-knowledge proof of well-formedness of its messages; however, given that the receiver is sending the first message, this seems problematic since, even with SPS-security, one-message ZK is impossible (with respect to non-uniform attackers [5, 36]).
To explain our solution to this problem, let us first assume that we have access to a witness encryption scheme [18]. Recall that a witness encryption scheme enables encrypting a message m with a statement \(\tilde{x}\) so that anyone having a witness w to \(\tilde{x}\) can decrypt the message; if the statement is false, however, the encryption scheme conceals the message m. If we had access to such a witness encryption scheme, we could have the functionality in the NISC compute a witness encryption of \(\mathsf {ct}_\mathsf {out}\) with the statement being that the public keys have been correctly generated. This method ensures that the receiver does not get any meaningful output unless it actually generated the public keys correctly. Of course, it may still use “bad” randomness—we can only verify that the public keys are in the range of the key generating function. But, if the delegation scheme also satisfies a “perfect correctness” property (specifically, both correctness of the computation and perfect completeness of the generated proof), this enables us to simulate the verification of the delegation scheme (as once again, in this case, perfect correctness guarantees that there is no “bad” randomness).
We still have an issue: perfect correctness of the FHE will ensure that the decryption of the output is correct, but we also need to ensure that we can simulate the ciphertext output by the NISC. While this can be handled using an FHE satisfying an appropriate rerandomizability/simulatability property (also with respect to maliciously selected ciphertext), doing so introduces additional complications. Furthermore, while we motivated the above modification using witness encryption, currently known constructions of witness encryption rely on non-standard, and less understood, hardness assumptions; as such, we would like to altogether avoid using it as an underlying primitive.
So, to circumvent the use of witness encryption—while at the same time ensuring that the output of the NISC is simulatable—we realize that in our context, it in fact suffices to use a two-round version of witness encryption, where the receiver of the encryption chooses the statement and can first send a message corresponding to the statement. And such a non-interactive version of witness encryption can be readily implemented using a NISC! As we are already running an instance of a NISC, we can simply have the NISC also implement this interactive witness encryption. More precisely, we now additionally require the receiver to provide its witness—i.e., the randomness for the key generation algorithms—as an input to the NISC, while the sender additionally provides the public keys  and
and  which it receives. The functionality will now only release the output \(\mathsf {ct}_\mathsf {out}\) if it verifies that the keys input by the sender are correctly generated from the respective randomness input by the receiver. Better still, since the randomness used to generate the public/secret key-pair is now an input to the functionality, the functionality can also recover the secret key for the FHE, and next also decrypt \(\mathsf {ct}_\mathsf {out}\) and simply output plain text corresponding to \(\mathsf {ct}_\mathsf {out}\). This prevents the need for rerandomizing \(\mathsf {ct}_\mathsf {out}\), since it is now internal to the NISC instance (and is no longer output). With all of the above modifications, we can now prove that the protocol satisfies SPS security.
which it receives. The functionality will now only release the output \(\mathsf {ct}_\mathsf {out}\) if it verifies that the keys input by the sender are correctly generated from the respective randomness input by the receiver. Better still, since the randomness used to generate the public/secret key-pair is now an input to the functionality, the functionality can also recover the secret key for the FHE, and next also decrypt \(\mathsf {ct}_\mathsf {out}\) and simply output plain text corresponding to \(\mathsf {ct}_\mathsf {out}\). This prevents the need for rerandomizing \(\mathsf {ct}_\mathsf {out}\), since it is now internal to the NISC instance (and is no longer output). With all of the above modifications, we can now prove that the protocol satisfies SPS security.
The Final Protocol. For clarity, let us summarize the final protocol.
-
The Receiver generates
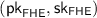 and
and 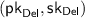 using randomness \(r_{\mathsf {FHE}}\) and \(r_{\mathsf {Del}}\) (respectively) and generates an encryption \(\mathsf {ct}_x\) of its input x using randomness \(r_x\). It then sends
using randomness \(r_{\mathsf {FHE}}\) and \(r_{\mathsf {Del}}\) (respectively) and generates an encryption \(\mathsf {ct}_x\) of its input x using randomness \(r_x\). It then sends  and the first message \(\mathsf {msg}_1\) of a NISC using the input \(x' = (x, r_{\mathsf {FHE}}, r_{\mathsf {Del}}, r_x)\) (for a functionality to be specified shortly).
and the first message \(\mathsf {msg}_1\) of a NISC using the input \(x' = (x, r_{\mathsf {FHE}}, r_{\mathsf {Del}}, r_x)\) (for a functionality to be specified shortly). -
The Sender, upon receiving
 generates an encryption \(\mathsf {ct}_y\) of its input y using randomness \(r_y\), applies the homomorphic evaluation of f to \(\mathsf {ct}_x\) and \(\mathsf {ct}_y\) to obtain a ciphertext \(\mathsf {ct}_\mathsf {out}= g(\mathsf {ct}_x,\mathsf {ct}_y)\), generates a proof \(\pi \) using the delegation scheme (w.r.t.
generates an encryption \(\mathsf {ct}_y\) of its input y using randomness \(r_y\), applies the homomorphic evaluation of f to \(\mathsf {ct}_x\) and \(\mathsf {ct}_y\) to obtain a ciphertext \(\mathsf {ct}_\mathsf {out}= g(\mathsf {ct}_x,\mathsf {ct}_y)\), generates a proof \(\pi \) using the delegation scheme (w.r.t.  ) of the correctness of the computation that \(\mathsf {ct}_\mathsf {out}= g(\mathsf {ct}_x,\mathsf {ct}_y)\), and finally sends the second message \(\mathsf {msg}_2\) of the NISC using the input
) of the correctness of the computation that \(\mathsf {ct}_\mathsf {out}= g(\mathsf {ct}_x,\mathsf {ct}_y)\), and finally sends the second message \(\mathsf {msg}_2\) of the NISC using the input  .
. -
Finally, the receiver, upon getting \(\mathsf {msg}_2\), computes the output z of the NISC protocol and outputs it.
-
The functionality computed by the NISC on input \(x' = (x, r_{\mathsf {FHE}}, r_{\mathsf {Del}}, r_x)\) and
 does the following: it checks that:
does the following: it checks that: -
1.
the public keys
 were respectively generated using randomness \(r_{\mathsf {FHE}}, r_{\mathsf {Del}}\);
were respectively generated using randomness \(r_{\mathsf {FHE}}, r_{\mathsf {Del}}\); -
2.
the ciphertexts \(\mathsf {ct}_x, \mathsf {ct}_y\) are respectively encryptions of x, y using randomness \(r_x,r_y\); and,
-
3.
\(\pi \) is a valid proof of \(\mathsf {ct}_\mathsf {out}= g(\mathsf {ct}_x,\mathsf {ct}_y)\) w.r.t.
 (as generated from \(r_{\mathsf {Del}}\)).
(as generated from \(r_{\mathsf {Del}}\)).
If the checks pass, it decrypts \(\mathsf {ct}_\mathsf {out}\) (by first generating
 from \(r_{\mathsf {FHE}}\)), obtaining the plaintext z, and finally outputs z. (If any of the checks fail, it instead outputs \(\bot \).)
from \(r_{\mathsf {FHE}}\)), obtaining the plaintext z, and finally outputs z. (If any of the checks fail, it instead outputs \(\bot \).) -
1.
A summary of the message flow can be found in Fig. 1.
A Subtlety in the Security Proof. One subtle point that arises in the proof of security is that, to simulate a malicious sender, we need to simulate the ciphertext \(\mathsf {ct}_x\) without knowledge of x. But the functionality of the underlying NISC takes as input the randomness used for both the key generation of  and for encrypting \(\mathsf {ct}_x\), and thus the functionality implicitly knows how to decrypt \(\mathsf {ct}_x\). A similar issue has arisen in the related context of constructing delegation schemes from FHE and related primitives (see [17]), where it was shown that so-called “spooky interactions” can arise, where a malicious sender (even though it does not how to decrypt the ciphertext) can in fact use this dependence to make the receiver output values that correlate in undesirable ways with the input x (in particular, in ways that would not have been possible if using an “idealized” FHE). Fortunately, in our context, we are able to overcome this issue by using the perfect correctness of the FHE scheme and soundness of our underlying delegation scheme to perform a carefully designed hybrid argument.
and for encrypting \(\mathsf {ct}_x\), and thus the functionality implicitly knows how to decrypt \(\mathsf {ct}_x\). A similar issue has arisen in the related context of constructing delegation schemes from FHE and related primitives (see [17]), where it was shown that so-called “spooky interactions” can arise, where a malicious sender (even though it does not how to decrypt the ciphertext) can in fact use this dependence to make the receiver output values that correlate in undesirable ways with the input x (in particular, in ways that would not have been possible if using an “idealized” FHE). Fortunately, in our context, we are able to overcome this issue by using the perfect correctness of the FHE scheme and soundness of our underlying delegation scheme to perform a carefully designed hybrid argument.
A bit more precisely, the key point is that when simulating a malicious sender in communication with an honest receiver, the receiver’s public key and ciphertext \(\mathsf {ct}_x\) will always be correctly generated (as such, we do not have to perform the checks involving the receiver to simulate the underlying NISC’s output); furthermore, by soundness of delegation and the perfect correctness of the FHE, the decryption of \(\mathsf {ct}_\mathsf {out}\) must equal f(x, y) (with overwhelming probability) if \(\pi \) is accepting, so we can use this fact to show that decrypting \(\mathsf {ct}_\mathsf {out}\) is actually also unnecessary. As such, we do not need to use either \(r_{\mathsf {FHE}}\) or \(r_x\) to emulate the experiment for a malicious sender, and we can create (and prove security in) a hybrid functionality for the underlying NISC which is independent of this randomness (and only depends on  ).
).
2 Preliminaries
2.1 Fully Homomorphic Encryption
Definition 1
(based on [21]). A fully homomorphic encryption (or FHE) scheme consists of a tuple of algorithms \((\mathsf {Gen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\), where \(\mathsf {Gen}\), \(\mathsf {Enc}\) are PPT and \(\mathsf {Eval}\), \(\mathsf {Dec}\) are (deterministic) polynomial-time algorithms, such that:
-
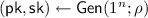 : takes the security parameter n as input and outputs a public key
: takes the security parameter n as input and outputs a public key  and secret key
and secret key 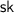 .
. -
 : takes as input a public key
: takes as input a public key 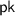 and a message \(m \in \lbrace 0,1 \rbrace \), and outputs a ciphertext \(\mathsf {ct}\). (For multi-bit messages \(\overrightarrow{m} \in \lbrace 0,1 \rbrace ^{p(n)}\), we let
and a message \(m \in \lbrace 0,1 \rbrace \), and outputs a ciphertext \(\mathsf {ct}\). (For multi-bit messages \(\overrightarrow{m} \in \lbrace 0,1 \rbrace ^{p(n)}\), we let  be such that
be such that 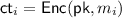 .)
.) -
 : takes as input a list of ciphertexts \(\overrightarrow{\mathsf {ct}}\) and a circuit description C of some function to evaluate and outputs a ciphertext \(\mathsf {ct}'\).
: takes as input a list of ciphertexts \(\overrightarrow{\mathsf {ct}}\) and a circuit description C of some function to evaluate and outputs a ciphertext \(\mathsf {ct}'\). -
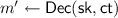 : takes as input a ciphertext \(\mathsf {ct}\) and outputs a message \(m'\).
: takes as input a ciphertext \(\mathsf {ct}\) and outputs a message \(m'\).
We furthermore require that the following properties are satisfied:
-
1.
Full homomorphism: There exist sets of boolean circuits \(\lbrace \mathcal {C}_n \rbrace _{n \in \mathbb {N}}\), negligible function \(\epsilon (n)\), and polynomial \(p(\cdot )\) such that \(\mathcal {C}= \bigcup _n \mathcal {C}_n\) includes the set of all arithmetic circuits over \(\textsf {GF}(2)\)Footnote 7, and, for any \(n \in \mathbb {N}\), we have that, for all \(C \in \mathcal {C}_n\) and \(\overrightarrow{m} \in \lbrace 0,1 \rbrace ^{p(n)}\):

Furthermore, if this probability is identically zero, we refer to the scheme as having perfect correctness.
-
2.
Compactness: There exists a polynomial \(q(\cdot )\) such that the output length of \(\mathsf {Eval}\) given (any number of) inputs generated with security parameter n is at most q(n).
Definition 2
(based on [25]). We say that an FHE \((\mathsf {Gen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) is secure if, for all non-uniform PPT D, there exists a negligible \(\epsilon (\cdot )\) such that for any \(n\in \mathbb {N}\):

over  . If this condition holds also with respect to subexponential size distinguishers D (i.e., algorithms implemented by circuits of size \(poly(2^{n^{\epsilon }})\) for some \(\epsilon >0\)), we refer to the scheme as being subexponentially secure.
. If this condition holds also with respect to subexponential size distinguishers D (i.e., algorithms implemented by circuits of size \(poly(2^{n^{\epsilon }})\) for some \(\epsilon >0\)), we refer to the scheme as being subexponentially secure.
We have the following consequence for encryptions of \(\textsf {poly}(n)\)-bit messages \(\overrightarrow{m_0}\) and \(\overrightarrow{m_1}\):
Fact 1
If an FHE scheme \((\mathsf {Gen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) is secure (resp., subexponentially secure), then, for any polynomial \(p(\cdot )\) and for any non-uniform PPT (resp., subexponential-size) \((\mathcal {A}, D)\) where \(\mathcal {A}\) outputs messages \(\overrightarrow{m_0}, \overrightarrow{m_1} \in \lbrace 0,1 \rbrace ^{p(n)}\) for polynomial \(p(\cdot )\), there exists a negligible \(\epsilon (\cdot )\) such that for any \(n\in \mathbb {N}\):

where

We can construct an FHE scheme with all of the above properties based on the Learning With Errors (LWE) assumption:
Theorem 3
([2, 11, 24]). Based on computational (resp., subexponential) hardness of the Learning With Errors assumption, there exists a secure (resp., subexponentially secure) fully homomorphic encryption scheme satisfying perfect correctness.
2.2 Adaptive Delegation Schemes
A delegation scheme allows for the effective “outsourcing” of computation from one party to another; that is, using delegation, the sender can compute both the correct result of some (possibly expensive) computation on a receiver’s input and a (short) proof which can convince the receiver of the correctness of the computation without requiring the receiver to perform the computation themselves. We consider a notion of delegation with the additional property, formalized in [12], that the functionality \(f(\cdot )\) whose computation is to be delegated can be decided adaptively after the keys  are computed (i.e., the key-generation algorithm \(\mathsf {Gen}\) is independent from f). Formally:
are computed (i.e., the key-generation algorithm \(\mathsf {Gen}\) is independent from f). Formally:
Definition 3
(based on [12]). An adaptive delegation scheme is given by a triple of algorithms \((\mathsf {Gen}, \mathsf {Comp}, \mathsf {Ver})\), where \(\mathsf {Comp}\) and \(\mathsf {Ver}\) are (deterministic) polynomial-time algorithms and \(\mathsf {Gen}\) is PPT, such that:
-
 takes as input a security parameter n and probabilistically outputs a public key
takes as input a security parameter n and probabilistically outputs a public key  and secret key
and secret key  .
. -
 takes as input a Turing machine description of the functionality f to be computed, as well as the inputs \(\overrightarrow{x}\) to f, and produces a result y which the sender claims to be the result of the computation, a \(\textsf {poly}(n)\)-size proof \(\pi \) of its correctness, and the running time T of the computation in unary.
takes as input a Turing machine description of the functionality f to be computed, as well as the inputs \(\overrightarrow{x}\) to f, and produces a result y which the sender claims to be the result of the computation, a \(\textsf {poly}(n)\)-size proof \(\pi \) of its correctness, and the running time T of the computation in unary. -
 takes as input the functionality f to be computed, inputs \(\overrightarrow{x}\), result y, proof \(\pi \), and running time T, and returns \(\mathsf {Accept}\) or \(\mathsf {Reject}\) depending on whether \(\pi \) is a valid proof of \(f(\overrightarrow{x}) = y\).
takes as input the functionality f to be computed, inputs \(\overrightarrow{x}\), result y, proof \(\pi \), and running time T, and returns \(\mathsf {Accept}\) or \(\mathsf {Reject}\) depending on whether \(\pi \) is a valid proof of \(f(\overrightarrow{x}) = y\).
Furthermore, we require the following properties:
-
1.
Completeness: There exists a negligible function \(\epsilon (\cdot )\) such that, for any \(n \in \mathbb {N}\), any f computable by a Turing machine that runs in time at most \(2^n\), and any \(\overrightarrow{x}\) in the domain of f:

In addition, if the above probability is identically zero, we say that the adaptive delegation scheme satisfies perfect completeness.
-
2.
Correctness: For any \(n \in \mathbb {N}\), any f computable by a Turing machine that runs in time at most \(2^n\), and any \(\overrightarrow{x}\) in the domain of f:

-
3.
Soundness: For any non-uniform PPT adversary \(\mathcal {A}\), there exists a negligible function \(\epsilon (\cdot )\) such that, for any \(n \in \mathbb {N}\):

Furthermore, if this condition holds with respect to subexponential-size adversaries, we say that the scheme is subexponentially sound.
A construction of an adaptive delegation scheme with perfect completeness can be found in the work of Brakerski et al. [12], and is based on a secure private information retrieval (PIR) scheme, which in turn can be constructed based on a leveled FHE scheme (including the one presented in Theorem 3). Hence:
Theorem 4
([2, 11, 12, 24]). Given computational (resp., subexponential) hardness of the Learning With Errors assumption, there exists a sound (resp., subexponentially sound) adaptive delegation scheme satisfying perfect completeness.
2.3 Non-interactive Secure Computation
Definition 4
(based on [3, 22, 42]). A non-interactive two-party computation protocol for computing some functionality \(f(\cdot , \cdot )\) (we assume f to be computable by a polynomial-time Turing machine) is given by three PPT algorithms \((\mathsf {NISC}_1, \mathsf {NISC}_2, \mathsf {NISC}_3)\) defining an interaction between a sender S and a receiver R, where only R will receive the final output. The protocol will have common input \(1^n\) (the security parameter); the receiver R will have input x, and the sender will have input y. The algorithms \((\mathsf {NISC}_1, \mathsf {NISC}_2, \mathsf {NISC}_3)\) are such that:
-
\((\mathsf {msg}_1, \sigma ) \leftarrow \mathsf {NISC}_1(1^n, x)\) generates R’s message \(\mathsf {msg}_1\) and persistent state \(\sigma \) (which is not sent to S) given the security parameter n and R’s input x.
-
\(\mathsf {msg}_2 \leftarrow \mathsf {NISC}_2(\mathsf {msg}_1,y ) \) generates S’s message \(\mathsf {msg}_2\) given S’s input y and R’s message \(\mathsf {msg}_1\).
-
\( out \leftarrow \mathsf {NISC}_3(\sigma , \mathsf {msg}_2)\) generates R’s output out given the state \(\sigma \) and S’s message \(\mathsf {msg}_2\).
Furthermore, we require the following property:
-
Correctness. For any parameter \(n \in \mathbb {N}\) and inputs x, y:
$$\text {Pr} \left[ (\mathsf {msg}_1, \sigma ) \leftarrow \mathsf {NISC}_1(1^n, x) : \mathsf {NISC}_3(\sigma , \mathsf {NISC}_2(\mathsf {msg}_1,y)) \ne f(x, y) \right] \le \epsilon (n)$$
Defining non-interactive secure computation will require us to add a security definition, which we formalize as follows:
Security. We adopt a standard notion of simulation-based security, with the relaxation that we allow superpolynomial-time simulation (as originally proposed in [36, 38]). We define security by comparing two experiments conducted between the sender and receiver, either of whom may be corrupted and act arbitrarily (while the other is honest and follows the protocol). In the real experiment, the two parties will perform the actual protocol; in the ideal experiment, the two parties will instead send their inputs to a “trusted third party” who performs the computation and returns the result only to, in this case (because the protocol is one-sided), the receiver. Informally, we say that a protocol is secure if, for any adversary \(\mathcal {A}\) against the real experiment, acting either as the sender or receiver, there is a simulated adversary \(\mathcal {S}\) in the ideal experiment which produces a near-identical (i.e., computationally indistinguishable) result; intuitively, if this is the case, we can assert that the real adversary cannot “learn” anything more than they could by interacting with a trusted intermediary. Let us formalize this notion for the case of SNISC:
-
Let the real experiment be defined as an interaction between a sender S with input y and a receiver R with input x, defined as follows:
-
R computes \((\mathsf {msg}_1, \sigma )\leftarrow \mathsf {NISC}_1(1^n, x)\), stores \(\sigma \), and sends \(\mathsf {msg}_1\) to S.
-
S, on receiving \(\mathsf {msg}_1\), computes \( \mathsf {msg}_2 \leftarrow \mathsf {NISC}_2(\mathsf {msg}_1,y)\) and sends \(\mathsf {msg}_2\) to R.
-
R, on receiving \(\mathsf {msg}_2\) computes \(out \leftarrow \mathsf {NISC}_3(\sigma , \mathsf {msg}_2) \) and outputs out.
In this interaction, one party \(I \in \lbrace S,R \rbrace \) is defined as the corrupted party; we additionally define an adversary, or a polynomial-time machine \(\mathcal {A}\), which receives the security parameter \(1^n\), an auxiliary input z, and the inputs of the corrupted party I, and sends messages (which it may determine arbitrarily) in place of I.
Letting \(\varPi \) denote the protocol to be proven secure, we shall denote by \(\mathsf {Out}_{\varPi , \mathcal {A}, I}(1^n, x, y, z)\) the random variable, taken over all randomness used by the honest party and the adversary, whose output is given by the outputs of the honest receiver (if \(I = S\)) and the adversary (which may output an arbitrary function of its view).
-
-
Let the ideal experiment be defined as an interaction between a sender S, a receiver R, and a trusted party \(\mathcal {T}_f\), defined as follows:
-
R sends x to \(\mathcal {T}_f\), and S sends y to \(\mathcal {T}_f\).
-
\(\mathcal {T}_f\), on receiving x and y, computes \(out = f(x,y)\) and returns it to R.
-
R, on receiving out, outputs it.
As with the real experiment, we say that one party \(I \in \lbrace S,R \rbrace \) is corrupted in that, as before, their behavior is controlled by an adversary \(\mathcal {A}\). We shall denote by \(\mathsf {Out}^{\mathcal {T}_f}_{\varPi _f, \mathcal {A}, I}(1^n, x, y, z)\) the random variable, once again taken over all randomness used by the honest party and the adversary, whose output is again given by the outputs of the honest receiver (if \(I = S\)) and the adversary.
-
Given the above, we can now formally define non-interactive secure computation:
Definition 5
(based on [3, 22, 36, 38, 42]). Given a function \(T(\cdot )\), a non-inter-active two-party protocol \(\varPi = (\mathsf {NISC}_1, \mathsf {NISC}_2, \mathsf {NISC}_3)\) between a sender S and a receiver R, and functionality \(f(\cdot , \cdot )\) computable by a polynomial-time Turing machine, we say that \(\varPi \) securely computes f with \(T(\cdot )\)-time simulation, or that \(\varPi \) is a non-interactive secure computation (NISC) protocol (with \(T(\cdot )\)-time simulation) for computing f, if \(\varPi \) is a non-interactive two-party computation protocol for computing f and, for any polynomial-time adversary \(\mathcal {A}\) corrupting party \(I \in \lbrace S, R \rbrace \), there exists a \(T(n) \cdot \textsf {poly}(n)\)-time simulator \(\mathcal {S}\) such that, for any \(T(n) \cdot \textsf {poly}(n)\)-time algorithm \(D : \lbrace 0,1 \rbrace ^* \rightarrow \lbrace 0,1 \rbrace \), there exists negligible \(\epsilon (\cdot )\) such that for any \(n \in \mathbb {N}\) and any inputs \(x, y \in \lbrace 0,1 \rbrace ^n, z \in \lbrace 0,1 \rbrace ^*\), we have:
where the experiments and distributions \(\mathsf {Out}\) are as defined above.
Furthermore, if \(\varPi \) securely computes f with \(T(\cdot )\)-time simulation for \(T(n) = n^{\log ^c(n)}\) for some constant c, we say that \(\varPi \) securely computes f with quasi-polynomial simulation.
Succinctness. The defining feature of our construction will be a notion of succinctness; specifically, for functionality \(f(\cdot , \cdot )\) with Turing machine description M and running time bounded by \(T_f\), we show the existence of a NISC protocol \(\varPi = (\mathsf {NISC}_1, \mathsf {NISC}_2, \mathsf {NISC}_3)\) for computing f whose message length (i.e., the combined output length of \(\mathsf {NISC}_1\) and \(\mathsf {NISC}_2\)) and total receiver running time on input \(1^n\) are relatively short and essentially independent of the running time of f. Formally:
Definition 6
We say that a NISC protocol \(\varPi = (\mathsf {NISC}_1, \mathsf {NISC}_2, \mathsf {NISC}_3)\) has communication complexity \(\rho (\cdot )\) if, for any \(n \in \mathbb {N}\), \(x, y \in \lbrace 0,1 \rbrace ^n\), and \(z \in \lbrace 0,1 \rbrace ^*\), the outputs of \(\mathsf {NISC}_1 (1^n, x)\) and \(\mathsf {NISC}_2 (1^n, y, z)\) contain at most \(\rho (n)\) bits.
We shall define a NISC protocol which, given functionality \(f : \lbrace 0,1 \rbrace ^n \times \lbrace 0,1 \rbrace ^n \leftarrow \lbrace 0,1 \rbrace ^{\ell (n)}\) computable by a Turing machine M with running time \(T_f (n)\), features communication complexity and receiver running time bounded above by \(p(n, \text {log}(T_f(n)), |M|, \ell (n))\) for an a priori fixed polynomial p.
There exist non-succinct non-interactive secure computation protocols in the standard model based on a notion of “weak oblivious transfer” [3], which in turn can be based on subexponential security of the Learning With Errors assumption [10]:
Theorem 5
([3, 10]). Assuming subexponential hardness of the Learning With Errors assumption, for any functionality \(f(\cdot , \cdot )\) computable by a polynomial-time Turing machine there exists a (non-succinct) non-interactive secure computation protocol with quasi-polynomial simulation for computing f.
We note that this theorem essentially follows from [3, 10]; however, [3] required as an additional assumption the existence of an onto one-way function. In the full version of our paper [34], we present a variant which demonstrates how to prove Theorem 5 without this added assumption.
3 Protocol
We state our main theorem:
Theorem 6
Assuming subexponential hardness of the Learning With Errors assumption, there exists polynomial \(p(\cdot , \cdot , \cdot , \cdot )\) such that, for any polynomials \(T_f(\cdot )\) and \(\ell (\cdot )\) and any Turing machine M with running time bounded by \(T_f(\cdot )\) computing functionality \(f(\cdot , \cdot ) : \lbrace 0,1 \rbrace ^n \times \lbrace 0,1 \rbrace ^n \leftarrow \lbrace 0,1 \rbrace ^{\ell (n)}\), there exists a non-interactive secure computation protocol for computing f with quasi-polynomial simulation which is additionally succinct in that both its communication complexity and the running time of the honest receiver are at most \(p(n, \text {log}(T_f (n)), |M|, \ell (n))\).
We propose the protocol \(\varPi \) given in Fig. 2 for secure non-interactive secure computation of a function f(x, y) given a receiver input x and sender input y, where \(\varPi \) shall use the following primitives:
-
Let \(\pi = (\mathsf {NISC}_1, \mathsf {NISC}_2, \mathsf {NISC}_3)\) be a non-succinct NISC protocol with T(n)-time simulation for \(T(n) = n^{\log ^c(n)}\) (i.e., quasi-polynomial simulation), for which the functionality h will be determined in the first round of the protocol. (The existence of such a primitive is guaranteed by Theorem 5 under subexponential LWE.)
-
Let \((\mathsf {Gen}_\mathsf {FHE}, \mathsf {Enc}_\mathsf {FHE}, \mathsf {Dec}_\mathsf {FHE}, \mathsf {Eval}_\mathsf {FHE})\) be a fully homomorphic encryption scheme satisfying perfect correctness, compactness, and subexponential security (in particular, with respect to \(T(n) \cdot \textsf {poly}(n)\)-time adversaries). (The existence of such a primitive is guaranteed by Theorem 3 under subexponential LWE.)
-
Let \((\mathsf {Gen}_\mathsf {Del}, \mathsf {Comp}_\mathsf {Del}, \mathsf {Ver}_\mathsf {Del})\) be an adaptive delegation scheme with perfect completeness, correctness, and subexponential soundness (in particular, with respect to \(T(n) \cdot \textsf {poly}(n)\)-time adversaries). (The existence of such a primitive is guaranteed by Theorem 4 under subexponential LWE.)
4 Proof
Overview. After first proving the succinctness and correctness of the protocol, we turn to proving its security. We do this in two steps. In the first step, we consider a “hybrid” model in which the underlying NISC protocol is replaced by an “ideal” third party \(\mathcal {T}_h\). If the underlying protocol were universally composable [14], this step would be trivial; unfortunately, it is not, so we need to take care to formally reduce this transformation to the simulation-based security of the underlying protocol. Crucially, this will rely on the fact that we restrict our attention to two-round protocols.
Next, in the second step, we can create and prove the respective simulators for a corrupted sender and corrupted receiver in the \(\mathcal {T}_h\)-hybrid model. The corrupted receiver case follows in a fairly straightforward way, relying on the perfect correctness and completeness of the delegation and FHE schemes. The corrupted sender case, however, has some interesting subtleties in the reduction, and in fact will require another hybrid with a slightly different third party \(\mathcal {T}_{h'}\) to complete; we discuss these subtleties in more detail when they arise during the proof. We begin the formal proof by proving that the protocol \(\varPi \) is succinct:
Lemma 1
There exists polynomial \(p(\cdot , \cdot , \cdot , \cdot )\) such that, for any polynomials \(T_f(\cdot )\) and \(\ell (\cdot )\) and any Turing machine M with running time bounded by \(T_f(\cdot )\) computing functionality \(f(\cdot , \cdot ) : \lbrace 0,1 \rbrace ^n \times \lbrace 0,1 \rbrace ^n \leftarrow \lbrace 0,1 \rbrace ^{\ell (n)}\), the respective non-interactive secure computation protocol \(\varPi \) has communication complexity and honest receiver running time bounded above by \(p(n, \text {log}(T_f (n)), |M|, \ell (n))\).
Proof
We begin by analyzing the communication complexity, as succinctness of the receiver’s running time will follow immediately from this analysis. Aside from messages \(\mathsf {msg}_1\) and \(\mathsf {msg}_2\) for the underlying NISC \(\pi \), the only communication consists of the public keys  and
and  and the ciphertext \(\mathsf {ct}_x\).
and the ciphertext \(\mathsf {ct}_x\).  has length \(\textsf {poly}(n)\) since \(\mathsf {Gen}_\mathsf {FHE}\) is a polynomial-time algorithm running on input \(1^n\), and the ciphertext \(\mathsf {ct}_x\) (which consists of a ciphertext for each bit in \(x \in \lbrace 0,1 \rbrace ^n\)) also has length \(\textsf {poly}(n)\) since \(\mathsf {Enc}_\mathsf {FHE}\) is polynomial-time and is run on inputs of length \(\textsf {poly}(n)\).
has length \(\textsf {poly}(n)\) since \(\mathsf {Gen}_\mathsf {FHE}\) is a polynomial-time algorithm running on input \(1^n\), and the ciphertext \(\mathsf {ct}_x\) (which consists of a ciphertext for each bit in \(x \in \lbrace 0,1 \rbrace ^n\)) also has length \(\textsf {poly}(n)\) since \(\mathsf {Enc}_\mathsf {FHE}\) is polynomial-time and is run on inputs of length \(\textsf {poly}(n)\).  will have length \(\textsf {poly}(n, \text {log}(T_f))\); specifically, its length is given to be \(\textsf {poly}(\lambda ) = \textsf {poly}(n, \text {log}(T_g))\), where \(T_g\) is the running time of the functionality
will have length \(\textsf {poly}(n, \text {log}(T_f))\); specifically, its length is given to be \(\textsf {poly}(\lambda ) = \textsf {poly}(n, \text {log}(T_g))\), where \(T_g\) is the running time of the functionality  with inputs generated from common input \(1^n\). However, since
with inputs generated from common input \(1^n\). However, since  has \(\textsf {poly}(n)\) length, the input ciphertexts both have \(\textsf {poly}(n)\) length by the efficiency of \(\mathsf {Enc}_\mathsf {FHE}\), and f in this case is given as a circuit description, which will have size \(\textsf {poly}(T_f(n))\), we have by the efficiency of \(\mathsf {Eval}_\mathsf {FHE}\) that \(T_g = \textsf {poly}(n, T_f(n))\), implying \(\textsf {poly}(\lambda ) = \textsf {poly}(n, \text {log}(T_f(n)))\).
has \(\textsf {poly}(n)\) length, the input ciphertexts both have \(\textsf {poly}(n)\) length by the efficiency of \(\mathsf {Enc}_\mathsf {FHE}\), and f in this case is given as a circuit description, which will have size \(\textsf {poly}(T_f(n))\), we have by the efficiency of \(\mathsf {Eval}_\mathsf {FHE}\) that \(T_g = \textsf {poly}(n, T_f(n))\), implying \(\textsf {poly}(\lambda ) = \textsf {poly}(n, \text {log}(T_f(n)))\).
So it suffices now to bound the length of the NISC messages \(\mathsf {msg}_1\) and \(\mathsf {msg}_2\). Specifically, even for a non-succinct NISC protocol \(\pi \), the honest sender and receiver must be efficient, and so the message length is still at most polynomial in the input length and running time of the functionality h. We argue that these are \(\textsf {poly}(n, \text {log}(T_f(n)), |M|, \ell (n))\) to complete the proof of the claim:
-
The input length to \(\pi \) is given as the size of the inputs \((x, r_{\mathsf {FHE}}, r_\mathsf {Del}, r_{\mathsf {Enc}(x)})\) from the receiver and
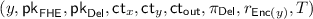 from the sender. x and y have length n by assumption.
from the sender. x and y have length n by assumption. 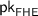 , \(\mathsf {ct}_x\), and \(\mathsf {ct}_y\) have length \(\textsf {poly}(n)\) as argued above, and \(\mathsf {ct}_\mathsf {out}\) (which consists of a ciphertext output from \(\mathsf {Eval}_\mathsf {FHE}\) for each bit of \(f(x,y) \in \lbrace 0,1 \rbrace ^{\ell (n)}\)) has length \(\textsf {poly}(n, \ell (n))\) by the compactness of the FHE scheme.
, \(\mathsf {ct}_x\), and \(\mathsf {ct}_y\) have length \(\textsf {poly}(n)\) as argued above, and \(\mathsf {ct}_\mathsf {out}\) (which consists of a ciphertext output from \(\mathsf {Eval}_\mathsf {FHE}\) for each bit of \(f(x,y) \in \lbrace 0,1 \rbrace ^{\ell (n)}\)) has length \(\textsf {poly}(n, \ell (n))\) by the compactness of the FHE scheme. 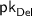 has length \(\textsf {poly}(n, \text {log}(T_f(n)))\) as argued above, and \(\pi _\mathsf {Del}\) also has length \(\textsf {poly}(\lambda ) = \textsf {poly}(n, \text {log}(T_f(n)))\); T will have size \(\lambda = \textsf {poly}(n, \text {log}(T_f(n)))\) as \(T \le 2^\lambda \) is required by the properties of the delegation scheme. Lastly, the randomness \(r_{\mathsf {FHE}}, r_\mathsf {Del}, r_{\mathsf {Enc}(x)}, r_{\mathsf {Enc}(y)}\) cannot have length greater than the running times of the respective algorithms \(\mathsf {Gen}_\mathsf {FHE}, \mathsf {Gen}_\mathsf {Del}, \mathsf {Enc}_\mathsf {FHE}\), all of which we have already noted are at most \(\textsf {poly}(n, \text {log}(T_f(n)))\).
has length \(\textsf {poly}(n, \text {log}(T_f(n)))\) as argued above, and \(\pi _\mathsf {Del}\) also has length \(\textsf {poly}(\lambda ) = \textsf {poly}(n, \text {log}(T_f(n)))\); T will have size \(\lambda = \textsf {poly}(n, \text {log}(T_f(n)))\) as \(T \le 2^\lambda \) is required by the properties of the delegation scheme. Lastly, the randomness \(r_{\mathsf {FHE}}, r_\mathsf {Del}, r_{\mathsf {Enc}(x)}, r_{\mathsf {Enc}(y)}\) cannot have length greater than the running times of the respective algorithms \(\mathsf {Gen}_\mathsf {FHE}, \mathsf {Gen}_\mathsf {Del}, \mathsf {Enc}_\mathsf {FHE}\), all of which we have already noted are at most \(\textsf {poly}(n, \text {log}(T_f(n)))\). -
To bound the running time of the functionality h, notice that it consists of the following:
-
\(\mathsf {Gen}_\mathsf {FHE}\) (run twice), \(\mathsf {Enc}_\mathsf {FHE}\) (run 2n times, once for each bit of x and y), \(\mathsf {Eval}_\mathsf {FHE}\) (run \(\ell (n)\) times, once for each bit of \(\mathsf {out}\)), all of which are efficient algorithms run on inputs of at most length \(\textsf {poly}(n)\) (and hence have running time \(\textsf {poly}(n)\));
-
\(\mathsf {Dec}_\mathsf {FHE}\) (run \(\ell (n)\) times), which has inputs
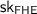 with size \(\textsf {poly}(n)\) and \(\mathsf {ct}_\mathsf {out}\) with size \(\textsf {poly}(n, \ell (n))\), and hence has running time \(\textsf {poly}(n, \ell (n))\);
with size \(\textsf {poly}(n)\) and \(\mathsf {ct}_\mathsf {out}\) with size \(\textsf {poly}(n, \ell (n))\), and hence has running time \(\textsf {poly}(n, \ell (n))\); -
\(\mathsf {Gen}_\mathsf {Del}\) (run twice), which runs in time \(\textsf {poly}(\lambda ) = \textsf {poly}(n, \text {log}(T_f(n)))\);
-
\(\mathsf {Ver}_\mathsf {Del}\) (run once), which, given inputs
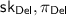 of size \(\textsf {poly}(\lambda ) = \textsf {poly}(n, \text {log}(T_f(n)))\), \(\mathsf {ct}_x, \mathsf {ct}_y\) of size \(\textsf {poly}(n)\), \(\mathsf {ct}_\mathsf {out}\) of size \(\textsf {poly}(n, \ell (n))\), g (the description of
of size \(\textsf {poly}(\lambda ) = \textsf {poly}(n, \text {log}(T_f(n)))\), \(\mathsf {ct}_x, \mathsf {ct}_y\) of size \(\textsf {poly}(n)\), \(\mathsf {ct}_\mathsf {out}\) of size \(\textsf {poly}(n, \ell (n))\), g (the description of  , where we here interpret f as the Turing machine M) of size \(\textsf {poly}(|M|)\), and \(T \le 2^\lambda \) of size at most \(\lambda = \textsf {poly}(n, \text {log}(T_f(n)))\), has running time which is at most \(\textsf {poly}(n, \text {log}(T_f(n)), |M|, \ell (n))\);
, where we here interpret f as the Turing machine M) of size \(\textsf {poly}(|M|)\), and \(T \le 2^\lambda \) of size at most \(\lambda = \textsf {poly}(n, \text {log}(T_f(n)))\), has running time which is at most \(\textsf {poly}(n, \text {log}(T_f(n)), |M|, \ell (n))\);
and a \(\textsf {poly}(n)\) number of comparisons between input values and function outputs which have already been established to have at most \(\textsf {poly}(n, \text {log}(T_f(n)))\) length.
-
The above shows that the communication complexity of \(\varPi \) is succinct. Furthermore, as the honest receiver runs only \(\mathsf {Gen}_\mathsf {FHE}\), \(\mathsf {Gen}_\mathsf {Del}\), \(\mathsf {Enc}_\mathsf {FHE}\), and the (efficient) receiver protocol for the underlying NISC on the aforementioned inputs, and as we have already established that all of these algorithms have running time \(\textsf {poly}(n, \text {log}(T_f(n)), |M|, \ell (n))\), the receiver will inherit the same running time bound. \(\square \)
Towards proving security for \(\varPi \), let \(\mathsf {Out}_{\varPi , \mathcal {A}, I} (1^n, x, y, z)\) denote the random variable, taken over all randomness used by the honest party and the adversary, of the outputs of the honest receiver (if \(I = S\)) and the adversary in the execution of protocol \(\varPi \) given adversary \(\mathcal {A}\) controlling corrupted party \(I \in \lbrace S, R \rbrace \), receiver input x, sender input y, and adversary auxiliary input z. Let \(\mathsf {Exec}_{\varPi , \mathcal {A}, I} (1^n, x, y, z)\) denote the respective experiment.
Let us also define the “ideal” execution by letting \(\mathcal {T}_f\) denote the ideal functionality corresponding to the computation target f(x, y) and letting \(\varPi _f\) be the “ideal” version of the protocol where R sends x to \(\mathcal {T}_f\), S sends y to \(\mathcal {T}_f\), and then R finally outputs the result \(\mathsf {out}\) output by \(\mathcal {T}_f\). We want to show the following theorem:
Theorem 7
Assume, given functionality \(f(\cdot , \cdot )\), the respective protocol \(\varPi \) described in Fig. 2 and the assumptions required in Theorem 6, and let \(T(\cdot )\) be such that the underlying NISC \(\pi \) is secure with \(T(\cdot )\)-time simulation. For any efficient adversary \(\mathcal {A}\) corrupting party \(I \in \lbrace S,R \rbrace \), there exists a \(T(n) \cdot \textsf {poly}(n)\)-time simulator \(\mathcal {S}\) such that, for any non-uniform polynomial-time distinguisher D, there exists a negligible function \(\epsilon (\cdot )\) such that, for all \(n \in \mathbb {N}\), \(x, y \in \lbrace 0,1 \rbrace ^n\), and auxiliary input z, D distinguishes the distributions \(\mathsf {Out}_{\varPi , \mathcal {A}, I} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}, I} (1^n, x, y, z)\) with at most probability \(\epsilon (n)\).
Notice that correctness of \(\varPi \) holds trivially from the perfect correctness of the underlying FHE, the correctness and perfect completeness of the underlying adaptive delegation scheme, and the correctness of the underlying NISC protocol \(\pi \); hence, Theorem 7, which proves security, and Lemma 1, which proves succinctness, will in conjunction directly imply Theorem 6 (where quasi-polynomial simulation results from our use of an underlying NISC protocol with quasi-polynomial simulation, as given in Theorem 5). The remainder of the section, then, is devoted to proving Theorem 7.
We begin by defining a “trusted third party” \(\mathcal {T}_h\) which executes the ideal functionality for h—that is, given the corresponding sender and receiver inputs, \(\mathcal {T}_h\) outputs the correct value of h computed on those inputs. Our first task is to show, then, that the “real” experiment’s outputs \(\mathsf {Out}_{\varPi , \mathcal {A}, I} (1^n, x, y, z)\) cannot be distinguished from those of a “hybrid” experiment, which we shall denote by \(\mathsf {Out}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', I} (1^n, x, y, z)\).
Formally, we let \(\varPi _h\) denote a protocol which is identical to \(\varPi \) with the exception that, in rounds 1 and 2, rather than generating \(\mathsf {msg}_1\) and \(\mathsf {msg}_2\), R and S instead send the respective inputs to \(\mathcal {T}_h\), and, in the output phase, R receives and returns the output from \(\mathcal {T}_h\) rather than unpacking \(\mathsf {msg}_2\). We then state the following lemma, the proof of which is deferred to the full version of our paper [34] as it is rather straightforward.
Lemma 2
For any efficient adversary \(\mathcal {A}\) corrupting party \(I \in \lbrace S,R \rbrace \), there is a \(T(n) \cdot \textsf {poly}(n)\)-time adversary \(\mathcal {A}'\) such that, for any non-uniform polynomial-time distinguisher D, there exists a negligible function \(\epsilon (\cdot )\) such that, for all \(n \in \mathbb {N}\), \(x, y \in \lbrace 0,1 \rbrace ^n\), and auxiliary input z, D distinguishes the distributions \(\mathsf {Out}_{\varPi , \mathcal {A}, I} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', I} (1^n, x, y, z)\) with at most probability \(\epsilon (n)\).
4.1 Comparing Hybrid and Ideal Executions
Next, we need to compare the hybrid execution \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', I} (1^n, x, y, z)\) to the “ideal” execution \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}, I} (1^n, x, y, z)\) to finish the proof of Theorem 7.
Lemma 3
For any \(T(n) \cdot \textsf {poly}(n)\)-time adversary \(\mathcal {A}'\) corrupting some party \(I \in \lbrace S,R \rbrace \), there exists a \(T(n) \cdot \textsf {poly}(n)\)-time simulator \(\mathcal {S}\) such that, for any non-uniform polynomial-time distinguisher D, there exists a negligible function \(\epsilon (\cdot )\) such that, for all \(n \in \mathbb {N}\), \(x, y \in \lbrace 0,1 \rbrace ^n\), and auxiliary input z, D distinguishes the distributions \(\mathsf {Out}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', I} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}, I} (1^n, x, y, z)\) with at most probability \(\epsilon (n)\).
Proof
We again separate into two cases, based on whether \(I = R\) (the receiver is corrupted) or \(I = S\) (the sender is corrupted).
Corrupted Receiver. In this case, define a \(T(n) \cdot \textsf {poly}(n)\)-time simulator \(\mathcal {S}_R\) which does as follows:
-
1.
Run the corrupted receiver \(\mathcal {A}'\). \(\mathcal {A}'\), in the first round, will output a message \((x, r_\mathsf {FHE}, r_\mathsf {Del}, r_\mathsf {Enc})\) to be sent to \(\mathcal {T}_h\). Send x to the ideal functionality \(\mathcal {T}_f\).
-
2.
Receive an output message \(\mathsf {out}\) from the ideal functionality \(\mathcal {T}_f\). If \(\mathsf {out}\) is \(\bot \), return \(\bot \) to \(\mathcal {A}'\) (as the output of \(\mathcal {T}_h\)).
-
3.
Verify the following. If any checks fail, return \(\bot \) to \(\mathcal {A}'\).
-
(a)

-
(b)

-
(c)
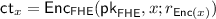
-
(a)
-
4.
If all checks in the previous step pass, return \(\mathsf {out}\) to \(\mathcal {A}'\). Finally, output whatever \(\mathcal {A}'\) outputs.
It suffices here to argue that the output which \(\mathcal {S}_R\) returns to \(\mathcal {A}'\) in the ideal experiment is identically distributed to the output which \(\mathcal {T}_h\) would return to \(\mathcal {A}'\) in the hybrid experiment, as this, combined with the observation that the only input \(\mathcal {A}'\) receives (aside from the auxiliary input z) is the output from \(\mathcal {T}_h\), allows us to conclude that \(\mathcal {A}'\)’s views in \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', R} (1^n, x, y, z)\) and \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_R, R} (1^n, x, y, z)\) (and hence \(\mathcal {A}'\)’s outputs) are likewise identically distributed. We can argue this using the following claims:
Claim 1
If S is honest, then, given the messages \((x, r_\mathsf {FHE}, r_\mathsf {Del}, r_\mathsf {Enc})\) and  from \(\mathcal {A}'\), step (4) of \(\mathcal {S}_R\) succeeds (i.e., does not return \(\bot \)) in \(\varPi _f\) if and only if all checks in step (1) of the functionality h described in Fig. 3 succeed in the respective instance of \(\varPi _h\).
from \(\mathcal {A}'\), step (4) of \(\mathcal {S}_R\) succeeds (i.e., does not return \(\bot \)) in \(\varPi _f\) if and only if all checks in step (1) of the functionality h described in Fig. 3 succeed in the respective instance of \(\varPi _h\).
Proof
The “if” direction is trivial since the checks in step (4) of \(\mathcal {S}_R\) are a strict subset of the checks in step (1) of h.
The “only if” direction follows from the assumption that S is honest, and will hence compute  correctly using the correct inputs. \(\square \)
correctly using the correct inputs. \(\square \)
Claim 2
If S is honest and all checks in step (1) of the functionality h described in Fig. 3 succeed in \(\varPi _h\), then, with probability 1, step (3) of the functionality h will not return \(\bot \).
Proof
Since step (1) is successful, we know that  ; moreover, since S is honest, we know that it must have computed
; moreover, since S is honest, we know that it must have computed  correctly (and using the correct
correctly (and using the correct  and \(\mathsf {ct}_x\), since the checks in step (1) passed). It follows by perfect completeness of the delegation scheme \((\mathsf {Gen}_\mathsf {Del}, \mathsf {Comp}_\mathsf {Del}, \mathsf {Ver}_\mathsf {Del})\) that
and \(\mathsf {ct}_x\), since the checks in step (1) passed). It follows by perfect completeness of the delegation scheme \((\mathsf {Gen}_\mathsf {Del}, \mathsf {Comp}_\mathsf {Del}, \mathsf {Ver}_\mathsf {Del})\) that

as desired. \(\square \)
Claim 3
If S is honest and, in \(\varPi _h\), all checks in step (1) of the functionality h described in Fig. 3 succeed, and step (3) of the functionality h does not return \(\bot \), then the value of \(\mathsf {out}\) returned by step (4) of h will be equal to f(x, y) with probability 1.
Proof
Since S is honest and step (1) is successful, we know, as in the previous claim, that  and furthermore
and furthermore  . It follows by correctness of the delegation scheme \((\mathsf {Gen}_\mathsf {Del}, \mathsf {Comp}_\mathsf {Del}, \mathsf {Ver}_\mathsf {Del})\) that
. It follows by correctness of the delegation scheme \((\mathsf {Gen}_\mathsf {Del}, \mathsf {Comp}_\mathsf {Del}, \mathsf {Ver}_\mathsf {Del})\) that

It suffices to show that this will decrypt to the correct output \({\mathsf {out}= f(x,y)}\). This holds due to perfect correctness of \((\mathsf {Gen}_\mathsf {FHE}, \mathsf {Enc}_\mathsf {FHE}, \mathsf {Dec}_\mathsf {FHE}, \mathsf {Eval}_\mathsf {FHE})\); specifically, since \(\mathsf {ct}_x\) and \(\mathsf {ct}_y\) are encryptions of x and y, respectively:

\(\square \)
Chaining together Claims 1, 2, and 3 leads us to the conclusion that (by Claim 1), \(\mathcal {S}_R\) returns \(\bot \) in \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_R, R} (1^n, x, y, z)\) if and only if \(\mathcal {T}_h\) would return \(\bot \) (from step (1)) in the respective execution of \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', R} (1^n, x, y, z)\), and furthermore, if this event does not occur, then (by Claims 2 and 3 as well as the definition of \(\mathcal {S}_R\)) both \(\mathcal {S}_R\) (in \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_R, R} (1^n, x, y, z)\)) and \(\mathcal {T}_h\) (in the respective execution of \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', R} (1^n, x, y, z)\)) will return an output \(\mathsf {out}\) that is precisely equal to f(x, y), where x is the value sent by the adversary to \(\mathcal {T}_h\) and y is the (honest) sender’s input. This completes the argument for the case \(I = R\).
Corrupted Sender. In the case \(I = S\), define a \(T(n) \cdot \textsf {poly}(n)\)-time simulator \(\mathcal {S}_S\) which does as follows:
-
1.
Generate \({r_\mathsf {FHE}, r_\mathsf {Del}, r_{\mathsf {Enc}(x)} \leftarrow \lbrace 0,1 \rbrace ^*}\),

 .
. -
2.
Run the corrupted sender \(\mathcal {A}'\) using input
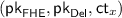 . \(\mathcal {A}'\) will generate a message
. \(\mathcal {A}'\) will generate a message 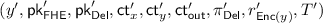 to send to \(\mathcal {T}_h\). Perform the following checks to verify this message, and return \(\bot \) to \(\mathcal {T}_f\) (causing it to output \(\bot \)) if any of them fail.
to send to \(\mathcal {T}_h\). Perform the following checks to verify this message, and return \(\bot \) to \(\mathcal {T}_f\) (causing it to output \(\bot \)) if any of them fail.-
(a)
 ,
,  , \(\mathsf {ct}_x = \mathsf {ct}'_x\).
, \(\mathsf {ct}_x = \mathsf {ct}'_x\). -
(b)

-
(c)
 for the functionality given by
for the functionality given by  .
.
-
(a)
-
3.
Otherwise (if the above checks pass), send \(y'\) to \(\mathcal {T}_f\). Finally, output whatever \(\mathcal {A}'\) outputs.
As this case has interesting subtleties, we lead the formal proof with a brief overview. Recall that, for this case, we need not only to verify that the adversary \(\mathcal {A}'\)’s views in the experiments \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_S, S} (1^n, x, y, z)\) (and hence \(\mathcal {A}'\)’s outputs) cannot be distinguished, but also that the honest receiver R’s outputs cannot be distinguished between the two experiments.
The natural way to do this would be to begin by creating a hybrid protocol \(\varPi '_h\) where the receiver, instead of sending a ciphertext of their input x in the first round, sends the corresponding ciphertext of 0 (as the simulator does when running \(\mathcal {A}'\) in \(\varPi _f\)). Ostensibly, this would allow us to show that the output distributions between \(\varPi _h\) and \(\varPi '_h\) are close by using the CPA-security of the underlying FHE protocol to assert that the ciphertexts, and hence the views of \(\mathcal {A}'\), are indistinguishable between the two experiments. And while this does indeed directly imply that the adversary’s outputs are close, we run into an issue the moment we consider the receiver’s output; specifically, the receiver’s output is the output from the ideal functionality \(\mathcal {T}_h\), which among other things depends on the secret key  and the randomness \(r_\mathsf {FHE}\) used to generate it. In fact, this makes a reduction from \(\varPi '_h\) to the security of the FHE scheme impossible (using current techniques), since a hypothetical adversary simulating this functionality would only know
and the randomness \(r_\mathsf {FHE}\) used to generate it. In fact, this makes a reduction from \(\varPi '_h\) to the security of the FHE scheme impossible (using current techniques), since a hypothetical adversary simulating this functionality would only know  .
.
Instead we will have to consider an alternate functionality \(h'\) which only depends on the public key  and does not use the randomness or secret key. Specifically, rather than decrypting the final result \(\mathsf {ct}_\mathsf {out}\), \(h'\) will instead simply return \(f(x,y')\). We then show that the output distribution of \(\varPi _{h'}\) is statistically close to that of \(\varPi _h\). Specifically, they are identical except when the adversary \(\mathcal {A}'\) can force the ideal functionality \(h'\) to verify a proof \(\pi _\mathsf {Del}\) of an incorrect ciphertext \(\mathsf {ct}_\mathsf {Out}\)—this implies that their statistical distance must be at most the (negligible) soundness error of delegation.Footnote 8 Now, given \(\varPi _{h'}\), we can finally consider a protocol \(\varPi '_{h'}\) where the receiver uses a ciphertext of 0; now that \(h'\) no longer depends on
and does not use the randomness or secret key. Specifically, rather than decrypting the final result \(\mathsf {ct}_\mathsf {out}\), \(h'\) will instead simply return \(f(x,y')\). We then show that the output distribution of \(\varPi _{h'}\) is statistically close to that of \(\varPi _h\). Specifically, they are identical except when the adversary \(\mathcal {A}'\) can force the ideal functionality \(h'\) to verify a proof \(\pi _\mathsf {Del}\) of an incorrect ciphertext \(\mathsf {ct}_\mathsf {Out}\)—this implies that their statistical distance must be at most the (negligible) soundness error of delegation.Footnote 8 Now, given \(\varPi _{h'}\), we can finally consider a protocol \(\varPi '_{h'}\) where the receiver uses a ciphertext of 0; now that \(h'\) no longer depends on  , the reduction to the CPA-security will go through (for both the adversary’s and receiver’s outputs), and we can lastly compare \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_S, S} (1^n, x, y, z)\) to show that, actually, the output distributions are identically distributed.
, the reduction to the CPA-security will go through (for both the adversary’s and receiver’s outputs), and we can lastly compare \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_S, S} (1^n, x, y, z)\) to show that, actually, the output distributions are identically distributed.
We continue to the formal proof. Let \(h'\) be the functionality defined as h, but with four key differences:
-
\(h'\), instead of taking input \(r_\mathsf {FHE}\) from the receiver, takes input
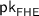 .
. -
In step (1), instead of verifying that
 , \(h'\) verifies that the sender’s and receiver’s inputs
, \(h'\) verifies that the sender’s and receiver’s inputs  match.
match. -
In step (2), \(h'\) no longer computes
 .
. -
In step (4), \(h'\) returns f(x, y) rather than
 .
.
Let \(\varPi _{h'}\) be defined identically to \(\varPi _h\) except that both parties use the ideal functionality \(\mathcal {T}_{h'}\) in place of \(\mathcal {T}_h\) and the receiver inputs  to \(\mathcal {T}_{h'}\) instead of \(r_\mathsf {FHE}\) as specified above. We state the following claim:
to \(\mathcal {T}_{h'}\) instead of \(r_\mathsf {FHE}\) as specified above. We state the following claim:
Claim 4
There exists negligible \(\epsilon (\cdot )\) such that, for all \({n \in \mathbb {N}}\) and inputs x, y, z, the output distributions \(\mathsf {Out}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) are \(\epsilon (n)\)-statistically close.
Proof
Intuitively, this will follow from the soundness of the delegation scheme \((\mathsf {Gen}_\mathsf {Del}, \mathsf {Comp}_\mathsf {Del}, \mathsf {Ver}_\mathsf {Del})\). First, observe that the adversary’s views in experiments \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\), and thus the adversary’s outputs, are identically distributed; hence, it suffices to argue about the honest receiver’s output, i.e., the output of \(\mathcal {T}_h\) or \(\mathcal {T}_{h'}\).
Second, since the receiver R is honest, the fact that \(h'\) verifies that the sender’s and receiver’s inputs  match is equivalent to the verification in h of the sender’s
match is equivalent to the verification in h of the sender’s  (that
(that  ), since the receiver’s input
), since the receiver’s input  will always be equal to \(\mathsf {Gen}_\mathsf {FHE}(1^n, r_\mathsf {FHE})\). So the only change that can possibly affect the output of \(\mathcal {T}_{h'}\) compared to \(\mathcal {T}_h\) in the corrupted sender case is the fact that \(h'\) returns f(x, y) rather than
will always be equal to \(\mathsf {Gen}_\mathsf {FHE}(1^n, r_\mathsf {FHE})\). So the only change that can possibly affect the output of \(\mathcal {T}_{h'}\) compared to \(\mathcal {T}_h\) in the corrupted sender case is the fact that \(h'\) returns f(x, y) rather than  .
.
Now, assume for the sake of contradiction that there is some polynomial \(p(\cdot )\) such that, for infinitely many \({n \in \mathbb {N}}\), there exist x, y, z so that the ideal functionality’s output is different between \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) with probability 1/p(n). We shall use this to construct a \(T(n) \cdot \textsf {poly}(n)\)-time adversary \(\mathcal {A}_\mathsf {Del}\) to break the soundness of the delegation scheme with probability 1/p(n). Specifically, let \(\mathcal {A}_\mathsf {Del}\) do as follows on input  :
:
-
1.
Generate \({r_\mathsf {FHE}, r_{\mathsf {Enc}(x)} \leftarrow \lbrace 0,1 \rbrace ^*}\) and
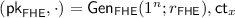
 .
. -
2.
Run the corrupted sender \(\mathcal {A}'\) on input y, auxiliary input z, and first-round message
 . \(\mathcal {A}'\) will generate the message
. \(\mathcal {A}'\) will generate the message 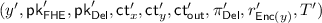 to send to the ideal functionality (\(\mathcal {T}_h\) or \(\mathcal {T}_{h'}\)).
to send to the ideal functionality (\(\mathcal {T}_h\) or \(\mathcal {T}_{h'}\)). -
3.
Run
 for the functionality given by
for the functionality given by 
-
4.
Verify the following and abort if any are false.
-
(a)
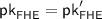 ,
,  , \(\mathsf {ct}_x = \mathsf {ct}'_x\)
, \(\mathsf {ct}_x = \mathsf {ct}'_x\) -
(b)
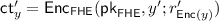
-
(a)
-
5.
Otherwise, return \((g, \mathsf {ct}_x, \mathsf {ct}'_y, \mathsf {ct}_\mathsf {out}, \mathsf {ct}'_\mathsf {out}, \pi _\mathsf {Del}, \pi '_\mathsf {Del}, 1^T, 1^{T'})\).
We claim that \(\mathcal {A}_\mathsf {Del}\) returns a tuple \({(g, \mathsf {ct}_x, \mathsf {ct}'_y, \mathsf {ct}_\mathsf {out}, \mathsf {ct}'_\mathsf {out}, \pi _\mathsf {Del}, \pi '_\mathsf {Del}, 1^T, 1^{T'})}\) such that \({\mathsf {ct}_\mathsf {out}\ne \mathsf {ct}'_\mathsf {out}}\) but 
 —that is, \(\mathcal {A}_\mathsf {Del}\) breaks soundness of the delegation scheme—precisely when h decrypts a ciphertext that is not equal to \(\mathsf {ct}_\mathsf {out}\) as returned by
—that is, \(\mathcal {A}_\mathsf {Del}\) breaks soundness of the delegation scheme—precisely when h decrypts a ciphertext that is not equal to \(\mathsf {ct}_\mathsf {out}\) as returned by  for the corresponding functionality and inputs; furthermore, we claim that this is the only case where h and \(h'\) may not be identically distributed.
for the corresponding functionality and inputs; furthermore, we claim that this is the only case where h and \(h'\) may not be identically distributed.
To verify this, we start by observing that the input to \(\mathcal {A}'\) in step (2) of \(\mathcal {A}_\mathsf {Del}\) is identically distributed to the inputs in the experiments \(\mathsf {Exec}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\), since  is honestly generated and the receiver is honest. Furthermore, given the message from \(\mathcal {A}'\) to the ideal functionality, as well as the fact that R is honest, we can assert that the checks in step (4) of \(\mathcal {A}_\mathsf {Del}\) are equivalent to the checks in step (1) of h or \(h'\), since the receiver’s inputs
is honestly generated and the receiver is honest. Furthermore, given the message from \(\mathcal {A}'\) to the ideal functionality, as well as the fact that R is honest, we can assert that the checks in step (4) of \(\mathcal {A}_\mathsf {Del}\) are equivalent to the checks in step (1) of h or \(h'\), since the receiver’s inputs  are guaranteed to be honestly generated. So, comparing \(\mathcal {T}_h\) and \(\mathcal {T}_{h'}\) for a particular interaction, there are four possible outcomes, which we shall analyze:
are guaranteed to be honestly generated. So, comparing \(\mathcal {T}_h\) and \(\mathcal {T}_{h'}\) for a particular interaction, there are four possible outcomes, which we shall analyze:
-
1.
Step (1) of h or \(h'\) fails, in which case both return \(\bot \) (and \(\mathcal {A}_\mathsf {Del}\) will abort).
-
2.
Step (1) succeeds, but the verification in step (3) fails, in which case both will return \(\bot \) (and \(\mathcal {A}_\mathsf {Del}\) will produce output \((g, \mathsf {ct}_x, \mathsf {ct}'_y, \mathsf {ct}_\mathsf {out}, \mathsf {ct}'_\mathsf {out}, \pi _\mathsf {Del}, \pi '_\mathsf {Del}, 1^T, 1^{T'})\) which is rejected because \((\mathsf {ct}'_\mathsf {out}, \pi '_\mathsf {Del})\) fails to verify).
-
3.
Steps (1) and (3) succeed, and \(\mathsf {ct}'_\mathsf {out}\) given by the adversary is the same as the correct
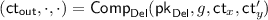 , in which case the outputs of h and \(h'\) are identical and not \(\bot \) by perfect correctness of \(\mathsf {Enc}\) and \(\mathsf {Eval}\), as well as correctness of the delegation scheme.
, in which case the outputs of h and \(h'\) are identical and not \(\bot \) by perfect correctness of \(\mathsf {Enc}\) and \(\mathsf {Eval}\), as well as correctness of the delegation scheme.Specifically, considering the inputs to h, we know by correctness of delegation that, since
 ,
,  . Furthermore, by perfect correctness of the FHE scheme and the fact that \(\mathsf {ct}_x\) and \(\mathsf {ct}'_y\) are encryptions of x and y, respectively:
. Furthermore, by perfect correctness of the FHE scheme and the fact that \(\mathsf {ct}_x\) and \(\mathsf {ct}'_y\) are encryptions of x and y, respectively: 
that is, the output of h will be identical to the output \(f(x, y')\) of \(h'\). In this case, \(\mathcal {A}_\mathsf {Del}\) will produce output \((g, \mathsf {ct}_x, \mathsf {ct}'_y, \mathsf {ct}_\mathsf {out}, \mathsf {ct}'_\mathsf {out}, \pi _\mathsf {Del}, \pi '_\mathsf {Del}, 1^T, 1^{T'})\) which is rejected because \(\mathsf {ct}'_\mathsf {out}= \mathsf {ct}_\mathsf {out}\).
-
4.
Steps (1) and (3) succeed, and \(\mathsf {ct}'_\mathsf {out}\) given by the adversary is not the same as the correct
 , in which case the outputs of h and \(h'\) may be different (and \(\mathcal {A}_\mathsf {Del}\) will produce output \((g, \mathsf {ct}_x, \mathsf {ct}'_y, \mathsf {ct}_\mathsf {out}, \mathsf {ct}'_\mathsf {out}, \pi _\mathsf {Del}, \pi '_\mathsf {Del}, 1^T, 1^{T'})\) which is accepted because \(\mathsf {ct}'_\mathsf {out}\ne \mathsf {ct}_\mathsf {out}\) and \((\mathsf {ct}'_\mathsf {out}, \pi '_\mathsf {Del}, 1^{T'})\) verifies successfully).
, in which case the outputs of h and \(h'\) may be different (and \(\mathcal {A}_\mathsf {Del}\) will produce output \((g, \mathsf {ct}_x, \mathsf {ct}'_y, \mathsf {ct}_\mathsf {out}, \mathsf {ct}'_\mathsf {out}, \pi _\mathsf {Del}, \pi '_\mathsf {Del}, 1^T, 1^{T'})\) which is accepted because \(\mathsf {ct}'_\mathsf {out}\ne \mathsf {ct}_\mathsf {out}\) and \((\mathsf {ct}'_\mathsf {out}, \pi '_\mathsf {Del}, 1^{T'})\) verifies successfully).
The above implies that the probability over possible interactions that the outputs of h and \(h'\) are different—which, as we have argued above, is equal to the statistical distance between the distributions \(\mathsf {Out}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\)—is no greaterFootnote 9 than the probability with which \(\mathcal {A}_\mathsf {Del}\)’s output is accepted. In particular, by our assumption that, for infinitely many \(n \in \mathbb {N}\), there were x, y, z such that this statistical distance was greater than 1/p(n), this implies that the probability that \(\mathcal {A}_\mathsf {Del}\)’s output is accepted (for the corresponding inputs) must be greater than 1/p(n) for infinitely many \(n \in \mathbb {N}\). But this contradicts the soundness of delegation, so the claim is proven. \(\square \)
Now let \(\varPi '_{h'}\) be identical to \(\varPi _{h'}\), with the sole exception that the receiver’s first-round message to the sender replaces the correctly generated  with the simulated encryption
with the simulated encryption  of 0. We present the following claim comparing \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\):
of 0. We present the following claim comparing \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\):
Claim 5
For any polynomial-time non-uniform distinguisher D, there exists negligible \(\epsilon (\cdot )\) such that, for any \(n \in \mathbb {N}\) and inputs x, y, z, the distributions \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) cannot be distinguished by D with probability greater than \(\epsilon (n)\).
Proof
Intuitively, this follows from the CPA-security of the FHE scheme with respect to \(T(n) \cdot \textsf {poly}(n)\)-time adversaries and the fact that both \(h'\) and the view of \(\mathcal {A}'\) are independent of \(r_\mathsf {FHE}\) and  .
.
Formally, assume for contradiction that there exist some non-uniform polynomial-time distinguisher D and polynomial \(p(\cdot )\) such that, for infinitely many \({n \in \mathbb {N}}\), there are inputs x, y, z such that D is able to distinguish the distributions \({\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)}\) and \({\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)}\) with probability 1/p(n). We define a tuple of \(T(n) \cdot \textsf {poly}(n)\)-time algorithms \((\mathcal {A}_\mathsf {FHE}, D')\) that can break the CPA-security of the FHE scheme \((\mathsf {Gen}_\mathsf {FHE}, \mathsf {Enc}_\mathsf {FHE}, \mathsf {Eval}_\mathsf {FHE}, \mathsf {Dec}_\mathsf {FHE})\) with probability 1/p(n) as follows:
-
\(\mathcal {A}_\mathsf {FHE}\), on input \(1^n\), outputs (0, x).
-
\(D'\), on input
 , where c is given as either
, where c is given as either  or
or  , does the following:
, does the following: -
1.
Generate \(r_\mathsf {Del}\leftarrow \lbrace 0,1 \rbrace ^*\) and
 .
. -
2.
Run the corrupted sender \(\mathcal {A}'\) with sender input y, auxiliary input z, and first-round message
 . \(\mathcal {A}'\) will generate a message
. \(\mathcal {A}'\) will generate a message 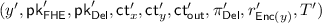 to send to \(\mathcal {T}_{h'}\) and output \(\mathsf {out}_{\mathcal {A}'}\). Store \(\mathsf {out}_{\mathcal {A}'}\).
to send to \(\mathcal {T}_{h'}\) and output \(\mathsf {out}_{\mathcal {A}'}\). Store \(\mathsf {out}_{\mathcal {A}'}\). -
3.
Verify the following and set \(\mathsf {out}_R = \bot \) if any are false. Otherwise, set \(\mathsf {out}_R = f(x,y')\).
-
(a)
 ,
,  , \(\mathsf {ct}_x = \mathsf {ct}'_x\)
, \(\mathsf {ct}_x = \mathsf {ct}'_x\) -
(b)

-
(c)
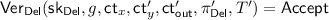 for the functionality given by
for the functionality given by 
-
(a)
-
4.
Return \(D(1^n, (\mathsf {out}_{\mathcal {A}'}, \mathsf {out}_R))\).
-
1.
First, notice that (given that the inputs  and
and  for either \(m = 0\) or \(m = x\) are generated correctly) the inputs to \(\mathcal {A}'\) in step (2) of \(D'\) are identically distributed to either the inputs in \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) (if \(m=x\)) or the inputs in \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) (if \(m=0\)). Hence, the view of \(\mathcal {A}'\) in \(D'\) is identically distributed to the corresponding view in the respective experiment, which implies that the output \(\mathsf {out}_{\mathcal {A}'}\) must be as well, as must the message sent to \(\mathcal {T}_{h'}\).
for either \(m = 0\) or \(m = x\) are generated correctly) the inputs to \(\mathcal {A}'\) in step (2) of \(D'\) are identically distributed to either the inputs in \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) (if \(m=x\)) or the inputs in \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) (if \(m=0\)). Hence, the view of \(\mathcal {A}'\) in \(D'\) is identically distributed to the corresponding view in the respective experiment, which implies that the output \(\mathsf {out}_{\mathcal {A}'}\) must be as well, as must the message sent to \(\mathcal {T}_{h'}\).
It remains to argue about the receiver’s output \(\mathsf {out}_R\); recall that the honest receiver’s output in either experiment is given by the output of the ideal functionality \(\mathcal {T}_{h'}\). However, \(\mathsf {out}_R\) as defined in step (3) of \(D'\) can easily be seen to be identically distributed to the output of \(h'\) in the respective experiment \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) (if \(m=x\)) or \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) (if \(m=0\)). This holds because, since R is honest, R’s inputs  are honestly generated and so the verifications in steps (3a) and (3b) are identical to the respective checks in step (1) of h. Furthermore, the verification in step (3c) of \(D'\) is identical to the verification in step (3) of h, so it follows that \(\mathsf {out}_R = \bot \) exactly when \(h'\) in the respective experiment would return \(\bot \), and that, otherwise, \(\mathsf {out}_R = f(x,y')\), which by the definition of \(h'\) is identical to what \(h'\) would return if not \(\bot \).
are honestly generated and so the verifications in steps (3a) and (3b) are identical to the respective checks in step (1) of h. Furthermore, the verification in step (3c) of \(D'\) is identical to the verification in step (3) of h, so it follows that \(\mathsf {out}_R = \bot \) exactly when \(h'\) in the respective experiment would return \(\bot \), and that, otherwise, \(\mathsf {out}_R = f(x,y')\), which by the definition of \(h'\) is identical to what \(h'\) would return if not \(\bot \).
So we have argued that the distribution \((\mathsf {out}_{\mathcal {A}'}, \mathsf {out}_R)\) is identical to the distribution \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) when \(m = x\) and to \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) when \({m = 0}\). But we have assumed that for infinitely many \({n \in \mathbb {N}}\) there exist x, y, z so that D can distinguish \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) with probability 1/p(n), i.e., that there is at least a 1/p(n) difference between the probability that \(D(1^n, (\mathsf {out}_{\mathcal {A}'}, \mathsf {out}_R))\) returns 1 in the \(m = x\) case and the respective probability in the \(m = 0\) case. But, since \(D'\) returns precisely \(D(1^n, (\mathsf {out}_{\mathcal {A}'}, \mathsf {out}_R))\), this gives us

which, since \(\mathcal {A}_\mathsf {FHE}\) always returns (0, x), means that \((\mathcal {A}_\mathsf {FHE}, D')\) is able to break the CPA-security of the underlying FHE scheme (w.r.t. \(T(n) \cdot \textsf {poly}(n)\)-time adversaries) with probability 1/p(n) for infinitely many \(n \in \mathbb {N}\), a contradiction. \(\square \)
It remains to compare \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_S, S} (1^n, x, y, z)\); we claim that in fact these distributions are already identical. First, observe that the input provided to \(\mathcal {A}'\) in \(\mathcal {S}_S\) is identically distributed to the input provided to \(\mathcal {A}'\) in \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\); in both cases this consists of an honestly generated  such that \(\mathsf {ct}_x\) is the respective encryption of 0. So it follows that the adversary’s output, as well as the message sent by the adversary to the ideal functionality, must be identically distributed between the two experiments. Demonstrating that the receiver’s outputs are identical—that is, that the output of \(h'\) in \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) is always equal to the output f(x, y) in \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_S, S} (1^n, x, y, z)\)—will follow from the following claim, to which we have already alluded in the previous two reductions:
such that \(\mathsf {ct}_x\) is the respective encryption of 0. So it follows that the adversary’s output, as well as the message sent by the adversary to the ideal functionality, must be identically distributed between the two experiments. Demonstrating that the receiver’s outputs are identical—that is, that the output of \(h'\) in \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) is always equal to the output f(x, y) in \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_S, S} (1^n, x, y, z)\)—will follow from the following claim, to which we have already alluded in the previous two reductions:
Claim 6
If R is honest, then, given messages  sent to \(\mathcal {T}_{h'}\),
sent to \(\mathcal {T}_{h'}\),  sent to \(\mathcal {A}'\), and
sent to \(\mathcal {A}'\), and  sent by \(\mathcal {A}'\) to \(\mathcal {T}_{h'}\), the checks in step (2) of \(\mathcal {S}_S\) succeed if and only if all checks in steps (1) and (3) of the functionality \(h'\) succeed.
sent by \(\mathcal {A}'\) to \(\mathcal {T}_{h'}\), the checks in step (2) of \(\mathcal {S}_S\) succeed if and only if all checks in steps (1) and (3) of the functionality \(h'\) succeed.
Proof
If R is honest, it must be the case that  and
and  ; hence step (2a) of \(\mathcal {S}_S\) is equivalent to verifying
; hence step (2a) of \(\mathcal {S}_S\) is equivalent to verifying  ,
,  , and
, and  , i.e., the first three checks of step (1) of \(h'\). Step (2b) is trivially equivalent to the last check in step (1) of \(h'\) and step (2c) is trivially equivalent to the check in step (3) of \(h'\), completing the argument. \(\square \)
, i.e., the first three checks of step (1) of \(h'\). Step (2b) is trivially equivalent to the last check in step (1) of \(h'\) and step (2c) is trivially equivalent to the check in step (3) of \(h'\), completing the argument. \(\square \)
This implies that the receiver in \(\mathsf {Exec}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) will return \(\bot \) as the output from \(h'\) precisely when \(\mathcal {S}_S\) will return \(\bot \) to the ideal functionality (based on the checks in step (2)) and cause the receiver in \(\mathsf {Exec}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_S, S} (1^n, x, y, z)\) to return \(\bot \). However, when \(\mathcal {T}_f\) does not output \(\bot \), it will always output \(f(x,y')\) on the respective inputs x from the honest receiver and \(y'\) from \(\mathcal {S}_S\); similarly, when \(\mathcal {T}_{h'}\) does not return \(\bot \), it will, by definition, also always output \(f(x, y')\) on the respective input x from the honest receiver and \(y'\) from \(\mathcal {A}'\). The above, then, is sufficient to conclude that the distributions \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}_S, S} (1^n, x, y, z)\) are identical.
We conclude the proof of the lemma with a standard hybrid argument; specifically, if there exists some non-uniform polynomial-time distinguisher D and polynomial \(p(\cdot )\) such that, for infinitely many \(n \in \mathbb {N}\), there are inputs x, y, z so that D can distinguish \(\mathsf {Out}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}, S} (1^n, x, y, z)\) with probability 1/p(n), then D must likewise be able to distinguish one of the following pairs with probability \(1/p'(n)\) for some polynomial \(p'(\cdot )\):
-
\(\mathsf {Out}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\)
-
\(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi _{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\)
-
\(\mathsf {Out}^{\mathcal {T}_{h'}}_{\varPi '_{h'}, \mathcal {A}', S} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}, S} (1^n, x, y, z)\)
The first case would contradict Claim 4, the second case would contradict Claim 5, and the third case is impossible because we showed the distributions to be identical. Therefore, such a distinguisher D cannot exist. \(\square \)
By the same logic, a standard hybrid argument shows that Lemmas 2 and 3 imply Theorem 7: if there were some non-uniform polynomial-time distinguisher D and polynomial \(p(\cdot )\) such that, for infinitely many \(n \in \mathbb {N}\), there were inputs x, y, z so that D could distinguish \(\mathsf {Out}_{\varPi , \mathcal {A}, I} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}, I} (1^n, x, y, z)\) with probability 1/p(n), then D would be able to distinguish either:
-
\(\mathsf {Out}_{\varPi , \mathcal {A}, I} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', I} (1^n, x, y, z)\), or
-
\(\mathsf {Out}^{\mathcal {T}_h}_{\varPi _h, \mathcal {A}', I} (1^n, x, y, z)\) and \(\mathsf {Out}^{\mathcal {T}_f}_{\varPi _f, \mathcal {S}, I} (1^n, x, y, z)\)
with probability \(1/p'(n)\) for some polynomial \(p'(\cdot )\). The first case would contradict Lemma 2 and the second Lemma 3; hence, Theorem 7 is proven.
Notes
- 1.
- 2.
- 3.
In the context of interactive proofs, WI is equivalent to a relaxed form of SPS security where the simulator’s running time is unbounded (as opposed to some “small” superpolynomial time).
- 4.
Roughly speaking, a weak oblivious transfer protocol is an OT protocol that satisfies SPS-security against a malicious receiver, but only indistinguishability-based (“game-based”) security against a malicious sender.
- 5.
While [3] claim a construction of SPS NISC from just the existence of a weak OT protocol, their security proof additionally relies on the existence of an onto one-way function. As far as we know, onto one-way functions are not known based on the existence of Weak OT. Consequently, in the full version [34] we present a variant of their protocol that dispenses of this additional assumption.
- 6.
The only work we are aware that uses perfect correctness of a FHE is a very recent work [2] which uses perfectly correct FHE as a tool to get perfectly correct iO.
- 7.
\(\textsf {GF}(2)\) is the set of arithmetic circuits consisting only of \(+\) and \(\times \) gates over the field \(\mathbb {F}_2\).
- 8.
An attentive reader might wonder at this point why, in doing this, we are not simply backing ourselves into the same corner, since indeed \(\mathcal {T}_h\) and even \(\mathcal {T}_{h'}\) are very much dependent on the randomness \(r_\mathsf {Del}\) and secret key
 . The intuitive answer is that, unlike with the reduction to FHE, we are able to “outsource” the dependence on
. The intuitive answer is that, unlike with the reduction to FHE, we are able to “outsource” the dependence on 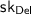 in \(\mathcal {T}_{h'}\) to the security game for the soundness of delegation, allowing us to effectively emulate \(h'\) without said secret key in the adversary we construct.
in \(\mathcal {T}_{h'}\) to the security game for the soundness of delegation, allowing us to effectively emulate \(h'\) without said secret key in the adversary we construct. - 9.
Note that equality is not guaranteed, as h could possibly accept a ciphertext \(\mathsf {ct}'_\mathsf {out}\ne \mathsf {ct}_\mathsf {out}\) that still decrypts to f(x, y).
References
Afshar, A., Mohassel, P., Pinkas, B., Riva, B.: Non-interactive secure computation based on cut-and-choose. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 387–404. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_22
Asharov, G., Ephraim, N., Komargodski, I., Pass, R.: On perfect correctness without derandomization. Cryptology ePrint Archive, Report 2019/1025 (2019). https://eprint.iacr.org/2019/1025
Badrinarayanan, S., Garg, S., Ishai, Y., Sahai, A., Wadia, A.: Two-message witness indistinguishability and secure computation in the plain model from new assumptions. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part III. LNCS, vol. 10626, pp. 275–303. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_10
Badrinarayanan, S., Jain, A., Ostrovsky, R., Visconti, I.: Non-interactive secure computation from one-way functions. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018, Part III. LNCS, vol. 11274, pp. 118–138. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03332-3_5
Barak, B., Pass, R.: On the possibility of one-message weak zero-knowledge. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 121–132. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_7
Bitansky, N., Canetti, R., Chiesa, A., Tromer, E.: Recursive composition and bootstrapping for SNARKS and proof-carrying data. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 111–120. ACM Press, June 2013. https://doi.org/10.1145/2488608.2488623
Bitansky, N., Canetti, R., Paneth, O., Rosen, A.: On the existence of extractable one-way functions. In: Shmoys, D.B. (ed.) 46th ACM STOC, pp. 505–514. ACM Press, May/June 2014. https://doi.org/10.1145/2591796.2591859
Bitansky, N., Chiesa, A., Ishai, Y., Paneth, O., Ostrovsky, R.: Succinct non-interactive arguments via linear interactive proofs. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 315–333. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_18
Boyle, E., Pass, R.: Limits of extractability assumptions with distributional auxiliary input. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part II. LNCS, vol. 9453, pp. 236–261. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_10
Brakerski, Z., Döttling, N.: Two-message statistically sender-private OT from LWE. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part II. LNCS, vol. 11240, pp. 370–390. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_14
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: (Leveled) fully homomorphic encryption without bootstrapping. In: Goldwasser, S. (ed.) ITCS 2012, pp. 309–325. ACM, January 2012. https://doi.org/10.1145/2090236.2090262
Brakerski, Z., Holmgren, J., Kalai, Y.T.: Non-interactive delegation and batch NP verification from standard computational assumptions. In: Hatami, H., McKenzie, P., King, V. (eds.) 49th ACM STOC, pp. 474–482. ACM Press, June 2017. https://doi.org/10.1145/3055399.3055497
Brakerski, Z., Kalai, Y.T.: Monotone batch NP-delegation with applications to access control. Cryptology ePrint Archive, Report 2018/375 (2018). https://eprint.iacr.org/2018/375
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145. IEEE Computer Society Press, October 2001. https://doi.org/10.1109/SFCS.2001.959888
Canetti, R., Jain, A., Scafuro, A.: Practical UC security with a global random oracle. In: Ahn, G.J., Yung, M., Li, N. (eds.) ACM CCS 2014, pp. 597–608. ACM Press, November 2014. https://doi.org/10.1145/2660267.2660374
Cho, C., Döttling, N., Garg, S., Gupta, D., Miao, P., Polychroniadou, A.: Laconic oblivious transfer and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 33–65. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_2
Dwork, C., Langberg, M., Naor, M., Nissim, K., Reingold, O.: Succinct proofs for NP and spooky interactions (2004)
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 467–476. ACM Press, June 2013. https://doi.org/10.1145/2488608.2488667
Garg, S., Mukherjee, P., Pandey, O., Polychroniadou, A.: The exact round complexity of secure computation. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 448–476. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_16
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Mitzenmacher, M. (ed.) 41st ACM STOC, pp. 169–178. ACM Press, May/June 2009. https://doi.org/10.1145/1536414.1536440
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: Aho, A. (ed.) 19th ACM STOC, pp. 218–229. ACM Press, May 1987. https://doi.org/10.1145/28395.28420
Goldreich, O., Oren, Y.: Definitions and properties of zero-knowledge proof systems. J. Cryptol. 7(1), 1–32 (1994). https://doi.org/10.1007/BF00195207
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 555–564. ACM Press, June 2013. https://doi.org/10.1145/2488608.2488678
Goldwasser, S., Micali, S.: Probabilistic encryption. J. Comput. Syst. Sci. 28(2), 270–299 (1984)
Goyal, V., Ishai, Y., Sahai, A., Venkatesan, R., Wadia, A.: Founding cryptography on tamper-proof hardware tokens. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 308–326. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_19
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Halevi, S., Kalai, Y.T.: Smooth projective hashing and two-message oblivious transfer. J. Cryptol. 25(1), 158–193 (2012)
Hazay, C., Polychroniadou, A., Venkitasubramaniam, M.: Composable security in the tamper-proof hardware model under minimal complexity. In: Hirt, M., Smith, A. (eds.) TCC 2016, Part I. LNCS, vol. 9985, pp. 367–399. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_15
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Prabhakaran, M., Sahai, A.: Efficient non-interactive secure computation. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 406–425. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_23
Katz, J., Ostrovsky, R.: Round-optimal secure two-party computation. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 335–354. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_21
Micali, S.: CS proofs (extended abstracts). In: 35th FOCS, pp. 436–453. IEEE Computer Society Press, November 1994. https://doi.org/10.1109/SFCS.1994.365746
Mohassel, P., Rosulek, M.: Non-interactive secure 2PC in the offline/online and batch settings. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part III. LNCS, vol. 10212, pp. 425–455. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_15
Morgan, A., Pass, R., Polychroniadou, A.: Succinct non-interactive secure computation (full version). Cryptology ePrint Archive, Report 2019/1341 (2019). https://eprint.iacr.org/2019/1341
Naor, M., Pinkas, B.: Efficient oblivious transfer protocols. In: SODA, pp. 448–457 (2001)
Pass, R.: Simulation in quasi-polynomial time, and its application to protocol composition. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 160–176. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_10
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Prabhakaran, M., Sahai, A.: New notions of security: achieving universal composability without trusted setup. In: Babai, L. (ed.) 36th ACM STOC, pp. 242–251. ACM Press, June 2004. https://doi.org/10.1145/1007352.1007394
Quach, W., Wee, H., Wichs, D.: Laconic function evaluation and applications. In: Thorup, M. (ed.) 59th FOCS, pp. 859–870. IEEE Computer Society Press, October 2018. https://doi.org/10.1109/FOCS.2018.00086
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) 37th ACM STOC, pp. 84–93. ACM Press, May 2005. https://doi.org/10.1145/1060590.1060603
Schröder, D., Unruh, D.: Round optimal blind signatures. Cryptology ePrint Archive, Report 2011/264 (2011). https://eprint.iacr.org/2011/264
Yao, A.C.: Protocols for secure computations (extended abstract). In: FOCS, pp. 160–164 (1982)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Morgan, A., Pass, R., Polychroniadou, A. (2020). Succinct Non-interactive Secure Computation. In: Canteaut, A., Ishai, Y. (eds) Advances in Cryptology – EUROCRYPT 2020. EUROCRYPT 2020. Lecture Notes in Computer Science(), vol 12106. Springer, Cham. https://doi.org/10.1007/978-3-030-45724-2_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-45724-2_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45723-5
Online ISBN: 978-3-030-45724-2
eBook Packages: Computer ScienceComputer Science (R0)





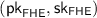 and
and 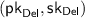 using randomness
using randomness  and the first message
and the first message  generates an encryption
generates an encryption  ) of the correctness of the computation that
) of the correctness of the computation that  .
. does the following: it checks that:
does the following: it checks that:  were respectively generated using randomness
were respectively generated using randomness  (as generated from
(as generated from  from
from 
 .
.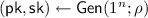 : takes the security parameter n as input and outputs a public key
: takes the security parameter n as input and outputs a public key  and secret key
and secret key 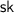 .
. : takes as input a public key
: takes as input a public key 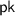 and a message
and a message  be such that
be such that 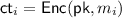 .)
.) : takes as input a list of ciphertexts
: takes as input a list of ciphertexts 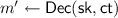 : takes as input a ciphertext
: takes as input a ciphertext 
 takes as input a security parameter n and probabilistically outputs a public key
takes as input a security parameter n and probabilistically outputs a public key  and secret key
and secret key  .
. takes as input a Turing machine description of the functionality f to be computed, as well as the inputs
takes as input a Turing machine description of the functionality f to be computed, as well as the inputs  takes as input the functionality f to be computed, inputs
takes as input the functionality f to be computed, inputs 




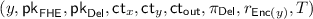 from the sender. x and y have length n by assumption.
from the sender. x and y have length n by assumption. 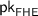 ,
, 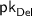 has length
has length 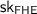 with size
with size 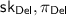 of size
of size  , where we here interpret f as the Turing machine M) of size
, where we here interpret f as the Turing machine M) of size 

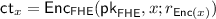

 .
.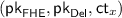 .
. 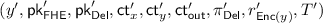 to send to
to send to  ,
,  ,
, 
 for the functionality given by
for the functionality given by  .
.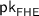 .
. ,
,  match.
match. .
. .
.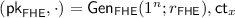
 .
. .
. 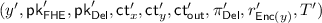 to send to the ideal functionality (
to send to the ideal functionality ( for the functionality given by
for the functionality given by 
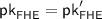 ,
,  ,
, 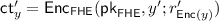
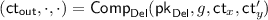 , in which case the outputs of h and
, in which case the outputs of h and  ,
,  . Furthermore, by perfect correctness of the FHE scheme and the fact that
. Furthermore, by perfect correctness of the FHE scheme and the fact that 
 , in which case the outputs of h and
, in which case the outputs of h and  , where c is given as either
, where c is given as either  or
or  , does the following:
, does the following:  .
. .
. 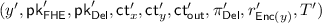 to send to
to send to  ,
,  ,
, 
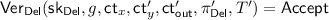 for the functionality given by
for the functionality given by 
 . The intuitive answer is that, unlike with the reduction to FHE, we are able to “outsource” the dependence on
. The intuitive answer is that, unlike with the reduction to FHE, we are able to “outsource” the dependence on  in
in 