Abstract
A non-interactive zero-knowledge (NIZK) protocol enables a prover to convince a verifier of the truth of a statement without leaking any other information by sending a single message. The main focus of this work is on exploring short pairing-based NIZKs for all \(\mathbf{NP} \) languages based on standard assumptions. In this regime, the seminal work of Groth, Ostrovsky, and Sahai (J.ACM’12) (GOS-NIZK) is still considered to be the state-of-the-art. Although fairly efficient, one drawback of GOS-NIZK is that the proof size is multiplicative in the circuit size computing the \(\mathbf{NP} \) relation. That is, the proof size grows by \(O(|C|\kappa )\), where C is the circuit for the \(\mathbf{NP} \) relation and \(\kappa \) is the security parameter. By now, there have been numerous follow-up works focusing on shortening the proof size of pairing-based NIZKs, however, thus far, all works come at the cost of relying either on a non-standard knowledge-type assumption or a non-static q-type assumption. Specifically, improving the proof size of the original GOS-NIZK under the same standard assumption has remained as an open problem.
Our main result is a construction of a pairing-based NIZK for all of \(\mathbf{NP} \) whose proof size is additive in |C|, that is, the proof size only grows by \(|C| +\mathsf {poly}(\kappa )\), based on the decisional linear (DLIN) assumption. Since the DLIN assumption is the same assumption underlying GOS-NIZK, our NIZK is a strict improvement on their proof size.
As by-products of our main result, we also obtain the following two results: (1) We construct a perfectly zero-knowledge NIZK (NIPZK) for \(\mathbf{NP} \) relations computable in \(\mathbf{NC} ^1\) with proof size \(|w| \cdot \mathsf {poly}(\kappa )\) where |w| is the witness length based on the DLIN assumption. This is the first pairing-based NIPZK for a non-trivial class of \(\mathbf{NP} \) languages whose proof size is independent of |C| based on a standard assumption. (2) We construct a universally composable (UC) NIZK for \(\mathbf{NP} \) relations computable in \(\mathbf{NC} ^1\) in the erasure-free adaptive setting whose proof size is \(|w| \cdot \mathsf {poly}(\kappa )\) from the DLIN assumption. This is an improvement over the recent result of Katsumata, Nishimaki, Yamada, and Yamakawa (CRYPTO’19), which gave a similar result based on a non-static q-type assumption.
The main building block for all of our NIZKs is a constrained signature scheme with decomposable online-offline efficiency. This is a property which we newly introduce in this paper and construct from the DLIN assumption. We believe this construction is of an independent interest.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
1.1 Background
Zero-knowledge proof system [26] is an interactive protocol that allows a prover to convince a verifier about the validity of a statement without revealing anything beyond the fact that the statement is true. A variant of this, which is both practically and theoretically important, are non-interactive zero-knowledge (NIZK) proofsFootnote 1 [6] where the prover is only required to send one message to the verifier to prove the validity of the statement in question. Not only have NIZKs shown to be a ubiquitous building block for cryptographic primitives and protocols, but it has also shown to be a mine of theoretical questions with interesting technical challenges.
Unfortunately, it is known that NIZKs for non-trivial languages (i.e., \(\mathbf{NP} \)) do not exist in the plain model where there is no trusted setup [25]. Therefore, NIZKs for non-trivial languages are typically constructed in the common reference string (CRS) model where the prover and verifier have access to a CRS generated by a trusted entity. We will call such NIZKs in the CRS model simply as NIZKs.
The most successful NIZK for all of \(\mathbf{NP} \) is arguably the pairing-based NIZK of Groth, Ostrovsky, and Sahai [30] (GOS-NIZK). GOS-NIZKs are based on the standard decisional linear (DLIN) or the subgroup decision (SD) assumptions. Due to its simplicity and efficiency, pairing-based NIZKs have flourished into a research topic on its own, and the original GOS-NIZK has been followed by many subsequent works trying to improve on it through various approaches. For example, many works such as [31, 37, 38, 42] aim to make GOS-NIZK more efficient by limiting the language to very specific pairing induced languages, while other works such as [14, 20, 28, 29, 45] aim to gain efficiency by relying on a much stronger assumption known as knowledge assumptions (i.e., a type of non-falsifiable [23, 48] assumption). In fact, all works that achieve any notion of “better efficiency” compared to GOS-NIZK only succeeds by either restricting the language or by resorting to use stronger assumptions compared to DLIN or SD.
Similarly with many prior works, the main focus of “efficiency” in our work will be the proof size of the NIZK. Denoting \(C\) as the circuit computing the \(\mathbf{NP} \) relation, GOS-NIZK requires a proof size as large as \(O(|C| \kappa )\), where \(\kappa \) is the security parameter. Borrowing terminology from the recent work of Katsumata et al. [40, 41], what we would like instead is a more compact proof size, that is, a proof size with only an additive overhead \(|C| + \mathsf {poly}(\kappa )\) rather than a multiplicative overhead. For instance, the above latter approach using knowledge assumptions are known to achieve pairing-based NIZKs for \(\mathbf{NP} \) with a significantly short proof size that only depends on the security parameter; in particular, the proof size does not even depend on the witness size. However, unfortunately, it is known that NIZKs with such an unusually short proof (i.e., proof size \(\mathsf {poly}(\kappa ) \cdot (|x| + |w|)^{o(1)}\) where x is the statement and w is the witness) inevitably require strong non-falsifiable assumptions [23]. The most compact NIZK based on any falsifiable assumption is due to [21, 22] which achieves proof size \(|w| + \mathsf {poly}(\kappa )\). However, since it uses (circular secure) fully homomorphic encryption (FHE) its instantiation is solely limited to lattice-based assumptions. Other than lattice-based constructions, Groth [27] proposed a NIZK based on the security of Naccache-Stern public key encryption scheme [47] with a proof size \(|C|\cdot \mathsf{polylog}(\kappa )\), which is asymptotically shorter than that of GOS-NIZK. Very recently, Katsumata et al. [41] provided the first compact NIZK based on any falsifiable pairing-based assumption achieving a proof size of \(|C|+ \mathsf {poly}(\kappa )\). Their construction relies on a new primitive called homomorphic equivocal commitment (HEC), and they instantiate HEC using a non-static Diffie-Hellman type assumption recently introduced in [40]. Unfortunately, the construction of HEC seems to be tailored to their specific non-static assumption, and it seems quite difficult to construct HEC based on a clean static assumption such as DLIN.
In summary, despite the considerable work that has been put into paring-based NIZKs, improving the proof size of GOS-NIZK while simultaneously maintaining the language and assumption has shown to be elusive. Therefore, in this work, the main question we ask is:
Can we construct compact NIZKs for all of \(\mathbf{NP} \) based on standard assumptions over a pairing group?
1.2 Our Result
In this work, we present the first compact pairing-based NIZK for all of \(\mathbf{NP} \) with proof size \(|C| + \mathsf {poly}(\kappa )\) based on the DLIN assumption.More precisely, we can base it on the weaker MDDH assumption, which includes the DLIN and symmetric external Diffie-Hellman (SXDH) assumptions as a special case. Along the way, we also obtain several interesting compact variants of our NIZK such as non-interactive perfect zero-knowledge (NIPZK) and universally composable NIZK (UC-NIZK) [30] from the DLIN assumption. We provide a list of NIZKs which we achieve below and refer to Tables 1 and 2 for comparison between prior works. We note that the table only includes NIZKs for \(\mathbf{NP} \) based on falsifiable assumptions.
-
1.
We construct a compact NIZK for all of \(\mathbf{NP} \) languages with proof size \(|C|+\mathsf {poly}(\kappa )\) based on the DLIN assumption. This is the first NIZK to achieve a proof size shorter than that of GOS-NIZK under the same assumption required by GOS-NIZK. Moreover, if we assume the \(\mathbf{NP} \) relation to be computable in \(\mathbf{NC} ^1\), the proof size can be made as small as \(|w|+\mathsf {poly}(\kappa )\), which matches the state-of-the-art of compact NIZKs from any primitive based on (possibly non-pairing) falsifiable assumptions, e.g., fully-homomorphic encryption [22]. Our NIZK can also be seen as an improvement of the recently proposed compact NIZK of Katsumata et al. [41] in the following two aspects. First, our construction relies on a standard assumption, whereas theirs rely on a non-static q-type assumption. Second, our construction is fairly efficient since we only use pairing group operations in a black-box manner, whereas their construction is highly inefficient since they require pairing group operations in a non-black-box way.
-
2.
We construct NIPZKs for \(\mathbf{NP} \) languages that are computable in \(\mathbf{NC} ^1\) with proof size \(|w|\cdot \mathsf {poly}(\kappa )\) from the DLIN assumption. This is the first pairing-based perfectly zero-knowledge NIZK for a non-trivial class of \(\mathbf{NP} \) languages whose proof size is independent of |C| based on a standard assumption.
-
3.
We construct UC-NIZKs for \(\mathbf{NP} \) languages that are computable in \(\mathbf{NC} ^1\) with proof size \(|w|\cdot \mathsf {poly}(\kappa )\) from the DLIN assumption. This is an improvement over the recent result of Katsumata et al. [41], which gave a similar result based on a non-static q-type assumption.
In column “CRS size” and “Proof size”, \(\kappa \) is the security parameter, |x|, |w| is the statement and witness size, |C| and d are the size and depth of the circuit computing the \(\mathbf{NP} \) relation, and \(k_\mathsf{tpm}\) is the length of the domain of the trapdoor permutation. In column “Assumption”, (n, m)-CDHER stands for the (parameterized) computational DH exponent and ratio assumption, LFE stands for laconic functional evaluation, and sub-exp. LWE stands for sub-exponentially secure learning with errors (LWE).
\(\dagger \)If the domain of the permutation is not \(\{0,1\}^{n}\), we further assume they are doubly enhanced [24].
\(\ddagger \)We additionally require a mild assumption that the prover run time is linear in the size of the circuit computing the \(\mathbf{NP} \) relation.
The main building block for all of our NIZKs is a constrained signature scheme with decomposable online-offline efficiency. This is a property which we newly introduce in this paper and construct from the DLIN assumption. We believe this construction is of independent interest.
1.3 Technical Overview
Reviewing Previous Results. Here, we review definitions and previous results that are required for explaining our approach. We remark that we explain previous works [40, 41, 43] in terms of constrained signatures (CS) instead of homomorphic signatures, even though they are based on the latter primitive. This is because these primitives are actually equivalent as shown by Tsabary [52] and explaining in this way allows us to ignore small differences between our approach and previous ones that stem from the syntactic difference between them.
 We first explain the notion of designated prover NIZK (DP-NIZK), which is a relaxed notion of the standard notion of NIZK. In order to differentiate them, we call the latter CRS-NIZK in the following. In DP-NIZK, only a prover who possesses a secret proving key can generate a proof for an NP statement, and the verification can be done publicly by any entity. Here, the secret proving key is generated along with the CRS by a trusted entity. We require that soundness holds against a malicious prover who possesses the secret proving key and that zero-knowledge holds against a malicious verifier who only accesses the CRS and the proofs, but not the secret proving key. We then explain the notion of CS, which is a slightly simplified version of attribute-based signature [46]. CS is an advanced form of signature where a signing key is associated with some circuit \(C: \{ 0,1 \} ^\ell \rightarrow \{ 0,1 \} \) and using the signing key, one can sign on a message x if \(C(x)=1\). The signature can be verified by a public verification key. As for security, we require unforgeability and privacy. The former requires that one cannot forge a valid signature on a message x if it only has a signing key \(\mathsf {CS}.\mathsf {sk}_C\) for C such that \(C(x)=0\). The latter requires that an honestly generated signature reveals nothing about the circuit C associated with the signing key that is used for generating the signature. In addition to the above security notions, we also require CS to have compact signatures in the sense that the size of the signatures is a fixed polynomial that is independent of the size of the circuit C and the length of the message x.
We first explain the notion of designated prover NIZK (DP-NIZK), which is a relaxed notion of the standard notion of NIZK. In order to differentiate them, we call the latter CRS-NIZK in the following. In DP-NIZK, only a prover who possesses a secret proving key can generate a proof for an NP statement, and the verification can be done publicly by any entity. Here, the secret proving key is generated along with the CRS by a trusted entity. We require that soundness holds against a malicious prover who possesses the secret proving key and that zero-knowledge holds against a malicious verifier who only accesses the CRS and the proofs, but not the secret proving key. We then explain the notion of CS, which is a slightly simplified version of attribute-based signature [46]. CS is an advanced form of signature where a signing key is associated with some circuit \(C: \{ 0,1 \} ^\ell \rightarrow \{ 0,1 \} \) and using the signing key, one can sign on a message x if \(C(x)=1\). The signature can be verified by a public verification key. As for security, we require unforgeability and privacy. The former requires that one cannot forge a valid signature on a message x if it only has a signing key \(\mathsf {CS}.\mathsf {sk}_C\) for C such that \(C(x)=0\). The latter requires that an honestly generated signature reveals nothing about the circuit C associated with the signing key that is used for generating the signature. In addition to the above security notions, we also require CS to have compact signatures in the sense that the size of the signatures is a fixed polynomial that is independent of the size of the circuit C and the length of the message x.
 [43]: We then explain the generic construction of DP-NIZK from CS shown by Kim and Wu [43]. This will serve as a good starting point for us because their conversion allows us to convert a compact CS into a compact DP-NIZK as we will see. Let us fix an NP language L that is verified by a circuit R that takes as input a statement x and a witness w and outputs \(R(x,w)\in \{ 0,1 \} \). In their construction, they set the CRS of the DP-NIZK to be a verification key of the CS. Furthermore, they set the secret proving key for the DP-NIZK to be a secret key K of an SKE and a CS signing key \(\mathsf {CS}.\mathsf {sk}_{C_K}\) for circuit \(C_K\). Here, \(C_K\) is a circuit that takes as input an SKE ciphertext \(\mathsf {SKE}.\mathsf {ct}\) and a statement x and outputs 1 if \(R(x,\mathsf {SKE}.\mathsf {Dec}(K,\mathsf {SKE}.\mathsf {ct})) = 1\) and 0 otherwise. To generate a proof for an NP statement x corresponding to a witness w, the prover encrypts the witness w by the SKE to obtain \(\mathsf {SKE}.\mathsf {ct}=\mathsf {SKE}.\mathsf {Enc}(K,w)\) and then signs on the message \((x, \mathsf {SKE}.\mathsf {ct} )\) using the CS signing key for \(C_K\). By the correctness of the SKE, we have \(C_K(x,\mathsf {SKE}.\mathsf {ct}) = R(x,w)=1\), which implies the completeness of the DP-NIZK. The soundness of the protocol follows from the unforgeability of the underlying CS. This is because any valid proof for an invalid statement \(x^* \not \in L\) is a valid signature on \((x^*,\mathsf {SKE}.\mathsf {ct}^*)\) for some \(\mathsf {SKE}.\mathsf {ct}^*\), for which we have \(C_K(x^*,\mathsf {SKE}.\mathsf {ct}^*) = R(x^*, \mathsf {SKE}.\mathsf {Dec}(K,\mathsf {SKE}.\mathsf {ct}^*))=0\). The zero-knowledge property of the protocol follows from the following intuition. From the privacy of the CS, information of K hardwired into the circuit \(C_K\) is not leaked from the CS signature. We, therefore, can use the security of SKE to conclude that \(\mathsf {SKE}.\mathsf {ct}\) leaks no information of the witness w.
[43]: We then explain the generic construction of DP-NIZK from CS shown by Kim and Wu [43]. This will serve as a good starting point for us because their conversion allows us to convert a compact CS into a compact DP-NIZK as we will see. Let us fix an NP language L that is verified by a circuit R that takes as input a statement x and a witness w and outputs \(R(x,w)\in \{ 0,1 \} \). In their construction, they set the CRS of the DP-NIZK to be a verification key of the CS. Furthermore, they set the secret proving key for the DP-NIZK to be a secret key K of an SKE and a CS signing key \(\mathsf {CS}.\mathsf {sk}_{C_K}\) for circuit \(C_K\). Here, \(C_K\) is a circuit that takes as input an SKE ciphertext \(\mathsf {SKE}.\mathsf {ct}\) and a statement x and outputs 1 if \(R(x,\mathsf {SKE}.\mathsf {Dec}(K,\mathsf {SKE}.\mathsf {ct})) = 1\) and 0 otherwise. To generate a proof for an NP statement x corresponding to a witness w, the prover encrypts the witness w by the SKE to obtain \(\mathsf {SKE}.\mathsf {ct}=\mathsf {SKE}.\mathsf {Enc}(K,w)\) and then signs on the message \((x, \mathsf {SKE}.\mathsf {ct} )\) using the CS signing key for \(C_K\). By the correctness of the SKE, we have \(C_K(x,\mathsf {SKE}.\mathsf {ct}) = R(x,w)=1\), which implies the completeness of the DP-NIZK. The soundness of the protocol follows from the unforgeability of the underlying CS. This is because any valid proof for an invalid statement \(x^* \not \in L\) is a valid signature on \((x^*,\mathsf {SKE}.\mathsf {ct}^*)\) for some \(\mathsf {SKE}.\mathsf {ct}^*\), for which we have \(C_K(x^*,\mathsf {SKE}.\mathsf {ct}^*) = R(x^*, \mathsf {SKE}.\mathsf {Dec}(K,\mathsf {SKE}.\mathsf {ct}^*))=0\). The zero-knowledge property of the protocol follows from the following intuition. From the privacy of the CS, information of K hardwired into the circuit \(C_K\) is not leaked from the CS signature. We, therefore, can use the security of SKE to conclude that \(\mathsf {SKE}.\mathsf {ct}\) leaks no information of the witness w.
We now focus on the efficiency of the resultant DP-NIZK. If we instantiate the DP-NIZK with an SKE with additive ciphertext overhead and a CS with compact signatures, this gives us a compact DP-NIZK. Note that an SKE scheme with additive ciphertext overhead can be realized from very mild assumptions such as CDH. Therefore, their result suggests that it suffices to construct compact CS in order to construct a compact DP-NIZK.
Overview of Our Approach. Here, we provide an overview of our approach. In high level, we follow the same approach as Katsumata et al. [40, 41], who constructed a compact CRS-NIZK from a non-static assumption over bilinear maps. Specifically, we will first construct a CS, then convert it into a DP-NIZK, and then modify it into a CRS-NIZK. However, our approach significantly differs from theirs in low level details. We will provide a comparison with their work after describing our approach in the following.
 We set the construction of compact DP-NIZK from a static assumption as an intermediate goal. Thanks to the Kim-Wu conversion, the problem is reduced to the construction of a CS scheme with compact signatures from a static assumption. To achieve the goal, we follow the folklore conversion that converts an attribute-based encryption (ABE) into a CS that is somewhat reminiscent of the Naor conversion [7] (See e.g., [49]). In order to obtain the CS scheme with the desired properties, it turns out that we need to construct an adaptively secure ABE scheme whose ciphertext size is bounded by some fixed polynomial. Although there is no ABE scheme with the required properties from a static assumption in the literature, we are able to construct it by modifying the very recent ABE scheme proposed by Kowalczyk and Wee [44], who resolved the long-standing open problem of constructing adaptively secure ABE for \(\mathbf{NC} ^1\) whose ciphertext length is independent of the circuit size from a static assumption by cleverly adapting the piecewise guessing frameworks [17, 18, 32, 35, 36, 44] to the setting of ABE. We modify their scheme so that it has even shorter ciphertexts by aggregating the ciphertext components and adding extra components to the secret keys as was done in previous works on ABE with short ciphertexts [2, 33]. The security proof for the scheme is again similar to that of Kowalczyk and Wee, where we decompose the secret keys into smaller pieces and gradually randomize them via carefully chosen sequence of hybrid games. The additional challenge for the proof in our setting is to deal with the extra components in the secret keys. We handle this by observing that the originally proof strategy by Kowalczyk and Wee for randomizing the secret keys works even with these extra components. From this ABE scheme, we can obtain a CS scheme with the desired properties. Furthermore, by applying the Kim-Wu conversion to the CS scheme, we obtain a new compact DP-NIZK from a static assumption. Although this is not our main goal, we note that this improves the compact DP-NIZK scheme from a non-static assumption by Katsumata et al. [40].
We set the construction of compact DP-NIZK from a static assumption as an intermediate goal. Thanks to the Kim-Wu conversion, the problem is reduced to the construction of a CS scheme with compact signatures from a static assumption. To achieve the goal, we follow the folklore conversion that converts an attribute-based encryption (ABE) into a CS that is somewhat reminiscent of the Naor conversion [7] (See e.g., [49]). In order to obtain the CS scheme with the desired properties, it turns out that we need to construct an adaptively secure ABE scheme whose ciphertext size is bounded by some fixed polynomial. Although there is no ABE scheme with the required properties from a static assumption in the literature, we are able to construct it by modifying the very recent ABE scheme proposed by Kowalczyk and Wee [44], who resolved the long-standing open problem of constructing adaptively secure ABE for \(\mathbf{NC} ^1\) whose ciphertext length is independent of the circuit size from a static assumption by cleverly adapting the piecewise guessing frameworks [17, 18, 32, 35, 36, 44] to the setting of ABE. We modify their scheme so that it has even shorter ciphertexts by aggregating the ciphertext components and adding extra components to the secret keys as was done in previous works on ABE with short ciphertexts [2, 33]. The security proof for the scheme is again similar to that of Kowalczyk and Wee, where we decompose the secret keys into smaller pieces and gradually randomize them via carefully chosen sequence of hybrid games. The additional challenge for the proof in our setting is to deal with the extra components in the secret keys. We handle this by observing that the originally proof strategy by Kowalczyk and Wee for randomizing the secret keys works even with these extra components. From this ABE scheme, we can obtain a CS scheme with the desired properties. Furthermore, by applying the Kim-Wu conversion to the CS scheme, we obtain a new compact DP-NIZK from a static assumption. Although this is not our main goal, we note that this improves the compact DP-NIZK scheme from a non-static assumption by Katsumata et al. [40].
 We then try to remove the necessity of the secret proving key from the DP-NIZK described above to obtain a CRS-NIZK. Toward this goal, our first idea is to make the signing key of the CS scheme public by including it into the CRS. When we do so, we stop hardwiring the secret key K of the SKE into the circuit associated with the signing key and change the circuit so that it takes K as an input. The obvious reason for this is because we would like to use the security of SKE at some later point. More concretely, we include \(\mathsf {CS}.\mathsf {sk}_C\) into the CRS, where C is a circuit that takes as input the secret key K of SKE, a statement x, and a ciphertext \(\mathsf {SKE}.\mathsf {ct}\) of SKE and outputs \(R(x,\mathsf {SKE}.\mathsf {Dec}(K,\mathsf {SKE}.\mathsf {ct}))\). When generating a proof, the prover chooses a random K on its own, computes \(\mathsf {SKE}.\mathsf {ct} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {Enc}(K,w)\), and signs on the message \((x,\mathsf {SKE}.\mathsf {ct},K)\) by using \(\mathsf {CS}.\mathsf {sk}_C\) to obtain a signature \(\mathsf {CS}.\sigma \), which is possible because we have \(C(x,\mathsf {SKE}.\mathsf {ct},K)=1\) by the definition of C. The problem with this approach is that we do not know what components to publish as the final proof. More specifically, we run into the following deadlock: If we include K into the proof, then the scheme is not zero-knowledge anymore because one can decrypt \(\mathsf {SKE}.\mathsf {ct}\) by using K to retrieve w. On the other hand, if we do not include K into the proof, we can no longer verify the validity of \(\mathsf {CS}.\sigma \) since K, which is now a part of the message, is required to verify the signature.
We then try to remove the necessity of the secret proving key from the DP-NIZK described above to obtain a CRS-NIZK. Toward this goal, our first idea is to make the signing key of the CS scheme public by including it into the CRS. When we do so, we stop hardwiring the secret key K of the SKE into the circuit associated with the signing key and change the circuit so that it takes K as an input. The obvious reason for this is because we would like to use the security of SKE at some later point. More concretely, we include \(\mathsf {CS}.\mathsf {sk}_C\) into the CRS, where C is a circuit that takes as input the secret key K of SKE, a statement x, and a ciphertext \(\mathsf {SKE}.\mathsf {ct}\) of SKE and outputs \(R(x,\mathsf {SKE}.\mathsf {Dec}(K,\mathsf {SKE}.\mathsf {ct}))\). When generating a proof, the prover chooses a random K on its own, computes \(\mathsf {SKE}.\mathsf {ct} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {Enc}(K,w)\), and signs on the message \((x,\mathsf {SKE}.\mathsf {ct},K)\) by using \(\mathsf {CS}.\mathsf {sk}_C\) to obtain a signature \(\mathsf {CS}.\sigma \), which is possible because we have \(C(x,\mathsf {SKE}.\mathsf {ct},K)=1\) by the definition of C. The problem with this approach is that we do not know what components to publish as the final proof. More specifically, we run into the following deadlock: If we include K into the proof, then the scheme is not zero-knowledge anymore because one can decrypt \(\mathsf {SKE}.\mathsf {ct}\) by using K to retrieve w. On the other hand, if we do not include K into the proof, we can no longer verify the validity of \(\mathsf {CS}.\sigma \) since K, which is now a part of the message, is required to verify the signature.
 We resolve the above issue by using a CRS-NIZK that is not necessarily compact (non-compact NIZK in the following) and change the scheme so that it proves the validity of the CS signature without revealing K nor the signature. In more detail, the prover generates \(K,\mathsf {SKE}.\mathsf {ct}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {Enc}(K,w),\mathsf {CS}.\sigma \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Sign}(\mathsf {CS}.\mathsf {sk}_C, (x,\mathsf {SKE}.\mathsf {ct},K) )\) as above. It then proves that there exists \((K, \mathsf {CS}.\sigma )\) such that \(\mathsf {CS}.\sigma \) is a valid signature on a message \((x,\mathsf {SKE}.\mathsf {ct},K)\) under the verification key \(\mathsf {CS}.\mathsf {vk}\) by using the non-compact NIZK. It then outputs \((\mathsf {SKE}.\mathsf {ct},\mathsf {CS}.\sigma ,\pi )\) as the final proof, where \(\pi \) is the non-compact proof for the above statement.
We resolve the above issue by using a CRS-NIZK that is not necessarily compact (non-compact NIZK in the following) and change the scheme so that it proves the validity of the CS signature without revealing K nor the signature. In more detail, the prover generates \(K,\mathsf {SKE}.\mathsf {ct}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {Enc}(K,w),\mathsf {CS}.\sigma \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Sign}(\mathsf {CS}.\mathsf {sk}_C, (x,\mathsf {SKE}.\mathsf {ct},K) )\) as above. It then proves that there exists \((K, \mathsf {CS}.\sigma )\) such that \(\mathsf {CS}.\sigma \) is a valid signature on a message \((x,\mathsf {SKE}.\mathsf {ct},K)\) under the verification key \(\mathsf {CS}.\mathsf {vk}\) by using the non-compact NIZK. It then outputs \((\mathsf {SKE}.\mathsf {ct},\mathsf {CS}.\sigma ,\pi )\) as the final proof, where \(\pi \) is the non-compact proof for the above statement.
We then explain that the scheme satisfies soundness and zero-knowledge. To see this, we first observe that to break the soundness of the resultant NIZK scheme, it is necessary to break the soundness of the underlying non-compact NIZK or generate a valid CS signature on \((x^*,\mathsf {SKE}.\mathsf {ct}^*,K^*)\) such that \(x^*\not \in L\). By our assumption, the former is impossible. Furthermore, the latter is also impossible, since we have \(C(x^*,\mathsf {SKE}.\mathsf {ct}^*,K^*)=0\) for any choice of \(K^*\) and \(\mathsf {SKE}.\mathsf {ct}^*\) and thus it implies a forgery against the CS scheme. The zero-knowledge property of the scheme holds since the proof consists of the SKE ciphertext and the proof of the non-compact NIZK. Intuitively, since the latter does not leak the information about K, we can use the security of SKE to conclude that w is hidden from the adversary.
While this gives a secure construction, it is unclear whether this is a step forward at this point since we merely constructed a NIZK from a CS by further assuming a NIZK, which seems to be a vacuous statement. Furthermore, the construction we described so far is not compact since the relation proven by the underlying non-compact NIZK is verified by a circuit whose size depends on |C|. To see this, we recall that the verification circuit for the relation proven by the non-compact NIZK takes as input the statement \(x' = (\mathsf {CS}.\mathsf {vk}, x,\mathsf {SKE}.\mathsf {ct})\) and witness \(w'=(K,\mathsf {CS}.\sigma )\) and outputs 1 if and only if \(\mathsf {CS}.\sigma \) is a valid signature on \((x,\mathsf {SKE}.\mathsf {ct},K)\). This circuit is not compact, since it takes as input x, which can be as large as |C| in general and \(\mathsf {CS}.\mathsf {vk}\), which is much larger than |C| in our specific CS scheme.
 We observe that what should be kept secret in the above construction are K and \(\mathsf {CS}.\sigma \),Footnote 2 and \((x,\mathsf {SKE}.\mathsf {ct})\) can be made public without losing the zero-knowledge property. To get a clearer understanding of the problem, we slightly generalize and simplify the problem as follows. What we would like to do is to give a compact proof that we have a valid signature \(\mathsf {CS}.\sigma \) on a message (y, z) for public y and secret z without revealing z nor \(\mathsf {CS}.\sigma \) using a non-compact NIZK. Here, y is not compact while z and \(\mathsf {CS}.\sigma \) are compact. In our context, \( y = (x,\mathsf {SKE}.\mathsf {ct})\) and \(z=K\). In this generalized setting, the above approach is equivalent to proving that \(\mathsf {CS}.\sigma \) is a valid signature on (y, z) under the verification key \(\mathsf {CS}.\mathsf {vk}\). This relation is verified by a circuit that directly takes \(( \mathsf {CS}.\mathsf {vk},(y,z),\mathsf {CS}.\sigma )\) as inputs. This approach does not work simply because the input is not compact.
We observe that what should be kept secret in the above construction are K and \(\mathsf {CS}.\sigma \),Footnote 2 and \((x,\mathsf {SKE}.\mathsf {ct})\) can be made public without losing the zero-knowledge property. To get a clearer understanding of the problem, we slightly generalize and simplify the problem as follows. What we would like to do is to give a compact proof that we have a valid signature \(\mathsf {CS}.\sigma \) on a message (y, z) for public y and secret z without revealing z nor \(\mathsf {CS}.\sigma \) using a non-compact NIZK. Here, y is not compact while z and \(\mathsf {CS}.\sigma \) are compact. In our context, \( y = (x,\mathsf {SKE}.\mathsf {ct})\) and \(z=K\). In this generalized setting, the above approach is equivalent to proving that \(\mathsf {CS}.\sigma \) is a valid signature on (y, z) under the verification key \(\mathsf {CS}.\mathsf {vk}\). This relation is verified by a circuit that directly takes \(( \mathsf {CS}.\mathsf {vk},(y,z),\mathsf {CS}.\sigma )\) as inputs. This approach does not work simply because the input is not compact.
Our first observation is that if we were somehow able to compress the verification circuit size of the relation proven by the non-compact NIZK to be a fixed polynomial without changing the functionality, then the resultant NIZK scheme will have compact proofs. Fortunately, our CS scheme has a nice property that brings us closer to this goal. Namely, in the scheme, the verifier can aggregate the verification key \(\mathsf {CS}.\mathsf {vk}\) depending on a message m to obtain an aggregated verification key \(\mathsf {CS}.\mathsf {vk}_m\), which is of fixed polynomial size. Then, a signature \(\mathsf {CS}.\sigma \) can be verified by using only the aggregated verification key \(\mathsf {CS}.\mathsf {vk}_m\). In particular, the verification circuit no longer takes m as an input. Typically, the aggregation of the verification key is done offline, where one is allowed to perform heavy computation, and the actual verification step is done online, where the computation is very fast even if m is a very long string. We call this property online-offline efficiency. We note that our CS scheme inherits this property from the underlying ABE scheme, where secret keys can be aggregated depending on an attribute in offline phase so that the decryption of a ciphertext corresponding to the same attribute in the online phase is very fast.
A natural approach to compress the verification circuit (for the non-compact NIZK) would be to replace the inputs \(\mathsf {CS}.\mathsf {vk}\) and (y, z) with its aggregated version \(\mathsf {CS}.\mathsf {vk}_{( y,z )}\). In particular, we replace the verification circuit which takes as input \(\mathsf {CS}.\mathsf {vk}\), (y, z), and \(\mathsf {CS}.\sigma \) and verifies the signature with the corresponding online verification circuit which takes \(\mathsf {CS}.\mathsf {vk}_{( y,z )}\) and \(\mathsf {CS}.\sigma \) as inputs. This circuit is compact thanks to the online-offline efficiency of the CS. However, since \(\mathsf {CS}.\mathsf {vk}_{( y,z )}\) cannot be publicly computed, we would have to move the term \(\mathsf {CS}.\mathsf {vk}_{( y,z )}\) into the witness. Furthermore, we additionally have to prove that \(\mathsf {CS}.\mathsf {vk}_{( y,z )}\) is honestly computed from \(\mathsf {CS}.\mathsf {vk}\) and (y, z) using the non-compact NIZK. The problem is that the resulting proof is not compact since this is a statement that involves non-compact terms. Put differently, even though we can compactly prove that we have a signature that passes the online verification under a compressed verification key, we cannot compactly prove that we honestly execute the offline phase to compute the compressed verification key.
As we saw above, the idea of compressing \(\mathsf {CS}.\mathsf {vk}\) depending on the entire string (y, z) does not work. Our idea is to “partially” compress \(\mathsf {CS}.\mathsf {vk}\) depending on the public part y and then use this compressed version of the verification key to construct the verification circuit for the non-compact NIZK. To enable the idea, let us assume that we can compress \(\mathsf {CS}.\mathsf {vk}\) with respect to a string y and obtain \(\mathsf {CS}.\mathsf {vk}_y\). Then, further assume that we can compress \(\mathsf {CS}.\mathsf {vk}_y\) into \(\mathsf {CS}.\mathsf {vk}_{(y,z)}\) using z, so that the verification of a message (y, z) is possible using \(\mathsf {CS}.\mathsf {vk}_{(y,z)}\). Furthermore, we require that the computational cost of compressing \(\mathsf {CS}.\mathsf {vk}_y\) into \(\mathsf {CS}.\mathsf {vk}_{(y,z)}\) depends only on |z|, not on |y|. Therefore if z is compact, we can compute \(\mathsf {CS}.\mathsf {vk}_{(y,z)}\) from \(\mathsf {CS}.\mathsf {vk}_y\) and z by a compact circuit. Assuming this property, we can solve the above generalized problem as follows: We first compress \(\mathsf {CS}.\mathsf {vk}\) depending on y to obtain \(\mathsf {CS}.\mathsf {vk}_y\). We then prove that there exists \(\mathsf {CS}.\sigma \) and z such that \(\mathsf {CS}.\sigma \) is a valid signature under \(\mathsf {CS}.\mathsf {vk}_{(y,z)}\), where \(\mathsf {CS}.\mathsf {vk}_{(y,z)}\) is obtained by compressing \(\mathsf {CS}.\mathsf {vk}_y\) depending on the string z. This statement can be proven compactly, since both verification under the verification key \(\mathsf {CS}.\mathsf {vk}_{(y,z)}\) and the compression of \(\mathsf {CS}.\mathsf {vk}_y\) into \(\mathsf {CS}.\mathsf {vk}_{(y,z)}\) can be done compactly. Furthermore, unlike the previous attempt, we do not have to prove that we honestly executed the offline computation. Namely, we do not have to prove the consistency between \(\mathsf {CS}.\mathsf {vk}\), y, and \(\mathsf {CS}.\mathsf {vk}_y\), since \(\mathsf {CS}.\mathsf {vk}_y\) is publicly computable from \(\mathsf {CS}.\mathsf {vk}\) and y. Therefore, it suffices to show that our CS scheme has the structure that allows one to compress the verification key in two steps. We name this property online-offline decomposability and show that our construction indeed has the property.Footnote 3
Comparison with Katsumata et al. [41]. Here, we compare our approach with the one by Katsumata et al. [40, 41], who showed a similar result from a non-static assumption. As we already mentioned, at the highest level, their approach is the same as ours in that they first construct a CS [40], then convert it into a DP-NIZK, and then modify it into a CRS-NIZK [41]. However, the way they obtained the CS, and the way they modify their DP-NIZK into a CRS-NIZK is significantly different from ours. We elaborate on this below.
 [40]: Similarly to us, their approach is to construct an ABE scheme and then convert it into a CS scheme. However, the requirements for the ABE are different from ours. For the ABE scheme, they require short secret keys, whereas we require short ciphertexts. Furthermore, they require the ABE scheme to be secure following a so-called “single-shot” reduction, where the reduction algorithm runs the adversary only once and perfectly simulates the view of the game. Roughly, this is equivalent to saying that the proof cannot go through hybrid arguments. Therefore, their approach does not seem to be promising when we try to construct a compact CS scheme from a static assumption. Notably, their single-shot reduction requirement excludes the dual system encryption methodology [54], which is a powerful tool for proving the security of an ABE scheme from static assumptions. On the other hand, we manage to employ the dual system encryption methodology to obtain an ABE scheme with the desired properties from static assumptions.
[40]: Similarly to us, their approach is to construct an ABE scheme and then convert it into a CS scheme. However, the requirements for the ABE are different from ours. For the ABE scheme, they require short secret keys, whereas we require short ciphertexts. Furthermore, they require the ABE scheme to be secure following a so-called “single-shot” reduction, where the reduction algorithm runs the adversary only once and perfectly simulates the view of the game. Roughly, this is equivalent to saying that the proof cannot go through hybrid arguments. Therefore, their approach does not seem to be promising when we try to construct a compact CS scheme from a static assumption. Notably, their single-shot reduction requirement excludes the dual system encryption methodology [54], which is a powerful tool for proving the security of an ABE scheme from static assumptions. On the other hand, we manage to employ the dual system encryption methodology to obtain an ABE scheme with the desired properties from static assumptions.
 [41]: They construct a DP-NIZK (as an intermediate goal) by applying the Kim-Wu conversion on their CS scheme. They then modify their DP-NIZK to a CRS-NIZK scheme by a non-generic technique. Here, we review their approach and compare it with ours. Recall that, in general, a DP-NIZK constructed from a CS via the Kim-Wu conversion, the CRS consists of the verification key of the CS \(\mathsf {CS}.\mathsf {vk}\), and the secret proving key consists of the secret key of an SKE K and a signing key of the CS \(\mathsf {CS}.\mathsf {sk}_{ C_K }\). Their observation was that they can divide the CS verification key \(\mathsf {CS}.\mathsf {vk}\) into two components \(\mathsf {CS}.\mathsf {vk}:= (\mathsf {CS}.\mathsf {vk}_0, \mathsf {CS}\mathsf {vk}_1)\) such that \(\mathsf {CS}.\mathsf {vk}_1\) is very short and anyone can compute \(\mathsf {CS}.\mathsf {vk}_1\) from \(\mathsf {CS}.\mathsf {sk}_{ C_K }\) and K. Note that as a stand-alone CS scheme, the secret key \(\mathsf {CS}.\mathsf {sk}_{ C_K }\) is computed using the master key of the CS only after \(\mathsf {CS}.\mathsf {vk}= ( \mathsf {vk}_0, \mathsf {vk}_1 ) \) is defined. What they observe is that the other direction of the computation is possible using the specific structure of their CS scheme. In order to construct a CRS-NIZK using this special structure, they remove \(\mathsf {CS}.\mathsf {vk}_1\) from the CRS. Then they let the prover pick K and \(\mathsf {CS}.\mathsf {sk}_{ C_K }\) on their own and let it compute \(\mathsf {CS}.\mathsf {vk}_1\). At this point, the prover can generate a proof as in the original DP-NIZK. In order to prevent the adversary to maliciously choose K, \(\mathsf {CS}.\mathsf {sk}_{ C_K }\), and \(\mathsf {CS}.\mathsf {vk}_1\), they let the prover prove consistency among the components using a non-compact NIZK and outputs the proof along with \(\mathsf {CS}.\mathsf {vk}_1\). The additional consistency proof by the non-compact NIZK as well as \(\mathsf {CS}.\mathsf {vk}_1\) appended to the final proof does not harm the compactness of the resulting NIZK, since all parameters involved are compact.
[41]: They construct a DP-NIZK (as an intermediate goal) by applying the Kim-Wu conversion on their CS scheme. They then modify their DP-NIZK to a CRS-NIZK scheme by a non-generic technique. Here, we review their approach and compare it with ours. Recall that, in general, a DP-NIZK constructed from a CS via the Kim-Wu conversion, the CRS consists of the verification key of the CS \(\mathsf {CS}.\mathsf {vk}\), and the secret proving key consists of the secret key of an SKE K and a signing key of the CS \(\mathsf {CS}.\mathsf {sk}_{ C_K }\). Their observation was that they can divide the CS verification key \(\mathsf {CS}.\mathsf {vk}\) into two components \(\mathsf {CS}.\mathsf {vk}:= (\mathsf {CS}.\mathsf {vk}_0, \mathsf {CS}\mathsf {vk}_1)\) such that \(\mathsf {CS}.\mathsf {vk}_1\) is very short and anyone can compute \(\mathsf {CS}.\mathsf {vk}_1\) from \(\mathsf {CS}.\mathsf {sk}_{ C_K }\) and K. Note that as a stand-alone CS scheme, the secret key \(\mathsf {CS}.\mathsf {sk}_{ C_K }\) is computed using the master key of the CS only after \(\mathsf {CS}.\mathsf {vk}= ( \mathsf {vk}_0, \mathsf {vk}_1 ) \) is defined. What they observe is that the other direction of the computation is possible using the specific structure of their CS scheme. In order to construct a CRS-NIZK using this special structure, they remove \(\mathsf {CS}.\mathsf {vk}_1\) from the CRS. Then they let the prover pick K and \(\mathsf {CS}.\mathsf {sk}_{ C_K }\) on their own and let it compute \(\mathsf {CS}.\mathsf {vk}_1\). At this point, the prover can generate a proof as in the original DP-NIZK. In order to prevent the adversary to maliciously choose K, \(\mathsf {CS}.\mathsf {sk}_{ C_K }\), and \(\mathsf {CS}.\mathsf {vk}_1\), they let the prover prove consistency among the components using a non-compact NIZK and outputs the proof along with \(\mathsf {CS}.\mathsf {vk}_1\). The additional consistency proof by the non-compact NIZK as well as \(\mathsf {CS}.\mathsf {vk}_1\) appended to the final proof does not harm the compactness of the resulting NIZK, since all parameters involved are compact.
We note that their approach is not applicable to our specific CS scheme. The reason is that our signing key for the CS is as large as the circuit size and we cannot prove the consistency between K, \(\mathsf {CS}.\mathsf {sk}_{ C_K }\), and \(\mathsf {CS}.\mathsf {vk}_1\) compactly no matter how we divide the CS verification key. We, therefore, take a different path from theirs and this entails several challenges that are not present in their approach.
1.4 Related Work
The first NIZK for \(\mathbf{NP} \) was given by [16] based on the existence of trapdoor permutations (whose arguments were later refined by several works [3, 24]). The next generation of NIZK following a completely different set of approaches were provided by Groth, Ostrovsky, and Sahai [30] (GOS-NIZK) based on pairings. Due to its simplicity and efficiency, pairing-based NIZKs have flourished into a research topic on its own, and the original GOS-NIZK has been followed by many subsequent works [20, 27, 28, 31, 45]. More than roughly a decade later, a new type of NIZKs based on indistinguishable obfuscation (iO) were proposed [4, 5, 12, 51]. Finally, very recently, a different path for designing NIZKs based on correlation intractable hash functions (CIH) [9, 10, 39] have gained much attention and has finally lead to the closing of a long-standing problem of constructing NIZKs based on lattice-based assumptions [50].
2 Definitions
We omit definitions of standard cryptographic primitives due to limited space.
2.1 Preliminaries on Bilinear Maps
A bilinear group generator \(\mathsf {GGen}\) takes as input \(1^\kappa \) and outputs a group description \(\mathbb {G}=(p,G_1,G_2,G_T,e, g_1, g_2)\), where p is a prime such that \(p>2^{2\kappa }\), \(G_1\), \(G_2\), and \(G_T\) are cyclic groups of order q, \(e:G_1\times G_2 \rightarrow G_T\) is a non-degenerate bilinear map, and \(g_1\) and \(g_2\) are generators of \(G_1\) and \(G_2\), respectively. We require that the group operations in \(G_1\), \(G_2\), and \(G_T\) as well as the bilinear map e can be efficiently computed. We employ the implicit representation of group elements: for a matrix \(\mathbf {A}\) over \(\mathbb {Z}_q\), we define \([ \mathbf {A}]_1 := g_1^{\mathbf {A}}\), \([ \mathbf {A}]_2 := g_2^{\mathbf {A}}\), \([ \mathbf {A}]_T := g_T^{\mathbf {A}}\), where exponentiation is carried out component-wise.
Definition 2.1
(\(\mathrm {MDDH}_{k}\) assumption [15]). Let \(\mathsf {GGen}\) be a group generator. We say that the matrix DDH (\(\mathrm {MDDH}_{k}\)) assumption holds on \(G_1\) with respect to \(\mathsf {GGen}\), if for all PPT adversaries \(\mathcal {A}\), we have
is negligible, where the probability is taken over the choice of \(\mathbb {G}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {GGen}(1^\kappa )\), \(\mathbf {M}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^{(k+1)\times k}\), \(\mathbf {s}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^k\), and \(\mathbf {u}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^{k+1}\). We can similarly define \(\mathrm {MDDH}_{k}\) assumption on \(G_2\).
In fact, the above assumption is called \(\mathrm {MDDH}_{k}\) assumption for uniform distribution by Escala et al. [15] since \(\mathbf {M}\) is chosen uniformly at random. As shown by them, \(\mathrm {MDDH}_{k}\) assumptions for uniform distribution is weaker than \(\mathrm {MDDH}_{k}\) assumption for all other distributions and in particular is implied by the k-LIN assumption.
2.2 Non-interactive Zero-Knowledge Arguments
Let \(\mathcal {R}\subseteq \{ 0,1 \} ^* \times \{ 0,1 \} ^*\) be a polynomial time recognizable binary relation. For \((x, w) \in \mathcal {R}\), we call x as the statement and w as the witness. Let \(\mathcal {L}\) be the corresponding \(\mathbf{NP} \) language \(\mathcal {L}= \{ x \mid \exists w ~\text {s.t.}~ (x, w)\in \mathcal {R} \}\). Below, we define non-interactive zero-knowledge arguments for \(\mathbf{NP} \) languages.Footnote 4
Definition 2.2
(NIZK Arguments). A non-interactive zero-knowledge (NIZK) argument \(\Pi _\mathsf{NIZK}\) for the relation \(\mathcal {R}\) consists of PPT algorithms \((\mathsf {Setup}, \mathsf {Prove}, \mathsf {Verify})\).
-
\(\mathsf {Setup}(1^\kappa ) \rightarrow \mathsf {crs}\): The setup algorithm takes as input the security parameter \(1^\kappa \) and outputs a common reference string \(\mathsf {crs}\).
-
\(\mathsf {Prove}(\mathsf {crs}, x, w) \rightarrow \pi \): The prover’s algorithm takes as input a common reference string \(\mathsf {crs}\), a statement x, and a witness w and outputs a proof \(\pi \).
-
\(\mathsf {Verify}(\mathsf {crs}, x, \pi ) \rightarrow \top \text{ or } \bot \): The verifier’s algorithm takes as input a common reference string, a statement x, and a proof \(\pi \) and outputs \( \top \) to indicate acceptance of the proof and \(\bot \) otherwise.
We consider the following requirements for a NIZK argument \(\Pi _\mathsf{NIZK}\), where the probabilities are taken over the random choice of the algorithms.
 For all pairs \((x, w) \in \mathcal {R}\), if we run \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\), then we have \( \Pr [\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Prove}(\mathsf {crs}, x, w) : \mathsf {Verify}(\mathsf {crs}, x, \pi ) = \top ] = 1. \)
For all pairs \((x, w) \in \mathcal {R}\), if we run \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\), then we have \( \Pr [\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Prove}(\mathsf {crs}, x, w) : \mathsf {Verify}(\mathsf {crs}, x, \pi ) = \top ] = 1. \)
 For all PPT adversaries \(\mathcal {A}\), if we run \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\), then we have
For all PPT adversaries \(\mathcal {A}\), if we run \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\), then we have
 We also consider the slightly weaker variant of adaptive soundness above. For all PPT adversaries \(\mathcal {A}\) and for all \(x \not \in \mathcal {L}\), if we run \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\), then we have
We also consider the slightly weaker variant of adaptive soundness above. For all PPT adversaries \(\mathcal {A}\) and for all \(x \not \in \mathcal {L}\), if we run \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\), then we have
 For all adversaries \(\mathcal {A}\), there exists a PPT simulator \(\mathcal {S}= (\mathcal {S}_1, \mathcal {S}_2)\) such that if we run \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\) and \((\overline{\mathsf {crs}}, \bar{\tau }) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {S}_1(1^\kappa )\), then we have
For all adversaries \(\mathcal {A}\), there exists a PPT simulator \(\mathcal {S}= (\mathcal {S}_1, \mathcal {S}_2)\) such that if we run \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\) and \((\overline{\mathsf {crs}}, \bar{\tau }) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {S}_1(1^\kappa )\), then we have
where \(\mathcal {O}_0(\mathsf {crs}, x, w)\) outputs \(\mathsf {Prove}(\mathsf {crs}, x, w)\) if \( (x, w) \in \mathcal {R}\) and \(\bot \) otherwise, and \(\mathcal {O}_1( \overline{\mathsf {crs}}, \bar{\tau }, x, w)\) outputs \(\mathcal {S}_2( \overline{\mathsf {crs}}, \bar{\tau }, x)\) if \((x, w) \in \mathcal {R}\) and \(\bot \) otherwise. We say it is computational (resp. statistical) zero-knowledge if the adversary is computationally bounded (resp. unbounded). Moreover, we further say it is perfect zero-knowledge if the above r.h.s. equals 0 for computationally unbounded adversaries.
We also define a stronger notion of soundness called extractability following [41].
Definition 2.3
(Extractability). An NIZK argument is said to be extractable if the following is satisfied:
 There is a deterministic algorithm \(\mathsf {Extract}\) (called extractor) such that for all PPT adversary \(\mathcal {A}\), we have
There is a deterministic algorithm \(\mathsf {Extract}\) (called extractor) such that for all PPT adversary \(\mathcal {A}\), we have
where \(r_{\mathsf {Setup}}\) is the randomness used in \(\mathsf {Setup}\) to generate \(\mathsf {crs}\).
We can convert any adaptively sound NIZK into an extractable one additionally assuming the existence of PKE [41].
Lemma 2.1
If there exist an adaptively sound NIZK for all of \(\mathbf{NP} \) and a CPA-secure PKE scheme, then there exists an extractable NIZK for all of \(\mathbf{NP} \).
2.3 \(\mathbf{NC} ^1\) Circuits and Monotone Formulae
Here, we define Monotone Boolean formula following Kowalczyk and Wee [44].
Monotone Boolean Formula. A monotone Boolean formula \(f: \{ 0,1 \} ^n \rightarrow \{ 0,1 \} \) is specified by a directed acyclic graph (DAG) with three kinds of nodes: input gate nodes, gate nodes, and a single output node. Input nodes have in-degree 0 and out-degree 1, AND/OR nodes have in-degree (fan-in) 2 and out-degree (fan-out) 1, and the output node has in-degree 1 and out-degree 0. We number the edges (wires) \(1, 2,\ldots , m\), and each gate node is defined by a tuple \((g,a_g,b_g,c_g)\) where \(g: \{ 0,1 \} ^2 \rightarrow \{ 0,1 \} \) is either AND or OR, \(a_g\) and \(b_g\) are the incoming wires, \(c_g\) is the outgoing wire and \(a_g, b_g < c_g\). The size of a formula m is the number of edges in the underlying DAG and the depth of a formula d is the length of the longest path from the output node.
\(\mathbf{NC} ^1\) and Boolean Formulae. The following lemma summarizes the well-known equivalence between the monotone formulae and \(\mathbf{NC} ^1\) circuits.
Lemma 2.2
Let \(d=d(\kappa ), n=n(\kappa )\), and \(s=s(\kappa )\) be integers. There exist integer parameters \(m=m(d,n,s)\) and deterministic algorithms \(\mathsf {EncInp}\) and \(\mathsf {EncCir}\) with the following properties.
-
\(\mathsf {EncInp}(x ) \rightarrow \hat{x} \in \{0,1\}^{2n} \), where \(x \in \{ 0,1 \} ^n \).
-
\(\mathsf {EncCir}(C) \rightarrow f \), where \(C: \{ 0,1 \} ^n \rightarrow \{ 0,1 \} \) is a circuit with depth and size bounded by d and s, respectively and f is a monotone Boolean formula of size m with input space being \( \{ 0,1 \} ^{2n}\).
We have \(f(\hat{x})=1\) if and only if \(C(x)=1\). Furthermore, the running time of \(\mathsf {EncCir}\) is \(\mathsf {poly}(n,s,2^d)\). In particular, if C is a polynomial-sized circuit with logarithmic depth (i.e., if the circuit is in \(\mathbf{NC} ^1\)), \(\mathsf {EncCir}\) runs in polynomial time and we have \(m=\mathsf {poly}(\kappa )\). Furthermore, for \(x\in \{ 0,1 \} ^n\), we have \(\hat{x} = x_1 \bar{x}_1 x_2 \bar{x}_2 \cdots x_n \bar{x}_n,\) where \(\bar{x}_i\) is the flip of \(x_i\).
See the full version for the details.
3 KP-ABE with Compact Ciphertexts
In this section, we give the construction of KP-ABE scheme for monotone Boolean formulae with constant-size ciphertexts by extending the scheme by Kowalczyk and Wee [44]. The scheme will be used in the construction of compact constrained signature scheme in Sect. 4, which will in turn be used for the construction of our compact NIZKs in Sect. 5. Our KP-ABE scheme would be of independent interest, since this is the first KP-ABE scheme for Boolean formulae with constant-size ciphertexts that is secure under a static assumption (rather than non-static q-type assumption).
3.1 Preliminaries
First, we review the secret sharing scheme for monotone Boolean formulae used by Kowalczyk and Wee, which is based on secret sharing schemes in [34, 35, 53].
Definition 3.1
(Secret Sharing). A secret sharing scheme consists of two algorithms \((\mathsf {share},\mathsf {reconstruct})\).
-
\(\mathsf {share}(f,\mu )\): This algorithm takes a (monotone) Boolean formula \(f: \{0,1\}^n \rightarrow \{0,1\}\) and \(\mu \in \mathbb {Z}_p\) and outputs shares \(\mu _1,\ldots ,\mu _{\hat{m}} \in \mathbb {Z}_p\) and a function \(\rho :[\hat{m}] \rightarrow \{0,1,\ldots ,n\}\). We assume that \(\rho \) is deterministically determined from f.
-
\(\mathsf {reconstruct}(f,x,\{\mu _j\}_{j\in S})\): This algorithms takes an input \(x \in \{0,1\}^n\) for f, f, and a subset of shares \(\{\mu _j\}_{j\in S}\) where \(S\subseteq [\hat{m}]\) and outputs the original value \(\mu \).
A secret sharing scheme satisfies the following properties.
-
Correctness: For all \(x\in \{0,1\}^n\), \(f:\{0,1\}^n \rightarrow \{0,1\}\), \(\mu \in \mathbb {Z}_p\), \((\{\mu _j\}_{j \in [\hat{m}]},\rho )\leftarrow \mathsf {share}(f,\mu )\) such that \(f(x)=1\), it holds that \(\mathsf {reconstruct}(f,x,\{\mu _j\}_{\rho (j)=0 \vee }\) \({ x_{\rho (j)}=1})=\mu \).
-
Security: For all \(x\in \{0,1\}^n\), \(f:\{0,1\}^n \rightarrow \{0,1\}\), \(\mu ,\mu ' \in \mathbb {Z}_p\) such that \(f(x)=0\), the following distributions are the same:
$$\begin{aligned} \{\{\mu _j\}_{\rho (j)=0 \vee x_{\rho (j)}=1} \mid (\{\mu _j\}_{j\in [\hat{m}]},\rho ) \leftarrow \mathsf {share}(f,\mu )\} \\ \equiv \{\{\mu '_j\}_{\rho (j)=0 \vee x_{\rho (j)}=1} \mid (\{\mu '_j\}_{j\in [\hat{m}]},\rho ) \leftarrow \mathsf {share}(f,\mu ')\} \end{aligned}$$ -
Linearity: The algorithm \(\mathsf {reconstruct}\) is a linear function of the shares over \(\mathbb {Z}_p\). That is, there exists \(\omega _j \in \mathbb {Z}_p\) for \(j\in [\hat{m}]\) and we can compute \(\mu = \sum _{\rho (j)=0 \vee x_{\rho (j)}=1}\omega _j\mu _j\).
We present their secret sharing scheme \((\mathsf {share},\mathsf {reconstruct})\) in Fig. 1 as it is. The scheme satisfies Definition 3.1. As Kowalczyk and Wee observed, it is easy to extend the secret sharing scheme to treat vectors of secrets. That is, for a vector \(\mathbf {v}\in \mathbb {Z}_p^k\), we define \(\mathsf {share}(f,\mathbf {v}) := (\{\mathbf {v}_j = (v_{1,j},\ldots ,\) \(v_{k,j})\}_{j \in [\hat{m}]},\rho )\) where \((\{v_{i,j}\}_{j\in [\hat{m}]},\rho ) \leftarrow \mathsf {share}(f,v_i)\) and \(\mathsf {reconstruct}(f,x,\) \(\{\mathbf {v}_j\}_{\rho (j)=0 \vee x_{\rho (j)}=1}) := \sum _{\rho (j)=0 \vee x_{\rho (j)}=1} \omega _j \mathbf {v}_j\) where \(\{\omega _{j}\}_{j\in [\hat{m}]}\) is defined as above.
Information-theoretic linear secret sharing for monotone Boolean formulae by Kowalczyk and Wee [44]
3.2 Construction
Here, we give the construction of KP-ABE with short ciphertext from the \(\mathrm {MDDH}_{k}\) assumption.
-
\(\mathsf {Setup}(1^\kappa , 1^n )\): Run \(\mathbb {G}= (p, G_1, G_2, G_T, e) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {GGen}(1^\kappa )\). Sample \(\mathbf {A}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^{k \times (k+1)}\), \(\mathbf {W}_i \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^{(k+1) \times k }\) for \(i\in [n]\), \(\mathbf {v}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^{k +1}\) and output
$$ \mathsf {mpk}= ( [\mathbf {A}]_1, [\mathbf {A}\mathbf {W}_1]_1,\ldots , [\mathbf {A}\mathbf {W}_n]_1, e( [\mathbf {A}]_1, [\mathbf {v}]_2 ) ), \quad \mathsf {msk}= (\mathbf {v}, \mathbf {W}_1, \ldots , \mathbf {W}_n ). $$ -
\(\mathsf {Enc}( \mathsf {mpk}, x, M)\): To encrypt a message \(M\in G_T\) for a string \(x\in \{ 0,1 \} ^n\), sample \(\mathbf {s}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^k \) and output
$$ \mathsf {ct}_x = \left( \mathsf {ct}_1 := [\mathbf {s}^\top \mathbf {A}]_1, \quad \mathsf {ct}_2 = \left[ \mathbf {s}^\top \sum _{i: x_i=1 } \mathbf {A}\mathbf {W}_i \right] _1 , \quad \mathsf {ct}_3 := e( [\mathbf {s}^\top \mathbf {A}]_1, [\mathbf {v}]_2 )\cdot M \right) . $$ -
\(\mathsf {KeyGen}( \mathsf {msk}, f)\): To generate a secret key for a Boolean formula f, sample \((\{ \mathbf {v}_j \}_{j\in [\hat{m}]}, \rho ) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {share}(f, \mathbf {v})\), \(\mathbf {r}_j \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^k\) and output \(\mathsf {sk}_f\), which consists of the following.
$$ \left( \Bigl \{ \mathsf {sk}_{ j } := [\mathbf {r}_j]_2,~ \mathsf {sk}_{ \rho (j), j }:= [\mathbf {v}_j + \mathbf {W}_{\rho (j)}\mathbf {r}_j]_2,~ \{\mathsf {sk}_{i,j} := [\mathbf {W}_i \mathbf {r}_j]_2 ~ \}_{ i\in [n] \backslash \{\rho (j) \} } \Bigr \}_{j\in [\hat{m}]} \right) $$where \(\mathbf {W}_0 = \mathbf {0}\) and \(\hat{m}\) is the number of shares. We note that for j such that \(\rho (j)=0\), we have \([n]\backslash \{ \rho (j) \} =[n]\).
-
\(\mathsf {Dec}(\mathsf {mpk}, \mathsf {sk}_f, \mathsf {ct}_\mathbf {x}) \): Compute \(\omega _j\) such that \(\mathbf {v}= \sum _{j: \rho (j)=0\vee x_{\rho (j)}=1 } \omega _j \mathbf {v}_j\) and output
$$ \mathsf {ct}_3 \cdot e\left( \mathsf {ct}_2, \prod _{j: \rho (j)=0 \vee x_{\rho (j)=1} } \mathsf {sk}_{ j}^{\omega _j } \right) \cdot e\left( \mathsf {ct}_1, \prod _{j:\rho (j)=0 \vee x_{\rho (j)}=1 } \left( \prod _{i: x_i = 1 } \mathsf {sk}_{i,j} \right) ^{\omega _j } \right) ^{-1}. $$
Correctness. The correctness follows since we have
where \(\mathbf {r}= \sum _{j:\rho (j)=0 \vee \hat{x}_{\rho (j)} = 1 } \omega _j \mathbf {r}_j\) for honestly generated secret key \(\mathsf {sk}\) for f such that \(f(x)=1\) from the correctness of the secret sharing.
3.3 Security
We prove the following theorem.
Theorem 3.1
The above construction is adaptively secure under the \(\mathrm {MDDH}_{k}\) assumption.
For proving this theorem, we first prove the following lemma.
Lemma 3.1
Under the \(\mathrm {MDDH}_{k}\) assumption,
is negligible where \(\mathcal {A}\) adaptively interacts with three oracles:
-
\(\mathcal {O}_{\mathsf {F},\beta }(f) := \) \(\left( \{ \mu _j \}_{j : \rho (j)=0} \cup \Bigl \{ [\mathbf {r}_j ]_2, [ \mu _j + \mathbf {w}_{\rho (j)}^\top \mathbf {r}_j ]_2, \bigl \{ [\mathbf {w}_i^\top \mathbf {r}_j]_2 \bigr \}_{ i\in [n] \backslash \{ \rho (j) \}} \Bigr \}_{ j\in [\hat{m}] } \right) \) where \( ( \{\mu _j \}_{j \in [\hat{m}]}, \rho ) \leftarrow \mathsf {share}(f, \mu ^{(\beta )} )\)
-
\( \mathcal {O}_{\mathsf {X}}(x) := \left( \{ \mathbf {w}_i \}_{i: x_i=1 } \right) \)
-
\( \mathcal {O}_{\mathsf {E}}() := \) \( \left( [\mathbf {r}]_2, \bigl \{ [\mathbf {w}_i^\top \mathbf {r}]_2 \bigr \}_{ i\in [n] } \right) \) where \(\mathbf {r}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^k\)
with the restriction that (i) only one query is made to each of \(\mathcal {O}_{\mathsf {F},\beta }(\cdot )\) and \(\mathcal {O}_{\mathsf {X}}(\cdot )\), and (ii) the queries f and x to \(\mathcal {O}_{\mathsf {F},\beta }(\cdot )\) and \(\mathcal {O}_{\mathsf {X}}(\cdot )\) respectively, satisfy \(f(x)=0\).
Note that the statement of the lemma is similar to that of Theorem 2 in [44]. There, \( \mathcal {O}_{\mathsf {F},\beta }(f)\) returns
and \( \mathcal {O}_{\mathsf {E}} \) takes as input \(i \in [m]\) and returns \(([\mathbf {r}]_2, [\mathbf {w}_i^\top \mathbf {r}]_2 )\).Footnote 5 Since the answers by the oracles in [44] can be simulated by our oracles by just stripping off appropriate components, our statement is stronger than theirs. Nonetheless, we can prove the above lemma with very similar proof to that of Theorem 2 in [44]. See the full version for the details.
Then we prove Theorem 3.1. The proof of the theorem is again similar to the equivalent in [44], but with some appropriate adaptations.
Proof of Theorem 3.1. We prove the theorem by considering a sequence of hybrid games. To define the hybrid distributions, it would be helpful to first give names of various forms of ciphertext and secret keys that will be used. A ciphertext (of message M under attribute x) can be one of the following forms:
-
Normal: A normal ciphertext is generated as in the scheme.
-
SF: This is the same as normal ciphertext except that \(\mathbf {s}^\top \mathbf {A}\) is replaced by a random vector \(\mathbf {c}^\top \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^{k+1}\). That is,
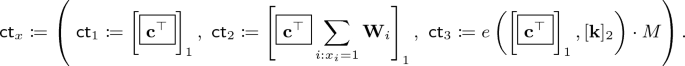
A secret key (for a Boolean formula f) can be one of the following forms:
-
Normal: A normal key is generated by \(\mathsf {KeyGen}\).
-
SF: An SF key is sampled as a normal key except that \(\mathbf {v}\) is replaced by \(\mathbf {v}+ \delta \mathbf {a}^{\perp }\), where a fresh \(\delta \) is chosen per SF key and \(\mathbf {a}^\perp \) is any fixed \(\mathbf {a}^\perp \in \mathbb {Z}_p^{k+1} \backslash \{ \mathbf {0} \}\). That is, \(\mathsf {sk}_f\) consists of
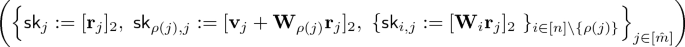
where
 , \(\mathbf {r}_j \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^k\).
, \(\mathbf {r}_j \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^k\).
We then define the following sequence of games to prove the security. Let the number of key generation queries made by an adversary be Q.
-
\(\mathsf {H}_0:\) This is the real security game for adaptive security where all ciphertexts and keys are normal.
-
\(\mathsf {H}_{1}:\) This game is the same as \(\mathsf {H}_0\) except that the challenge ciphertext is SF.
-
\(\mathsf {H}_{2,\ell }:\) This game is the same as \(\mathsf {H}_{1}\) except that the first \(\ell \) keys are SF and the remaining \(Q-\ell \) keys are normal. The game is defined for \(\ell =0,1,\ldots , Q\).
-
\(\mathsf {H}_{3}:\) This is the same as \(\mathsf {H}_{Q}\) except that the message to be encrypted is replaced by a random group element \(\widetilde{M}\).
Let us fix a PPT adversary \(\mathcal {A}\) and denote the advantage of \(\mathcal {A}\) in \(\mathsf {H}_\mathrm{xx}\) by \(\mathsf {Adv}_\mathrm{xx}\). We can easily see that \(\mathsf {H}_{1} \equiv \mathsf {H}_{2,0}\) and \(\mathsf {Adv}_{3}= 0\). Therefore, to complete the proof of Theorem 3.1, it suffices to prove any neighboring games are computationally indistinguishable from the adversary’s view. We omit proofs of them since they are proven similarly to their counterparts in [44] except that we need some adaptations for the analysis of the game hop from \(\mathsf {H}_{2,\ell }\) to \(\mathsf {H}_{2,\ell +1}\) by using Lemma 3.1. See the full version for the full proof. \(\square \)
4 Compact Constrained Signature
4.1 Constrained Signature
We provide definition of a constrained signature (CS) scheme. We also provide an additional feature (i.e., online/offline efficiency) for CS schemes which will play a vital role in our compact NIZK construction in Sect. 5.
Definition 4.1
(Constrained Signature). A constrained signature (CS) scheme with message space \( \{ 0,1 \} ^n\) for a circuit class  consists of PPT algorithms \((\mathsf {CS.Setup}, \mathsf {CS.KeyGen}, \mathsf {CS.Sign}, \mathsf {CS.Vrfy})\).
consists of PPT algorithms \((\mathsf {CS.Setup}, \mathsf {CS.KeyGen}, \mathsf {CS.Sign}, \mathsf {CS.Vrfy})\).
-
\(\mathsf {CS.Setup}(1^\kappa , 1^n) \rightarrow (\mathsf {msk}, \mathsf {vk})\): The setup algorithm on input the security parameter \(1^\lambda \) and the input length \(1^n\), outputs a master secret key \(\mathsf {msk}\) and a verification key \(\mathsf {vk}\).
-
\(\mathsf {CS.KeyGen}(\mathsf {msk}, C) \rightarrow \mathsf {sk}_C\): The key generation algorithm on input a master secret key \(\mathsf {msk}\) and a circuit \(C\in \mathcal {C}\), outputs a signing key \(\mathsf {sk}_C\).
-
\(\mathsf {CS.Sign}(\mathsf {sk}_C, x) \rightarrow \sigma \): The signing algorithm on input the signing key \(\mathsf {sk}_C\) and message \(x \in \{ 0,1 \} ^n\), outputs a signature \(\sigma \).
-
\(\mathsf {CS.Vrfy}(\mathsf {vk}, x, \sigma ) \rightarrow \top \text { or } \bot \): The verification algorithm on input the verification key \(\mathsf {vk}\), message x, and signature \(\sigma \), outputs either \(\bot \) (indicating the signature is valid) or \(\top \) (indicating the signature is invalid).
A CS scheme must satisfy the following requirements.
 For all \(\kappa \in \mathbb {N}\), \(n = n(\kappa ) \in \mathbb {N}\), \((\mathsf {msk}, \mathsf {vk}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Setup}(1^\kappa , 1^n)\), \(x \in \{ 0,1 \} ^n\), \(C\in \mathcal {C}\) such that \(C(x) = 1\), and \(\mathsf {sk}_C\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk}, C)\), we have
For all \(\kappa \in \mathbb {N}\), \(n = n(\kappa ) \in \mathbb {N}\), \((\mathsf {msk}, \mathsf {vk}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Setup}(1^\kappa , 1^n)\), \(x \in \{ 0,1 \} ^n\), \(C\in \mathcal {C}\) such that \(C(x) = 1\), and \(\mathsf {sk}_C\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk}, C)\), we have
 We define (adaptive) unforgeability for a CS scheme. The security notion is defined by the following game between a challenger and an adversary \(\mathcal {A}\).
We define (adaptive) unforgeability for a CS scheme. The security notion is defined by the following game between a challenger and an adversary \(\mathcal {A}\).
-
Setup: The challenger runs \((\mathsf {msk}, \mathsf {vk}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Setup}(1^\kappa , 1^n)\) and gives \(\mathsf {vk}\) to \(\mathcal {A}\). It also prepares an empty list \(\mathcal Q\).
-
Key Queries: \(\mathcal {A}\) can adaptively make key queries unbounded polynomially many times throughout the game. When \(\mathcal {A}\) queries \(C\in \mathcal {C}\), the challenger runs \(\mathsf {sk}_C\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk}, C)\) and returns \(\mathsf {sk}_C\) to \(\mathcal {A}\). Finally, the challenger updates
 .
. -
Forgery: Eventually, \(\mathcal {A}\) outputs \((x^*, \sigma ^*)\) as the forgery. We say \(\mathcal {A}\) wins if \(\mathsf {CS.Vrfy}( \mathsf {vk}, x^*, \sigma ^* ) = \top \) holds. Furthermore, we say that \(\mathcal {A}\) is admissible if \(C(x^*) = 0\) holds for all \(C\in \mathcal Q\) at the end of the game.
We say the CS scheme is (adaptively) unforgeable if the winning probability for all admissible PPT adversaries \(\mathcal {A}\) in the above game is \( \mathsf {negl}(\kappa )\), where the probability is taken over the randomness of all algorithms.
The following property is optional in the sense that our CS scheme can achieve the following property, but the property is not strictly necessary for our application of CS to the construction of compact NIZKs.
 For all \(\kappa , n\in \mathbb {N}\), \((\mathsf {mpk},\mathsf {msk})\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^{\kappa },1^n)\), \(x\in \{ 0,1 \} ^n\), \(C_0,C_1\in \mathcal {C}\), \((\mathsf {msk}, \mathsf {vk}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Setup}(1^\kappa , 1^n)\), \(\mathsf {sk}_{C_0} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk},\) \(C_0)\), and \(\mathsf {sk}_{C_1} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk}, C_1)\), we need that the following distributions are statistically close:
For all \(\kappa , n\in \mathbb {N}\), \((\mathsf {mpk},\mathsf {msk})\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^{\kappa },1^n)\), \(x\in \{ 0,1 \} ^n\), \(C_0,C_1\in \mathcal {C}\), \((\mathsf {msk}, \mathsf {vk}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Setup}(1^\kappa , 1^n)\), \(\mathsf {sk}_{C_0} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk},\) \(C_0)\), and \(\mathsf {sk}_{C_1} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk}, C_1)\), we need that the following distributions are statistically close:
where the probability is only over the randomness used by \(\mathsf {CS.Sign}\).
Additionally to the above essential requirements for CS, we introduce a natural notion of decomposable online-offline efficiency. At a high level, this notion states that if we (partially) knew the message x to be signed in advance, then we can modify the verification key \(\mathsf {vk}\) to a message specific verification key \(\mathsf {vk}_x\) which allows for an efficient verification of signature \(\sigma \) with running time independent of |x|. More formally, the notion is defined as follows.
Definition 4.2
(Decomposable Online-Offline Efficiency). A constrained signature with message space \( \{ 0,1 \} ^n\) for a circuit class  is said to have decomposable online-offline efficiency if there further exists PPT algorithms \((\mathsf {CS.Aggrgt}, \mathsf {CS.VrfyOnL})\) exhibiting the following properties.
is said to have decomposable online-offline efficiency if there further exists PPT algorithms \((\mathsf {CS.Aggrgt}, \mathsf {CS.VrfyOnL})\) exhibiting the following properties.
-
The verification key \(\mathsf {vk}\) can be decomposed into \(\mathsf {vk}=( \mathsf {vk}_0, \{\mathsf {vk}_{i,b} \in \mathcal {VK}\}_{i\in [n] , b\in \{ 0,1 \} } )\), where \(\mathcal {VK}\) is a space of verification key component.
-
Any component in \(\mathcal {VK}\), any honestly generated \(\mathsf {vk}_0\), and any honestly generated signature \(\sigma \) can be represented as binary strings of fixed polynomial length \(\mathsf {poly}(\kappa )\). In particular, length of these components are independent from n.
-
Algorithm \(\mathsf {CS.Aggrgt}\) takes as input an element of \(\mathcal {VK}^*=\cup _{\ell \in \mathbb {N}}\mathcal {VK}^\ell \) and outputs an element in \(\mathcal {VK}\). We require that for any \(y,z \in \{ 0,1 \} ^*\) such that \(x=y\Vert z \in \{ 0,1 \} ^n\), we have
$$\begin{aligned}&\mathsf {CS.Aggrgt}\left( \{ \mathsf {vk}_{i,x_i} \}_{i\in [n] } \right) \\ =&\mathsf {CS.Aggrgt}\left( \mathsf {CS.Aggrgt}\left( \{ \mathsf {vk}_{i,y_i} \}_{i\in [|y|]} \right) , \mathsf {CS.Aggrgt}\left( \{ \mathsf {vk}_{|y|+ i,z_i} \}_{i\in [|z|]}\right) \right) . \end{aligned}$$ -
Algorithm \(\mathsf {CS.VrfyOnL}\) takes as input \(\mathsf {vk}_0\), a component in \(\mathcal {VK}\) and a signature in \(\sigma \), and outputs either \(\top \) or \(\bot \). We require that for any \(x\in \{ 0,1 \} ^n\), for any honestly generated \(\mathsf {vk}\), and for any (possibly maliciously generated) \(\sigma \), we have
$$ \mathsf {CS.Vrfy}( \mathsf {vk}, x, \sigma ) = \mathsf {CS.VrfyOnL}\left( \mathsf {vk}_0, \mathsf {CS.Aggrgt}\left( \{ \mathsf {vk}_{i,x_i} \}_{i\in [n]} \right) , \sigma \right) . $$Observe that the input length of \(\mathsf {CS.VrfyOnL}\) is independent from n, which follows from the second item of this definition. We require that the running time of \(\mathsf {CS.VrfyOnL}\) is independent from n as well.
4.2 Construction and Security
Here, we give the construction of our constrained signature (CS) scheme that will be used for the construction of the compact NIZK. The CS scheme has very compact signature size and the decomposable online-offline efficiency defined in Definition 4.2. In order to get the CS scheme, we apply the folklore conversion that converts ABE into CS to our compact KP-ABE scheme in Sect. 3, where the signing key \(\mathsf {sk}_f\) for the function f in the CS scheme is the same as the secret key \(\mathsf {sk}_f\) for the same function f in the ABE scheme, and the signature on a string x in the CS scheme is certain “aggregated form” of the secret key that is derived when decrypting an ABE ciphertext encrypted for the attribute x. To verify a signature on x in the CS, we encrypt a random message for x in the underlying ABE and then see if the message is recovered or not when decrypting the ciphertext using the signature as an (aggregated form of) secret key.
The CS scheme obtained by the above conversion can only deal with monotone Boolean formulae, since the original ABE is for the same class of functions. For our purpose, we need CS scheme for \(\mathbf{NC} ^1\) circuits, which is more general class than monotone Boolean formulae. This gap can be filled using Lemma 2.2.
We then provide the description of the construction.
-
\(\mathsf {CS.Setup}(1^\kappa , 1^n )\): Run \(\mathbb {G}= (p, G_1, G_2, G_T, e) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {GGen}(1^\kappa )\). Sample \(\mathbf {A}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^{k \times (k+1)}\), \(\mathbf {W}_{i} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^{(k+1) \times k }\) for \(i\in [2n]\) and \(\mathbf {v}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^{k +1}\) and output
$$ \mathsf {vk}= ( [\mathbf {A}]_1, [\mathbf {A}\mathbf {W}_1]_1,\ldots , [\mathbf {A}\mathbf {W}_{2n}]_1, e( [\mathbf {A}]_1, [\mathbf {v}]_2 ) ), \quad \mathsf {msk}= (\mathbf {v}, \mathbf {W}_1, \ldots , \mathbf {W}_{2n} ). $$ -
\(\mathsf {CS.KeyGen}( \mathsf {msk}, C )\): To generate a signing key for a circuit C, run \(\mathsf {EncCir}(C) \rightarrow f\). Then sample \((\{ \mathbf {v}_j \}_{j\in [ \hat{m} ]}, \rho ) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {share}(f, \mathbf {v})\) and \(\mathbf {r}_j \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathbb {Z}_p^k\) for \(j\in [\hat{m} ]\) and output \(\mathsf {sk}_f\), which consists of the following.
$$ \left( \Bigl \{ \mathsf {sk}_{ j } := [\mathbf {r}_j]_2,~ \mathsf {sk}_{ \rho (j), j }:= [\mathbf {v}_j + \mathbf {W}_{\rho (j)}\mathbf {r}_j]_2,~ \{\mathsf {sk}_{i,j} := [\mathbf {W}_{i} \mathbf {r}_j]_2 ~ \}_{ i\in [2n] \backslash \{\rho (j) \}} \Bigr \}_{j\in [\hat{m}]} \right) $$where \(\mathbf {W}_{0} = \mathbf {0}\) and \(\hat{m}\) is the number of shares that are generated by \(\mathsf {share}(f,\mathbf {v})\).
-
\(\mathsf {CS.Sign}( \mathsf {sk}_f, x ) \): Set \(\hat{x} := \mathsf {EncInp}(x ) \) and compute \(\omega _j\) such that \(\mathbf {v}= \sum _{j: \rho (j)=0\vee \hat{x}_{\rho (j)}=1 } \omega _j \mathbf {v}_j\) and output
$$ \sigma = \left( \sigma _1 = \prod _{j:\rho (j)=0 \vee \hat{x}_{\rho (j)}=1 } \left( \prod _{i: \hat{x}_i = 1 } \mathsf {sk}_{i,j} \right) ^{\omega _j } , \quad \sigma _2= \prod _{j: \rho (j)=0 \vee \hat{x}_{\rho (j)=1} } \mathsf {sk}_{j}^{\omega _j } \right) . $$ -
\(\mathsf {CS.Vrfy}(\mathsf {vk}, x, \sigma ) \): Parse \(\sigma \rightarrow (\sigma _1, \sigma _2 )\in G_2^k \times G_2^k\) and output \(\bot \) if the signature is not in this form. Otherwise, compute \(\hat{x}= \mathsf {EncInp}(x)\) and
$$\begin{aligned} \mathsf {vk}' = \prod _{i: \hat{x}_i =1} [ \mathbf {A}\mathbf {W}_{i} ]_1 . \end{aligned}$$(1)Then output \(\top \) if the following holds and \(\bot \) otherwise:
$$\begin{aligned} e( [\mathbf {A}]_1 , \sigma _1) \cdot e(\mathsf {vk}', \sigma _2 )^{-1} = e( [\mathbf {A}]_1, [\mathbf {v}]_2 ). \end{aligned}$$
Correctness. The correctness follows since we have \(f(\hat{x})=1\) when \(C(x)=1\) from Lemma 2.2 and
Online-Offline Decomposability
Theorem 4.1
The CS scheme above has decomposable online-offline efficiency defined as per Definition 4.2.
Proof
To prove the theorem, we define \(\mathcal {VK}\), \(\mathsf {vk}_0\), and \(\mathsf {vk}_{i,b}\) for \(i\in [n]\), \(b\in \{ 0,1 \} \) as
It is easy to see that the first and the second items in Definition 4.2 are satisfied. We then define additional algorithms \(\mathsf {CS.VrfyOnL}\) and \(\mathsf {CS.Aggrgt}\) as follows:
-
\(\mathsf {CS.Aggrgt}( \{ \mathsf {vk}_i \}_{i\in [n']} ) \): If there exists \(i\in [n']\) such that \(\mathsf {vk}_i \not \in \mathcal {VK}= G_1^{k\times k}\), output \(\bot \). Otherwise, output \( X := \prod _{i\in [n']} \mathsf {vk}_i \), where the product represents the component-wise multiplication in \(G_1\).
-
\(\mathsf {CS.VrfyOnL}( \mathsf {vk}_0, \mathsf {vk}', \sigma ) \): Parse \(\mathsf {vk}_0 \rightarrow ( A\in G_1^{k\times (k+1)} , V\in G_T^k )\), \(\mathsf {vk}' \in G_1^{k\times k}\), and \(\sigma \rightarrow (\sigma _1, \sigma _2 )\in G_2^k \times G_2^k\). Then output \(\top \) if the following holds and \(\bot \) otherwise:
$$\begin{aligned} e( A , \sigma _1) \cdot e(\mathsf {vk}', \sigma _2 )^{-1} = V. \end{aligned}$$
The third item in Definition 4.2 follows from the fact that the following equation holds for any \(x= y\Vert z \in \{ 0,1 \} ^n\):
To prove the fourth item, it suffices to show that \(\mathsf {vk}'\) computed as Eq. 1 equals to \(\mathsf {CS.Aggrgt}( \{ \mathsf {vk}_{i,x_i} \}_{i\in [n]} )\). This follows since the former is the product of \([\mathbf {A}\mathbf {W}_i]_1\) over i in \(S:= \{ i\in [2n]: \hat{x}_i=1 \}\) and the latter is over i in \(S' := \{ 2j-x_j : j\in [n] \}\), and we have \(S=S'\) by the definition of \(\hat{x}\) (See Lemma 2.2). \(\square \)
Security. In the following, we show that the above construction is unforgeable and then discuss how to extend the scheme to satisfy context-hiding. While the latter property is not necessary for our application of CS in Sect. 5, this property may be useful when we use the CS scheme stand-alone.
Theorem 4.2
The above construction is (adaptively) unforgeable under the \(\mathrm {MDDH}_{k}\) assumption.
Proof
For the sake of contradiction, suppose that there exists an adversary \(\mathcal {A}\) that breaks unforgeability of the \(\Pi _\mathsf {CS}\) with non-negligible probability \(\epsilon \). We then construct a PPT adversary \(\mathcal {B}\) that breaks the adaptive security of the ABE with advantage \(\epsilon \) for the attribute length 2n as follows.
-
\(\mathcal {B}(\mathsf {mpk})\): It sets \(\mathsf {vk}:= \mathsf {mpk}\) and gives the master public key to \(\mathcal {A}\). When \(\mathcal {A}\) makes a signing key query for a circuit C, \(\mathcal {B}\) runs \(\mathsf {EncCir}(C) \rightarrow f\) and makes a key generation query for f to obtain \(\mathsf {sk}_f\). Then, \(\mathcal {B}\) passes \(\mathsf {sk}_f\) to \(\mathcal {A}\). At some point, \(\mathcal {A}\) outputs a forgery \((x^*, \sigma ^*)\). Then, \(\mathcal {B}\) outputs a random bit and abort if \(\mathsf {CS.Vrfy}(\mathsf {vk}, x^*, \sigma ^* ) = \bot \). Otherwise, \(\mathcal {B}\) samples two random distinctive messages \(M_0, M_1 \in G_T\) and makes a challenge query for \(( \hat{x}^*, (M_0,M_1) )\), where \(\hat{x}^* = \mathsf {EncInp}(x^*)\). Given the challenge ciphertext \(\mathsf {ct}\), it first parses \(\mathsf {ct} \rightarrow (\mathsf {ct}_1 \in G_1^{k+1}, \mathsf {ct}_2 \in G_1^k, \mathsf {ct}_3 \in G_T )\) and \(\sigma ^* \rightarrow (\sigma ^*_1 \in G_2^{k+1}, \sigma ^*_2 \in G_2^{k+1})\) and computes \(M' := e( \mathsf {ct}_1 , \sigma ^*_1)^{-1} \cdot e(\mathsf {ct}_2, \sigma ^*_2 ) \cdot \mathsf {ct}_3\). It outputs 0 if \(M'=M_0\) and 1 otherwise.
We first check that \(\mathcal {B}\) is an admissible adversary if so is \(\mathcal {A}\), since we have \(C(x^*)=0\) iff \(f(\hat{x}^*)=0\) for any C and \(f=\mathsf {EncCir}(C)\) from Lemma 2.2. We then claim that whenever \(\mathsf {CS.Vrfy}(\mathsf {vk}, x^*, \sigma ^* ) = \top \), we have \(M'= M_\mathsf {coin}\). To prove the claim, let us assume that \(\mathsf {CS.Vrfy}(\mathsf {vk}, \hat{x}^*, \sigma ^* ) = \top \) holds. Then, we have
by the definition of \(\mathsf {CS.Vrfy}\). Furthermore, there exists \(\mathbf {s}\in \mathbb {Z}_p^k\) such that \(\mathsf {ct}_1 = [\mathbf {s}^\top \mathbf {A}]_1\), \(\mathsf {ct}_2 = [ \mathbf {s}^\top \sum _{i: y^*_i =1} \mathbf {A}\mathbf {W}_{i} ]_1\), and \(\mathsf {ct}_3 = e( [\mathbf {s}^\top \mathbf {A}]_1, [\mathbf {v}]_2 )\cdot M_\mathsf {coin}\) by the definition of \(\mathsf {Enc}\). Then, the above equation implies \( e( \mathsf {ct}_1 , \sigma ^*_1) \cdot e( \mathsf {ct}_2 , \sigma ^*_2 )^{-1} = e( [\mathbf {s}^\top \mathbf {A}]_1, [\mathbf {v}]_2 ) \) which in turns implies \(M'=M_\mathsf {coin}\). Thus, \(\mathcal {B}\) correctly guesses \(\mathsf {coin}\) when \(\mathcal {A}\) breaks the unforgeability of \(\Pi _\mathsf {CS}\) and outputs a random bit otherwise. This implies that the advantage of \(\mathcal {B}\) is \(\epsilon \), which is non-negligible as desired. \(\square \)
Remark 1
(Adding Context-Hiding for the Scheme). We remark that it is possible to make the above scheme context-hiding by adding the following modification. Namely, we change the scheme so that it contains \( [\mathbf {R}]_2, [\mathbf {W}_1\mathbf {R}]_2, \ldots , [\mathbf {W}_{2n}\mathbf {R}]_2, \) for random \(\mathbf {R}\in \mathbb {Z}_p^{k\times k}\) in \(\mathsf {vk}\). This modification allows us to randomize \(\mathbf {r}\) in Eq. 2, which makes the scheme context-hiding. The scheme remains adaptively unforgeable even with this change. For proving this, it suffices to show that our KP-ABE scheme in Sect. 3 remains adaptively secure even if we add \(([\mathbf {R}]_2, [\mathbf {W}_1\mathbf {R}]_2, \ldots , [\mathbf {W}_{n}\mathbf {R}]_2)\) to the master public key. Although we need to slightly modify the proof of Theorem 3.1, the proof is not difficult. We omit it due to limited space. See the full version for the detail.
5 Compact NIZK from Compact Constrained Signatures
5.1 Main Construction
Here, we construct a compact NIZK based on the compact CS scheme which we constructed in Sect. 4. Let \(\mathcal {L}\) be an \(\mathbf{NP} \) language defined by a relation \(\mathcal {R}\subseteq \{0,1\}^*\times \{0,1\}^* \). Let \(n(\kappa )\) and \(m(\kappa )\) be any fixed polynomials. Let C be a circuit that computes the relation \(\mathcal {R}\) on \(\{0,1\}^{n}\times \{0,1\}^{m}\), i.e., for \((x,w)\in \{0,1\}^{n}\times \{0,1\}^{m}\), we have \(C(x,w)=1\) if and only if \((x,w)\in \mathcal {R}\).
The construction will be given by combining following ingredients.
-
A symmetric key encryption (SKE) scheme \(\Pi _\mathsf {SKE}= (\mathsf {SKE}.\mathsf {KeyGen},\mathsf {SKE}.\mathsf {Enc}, \mathsf {SKE}.\mathsf {Dec})\) with message space \( \{ 0,1 \} ^{m}\), key space \( \{ 0,1 \} ^{\ell }\) and ciphertext space \( \{ 0,1 \} ^{|\mathsf {ct}|}\). We require that its decryption circuit can be computed in \(\mathbf{NC} ^1\), and it has an additive ciphertext overhead (i.e., \(|\mathsf {ct}|=m+\mathsf {poly}(\kappa )\)).
-
A constrained signature scheme \( (\mathsf {CS.Setup}, \mathsf {CS.KeyGen}, \mathsf {CS.Sign}, \mathsf {CS.Vrfy}, \mathsf {CS.Aggrgt}, \mathsf {CS.VrfyOnL})\) we constructed in Sect. 4. The scheme should support the circuit f that computes \(f( K, x,\mathsf {ct}) = C(x, \mathsf {SKE}.\mathsf {Dec}( K, \mathsf {ct}) )\).
-
(Not necessarily compact) extractable NIZK scheme \(\Pi _\mathsf {NIZK}= (\mathsf {Setup}, \mathsf {Prove}, \mathsf {Verify})\) for the language corresponding to the relation \(\widetilde{\mathcal {R}}\) defined below: \(( ( \mathsf {vk}_0, \{ \mathsf {vk}_{i,b}\}_{i\in [\ell ], b\in \{ 0,1 \} }, Y ),(K,\sigma ))\in \widetilde{\mathcal {R}}\) if and only if the followings are satisfied:
-
1.
\(K \in \{0,1\}^{\ell },\)
-
2.
\(\mathsf {CS.VrfyOnL}( \mathsf {vk}_0, Z , \sigma ) = \top \) where \(Z = \mathsf {CS.Aggrgt}\bigl ( \mathsf {CS.Aggrgt}\)\(( \{ \mathsf {vk}_{i,K_i} \}_{i\in [\ell ]} ) , Y \bigr ) \)
-
1.
Our compact NIZK is described as follows.
-
\(\mathsf {Setup}'(1^\kappa )\):
-
1.
Generate \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\).
-
2.
Generate \((\mathsf {vk}=(\mathsf {vk}_0, \{ \mathsf {vk}_{i,b}\}_{i\in [\ell +n+|\mathsf {ct}|], b\in \{ 0,1 \} }), \mathsf {msk}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Setup}(1^\kappa ,\) \(1^{\ell +n+|\mathsf {ct}|})\).
-
3.
Generate \(\mathsf {sk}_f \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk}, f)\).
-
4.
Output \(\mathsf {crs}'= (\mathsf {crs}, \mathsf {vk}, \mathsf {sk}_f )\).
-
1.
-
\(\mathsf {Prove}'(\mathsf {crs}',x,w)\):
-
1.
Abort if \(\mathcal {R}(x,w)=0\). Otherwise, do the following.
-
2.
Parse \(\mathsf {crs}' \rightarrow (\mathsf {crs}, \mathsf {vk}=(\mathsf {vk}_0, \{ \mathsf {vk}_{i,b}\}_{i\in [\ell +n+|\mathsf {ct}|], b\in \{ 0,1 \} }), \mathsf {sk}_f )\).
-
3.
Generate \(K\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {KeyGen}(1^\kappa )\) and \(\mathsf {ct}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {Enc}(K,w)\).
-
4.
Compute \( \sigma \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Sign}(\mathsf {sk}_f, ( K, x, \mathsf {ct}) ). \)
-
5.
Compute \( Y := \mathsf {CS.Aggrgt}( \{ \mathsf {vk}_{\ell + i,y_i} \}_{i\in [n+|\mathsf {ct}| ] } ) \) where \(y := ( x,\mathsf {ct})\in \{ 0,1 \} ^{n+|\mathsf {ct}|} \).
-
6.
Compute \( \pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Prove}( ( \mathsf {vk}_0, \{ \mathsf {vk}_{i,b}\}_{i\in [\ell ], b\in \{ 0,1 \} }, Y ),(K,\sigma ) ). \)
-
7.
Output \(\pi ' := (\mathsf {ct}, \pi )\).
-
1.
-
\(\mathsf {Verify}'(\mathsf {crs}',x,\pi ')\):
-
1.
Parse \(\pi ' \rightarrow (\mathsf {ct}, \pi )\). If it is not in this form, reject it. Otherwise, do the following.
-
2.
Parse \(\mathsf {crs}' \rightarrow (\mathsf {crs}, \mathsf {vk}=(\mathsf {vk}_0, \{ \mathsf {vk}_{i,b}\}_{i\in [\ell +n+|\mathsf {ct}|], b\in \{ 0,1 \} }), \mathsf {sk}_f )\).
-
3.
Compute \( Y := \mathsf {CS.Aggrgt}( \{ \mathsf {vk}_{\ell + i,y_i} \}_{i\in [n+|\mathsf {ct}| ] } ) \) where \(y := ( x,\mathsf {ct})\in \{ 0,1 \} ^{n+|\mathsf {ct}|} \).
-
4.
Output \(\top \) if \(\mathsf {Verify}( (\mathsf {vk}_0, \{ \mathsf {vk}_{i,b} \}_{i\in [\ell ], b\in \{ 0,1 \} } ,Y ), \pi ) = \top \) and otherwise \(\bot \).
-
1.
Correctness. Suppose that \((\mathsf {ct},\pi )\) is an honestly generated proof on \((x,w)\in \mathcal {R}\). Then we have \(\mathsf {ct}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {Enc}(K,w)\) and \(\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Prove}( ( \mathsf {vk}_0,\) \(\{ \mathsf {vk}_{i,b}\}_{i\in [\ell ], b\in \{ 0,1 \} }, Y ),(K,\sigma ) )\) where \(K\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {KeyGen}(1^\kappa )\), \(\sigma \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Sign}(\mathsf {sk}_f,\) \(( K, x, \mathsf {ct}) )\), and
By the correctness of \(\Pi _\mathsf{SKE}\), we have \(f(K,x,\mathsf {ct})=1\). Furthermore, by the correctness of \(\Pi _\mathsf {CS}\), we have \(\mathsf {CS.Vrfy}(\mathsf {vk},(K,x,\mathsf {ct}),\sigma )=\top \), which is equivalent to
Therefore we have \(( ( \mathsf {vk}_0, \{ \mathsf {vk}_{i,b}\}_{i\in [\ell ], b\in \{ 0,1 \} }, Y ),(K,\sigma ))\in \widetilde{\mathcal {R}}\) and thus we have \(\mathsf {Verify}( (\mathsf {vk}_0, \{ \mathsf {vk}_{i,b} \}_{i\in [\ell ], b\in \{ 0,1 \} } ,Y ), \pi ) = \top \) by the correctness of \(\Pi _\mathsf {NIZK}\).
Efficiency. We first observe that the size of the verification circuit for the relation \(\widetilde{\mathcal {R}}\) is \(\mathsf {poly}(\kappa )\), which is independent of the size of the verification circuit for \(\mathcal {R}\). This is because \(Z = \mathsf {CS.Aggrgt}\bigl ( \mathsf {CS.Aggrgt}( \{ \mathsf {vk}_{i,K_i} \}_{i\in [\ell ]} ) , Y \bigr ) \) can be computed in polynomial time in \(\kappa \) and the length \(\ell =\mathsf {poly}(\kappa )\) of K and the running time of \(\mathsf {CS.VrfyOnL}(\mathsf {vk}_0,Z,\sigma )\) does not depend on the length of \((x,\mathsf {ct})\) (and in particular the complexity of the circuit f) as required in Definition 4.2. Therefore, the size of \(\pi \) is \(\mathsf {poly}(\kappa )\) and independent of |x|, |w|, or |C| even though we do not require any compactness requirement for the underlying NIZK \(\Pi _\mathsf{NIZK}\). Since we assume \(|\mathsf {ct}|=m+\mathsf {poly}(\kappa )\), the total proof size is \(|w|+\mathsf {poly}(\kappa )\). We note that this scheme can be directly implemented only when the relation \(\mathcal {R}\) can be verified in \(\mathbf{NC} ^1\). Otherwise, we have to first expand the witness to make the relation verifiable in \(\mathbf{NC} ^1\) similarly to [19, 41]. This is done by considering all values corresponding to all gates when computing the circuit C on input (x, w) to be the new witness and have the new circuit verify the consistency of the values for all gates in C. In this case, the proof size becomes \(|C|+\mathsf {poly}(\kappa )\).
Since the relation \(\widetilde{R}\) is well-suited to be proven by the Groth-Sahai proof, a fairly efficient instantiation is possible based on the Groth-Sahai proof. Especially, a proof consists of |C| bits, \(6\kappa +14\) elements of \(\mathbb {G}_1\) and \(7\kappa +25\) elements of \(\mathbb {G}_2\) when instantiated under the SXDH assumption. See the full version for the detail. We also note that if the relation \(\mathcal {R}\) can be verified by a “leveled circuit” [8], we can further reduce the proof size to \(|w|+|C|/\log \kappa + \mathsf {poly}(\kappa )\) which is sublinear in |C| similarly to [41]. (See [41] for details.)
Security. In the following, we prove the soundness and the zero-knowledge property of \(\Pi '_\mathsf {NIZK}\).
Theorem 5.1
(Soundness). The above NIZK scheme \(\Pi '_\mathsf {NIZK}\) is computationally (adaptive) sound if \(\Pi _\mathsf {NIZK}\) satisfies extractability and \(\Pi _\mathsf {CS}\) is unforgeable.
Proof
Suppose that there is a PPT adversary \(\mathcal {A}\) that breaks soundness. Then we construct a PPT adversary \(\mathcal {B}\) that breaks the unforgeability of \(\Pi _\mathsf {CS}\) as follows.
-
\(\mathcal {B}(\mathsf {vk})\): It queries f to the key generation oracle to obtain \(\mathsf {sk}_f\) where f is the circuit as defined in the description of the scheme. Then it generates \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa ;r_{\mathsf {Setup}})\), runs \(\mathcal {A}(\mathsf {crs}')\) to obtain \((x^*,{\pi '}^*=(\mathsf {ct}, \pi ))\) where \(\mathsf {crs}' := (\mathsf {crs},\mathsf {vk}, \mathsf {sk}_f)\). Then it computes \((K,\sigma )\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Extract}(r_{\mathsf {Setup}}, \pi )\) and outputs \(((K,x^*,\mathsf {ct}),\sigma )\) as a forgery.
This completes the description of \(\mathcal {B}\). In the following, we show that \(\mathcal {B}\) breaks the unforgeability of \(\Pi _\mathsf {CS}\). Let \(\mathsf {VK}_{[0,\ell ]} := (\mathsf {vk}_0, \{ \mathsf {vk}_{i,b} \}_{i\in [\ell ], b\in \{ 0,1 \} })\). Since we assume \(\mathcal {A}\) breaks the soundness of \(\Pi _\mathsf {NIZK}'\),
is non-negligible where \( Y^* = \mathsf {CS.Aggrgt}( \{ \mathsf {vk}_{\ell + i,y^*_i} \}_{i\in [n+|\mathsf {ct}| ] } ) \) and \(y^* := ( x^*,\mathsf {ct})\in \{ 0,1 \} ^{n+|\mathsf {ct}|} \). On the other hand, by the extractability of \(\Pi _\mathsf {NIZK}\),
is negligible. Therefore
is non-negligible. Suppose that this event happens. Since we have \(x^*\notin \mathcal {L}\), we have \(f(K,x^*,\mathsf {ct})=0\). On the other hand, \(((\mathsf {VK}_{[0,\ell ]} ,Y^*),(K,\sigma ))\in \widetilde{\mathcal {R}}\) implies that we have \(K \in \{0,1\}^{\ell } \wedge \mathsf {CS.VrfyOnL}( \mathsf {vk}_0, Z , \sigma ) = \top \) where \(Z = \mathsf {CS.Aggrgt}\bigl ( \mathsf {CS.Aggrgt}(\{ \mathsf {vk}_{i,K_i} \}_{i\in [\ell ]} ) , Y^* \bigr ) \), which implies \(\mathsf {CS.Vrfy}( \mathsf {vk}, (K,x^*,\mathsf {ct}) , \sigma ) = \top \). This means that \(\mathcal {B}\) succeeds in breaking the unforgeability of \(\Pi _\mathsf {CS}\). \(\square \)
Theorem 5.2
(Zero-Knowledge). The above NIZK scheme \(\Pi '_\mathsf {NIZK}\) is computationally zero-knowledge if \(\Pi _\mathsf {NIZK}\) is computationally zero-knowledge and \(\Pi _\mathsf {SKE}\) is CPA-secure.
Proof
Let \((\mathcal {S}_1,\mathcal {S}_2)\) be the simulator for \(\Pi _\mathsf {NIZK}\). We describe the simulator \((\mathcal {S}'_1,\mathcal {S}'_2)\) for \(\Pi '_\mathsf {NIZK}\) below.
-
\(\mathcal {S}'_1(1^{\kappa })\): It generates \((\mathsf {crs},\tau _\mathsf{V})\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {S}_1(1^{\kappa })\), \((\mathsf {vk}=(\mathsf {vk}_0,\) \(\{ \mathsf {vk}_{i,b}\}_{i\in [\ell +n+|\mathsf {ct}|], b\in \{ 0,1 \} }), \mathsf {msk}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Setup}(1^\kappa ,1^{\ell +n+|\mathsf {ct}|})\), and \(\mathsf {sk}_f \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk}, f)\), and outputs \(\mathsf {crs}':=(\mathsf {crs},\mathsf {vk},\mathsf {sk}_f)\) and \(\tau _\mathsf{V}':= \tau _\mathsf{V}\).
-
\(\mathcal {S}'_2(\mathsf {crs}':=(\mathsf {crs},\mathsf {vk},\mathsf {sk}_f),\tau _\mathsf{V}'=\tau _\mathsf{V},x)\): It picks \(K\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {KeyGen}(1^{\kappa })\), computes \(\mathsf {ct}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {Enc}(K,0^{m})\), \(Y := \mathsf {CS.Aggrgt}( \{ \mathsf {vk}_{\ell + i,y_i} \}_{i\in [n+|\mathsf {ct}| ] } )\) where \(y := ( x,\mathsf {ct})\in \{ 0,1 \} ^{n+|\mathsf {ct}|} \), and \(\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {S}_2(\mathsf {crs},\tau _\mathsf{V},(\mathsf {vk}_0, \{ \mathsf {vk}_{i,b} \}_{i\in [\ell ], b\in \{ 0,1 \} } ,Y))\), and outputs \(\pi ':=(\mathsf {ct},\pi )\).
This completes the description of the simulator. We prove that proofs simulated by the above simulator are computationally indistinguishable from the honestly generated proofs. To prove this, we consider the following sequence of games between a PPT adversary \(\mathcal {A}\) and a challenger.
-
\(\mathsf {G}_0\): In this game, proofs are generated honestly. Namely,
-
1.
The challenger generates \(\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\kappa )\), \((\mathsf {vk}=(\mathsf {vk}_0,\) \(\{ \mathsf {vk}_{i,b}\}_{i\in [\ell +n+|\mathsf {ct}|], b\in \{ 0,1 \} }), \mathsf {msk}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Setup}(1^\kappa ,1^{\ell +n+|\mathsf {ct}|})\), and \(\mathsf {sk}_f \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.KeyGen}(\mathsf {msk}, f)\), and gives \(\mathsf {crs}':=(\mathsf {crs},\mathsf {vk},\mathsf {sk}_f )\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) is given \((1^{\kappa }, \mathsf {crs}')\) and is allowed to query \(\mathcal {O}(\mathsf {crs}',\cdot , \cdot )\), which works as follows. When \(\mathcal {A}\) queries (x, w), if \((x,w)\notin \mathcal {R}\), then the oracle returns \(\bot \). Otherwise, it picks \(K \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {KeyGen}(1^{\kappa })\), computes \(\mathsf {ct}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {Enc}(K,w)\), \( \sigma \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {CS.Sign}(\mathsf {sk}_f, ( K, x, \mathsf {ct}) ), \) \( Y := \mathsf {CS.Aggrgt}( \{ \mathsf {vk}_{\ell + i,y_i} \}_{i\in [n+|\mathsf {ct}| ] } ) \) where \(y := ( x,\mathsf {ct})\in \{ 0,1 \} ^{n+|\mathsf {ct}|} \), and \( \pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Prove}( \mathsf {crs}, ( \mathsf {vk}_0, \{ \mathsf {vk}_{i,b}\}_{i\in [\ell ], b\in \{ 0,1 \} }, Y ),(K,\sigma ) ), \) and returns a proof \(\pi ':= (\mathsf {ct},\pi )\).
-
3.
Finally, \(\mathcal {A}\) returns a bit \(\beta \).
-
1.
-
\(\mathsf {G}_1\): This game is identical to the previous game except that \(\mathsf {crs}\) and \(\pi \) are generated differently. Namely, the challenger generates \((\mathsf {crs},\tau _\mathsf{V})\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {S}_1(1^{\kappa })\) at the beginning of the game, and \(\pi \) is generated as \(\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {S}_2(\mathsf {crs},\tau _\mathsf{V},(\mathsf {vk}_0, \{ \mathsf {vk}_{i,b}\}_{i\in [\ell ], b\in \{ 0,1 \} }, Y))\) for each oracle query.
-
\(\mathsf {G}_2\): This game is identical to the previous game except that \(\mathsf {ct}\) is generated as \(\mathsf {ct}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SKE}.\mathsf {Enc}(K,0^{m})\) for each oracle query.
Let \(\mathsf {T}_i\) be the event that \(\mathcal {A}\) returns 1 in \(\mathsf {G}_i\) for \(i=0,1,2\). It is easy to see that proofs are generated by \(\mathcal {S}'=(\mathcal {S}'_1,\mathcal {S}'_2)\) in \(\mathsf {G}_2\). Thus we have to prove that \(|\Pr [\mathsf {T}_0]-\Pr [\mathsf {T}_2]|\) is negligible. The following lemmas are straightforward to prove.
Lemma 5.1
If \(\Pi _\mathsf {NIZK}\) satisfies computational zero-knowledge w.r.t. the simulator \(\mathcal {S}\), then \(|\Pr [\mathsf {T}_0]-\Pr [\mathsf {T}_1]|=\mathsf {negl}(\kappa )\).
Proof
We observe that every proof \(\pi \) given to \(\mathcal {A}\) is created for a correct statement in both games. Therefore, the indistinguishability of the games can be reduced to the zero-knowledge property of \(\Pi _\mathsf {NIZK}\). \(\square \)
Lemma 5.2
If \(\Pi _\mathsf {SKE}\) is CPA-secure, then \(|\Pr [\mathsf {T}_1]-\Pr [\mathsf {T}_2]|=\mathsf {negl}(\kappa )\).
Proof
Due to the change we introduced in \(\mathsf {G}_1\), the secret key K of \(\mathsf {SKE}\) that is used to generate \(\mathsf {ct}\) is not used anywhere else in both games. therefore, the indistinguishability of these games can be reduced to the CPA security of \(\Pi _\mathsf {SKE}\). \(\square \)
This completes the proof of Theorem 5.2. \(\square \)
5.2 Variants of Our NIZK
Perfect Zero-Knowledge Variant. Observe that the assumptions required to prove the zero-knowledge property of our NIZK was the zero-knowledge property of the underlying non-compact NIZK and the security of SKE. Therefore if we assume that the underlying non-compact NIZK is perfect zero-knowledgeFootnote 6 and modify the scheme somehow so that we do not use an SKE anymore, the resulting NIZK can be made perfect zero-knowledge. Indeed, the latter can be done by using the witness w itself in place of the SKE key K in the definition of the circuit f supported by the CS scheme. By instantiating the non-compact NIZK with the Groth-Sahai proof, which is perfect zero-knowledge, we obtain the following theorem. (See the full version for the full detail.)
Theorem 5.3
There exists a NIPZK for \(\mathbf{NP} \) relations computable in \(\mathbf{NC} ^1\) with proof size \(|w|\cdot \mathsf {poly}(\kappa )\) if the DLIN assumption holds.
UC Variant. If we further modify the perfect zero-knowledge variant to have non-malleability by using one-time signatures and assume that the underlying non-compact NIZK is a UC-NIZK, then we can show that the resulting scheme is also UC-NIZK. In particular, we obtain the following theorem. (See the full version for the full detail.)
Theorem 5.4
There exists a UC-NIZK for \(\mathbf{NP} \) relations computable in \(\mathbf{NC} ^1\) with proof size \(|w|\cdot \mathsf {poly}(\kappa )\) if the DLIN assumption holds.
Notes
- 1.
In the introduction, we do not distinguish between proofs and arguments for simplicity.
- 2.
Note that \(\mathsf {CS}.\sigma \) should be kept secret since it reveals partial information of K.
- 3.
Actually, the definition of online-offline decomposability is slightly different from the one in the main body, but the latter implies the former.
- 4.
We say it is a non-interactive zero-knowledge proofs when the soundness property holds for even unbounded adversaries. In this paper, we will only be interested in computationally bounded adversaries.
- 5.
More accurately, \( \mathcal {O}_{\mathsf {E}} \) takes as input \([M]_2 \in G_2\) in addition to i in [44]. But we can ignore the additional input \([M]_2\) without loss of generality.
- 6.
Actually, we have to assume the underlying non-compact NIZK is dual-mode NIZK for proving the soundness.
References
Abusalah, H.: Generic instantiations of the hidden bits model for non-interactive zero-knowledge proofs for NP. Master’s thesis, RWTH-Aachen University (2013)
Attrapadung, N., Libert, B., de Panafieu, E.: Expressive key-policy attribute-based encryption with constant-size ciphertexts. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 90–108. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_6
Bellare, M., Yung, M.: Certifying permutations: noninteractive zero-knowledge based on any trapdoor permutation. J. Cryptol. 9(3), 149–166 (1996)
Bitansky, N., Paneth, O.: ZAPs and non-interactive witness indistinguishability from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 401–427. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_16
Bitansky, N., Paneth, O., Wichs, D.: Perfect structure on the edge of chaos. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part I. LNCS, vol. 9562, pp. 474–502. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_20
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications (extended abstract). In: 20th ACM STOC, pp. 103–112 (1988)
Boneh, D., Franklin, M.: Identity-based encryption from the Weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13
Boyle, E., Gilboa, N., Ishai, Y.: Breaking the circuit size barrier for secure computation under DDH. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part I. LNCS, vol. 9814, pp. 509–539. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_19
Canetti, R., et al.: Fiat-Shamir: from practice to theory. In: 51st ACM STOC, pp. 1082–1090 (2019)
Canetti, R., Chen, Y., Reyzin, L., Rothblum, R.D.: Fiat-Shamir and correlation intractability from strong KDM-secure encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 91–122. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_4
Canetti, R., Halevi, S., Katz, J.: A forward-secure public-key encryption scheme. J. Cryptol. 20(3), 265–294 (2007)
Canetti, R., Lichtenberg, A.: Certifying trapdoor permutations, revisited. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part I. LNCS, vol. 11239, pp. 476–506. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_18
Cohen, R., Shelat, A., Wichs, D.: Adaptively secure MPC with sublinear communication complexity. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 30–60. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_2
Danezis, G., Fournet, C., Groth, J., Kohlweiss, M.: Square span programs with applications to succinct NIZK arguments. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part I. LNCS, vol. 8873, pp. 532–550. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_28
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie–Hellman assumptions. J. Cryptol. 30(1), 242–288 (2015). https://doi.org/10.1007/s00145-015-9220-6
Feige, U., Lapidot, D., Shamir, A.: Multiple noninteractive zero knowledge proofs under general assumptions. SIAM J. Comput. 29(1), 1–28 (1999)
Fuchsbauer, G., Jafargholi, Z., Pietrzak, K.: A quasipolynomial reduction for generalized selective decryption on trees. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part I. LNCS, vol. 9215, pp. 601–620. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_29
Fuchsbauer, G., Konstantinov, M., Pietrzak, K., Rao, V.: Adaptive security of constrained PRFs. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 82–101. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_5
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. SIAM J. Comput. 45(3), 882–929 (2016)
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Gentry, C.: A fully homomorphic encryption scheme. Ph.D. thesis, Stanford University (2009)
Gentry, C., Groth, J., Ishai, Y., Peikert, C., Sahai, A., Smith, A.D.: Using fully homomorphic hybrid encryption to minimize non-interative zero-knowledge proofs. J. Cryptol. 28(4), 820–843 (2015)
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: 43rd ACM STOC, pp. 99–108 (2011)
Goldreich, O.: Foundations of Cryptography: Volume 2, Basic Applications (2004)
Goldreich, O., Oren, Y.: Definitions and properties of zero-knowledge proof systems. J. Cryptol. 7(1), 1–32 (1994)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Groth, J.: Short non-interactive zero-knowledge proofs. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 341–358. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_20
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Groth, J.: On the size of pairing-based non-interactive arguments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 305–326. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_11
Groth, J., Ostrovsky, R., Sahai, A.: New techniques for noninteractive zero-knowledge. J. ACM 59(3), 1–35 (2012)
Groth, J., Sahai, A.: Efficient noninteractive proof systems for bilinear groups. SIAM J. Comput. 41(5), 1193–1232 (2012)
Hemenway, B., Jafargholi, Z., Ostrovsky, R., Scafuro, A., Wichs, D.: Adaptively secure garbled circuits from one-way functions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part III. LNCS, vol. 9816, pp. 149–178. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_6
Hohenberger, S., Waters, B.: Attribute-based encryption with fast decryption. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 162–179. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_11
Ishai, Y., Kushilevitz, E.: Perfect constant-round secure computation via perfect randomizing polynomials. In: Widmayer, P., Eidenbenz, S., Triguero, F., Morales, R., Conejo, R., Hennessy, M. (eds.) ICALP 2002. LNCS, vol. 2380, pp. 244–256. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45465-9_22
Jafargholi, Z., Kamath, C., Klein, K., Komargodski, I., Pietrzak, K., Wichs, D.: Be adaptive, avoid overcommitting. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 133–163. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_5
Jafargholi, Z., Wichs, D.: Adaptive security of Yao’s garbled circuits. In: Hirt, M., Smith, A. (eds.) TCC 2016, Part I. LNCS, vol. 9985, pp. 433–458. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_17
Jutla, C.S., Roy, A.: Switching lemma for bilinear tests and constant-size NIZK proofs for linear subspaces. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 295–312. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_17
Jutla, C.S., Roy, A.: Shorter quasi-adaptive NIZK proofs for linear subspaces. J. Cryptol. 30(4), 1116–1156 (2017)
Kalai, Y.T., Rothblum, G.N., Rothblum, R.D.: From obfuscation to the security of Fiat-Shamir for proofs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 224–251. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_8
Katsumata, S., Nishimaki, R., Yamada, S., Yamakawa, T.: Designated verifier/prover and preprocessing NIZKs from Diffie-Hellman assumptions. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part II. LNCS, vol. 11477, pp. 622–651. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_22
Katsumata, S., Nishimaki, R., Yamada, S., Yamakawa, T.: Exploring constructions of compact NIZKs from various assumptions. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part III. LNCS, vol. 11694, pp. 639–669. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_21
Kiltz, E., Wee, H.: Quasi-adaptive NIZK for linear subspaces revisited. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 101–128. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_4
Kim, S., Wu, D.J.: Multi-theo preprocessing NIZKs from lattices. In: CRYPTO 2018, Part II, pp. 733–765 (2018)
Kowalczyk, L., Wee, H.: Compact adaptively secure ABE for \(\sf NC^1\) from k-Lin. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 3–33. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_1
Lipmaa, H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 169–189. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_10
Maji, H.K., Prabhakaran, M., Rosulek, M.: Attribute-based signatures. In: Kiayias, A. (ed.) CT-RSA 2011. LNCS, vol. 6558, pp. 376–392. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19074-2_24
Naccache, D., Stern, J.: A new public key cryptosystem based on higher residues. In: ACM CCS 1998, pp. 59–66 (1998)
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_6
Okamoto, T., Takashima, K.: Efficient attribute-based signatures for non-monotone predicates in the standard model. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 35–52. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_3
Peikert, C., Shiehian, S.: Noninteractive zero knowledge for NP from (plain) learning with errors. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 89–114. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_4
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: 46th ACM STOC, pp. 475–484 (2014)
Tsabary, R.: An equivalence between attribute-based signatures and homomorphic signatures, and new constructions for both. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part II. LNCS, vol. 10678, pp. 489–518. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_16
Vinod, V., Narayanan, A., Srinathan, K., Rangan, C.P., Kim, K.: On the power of computational secret sharing. In: Johansson, T., Maitra, S. (eds.) INDOCRYPT 2003. LNCS, vol. 2904, pp. 162–176. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-24582-7_12
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Acknowledgement
We thank anonymous reviewers of Eurocrypt 2020 for their helpful comments. The first and the third authors were supported by JST CREST Grant Number JPMJCR19F6. The third author was supported by JSPS KAKENHI Grant Number 16K16068.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Katsumata, S., Nishimaki, R., Yamada, S., Yamakawa, T. (2020). Compact NIZKs from Standard Assumptions on Bilinear Maps. In: Canteaut, A., Ishai, Y. (eds) Advances in Cryptology – EUROCRYPT 2020. EUROCRYPT 2020. Lecture Notes in Computer Science(), vol 12107. Springer, Cham. https://doi.org/10.1007/978-3-030-45727-3_13
Download citation
DOI: https://doi.org/10.1007/978-3-030-45727-3_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45726-6
Online ISBN: 978-3-030-45727-3
eBook Packages: Computer ScienceComputer Science (R0)



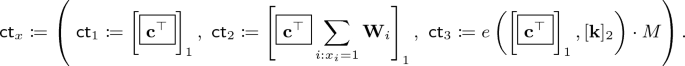
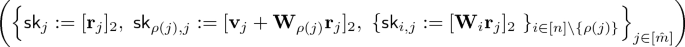
 ,
,  .
.