Sigma Protocols for MQ, PKP and SIS, and Fishy Signature Schemes

Abstract

This work presents sigma protocols to prove knowledge of:

• a solution to a system of quadratic polynomials,

• a solution to an instance of the Permuted Kernel Problem and

• a witness for a variety of lattice statements (including SIS).

Our sigma protocols have soundness error 1/$q'$, where $q'$ is any number bounded by the size of the underlying finite field. This is much better than existing proofs, which have soundness error 2/3 or $(q'+1)/2q'$. The prover and verifier time our proofs are $O(q')$. We achieve this by first constructing so-called sigma protocols with helper, which are sigma protocols where the prover and the verifier are assisted by a trusted third party, and then eliminating the helper from the proof with a “cut-and-choose” protocol. We apply the Fiat-Shamir transform to obtain signature schemes with security proof in the QROM. We show that the resulting signature schemes, which we call the “MUltivariate quaDratic FIat-SHamir” scheme (MUDFISH) and the “ShUffled Solution to Homogeneous linear SYstem FIat-SHamir” scheme (SUSHSYFISH), are more efficient than existing signatures based on the MQ problem and the Permuted Kernel Problem. Our proof system can be used to improve the efficiency of applications relying on (generalizations of) Stern’s protocol. We show that the proof size of our SIS proof is smaller than that of Stern’s protocol by an order of magnitude and that our proof is more efficient than existing post-quantum secure SIS proofs.

1 Introduction

Zero-knowledge proofs of knowledge and more specifically Sigma protocols are a technique in cryptography that allows a prover to prove to a verifier that they know a value x that satisfies some relation, without revealing any additional information about x [19]. Sigma protocols are useful to build a wide variety of cryptographic applications, including digital signatures, group/ring signatures, e-voting protocols, and privacy-preserving cryptocurrencies. In some cases these sigma protocols are not completely sound, meaning that a cheating prover can convince a verifier he knows some value, without actually knowing it. If a prover can do this with a probability at most $\epsilon$, then $\epsilon$ is said to be the soundness error of the sigma protocol. The soundness of a sigma protocol can be amplified; by repeating the protocol k times the soundness error of the entire protocol becomes $\epsilon ^k$. Therefore, if one repeats a protocol with soundness error ${\le }1$ often enough, one can obtain a sound protocol. However, if a large number of repetitions is required, this makes the protocol less efficient and makes applications of the protocol less practical. This is the case for Stern’s protocol [34] and the sigma protocols underlying some post-quantum signature schemes [10, 12, 14]. The goal of this paper is to develop new variants of these sigma protocols that have a smaller soundness error, such that fewer repetitions are necessary and such that the overall efficiency of the protocols is improved.

Zero-Knowledge Based Post-Quantum Signatures. One way to construct a signature scheme is to first construct a zero-knowledge identification scheme and then make it into a non-interactive signature scheme with a transformation such as the Fiat-Shamir transform [17] or the Unruh transform [35]. Looking at the NIST Post-Quantum Standardization project, three of the Round II signature schemes, MQDSS, Picnic, and Dilithium use this approach. MQDSS [13] uses a zero-knowledge proof that, given a multivariate quadratic map $\mathcal {P}: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^m$ proves knowledge of a solution $\mathbf {s} \in \mathbb {F}_q^n$ such that $\mathcal {P}(\mathbf {s}) = \mathbf {0}$. Picnic [12] uses an identification scheme constructed using the “MPC-in-the-head” technique [20] that relies on symmetric primitives. Dilithium is a lattice-based signature scheme that relies on the Fiat-Shamir with aborts technique [29]. Another example is PKP-DSS [10], which uses a zero-knowledge proof introduced by Shamir in 1989 for proving knowledge of a solution of an instance of the Permuted Kernel Problem (PKP) [33]. This means that, given a matrix $\mathbf {A} \in \mathbb {F}_q^{m \times n}$ and a vector $\mathbf {v} \in \mathbb {F}_q^{n}$, the proof system can prove knowledge of a permutation $\pi \in S_n$ such that $\mathbf {A}\mathbf {v}_\pi = 0$, where $\mathbf {v}_\pi$ is the vector obtained by permuting the entries of the vector $\mathbf {v}$ with the permutation $\pi$. A drawback of these schemes (with exception of Dilithium) is that the underlying identification schemes have a large soundness error, so a large number of parallel repetitions are required to get a secure signature scheme. This increases the signature sizes and the signing and verification times. For example, the protocol underlying the Picnic signature scheme has a soundness error of $\frac{2}{3}$ and hence requires $k = 219$ repetitions to get the soundness error down to less than $2^{-128}$.

Recently, Katz et al. [24] improved on the approach of Picnic by building a zero-knowledge proof from MPC in the preprocessing model, where the parties can use some auxiliary data that was generated during a preprocessing phase. The advantage of moving to the new MPC protocol is that it allows for secure computation with dishonest majority with an arbitrary number of parties n, which results in a zero-knowledge proof with a soundness error of $\frac{1}{n}$. Hence, fewer parallel rounds are required to get a secure signature scheme. A “cut-and-choose” protocol is used to deal with the preprocessing phase, which makes signing and verification slower compared to the original Picnic scheme. This new signature scheme is called Picnic2 and is, together with the original Picnic scheme, one of the Round 2 candidates of the NIST PQC standardization project.

Stern’s Protocol. In 1993, Stern proposed a code based sigma protocol [34]. For a publicly known parity check matrix $\mathbf {H} \in \mathbb {F}_{2}^{m \times n}$, syndrome $\mathbf {s} \in \mathbb {F}_2^{m}$ and weight t, Stern’s zero-knowledge proof can prove knowledge of an error vector $\mathbf {e} \in \mathbb {F}_2^n$ with hamming weight t such that $\mathbf {H} \mathbf {e} = \mathbf {s}$. Internally, Stern’s protocol is very similar to Shamir’s protocol for PKP, and in fact, Stern’s protocol generalizes easily to proving knowledge of a witness of the inhomogeneous PKP (IPKP) relation. The motivation behind Stern’s protocol was to obtain a code-based identification scheme (and hence also a signature scheme with the Fiat-Shamir transform). However, Stern’s protocol has been used extensively in lattice-based cryptography, because the IPKP relation can be bootstrapped to prove knowledge of a solution to the SIS problem, knowledge of an LWE secret and more complex lattice statements such as proving that a given LWE ciphertext is a valid encryption of a known message satisfying certain constraints [28]. This led to the construction of many advanced primitives from lattices, such as identity-based identification schemes, group signatures (with verifier local revocation), logarithmic size ring signatures and group encryption [25,26,27,28]. Improving Stern’s protocol is an important and long-standing open problem because this would improve the efficiency of all these constructions.

Contributions. In this paper we generalize the idea behind Picnic2 [24] to something we call “sigma protocols with helper”. Concretely, a sigma protocol with helper is a 3-party protocol between a prover, a verifier and a trusted third party called the “helper”. The protocol begins with the helper who honestly generates some auxiliary information that he sends to the verifier. The helper also sends the randomness seed that he used to generate his randomness to the prover. Then, the protocol resumes like a normal sigma protocol. A sigma protocol with helper is similar to a sigma protocol in the Common Reference String (CRS) model, except that the trusted third party sends some secret information (the randomness seed) to the prover and that the trusted third party needs to participate in every execution, rather than just doing the trusted setup once.

We then construct a sigma protocol with helper to prove knowledge of a solution of a system of quadratic equations and a sigma protocol with helper for proving knowledge of a solution of an inhomogeneous PKP instance (i.e. the same relation as the Shamir and Stern protocols). Our proofs have soundness error $\frac{1}{q'}$ and prover time $\varTheta (q')$, where $q'$ is any number bounded by the size of the finite fields that are used. This soundness error is much better than existing proofs which have soundness error $\frac{1}{2}+\frac{1}{2q}$ or soundness error 2/3. We then show how to remove the helper with a “cut-and-choose” protocol, analogous to the approach used by Katz et al. [24]. This transformation gives rise to standard sigma protocols (i.e. without helper) which can then be transformed into signature schemes using the Fiat-Shamir transform or used as a more efficient variant of Stern’s protocol as a building block for advanced privacy-preserving constructions.

Note that, even though the soundness error is $q'$, it is not possible to do one-shot proofs if the field size is exponential because the prover time is $\varTheta (q')$. However, we can still realize a large practical improvement over existing proofs: The proof size of existing proofs is $\mathcal {O}(\lambda X)$, where $\lambda$ is the security parameter and X is the proof size of a single iteration of the protocol. In comparison, the proof size of our proofs is $\mathcal {O}(\frac{\lambda }{\log q'}(X + \log q' * |\mathsf {seed}|))$, because the number of iterations is now $O(\frac{\lambda }{\log q'})$, and each iteration incurs an overhead of $\log q' |\mathsf {seed}|$ (a path in a Merkle tree of size $q'$). In practice, the proof size is often dominated by the $\mathcal {O}(\lambda |\mathsf {seed}|)$ term even for small values of $q'$. Since X is usually much larger than $|\mathsf {seed}| = \lambda$, this gives a large improvement in practice. X and $|\mathsf {seed}|$ are both linear in $\lambda$, so the improvement factor remains the same at higher security levels.

We apply the Fiat-Shamir transform to our Sigma protocol for the MQ relation to get a signature scheme whose security reduces to the problem of finding a solution to a random system of multivariate quadratic polynomials. We call this the “MUltivarite quaDratic FIat-SHamir” scheme (MUDFISH). MUDFISH is more efficient than MQDSS, the existing signature scheme based on the same hard problem. At NIST security level 1, the MUDFISH signatures are roughly half as big as the MQDSS signatures, while our constant-time MUDFISH implementation is roughly twice as fast as the optimized MQDSS implementation that was submitted to the NIST PQC standardization project. Using the Fiat-Shamir transform on our sigma protocol for the PKP relation, we obtain the “ShUffled Solution to Homogeneous linear SYstem FIat-SHamir” scheme (SUSHSYFISH), a signature scheme whose security reduces to finding a solution of a random PKP instance. SUSHSYFISH has smaller signatures than PKP-DSS, the existing scheme based on the PKP problem while being only slightly slower. Moreover, unlike MQDSS and PKP-DSS, the MUDFISH and SUSHSYFISH signature schemes are based on sigma protocols (i.e. 3-round proofs) rather than 5-round proofs, which results in tighter security proofs in the ROM and even allows us to use the recent results of Don et al. [16] to prove their security in the QROM. A comparison of the signature sizes and signing speed of MUDFISH and multiple instantiations of SUSHSYFISH with those of existing Post-Quantum Fiat-Shamir signatures is given in Fig. 1. Our implementation is available on GitHub [9].

We can improve the lattice-based constructions such as identity-based identification schemes, group signatures (with verifier local revocation), logarithmic size ring signatures and group encryption that rely on Stern’s protocol [25,26,27,28], by replacing Sterns protocol by our more efficient proof for IPKP. In particular, we make a case study for the SIS problem, where we see that with our proof system, the proof size is a factor 10 smaller than with Stern’s protocol. And smaller than proof sizes arising from other post-quantum exact proofs for SIS, such as using “MPC-in-the-head” techniques [5] or an algebraic approach [11].

Fig. 1.

taken from [10].

Comparison of MUDFISH and SUSHSYFISH to existing signatures based on the MQ problem (MQDSS) and PKP problem (PKP-DSS). Cycle counts of picnic and MQDSS are taken from the NIST Round2 submission packages (the optimized, but not AVX2 optimized implementations, updated to take the attack of Kales and Zaverucha into account [23]), cycle counts for PKP-DSS are

Roadmap. In Sect. 2 we lay out some basic preliminaries required for the remainder of the paper. In Sect. 3 we formalize the notion of a sigma protocol with helper, then we construct sigma protocols with helper for the MQ problem and the Permuted Kernel Problem in Sects. 4 and 5. In Sect. 6 we show how to convert a sigma protocol with helper in a normal zero-knowledge proof (without helper). Then, we convert our zero-knowledge proofs into signature schemes in Sect. 8, where we also briefly discuss our proof-of-concept implementations. Finally, in Sect. 9 we show how to use the IPKP proof to construct a zero-knowledge proof for the SIS relation, and we compare our SIS proof to existing SIS proofs.

2 Preliminaries

2.1 Hard Problems

We introduce (variants of) the Permuted Kernel Problem (PKP), the Multivariate quadratic problem (MQ) and the Short Integer Solution problem (SIS), three computationally hard problems that are used in the remainder of the paper.

Permuted Kernel Problem (PKP/IPKP). Given a matrix $\mathbf {A} \in \mathbb {F}_q^{m\times n}$ and a vector $\mathbf {v} \in \mathbb {F}_q^n$ defined over a finite field $\mathbb {F}_q$, the Permuted Kernel Problem is to find a permutation $\pi \in S_n$, such that $\mathbf {A} \mathbf {v}_\pi = 0$, where $\mathbf {v}_\pi$ is the vector obtained by permuting the entries of $\mathbf {v}$ with the permutation $\pi$, that is, the vector defined by $(\mathbf {v}_\pi )_i = v_{\pi (i)}$. There is also a inhomogeneous version of the problem, where given $\mathbf {A} \in \mathbb {F}_q^{m\times n}$, $\mathbf {v} \in \mathbb {F}_q^n$ and a target vector $\mathbf {t} \in \mathbb {F}_q^m$, the task is to find a permutation $\pi \in S_n$, such that $\mathbf {A}\mathbf {v}_\pi = \mathbf {t}$.

The permuted kernel problem is a classical NP-Hard problem that was first introduced in cryptography by Shamir, who designed an identification scheme, whose security reduces to the problem of solving a random PKP instance [33]. Several works have introduced new algorithms and time-memory trade-offs for solving the PKP [3, 18, 21, 30], but solving the problem remains prohibitively difficult, even for small parameters (see Table 3).

Subgroup IPKP. The Subgroup Inhomogeneous Permuted Kernel Problem (SIPKP) is the same as the IPKP problem, with the additional constraint that the solution is a member of a certain subgroup of $S_n$. Concretely, a solution to the a SIPKP instance $(\mathbf {A},\mathbf {v},\mathbf {t},H)$, with $\mathbf {A} \in \mathbb {F}_q^{m\times n}, \mathbf {v} \in \mathbb {F}_q^n, \mathbf {t} \in \mathbb {F}_q^m$ and H a subgroup of $S_n$ is a permutation $\pi \in H$ such that $\mathbf {A}\mathbf {v}_\pi = \mathbf {t}$.

Multivariate Quadratic (MQ). Given a multivariate quadratic map $\mathcal {P} : \mathbb {F}_q^n \rightarrow \mathbb {F}_q^m$ of m quadratic polynomials in n variables defined over a finite field $\mathbb {F}_q$, the MQ problem asks to find a solution $\mathbf {s}\in \mathbb {F}_q^n$ such that $\mathcal {P}(\mathbf {s}) = 0$. The best known methods for solving this problem rely on Grobner basis methods or linearization methods in combination with guessing a number of the variables [8, 22]. This is the central problem underlying most of multivariate cryptography, and for random systems $\mathcal {F}$, the hardness of the problem is well understood.

Short Integer Solution (SIS/ISIS). The well known Short Integer Solution problem, introduced in the seminal work of Ajtai [1] asks to, given a matrix $\mathbf {A} \in \mathbb {Z}_q^{n \times m}$, and a bound $\beta$, find a vector $\mathbf {x}$, such that $\mathbf {A}\mathbf {x} = 0$ whose norm is bounded by $||\mathbf {x}|| \le \beta$. There is also a inhomogeneous version of the problem (ISIS), where, given $\mathbf {A} \in \mathbb {Z}_q^{n \times m}$, $\mathbf {t} \in \mathbb {Z}_q^n$ and a bound $\beta$ the task is to find $\mathbf {x} \in \mathbb {Z}_q^m$ such that $\mathbf {A}\mathbf {x} = \mathbf {t}$, again subject to $||\mathbf {x}|| \le \beta$. The problem enjoys reductions from worst case lattice problems, and is one of the fundamental problems underlying lattice-based cryptography.

2.2 Commitment Schemes

Many sigma protocols, including ours, depend heavily on secure non-interactive commitment schemes. In the remainder of the paper we assume a non-interactive commitment function $\mathsf {Com}: \{0,1\}^{\lambda } \times \{0,1\}^\star \rightarrow \{0,1\}^{2 \lambda }$, that takes as input $\lambda$ uniformly random bits $\mathsf {bits}$, where $\lambda$ is the security parameter, and a message $m \in \{0,1\}^\star$ and outputs a $2\lambda$ bit long commitment $\mathsf {Com}(\mathsf {bits},m)$.

Intuitively, the commitment scheme should not reveal anything the message it commits to, and it should not be possible to open the commitment to some different message. These properties are formalized as follows:

Definition 1

(Computational binding). For an adversary $\mathcal {A}$ we define its advantage for the commitment binding game as

$$ \mathsf {Adv}^{\mathsf {Binding}}_{\mathsf {Com}}(\mathcal {A}) = \Pr [ \mathsf {Com}(\mathsf {bits},m) = \mathsf {Com}(\mathsf {bits}',m') | (\mathsf {bits},m,\mathsf {bits}',m') \leftarrow \mathcal {A}(1^\lambda ) ] $$

We say that $\mathsf {Com}$ is computationally binding if for all polynomial time algorithms $\mathcal {A}$, the advantage $\mathsf {Adv}^{\mathsf {Binding}}_{\mathsf {Com}}(\mathcal {A})$ is a negligible function of the security parameter $\lambda$.

Definition 2

(Computational hiding). For an adversary $\mathcal {A}$ we define the advantage for the commitment hiding game for a pair of messages $m,m'$ as

We say that $\mathsf {Com}$ is computationally hiding if for all polynomial time algorithms $\mathcal {A}$, and every pair of messages $m,m'$ the advantage $\mathsf {Adv}^{\mathsf {Hiding}}_{\mathsf {Com}}(\mathcal {A},m,m')$ is a negligible function of the security parameter $\lambda$.

In our implementations, we use SHAKE256 as commitment function. If we model SHAKE256 as a quantum random oracle, then it satisfies the computational binding and hiding properties.

3 Sigma Protocols with Helper

This paper introduces two Sigma protocols with helper, which are like normal sigma protocols, with the addition of a trusted third party (called the helper) that runs a setup algorithm based on a random seed at the beginning of each execution of the protocol. The helper then sends some auxiliary information to the verifier and sends the seed value that was used to seed the setup algorithm to the prover. A more formal definition is as follows:

Definition 3

(Sigma protocol with helper). A protocol is a sigma protocol with helper for relation R with challenge space $\mathcal {C}$ if it is of the form of Fig. 2 and satisfies:

• Completeness. If all parties (Helper, Prover and Verifier) follow the protocol on input $(x,w) \in R$, then the verifier always accepts.

• 2-Special soundness. From an adversary $\mathcal {A}$ that outputs with noticeable probability two valid transcripts $(x,\mathsf {aux},\mathsf {com},ch,\mathsf {rsp})$ and $(x,\mathsf {aux},\mathsf {com},ch',\mathsf {rsp}' )$ with $ch \not = ch'$ and where $\mathsf {aux} = Setup(\mathsf {seed})$ for some seed value $\mathsf {seed}$ (not necessarily known to the extractor) one can efficiently extract a witness w such that $(x,w) \in R$.

• Special honest-verifier zero-knowledge. There exists a PPT simulator $\mathcal {S}$ that on input x, a random seed value $\mathsf {seed}$ and a random challenge ch outputs a transcript $(x,\mathsf {aux},\mathsf {com},ch,\mathsf {rsp})$ with $\mathsf {aux} =$ Setup$(\mathsf {seed})$ that is computationally indistinguishable from the probability distribution of transcripts of honest executions of the protocol on input (x, w) for some w such that $(x,w) \in R$, conditioned on the auxiliary information being equal to $\mathsf {aux}$ and the challenge being equal to ch.

4 Proving Knowledge of a Solution to a System of Quadratic Equations

Two zero-knowledge proofs to prove knowledge of a solution of a system of multivariate quadratic equations over a finite field $\mathbb {F}_q$ were proposed by Sakumoto et al. [32]. The first proof is a 3-round protocol which has soundness error $\frac{2}{3}$, while the second proof is a 5-round protocol with soundness error $\frac{1}{2}+\frac{1}{2q}$, where q is the size of the finite field over which the system of polynomials is defined. The MQDSS [13] signature scheme is obtained by applying the Fiat-Shamir transform to the 5-round protocol of Sakumoto et al. Because the soundness error of $\frac{1}{2}+\frac{1}{2q}$ is rather big, and because the Fiat-Shamir transformation does not tightly preserve security for 5-round protocols [23] a large number (e.g. 184 for the NIST security level I parameter set) of parallel rounds is required to obtain a secure signature scheme.

Fig. 2.

The structure of a sigma protocol with trusted setup.

In this section, we present a sigma protocol with helper to prove knowledge of a solution of a system of multivariate quadratic equations. The scheme improves the knowledge error to only 1/q, but this comes at the cost of having an honest party that helps the prover and the verifier in their execution of the protocol. Similar to the schemes of Sakumoto et al. the new protocol relies on the fact that if $\mathcal {F} : \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ is a multivariate quadratic map of m polynomials in n variables, then the polar form of $\mathcal {F}$, which is defined as

(1)

is linear in both $\mathbf {x}$ and $\mathbf {y}$.

To prove knowledge of a secret $\mathbf {s}$ such that $\mathcal {F}(\mathbf {s}) = \mathbf {v}$ the protocol goes as follows: During the first phase the helper picks a random vector $\mathbf {r_0}$ and commits to linear secret sharings $\mathbf {t} + \mathbf {t}_c = c\mathbf {r}_0, \mathbf {e} + \mathbf {e}_c = c\mathcal {F}(\mathbf {r}_0)$ for each $c \in \mathbb {F}_q$. These commitments are public auxiliary information which the helper sends to the verifier. The helper also sends the $\mathsf {seed}$ that he used to generate his randomness to the prover. Then, the prover publishes the masked secret $\mathbf {r}_1 = \mathbf {s} - \mathbf {r}_0$ and commits to the value of $\mathbf {e} + \mathcal {G}(\mathbf {r}_1,\mathbf {t})$. Finally the verifier challenges the prover to reveal $\mathbf {e}_\alpha$ and $\mathbf {t}_\alpha$ for a random choice of $\alpha \in \mathbb {F}_q$ and checks whether the following equation, which is equivalent to Eq. 1, holds.

$$\begin{aligned} \mathbf {e} + \mathcal {G}(\mathbf {r}_1,\mathbf {t}) = c \left( \mathcal {F}(\mathbf {s}) - \mathcal {F}(\mathbf {r}_1) \right) - \mathbf {e}_c - \mathcal {G}(\mathbf {r}_1,\mathbf {t}_c)\, , \quad \forall c \in \mathbb {F}_q\, \end{aligned}$$

(2)

A more detailed version of the protocol is displayed in Fig. 3.

Theorem 1

Suppose the used commitment scheme is computationally binding and computationally hiding, then the protocol of Fig. 3 is a sigma protocol with trusted setup as in Definition 3 with challenge space $\mathbb {F}_q$.

Proof

We prove completeness, 2-special soundness and special honest-verifier zero knowledge separately:

Completeness: The fact that in a honest execution of the protocol $\mathbf {x} = \mathbf {e}+\mathcal {G}(\mathbf {r}_1,\mathbf {t})$ follows from Eq. 2, so completeness follows immediately.

2-Special Soundness: Suppose an extractor is given two transcripts $(\mathsf {aux},\mathsf {com},\alpha ,(\mathsf {r},\mathsf {r}_\alpha ,\mathbf {r}_1,\mathbf {e}_\alpha ,\mathbf {t}_\alpha ))$, $(\mathsf {aux},\mathsf {com},\alpha ,(\mathsf {r}',\mathsf {r}_\alpha ',\mathbf {r}_1',\mathbf {e}_{\alpha '},\mathbf {t}_{\alpha '}))$ with $\alpha \not = \alpha '$ that are accepted by the verifier and such that $\mathsf {aux} =$ Setup$(\mathsf {seed})$ (for some $\mathsf {seed}$ value unknown to the extractor). Then we show how to extract a witness $\mathbf {s}$ such that $\mathcal {P}(\mathbf {s}) = \mathbf {v}$ if the binding of the commitments does not fail.

Let and , then the verifier only accepts if we have $\mathsf {com} = \mathsf {Com}(\mathsf {r},\mathbf {r}_1,\mathbf {x}) = \mathsf {Com}(\mathsf {r}',\mathbf {r}_1',\mathbf {x'})$, so the binding property of $\mathsf {Com}$ implies that $\mathbf {r}_1 = \mathbf {r}_1'$ and $\mathbf {x} = \mathbf {x}'$.

Even though the extractor does not know $\mathbf {e},\mathbf {t},\mathbf {r}_0$ or the commitment random strings $\{\mathsf {r}_c \, | \, c \in \mathbb {F}_q \}$, the extractor still knows that

$$ \mathsf {aux} = \{ \mathsf {Com}(\tilde{\mathsf {r}}_c, (c\mathcal {F}(\mathbf {r}_0) - \mathbf {e} , c \mathbf {r}_0 - \mathbf {t}) ) \, | \, c \in \mathbb {F}_q \} $$

for some values of $\mathbf {e},\mathbf {t},\mathbf {r}_0$ and $\{\tilde{\mathsf {r}}_c \, | \, c \in \mathbb {F}_q \}$, because the helper computed $\mathsf {aux} =$ Setup$(\mathsf {seed})$ honestly.

The verifier only accepts both transcripts if $\mathsf {Com}(\tilde{\mathsf {r}}_\alpha , (\alpha \mathcal {F}(\mathbf {r}_0) - \mathbf {e} , \alpha \mathbf {r}_0 - \mathbf {t}) ) = \mathsf {Com}(\mathsf {r}_\alpha ,(\mathbf {e}_\alpha ,\mathbf {t}_\alpha ))$ and $\mathsf {Com}(\tilde{\mathsf {r}}_{\alpha '}, ({\alpha '}\mathcal {F}(\mathbf {r}_0) - \mathbf {e} , {\alpha '} \mathbf {r}_0 - \mathbf {t}) ) = \mathsf {Com}(\mathsf {r}_\alpha ',(\mathbf {e}_{\alpha '},\mathbf {t}_{\alpha '}))$, so the binding property of $\mathsf {Com}$ implies that

$$\begin{aligned} \alpha \mathcal {F}(\mathbf {r}_0) - \mathbf {e}&= \mathbf {e}_\alpha \, ,&\alpha \mathbf {r}_0 - \mathbf {t}&= \mathbf {t}_\alpha \, , \\ \alpha ' \mathcal {F}(\mathbf {r}_0) - \mathbf {e}&= \mathbf {e}_{\alpha '} \quad \quad \quad \text { and }&\alpha ' \mathbf {r}_0 - \mathbf {t}&= \mathbf {t}_{\alpha '} \, . \end{aligned}$$

Substituting this into $\mathbf {x} = \mathbf {x'}$ we get

$$ \alpha ( \mathbf {v} - \mathcal {F}(\mathbf {r}_1))+\mathbf {e}-\alpha \mathcal {F}(\mathbf {r}_0) - \mathcal {G}(\mathbf {r}_1,\alpha \mathbf {r}_0 - \mathbf {t}) = \alpha '( \mathbf {v} - \mathcal {F}(\mathbf {r}_1))+\mathbf {e}-\alpha '\mathcal {F}(\mathbf {r}_0) - \mathcal {G}(\mathbf {r}_1,\alpha ' \mathbf {r}_0 - \mathbf {t}) \, , $$

which simplifies to

$$\begin{aligned} (\alpha - \alpha ') \left( \mathcal {F}(\mathbf {r}_1) + \mathcal {F}(\mathbf {r}_0) + \mathcal {G}(\mathbf {r}_0,\mathbf {r_1}) - \mathbf {v} \right)&= \\ (\alpha - \alpha ') \left( \mathcal {F}(\mathbf {r}_0 + \mathbf {r}_1) - \mathbf {v}) \right)&= 0\, , \end{aligned}$$

so $\mathbf {r}_0 + \mathbf {r}_1 = \frac{\mathbf {t}_\alpha - \mathbf {t}_{\alpha '}}{\alpha - \alpha '} + \mathbf {r}_1$ is a solution to $\mathcal {F}(\mathbf {x}) = \mathbf {v}$. Notice that all the values on the right hand side of this equation are included in the 2 transcripts, so extracting the solution from the two transcripts is trivial.

Special Honest-Verifier Zero-Knowledge: Define a simulator $\mathcal {S}$, that on input $\mathbf {v}$, a random seed value $\mathsf {seed}$ and a random challenge $\alpha \in \mathbb {F}_q$ does the following things:

• 1. recompute $\mathsf {aux},\mathsf {r}_\alpha , \mathbf {e}_\alpha$ and $\mathbf {t}_\alpha$ from $\mathsf {seed}$.

• 2. pick a uniformly random vector $\mathbf {u}\in \mathbb {F}_q^n$.

• 3. compute $f_{\alpha ,\mathbf {e}_\alpha , \mathbf {t}_\alpha }(\mathbf {u})$, where .

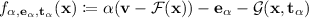• 4. produce commitment randomness $\mathsf {r}$ and a commitment $\mathsf {com}'$ to $(\mathbf {u},f_{\alpha ,\mathbf {e}_\alpha , \mathbf {t}_\alpha }(\mathbf {u}))\, .$

• 5. output $(\mathsf {aux},\mathsf {com}',\alpha ,(\mathsf {r},\mathsf {r}_\alpha ,\mathbf {u},\mathbf {e}_\alpha ,\mathbf {t}_\alpha ))$.

Then the Simulator is identical to an honest prover, except for step 2, where the honest prover sets $\mathbf {u}$ equal to $\mathbf {s} - \mathbf {r}_0$ rather than a uniformly random value. It is clear that $(\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\mathbf {u},\mathbf {e}_\alpha ,\mathbf {t}_\alpha )$ and $(\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\mathbf {s}-\mathbf {r}_0,\mathbf {e}_\alpha ,\mathbf {t}_\alpha )$ are both uniformly distributed in $\mathbb {F}_q \times \{0,1\}^{2\lambda } \times \left( \mathbb {F}_q^n \right) ^3$ and hence follow the same distribution. Since $\mathsf {com}$ and $\mathsf {com}_\alpha$ are completely determined by $(\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\mathbf {s}-\mathbf {r}_0,\mathbf {e}_\alpha ,\mathbf {t}_\alpha )$ it follows that $(\mathsf {com}_\alpha ,\mathsf {com}',\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\mathbf {u},\mathbf {e}_\alpha ,\mathbf {t}_\alpha )$ and $(\mathsf {com}_\alpha ,\mathsf {com},\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\mathbf {s}-\mathbf {r}_0,\mathbf {e}_\alpha ,\mathbf {t}_\alpha )$ also follow the same distribution. Finally, since the commitments $\mathsf {com}_{c\not = \alpha }$ are never opened, it follows from the hiding property of the commitment scheme with the standard hybrid argument that $(\mathsf {aux},\mathsf {com}',\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\mathbf {u},\mathbf {e}_\alpha ,\mathbf {t}_\alpha )$ and $(\mathsf {aux},\mathsf {com},\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\mathbf {s}-\mathbf {r}_0,\mathbf {e}_\alpha ,\mathbf {t}_\alpha )$ are computationally indistinguishable.

Fig. 3.

A sigma protocol with helper for proving knowledge of a solution to the MQ problem.

5 Proving Knowledge of a Solution to a (inhomogeneous) PKP Instance

In this section we give a Sigma protocol with helper with challenge space $\mathbb {F}_p$ to prove knowledge of a solution for an inhomogeneous PKP instance, i.e. given $\mathbf {A},\mathbf {v},\mathbf {t}$ our proof system proves knowledge of a permutation $\pi$ such that $\mathbf {A}\mathbf {v}_\pi = \mathbf {t}$. The soundness error of our proof is only 1/p, which is much better than the 5-round proof of Shamir, which has a soundness error of $\frac{1}{2}+\frac{1}{2p}$ [33], and Stern’s 3-round protocol, which has a soundness error of 2/3 [34].

To prove knowledge of a solution $\pi$ to the instance $(\mathbf {A},\mathbf {v},\mathbf {t})$ the protocol goes as follows: The helper picks a random vector $\mathbf {r} \in \mathbb {F}_p^n$, and a random permutation $\sigma \in S_n$, it then commits to $\mathbf {r} + c \mathbf {v}_\sigma$ for all values of $c \in \mathbb {F}_p$. The helper sends these commitments as public auxiliary information to the verifier, and he sends the seed that he used to generate his randomness to the prover. Then the prover sends $\rho = \pi \sigma ^{-1}$ to the verifier and commits to the value of $\mathbf {Ar}_{\pi \sigma ^{-1}}$. Finally, the verifier challenges the prover to reveal $\mathbf {x} = \mathbf {r}+\alpha \mathbf {v}_\sigma$ for a random choice of $\alpha$. Once the prover reveals $\mathbf {x}$ the verifier checks if $\mathbf {A}\mathbf {x}_{\rho } - \alpha \mathbf {t} = \mathbf {A}\left( \mathbf {r}_{\pi \sigma ^{-1}} + \alpha \mathbf {v}_\pi \right) - \alpha \mathbf {t} = \mathbf {Ar}_{\pi \sigma ^{-1}}$. For a more detailed description of the protocol we refer to Fig. 4.

Theorem 2

Suppose the used commitment scheme is computationally binding and computationally hiding, then the protocol of Fig. 4 is a sigma protocol with trusted setup as in Definition 3 with challenge space $\mathbb {F}_p$.

Proof

We prove completeness, 2-special soundness and special honest-verifier zero knowledge separately:

Completeness: In an honest execution of the protocol we have

$$\begin{aligned} \mathbf {y} = \mathbf {A}\mathbf {x}_{\rho } - \alpha \mathbf {t} = \mathbf {A}\left( \mathbf {r}_{\pi \sigma ^{-1}} + \alpha \mathbf {v}_\pi \right) - \alpha \mathbf {t}, \end{aligned}$$

so if $\pi$ is a solution to the PKP instance ($\mathbf {A},\mathbf {v}$,$\mathbf {t}$), then $\mathbf {A}\mathbf {v}_\pi = \mathbf {t}$, which means $\mathbf {y} = \mathbf {Ar}_{\pi \sigma ^{-1}}$ and hence the completeness follows from the completeness of the commitment scheme.

2-Special Soundness: Given two transcripts $(\mathsf {aux},\mathsf {com},\alpha ,(\mathsf {r},\mathsf {r}_\alpha ,\rho ,\mathbf {x}))$ and $(\mathsf {aux},\mathsf {com},\alpha ',(\mathsf {r}',\mathsf {r}_\alpha ',\rho ',\mathbf {x}'))$ with $\alpha \not = \alpha '$ that are accepted by the verifier and such that $\mathsf {aux} =\$Setup$(\mathsf {seed})$, for some value of $\mathsf {seed}$ (not necessarily known to the extractor). Then, if the binding of the commitment scheme does not fail (which, by assumption, happens with overwhelming probability), one can efficiently extract a witness $\pi$ such that $\mathbf {A}\mathbf {v}_\pi = \mathbf {t}$.

Let and , then the verifier only accepts if we have $\mathsf {com} = \mathsf {Com}(\mathsf {r},(\rho ,\mathbf {y})) = \mathsf {Com}(\mathsf {r}',(\rho ',\mathbf {y'}))$, so the binding property of $\mathsf {Com}$ implies that $\rho = \rho '$ and $\mathbf {y} = \mathbf {y}'$.

Note that even though the extractor does not know $\mathbf {r}, \sigma$ or any of the commitment randomness strings $\mathsf {r}_c$, he still knows that $\mathsf {aux}$ is of the form

$$\begin{aligned} \mathsf {aux} = \left\{ \mathsf {Com}(\mathsf {r_c},\mathbf {r} + c \mathbf {v}_{\sigma } ) \, | \, c \in \mathbb {F}_q \right\} \end{aligned}$$

for some values of $\mathbf {r},\sigma$ and $\{ \mathsf {r_c} \}_{c \in \mathbb {F}_q }$, because the helper computed $\mathsf {aux}\, =\,$Setup$(\mathsf {seed})$ honestly.

The verifier only accepts both transcripts if $\mathsf {Com}(\mathsf {r_\alpha },\mathbf {r} + \alpha \mathbf {v}_{\sigma } ) = \mathsf {Com}(\mathsf {r}_\alpha ,\mathbf {x})$ and $\mathsf {Com}(\mathsf {r_{\alpha '}},\mathbf {r} + \alpha ' \mathbf {v}_{\sigma } ) = \mathsf {Com}(\mathsf {r}_{\alpha '},\mathbf {x}')$, so the binding property of $\mathsf {Com}$ implies that $\mathbf {x} = \mathbf {r} + \alpha \mathbf {v}_{\sigma }$, and that $\mathbf {x}' = \mathbf {r} + \alpha ' \mathbf {v}_\sigma$.

Putting everything together we get

$$ \mathbf {A}\left( \mathbf {r}_\rho + \alpha \mathbf {v}_{\rho \sigma } \right) - \alpha \mathbf {t} = \mathbf {A}\left( \mathbf {r}_\rho + \alpha ' \mathbf {v}_{\rho \sigma } \right) - \alpha ' \mathbf {t} $$

which simplifies to

$$\begin{aligned} (\alpha - \alpha ') \left( \mathbf {A} \mathbf {v}_{\rho \sigma } - \mathbf {t} \right) = 0, \end{aligned}$$

so $\rho \sigma$ is a solution to the instance of the permuted kernel problem. The value of $\rho$ is known to the extractor because it is included in the transcripts, and the value of $\sigma$ can be deduced from $\alpha ,\alpha ',\mathbf {x},\mathbf {x'}$ and $\mathbf {v}$, because $\mathbf {x}-\mathbf {x}' = (\alpha - \alpha ')\mathbf {v}_\sigma$. (If the entries of $\mathbf {v}$ are not unique, multiple values of $\sigma$ are possible, but they will all give valid solutions to the PKP problem.)

Special Honest-Verifier Zero Knowledge: Define a simulator $\mathcal {S}$, that on input $\mathbf {A}, \mathbf {v}$, a random seed value $\mathsf {seed}$ and a random challenge $\alpha \in \mathbb {F}_p$ does the following things:

• 1. recompute $\mathsf {aux},\mathsf {r}_\alpha$ and $\mathbf {x} = \mathbf {r} + \alpha \mathbf {v}_\sigma$ from $\mathsf {seed}$.

• 2. pick a uniformly random permutation $\tau \in S_n$.

• 3. produce commitment randomness $\mathsf {r}$, and a commitment $\mathsf {com}'$ to $(\tau ,\mathbf {Ax}_\tau )$.

• 4. output $(\mathsf {aux},\mathsf {com}',\alpha ,(\mathsf {r},\mathsf {r}_\alpha ,\tau ,\mathbf {Ax}_\tau ))$.

Then the Simulator is identical to an honest prover, except for step 2, where the honest prover sets $\rho$ equal to $\pi \sigma ^{-1}$ rather than a uniformly random value. It is clear that $(\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\tau ,\mathbf {Ax}_\tau )$ and $(\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\rho ,\mathbf {Ax}_\rho )$ are both uniformly distributed in $\mathbb {F}_q \times \{0,1\}^{2\lambda } \times S_n \times \mathbb {F}_q^n$ and hence follow the same distribution. Since $\mathsf {com}$ and $\mathsf {com}_\alpha$ are completely determined by $(\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\rho ,\mathbf {Ax}_\rho )$ it follows that $(\mathsf {com}_\alpha ,\mathsf {com}',\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\tau ,\mathbf {Ax}_\tau )$ and $(\mathsf {com}_\alpha ,\mathsf {com},\alpha ,\mathsf {r},\mathsf {r}_\alpha ,\rho ,\mathbf {Ax}_\rho )$ also follow the same distribution. Finally, since the commitments $\mathsf {com}_{c\not = \alpha }$ are never opened, it follows from the hiding property of the commitment scheme and the standard hybrid argument that $(\mathsf {aux},\mathsf {com}',\alpha ,(\mathsf {r},\mathsf {r}_\alpha ,\tau ,\mathbf {Ax}_\tau ))$ and $(\mathsf {aux},\mathsf {com},\alpha ,(\mathsf {r},\mathsf {r}_\alpha ,\rho ,\mathbf {Ax}_\rho ))$ are computationally indistinguishable.

6 Removing the Helper

In this section, we show how to transform a Sigma protocol with helper into a standard zero-knowledge proof of knowledge (without helper). We use the same “Cut-and-choose” approach that was used by Katz et al. to get rid of the preprocessing phase [24].

The idea is to let the prover pick k seeds $\mathsf {seed}_1,\cdots ,\mathsf {seed}_k$ and generate k sets of auxiliary information $\mathsf {aux}_i =$ Setup $(\mathsf {seed}_i)$ which the prover sends to the verifier, along with the first messages of the protocol $\mathsf {com}_i = P_1(x,w,\mathsf {seed}_i)$ for all i from 1 to k. The verifier then picks a random index I and a single challenge $ch \in \mathcal {C}$ and sends this to the prover. The prover then sends $\mathsf {seed}_i$ for $i \not = I$ as well as a response $\mathsf {rsp}$ to the challenge at index I. Using the seeds, the verifier then checks if all the auxiliary information $\mathsf {aux}_{i \not = I}$ was generated properly and checks if $\mathsf {rsp}$ is a correct response to the challenge at index I. The details of the protocol are displayed in Fig. 5. We prove that this is a honest-verifier zero knowledge protocol with soundness error $\max (\frac{1}{k},\frac{1}{|\mathcal {C}|})$.

Theorem 3

Let (Setup, $P_1, P_2, V$) be a sigma protocol with helper and challenge space $\mathcal {C}$, if the used commitment scheme is hiding, then the protocol of Fig. 5 is an honest-verifier zero knowledge proof of knowledge with challenge space $\{1,\cdots ,k\} \times \mathcal {C}$ and $\max (k,|\mathcal {C}|)+1$-special soundness (and hence it has soundness error $\max (\frac{1}{k},\frac{1}{|\mathcal {C}|})$).

Proof

We prove completeness, special soundness and special honest-verifier zero knowledge separately.

Fig. 4.

A sigma protocol with helper for proving knowledge of a solution to the inhomogeneous PKP problem.

Completeness: Follows immediately from the completeness of the underlying Sigma protocol with trusted setup.

$(\max (k,|\mathcal {C}|)+1)$ -special Soundness: If there are $\max (k,|\mathcal {C}|)+1$ valid transcripts then there are at least two valid transcripts with different values of I, which implies that all k setups were done honestly. The pigeon hole principle says there are at least two accepted transcripts with the same value of I, but different ch, so the extractor can use special soundness of the underlying Sigma protocol with trusted setup to extract a witness w.

Special Honest-Verifier Zero-Knowledge: On input (I, ch), the simulator generates all the setups honestly, and commits to random dummy values to create the commitments $\mathsf {com}_{i \not = I}$. The simulator then uses the simulator of the underlying sigma protocol with trusted setup to simulate the transcript at index I. Indistinguishability follows from the hiding property of the commitment scheme and the honest-verifier zero-knowledge property of the underlying sigma protocol with trusted setup.

Fig. 5.

A zero knowledge proof (without trusted setup) from a Sigma protocol with trusted setup.

7 Optimizations

In this section, we describe optimizations for the MQ and PKP zero-knowledge proofs with trusted setup, as well as for the transformation that removes the trusted setup. The first two optimizations are applications of standard techniques and the last optimization was proposed by Katz et al. [24], and proven secure by Baum and Nof [5].

Hashing and Merkle Trees. In both the MQ proof and the PKP proof the auxiliary information consists of q commitments $\mathsf {com}_i$ for $i \in \mathbb {F}_q$, but only one of these commitments, $\mathsf {com}_\alpha$, is opened in each honest execution of the protocol. To reduce the communication cost (and hence the signature size after the Fiat-Shamir transform) we can build a Merkle tree on these commitments and only send the root of the tree. Then the prover includes in his response the $\left\lceil \log _2(q) \right\rceil$ nodes of the Merkle tree required to reconstruct the root of the Merkle tree.

When we are doing the transformation to get rid of the trusted party, we do not have to send all the k roots separately. Instead, it suffices to send a hash of all the roots to the verifier. Then, during verification, the verifier recomputes all the roots (either from $\mathsf {seed}_i$ if $i \not = I$, or through the verification algorithm if $i = I$) and hashes the roots to verify that they were correct.

The prover sends k commitments $\mathsf {com}_i$, but only the commitment $\mathsf {com}_I$ is used. Therefore, similar to the first optimization, the prover can build a Merkle tree on his commitments and send the root to the verifier. Then, he includes $\mathsf {com}_I$ and some nodes of the Merkle tree in his response, so the verifier can recompute the root and authenticate $\mathsf {com}_I$.

Sending Fewer Seeds. The prover chooses k seed values and sends all but one of these seeds to the verifier. We can use a tree strategy to reduce the communication cost. The prover constructs a binary tree of seed values. First, he picks the value of the root at random. Then, the value of each internal node is used to seed a PRNG which generates the values of its two children. In the end, the leaf nodes act as the $\mathsf {seed}_i$ values. Now, instead of sending $k-1$ seed values, the prover can send $\left\lceil \log _2(k) \right\rceil$ node values in the tree and the prover can recompute the $k-1$ seeds himself (but not $\mathsf {seed}_I$).

Smaller Challenge Space. For some applications, the finite field $\mathbb {F}_q$ is so large that it would not be practical to compute Merkle trees of size q. In that case, we can simply reduce the challenge space to some subset of $\mathbb {F}_q$ of size $q' \le q$. The soundness error of the scheme then becomes $1/q'$ instead of 1/q.

Beating Parallel Repetition. The basic scheme has soundness error $\frac{1}{q'}$, so to reach a soundness error of $2^{-\lambda }$ we would need to perform $r = \left\lceil \frac{\lambda }{log_2(q')} \right\rceil$ parallel executions of the protocol. The optimization of Katz et al. [24] gives a more efficient approach: The idea is that instead of letting the verifier choose 1 out of k setups to execute, we now let him choose $\tau$ out of M setups to execute. Now suppose a cheating prover does $e \le \tau$ out of the M setups incorrectly. Since he cannot produce $\mathsf {seed}_i$ values for the cheated setups, he can only convince the verifier if all the setups in which he cheated end up being executed. This happens with probability $\left( {\begin{array}{c}M-e\\ \tau -e\end{array}}\right) \cdot \left( {\begin{array}{c}M\\ \tau \end{array}}\right) ^{-1}$. Then, the prover still needs to generate responses for $\tau - e$ honest setups, which he can do with probability at most $\left( \frac{1}{q'} \right) ^{\tau - e}$. Therefore the soundness error of the adapted scheme is bounded by

$$ \max _{0\le e \le \tau } \frac{\left( {\begin{array}{c}M-e\\ \tau -e\end{array}}\right) }{\left( {\begin{array}{c}M\\ \tau \end{array}}\right) q'^{\tau -e}}. $$

For a more formal proof we refer to [5].

Example 1

Suppose $q = 128$, then without the optimization, we would need 19 parallel executions of the basic protocol to reach a soundness error of $2^{-128}$, which amounts to $19*128$ = 2432 setups and 19 executions of the protocol. With the optimization, it turns out that 916 setups and 20 executions are sufficient. So, in this case, the optimization reduces the number of setups by a factor 2.6 at the cost of a single extra execution.

8 Signature Schemes

In this section, we apply the Fiat-Shamir transformation to the zero-knowledge proofs for MQ and PKP (after applying the transformation of Sect. 6) to obtain 2 signature schemes. We call these schemes the “MUltivariate quaDratic FIat-SHamir” scheme (MUDFISH) and the “ShUffled Solution to Homogeneous linear SYstem FIat-SHamir” scheme (SUSHSYFISH). First, we observe that the recent results on Post-Quantum Fiat-Shamir by Don et al. [15] apply and thus that our signature scheme are provably secure in the QROM (with non-tight reductions). We then give some generic optimizations for the signature scheme and parameter choices for MUDFISH and SUSHSYFISH. We provide a proof-of-concept implementation to show that MUDFISH and SUSHSYFISH are more efficient than existing signature schemes based on the MQ and PKP assumptions (i.e. MQDSS and PKP-DSS respectively) in terms of signature size and speed (on the NIST reference platform).

8.1 Fiat-Shamir Transform

The Fiat-Shamir transform allows us to convert the sigma protocols for MQ and PKP into signatures. The idea is that instead of letting the verifier choose the challenge at random, we derive the challenge deterministically from the commitment and the message that we want to sign. Concretely, to sign a message m, the signer executes the first part of the identification scheme to produce a commitment $\mathsf {com}$, then he derives a challenge ch by applying a random oracle to $\mathsf {com}|m$. Finally, the signer completes his part of the identification scheme to produce the response $\mathsf {rsp}$. The signature is then simply $(\mathsf {com},\mathsf {resp})$. To verify a signature $(\mathsf {com},\mathsf {resp})$ for a message m, the verifier simply computes ch by querying the random oracle at $\mathsf {com}|m$, and then he accepts the signature if and only if $(\mathsf {com},ch,\mathsf {resp})$ is a valid transcript of the identification protocol. Using the results of [15], it is straightforward to prove that MUDFISH and SUSHSYFISH are strongly unforgeable in the QROM.

Theorem 4

Assume that a hash function modeled as a Quantum Random Oracle is used as commitment scheme and that a Quantum random oracle model is used as PRG, then the non-optimized variants of MUDFISH and SUSHSYFISH signature schemes are strongly existentially unforgeable in the QROM.

Proof

(The argument is similar to the proof for the FS variant of Picnic, see Sect. 6.1 of [15].) First, we prove that the Setup function is collapsing: If we model the commitment functions as Quantum random oracles, then they are collapsing [36]. In both the MUDFISH and SUSHYFISH schemes, the Setup algorithm consists of expanding a randomness seed, computing some values based on the output of the PRG, and committing to them. In both cases, the PRG output is more than three times longer than the input, so this function is injective with overwhelming probability. Also, it is easily verified that the computing of the values from the output of the PRG is injective. Since the concurrent composition of collapsing functions is collapsing [16] and composing a collapsing function with an injective function preserves collapsingness, it follows that the entire Setup algorithm is collapsing.

Since the responses of the sigma protocol only consist of openings of commitments (which are preimages to $\mathsf {Com}$), and preimages to the Setup function it follows from the collapsingness of $\mathsf {Com}$ and Setup that the MUDFISH and SUSHSYFISH sigma protocols have quantum computationally unique responses. Moreover, the protocols have k-special soundness, so theorem 25 of [15] says that the non-optimized versions of MUDFISH and SUSHSYFISH are quantum computational proofs of knowledge. Together with their theorem 22, this implies that MUDFISH and SUSHSYFISH are sEUF-CMA secure.

8.2 MUDFISH

Parameter Choices. For ease of implementation, we have chosen to use the same finite field $\mathbb {F}_4$ for all the parameter sets. To have a fair comparison with the MQDSS scheme, and to avoid the technicalities of choosing secure parameters for the MQ problem, we use the parameters proposed in the MQDSS submission to the NIST PQC standardization project. These parameter choices for the MQ problem are displayed in Table 1.

We still need to pick parameters for the ZK proof (i.e. $\tau$, the number of executions and M, the number of setups). The choice of $\tau$ and M allows for a trade-off: If one is willing to increase $\tau$, which mainly impacts signature size, then one can decrease M, which mainly impacts signing and verification time.

Table 1. Parameters for the MQ problem used by MUDFISH, and the complexity of solving them with the Crossbred algorithm. The parameter sets and the complexity estimates are taken from Table 8.4 of [14].

Table 2. Parameters for MUDFISH, key and signature sizes and performance measurements (average over 1000 signatures).

Implementation Results. The signing and verification algorithms require to do a lot of setups and executions of the ZK proof on independent data. We take advantage of this by fitting data from 64 independent rounds into one word. Hence, we can do 64 setups or 64 executions of the protocol in parallel on a 64-bit machine. Since the MUDFISH algorithm is inherently constant-time, there was no performance penalty for making the implementation constant-time. Our proof-of-concept implementation uses SHAKE256 as hash function and to expand randomness. The performance results of the implementation are displayed in Table 2. We see that MUDFISH is more efficient than MQDSS: Comparing the parameter sets that achieve NIST security level I, the signatures of MUDFISH are only half as big as those of MQDSS. At the same time, the signing and verification speed of our proof-of-concept implementation of MUDFISH is a factor 2.5 and 1.8 faster than those of the optimized implementation of MQDSS submitted to the second round of the NIST PQC standardization project. We leave the task of making an AVX2 optimized implementation of MUDFISH and comparing its performance to the AVX2 optimized implementation of MQDSS for future work.

8.3 SUSHSYFISH

Parameter Choices. An advantage of building cryptography on PKP is that the best attack algorithms are quite simple and easy to analyze. We use the PKP parameter sets proposed by Faugère et al. [10] to achieve the NIST security levels 1, 3 and 5. The choice of the remaining parameters $q',\tau$ and M allows for a trade-off between signature size and signing and verification speed. For each of the NIST PQC security levels 1, 3 and 5 we propose a parameter set which aims to be fast $(q' = 4)$, a parameter sets which aims to have small signatures $q' = 128$ and an intermediate parameter set $q'=16$.

Table 3. Parameters for SUSHSYFISH, key and signature sizes and performance measurements (average over 1000 signatures).

Making the Implementation Constant-Time. Most of the SUSHSYFISH algorithm is inherently constant-time, except for some operations involving permutations such as composing permutations, applying a permutation to a vector and sampling random permutations. Naive implementations of these operations involve accessing memory at secret indices, which could make the implementation vulnerable to cache timing attacks. In our implementation, we leverage the djbsort constant-time sorting software library [7] to do these operations in constant-time. For example, to apply a permutation $\pi \in S_n$ to a vector $\mathbf {v} \in \mathbb {F}_p^n$ we first construct a list of integers $x_i$, such that the high-order bits of $x_i$ correspond to $\pi _i$, and such that the low-order bits of $x_i$ correspond to $v_i$. We then call the djbsort library to sort this list of integers in constant-time, and we extract the low-order bits from the sorted list, which correspond to $\mathbf {v}_\pi$. Since the performance bottleneck of SUSHSYFISH is hashing, a slight increase in the cost of the operations involving permutations has a negligible effect on the total performance of the signature scheme.

Implementation Results. Our implementation uses SHAKE256 as hash function and to expand randomness. The signing and verification times are dominated by the use of SHAKE256, and hence there is a lot of potential for speedups by choosing different symmetric primitives or by parallelizing independent calls of the SHAKE function. The key and signature sizes and the performance measurements for the 9 proposed parameter sets are displayed in Table 3. We see that SUSHSYFISH has smaller signatures than PKP-DSS while being only slightly slower. For NIST PQC security level I, the performance of the “Fast” SUSHSYFISH parameter set is the close to the performance of PKP-DSS: Signatures are $12\%$ smaller, while with the current implementations signing and verification are $44\%$ and $80\%$ slower respectively. The “Middle” and “Fast” parameter sets offer more compact signatures at the cost of slower signing and verification.

Comparison to Previous Works. In this section, we compare the MUDFISH and SUSHSYFISH non-interactive zero-knowledge proof systems to existing methods for proving knowledge of a solution to the MQ or PKP problem. We compare to MQDSS [14] and PKP-DSS [10] that are dedicated proof systems for MQ and PKP respectively, and we compare to Ligero [2] and Aurora [6], which are generic ZK-proof systems capable of proving knowledge of a witness for any NP statement. To compare with generic ZK systems we construct a verification circuit with a minimal number of multiplication gates (since linear gates are for free). For the MQ problem, the verification circuit just evaluates the multivariate system, which requires $n(n+1)/2$ secret multiplications. Using a permutation network [37], we can encode a permutation as a sequence of bits, where each bit controls if a switch in the network is active or not. With this representation, we can verify if a permutation is a solution of a PKP problem with a small number of non-linear gates. If the permutation network has k switches the verification can be done with 2k non-linear gates; k multiplications for applying the k switches and an additional k multiplications to verify that the witness consists of bits. Tables 4 and 5 show that our proof systems have significantly lower proof sizes compared to existing solutions.

Table 4. Comparison of proof sizes of various ZK-proof systems for proving knowledge of a solution of an MQ instance. For the MQDSS system the number of iterations is 315, 478 and 637 respectively. At security level $\lambda$, the hashes and commitments are $2\lambda$ bits long. The parameter choices do not compensate for the non-tightness of the Fiat-Shamir transform, instead they only guarantee $\lambda$ bits of soundness for the interactive version of the protocols.

Table 5. Comparison of proof sizes of various ZK-proof systems for proving knowledge of a solution of a PKP instance.

9 Zero Knowledge Proofs for Lattice Statements

Stern’s zero-knowledge protocol has been used extensively in lattice-based cryptography because it can be used to prove a wide variety of statements. It has been used to construct, among other things, identity-based identification schemes, group signatures (with verifier local revocation), logarithmic size ring signatures and group encryption [25,26,27,28]. The way this works is to transform the lattice statement into an instance of the IPKP problem, in such a way that from a solution to the IPKP instance one can efficiently derive a witness for the lattice statement and conversely, that given a witness for the statement one can efficiently compute a solution to the IPKP instance. Then, one just uses Stern’s protocol to prove knowledge of a solution to the IPKP instance, which is equivalent to proving knowledge of a witness of the lattice statement. However, it is often the case that witnesses for the lattice statement correspond to IPKP solutions that lie in a certain subgroup $H \subset S_n$. If this is the case, then the prover needs to prove that he knows a solution $\pi$ to the IPKP instance subject to $\pi \in H$. Luckily, Stern’s protocol (and as we will see also our IPKP proof) can be easily adapted to prove knowledge of an IPKP solution that lies in any subgroup H (assuming one can sample uniformly from H and efficiently verify membership of H).

In the remainder of this section, we prove that our IPKP proof can handle proving that a solution lies in a subgroup $H \subset S_n$, which implies that we can improve all the applications of Sterns protocol by replacing Stern’s proof by our more efficient protocol. Then, we will focus on proving knowledge of a solution to the inhomogeneous SIS problem. We briefly illustrate how the ISIS problem can be embedded into IPKP with the decomposition-extension technique of Ling et al. [28]. Then, we compare the efficiency of our IPKP proof against the efficiency of Stern’s protocol for proving knowledge of a solution of an ISIS problem. Finally, we compare our approach to some recent works that use different techniques to prove knowledge of a solution of an ISIS instance.

9.1 Generalizing to Subgroup IPKP

It is trivial to generalize the protocol of Sect. 5 to prove knowledge of a solution $\pi$ of an IPKP instance with the additional constraint that $\pi$ lies in a subgroup $H \subset S_n$, assuming that one can efficiently sample uniformly from H and efficiently test if a group element is a member of H. The only modification required is that the prover now samples $\sigma$ from H instead of from $S_n$ and that the verifier checks that $\rho$ lies in H.

Theorem 5

The modified version of the protocol for IPKP of Sect. 5 is a sigma protocol with helper as in Definition 3 with challenge space $\mathbb {F}_q$.

Proof

Completeness. If $\pi$ is a solution of the IPKP instance, then since the unmodified protocol is complete, the verifier will accept a transcript unless the additional check that $\rho$ lies in H fails. However, if $\pi \in H$, then also $\rho = \pi \sigma ^{-1}$ lies in H, because $\sigma$ is sampled from H. Therefore, the verifier will accept with probability 1 if $\pi$ is a solution to the SIPKP problem.

2-Special Soundness. The extractor from the security proof of the IPKP proof system extracts $\rho \sigma$, which is a solution to the IPKP problem. We only need to show that $\rho \sigma \in H$. The verifier only accepts if $\rho \in H$, and we know that $\sigma \in H$, because it is sampled from H by the honest helper. Therefore the extracted solution to the IPKP solution is also a solution to the SIPKP problem.

Honest-Verifier Zero-Knowledge. The proof is the same as in the proof of Theorem 2, except that the simulator samples $\tau$ uniformly from H instead of from $S_n$.

Remark 1

The proof of Theorem 2 does not use any specific properties of the action of $S_n$ apart from the property that $\mathbf {v}_\sigma + \mathbf {w}_\sigma = (\mathbf {v}+\mathbf {w})_\sigma$, which is required for correctness. Therefore, it is clear that the proof system generalizes to any representation of a finite group G on $\mathbb {F}_q^n$. In particular, we can also consider the group of signed permutations with it natural representation on $\mathbb {F}_q^n$.

9.2 Embedding ISIS into IPKP

To illustrate the embedding first suppose that $(\mathbf {A},\mathbf {t}) \in \mathbb {F}_q^{m \times n} \times \mathbb {F}_q^m$ is an instance of the ISIS problem where a solution is a vector $\mathbf {s} \in \mathbb {F}_q^n$ such that $\mathbf {A}\mathbf {s} = \mathbf {t}$ and the coefficients of $\mathbf {s}$ are 0 or 1. In that case we define the extended matrix $\mathbf {A}' = \begin{pmatrix} \mathbf {A} \mathbf {0}_{m \times n} \end{pmatrix}$ and a vector $\mathbf {v} \in \mathbb {F}_q$ whose first n entries are 1 and whose last n entries are equal to 0. Then finding a solution to the ISIS instance $(\mathbf {A},\mathbf {t})$ is equivalent to finding a solution to the IPKP instance $(\mathbf {A'},\mathbf {v},\mathbf {t})$: Given a solution $\mathbf {s}$ to the ISIS instance it is trivial to find a permutation $\pi$ such that the first half of $\mathbf {v}_\pi$ equals $\mathbf {s}$, which is then a solution to the IPKP instance. Conversely, if $\pi$ is a solution to the IPKP instance, then the first half of $\mathbf {v}_\pi$ is a solution to the ISIS instance. Therefore, proving knowledge of $\pi$ is equivalent to proving knowledge of $\mathbf {s}$.

To improve the efficiency of the proof system we can restrict the IPKP solutions to the subgroup of $S_{2n}$ generated by the transpositions $(i \quad i+n)$ for $0 \le i < n$. This approach reduces the proof size because elements of the subgroup can be represented with only n bits, rather than the $\log _2((2n) !) \approx 2n \log _2 (2n)$ bits required to represent an arbitrary permutation of 2n elements.

More generally, if the coefficients of $\mathbf {s}$ are required to lie in a range of size B, one can use the decomposition-extension technique [28] to transform an instance of the ISIS problem into an equivalent instance of the IPKP with a matrix $\mathbf {A'}$ with $2n \lceil \log _{2} B \rceil$ columns [28]. Moreover, we can restrict to a subgroup of size $2^{2 \lceil \log _{2} B \rceil }$ to reduce the proof size.

9.3 Concrete Examples and Comparison to Previous Works

To compare the concrete efficiency of our work with the recent work of Bootle et al. [11] and Baum and Nof [5] we apply our proof system to the following two SIS parameters sets:

• 1. $q \approx 2^{32}, m = 512, n = 2048, \beta = 1$: This is the parameter set considered by Bootle et al [11]. This parameter set is relevant for FHE schemes and group signature schemes.

• 2. $q \approx 2^{61}, m = 1024, n = 4092, \text { binary solution}$: This is one of the parameter sets considered by Baum and Nof. [5], they claim that this parameter set is relevant for applications such as somewhat homomorphic encryption.

Let $\mathbf {A} \in \mathbb {F}_q^{512 \times 2048}$ be an instance of the SIS problem from the first parameter set, define the matrix $\mathbf {A'} = \begin{pmatrix} \mathbf {A}&\mathbf {0}_{512 \times 2048} \end{pmatrix}$ and let $\mathbf {v} \in \{0,1\}^{4096}$ be the vector whose first 2048 entries are equal to 1 and whose remaining 2048 entries are equal to 0. Then finding a solution to the SIS instance $\mathbf {A}$ is equivalent to finding a solution to the generalized PKP instance that asks to find a signed permutation $\pi$ such that $\mathbf {A}' \mathbf {v}_\pi = \mathbf {0}$. Moreover, this still holds if we restrict the solutions of the PKP problem to lie in the subgroup H generated by sign swaps and the transpositions $\{ (i \quad i+2048 ) | \text { for } i \text { from } 1 \text { to } 2048 \}$. This subgroup has $8^{2048}$ elements, and we can represent each element by $3*2048$ bits.

Therefore, to prove knowledge of a short integer solution it suffices to prove knowledge of a signed permutation $\pi$ in H such that $\mathbf {A}'\mathbf {v}_\pi = 0$. We choose parameters $\tau = 14, M=4040, q' = 2^{10}$ to achieve a soundness error less than $2^{-128}$. The proof size is dominated by the vectors and signed permutations in the proof, of which there is one per execution. A vector can be represented with $4069 \log _2 (q)$ bits and each permutation in H can be represented with $2048 * 3$ bits. Therefore the total proof size is roughly equal to

$$ 14 \cdot (4069 \cdot 32 + 2048 \cdot 3 ) \text { bits } = 233 \text { KB}. $$

Observe that (in a field of characteristic $>\!2$) if $\overline{1}$ is the vector with a 1 in each entry, then

$$ A\mathbf {s} = \mathbf {t} \iff A(2\mathbf {s}-\overline{\mathbf {1}}) = 2\mathbf {t} + A\overline{\mathbf {1}}, $$

which means that binary SIS is equivalent to a SIS instance where the entries of $\mathbf {s}$ are restricted to $\{-1,1\}$. Therefore, for the second parameter set, we can embed the binary SIS problem into a generalized PKP problem of the form $\mathbf {A} \overline{\mathbf {1}}_\pi = \mathbf {t}'$ with $\pi$ in the group with $2^{4092}$ elements generated by sign flips. If we again pick $\tau = 14, M=4040, q' = 2^{10}$ to achieve a soundness error less than $2^{-128}$ the total proof size is approximately

$$ 14 \cdot ( 4092 \cdot 61 + 4092 ) \text { bits } = \text { 444 KB } $$

Comparison to Previous Works. Table 6 makes a comparison of the proof sizes of our proof system with that of previous works. First of all, an application of Stern’s protocol to the generalized PKP problems derived from the two parameter sets results in proofs of 2.3 MB and 4.3 MB respectively. This is an order of magnitude larger than our proof system for both parameter sets. The work of Bootle et al. [11] uses algebraic techniques rather than combinatorial ones and achieves a proof size of 384 KB for the first parameter set, which is $65\%$ larger than our proofs.

The proof system of Baum and Nof uses MPC-in-the-head techniques and has a proof size of 4.0 MB for the second parameter set. This is almost an order of magnitude larger than our proofs. Baum and Nof also include timings of the implementation of their protocol. An implementation with 80 bits of statistical security for the second SIS parameter takes 2.4 s, with a proof size of 7.5 MB. (Note that this proof size is larger than for their 128 bits variant, because this choice was optimized for speed rather than proof size.) If we choose the parameters for our proof scheme as $q' = 2^4, M = 149, \tau =23$ to reach 80 bits of statistical security and optimize for speed, our proof size would be 1.4 MB (still 5 times smaller). Extrapolating from our SUSHSYFISH measurements, we claim that with these parameter choices our proof system will be significantly faster than the system of Baum and Nof.

Compared to the generic sub-linear Zero-Knowledge systems Ligero and Aurora [6] our proof systems are asymptotically worse, and for the large examples in Table 6 aiming at applications such as FHE we also perform significantly worse in terms of concrete proof sizes. However, for smaller applications, such as proving knowledge of a secret key that corresponds to a MLWE-encryption public key. ($q \approx 2^{13}, n = 1024, m = 512, \beta = 3$) we expect our proof size to be smaller than those of Ligero and similar to those of Aurora. Moreover, an important advantage of our proof system, as well as Stern’s protocol and the method of Baum and Nof is that they do not require $\mathbb {F}_q$ (or a field extension thereof) to be NTT friendly, this is in contrast to Ligero, Aurora and the work of Bootle et al.

Table 6. Proof sizes of various protocols for our two SIS parameter sets aiming at 128 bits of security. The hashes and commitments are 256 bits long. The parameter choices do not compensate for the non-tightness of the Fiat-Shamir transform, instead they only guarantee 128 bits of soundness for the interactive version of the protocols.

The work of Del Pino et al. [31] uses so-called bulletproofs to achieve much smaller proof sizes for SIS (for example 1.25 KB for $q \approx 2^{13}, m = 2048, n = 4096$) at the cost of longer running times. However, one cannot make a direct comparison with our work and the other works in Table 6, because bulletproofs rely on the discrete logarithm problem and are hence not post-quantum secure. Also, there has been a lot of work on “relaxed” proofs for SIS, where the extractor does not output the witness that is known to the prover, but instead some other solution that is somewhat short, but bigger than the witness [4, 29]. For some applications, such as post-quantum signatures [29], this is not a problem, but for other applications, exact proofs are required.