Abstract
We present a cryptographic construction for anonymous tokens with private metadata bit, called PMBTokens. This primitive enables an issuer to provide a user with a lightweight, single-use anonymous trust token that can embed a single private bit, which is accessible only to the party who holds the secret authority key and is private with respect to anyone else. Our construction generalizes and extends the functionality of Privacy Pass (PETS’18) with this private metadata bit capability. It provides unforgeability, unlinkability, and privacy for the metadata bit properties based on the DDH and CTDH assumptions in the random oracle model. Both Privacy Pass and PMBTokens rely on non-interactive zero-knowledge proofs (NIZKs). We present new techniques to remove the need for NIZKs, while still achieving unlinkability. We implement our constructions and we report their efficiency costs.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The need to propagate trust signals while protecting anonymity has motivated cryptographic constructions for anonymous credentials [Cha82, CL01]. While we have constructions that support complex statements, this comes with computation and communication costs. On the other hand, some practical uses require very simple functionality from the anonymous credential, while having very strict efficiency requirements. One such example is the setting of Privacy Pass [DGS+18]. Privacy Pass was designed as a tool for content delivery networks (CDNs), which need a way to distinguish honest from malicious content requests, so as to block illegitimate traffic that could drain network resources causing a denial of service (DoS). Previous solutions leveraged IP reputation to assess the reputation of users. While helpful in many cases, IP reputation may also lead to a high rate of false positives because of shared IP use. In particular, this is the case for users of privacy tools, such as Tor, VPNs, and I2P. Privacy Pass [DGS+18] proposes a solution for this problem using anonymous tokens as a mechanism to prove trustworthiness of the requests, without compromising the privacy of the user. Since CDNs need to potentially handle millions of requests per second, efficiency of the cryptographic construction is of extreme importance.
In this paper, we consider anonymous tokens that can convey two trust signals, in such a way that the user cannot distinguish which of the two signals is embedded in her tokens. This extension is motivated by the fact that in a system relying on anonymous trust tokens, malicious users be identified as a threat if the issuer stops providing them with tokens. Since real-world attackers have means to corrupt honest users, finding out when they have been detected could serve as an incentive to corrupt more users or adversarial learning against spam detectors. Being able to pass on the information whether a user is on an allow or disallow list, and consume it in appropriate ways on the authentication side, mitigates such behavior. There has been recent interest in primitives that provide such functionality in standardization bodies such as the IETF and W3C. This includes a recent draft proposal for a Trusted Token API submitted by Google at the W3C, which calls for a secret metadata bit functionality.Footnote 1 Also an IETF working groupFootnote 2 is discussing standardization of the core protocol of Privacy Pass used by CloudflareFootnote 3 together with extensions including private metadata bit.
More concretely, we consider an anonymous token primitive that provides the following functionality: a user and an issuer interact and, as a result of this interaction, the user obtains a token with a private metadata bit (PMB) embedded in it. The private metadata bit can be read from a token using the secret key held by the issuer, at redemption time. Each token is one-time use, which enables the issuer to update the trust assigned to each user without requiring a complex revocation process, by just adjusting the number of tokens that can be issued at once and the frequency of serving new token requests. Anonymous token schemes offer the following security properties: unforgeability, unlinkability, and privacy of the metadata bit. Unforgeability guarantees that nobody but the issuer can generate new valid tokens. Unlinkability guarantees that the tokens that were issued with the same private metadata bit are indistinguishable to the issuer when redeemed. Privacy of the metadata bit states that no party that does not have the secret key can distinguish any two tokens, including tokens issued with different metadata bits.
Our goal is to construct a primitive which achieves the above properties, and has competitive efficiency introducing minimal overhead over Privacy Pass.
1.1 Our Contributions
Our work includes the following contributions. We formalize the security properties of the primitive of anonymous tokens with private metadata bit. We present a new construction for this primitive, called PMBToken, which extends Privacy Pass (PP) to support private metadata bit, while maintaining competitive efficiency. Further, we introduce new techniques that allow to remove the need for NIZK in the constructions of both Privacy Pass and PMBToken. This simplifies and optimizes the constructions in which the NIZK proof computation is a major bottleneck. The resulting schemes satisfy a weaker unlinkability notion. Finally, we implement all the above candidate constructions in Rust, and we summarize the performance of our schemes.
A Failed Approach and Its Insight. The starting point of our study is Privacy Pass, which uses the verifiable oblivious PRF (VOPRF) primitive of Jarecki et al. [JKK14] \(F_x(t) = x\mathsf {H}_t(t)\) (additively denoted). In the oblivious PRF evaluation mechanism, the user sends to the issuer \(r\mathsf {H}_t(t)\) for a randomly selected value r, receives back \(rx\mathsf {H}_t(t)\) from which she recovers the output \(x\mathsf {H}_t(t)\).Footnote 4 Obliviousness is guaranteed by the blinding factor r, which makes the distribution of \(r\mathsf {H}_t(t)\) uniform even when knowing t. The PRF output can be verified by the user providing her with a DLEQ proof, which guarantees that \(\log _{\mathsf {H}_t(t)}(F_x(t)) = \log _G X\), where G is the base point and \(X :=xG\) is published by the issuer as a public parameter for the scheme.
There is a natural idea to upgrade the above functionality to support a private metadata bit, which is to have two secret keys and use each of these keys for one of the bits. However, this idea does not work directly; the reason for this stems from the fact that the underlying VOPRF is a deterministic primitive. In particular, this means that if we are using two different keys for tokens issued with different private metadata bit values, the VOPRF evaluations on the same input t will be the same if they are issued with the same key and will be different with high probability if used with different keys. Thus, if the user obtains multiple tokens using the same input value t (the issuer, by blindness, has no way of telling), she will be able to distinguish which ones were issued with the same bit.
New Randomized Tokens and Private Metadata. To resolve the above issue we introduce a construction which makes the token issuance a randomized functionality where the randomness is shared between the user and the issuer. We use the following function \(F_{(x, y)}(t; S) = x\mathsf {H}_t(t)+yS\), where t is the value that will be input of the user and S is the randomness of the evaluation, which will be determined by the two parties, more specifically \(S = r^{-1} \mathsf {H}_s(r\mathsf {H}_t(t); s)\) where r is the blinding factor chosen by the user and s is a random value chosen by the issuer. This functionality suffices to construct a new anonymized token where during the oblivious evaluation the user sends \(T' = r\mathsf {H}_t(t)\), receives back from the issuer \(s, W' = xT' + y\mathsf {H}_s(T'; s)\), unblinds the values \(S = r^{-1} \mathsf {H}_s(T'; s)\) and \(W = r^{-1}W'\), and outputs (S, W).
The token verification checks that \(W = x\mathsf {H}_t(t)+yS\). In order to provide verifiability, the issuer provides an element of the form \(X = xG + yH\) and sends a proof that \(X = xG + yH\) and \(W = x\mathsf {H}_t(t)+yS\) are computed using the same secret key (x, y). This is similar to Okamoto–Schnorr blind signatures [Oka92], with the key difference that we redefine this as a secret key primitive which enables us to have a round-optimal blind evaluation algorithm.
We apply the idea of using two different keys for each private metadata bit value to the above randomized construction; the resulting construction is called PMBTokens. The public parameters are now a pair \((X_0 :=x_0G + y_0H, X_1 :=x_1G + y_1H)\), a token issued with a private metadata bit b is of the form \(W' = x_b \mathsf {H}_t(t) + y_b S\) and the DLEQ proof is replaced with a DLEQOR proof stating that either \(W'\) and \(X_0\), or \(W'\) and \(X_1\), are computed using the same secret key \((x_0, y_0)\) or \((x_1, y_1)\).
Removing the NIZK. Both Privacy Pass and PMBTokens employ zero-knowledge arguments of knowledge to achieve unlinkability. This approach guarantees that the user can verify that she has obtained a token issued under the same secret key as in the issuer’s public parameters. Unlinkability follows from the fact that tokens issued under the same secret key are indistinguishable. We consider a slightly weaker unlinkability guarantee for the user during token issuance, which is that either the token she has received is issued under the public key or the token is indistinguishable from a random value, however, the user cannot distinguish these two cases. Now, a user will not be able to know in advance whether she has a token that will be valid at redemption. Another difference is that, if the issuer misbehaves, incorrectly issued tokens will be indistinguishable for the issuer from incorrectly formed tokens that a malicious user may try to use. Note that in any of the above constructions the issuer also distinguishes valid from invalid, however, the difference is that the she can check if the received tokens are valid.
We present modifications of both Privacy Pass and PMBTokens that satisfy this version of unlinkability, while removing the need for DLEQ or DLEQOR proofs and improving the computational cost for the issuer, which is the bottleneck in systems that need to support large number of users who perform many transactions and hence need to obtain tokens regularly.
Our approach for removing the DLEQ proof from Privacy Pass borrows ideas from the construction of a verifiable partially oblivious PRF of Jarecki et al. [JKR18], but simplifies their construction which has additional complexity in order to achieve user verifiability. We use the idea to use not only multiplicative but also additive blinding of the user’s input in the form \(T' = r(\mathsf {H}_t(t) - \rho G)\). Now, an honest evaluation of the issuer \(W' = xr(\mathsf {H}_t(t)-\rho G)\) can be unblinded by the user by computing \(r^{-1} W + \rho X = x\mathsf {H}_t(t) - \rho (xG) + \rho X = x\mathsf {H}_t(t)\), where \(X = xG\) is the issuer’s public key. On the other hand, any dishonestly computed \(W'\) which is of the form \(W' = r^{-1} T' + P\) for some \(P\ne 0\) when unblinded will contain a random additive factor \(r^{-1}P\), thus the resulting value will be random. Similarly to Jarecki et al. [JKR18], we can recover verifiability by doing another oblivious evaluation on the same value t and comparing the outputs, which will be equal only if the issuer used the public key for both executions. We also observe that these checks can be batched for an arbitrary number of issued tokens by computing a random linear combination of the values \(\mathsf {H}_t(t_i)\), obtaining a VOPRF evaluation on that value, and comparing with the same linear combination of the other tokens. Thus a user can verify n tokens by running one additional token request only. We note further that removing the zero knowledge argument significantly simplifies the issuer work, which now consist only of one multiplication.
Applying the above idea to the anonymous token construction with private metadata bit is more challenging since the user does not know which of the two public keys the issuer will use. However, the user can unblind the response from the issuer using each of the public keys and thus obtain one valid and one random token. This property turns out to be true if the issuer behaves honestly but if the issuer is malicious, he can create public keys and a response \(W'\) such that the two values obtained from the unblinding with each of the public keys are correlated and this correlation can be used for fingerprinting the user. Thus, in our construction the user computes two values \(T'_d = r_d(\mathsf {H}_t(t) - \rho _d G)\), for \(d = 0, 1\), and the issuer uses one of them to compute his response \(W' = x_b T'_b + y_b S'_b\) with a private bit b. The user unblinds \(W'\) using both public keys and the scalars \(r_d, \rho _d\) for \(d\in \{0,1\}\) to obtain \(S_0, W_0, S_1, W_1\), which she uses for the final token. The resulting token verifies with only one of the issuer’s keys: the key corresponding to the private metadata value.
Verification Oracle. One last wrinkle in the security proof is whether the adversary for unforgeability and privacy of the metadata bit properties should have access to a verification oracle for tokens of his choice. This is not explicitly supported in the current Privacy Pass security proof [DGS+18]. We provide a new proof for unforgeability of Privacy Pass in the presence of a verification oracle based on a different hardness assumption, the Chosen Target Gap Diffie–Hellman assumption, which is a formalization of the Chosen Target Diffie–Hellman in a Gap DH group, which was defined by Boneh et al. [BLS01]. In the context of anonymous tokens with private metadata bit, we distinguish a \(\textsc {Verify}\) oracle which just simply checks validity of the token, and a \(\textsc {Read}\) oracle that returns the value of the private metadata bit (which could be 0, 1, or invalid, and in some applications, e.g. blocklisting, we can merge the states of value 0 and invalid bit). We present an anonymous token construction that provides unforgeability and privacy for the metadata bit even when the adversary has access to the \(\textsc {Verify}\) oracle, but we crucially require that the adversary does not get an oracle access that reads the private metadata bit of a token.
Efficiency of Our Constructions. We consider the most expensive computation operation in the above protocols (scalar multiplication) and the largest communication overhead (the number of group elements transferred). We report in Table 1 the efficiency of our constructions. Additionally, the variant of our constructions that supports a verification oracle in the PMB security game adds the overhead of Okamoto–Schnorr Privacy Pass to the overhead of PMBTokens. The modifications of the constructions that do not use DLEQ or DLEQOR proofs save work for the issuer with no or moderate increase in communication and increased user computation. This computation trade-off is beneficial for settings where the issuer handles orders of magnitude more token issuance requests than any particular user. We further implement our constructions in Rust, and report their practicals costs in Sect. 8. Using a Ristretto group on Curve25519, PMBTokens issuance runs in 845 \(\upmu \)s and redemption takes 235 \(\upmu \)s, while Privacy Pass issuance runs in 303 \(\upmu \)s and redemption takes 95 \(\upmu \)s. Without the issuance NIZK, Construction 5 introduces a small overhead over Privacy Pass.
Paper Organization. We overview the hardness assumptions and the building block primitives we use in Sect. 2. Section 3 defines our new anonymous tokens primitive and its security notions. We recall the Privacy Pass construction in Sect. 4, and present a (randomized) Okamoto–Schnorr anonymous tokens construction in Sect. 5. Next, Sect. 6 presents our construction for anonymous tokens with private metadata bit, called PMBTokens. Section 7 proposes modifications of Privacy Pass and PMBTokens that avoid the need of zero-knowledge proofs. Finally, Sect. 8 reports on the efficiency costs of our implementation.
Due to space constraints, the security proofs are provided in the full version of this paper [KLOR20].
1.2 Related Work
Starting with the work of Chaum [Cha82], the concept of blind signatures has been widely used as a tool for building anonymous credentials. Blind Schnorr and Okamoto–Schnorr signatures, which have been studied and analyzed in the random oracle model [CP92, Oka92, PS00, Sch01, Sch06, FPS19], require three moves of interaction between the user and the issuer. Blind signatures constructions that achieve one round, which is the goal for our construction, rely on more expensive building blocks. Partially blind signatures, for which we also have round-optimal constructions [Fis06, SC12, BPV12], allow the issuer to embed some information in the signature, however, this information is public, unlike the private metadata bit that is the goal of our construction. The works of Boldyareva [Bol03] and Bellare et al. [BNPS03] achieve round optimal (one round) constructions in the random oracle model under interactive assumptions. These constructions use the same blinding idea as the VOPRF [JKK14] used by Privacy Pass, but are defined over groups where DDH is easy and CDH holds (or where the RSA assumptions hold), which enables public verifiability but requires larger group parameters. Other blind signature constructions have evolved from constructions that need a CRS [Fis06, SC12, BFPV11] to constructions in the standard model [GG14, FHS15, FHKS16], but they rely on bilinear groups. This adds complexity to the group instantiations for schemes and computational cost, which we aim to minimize.
Group signatures [CvH91, Cam97, BMW03] present functionality which allows all member of the group to sign messages, with the property that signatures from different signers are indistinguishable. At the same time there is a master secret key that belongs to a group manager, which can be used to identify the signer of a message. We can view different signer keys as signing keys for the private metadata bits, and the master secret key as a way to read that bit value. Group blind signatures [LR98], which provide also the oblivious evaluation for the signing algorithm we aim at, provide a solution for the anonymous token functionality with a private metadata bit. Existing blind group signatures constructions [LR98, Ram13, Gha13] require multiple rounds of interaction for the oblivious signing and communication of many group elements.
Abdalla et al. [ANN06] introduced a notion of blind message authentication codes (MACs), a secret key analog to blind signatures. They showed that this notion can exist only assuming a commitment of the private key, and showed how to instantiate that primitive with Chaum’s blind signatures [Cha82]. Davidson et al. [DGS+18] construct a similar private key functionality for anonymous tokens using a VOPRF [JKK14]; it is called Privacy Pass and is the basis of this work.
Everspaugh et al. [ECS+15] introduce the primitive of a partially oblivious PRF, which analogously to blind signatures allows the party with the secret key to determine part of the input for the PRF evaluation. However, this input needs to be public for verifiability. The presented partially blind PRF uses bilinear groups and pairings. Jarecki et al. [JKR18] show how to obtain a threshold variant of the partially oblivious PRF.
The work of Tsang et al. [TAKS07] presents a construction for blacklistable anonymous credentials using bilinear maps, which enables the issuer to create a blacklist of identities and the user can only generate an authentication token if she is not blacklisted; hence the user does find out whether she has been blacklisted in this process.
In keyed-verification anonymous credentials [CMZ14], the issuer and verifier are the same party. They use an algebraic MAC in place of a signature scheme, where the message space is a n-tuple of elements in \(\mathbb {Z}_p\) (or in \(\mathbb {G}\)). They can be used to provide an anonymous token primitive (at a slightly higher cost) but they’re overall meant for multi-use credentials. We are not aware of any extension that allows for the embedding of a private metadata bit.
2 Preliminaries
Notation. When sampling the value x uniformly at random from the set S, we write  . When sampling the value x from a probabilistic algorithm \(\mathsf {M}\), we write \(x \leftarrow \mathsf {M}\). We use \(:=\) to denote assignment. For an integer \(n \in \mathbb {N}\), we denote with [n] the interval \(\left\{ 0, \dots , n-1\right\} \). We denote vectors in bold. For a vector \(\mathbf {a}\), we denote with \(a_i\) the i-th element of \(\mathbf {a}\).
. When sampling the value x from a probabilistic algorithm \(\mathsf {M}\), we write \(x \leftarrow \mathsf {M}\). We use \(:=\) to denote assignment. For an integer \(n \in \mathbb {N}\), we denote with [n] the interval \(\left\{ 0, \dots , n-1\right\} \). We denote vectors in bold. For a vector \(\mathbf {a}\), we denote with \(a_i\) the i-th element of \(\mathbf {a}\).
The output resulting form the interaction of two (interactive) \(\mathsf {PPT}\) algorithms \(\mathsf {A}, \mathsf {B}\) is denoted as \(\llbracket a, b\rrbracket \leftarrow \langle \mathsf {A}, \mathsf {B}\rangle \). If only the first party receives a value at the end of the interaction, we write \(a \leftarrow \left\langle \mathsf {A}, \mathsf {B}\right\rangle \) instead of \(\llbracket a, \perp \rrbracket \leftarrow \left\langle \mathsf {A}, \mathsf {B}\right\rangle \).
We assume the existence of a group generator algorithm \(\mathsf {GrGen}(1^\lambda )\) that, given as input the security parameter in unary form outputs the description \(\varGamma = (\mathbb {G}, p, G, H)\) of a group \(\mathbb {G}\) of prime order p; G and H are two nothing-up-my-sleeve (NUMS) generators of \(\mathbb {G}\). For simplicity, we will assume that the prime p is of length \(\lambda \).
2.1 Security Assumptions
We assume the reader to be familiar with the discrete logarithm (DLOG), decisional Diffie–Hellman (DDH), and computational Diffie–Hellman (CDH) assumptions. In this work, we will use the chosen-target gap Diffie–Hellman (CTGDH) assumption.
Chosen-Target Gap Diffie–Hellman. The chosen-target Diffie–Hellman (CTDH) assumption [Bol03, HL06] states that any \(\mathsf {PPT}\) adversary \(\mathsf {A}\) has negligible advantage in solving CDH on \(\ell +1\) target group elements, even when given access to a CDH helper oracle for \(\ell \) instances. We formalize here its gap [OP01] flavor, in which the adversary has, in addition, access to a DDH oracle for arbitrary group elements. Note that the CTDH assumption was originally introduced by Boldyreva [Bol03] in gap DH groups [BLS01], that is, in groups where CDH is hard but DDH is assumed to be easy. In other words, the original definition of CTDH was already in groups where the adversary has access to a DDH oracle. Here, we introduce the chosen-target gap Diffie–Hellman assumption (CTGDH, that is, the gap version of CTDH) as a security experiment where the adversary is provided a challenge \(X \in \mathbb {G}\), and has access to three oracles: the \(\textsc {Target}\) oracle, that given as input a string \(t \in \{0,1\}^*\), outputs a random group element; the \(\textsc {Help}\) oracle, that outputs the CDH of X with an arbitrary group element \(Y \in \mathbb {G}\), and the \(\textsc {Ddh}\) oracle, that given as input two group elements \((Y, Z) \in \mathbb {G}^2\) returns 1 if and only if (X, Y, Z) is a Diffie–Hellman tuple. We describe the \(\textsc {Target}\) oracle in this cumbersome way to ease readability of the security proofs later.
Formally, we say that CTGDH holds for the group generator \(\mathsf {GrGen}\) if for any \(\mathsf {PPT}\) adversary \(\mathsf {A}\), and any \(\ell \ge 0\):

where \({\text {CTGDH}}^{}_{\mathsf {GrGen}, \mathsf {A}, \ell }(\lambda )\) is defined in Fig. 1. Note that for \(\ell =0\), the game \({\text {CTGDH}}^{}_{\mathsf {GrGen}, \mathsf {A}, 0}(\lambda )\) is equivalent to gap CDH.
2.2 Non-interactive Arguments of Knowledge
A non-interactive proof system \(\mathsf {\Pi }\) for relation \(\mathsf {R}\) consists of the following three algorithms:
-
\((\textsf {crs}, \textsf {td}) \leftarrow \mathsf {\Pi }.\!\mathsf {Setup}(\varGamma )\), the setup algorithm that outputs a common reference string (CRS) \(\textsf {crs}\) together with some trapdoor information \(\textsf {td}\).
-
\(\pi \leftarrow \mathsf {\Pi }.\!\mathsf {Prove}(\textsf {crs}, \phi , w)\), a prover which takes as input some \((\phi , w) \in \mathsf {R}\) and a CRS \(\textsf {crs}\), and outputs a proof \(\pi \).
-
\(\textit{bool}\leftarrow \mathsf {\Pi }.\!\mathsf {Verify}(\textsf {crs}, \phi , \pi )\) a verifier that, given as input a statement \(\phi \) together with a proof \(\pi \) outputs \(\mathbf{true} \) or \(\mathbf{false} \), indicating acceptance of the proof.
The proof system \(\mathsf {\Pi }\) is a non-interactive zero-knowledge (NIZK) argument of knowledge if it satisfies the following properties:
Completeness. \(\mathsf {\Pi }\) is complete if every correctly generated proof verifies. More formally, a proof system \(\mathsf {\Pi }\) is complete if for any \(\varGamma \in [\mathsf {GrGen}(1^\lambda )]\), \(\textsf {crs}\in [\mathsf {\Pi }.\!\mathsf {Setup}(\varGamma )]\) and \((\phi , w) \in \mathsf {R}\):

Knowledge Soundness. A proof system \(\mathsf {\Pi }\) for relation \(\mathsf {R}\) is knowledge-sound if for any \(\mathsf {PPT}\) adversary \(\mathsf {A}\) there exists a \(\mathsf {PPT}\) extractor \(\mathsf {Ext}\) such that:

where \({\text {KSND}}^{}_{\mathsf {\Pi }, \mathsf {R}, \mathsf {A}, \mathsf {Ext}}(\lambda )\) is defined in Fig. 2 and \(\mathsf {A}.\!\mathsf {rl}(\lambda )\) is the randomness length for the machine \(\mathsf {A}\). An argument of knowledge is a knowledge-sound proof system. In our proofs, for ease of notation, we will omit to specify explicitly that the extractor takes as input the coins of the adversary.
Zero Knowledge. A proof system \(\mathsf {\Pi }\) for \(\mathsf {R}\) is zero-knowledge if no information about the witness is leaked by the proof, besides membership in the relation. This is formalized by specifying an additional \(\mathsf {PPT}\) algorithm \(\mathsf {\Pi }.\!\mathsf {Sim}\), that takes as input the trapdoor information \(\textsf {td}\) and a statement \(\phi \), and outputs a valid proof \(\pi \) indistinguishable from those generated via \(\mathsf {\Pi }.\!\mathsf {Prove}\). Formally, A proof system \(\mathsf {\Pi }\) for relation \(\mathsf {R}\) is zero-knowledge if for any \(\mathsf {PPT}\) adversary \(\mathsf {A}\):

where \({\text {ZK}}^{\beta }_{\mathsf {\Pi }, \mathsf {R}, \mathsf {A}}(\lambda )\) is defined in Fig. 2.
Throughout this paper, we will assume the existence of the following proof systems, that we summarize here in Camenisch-Stadler notation [Cam97]:
Equation (1) and Eq. (4) are discrete logarithm proofs for one, respectively two generators. Equation (2) and Eq. (3) prove discrete logarithm equality under one, respectively two generators. Finally, Eq. (5) proves discrete logarithm equality for one out of two group elements (in the witness, the index is denoted as \(i \in \{0,1\}\)). In the full version [KLOR20], we provide a more formal description of the above relations, and efficient instantiations with techniques for batching proofs at issuance time.
3 Anonymous Tokens
We describe two flavors of anonymous tokens. The first flavor enables a user to obtain a token from an issuer; the user can later use this token as a trust signal, for one-time authentication. In the second flavor, the issuer has an additional input during the token issuance, a private metadata bit, that is hidden within the token. The private metadata bit can later be recovered by the issuer at redemption time. The following definition captures both functionalities; in
 , we refer only to the anonymous token with private metadata bit.
, we refer only to the anonymous token with private metadata bit.
Anonymous Token. An anonymous token scheme
 \(\mathsf {AT}\) consists of the following algorithms:
\(\mathsf {AT}\) consists of the following algorithms:
-
\((\textsf {crs}, \textsf {td}) \leftarrow \mathsf {AT}.\!\mathsf {Setup}(1^\lambda )\), the setup algorithm that takes as input the security parameter \(\lambda \) in unary form, and returns a CRS \(\textsf {crs}\) and a trapdoor \(\textsf {td}\).
All the remaining algorithms take \(\textsf {crs}\) as their first input, but for notational clarity, we usually omit it from their lists of arguments.
-
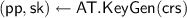 , the key generation algorithm that generates a private key
, the key generation algorithm that generates a private key
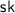 along with a set of public parameters \(\mathsf {pp}\);
along with a set of public parameters \(\mathsf {pp}\); -
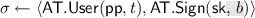 , the token issuance protocol, that involves interactive algorithms \(\mathsf {AT}.\!\mathsf {User}\) (run by the user) with input a value \(t \in \{0,1\}^\lambda \), and \(\mathsf {AT}.\!\mathsf {Sign}\) (run by the issuer) with input the private key
, the token issuance protocol, that involves interactive algorithms \(\mathsf {AT}.\!\mathsf {User}\) (run by the user) with input a value \(t \in \{0,1\}^\lambda \), and \(\mathsf {AT}.\!\mathsf {Sign}\) (run by the issuer) with input the private key
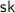
 . At the end of the interaction, the issuer outputs nothing, while the user outputs \(\sigma \), or \(\perp \).
. At the end of the interaction, the issuer outputs nothing, while the user outputs \(\sigma \), or \(\perp \). -
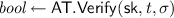 , the verification algorithm that takes as input the private key
, the verification algorithm that takes as input the private key
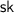 and a token \((t, \sigma )\). It returns a boolean indicating if the token was valid or not.
and a token \((t, \sigma )\). It returns a boolean indicating if the token was valid or not. -
 , the metadata extraction algorithm that takes as input the private key
, the metadata extraction algorithm that takes as input the private key
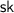 , and a token \((t, \sigma )\). It returns an indicator \(\mathsf {ind}\in \{\perp , 0, 1\}\), which is either the private metadata bit, or \(\perp \).
, and a token \((t, \sigma )\). It returns an indicator \(\mathsf {ind}\in \{\perp , 0, 1\}\), which is either the private metadata bit, or \(\perp \).
Throughout the rest of this paper, we assume that \(\mathsf {AT}\) has a one-round signing protocol initiated by the user. Thus, for simplicity, we split the signing algorithms (\(\mathsf {AT}.\!\mathsf {Sign}\) and \(\mathsf {AT}.\!\mathsf {User}\)) into non-interactive algorithms that take as input a message, and the partial state (if any). They will return the next message together with the updated state \(\mathsf {st}_i\). Concretely, the signing protocol will be composed of the following (non-interactive) algorithms:
-
\((\textsf {usr\_msg}_0, \textsf {st}_{0}) \leftarrow \mathsf {AT}.\!\mathsf {User}_0(\mathsf {pp}, t)\);
-
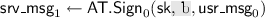 ;
; -
\(\sigma \leftarrow \mathsf {AT}.\!\mathsf {User}_1(\textsf {st}_0, \textsf {srv\_msg}_{1})\)
We demand that anonymous token schemes satisfies correctness, unforgeability, unlinkability
 .
.
Correctness. An anonymous token scheme \(\mathsf {AT}\) is correct if any honestly-generated token verifies
 . That is, for any \(\textsf {crs}\in [\mathsf {AT}.\!\mathsf {Setup}(1^\lambda )]\), any
. That is, for any \(\textsf {crs}\in [\mathsf {AT}.\!\mathsf {Setup}(1^\lambda )]\), any
 , any \(t \in \{0,1\}^\lambda \),
, any \(t \in \{0,1\}^\lambda \),
 :
:


Unforgeability. The first security property that we require from an anonymous token is unforgeability, which guarantees that no adversary can redeem more tokens than it is allowed. This is formalized with a standard one-more security game where the adversary can interact with the issuer at most \(\ell \) times, and at the end must output \(\ell +1\) valid tokens. The adversary has also access to a verification oracle for tokens of its choice. In the private metadata bit variant, the adversary can interact with the issuer \(\ell \) times for each private metadata bit, but should not be able to generate \(\ell +1\) valid tokens with the same private metadata.
Definition 1
(One-more unforgeability). An anonymous token scheme \(\mathsf {AT}\) is one-more unforgeable if for any \(\mathsf {PPT}\) adversary \(\mathsf {A}\), and any \(\ell \ge 0\):

where \({\text {OMUF}}^{}_{\mathsf {AT}, \mathsf {A}, \ell }(\lambda )\) is defined in Fig. 3.
Unlinkability. This security property is concerned with user anonymity, and guarantees that a malicious issuer cannot link the redemption of a token with a particular execution of the token issuance protocol. More precisely, in \(\kappa \)-unlinkability, if m tokens were issued but not yet redeemed, the adversary cannot link the relative issuance session of a token with probability better than \(\kappa /m\), even after seeing the remaining \(m-1\) tokens in a random order.
Definition 2
(Unlinkability). An anonymous token scheme \(\mathsf {AT}\) is \(\kappa \)-unlinkable if for any \(\mathsf {PPT}\) adversary \(\mathsf {A}\), and any \(m > 0\):

where \({\text {UNLINK}}^{}_{\mathsf {AT}, \mathsf {A}, m}(\lambda )\) is defined in Fig. 4.
Private Metadata Bit. The last security property protects the private metadata bit in the issued tokens.Footnote 5 It guarantees that the private metadata embedded in a token is entirely hidden from anyone who does not possess the private key including the user. More precisely, we require that, even if the adversary corrupts a large number of users, it cannot guess with probability non-negligibly bigger than 1/2 if newly issued tokens have private metadata 0 or 1.
Formally, this is modeled as an indistinguishability game where the adversary has access to two signing oracles: one where it can provide both the message to be signed and the private metadata bit to be used, and one where the adversary chooses only the message (the metadata bit is fixed), and a verification oracle for the validity of the tokens. The adversary’s goal is to guess the challenge private metadata bit used.
Definition 3
(Private metadata bit). An anonymous token scheme \(\mathsf {AT}\) provides private metadata bit if for any \(\mathsf {PPT}\) adversary \(\mathsf {A}\):

where \({\text {PMB}}^{\beta }_{\mathsf {AT}, \mathsf {A}}(\lambda )\) is defined in Fig. 5.
Token Hijacking. In our formalization, we do not consider man-in-the-middle adversaries that can steal tokens from honest users. This attack vector, called token hijacking, can be mitigated with the use of message authentication codes (MACs). Roughly speaking, instead of sending the entire token \((t, \sigma )\) over the wire, the user can derive a symmetric key  to MAC a shared message (e.g., the resource or the URL she’s trying to access). The resulting message authentication code is sent together with t to the issuer (and any supplementary randomness that the user needs to recompute \(\sigma \)). We discuss in detail such concerns in the full version of this paper
[KLOR20].
to MAC a shared message (e.g., the resource or the URL she’s trying to access). The resulting message authentication code is sent together with t to the issuer (and any supplementary randomness that the user needs to recompute \(\sigma \)). We discuss in detail such concerns in the full version of this paper
[KLOR20].
Token issuance for \(\mathsf {PP}\) (Construction 1).
4 Review: Privacy Pass
We start by recalling, using the notation from Sect. 3, the anonymous token scheme proposed in [DGS+18] (under the name Privacy Pass) and built on top of the verifiable oblivious PRF (VOPRF) “2HashDH-NIZK” [JKK14]. Privacy Pass uses a Schnorr proof in the issuance phase, that we generalize here to any NIZK. Differently from the initial proof of Goldberg et al. [DGS+18], our proof takes into account the presence of a verification oracle, and the knowledge error of the proof system.
Construction 1
(Privacy Pass). Let \(\mathsf {\Pi }_\mathsf {DLEQ}\) be a proof system for relation \(\mathsf {R}_\textsf {DLEQ}\); let \(\mathsf {H}_t\) be a random oracle \(\{0,1\}^*\rightarrow \mathbb {G}\). The anonymous token scheme \(\mathsf {PP}\) [DGS+18] is composed of the following algorithms:
-
\((\textsf {crs}, \textsf {td}) \leftarrow \mathsf {PP}.\!\mathsf {Setup}(1^\lambda )\): invoke the group generator \(\varGamma \leftarrow \mathsf {GrGen}(1^\lambda )\) and the CRS generation algorithm of the underlying proof system \((\textsf {pcrs}, \textsf {ptd}) \leftarrow \mathsf {\Pi }_\mathsf {DLEQ}.\!\mathsf {Setup}(\varGamma )\). Return \(\textsf {crs}:=(\varGamma , \textsf {pcrs})\) and \(\textsf {td}:=\textsf {ptd}\).
-
\((X, x) \leftarrow \mathsf {PP}.\!\mathsf {KeyGen}(\textsf {crs})\): sample a uniformly random element
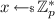 , that will constitute the secret key. Let \(X :=xG\) be the public parameter. Return (X, x).
, that will constitute the secret key. Let \(X :=xG\) be the public parameter. Return (X, x). -
\(W \leftarrow \langle \mathsf {PP}.\!\mathsf {User}(X, t), \mathsf {PP}.\!\mathsf {Sign}(x)\rangle \): illustrated in Fig. 6.
-
\( \textit{bool}\leftarrow \mathsf {PP}.\!\mathsf {Verify}(x, t, W)\): return \(\mathbf{true} \) if \(W = x \mathsf {H}_t(t)\); else, return \(\mathbf{false} \).
Note that this anonymous token protocol is deterministic, i.e., there will exist a unique value \(W\in \mathbb {G}\) corresponding to a string \(t\in \{0,1\}^\lambda \) that verifies. This property will make difficult to directly extend the construction to support private metadata bit.
Correctness. By correctness of the underlying proof system, at the end of the protocol the user returns \(\perp \) only with negligible probability. If the user returns \(W \in \mathbb {G}\), then W always satisfies the verification equation, since: \(W = rW' = r(x T') = x T = x \mathsf {H}_t(t)\).
Security. \(\mathsf {PP}\) satisfies both unforgeability and 1-unlinkability.
Theorem 4
If CTGDH holds for \(\mathsf {GrGen}\) and \(\mathsf {\Pi }_\mathsf {DLEQ}\) is a zero-knowledge proof system for relation \(\mathsf {R}_\textsf {DLEQ}\), then \(\mathsf {PP}[\mathsf {GrGen}, \mathsf {\Pi }_\mathsf {DLEQ}]\) is one-more unforgeable with advantage:

The proof can be found in the full version, and follows directly from chosen-target gap Diffie–Hellman for \(\mathsf {GrGen}\), and zero-knowledge of \(\mathsf {\Pi }_\mathsf {DLEQ}\). Consider an adversary \(\mathsf {A}\) in the game \({\text {OMUF}}^{}_{\mathsf {PP}, \mathsf {A}}(\lambda )\). To win the game, \(\mathsf {A}\) must return \(\ell +1\) tokens \((t_i, W_i)_{i \in [\ell +1]}\) such that, for all \(i \in [\ell +1]\):
During its execution, the adversary \(\mathsf {A}\) can query at most \(\ell \) times the signing oracle, which given as input \(T^* \in \mathbb {G}\) computes the Diffie–Hellman \(W = xT^*\), and sends it together with a proof \(\pi \) that W was correctly computed; additionally, \(\mathsf {A}\) can query the oracle \(\textsc {Verify}(t^*, W^*)\) that returns 1 if \(W^* = x\mathsf {H}_t(t^*)\), that is, if \((X, \mathsf {H}_t(t^*), W^*)\) is a DH tuple. Since \(\mathsf {\Pi }_\mathsf {DLEQ}\) is zero-knowledge, it is possible to simulate the proof \(\pi \). We are thus left with the game CTGDH (Fig. 1), where \(\textsc {Verify}\) can be replaced by the oracle \(\textsc {Ddh}\), \(\mathsf {H}_t\) by \(\textsc {Target}\), and \(\textsc {Sign}\) by the oracle \(\textsc {Help}\) (together with \(\mathsf {\Pi }_\mathsf {DLEQ}.\!\mathsf {Sim}\)).
Theorem 5
Let \(\mathsf {GrGen}\) be a group generator algorithm. If \(\mathsf {\Pi }_\mathsf {DLEQ}\) is a knowledge-sound proof system for relation \(\mathsf {R}_\textsf {DLEQ}\), then \(\mathsf {PP}[\mathsf {GrGen}, \mathsf {\Pi }_\mathsf {DLEQ}]\) is 1-unlinkable.
We remark that the i-th message sent by \(\mathsf {PP}.\!\mathsf {User}_0\) is \(T_i' = r^{-1}T_i\), for a uniformly random \(r_i \in \mathbb {Z}_p^*\). Therefore, \(T'_i\) contains no information about \(T_i\) or \(t_i\). Additionally, by knowledge soundness of \(\mathsf {\Pi }_\mathsf {DLEQ}\), it is possible to extract the witness \(x \in \mathbb {Z}_p\) used to compute the signatures. With it, the user can compute \(W_i\) herself, without ever using the responses from the issuer. It follows that the view of the adversary is limited to random group elements and \(\mathsf {PP}\) is 1-unlinkable, as long as the proof system is knowledge-sound.
5 Okamoto–Schnorr Privacy Pass
In this section, we describe a novel anonymous token scheme that generalizes \(\mathsf {PP}\) (Sect. 4) and allows for randomized tokens, which will be an important property when we extend the construction to support private metadata bit (Sect. 6). Roughly speaking, while in \(\mathsf {PP}\) we issue tokens (and DLEQ proofs) using one generator G of \(\mathbb {G}\), in this construction we will issue tokens under two generators (G, H), in a similar way to Okamoto–Schnorr [Oka92] signatures. Similarly to Okamoto–Schnorr, it is important here that the discrete logarithm of H base G is unknown. Fixing \(y = 0\) in the protocol below, we obtain \(\mathsf {PP}\) (cf. Sect. 4).
Token issuance for \(\mathsf {OSPP}\) (Construction 2).
Construction 2
(Okamoto–Schnorr Privacy Pass). Let \(\mathsf {GrGen}\) be a group generator algorithm; let \(\mathsf {\Pi }_\mathsf {DLEQ2}\) be a proof system for relation \(\mathsf {R}_\textsf {DLEQ2}\); let \(\mathsf {H}_t, \mathsf {H}_s\) be two random oracles \(\{0,1\}^* \rightarrow \mathbb {G}\). We construct an anonymous token scheme \(\mathsf {OSPP}\) defined by the following algorithms:
-
\((\textsf {crs}, \textsf {td}) \leftarrow \mathsf {OSPP}.\!\mathsf {Setup}(1^\lambda )\): invoke the group generator \(\varGamma \leftarrow \mathsf {GrGen}(1^\lambda )\) and the CRS generation algorithm of the underlying proof system \((\textsf {pcrs}, \textsf {ptd}) \leftarrow \mathsf {\Pi }_\mathsf {DLEQ2}.\!\mathsf {Setup}(\varGamma )\). Return \(\textsf {crs}:=(\varGamma , \textsf {pcrs})\) and \(\textsf {td}:=\textsf {ptd}\).
-
\((X, (x, y)) \leftarrow \mathsf {OSPP}.\!\mathsf {KeyGen}(\textsf {crs})\): sample the secret key
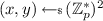 . Let \(X :=xG+yH\) be the public parameter. Return (X, (x, y)).
. Let \(X :=xG+yH\) be the public parameter. Return (X, (x, y)). -
\(\sigma \leftarrow \langle \mathsf {OSPP}.\!\mathsf {User}(X, t), \mathsf {OSPP}.\!\mathsf {Sign}((x, y))\rangle \): illustrated in Fig. 7.
-
\(\textit{bool}\leftarrow \mathsf {OSPP}.\!\mathsf {Verify}((x, y), t, \sigma )\): read \((S, W) :=\sigma \). Return \(\mathbf{true} \) if \(W = x\mathsf {H}_t(t) + yS\); else, return \(\mathbf{false} \).
Correctness. By correctness of the underlying proof system, the protocol aborts only with negligible probability. If the user returns \(\sigma :=(S, W) \in \mathbb {G}^2\), then \(\sigma \) always satisfies the verification equation, since \(W = rW' = r(x T' + yS') = x T + y S = x \mathsf {H}_t(t) + y S\).
Security. \(\mathsf {OSPP}\) satisfies both unforgeability and 1-unlinkability.
Theorem 6
If CTGDH holds for \(\mathsf {GrGen}\), and \(\mathsf {\Pi }_\mathsf {DLEQ2}\) is a zero-knowledge proof system for relation \(\mathsf {R}_\textsf {DLEQ2}\), then \(\mathsf {OSPP}[\mathsf {GrGen}, \mathsf {\Pi }_\mathsf {DLEQ2}]\) is one-more unforgeable with advantage:

The proof of unforgeability is essentially the same argument of the previous section, with a slightly more careful analysis to deal with the additional element \(s \in \{0,1\}^\lambda \). The reduction for CTGDH receives a challenge \(A \in \mathbb {G}\), that is now embedded in the public parameters as \(X = A + y H\) for some  ; the signing oracle computes \(W' =\textsc {Help}(T') + yS'\), and the read oracle \(\textsc {Ddh}(W - yS)\). The tokens returned by the adversary can be converted in CDH solutions computing \(W_i -yS_i\), for all \(i \in [\ell +1]\).
; the signing oracle computes \(W' =\textsc {Help}(T') + yS'\), and the read oracle \(\textsc {Ddh}(W - yS)\). The tokens returned by the adversary can be converted in CDH solutions computing \(W_i -yS_i\), for all \(i \in [\ell +1]\).
Theorem 7
If DDH holds for \(\mathsf {GrGen}\) and \(\mathsf {\Pi }_\mathsf {DLEQ2}\) is an argument of knowledge for relation \(\mathsf {R}_\textsf {DLEQ2}\), then \(\mathsf {OSPP}[\mathsf {GrGen}, \mathsf {\Pi }_\mathsf {DLEQ2}]\) is 1-unlinkable.
Similarly to the previous proof, we first notice that in the i-th message, \(T'_i\) contains no information about t; additionally, by knowledge soundness of the proof system, \(W_i\) must be computed with the same “witness” (x, y) satisfying \(X = xG + yH\) (if there exists \((x', y') \ne (x, y)\), then it is possible to construct an adversary for discrete log for \(\mathsf {GrGen}\)). The core difference now is that we use the same blinding factor r both on \(S' \) and \(W'\). The proof hence proceeds in two steps: first, \(W:=rW'\) is computed as \(W:=xT+yS\) with the extracted witness, and next \(S:=rS'\) is replaced by  . This last step can be reduced to DDH: if the adversary manages to distinguish \((T', T = rT', S', S=rS')\) from \((T', T = rT', S', U)\) for
. This last step can be reduced to DDH: if the adversary manages to distinguish \((T', T = rT', S', S=rS')\) from \((T', T = rT', S', U)\) for  , then it is possible to construct an adversary \(\mathsf {B}\) for game \({\text {DDH}}^{\beta }_{\mathsf {GrGen}, \mathsf {B}}(\lambda )\).
, then it is possible to construct an adversary \(\mathsf {B}\) for game \({\text {DDH}}^{\beta }_{\mathsf {GrGen}, \mathsf {B}}(\lambda )\).
6 Private Metadata Bit Tokens
In this section, we present PMBTokens, an extension of the anonymous token construction from Sect. 5 that supports a private metadata bit. The high-level idea is that we use two different secret keys, one for each private metadata bit. In order to hide which bit is associated with the token, we will use OR proofs (i.e., \(\mathsf {\Pi }_\mathsf {DLEQOR2}\) of Eq. (5)).
Token issuance for \(\mathsf {PMBT}\) (Construction 3).
Construction 3
(PMBTokens). Let \(\mathsf {GrGen}\) be a group generator algorithm; let \(\mathsf {\Pi }_\mathsf {DLEQOR2}\) be a proof system for relation \(\mathsf {R}_\mathsf {DLEQOR2}\); let \(\mathsf {H}_t, \mathsf {H}_s\) be two random oracles \(\{0,1\}^* \rightarrow \mathbb {G}\). We construct an anonymous token scheme \(\mathsf {PMBT}\) defined by the following algorithms:
-
\((\textsf {crs}, \textsf {td}) \leftarrow \mathsf {PMBT}.\!\mathsf {Setup}(1^\lambda )\): invoke the group generator \(\varGamma \leftarrow \mathsf {GrGen}(1^\lambda )\) and the CRS generation algorithm of the underlying proof system \((\textsf {pcrs}, \textsf {ptd}) \leftarrow \mathsf {\Pi }_\mathsf {DLEQOR2}.\!\mathsf {Setup}(\varGamma )\). Return \(\textsf {crs}:=(\varGamma , \textsf {pcrs})\) and \(\textsf {td}:=\textsf {ptd}\).
-
\((\mathbf {X}, (\mathbf {x}, \mathbf {y})) \leftarrow \mathsf {PMBT}.\!\mathsf {KeyGen}(\textsf {crs})\): let
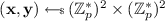 be the secret key. Define the public parameters as: $$ \mathbf {X} :=\begin{bmatrix}X_0 \\ X_1\end{bmatrix} :=\begin{bmatrix} x_0G + y_0 H \\ x_1G + y_1 H \end{bmatrix}; $$
be the secret key. Define the public parameters as: $$ \mathbf {X} :=\begin{bmatrix}X_0 \\ X_1\end{bmatrix} :=\begin{bmatrix} x_0G + y_0 H \\ x_1G + y_1 H \end{bmatrix}; $$restart if \(X_0 = X_1\). Return \((\mathbf {X}, (\mathbf {x}, \mathbf {y}))\).
-
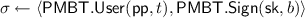 : illustrated in Fig. 8.
: illustrated in Fig. 8. -
\( \textit{bool}\leftarrow \mathsf {PMBT}.\!\mathsf {Verify}((\mathbf {x}, \mathbf {y}), t, \sigma )\): return \(\mathbf{true} \).
-
\( \mathsf {ind}\leftarrow \mathsf {PMBT}.\!\mathsf {ReadBit}((\mathbf {x}, \mathbf {y}), t, \sigma )\): read \((S, W) :=\sigma \). Then:
-
(a)
if \(W = x_0\mathsf {H}_t(t) + y_0S\) and \(W \ne x_1\mathsf {H}_t(t) + y_1S\), return 0;
-
(b)
if \(W \ne x_0\mathsf {H}_t(t) + y_0S\) and \(W = x_1\mathsf {H}_t(t) + y_1S\), return 1;
-
(c)
else, return \(\perp \).
-
(a)
Our construction does not provide a (meaningful) implementation of \(\mathsf {Verify}\), but only a \(\mathsf {ReadBit}\) functionality. We elaborate this point in Sect. 6.1; this construction can be combined with \(\mathsf {OSPP}\) to provide an actual verification procedure (described in the full version).
Correctness. Validity of honestly-generated tokens (cf. Eq. (6)) holds perfectly because \(\mathsf {PMBT}.\!\mathsf {Verify}\) always returns \(\mathbf{true} \); we focus here on proving that the bit embedded is read correctly with overwhelming probability (Eq. (7)). By correctness of the underlying proof system, the protocol aborts only with negligible probability. If the user returns \((S, W) \in \mathbb {G}^2\), then there exists \(b \in \{0,1\}\) such that \( W = rW' = r(x_b T' + y_b S') = x_b T + x_b S = x_b \mathsf {H}_t(t) + y_b S\). The probability that the above equation holds for both \(b=0\) and \(b=1\) (in which case, \(\mathsf {PMBT}.\!\mathsf {ReadBit}\) returns \(\perp \)), is statistically negligible. In fact, if:
then we have two possibilities:
-
(a)
\(y_0 = y_1\), which in turn implies that \(x_0\mathsf {H}_t(t) = x_1\mathsf {H}_t(t)\). Because \(x_0 \ne x_1\) (by construction of \(\mathsf {PMBT}.\!\mathsf {KeyGen}\)), this happens only if \(\mathsf {H}_t(t)\) is the identity element. This event happens with probability 1/p;
-
(b)
\(y_0\ne y_1\), which in turn means that: \(\mathsf {H}_t (t) = \frac{x_0-x_1}{y_0-y_1}S\). However, the left-hand side of the equation is distributed uniformly at random in \(\mathbb {G}\) and independently from the terms on the right-hand side. This event happens with probability 1/p.
Security. In the full version, we prove the one-more unforgeability and \(\mathbf {2}\)-unlinkability of \(\mathsf {PMBT}\).
Theorem 8
If CTGDH holds for \(\mathsf {GrGen}\) and \(\mathsf {\Pi }_\mathsf {DLEQ2}\) is a zero-knowledge proof system for relation \(\mathsf {R}_\textsf {DLEQ2}\), then \(\mathsf {PMBT}[\mathsf {GrGen}, \mathsf {\Pi }_\mathsf {DLEQ2}]\) is one-more unforgeable with advantage:

Consider an adversary \(\mathsf {A}\) in the game \({\text {OMUF}}^{}_{\mathsf {PMBT}, \mathsf {A}}(\lambda )\). \(\mathsf {A}\) wins the game if it returns \(\ell +1\) tokens \((t_i, (S_i,W_i))_{i \in [\ell +1]}\) such that there exists a \(b \in \{0,1\}\) satisfying:
During its execution, \(\mathsf {A}\) can query \(\ell +1\) times the signing oracle for \(b=0\), and \(\ell +1\) times for \(b=1\). We claim (in a similar way to Eq. (8)), that \(\mathsf {A}\) can be used to construct an adversary \(\mathsf {B}\) that solves CTGDH. We embed the CTGDH challenge \(A \in \mathbb {G}\) in one of the two keys: we sample  , where
, where  . We construct \(X_{1-{b^*}}\) following the key generation algorithm. Queries by \(\mathsf {A}\) to the oracle \(\textsc {Sign}\) are responded in the following way: if the adversary demands issuance for hidden metadata \(b^*\), we use the \(\textsc {Help}\) oracle to return \(W' = \textsc {Help}(t, T') + y_{b^*} S'\); otherwise \(\mathsf {B}\) just follows the signing protocol and computes \(W'\) using \((x_{1-{b^*}}, y_{1-{b^*}})\). The zero-knowledge proof is simulated. Queries to the oracle \(\textsc {Read}\) can still be answered by \(\mathsf {B}\) with the help of the oracle \(\textsc {Ddh}\) available in the game \({\text {CTGDH}}^{}_{\mathsf {GrGen}, \mathsf {B}, \ell }(\lambda )\). Queries to \(\textsc {Verify}\) are trivially dealt with, by answering \(\mathbf{true} \). If at the end of its execution \(\mathsf {A}\) presents forgeries for the bit \(b=b^*\), then by winning condition (a) (cf. Eq. (9)), for all \(i \in [\ell +1]\), \((W_i- y_{b^*}S_i)\) is the CDH of the challenge A with \(\mathsf {H}_t(t_i)\), which we replace with the CTGDH oracle \(\textsc {Target}\) thus presenting \(\ell +1\) CDH solutions for the challenge \(A \in \mathbb {G}\). If the guess \(b^*\) was not correct, then \(\mathsf {B}\) outputs \(\perp \), and we consider the game lost. It follows that \(\mathsf {B}\) wins the game \({\text {CTGDH}}^{}_{\mathsf {GrGen}, \mathsf {B}, \ell }(\lambda )\) half the time that \(\mathsf {A}\) wins \({\text {OMUF}}^{}_{\mathsf {PMBT}, \mathsf {A}, \ell }(\lambda )\).
. We construct \(X_{1-{b^*}}\) following the key generation algorithm. Queries by \(\mathsf {A}\) to the oracle \(\textsc {Sign}\) are responded in the following way: if the adversary demands issuance for hidden metadata \(b^*\), we use the \(\textsc {Help}\) oracle to return \(W' = \textsc {Help}(t, T') + y_{b^*} S'\); otherwise \(\mathsf {B}\) just follows the signing protocol and computes \(W'\) using \((x_{1-{b^*}}, y_{1-{b^*}})\). The zero-knowledge proof is simulated. Queries to the oracle \(\textsc {Read}\) can still be answered by \(\mathsf {B}\) with the help of the oracle \(\textsc {Ddh}\) available in the game \({\text {CTGDH}}^{}_{\mathsf {GrGen}, \mathsf {B}, \ell }(\lambda )\). Queries to \(\textsc {Verify}\) are trivially dealt with, by answering \(\mathbf{true} \). If at the end of its execution \(\mathsf {A}\) presents forgeries for the bit \(b=b^*\), then by winning condition (a) (cf. Eq. (9)), for all \(i \in [\ell +1]\), \((W_i- y_{b^*}S_i)\) is the CDH of the challenge A with \(\mathsf {H}_t(t_i)\), which we replace with the CTGDH oracle \(\textsc {Target}\) thus presenting \(\ell +1\) CDH solutions for the challenge \(A \in \mathbb {G}\). If the guess \(b^*\) was not correct, then \(\mathsf {B}\) outputs \(\perp \), and we consider the game lost. It follows that \(\mathsf {B}\) wins the game \({\text {CTGDH}}^{}_{\mathsf {GrGen}, \mathsf {B}, \ell }(\lambda )\) half the time that \(\mathsf {A}\) wins \({\text {OMUF}}^{}_{\mathsf {PMBT}, \mathsf {A}, \ell }(\lambda )\).
Theorem 9
If DDH holds for \(\mathsf {GrGen}\) and \(\mathsf {\Pi }_\mathsf {DLEQOR2}\) is a knowledge-sound proof system for relation \(\mathsf {R}_\mathsf {DLEQOR2}\), then \(\mathsf {PMBT}[\mathsf {GrGen}, \mathsf {\Pi }_\mathsf {DLEQOR2}]\) is 2-unlinkable.
The key idea is that adversary can now embed different private metadata bits at issuance time, at most halving the anonymity set. We use the knowledge extractor to partition the sessions in two buckets: \(U_0\), those associated to the bit 0, and \(U_1\), those with bit 1. We sample a biased \(b \in \{0,1\}\) (depending on the distribution of the private metadata bit in the tokens) and select two sessions coming from the same bucket \(U_b\). The probability of success of the adversary will be upper bounded by
 .
.
Theorem 10
If DDH holds for the group generator \(\mathsf {GrGen}\), and \(\mathsf {\Pi }_\mathsf {DLEQOR2}\) is a zero-knowledge proof system for relation \(\mathsf {R}_\mathsf {DLEQOR2}\) then \(\mathsf {PMBT}[\mathsf {GrGen},\mathsf {\Pi }_\mathsf {DLEQOR2}]\) provides private metadata bit with advantage:

where q is the number of queries the adversary makes to \(\mathsf {H}_s\) or \(\textsc {Sign}\).
The proof is done by means of a hybrid argument, where the first hybrid is \({\text {PMB}}^{0}_{\mathsf {A}, \mathsf {PMBT}}(\lambda )\) and the last hybrid is \({\text {PMB}}^{1}_{\mathsf {A}, \mathsf {PMBT}}(\lambda )\). In the first hybrid, instead of generating the proof using the prover \(\mathsf {\Pi }_\mathsf {DLEQOR2}.\!\mathsf {Prove}\) in the \(\textsc {Sign}^\prime \) oracle, we use the zero-knowledge simulator \(\mathsf {\Pi }_\mathsf {DLEQOR2}.\!\mathsf {Sim}\). The advantage in distinguishing is trivially
 . Then, instead of computing the signature as \(W' = x_0 T' + y_0 S'\), it computes \(W' :=x_0 T' + y'S'\), for some
. Then, instead of computing the signature as \(W' = x_0 T' + y_0 S'\), it computes \(W' :=x_0 T' + y'S'\), for some  sampled after the key generation phase. This hybrid can be shown indistinguishable from the previous one under DDH assumption: \((X-x_0G, S', W'-x_0T') \in \mathbb {G}\) is in fact a DDH triple in the previous hybrid, and a random triple now. Using random self-reducibility of DDH we can answer all queries to \(\textsc {Sign}^\prime \) using a single DDH challenge. At this point, we remark that \(W'\) is distributed uniformly at random (because \(y'S'\) is so) and we can therefore swap \(x_0\) with \(x_1\). A final sequence of hybrid replaces \(y'\) with \(y_1\) (again indistinguishable from DDH) and then the simulator with the honest prover. The full proof is available in the full version of this paper
[KLOR20].
sampled after the key generation phase. This hybrid can be shown indistinguishable from the previous one under DDH assumption: \((X-x_0G, S', W'-x_0T') \in \mathbb {G}\) is in fact a DDH triple in the previous hybrid, and a random triple now. Using random self-reducibility of DDH we can answer all queries to \(\textsc {Sign}^\prime \) using a single DDH challenge. At this point, we remark that \(W'\) is distributed uniformly at random (because \(y'S'\) is so) and we can therefore swap \(x_0\) with \(x_1\). A final sequence of hybrid replaces \(y'\) with \(y_1\) (again indistinguishable from DDH) and then the simulator with the honest prover. The full proof is available in the full version of this paper
[KLOR20].
6.1 Enabling Token Verification
The anonymous token scheme \(\mathsf {PMBT}\) (Construction 3) does not provide a meaningful verification algorithm, as it always output \(\mathbf{true} \). Indeed, we note that, given two tokens \((t_0, (S_0, W_0))\) and \((t_1,(S_1, W_1))\), if \(t_0 =t_1\), then \(\big (t^*=t_0=t_1, (S^*=2S_0 - S_1, W^*=2W_0-W_1)\big )\) is a triple of random elements satisfying \(W^*= x_b \mathsf {H}(t^*) + y_b S^*\) only if the same metadata bit b was used. Henceforth, having a verification oracle that checks for the above relation allows an adversary in the game \({\text {PMB}}^{\beta }_{\mathsf {PMBT}, \mathsf {A}}(\lambda )\) to check if two tokens corresponding to the same t were issued with the same private metadata bit.
Instead, we propose to enable such a functionality by combining the \(\mathsf {PMBT}\) scheme with Okamoto–Schnorr Privacy Pass, into one token that has two parts: a token that has no private metadata and can be used for validity verification, and a second token, which provides a private metadata bit. It is important that these two parts could not be separated (they will depend on the same \(\mathsf {H}_t(t), S\) values) and used independently for the purpose of reading the metadata bit. We present in details the design combining Constrs. 2 and 3 in the full version [KLOR20].
Jumping ahead, we can also instantiate this design by combining Constrs. 4 and 5 that do not use NIZK during issuance. In the later case the unlinkability will degrade to 6-unlinkability since the issuer can cause each of the two token to be invalid independently.
7 Removing the NIZKs During Issuance
In this section, we present a general technique for removing the NIZK sent at issuance time in the previous schemes, and replace it with a proof of possession sent only once. We present a formal analysis of it for \(\mathsf {PP}\) and \(\mathsf {PMBT}\) (Constructions 1 and 3). We recall that the role of the NIZK is to provide unlinkability for the user, as they can check that the tokens received are consistent with the issuer’s public parameters. In particular they prevent the issuer from fingerprinting users by using a unique key per user. In this section, we consider a weaker notion of unlinkability, which guarantees that the user either receives a valid token, or a completely random value (unpredictable by the issuer). This implies that the issuer can distinguish valid tokens from invalid tokens since the user cannot verify herself whether they have a valid token or not. In other words, the issuer can partition the users into two sets: one that receives valid tokens, and one that receives invalid tokens. The issuer will be able to identify which of these sets a user belongs to, at redemption time. For a more careful analysis on how this affect the success probability of the adversary in the unlinkability game, we refer the reader to the full version [KLOR20].
7.1 \(\mathsf {PP}\) Without Issuance NIZK
We start with our new construction for the functionality of Privacy Pass. The change that we make is that the user blinds her token hash \(\mathsf {H}_t(t)\) using both multiplicative and additive blinding. The additive part can be removed during the unblinding if the issuer used the correct secret key. Otherwise, the generated token \((t, W) \in \{0,1\}^{\lambda }\times \mathbb {G}\) will be invalid and distributed uniformly at random.
Token issuance for \(\mathsf {PPB}\) (Construction 4).
Construction 4
(Privacy Pass without issuance NIZK). Let \(\mathsf {GrGen}\) be a group generator algorithm; let \(\mathsf {\Pi }_\mathsf {DLOG}\) be a proof system for relation \(\mathsf {R}_\mathsf {DLOG}\); let \(\mathsf {H}_t\) be a random oracle \(\{0,1\}^* \rightarrow \mathbb {G}\). We construct an anonymous token scheme \(\mathsf {PPB}\) defined by the following algorithms:
-
\((\textsf {crs}, \textsf {td}) \leftarrow \mathsf {PPB}.\!\mathsf {Setup}(1^\lambda )\): invoke the group generator \(\varGamma \leftarrow \mathsf {GrGen}(1^\lambda )\) and the CRS generation algorithm of the underlying proof system \((\textsf {pcrs}, \textsf {ptd}) \leftarrow \mathsf {\Pi }_\mathsf {DLOG}.\!\mathsf {Setup}(\varGamma )\). Return \(\textsf {crs}:=(\varGamma , \textsf {pcrs})\) and \(\textsf {td}:=\textsf {ptd}\).
-
\(((X, \pi ), x) \leftarrow \mathsf {PPB}.\!\mathsf {KeyGen}(\textsf {crs})\): sample the secret key
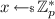 . Define \(\pi \leftarrow \mathsf {\Pi }_\mathsf {DLOG}.\!\mathsf {Prove}(\textsf {pcrs}, X, x)\). Return the public parameters \((X, \pi )\), and the secret key x.
. Define \(\pi \leftarrow \mathsf {\Pi }_\mathsf {DLOG}.\!\mathsf {Prove}(\textsf {pcrs}, X, x)\). Return the public parameters \((X, \pi )\), and the secret key x. -
\(W \leftarrow \langle \mathsf {PPB}.\!\mathsf {User}((X, \pi ), t), \mathsf {PPB}.\!\mathsf {Sign}(x)\rangle \): illustrated in Fig. 9.
-
\(\textit{bool}\leftarrow \mathsf {PPB}.\!\mathsf {Verify}(x, t, W)\): return \(\mathbf{true} \) if \(W = x \mathsf {H}_t(t)\); else, return \(\mathbf{false} \).
Correctness. By correctness of \(\mathsf {\Pi }_\mathsf {DLOG}\), at the end of the protocol the user returns \(\perp \) only with negligible probability. If the user returns \(W \in \mathbb {G}\), then W always satisfies the verification equation, since: \(W = rW' + \rho X = rxr^{-1} (T - \rho G) + \rho X = xT - \rho (xG) + \rho X = xT. \)
Security. \(\mathsf {PPB}\) satisfies unforgeability and 2-unlinkability.
Theorem 11
If CTGDH holds for \(\mathsf {GrGen}\), and \(\mathsf {\Pi }_\mathsf {DLEQ}\) is a zero-knowledge proof system for relation \(\mathsf {\Pi }_\mathsf {DLOG}\), then \(\mathsf {PPB}\) is one-more unforgeable with advantage:

The proof can be found in the full version. Intuitively, unforgeability must hold because the issuer is sending strictly less information than in \(\mathsf {PP}\). The adversary \(\mathsf {A}\) in game \({\text {OMUF}}^{}_{\mathsf {PPB}, \mathsf {A}}(\lambda )\) takes as input the pair \((X, \pi )\), where \(X \in \mathbb {G}\) is the CTGDH challenge, and \(\pi \) is a DLOG proof. By zero-knowledge of \(\mathsf {\Pi }_\mathsf {DLOG}\), the proof can be simulated; the adversary is now asked to return \(\ell +1\) pairs \((t_i, W_i)\), all different, such that \(W_i\) is the CDH of \((X, \mathsf {H}_t(t_i))\). During its execution, the adversary has at disposal the random oracle \(\mathsf {H}_t\) (which behaves exactly as the \(\textsc {Target}\) oracle), the \(\textsc {Verify}\) oracle, which given as input \((Y, W) \in \mathbb {G}^2\) returns 1 if (X, Y, W) is a DH tuple (just as the \(\textsc {Ddh}\) oracle in the game for CTGDH), and the \(\textsc {Sign}\) oracle, which computes at most \(\ell \) times the CDH with an arbitrary group element (just as the \(\textsc {Help}\) oracle in the game for CTGDH).
Theorem 12
Let \(\mathsf {GrGen}\) be a group generator. If \(\mathsf {\Pi }_\mathsf {DLOG}\) is a knowledge-sound proof system for relation \(\mathsf {R}_\mathsf {DLOG}\), then \(\mathsf {PPB}\) is 2-unlinkable with advantage:

First of all, we note that by knowledge soundness of \(\mathsf {\Pi }_\mathsf {DLOG}\), for any adversary \(\mathsf {A}\) that produces th public parameters \((X, \pi )\) with \(X \in \mathbb {G}\), it is possible to extract a witness \(x \in \mathbb {Z}_p\) such that \(x G=X\), except with negligible probability
 . We use this witness to partition the sessions in two sets, \(U_0\) where W is correctly computed, and \(U_1\) where W isn’t. In the latter case, we remark that because the additive blinding \(\rho \in \mathbb {Z}_p\) is sampled uniformly at random, in \(U_1\) all tokens are distributed uniformly at random. In a similar way to Theorem 7, we select two sessions k and j from the same \(U_b\) (for a \(b \in \{0,1\}\) that sampled at random, following the distribution of the open sessions) and swap them. If k and j are in \(U_0\), unlinkability follows the same reasoning used for proving unlinkability of \(\mathsf {PP}\). If k and j are in \(U_1\), then both tokens are uniformly random elements in \(\mathbb {G}\) independent from the elements used at issuance time.
. We use this witness to partition the sessions in two sets, \(U_0\) where W is correctly computed, and \(U_1\) where W isn’t. In the latter case, we remark that because the additive blinding \(\rho \in \mathbb {Z}_p\) is sampled uniformly at random, in \(U_1\) all tokens are distributed uniformly at random. In a similar way to Theorem 7, we select two sessions k and j from the same \(U_b\) (for a \(b \in \{0,1\}\) that sampled at random, following the distribution of the open sessions) and swap them. If k and j are in \(U_0\), unlinkability follows the same reasoning used for proving unlinkability of \(\mathsf {PP}\). If k and j are in \(U_1\), then both tokens are uniformly random elements in \(\mathbb {G}\) independent from the elements used at issuance time.
User Verifiability. The protocol presented in the previous section does not enable the user to verify that she has received valid token at the end of an execution. We can enable such verifiability for any number of tokens at the cost of one additional issuance interaction between the user and the issuer. In particular, let \((t_i, W_i)_{i \in [m]}\) be m tokens that the user has been issued. She sends a token issuance request \(T' = \sum _{i \in [m]} c_i \mathsf {H}_t(t_i)\) where  for \(i \in [m]\). Let W be the issuer’s response after unblinding, then the user checks that \(W = \sum _{i \in [m]} c_i W_i\).
for \(i \in [m]\). Let W be the issuer’s response after unblinding, then the user checks that \(W = \sum _{i \in [m]} c_i W_i\).
If the issuer was honest, then \(W_i = x\mathsf {H}_t(t_i)\) and
Next, we argue that if \(W = \sum _{i \in [m]} c_iW_i\), then the issuer could be cheating on any of the m token executions only with negligible probability. We will prove this by induction on m. Let \(m=1\), then we have \(W = c_1 W_1\) and at the same time \(W_1 \ne x\mathsf {H}_t(t_1)\). By the unlinkability argument above we know that \(W_1\) and hence \(c_1W_1\) are uniformly distributed. Hence, the adversary has only negligible probability to guess the value W.
Now, let us assume that the statement holds for \(m \le k\) and we will be prove it for \(m=k+1\). We have \(W = \sum _{i \in [m]} c_i W_i\) and at the same time there exists an index j such that \(W_j \ne x \mathsf {H}_t(t_j)\). If there is an index k such that \(W_k = x \mathsf {H}_t(t_k)\), then \(W - x \mathsf {H}_t(t_k) = \sum _{i \in [m]\backslash \{k\}} c_i W_i\) and \(j \in [m]\backslash \{k\}\), which contradicts the induction assumption. Therefore, it must be the case that \(W_i \ne x \mathsf {H}_t(t_i)\) for any \(i \in [m]\). However, by the arguments in the unlinkability proof, we know that all \(W_i\)’s, and hence \(\sum _{i \in [m]} c_i W_i\), will be distributed uniformly at random. Hence, the adversary has only negligible probability in guessing the value of W, which concludes the inductive step.
7.2 \(\mathsf {PMBT}\) Without Issuance NIZK
The challenge to generalizing the construction of the previous section to the setting of private metadata is that the user should not find out what metadata bit value the issuer used and hence which public key it should use when unblinding. Our solution will be to have the user run the unblinding with both keys where only one of the resulting values will be a valid token under the corresponding key for the bit value while the other unblinded value will be completely random. When we do this we need to be careful that the issuer who also generates the public keys should not be able to make the two unblinded values correlated, which would open an avenue for fingerprinting.
To guarantee that the unblinded value with the public key that does not correspond to the embedded private metadata bit is random and hence it is independent of the other unblinded value, even in the case when the issuer is misbehaving, we will need to have that the user generate two independent blinded values which it sends in its first message. The issuer will be using only one of the received blinded tokens to sign and embed his metadata bit, however, the user will be unblinding the message coming from the issuer using two independent sets of blinding parameters, which would thwart the issuer from embedding correlations.
Construction 5
(PMBTokens without issuance NIZK). Let \(\mathsf {GrGen}\) be a group generator algorithm; let \(\mathsf {\Pi }_\mathsf {DLOGAND2}\) be a proof system for the relation \(\mathsf {R}_\mathsf {DLOGAND2}\); let \(\mathsf {H}_t, \mathsf {H}_s\) be two random oracles \(\{0,1\}^* \rightarrow \mathbb {G}\). We construct an anonymous token scheme \(\mathsf {PMBTB}\) defined by the following algorithms:
-
\((\textsf {crs}, \textsf {td}) \leftarrow \mathsf {PMBTB}.\!\mathsf {Setup}(1^\lambda )\): invoke the group generator \(\varGamma \leftarrow \mathsf {GrGen}(1^\lambda )\) and the CRS generation algorithm \((\textsf {pcrs}, \textsf {ptd}) \leftarrow \mathsf {\Pi }_\mathsf {DLOGAND2}.\!\mathsf {Setup}(\varGamma )\). Return \(\textsf {crs}:=(\varGamma , \textsf {pcrs})\) and \(\textsf {td}:=\textsf {ptd}\).
-
\(((\mathbf {X}, \pi ), (\mathbf {x}, \mathbf {y})) \leftarrow \mathsf {PMBTB}.\!\mathsf {KeyGen}(1^\lambda )\): let
 be the secret key. Define: $$ \mathbf {X} :=\begin{bmatrix}X_0 \\ X_1\end{bmatrix} :=\begin{bmatrix} x_0G + y_0 H \\ x_1G + y_1 H \end{bmatrix}, $$
be the secret key. Define: $$ \mathbf {X} :=\begin{bmatrix}X_0 \\ X_1\end{bmatrix} :=\begin{bmatrix} x_0G + y_0 H \\ x_1G + y_1 H \end{bmatrix}, $$and let \(\pi \leftarrow \mathsf {\Pi }_\mathsf {DLOGAND2}.\!\mathsf {Prove}(\textsf {pcrs}, \mathbf {X}, (\mathbf {x}, \mathbf {y}))\). The public parameters are \((\mathbf {X}, \pi )\). Return \(((\mathbf {X}, \pi ), (\mathbf {x}, \mathbf {y}))\).
-
\(\sigma \leftarrow \langle \mathsf {PMBTB}.\!\mathsf {User}((\mathbf {X}, \pi ), t), \mathsf {PMBTB}.\!\mathsf {Sign}((\mathbf {x}, \mathbf {y}))\rangle \): illustrated in Fig. 10.
-
\(\textit{bool}\leftarrow \mathsf {PMBTB}.\!\mathsf {Verify}((\mathbf {x}, \mathbf {y}), t, \sigma )\): return \(\mathbf{true} \).
-
\( \mathsf {ind}\leftarrow \mathsf {PMBTB}.\!\mathsf {ReadBit}((\mathbf {x}, \mathbf {y}), t, \sigma )\): read \(\sigma \) as \((S_0, S_1, W_0, W_1) \in \mathbb {G}^4\). Then,
-
(a)
if \(W_0 = x_0\mathsf {H}_t(t) + y_0S_0\) and \(W_1 \ne x_1\mathsf {H}_t(t) + y_1S_1\), return 0;
-
(b)
if \(W_0 \ne x_0\mathsf {H}_t(t) + y_0S_0\) and \(W_1 = x_1\mathsf {H}_t(t) + y_1S_1\), return 1;
-
(c)
else, return \(\perp \).
-
(a)
Token issuance for \(\mathsf {PMBTB}\) (Construction 5).
Correctness. Honestly-generated tokens are always valid, because the verification algorithm \(\mathsf {PMBTB}.\!\mathsf {Verify}\) always outputs \(\mathbf{true} \). We thus focus on Eq. (7). By correctness of the underlying proof system, the protocol aborts only with negligible probability. If the user returns a tuple \((S_0, S_1, W_0, W_1) \in \mathbb {G}^4\), then there exists \(b \in \{0,1\}\) such that:
The probability that the above equation holds for both \(b=0\) and \(b=1\) (in which case, \(\mathsf {PMBTB}.\!\mathsf {ReadBit}\) returns \(\perp \)) is statistically negligible. In fact, if:
we have two possible cases:
-
(a)
\(x_0 = x_1\), which in turn implies that: \( S_0 = {y_1}^{-1}{y_0} S_1\). However, because \(S_0\) is distributed uniformly at random in \(\mathbb {G}\), this happens with probability 1/p.
-
(b)
\(x_0 \ne x_1\), which in turn implies that \(\ \mathsf {H}_t(t) = \frac{1}{x_1-x_0} (y_0 S_0 - y_1 S_1)\), which happens with probability 1/p.
Security. We provide the proofs for the security properties of the construction in the full version.
Theorem 13
If CTGDH holds for the group generator algorithm \(\mathsf {GrGen}\) and \(\mathsf {\Pi }_\mathsf {DLOGAND2}\) is a zero-knowledge proof system for \(\mathsf {R}_\mathsf {DLOGAND2}\), then \(\mathsf {PMBTB}[\mathsf {GrGen},\mathsf {\Pi }_\mathsf {DLOGAND2}]\) is one-more unforgeable with advantage:

Intuitively, unforgeability follows a similar reasoning of Theorem 8 (unforgeability of \(\mathsf {PMBT}\)) except that here, at issuance time, we are sending strictly less information to the user, since we removed the NIZK at issuance time. The proof of knowledge of the discrete log, published at the beginning within the public parameters, can be simulated by zero knowledge.
Theorem 14
If DDH holds for the group generator \(\mathsf {GrGen}\) and \(\mathsf {\Pi }_\mathsf {DLOGAND2}\) is a knowledge-sound proof system for relation \(\mathsf {R}_\mathsf {DLOGAND2}\), then \(\mathsf {PMBTB}[\mathsf {GrGen},\mathsf {\Pi }_\mathsf {DLOGAND2}]\) is 3-unlinkable.
A \(\mathsf {PPT}\) adversary in the game \({\text {UNLINK}}^{}_{\mathsf {PMBTB}, \mathsf {A}}(\lambda )\) can now: compute \(W'\) using \((x_0, y_0)\), using \((x_1, y_1)\), or yet another key. Specifically in the latter case, the token \(\sigma \) will be distributed at random independently from \(W'\). In the full version, we prove that now the adversary can partition the set of open sessions at most in 3, and that therefore the advantage in the game
 .
.
Theorem 15
If DDH holds for the group generator \(\mathsf {GrGen}\) and \(\mathsf {\Pi }_\mathsf {DLOGAND2}\) is a zero-knowledge proof system for relation \(\mathsf {R}_\mathsf {DLOGAND2}\), then \(\mathsf {PMBTB}[\mathsf {GrGen},\mathsf {\Pi }_\mathsf {DLOGAND2}]\) provides private metadata bit with advantage:

where q is the number of queries the adversary makes either to \(\mathsf {H}_s\) or \(\textsc {Sign}\).
As for unforgeability, the proof follows a similar reasoning to the case of \(\mathsf {PMBT}\). We notice that now the issuer is sending strictly less information during signing, and that the zero-knowledge proof \(\pi \) can be simulated.
8 Implementation
We implemented our construction in pure Rust (stable, version 1.41.0), The second generator \(H \in \mathbb {G}\) is chosen by hashing into the group the public generator G. Hashing into the group is done with a Elligator 2 map [Tib14] with SHA-512. Our implementation is not copyrighted and is released in the public domain.Footnote 6
We benchmarked our own implementation on a single thread of an Intel(R) Xeon(R) CPU E5-2650 v4 @ 2.20 GHz, running Ubuntu 18.04.3 LTS (kernel version 4.15.0). They are summarized in Table 2. As expected, Constructions 4 and 5 feature very fast issuance time at a slight increase in the user computation. Our results are between ten and one thousand faster than the previous implementation proposed in [DGS+18] due to the different choiceFootnote 7 of elliptic curve (NIST P-256) as well as the programming language used.
Notes
- 1.
- 2.
- 3.
- 4.
In Privacy Pass the resulting value \(x \mathsf {H}_t(t)\) is used for the derivation of a HMAC key in order to avoid credential hijacking. We cover token hijacking in the full version. Throughout this work, we assume that the communication channel between user and issuer is encrypted and authenticated.
- 5.
Consider, e.g., the following practical scenario: the issuer is suspecting that it is targeted by a DoS attack, and decides to tag users that it believes are controlled by a bot using the private metadata bit. The private metadata bit property ensures it is difficult for anyone, but the issuer, to learn how malicious traffic is classified.
- 6.
- 7.
We comment on the choice of curve and its security in the full version of this paper [KLOR20].
References
Abdalla, M., Namprempre, C., Neven, G.: On the (im)possibility of blind message authentication codes. In: Pointcheval, D. (ed.) CT-RSA 2006. LNCS, vol. 3860, pp. 262–279. Springer, Heidelberg (2006). https://doi.org/10.1007/11605805_17
Blazy, O., Fuchsbauer, G., Pointcheval, D., Vergnaud, D.: Signatures on randomizable ciphertexts. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 403–422. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_25
Boneh, D., Lynn, B., Shacham, H.: Short signatures from the Weil pairing. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 514–532. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_30
Bellare, M., Micciancio, D., Warinschi, B.: Foundations of group signatures: formal definitions, simplified requirements, and a construction based on general assumptions. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 614–629. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_38
Bellare, M., Namprempre, C., Pointcheval, D., Semanko, M.: The one-more-RSA-inversion problems and the security of Chaum’s blind signature scheme. J. Cryptol. 16(3), 185–215 (2003)
Boldyreva, A.: Threshold signatures, multisignatures and blind signatures based on the Gap-Diffie-Hellman-Group signature scheme. In: Desmedt, Y.G. (ed.) PKC 2003. LNCS, vol. 2567, pp. 31–46. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36288-6_3
Blazy, O., Pointcheval, D., Vergnaud, D.: Compact round-optimal partially-blind signatures. In: Visconti, I., De Prisco, R. (eds.) SCN 2012. LNCS, vol. 7485, pp. 95–112. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32928-9_6
Camenisch, J.: Efficient and generalized group signatures. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 465–479. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_32
Chaum, D.: Blind signatures for untraceable payments. In: CRYPTO, pp. 199–203. Plenum Press, New York (1982)
Camenisch, J., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 93–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_7
Chase, M., Meiklejohn, S., Zaverucha, G.: Algebraic MACs and keyed-verification anonymous credentials, pp. 1205–1216 (2014)
Chaum, D., Pedersen, T.P.: Wallet databases with observers. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 89–105. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_7
Chaum, D., van Heyst, E.: Group signatures. In: Davies, D.W. (ed.) EUROCRYPT 1991. LNCS, vol. 547, pp. 257–265. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-46416-6_22
Davidson, A., Goldberg, I., Sullivan, N., Tankersley, G., Valsorda, F.: Privacy pass: bypassing internet challenges anonymously. PoPETs 2018(3), 164–180 (2018)
Everspaugh, A., Chatterjee, R., Scott, S., Juels, A., Ristenpart, T.: The Pythia PRF service. In: USENIX Security Symposium, pp. 547–562. USENIX Association (2015)
Fuchsbauer, G., Hanser, C., Kamath, C., Slamanig, D.: Practical round-optimal blind signatures in the standard model from weaker assumptions. In: Zikas, V., De Prisco, R. (eds.) SCN 2016. LNCS, vol. 9841, pp. 391–408. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44618-9_21
Fuchsbauer, G., Hanser, C., Slamanig, D.: Practical round-optimal blind signatures in the standard model. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 233–253. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_12
Fischlin, M.: Round-optimal composable blind signatures in the common reference string model. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 60–77. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_4
Fuchsbauer, G., Plouviez, A., Seurin, Y.: Blind schnorr signatures in the algebraic group model. Cryptology ePrint Archive, Report 2019/877 (2019)
Garg, S., Gupta, D.: Efficient round optimal blind signatures. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 477–495. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_27
Ghadafi, E.: Formalizing group blind signatures and practical constructions without random oracles. In: Boyd, C., Simpson, L. (eds.) ACISP 2013. LNCS, vol. 7959, pp. 330–346. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39059-3_23
Herranz, J., Laguillaumie, F.: Blind ring signatures secure under the chosen-target-CDH assumption. In: Katsikas, S.K., López, J., Backes, M., Gritzalis, S., Preneel, B. (eds.) ISC 2006. LNCS, vol. 4176, pp. 117–130. Springer, Heidelberg (2006). https://doi.org/10.1007/11836810_9
Jarecki, S., Kiayias, A., Krawczyk, H.: Round-optimal password-protected secret sharing and T-PAKE in the password-only model. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 233–253. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_13
Jarecki, S., Krawczyk, H., Resch, J.K.: Threshold partially-oblivious PRFs with applications to key management. IACR Cryptology ePrint Archive, 2018/733 (2018)
Kreuter, B., Lepoint, T., Orru, M., Raykova, M.: Anonymous tokens with private metadata bit. Cryptology ePrint Archive, Report 2020/072 (2020). https://eprint.iacr.org/2020/072
Lysyanskaya, A., Ramzan, Z.: Group blind digital signatures: a scalable solution to electronic cash. In: Hirchfeld, R. (ed.) FC 1998. LNCS, vol. 1465, pp. 184–197. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055483
Okamoto, T.: Provably secure and practical identification schemes and corresponding signature schemes. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 31–53. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_3
Okamoto, T., Pointcheval, D.: The gap-problems: a new class of problems for the security of cryptographic schemes. In: Kim, K. (ed.) PKC 2001. LNCS, vol. 1992, pp. 104–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44586-2_8
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptol. 13, 361–396 (2000)
Ramzan, Z.: Group blind digital signatures: theory and applications (2013). https://dspace.mit.edu/bitstream/handle/1721.1/80561/43557700-MIT.pdf?sequence=2&isAllowed=y
Seo, J.H., Cheon, J.H.: Beyond the limitation of prime-order bilinear groups, and round optimal blind signatures. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 133–150. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_8
Schnorr, C.P.: Security of blind discrete log signatures against interactive attacks. In: Qing, S., Okamoto, T., Zhou, J. (eds.) ICICS 2001. LNCS, vol. 2229, pp. 1–12. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45600-7_1
Schnorr, C.P.: Enhancing the security of perfect blind DL-signatures. Inf. Sci. 176(10), 1305–1320 (2006)
Tsang, P.P., Au, M.H., Kapadia, A., Smith, S.W.: Blacklistable anonymous credentials: blocking misbehaving users without TTPs. In: ACM Conference on Computer and Communications Security, pp. 72–81. ACM (2007)
Tibouchi, M.: Elligator squared: uniform points on elliptic curves of prime order as uniform random strings. In: Christin, N., Safavi-Naini, R. (eds.) FC 2014. LNCS, vol. 8437, pp. 139–156. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45472-5_10
Acknowledgments
The authors thank Fabrice Benhamouda, Dan Boneh, Charlie Harrison, Michael Kleber, Hugo Krawczyk, Steven Valdez, and Moti Yung for helpful discussions. A part this work was completed while Michele Orrù was an intern at Google and at Web3 Foundation.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Kreuter, B., Lepoint, T., Orrù, M., Raykova, M. (2020). Anonymous Tokens with Private Metadata Bit. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12170. Springer, Cham. https://doi.org/10.1007/978-3-030-56784-2_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-56784-2_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56783-5
Online ISBN: 978-3-030-56784-2
eBook Packages: Computer ScienceComputer Science (R0)




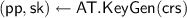 , the key generation algorithm that generates a private key
, the key generation algorithm that generates a private key
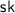 along with a set of public parameters
along with a set of public parameters 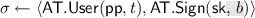 , the token issuance protocol, that involves interactive algorithms
, the token issuance protocol, that involves interactive algorithms 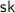
 . At the end of the interaction, the issuer outputs nothing, while the user outputs
. At the end of the interaction, the issuer outputs nothing, while the user outputs  , the verification algorithm that takes as input the private key
, the verification algorithm that takes as input the private key
 and a token
and a token  , the metadata extraction algorithm that takes as input the private key
, the metadata extraction algorithm that takes as input the private key
 , and a token
, and a token 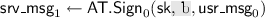 ;
;



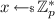 , that will constitute the secret key. Let
, that will constitute the secret key. Let 
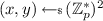 . Let
. Let 
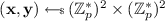 be the secret key. Define the public parameters as:
be the secret key. Define the public parameters as: 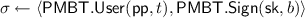 : illustrated in Fig.
: illustrated in Fig. 
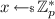 . Define
. Define  be the secret key. Define:
be the secret key. Define: 
