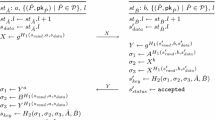Leakage-Resilient Key Exchange and Two-Seed Extractors

Abstract

Can Alice and Bob agree on a uniformly random secret key without having any truly secret randomness to begin with? Here we consider a setting where Eve can get partial leakage on the internal state of both Alice and Bob individually before the protocol starts. They then run a protocol using their states without any additional randomness and need to agree on a shared key that looks uniform to Eve, even after observing the leakage and the protocol transcript. We focus on non-interactive (one round) key exchange (NIKE), where Alice and Bob send one message each without waiting for one another.

We first consider this problem in the symmetric-key setting, where the states of Alice and Bob include a shared secret as well as individual uniform randomness. However, since Eve gets leakage on these states, Alice and Bob need to perform privacy amplification to derive a fresh secret key from them. Prior solutions require Alice and Bob to sample fresh uniform randomness during the protocol, while in our setting all of their randomness was already part of their individual states a priori and was therefore subject to leakage. We show an information-theoretic solution to this problem using a novel primitive that we call a two-seed extractor, which we in turn construct by drawing a connection to communication-complexity lower-bounds in the number-on-forehead (NOF) model.

We then turn to studying this problem in the public-key setting, where the states of Alice and Bob consist of independent uniform randomness. Unfortunately, we give a black-box separation showing that leakage-resilient NIKE in this setting cannot be proven secure via a black-box reduction under any game-based assumption when the leakage is super-logarithmic. This includes virtually all assumptions used in cryptography, and even very strong assumptions such as indistinguishability obfuscation ($\textit{i}\mathcal {O}$). Nevertheless, we also provide positive results that get around the above separation:

• We show that every key exchange protocol (e.g., Diffie-Hellman) is secure when the leakage amount is logarithmic, or potentially even greater if we assume sub-exponential security without leakage.

• We notice that the black-box separation does not extend to schemes in the common reference string (CRS) model, or to schemes with preprocessing, where Alice and Bob can individually pre-process their random coins to derive their secret state prior to leakage. We give a solution in the CRS model with preprocessing using bilinear maps. We also give solutions in just the CRS model alone (without preprocessing) or just with preprocessing (without a CRS), using $\textit{i}\mathcal {O}$ and lossy functions.

1 Introduction

Leakage-resilient cryptography [1, 2, 3, 17, 20, 23, 28, 30, ...] studies the security of cryptosystems when the adversary can get some partial information about the secret keys of honest users. However, in almost all cases, the schemes rely on some leak-free randomness to guarantee security. For example, leakage-resilient encryption [1, 30] only guarantees security when the adversary gets leakage on the secret key, but requires the encryption randomness to be leak-free. In fact, leakage-resilience is closely related to cryptography with imperfect randomness (conditioned on the leakage, the randomness is no longer uniform) where it was shown that many cryptographic tasks are impossible with imperfect randomness [15].

In this work, we study the question of leakage-resilient key exchange, where Alice and Bob wish to agree on a nearly uniform secret key by communicating over a public channel whose contents are being observed by an adversary Eve. Before the protocol starts, Eve can additionally get partial leakage on the internal states of each of Alice and Bob individually. In particular, Eve can choose two functions $f_A, f_B$ with $\ell$-bit output, where $\ell$ is some leakage bound, and learn the output of these functions when applied on the states of Alice and Bob respectively. We assume that the state of each user includes all of the randomness that will be available to them during the protocol and they cannot sample any fresh randomness after the leakage occurs. Throughout this work, we focus on non-interactive key-exchange (NIKE) protocols (e.g., in the style of Diffie-Hellman key exchange) where Alice and Bob each non-adaptively send one message as a function of their state.

Symmetric-Key Setting. We first study leakage-resilient NIKE in the symmetric-key setting, where Alice and Bob share a uniformly random secret $\mathsf {sk}$. Each of them has some additional independent randomness $r_A,r_B$ and their states are $\mathsf {state}_A = (\mathsf {sk}, r_A)$ and $\mathsf {state}_B = (\mathsf {sk}, r_B)$ respectively. The adversary Eve can get $\ell$ bits of leakage on each of $\mathsf {state}_A$ and $\mathsf {state}_B$, and therefore the secret key $\mathsf {sk}$ is no longer fully secure from her point of view. Alice and Bob wish to run a protocol to derive a fresh key k that looks (nearly) uniformly random to Eve. We study this problem in the information-theoretic setting.

The above problem is similar to that of privacy amplification [6,7,8, 27], where Alice and Bob have a weakly random shared secret and want to agree on a (nearly) uniform key. The crucial difference is that privacy amplification allows Alice and Bob to sample fresh randomness, whereas our problem does not. In particular, the privacy amplification problem can be easily solved using a (strong) seeded randomness extractor $\mathsf {Ext}$: Alice chooses a fresh random seed $r_A$ that she sends to Bob, and then both Alice and Bob set their key to be $k = \mathsf {Ext}(\mathsf {sk};r_A)$. However, this solution does not work in our setting if we think of $r_A$ as a part of Alice’s state, since the adversary can then get leakage on k via leakage on $\mathsf {state}_A=(\mathsf {sk},r_A)$.

Instead, we introduce a new primitive called a (strong) two-seed extractor where two seeds $r_A,r_B$ are used to extract randomness $k = \mathsf {Ext}(\mathsf {sk}; r_A,r_B)$. We require that the extracted randomness looks uniform even to an adversary that gets partial leakage on each of the tuples $(\mathsf {sk}, r_A)$ and $(\mathsf {sk}, r_b)$ together with the seeds $r_A,r_B$. Such extractors do not seem to follow easily from standard (strong) seeded extractors or even two-source extractors. Instead, we construct two-seed extractors by drawing a new connection to communication-complexity lower bounds in the number-on-forehead model [4]. Using two-seed extractors, we can easily solve our problem by having Alice and Bob exchange the messages $r_A,r_B$ respectively and having them agree on the new key $k = \mathsf {Ext}(\mathsf {sk}; r_A,r_B)$.

As our final result in this setting, we show that if Alice and Bob have a shared secret of length n, we get a scheme where the randomness $r_A,r_B$ is of length O(n), we tolerate a leakage bound of $\ell = \varOmega (n)$, the exchanged key k is of length $\varOmega (n)$, and the statistical distance from uniform is $\epsilon = 2^{-\varOmega (n)}$. It remains an interesting open problem to optimize the constants in the scheme.

Public-Key Setting: A Negative Result. We next turn to studying leakage-resilient NIKE in the public-key setting, where the states of Alice and Bob consist of independent uniform randomness $\mathsf {state}_A = r_A$ and $\mathsf {state}_B = r_B$ with no shared key.

We begin by giving a black-box separation showing that such schemes cannot be proven secure via a black-box reduction under any “(single-stage) game-based assumption,” when the leakage bound $\ell$ is super-logarithmic in the security parameter. Game-based assumptions are ones that can be expressed via a game between a (potentially inefficient) challenger and a stateful adversary, where any polynomial-time adversary should have at most a negligible advantage. In particular, this includes essentially all assumptions used in cryptography such as DDH and LWE, and even very strong assumptions such as the existence of indistinguishability obfuscation ($\textit{i}\mathcal {O}$). Our results rule out black-box reductions that treat the adversary as well as the leakage-functions as a black box, which is the case for all known positive results in leakage-resilient cryptography we are aware of. Our separation closely follows the framework of [35], which gave similar separations for other leakage-resilient primitives (e.g., leakage-resilient injective one-way functions).

Pinpointing the above barrier allows us to look for ways to overcome it. We identify three avenues toward getting around the negative result, and follow them to get positive results.

Public-Key Setting: Small Leakage. The first and most obvious avenue is to consider small leakage, where $\ell$ is only logarithmic in the security parameter. Interestingly, some types of cryptosystems (e.g., one-way functions, signatures, public-key encryption, weak pseudorandom functions) are known to be automatically secure with small leakage while others (pseudorandom generators/functions, semantically secure symmetric-key encryption) are known not to be [16, 32]. Where does leakage-resilient NIKE fit in? The work of [16] gave a partial characterization of primitives that are automatically secure, but it does not appear to capture NIKE directly. Instead, we adapt the techniques of [16] for our purposes and show that any NIKE protocol is automatically secure when the leakage $\ell$ is logarithmic. The result also extends to allowing larger leakage $\ell$ by assuming stronger (sub-exponential) security of the underlying NIKE.

As an example, this shows that the Diffie-Hellman key agreement is secure with small leakage: even if an adversary gets small leakage on $r_A$ and $r_B$ individually and then sees $g^{r_A}, g^{r_B}$, the exchanged key $g^{r_Ar_B}$ is indistinguishable from uniform.

Public-Key Setting: CRS or Preprocessing. The other two avenues for overcoming the negative result require us to add some flexibility to our setting to make the black-box separation fail. We can consider schemes in the common reference string (CRS) model, where the honest parties as well as the adversary get access to a CRS generated from some specified distribution. Note that, in this setting, the leakage functions can depend on the CRS. Alternately, we can consider schemes with preprocessing, where Alice and Bob can individually preprocess their random coins to derive their secret states prior to leakage. In particular, instead of having the two states $r_A, r_B$ consist of uniformly random coins, we allow $r_A \leftarrow \mathsf {Gen}(\rho _A), r_B \leftarrow \mathsf {Gen}(\rho _B)$ to be sampled from some specified distribution using uniformly random coins $\rho _A,\rho _B$. We assume the adversary only gets leakage on the secret states $r_A, r_B$ but not on the underlying random coins $\rho _A,\rho _B$ used to sample them.

We construct a leakage-resilient NIKE using bilinear maps, which simultaneously requires a CRS and preprocessing. It can flexibly tolerate any polynomial leakage bound $\ell$ with states of size $|r_A|, |r_B| = O(\ell )$. We prove security under either the subgroup decision assumption in composite-order bilinear groups or the decision-linear (DLIN) assumption in prime order groups. Interestingly, we rely on two-seed extractors, which solved the problem in the symmetric setting, as a crucial tool to aid our construction in the public-key setting.

We also give an alternate construction of leakage-resilient NIKE using indistinguishability obfuscation ($\textit{i}\mathcal {O}$) and lossy functions, which can be initialized with either just a CRS (without preprocessing) or just preprocessing (without a CRS). It can flexibly tolerate any polynomial leakage $\ell$ with states of size $(2+o(1))\ell$.

Other Related Work. Prior works have proposed constructions of leakage-resilient NIKE, albeit under a leak-free hardware assumption, which, in particular, gives both parties access to some (limited) leak-free randomness during the protocol execution [11, 12]. These results do not address the central goal of our work, which is for two parties to non-interactively agree on a shared key without relying on any fresh randomness after the leakage occurs.

Organization. In Sect. 4, we define and construct leakage-resilient symmetric-key NIKE and two-seed extractors. In Sect. 5, we define leakage-resilient NIKE in the public-key setting. In Sect. 6, we give a black-box separation of leakage-resilient NIKE from any single-stage assumption. In Sect. 7, we build a leakage-resilient NIKE in the CRS model with preprocessing from bilinear maps over composite-order groups.

2 Technical Overview

2.1 Symmetric-Key NIKE

We first consider the problem of leakage-resilient NIKE in the symmetric-key setting, where Alice and Bob start with a secret $\mathsf {sk}$, and want to agree on a fresh uniform key k. We assume they each have internal randomness $r_A$ and $r_B$, respectively. Here we want security to hold even given the protocol transcript together with leakages on the states of both Alice and Bob, $\mathsf {state}_A = (\mathsf {sk}, r_A)$ and $\mathsf {state}_B = (\mathsf {sk}, r_B)$, prior to the protocol execution. We study this problem in the information-theoretic setting.

We remark that the particular case when the messages sent by Alice and Bob consist of their entire randomness $r_A$ and $r_B$ corresponds to a natural notion of randomness extractors that we name (strong) two-seed extractors. Namely, a (strong) two-seed extractor $\mathsf {Ext}(x;r_A,r_B)$ uses two seeds $r_A,r_B$ to extract randomness from a high-entropy source x in a setting where the distinguisher gets leakages on $(x,r_A)$ and $(x,r_B)$, as well as the entire seeds $r_A$ and $r_B$. Given such an extractor, Alice and Bob, sharing a secret key $x = \mathsf {sk}$ can send their individual randomness $r_A$ and $r_B$ respectively to each other and compute $k = \mathsf {Ext}(x;r_A,r_B)$ as the exchanged key. Leakage resilience of this symmetric-key NIKE exactly follows from the security of the two-seed extractor described above.

We initially suspected that there should be simple solutions to the two-seed extractor problem via standard (strong) seeded extractors and/or two-source extractors. For example, we thought of applying a 2-source extractor on $(r_A,r_B)$ to derive a seed $s = 2\mathsf {Source}\mathsf {Ext}(r_A,r_B)$ and then plugging it into a strong seeded extractor to extract $k = \mathsf {Seeded}\mathsf {Ext}(x; s)$. Our intuition was that the leakage would not be able to predict s and therefore could not leak any information on x that depends on s. However, we were unable to prove security of this candidate (or other simple variants). The problem is that, although the leakage cannot predict s, it can cause x to be correlated with s once $r_A,r_B$ are made public. We leave it as an open problem to explore the possibility of this construction or some variant and either show it secure via a more complex argument or find counter-examples.

Instead, we construct two-seed extractors by leveraging a connection with communication complexity lower bounds in the number-on-forehead (NOF) model [4]. Such lower bounds were also recently used in the context of leakage-resilient secret sharing in [24]. At a high level, the NOF communication complexity of a boolean function $f:(x_1, \cdots , x_N) \rightarrow \{0,1\}$ is the minimal transcript size required to predict f with noticeable probability, over protocols where every party can exactly see all the others parties’ inputs (but not their own; imagine it is on their forehead), and where parties speak one at a time. A NOF lower bound says that no such communication protocol of transcript length $\ell$ is sufficient to predict the output of f on uniformly random inputs.

To see the connection with two-seed extractors, consider the case where $N=3$ and think of $x_1=x, x_2 = r_A, x_3=r_B$. Then an NOF lower bound implies that small leakage on each of the tuples $(x,r_A), (x,r_B), (r_A,r_B)$ does not allow one to predict $\mathsf {Ext}(x;r_A,r_B) {\mathop {=}\limits ^{\mathsf {def}}}f(x_1,x_2,x_2)$. However, in the setting of (strong) two-seed extractors, the adversary does not just get leakage on $(r_A,r_B)$ but rather gets the entire values $r_A,r_B$ in full. We show that security is preserved in the latter setting. At a high level, if a distinguisher succeeds in the latter setting given $r_A,r_B$ in full, then we could also run that distinguisher as the leakage on $(r_A,r_B)$ to distinguish in the former setting. This is not entirely accurate, since the distinguisher in the latter setting also expects to get the challenge value z which is either $z = \mathsf {Ext}(x;r_A,r_B)$ or z uniform, while leakage on $(r_A,r_B)$ in the former setting cannot depend on z. However, we can remedy this by guessing z ahead of time and taking a statistical security loss proportional to the length of the extracted output.

Combining the above with explicit constructions of efficiently computable boolean functions f with high NOF communication complexity [4, 13], we get two-seed extractors with $|x|=|r_A|=|r_B| =n$ that tolerate $\ell = \varOmega (n)$ leakage and have security $2^{-\varOmega (n)}$, but only extract 1 bit of output. We show a simple generic method to get output length $m=\varOmega (n)$ by choosing m independent seeds $r_A=(r_A^1,\ldots ,r_A^m),r_B= (r_B^1,\ldots ,r_B^m)$ and outputting $\mathsf {Ext}(x;r_A^i,r_B^i)_{i=1}^m$. However, this leads to seed length $\varOmega (n^2)$. We also give an alternate construction using the techniques of [14] that relies on the linearity of the underlying 1-bit extractor and allows us to extract $\varOmega (n)$ bits while preserving the seed length.

2.2 A Black-Box Separation

In the public-key setting, we show that it is impossible to construct leakage-resilient NIKE with perfect correctness, and prove security via a black-box reduction from any single-stage game assumption (also called cryptographic games in  [21, 35]). An assumption is a single-stage game assumption if it can be written in the format of an interactive game between a (potentially inefficient) challenger and a single stateful adversary, where the challenger decides whether or not the adversary succeeded at the end of the game. The assumption states that no polynomial time adversary can succeed with better than negligible probability. (This is a more general class than falsifiable assumptions [18, 29], where the challenger is also required to be efficient.) Such single-stage game assumptions capture essentially all standard assumptions used in cryptography, such as the hardness of DDH, Factoring or LWE, as well as less standard assumptions such as the security of indistinguishability obfuscation $\textit{i}\mathcal {O}$.

However, the security definition for leakage-resilient NIKE (and most other leakage-resilient primitives) is not a single-stage game. This is because the adversary consists three separate components—the two leakage functions and the distinguisher—that cannot fully communicate together or keep arbitrary state between invocations. In particular, the distinguisher does not get to see the inputs given to the leakage functions as this would make its task trivial. It was already observed in [35] that this potentially allows us to separate some cases of leakage-resilient security from all single-stage game assumptions. However, it was only shown to hold for a few very select cases. For example, a black-box separation was given for leakage-resilient one-way permutations with sufficiently large leakage, but not for one-way functions; the latter can be easily constructed from any standard one-way function. Where does leakage-resilient NIKE fit in?

In this work, we use the framework of [35] to separate leakage-resilient NIKE from all single-stage game assumptions. In fact, our separation even rules out “unpredictable NIKE” where the adversary has to predict the entire exchanged key, rather than just distinguish it from uniform. The proof follows the “simulatable attacker paradigm”. We construct an inefficient attacker $\mathcal {A}$ that breaks the security of the primitive using brute force. However, by constructing $\mathcal {A}$ carefully, we show that there also exists an efficient simulator $\mathcal {S}$ such that no (even inefficient) distinguisher can distinguish between black-box access to $\mathcal {A}$ versus $\mathcal {S}$. The attacker $\mathcal {A}= (\mathcal {A}{.}f_A, \mathcal {A}{.}f_B, \mathcal {A}{.}\mathsf {Pred})$ is a multi-stage attacker consisting of three separate entities which do not communicate or keep state between invocations: the two leakage functions $\mathcal {A}{.}f_A, \mathcal {A}{.}f_B$ and the predictor $\mathcal {A}{.}\mathsf {Pred}$ who predicts the exchanged key given the leakage and the protocol transcript. However, the simulator $\mathcal {S}= (\mathcal {S}{.}f_A, \mathcal {S}{.}f_B, \mathcal {S}{.}\mathsf {Pred})$ is a single fully stateful entity and can remember any inputs given to $\mathcal {S}{.}f_A, \mathcal {S}{.}f_B$ and use them to answer calls to $\mathcal {S}{.}\mathsf {Pred}$. Therefore, $\mathcal {S}$ is not a valid attacker on leakage-resilient NIKE. Nevertheless, if we had a black-box reduction from any single-stage assumption, then the reduction would have to break the assumption given black-box oracle access to $\mathcal {A}$. However, since the reduction and the assumption challenger together cannot distinguish between black-box access to $\mathcal {A}$ versus $\mathcal {S}$, the reduction would also break the assumption given the latter. But this means that the reduction together with $\mathcal {S}$ give a fully efficient attack against the assumption and therefore the assumption must be insecure to begin with!

The high level idea of how to construct $\mathcal {A}$ and $\mathcal {S}$ is simple. The leakage function $\mathcal {A}{.}f_A$ gets as input Alice’s randomness $r_A$, computes the protocol message $p_A$ that Alice will send as a function of $r_A$, and outputs a random $\ell$-bit hash $\sigma _A = H(p_A)$ as the leakage. The leakage function $\mathcal {A}{.}f_B$ works analogously. The predictor $\mathcal {A}{.}\mathsf {Pred}(p_A,p_B,\sigma _A,\sigma _B)$ gets the protocol messages $p_A,p_B$ and the leakages $\sigma _A,\sigma _B$: it checks if $\sigma _A = H(p_A)$ and $\sigma _B = H(p_B)$ and if this does not hold it outputs $\bot$; otherwise, it performs a brute-force search on $p_A,p_B$ to recover the exchanged key k and outputs it. We think of H as a completely random function, which is part of the description of the inefficient attacker $\mathcal {A}$. The simulator $\mathcal {S}$ simulates the leakage queries to $\mathcal {S}{.}f_A,\mathcal {S}{.}f_B$ by keeping a table of the inputs $r_A$ and $r_B$ that were queried so far and simulating H by choosing its outputs randomly on the fly for each new corresponding $p_A$ or $p_B$. It simulates the predictor $\mathcal {S}{.}\mathsf {Pred}(p_A,p_B,\sigma _A,\sigma _B)$ by checking its table to see if it contains some values $r_A,r_B$ that yield protocol messages $p_A,p_B$ and on which the leakage functions outputted $\sigma _A,\sigma _B$ respectively; if so, it uses these values to efficiently recover the exchanged key k and else it outputs $\bot$. If the key exchange has perfect correctness, then the only way to to distinguish between oracle access to $\mathcal {A}$ versus $\mathcal {S}$ is to “guess” some valid value $\sigma _A = H(p_A)$ or $\sigma _B = H(p_B)$ without querying the leakage functions, and the probability of this happening is $2^{-\ell }$. Therefore, if $\ell$ is super-logarithmic, then $\mathcal {A}$ and $\mathcal {S}$ are indistinguishable with polynomially many queries except with negligible probability.

2.3 Circumventing the Black-Box Separation

Unfortunately, we are not aware of any useful non-black-box techniques in the context of leakage-resilient cryptography. Therefore, to circumvent the black-box separation, we consider two options. First, we consider the case of small leakage, where $\ell$ is logarithmic in the security parameter. Second, we consider extensions of the basic NIKE setting that are not covered by the negative result.

The Small Leakage Setting. Our black-box impossibility result holds whenever the size of the leakage is super-logarithmic in the security parameter. It also only applies to poly/negligible single-stage assumptions that require polynomial-time attackers to have negligible success probability, but does not extend to assuming stronger levels of security. We demonstrate that this dependence on leakage size is in fact “tight.” In particular, we show that any NIKE that is secure in a setting without leakage is also automatically leakage-resilient when the leakage bound $\ell$ is logarithmic in the security parameter. This can be extended to leakage bound $\ell = \omega (\log \lambda )$ if the original NIKE has $\mathrm{poly}(2^{\ell })$-security without leakage.

Similar results were previously known to hold for all unpredictability primitives (e.g., one-way functions, message-authentication codes, signatures, etc.), where the goal of the attacker is to win some game with non-negligible probability. In such cases, it is always possible to guess the small leakage and get a $2^\ell$ loss in security. It is also known that similar positive results hold for some but not all indistinguishability primitives, where the goal of the attacker is to win some game with probability that is non-negligibly larger than 1/2. In particular, it holds for public-key encryption, CPA-secure symmetric-key encryption, and weak pseudorandom functions, but it does not hold for pseudorandom generators, pseudorandom functions, or one-time semantically secure symmetric-key encryption; in all of the latter cases even 1 bit of leakage can completely break security (see [16, 32]). The aforementioned positive results can be proven using techniques due to [5, 16] showing that any indistinguishability primitive satisfying a so-called “square friendliness” property is resilient to small leakage. However, it is not a priori clear if these techniques apply to leakage-resilient NIKE.

To illustrate the difficulty, we briefly recall what it means for a generic (indistinguishability) primitive to be “square-friendly” in the sense of  [16]. Take an arbitrary partition of the challenger’s random coins $\mathsf {rand}_{\mathcal{C}}$ into $\mathsf {rand}_{\mathcal{C}} = (\mathsf {rand}^{\text {fix}}_{\mathcal{C}},\mathsf {rand}^{\text {exp}}_{\mathcal{C}})$ (e.g. for CPA-secure symmetric-key encryption, $\mathsf {rand}^{\text {fix}}_{\mathcal{C}}$ could be the randomness of the secret key while $\mathsf {rand}^{\text {exp}}_{\mathcal{C}}$ could be the challenge bit and the encryption randomness for chosen plaintext queries). The following “square-security” game is then defined with respect to this partition: an attacker (for the original primitive) is asked to play the standard security game twice, where in the first run the challenger samples both $\mathsf {rand}^{\text {fix}}_{\mathcal{C}}$ and $\mathsf {rand}^{\text {exp}}_{\mathcal{C}}$ at random as in the standard game, but in the second run, the challenger re-uses the same $\mathsf {rand}^{\text {fix}}_{\mathcal{C}}$ coins and re-samples fresh $\mathsf {rand}^{\text {exp}}_{\mathcal{C}}$ coins. The attacker wins the square-security game only if it obtains the same result in both runs (win-win or lose-lose); square-security holds if any efficient attacker’s can only win the square-security game with probability negligibly greater than its chance of losing. [16] refer to a primitive as “square-friendly” if standard security implies square security. As previously mentioned, [16] prove that any square-friendly primitive with $\mathrm{poly}(2^\ell )$-security can withstand $\ell$ bits of leakage on $\mathsf {rand}^{\text {fix}}_{\mathcal{C}}$.

In the NIKE setting, we would like to argue security even given leakage on $r_A$ and $r_B$, where $r_A$ and $r_B$ and Alice and Bob’s secret values. A naive attempt to invoke the [16] lemma might set $\mathsf {rand}^{\text {fix}}_{\mathcal{C}} = (r_A,r_B)$, but then leakage-resilience/square-friendliness cannot possibly hold since even 1 bit of leakage on $\mathsf {rand}^{\text {fix}}_{\mathcal{C}}$ completely breaks security (simply leak the first bit of the shared key).

Instead, we take the following two-step approach. We first consider an alternate partitioning of the challenger’s randomness where $\mathsf {rand}^{\text {fix}}_{\mathcal{C}} = r_A$, and $r_B$ is now viewed as part of the experiment randomness $\mathsf {rand}^{\text {exp}}_{\mathcal{C}}$. Under this partitioning, the NIKE security experiment is square-friendly, but now the [16] lemma only implies security given leakage on $r_A$ alone.

To handle independent leakage on $r_A$ and $r_B$, we consider yet another partitioning of the challenger’s randomness. However, we start from a syntactically different NIKE security game—parameterized by leakage function $f_A$—in which the attacker is given leakage $f_A(r_A)$ on Alice’s random coins in addition to Alice and Bob’s public values. By our previous argument, security of the original NIKE scheme implies security of this modified primitive provided $f_A$ has bounded-length outputs. Since we want to handle leakage on Bob’s coins $r_B$, we partition the challenger’s random coins so that $\mathsf {rand}^{\text {fix}}_{\mathcal{C}} = r_B$, and $r_A$ is now part of $\mathsf {rand}^{\text {exp}}_{\mathcal{C}}$. We prove that this is indeed square-friendly, so by [16], security holds with independent leakage on $r_A$ and $r_B$.

Adding Setups: CRS or Preprocessing. On an intuitive level, our black-box separation result went through because, when everything can leak, there is no meaningful place for a reduction to embed its challenge. We consider two settings with some additional setup that allows us to overcome the black-box separation, precisely by creating a place for the reduction to meaningfully embed a challenge.

The first such setting considers a NIKE scheme with a common reference string (CRS). We assume that the CRS is generated using some potentially secret, leak-free coins. The second setting considers NIKE where users preprocess their individual random coins to derive their secret state. In particular, instead of having the two secret states $r_A, r_B$ consist of the uniformly random coins of Alice and Bob, we allow Alice and Bob to sample their internal secret states from some specified (secret coin) distribution by running $r_A \leftarrow \mathsf {Gen}(\rho _A)$, $r_B \leftarrow \mathsf {Gen}(\rho _B)$ on their secret random coins $\rho _A,\rho _B$ respectively. The secret coins $\rho _A,\rho _B$ are discarded afterwards, and Alice and Bob can run the NIKE protocol using only their preprocessed states $r_A,r_B$. We assume the adversary only gets leakage on the preprocessed states $r_A, r_B$ but not on the underlying random coins $\rho _A,\rho _B$ used to sample them. The above two settings give the reduction an opportunity to embed its challenge in either the CRS or in the states $r_A,r_B$ without having to explain the underlying randomness.

Construction from Bilinear Maps. We first begin by constructing leakage-resilient NIKE in a model with both a CRS and preprocessing. We give two constructions. A simpler one under the subgroup decision assumption on composite-order groups with a bilinear map, and a slightly more complex one under the decision-linear assumption (DLIN) in prime-order groups with a bilinear map. We give a high-level overview of the first result.

The idea is inspired by “dual-system encryption” [25, 26, 34, ...]. In a nutshell, dual-system encryption allows us to switch regular ciphertexts and secret keys to so-called semi-functional counterparts, which individually look legitimate, but when “paired” together result in some randomness that is not dictated by the public key. In our case, we will switch the two states $r_A,r_B$ to be semi-functional so that when Alice and Bob run the NIKE with these values, the exchanged key k has true entropy even given the corresponding protocol messages $p_A,p_B$. To convert such a key into a uniformly random one, we additionally apply a two-seed extractor on it, where Alice and Bob each supply one seed.

In more detail, our construction uses a source group G which is a cyclic of composite order $N=p_1 p_2$, so that it can be decomposed using the Chinese Remainder Theorem into $G \simeq G_{p_1} \times G_{p_2}$, where $G_{p_1}$ and $G_{p_2}$ are cyclic of prime order $p_1$ and $p_2$ respectively. In our construction, everything happens in the subgroup $G_{p_1}$. The CRS consists of two elements $g\leftarrow G_{p_1}, h=g^x \in G_{p_1}$ where $x\leftarrow \mathbb {Z}_N$. The secret states of Alice and Bob are pairs of group elements $r_A = (g^a,h^a), r_B = (g^b, h^b) \in G_{p_1}^2$ where $a,b\leftarrow \mathbb {Z}_N$. The key exchange protocol consists of Alice sending $p_A = g^a$ and Bob sending $p_B = g^b$. The exchanged key is set to $k = e(g,h)^{ab}$ which can be computed by Alice as $e(p_B,h^a)$ and by Bob as $e(p_A,h^b)$. Note that, both the CRS and secret states of Alice and Bob in the above construction, are sampled from some distributions using secret coins (namely the group G, and the exponents x, a and b) that we assume do not leak.

To argue leakage-resilience, we switch the secret states $r_A,r_B$ to being sampled from the whole group G rather than the subgroup $G_{p_1}$. Namely, the whole execution of the NIKE is indistinguishable from sampling $x\leftarrow \mathbb {Z}_N$, $u \leftarrow G$, $v = u^x \in G$, and setting $r_A = (u^a, v^a)$ and $r_B = (u^b, v^b)$, while still keeping the CRS elements $g\leftarrow G_{p_1}$ and $h = g^x \in G_{p_1}$ in the subgroup. Indistinguishability follows from a standard subgroup decision assumption, even if the adversary gets to see the entire secret states $r_A, r_B$ in full.

With the above change, even if an adversary sees the CRS $(g,h= g^x)$ and the protocol transcript $(p_A = u^a, p_B = u^b)$, the value of $x \bmod p_2$ is uniformly random since $h=g^x$ only reveals $x \bmod p_1$. Therefore the exchanged key $k = e(u^b, v^a) = e(u^a,v^b) = e(u,v)^{ab} = e(u,u)^{xab}$ also has $\log p_2$ bits of entropy conditioned on the above. This means that given $\ell$ bits of leakage on each of $r_A,r_B$, the exchanged key k has $\log p_2 - 2\ell$ bits of entropy. As mentioned previously, we can upgrade this to a scheme where the exchanged key is indistinguishable from uniform under leakage, by adding the two seeds of a two-seed extractor to the states of Alice and Bob respectively, and having them exchange these seeds during the protocol and use them to extract randomness from k as their final exchanged key.

To allow for a larger leakage bound $\ell$, we can either choose a larger prime $p_2$, or we can execute many copies of this protocol in parallel. Overall, the scheme can flexibly tolerate any polynomial leakage bound $\ell$ while keeping the size of Alice’s and Bob’s secret states bounded by $O(\ell )$.

Constructions from Indistinguishability Obfuscation. We also give a construction from indistinguishability obfuscation ($\textit{i}\mathcal {O}$) and lossy functions (which can be instantiated from either DDH or LWE [31]). This construction can be initialized with either just a CRS (without preprocessing) or just preprocessing (without a CRS). Let us start with the CRS version of the scheme. The idea starts with the construction of (multiparty) NIKE from $\textit{i}\mathcal {O}$ due to Boneh and Zhandry [10]. Each party has randomness r and sets its protocol message to $p = G(r)$ where G is some function that we specify later. The CRS includes an obfuscated program that has a hard-coded PRF F: it takes as input two protocol messages $p_A,p_B$ and r, and checks that either $p_A = G(r)$ or $p_B = G(r)$; if so it outputs an evaluation of the PRF $F(p_A,p_B)$ and else it outputs $\bot$. It is easy to see that this gives correctness.

To argue security, we will set G to be a function whose description is a part of the CRS and can be indistinguishably created in either lossy or injective mode. We puncture the PRF F on the point $(p_A,p_B)$ and program a random output k. But instead of hard-coding k directly, we hard-code $k \oplus r_A$ and $k \oplus r_B$; i.e., two one-time pad encryptions of k under $r_A$ and $r_B$ respectively. This allows the obfuscated program to decrypt k given either $r_A$ or $r_B$ and so preserves correctness. But now we can switch G to lossy mode and argue that even given the obfuscated program with the hard-coded ciphertexts, the protocol transcript, and the leakages on $r_A,r_B$, the exchanged key k has high entropy. We can then convert this into a uniformly random exchanged key by additionally applying a two-seed extractor on top. (Our actual construction does something slightly more complicated to avoid two-seed extractors and gets better parameters via standard seeded extractors.)

The above can also be converted into a scheme with preprocessing and without a CRS. In this case, Alice creates the obfuscated program as part of the preprocessed state and sends it as her protocol message. Furthermore, instead of putting the description of G in the CRS, we will have each of Alice and Bob sample different functions $G_1,G_2$ that they send as part of their messages and are used as inputs to the obfuscated program; the obfuscated program also adds them to the input on which it evaluates the PRF $F(G_1,G_2, p_A,p_B)$.

3 Preliminaries

Basic Notation. For an integer N, we let . For a set S we let $x \leftarrow S$ denote sampling x uniformly at random from S. For a distribution $\mathcal{D}$ we let $x \leftarrow \mathcal{D}$ denote sampling x according to the distribution. We will denote the security parameter by $\lambda$. We say a function $f(\lambda )$ is negligible, denoted $f(\lambda ) = \mathrm{negl}(\lambda )$, if $f(\lambda ) = O(\lambda ^{-c})$ for every constant $c > 0$. A function is $f(\lambda )$ is polynomial, denoted $f(\lambda ) = \mathrm{poly}(\lambda )$, if $f(\lambda ) = O(\lambda ^c)$ for some constant $c > 0$.

Information Theory. For two random variables X, Y with support $\mathsf {supp}(X)$ and $\mathsf {supp}(Y)$ respectively, we define their statistical distance $\mathbf {SD}(X,Y)$ as

For two random variables X, Y with statistical distance $\mathbf {SD}(X,Y) \le \epsilon$, we will sometimes use the shorthand $X\approx _\epsilon Y$.

Two ensembles of random variables $X=\{X_\lambda \}_\lambda , Y=\{Y_\lambda \}_{\lambda }$ are statistically close if $\mathbf {SD}(X_\lambda ,Y_\lambda ) = \mathrm{negl}(\lambda )$. We will occasionally denote this as $X \approx _S Y$.

The min-entropy $\mathbf {H}_{\infty }(X)$ of a random variable X is defined as

A random variable X with min-entropy k is referred to as a k-source. When X is supported over $\{0,1\}^n$, we refer to it as an (n, k)-source. We denote the uniform distribution over $\{0,1\}^n$ by $U_n$.

Definition 1

(Strong Seeded Extractors). An efficient function $\mathsf {Ext}:\{0,1\}^n \times \{0,1\}^d \rightarrow \{0,1\}^\ell$ is a strong $(k,\epsilon )$-extractor if for every (n, k)-source X,

$$\begin{aligned} \mathbf {SD}((U_d,\mathsf {Ext}(X,U_d)),(U_d,U_m)) \le \epsilon . \end{aligned}$$

3.1 Background on Bilinear Maps

We review some definitions pertaining to bilinear maps, adapted from  [26].

Composite-Order Bilinear Groups. Let $\mathcal{G}(1^\lambda )$ be a group generator, which outputs the description of a pairing-friendly group $\mathbb {G} = (G,G_T,N=p_1p_2, e)$, where G and $G_T$ are cyclic groups of order N, and $p_1, p_2$ are distinct primes of bit-size $\varOmega (\lambda )$, and $e:G \times G \rightarrow G_T$ is an efficiently computable bilinear map, that satisfies:

• 1. (Bilinearity) $\forall g,h \in G$, $\forall a,b \in \mathbb {Z}_N$, we have:

  $$\begin{aligned} e(g^a,h^b) = e(g,h)^{ab}. \end{aligned}$$

• 2. (Non-degeneracy): There exists $g\in G$ such that $e(g,g) \in G_T$ has order N.

We will assume that the descriptions of G and $G_T$ include respective generators. We also assume that the random coins of $\mathcal{G}$ reveal the factorization $N=p_1p_2$.¹ We will denote by $G_{p_1}$ and $G_{p_2}$ the subgroups of G of order $p_1$ and $p_2$, respectively. Observe that any $g\in G_{p_1}$ and any $h\in G_{p_2}$ are “orthogonal” with respect to e, i.e. e(g, h) is the identity element in $G_T$.

Assumption 1

Let $\mathcal{G}(1^\lambda )$ be a group generator. We define the following distributions:

$\begin{array}{c} \mathbb {G} = (G,G_T,N=p_1p_2, e) \leftarrow \mathcal{G}, g \leftarrow G_{p_1}, T_1 \leftarrow G_{p_1}, \, T_{1,2} \leftarrow G. \end{array}$

We say that $\mathcal{G}$ satisfies Assumption 1 if for all PPT adversaries $\mathcal{A}$:

$$ \big | \, \Pr [\mathcal{A}(\mathbb {G}, g, T_1)=1] - \Pr [\mathcal{A}(\mathbb {G}, g, T_{1,2})=1] \, \big | \le \mathrm{negl}(\lambda ). $$

4 Leakage-Resilient NIKE in the Symmetric-Key Setting

4.1 Definitions

We first define leakage-resilient NIKE in the symmetric setting, where both parties share a common secret key with sufficiently high min-entropy.

Definition 2

(Symmetric-Key Leakage-Resilient NIKE). A symmetric-key NIKE protocol $\mathsf {sk}\text {-}\mathsf {NIKE}$ with secret key space $\mathcal{S}\mathcal{K}$, private state space $\mathcal{R}$, public message space $\mathcal{P}$ and output key space $\mathcal{K}$ consists of the algorithms:

• $\mathsf {Publish}(\mathsf {sk},r)$ is a deterministic algorithm which takes as input a secret key $\mathsf {sk}\in \mathcal{S}\mathcal{K}$, a private state $r \in \mathcal{R}$ and outputs a public message $p\in \mathcal{P}$.

• $\mathsf {SharedKey}(\mathsf {sk}, r,p)$ takes as input a secret key $\mathsf {sk}\in \mathcal{S}\mathcal{K}$, a private state $r \in \mathcal{R}$ and a public message $p\in \mathcal{P}$, and outputs a key $K\in \mathcal{K}$.

We require $\mathsf {sk}\text {-}\mathsf {NIKE}$ to satisfy the following properties.

Perfect Correctness. An $\mathsf {sk}\text {-}\mathsf {NIKE}=(\mathsf {Publish}, \mathsf {SharedKey})$ protocol is perfectly correct if for all secret keys $\mathsf {sk}\in \mathcal{S}\mathcal{K}$ and all private states $r_A,r_B \in \mathcal{R}$:

$$\begin{aligned} \mathsf {SharedKey}(\mathsf {sk},r_A,p_B) = \mathsf {SharedKey}(\mathsf {sk}, r_B,p_A), \end{aligned}$$

where $p_A = \mathsf {Publish}(\mathsf {sk}, r_A)$ and $p_B = \mathsf {Publish}(\mathsf {sk}, r_B)$.

Information-Theoretic Leakage Resilience. We say that a symmetric-key NIKE protocol is $(k,\ell ,\epsilon )$-secure if for any distribution $\mathcal{L}$ such that $H_\infty (\mathcal{L}) \ge k$ and all (potentially inefficiently computable) functions $f_A, f_B:\mathcal{S}\mathcal{K}\times \mathcal{R}\rightarrow \{0,1\}^\ell$, we have:

$$\begin{aligned} (p_A, p_B, f_A(\mathsf {sk}, r_A), f_B(\mathsf {sk}, r_B), K_0) \approx _\epsilon (p_A, p_B, f_A(\mathsf {sk}, r_A), f_B(\mathsf {sk}, r_B), K_1), \end{aligned}$$

where $\mathsf {sk}\leftarrow \mathcal{L}$, $r_A, r_B \leftarrow \mathcal{R}$, $p_A = \mathsf {Publish}(\mathsf {sk}, r_A)$, $p_B = \mathsf {Publish}(\mathsf {sk}, r_B)$, $K_0 = \mathsf {SharedKey}(\mathsf {sk},p_A,r_B)$, and $K_1 \leftarrow \mathcal{K}$.

Definition 3

(Leakage Rate). For a $(k,\ell ,\epsilon )$-secure symmetric-key NIKE, we define its leakage rate as

$$\begin{aligned} \frac{\ell }{\max _{r \in \mathcal{R}} |r|}. \end{aligned}$$

4.2 Two-Seed Extractors

We consider a new type of extractor called a two-seed extractor which suffices to construct leakage-resilient symmetric-key NIKE.

Definition 4

(Two-Seed Extractors). A $(k,2\ell )$-two-seed extractor $\mathsf {Ext}(X; R,S):\{0,1\}^n \times \{0,1\}^{d_1}\times \{0,1\}^{d_2} \rightarrow \{0,1\}^{m}$ with error $\epsilon$ is an efficient function such that for all (potentially inefficient) leakage functions $f:\{0,1\}^{n}\times \{0,1\}^{d_1} \rightarrow \{0,1\}^a$, $g:\{0,1\}^{n}\times \{0,1\}^{d_2} \rightarrow \{0,1\}^b$ with $a+b=2\ell$, and any (n, k)-source X, we have:

$$ \big ( \mathsf {Ext}(X;R,S), R,S, f(X,R), g(X,S) \big ) \approx _{\epsilon } \big ( U_m, R,S, f(X,R), g(X,S) \big ), $$

where R, S are independent uniform random bits of length $d_1$ and $d_2$ respectively.

Remark 1

Our definition of a two-seed extractor corresponds to strong two-seed extractors in the sense that the output is close to uniform even given the two seeds R and S. For simplicity, when we say a two-seed extractor in this paper, we always mean a strong two-seed extractor. Without the “strong” condition, a two-seed extractor is implied by any two source extractor on R and S.

Remark 2

For all applications in this paper, we only need two-seed extractors for full entropy $k=n$. However such a construction also trivially implies a two-seed extractor for min-entropy k where the error becomes $2^{n-k}\epsilon$.

Claim 2

Any $(k,2\ell )$-two-seed extractor $\mathsf {Ext}$ with error $\epsilon$ induces a symmetric-key NIKE that is $(k,\ell ,\epsilon )$-secure.

Proof

Let $\mathsf {Ext}$ be a $(k,2\ell )$-two-seed extractor $\mathsf {Ext}: \{0,1\}^{n}\,\times \,\{0,1\}^{d_1}\,\times \,\{0,1\}^{d_2} \rightarrow \{0,1\}^{m}$ with leakage size $2\ell$ and error $\epsilon$. We can construct an $\mathsf {sk}\text {-}\mathsf {NIKE}$ as follows. Let the secret key space $\mathcal{S}\mathcal{K}$ be $\{0,1\}^n$, let both the private state space $\mathcal{R}$ and the public message space $\mathcal{P}$ be $\{0,1\}^{\min (d_1, d_2)}$, and let the key space $\mathcal{K}$ be $\{0,1\}^m$. Suppose without loss of generality that $d_1 \ge d_2$. Define $\mathsf {Publish}(\mathsf {sk}, r) = r \in \{0,1\}^{d_2}$ and $\mathsf {SharedKey}(\mathsf {sk}, r, p) = \mathsf {Ext}(\mathsf {sk}, (r\Vert 0^{d_1-d_2}), p)$. Then any (potentially unbounded) distinguisher for $\mathsf {sk}\text {-}\mathsf {NIKE}$ is a distinguisher for $\mathsf {Ext}$ with the same advantage $\epsilon$.    $\square$

4.3 Construction

We show how to construct two-seed extractors from what we call BCP extractors, which are first studied implicitly in [4] and then explicitly defined in [24].² Looking ahead, we will build both two-seed extractors and symmetric-key NIKE that satisfy slightly stronger security definitions than standard leakage-resilience (Definition 6 and Definition 7).

We first recall the definition of a bounded collusion protocol, following [24].

Definition 5

(Bounded Collusion Protocol (BCP) [24]). An (interactive, potentially randomized) communication protocol $\pi$ among N parties is called a $(p, N, \mu )$-bounded collusion protocol (BCP) if:

• the N parties start the protocol with input $X_1,\dots ,X_N$, and the transcript $\tau$ is empty at the beginning of the protocol;

• there is a function $\mathsf {Next}(\tau )\rightarrow S$ takes as input a (partial) transcript $\tau$, and outputs either a set $S\subset [N]$ with $|S| \le p$ along with a function g, or $\bot$;

• at each round with current transcript $\tau$, the protocol computes $\mathsf {Next}(\tau )$. If $\mathsf {Next}(\tau ) = (S,f)$, the message $g(\{X_i\}_{i\in S})$ is appended to the current transcript $\tau$; otherwise the protocol stops and outputs $\tau$ as the final transcript.

• the final transcript $\tau$ has size at most $\mu$.

We say that a $(p,N,\mu )$-BCP $\pi$ $\epsilon$-computes a (deterministic) boolean function $f:(X_1,\dots , X_N) \rightarrow b \in \{0,1\}$ if there exists a (potentially unbounded) predictor $\mathcal{P}$, given a BCP transcript $\tau$ of $\pi$, that computes b with probability $1/2+\epsilon$ (over the randomness of $\{X_i\}_i, \pi$ and $\mathcal{P}$).

In this section, we will actually build a two-seed extractor with a stronger security property than Definition 4; namely, it remains secure against leakages computed as 3-party BCP transcripts over inputs X, R, S. This results in a symmetric-key NIKE that is secure against the same type of leakage, by directly adapting Claim 2.

Definition 6

(Two-Seed Extractors with BCP Leakage Resilience). A $(k,2\ell )$-two-seed extractor $\mathsf {Ext}(X; R,S):\{0,1\}^n \times \{0,1\}^{d_1}\times \{0,1\}^{d_2} \rightarrow \{0,1\}^{m}$ with error $\epsilon$ is an efficient function such that for all $(1,2,2\ell )$-BCP protocol $\pi :(\{0,1\}^n \times \{0,1\}^{d_1}) \times (\{0,1\}^n \times \{0,1\}^{d_2} \rightarrow \{0,1\}^{2\ell }$ and any (n, k)-source X, we have:

$$ \big ( \mathsf {Ext}(X;R,S), R,S, \pi ((X,R),(X,S)) \big ) \approx _{\epsilon } \big ( U_m, R,S, \pi ((X,R),(X,S)) \big ), $$

where R, S are independent uniform random bits of length $d_1$ and $d_2$ respectively.

Definition 7

(Symmetric-Key NIKE with BCP Leakage Resilience). We say that a symmetric-key NIKE $\mathsf {sk}\text {-}\mathsf {NIKE}= (\mathsf {Publish}, \mathsf {SharedKey})$ is $(k,\ell ,\epsilon )$-secure against interactive leakages if for any distribution $\mathcal{L}$ such that $H_\infty (\mathcal{L}) \ge k$ all $(1,2,2\ell )$-BCP protocol $\pi ((\mathsf {sk},r_A),(\mathsf {sk},r_B))$ (Definition 5), we have:

$$\begin{aligned} (p_A, p_B, \pi ((\mathsf {sk},r_A),(\mathsf {sk},r_B)), K_0) \approx _\epsilon (p_A, p_B, \pi ((\mathsf {sk},r_A),(\mathsf {sk},r_B)), K_1), \end{aligned}$$

where $\mathsf {sk}\leftarrow \mathcal{L}$, $r_A, r_B \leftarrow \mathcal{R}$, $p_A = \mathsf {Publish}(\mathsf {sk}, r_A)$, $p_B = \mathsf {Publish}(\mathsf {sk}, r_B)$, $K_0 = \mathsf {SharedKey}(\mathsf {sk},p_A,r_B)$, and $K_1 \leftarrow \mathcal{K}$.

Definition 8

(BCP Extractor). Let $X_1, \cdots , X_N$ be N independent (n, k)-sources. Let $\pi$ be a (possibly randomized) $(p, N, \mu )$-BCP and $\pi (X_1, \cdots , X_N)$ be the transcript. A deterministic function $\mathsf {Ext}: (\{0,1\}^n)^N \rightarrow \{0,1\}^m$ is an $(n, k, p, N, \mu )$-BCP extractor with error $\epsilon$ if

$$\begin{aligned} (\mathsf {Ext}(X_1, \cdots , X_N), \pi (X_1, \cdots , X_N)) \approx _{\epsilon } (U_m, \pi (X_1, \cdots , X_N)). \end{aligned}$$

Definition 9

The $\epsilon$-distributional communication complexity of a Boolean function $f: (\{0,1\}^n)^N \rightarrow \{0,1\}$, $C_{\epsilon }(f)$ in a (p, N) bounded collusion model, is the minimum number $\mu$ of any $(p, N, \mu )$-BCP that $\epsilon$-computes f.

Using the standard argument that unpredictability is the same as indistinguishability for any 1-bit random variable, we have the following theorem.

Theorem 3

A Boolean function $f: (\{0,1\}^n)^N \rightarrow \{0,1\}$ with $C_{\epsilon }(f) \ge \mu +1$ gives an $(n, n, p, N, \mu )$-BCP extractor with error $\epsilon$, and vice versa.

Next we show that any $(n, k, p, N, \mu +1)$-BCP extractor with sufficiently small error must be strong in any subset of p sources if the transcript size is at most $\mu$.

Theorem 4

Suppose $\mathsf {Ext}: (\{0,1\}^n)^N \rightarrow \{0,1\}^m$ is an $(n, k, p, N, \mu +1)$-BCP extractor with error $\epsilon$. Then for any $(p, N, \mu )$-BCP transcript $\pi (X_1, \cdots , X_N)$ and any subset $S \subset [N]$ with $|S|=p$, we have

$$\begin{aligned} (\mathsf {Ext}(X_1, \cdots , X_N), \pi (X_1, \cdots , X_N), X_S) \approx _{2^m \cdot \epsilon } (U_m, \pi (X_1, \cdots , X_N), X_S), \end{aligned}$$

where $X_S=\{X_i, i \in S\}$.

Proof

Assume that there exists a set $S \subset [N]$, a transcript $\pi (X_1, \cdots , X_N)$ of a $(p, N, \mu )$-BCP, and a distinguisher D such that

$$\begin{aligned} \big | \Pr [D(\mathsf {Ext}(X_1, \cdots , X_N), \pi (X_1, \cdots , X_N), X_S)=1]\\ -\Pr [D(U_m, \pi (X_1, \cdots , X_N), X_S)=1] \big | = \epsilon '. \end{aligned}$$

Let V be a uniformly random m-bit string, and consider the following $(p, N, \mu +1)$-BCP where the transcript is $(\pi (X_1, \cdots , X_N), D(V, \pi (X_1, \cdots , X_N), X_S))$. Now define another distinguisher $T_V$ as follows. Given input

$$\begin{aligned} (W, \pi (X_1, \cdots , X_N), D(V, \pi (X_1, \cdots , X_N), X_S)), \end{aligned}$$

$T_V$ outputs $D(V, \pi (X_1, \cdots , X_N), X_S)$ if $W=V$ and outputs a uniformly random bit otherwise. We have

$$\begin{aligned}&\big | \Pr [T_V(\mathsf {Ext}(X_1, \cdots , X_N), \pi (X_1, \cdots , X_N), D(V, \pi (X_1, \cdots , X_N), X_S))=1] \\&- \Pr [T_V(U_m, \pi (X_1, \cdots , X_N), D(V, \pi (X_1, \cdots , X_N), X_S))=1] \big | \\ =&\, \big | 2^{-m} (\Pr [D(\mathsf {Ext}(X_1, \cdots , X_N), \pi (X_1, \cdots , X_N), X_s)=1]\\&-\Pr [D(U_m, \pi (X_1, \cdots , X_N), X_S)=1]) \big | \\ =&\, 2^{-m} \epsilon ' \end{aligned}$$

However, note that the new protocol is a $(p, N, \mu +1)$-BCP, thus we have $2^{-m} \epsilon ' \le \epsilon$. This means that $\epsilon ' \le 2^m \cdot \epsilon$.    $\square$

In the case of $p=N-1$, BCP extractors with one bit of output are equivalent to hard functions in the number-on-forehead (NOF) communication model. The communication in the NOF model is exactly an $(N-1, N, \mu )$-BCP, and thus we can use the results in [4] on hard functions in the NOF model. Specifically, [4] showed two explicit functions that are hard in the NOF model.

• Generalized Inner Product (GIP): $\mathsf {GIP}_{N, n}: (\{0,1\}^n)^N \rightarrow \{0,1\}$ is defined as $\mathsf {GIP}_{N, n}(x_1, \cdots , x_N)=1$ iff the number of positions where all the $x_i$’s have 1 is odd.

• Quadratic Residue (QR) $\mathsf {QR}_{N, n}: (\{0,1\}^n)^N \rightarrow \{0,1\}$ is defined as $\mathsf {QR}_{N, n}(x_1, \cdots , x_N)=1$ iff $\sum _{i=1}^{N} x_i$ is a quadratic residue mod p.

Theorem 5

In the NOF model with N parties, we have

• 1. [4] For any n-bit long prime number p, $C_{\epsilon }(\mathsf {QR})=\varOmega (\frac{n}{2^N}+\log \epsilon )$.

• 2. [13] $C_{\epsilon }(\mathsf {GIP})=\varOmega (\frac{n}{2^N}+\log \epsilon )$.

Using this theorem together with Theorem 3, we obtain explicit, efficient BCP extractors, which are also two-seed extractors by Theorem 4 with $N=3$:

Theorem 6

There exist explicit constructions of $(n, \ell )$-two-seed extractors $\mathsf {Ext}: \{0,1\}^n \times \{0,1\}^n \times \{0,1\}^n \rightarrow \{0,1\}$, with leakage size $\ell =\varOmega (n)$ and error $\epsilon =2^{-\varOmega (n)}$.

We would like to get more output bits. Below we show two different methods to achieve this. The first method is quite general and applies to any two-seed extractor, while the second method achieves better seed length but only applied to the GIP extractor.

Construction 1: Take any two-seed extractor $\mathsf {Ext}$ which outputs one bit, choose m independent copies of seeds $(R_1, \cdots R_m)$ and another independent copy of seed S. Compute $Z_i=\mathsf {Ext}(X, R_i, S)$ for each i. The final output is $Z=(Z_1, \cdots , Z_m)$.

We have the following lemma.

Lemma 1

If $\mathsf {Ext}$ is a $(k , \ell +m)$-two-seed extractor with error $\epsilon$, then Construction 1 gives a $(k , \ell )$-two-seed extractor with error $m \epsilon$.

Proof

Let $R=(R_1, \cdots , R_m)$. Let the leakage be $L_1=f(X, R)$ and $L_2=g(X, S)$. Define $Z_{-i}=(Z_1, \cdots , Z_{i-1}, Z_{i+1}, \cdots , Z_m)$. We show that for any i,

$$\begin{aligned} (Z_i, Z_{-i}, L_1, L_2, R, S) \approx _{\epsilon } (U_1, Z_{-i}, L_1, L_2, R, S). \end{aligned}$$

To see this, first fix all the $R_j$’s except $R_i$. Note that after this fixing, $(R_i, S)$ are still independent and uniform. Further note that conditioned on this fixing, $L_1$ becomes a deterministic function of X and $R_i$, while $L_2$ is a deterministic function of X and S. Now $Z_{-i}$ can be viewed as an extra deterministic leakage from (X, S) with size $m-1$ and therefore the total size of leakage is at most $m+\ell$.

Thus we have

$$\begin{aligned} (Z_i, Z_{-i}, L_1, L_2, R, S) \approx _{\epsilon } (U_1, Z_{-i}, L_1, L_2, R, S). \end{aligned}$$

Now a standard hybrid argument implies that

$$\begin{aligned} (Z, L_1, L_2, R, S) \approx _{m \epsilon } (U_m, L_1, L_2, R, S). \end{aligned}$$

   $\square$

This gives the following theorem.

Theorem 7

There exist explicit constructions of $(n, \ell )$-two-seed extractors $\mathsf {Ext}: \{0,1\}^n \times \{0,1\}^{mn} \times \{0,1\}^{n} \rightarrow \{0,1\}^m$ with leakage size $\ell =\varOmega (n)$, error $\epsilon =2^{-\varOmega (n)}$ and output length $m=\varOmega (n)$. One seed has length mn and the other has length n.

Next we show a construction that uses smaller seed length. First we recall the following lemma from [14].

Lemma 2

[14] For any number n, there exists an explicit construction of n matrices $A_1, \cdots , A_n$, where each $A_i$ is an $n \times n$ matrix over ${\mathbb {F}}_2$, such that for any $S \subseteq [n]$ with $S \ne \emptyset$, we have that $\sum _{i \in S} A_i$ has full rank.

We can now describe our second construction.

Construction 2: Let $\mathsf {Ext}$ be the two-seed extractor constructed from $\mathsf {GIP}_{3, n}$. For some $m < n$, let $A_1, \cdots , A_m$ be the first m matrices from Lemma 2. Let the seed be $(R, S) \in \mathbb {F}_2^n$. For each $i \in [m]$ compute $Z_i=\mathsf {Ext}(X, A_i R, S)$ and let $Z=(Z_1, \cdots , Z_m)$.

To analyze the lemma we will use a standard XOR lemma.

Lemma 3

[19] For any m-bit random variable T, we have:

$$\begin{aligned} \mathbf {SD}(T,U_m) \le \sqrt{\sum _{0^m \ne a \in \{0,1\}^m} \mathbf {SD}(T \cdot a ,\, U_1)^2}, \end{aligned}$$

where $T \cdot a$ denotes the inner product of T and a over ${\mathbb {F}}_2$.

We have the following lemma.

Lemma 4

Construction 2 gives an $(n, \ell )$-two-seed extractor with leakage size $\ell =\varOmega (n)$ and error $\epsilon =2^{m-\varOmega (n)}$.

Proof

Let the leakage be $L_1=f(X, R)$ and $L_2=g(X, S)$. For any $a \in \{0,1\}^m$ with $a \ne 0^m$, let $S_a \subseteq [m]$ denote the set of indices of a where the corresponding bit is 1. Then $S_a \ne \emptyset$. Observe that

$$\begin{aligned} Z \cdot a = \mathsf {GIP}(X, \sum _{i \in S_a} A_i R, S)=\mathsf {GIP}(X, (\sum _{i \in S_a} A_i) R, S). \end{aligned}$$

Since $\sum _{i \in S_a} A_i$ has full rank, $(\sum _{i \in S_a} A_i) R$ is uniform in $\mathbb {F}_2^n$. Thus we have

$$\begin{aligned} (Z \cdot a, L_1, L_2, R, S) \approx _{\epsilon } (U_1, L_1, L_2, R, S), \end{aligned}$$

where $\epsilon =2^{-\varOmega (n)}$. By Markov’s inequality, with probability $1-\sqrt{\epsilon }$ over the fixing of $(L_1, L_2, R, S)$, we have that $Z \cdot a$ is $\sqrt{\epsilon }$-close to uniform. By a union bound, with probability $1-2^m \sqrt{\epsilon }$ over the fixing of $(L_1, L_2, R, S)$, we have that for all $a \in \{0,1\}^m$ with $a \ne 0^m$, $Z \cdot a$ is $\sqrt{\epsilon }$-close to uniform. When this happens, by Lemma 3 we have that

$$\begin{aligned} |Z-U_m| \le 2^{m/2}\sqrt{\epsilon }. \end{aligned}$$

Thus overall we have that

$$\begin{aligned} (Z, L_1, L_2, R, S) \approx _{\epsilon '} (U_m, L_1, L_2, R, S), \end{aligned}$$

where $\epsilon ' \le 2^m \sqrt{\epsilon }+2^{m/2} \sqrt{\epsilon } =2^{m-\varOmega (n)}$.    $\square$

This yields the following theorem.

Theorem 8

There exist explicit constructions of $(n, \ell )$-two-seed extractors $\mathsf {Ext}: \{0,1\}^n \times \{0,1\}^{n} \times \{0,1\}^{n} \rightarrow \{0,1\}^m$ with leakage size $\ell =\varOmega (n)$, error $\epsilon =2^{-\varOmega (n)}$ and output length $m=\varOmega (n)$. Each seed has length n.

5 Definitions for Leakage-Resilient NIKE in the Public-Key Setting

We define NIKE in the public-key setting.

Definition 10

(Non-Interactive Key Exchange). A Non-Interactive Key Exchange $\mathsf {NIKE}$ over parameter space $\mathcal{C}$, state space $\mathcal{R}$, public message space $\mathcal{P}$ and key space $\mathcal{K}$ consists of the following efficient algorithms:

• $\mathsf {Setup}(1^\lambda )$ is a randomized algorithm that takes as input the security parameter $1^\lambda$ and outputs public parameters $\mathsf {params}\in \mathcal{C}$.

• $\mathsf {Gen}(\mathsf {params})$ is a randomized algorithm that takes as input public parameters $\mathsf {params}\in \mathcal{C}$ and outputs a state $r \in \mathcal{R}$.

• $\mathsf {Publish}(\mathsf {params}, r)$ is a deterministic algorithm that takes as input public parameters $\mathsf {params}\in \mathcal{C}$ and a state $r\in \mathcal{R}$ and outputs a public message $p\in \mathcal{P}$.

• $\mathsf {SharedKey}(\mathsf {params},r,p)$ is a deterministic algorithm that takes as input public parameters $\mathsf {params}\in \mathcal{C}$, a state $r\in \mathcal{R}$ and a public message $p\in \mathcal{P}$, and outputs a key $K \in \mathcal{K}$.

For notational simplicity, we will omit the input $\mathsf {params}$ from these algorithms in the rest of the paper.

We require a $\mathsf {NIKE}$ protocol to satisfy the two following properties: Perfect Correctness. We say that $\mathsf {NIKE}$ is perfectly correct if, over the randomness of $\mathsf {Setup}$ and $\mathsf {Gen}$:

$$\begin{aligned} \Pr [\mathsf {SharedKey}(r_A,p_B) = \mathsf {SharedKey}(r_B,p_A)] = 1 \end{aligned}$$

where $\mathsf {params}\leftarrow \mathsf {Setup}(1^\lambda )$, $r_A \leftarrow \mathsf {Gen}(\mathsf {params}),\, p_A = \mathsf {Publish}(r_A),\, r_B \leftarrow \mathsf {Gen}(\mathsf {params})$, $p_B = \mathsf {Publish}(r_B)$.

Security Against $\ell$-bit Leakage. We say that a $\mathsf {NIKE}$ protocol is secure against $\ell$-bit leakage if for all PPT distinguishers $\mathcal{D}$, and for all efficiently computable leakage functions $f_A, f_B: \mathcal{C}\times \mathcal{R}\rightarrow \{0,1\}^\ell$, we have (where we omit also $\mathsf {params}$ as an input to the distinguisher $\mathcal{D}$ and the leakage functions $f_A, f_B$ in the rest of the paper):

$$\begin{aligned} \big |&\Pr \left[ \mathcal{D}\left( p_A, p_B, f_A(r_A), f_B(r_B), K_0) \right) =1 \right] \\&- \Pr \left[ \mathcal{D}\left( p_A, p_B, f_A(r_A), f_B(r_B), K_1\, \right) =1 \right] \big | \le \mathrm{negl}(\lambda ), \end{aligned}$$

where $\mathsf {params}\leftarrow \mathsf {Setup}(1^\lambda )$, $r_A \leftarrow \mathsf {Gen}(\mathsf {params})$, $p_A = \mathsf {Publish}(r_A)$, $r_B \leftarrow$ $\mathsf {Gen}(\mathsf {params})$, $p_B = \mathsf {Publish}(r_B)$, $K_0 = \mathsf {SharedKey}(r_A, p_B)$, and $K_1 \leftarrow \mathcal{K}$.

Default Definition versus Variants. We define several variants of NIKE depending on whether the $\mathsf {Setup}$ algorithm and the $\mathsf {Gen}$ algorithm just output uniformly random coins or sample from some more complex distribution. By default, we will only allow them to output uniformly random coins, which means that the leakage can depend on all of the random coins used by the scheme and there is no reliance on leak-free randomness. In particular, we say that a NIKE scheme is:

• a plain NIKE (default), if both $\mathsf {Setup}(1^\lambda )$ and $\mathsf {Gen}(\mathsf {params})$ just output (some specified number of) uniformly random bits. In particular $\mathsf {Setup}(1^\lambda ; \rho _S) = \rho _S$ and $\mathsf {Gen}(\mathsf {params};\rho _G) = \rho _G$. In this case, we will often exclude the algorithms $\mathsf {Setup},\mathsf {Gen}$ from the description of NIKE.

• a NIKE in the common reference string model, if the algorithm $\mathsf {Setup}(1^\lambda )$ can be arbitrary (sample from an arbitrary distribution). Note that this means that we rely on leak-free randomness to run the $\mathsf {Setup}$ algorithm.

• a NIKE in the preprocessing model, if the algorithm $\mathsf {Gen}(\mathsf {params})$ can be arbitrary (sample from an arbitrary distribution). Note that this means we rely on leak-free randomness to generate the states $r_A,r_B$ of each party before the protocol starts (but we do not rely on any additional leak-free randomness during the protocol execution).

• a NIKE in the common reference string and preprocessinf model, if both the algorithms $\mathsf {Setup},\mathsf {Gen}$ can be arbitrary (sample from an arbitrary distribution).

6 A Black-Box Separation

In this section, we show a broad black-box separation result, which rules out any efficient black-box reduction from any single-stage assumption to the leakage-resilience of plain NIKE with sufficiently large leakage.

6.1 Single-Stage Assumptions

Roughly following [21, 35], we define single-stage (game-based) assumptions (also called cryptographic games). For comparison, single-stage assumptions differ from falsifiable assumptions [18, 29] as challengers can be potentially unbounded.

Definition 11

(Single-Stage Assumption). A single-stage assumption consists of an interactive (potentially inefficient, stateful) challenger $\mathcal{C}$ and a constant $c \in [0,1)$. On security parameter $\lambda$, the challenger $\mathcal{C}(1^\lambda )$ interacts with a (stateful) machine $\mathcal{A}(1^\lambda )$ called the adversary and may output a special symbol $\mathsf {win}$. If this occurs, we say that $\mathcal{A}(1^\lambda )$ wins $\mathcal{C}(1^\lambda )$. The assumption associated with the tuple $(\mathcal{C},c)$ states that for any PPT adversary $\mathcal{A}$, we have

$$\begin{aligned} \Pr [\mathcal{A}(1^\lambda ) \text { wins } \mathcal{C}(1^\lambda )] \le c + \mathrm{negl}(\lambda ) \end{aligned}$$

where the probability is over the random coins of $\mathcal{C}$ and $\mathcal{A}$.

Which assumptions are not single-stage? The definition above seems to cover all most common cryptographic assumptions, so one can naturally ask which assumptions our black-box impossibility does not cover. An example of a multi-stage assumption is the leakage resilience of NIKE itself (defined in Sect. 5)! In particular, one can equivalently define leakage-resilience as a two-stage game, where the adversary is split into two distinct entities: a leaker that produces the leakages $f_A(r_A), f_B(r_B)$, and a distinguisher that uses this leakage to distinguish the final key from uniform. Unlike the leaker, the distinguisher in that game does not see the secret states $r_A, r_B$, and the only state kept by the adversary between the two stages are the leakages $f_A(r_A)$ and $f_B(r_B)$.

6.2 Separating Leakage-Resilient NIKE from Single-Stage Assumptions

Next, we recall the notion of black-box reductions.

Definition 12

(Black-Box Reduction). A black-box reduction showing the leakage-resilience (for $\ell$-bit leakage) of $\mathsf {NIKE}$ based on a single-stage assumption $(\mathcal{C}, c)$ is an efficient oracle-access machine $\mathcal{R}(\cdot )$ such that, for every (possibly inefficient, non-uniform) distinguisher $\mathcal{D}$ to the NIKE with (possibily inefficient, non-uniform) leakage functions $f_A, f_B: \mathcal{R}\rightarrow \{0,1\}^\ell$, the machine $\mathcal{R}^{\mathcal{D}, f_A, f_B}$ breaks the assumption $(\mathcal{C}, c)$.

We are ready to state our black-box impossibility result.

Theorem 9

(Black-Box Separation). Let $\ell = \omega (\log \lambda )$. Let $\mathsf {NIKE}= ( \mathsf {Publish}, \mathsf {SharedKey})$ be a candidate plain NIKE satisfying perfect correctness. Then for any single-stage assumption $(\mathcal{C},c)$, one of the following must hold:

• $(\mathcal{C},c)$ is false.

• There is no black-box security reduction showing the leakage resilience of $\mathsf {NIKE}$ against $\ell$-bit leakages based on the assumption $(\mathcal{C},c)$.

Proof

Our proof strategy closely follows the ideas of [35]. Looking ahead, our inefficient distinguisher against NIKE is a simulatable attacker in the sense of [35, Definition 4.1].

Let $(\mathcal{C}, c)$ be a single-stage assumption, and let $\mathcal{R}$ be a black-box reduction from the security of $\mathsf {NIKE}$ against $\ell$-bit leakage to the assumption $(\mathcal{C}, c)$. In other words, for any (potentially inefficient, non-uniform) distinguisher $\mathcal{D}$ with non-negligible advantage along with (potentially inefficient, non-uniform) leakage functions $f_A, f_B:\mathcal{R}\rightarrow \{0,1\}^\ell$, the machine $\mathcal{R}^{\mathcal{D}, f_A, f_B}$ breaks $(\mathcal{C},c)$ with non-negligible advantage.

Let $H:\mathcal{P}\rightarrow \{0,1\}^\ell$ be a random function. We first define a family of inefficient distinguishers $\overline{\mathcal{D}}^{(H)}$ along with (inefficient) leakage functions $\overline{f_A}^{(H)}, \overline{f_B}^{(H)}$ as follows.

• $\overline{f_A}^{(H)}$ takes as input a state $r_A \in \mathcal{R}$. It has the function H hard-coded (say as a truth table). It computes $p_A = \mathsf {Publish}(r_A)$ and outputs $\sigma _A = H(p_A)$.

• $\overline{f_B}^{(H)}$ takes as input a state $r_B \in \mathcal{R}$. It has the function H hard-coded (say as a truth table). It computes $p_B = \mathsf {Publish}(r_B)$ and outputs $\sigma _B = H(p_B)$.

• $\overline{\mathcal{D}}^{(H)}(p_A, p_B, \sigma _A, \sigma _B, K)$ takes as input public messages $p_A, p_B \in \mathcal{P}$, leakages $\sigma _A, \sigma _B \in \{0,1\}^\ell$ and a key $K\in \mathcal{K}$. It checks that $H(p_A) = \sigma _A$ and $H(p_B)=\sigma _B$.

  If this equality holds, brute-force search for any $r_A\in R$ such that $\mathsf {Publish}(r_A) = p_A$; output 1 if $K=\mathsf {SharedKey}(r_A, p_B)$ and 0 otherwise.

  Otherwise output a random bit $b\in \{0,1\}$.

Claim 10

Assume $\mathsf {NIKE}$ is perfectly correct. Then $\overline{\mathcal{D}}^{(H)}$ along with $\overline{f_A}^{(H)}, \overline{f_B}^{(H)}$ is an (inefficient) distinguisher with leakage size $\ell$ and advantage $1-1/|\mathcal{K}|$.

Proof

By perfect correctness of $\mathsf {NIKE}$, for any $p_B$ in the image of $\mathsf {Publish}$ and any $r_A, r_A'$ such that $\mathsf {Publish}(r_A) = \mathsf {Publish}(r_A')$, we have $\mathsf {SharedKey}(r_A, p_B) = \mathsf {SharedKey}(r_A', p_B)$.

In particular, on input $\big (p_A, p_B, \overline{f_A}^{(H)}(r_A), \overline{f_B}^{(H)}(r_B), K_0\big )$ where $p_A = \mathsf {Publish}(r_A)$ and $K_0 = \mathsf {SharedKey}(r_A, p_B)$, the distinguisher $\overline{\mathcal{D}}^{(H)}$ always outputs 1.

Similarly, on input $\big (p_A, p_B, \overline{f_A}^{(H)}(r_A), \overline{f_B}^{(H)}(r_B), K_1\big )$ where $K_1\leftarrow \mathcal{K}$, the distinguisher $\overline{\mathcal{D}}^{(H)}$ outputs 1 if and only if $K = \mathsf {SharedKey}(r_A, p_B)$ (for any $r_A$ such that $p_A = \mathsf {Publish}(r_A)$), which happens with probability $1/|\mathcal{K}|$.    $\square$

We now consider the following efficient algorithm $\mathcal{D}_{\mathsf {Sim}}$ along with efficient leakage functions $f_A^*, f_B^*$. These three algorithms share a look-up table T of entries in $\mathcal{R}\times \{0,1\}^\ell$ indexed by elements in $\mathcal{P}$; we will write $T[p\in \mathcal{P}] = (r,\sigma )\in \mathcal{R}\times \{0,1\}^\ell$. We stress that $\mathcal{D}_{\mathsf {Sim}}$ is not a distinguisher against $\mathsf {NIKE}$ because of this shared state T.

• $f_A^*(r)$ takes as input $r\in \mathcal{R}$. It computes $p = \mathsf {Publish}(r)$. If the entry of T indexed by p has not yet been assigned, it samples a uniform $\sigma \leftarrow \{0,1\}^\ell$, and define $T[p] = (r,\sigma )$. Otherwise it outputs the second element of T[p].

• $f_B^*(r)$ takes as input $r\in \mathcal{R}$. It computes $p = \mathsf {Publish}(r)$. If the entry of T indexed by p has not yet been assigned, it samples a uniform $\sigma \leftarrow \{0,1\}^\ell$, and define $T[p] = (r,\sigma )$. Otherwise it outputs the second element of T[p].

• $\mathcal{D}_{\mathsf {Sim}}$ takes as input public messages $p_A, p_B \in \mathcal{P}$, leakages $\sigma _A, \sigma _B \in \{0,1\}^\ell$ and a key $K\in \mathcal{K}$.

  It looks up in T whether both $T[p_A]$ and $T[p_B]$ are defined; if so it checks that the second elements of $T[p_A]$ and $T[p_B]$ equal $\sigma _A$ and $\sigma _B$, respectively. If this is the case, let $r_A$ be the first element of $T[p_A] \in \mathcal{R}\times \{0,1\}^\ell$. It outputs 1 if $\mathsf {SharedKey}(r_A, p_B) = K$, and 0 otherwise.

  Otherwise, it outputs a random bit b.

Claim 11

Suppose $\mathsf {NIKE}$ is perfectly correct. Let $\mathcal{R}$ be an efficient oracle-access machine. Then the outputs of $\mathcal{R}^{\overline{\mathcal{D}}^{(H)}, \, \overline{f_A}^{(H)}, \, \overline{f_B}^{(H)}}$ and $\mathcal{R}^{\mathcal{D}_{\mathsf {Sim}},\, f_A^*, \, f_B^*}$ are within statistical distance $Q/2^\ell$ over the randomness of $\mathcal{R}$ and H, where Q is the number of oracle queries of $\mathcal{R}$, and $\ell$ is the size of the leakages.

Proof

Let $Q = \mathrm{poly}(\lambda )$ be the total number of oracle queries performed by $\mathcal{R}^{\mathcal{D}, f_A, f_B}$ to $\mathcal{D}, f_A, f_B$. It suffices to argue that the transcripts of the calls of $\mathcal{R}$ to $(\overline{\mathcal{D}}^{(H)}, \, \overline{f_A}^{(H)}, \, \overline{f_B}^{(H)})$ and to $(\mathcal{R}^{\mathcal{D}_{\mathsf {Sim}},\, f_A^*, \, f_B^*})$ are within statistical distance $Q/2^\ell$.

We first note that the (transcripts of the) outputs of the calls to $\overline{f_A}^{(H)}, \, \overline{f_B}^{(H)}$ and $f_A^*, f_B^*$ are identically distributed. We then distinguish two cases:

• $\mathcal{R}^{\mathcal{D}, f_A, f_B}$ calls $\mathcal{D}$ on input $p_A, p_B, \sigma _A, \sigma _B$ but has either not previously called $f_A$ on any input $r_A$ such that $\mathsf {Publish}(r_A) = p_A$, or has not previously called $f_B$ on any input $r_B$ such that $\mathsf {Publish}(r_B) = p_B$. Then $\mathcal{R}^{\mathcal{D}_{\mathsf {Sim}},\, f_A^*, \, f_B^*}$ obtains a uniformly random output bit over such calls as either $T[p_A]$ or $T[p_B]$ has not been defined. Further, the probability that $\mathcal{R}^{\overline{\mathcal{D}}^{(H)}, \, \overline{f_A}^{(H)}, \, \overline{f_B}^{(H)}}$ does not get a random output bit over any such call to $\overline{\mathcal{D}}^{(H)}$ is at most $Q/2^\ell$ (over the randomness of $H(p_A)$ and $H(p_B)$).

• Otherwise for every call to $\mathcal{D}$ that does not result in a random output bit, $\mathcal{R}^{\mathcal{D}, f_A, f_B}$ has previously queried both $f_A$ on $r_A$ such that $\mathsf {Publish}(r_A) = p_A$ and $f_B$ on $r_B$ such that $\mathsf {Publish}(r_B) = p_B$. In particular $p_B$ is in the image of $\mathsf {Publish}$, and by perfect correctness, both $\mathcal{D}_{\mathsf {Sim}}$ and $\overline{\mathcal{D}}^{(H)}$ compute the same value $\mathsf {SharedKey}(r_A, p_B)$. Therefore the two resulting distributions are identically distributed.    $\square$

By Claim 11, we have in particular:

$$ \Pr [\mathcal{R}^{\mathcal{D}_{\mathsf {Sim}}, f_A^*, f_B^*}\text { wins }\mathcal{C}] \ge \Pr [\mathcal{R}^{\overline{\mathcal{D}}^{(H)}, \overline{f_A}^{(H)}, \overline{f_B}^{(H)}}\text { wins }\mathcal{C}] - Q/2^\ell , $$

over the randomness of $\mathcal{R}$, $\mathcal{C}$ and H. Note that $\mathcal{R}^{\mathcal{D}_{\mathsf {Sim}}, f_A^*, f_B^*}$ is a PPT algorithm. Now by Claim 10, $\mathcal{R}^{\mathcal{D}_{\mathsf {Sim}}, f_A^*, f_B^*}$ is an efficient adversary that wins $(\mathcal{C}, c)$ with advantage at least $1-1/|\mathcal{K}| - Q/2^\ell$, which concludes the proof.    $\square$

6.3 Circumventing the Impossibility Result

The black-box impossibility result of Theorem 9 suggests several natural avenues to avoid it. We mention below several such options, some of which lead to positive results in subsequent sections of the paper.

Small Leakage. Our impossibility result only covers super-logarithmically-sized leakages, and assumptions asserting security against PPT adversary with negligible advantage. One natural way around this is to restrict security to small leakages and/or to use stronger assumptions. In the full version, we show that any standard NIKE is actually directly secure against $\mathcal{O}(\log \lambda )$-bit leakages, and, more generally, that any $\epsilon$-secure standard NIKE (where the advantage of any PPT distinguisher is at most $\epsilon$) is $(\epsilon \cdot 2^{\mathcal{O}(\ell )})$-secure with $\ell$-bit leakage.

Multi-Stage Assumptions and Non-Black-Box Reductions. Our impossibility result only covers single-stage assumptions under black-box reductions. All the constructions we are aware of for leakage resilience use black-box reductions, and essentially all standard cryptographic assumptions are phrased as single-stage game-based assumptions.

Imperfect Correctness. We crucially use in several steps of our proof that the NIKE is perfectly correct, to ensure that both $\overline{\mathcal{D}}^{(H)}$ is an (inefficient) distinguisher for $\mathsf {NIKE}$, and that $\overline{\mathcal{D}}^{(H)}$ and $\mathcal{D}_{\mathsf {Sim}}$ compute the same shared key. However we do not see a way to leverage this gap alone to build a secure construction.

The Common Reference String Model. On a more constructive side, an interesting way to get around Theorem 9 is to further rely on trusted setup. A common setting is to assume the availability of a common reference string (CRS), where the randomness used to generate the CRS cannot leak. The reason our black-box impossibility result does not apply in that case is somewhat subtle: the reduction $\mathcal{R}$ can call $(\mathcal{D}, f_A, f_B)$ using a malformed CRS (not in the image of $\mathsf {Setup}$), where perfect correctness might not hold. As a matter of fact, our black-box impossibility result does extend to the common random string model. In the full version, we build a leakage-resilient NIKE in the CRS model from $\textit{i}\mathcal {O}$.

The Preprocessing Model. A very similar workaround is to consider what we call the preprocessing model, where parties generate their secret states r using some leak-free randomness. In the preprocessing model, our impossibility result does not apply for the same reason it does not apply in the CRS setting. This preprocessing could either be performed by the parties themselves during an earlier leak-free preprocessing stage, or it could be generated by a trusted third party. In Sect. 7, we build a leakage-resilient NIKE in the CRS model with preprocessing from bilinear maps; in the full version we build a leakage-resilient NIKE in the pure preprocessing model from $\textit{i}\mathcal {O}$ and lossy functions.

7 Constructions from Bilinear Maps

In this section we leverage bilinear maps to build leakage-resilent NIKE in the CRS model with preprocessing. We first provide a construction using composite-order bilinear groups. In the full version, we give an alternate construction from the decisional linear assumption (DLIN) over prime order groups.

Construction 12

Let $\mathsf {sk}\text {-}\mathsf {NIKE}= (\mathsf {sk}\text {-}\mathsf {NIKE}.\mathsf {Publish}, \mathsf {sk}\text {-}\mathsf {NIKE}.\mathsf {SharedKey})$ be a leakage-resilient symmetric key NIKE (Definition 2) over secret key space $\mathcal{S}\mathcal{K}$, internal randomness space $\mathcal{R}$, public message space $\mathcal{P}$ and output key space $\mathcal{K}$. We will assume that $\mathsf {sk}\text {-}\mathsf {NIKE}.\mathsf {Publish}$ does not take any secret key $\mathsf {sk}$ as input; all our constructions from two-seed extractors in Sect. 4 satisfy this property.

Let $\mathcal{G}$ be a group generator for a composite-order group (defined in Sect. 3.1). We will assume that there is a natural bijection $G_T \simeq \mathcal{S}\mathcal{K}$.

We construct $\mathsf {NIKE}=(\mathsf {Setup}, \mathsf {Gen}, \mathsf {Publish}, \mathsf {SharedKey})$ as follows:

• $\mathsf {Setup}(1^\lambda )$: on input the security parameter, generate $\mathbb {G} = (G,G_T,N=p_1p_2, e) \leftarrow \mathcal{G}(1^\lambda )$ of order $N=p_1p_2$ where $p_1$ and $p_2$ are primes. Let u be a generator of G.

  Sample $\alpha ,x\leftarrow \mathbb {Z}_N$ and use $p_2$ (given by the random coins used to run $\mathcal{G}$) to compute $g = u^{\alpha \cdot p_2} \in G_{p_1}$ and $h = g^x \in G_{p_1}$. Output $\mathsf {params}= (\mathbb {G}, g,h)$.

• $\mathsf {Gen}(\mathsf {params})$: on input $\mathsf {params}$, sample $\rho \leftarrow \mathcal{R}$. Sample $a\leftarrow \mathbb {Z}_N$, and output the state $r = (\rho , (g^a, h^a)) \in \mathcal{R}\times G^2$.

• $\mathsf {Publish}(r)$: on input a state $r=(\rho , (X,Y))\in \mathcal{R}\times G^2$, output the public message $p=(\mathsf {sk}\text {-}\mathsf {NIKE}.\mathsf {Publish}(\rho ), X)$.

• $\mathsf {SharedKey}(r,p)$: on input a state $r=(\rho , (X,Y)) \in \mathcal{R}\times G^2$ and a public message $p=(P, Z) \in \mathcal{P}\times G$, compute:

  $$\begin{aligned} \mathsf {sk}= e(Y,Z), \end{aligned}$$

  that we identify as an element of $\mathcal{S}\mathcal{K}$, and output:

  $$\begin{aligned} K = \mathsf {sk}\text {-}\mathsf {NIKE}.\mathsf {SharedKey}(\mathsf {sk}, \rho , P). \end{aligned}$$

Theorem 13

(Correctness). Assuming $\mathsf {sk}\text {-}\mathsf {NIKE}$ is perfectly correct, Construction 12 is perfectly correct.

Proof

Let $r_A, r_B$ be elements of $\mathcal{R}\times G^2$, $p_A = \mathsf {Publish}(r_A)$, $p_B = \mathsf {Publish}(r_B)$. By perfect correctness of $\mathsf {sk}\text {-}\mathsf {NIKE}$, it suffices to show that $\mathsf {SharedKey}(r_A, p_B)$ and $\mathsf {SharedKey}(r_B, p_A)$ compute the same intermediate secret key $\mathsf {sk}$. But this follows as for all $Y,Z\in G^2$, $e(Y,Z) = e(Z,Y)$.    $\square$

Theorem 14

(NIKE in the CRS model with Preprocessing). Assume that Assumption 1 holds, and that $\mathsf {sk}\text {-}\mathsf {NIKE}$ is leakage resilient. Then Construction 12 is leakage-resilient.

Proof

Let $\mathcal{D}$ be an efficient algorithm which breaks the leakage resilience of $\mathsf {NIKE}$ with leakage functions $f_A,f_B$. We proceed via a sequence of hybrid games.

Hybrid 0. This is the real security experiment: $\mathcal{D}$ is given as input

$$\begin{aligned} (\mathsf {params}, p_A, p_B, f_A(r_A), f_B(r_B),K_b) \end{aligned}$$

where b is the challenger’s bit.

Hybrid 1. We change how we compute $\mathsf {params}, r_A, r_B$ given to the distinguisher. We now sample $g\leftarrow G_{p_1}$, $x,y\leftarrow \mathbb {Z}_N$, $v \leftarrow G_{p_1}$, and set:

$$ h = g^x, \quad r_A = (\rho _A, v, v^x), \quad r_B = (\rho _A, v^y, v^{xy}). $$

The resulting input distributions to the distinguisher $\mathcal{D}$ in Hybrid 0 and Hybrid 1 are statistically close. Indeed, g is uniform in $G_{p_1}$ in both cases, and for $a\leftarrow \mathbb {Z}_N$, $g^a$ is uniform in $G_{p_1}$, except when $g = 1_G$ which happens with negligible probability $1/p_1$. If this is not the case, then $h^a$ can be computed as $(g^a)^x$. Similarly, $g^y$ is in this case uniformly distributed in $G_{p_1}$, and therefore follows the same distribution as $(g^a)^y$ where $y\leftarrow \mathbb {Z}_N$, except if $(g^a) = 1_G$, which happens with probability $1/p_1$ over the randomness of $a \leftarrow \mathbb {Z}_N$. Overall, the statistical distance between the distributions is at most $2/p_1$ which is negligible.

Hybrid 2. We change how we compute $r_A, r_B$ given to the distinguisher. We now pick , and set:

This change is undetectable to any efficient distinguisher, even given $r_A, r_B$:

Lemma 5

Under Assumption 1, the following distributions are computationally indistinguishable:

$$\begin{aligned} \big ( \mathbb {G}, g, h=g^x, r_A=(\rho _A, (v,v^x)),\, r_B=(\rho _B, (v^y,v^{xy})), K_b \big )\\ \big ( \mathbb {G}, g, h=g^x, r_A=(\rho _A, (w,w^x)),\, r_B=(\rho _B, (w^y,w^{xy})), K_b \big ), \end{aligned}$$

where $\mathbb {G} \leftarrow \mathcal{G}$, $g \leftarrow G_{p_1}$, $x, y \leftarrow \mathbb {Z}_N$, $v \leftarrow G_1$, $w\leftarrow G$; and $\rho _A, \rho _B \leftarrow \mathcal{R}$, $K_0 = \mathsf {SharedKey}(r_A, \mathsf {Publish}(r_B))$ and $K_1 \leftarrow \mathcal{K}$.

In particular since $\mathsf {Publish}$, $f_A$ and $f_B$ are efficiently computable, the input distributions—and therefore the outputs of $\mathcal{D}$ in Hybrid 1 and Hybrid 2—are statistically indistinguishable.

Proof

We define a reduction R to Assumption 1 that takes as input $\mathbb {G}, g, T$, where $\mathbb {G} \leftarrow \mathcal{G}$, $g \leftarrow G_{p_1}$ and T is either uniform in $G_{p_1}$ or in G. R does the following:

• Samples $x\leftarrow \mathbb {Z}_N$ and sets $h=g^x$,

• Samples $\rho _A, \rho _B \leftarrow \mathcal{R}$, $y \leftarrow \mathbb {Z}_N$, and sets $r_A = (\rho _A, T, T^x)$ and $r_B = (\rho _B, T^y, T^{xy})$,

• Computes

  $$\begin{aligned} K_0 = \mathsf {sk}\text {-}\mathsf {NIKE}.\mathsf {SharedKey}(e(T,T)^{xy}, \rho _A, \mathsf {sk}\text {-}\mathsf {NIKE}.\mathsf {Publish}(\rho _B)), \end{aligned}$$

• Samples $K_1 \leftarrow \mathcal{K}$,

• Outputs

  $$ \big ( \mathbb {G}, g, h, r_A,\, r_B, K_b \big ). $$

If $T \leftarrow G_{p_1}$ then R produces the first distribution of Lemma 5, and if $T \leftarrow G$ then it produces the second distribution.    $\square$

Hybrid 3. We again change how we compute $r_A, r_B$ given to the distinguisher. In this experiment we sample $x \leftarrow \mathbb {Z}_N$. We now compute $h = g^x$, and generate the state as $r= (\rho , (u^{a}, u^{ax}))$ where $a \leftarrow \mathbb {Z}_N$.

The distributions induced by Hybrid 2 and Hybrid 3 are statistically indistinguishable. Indeed, they only differ when $w\in G_{p_1}$ or $w\in G_{p_2}$, which happens with probability $(p_1+p_2-1)/(p_1p_2) = \mathrm{negl}(\lambda )$.

Lemma 6

Assume $\mathsf {sk}\text {-}\mathsf {NIKE}$ is an $(n, \ell + (\log p_1)/2, \epsilon )$-secure symmetric key NIKE with error $\epsilon = \mathrm{negl}(\lambda )$. Then the advantage of any (even potentially unbounded) distinguisher in Hybrid 3 is negligible.

Proof

In Hybrid 3, the secret key $\mathsf {sk}$ for $\mathsf {sk}\text {-}\mathsf {NIKE}$ is computed as $\mathsf {sk}= e(u^a, u^{xy}) = e(u,u)^{axy}$. In particular, over the randomness of x alone (with high probability over a and y), $\mathsf {sk}$ is uniform in $G_T$ conditioned on $h^x \in G_{p_1}$, $f_A(r_A)$ and $f_B(r_B)$. In particular, $h^x$ can be computed given $x\bmod p_1$, and therefore the view of the distinguisher can be generated using $(f_A^*(r_A), f_B^*(r_B)) = (x\bmod p_1, f_A(r_A), f_B(r_B))$ which is of size $\log p_1 + 2\ell$.

By $(n,\ell + (\log p_1)/2,\epsilon )$-security of $\mathsf {sk}\text {-}\mathsf {NIKE}$, the advantage of any (potentially unbounded) distinguisher is therefore at most $\epsilon = \mathrm{negl}(\lambda )$.    $\square$

Overall we conclude that the advantage of $\mathcal{D}, f_A, f_B$ against Construction 12 is at most negligible.    $\square$

The scheme above allows for a constant leakage rate. We refer to the full version for a short discussion on the parameters involved.