Abstract
We study the security of \(\mathsf {CTR\text {-}DRBG}\), one of NIST’s recommended Pseudorandom Number Generator (PRNG) designs. Recently, Woodage and Shumow (Eurocrypt’ 19), and then Cohney et al. (S&P’ 20) point out some potential vulnerabilities in both NIST specification and common implementations of \(\mathsf {CTR\text {-}DRBG}\). While these researchers do suggest counter-measures, the security of the patched \(\mathsf {CTR\text {-}DRBG}\) is still questionable. Our work fills this gap, proving that \(\mathsf {CTR\text {-}DRBG}\) satisfies the robustness notion of Dodis et al. (CCS’13), the standard security goal for PRNGs.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Cryptography ubiquitously relies on the assumption that high-quality randomness is available. Violation of this assumption would often lead to security disasters [9, 12, 20], and thus a good Pseudorandom Number Generator (PRNG) is a fundamental primitive in cryptography, in both theory and practice. In this work we study the security of \(\mathsf {CTR\text {-}DRBG}\), the most popular standardized PRNG.Footnote 1
A Troubled History. \(\mathsf {CTR\text {-}DRBG}\) is one of the recommended designs of NIST standard SP 800-90A, which initially included the now infamous Dual-EC. While the latter has received lots of scrutiny [8, 9], the former had attracted little attention until Woodage and Shumow [31] point out vulnerabilities in a NIST-compliant version. Even worse, very recently, Cohney et al. [12] discover that many common implementations of \(\mathsf {CTR\text {-}DRBG}\) still rely on table-based AES and thus are susceptible to cache side-channel attacks [5, 18, 24, 25].
While the attacks above are catastrophic, they only show that (i) some insecure options in the overly flexible specification of \(\mathsf {CTR\text {-}DRBG}\) should be deprecated, and (ii) developers of \(\mathsf {CTR\text {-}DRBG}\) implementation should be mindful of misuses such as leaky table-based AES, failure to refresh periodically, or using low-entropy inputs. Following these counter-measures will thwart the known attacks, but security of \(\mathsf {CTR\text {-}DRBG}\) remains questionable. A full-fledged provable-security treatment of \(\mathsf {CTR\text {-}DRBG}\) is therefore highly desirable—Woodage and Shumow consider it an important open problem [31].
Prior Provable Security. Most prior works [7, 30] only consider a simplified variant of \(\mathsf {CTR\text {-}DRBG}\) that takes no random input, and assume that the initial state is truly random. These analyses fail to capture scenarios where the PRNG’s state is either compromised or updated with adversarial random inputs. Consequently, their results are limited and cannot support security claims in NIST SP 800-90A.
A recent Ph.D. thesis of Hutchinson [23] aims to do better, analyzing security of \(\mathsf {CTR\text {-}DRBG}\) via the robustness notion of Dodis et al. [15]. But upon examining this work, we find numerous issues, effectively invalidating the results. A detailed discussion of the problems in Hutchinson’s analysis can be found in Appendix A.
Contributions. In this work, we prove that the patched \(\mathsf {CTR\text {-}DRBG}\) satisfies the robustness security of Dodis et al. [15]. Obtaining a good bound for \(\mathsf {CTR\text {-}DRBG}\) requires surmounting several theoretical obstacles, which we will elaborate below.
An important stepping stone in proving robustness of \(\mathsf {CTR\text {-}DRBG}\) is to analyze the security of the underlying randomness extractor that we name Condense-then-Encrypt (\(\mathrm {CtE}\)); see Fig. 2 for the code and an illustration of \(\mathrm {CtE}\). The conventional approach [15, 29, 31] requires that the extracted outputs be pseudorandom. However, \(\mathrm {CtE}\) oddly applies \(\mathsf {CBCMAC}\) multiple times on the same random input (with different constant prefixes), foiling attempts to use existing analysis of \(\mathsf {CBCMAC}\) [14].
To address the issue above, we observe that under \(\mathsf {CTR\text {-}DRBG}\), the outputs of \(\mathrm {CtE}\) are used for deriving keys and IVs of the CTR mode. If we model the underlying blockcipher of CTR as an ideal cipher then the extracted outputs only need to be unpredictable. In other words, \(\mathrm {CtE}\) only needs to be a good randomness condenser [27]. In light of the Generalized Leftover Hash Lemma [1], one thus needs to prove that \(\mathrm {CtE}\) is a good almost-universal hash function, which is justified by the prior \(\mathsf {CBCMAC}\) analysis of Dodis et al. [14]. As an added plus, aiming for just unpredictability allows us to reduce the min-entropy threshold on random inputs from 280 bits to 216 bits.
Still, the analysis above relies on the \(\mathsf {CBCMAC}\) result in [14], but the latter implicitly assumes that each random input is sampled from a set of equal-length strings. (Alternatively, one can view that each random input is sampled from a general universe, but then its exact length is revealed to the adversary.) This assumption may unnecessarily limit the choices of random sources for \(\mathrm {CtE}\) or squander entropy of random inputs, and thus removing it is desirable. Unfortunately, one cannot simply replace the result of [14] by existing \(\mathsf {CBCMAC}\) analysis for variable-length inputs [4], as the resulting unpredictability bound for \(\mathrm {CtE}\) will be poor. Specifically, we would end up with an inferior term \({\sqrt{q} \cdot p}/{2^{64}}\) in bounding the unpredictability of \(p\) extracted outputs against q guesses.
To circumvent the obstacle above, we uncover a neat idea behind the seemingly cumbersome design of \(\mathrm {CtE}\). In particular, given a random input I, \(\mathrm {CtE}\) first condenses it to a key \(K \leftarrow \mathsf {CBCMAC}(0 \,\Vert \,I)\) and an initialization vector \(\mathrm {IV}\leftarrow \mathsf {CBCMAC}(1 \,\Vert \,I)\), and then uses CBC mode to encrypt a constant string under K and \(\mathrm {IV}\). To predict the CBC ciphertext, an adversary must guess both K and \(\mathrm {IV}\) simultaneously. Apparently, the designers of \(\mathrm {CtE}\) intend to use the iteration of \(\mathsf {CBCMAC}\) to undo the square-root effect in the Leftover Hash Lemma [14, 19] that has plagued existing \(\mathsf {CBCMAC}\) analysis [14]. Still, giving a good unpredictability bound for \((K, \mathrm {IV})\) is nontrivial, as (i) they are derived from the same random input I, and (ii) prior results [4], relying on analysis of ordinary collision on \(\mathsf {CBCMAC}\), can only be used to bound the marginal unpredictability of either K or \(\mathrm {IV}\). We instead analyze a multi-collision property for \(\mathsf {CBCMAC}\), and thus can obtain a tighter bound on the unpredictability of \((K, \mathrm {IV})\). Concretely, we can improve the term \({\sqrt{q} \cdot p}{/2^{64}}\) above to \({\sqrt{qL} \cdot \sigma }/{2^{128}}\), where L is the maximum block length of the random inputs, and \(\sigma \) is their total block length.Footnote 2
Even with the good security of \(\mathrm {CtE}\), obtaining a strong robustness bound for \(\mathsf {CTR\text {-}DRBG}\) is still challenging. The typical approach [15, 17, 31] is to decompose the complex robustness notion into simpler ones, preserving and recovering. But this simplicity comes with a cost: if we can bound the recovering and preserving advantage by \(\epsilon \) and \(\epsilon '\) respectively, then we only obtain a loose bound \(p(\epsilon + \epsilon ')\) in the robustness advantage, where \(p\) is the number of random inputs. In our context, the blowup factor \(p\) will lead to a rather poor bound.
Even worse, as pointed out by Dodis et al. [15], there is an adaptivity issue in proving recovering security of PRNGs that are built on top of a universal hash H. In particular, here an adversary, given a uniform hash key K, needs to pick an index \(i \in \{1, \ldots , p\}\) to indicate which random input \(I_i\) that it wants to attack, and then predicts the output of \(H_K(I_i)\) via q guesses. The subtlety here is that the adversary can adaptively pick the index i that depends on the key K, creating a situation similar to selective-opening attacks [3, 16]. Dodis et al. [15] give a simple solution for this issue, but their treatment leads to another blowup factor \(p\) in the security bound. In Sect. 6.1 we explore this problem further, showing that the blowup factor \(p\) is inherent via a counter-example. Our example is based on a contrived universal hash function, so it does not imply that \(\mathsf {CTR\text {-}DRBG}\) has inferior recovering security per se. Still, it shows that if one wants to prove a good recovering bound for \(\mathsf {CTR\text {-}DRBG}\), one must go beyond treating \(\mathrm {CtE}\) as a universal hash function.
Given the situation above, instead of using the decomposition approach, we give a direct proof for the robustness security via the H-coefficient technique [10, 26]. We carefully exercise the union bound to sidestep pesky adaptivity pitfalls and obtain a tight bound.Footnote 3
Limitations. In this work, we assume that each random input has sufficient min entropy. This restriction is admittedly limited, failing to show that \(\mathsf {CTR\text {-}DRBG}\) can slowly accumulate entropy in multiple low-entropy inputs, which is an important property in the robustness notion. Achieving full robustness for \(\mathsf {CTR\text {-}DRBG}\) is an important future direction. Still, our setting is meaningful, comparable to the notion of Barak and Halevi [2]. This is also the setting that the standard NIST SP 800-90A assumes. We note that Woodage and Shumow [31] use the same setting for analyzing HMAC-DRBG, and Hutchinson [23] for \(\mathsf {CTR\text {-}DRBG}\).
Seed-Dependent Inputs. Our work makes a standard assumption that the random inputs are independent of the seed of the randomness extractor.Footnote 4 This assumption seems unavoidable as deterministic extraction from a general source is impossible [11]. In a recent work, Coretti et al. [13] challenge the conventional wisdom with meaningful notions for seedless extractors and PRNGs, and show that \(\mathsf {CBCMAC}\) is insecure in their model. In Sect. 7, we extend their ideas to attack \(\mathsf {CTR\text {-}DRBG}\). We note that this is just a theoretical attack with a contrived sampler of random inputs, and does not directly translate into an exploit of real-world \(\mathsf {CTR\text {-}DRBG}\) implementations.
Ruhault [28] also considers attacking \(\mathsf {CTR\text {-}DRBG}\) with a seed-dependent sampler. But his attack, as noted by Woodage and Shumow [31], only applies to a variant of \(\mathsf {CTR\text {-}DRBG}\) that does not comply with NIST standard. It is unclear how to use his ideas to break the actual \(\mathsf {CTR\text {-}DRBG}\).
2 Preliminaries
Notation. Let \(\varepsilon \) denote the empty string. For an integer i, we let \([i]_{t}\) denote a t-bit representation of i. For a finite set S, we let  denote the uniform sampling from S and assigning the value to x. Let |x| denote the length of the string x, and for \(1 \le i < j \le |x|\), let x[i : j] denote the substring from the i-th bit to the j-th bit (inclusive) of x. If A is an algorithm, we let \(y \leftarrow A(x_1,\ldots ;r)\) denote running A with randomness r on inputs \(x_1,\ldots \) and assigning the output to y. We let
denote the uniform sampling from S and assigning the value to x. Let |x| denote the length of the string x, and for \(1 \le i < j \le |x|\), let x[i : j] denote the substring from the i-th bit to the j-th bit (inclusive) of x. If A is an algorithm, we let \(y \leftarrow A(x_1,\ldots ;r)\) denote running A with randomness r on inputs \(x_1,\ldots \) and assigning the output to y. We let  be the result of picking r at random and letting \(y \leftarrow A(x_1,\ldots ;r)\).
be the result of picking r at random and letting \(y \leftarrow A(x_1,\ldots ;r)\).
Conditional Min-entropy and Statistical Distance. For two random variables X and Y, the (average-case) conditional min-entropy of X given Y is
The statistical distance between X and Y is
The statistical distance \(\mathsf {SD}(X, Y)\) is the best possible advantage of an (even computationally unbounded) adversary in distinguishing X and Y.
Systems and Transcripts. Following the notation from [22], it is convenient to consider interactions of a distinguisher \(A\) with an abstract system \(\mathbf {S}\) which answers \(A\)’s queries. The resulting interaction then generates a transcript \(\tau = ((X_1, Y_1), \ldots , (X_q, Y_q))\) of query-answer pairs. It is known that \(\mathbf {S}\) is entirely described by the probabilities \(\mathsf {p}_{\mathbf {S}}(\tau )\) that correspond to the system \(\mathbf {S}\) responding with answers as indicated by \(\tau \) when the queries in \(\tau \) are made.
We will generally describe systems informally, or more formally in terms of a set of oracles they provide, and only use the fact that they define corresponding probabilities \(\mathsf {p}_{\mathbf {S}}(\tau )\) without explicitly giving these probabilities. We say that a transcript \(\tau \) is valid for system \(\mathbf {S}\) if \(\mathsf {p}_{\mathbf {S}}(\tau ) > 0\).
The H-coefficient Technique. We now describe the H-coefficient technique of Patarin [10, 26]. Generically, it considers a deterministic distinguisher \(A\) that tries to distinguish a “real” system \(\mathbf {S}_{1}\) from an “ideal” system \(\mathbf {S}_{0}\). The adversary’s interactions with those systems define transcripts \(X_1\) and \(X_0\), respectively, and a bound on the distinguishing advantage of \(A\) is given by the statistical distance \(\mathsf {SD}(X_1, X_0)\).
Lemma 1
[10, 26] Suppose we can partition the set of valid transcripts for the ideal system into good and bad ones. Further, suppose that there exists \(\epsilon \ge 0\) such that \(1 - \frac{\mathsf {p}_{\mathbf {S}_{1}}(\tau )}{\mathsf {p}_{\mathbf {S}_{0}}(\tau )} \le \epsilon \) for every good transcript \(\tau \). Then,
3 Modeling Security of PRNGs
In this section we recall the syntax and security notion of Pseudorandom Number Generator (PRNG) from Dodis et al. [15].
Syntax. A PRNG with state space \(\mathrm {State}\) and seed space \(\mathrm {Seed}\) is a tuple of deterministic algorithms \(\mathcal{G}= (\mathsf {setup}, \mathsf {refresh}, \mathsf {next})\). Under the syntax of
[15], \(\mathsf {setup}\) is instead probabilistic: it takes no input, and returns  and
and  . However, as pointed out by Shrimpton and Terashima
[29], this fails to capture real-world PRNGs, where the state may include, for example, counters. Moreover, real-world \(\mathsf {setup}\) typically gets its coins from an entropy source, and thus the coins may be non-uniform. Therefore, following
[29, 31], we instead require that the algorithm
. However, as pointed out by Shrimpton and Terashima
[29], this fails to capture real-world PRNGs, where the state may include, for example, counters. Moreover, real-world \(\mathsf {setup}\) typically gets its coins from an entropy source, and thus the coins may be non-uniform. Therefore, following
[29, 31], we instead require that the algorithm  take as input a seed
take as input a seed  and a string I, and then output an initial state \(S \in \mathrm {State}\); there is no explicit requirement on the distribution of S.
and a string I, and then output an initial state \(S \in \mathrm {State}\); there is no explicit requirement on the distribution of S.
Next, algorithm  takes as input a seed
takes as input a seed  , a state S, and a string I, and then outputs a new state. Finally algorithm
, a state S, and a string I, and then outputs a new state. Finally algorithm  takes as input a seed
takes as input a seed  , a state S, and a number \(\ell \in \mathbb {N}\), and then outputs a new state and an \(\ell \)-bit output string. Here we follow the recent work of Woodage and Shumow
[31] to allow variable output length.
, a state S, and a number \(\ell \in \mathbb {N}\), and then outputs a new state and an \(\ell \)-bit output string. Here we follow the recent work of Woodage and Shumow
[31] to allow variable output length.
Distribution Samplers. A distribution sampler \(\mathcal {D}\) is a stateful, probabilistic algorithm. Given the current state s, it will output a tuple \((s', I, \gamma , z)\) in which \(s'\) is the updated state, I is the next randomness input for the PRNG \(\mathcal{G}\), \(\gamma \ge 0\) is a real number, and z is some side information of I given to an adversary attacking \(\mathcal{G}\). Let \(p\) be an upper bound of the number of calls to \(\mathcal {D}\) in our security games. Let \(s_0\) be the empty string, and let  for every \(i \in \{1, \ldots , p\}\). For each \(i \le p\), let
for every \(i \in \{1, \ldots , p\}\). For each \(i \le p\), let
We say that sampler \(\mathcal {D}\) is legitimate if \(H_\infty (I_i \mid {\mathcal {I}}_{p, i}) \ge \gamma _i\) for every \(i \in \{1, \ldots , p\}\). A legitimate sampler is \(\lambda \)-simple if \(\gamma _i \ge \lambda \) for every i.
In this work, we will consider only simple samplers for a sufficiently large min-entropy threshold \(\lambda \). In other words, we will assume that each random input has sufficient min entropy. This setting is somewhat limited, as it fails to show that the PRNG can slowly accumulate entropy in multiple low-entropy inputs. However, it is still meaningful—this is actually the setting that the standard NIST SP 800-90A assumes. We note that Woodage and Shumow [31] also analyze the HMAC-DRBG construction under the same setting.
Robustness. Let \(\lambda > 0\) be a real number, \(A\) be an adversary attacking \(\mathcal{G}\), and \(\mathcal {D}\) be a legitimate distribution sampler. Define

where game \(\mathbf {G}^{\mathrm {rob}}_{\mathcal{G}, \lambda }(A, \mathcal {D})\) is defined in Fig. 1.
Informally, the game picks a challenge bit  and maintains a counter c of the current estimated amount of accumulated entropy that is initialized to 0. It runs the distribution sampler \(\mathcal {D}\) on an empty-string state to generate the first randomness input I. It then calls the \(\mathsf {setup}\) algorithm on a uniformly random seed to generate the initial state S, and increments c to \(\gamma \). The adversary \(A\), given the seed and the side information z and entropy estimation \(\gamma \) of I, has access to the following:
and maintains a counter c of the current estimated amount of accumulated entropy that is initialized to 0. It runs the distribution sampler \(\mathcal {D}\) on an empty-string state to generate the first randomness input I. It then calls the \(\mathsf {setup}\) algorithm on a uniformly random seed to generate the initial state S, and increments c to \(\gamma \). The adversary \(A\), given the seed and the side information z and entropy estimation \(\gamma \) of I, has access to the following:
-
(i)
An oracle \(\textsc {Ref}()\) to update the state S via the algorithm \(\mathsf {refresh}\) with the next randomness input I. The adversary learns the corresponding side information z and the entropy estimation \(\gamma \) of I. The counter c is incremented by \(\gamma \).
-
(ii)
An oracle \(\textsc {Get}()\) to obtain the current state S. The counter c is reset to 0.
-
(iii)
An oracle \(\textsc {Set}()\) to set the current state to an adversarial value \(S^*\). The counter c is reset to 0.
-
(iv)
An oracle \(\textsc {RoR}(1^\ell )\) to get the next \(\ell \)-bit output. The game runs the \(\mathsf {next}\) algorithm on the current state S to update it and get an \(\ell \)-bit output \(R_1\), and also samples a uniformly random string
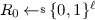 . If the accumulated entropy is insufficient (meaning \(c < \lambda \)) then c is reset to 0 and \(R_1\) is returned to the adversary. Otherwise, \(R_b\) is given to the adversary.
. If the accumulated entropy is insufficient (meaning \(c < \lambda \)) then c is reset to 0 and \(R_1\) is returned to the adversary. Otherwise, \(R_b\) is given to the adversary.
The goal of the adversary is to guess the challenge bit b, by outputting a bit \(b'\). The advantage  measures the normalized probability that the adversary’s guess is correct.
measures the normalized probability that the adversary’s guess is correct.
Extension for Ideal Models. In many cases, the PRNG is based on an ideal primitive \(\varPi \) such as an ideal cipher or a random oracle. One then can imagine that the PRNG uses a huge seed that encodes \(\varPi \). In the robustness notion, the adversary \(A\) would be given oracle access to \(\varPi \) but the distribution sampler \(\mathcal {D}\) is assumed to be independent of the seed, and thus has no access to \(\varPi \). This extension for ideal models is also used in prior work [6, 31].
Some PRNGs, such as \(\mathsf {CTR\text {-}DRBG}\) or the Intel PRNG [29], use AES with a constant key \(K_0\). For example, \(K_0 \leftarrow \mathrm {AES}(0^{128}, 0^{127} \,\Vert \,1)\) for the Intel PRNG, and \(K_0 \leftarrow \mathtt {0x}00010203 \cdots \) for \(\mathsf {CTR\text {-}DRBG}\). An alternative treatment for ideal models in this case is to let both \(\mathcal {D}\) and \(A\) have access to the ideal primitive, but pretend that \(K_0\) is truly random, independent of \(\mathcal {D}\). This approach does not work well in our situation because (i) the constant key of \(\mathsf {CTR\text {-}DRBG}\) does not look random at all, and (ii) allowing \(\mathcal {D}\) access to the ideal primitive substantially complicates the robustness proof of \(\mathsf {CTR\text {-}DRBG}\). We therefore avoid this approach to keep the proof simple.
4 The Randomness Extractor of \(\mathsf {CTR\text {-}DRBG}\)
A PRNG is often built on top of an internal (seeded) randomness extractor \(\mathsf {Ext}: \mathrm {Seed}\times \{0,1\}^* \rightarrow \{0,1\}^s\) that takes as input a seed  and a random input \(I \in \{0,1\}^*\) to deterministically output a string \(V \in \{0,1\}^s\). For example, the Intel PRNG
[29] is built on top of CBCMAC, or HMAC-DRBG on top of HMAC. In this section we will analyze the security of the randomness extractor of \(\mathsf {CTR\text {-}DRBG}\), which we call Condense-then-Encrypt (\(\mathrm {CtE}\)). We shall assume that the underlying blockcipher is AES.Footnote 5
and a random input \(I \in \{0,1\}^*\) to deterministically output a string \(V \in \{0,1\}^s\). For example, the Intel PRNG
[29] is built on top of CBCMAC, or HMAC-DRBG on top of HMAC. In this section we will analyze the security of the randomness extractor of \(\mathsf {CTR\text {-}DRBG}\), which we call Condense-then-Encrypt (\(\mathrm {CtE}\)). We shall assume that the underlying blockcipher is AES.Footnote 5
4.1 The \(\mathrm {CtE}\) Construction
The randomness extractor \(\mathrm {CtE}\) is based on two standard components: CBCMAC and CBC encryption. Below, we first recall the two components of \(\mathrm {CtE}\), and then describe how to compose them in \(\mathrm {CtE}\).
The CBCMAC Construction. Let \(\pi : \{0,1\}^n \rightarrow \{0,1\}^n\) be a permutation. For the sake of convenience, we will describe CBCMAC with a general IV; one would set \(\mathrm {IV}\leftarrow 0^n\) in the standard CBCMAC algorithm. For an initialization vector \(\mathrm {IV}\in \{0,1\}^n\) and a message \(M = M_1 \cdots M_t\), with each \(|M_i| = n\), we recursively define
where \(R \leftarrow \pi (\mathrm {IV}\oplus M_1)\), and in the base case of the empty-string message, let \(\mathsf {CBCMAC}^\mathrm {IV}[\pi ]( \varepsilon ) = \mathrm {IV}\). In the case that \(\mathrm {IV}= 0^n\), we simply write \(\mathsf {CBCMAC}[\pi ](M)\) instead of \(\mathsf {CBCMAC}^\mathrm {IV}[\pi ](M)\).
The CBC Encryption Construction. In the context of \(\mathrm {CtE}\), the CBC encryption is only used for full-block messages. Let \(E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\) be a blockcipher. For a key \(K \in \{0,1\}^k\), an initialization vector \(\mathrm {IV}\in \{0,1\}^n\), and a message \(M = M_1 \cdots M_t\), with each \(|M_i| = n\), let
where \(C_1, \ldots , C_t\) are defined recursively via \(C_0 \leftarrow \mathrm {IV}\) and \(C_i \leftarrow E_K(C_{i - 1} \oplus M_i)\) for every \(1 \le i \le t\). In our context, since we do not need decryptability, the IV is excluded in the output of CBC.
The \(\mathrm {CtE}[E, m]\) construction, built on top of a blockcipher \(E:\{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\). Here the random input I is a byte string. For an integer i, we let \([i]_{t}\) denote a t-bit representation of i, and the permutation \(\pi \) is instantiated from E with the k-bit constant key \(\mathtt {0x}00010203 \cdots \).
The \(\mathrm {CtE}\) Construction. Let \(E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\) be a blockcipher, such that k and n are divisible by 8, and \(n \le k \le 2n\)—this captures all choices of AES key length. Let \(\mathrm {pad}: \{0,1\}^* \rightarrow (\{0,1\}^n)^+\) be the padding scheme that first appends the byte \(\mathtt {0x08}\), and then appends 0’s until the length is a multiple of n. Note that \(\mathrm {pad}(X) \ne \mathrm {pad}(Y)\) for any \(X \ne Y\). For the sake of convenience, we shall describe a more generalized construction \(\mathrm {CtE}[E, m]\), with \(m \le 3n\). The code of this construction is shown in Fig. 2. The randomness extractor of \(\mathsf {CTR\text {-}DRBG}\) corresponds to \(\mathrm {CtE}[E, k + n]\); we also write \(\mathrm {CtE}[E]\) for simplicity.
4.2 Security of \(\mathrm {CtE}\)
Security Modeling. In modeling the security of a randomness extractor \(\mathsf {Ext}\), prior work
[14, 29, 31] usually requires that  be pseudorandom for an adversary that is given the seed S, provided that (i) the random input I has sufficiently high min entropy, and (ii) the seed S is uniformly random. In our situation, following the conventional route would require each random input to have at least 280 bits of min entropy for \(\mathsf {CTR\text {-}DRBG}\) to achieve birthday-bound security. However, for the way that \(\mathrm {CtE}\) is used in \(\mathsf {CTR\text {-}DRBG}\), we only need the n-bit prefix of the output to be unpredictable, allowing us to reduce the min-entropy threshold to 216 bits. In other words, we only need \(\mathrm {CtE}[E, n]\) to be a good condenser
[27].
be pseudorandom for an adversary that is given the seed S, provided that (i) the random input I has sufficiently high min entropy, and (ii) the seed S is uniformly random. In our situation, following the conventional route would require each random input to have at least 280 bits of min entropy for \(\mathsf {CTR\text {-}DRBG}\) to achieve birthday-bound security. However, for the way that \(\mathrm {CtE}\) is used in \(\mathsf {CTR\text {-}DRBG}\), we only need the n-bit prefix of the output to be unpredictable, allowing us to reduce the min-entropy threshold to 216 bits. In other words, we only need \(\mathrm {CtE}[E, n]\) to be a good condenser
[27].
We now recall the security notion for randomness condensers. Let \(\mathsf {Cond}: \mathrm {Seed}\times \{0,1\}^* \rightarrow \{0,1\}^n\) be a deterministic algorithm. Let \(\mathcal {S}\) be a \(\lambda \)-source, meaning a stateless, probabilistic algorithm that outputs a random input I and some side information z such that \(H_\infty (I \mid z) \ge \lambda \). For an adversary \(A\), define

as the guessing advantage of \(A\) against the condenser \(\mathsf {Cond}\) on the source \(\mathcal {S}\), where game \(\mathbf {G}^{\mathrm {guess}}_\mathsf {Cond}(A, \mathcal {S})\) is defined in Fig. 3. Informally, the game measures the chance that the adversary can guess the output  given the seed
given the seed  and some side information z of the random input I.
and some side information z of the random input I.
When the condenser \(\mathsf {Cond}\) is built on an ideal primitive \(\varPi \) such as a random oracle or an ideal cipher, we only consider sources independent of \(\varPi \). Following [14], instead of giving \(A\) oracle access to \(\varPi \), we will give the adversary \(A\) the entire (huge) encoding of \(\varPi \), which can only help the adversary. In other words, we view the encoding of \(\varPi \) as the seed of \(\mathsf {Cond}\), and as defined in game \(\mathbf {G}^{\mathrm {guess}}_\mathsf {Cond}(A, \mathcal {S})\), the adversary \(A\) is given the seed.
To show that \(\mathrm {CtE}[E, n]\) is a good condenser, we will first show that it is an almost universal (AU) hash, and then apply a Generalized Leftover Hash Lemma of Barak et al. [1]. Below, we will recall the notion of AU hash.
AU Hash. Let \(\mathsf {Cond}: \mathrm {Seed}\times \mathrm {Dom}\rightarrow \{0,1\}^n\) be a (keyed) hash function. For each string X, define its block length to be \(\max \{1, |X|/n\}\). For a function \(\delta : \mathbb {N}\rightarrow [1, \infty )\), we say that \(\mathsf {Cond}\) is a \(\delta \)-almost universal hash if for every distinct strings \(X_1, X_2\) whose block lengths are at most \(\ell \), we have

The following Generalized Leftover Hash Lemma of Barak et al. [1] shows that an AU hash function is a good condenser.
Lemma 2 (Generalized Leftover Hash Lemma)
[1] Let \(\mathsf {Cond}: \mathrm {Seed}\times \mathrm {Dom}\rightarrow \{0,1\}^n\) be a \(\delta \)-AU hash function, and let \(\lambda > 0\) be a real number. Let \(\mathcal {S}\) be a \(\lambda \)-source whose random input I has at most \(\ell \) blocks. For any adversary \(A\) making at most q guesses,

Discussion. A common way to analyze \(\mathsf {CBCMAC}\)-based extractors is to use a result by Dodis et al. [14]. However, this analysis is restricted to the situation in which either (i) the length of the random input is fixed, or (ii) the side information reveals the exact length of the random input. On the one hand, while the assumption (i) is true in Linux PRNG where the kernel entropy pool has size 4,096 bits, it does not hold in, say Intel PRNG where the system keeps collecting entropy and lengthening the random input. On the other hand, the assumption (ii) may unnecessarily squander entropy of random inputs by intentionally leaking their lengths. Given that \(\mathsf {CTR\text {-}DRBG}\) is supposed to deal with a generic source of potentially limited entropy, it is desirable to remove the assumptions (i) and (ii) in the analysis.
At the first glance, one can deal with variable input length by using the following analysis of Bellare et al. [4] of \(\mathsf {CBCMAC}\). Let \(\mathrm {Perm}(n)\) be the set of permutations on \(\{0,1\}^n\). Then for any distinct, full-block messages \(X_1\) and \(X_2\) of at most \(\ell \le 2^{n/4}\) blocks, Bellare et al. show that

However, this bound is too weak for our purpose due to the square root in Lemma 2. In particular, using this formula leads to an inferior term \(\frac{\sqrt{q} \cdot p}{2^{n / 2}}\) in bounding the unpredictability of \(p\) extracted outputs against q guesses.
To improve the concrete bound, we observe that to guess the output of \(\mathrm {CtE}[E, n]\), the adversary has to guess both the key and IV of the CBC encryption simultaneously. Giving a good bound for this joint unpredictability is nontrivial, since the key and the IV are derived from the same source of randomness (but with different constant prefixes). This requires us to handle a multi-collision property of CBCMAC.
Security Analysis of \(\mathrm {CtE}\) . The following Lemma 3 gives a multi-collision property of CBCMAC that \(\mathrm {CtE}\) needs;
Lemma 3 (Multi-collision of CBCMAC)
Let \(n \ge 32\) be an integer. Let \(X_1, \ldots , X_4\) be distinct, non-empty, full-block messages such that
-
(i)
\(X_1\) and \(X_2\) have the same first block, and \(X_3\) and \(X_4\) have the same first block, but these two blocks are different, and
-
(ii)
the block length of each message is at most \(\ell \), with \(4 \le \ell \le 2^{n/3 -4}\).
Then for a truly random permutation  , the probability that both \(\mathsf {CBCMAC}[\pi ](X_1) = \mathsf {CBCMAC}[\pi ](X_2)\) and \(\mathsf {CBCMAC}[\pi ](X_3) = \mathsf {CBCMAC}[\pi ](X_4)\) happen is at most \(64\ell ^3/2^{2n}\).
, the probability that both \(\mathsf {CBCMAC}[\pi ](X_1) = \mathsf {CBCMAC}[\pi ](X_2)\) and \(\mathsf {CBCMAC}[\pi ](X_3) = \mathsf {CBCMAC}[\pi ](X_4)\) happen is at most \(64\ell ^3/2^{2n}\).
Armed with the result above, we now can show in Lemma 4 below that \(\mathrm {CtE}[E, n]\) is a good AU hash. Had we used the naive bound in Eq. (1), we would have obtained an inferior bound \(\frac{2\sqrt{\ell }}{2^n} + \frac{64\ell ^4}{2^{2n}}\).
Lemma 4
Let \(n \ge 32\) and \(k \in \{n, n + 1, \ldots , 2n\}\) be integers. Let \(E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\) that we model as an ideal cipher. Let \(\mathrm {CtE}[E, n]\) be described as above. Let \(I_1, I_2\) be distinct strings of at most \(\ell \) blocks, with \(\ell + 2 \le 2^{n/3 - 4}\). Then
where the randomness is taken over the choices of E.
Proof
Recall that in \(\mathrm {CtE}[E, n](I_b)\), with \(b \in \{1,2\}\), we first iterate through \(\mathsf {CBCMAC}\) three times to derive a key \(K_b\) and an IV \(J_b\), and then output \(E(K_b, J_b)\). Let \(Y_b\) and \(Z_b\) be the first block and the second block of \(K_b \,\Vert \,J_b\), respectively. We consider the following cases:
Case 1: \((Y_1, Z_1) \ne (Y_2, Z_2)\). Hence \((K_1, J_1) \ne (K_2, J_2)\). If \(K_1 = K_2\) then since E is a blockcipher, \(E(K_1, J_1) \ne E(K_2, J_2)\). Suppose that \(K_1 \ne K_2\). Without loss of generality, assume that \(K_1\) is not the constant key in CBCMAC. Since E is modeled as an ideal cipher, \(E(K_1, J_1)\) is a uniformly random string, independent of \(E(K_2, J_2)\), and thus the chance that \(E(K_1, J_1) = E(K_2, J_2)\) is \(1/2^n\). Therefore, in this case, the probability that \(\mathrm {CtE}[E,n](I_1) = \mathrm {CtE}[E, n](I_2)\) is at most \(1/2^n\).
Case 2: \((Y_1, Z_1) = (Y_2, Z_2)\). It suffices to show that this case happens with probability at most \(64(\ell + 2)^3 / 2^{2n}\). For each \(a \in \{0, 1\}\), let \(P_a \leftarrow [a]_{32} \,\Vert \,0^{n - 32}\). For \(b \in \{1, 2\}\), let
Let \(\pi \) be the permutation in CBCMAC. Note that \(Y_b \leftarrow \mathsf {CBCMAC}[\pi ](P_0 \,\Vert \,U_b)\) and \(Z_b \leftarrow \mathsf {CBCMAC}[\pi ](P_1 \,\Vert \,U_b)\) for every \(b \in \{1, 2\}\). Applying Lemma 3 with \(X_1 = P_0 \,\Vert \,U_1\), \(X_2 = P_0 \,\Vert \,U_2\), \(X_3 = P_1 \,\Vert \,U_1\), and \(X_4 = P_1 \,\Vert \,U_2\) (note that these strings have block length at most \(\ell + 2\)), the chance that \(Y_1 = Y_2\) and \(Z_1 = Z_2\) is at most \(64(\ell + 2)^3 / 2^{2n}\). \(\square \)
Combining Lemma 2 and Lemma 4, we immediately obtain the following result, establishing that \(\mathrm {CtE}[E, n]\) is a good condenser.
Theorem 1
Let \(n \ge 32\) and \(k \in \{n, n + 1, \ldots , 2n\}\) be integers. Let \(E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\) that we model as an ideal cipher. Let \(\mathrm {CtE}[E, n]\) be described as above. Let \(\mathcal {S}\) be a \(\lambda \)-source that is independent of E and outputs random inputs of at most \(\ell \) blocks. Then for any adversary \(A\) making at most q guesses,

Another Requirement of \(\mathrm {CtE}\) . In proving security of \(\mathsf {CTR\text {-}DRBG}\), one would encounter the following situation. We first derive the key \(J \leftarrow \mathrm {CtE}[E](I)\) on a random input I, and let K be the key of \(\mathsf {CBC}\) encryption in \(\mathrm {CtE}[E](I)\). The adversary then specifies a mask P. It wins if \(K = J \oplus P\); that is, the adversary wins if it can predict \(K \oplus J\). To bound the winning probability of the adversary, our strategy is to show that even the n-bit prefix of \(K \oplus J\) is hard to guess. In particular, we consider a construction Xor-Prefix (\(\mathrm {XP}\)) such that \(\mathrm {XP}[E](I)\) outputs the n-bit prefix of \(K \oplus J\), and then show that \(\mathrm {XP}[E]\) is a good condenser.
The code of \(\mathrm {XP}[E]\) is given in Fig. 4. Informally, \(\mathrm {XP}[E](I)\) first runs \(\mathrm {CtE}[E, n](I)\) to obtain an n-bit string C, and then outputs \(C \oplus K[1:n]\), where K is the key of \(\mathsf {CBC}\) encryption in \(\mathrm {CtE}[E, n](I)\).
The \(\mathrm {XP}[E]\) construction, built on top of a blockcipher \(E:\{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\). Here the random input I is a byte string. For an integer i, we let \([i]_{t}\) denote a t-bit representation of i, and the permutation \(\pi \) is instantiated from E with the k-bit constant key \(\mathtt {0x}00010203 \cdots \).
The following result shows that \(\mathrm {XP}[E]\) is a good AU hash.
Lemma 5
Let \(n \ge 32\) and \(k \in \{n, n + 1, \ldots , 2n\}\) be integers. Let \(E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\) that we model as an ideal cipher. Let \(\mathrm {XP}[E]\) be described as above. Let \(I_1, I_2\) be distinct strings of at most \(\ell \) blocks, with \(\ell + 2 \le 2^{n/3 - 4}\). Then
where the randomness is taken over the choices of E.
Proof
Recall that in \(\mathrm {XP}[E](I_b)\), with \(b \in \{1, 2\}\), we first iterate through \(\mathsf {CBCMAC}\) to derive a key \(K_b\) and an IV \(J_b\), and then output \(E(K_b, J_b) \oplus K_b[1:n]\). Let \(Y_b\) and \(Z_b\) be the first block and the second block of \(K_b \,\Vert \,J_b\), respectively. We consider the following cases:
Case 1: \((Y_1, Z_1) \ne (Y_2, Z_2)\). Hence \((K_1, J_1) \ne (K_2, J_2)\). If \(K_1 = K_2\) then since E is a blockcipher, \(E(K_1, J_1) \ne E(K_2, J_2)\) and thus
Suppose that \(K_1 \ne K_2\). Without loss of generality, assume that \(K_1\) is not the constant key in CBCMAC. Since E is modeled as an ideal cipher, the string \(E(K_1, J_1) \oplus K_1[1:n]\) is uniformly random, independent of \(E(K_2, J_2) \oplus K_2[1:n]\), and thus the chance that these two strings are the same is \(1/2^n\). Therefore, in this case, the probability that \(\mathrm {XP}[E](I_1) = \mathrm {XP}[E](I_2)\) is at most \(1/2^n\).
Case 2: \((Y_1, Z_1) = (Y_2, Z_2)\). It suffices to show that this case happens with probability at most \(64(\ell + 2)^3 / 2^{2n}\). For each \(a \in \{0, 1\}\), let \(P_b \leftarrow [b]_{32} \,\Vert \,0^{n - 32}\). For \(b \in \{1, 2\}\), let
Let \(\pi \) be the permutation in CBCMAC. Note that \(Y_b \leftarrow \mathsf {CBCMAC}[\pi ](P_0 \,\Vert \,U_b)\) and \(Z_b \leftarrow \mathsf {CBCMAC}[\pi ](P_1 \,\Vert \,U_b)\) for every \(b \in \{1, 2\}\). Applying Lemma 3 with \(X_1 = P_0 \,\Vert \,U_1\), \(X_2 = P_0 \,\Vert \,U_2\), \(X_3 = P_1 \,\Vert \,U_1\), and \(X_4 = P_1 \,\Vert \,U_2\) (note that these strings have block length at most \(\ell + 2\)), the chance that \(Y_1 = Y_2\) and \(Z_1 = Z_2\) is at most \(64(\ell + 2)^3 / 2^{2n}\). \(\square \)
Combining Lemma 2 and Lemma 5, we immediately obtain the following result, establishing that \(\mathrm {XP}[E]\) is a good condenser.
Lemma 6
Let \(n \ge 32\) and \(k \in \{n, n + 1, \ldots , 2n\}\) be integers. Let \(E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\) that we model as an ideal cipher. Let \(\mathrm {XP}[E]\) be described as above. Let \(\mathcal {S}\) be a \(\lambda \)-source that is independent of E and outputs random inputs of at most \(\ell \) blocks. Then for any adversary \(A\) making at most q guesses,

5 The \(\mathsf {CTR\text {-}DRBG}\) Construction
The \(\mathsf {CTR\text {-}DRBG}\) construction is based on the randomness extractor \(\mathrm {CtE}\) in Sect. 4 and the Counter (CTR) mode of encryption. Below, we will first recall the CTR mode before describing \(\mathsf {CTR\text {-}DRBG}\).
The Counter Mode. Let \(E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\) be a blockcipher. For a key \(K \in \{0,1\}^k\), an \(\mathrm {IV}\in \{0,1\}^n\), and a message M, let \(r \leftarrow \lceil |M| / n \rceil \), and let
in which \(Y \leftarrow Y_1 \,\Vert \,\cdots \,\Vert \,Y_r\) and each \(Y_i \leftarrow E(K, \mathrm {IV}+ i \bmod 2^n)\). Since we do not need decryptability, the IV is excluded in the output of CTR.
The \(\mathsf {CTR\text {-}DRBG}\) Construction. The code of \(\mathsf {CTR\text {-}DRBG}[E]\) is given in Fig. 5. Recall that here we model E as an ideal cipher, and thus the algorithms of \(\mathsf {CTR\text {-}DRBG}\) are given oracle access to E instead of being given a seed.
Remarks. The specification of \(\mathsf {CTR\text {-}DRBG}\) in NIST 800-90A is actually very flexible, allowing a wide range of options that do not conform to the specification in Fig. 5:
-
Bypassing randomness extraction: The use of \(\mathrm {CtE}\) to extract randomness is actually optional, but if \(\mathrm {CtE}\) is not used then the random inputs are required to be uniformly random. In practice, it is unclear how to enforce the full-entropy requirement. In fact, as Woodage and Shumow [31] point out, OpenSSL implementation of \(\mathsf {CTR\text {-}DRBG}\) allows one to turn off the use of \(\mathrm {CtE}\), yet directly use raw random inputs. Bypassing \(\mathrm {CtE}\), coupled with the negligence of properly sanitizing random inputs, may lead to security vulnerabilities, as demonstrated via an attack of Woodage and Shumow. We therefore suggest making the use of \(\mathrm {CtE}\) mandatory.
-
Use of nonces: Procedures \(\mathsf {setup}\) and \(\mathsf {refresh}\) may take an additional nonce as input. This extension allows one to run multiple instances of \(\mathsf {CTR\text {-}DRBG}\) on the same source of randomness, provided that they are given different nonces. In this work we do not consider multi-instance security.
-
Use of additional inputs: Procedure \(\mathsf {next}\) may take an additional random input. If \(\mathrm {CtE}\) is used, this extension is simply a composition of \(\mathsf {refresh}\) and the basic \(\mathsf {next}\) (without additional inputs). Therefore, without loss of generality, we can omit the use of addition inputs in \(\mathsf {next}\).
6 Security Analysis of \(\mathsf {CTR\text {-}DRBG}\)
6.1 Results and Discussion
Consider an adversary \(A\) attacking \(\mathsf {CTR\text {-}DRBG}\) that makes at most q oracle queries (including ideal-cipher ones) in which each \(\mathsf {next}\) query is called to output at most B blocks, and the total block length of those outputs is at most s. Let \(\mathcal {D}\) be a \(\lambda \)-simple distribution sampler. Assume that under \(A\)’s queries, \(\mathcal {D}\) produces at most \(p\) random inputs, in which the i-th random input has maximum block length \(\ell _i\). Let
be the maximum block length of the random inputs, and let
be their maximum total block length. The following Theorem 2 gives a bound on the robustness of \(\mathsf {CTR\text {-}DRBG}\) on simple samplers.
Theorem 2
Let \(E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\) be a blockcipher. Let \(\mathcal{G}\) be the construction \(\mathsf {CTR\text {-}DRBG}[E]\) as described above. Let \(\mathcal {D}\) be a \(\lambda \)-simple distribution sampler and \(A\) be an adversary attacking \(\mathcal{G}\) whose accounting of queries is given above. Then

Interpreting Our Bound. Under NIST SP 800-90A, \(L \le 2^{28}\) and \(B \le 2^{12}\). Assuming that \(q, p\le 2^{45}\) and \(s, \sigma \le 2^{50}\), if the min-entropy threshold \(\lambda \) is at least 216, the adversary’s advantage is at most \(2^{-32}\). This is comparable to what conventional blockcipher-based constructions (such as \(\mathsf {CBCMAC}\)) offer.Footnote 6
Caveat. Under our security notion, if an adversary can learn the state of \(\mathsf {CTR\text {-}DRBG}\), the outputs of \(\mathsf {next}\) are compromised until \(\mathsf {refresh}\) is called. Thus Theorem 2 does not contradict the recent (side-channel) attack of Cohney et al. [12] on common implementations of \(\mathsf {CTR\text {-}DRBG}\). Our results indicate that such an attack can be mitigated by calling \(\mathsf {refresh}\) frequently, assuming that each random input has sufficient min entropy. This is consistent with the recommendation of Cohney et al., and thus our work can be viewed as a theoretical justification for their counter-measures.
Security Recommendation. NIST SP 800-90A only requires that random inputs have min entropy of at least 128 bits. This threshold is too low, even for the modest goal of using \(\mathrm {CtE}\) to extract randomness from \(p\) random inputs. We therefore recommend increasing the min-entropy threshold to at least 216 bits. On the other hand, the standard only requires calling \(\mathsf {refresh}\) after producing \(2^{48}\) bits for the outputs. We suggest reducing this limit to, say \(2^{24}\) to force implementations to refresh more frequently.
Obstacles in the Proof of Theorem 2. A common way to prove robustness of a PRGN is to decompose the complex notion of robustness into two simpler notions: preserving and recovering [15, 17, 31]. In particular, if we can bound the recovering and preserving advantages by \(\epsilon \) and \(\epsilon '\) respectively, then this gives a bound \(p(\epsilon + \epsilon ')\) on robustness. However, if one uses the decomposition approach above to deal with \(\mathsf {CTR\text {-}DRBG}\) then one would run into the following issues.
First, at best one can only obtain a birthday bound \(B^2 / 2^n\) for the preserving and recovering security: a birthday security is unavoidable since under these two notions, the adversary has to distinguish a CTR output with a truly random string. Combining this birthday bound with the blowup factor \(p\) leads to an inferior bound \(B^2p/ 2^n\).
Next, there lies a trap in proving recovering security of any PRNG that is built on top of an AU hash function H. In particular, under the recovering notion, the adversary needs to pick an index \(i \in \{1, \ldots , p\}\) to indicate which random input \(I_i\) that it wants to attack, and then predicts the output of \(H_K(I_i)\) via q guesses. At the first glance, one can trivially use the Generalized Leftover Hash Lemma to bound the guessing advantage of each \(I_j\) as \(\delta \); the recovering advantage should be also at most \(\delta \). However, this argument is wrong, because here the adversary can adaptively pick the index i after seeing the hash key K. The correct bound for the recovering advantage should be \(p\cdot \delta \). This subtlety is somewhat similar to selective-opening security on encryption schemes [3, 16].
To understand the adaptivity issue above, consider the following counter-example. Let \(H: \{0,1\}^t \times \mathrm {Dom}\rightarrow \{0,1\}^n\) be a hash function, and let \(p= 2^t\). Let \(\mathrm {Dom}_1, \ldots , \mathrm {Dom}_p\) be a partition of \(\mathrm {Dom}\). Suppose that we have \(p\) random inputs \(I_1 \in \mathrm {Dom}_1, \ldots , I_p\in \mathrm {Dom}_{p}\), each of at least \(\lambda \) min entropy. Assume that if the key K is a t-bit encoding of an integer i and the input X belongs to \(\mathrm {Dom}_i\) then H misbehaves, outputting \(0^n\); otherwise it is a good cryptographic hash function that we can model as a (keyed) random oracle. Then H is still a good condenser: for each fixed \(i \in \{1, \ldots , p\}\) and for a uniformly random key  , the chance that one can predict \(H_K(I_i)\) after q guesses is at most \(\frac{1}{2^t} + \frac{q}{2^\lambda } + \frac{q}{2^n}\). Now, under the recovering notion, the adversary can choose the index i after seeing the key K. If the adversary chooses i as the integer that K encodes, then \(H(K, I_i) = 0^n\), and thus the adversary can trivially predict \(H(K, I_i)\).
, the chance that one can predict \(H_K(I_i)\) after q guesses is at most \(\frac{1}{2^t} + \frac{q}{2^\lambda } + \frac{q}{2^n}\). Now, under the recovering notion, the adversary can choose the index i after seeing the key K. If the adversary chooses i as the integer that K encodes, then \(H(K, I_i) = 0^n\), and thus the adversary can trivially predict \(H(K, I_i)\).
The subtlety above also arises in the proof of a theoretical PRNG by Dodis et al. [15]. These authors are aware of the adaptivity issue, and give a proper treatment of the recovering bound at the expense of a blowup factor \(p\). The counter-example above suggests that this factor \(p\) is inherent, and there is no hope to improve the recovering advantage.
To cope with the issues above, instead of using the decomposition approach, we give a direct proof for the robustness security via the H-coefficient technique. By considering all \(\mathsf {CTR}\) outputs at once, we can replace the term \(B^2 p/ 2^n\) by a better one \(B s / 2^n\). Likewise, a direct proof helps us to avoid the blowup factor \(p\) in bounding the guessing advantage of the extracted randomness \(\mathrm {CtE}(I_i)\).
Tightness of the Bound. Our bound is probably not tight. First, the term \(p \cdot \sqrt{q} / 2^{\lambda / 2}\) is from our use of the Generalized Leftover Hash Lemma to analyze the guessing advantage of \(\mathrm {CtE}[E, n]\). It is unclear if a dedicated analysis of the guessing advantage of \(\mathrm {CtE}\) can improve this term. Next, the term \(pq / 2^n\) is an artifact of our analysis in which we only consider the unpredictability of the n-bit prefix of each \(\mathsf {CTR}\) key instead of the entire key. It seems possible to improve this to \(pq / 2^k\), leading to a better security bound if the underlying blockcipher is either AES-192 or AES-256. Finally, the term \(\sqrt{qL} \cdot \sigma / 2^n\) is the result of our multi-collision analysis of \(\mathsf {CBCMAC}\), but the bound in Lemma 3 is rather loose. We leave this as an open problem to improve our bound.
6.2 Proof of Theorem 2
Setup. Since we consider computationally unbounded adversaries, without loss of generality, assume that \(A\) is deterministic. Let \(\mathbf {S}_{\mathrm {real}}\) and \(\mathbf {S}_{\mathrm {ideal}}\) be the systems that model the oracles accessed by \(A\) in game \(\mathbf {G}^{\mathrm {rob}}_{\mathcal{G},\lambda }(A,\mathcal {D})\) with the challenge bit \(b = 1\) and \(b = 0\) respectively. For bookkeeping purpose, the system \(\mathbf {S}_{\mathrm {real}}\) also maintains two ordered lists \(\mathsf {Keys}\) and \(\mathsf {Queries}\) that are initialized to be \(\emptyset \). Those lists shall be updated within procedure \(\mathsf {CTR}\) of \(\mathbf {S}_{\mathrm {real}}\); the extended code of \(\mathsf {CTR}\) is shown in Fig. 6. Informally, \(\mathsf {Keys}\) keeps track of CTR keys whose min-entropy counter is at least \(\lambda \), and \(\mathsf {Queries}\) maintains the corresponding ideal-cipher queries of \(\mathsf {CTR}\).
The extended code of procedures \(\mathsf {CTR}\) of \(\mathbf {S}_{\mathrm {real}}\). The code maintains two lists \(\mathsf {Keys}\) and \(\mathsf {Queries}\) that are initialized to \(\emptyset \). Here c is the global counter estimating min entropy of the state of \(\mathbf {S}_{\mathrm {real}}\).
A Hybrid Argument. We will now create a hybrid system \(\mathbf {S}_{\mathrm {hybrid}}\). The hybrid system will implement \(\mathbf {S}_{\mathrm {real}}\), but each time it’s asked to run CTR, if the min-entropy level c is at least the threshold \(\lambda \), our hybrid system will use a fresh, uniformly random string instead of the CTR output. In particular, the outputs of \(\textsc {RoR}\) of \(\mathbf {S}_{\mathrm {hybrid}}\), when \(c \ge \lambda \), are uniformly random strings. The code of procedure \(\mathsf {CTR}\) of \(\mathbf {S}_{\mathrm {hybrid}}\) is shown in Fig. 7. It also maintains the lists \(\mathsf {Keys}\) and \(\mathsf {Queries}\). To avoid confusion, we shall write \(\mathsf {Keys}(\mathbf {S})\) and \(\mathsf {Queries}(\mathbf {S})\) to refer to the corresponding lists of system \(\mathbf {S}\in \{\mathbf {S}_{\mathrm {real}}, \mathbf {S}_{\mathrm {hybrid}}\}\).
For any systems \(\mathbf {S}_{1}\) and \(\mathbf {S}_{0}\), let \(\varDelta _A(\mathbf {S}_{1}, \mathbf {S}_{0})\) denote the distinguishing advantage of the adversary A against the “real” system \(\mathbf {S}_{1}\) and “ideal” system \(\mathbf {S}_{0}\). We now construct an adversary \({A^*}\) of about the same efficiency as \(A\) such that
Adversary \({A^*}\) runs \(A\) and provides the latter with access to its oracles. However, for each \(\textsc {RoR}\) query, if \(c \ge \lambda \) (which \({A^*}\) can calculate), instead of giving \(A\) the true output, \({A^*}\) will instead give \(A\) a uniformly random string of the same length. Finally, when \(A\) outputs its guess \(b'\), adversary \({A^*}\) will output the same guess. Adversary \({A^*}\) perfectly simulates the systems \(\mathbf {S}_{\mathrm {ideal}}\) (in the real world) and \(\mathbf {S}_{\mathrm {hybrid}}\) (in the hybrid world) for \(A\), and thus achieves the same distinguishing advantage.
Below, we will show that
Since this bound applies to any adversary of the same accounting of queries, it applies to adversary \({A^*}\) as well, meaning that
By the triangle inequality,


We now justify Eq. (2) by the H-coefficient technique.
Defining Bad Transcripts. Recall that when \(A\) interacts with a system \(\mathbf {S}\in \{\mathbf {S}_{\mathrm {real}}, \mathbf {S}_{\mathrm {hybrid}}\}\), the system \(\mathbf {S}\) maintains a \((k + n)\)-bit state \(S = (K, V)\). This state starts as \((K_0, V_0) = (0^k, 0^n)\), and then \(\mathsf {setup}\) is called to update the state to \((K_1, V_1)\). The queries of \(A\) will cause it to be updated to \((K_2, V_2), (K_3, V_3),\) and so on. When the adversary \(A\) finishes querying \(\mathbf {S}\), we’ll grant it all states \((K_i, V_i)\), all random inputs \(I_j\) and their extracted randomness \(\mathrm {CtE}[E](I_j)\), the list \(\mathsf {Queries}\), and triples (J, X, E(J, X)) for any \(J \in \{0,1\}^k \backslash \mathsf {Keys}(\mathbf {S})\) and \(X \in \{0,1\}^n\). This extra information can only help the adversary. A transcript is bad if one of the following conditions happens:
-
(i)
There are different triples \((J, X_1, Y_1), (J, X_2, Y_2) \in \mathsf {Queries}(\mathbf {S})\) that are generated under the same call of \(\mathsf {CTR}\) (meaning that \(X_1 \ne X_2\)) such that \(Y_1 = Y_2\).Footnote 7 This cannot happen in \(\mathbf {S}_{\mathrm {real}}\) but may happen in \(\mathbf {S}_{\mathrm {hybrid}}\).
-
(ii)
The transcript contains a query (J, X) of \(A\) to \(E/E^{-1}\) such that \(J \in \mathsf {Keys}(\mathbf {S})\). In other words, the adversary somehow managed to guess a secret key of the CTR mode before it is granted extra information.
-
(iii)
There are distinct i and j, with \(K_j \in \mathsf {Keys}(\mathbf {S})\), such that \(K_i = K_j\). That is, there is a collision between the keys \(K_i\) and \(K_j\), in which \(K_j\) is the secret keys for CTR mode that we want to protect. The other key \(K_i\) may either be a secret CTR key, or a compromised key that the adversary knows.
-
(iv)
There is some key \(K_i \in \mathsf {Keys}(\mathbf {S})\) that is also the constant key in \(\mathsf {CBCMAC}\).
-
(v)
There is some key \(J \in \mathsf {Keys}(\mathbf {S})\) that is derived from \(I_j\) and there is an index \(i \ne j\) such that J is also the key of \(\mathsf {CBC}\) encryption in \(\mathrm {CtE}[E](I_i)\).
-
(vi)
There is some key \(J \in \mathsf {Keys}(\mathbf {S})\) that is derived from \(I_j\) such that J is also the key of \(\mathsf {CBC}\) encryption in \(\mathrm {CtE}[E](I_j)\).
If a transcript is not bad then we say that it’s good. Let \(\mathcal {T}_{\mathrm {real}}\) and \(\mathcal {T}_{\mathrm {hybrid}}\) be the random variables of the transcript for \(\mathbf {S}_{\mathrm {real}}\) and \(\mathbf {S}_{\mathrm {hybrid}}\) respectively.
Probability of Bad Transcripts. We now bound the chance that \(\mathcal {T}_{\mathrm {hybrid}}\) is bad. Let \(\mathrm {Bad}_i\) be the event that \(\mathcal {T}_{\mathrm {hybrid}}\) violates the i-th condition. By the union bound,
We first bound \(\Pr [\mathrm {Bad}_1]\). Suppose that \(\mathsf {Queries}(\mathbf {S}_{\mathrm {hybrid}})\) are generated from Q calls of \(\mathsf {CTR}\), and let \(P_1, \ldots , P_Q\) be the corresponding \(\mathsf {CTR}\) outputs. Let \(T_1, \ldots , T_Q\) be the block length of \(P_1, \ldots , P_Q\). Note that \(Q, T_1, \ldots , T_Q\) are random variables, but since \(k \le 2n\), we have \(T_i \le B + 3\) for every i, and \(T_1 + \cdots + T_Q \le s + 3p\). The event \(\mathrm {Bad}_1\) happens if among \(T_i\) blocks of some \(P_i\), there are two duplicate blocks. Since the blocks of each \(P_i\) are uniformly random,
Next, we shall bound \(\Pr [\mathrm {Bad}_2]\). Note that the keys in \(\mathsf {Keys}(\mathbf {S}_{\mathrm {hybrid}})\) can be categorized as follows.
-
Strong keys: Those keys are picked uniformly at random.
-
Weak keys: Those keys \(K_i\) are generated via
$$\begin{aligned} K_i \leftarrow \mathsf {CTR}_{K_{i - 1}}^{V_{i - 1}}[E]\bigl (\mathrm {CtE}[E](I) \bigr )[1:k] \end{aligned}$$for a random input I of \(\mathcal {D}\).
For a strong key, the chance that the adversary can guess it using q ideal-cipher queries is at most \(q / 2^k\). Since there are at most q strong keys, the chance that one of the strong keys causes \(\mathrm {Bad}_2\) to happen is at most \(q^2 / 2^k\). For each \(j \le p\), let \(\mathsf {Hit}_2(j)\) be the event that the key derived from the random input \(I_j\) is a weak key, and it causes \(\mathrm {Bad}_2\) to happen. From the union bound,
We now bound each \(\Pr [\mathsf {Hit}_2(j)]\). Let J be the key derived from the random input \(I_j\) and assume that J is weak. Since \(J \in \mathsf {Keys}(\mathbf {S}_{\mathrm {hybrid}})\), the next state of \(\mathbf {S}_{\mathrm {hybrid}}\) is generated (as shown in Fig. 7) by picking a uniformly random string, and thus subsequent queries give no information on J. In addition, recall that the n-bit prefix of J is the xor of \(\mathrm {CtE}[E, n](I_j)\) with a mask \(P_j\). If we grant \(P_j\) to the adversary then it only increases \(\Pr [\mathsf {Hit}_2(j)]\). The event \(\mathsf {Hit}_2(j)\) happens only if the adversary can somehow guess \(\mathrm {CtE}[E, n](I_j)\) via q choices of its ideal-cipher queries. But anything that the adversary receives is derived from the blockcipher E, the side information \(z_j\) and the entropy estimation \(\gamma _j\) of \(I_j\), the other \((I_i, \gamma _i, z_i)\) with \(i \ne j\). Thus from Theorem 1,
Summing up over all events \(\mathsf {Hit}_2(1), \ldots , \mathsf {Hit}_2(p)\),
We now bound \(\Pr [\mathrm {Bad}_3]\). For a strong key, the chance that it collides with one of the other q keys in the system in at most \(q / 2^k\). Since there are at most q strong keys, the chance that some strong key causes \(\mathrm {Bad}_3\) to happen is at most \(q^2 / 2^k\). For each \(j \le p\), let \(\mathsf {Hit}_3(j)\) be the event that the key derived from the random input \(I_j\) is a weak key, and it causes \(\mathrm {Bad}_3\) to happen. From the union bound,
We now bound each \(\Pr [\mathsf {Hit}_3(j)]\). The event \(\mathsf {Hit}_3(j)\) happens only if the environment somehow can “guess” \(\mathrm {CtE}[E, n](I_j)\) via q choices of its other keys, using just information from the blockcipher E, the side information \(z_j\) and the entropy estimation \(\gamma _j\) of \(I_j\), the other \((I_i, \gamma _i, z_i)\) with \(i \ne j\). Thus from Theorem 1,
Summing up over all events \(\mathsf {Hit}_3(1), \ldots , \mathsf {Hit}_3(p)\),
Bounding \(\Pr [\mathrm {Bad}_4]\) is similar to handling \(\mathrm {Bad}_3\), but now the environment has just a single choice, instead of q choices. Thus
Bounding \(\Pr [\mathrm {Bad}_5]\) is similar to handling \(\mathrm {Bad}_3\), but now the environment has p choices instead of q ones. Thus
Finally, consider \(\mathrm {Bad}_6\). Again, the chance that some strong key causes \(\mathrm {Bad}_6\) to happen is at most \(q / 2^k\). For each \(j \le p\), let \(\mathsf {Hit}_6(j)\) be the event that the key derived from the random input \(I_j\) is a weak key, and it causes \(\mathrm {Bad}_6\) to happen. From the union bound,
We now bound each \(\Pr [\mathsf {Hit}_6(j)]\). The event \(\mathsf {Hit}_6(j)\) happens only if the environment somehow can “guess” \(\mathrm {XP}[E](I_j)\) via a single choice of the \(\mathsf {CTR}\) mask, using just information from the blockcipher E, the side information \(z_j\) and the entropy estimation \(\gamma _j\) of \(I_j\), the other \((I_i, \gamma _i, z_i)\) with \(i \ne j\). From Lemma 6 with a single guess,
Summing up over all events \(\mathsf {Hit}_6(1), \ldots , \mathsf {Hit}_6(p)\),
Summing up, and taking into account that \(q \ge p\),
Transcript Ratio. Let \(\tau \) be a good transcript such that \(\Pr [\mathcal {T}_{\mathrm {hybrid}}= \tau ] > 0\). We now prove that
If \(\mathcal {T}_{\mathrm {real}}\) is good then \(\mathsf {Queries}(\mathbf {S}_{\mathrm {real}})\) and the granted triples (K, X, Y) at the end of the game (with all \(K \in \{0,1\}^n \backslash \mathsf {Keys}(\mathbf {S}_{\mathrm {real}})\) and \(X \in \{0,1\}^n\)), would contain all adversary’s queries to \(E/E^{-1}\) and \(\mathbf {S}_{\mathrm {real}}\)’s queries to E in its \(\mathsf {setup}, \mathsf {next}, \mathsf {refresh}\) procedures. Since \(A\) is deterministic, when \(\mathcal {T}_{\mathrm {real}}\) is good, it is completely determined from \(\mathcal {D}\)’s outputs, \(\mathsf {Queries}(\mathbf {S}_{\mathrm {real}})\), and the granted triples (K, X, Y) at the end of the game. Let \(\mathsf {Queries}(\tau )\) and \(\mathsf {Keys}(\tau )\) be the value of \(\mathsf {Queries}(\mathbf {S})\) and \(\mathsf {Keys}(\mathbf {S})\) for \(\mathbf {S}\in \{\mathbf {S}_{\mathrm {real}}, \mathbf {S}_{\mathrm {hybrid}}\}\) indicated by \(\tau \). Thus the event that \(\mathcal {T}_{\mathrm {real}}= \tau \) can be factored into the following sub-events:
-
\(\mathsf {Inputs}\): The distribution sampler \(\mathcal {D}\) outputs as instructed in \(\tau \).
-
\(\mathsf {Prim}\): The blockcipher E agrees with the granted queries (K, X, Y) in \(\tau \), with \(K \in \{0,1\}^n \backslash \mathsf {Keys}(\tau )\). That is, for any such triple (K, X, Y), if we query E(K, X), we’ll get the answer Y.
-
\(\mathsf {Coll}_{\mathrm {real}}\): The blockcipher E agrees with the triples in \(\mathsf {Queries}(\tau )\). Note that for any \((K, X, Y) \in \mathsf {Queries}(\tau )\), we have \(K \in \mathsf {Keys}(\tau )\).
Due to the key separation in \(\mathsf {Prim}\) and \(\mathsf {Coll}_{\mathrm {real}}\) and due to the fact that \(\mathcal {D}\) has no access to E,
Likewise, if \(\mathcal {T}_{\mathrm {hybrid}}\) is good then the granted triples (K, X, Y) at the end of the game (with all \(K \in \{0,1\}^n \backslash \mathsf {Keys}(\mathbf {S}_{\mathrm {hybrid}})\) and \(X \in \{0,1\}^n\)), would contain all adversary’s queries to \(E/E^{-1}\) and \(\mathbf {S}_{\mathrm {hybrid}}\)’s queries to E in its \(\mathsf {setup}, \mathsf {next}, \mathsf {refresh}\) procedures. Thus if \(\mathcal {T}_{\mathrm {hybrid}}\) is good then it is completely determined from \(\mathcal {D}\)’s outputs, \(\mathsf {Queries}(\mathbf {S}_{\mathrm {hybrid}})\), and the granted triples (K, X, Y) at the end of the game. Hence the event that \(\mathcal {T}_{\mathrm {hybrid}}= \tau \) can be factored into \(\mathsf {Inputs}, \mathsf {Prim}\) and the following sub-event:
-
\(\mathsf {Coll}_{\mathrm {ideal}}\): For any triple \((K, X, Y) \in \mathsf {Queries}(\tau )\), if we pick
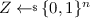 , we’ll have \(Z = Y\). This random variable Z stands for the uniformly random block that \(\mathbf {S}_{\mathrm {hybrid}}\) samples when it is supposed to run E(K, X) (but actually does not do) under procedure \(\mathsf {CTR}\) on key \(K \in \mathsf {Keys}(\tau )\).
, we’ll have \(Z = Y\). This random variable Z stands for the uniformly random block that \(\mathbf {S}_{\mathrm {hybrid}}\) samples when it is supposed to run E(K, X) (but actually does not do) under procedure \(\mathsf {CTR}\) on key \(K \in \mathsf {Keys}(\tau )\).
Then
Therefore,
Now, suppose that \(\mathsf {Queries}(\tau )\) contains exactly r keys, and the i-th key contains exactly \(t_i\) tuples. Since \(\tau \) is good, for any two tuples (K, X, Y) and \((K, X', Y')\) of the i-th key, we have \(X \ne X'\) and \(Y \ne Y'\). Thus on the one hand,
On the other hand,
Hence
and thus
as claimed.
Wrapping it Up. From Lemma 1 and Eqs. (5) and (6), we conclude that
as claimed.
7 Breaking \(\mathsf {CTR\text {-}DRBG}\) with a Seed-Dependent Sampler
In this section, we show that if the underlying blockcipher is AES-128 then \(\mathsf {CTR\text {-}DRBG}\) is insecure in the new security model of Coretti et al. [13].
Seedless PRNGs. A seedless PRNG that is built on top of an ideal primitive \(\varPi \) is a tuple of deterministic algorithms \(\mathcal{G}= (\mathsf {setup}, \mathsf {refresh}, \mathsf {next})\), any of which has oracle access to \(\varPi \). Algorithm \(\mathsf {setup}^\varPi (I)\), on a random input I, outputs a state S. Next, algorithm \(\mathsf {refresh}^\varPi (S, I)\) takes as input a state S and a string I and then outputs a new state. Finally algorithm \(\mathsf {next}^\varPi (S, \ell )\) takes as input a state S and a number \(\ell \in \mathbb {N}\), and then outputs a new state and an \(\ell \)-bit output string. Note that the description of \(\mathsf {CTR\text {-}DRBG}\) in Fig. 5 also conforms to this syntax.
Security Modeling. Instead of using the full notion of Coretti et al. [13], we levy some additional restrictions on the adversary to simplify the definition and to make our attack more practical. In particular, we (i) strip away the adversary’s ability to read or modify the PRNG’s state, (ii) require that each random input must have sufficient min entropy, and (iii) forbid the adversary from calling \(\mathsf {next}\) when the accumulated entropy is insufficient. The simplified notion, which we call resilience, is described in Fig. 8. Define

as the advantage of \(A\) breaking the resilience of \(\mathcal{G}\). Informally, the game begins by picking a challenge bit  . In the first phase, the adversary \(A\), given just oracle access to \(\varPi \), outputs a random input I and keeps some state s. The game then runs \(\mathsf {setup}^\varPi (I)\) to generate an initial state S for the PRNG. In the second phase, the adversary, in addition to \(\varPi \), is given the following oracles:
. In the first phase, the adversary \(A\), given just oracle access to \(\varPi \), outputs a random input I and keeps some state s. The game then runs \(\mathsf {setup}^\varPi (I)\) to generate an initial state S for the PRNG. In the second phase, the adversary, in addition to \(\varPi \), is given the following oracles:
-
(i)
An oracle \(\textsc {Ref}(I)\) to update the state S via \(S \leftarrow \mathsf {refresh}^\varPi (I)\).
-
(ii)
An oracle \(\textsc {RoR}(1^\ell )\) to get the next \(\ell \)-bit output. The game runs the \(\mathsf {next}\) algorithm on the current state S to update it and get an \(\ell \)-bit output \(R_1\), and also samples a uniformly random string
 . It then returns \(R_b\) to the adversary.
. It then returns \(R_b\) to the adversary.
The goal of the adversary is to guess the challenge bit b, by outputting a bit \(b'\).
To avoid known impossibility results
[11], one needs to carefully impose restrictions on the adversary \(A\). Consider game \(\mathbf {G}^{\mathrm {res}}_{\mathcal{G},\varPi }(A)\) in which the challenge bit \(b = 0\). Note that this game is independent of the construction \(\mathcal{G}\): one can implement the oracle \(\textsc {Ref}(I)\) to do nothing, and oracle \(\textsc {RoR}(1^\ell )\) to return  . Let \(s_i\) and \(L_i\) be the random variables for the adversary’s state and its current list of queries/answers to \(\varPi \) right before the adversary makes the i-th query to \(\textsc {RoR}\), respectively. Let \({\mathcal {I}}_i\) be the list of random inputs before the adversary makes the i-th query to \(\textsc {RoR}\). We say that \(A\) is \(\lambda \)-legitimate if \(H_\infty (I \mid s_i, L_i) \ge \lambda \), for any \(i \in \mathbb {N}\) and any \(I \in {\mathcal {I}}_i\).
. Let \(s_i\) and \(L_i\) be the random variables for the adversary’s state and its current list of queries/answers to \(\varPi \) right before the adversary makes the i-th query to \(\textsc {RoR}\), respectively. Let \({\mathcal {I}}_i\) be the list of random inputs before the adversary makes the i-th query to \(\textsc {RoR}\). We say that \(A\) is \(\lambda \)-legitimate if \(H_\infty (I \mid s_i, L_i) \ge \lambda \), for any \(i \in \mathbb {N}\) and any \(I \in {\mathcal {I}}_i\).
The Attack. We adapt the ideas of the \(\mathsf {CBCMAC}\) attack in [13] to attack \(\mathsf {CTR\text {-}DRBG}\), assuming that the key length and block length of the underlying blockcipher are the same. In other words, our attack only applies if the underlying blockcipher is AES-128. Still, it works for any fixed entropy threshold \(\lambda > 0\).
Let \(E: \{0,1\}^k\times \{0,1\}^n \rightarrow \{0,1\}^n\) be the underlying blockcipher of \(\mathsf {CTR\text {-}DRBG}\), and let \(\pi \) be the permutation in \(\mathsf {CBCMAC}\). Pick an arbitrary integer \(m \ge \lambda \). For each \(a \in \{0,1\}\), let
and let
For each integer \(i \ge 0\) and any string \(x \in \{0,1\}^n\), define \(\pi ^i(x)\) recursively via \(\pi ^i(x) \leftarrow \pi \bigl (\pi ^{i - 1}(x) \bigr )\) and \(\pi ^0(x) \leftarrow x\). In the first phase, for each \(i \in \{ 0, \ldots , m - 1\}\), the adversary \(A\) picks  . It then outputs
. It then outputs
and also outputs the empty string as its state s. In the second phase, \(A\) queries \(\textsc {RoR}(1^n)\) to get an answer Y. Next, recall that in the real world (where the challenge bit \(b = 1\)), to set up the initial state, \(\mathsf {setup}(I)\) first derives
where \(P \leftarrow \mathrm {pad}(\varepsilon )\), and then runs \(\mathsf {CBC}^{\mathrm {IV}}_K[E](0^{2n})\). Our adversary aims to predict two possible pairs \((K_0, V_0)\) and \((K_1, V_1)\) for \((K, \mathrm {IV})\), and then compare Y with the corresponding \(\textsc {RoR}\) outputs \(Z_0\) and \(Z_1\). Specifically, \(A\)

In summary, \(A\) makes 2m queries to \(\pi \) in the first phase, and \(2m + 4\) queries to \(\pi \) and 6 queries to E in the second phase. Let L be the list of queries and answers to \(\pi \) and E. Since the state s of \(A\) right before it queries \(\textsc {RoR}\) is the empty string, in the ideal world, we have \(H_\infty (I \mid s, L) = m \ge \lambda \), and thus the adversary is \(\lambda \)-legitimate.
We now analyze the adversary’s advantage. In the ideal world, the answer Y is a uniformly random string, independent of \(Z_0\) and \(Z_1\), and thus the chance that \(Y \in \{Z_0, Z_1\}\) is \(2^{1 - n}\). As a result, the chance that \(A\) outputs 1 in the ideal world is \(2^{1-n}\). In the real world, we claim that \(A\)’s prediction of (K, V) is correct. Consequently, the chance that it outputs 1 in the real world is 1, and thus  .
.
To justify the claim above, note that \(K \leftarrow \mathsf {CBCMAC}[\pi ](B_0, M_0 \cdots M_{m - 1} \,\Vert \,P)\) and \(\mathrm {IV}\leftarrow \mathsf {CBCMAC}[\pi ](B_1, M_0 \cdots M_{m - 1} \,\Vert \,P)\). From the definition of \(\mathsf {CBCMAC}\), the two \(\mathsf {CBCMAC}\) calls above can be rewritten as follows:

We will prove by induction that in the code above, \(\{ X_i, Y_i \} = \{\pi ^i(B_0), \pi ^{i}(B_1)\}\) for every \(i \in \{0, \ldots , m\}\); the claim above corresponds to the special case \(i = m\). The statement is true for the base case \(i = 0\), from the definition of \(X_0\) and \(Y_0\). Assume that our statement is true for \(i < m\), we now prove that it also holds for \(i + 1\). Since \(M_i \in \{\pi ^{i}(B_0) \oplus \pi ^i(B_1), 0^n\}\), from the inductive hypothesis, \(\{ X_i \oplus M_i, Y_i \oplus M_i \} = \{ \pi ^i(B_{0}), \pi ^i(B_1) \}\). As \(X_{i + 1} \leftarrow \pi (X_i \oplus M_i)\) and \(Y_{i + 1} \leftarrow \pi (X_i \oplus M_i)\), our statement also holds for \(i + 1\).
Discussion. The key idea of the attack above is to craft a random input I such that it is easy to learn both the key K and the initialization vector \(\mathrm {IV}\) of \(\mathsf {CBC}\) in \(\mathrm {CtE}[E](I)\). This attack can be extended for a general key length \(k \in \{n, \ldots , 2n\}\), but now the adversary can only learn just K and the \((2n -k)\)-bit prefix of \(\mathrm {IV}\). Still, the adversary can make \(2^{k - n}\) guesses to determine the remaining \(k - n\) bits of \(\mathrm {IV}\). This leads to a theoretical attack of about \(2^{64}\) operations for AES-192, but for AES-256, the cost (\(2^{128}\) operations) is prohibitive. We leave it as an open problem to either extend our attack for \(\mathsf {CTR\text {-}DRBG}\) with AES-256, or to prove that it is actually resilient.
Notes
- 1.
A recent study by Cohney et al. [12] finds that \(\mathsf {CTR\text {-}DRBG}\) is supported by 67.8% of validated implementations in NIST’s Cryptographic Module Validation Program (CMVP). The other recommended schemes in NISP SP 800-90A, Hash-DRBG and HMAC-DRBG, are only supported by 36.3% and 37.0% of CMVP-certified uses, respectively.
- 2.
For a simple comparison of the two bounds, assume that \(\sigma \lessapprox 2^{18} \cdot p\), meaning that a random input is at most 4 MB on average, which seems to be a realistic assumption for typical applications. The standard NIST SP 800-90A dictates that \(L \le 2^{28}\). Then our bound \({\sqrt{qL} \cdot \sigma }/{2^{128}}\) is around \(\sqrt{q} \cdot p / 2^{96}\). If we instead consider the worst case where \(\sigma \approx L p\), then our bound is around \(\sqrt{q} \cdot p / 2^{86}\).
- 3.
Using the same treatment for recovering security still ends up with the blowup factor \(p\), as it is inherent.
- 4.
In the context of \(\mathrm {CtE}\), the seed is the encoding of the ideal cipher. In other words, we assume that the sampler of the random inputs has no access to the ideal cipher.
- 5.
While \(\mathsf {CTR\text {-}DRBG}\) does support 3DES, the actual deployment is rare: among the CMVP-certified implementations that support \(\mathsf {CTR\text {-}DRBG}\), only 1% of them use 3DES [12].
- 6.
We choose the bound \(2^{-32}\) in this example because this is a failure probability that NIST standards usually accept. For instance, NIST 800-38B requires \(\mathsf {CBCMAC}\) implementation to rekey after \(2^{48}\) messages so that the probability of IV collision in \(\mathsf {CBCMAC}\) under a single key is below \(2^{-32}\).
- 7.
One can tell whether two triples in \(\mathsf {Queries}(\mathbf {S})\) belong to the same call of \(\mathsf {CTR}\) since the list \(\mathsf {Queries}(\mathbf {S})\) is ordered, and the lengths of the messages of \(\mathsf {CTR}\) are known.
References
Barak, B., et al.: Leftover hash lemma, revisited. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 1–20. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_1
Barak, B., Halevi, S.: A model and architecture for pseudo-random generation with applications to /dev/random. In: Atluri, V., Meadows, C., Juels, A. (eds.) ACM CCS 05, pp. 203–212. ACM Press, November 2005
Bellare, M., Hofheinz, D., Yilek, S.: Possibility and impossibility results for encryption and commitment secure under selective opening. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 1–35. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_1
Bellare, M., Pietrzak, K., Rogaway, P.: Improved security analyses for CBC MACs. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 527–545. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_32
Bernstein, D.J.: Cache-timing attacks on AES (2005)
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: Sponge-based pseudo-random number generators. In: Mangard, S., Standaert, F.-X. (eds.) CHES 2010. LNCS, vol. 6225, pp. 33–47. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15031-9_3
Campagna, M.: Security bounds for the NIST codebook-based deterministic random bit generator. Cryptology ePrint Archive, Report 2006/379 (2006). https://eprint.iacr.org/2006/379
Checkoway, S., et al.: A systematic analysis of the Juniper Dual EC incident. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pp. 468–479. ACM (2016)
Checkoway, S., et al.: On the practical exploitability of dual EC in TLS implementations. In: Proceedings of the 23rd USENIX Security Symposium, pp. 319–335, August 2014
Chen, S., Steinberger, J.: Tight security bounds for key-alternating ciphers. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 327–350. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_19
Chor, B., Goldreich, O.: Unbiased bits from sources of weak randomness and probabilistic communication complexity (extended abstract). In: 26th FOCS, pp. 429–442. IEEE Computer Society Press, October 1985
Cohney, S., et al.: Pseudorandom black swans: cache attacks on CTR DRBG. In: IEEE Security and Privacy 2020 (2020)
Coretti, S., Dodis, Y., Karthikeyan, H., Tessaro, S.: Seedless fruit is the sweetest: random number generation, revisited. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11692, pp. 205–234. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_8
Dodis, Y., Gennaro, R., Håstad, J., Krawczyk, H., Rabin, T.: Randomness extraction and key derivation using the CBC, cascade and HMAC modes. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 494–510. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_30
Dodis, Y., Pointcheval, D., Ruhault, S., Vergnaud, D., Wichs, D.: Security analysis of pseudo-random number generators with input: /dev/random is not robust. In: Sadeghi, A.R., Gligor, V.D., Yung, M. (eds.) ACM CCS 13, pp. 647–658. ACM Press, November 2013
Dwork, C., Naor, M., Reingold, O., Stockmeyer, L.J.: Magic functions. In: 40th FOCS, pp. 523–534. IEEE Computer Society Press, October 1999
Gaži, P., Tessaro, S.: Provably robust sponge-based PRNGs and KDFs. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 87–116. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_4
Gullasch, D., Bangerter, E., Krenn, S.: Cache games - bringing access-based cache attacks on AES to practice. In: 2011 IEEE Symposium on Security and Privacy, pp. 490–505. IEEE Computer Society Press, May 2011
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Heninger, N., Durumeric, Z., Wustrow, E., Halderman, J.A.: Mining your Ps and Qs: detection of widespread weak keys in network devices. In: Proceedings of the 21st USENIX Security Symposium, pp. 205–220, August 2012
Hoang, V.T., Shen, Y.: Security analysis of NIST CTR-DRBG. Cryptology ePrint Archive, Report 2020/619 (2020). https://eprint.iacr.org/2020/619
Hoang, V.T., Tessaro, S.: Key-alternating ciphers and key-length extension: exact bounds and multi-user security. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part I. LNCS, vol. 9814, pp. 3–32. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_1
Hutchinson, D.: Randomness in cryptography: theory meets practice. Ph.D. thesis, Royal Holloway, University of London (2018)
Neve, M., Seifert, J.-P.: Advances on access-driven cache attacks on AES. In: Biham, E., Youssef, A.M. (eds.) SAC 2006. LNCS, vol. 4356, pp. 147–162. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74462-7_11
Osvik, D.A., Shamir, A., Tromer, E.: Cache attacks and countermeasures: the case of AES. In: Pointcheval, D. (ed.) CT-RSA 2006. LNCS, vol. 3860, pp. 1–20. Springer, Heidelberg (2006). https://doi.org/10.1007/11605805_1
Patarin, J.: The “Coefficients H” technique. In: Avanzi, R.M., Keliher, L., Sica, F. (eds.) SAC 2008. LNCS, vol. 5381, pp. 328–345. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04159-4_21
Raz, R., Reingold, O.: On recycling the randomness of states in space bounded computation. In: 31st ACM STOC, pp. 159–168. ACM Press, May 1999
Ruhault, S.: SoK: security models for pseudo-random number generators. IACR Trans. Symm. Crypt. 2017(1), 506–544 (2017)
Shrimpton, T., Terashima, R.S.: A provable-security analysis of intel’s secure key RNG. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part I. LNCS, vol. 9056, pp. 77–100. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_4
Shrimpton, T., Terashima, R.S.: Salvaging weak security bounds for blockcipher-based constructions. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part I. LNCS, vol. 10031, pp. 429–454. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_16
Woodage, J., Shumow, D.: An analysis of NIST SP 800-90A. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 151–180. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_6
Acknowledgments
We thank Stefano Tessaro for insightful discussions, Yevgeniy Dodis for suggesting the study of \(\mathsf {CTR\text {-}DRBG}\) in the seedless setting, and CRYPTO reviewers for useful feedback. Viet Tung Hoang was supported in part by NSF grants CICI-1738912 and CRII-1755539. Yaobin Shen was supported in part by National Key Research and Development Program of China (No. 2019YFB2101601, No. 2018YFB0803400), 13th five-year National Development Fund of Cryptography (MMJJ20170114), and China Scholarship Council (No. 201806230107). Much of this work was done while Yaobin Shen was visiting Florida State University.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
A Problems in Hutchinson’s Analysis of \(\mathsf {CTR\text {-}DRBG}\)
A Problems in Hutchinson’s Analysis of \(\mathsf {CTR\text {-}DRBG}\)
In this section, we describe the issues in Hutchinson’s analysis of \(\mathsf {CTR\text {-}DRBG}\) [23]. For convenience, we shall use the notation and terminology in Sect. 4.
First, under \(\mathsf {CTR\text {-}DRBG}\), one uses \(\mathsf {CBCMAC}\) to extract randomness multiple times from basically the same random input (with different constant prefixes). Conventional analysis of \(\mathsf {CBCMAC}\) [14] via the Leftover Hash Lemma [19] only implies that each of the corresponding outputs is marginally pseudorandom, but in the proof of his Lemma 5.5.4, Hutchinson incorrectly concludes that they are jointly pseudorandom.
Next, in the proof of his Lemma 5.5.14, Hutchinson considers a multicollision
with \(r \in \{2, 3\}\) and a truly random permutation \(\pi : \{0,1\}^{n} \rightarrow \{0,1\}^{n}\). Assume that each individual collision \(\mathsf {CBCMAC}[\pi ](M_i) = \mathsf {CBCMAC}[\pi ](M^*_i)\) happens with probability at most \(\epsilon \). Hutchinson claims (without proof) that the multicollision happens with probability at most \(\epsilon ^3\), but this is obviously wrong for \(r = 2\). While one may try to salvage the proof by changing the multicollision probability to \(\epsilon ^r\), proving such a bound is difficult.
Next, in several places, his probabilistic reasoning is problematic. For instance, in the proof of his Lemma 5.5.14, he considers \(X_1 \leftarrow \mathsf {CBC}_{K_1}^{\mathrm {IV}_1}[E](0^{3n})\) and \(X_2 \leftarrow \mathsf {CBC}_{K_2}^{\mathrm {IV}_2}[E](0^{3n})\), for \(K_1 \ne K_2\) and \(\mathrm {IV}_1 \ne \mathrm {IV}_2\), and \(E: \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n\) is modeled as an ideal cipher. He claims that
but this collision probability is actually around \(\frac{1}{2^{3n}}\), which is much bigger than the claimed bound.
In addition, while Hutchinson appears to consider random inputs of a general block length L, he actually uses \(L = 3\) in the proof of his Lemma 5.5.4, and the resulting incorrect bound propagates to other places.
Finally, even if all the bugs above are fixed, Hutchinson’s approach is doomed to yield a weak bound
assuming that we have \(p\) random inputs, each of at least \(\lambda \ge n\) bits of min entropy, and their total block length is at most \(\sigma \). This poor bound is due to: (i) the decomposition of robustness to two other notions (preserving and recovering) that leads to a p-blowup, and (ii) the unnecessary requirement that \(\mathsf {CBCMAC}\) on random inputs yield pseudorandom (instead of just unpredictable) outputs.
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Hoang, V.T., Shen, Y. (2020). Security Analysis of NIST CTR-DRBG. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12170. Springer, Cham. https://doi.org/10.1007/978-3-030-56784-2_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-56784-2_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56783-5
Online ISBN: 978-3-030-56784-2
eBook Packages: Computer ScienceComputer Science (R0)






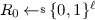 . If the accumulated entropy is insufficient (meaning
. If the accumulated entropy is insufficient (meaning 





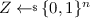 , we’ll have
, we’ll have  . It then returns
. It then returns 
