Abstract
Secret sharing enables a dealer to split a secret into a set of shares, in such a way that certain authorized subsets of share holders can reconstruct the secret, whereas all unauthorized subsets cannot. Non-malleable secret sharing (Goyal and Kumar, STOC 2018) additionally requires that, even if the shares have been tampered with, the reconstructed secret is either the original or a completely unrelated one.
In this work, we construct non-malleable secret sharing tolerating \(p\)-time joint-tampering attacks in the plain model (in the computational setting), where the latter means that, for any \(p>0\) fixed a priori, the attacker can tamper with the same target secret sharing up to \(p\) times. In particular, assuming one-to-one one-way functions, we obtain:
-
A secret sharing scheme for threshold access structures which tolerates joint \(p\)-time tampering with subsets of the shares of maximal size (i.e., matching the privacy threshold of the scheme). This holds in a model where the attacker commits to a partition of the shares into non-overlapping subsets, and keeps tampering jointly with the shares within such a partition (so-called selective partitioning).
-
A secret sharing scheme for general access structures which tolerates joint \(p\)-time tampering with subsets of the shares of size \(O(\sqrt{\log n})\), where \(n\) is the number of parties. This holds in a stronger model where the attacker is allowed to adaptively change the partition within each tampering query, under the restriction that once a subset of the shares has been tampered with jointly, that subset is always either tampered jointly or not modified by other tampering queries (so-called semi-adaptive partitioning).
At the heart of our result for selective partitioning lies a new technique showing that every one-time statistically non-malleable secret sharing against joint tampering is in fact leakage-resilient non-malleable (i.e., the attacker can leak jointly from the shares prior to tampering). We believe this may be of independent interest, and in fact we show it implies lower bounds on the share size and randomness complexity of statistically non-malleable secret sharing against independent tampering.
A. Faonio—Supported by the Spanish Government under projects SCUM (ref. RTI2018-102043-B-I00), CRYPTOEPIC (ref. EUR2019-103816), and SECURITAS (ref. RED2018-102321-T), by the Madrid Regional Government under project BLOQUES (ref. S2018/TCS-4339).
M. Obremski—Supported by MOE2019-T2-1-145 Foundations of quantum-safe cryptography.
M. Simkin—Supported by the European Research Council (ERC) under the European Unions’s Horizon 2020 research and innovation programme under grant agreement No 669255 (MPCPRO), grant agreement No 803096 (SPEC), Danish Independent Research Council under Grant-ID DFF-6108-00169 (FoCC), and the Concordium Blockhain Research Center.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
In the past 40 years, secret sharing [9, 32] became one of the most fundamental cryptographic primitives. Secret sharing schemes allow a trusted dealer to split a message \(m\) into shares \(s_1, \dots , s_n\) and distribute them among \(n\) participants, such that only certain authorized subsets of share holders are allowed to recover \(m\). The collection \(\mathcal {A} \) of authorized subsets is called the access structure. The most basic security guarantee is that any unauthorized subset outside \(\mathcal {A} \) collectively has no information about the shared message. Shamir [32] and Blakley [9] showed how to construct secret sharing schemes with information-theoretic security, and Krawczyk [25] presented the first computationally-secure construction with improved efficiency parameters.
Non-malleable Secret Sharing. A long line of research [2, 8, 11, 12, 14, 21, 23, 24, 26, 31, 33] has focused on different settings with active adversaries that were allowed to tamper with the shares in one or another way. In verifiable secret sharing [31] the dealer is considered to be untrusted and the share holders want to ensure they hold shares of a consistent secret. In robust secret sharing [12] some parties may act maliciously and try to prevent the correct reconstruction of the shared secret by providing incorrect shares. It is well known that robust secret sharing is impossible when more than half of the parties are malicious.
A recent line of works considers an adversary that has some form of restricted access to all shares. In non-malleable secret sharing [23] the adversary can partition the shares in disjoint sets and can then independently tamper with each set of shares. Security guarantees that whatever is reconstructed from the tampered shares is either the original secret, or a completely unrelated value. Most previous works have focused on the setting of independent tampering [2, 8, 11, 21, 23, 24, 26, 33], where the adversary is only allowed to tamper with each share independently. Only a few papers [11, 14, 23, 24] have considered the stronger setting where the adversary is allowed to tamper with subsets of shares jointly.
Continuous Non-malleability. The first notions of non-malleability only focused on security against a single round of tampering. A natural extension of this setting is to consider adversaries that may perform several rounds of tampering attacks on a secret sharing scheme. Badrinarayanan and Srinivasan [8] and Aggarwal et al. [2] considered \(p\)-time tampering attacks in the information-theoretic setting, where \(p\) must be a-priori bounded. The works of Faonio and Venturi [21] and Brian, Faonio and Venturi [11] considered continuous, i.e., poly-many tampering attacks in the computational setting. It is well known that cryptographic assumptions are inherent in the latter case [8, 21, 22].
An important limitation of all works mentioned above is that, with the exception of [11], they only consider the setting of independent tampering. Brian Faonio, and Venturi [11] achieve continuous non-malleability against joint tampering, where each tampering function can tamper with \(O(\log n)\)-large sets of shares assuming a trusted setup in the form of a common reference string. This leads to the following question:
Can we obtain continuously non-malleable secret sharing against joint tampering in the plain model?
1.1 Our Contributions
In this work, we make progress towards answering the above question. Our main contribution is a general framework for reducing computational \(p\)-time non-malleability against joint tampering to statistical one-time non-malleability against joint tampering. Our framework encompasses the following models:
-
Selective partitioning. Here, the adversary has to initially fix any \(k\)-sized partitionFootnote 1 of the \(n\) shares, at the beginning of the experiment. Afterwards, the adversary can tamper \(p\) times with the shares within each subset in a joint manner. We call this notion \(k\)-joint \(p\)-time non-malleability under selective partitioning.
-
Semi-adaptive partitioning. In this setting, the adversary can adaptively choose different \(k\)-sized partitions for each tampering query. However, once a subset of the shares has been tampered with jointly, that subset is always either tampered jointly or not modified by other tampering queries. We call this notion \(k\)-joint \(p\)-time non-malleability under semi-adaptive partitioning.
Combining known constructions of one-time statistically non-malleable secret sharing schemes against joint tampering [14, 23, 24] with a new secret sharing scheme that we present in this work, we obtain the following result:
Theorem 1
(Main Theorem, Informal). Assuming the existence of one-to-one one-way functions, there exist:
-
(i)
A \(\tau \)-out-of-\(n\) secret sharing scheme satisfying \(k\)-joint \(p\)-time non-malleability under selective partitioning,Footnote 2 for any \(\tau \le n\), \(k\le \tau - 1\), and \(p> 0\).
-
(ii)
An \((n,\tau )\)-rampFootnote 3 secret sharing scheme with binary shares satisfying \(k\)-joint \(p\)-time non-malleability under selective partitioning, for \(\tau = n- n^\beta \), \(k\le \tau - 1\), \(\beta <1\), and \(p\in O(\sqrt{n})\).
-
(iii)
A secret sharing scheme satisfying \(k\)-joint \(p\)-time non-malleability under semi-adaptive partitioning, for \(k\in O(\sqrt{\log n})\) and \(p>0\), and for any access structure that can be described by a polynomial-size monotone span program for which authorized sets have size greater than \(k\).
1.2 Technical Overview
Our initial observation is that a slight variant of a transformation by Ostrovsky et al. [30] allows to turn a bounded leakage-resilient, statistically one-time non-malleable secret sharing \(\varSigma \) into a bounded-time non-malleable secret sharing \(\varSigma ^*\) against joint tampering. Bounded leakage resilience here means that, prior to tampering, the attacker may also repeatedly leak information jointly from the shares of \(\varSigma \), as long as the overall leakage is bounded.
In the setting of joint tampering under selective partitioning, the leakage resilience property of \(\varSigma \) has to hold w.r.t. the same partition used for tampering. For joint tampering under semi-adaptive partitioning, we need \(\varSigma \) to be leakage-resilient under a semi-adaptive choice of the partitions too. A nice feature of this transformation is that it only requires perfectly binding commitments, which can be built from injective one-way functions. Moreover, it preserves the access structure of the underlying secret sharing scheme \(\varSigma \).
Given the above result, we can focus on the simpler task of constructing bounded leakage-resilient, statistically one-time non-malleable secret sharing, instead of directly attempting to construct their multi-time counterparts. We show different ways of doing that for both settings of selective and semi-adaptive partitioning.
Selective Partitioning. First, we show that every statistically one-time non-malleable secret sharing scheme \(\varSigma \) is also resilient to bounded leakage under selective partitioning. Let \(\ell \) be an upper bound on the total bit-length of the leakage over all shares. We use an argument reminiscent to standard complexity leveraging to prove that every one-time non-malleable secret sharing scheme with statistical security \(\epsilon \in [0,1)\) is also \(\ell \)-bounded leakage-resilient one-time non-malleable under selective partitioning with statistical security \(\epsilon /2^\ell \). The proof roughly works as follows. Given an unbounded attacker \(\mathsf {A}\) breaking the leakage-resilient one-time non-malleability of \(\varSigma \), we construct an unbounded attacker \(\hat{\mathsf {A}}\) against one-time non-malleability of \(\varSigma \) (without leakage). The challenge is how \(\hat{\mathsf {A}}\) can answer the leakage queries done by \(\mathsf {A}\). Our strategy is to simply guess the overall leakage \(\varLambda \) by sampling it uniformly at random, and use this guess to answer all of \(\mathsf {A}\)’s leakage queries.
The problem with this approach is that, whenever our guess was incorrect, the attacker \(\mathsf {A}\) may notice that it is being used in a simulation and start behaving arbitrarily. We solve this issue with the help of \(\hat{\mathsf {A}}\)’s final tampering query. Recall that in the model of selective partitioning, all leakage queries and the tampering query, act on the same arbitrary but fixed subsets \(\mathcal {B} _1,\ldots ,\mathcal {B} _t\) of a \(k\)-sized partition of the shares. Hence, when \(\mathsf {A}\) outputs its tampering query \((f_1,\ldots ,f_t)\), the reduction \(\hat{\mathsf {A}}\) defines a modified tampering query \((\hat{f}_1,\ldots ,\hat{f}_t)\) that first checks whether the guessed leakage from each subset \(\mathcal {B} _i\) was correct; if not, the tampering function setsFootnote 4 the modified shares within \(\mathcal {B} _i\) to \(\bot \), else it acts identically to \(f_i\). This strategy ensures that our reduction either performs a correct simulation or destroys the secret. In turn, destroying the secret whenever we guessed incorrectly implies that the success probability of \(\hat{\mathsf {A}}\) is exactly that of \(\mathsf {A}\) times the probability of guessing the leakage correctly, which is \(2^{-\ell }\).
By plugging the schemes from [23, Thm. 2], [24, Thm. 6], and [14, Thm. 3], together with our refined analysis of the transformation by Ostrovsky et al. [30], the above insights directly imply items i and ii of Theorem 1.
Semi-adaptive Partitioning. Unfortunately, the argument for showing that one-time non-malleability implies bounded leakage resilience breaks in the setting of adaptive (or even semi-adaptive) partitioning. Intuitively, the problem is that the adversary can leak jointly from adaptively chosen partitions, and thus it is unclear how the reduction can check whether the simulated leakage was correct using a single tampering query.
Hence, we take a different approach. We directly construct a bounded leakage-resilient, statistically one-time non-malleable secret sharing scheme for general access structures. Our construction \(\varSigma \) combines a 2-out-of-2 non-malleable secret sharing scheme \(\varSigma _2\) with two auxiliary leakage-resilient secret sharing schemes \(\varSigma _0\) and \(\varSigma _1\) realizing different access structures. When taking \(\varSigma _0\) to be the secret sharing scheme from [26, Thm. 1], our construction achieves \(k\)-joint bounded leakage-resilient statistical one-time non-malleability under semi-adaptive partitioning for \(k\in O(\sqrt{\log n})\). This implies item iii of Theorem 1. We refer the reader directly to Sect. 5 for a thorough description of our new secret sharing scheme and its security analysis.
Lower Bounds. Our complexity leveraging argument implies that every statistically one-time non-malleable secret sharing scheme against independent tampering with the shares is also statistically bounded leakage resilient against independent leakage (and no tampering).
By invoking a recent result of Nielsen and Simkin [29], we immediately obtain lower bounds on the share size and randomness complexity of any statistically one-time non-malleable secret sharing scheme against independent tampering.
1.3 Related Works
Non-malleable secret sharing is intimately related to non-malleable codes [19]. The difference between the two lies in the privacy property: While any non-malleable code in the split-state model [1, 3, 5,6,7, 13, 15,16,17, 19, 20, 22, 27, 28, 30] is also a 2-out-of-2 secret sharing [17], for any \(n\ge 3\) there are \(n\)-split-state non-malleable codes that are not private.
Continuously non-malleable codes in the \(n\)-split-state model are currently known for \(n= 8\) [4] (with statistical security), and for \(n= 2\) [16, 20, 22, 30] (with computational security).
Non-malleable secret sharing schemes have useful cryptographic applications, such as non-malleable message transmission [23] and continuously non-malleable threshold signatures [2, 21].
1.4 Paper Organization
The rest of this paper is organized as follows. In Sect. 2, we recall a few standard definitions. In Sect. 3, we define our model of \(k\)-joint non-malleability under selective and semi-adaptive partitioning.
In Sect. 4 and Sect. 5, we describe our constructions of bounded leakage-resilient statistically one-time non-malleable secret sharing schemes under selective and semi-adaptive partitioning. The lower bounds for non-malleable secret sharing, and the compiler for achieving \(p\)-time non-malleability against joint tampering are presented in Sect. 6. Finally, in Sect. 7, we conclude the paper with a list of open problems for further research.
2 Preliminaries
2.1 Standard Notation
For a string \(x \in \{0,1\}^*\), we denote its length by |x|; if \(\mathcal {X} \) is a set, \(|\mathcal {X} |\) represents the number of elements in \(\mathcal {X} \). We denote by [n] the set \(\{1, \ldots , n\}\). For a set of indices \(\mathcal {I} = (i_1, \ldots , i_t)\) and a vector \(x = (x_1, \ldots , x_n)\), we write \(x_\mathcal {I} \) to denote the vector \((x_{i_1}, \ldots , x_{i_t})\). When x is chosen randomly in \(\mathcal {X} \), we write  . When \(\mathsf {A}\) is a randomized algorithm, we write
. When \(\mathsf {A}\) is a randomized algorithm, we write  to denote a run of \(\mathsf {A}\) on input x (and implicit random coins r) and output y; the value y is a random variable and \(\mathsf {A}(x; r)\) denotes a run of \(\mathsf {A}\) on input x and randomness r. An algorithm \(\mathsf {A}\) is probabilistic polynomial-time (PPT for short) if \(\mathsf {A}\) is randomized and for any input \(x, r \in \{0,1\}^*\), the computation of \(\mathsf {A}(x; r)\) terminates in a polynomial number of steps (in the size of the input).
to denote a run of \(\mathsf {A}\) on input x (and implicit random coins r) and output y; the value y is a random variable and \(\mathsf {A}(x; r)\) denotes a run of \(\mathsf {A}\) on input x and randomness r. An algorithm \(\mathsf {A}\) is probabilistic polynomial-time (PPT for short) if \(\mathsf {A}\) is randomized and for any input \(x, r \in \{0,1\}^*\), the computation of \(\mathsf {A}(x; r)\) terminates in a polynomial number of steps (in the size of the input).
Negligible Functions. We denote with  the security parameter. A function p is polynomial (in the security parameter), denoted
the security parameter. A function p is polynomial (in the security parameter), denoted  , if
, if  for some constant \(c > 0\). A function
for some constant \(c > 0\). A function  is negligible (in the security parameter) if it vanishes faster than the inverse of any polynomial in
is negligible (in the security parameter) if it vanishes faster than the inverse of any polynomial in  , i.e.
, i.e.  for all positive polynomials
for all positive polynomials  . We often write
. We often write  to denote that
to denote that  is negligible. Unless stated otherwise, throughout the paper, we implicitly assume that the security parameter is given as input (in unary) to all algorithms.
is negligible. Unless stated otherwise, throughout the paper, we implicitly assume that the security parameter is given as input (in unary) to all algorithms.
Random Variables. For a random variable \(\mathbf {X}\), we write \(\mathbb {P}[\mathbf {X} = x]\) for the probability that \(\mathbf {X}\) takes on a particular value \(x \in \mathcal {X} \), with \(\mathcal {X} \) being the set where \(\mathbf {X}\) is defined. The statistical distance between two random variables \(\mathbf {X}\) and \(\mathbf {Y}\) over the same set \(\mathcal {X} \) is defined as
Given two ensembles  and
and  , we write \(\mathbf {X} \equiv \mathbf {Y}\) to denote that they are identically distributed, \(\mathbf {X} {\mathop {\approx }\limits ^{\mathsf {s}}}\mathbf {Y}\) to denote that they are statistically close, i.e.
, we write \(\mathbf {X} \equiv \mathbf {Y}\) to denote that they are identically distributed, \(\mathbf {X} {\mathop {\approx }\limits ^{\mathsf {s}}}\mathbf {Y}\) to denote that they are statistically close, i.e.  , and \(\mathbf {X} {\mathop {\approx }\limits ^{\mathsf {c}}}\mathbf {Y}\) to denote that they are computationally indistinguishable, i.e. for all PPT distinguishers \(\mathsf {D}\):
, and \(\mathbf {X} {\mathop {\approx }\limits ^{\mathsf {c}}}\mathbf {Y}\) to denote that they are computationally indistinguishable, i.e. for all PPT distinguishers \(\mathsf {D}\):

Sometimes we explicitly denote by \(\mathbf {X} {\mathop {\approx }\limits ^{\mathsf {s}}}_\epsilon \mathbf {Y}\) the fact that  for a parameter
for a parameter  . We also extend the notion of computational indistinguishability to the case of interactive experiments (a.k.a. games) featuring an adversary \(\mathsf {A}\). In particular, let
. We also extend the notion of computational indistinguishability to the case of interactive experiments (a.k.a. games) featuring an adversary \(\mathsf {A}\). In particular, let  be the random variable corresponding to the output of \(\mathsf {A}\) at the end of the experiment, where wlog. we may assume \(\mathsf {A}\) outputs a decision bit. Given two experiments
be the random variable corresponding to the output of \(\mathsf {A}\) at the end of the experiment, where wlog. we may assume \(\mathsf {A}\) outputs a decision bit. Given two experiments  and
and  , we write
, we write  as a shorthand for
as a shorthand for

The above naturally generalizes to statistical distance, which we denote by  , in case of unbounded adversaries.
, in case of unbounded adversaries.
We recall a lemma from Dziembowski and Pietrzak [18]:
Lemma 1
Let \(\mathbf{X}\) and \(\mathbf{Y}\) be two independent random variables, and \(\mathcal {O}_\mathsf {leak}(\cdot ,\cdot )\) be an oracle that upon input arbitrary functions \((g_0,g_1)\) returns \((g_0(\mathbf{X}),g_1(\mathbf{Y}))\). Then, for any adversary \(\mathsf {A}\) outputting  , it holds that the random variables \(\mathbf{X} |\mathbf{Z}\) and \(\mathbf{Y}|\mathbf{Z}\) are independent.
, it holds that the random variables \(\mathbf{X} |\mathbf{Z}\) and \(\mathbf{Y}|\mathbf{Z}\) are independent.
2.2 Secret Sharing Schemes
An n-party secret sharing scheme \(\varSigma \) consists of polynomial-time algorithms \((\mathsf {Share}, \mathsf {Rec})\) specified as follows. The randomized sharing algorithm \(\mathsf {Share}\) takes a message \(m\in \mathcal {M} \) as input and outputs \(n\) shares \(s_1, \ldots , s_n\), where each \(s_i \in \mathcal {S}_i\). The deterministic algorithm \(\mathsf {Rec}\) takes some number of shares as input and outputs a value in \(\mathcal {M} \cup \{ \bot \}\). We define \(\mu := \log |\mathcal {M} |\) and \(\sigma _i := \log |\mathcal {S}_i|\) respectively, to be the bit length of the message and of the ith share.
Which subsets of shares are authorized to reconstruct the secret and which are not is defined via an access structure, which is the set of all authorized subsets.
Definition 1
(Access structure). We say that \(\mathcal {A}\) is an access structure for \(n\) parties if \(\mathcal {A}\) is a monotone class of subsets of \([n]\), i.e., if \(\mathcal {I} _1 \in \mathcal {A}\) and \(\mathcal {I} _1 \subseteq \mathcal {I} _2\), then \(\mathcal {I} _2 \in \mathcal {A}\). We call authorized or qualified any set \(\mathcal {I} \in \mathcal {A}\), and unauthorized or unqualified any other set. We say that an authorized set \(\mathcal {I} \in \mathcal {A}\) is minimal if any proper subset of \(\mathcal {I} \) is unauthorized, i.e., if \(\mathcal {U} \subsetneq \mathcal {I} \), then \(\mathcal {U} \notin \mathcal {A}\).
Intuitively, a perfectly secure secret sharing scheme must be such that all qualified subsets of players can efficiently reconstruct the secret, whereas all unqualified subsets have no information (possibly in a computational sense) about the secret.
Definition 2
(Secret sharing scheme). Let  and \(\mathcal {A}\) be an access structure for \(n\) parties. We say that \(\varSigma = (\mathsf {Share}, \mathsf {Rec})\) is a secret sharing scheme realizing access structure \(\mathcal {A}\) with message space \(\mathcal {M} \) and share space \(\mathcal {S}= \mathcal {S}_1 \times \ldots \times \mathcal {S}_n\) if it is an \(n\)-party secret sharing with the following properties.
and \(\mathcal {A}\) be an access structure for \(n\) parties. We say that \(\varSigma = (\mathsf {Share}, \mathsf {Rec})\) is a secret sharing scheme realizing access structure \(\mathcal {A}\) with message space \(\mathcal {M} \) and share space \(\mathcal {S}= \mathcal {S}_1 \times \ldots \times \mathcal {S}_n\) if it is an \(n\)-party secret sharing with the following properties.
-
(i)
Correctness: For all
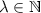 , all messages \(m\in \mathcal {M} \) and all authorized subsets \(\mathcal {I} \in \mathcal {A}\), we have that \(\mathsf {Rec}((\mathsf {Share}(m))_\mathcal {I}) = m\) with overwhelming probability over the randomness of the sharing algorithm.
, all messages \(m\in \mathcal {M} \) and all authorized subsets \(\mathcal {I} \in \mathcal {A}\), we have that \(\mathsf {Rec}((\mathsf {Share}(m))_\mathcal {I}) = m\) with overwhelming probability over the randomness of the sharing algorithm. -
(ii)
Privacy: For all PPT adversaries \(\mathsf {A}\), all pairs of messages \(m_0, m_1 \in \mathcal {M} \) and all unauthorized subsets \(\mathcal {U} \notin \mathcal {A}\), we have that
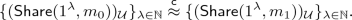
If the above ensembles are statistically close (resp. identically distributed), we speak of statistical (resp. perfect) privacy.
2.3 Non-interactive Commitments
A non-interactive commitment scheme \(\mathsf {Commit}\) is a randomized algorithm taking as input a message \(m\in \mathcal {M} \) and outputting a value \(c= \mathsf {Commit}(m; r)\) called commitment, using random coins \(r\in \mathcal {R} \). The pair \((m, r)\) is called the opening.
Intuitively, a secure commitment satisfies two properties called binding and hiding. The first property says that it is hard to open a commitment in two different ways. The second property says that a commitment hides the underlying message. The formal definition follows.
Definition 3
(Binding). We say that a non-interactive commitment scheme \(\mathsf {Commit}\) is computationally binding if for all PPT adversaries \(\mathsf {A}\), all messages \(m\in \mathcal {M} \), and all random coins \(r\in \mathcal {R} \), the following probability is negligible:

If the above holds even in the case of unbounded adversaries, we say that \(\mathsf {Commit}\) is statistically binding. Finally, if the above probability is exactly 0 for all adversaries (i.e., each commitment can be opened to at most a single message), then we say that \(\mathsf {Commit}\) is perfectly binding.
Definition 4
(Hiding). We say that a non-interactive commitment scheme \(\mathsf {Commit}\) is computationally hiding if, for all \(m_0, m_1 \in \mathcal {M} \), it holds that

In case the above ensembles are statistically close (resp. identically distributed), we say that \(\mathsf {Commit}\) is statistically (resp. perfectly) hiding.
3 Our Leakage and Tampering Model
In this section we define various notions of non-malleability against joint tampering and leakage for secret sharing. Very roughly, in our model the attacker is allowed to partition the set of share holders into \(t\) (non-overlapping) blocks with size at most \(k\), covering the entire set \([n]\). This is formalized through the notion of a \(k\)-sized partition.
Definition 5
(\(k\)-sized partition). Let  . We call \(\mathcal {B} = (\mathcal {B} _1, \ldots , \mathcal {B} _t)\) a \(k\)-sized partition of \([n]\) when: (i) \(\bigcup _{i=1}^t\mathcal {B} _i = [n]\); (ii) \(\forall i_1, i_2 \in [t]\) such that \(i_1 \ne i_2\), \(\mathcal {B} _{i_1} \cap \mathcal {B} _{i_2} = \emptyset \); (iii) \(\forall i \in [t],~|\mathcal {B} _i| \le k\).
. We call \(\mathcal {B} = (\mathcal {B} _1, \ldots , \mathcal {B} _t)\) a \(k\)-sized partition of \([n]\) when: (i) \(\bigcup _{i=1}^t\mathcal {B} _i = [n]\); (ii) \(\forall i_1, i_2 \in [t]\) such that \(i_1 \ne i_2\), \(\mathcal {B} _{i_1} \cap \mathcal {B} _{i_2} = \emptyset \); (iii) \(\forall i \in [t],~|\mathcal {B} _i| \le k\).
Let \(\mathcal {B} = (\mathcal {B} _1, \ldots , \mathcal {B} _t)\) be a \(k\)-sized partition of \([n]\). To define non-malleability, we consider an adversary \(\mathsf {A}\) interacting with a target secret sharing \(s= (s_1, \ldots , s_n)\) via the following queries:
-
Leakage queries. For each \(i \in [t]\), the attacker can leak jointly from the shares \(s_{\mathcal {B} _i}\). This can be done repeatedly and in an adaptiveFootnote 5 fashion, as long as the total number of bits that the adversary leaks from each share does not exceed
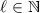 .
. -
Tampering queries. For each \(i \in [t]\), the attacker can tamper jointly with the shares \(s_{\mathcal {B} _i}\). Each such query yields mauled shares \((\tilde{s}_1, \ldots , \tilde{s}_n)\), for which the adversary is allowed to see the corresponding reconstructed message w.r.t. a reconstruction set \(\mathcal {T} \in \mathcal {A}\) of his choice. This can be done for at most
 times, and in an adaptive fashion.
times, and in an adaptive fashion.
Depending on the partition \(\mathcal {B} \) being fixed, or chosen adaptively with each leakage/tampering query, we obtain two different flavors of non-malleability, as defined in the following subsections.
3.1 Selective Partitioning
Here, we restrict the adversary to jointly leak from and tamper with subsets of shares belonging to a fixed partition of \([n]\).
Definition 6
(Selective bounded-leakage and tampering admissible adversary). Let  , and fix an arbitrary message space \(\mathcal {M} \), sharing space \(\mathcal {S}= \mathcal {S}_1 \times \cdots \times \mathcal {S}_n\), and access structure \(\mathcal {A} \) for \(n\) parties. We say that a (possibly unbounded) adversary \(\mathsf {A}\) is selective \(k\)-joint \(\ell \)-bounded leakage \(p\)-tampering admissible (selective \((k,\ell ,p)\)-BLTA for short) if, for every fixed \(k\)-sized partition \((\mathcal {B} _1, \ldots , \mathcal {B} _{t})\) of \([n]\), \(\mathsf {A}\) satisfies the following conditions:
, and fix an arbitrary message space \(\mathcal {M} \), sharing space \(\mathcal {S}= \mathcal {S}_1 \times \cdots \times \mathcal {S}_n\), and access structure \(\mathcal {A} \) for \(n\) parties. We say that a (possibly unbounded) adversary \(\mathsf {A}\) is selective \(k\)-joint \(\ell \)-bounded leakage \(p\)-tampering admissible (selective \((k,\ell ,p)\)-BLTA for short) if, for every fixed \(k\)-sized partition \((\mathcal {B} _1, \ldots , \mathcal {B} _{t})\) of \([n]\), \(\mathsf {A}\) satisfies the following conditions:
-
\(\mathsf {A}\) outputs a sequence of poly-many leakage queries \((g_1^{(q)}, \ldots , g_t^{(q)})\), such that for all
 and all \(i \in [t]\),
and all \(i \in [t]\), 
where \(\ell _i^{(q)}\) is the length of the output \(\varLambda _i^{(q)}\) of \(g_i^{(q)}\). The only restriction is that \(|\varLambda | \le \ell \), where \(\varLambda \) is the string containing the total leakage performed (over all queries).
-
\(\mathsf {A}\) outputs a sequence of tampering queries \((\mathcal {T} ^{(q)}, (f_1^{(q)}, \ldots , f_t^{(q)}))\), such that, for all \(q \in [p]\), and for all \(i \in [t]\), it holds that

and moreover \(\mathcal {T} ^{(q)} \in \mathcal {A}\) is a minimal authorized subset.
-
All queries performed by \(\mathsf {A}\) are chosen adaptively, i.e. each query may depend on the information obtained from all the previous queries.
-
If \(p> 0\), the last query performed by \(\mathsf {A}\) is a tampering query.
Note that \(\mathsf {A}\) can choose a different reconstruction set \(\mathcal {T} ^{(q)}\) with each tampering query, in a fully adaptive manner. This feature is known as adaptive reconstruction [21]. However, we consider the following two restrictions (that were not present in previous works): (i) Each set \(\mathcal {T} ^{(q)}\) must be minimal and contain at least one mauled share from each subset \(\mathcal {B} _i\); (ii) The last query asked by \(\mathsf {A}\) is a tampering query. Looking ahead, these technical conditions are needed for the complexity leveraging argument used in Theorem 3. Note that the above restrictions are still meaningful, as they allow, e.g., to capture the setting in which the attacker first leaks from all the shares and then tampers with the shares in a minimal authorized subset.
3.2 Semi-adaptive Partitioning
Next, we generalize the above definition to the stronger setting in which the adversary is allowed to change the \(k\)-sized partition with each leakage and tampering query. Here, we do not consider the restriction (i) mentioned above as it is not needed for the analysis of our secret sharing scheme in Sect. 5; yet we still consider the restriction (ii), and we will need to restrict the way in which the attacker specifies the partitions corresponding to each leakage and tampering query. For this reason, we refer to our model as semi-adaptive partitioning.
Definition 7
(Semi-adaptive bounded-leakage and tampering admissible adversary). Let  and \(\mathcal {M}, \mathcal {S}, \mathcal {A}\) as in Definition 6. We say that a (possibly unbounded) adversary \(\mathsf {A}\) is semi-adaptive \(k\)-joint \(\ell \)-bounded leakage \(p\)-tampering admissible (semi-adaptive \((k,\ell ,p)\)-BLTA for short) if it satisfies the following conditions:
and \(\mathcal {M}, \mathcal {S}, \mathcal {A}\) as in Definition 6. We say that a (possibly unbounded) adversary \(\mathsf {A}\) is semi-adaptive \(k\)-joint \(\ell \)-bounded leakage \(p\)-tampering admissible (semi-adaptive \((k,\ell ,p)\)-BLTA for short) if it satisfies the following conditions:
-
\(\mathsf {A}\) outputs a sequence of poly-many leakage queries \((\mathcal {B} ^{(q)}, (g_1^{(q)}, \ldots , g_{t^{(q)}}^{(q)}))\), chosen adaptively, such that, for all
 , and for all \(i \in [t^{(q)}]\), it holds that \(\mathcal {B} ^{(q)} = (\mathcal {B} _1^{(q)}, \ldots , \mathcal {B} _{t^{(q)}}^{(q)})\) is a \(k\)-sized partition of \([n]\) and
, and for all \(i \in [t^{(q)}]\), it holds that \(\mathcal {B} ^{(q)} = (\mathcal {B} _1^{(q)}, \ldots , \mathcal {B} _{t^{(q)}}^{(q)})\) is a \(k\)-sized partition of \([n]\) and 
where \(\ell _i^{(q)}\) is the length of the output. The only restriction is that \(|\varLambda | \le \ell \), where \(\varLambda = (\varLambda ^{(1)}, \varLambda ^{(2)}, \ldots )\) is the total leakage (over all queries).
-
\(\mathsf {A}\) outputs a sequence of \(p\) tampering queries \((\mathcal {B} ^{(q)}, \mathcal {T} ^{(q)}, (f_1^{(q)}, \ldots , f_t^{(q)}))\), chosen adaptively, such that, for all \(q \in [p]\), and for all \(i \in [t^{(q)}]\), it holds that \(\mathcal {B} ^{(q)}\) is a \(k\)-sized partition of \([n]\) and

-
All queries performed by \(\mathsf {A}\) are chosen adaptively, i.e. each query may depend on the information obtained from all the previous queries.
-
If \(p> 0\), the last query performed by \(\mathsf {A}\) is a tampering query.
-
Given a tampering query \((\mathcal {B},\mathcal {T},f)\), let \(\mathcal {T} = \{\beta _1, \ldots , \beta _\tau \}\) for
 . We write \(\xi (i)\) for the index such that \(\beta _i \in \mathcal {B} _{\xi (i)}\); namely, the i-th share used in the reconstruction is tampered by the \(\xi (i)\)-th tampering function. Then:
. We write \(\xi (i)\) for the index such that \(\beta _i \in \mathcal {B} _{\xi (i)}\); namely, the i-th share used in the reconstruction is tampered by the \(\xi (i)\)-th tampering function. Then: -
(i)
For all leakage queries \((\mathcal {B}, g)\) and all tampering queries \((\mathcal {B} ', \mathcal {T} ', f')\), where \(\mathcal {B} = (\mathcal {B} _1, \ldots , \mathcal {B} _{t})\) and \(\mathcal {B} ' = (\mathcal {B} _1', \ldots , \mathcal {B} _{t'}')\), the following holds: for all indices \(i \in [t]\), either there exists \(j \in \mathcal {T} '\) such that \(\mathcal {B} _i \subseteq \mathcal {B} _{\xi (j)}'\), or for all \(j\in \mathcal {T} '\) we have \(\mathcal {B} _i \cap \mathcal {B} '_{\xi (j)} = \emptyset \).
-
(ii)
For any pair of tampering queries \((\mathcal {B} ', \mathcal {T} ', f')\) and \((\mathcal {B} '', \mathcal {T} '', f'')\), where \(\mathcal {B} '=\{\mathcal {B} '_1,\dots ,\mathcal {B} '_{t'}\}\) and \(\mathcal {B} ''=\{\mathcal {B} ''_1,\dots ,\mathcal {B} ''_{t''}\}\), the following holds: for all \(i \in \mathcal {T} '\), either there exists \(j\in \mathcal {T} ''\) such that \(\mathcal {B} '_{\xi (i)} \subseteq \mathcal {B} ''_{\xi (j)}\), or for all \(j \in \mathcal {T} ''\) we have \(\mathcal {B} '_{\xi (i)} \cap \mathcal {B} ''_{\xi (j)} = \emptyset \).
-
(i)
Intuitively, condition (i) means that whenever the attacker leaks jointly from the shares within a subset \(\mathcal {B} _i\), then for any tampering query the adversary must either tamper jointly with the shares within \(\mathcal {B} _i\), or do not modify those shares at all. Condition (ii) is the same translated to the partitions corresponding to different tampering queries. Looking ahead, condition (i) is needed for the proof in Sect. 5.3, whereas condition (ii) is needed for the proof in Sect. 6.2. Note that the above restrictions are still meaningful, as they allow, e.g., to capture the setting in which the attacker defines two non-overlappingFootnote 6 subsets of \([n]\) and then performs joint leakage under adaptive partitioning within the first subset and joint leakage/tampering under selective partitioning within the second subset.
3.3 The Definition
Very roughly, leakage-resilient non-malleability states that no admissible adversary, as defined above, can distinguish whether it is interacting with a secret sharing of \(m_0\) or of \(m_1\).
Definition 8
(Leakage-resilient non-malleability). Let  and \(\epsilon \in [0, 1]\) be parameters, and \(\mathcal {A}\) be an access structure for \(n\) parties. We say that \(\varSigma = (\mathsf {Share}, \mathsf {Rec})\) is a \(k\)-joint \(\ell \)-bounded leakage-resilient \(p\)-time \(\epsilon \)-non-malleable secret sharing scheme realizing \(\mathcal {A} \), shortened \((k, \ell , p, \epsilon )\)-BLR-NMSS, if it is an \(n\)-party secret sharing scheme realizing \(\mathcal {A} \), and additionally, for all pairs of messages \(m_0, m_1 \in \mathcal {M} \), we have one of the following:
and \(\epsilon \in [0, 1]\) be parameters, and \(\mathcal {A}\) be an access structure for \(n\) parties. We say that \(\varSigma = (\mathsf {Share}, \mathsf {Rec})\) is a \(k\)-joint \(\ell \)-bounded leakage-resilient \(p\)-time \(\epsilon \)-non-malleable secret sharing scheme realizing \(\mathcal {A} \), shortened \((k, \ell , p, \epsilon )\)-BLR-NMSS, if it is an \(n\)-party secret sharing scheme realizing \(\mathcal {A} \), and additionally, for all pairs of messages \(m_0, m_1 \in \mathcal {M} \), we have one of the following:
-
For all selective \((k, \ell , p)\)-BLTA adversaries \(\mathsf {A}\), and for all \(k\)-sized partitions \(\mathcal {B} \) of \([n]\),
 (1)
(1)In this case, we speak of \((k, \ell , p, \epsilon )\)-BLR-NMSS under selective partitioning.
-
For all semi-adaptive \((k, \ell , p)\)-BLTA adversaries \(\mathsf {A}\),
 (2)
(2)In this case, we speak of \((k, \ell , p, \epsilon )\)-BLR-NMSS under semi-adaptive partitioning.
Experiments  and
and  , for \(b\in \{0,1\}\), are depicted in Fig. 1.
, for \(b\in \{0,1\}\), are depicted in Fig. 1.
In case there exists  such that indistinguishability still holds computationally in the above definitions for any
such that indistinguishability still holds computationally in the above definitions for any  , and any PPT adversaries \(\mathsf {A}\), we call \(\varSigma \) bounded leakage-resilient continuously non-malleable, shortened \((k, \ell )\)-BLR-CNMSS, under selective/semi-adaptive partitioning.
, and any PPT adversaries \(\mathsf {A}\), we call \(\varSigma \) bounded leakage-resilient continuously non-malleable, shortened \((k, \ell )\)-BLR-CNMSS, under selective/semi-adaptive partitioning.
Non-malleable Secret Sharing. When no leakage is allowed (i.e., \(\ell = 0\)), we obtain the notion of non-malleable secret sharing as a special case. In particular, an adversary is \(k\)-joint \(p\)-time tampering admissible, shortened \((k, p)\)-TA, if it is \((k, 0, p)\)-BLTA. Furthermore, we say that \(\varSigma \) is a \(k\)-joint \(p\)-time \(\epsilon \)-non-malleable secret sharing, shortened \((k, p, \epsilon )\)-NMSS, if \(\varSigma \) is a \((k, 0, p, \epsilon )\)-BLR-NMSS scheme.
Leakage-Resilient Secret Sharing. When no tampering is allowed (i.e., \(p= 0\)), we obtain the notion of leakage-resilient secret sharing as a special case. In particular, an adversary is \(k\)-joint \(\ell \)-bounded leakage admissible, shortened \((k, \ell )\)-BLA, if it is \((k, \ell , 0)\)-BLTA. Furthermore, we say that \(\varSigma \) is a \(k\)-joint \(\ell \)-bounded \(\epsilon \)-leakage-resilient secret sharing, shortened \((k, \ell , \epsilon )\)-BLRSS, if \(\varSigma \) is a \((k, \ell , 0, \epsilon )\)-BLR-NMSS scheme.
Finally, we denote by  and
and  the experiments in Definition 8 defining leakage resilience against selective and semi-adaptive partitioning respectively. However, note that when no tampering happens the conditions (i) and (ii) of Definition 7 are irrelevant, and thus we simply speak of \((k, \ell , \epsilon )\)-BLRSS under adaptive partitioning.
the experiments in Definition 8 defining leakage resilience against selective and semi-adaptive partitioning respectively. However, note that when no tampering happens the conditions (i) and (ii) of Definition 7 are irrelevant, and thus we simply speak of \((k, \ell , \epsilon )\)-BLRSS under adaptive partitioning.
Augmented Leakage Resilience. We also define a seemingly stronger variant of leakage-resilient secret sharing, in which \(\mathsf {A}\) is allowed to obtain the shares within a subset of the partition \(\mathcal {B} \) (in the case of selective partitioning, or any unauthorized subset of at most \(k\) shares in the case of adaptive partitioning) at the end of the experiment. In particular, in the case of selective partitioning, an augmented admissible adversary is an attacker \(\mathsf {A}^+ = (\mathsf {A}_1^+, \mathsf {A}_2^+)\) such that:
-
\(\mathsf {A}_1^+\) is an admissible adversary in the sense of Definition 6, the only difference being that \(\mathsf {A}_1^+\) outputs a tuple \((\alpha , i^*)\), where \(\alpha \) is an auxiliary state, and \(i^*\in [t]\);
-
\(\mathsf {A}_2^+\) takes as input \(\alpha \) and all the shares \(s_{\mathcal {B} _{i^*}}\), and outputs a decision bit.
In case of adaptive partitioning, the definition changes as follows: the adversary \(\mathsf {A}_1^+\) is admissible in the sense of Definition 7 and outputs an unauthorized subset \(\mathcal {U} \notin \mathcal {A}\) of size at most \(k\) instead of the index \(i^*\), and \(\mathsf {A}_2^+\) takes as input the shares \(s_\mathcal {U} \) instead of the shares \(s_{\mathcal {B} _{i^*}}\).
This flavor of security is called augmented leakage resilience. The theorem below, which was established by [11, 26] for the case of independent leakage, shows that any joint LRSS is also an augmented LRSS at the cost of an extra bit of leakage.
Theorem 2
Let \(\varSigma \) be a \((k, \ell + 1, \epsilon )\)-BLRSS realizing access structure \(\mathcal {A}\) under selective/adaptive partitioning. Then, \(\varSigma \) is an augmented \((k, \ell , \epsilon )\)-BLRSS realizing \(\mathcal {A}\) under selective/adaptive partitioning.
Proof
By reduction to non-augmented leakage resilience. Let \(\mathsf {A}^+ = (\mathsf {A}_1^+, \mathsf {A}_2^+)\) be a \((k, \ell , \epsilon )\)-BLA adversary violating augmented leakage-resilience; we construct an adversary \(\mathsf {A}\) breaking the non-augmented variant of leakage resilience. Fix \(m_0, m_1 \in \mathcal {M} \) and a \(k\)-sized partition \(\mathcal {B} = (\mathcal {B} _1, \ldots , \mathcal {B} _t)\). Attacker \(\mathsf {A}\) works as follows.
-
Run \(\mathsf {A}_1^+\) and, upon input a leakage query \((g_1, \ldots , g_t)\), forward the same query to the target leakage oracle and return the answer to \(\mathsf {A}_1^+\).
-
Let \((\alpha , i^*)\) be the final output of \(\mathsf {A}_1^+\). Define the leakage function \(\hat{g}_{i^*}^{\alpha , \mathsf {A}_2^+}\) which hard-wires \(\alpha \) and a description of \(\mathsf {A}_2^+\), takes as input the shares \(s_{\mathcal {B} _{i^*}}\) and returns the decision bit
 .
. -
Forward \((\varepsilon , \ldots , \varepsilon , \hat{g}_{i^*}^{\alpha , \mathsf {A}_2^+}, \varepsilon , \ldots , \varepsilon )\) to the target leakage oracle, obtaining a bit \(b'\).
-
Output \(b'\).
The statement follows by observing that \(\mathsf {A}\)’s simulation to \(\mathsf {A}^+\)’s leakage queries is perfect, thus \(\mathsf {A}\) and \(\mathsf {A}^+\) have the same advantage, and moreover \(\mathsf {A}\) leaks a total of at most \(\ell + 1\) bits. \(\square \)
4 Selective Partitioning
In this section, we construct bounded leakage-resilient, statistically one-time non-malleable secret sharing under selective partitioning. We achieve this in two steps. First, in Sect. 4.1, we prove that every statistically one-time non-malleable secret sharing is in fact bounded leakage-resilient, statistically one-time non-malleable under selective partitioning at the price of a security loss exponential in the size of the leakage. Then, in Sect. 4.2, we provide concrete instantiations using known results from the literature.
4.1 Non-malleability Implies Bounded Leakage Resilience
Theorem 3
Let \(\varSigma = (\mathsf {Share}, \mathsf {Rec})\) be a \((k, 1, \epsilon /2^{\ell })\)-NMSS realizing \(\mathcal {A}\). Then, \(\varSigma \) is also a \((k, \ell , 1, \epsilon )\)-BLR-NMSS realizing \(\mathcal {A}\) under selective partitioning.
Proof
By contradiction, assume that there exist a pair of messages \(m_0, m_1 \in \mathcal {M} \), a \(k\)-partition \(\mathcal {B} = (\mathcal {B} _1, \ldots , \mathcal {B} _t)\) of [n], and a \((k, \ell , 1)\)-BLTA unbounded adversary \(\mathsf {A}\) such that

Consider the following unbounded reduction \(\hat{\mathsf {A}}\) trying to break \((k, 0, 1, \epsilon /2^{\ell })\)-non-malleability using the same partition \(\mathcal {B} \), and the same messages \(m_0, m_1\).
-
1.
Run
 .
. -
2.
Upon input the q-th leakage query \(g^{(q)} = (g_1^{(q)}, \ldots , g_t^{(q)})\), generate a uniformly random string \(\varLambda ^{(q)} = (\varLambda _1^{(q)}, \ldots , \varLambda _t^{(q)})\) compatible with the range of \(g^{(q)}\), and output \(\varLambda ^{(q)}\) to \(\mathsf {A}\).
-
3.
Upon input the final tampering query \(f= (f_1, \ldots , f_t)\), construct the following tampering function \(\hat{f} = (\hat{f}_1, \ldots , \hat{f}_t)\):
-
The function hard-wires (a description of) all the leakage functions \(g^{(q)}\), the tampering query \(f\), and the guess on the leakage \(\varLambda = \varLambda ^{(1)} || \varLambda ^{(2)} || \cdots \).
-
Upon input the shares \((s_j)_{j \in \mathcal {B} _i}\), the function \(\hat{f}_i\) checks that the guess on the leakage was correct, i.e. \(g_i^{(q)}((s_j)_{j \in \mathcal {B} _i}) = \varLambda _i^{(q)}\) for all q. If the guess was correct, compute and output \(f_i((s_j)_{j \in \mathcal {B} _i})\); else, output \(\bot \).
-
-
4.
Send \(\hat{f}\) to the tampering oracle and pass the answer \(\tilde{m}\in \mathcal {M} \cup \{\diamond , \bot \}\) to \(\mathsf {A}\).
-
5.
Output the same guessing bit as \(\mathsf {A}\).
For the analysis, we now compute the distinguishing advantage of \(\hat{\mathsf {A}}\). In particular, call \(\mathbf {Miss}_{b}\) the event in which the guess on the leakage was wrong in experiment  , i.e. there exists \(i \in [t]\) such that \(\hat{f}_i\) outputs \(\bot \) in step 3, and call \(\mathbf {Hit}_{b}\) its complementary event. We notice that the probability of \(\mathbf {Hit}_0\) is equal to the probability of \(\mathbf {Hit}_1\), since the strings \(\varLambda ^{(q)}\) are sampled uniformly at random:
, i.e. there exists \(i \in [t]\) such that \(\hat{f}_i\) outputs \(\bot \) in step 3, and call \(\mathbf {Hit}_{b}\) its complementary event. We notice that the probability of \(\mathbf {Hit}_0\) is equal to the probability of \(\mathbf {Hit}_1\), since the strings \(\varLambda ^{(q)}\) are sampled uniformly at random:
where \(\mathbf{S}^b\) is the random variable corresponding to \(\mathsf {Share}(m_b)\), \(\mathbf {U}_\ell \) is the uniform distribution over \(\{0,1\}^\ell \), and \(g\) is the concatenation of all the leakage functions. Then, we can write:
In the above derivation, Eq. (3) follows from the law of total probability, Eq. (4) comes from the fact that, when \(\mathbf {Miss}\) happens, the view of \(\mathsf {A}\) (i.e. the leakage \(\varLambda \) and the output of the tampering query) is independentFootnote 7 of the target secret sharing, and thus its distinguishing advantage is zero, and Eq. (5) follows because \(\mathbb {P}[\mathbf {Hit}]=2^{-\ell }\) and moreover, when \(\mathbf {Hit}\) happens, the view of \(\mathsf {A}\) is perfectly simulated and thus \(\hat{\mathsf {A}}\) has the same distinguishing advantage of \(\mathsf {A}\), which is at least \(\epsilon \) by assumption.
Therefore, \(\hat{\mathsf {A}}\) has a distinguishing advantage of at least \(\epsilon /2^{\ell }\). Finally, note that \(\hat{\mathsf {A}}\) performs no leakage and uses only one tampering query, and thus \(\hat{\mathsf {A}}\) is \((k, 1)\)-TA. The lemma follows. \(\square \)
4.2 Instantiations
Using known constructions of one-time non-malleable secret sharing schemes against joint tampering, we obtain the following:
Corollary 1
For every  , and every \(k,\tau \ge 0\) such that \(k< \tau \le n\), there exists a \(\tau \)-out-of-\(n\) secret sharing \(\varSigma \) that is a
, and every \(k,\tau \ge 0\) such that \(k< \tau \le n\), there exists a \(\tau \)-out-of-\(n\) secret sharing \(\varSigma \) that is a  -BLR-NMSS under selective partitioning.
-BLR-NMSS under selective partitioning.
Proof
Follows by combining Theorem 3 with the secret sharing schemeFootnote 8 of
[23, Thm. 4], using security parameter  and choosing
and choosing  in order to obtain
in order to obtain

\(\square \)
Corollary 2
For every \(\ell ,n\ge 0\), any \(\beta <1\), and every \(k,\tau \ge 0\) such that \(k< \tau \le n\), there exists an \((n,\tau )\)-ramp secret sharing \(\varSigma \) that is a \((k, \ell , 1, 2^\ell \cdot 2^{-n^{\varOmega (1)}})\)-BLR-NMSS under selective partitioning with binary shares.
Proof
Follows by combining Theorem 3 with the secret sharing scheme of [14, Thm. 4.1].
5 Semi-adaptive Partitioning
As mentioned in the introduction, the proof of Theorem 3 breaks in the setting of semi-adaptive partitioning. To overcome this issue, in Sect. 5.1, we give a direct construction of a bounded leakage-resilient, one-time statistically non-malleable secret sharing (for general access structures) under semi-adaptive partitioning. We explain the main intuition behind our design in Sect. 5.2, and formally prove security in Sect. 5.3. Finally, in Sect. 5.4, we explain how to instantiate our construction using known results from the literature.
5.1 Our New Secret Sharing Scheme
Let \(\varSigma _0\) be a secret sharing realizing access structure \(\mathcal {A}\), let \(\varSigma _1\) be a \(k_1\)-out-of-\(n\) secret sharing, and let \(\varSigma _2\) be a 2-out-of-2 secret sharing. Consider the following scheme \(\varSigma = (\mathsf {Share}, \mathsf {Rec})\):
-
Algorithm \(\mathsf {Share}\): Upon input \(m\), first compute
 ,
,  , and
, and  . Then set \(s_i := (s_{0, i}, s_{1, i})\) for all \(i \in [n]\), and output \((s_1, \ldots , s_n)\).
. Then set \(s_i := (s_{0, i}, s_{1, i})\) for all \(i \in [n]\), and output \((s_1, \ldots , s_n)\). -
Algorithm \(\mathsf {Rec}\): Upon input \((s_i)_{i \in \mathcal {I}}\), parse \(s_i = (s_{0, i}, s_{1, i})\) and \(\mathcal {I} = \{i_1, \ldots , i_{|\mathcal {I} |}\}\), and define \(\mathcal {I} _{|_{k_1}} := \{i_1, \ldots , i_{k_1}\}\); compute \(s_1= \mathsf {Rec}_1((s_{1, i})_{i \in \mathcal {I} _{|_{k_1}}})\) and \(s_0= \mathsf {Rec}_0((s_{0, i})_{i \in \mathcal {I}})\), and finally output \(m' = \mathsf {Rec}_2((s_0, s_1))\).
With the above defined scheme, we achieve the following:
Theorem 4
Let  and \(\epsilon _0, \epsilon _1, \epsilon _2\in [0, 1]\) be parameters, and set \(k_1:= \sqrt{k}\), \(\ell _0:= \ell + 1\) and \(\ell _1:= \ell + n\cdot \sigma _0\). Let \(\mathcal {A}\) be an arbitrary access structure for \(n\) parties, where for any \(\mathcal {I} \in \mathcal {A} \) we have \(|\mathcal {I} | > k_1\). Assume that:
and \(\epsilon _0, \epsilon _1, \epsilon _2\in [0, 1]\) be parameters, and set \(k_1:= \sqrt{k}\), \(\ell _0:= \ell + 1\) and \(\ell _1:= \ell + n\cdot \sigma _0\). Let \(\mathcal {A}\) be an arbitrary access structure for \(n\) parties, where for any \(\mathcal {I} \in \mathcal {A} \) we have \(|\mathcal {I} | > k_1\). Assume that:
-
1.
\(\varSigma _0\) is a \((k, \ell _0, \epsilon _0)\)-BLRSS realizing \(\mathcal {A}\) under adaptive partitioning, with share space such that \(\log |\mathcal {S}_{0, i}| \le \sigma _0\) (for any \(i \in [n]\));
-
2.
\(\varSigma _1\) is a \((k_1- 1, \ell _1, \epsilon _1)\)-BLRSS realizing the \(k_1\)-out-of-\(n\) threshold access structure under adaptive partitioning;
-
3.
\(\varSigma _2\) is a one-time \(\epsilon _2\)-non-malleable 2-out-of-2 secret sharing (i.e. a \((1, 1, \epsilon _2)\)-NMSS).
Then, the above defined \(\varSigma \) is a \((k_1- 1, \ell , 1, 2(\epsilon _0+ \epsilon _1) + \epsilon _2)\)-BLR-NMSS realizing \(\mathcal {A}\) under semi-adaptive partitioning.
5.2 Proof Overview
In order to prove Theorem 4, we first make some considerations on the tampering query \((\mathcal {T}, \mathcal {B}, f)\). In particular, we construct two disjoint sets \(\mathcal {T} _0^*\) and \(\mathcal {T} _1^*\) that are the union of subsets from the partition \(\mathcal {B} \), in such a way that (i) \(\mathcal {T} _0^* \cap \mathcal {T} \) contains at least \(k_1\) elements (so that it can be used as a reconstruction set for \(\mathsf {Rec}_1\)); and (ii) each subset \(\mathcal {B} _i\) of the partition \(\mathcal {B} \) intersects at most one of \(\mathcal {T} _0^*,\mathcal {T} _1^*\) (so that both leakage and tampering queries can be computed on \(\mathcal {T} _0^*\) and on \(\mathcal {T} _1^*\) independently). Hence, we define four hybrid experiments as described below.
-
First Hybrid: In the first hybrid experiment, we change how the tampering query is answered. Namely, after the last leakage query, we replace all the left shares \((s_{0,\beta })_{\beta \in \mathcal {T} ^*_1}\) with new shares \((s_{0,\beta }^*)_{\beta \in \mathcal {T} ^*_1}\) that are valid shares of \(s_0\) and consistent with the leakage obtained by the adversary and with the shares \((s_{0,\beta })_{\beta \in \mathcal {T} ^*_0}\). Here, we note that due to the fact that we only consider semi-adaptive partitioning,Footnote 9 the shares \((s_{0,\beta })_{\beta \in \mathcal {T} ^*_1}\) and \((s_{1,\beta })_{\beta \in \mathcal {T} ^*_0}\) are independent even given the leakage. In particular, the above shares are independent before the leakage occurs, and furthermore condition (i) in Definition 7 ensures that the adversary never leaks jointly from shares in \(\mathcal {T} _0^*\) and in \(\mathcal {T} _1^*\). Thus, since the old and the new shares are sampled from the same distribution, this change does not affect the view of the adversary and does not modify its advantage.
-
Second Hybrid: In the second hybrid experiment, we change the distribution of the left shares. Namely, we discard the original ones and we replace them with left shares of some unrelated message \(\hat{s}_0\), where
 . In order to prove that this hybrid experiment is \(\epsilon _0\)-close to the previous one, we construct an admissible reduction to leakage resilience of \(\varSigma _0\), thus proving that, if some admissible adversary is able to notice the difference between the old and the new experiment with advantage more than \(\epsilon _0\), then our reduction can distinguish between a secret sharing of \(s_0\) and a secret sharing of \(\hat{s}_0\) with exactly the same advantage.
. In order to prove that this hybrid experiment is \(\epsilon _0\)-close to the previous one, we construct an admissible reduction to leakage resilience of \(\varSigma _0\), thus proving that, if some admissible adversary is able to notice the difference between the old and the new experiment with advantage more than \(\epsilon _0\), then our reduction can distinguish between a secret sharing of \(s_0\) and a secret sharing of \(\hat{s}_0\) with exactly the same advantage.The key idea here is to forward leakage queries to the target oracle and, once the adversary outputs its tampering query, obtain all the shares in \(\mathcal {T} _0^*\) from the challenger, using the augmented property ensured by Theorem 2; the reduction remains admissible because \(\varSigma _0\) has security against adaptive \(k\)-partitioning and \(|\mathcal {T} _0^*| \le k\). After receiving such shares, the reduction can sample the shares \((s_{0, \beta }^*)_{\mathcal {T} _1^*}\) as in the first hybrid experiment and compute the tampering on both \(s_0\) (using the shares in \(\mathcal {T} _0^*\) and the sampled shares in \(\mathcal {T} _1^*\)) and \(s_1\) (only using the shares in \(\mathcal {T} _0^*\)), which allows to simulate the tampering query.
-
Third Hybrid: In the third hybrid experiment, we change how the tampering query is answered. Similarly to the modification introduced in the first hybrid experiment, after the last leakage query, we replace all the right shares \((s_{1,\beta })_{\beta \in \mathcal {T} ^*_0}\) with new shares \((s^*_{1,\beta })_{\beta \in \mathcal {T} ^*_0}\) that are valid shares of \(s_1\) and consistent with the leakage obtained by the adversary. However, we now further require that this change does not affect the outcome of the tampering query on the left shares; in particular, if the tampering function applied to \((\hat{s}_{0, \beta }, s_{1, \beta })\) leads to \((\tilde{s}_{0, \beta }, *)\), the same tampering function applied to \((\hat{s}_{0, \beta }, s_{1, \beta }^*)\) must lead to \((\tilde{s}_{0, \beta },*)\). This is required in order to keep consistency with the modifications introduced in the second hybrid experiment. As before, since the old and the new shares are sampled from the same distribution, this change does not modify the advantage of the adversary.
-
Fourth Hybrid: In the fourth hybrid experiment, we change the distribution of the right shares. Similarly to the modification introduced in the third hybrid experiment, we discard the original shares and replace them with the right shares of the previously computed unrelated message, i.e. \(\hat{s}_1\). In order to prove that this hybrid experiment is \(\epsilon _1\)-close to the previous one, we construct an admissible reduction to leakage resilience of \(\varSigma _1\).
The key idea here is to simulate the tampering query with a leakage query that yields the result of the tampering on all the left shares \((\tilde{s}_{0,\beta })_{\beta \in \mathcal {T} ^*}\), where \(\mathcal {T} ^* = \mathcal {T} _0^* \cup \mathcal {T} _1^*\). This is allowed because of the restriction on the shares of \(\varSigma _0\) being at most \(\sigma _0\) bits long, so that the total performed leakage is bounded by \(\ell + n\sigma _0\). In particular, after sampling the fake shares \((\hat{s}_{0, 1},\ldots ,\hat{s}_{0, n})\), forwarding the leakage queries to the target oracle and receiving the tampering query, the reduction samples the shares \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) as in the second hybrid experiment and hard-wires them, along with the shares \((\hat{s}_{0, 1},\ldots ,\hat{s}_{0, n})\), inside a leakage function that computes \((\tilde{s}_{0, \beta }, \tilde{s}_{1, \beta })_{\beta \in \mathcal {T} ^*}\) and outputs \((\tilde{s}_{0, \beta })_{\beta \in \mathcal {T} ^*}\). After receiving the mauled shares, the reduction samples the shares \((s^*_{1,\beta })_{\beta \in \mathcal {T} ^*_0}\) as in the third hybrid and computes the corresponding tampered shares \((\tilde{s}_{1, \beta })_{\beta \in \mathcal {T} _0^*}\). Given the mauled shares \((\tilde{s}_{0, \beta })_{\beta \in \mathcal {T} ^*}\) and \((\tilde{s}_{1, \beta })_{\beta \in \mathcal {T} _0^*}\), the reduction can then simulate the tampering query correctly.
Since the above defined hybrid experiments are all statistically close, it only remains to show that no adversary can distinguish between the last hybrid experiment with bit \(b = 0\) and the same experiment with \(b = 1\) with an advantage more than \(\epsilon _2\), thus proving the security of our scheme. Here, we once again construct a reduction, this time to one-time \(\epsilon _2\)-non-malleability, that achieves the same advantage of an adversary distinguishing between the two experiments.
The key idea is to use \(s_0\) to sample the shares \((s^*_{0,\beta })_{\beta \in \mathcal {T} ^*_1}\) and \(s_1\) to sample the shares \((s_{1,\beta }^*)_{\beta \in \mathcal {T} ^*_0}\). In particular, all the missing shares needed for the computation are the one sampled from \((\hat{s}_0, \hat{s}_1)\) and, since \(\mathcal {T} _0^* \cap \mathcal {T} _1^* = \emptyset \), there is no overlap and the tampering can be split between two functions \(f_0, f_1\) that hard-wire the sampled values. These two functions take as input \(s_0\) and \(s_1\), respectively, and can thus compute the mauled values \(\tilde{s}_0\) and \(\tilde{s}_1\), which in turn allows the reduction to simulate the tampering query.
5.3 Security Analysis
Before proceeding with the analysis, we introduce some useful notation. We will define a sequence of hybrid experiments  for
for  and \(b \in \{0,1\}\), starting with
and \(b \in \{0,1\}\), starting with  which is identical to the
which is identical to the  experiment. Recall that, after the leakage phase, the adversary sends a single tampering query \((\mathcal {T}, \mathcal {B}, f)\).
experiment. Recall that, after the leakage phase, the adversary sends a single tampering query \((\mathcal {T}, \mathcal {B}, f)\).
-
Let
 and \(\mathcal {T} = \{\beta _1, \ldots , \beta _\tau \}\), and write \(\xi (i)\) for the index such that \(\beta _i \in \mathcal {B} _{\xi (i)}\) (i.e., the i-th share of the reconstruction is tampered by the \(\xi (i)\)-th tampering function).
and \(\mathcal {T} = \{\beta _1, \ldots , \beta _\tau \}\), and write \(\xi (i)\) for the index such that \(\beta _i \in \mathcal {B} _{\xi (i)}\) (i.e., the i-th share of the reconstruction is tampered by the \(\xi (i)\)-th tampering function). -
We define some subsets starting from \(\mathcal {T} \). Call
$$ \mathcal {T} _0^* = \bigcup _{\beta \in \mathcal {T} _{|_{k_1}}} \mathcal {B} _{\xi (\beta )} \qquad \text { and } \qquad \mathcal {T} _0 = \mathcal {T} _0^* \cap \mathcal {T}. $$Then, use the above to define
$$ \mathcal {T} _1 = \mathcal {T} \setminus \mathcal {T} _0 \qquad \text { and } \qquad \mathcal {T} _1^* = \bigcup _{\beta \in \mathcal {T} _1} \mathcal {B} _{\xi (\beta )}. $$and let \(\mathcal {T} ^* = \mathcal {T} _0^* \cup \mathcal {T} _1^*\).
Note that, with the above notation, we can write:
Moreover, \(\mathcal {T} _0\) and \(\mathcal {T} _1\) are defined in such a way that \(|\mathcal {T} _0| \ge k_1\) and, if \(\mathcal {B} _i \cap \mathcal {T} \ne \emptyset \), then either \(\mathcal {B} _i \cap \mathcal {T} _0 \ne \emptyset \) or \(\mathcal {B} _i \cap \mathcal {T} _1 \ne \emptyset \), but not both. In this way, we also obtain that \(\mathcal {T} _0^* \cap \mathcal {T} _1^* = \emptyset \).
Finally recall that the adversary sends leakage queries \((\mathcal {B} ^{(1)},g^{(1)}),\dots ,(\mathcal {B} ^{(q)},g^{(q)})\), for  , and by condition (i) in the definition of semi-adaptive admissibility (cf. Definition 7) we have that for all \(\mathcal {B} ^*\in \bigcup _{i\in [q]} \mathcal {B} ^{(i)}\) either (1) \(\exists j\in \mathcal {T}: \mathcal {B} ^* \subseteq \mathcal {B} _{\xi (j)}\), or (2) \(\forall j\in \mathcal {T}: \mathcal {B} ^* \cap \mathcal {B} _{\xi (j)} = \emptyset \).
, and by condition (i) in the definition of semi-adaptive admissibility (cf. Definition 7) we have that for all \(\mathcal {B} ^*\in \bigcup _{i\in [q]} \mathcal {B} ^{(i)}\) either (1) \(\exists j\in \mathcal {T}: \mathcal {B} ^* \subseteq \mathcal {B} _{\xi (j)}\), or (2) \(\forall j\in \mathcal {T}: \mathcal {B} ^* \cap \mathcal {B} _{\xi (j)} = \emptyset \).
Hybrid 1. Let  be the same as
be the same as  except for the shares of \(s_0\) being re-sampled at the end of the leakage phase. Namely, in
except for the shares of \(s_0\) being re-sampled at the end of the leakage phase. Namely, in  we sample \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) such that \((s_{0, \beta })_{\beta \in \mathcal {T} _0^*}, (s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) are valid shares of \(s_0\) and consistent with the leakage. Then, we answer to \(\mathsf {A}\)’s queries as follows:
we sample \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) such that \((s_{0, \beta })_{\beta \in \mathcal {T} _0^*}, (s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) are valid shares of \(s_0\) and consistent with the leakage. Then, we answer to \(\mathsf {A}\)’s queries as follows:
-
upon receiving a leakage query, use \((s_{0, 1}, s_{1, 1}), \ldots , (s_{0, n}, s_{1, n})\) to compute the answer;
-
upon receiving the tampering query, use \((s_{0, \beta }, s_{1, \beta })_{\beta \in \mathcal {T} _0^*}, (s_{0, \beta }^*, s_{1, \beta })_{\beta \in \mathcal {T} _1^*}\) to compute the answer.
Lemma 2
For \(b\in \{0,1\}\),  .
.
Proof
Let \((\mathbf {S}_{0, \beta })_{\beta \in \mathcal {T} _1^*}\) and \((\mathbf {S}_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) be the random variables for the values \((s_{0, \beta })_{\beta \in \mathcal {T} _1^*}\) and \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) in experiments \(\mathbf {H}_0\) and \(\mathbf {H}_1\). More in details, the random variable \((\mathbf{S}_{0,\beta }^*)_{\beta \in \mathcal {T} _1^*}\) comes from the distribution of the shares \((s_{0,\beta })_{\beta \in \mathcal {T} _1^*}\) conditioned on the fixed values \((s_{0,\beta })_{\beta \in \mathcal {T} _0^*}\) and the overall leakage \(\varLambda \). We claim that \((\mathbf{S}_{0,\beta }^*)_{\beta \in \mathcal {T} _1^*}\) and \((\mathbf{S}_{1,\beta })_{\beta \in \mathcal {T} _0^*}\) are independent conditioned on the leakage \(\mathbf \varLambda \). This is because the random variables \((\mathbf{S}_{0,\beta })_{\beta \in \mathcal {T} _1^*}\) and \((\mathbf{S}_{1,\beta })_{\beta \in \mathcal {T} _0^*}\) are independent in isolation, and, by condition (i) in the definition of semi-adaptive admissibility, none of the leakage functions leaks simultaneously from a share in \(\mathcal {T} _0^*\) and a share in \(\mathcal {T} _1^*\). The latter holds as otherwise there would exist \(\mathcal {B} ^*\in \bigcup _{i\in [q]} \mathcal {B} ^{(i)}\) such that \(\mathcal {T} _1^* \cap \mathcal {B} ^* \ne \emptyset \) and \(\mathcal {T} _0^* \cap \mathcal {B} ^* \ne \emptyset \), and therefore: (1) \(\forall j\in \mathcal {T}: \mathcal {B} ^* \nsubseteq \mathcal {B} _{\xi (j)}\), and (2) \(\exists j\in \mathcal {T}: \mathcal {B} ^* \cap \mathcal {B} _{\xi (j)} \ne \emptyset \). Finally, by Lemma 1, we can conclude that the two random variables are independent even conditioned on the leakage.
For any string \(\bar{s}\), let \(\mathbf {B}_0^{\bar{s}}\) and \(\mathbf {B}_1^{\bar{s}}\) be, respectively, the event that \((\mathbf {S}_{0, \beta })_{\beta \in \mathcal {T} _1^*} = \bar{s}\) and \((\mathbf {S}_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*} = \bar{s}\). Then:
where Eq. (7) holds because of \((\mathbf {S}_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) is re-sampled from the distribution of the \((s_{0,\beta })_{\beta \in \mathcal {T} ^*_1}\) conditioned on the measured leakage \(\varLambda \) and fixed \((s_{0,\beta })_{\beta \in \mathcal {T} ^*_0}\) and moreover it is independent of \((s_{1,\beta })_{\beta \in \mathcal {T} ^*_0}\) thus is distributed exactly as the conditional distribution of the \((\mathbf {S}_{0, \beta })_{\beta \in \mathcal {T} _1^*}\). The Eq. (8) holds because, once fixed the value of \(\bar{s}\), if both \(\mathbf {B}_0^{\bar{s}}\) and \(\mathbf {B}_1^{\bar{s}}\) happen, then \((\mathbf {S}_{0, \beta })_{\beta \in \mathcal {T} _1^*} = \bar{s}= (\mathbf {S}_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) and the two hybrids are the same. \(\square \)
Hybrid 2. Let  be the same as
be the same as  except for the leakage being performed on fake shares of \(s_0\). Namely, compute
except for the leakage being performed on fake shares of \(s_0\). Namely, compute  , let \(\hat{s}_i = (\hat{s}_{0, i}, s_{1, i})\) where
, let \(\hat{s}_i = (\hat{s}_{0, i}, s_{1, i})\) where  , and sample the shares \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) of \(\mathbf {H}_1\) such that \((\hat{s}_{0, \beta })_{\beta \in \mathcal {T} _0^*}, (s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) are valid shares of \(s_0\) and consistent with the leakage. Then:
, and sample the shares \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) of \(\mathbf {H}_1\) such that \((\hat{s}_{0, \beta })_{\beta \in \mathcal {T} _0^*}, (s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) are valid shares of \(s_0\) and consistent with the leakage. Then:
-
upon receiving a leakage query, use \((\hat{s}_{0, 1}, s_{1, 1}), \ldots , (\hat{s}_{0, n}, s_{1, n})\) to compute the answer;
-
upon receiving the tampering query, use \((\hat{s}_{0, \beta }, s_{1, \beta })_{\beta \in \mathcal {T} _0^*}, (s_{0, \beta }^*, s_{1, \beta })_{\beta \in \mathcal {T} _1^*}\) to compute the answer.
Lemma 3
For \(b\in \{0,1\}\),  .
.
Proof
By reduction to leakage resilience of \(\varSigma _0\). Suppose towards contradiction that there exist \(b\in \{0,1\}\), messages \(m_0,m_1\), and an adversary \(\mathsf {A}\) able to tell apart  and
and  with advantage more than
with advantage more than  . Let \((s_0, s_1)\) and \((\hat{s}_0, \hat{s}_1)\) be, respectively, a secret sharing of \(m_b\) and of the all-zero string under \(\varSigma _2\). Consider the following reduction trying to distinguish a secret sharing of \(s_0\) and a secret sharing of \(\hat{s}_0\) under \(\varSigma _0\), where we call \(s_0^{\mathsf {target}}\) the target secret sharing in the leakage oracle.
. Let \((s_0, s_1)\) and \((\hat{s}_0, \hat{s}_1)\) be, respectively, a secret sharing of \(m_b\) and of the all-zero string under \(\varSigma _2\). Consider the following reduction trying to distinguish a secret sharing of \(s_0\) and a secret sharing of \(\hat{s}_0\) under \(\varSigma _0\), where we call \(s_0^{\mathsf {target}}\) the target secret sharing in the leakage oracle.

- 1.
Sample
and run the experiment as in \(\mathbf {H}_1\) with the adversary \(\mathsf {A}\); upon receiving each leakage function, hard-code into it the shares of \(s_1\) and forward it to the leakage oracle.
- 2.
Eventually, the adversary sends its tampering query. Obtain from the challenger the shares \((s_{0, \beta }^{\mathsf {target}})_{\beta \in \mathcal {T} _0^*}\) (using the augmented property from Theorem 2).
- 3.
For all \(\beta \in \mathcal {T} _0\), compute \((\tilde{s}_{0, j}, \tilde{s}_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}} = f_{\xi (\beta )}( (s_{0, j}^{\mathsf {target}}, s_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}} )\) and compute \(\tilde{s}_1= \mathsf {Rec}_1((\tilde{s}_{1, \beta })_{\beta \in \mathcal {T} _{|_{k_1}}})\).
- 4.
Sample \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) as described in \(\mathbf {H}_2\) and compute \(\tilde{s}_0\) as follows: for all \(\beta \in \mathcal {T} _1\), let \((\tilde{s}_{0, j}, \tilde{s}_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}} = f_{\xi (\beta )}( (s_{0, j}^*, s_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}} )\) and \(\tilde{s}_0= \mathsf {Rec}_0( (\tilde{s}_{0, \beta })_{\beta \in \mathcal {T}} )\).
- 5.
Compute the value \(\tilde{m}= \mathsf {Rec}_2(\tilde{s}_0, \tilde{s}_1)\). In case \(\tilde{m}\in \{m_0,m_1\}\) return \(\diamond \) to \(\mathsf {A}\), and else return \(\tilde{m}\).
- 6.
Output the same as \(\mathsf {A}\).
For the analysis, note that the reduction is perfect. In particular, the reduction perfectly simulates \(\mathbf {H}_1\) when \((s_{0, i}^{\mathsf {target}})_{i \in [n]}\) is a secret sharing of \(s_0\) and perfectly simulates \(\mathbf {H}_2\) when \((s_{0, i}^{\mathsf {target}})_{i \in [n]}\) is a secret sharing of \(\hat{s}_0\). Moreover, the leakage requested by \(\mathsf {A}\) is forwarded to the leakage oracle of \(\hat{\mathsf {A}}\) and perfectly simulated by it. Finally, the reduction gets in full \((s_{0, \beta }^{\mathsf {target}})_{\beta \in \mathcal {T} _0^*}\), which allows it to compute \(\tilde{s}_1\), and computes \(\tilde{s}_0\) by sampling the values \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) as in \(\mathbf {H}_1\).
Let us now analyze the admissibility of \(\hat{\mathsf {A}}\). The only leakage performed by \(\hat{\mathsf {A}}\) is the one requested by \(\mathsf {A}\), and augmented leakage resilience can be obtained with 1 extra bit of leakage by Theorem 2. Finally, since \(|\mathcal {T} _0^*| \le k_1(k_1- 1) \le k\), it follows that if \(\mathsf {A}\) is \((k_1- 1, \ell , 1)\)-BLTA, \(\hat{\mathsf {A}}\) is \((k, \ell +1)\)-BLA. \(\square \)
Hybrid 3. Let  be the same as
be the same as  except for the shares of \(s_1\) being re-sampled at the end of the leakage phase. Namely, in
except for the shares of \(s_1\) being re-sampled at the end of the leakage phase. Namely, in  we sample \((s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}\) such that (1) the shares \((s_{1, \beta })_{\beta \in \mathcal {T} _0^*}\) and \((s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}\) agree with the same leakage and the same reconstructed secret \(s_1\), and (2) for all \(\beta \in \mathcal {T} _0\), applying the tampering function \(f_{\xi (\beta )}\) to \((\hat{s}_{0, j}, s_{1, j}^*)_{j \in \mathcal {B} _{\xi (\beta )}}\) or to \((\hat{s}_{0, j}, s_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}}\) leads to the same values \((\tilde{s}_{0, j})_{j \in \mathcal {B} _{\xi (\beta )}}\). Then, we answer to \(\mathsf {A}\)’s queries as follows:
we sample \((s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}\) such that (1) the shares \((s_{1, \beta })_{\beta \in \mathcal {T} _0^*}\) and \((s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}\) agree with the same leakage and the same reconstructed secret \(s_1\), and (2) for all \(\beta \in \mathcal {T} _0\), applying the tampering function \(f_{\xi (\beta )}\) to \((\hat{s}_{0, j}, s_{1, j}^*)_{j \in \mathcal {B} _{\xi (\beta )}}\) or to \((\hat{s}_{0, j}, s_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}}\) leads to the same values \((\tilde{s}_{0, j})_{j \in \mathcal {B} _{\xi (\beta )}}\). Then, we answer to \(\mathsf {A}\)’s queries as follows:
-
upon receiving a leakage query, use \((\hat{s}_{0, 1}, s_{1, 1}), \ldots , (\hat{s}_{0, n}, s_{1, n})\) to compute the answer;
-
upon receiving the tampering query, use \((\hat{s}_{0, \beta }, s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}, (s_{0, \beta }^*, s_{1, \beta })_{\beta \in \mathcal {T} _1^*}\) to compute the answer.
Lemma 4
For \(b\in \{0,1\}\),  .
.
Proof
The proof is similar to that of Lemma 2, and thus omitted.
Hybrid 4. Let  be the same as
be the same as  except for the leakage being performed on fake shares of \(s_1\). Namely, let
except for the leakage being performed on fake shares of \(s_1\). Namely, let  , where \(\hat{s}_1\) comes from \(\mathsf {Share}_2(0)\) as in \(\mathbf {H}_2\). Then:
, where \(\hat{s}_1\) comes from \(\mathsf {Share}_2(0)\) as in \(\mathbf {H}_2\). Then:
-
upon receiving a leakage query, use \((\hat{s}_{0, 1}, \hat{s}_{1, 1}), \ldots , (\hat{s}_{0, n}, \hat{s}_{1, n})\) to compute the answer;
-
upon receiving the tampering query, use \((\hat{s}_{0, \beta }, s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}, (s_{0, \beta }^*, \hat{s}_{1, \beta })_{\beta \in \mathcal {T} _1^*}\) to compute the answer.
Lemma 5
For \(b\in \{0,1\}\),  .
.
Proof
By reduction to the leakage resilience of \(\varSigma _1\). Suppose towards contradiction that there exist \(b\in \{0,1\}\), messages \(m_0,m_1\), and an adversary \(\mathsf {A}\) able to tell apart  and
and  with advantage more than
with advantage more than  . Let \((s_0, s_1)\) and \((\hat{s}_0, \hat{s}_1)\) be, respectively, a secret sharing of \(m_b\) and of the all-zero string under \(\varSigma _2\). Consider the following reduction trying to distinguish a secret sharing of \(s_1\) and a secret sharing of \(\hat{s}_1\) under \(\varSigma _1\), where we call \(s_1^{\mathsf {target}}\) the target secret sharing in the leakage oracle.
. Let \((s_0, s_1)\) and \((\hat{s}_0, \hat{s}_1)\) be, respectively, a secret sharing of \(m_b\) and of the all-zero string under \(\varSigma _2\). Consider the following reduction trying to distinguish a secret sharing of \(s_1\) and a secret sharing of \(\hat{s}_1\) under \(\varSigma _1\), where we call \(s_1^{\mathsf {target}}\) the target secret sharing in the leakage oracle.

- 1.
Sample
and run the experiment as in \(\mathbf {H}_3\) with the adversary \(\mathsf {A}\); upon receiving each leakage function, hard-code into it the shares of \(\hat{s}_0\) and forward it to the leakage oracle.
- 2.
Eventually, the adversary sends its tampering query \((\mathcal {T}, \mathcal {B}, f)\).
- 3.
Sample \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) as in \(\mathbf {H}_2\). In particular, recall that we can sample these share as a function of just the shares \((s_{0,\beta })_{\beta \in \mathcal {T} _0^*}\) and the leakage. Then, set
$$ s_{0, \beta }' := {\left\{ \begin{array}{ll} \hat{s}_{0, \beta } &{} \text { if } \beta \in \mathcal {T} _0^*,\\ s_{0, \beta }^* &{} \text { if } \beta \in \mathcal {T} _1^*. \end{array}\right. } $$Note that this is well defined since \(\mathcal {T} _0^* \cap \mathcal {T} _1^* = \emptyset \).
- 4.
For all \(i \in [t]\), construct the leakage function \(g_i\) that, given as input \((s_{1, \beta }^{\mathsf {target}})_{\beta \in \mathcal {B} _i}\), computes \((\tilde{s}_{0, \beta }, \tilde{s}_{1, \beta })_{\beta \in \mathcal {B} _i} = f_j((s_{0, \beta }', s_{1, \beta }^{\mathsf {target}})_{\beta \in \mathcal {B} _i})\) and outputs \((\tilde{s}_{0, \beta })_{\beta \in \mathcal {B} _i}\). Send \((\mathcal {B}, (g_1, \ldots , g_t))\) to the leakage oracle obtaining values \((\tilde{s}_{0, \beta })_{\beta \in \mathcal {T} ^*}\).
- 5.
Sample the values \((s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}\) as in \(\mathbf {H}_3\) using \((\tilde{s}_{0, \beta })_{\beta \in \mathcal {T} ^*}\) and the leakage.
- 6.
For all \(j \in \mathcal {T} _0\), compute \((\tilde{s}_{0, \beta }, \tilde{s}_{1, \beta })_{\beta \in \mathcal {B} _{\xi (j)}} = f_j((s_{0, \beta }', s_{1, \beta }^*)_{\beta \in \mathcal {B} _{\xi (j)}})\); then, compute \(s_0= \mathsf {Rec}_0((\tilde{s}_{0, \beta })_{\beta \in \mathcal {T}})\) and \(s_1= \mathsf {Rec}_1((\tilde{s}_{1, \beta })_{\beta \in \mathcal {T} _{|_{k_1}}})\) and let \(\tilde{m}= \mathsf {Rec}_2(s_0, s_1)\). In case \(\tilde{m}\in \{m_0,m_1\}\) return \(\diamond \) to \(\mathsf {A}\), and else return \(\tilde{m}\) to \(\mathsf {A}\).
- 7.
Output the same as \(\mathsf {A}\).
For the analysis, note that the reduction is perfect. In particular, the reduction perfectly simulates \(\mathbf {H}_3\) when \((s_{1, i}^{\mathsf {target}})_{i \in [n]}\) is a secret sharing of \(s_1\) and perfectly simulates \(\mathbf {H}_4\) when \((s_{1, i}^{\mathsf {target}})_{i \in [n]}\) is a secret sharing of \(\hat{s}_1\). Moreover, the leakage requested by the adversary \(\mathsf {A}\) is forwarded to the leakage oracle of \(\hat{\mathsf {A}}\) and perfectly simulated by it. Finally, the reduction obtains all the shares \((\tilde{s}_{0, \beta })_{\beta \in \mathcal {T} ^*}\), and thus it is able to both compute \(\tilde{s}_0\) and sample the values \((s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}\).
Let us now analyze the admissibility of \(\hat{\mathsf {A}}\). The only leakage performed by \(\hat{\mathsf {A}}\) is the one requested by \(\mathsf {A}\) in step 1 plus the one needed in order to get the values \((\tilde{s}_{0, \beta })_{\beta \in \mathcal {T} ^*}\) in step 4; summing up, the overall leakage performed by \(\hat{\mathsf {A}}\) is:
where the last inequality follows by the fact that \(\log |\mathcal {S}_{0, i}| \le \sigma _0\) for all \(i \in [n]\). Therefore, we can conclude that \(\hat{\mathsf {A}}\) is \((k_1- 1, \ell + n\sigma _0)\)-BLA. \(\square \)
Final Step. Finally, we show:
Lemma 6
 .
.
Proof
By reduction to non-malleability of \(\varSigma _2\). Suppose by contradiction that there exist messages \(m_0,m_1\) and an adversary \(\mathsf {A}\) telling apart  and
and  with advantage more than
with advantage more than  . Fix values \((\hat{s}_i)_{i \in [n]} = ((\hat{s}_{0, i}, \hat{s}_{1, i})_{i \in [n]})\) and \((s_0, s_1)\) being either a (2-out-of-2) secret sharing of \(m_0\) or of \(m_1\). Consider the following reduction:
. Fix values \((\hat{s}_i)_{i \in [n]} = ((\hat{s}_{0, i}, \hat{s}_{1, i})_{i \in [n]})\) and \((s_0, s_1)\) being either a (2-out-of-2) secret sharing of \(m_0\) or of \(m_1\). Consider the following reduction:

- 1.
Run the experiment as in \(\mathbf {H}_4\) with the adversary \(\mathsf {A}\); upon receiving each leakage function, answer using the values \((\hat{s}_i)_{i \in [n]}\).
- 2.
Upon input the tampering query \((\mathcal {T}, \mathcal {B}, f)\), construct the following two tampering functions:
Function \(f_0\), upon input \(s_0\), samples \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) as in \(\mathbf {H}_2\); notice that the reduction knows all the information needed to re-sample the shares, as in particular it samples \((s_{0,\beta })_{\beta \in [n]}\) and simulates the leakage. Then, \(f_0\) computes \((\tilde{s}_{0, j}, \tilde{s}_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}} = f_{\xi (\beta )}((\hat{s}_{0, j}, \hat{s}_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}})\) for all \(\beta \in \mathcal {T} _0\) and \((\tilde{s}_{0, j}, \tilde{s}_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}} = f_{\xi (\beta )}((s_{0, j}^*, \hat{s}_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}})\) for all \(\beta \in \mathcal {T} _1\) and outputs \(\tilde{s}_0= \mathsf {Rec}_0( (\tilde{s}_{0, \beta })_{\beta \in \mathcal {T}} )\).
Function \(f_1\), upon input \(s_1\), samples \((s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}\) as in \(\mathbf {H}_3\). Then, \(f_{1}\) computes \((\tilde{s}_{0, j}, \tilde{s}_{1, j})_{j \in \mathcal {B} _{\xi (\beta )}} = f_{\xi (\beta )}((\hat{s}_{0, j}, s_{1, j}^*)_{j \in \mathcal {B} _{\xi (\beta )}})\) for all \(\beta \in \mathcal {T} _0\) and outputs \(\tilde{s}_1= \mathsf {Rec}_1( (\tilde{s}_{1, \beta })_{\beta \in \mathcal {T}} )\).
- 3.
Send \((f_0, f_1)\) to the tampering oracle, receiving an answer \(\tilde{m}\).
- 4.
Return \(\tilde{m}\) to \(\mathsf {A}\) and output the same as \(\mathsf {A}\).
For the analysis, note that the reduction is perfect. In particular, shares \((s_{0, \beta }^*)_{\beta \in \mathcal {T} _1^*}\) and \((s_{1, \beta }^*)_{\beta \in \mathcal {T} _0^*}\) are computed using \(s_0\) and \(s_1\) respectively; moreover, both \(\tilde{s}_0\) and \(\tilde{s}_1\) are computed as in experiment \(\mathbf {H}_4\) and thus the tampering query is perfectly simulated. Finally, the leakage is computed using the fake shares \((\hat{s}_i)_{i \in [n]}\) as in \(\mathbf {H}_4\) and thus, once again, perfectly simulated. The lemma follows.
Proof
(Theorem 4). Follows by the above lemmas and the triangular inequality:

\(\square \)
5.4 Instantiation
Using a previous construction of bounded leakage-resilient secret sharing scheme against joint leakage under adaptive partitioning, we obtain the following:
Corollary 3
For every  , every \(k\in O(\sqrt{\log n})\), and every access structure \(\mathcal {A} \) over \(n\) parties that can be described by a polynomial-size monotone span program for which authorized sets have size greater than \(k\), there exists a
, every \(k\in O(\sqrt{\log n})\), and every access structure \(\mathcal {A} \) over \(n\) parties that can be described by a polynomial-size monotone span program for which authorized sets have size greater than \(k\), there exists a  -BLR-NMSS with message length
-BLR-NMSS with message length  realizing \(\mathcal {A} \) under semi-adaptive partitioning.
realizing \(\mathcal {A} \) under semi-adaptive partitioning.
Proof
By Theorem 4, we need to instantiate \(\varSigma _{0}\), \(\varSigma _1\), and \(\varSigma _2\). Using
[26, Thm. 1] and
[26, Cor. 2], we can take  , \(k\in O(\log n)\), and thus \(k_1\in O(\sqrt{\log n})\),
, \(k\in O(\log n)\), and thus \(k_1\in O(\sqrt{\log n})\),  and any \(\ell _0,\ell _1> 0\). As for \(\varSigma _2\), we can take the split-state non-malleable code in
[27, Thm. 1.12], which achieves error
and any \(\ell _0,\ell _1> 0\). As for \(\varSigma _2\), we can take the split-state non-malleable code in
[27, Thm. 1.12], which achieves error  . \(\square \)
. \(\square \)
6 Applications
6.1 Lower Bounds for Non-malleable Secret Sharing
Combining our result from Theorem 3 with the lower bound of Nielsen and Simkin [29], we obtain a lower bound on the share size and randomness complexity of non-malleable secret sharing schemes. In particular, we obtain the following:
Corollary 4
Any \(\tau \)-out-of-\(n\) \((1, 1, \epsilon )\)-NMSS must satisfy
where \(\widehat{\tau }\) is the number of shares needed to reconstruct the full vector of shares and \(\sigma \) is the bit-length of each share.
Observe that \(\widehat{\tau }\) is a simplified notion of entropy. If \(\tau = \widehat{\tau }\), then any authorized set can reconstruct all remaining shares, meaning that those shares have no entropy left.
6.2 Bounded-Time Non-malleability
Here, we revisit the compiler from Ostrovsky et al. [30] in the setting of non-malleable secret sharing against joint tampering.
The basic idea is as follows. First, we commit to the message \(m\) using random coins \(r\), thus obtaining a cryptographic commitment \(c\). Then, we secret share the string \(m||r\) using an auxiliary secret sharing scheme \(\varSigma \), thus obtaining shares \(s_1,\ldots ,s_n\). The final share of the i-th party is set to be \(s^*_i = (c,s_i)\). Given an authorized set \(\mathcal {I} \), the reconstruction first checks that all commitments in \(s^*_\mathcal {I} \) are equal, and then uses \(s_\mathcal {I} \) to recover \(m||r\), and verifies consistency of the commitments. If any of these checks fails, it outputs \(\bot \); else, it returns \(m\).
The original analysis by Ostrovsky et al. shows that if \(\varSigma \) is a 2-out-of-2 secret sharing that is bounded leakage-resilient, statistically one-time non-malleable, and further satisfies additional non-standard properties, then \(\varSigma ^*\) is continuously non-malleable. In a follow up work, Brian et al. [11] proved that the additional properties on \(\varSigma \) can be avoided if one assumes that \(\varSigma \) satisfies a stronger form of leakage resilience known as noisy leakage resilience, and further extended the original analysis to any value \(n\ge 2\) and for arbitrary access structures.
Both the proofs in [11, 30] are for the setting of independent tampering. The theorem below says that the same construction works also in the case of joint \(p\)-time tampering under selective/semi-adaptive partitioning as long as \(\varSigma \) tolerates joint bounded leakage resilience, where there is a natural trade off between the leakage bound and the number of tampering queries. The main idea behind the proof is to reduce the security of \(\varSigma ^*\) to that of \(\varSigma \), where the bounded leakage is used to simulate multiple tampering queries. The main difference with the original proof is that we need a small leakage for each tampering query, and thus the analysis only works in case the number of tampering queries is a priori bounded. Moreover, in the case of semi-adaptive partitioning, we need to make sure that the leakage performed by the reduction does not violate condition (i) in the definition of semi-adaptive admissibility (cf. Definition 7); intuitively, the latter holds thanks to the fact that the tampering queries chosen by the attacker must satisfy condition (ii) in Definition 7. We refer to the full version of the paper for the details [10].
Theorem 5
Let \(n\in \mathbb {N}\) and let \(\mathcal {A}\) be an arbitrary access structure for \(n\) parties without singletons. Assume that:
-
1.
\(\mathsf {Commit}\) is a perfectly binding and computationally hiding non-interactive commitment;
-
2.
\(\varSigma \) is a \(n\)-party \(k\)-joint \(\ell \)-bounded leakage-resilient one-time non-malleable secret sharing scheme realizing access structure \(\mathcal {A}\) against joint semi-adaptive (resp., selective) partitioning with information-theoretic security and with message space \(\mathcal {M} \) such that
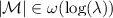 .
.
Then, the secret sharing scheme \(\varSigma ^*\) described in Fig. 2 is a \(n\)-party \(k\)-joint \(p\)-time non-malleable secret sharing scheme realizing access structure \(\mathcal {A}\) against joint semi-adaptive (resp., selective) partitioning with computational security, as long as \(\ell = p\cdot (\gamma + n) + 1\), where \(\gamma = \log |\mathcal {C} |\) is the size of a commitment.
7 Conclusions
We presented new constructions of non-malleable secret sharing schemes against joint tampering with the shares, both in the setting of selective and adaptive partitioning.
Our constructions for selective partitioning are for threshold access structures and tolerate joint tampering with maximal subsets of unauthorized parties, i.e., of size equal to the privacy threshold. Our construction for adaptive partitioning is for general access structures, but tolerates joint tampering with much smaller subsets of size \(k\in O(\sqrt{\log n})\) (where \(n\) is the number of parties) and under some restrictions on the way the partitions are determined by the attacker. Removing the latter limitation is an intriguing open question.
The above results hold for any a priori fixed bound \(p>0\) on the number of tampering queries, and under computational assumptions. We leave it as an open problem to design continuously non-malleable (i.e., for  being an arbitrary polynomial in the security parameter) secret sharing schemes tolerating joint tampering under selective/adaptive partitioning.
being an arbitrary polynomial in the security parameter) secret sharing schemes tolerating joint tampering under selective/adaptive partitioning.
Another interesting question would be to improve the rate, i.e., the ratio between message size and maximal size of a share, for non-malleable secret sharing against joint tampering. Note that, in the computational setting, it is always possible to boost the rate as follows: First, share the secret key  of an authenticated symmetric encryption using a secret sharing scheme with poor rate, obtaining shares \(s_1,\ldots ,s_n\); hence, encrypt the message \(m\) using \(\kappa \), obtaining a ciphertext \(c\), and define the final i-th share to be \(s^*_i = (c,s_i)\). Such a rate-optimizing compiler was originally analyzed in the setting of non-malleable codes
[1, 16, 19], and more recently in the setting of non-malleable secret sharing against independent tampering
[21]. While this transformation may be proven secure even in the setting of joint tampering with the shares, it yields a rate asymptotically approaching one, which is still far from the optimal share size of \(O(\mu /n)\)
[25] (where \(\mu \) is the message size).
of an authenticated symmetric encryption using a secret sharing scheme with poor rate, obtaining shares \(s_1,\ldots ,s_n\); hence, encrypt the message \(m\) using \(\kappa \), obtaining a ciphertext \(c\), and define the final i-th share to be \(s^*_i = (c,s_i)\). Such a rate-optimizing compiler was originally analyzed in the setting of non-malleable codes
[1, 16, 19], and more recently in the setting of non-malleable secret sharing against independent tampering
[21]. While this transformation may be proven secure even in the setting of joint tampering with the shares, it yields a rate asymptotically approaching one, which is still far from the optimal share size of \(O(\mu /n)\)
[25] (where \(\mu \) is the message size).
Notes
- 1.
This a sequence of non-overlapping subsets \(\mathcal {B} _1,\ldots ,\mathcal {B} _{t}\) covering \([n]\), such that each \(\mathcal {B} _i\) has size at most \(k\).
- 2.
Here, we inherit a few restrictions from [23]. Namely, the attacker is allowed to tamper jointly using a partition of a minimal reconstruction set in subsets of different sizes. We can remove these restrictions relying on the scheme from [24], which however only works for the \(n\)-out-of-\(n\) access structure.
- 3.
This means privacy holds with threshold \(\tau \), but all of the \(n\) shares are required to reconstruct the message.
- 4.
We assume that the reconstruction algorithm outputs \(\bot \) whenever one of the input shares is set to \(\bot \). As we will see later, this is without loss of generality.
- 5.
This means that the choice of the next leakage query depends on the overall leakage so far.
- 6.
In fact, the two subsets do not need to be fixed a priori.
- 7.
Here is where we use the restriction that the reconstruction set \(\mathcal {T} \) must be minimal and contain at least one share from each subset \(\mathcal {B} _i\); otherwise, we cannot argue that the output of the tampering query is \(\bot \), and thus independent of the target.
- 8.
The construction in [23, Thm. 4] actually only achieves security against joint tampering within a partition \(\mathcal {B} \) of the reconstruction set \(\mathcal {T} \) (rather than the entire set \([n]\)). Accordingly, in this case we can only tolerate joint leakage from the shares within the same partition \(\mathcal {B} \).
- 9.
We thank Ashutosh Kumar for pointing out to us that independence given the leakage does not necessarily hold in the case of fully adaptive (rather than semi-adaptive) partitioning.
References
Aggarwal, D., Agrawal, S., Gupta, D., Maji, H.K., Pandey, O., Prabhakaran, M.: Optimal computational split-state non-malleable codes. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part II. LNCS, vol. 9563, pp. 393–417. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_15
Aggarwal, D., et al.: Stronger leakage-resilient and non-malleable secret sharing schemes for general access structures. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 510–539. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_18
Aggarwal, D., Dodis, Y., Kazana, T., Obremski, M.: Non-malleable reductions and applications. In: Servedio, R.A., Rubinfeld, R. (eds.) 47th ACM STOC, pp. 459–468. ACM Press, June 2015
Aggarwal, D., Döttling, N., Nielsen, J.B., Obremski, M., Purwanto, E.: Continuous non-malleable codes in the 8-split-state model. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 531–561. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_18
Aggarwal, D., Dziembowski, S., Kazana, T., Obremski, M.: Leakage-resilient non-malleable codes. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 398–426. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_17
Aggarwal, D., Kazana, T., Obremski, M.: Inception makes non-malleable codes stronger. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part II. LNCS, vol. 10678, pp. 319–343. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_10
Aggarwal, D., Obremski, M.: A constant-rate non-malleable code in the split-state model. Cryptology ePrint Archive, Report 2019/1299 (2019). https://eprint.iacr.org/2019/1299
Badrinarayanan, S., Srinivasan, A.: Revisiting non-malleable secret sharing. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 593–622. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_20
Blakley, G.R.: Safeguarding cryptographic keys. In: Proceedings of AFIPS 1979 National Computer Conference, vol. 48, pp. 313–317 (1979)
Brian, G., Faonio, A., Obremski, M., Simkin, M., Venturi, D.: Non-malleable secret sharing against bounded joint-tampering attacks in the plain model. Cryptology ePrint Archive, Report 2020/725 (2020). https://eprint.iacr.org/2020/725
Brian, G., Faonio, A., Venturi, D.: Continuously non-malleable secret sharing for general access structures. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019, Part II. LNCS, vol. 11892, pp. 211–232. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36033-7_8
Carpentieri, M., De Santis, A., Vaccaro, U.: Size of shares and probability of cheating in threshold schemes. In: Helleseth, T. (ed.) EUROCRYPT 1993. LNCS, vol. 765, pp. 118–125. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48285-7_10
Chattopadhyay, E., Goyal, V., Li, X.: Non-malleable extractors and codes, with their many tampered extensions. In: Wichs, D., Mansour, Y. (eds.) 48th ACM STOC, pp. 285–298. ACM Press, June 2016
Chattopadhyay, E., Li, X.: Non-malleable extractors and codes for composition of tampering, interleaved tampering and more. Cryptology ePrint Archive, Report 2018/1069 (2018). https://eprint.iacr.org/2018/1069
Cheraghchi, M., Guruswami, V.: Non-malleable coding against bit-wise and split-state tampering. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 440–464. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_19
Coretti, S., Faonio, A., Venturi, D.: Rate-optimizing compilers for continuously non-malleable codes. In: Deng, R.H., Gauthier-Umaña, V., Ochoa, M., Yung, M. (eds.) ACNS 2019. LNCS, vol. 11464, pp. 3–23. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-21568-2_1
Dziembowski, S., Kazana, T., Obremski, M.: Non-malleable codes from two-source extractors. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 239–257. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_14
Dziembowski, S., Pietrzak, K.: Intrusion-resilient secret sharing. In: 48th FOCS, pp. 227–237. IEEE Computer Society Press, October 2007
Dziembowski, S., Pietrzak, K., Wichs, D.: Non-malleable codes. In: Yao, A.C.C. (ed.) ICS 2010, pp. 434–452. Tsinghua University Press, January 2010
Faonio, A., Nielsen, J.B., Simkin, M., Venturi, D.: Continuously non-malleable codes with split-state refresh. In: Preneel, B., Vercauteren, F. (eds.) ACNS 2018. LNCS, vol. 10892, pp. 121–139. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93387-0_7
Faonio, A., Venturi, D.: Non-malleable secret sharing in the computational setting: adaptive tampering, noisy-leakage resilience, and improved rate. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 448–479. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_16
Faust, S., Mukherjee, P., Nielsen, J.B., Venturi, D.: Continuous non-malleable codes. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 465–488. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_20
Goyal, V., Kumar, A.: Non-malleable secret sharing. In: Diakonikolas, I., Kempe, D., Henzinger, M. (eds.) 50th ACM STOC, pp. 685–698. ACM Press, June 2018
Goyal, V., Kumar, A.: Non-malleable secret sharing for general access structures. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part I. LNCS, vol. 10991, pp. 501–530. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_17
Krawczyk, H.: Secret sharing made short. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 136–146. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_12
Kumar, A., Meka, R., Sahai, A.: Leakage-resilient secret sharing against colluding parties. In: Zuckerman, D. (ed.) 60th FOCS, pp. 636–660. IEEE Computer Society Press, November 2019
Li, X.: Improved non-malleable extractors, non-malleable codes and independent source extractors. In: Hatami, H., McKenzie, P., King, V. (eds.) 49th ACM STOC, pp. 1144–1156. ACM Press, June 2017
Liu, F.-H., Lysyanskaya, A.: Tamper and leakage resilience in the split-state model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 517–532. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_30
Nielsen, J.B., Simkin, M.: Lower bounds for leakage-resilient secret sharing. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part I. LNCS, vol. 12105, pp. 556–577. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45721-1_20
Ostrovsky, R., Persiano, G., Venturi, D., Visconti, I.: Continuously non-malleable codes in the split-state model from minimal assumptions. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part III. LNCS, vol. 10993, pp. 608–639. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_21
Rabin, T., Ben-Or, M.: Verifiable secret sharing and multiparty protocols with honest majority (extended abstract). In: 21st ACM STOC, pp. 73–85. ACM Press, May 1989
Shamir, A.: How to share a secret. Commun. Assoc. Comput. Mach. 22(11), 612–613 (1979)
Srinivasan, A., Vasudevan, P.N.: Leakage resilient secret sharing and applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 480–509. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_17
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Brian, G., Faonio, A., Obremski, M., Simkin, M., Venturi, D. (2020). Non-malleable Secret Sharing Against Bounded Joint-Tampering Attacks in the Plain Model. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12172. Springer, Cham. https://doi.org/10.1007/978-3-030-56877-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-56877-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56876-4
Online ISBN: 978-3-030-56877-1
eBook Packages: Computer ScienceComputer Science (R0)





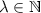 , all messages
, all messages 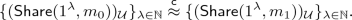
 .
. times, and in an adaptive fashion.
times, and in an adaptive fashion. and all
and all 

 , and for all
, and for all 

 . We write
. We write 


 .
. .
. ,
,  , and
, and  . Then set
. Then set  . In order to prove that this hybrid experiment is
. In order to prove that this hybrid experiment is  and
and 
 and run the experiment as in
and run the experiment as in 
 and run the experiment as in
and run the experiment as in 

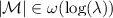 .
.