Abstract
A two-party fair coin-tossing protocol guarantees output delivery to the honest party even when the other party aborts during the protocol execution. Cleve (STOC–1986) demonstrated that a computationally bounded fail-stop adversary could alter the output distribution of the honest party by (roughly) 1/r (in the statistical distance) in an r-message coin-tossing protocol. An optimal fair coin-tossing protocol ensures that no adversary can alter the output distribution beyond 1/r.
In a seminal result, Moran, Naor, and Segev (TCC–2009) constructed the first optimal fair coin-tossing protocol using (unfair) oblivious transfer protocols. Whether the existence of oblivious transfer protocols is a necessary hardness of computation assumption for optimal fair coin-tossing remains among the most fundamental open problems in theoretical cryptography. The results of Impagliazzo and Luby (FOCS–1989) and Cleve and Impagliazzo (1993) prove that optimal fair coin-tossing implies the necessity of one-way functions’ existence; a significantly weaker hardness of computation assumption compared to the existence of secure oblivious transfer protocols. However, the sufficiency of the existence of one-way functions is not known.
Towards this research endeavor, our work proves a black-box separation of optimal fair coin-tossing from the existence of one-way functions. That is, the black-box use of one-way functions cannot enable optimal fair coin-tossing. Following the standard Impagliazzo and Rudich (STOC–1989) approach of proving black-box separations, our work considers any r-message fair coin-tossing protocol in the random oracle model where the parties have unbounded computational power. We demonstrate a fail-stop attack strategy for one of the parties to alter the honest party’s output distribution by \(1/\sqrt{r}\) by making polynomially-many additional queries to the random oracle. As a consequence, our result proves that the r-message coin-tossing protocol of Blum (COMPCON–1982) and Cleve (STOC–1986), which uses one-way functions in a black-box manner, is the best possible protocol because an adversary cannot change the honest party’s output distribution by more than \(1/\sqrt{r}\).
Several previous works, for example, Dachman–Soled, Lindell, Mahmoody, and Malkin (TCC–2011), Haitner, Omri, and Zarosim (TCC–2013), and Dachman–Soled, Mahmoody, and Malkin (TCC–2014), made partial progress on proving this black-box separation assuming some restrictions on the coin-tossing protocol. Our work diverges significantly from these previous approaches to prove this black-box separation in its full generality. The starting point is the recently introduced potential-based inductive proof techniques for demonstrating large gaps in martingales in the information-theoretic plain model. Our technical contribution lies in identifying a global invariant of communication protocols in the random oracle model that enables the extension of this technique to the random oracle model.
H. K. Maji and M. Wang—The research effort is supported in part by an NSF CRII Award CNS–1566499, an NSF SMALL Award CNS–1618822, the IARPA HECTOR project, MITRE Innovation Program Academic Cybersecurity Research Award, a Purdue Research Foundation (PRF) Award, and The Center for Science of Information, an NSF Science and Technology Center, Cooperative Agreement CCF–0939370.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Ideally, in any cryptographic task, one would like to ensure that the honest parties receive their output when adversarial parties refuse to participate any further. Ensuring guaranteed output delivery, a.k.a., fair computation, is challenging even for fundamental cryptographic primitives like two-party coin-tossing. A two-party fair coin-tossing protocol assures that the honest party receives her output bit even when the adversary aborts during the protocol execution. Cleve [24] demonstrated that, even for computationally bounded parties, a fail-stop adversaryFootnote 1 could alter the output distribution by 1/r (in the statistical distance) in any r-message interactive protocols. Intuitively, any r-message interactive protocol is 1/r-insecure. An optimal r-message two-party fair coin-tossing protocol ensures that it is only 1/r-insecure.
In a seminal result, nearly three decades after the introduction of optimal fair coin-tossing protocols, Moran, Naor, and Segev [88] presented the first optimal coin-tossing protocol construction based on the existence of (unfair) secure protocols for the oblivious transfer functionality.Footnote 2 Shortly after that, in a sequence of exciting results, several optimal/near-optimal fair protocols were constructed for diverse two-party and multi-party functionalities [3,4,5,6, 13, 14, 23, 58, 59, 64, 86]. However, each of these protocols assumes the existence of secure protocols for oblivious transfer as well.
In theoretical cryptography, a primary guiding principle of research is to realize a cryptographic primitive securely using the minimal computational hardness assumption. Consequently, the following fundamental question arises naturally.
For example, the results of Impagliazzo and Luby [74] and Cleve and Impagliazzo [25] prove that optimal fair coin-tossing implies that the existence of one-way functions is necessary; a significantly weaker hardness of computation assumption compared to the existence of secure oblivious transfer protocols. However, it is unclear whether one-way functions can help realize optimal fair coin-tossing or not. For instance, historically, for a long time, one-way functions were not known to imply several fundamental primitives like pseudorandom generators [66, 67, 73], pseudorandom functions [54, 55], pseudorandom permutations [81], statistically binding commitment [90], statistically hiding commitment [63, 92], zero-knowledge proofs [57], and digital signatures [93, 97]; eventually, however, secure constructions were discovered. On the other hand, cryptographic primitives like collision-resistant hash functions, key-agreement schemes, public-key encryption, trapdoor primitives, and oblivious transfer protocols do not have constructions based on the existence of one-way functions. Therefore, is it just that we have not yet been able to construct optimal fair coin-tossing protocols securely from one-way functions, or are there inherent barriers to such constructions?
Impagliazzo [72] introduced five possible worlds and their implications for computer science. In Minicrypt, one-way functions exist; however, public-key cryptography is impossible. In Cryptomania, complex public-key cryptographic primitives like key-agreement and oblivious transfer are feasible.
Among several possible approaches, a prominent technique to address the question above is to study it via the lens of black-box separations, as introduced by Impagliazzo and Rudich [75]. Suppose one “black-box separates the cryptographic primitive Q from another cryptographic primitive P”. Then, one interprets this result as indicating that the primitive P is unlikely to facilitate the secure construction of Q using black-box constructions.Footnote 3 Consequently, to reinforce the necessity of the existence of oblivious transfer protocols for optimal fair coin-tossing, one needs to provide black-box separation of optimal fair coin-tossing protocols from computational hardness assumptions that are weaker than the existence of oblivious transfer protocols; for example, the existence of one-way functions [74, 75].
Our Results. In this work, we prove the (fully) black-box separation [96] of optimal two-party fair coin-tossing protocol from the existence of one-way functions. In particular, we show that any r-message two-party coin-tossing protocol in the random oracle model, where parties have unbounded computational power, is \(1/\sqrt{r}\)-insecure. In turn, this result settles in the positive the longstanding open problem of determining whether the coin-tossing protocol of Blum [16] and Cleve [24] achieves the highest security while using one-way functions in a black-box manner.
Our proof relies on a potential-based argument that proceeds by identifying a global invariant (see Claim 4.3) across coin-tossing protocols in the random oracle model to guide the design of good fail-stop adversarial attacks. As a significant departure from previous approaches [29, 30], our analysis handles the entire sequence of curious random oracle query-answer pairs as a single instance of information exposure.
1.1 Our Contributions
Before we proceed to present a high-level informal summary of our results, we need a minimalist definition of two-party coin-tossing protocols in the random oracle model that are secure against fail-stop adversaries. An \((r,n,X_0)\)-coin-tossing protocol is a two-party interactive protocol with final output \(\in {\{0,1\}} \), and parties have oracle access to a random oracleFootnote 4 such that the following conditions are satisfied.
-
1.
Alice and Bob exchange a total of r messages (of arbitrary length) during the protocol.Footnote 5
-
2.
The oracle query complexity of both Alice and Bob is (at most) n in every execution of the protocol.
-
3.
At the end of the protocol, parties always agree on the output \(\in {\{0,1\}} \). Furthermore, the expectation of the output over all possible protocol executions is \(X_0\in [0,1]\).
-
4.
We consider only fail-stop adversarial strategies. If one party aborts during the protocol execution, then the honest party outputs a defense coin \(\in {\{0,1\}} \) based on her view without making additional queries to the random oracle. Such protocols are called instant protocols, and one may assume any coin-tossing protocol to be instant without loss of generality [29].Footnote 6
We emphasize that there are additional subtleties in defining coin-tossing protocols in the random oracle model, and Sect. 2.3 addresses them. In this section, we rely on a minimalist definition that suffices to introduce our results. Our main technical result is the following consequence for any \((r,n,X_0)\)-coin-tossing protocol.
Informal Theorem 1
(Main Technical Result). There exists a universal constant \(c>0\) and a polynomial \(p(\cdot )\) such that the following holds. Let \(\pi \) be any \((r,n,X_0)\)-coin-tossing protocol in the information-theoretic random oracle model, where \(r,n\in \mathbb {N}\), and \(X_0\in (0,1)\). Then, there exists a fail-stop adversarial strategy for one of the parties to alter the expected output of the honest party by \(\ge c\cdot X_0(1-X_0) / \sqrt{r}\) and performs at most \(p(nr/X_0(1-X_0))\) additional queries to the random oracle.
We remark that \(X_0\) may be a function of r and n itself. For example, the expected output \(X_0\) may be an inverse polynomial of r.
This technical result directly yields the following (fully) black-box separation result using techniques in [75, 96].
Corollary 1
(Black-box Separation from One-way Functions). There exists a universal constant \(c>0\) such that the following holds. Let \(\pi \) be any r-message two-party protocol that uses any one-way function in a fully black-box manner. Suppose, at the end of the execution of \(\pi \), both parties agree on their output \(\in {\{0,1\}} \). Before the beginning of the protocol, let the expectation of their common output be \(X_0\in (0,1)\). Then, there is a fail-stop adversarial strategy for one of the parties to alter the honest party’s expected output by \(\ge c\cdot X_0(1-X_0) / \sqrt{r}\).
That is, optimal fair coin-tossing lies in Cryptomania. All our hardness of computation results extend to the multi-party fair computation of arbitrary functionalities, where parties have private inputs if the output of the functionality has entropy and honest parties are not in the majority.
We emphasize that the black-box separation extends to any primitive (and their exponentially-hard versions) that one can construct in a black-box manner from random oracles or ideal ciphers, which turn out to be closely related to random oracles [28, 70]. Furthermore, the impossibility result in the random oracle model implies black-box separations from other (more structured) cryptographic primitives (and their exponentially-hard versions) like regular one-way functions, one-way permutations, and collision-resistant hash functions as well. Although these primitives cannot be constructed from random oracles/ideal cipher in a black-box manner, using by-now well-establish techniques in this field (see, for example, [75]), the main technical result suffices to prove the separations from these structured primitives.
This black-box separation from one-way functions indicates that the two-party coin-tossing protocol of Blum [16] and Cleve [24], which uses one-way functions in a black-box manner and builds on the protocols of [7, 21], achieves the best possible security for any r-message protocol. Their protocol is \(1/\sqrt{r}\)-insecure, and any r-message protocol cannot have asymptotically better security by only using one-way functions in a black-box manner, thus resolving this fundamental question after over three decades.
1.2 Prior Related Works and Comparison
There is a vast literature of defining and constructing fair protocols for two-party and multi-party functionalities [2,3,4,5,6, 13, 14, 23, 58, 59, 64, 86]. In this paper, our emphasis is on the intersection of this literature with black-box separation results. The field of meta-reductions [1, 8, 10, 15, 19, 20, 22, 27, 31, 34, 38, 39, 41,42,43, 50, 65, 68, 89, 94, 95, 101, 105], which demonstrates similar hardness of computation results from computational hardness assumptions like falsifiable assumptions [91], is outside the scope of this work.
In a seminal result, Impagliazzo and Rudich [75] introduced the notion of black-box separation for cryptographic primitives. After that, there have been other works [9, 96] undertaking this nuanced task of precisely defining black-box separation and its subtle variations. Intuitively, separating a primitive Q from a primitive P indicates that attempts to secure realize Q solely on the black-box use of P are unlikely to succeed. Reingold, Trevisan, and Vadhan [96] highlighted the subtleties involved in defining black-box separations by delineating several variants of separations. In their terminology, this work pertains to a fully black-box separation where the construction uses P in a black-box manner, and the security reduction uses the adversary in a black-box manner as well. Since the inception of black-box separations in 1989, this research direction has been a fertile ground for highly influential research [12, 17, 18, 29, 30, 32, 36, 37, 40, 44,45,46,47,48,49, 51,52,53, 62, 69, 71, 75, 77, 80, 82,83,85, 87, 98, 99, 102, 103]. Among these results, in this paper, we elaborate on the hardness of computation results about fair computation protocols.
A recent work of Haitner, Nissim, Omri, Shaltiel, and Silbak [61] introduces the notion of the “computational essence of key-agreement”. Haitner, Makriyannis, and Omri [60], for any constant r, prove that r-message coin-tossing protocols imply key-agreement protocols, if they are less than \(1/\sqrt{r}\)-insecure. Observe that proving the implication that key-agreement protocol exists is a significantly stronger result as compared to demonstrating a black-box separation from key-agreement.Footnote 7 However, their contribution is incomparable to our result because it shows a stronger consequence for any constant r.
Among the related works in black-box separation, the most relevant to our problem are the following. Haitner, Omri, and Zarosim
[62], for input-less functionalities, lift the hardness of computation results in the information-theoretic plain model against semi-honest adversaries to the random oracle model, i.e., random oracles are useless. However, coin-tossing is trivial to realize securely against semi-honest adversaries,Footnote 8 and fail-stop adversarial strategies are not semi-honest. Dachman–Soled, Lindell, Mahmoody, and Malkin
[29] proved that the random oracle could be “compiled away” if the coin-tossing protocol has  messages. Therefore, the fail-stop adversarial strategy of Cleve and Impagliazzo
[25] in the information-theoretic plain model also succeeds against the two-party coin-tossing protocol in the random oracle model. Finally, Dachman–Soled, Mahmoody, and Malkin
[30] show a fail-stop adversarial strategy against a particular class of fair coin-tossing protocols, namely, function oblivious protocols. An exciting feature of this work is that the attack performed by the adversarial party does not proceed by compiling away the random oracle. Similar proof techniques were independently introduced by
[82, 83] to study the computational complexity of two-party secure deterministic function evaluations.
messages. Therefore, the fail-stop adversarial strategy of Cleve and Impagliazzo
[25] in the information-theoretic plain model also succeeds against the two-party coin-tossing protocol in the random oracle model. Finally, Dachman–Soled, Mahmoody, and Malkin
[30] show a fail-stop adversarial strategy against a particular class of fair coin-tossing protocols, namely, function oblivious protocols. An exciting feature of this work is that the attack performed by the adversarial party does not proceed by compiling away the random oracle. Similar proof techniques were independently introduced by
[82, 83] to study the computational complexity of two-party secure deterministic function evaluations.
Recently, there have been two works providing improvements to the fail-stop adversarial attacks of Cleve and Impagliazzo [25] in the information-theoretic plain model. These results proceed by induction on r and employ a potential argument to lower-bound the performance of the most devastating fail-stop adversarial strategy against a coin-tossing protocol. Khorasgani, Maji, and Mukherjee [78] generalize (and improve) the fail-stop attack of Cleve and Impagliazzo [25] to arbitrary \(X_0\in (0,1)\), even when \(X_0\) depends on r and tends to 0 or 1. Khorasgani, Maji, and Wang [79] decouple the number of messages r in a coin-tossing protocol and the number of defense updates d that the two parties perform. They show that a two-party coin-tossing protocol in the information-theoretic plain model is \(1/\sqrt{d}\)-insecure, independent of the number of messages r in the protocol.
This result [79] is a good starting point for our work because our curious fail-stop attacker shall perform additional queries to the random oracle; however, the parties do not update their defense coins during this information exposure. Unfortunately, their approach only applies to interactive protocols in the information-theoretic plain model. Our work identifies a global invariant for communication protocols that enables the extension of the approach of [79] to the random oracle model. Furthermore, we simplify the proof of their result as well.
2 Preliminaries
We use uppercase letters for random variables, (corresponding) lowercase letters for their values, and calligraphic letters for sets. For a joint distribution (A, B), A and B represent the marginal distributions, and \(A\times B\) represents the product distribution where one samples from the marginal distributions A and B independently. For a random variable A distributed over \(\varOmega \), the support of A, denoted by  , is the set
, is the set  For two random variables A and B distributed over a (discrete) sample space \(\varOmega \), their statistical distance is defined as
For two random variables A and B distributed over a (discrete) sample space \(\varOmega \), their statistical distance is defined as 
For a sequence \((X_1,X_2,\ldots )\), we use \(X_{\le i}\) to denote the joint distribution \((X_1,X_2,\ldots ,X_i)\). Similarly, for any \((x_1,x_2,\dotsc )\in \varOmega _1\times \varOmega _2\times \cdots \), we define \(x_{{\le i}}\,{:}{=} (x_1,x_2,\dotsc ,x_i)\in \varOmega _1\times \varOmega _2\times \cdots \times \varOmega _i\). Let \((M_1,M_2,\ldots ,M_r)\) be a joint distribution over sample space \(\varOmega _1\times \varOmega _2\times \cdots \times \varOmega _r\), such that for any \(i\in \{1,2,\ldots ,n\}\), \(M_i\) is a random variable over \(\varOmega _i\). A (real-valued) random variable \(X_i\) is said to be \(M_{\le i}\) measurable if there exists a deterministic function \(f:\varOmega _1\times \cdots \times \varOmega _i\rightarrow {\mathbb {R}} \) such that \(X_i=f(M_1,\ldots ,M_i)\). A random variable \(\tau :\varOmega _1\times \cdots \times \varOmega _r\rightarrow \{1,2,\ldots ,r\}\) is called a stopping time, if the random variable \(\mathbbm {1}_{\tau \le i}\) is \(M_{\le i}\) measurable, where \(\mathbbm {1}\) is the indicator function. For a more formal treatment of probability spaces, \(\sigma \)-algebras, filtrations, and martingales, refer to, for example, [100].
The following inequality shall be helpful for our proof.
Theorem 2
(Jensen’s inequality). If f is a multivariate convex function, then  , for all probability distributions X over the domain of f.
, for all probability distributions X over the domain of f.
2.1 Two-Party Interactive Protocols in the Random Oracle Model
Alice and Bob speak in alternate rounds. We denote the \(i^{th}\) message by \(M_i\). For every message \(M_i\), we denote Alice’s private view immediately after sending/receiving message \(M_i\) as \(V^\mathsf {A}_i\), which consists of Alice’s random tape \(R^\mathsf {A}\), her private queries, and the first i messages exchanged. We use \(V^\mathsf {A}_0\) to represent Alice’s private view before the protocol begins. Similarly, we define Bob’s private view \(V^\mathsf {B}_i\) and use \(R^\mathsf {B}\) to denote his private random tape.
Query Operator \({\mathcal {Q}} \). For any view V, we use \({\mathcal {Q}} (V)\) to denote the set of all queries contained in the view V.
2.2 Heavy Querier and the Augmented Protocol
For two-party protocols in the random oracle model, [12, 75] introduced a standard algorithm, namely, the heavy querier. In this paper, we shall use the following imported theorem.
Imported Theorem 3
(Guarantees of Heavy Querier [12, 83]). Let \(\pi \) be any two-party protocol between Alice and Bob in the random oracle model, in which both parties ask at most n queries. For all threshold \(\epsilon \in (0,1)\), there exists a public algorithm, called the heavy querier, who has access to the transcript between Alice and Bob. After receiving each message \(M_i\), the heavy querier performs a sequence of queries and obtain its corresponding answers from the random oracle. Let \(H_i\) denote the sequence of query-answer pairs asked by the heavy querier after receiving message \(M_i\). Let \(T_i\) be the union of the \(i^{th}\) message \(M_i\) and the \(i^{th}\) heavy querier message \(H_i\). The heavy querier guarantees that the following conditions are simultaneously satisfied.
-
\(\epsilon \) -Lightness. For any i, any
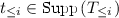 , and query \(q\notin {\mathcal {Q}} \left( h_{\le i}\right) \),
, and query \(q\notin {\mathcal {Q}} \left( h_{\le i}\right) \), 
-
\(n\epsilon \) -Dependence. Fix any i,

Intuitively, it states that on average, the statistical distance between (1) the joint distribution of Alice’s and Bob’s private view, and (2) the product of the marginal distributions of Alice’s private views and Bob’s private views is small.
-
 -Efficiency. The expected number of queries asked by the heavy querier is bounded by
-Efficiency. The expected number of queries asked by the heavy querier is bounded by 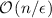 . Consequently, it has
. Consequently, it has 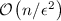 query complexity with probability (at least) \((1-\epsilon )\) by an averaging argument.
query complexity with probability (at least) \((1-\epsilon )\) by an averaging argument.
We refer to the protocol with the heavy querier’s messages attached as the augmented protocol. We call \(T_i\) the augmented message.
2.3 Coin-Tossing Protocol
We will prove our main result by induction on the message complexity of the protocol. Therefore, after any partial transcript \(t_{\le i}\), we will treat the remainder of the orginal protocol starting from the \((i+1)^{th}\) message, as a protocol of its own. Hence, it is helpful to define the coin-tossing protocol where, before the beginning of the protocol, Alice’s and Bob’s private views are already correlated with the random oracle. However, note that, in the augmented protocol, after each augmented message \(t_i\), the heavy querier has just ended. Thus, these correlations will satisfy Imported Theorem 3. Therefore, we need to define a general class of coin-tossing protocols in the random oracle model over which we shall perform our induction.
Definition 1
(\((\epsilon ,\varvec{\alpha },r,n,X_0)\)-Coin-Tossing). An interactive protocol \(\pi \) between Alice and Bob with random oracle \(O:{\{0,1\}} ^\lambda \rightarrow {\{0,1\}} ^\lambda \) is called an \((\epsilon ,\varvec{\alpha },r,n,X_0)\)-coin-tossing protocol if it satisfies the following.
-
Setup. There is an arbitrary set \({\mathcal {S}} \subseteq {\{0,1\}} ^\lambda \), which is publicly known, such that for all queries \(s\in {\mathcal {S}} \), the query answers O(s) are also publicly known. Let \(\varOmega ^\mathsf {A}\), \(\varOmega ^\mathsf {B}\), and \(\varOmega ^\mathsf {O}\) be the universes of Alice’s random tape, Bob’s random tape, and the random oracle, respectively. There are also publicly known sets \({\mathcal {A}} \subseteq \varOmega ^\mathsf {A}\times \varOmega ^\mathsf {O}\) and \({\mathcal {B}} \subseteq \varOmega ^\mathsf {B}\times \varOmega ^\mathsf {O}\). The random variables \(R^\mathsf {A}\), \(R^\mathsf {B}\), and O are sampled uniformly conditioned on that (1) \((R^\mathsf {A},O)\in {\mathcal {A}} \), (2) \((R^\mathsf {B},O)\in {\mathcal {B}} \), and (3) O is consistent with the publicly known answers at \({\mathcal {S}} \). Alice’s private view before the beginning of the protocol is a deterministic function of \(R^\mathsf {A}\) and O, which might contain private queries. Likewise, Bob’s private view is a deterministic function of \(R^\mathsf {B}\) and O.Footnote 9
-
Agreement. At the end of the protocol, both parties always agree on the output \(\in {\{0,1\}} \). Without loss of generality, we assume the output is concatenated to the last message in the protocol.Footnote 10
-
Defense preparation. At message \(M_i\), if Alice is supposed to speak, in addition to preparing the next-message \(M_i\), she will also prepare a defense coin for herself as well. If Bob decides to abort the next message, she shall not make any additional queries to the random oracle, and simply output the defense she has just prepared. [29, 30] introduced this constraint as the “instant construction.” They showed that, without loss of generality, one can assume this property for all the defense preparations except for the first defense (see Remark 2). We shall refer to this defense both as Alice’s \(i^{th}\) defense and also as her \((i+1)^{th}\) defense. Consequently, Alice’s defense for every i is well-defined. Bob’s defense is defined similarly. We assume the party who receives the first message has already prepared her defense for the first message before the protocol begins.
-
\(\epsilon \) -Lightness at Start. For any query \(q\notin {\mathcal {S}} \), the probability that Alice has asked query q before the protocol begins is upper bounded by \(\epsilon \in [0,1]\). Similarly, the probability that Bob has asked query q is at most \(\epsilon \).
-
\(\varvec{\alpha }\) -Dependence. For all \(i\in \{0,1,\ldots ,r\}\), Alice’s and Bob’s private views are \(\alpha _i\)-dependent on average immediate after the message \(T_i\). That is, the following condition is satisfied for every i.

-
r -Message complexity. The number of messages of this protocol is
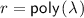 . We emphasize that the length of the message could be arbitrarily long.
. We emphasize that the length of the message could be arbitrarily long. -
n -Query complexity. For all possible complete executions of the protocol, the number of queries that Alice asks (including the queries asked before the protocol begins) is at most
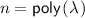 . This also includes the queries that are asked for the preparation of the defense coins. Likewise, Bob asks at most n queries as well.
. This also includes the queries that are asked for the preparation of the defense coins. Likewise, Bob asks at most n queries as well. -
\(X_0\) -Expected Output. The expectation of the output is \(X_0\in (0,1)\).
Remark 1
Let us justify the necessity of \(\varvec{\alpha }\)-dependence in the definition. We note that when heavy querier stops, Alice’s and Bob’s view are not necessarily close to the product of their respective marginal distributions.Footnote 11 However, to prove any meaningful bound on the susceptibility of this protocol, we have to treat \(\varvec{\alpha }\) as an additional error term. Therefore, we introduce this parameter in our definition. However, the introduction of this error shall not be a concern globally, because the heavy querier guarantees that over all possible executions this dependence is at most \(n\epsilon \) (on average), which we shall ensure to be sufficiently small.
Remark 2
We note that, after every heavy querier message, the remaining sub-protocol always satisfies the definition above. However, the original coin-tossing protocol might not meet these constraints. For example, consider a one-message protocol where Alice queries \(O(0^\lambda )\), and sends the parity of this string to Bob as the output. On the other hand, Bob also queries \(O(0^\lambda )\) and uses the parity of this string as his defense. This protocol is perfectly secure in the sense that no party can deviate the output of the protocol at all. However, the query \(0^\lambda \) is 1-heavy in Bob’s private view even before the protocol begins. Prior works [29, 30] rule out such protocols by banning Bob from making any queries when he prepares his first defense. In this paper, we consider protocols such that no queries are more than \(\epsilon \)-heavy when Bob prepares his first defense. We call this the \(\epsilon \)-lightness at start assumption. The set of protocols that prior works consider is identical to the set of protocols that satisfies 0-lightness at start assumption.
To justify our \(\epsilon \)-lightness at start assumption, we observe that one can always run a heavy querier with a threshold \(\epsilon \) before the beginning of the protocol as a pre-processing step. Note that this step fixes only a small part (of size  ) of the random oracle, and, hence, the random oracle continues to be an “idealized” one-way function. If this protocol is a black-box construction of a coin-tossing protocol with any one-way function, the choice of the one-way function should not change its expected output. Therefore, by running a heavy querier before the beginning of the protocol, it should not alter the expected output of the protocol. After this compilation step, all queries are \(\epsilon \)-light in Bob’s view before the protocol begins. Consequently, our inductive proof technique is applicable.
) of the random oracle, and, hence, the random oracle continues to be an “idealized” one-way function. If this protocol is a black-box construction of a coin-tossing protocol with any one-way function, the choice of the one-way function should not change its expected output. Therefore, by running a heavy querier before the beginning of the protocol, it should not alter the expected output of the protocol. After this compilation step, all queries are \(\epsilon \)-light in Bob’s view before the protocol begins. Consequently, our inductive proof technique is applicable.
Remark 3
Let us use the an example to further illustrate how we number Alice’s and Bob’s defense coins. Suppose Alice sends the first message in the protocol. Bob shall prepare his first defense coin even before the protocol begins. Alice, during her preparation of the first message, shall also prepare a defense coin as her first defense.
The second message in the protocol is sent by Bob. Since Alice is not speaking during this message preparation, her second defense coin remains identical to her first defense coin. Bob, on the other hand, shall update a new defense coin as his second defense during his preparation of the second message.
For the third message, Alice shall prepare a new third defense coin and Bob’s third defense coin is identical to his second defense coin. This process continues for r messages during the protocol execution.
Notation. Let \(X_i\) represent the expected output conditioned on the first i augmented messages, i.e., the random variable \(T_{\le i}\). Let \(D^\mathsf {A}_i\) be the expectation of Alice’s \(i^{th}\) defense coin conditioned on the first i augmented messages. Similarly, let \(D^\mathsf {B}_i\) be the expectation of Bob’s \(i^{th}\) defense coin conditioned on the first i augmented messages. (Refer to Definition 1 for the definition of \(i^{th}\) defense. Recall that, for both Alice and Bob, the \(i^{th}\) defense is defined for all \(i\in \{1,2,\ldots ,r\}\).) Note that random variables \(X_i,D^\mathsf {A}_i,\) and \(D^\mathsf {B}_i\) are all \(T_{\le i}\)-measurable.
3 Our Results
Given an \((\epsilon ,\varvec{\alpha },r,n,X_0)\)-coin-tossing protocol \(\pi \) and a stopping time \(\tau \), we define the following score function that captures the susceptibility of this protocol with respect to this particular stopping time.
Definition 2
Let \(\pi \) be an \((\epsilon ,\varvec{\alpha },r,n,X_0)\)-coin tossing protocol. Let \(\mathsf {P}\in \{\mathsf {A},\mathsf {B}\}\) be the party who sends the last message of the protocol. For any stopping time \(\tau \), define

We clarify that the binary operator \(\vee \) in the expression above represents the boolean OR operation, and not the “join” operator.
To provide additional perspectives to this definition, we make the following remarks similar to [79].
-
1.
Suppose Alice is about to send \((m_i^*,h_i^*)\) as the \(i^{th}\) message. In the information-theoretic plain model, prior works [25, 78] consider the gap between the expected output before and after this message. Intuitively, since Alice is sending this message, she could utilize this gap to attack Bob, because Bob’s defense cannot keep abreast of this new information. However, in the random oracle model, both parties are potentially vulnerable to this gap. This is due to the fact that the heavy querier message might also reveal information about Bob. For instance, it might reveal Bob’s commitments sent in previous messages using the random oracle as an idealized one-way function. Then, Alice’s defense cannot keep abreast of this new information either and thus Alice is potentially vulnerable.
-
2.
Due to the reasons above, for every message, we consider the potential deviations that both parties can cause by aborting appropriately. Suppose we are at transcript \(T_{\le i}=t_{\le i}^*\), which belongs to the stopping time, i.e., \(\tau =i\). And Alice sends the last message \((m_i^*,h_i^*)\). Naturally, Alice can abort without sending this message to Bob when she finds out her \(i^{th}\) message is \((m_i^*,h_i^*)\). This attack causes a deviation of
 . On the other hand, Bob can also attack by aborting when he receives Alice’s message \((m_i^*,h_i^*)\). This attack ensures a deviation of
. On the other hand, Bob can also attack by aborting when he receives Alice’s message \((m_i^*,h_i^*)\). This attack ensures a deviation of  . Note that for the \((i+1)^{th}\) message, Alice is not supposed to speak, her \((i+1)^{th}\) defense is exactly her \(i^{th}\) defense. Hence this deviation can be also written as
. Note that for the \((i+1)^{th}\) message, Alice is not supposed to speak, her \((i+1)^{th}\) defense is exactly her \(i^{th}\) defense. Hence this deviation can be also written as 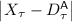 .
. -
3.
The above argument has a boundary case, which is the last message of the protocol. Suppose Alice sends the last message. Then, Bob, who receives this message, cannot abort anymore because the protocol has ended. Therefore, if our stopping time \(\tau =n\), the score function must exclude
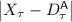 . This explains why we have the indicator function \(\mathbbm {1}\) in our score function.
. This explains why we have the indicator function \(\mathbbm {1}\) in our score function. -
4.
Lastly, we illustrate how one can translate this score function into a fail-stop attack strategy. Suppose we find a stopping time \(\tau ^*\) that witnesses a large score \(\mathsf {Score}(\pi ,\tau ^*)\). For Alice, we will partition the stopping time into two partitions depending on whether \(X_\tau \ge D^\mathsf {B}_\tau \) or not. Similarly, for Bob, we partition the stopping time into two partitions depending on whether \(X_\tau \ge D^\mathsf {A}_\tau \). These four attack strategies correspond to Alice or Bob deviating towards 0 or 1. And the summation of the deviations caused by these four attacks are exactly \(\mathsf {Score}(\pi ,\tau ^*)\). Hence, there must exist a fail-stop attack strategy for one of the parties that changes the honest party’s output distribution by \(\ge \frac{1}{4}\cdot \mathsf {Score}(\pi ,\tau ^*)\).
Given the definition of our score function, we are interested in finding the stopping time that witnesses the largest score. This motivates the following definition.
Definition 3
For any \((\epsilon ,\varvec{\alpha },r,n,X_0)\)-coin-tossing protocol \(\pi \), define
Intuitively, \(\mathsf {Opt}(\pi )\) represents the susceptibility of the protocol \(\pi \). Our main theorem states the following lower bound on this quantity.
Theorem 4
(Main Technical Result in the Random Oracle Model). For any \((\epsilon ,\varvec{\alpha },r,n,X_0)\)-coin-tossing protocol \(\pi \), the following holds.
where \(\varGamma _r\,{:}{=} \sqrt{\frac{\sqrt{2}-1}{r}}\), for all positive integers r. Furthermore, one needs to make an additional  queries to the random oracle (in expectation) to identify a stopping time \(\tau \) witnessing this lower bound.
queries to the random oracle (in expectation) to identify a stopping time \(\tau \) witnessing this lower bound.
We defer the proof to Sect. 4. In light of the remarks above, this theorem implies the following corollary.
Corollary 2
Let \(\pi \) be a coin-tossing protocol in the random oracle model that satisfies the \(\epsilon \)-lightness at start assumption (see Remark 2). Suppose \(\pi \) is an r-message protocol, and Alice and Bob ask at most n queries. The expected output of \(\pi \) is \(X_0\). Then, either Alice or Bob has a fail-stop attack strategy that deviates the honest party’s output distribution by
This attack strategy performs  additional queries to the random oracle in expectation.
additional queries to the random oracle in expectation.
This corollary is obtained by substituting \(\epsilon =\frac{X_0\left( 1-X_0\right) }{nr^2}\) in Theorem 4. Imported Theorem 3 guarantees that, for all i, the average dependencies after the \(i^{th}\) message are bounded by \(n\epsilon \). Hence, the error term is  .
.
The efficiency of the heavy querier is guaranteed by Imported Theorem 3. One can transform the average-case efficiency to worst-case efficiency by forcing the heavy querier to stop when it asks more than \(\frac{n^2 r^3}{\left( X_0\left( 1-X_0\right) \right) ^2}\) queries. By Markov’s inequality, this happens with probability at most  , and thus the quality of this attack is essentially identical to the averge-case attack.
, and thus the quality of this attack is essentially identical to the averge-case attack.
4 Proof of Theorem 4
In this section, we prove Theorem 4 using induction on the message complexity r. We first provide some useful lemmas in Sect. 4.1. Next, we prove the base case in Sect. 4.2. Finally, Sect. 4.3 proves the inductive step.
Throughout this section, without loss of generality, we shall assume that Alice sends the first message in the protocol.
4.1 Useful Imported Technical Lemmas
Firstly, it is implicit in [12] that if (1) Alice’s and Bob’s private view before the protocol begins are \(\alpha _0\)-dependent, (2) all the queries are \(\epsilon \)-light for Bob, and (3) Alice asks at most n queries to prepare her first message, then after the first message, Alice’s and Bob’s private view are \((\alpha _0+n\epsilon )\)-dependent.
Lemma 1
(Technical Lemma [12]). We have
Additionally, the following inequality from [79] shall be useful for our proof.
Lemma 2
(Imported Technical Lemma, Lemma 1 in [79]). For all \(P\in [0,1]\) and \(Q\in [0,1/2]\), if P, Q satisfies
then for all \(x,\alpha ,\beta \in [0,1]\), we have

In particular, for all \(r\ge 1\), the constraints are satisfied if we set \(P=\varGamma _r\) and \(Q=\varGamma _{r+1}\), where \(\varGamma _r\,{:}{=} \sqrt{\frac{\sqrt{2}-1}{r}}.\)
4.2 Base Case of the Induction: Message Complexity \(r=1\)
Let \(\pi \) be an \((\epsilon ,\varvec{\alpha },r,n,X_0)\)-coin-tossing protocol with \(r=1\). In this protocol, Alice sends the only message \(M_1\). We shall pick the stopping time \(\tau \) to be 1. Note that this is the last message of the protocol and hence Bob who receives it cannot abort any more. Therefore, our score function is the following

Let  , which is the expectation of Bob’s first defense before the protocol begins. Recall that in the augmented protocol \(T_1=(M_1,H_1)\), and \(X_1\) and \(D_1^\mathsf {B}\) are \(T_1\) measurable. We have
, which is the expectation of Bob’s first defense before the protocol begins. Recall that in the augmented protocol \(T_1=(M_1,H_1)\), and \(X_1\) and \(D_1^\mathsf {B}\) are \(T_1\) measurable. We have

In the above inequality, (i) and (ii) are because of triangle inequality. Since we assume the output is concatenated to the last message of the protocol,  . And by the definition of \(X_0\), the probability of the output being 1 is \(X_0\). Hence we have (iv).
. And by the definition of \(X_0\), the probability of the output being 1 is \(X_0\). Hence we have (iv).
To see (iii), note that

Hence,

Therefore,

This completes the proof for the base case.
4.3 Inductive Step
Suppose the theorem is true for \(r=r_0-1\), we are going to prove it for \(r=r_0\). Let \(\pi \) be an arbitrary \((\epsilon ,\varvec{\alpha },r_0,n, X_0)\)-coin-tossing protocol. Assume the first augmented message is \((M_1,H_1)=(m_1^*,h_1^*)\), and conditioned on that, \(X_1=x_1^*\), \(D_1^\mathsf {A}=d_1^{\mathsf {A},*}\), and \(D_1^\mathsf {B}=d_1^{\mathsf {B},*}\). Moreover, the remaining sub-protocol \(\pi ^*\) is an \((\epsilon ,\varvec{\alpha }^*,r_0-1,n,x_1^*)\)-coin-tossing protocol. By our induction hypothesis,
(For simplicity, we shall use \(\mathsf {Err}\left( {\varvec{\alpha },n,r}\right) \) to represent \(\alpha _0+\sum _{i=1}^r\alpha _i+nr\epsilon \) in the rest of the proof.) That is, there exists a stopping time \(\tau ^*\) for sub-protocol \(\pi ^*\), whose score is lower bounded by the quantity above. On the other hand, we may choose not to continue by picking this message \((M_1,H_1)=(m_1^*,h_1^*)\) as our stopping time. This would yield a score of

Hence, the optimal stopping time would decide on whether to abort now or defer the attack to sub-protocol \(\pi ^*\) by comparing which one of those two quantities is larger. This would yield a score of

where inequality (i) is because of Lemma 2. Now that we have a lower bound on how much score we can yield at every first augmented message, we are interested in how much they sum up to.
Without loss of generality, assume there are totally \(\ell \) possible first augmented messages, namely \(t_1^{(1)},t_1^{(2)},\ldots ,t_1^{(\ell )}\). The probability of the first message being \(t_1^{(i)}\) is \(p^{(i)}\) and conditioned that, \(X_1=x_1^{(i)}\), \(D_1^\mathsf {A}=d_1^{\mathsf {A},{(i)}}\), and \(D_1^\mathsf {B}=d_1^{\mathsf {B},{(i)}}\). Moreover, the remaining \(r_0-1\) protocol has dependence vector \(\varvec{\alpha }^{(i)}\). Therefore, we are interested in,
Define the tri-variate function \(\varPhi \) as
We make the crucial observation that this function can also be rewritten as
Therefore, we can rewrite the above quantity as
We observe the following case analysis for the three expressions in the potential function above.
-
1.
For the x term, we observe that the expectation of \(x_1^{(i)}\) is \(X_0\), i.e., we have \(\sum _{i=1}^\ell p^{(i)}\cdot x_1^{(i)}=X_0\).
-
2.
For the \((x-y-z)^2\) term, we note that it is a convex tri-variate function. Hence, Jensen’s inequality is applicable.
-
3.
For the \(y\cdot z\) term, we have the following claim.
Claim
4.3 (Global Invariant)

Proof
To see this, consider the expectation of the product of Alice and Bob defense when we sample from  . This expectation is \(\alpha _0+n\epsilon \) close to
. This expectation is \(\alpha _0+n\epsilon \) close to  because joint distribution \(\left. \left( V^\mathsf {A}_1,V^\mathsf {B}_0\right) \right. \) is \(\alpha _0+n\epsilon \) close to the product of its marginal distribution by Lemma 1.
because joint distribution \(\left. \left( V^\mathsf {A}_1,V^\mathsf {B}_0\right) \right. \) is \(\alpha _0+n\epsilon \) close to the product of its marginal distribution by Lemma 1.
On the other hand, this expectation is identical to the average (over all possible messages) of the expectation of the product of Alice and Bob defense when we sample from  . Conditioned on first message being \(t_1^{(i)}\), this expectation is \(\alpha _0^{(i)}\)-close to
. Conditioned on first message being \(t_1^{(i)}\), this expectation is \(\alpha _0^{(i)}\)-close to  because
because  has \(\alpha _0^{(i)}\)-dependence by definition.
has \(\alpha _0^{(i)}\)-dependence by definition.
Finally, we note that, by definition, \(\sum _{i=1}^\ell p^{(i)}\alpha _0^{(i)}=\alpha _1.\) Note that the indices between \(\alpha \) and \(\alpha ^{(i)}\) are shifted by 1. This is because of that the dependence after the first message of the original protocol is the average of the dependence before each sub-protocol begins.
This proves that \(\sum _{i=1}^\ell p^{(i)}\cdot d_1^{\mathsf {A},{(i)}}d_1^{\mathsf {B},{(i)}}\) and  are \((\alpha _0+n\epsilon )+\alpha _1\) close. \(\square \)
are \((\alpha _0+n\epsilon )+\alpha _1\) close. \(\square \)
Given these observations, we can push the expectation inside each term, and they imply that our score is lower bounded by

We note that by definition (again note that the indices of \(\alpha \) and \(\alpha ^{(i)}\) are shifted by 1),
Therefore, our score is at least

Switching back to the form of \(x(1-x)+(x-y)^2+(x-z)^2\), we get

This completes the proof of the inductive step and, hence, the proof of Theorem 4.
Notes
- 1.
A fail-stop adversary behaves honestly and follows the prescribed protocol. However, based on her private view, she may choose to abort the protocol execution.
- 2.
Oblivious transfer takes \((x_0,x_1)\in {\{0,1\}} ^2\) as input from the first party, and a choice bit \(b\in {\{0,1\}} \) from the second party. The functionality outputs the bit \(x_b\) to the second party, and the first party receives no output. The security of this functionality ensures that the first party has no advantage in predicting the choice bit b. Furthermore, the second party has no advantage in predicting the other input bit \(x_{1-b}\).
- 3.
Most constructions in theoretical computer science and cryptography are black-box in nature. That is, they rely only on the input-output behavior of the primitive P, and are oblivious to, for instance, the particular implementation of the primitive P. The security reduction in cryptographic black-box constructions also uses the adversary in a black-box manner. There are, however, some highly non-trivial non-black-box constructions in theoretical computer science, for example, [11, 26, 33, 35, 56, 57, 76, 104]. However, an infeasibility of black-box constructions to realize Q from P indicates the necessity of new non-black-box constructions, which, historically, have been significantly infrequent.
- 4.
A random oracle is a function sampled uniformly at random from the set of all functions mapping \({\{0,1\}} ^n\rightarrow {\{0,1\}} ^n\).
- 5.
In this paper, we avoid the use of “round.” Some literature assumes one round to contain only one message from some party. Other literature assumes that one round has one message from all the parties. Instead, for clarity, we refer to the total number of messages exchanged in the entire protocol.
- 6.
For a more detailed discussion, refer to Remark 2.
- 7.
For example, consider the following analogy from complexity theory. We know that the complexity class \(\varSigma _2\) is separated from the complexity class \(\varSigma _1\) via Cook reductions; unless the polynomial hierarchy collapses. However, the existence of an efficient protocol for \(\varSigma _1\), implies that the entire polynomial hierarchy collapses, and we have \(\varSigma _1=\varSigma _2\). Similarly, the existence of an efficient protocol for a cryptographic primitive may have several additional implicit consequences in addition to merely providing oracle access to an implementation of that primitive.
- 8.
Every party broadcasts one uniformly and independently random bit, and all the parties agree on the parity of all the broadcast bits. This protocol is semi-honest secure.
- 9.
Basically, \({\mathcal {S}} \) is the set of all the queries that the heavy querier has published. \({\mathcal {A}} \) is the set of all possible pairs of Alice’s private randomness \(r^\mathsf {A}\) and random oracle o that are consistent with Alice’s messages before this protocol begins. Similarly, \({\mathcal {B}} \) is the set of all consistent pairs of Bob’s private randomness \(r^\mathsf {B}\) and random oracle o.
- 10.
This generalization shall not make the protocol any more vulnerable. Any attack in this protocol shall also exist in the original protocol with the same amount of deviation. This only helps simplify the presentation of our proof.
- 11.
For instance, suppose Alice samples a uniform string \(u_1\xleftarrow {\$} {\{0,1\}} ^\lambda \) and sends \(O(u_1)\) to Bob. Next, Bob samples a uniform string \(u_2\xleftarrow {\$} {\{0,1\}} ^\lambda \) and sends \(O(u_2)\) to Alice. Assume the first message and the second message are the same, i.e., \(O(u_1)=O(u_2)\). Then, there are no heavy queries, but Alice’s and Bob’s private views are largely correlated.
References
Abe, M., Ambrona, M., Ohkubo, M.: On black-box extensions of non-interactive zero-knowledge arguments, and signatures directly from simulation soundness. In: Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V. (eds.) PKC 2020, Part I. LNCS, vol. 12110, pp. 558–589. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45374-9_19
Agrawal, S., Prabhakaran, M.: On fair exchange, fair coins and fair sampling. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 259–276. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_15
Alon, B., Omri, E.: Almost-optimally fair multiparty coin-tossing with nearly three-quarters malicious. In: Hirt, M., Smith, A. (eds.) TCC 2016, Part I. LNCS, vol. 9985, pp. 307–335. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_13
Asharov, G.: Towards characterizing complete fairness in secure two-party computation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 291–316. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_13
Asharov, G., Beimel, A., Makriyannis, N., Omri, E.: Complete characterization of fairness in secure two-party computation of boolean functions. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 199–228. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_10
Asharov, G., Lindell, Y., Rabin, T.: A full characterization of functions that imply fair coin tossing and ramifications to fairness. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 243–262. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_14
Awerbuch, B., Blum, M., Chor, B., Goldwasser, S., Micali, S.: How to implement Bracha’s o (log n) byzantine agreement algorithm. Unpublished manuscript (1985)
Bader, C., Jager, T., Li, Y., Schäge, S.: On the impossibility of tight cryptographic reductions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 273–304. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_10
Baecher, P., Brzuska, C., Fischlin, M.: Notions of black-box reductions, revisited. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part I. LNCS, vol. 8269, pp. 296–315. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_16
Baldimtsi, F., Lysyanskaya, A.: On the security of one-witness blind signature schemes. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 82–99. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_5
Barak, B.: Constant-round coin-tossing with a man in the middle or realizing the shared random string model. In: 43rd Annual Symposium on Foundations of Computer Science, Vancouver, BC, Canada, 16–19 November 2002, pp. 345–355. IEEE Computer Society Press (2002)
Barak, B., Mahmoody-Ghidary, M.: Merkle puzzles are optimal - an O(n2)-query attack on any key exchange from a random oracle. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 374–390. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_22
Beimel, A., Lindell, Y., Omri, E., Orlov, I.: 1/p-secure multiparty computation without honest majority and the best of both worlds. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 277–296. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_16
Beimel, A., Omri, E., Orlov, I.: Protocols for multiparty coin toss with dishonest majority. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 538–557. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_29
Bitansky, N., et al.: Why “Fiat-Shamir for Proofs” lacks a proof. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 182–201. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_11
Blum, M.: Coin flipping by telephone - a protocol for solving impossible problems, pp. 133–137 (1982)
Boldyreva, A., Cash, D., Fischlin, M., Warinschi, B.: Foundations of non-malleable hash and one-way functions. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 524–541. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_31
Boneh, D., Papakonstantinou, P.A., Rackoff, C., Vahlis, Y., Waters, B.: On the impossibility of basing identity based encryption on trapdoor permutations. In: 49th Annual Symposium on Foundations of Computer Science, Philadelphia, PA, USA, 25–28 October 2008, pp. 283–292. IEEE Computer Society Press (2008)
Boneh, D., Venkatesan, R.: Breaking RSA may not be equivalent to factoring. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 59–71. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054117
Brendel, J., Fischlin, M., Günther, F., Janson, C.: PRF-ODH: relations, instantiations, and impossibility results. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part III. LNCS, vol. 10403, pp. 651–681. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_22
Broder, A.Z., Dolev, D.: Flipping coins in many pockets (byzantine agreement on uniformly random values). In: 25th Annual Symposium on Foundations of Computer Science, Singer Island, Florida, 24–26 October 1984, pp. 157–170. IEEE Computer Society Press (1984)
Brown, D.R.L.: Breaking RSA may be as difficult as factoring. J. Cryptol. 29(1), 220–241 (2016)
Buchbinder, N., Haitner, I., Levi, N., Tsfadia, E.: Fair coin flipping: tighter analysis and the many-party case. In: Klein, P.N. (ed.) 28th Annual ACM-SIAM Symposium on Discrete Algorithms, Barcelona, Spain, 16–19 January 2017, pp. 2580–2600. ACM-SIAM (2017)
Cleve, R.: Limits on the security of coin flips when half the processors are faulty (extended abstract). In: 18th Annual ACM Symposium on Theory of Computing, Berkeley, CA, USA, 28–30 May 1986, pp. 364–369. ACM Press (1986)
Cleve, R., Impagliazzo, R.: Martingales, collective coin flipping and discrete control processes. Other Words 1, 5 (1993)
Cook, S.A.: The complexity of theorem-proving procedures. In: Harrison, M.A., Banerji, R.B., Ullman, J.D. (eds.) Proceedings of the 3rd Annual ACM Symposium on Theory of Computing, Shaker Heights, Ohio, USA, 3–5 May 1971, pp. 151–158. ACM (1971)
Coron, J.-S.: Security proof for partial-domain hash signature schemes. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 613–626. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_39
Coron, J.-S., Patarin, J., Seurin, Y.: The random oracle model and the ideal cipher model are equivalent. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 1–20. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_1
Dachman-Soled, D., Lindell, Y., Mahmoody, M., Malkin, T.: On the black-box complexity of optimally-fair coin tossing. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 450–467. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_27
Dachman-Soled, D., Mahmoody, M., Malkin, T.: Can optimally-fair coin tossing be based on one-way functions? In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 217–239. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_10
Dodis, Y., Haitner, I., Tentes, A.: On the instantiability of hash-and-sign RSA signatures. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 112–132. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_7
Dodis, Y., Oliveira, R., Pietrzak, K.: On the generic insecurity of the full domain hash. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 449–466. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_27
Dolev, D., Dwork, C., Naor, M.: Nonmalleable cryptography. SIAM J. Comput. 30(2), 391–437 (2000)
Drijvers, M., et al.: On the security of two-round multi-signatures. In: 2019 IEEE Symposium on Security and Privacy, SP 2019, San Francisco, CA, USA, 19–23 May 2019, pp. 1084–1101. IEEE (2019)
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: 22nd Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 14–16 May 1990, pp. 416–426. ACM Press (1990)
Fiore, D., Schröder, D.: Uniqueness is a different story: impossibility of verifiable random functions from trapdoor permutations. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 636–653. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_36
Fischlin, M.: On the impossibility of constructing non-interactive statistically-secret protocols from any trapdoor one-way function. In: Preneel, B. (ed.) CT-RSA 2002. LNCS, vol. 2271, pp. 79–95. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45760-7_7
Fischlin, M., Fleischhacker, N.: Limitations of the meta-reduction technique: the case of Schnorr signatures. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 444–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_27
Fischlin, M., Harasser, P., Janson, C.: Signatures from sequential-OR proofs. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part III. LNCS, vol. 12107, pp. 212–244. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_8
Fischlin, M., Lehmann, A., Ristenpart, T., Shrimpton, T., Stam, M., Tessaro, S.: Random oracles with(out) programmability. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 303–320. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_18
Fischlin, M., Schröder, D.: On the impossibility of three-move blind signature schemes. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 197–215. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_10
Fuchsbauer, G., Konstantinov, M., Pietrzak, K., Rao, V.: Adaptive security of constrained PRFs. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 82–101. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_5
Fukumitsu, M., Hasegawa, S.: One-more assumptions do not help Fiat-Shamir-type signature schemes in NPROM. In: Jarecki, S. (ed.) CT-RSA 2020. LNCS, vol. 12006, pp. 586–609. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-40186-3_25
Garg, S., Hajiabadi, M., Mahmoody, M., Mohammed, A.: Limits on the power of garbling techniques for public-key encryption. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part III. LNCS, vol. 10993, pp. 335–364. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_12
Garg, S., Mahmoody, M., Masny, D., Meckler, I.: On the round complexity of OT extension. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part III. LNCS, vol. 10993, pp. 545–574. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_19
Garg, S., Mahmoody, M., Mohammed, A.: Lower bounds on obfuscation from all-or-nothing encryption primitives. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 661–695. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_22
Garg, S., Mahmoody, M., Mohammed, A.: When does functional encryption imply obfuscation? In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part I. LNCS, vol. 10677, pp. 82–115. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_4
Gennaro, R., Gertner, Y., Katz, J.: Lower bounds on the efficiency of encryption and digital signature schemes. In: 35th Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 9–11 June 2003, pp. 417–425. ACM Press (2003)
Gennaro, R., Trevisan, L.: Lower bounds on the efficiency of generic cryptographic constructions. In: 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000, pp. 305–313. IEEE Computer Society Press (2000)
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd Annual ACM Symposium on Theory of Computing, San Jose, CA, USA, 6–8 June 2011, pp. 99–108. ACM Press (2011)
Gertner, Y., Kannan, S., Malkin, T., Reingold, O., Viswanathan, M.: The relationship between public key encryption and oblivious transfer. In: 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000, pp. 325–335. IEEE Computer Society Press (2000)
Gertner, Y., Malkin, T., Myers, S.: Towards a separation of semantic and CCA security for public key encryption. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 434–455. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_24
Gertner, Y., Malkin, T., Reingold, O.: On the impossibility of basing trapdoor functions on trapdoor predicates. In: 42nd Annual Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 14–17 October 2001, pp.126–135. IEEE Computer Society Press (2001)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions (extended abstract). In: 25th Annual Symposium on Foundations of Computer Science, Singer Island, Florida, 24–26 October 1984, pp. 464–479. IEEE Computer Society Press (1984)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: Aho, A. (ed.) 19th Annual ACM Symposium on Theory of Computing, New York City, NY, USA, 25–27 May 1987, pp. 218–229. ACM Press (1987)
Goldreich, O., Micali, S., Wigderson, A.: Proofs that yield nothing but their validity or all languages in NP have zero-knowledge proof systems. J. ACM 38(3), 691–729 (1991)
Gordon, S.D., Hazay, C., Katz, J., Lindell, Y.: Complete fairness in secure two-party computation. In: Ladner, R.E., Dwork, C. (eds.) 40th Annual ACM Symposium on Theory of Computing, Victoria, BC, Canada, 17–20 May 2008, pp. 413–422. ACM Press (2008)
Gordon, S.D., Katz, J.: Partial fairness in secure two-party computation. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 157–176. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_8
Haitner, I., Makriyannis, N., Omri, E.: On the complexity of fair coin flipping. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part I. LNCS, vol. 11239, pp. 539–562. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_20
Haitner, I., Nissim, K., Omri, E., Shaltiel, R., Silbak, J.: Computational two-party correlation: a dichotomy for key-agreement protocols. In: Thorup, M. (ed.) 59th Annual Symposium on Foundations of Computer Science, Paris, France, 7–9 October 2018, pp. 136–147. IEEE Computer Society Press (2018)
Haitner, I., Omri, E., Zarosim, H.: Limits on the usefulness of random oracles. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 437–456. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_25
Haitner, I., Reingold, O.: Statistically-hiding commitment from any one-way function. In: Johnson, D.S., Feige, U. (eds.) 39th Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 11–13 June 2007, pp. 1–10. ACM Press (2007)
Haitner, I., Tsfadia, E.: An almost-optimally fair three-party coin-flipping protocol. In: Shmoys, D.B. (ed.) 46th Annual ACM Symposium on Theory of Computing, New York, NY, USA, 31 May - 3 June 2014, pp. 408–416. ACM Press (2014)
Hanaoka, G., Matsuda, T., Schuldt, J.C.N.: On the impossibility of constructing efficient key encapsulation and programmable hash functions in prime order groups. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 812–831. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_47
Håstad, J.: Pseudo-random generators under uniform assumptions. In: 22nd Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 14–16 May 1990, pp. 395–404. ACM Press (1990)
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Hesse, J., Hofheinz, D., Kohl, L.: On tightly secure non-interactive key exchange. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part II. LNCS, vol. 10992, pp. 65–94. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_3
Hofheinz, D.: Possibility and impossibility results for selective decommitments. J. Cryptol. 24(3), 470–516 (2011)
Holenstein, T., Künzler, R., Tessaro, S.: The equivalence of the random oracle model and the ideal cipher model, revisited. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd Annual ACM Symposium on Theory of Computing, San Jose, CA, USA, 6–8 June 2011, pp. 89–98. ACM Press (2011)
Hsiao, C.-Y., Reyzin, L.: Finding collisions on a public road, or do secure hash functions need secret coins? In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 92–105. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_6
Impagliazzo, R.: A personal view of average-case complexity. In: Proceedings of the Tenth Annual Structure in Complexity Theory Conference, Minneapolis, Minnesota, USA, 19–22 June 1995, pp. 134–147. IEEE Computer Society (1995)
Impagliazzo, R., Levin, L.A., Luby, M.: Pseudo-random generation from one-way functions (extended abstracts). In: 21st Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 15–17 May 1989, pp. 12–24. ACM Press (1989)
Impagliazzo, R., Luby, M.: One-way functions are essential for complexity based cryptography (extended abstract). In: 30th Annual Symposium on Foundations of Computer Science, Research Triangle Park, NC, USA, 30 October–1 November 1989, pp. 230–235. IEEE Computer Society Press (1989)
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: 21st Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 15–17 May 1989, pp. 44–61. ACM Press (1989)
Karp, R.M.: Reducibility among combinatorial problems. In: Miller, R.E., Thatcher, J.W. (eds.) Proceedings of a Symposium on the Complexity of Computer Computations, Held 20–22 March 1972, at the IBM Thomas J. Watson Research Center, Yorktown Heights, New York, USA, The IBM Research Symposia Series, pp. 85–103. Plenum Press, New York (1972)
Katz, J., Schröder, D., Yerukhimovich, A.: Impossibility of blind signatures from one-way permutations. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 615–629. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_37
Khorasgani, H.A., Maji, H.K., Mukherjee, T.: Estimating gaps in martingales and applications to coin-tossing: constructions and hardness. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019, Part II. LNCS, vol. 11892, pp. 333–355. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36033-7_13
Khorasgani, H.A., Maji, H.K., Wang, M.: Coin tossing with lazy defense: hardness of computation results. IACR Cryptol. ePrint Arch. 2020:131 (2020)
Kim, J.H., Simon, D.R., Tetali, P.: Limits on the efficiency of one-way permutation-based hash functions. In: 40th Annual Symposium on Foundations of Computer Science, New York, NY, USA, 17–19 October 1999, pp. 535–542. IEEE Computer Society Press (1999)
Luby, M., Rackoff, C.: How to construct pseudorandom permutations from pseudorandom functions. SIAM J. Comput. 17(2), 373–386 (1988)
Mahmoody, M., Maji, H.K., Prabhakaran, M.: Limits of random oracles in secure computation. In: Naor, M. (ed.) ITCS 2014: 5th Conference on Innovations in Theoretical Computer Science, Princeton, NJ, USA, 12–14 January 2014, pp. 23–34. Association for Computing Machinery (2014)
Mahmoody, M., Maji, H.K., Prabhakaran, M.: On the power of public-key encryption in secure computation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 240–264. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_11
Mahmoody, M., Mohammed, A.: On the power of hierarchical identity-based encryption. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 243–272. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_9
Mahmoody, M., Mohammed, A., Nematihaji, S., Pass, R., Shelat, A.: Lower bounds on assumptions behind indistinguishability obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part I. LNCS, vol. 9562, pp. 49–66. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_3
Makriyannis, N.: On the classification of finite Boolean functions up to fairness. In: Abdalla, M., De Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 135–154. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10879-7_9
Matsuda, T., Matsuura, K.: On black-box separations among injective one-way functions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 597–614. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_36
Moran, T., Naor, M., Segev, G.: An optimally fair coin toss. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 1–18. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_1
Morgan, A., Pass, R.: On the security loss of unique signatures. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part I. LNCS, vol. 11239, pp. 507–536. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_19
Naor, M.: Bit commitment using pseudorandomness. J. Cryptol. 4(2), 151–158 (1991)
Naor, M.: On cryptographic assumptions and challenges (invited talk). In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_6
Naor, M., Ostrovsky, R., Venkatesan, R., Yung, M.: Perfect zero-knowledge arguments for NP using any one-way permutation. J. Cryptol. 11(2), 87–108 (1998)
Naor, M., Yung, M.: Universal one-way hash functions and their cryptographic applications. In: 21st Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 15–17 May 1989, pp. 33–43. ACM Press (1989)
Paillier, P., Vergnaud, D.: Discrete-log-based signatures may not be equivalent to discrete log. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 1–20. Springer, Heidelberg (2005). https://doi.org/10.1007/11593447_1
Pass, R.: Limits of provable security from standard assumptions. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd Annual ACM Symposium on Theory of Computing, San Jose, CA, USA, 6–8 June 2011, pp. 109–118. ACM Press (2011)
Reingold, O., Trevisan, L., Vadhan, S.: Notions of reducibility between cryptographic primitives. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 1–20. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_1
Rompel, J.: One-way functions are necessary and sufficient for secure signatures. In: 22nd Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 14–16 May 1990, pp. 387–394. ACM Press (1990)
Rudich, S.: Limits on the provable consequences of one-way functions (1988)
Rudich, S.: The use of interaction in public cryptosystems (extended abstract). In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 242–251. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_19
Schilling, R.L.: Measures, Integrals and Martingales. Cambridge University Press, Cambridge (2017)
Seurin, Y.: On the exact security of Schnorr-type signatures in the random oracle model. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 554–571. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_33
Simon, D.R.: Finding collisions on a one-way street: can secure hash functions be based on general assumptions? In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 334–345. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054137
Vahlis, Y.: Two is a crowd? A black-box separation of one-wayness and security under correlated inputs. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 165–182. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_11
Yao, A.C.-C.: How to generate and exchange secrets (extended abstract). In: 27th Annual Symposium on Foundations of Computer Science, Toronto, Ontario, Canada, 27–29 October 1986, pp. 162–167. IEEE Computer Society Press (1986)
Zhang, J., Zhang, Z., Chen, Y., Guo, Y., Zhang, Z.: Black-box separations for one-more (static) CDH and its generalization. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 366–385. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_20
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Maji, H.K., Wang, M. (2020). Black-Box Use of One-Way Functions is Useless for Optimal Fair Coin-Tossing. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12171. Springer, Cham. https://doi.org/10.1007/978-3-030-56880-1_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-56880-1_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56879-5
Online ISBN: 978-3-030-56880-1
eBook Packages: Computer ScienceComputer Science (R0)





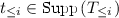 , and query
, and query 

 -Efficiency. The expected number of queries asked by the heavy querier is bounded by
-Efficiency. The expected number of queries asked by the heavy querier is bounded by 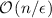 . Consequently, it has
. Consequently, it has 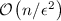 query complexity with probability (at least)
query complexity with probability (at least) 
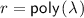 . We emphasize that the length of the message could be arbitrarily long.
. We emphasize that the length of the message could be arbitrarily long.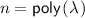 . This also includes the queries that are asked for the preparation of the defense coins. Likewise, Bob asks at most n queries as well.
. This also includes the queries that are asked for the preparation of the defense coins. Likewise, Bob asks at most n queries as well. . On the other hand, Bob can also attack by aborting when he receives Alice’s message
. On the other hand, Bob can also attack by aborting when he receives Alice’s message  . Note that for the
. Note that for the 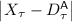 .
.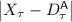 . This explains why we have the indicator function
. This explains why we have the indicator function 