Abstract
In the context of secure computation, protocols with security against covert adversaries ensure that any misbehavior by malicious parties will be detected by the honest parties with some constant probability. As such, these protocols provide better security guarantees than passively secure protocols and, moreover, are easier to construct than protocols with full security against active adversaries. Protocols that, upon detecting a cheating attempt, allow the honest parties to compute a certificate that enables third parties to verify whether an accused party misbehaved or not are called publicly verifiable.
In this work, we present the first generic compilers for constructing two-party protocols with covert security and public verifiability from protocols with passive security. We present two separate compilers, which are both fully blackbox in the underlying protocols they use. Both of them only incur a constant multiplicative factor in terms of bandwidth overhead and a constant additive factor in terms of round complexity on top of the passively secure protocols they use.
The first compiler applies to all two-party protocols that have no private inputs. This class of protocols covers the important class of preprocessing protocols that are used to setup correlated randomness among parties. We use our compiler to obtain the first secret-sharing based two-party protocol with covert security and public verifiability. Notably, the produced protocol achieves public verifiability essentially for free when compared with the best known previous solutions based on secret-sharing that did not provide public verifiability.
Our second compiler constructs protocols with covert security and public verifiability for arbitrary functionalities from passively secure protocols. It uses our first compiler to perform a setup phase, which is independent of the parties’ inputs as well as the protocol they would like to execute.
Finally, we show how to extend our techniques to obtain multiparty computation protocols with covert security and public verifiability against arbitrary constant fractions of corruptions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In secure computation two or more parties want to compute a joint function of their private inputs, while revealing nothing beyond what is already revealed by the output itself. Privacy of the inputs and correctness of the output should be maintained, even if some of the parties are corrupted by an adversary. Historically, this adversary has mostly been assumed to be either passive or active. Passive adversaries observe corrupted parties, learn their private inputs, the random coins they use, and see all messages that are being sent or received by them. Active adversaries take full control of the corrupted parties, they can deviate from the protocol description in an arbitrary fashion, or may just stop sending messages altogether. Protocols that are secure against active adversaries provide very strong security guarantees. They ensure that any deviation from the protocol description by the corrupted parties is detected by the honest parties with an overwhelming probability. Unfortunately, such strong security guarantees do not come for free and actively secure protocols are typically much slower than their passively secure counterparts.
To provide a compromise between efficiency and security, Aumann and Lindell [AL07] introduced the notion of security against covert adversariesFootnote 1. Loosely speaking, the adversary still has full control of the corrupted parties, but if any of them deviates from the protocol description, then this behavior will be detected with some constant probability, say 1/2, by all honest parties. The main rationale for why such an adversarial model may be sensible in the real world, is that in certain scenarios the loss of reputation that comes from being caught cheating outweighs the gain that comes from not being caught. Consider, for example, a large company that performs secure computations with its customers on a regular basis. It is reasonable to assume that the company’s general reputation is more valuable than whatever it could possibly earn by tricking a few of its customers.
Asharov and Orlandi [AO12] observed that despite being well-motivated in practice, the original notion of security against covert adversaries may be a bit too weak. More concretely, the original notion ensures that the honest parties detect cheating with some constant probability, but it does not ensure the existence of a mechanism for convincing third parties that the adversary really cheated. For our hypothetical large company from before, this means that no cheated customer could convince the others of the company’s misbehavior. Asharov and Orlandi therefore introduce the stronger notion of covert security with public verifiability, which, in case of detected cheating, ensures that the honest parties can compute a publicly verifiable certificate, which allows third parties to check that cheating by some accused party indeed happened.
Although covert security with and without public verifiability seems like a very natural security notion, comparatively few works focus on this security model. Goyal, Mohassel, and Smith [GMS08] present covertly secure two and multiparty protocols without public verifiability based on garbled circuits [Yao82] and its multiparty extension the BMR protocol [BMR90]. Subsequently, Damgård et al. [DKL+13] present a preprocessing protocol with covert security without public verifiability for SPDZ [DPSZ12]. Asharov and Orlandi [AO12] present a two-party protocol with covert security and public verifiability based on garbled circuits and a flavor of oblivious transfer (OT), which they call signed-OT. Kolesnikov and Malozemoff [KM15] improve upon the construction of Asharov and Orlandi by constructing a signed-OT extension protocol based on the OT extensionFootnote 2 protocol of Ishai et al. [IKNP03]. In a recent work by Hong et al. [HKK+19], the authors present a new approach for constructing two-party computation with covert security and public verifiability based on garbled circuits from plain standard OT.
Apart from the concrete constructions above, one can also use so called protocol compilers that generically transform protocols with weaker security guarantees into protocols with stronger ones. The main advantage of compilers over concrete protocols is that they allow us to automatically obtain protocols with the stronger security guarantee from any future insight into protocols with the weaker one. In case of covert security with and without public verifiability, for example, most of the existing concrete constructions are based on garbled circuits. If at some point in the future a new methodology for constructing more efficient passively secure protocols is discovered, then we may end up in the situation that the techniques that we used to lift garbled circuits from passive to covert security may not be applicable. Compilers, on the other hand, will still be useful as long as the new protocols satisfy the requirements the compiler imposes on the protocols it transforms.
In terms of generic approaches for efficiently transforming arbitrary passively secure protocols into covertly secure ones very little is known. Damgård, Geisler, and Nielsen [DGN10] present a blackbox compiler that transforms passively secure protocols that are based on secret sharing into covertly secure protocols. Their compiler only works for the honest majority setting, i.e., it assumes that the honest parties form a strict majority, and therefore their compiler is not applicable to the two-party setting. Lindell, Oxman, and Pinkas [LOP11] present a compiler, based on the work of Ishai, Prabhakaran, and Sahai [IPS08], that transforms passively secure protocols in the dishonest majority setting into covertly secure ones. Their compiler makes blackbox use of a passively secure “inner” and non-blackbox use of an information-theoretic “outer” multiparty computation protocol with active security. The bandwidth overhead and round complexity of their compiler depends on the complexity of both the inner and the outer protocol. Unfortunately this means that the protocols this compiler produces are either not constant-round protocols or have a large bandwidth overhead. Using an information-theoretic outer protocol results in a protocol that is not constant-round, since constructing information-theoretic multiparty computation with a constant number of rounds is a long standing open problem.Footnote 3 Alternatively, the authors of [IPS08] show how to combine their compiler with a variant of a computationally secure protocol of Damgård and Ishai [DI05], which only makes blackbox use of pseudorandom generators, as the outer protocol. This approach, however, results in a protocol, which incurs a bandwidth overhead that is multiplicative in the security parameter and the circuit size on top of the communication costs of the underlying passively secure protocol.
None of the above compilers is publicly verifiable and, more generally, there is currently no better approach for constructing covertly secure protocols with public verifiability in a generic way than just taking a compiler that already produces actively secure protocols.Footnote 4 Even without public verifiability, there is currently no compiler for the dishonest majority setting that is fully blackbox in the sense that the code of the used secure computation protocols does not need to be known.
1.1 Our Contribution
In this work, we present the first blackbox compilers for transforming protocols with passive security into two-party protocols with covert security and public verifiability. Our compilers are fully blackbox in the underlying primitives they use, they are conceptually simple, efficient and constant-round.
Our first compiler applies to all two-party protocols with passive security that have no private inputs. The class of protocols with no inputs covers the important class of preprocessing protocols which are commonly used to setup correlated randomness among the parties. For example, one can combine our compiler with a suitable preprocessing protocol and the SPDZ online phase, similarly to [DKL+13], to obtain the first protocol with covert security, public verifiability. The resulting protocol, somewhat surprisingly, achieves public verifiability essentially for free. That is, the efficiency of our resulting protocol is essentially the same as the efficiency of the best known secret-sharing based protocol for covert security without public verifiability [DKL+13].
Our second compiler uses the first compiler to perform a input and protocol independent setup phase after which the parties can efficiently transform any protocol with passive security into one with covert security and publicly verifiability. We would like to stress that during the setup phase, the parties do not need to know which standalone passively secure protocol they would like to use later on.Footnote 5 When compared to compilers without public verifiability, ours is the first one that is simultaneously blackbox and constant-round with only a constant multiplicative factor bandwidth overhead on top of the underlying passively secure protocol. Existing compilers for two-party protocols do not even achieve these properties separately. It is the first compiler to produce protocols with public verifiability.
Lastly, we sketch how to extend our compilers to the multiparty setting. The resulting protocols are secure against an arbitrary constant fraction of corruptions.
1.2 Technical Overview
Before presenting the main ideas behind our compilers, let us first revisit the main ideas as well as the main technical challenges in existing protocols. Generally speaking, most covertly secure two-party protocols [AL07, GMS08, AO12, HKK+19] follow the same blueprint. They all start from a passively secure protocol, which they run k times in parallel. They use \(k-1\) randomly chosen executions to check the behavior of the participating parties and then use the last unopened protocol execution to actually compute the desired functionality on their private inputs. The intuition behind these approaches is that, if cheating happened, it will be detected with a probability of \(1- 1/k\), since the adversary would need to guess which execution will remain unopened. Importantly, this blueprint relies on the ability to open \(k-1\) executions “late enough” to ensure that cheating in the unopened execution is not possible any more, while at the same time being able to open the checked executions “early enough” to ensure that no private inputs are leaked. Secure two- and multiparty computation protocols based on garbled circuits are a perfect match for the blueprint described above, since they consist of an input-independent garbling phase, and an actively secure evaluation phase. Checked executions are opened after circuit garbling, but before circuit evaluation. Unfortunately, however, it is not clear how to generalize this approach to arbitrary passively secure protocols, since it crucially relies on the concrete structure of garbled circuit based protocols.
Our first compiler focuses on a restricted class of two-party protocols, namely those that have no private inputs. Apart from being a good starting point for explaining some of the technical ideas behind our compiler for arbitrary protocols, this class also covers a large range of important protocols. Specifically, it includes so called preprocessing protocols that are used for setting up correlated randomness between the parties.
Not having to deal with private inputs, immediately suggests the following high-level approach for letting Alice and Bob compute some desired function with covert security: Both parties first jointly execute a given protocol \(\varPi \) with passive security k times in parallel. Once these executions are finished, Alice and Bob independently announce subsets \(I^A \subset [k]\) and \(I^B \subset [k]\) with \(\vert I^A\vert = \vert I^B\vert < k/2\). Alice reveals the randomness used in each execution \(i \in I^B\) and Bob does the same for all executions with an index in \(I^A\). Knowing these random tapes each party can verify whether the other party behaved honestly in the checked executions. Since \(I^A \cup I^B \subsetneq [k]\), the parties are guaranteed that there exists an execution that is not checked by either of the parties. If no cheating in any of the checked executions is detected, then both parties agree to accept the output of one of the unopened executions.
This straightforward approach works for the plain version of covert security, but fails to achieve public verifiability, since neither of the parties has any way of convincing a third party of a detected cheating attempt. Even if each party signs each message it sends, a cheating party might simply stop responding if it does not like which executions are being checked. To achieve public verifiability, rather than asking for \(I^A\) and \(I^B\) in the clear, both parties use oblivious transfer to obtain the random tapes that correspond to the executions they would like to check. As before, we run k copies of the passively secure protocol \(\varPi \), where Alice and Bob use the random tapes they input to the OT protocol. At the end of these executions, both parties sign the complete transcript of the protocol \(\varPi \) as well as the transcript of the OT. If, e.g., Alice detects cheating by Bob in some execution, then she can publish the signed transcripts of both the OT protocol and the protocol in which Bob cheated, together with the randomness she used in the OT protocol. Any third party can now use Alice’s opened random tape in combination with the signed transcript of the OT protocol to recover Bob’s random tape and use it to check whether Bob misbehaved or not in the protocol \(\varPi \). The general idea of derandomizing the parties to achieve public verifiability has previously been used by Hong et al. [HKK+19]. However, as it turns out there are quite a few subtleties to take care of to make sure that the approach outlined above actually works and is secure. We will elaborate on these challenges in the later technical sections.
Using our compiler for protocols with no private inputs, we can obtain efficient protocols with covert security and public verifiability in the preprocessing model. In this model, protocols are split into a preprocessing protocol \(\varPi _{\mathsf {OFF}} \) and an online phase \(\varPi _{\mathsf {ON}} \), where \(\varPi _{\mathsf {OFF}} \) generates correlated randomness and \(\varPi _{\mathsf {ON}} \) is a highly efficient protocol for computing a desired function using the correlated randomness and the parties’ private inputs. We can apply our compiler to a passively secure version of the preprocessing protocol of SPDZ [DPSZ12] and combine it with an actively secure online protocol \(\varPi _{\mathsf {ON}} \) to obtain an overall protocol with covert security and public verifiability.
Our second compiler for arbitrary protocols follows the player virtualization paradigm, which was first introduced by Bracha [Bra87] in the context of distributed computing and then first applied to secure computation protocols by Maurer and Hirth [HM00]. Very roughly speaking, the idea behind this paradigm is to let a set of real parties simulate a set of virtual parties, which execute some given protocol on behalf of the real parties. Despite the conceptual simplicity of this idea, it has led to many interesting results. Ishai, Prabhakaran, and Sahai [IPS08], for example, show how to use this paradigm in combination with OT to obtain actively secure protocols from passively secure ones in the dishonest majority setting. In another work, Ishai et al. [IKOS07] show how to transform secure multiparty computation protocols with passive security into zero-knowledge proofs. Cohen et al. [CDI+13] show how to transform three or four-party protocols that tolerate one active corruption into n-party protocols for arbitrary n that tolerate a constant fraction of active corruptions. Damgård, Orlandi, and Simkin [DOS18] show how to transform information-theoretically secure multiparty protocols that tolerate \(\varOmega (t)\) passive corruptions into information-theoretically secure ones that tolerate \(\varOmega (\sqrt{t})\) active corruptions.
In this work, we make use of this paradigm as follows: Assume Alice and Bob have inputs \(x^A\) and \(x^B\), would like to compute some function f, and are given access to some 2m-party protocol \(\varPi \) with security against \(m\,+\,t\) passive corruptions, where m and t are parameters that will determine the probability with which cheating will be caught. Alice imagines m virtual parties \(\mathbb {V}_{1} ^{A}, \dots , \mathbb {V}_{m} ^{A}\) in her head and Bob imagines virtual parties \(\mathbb {V}_{1} ^{B}, \dots , \mathbb {V}_{m} ^{B}\) in his. Alice splits her input \(x^A\) into an m-out-of-m secret sharing with shares \(x^A_1, \dots , x^A_m\) and she will use share \(x^A_i\) as the private input of her virtual party \(\mathbb {V}_{i} ^{A}\). Bob does the same with his input. All 2m virtual parties jointly execute \(\varPi \), which first reconstructs \(x^A\) and \(x^B\) from the given shares and then computes \(f(x^A, x^B)\). During the protocol execution, Alice and Bob send messages on behalf of the virtual parties they simulate. If both parties perform their simulations honestly, then the protocol computes the desired result. If either of the real parties misbehaves, then it will necessarily misbehave in at least one of its virtual parties. Similarly to before, our idea here is to let Alice and Bob check subsets of each other’s simulations. Assuming, for instance, Alice obtains the random tapes and inputs of t uniformly random virtual parties of Bob, then she can recompute all messages that those virtual parties should be sending. Since Bob does not know which of his virtual parties are checked, any attempt to cheat will be caught with a probability of t/m. Further, observe that as long as \(t < m\), the inputs remain hidden, since the protocol tolerates \(m\,+\,t\) corruptions and each input is m-out-of-m secret shared.
As in the case of the first compiler, the high-level idea of the simulation strategy above is reasonably simple, yet the details are in fact non-trivial and several subtle issues arise when trying to turn this idea into a working compiler.
What function to compute? The first question that needs to be addressed is that of which function exactly the virtual parties should compute. Using \(\varPi \) to reconstruct \(x^A\) and \(x^B\) and then directly compute \(f(x^A, x^B\)) is good enough for the intuition above, but is actually not secure. The reason is, that security against covert adversaries requires that the adversary’s decision to cheat is independent of the honest party’s input and output. A passively secure protocol, however, may reveal the output bit-by-bit, which would allow the adversary to learn parts of the output before deciding on whether to cheat or not. Consider for example the case, where \(x^A\) and \(x^B\) are bit-strings and \(f(x^A, x^B) = x^A \wedge x^B\). A passively secure protocol may simply compute and output the AND of each bit sequentially, which would enable an adversary to make its decision to cheat dependent on the output bits it has seen so far. To deal with this issue, we will use \(\varPi \) to secret share the output value among all virtual parties. This ensures that \(\varPi \) will not leak any information about any of the inputs or the output. At the same time all virtual parties can still reconstruct the output together by simply publishing their respective share.
How to check the behavior of virtual parties? The behavior of any virtual party is uniquely defined by its input, its random tape, and its current view of the protocol. Assuming, for example, Alice has access to input, random tape, and current view of some virtual party \(\mathbb {V}_{i} ^B\) of Bob, she can recompute the exact message this party should be sending. If the virtual party \(\mathbb {V}_{i} ^B\) deviates from that message, then Alice knows that a cheating attempt has happened. Assume for a second, that Alice somehow already obtained \(\mathbb {V}_{i} ^B\)’s input and random tape. The question now is how she can keep track of that virtual party’s view. If \(\mathbb {V}_{i} ^B\) is sending a protocol message to or receiving it from any \(\mathbb {V}_{j} ^A\), then Alice necessarily obtains that message and she can either check its validity or add it to \(\mathbb {V}_{i} ^B\)’s view. However, what happens when \(\mathbb {V}_{i} ^B\) is receiving a message from another one of Bob’s virtual parties \(\mathbb {V}_{j} ^B\)? In this case things are a little trickier. If Alice is checking \(\mathbb {V}_{i} ^B\), she should be able to read the message, but if she is not checking this virtual party, then the sent message should remain hidden from her. To solve this problem, we establish private communication channels between all virtual parties of Bob and separately also between all the ones of Alice. More precisely, for \(1 \le i,j \le m\), we will pick symmetric keys \(k^B_{(i,j)}\), which will be used to encrypt the communication between \(\mathbb {V}_{i} ^B\) and \(\mathbb {V}_{j} ^B\). When Alice initially obtains input and random tape of \(\mathbb {V}_{i} ^B\), she will also obtain all keys that belong to communication channels that are connected to \(\mathbb {V}_{i} ^B\). Now if during the protocol execution \(\mathbb {V}_{i} ^B\) should send a message to \(\mathbb {V}_{j} ^B\), we let Bob encrypt the message with the corresponding symmetric key and send it to Alice, who can decrypt the message only if she is checking the receiver or sender.
In our description here we have assumed that quite a lot of correlated randomness magically fell from the sky. For instance, we assumed that all random tapes and all symmetric keys were chosen honestly and distributed correctly. To realize this setup, we will use our first compiler, which we will apply to an appropriate protocol with passive security.
2 Preliminaries
2.1 Secure Multiparty Computation
All of our security definitions follow the ideal/real simulation paradigm in the standalone model. In the real protocol execution, all parties jointly execute the protocol \(\varPi \). Honest parties always follow the protocol description, whereas corrupted parties are controlled by an adversary  . In the ideal execution all parties simply send their inputs to a trusted party \(\mathcal {F}\), which computes the desired function and returns the output to the parties. Roughly speaking, we say that \(\varPi \) securely realizes \(\mathcal {F}\), if for every real-world adversary
. In the ideal execution all parties simply send their inputs to a trusted party \(\mathcal {F}\), which computes the desired function and returns the output to the parties. Roughly speaking, we say that \(\varPi \) securely realizes \(\mathcal {F}\), if for every real-world adversary  , there exists an ideal-world adversary \(\mathcal {S} \) such that the output distribution of the honest parties and \(\mathcal {S} \) in the ideal execution is indistinguishable from the output distribution of the honest parties and
, there exists an ideal-world adversary \(\mathcal {S} \) such that the output distribution of the honest parties and \(\mathcal {S} \) in the ideal execution is indistinguishable from the output distribution of the honest parties and  in the real execution. Different security notions, such as security against passive, covert, or malicious adversaries, differ in the capabilities the adversary has as well as the ideal functionalities they aim to implement. Throughout this paper we will consider synchronous protocols, static, rushing adversaries, and we assume the existence of secure authenticated point-to-point channels between the parties.
in the real execution. Different security notions, such as security against passive, covert, or malicious adversaries, differ in the capabilities the adversary has as well as the ideal functionalities they aim to implement. Throughout this paper we will consider synchronous protocols, static, rushing adversaries, and we assume the existence of secure authenticated point-to-point channels between the parties.
Let \(\mathrm {P}_{1}, \dots , \mathrm {P}_{n} \) be the involved parties and let \(I \subset [n ]\) be the set of indices of the corrupted parties that are controlled by the adversary  . Let
. Let  be an \(n\)-party protocol that takes one input from and returns one output to each party. \(\varPi \) internally may use an auxiliary ideal functionality \(\mathcal {G}\). For the sake of simplicity, we assume that parties have inputs of the same length. Let \(\bar{x} = (x_1, \dots , x_n)\) be the vector of the parties’ inputs and let z be an auxiliary input to
be an \(n\)-party protocol that takes one input from and returns one output to each party. \(\varPi \) internally may use an auxiliary ideal functionality \(\mathcal {G}\). For the sake of simplicity, we assume that parties have inputs of the same length. Let \(\bar{x} = (x_1, \dots , x_n)\) be the vector of the parties’ inputs and let z be an auxiliary input to  . We define
. We define
 as the output of the adversary
as the output of the adversary  and the outputs of the honest parties in an execution of \(\varPi \).
and the outputs of the honest parties in an execution of \(\varPi \).
Passive adversaries. Security against passive adversaries is modelled by considering an environment \(\mathcal {Z}\) that, in the real and ideal execution, picks the inputs of all parties. An adversary  gets access to views of the corrupted parties, but follows the protocol specification honestly. We consider the following ideal execution:
gets access to views of the corrupted parties, but follows the protocol specification honestly. We consider the following ideal execution:
-
Inputs: Environment \(\mathcal {Z}\) gets as input auxiliary information z and sends the vector of inputs \(\bar{x} = (x_1, \dots , x_n)\) to the ideal functionality \(\mathcal {F} _{\mathsf {PASSIVE}}\).
-
Ideal functionality reveals inputs: If the ideal world adversary \(\mathcal {S} \) sends \(\textsf {get\_inputs}\) to \(\mathcal {F} _{\mathsf {PASSIVE}}\), then it gets back the inputs of all corrupted parties, i.e. all \(x_i\), where \(i \in I\).
-
Output generation: The ideal functionality computes \((y_1, \dots , y_n) = f(x_1, \dots , x_n)\) and returns back \(y_i\) to each \(\mathrm {P}_{i}\). All honest parties output whatever they receive from \(\mathcal {F} _{\mathsf {PASSIVE}}\). The ideal world adversary \(\mathcal {S}\) outputs an arbitrary probabilistic polynomial-time computable function of the initial inputs of the corrupted parties, the auxiliary input z, and the messages received from the ideal functionality.
The joint distribution of the outputs of the honest parties and \(\mathcal {S}\) in an ideal execution is denoted by  .
.
Definition 1
Protocol \(\varPi \) is said to securely compute \(\mathcal {F}\) with security against passive adversaries in the \(\mathcal {G}\)-hybrid model if for every non-uniform probabilistic polynomial time adversary  in the real world, there exists a probabilistic polynomial time adversary \(\mathcal {S}\) in the ideal world such that for all
in the real world, there exists a probabilistic polynomial time adversary \(\mathcal {S}\) in the ideal world such that for all 

Covert adversaries. We use the security definition of Aumann and Lindell [AL07] for defining security against covert adversaries. The security notion we consider here is the strongest one of several and is known as the Strong Explicit Cheat Formulation (SECF). Covert adversaries are modelled by considering active adversaries, but relaxing the ideal functionality we aim to implement. The relaxed ideal functionality \(\mathcal {F} _{\mathsf {SECF}}\) allows the ideal-world adversary \(\mathcal {S}\) to perform a limited amount of cheating. That is, the ideal-world adversary, can attempt to cheat by sending \(\mathsf {cheat}\) to the ideal functionality, which randomly decides whether the attempt was successful or not. With probability \(\epsilon \), known as the deterrence factor, \(\mathcal {F} _{\mathsf {SECF}}\) will send back \(\mathsf {detected}\) and all parties will be informed of at least one corrupt party that attempted to cheat. With probability \(1 - \epsilon \), the simulator \(\mathcal {S}\) will receive \(\mathsf {undetected}\). In this case \(\mathcal {S}\) learns all parties’ inputs and can decide what the output of the ideal functionality is. The ideal execution proceeds as follows:
-
Inputs: Every honest party \(\mathrm {P}_{i}\) sends its inputs \(x_i\) to \(\mathcal {F} _{\mathsf {SECF}} \). The ideal world adversary \(\mathcal {S}\) gets auxiliary input z and sends inputs on behalf of all corrupted parties. Let \(\bar{x} = (x_1, \dots , x_n)\) be the vector of inputs that the ideal functionality receives.
-
Abort options: If a corrupted party sends \((\textsf {abort}, i)\) as its input to the \(\mathcal {F} _{\mathsf {SECF}}\), then the ideal functionality sends \((\textsf {abort}, i)\) to all honest parties and halts. If a corrupted party sends \((\textsf {corrupted}, i)\) as its input, then the functionality sends \((\textsf {corrupted}, i)\) to all honest parties and halts. If multiple corrupted parties send \((\textsf {abort}, i)\), respectively \((\textsf {corrupted}, i)\), then the ideal functionality only relates to one of them. If both \((\textsf {corrupted}, i)\) and \((\textsf {abort}, i)\) messages are sent, then the ideal functionality ignores the \((\textsf {corrupted}, i)\) messages.
-
Attempted cheat: If \(\mathcal {S}\) sends \((\textsf {cheat}, i)\) as the input of a corrupted \(\mathrm {P}_{i}\), then \(\mathcal {F} _{\mathsf {SECF}}\) decides randomly whether cheating was detected or not:
-
Detected: With probability \(\epsilon \), \(\mathcal {F} _{\mathsf {SECF}} \) sends \((\textsf {detected}, i)\) to the adversary and all honest parties.
-
Undetected: With probability \(1 - \epsilon \), \(\mathcal {F} _{\mathsf {SECF}} \) sends \(\textsf {undetected}\) to the adversary. In this case \(\mathcal {S}\) obtains the inputs \((x_1, \dots , x_n)\) of all honest parties from \(\mathcal {F} _{\mathsf {SECF}} \). It specifies an output \(y_i\) for each honest \(\mathrm {P}_{i}\) and \(\mathcal {F} _{\mathsf {SECF}} \) outputs \(y_i\) to \(\mathrm {P}_{i}\).
The ideal execution ends at this point. If no corrupted party sent \((\textsf {abort}, i)\), \((\textsf {corrupted}, i)\) or \((\textsf {cheat}, i)\), then the ideal execution continues below.
-
-
Ideal functionality answers adversary: The ideal functionality computes \((y_1, \dots , y_n) = f(x_1, \dots , x_n)\) and sends it to \(\mathcal {S}\).
-
Ideal functionality answers honest parties: The adversary \(\mathcal {S}\) either sends back \(\textsf {continue}\) or \((\textsf {abort, i})\) for a corrupted \(\mathrm {P}_{i}\). If the adversary sends \(\textsf {continue}\), then the ideal functionality returns \(y_i\) to each honest parties \(\mathrm {P}_{i}\). If the adversary sends \((\textsf {abort, i})\) for some i, then the ideal functionality sends back \((\textsf {abort, i})\) to all honest parties.
-
Output generation: An honest party always outputs the message it obtained from \(\mathcal {F} _{\mathsf {SECF}}\). The corrupted parties output nothing. The adversary outputs an arbitrary probabilistic polynomial-time computable function of the initial inputs of the corrupted parties, the auxiliary input z, and the messages received from the ideal functionality.
The outputs of the honest parties and \(\mathcal {S}\) in an ideal execution is denoted by
 . Note that the definition requires the adversary to either cheat or send the corrupted parties’ inputs to the ideal functionality, but not both.
. Note that the definition requires the adversary to either cheat or send the corrupted parties’ inputs to the ideal functionality, but not both.
Definition 2
Protocol \(\varPi \) is said to securely compute \(\mathcal {F}\) with security against covert adversaries with \(\epsilon \)-deterrent in the \(\mathcal {G}\)-hybrid model if for every non-uniform probabilistic polynomial time adversary  in the real world, there exists a probabilistic polynomial time adversary \(\mathcal {S}\) in the ideal world such that for all
in the real world, there exists a probabilistic polynomial time adversary \(\mathcal {S}\) in the ideal world such that for all 

Security against covert adversaries with public verifiability. This notion was first introduced by [AO12] and was later simplified by [HKK+19]. In covert security with public verifiability, each protocol \(\varPi \) is extended with an additional algorithm \(\mathsf {Judge}\). We assume that whenever a party detects cheating during an execution of \(\varPi \), it outputs a special message \(\mathsf {cert}\). The verification algorithm, \(\mathsf {Judge}\), takes as input a certificate \(\mathsf {cert}\) and outputs the identity, which is defined by the corresponding public key, of the party to blame or \(\bot \) in the case of an invalid certificate.
Definition 3
(Covert security with \(\epsilon \)-deterrent and public verifiability). Let  be the keys of parties Alice and Bob and f be a public function. We say that \((\pi ,\mathsf {Judge})\) securely computes f in the presence of a covert adversary with \(\epsilon \)-deterrent and public verifiability if the following conditions hold:
be the keys of parties Alice and Bob and f be a public function. We say that \((\pi ,\mathsf {Judge})\) securely computes f in the presence of a covert adversary with \(\epsilon \)-deterrent and public verifiability if the following conditions hold:
-
Covert Security: The protocol \(\varPi \) (which now might output \(\mathsf {cert}\) if an honest party detects cheating) is secure against a covert adversary according to the strong explicit cheat formulation above with \(\epsilon \)-deterrent.
-
Public Verifiability: If the honest party \(P \in \{A, B\}\) outputs \(\mathsf {cert}\) in an execution of the protocol, then
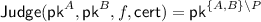 except with negligible probability.
except with negligible probability. -
Defamation-Freeness: If party \(P\in \{A,B\}\) is honest and runs the protocol with a corrupt party
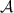 , then the probability that
, then the probability that 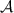 outputs \(\mathsf {cert}^*\) such that
outputs \(\mathsf {cert}^*\) such that  is negligible.
is negligible.
Next-Message Functionality. From time to time it may be convenient to go through a n-party protocol \(\varPi \) step-by-step. For this purpose we define a next-message functionality \((v_1, \dots , v_n) \leftarrow \varPi _{\mathsf {NEXT}} (i, x, r, T)\), which takes the party’s index i, its input x, its random tape r and the transcript T of messages the party has seen so far as input and computes a vector \((v_1, \dots , v_n)\) of messages, where party i should be sending message \(v_j\) to party j next. If \(v_j = \bot \), then party j does not receive a message from party i in that round. The protocol ends when \(\varPi _{\mathsf {NEXT}} \) outputs a special value \((\mathsf {out},z)\), where z is then interpreted as the output of that party.
2.2 Ideal Functionalities
We recall some basic ideal functionalities which we will make use of in our compiler. In the k-out-of-n oblivious transfer functionality \(\mathcal {F} _{\mathsf {OT}} \) (Fig. 1) a sender has a message vector \((m_0, \dots , m_n)\) and a receiver has index vector \((i_1, \dots , i_k)\). The receiver learns \((m_{i_1}, \dots , m_{i_k})\), but learns nothing about the other messages, whereas the sender learns nothing about the index vector.
The commitment functionality \(\mathcal {F} _{\mathsf {Com}} \) (Fig. 2) allows a party to first commit to a message and then later open this commitment to another party. The commitment should be binding, i.e. the committing party should not be able to open the commitment to more than one message, and hiding, i.e. the commitment should not reveal any information about the committed messages before the commitment is opened.
Our compilers requires commitments with non-interactive opening phase. To ease the notation, we will describe our protocols using commitments where the commitment phase is non-interactive as well, but our protocols could easily be extended to commitments with interactive commitment phases as well. To commit to a message m, we write: \((c,d)\leftarrow \mathsf {Com} (m;r)\) where c is the commitment and d is the opening information. The values d is then used to compute \(m'\leftarrow \mathsf {Open} (c,d)\) with \(m'=m\) or \(\bot \) in case of incorrect opening.
3 Compiler for Two-Party Protocols with No Inputs
We already provided a high level description of this compiler for protocols with no inputs in the introduction. The formal compiler is presented in Fig. 3. Before proving the security of our compiler, we discuss some of the subtle issues we encountered in the design of the protocol and the role they play in the proof. As the protocol is completely symmetric, and to ease the notation, we will explain all choices from the point of view of Alice. In the first step of the protocol both Alice and Bob pick random tapes \(s^A_i\) and \(s^B_i\) for all \(i\in [k]\), which are in turn parsed as \(s^P_i=(u^P_i, v^P_i, w^P_i)\) for \(P \in \{A, B\}\) during the protocol. There are several reasons for this. Since we want to compile any passively secure protocol, we can only guarantee security of the unopened execution if both parties use uniformly random tapes in this execution. Therefore, the actual random tape \(r^A_i\) which is used by A in the execution of the i-th copy of \(\varPi \) is obtained as  in step 5 of the protocol, thus, if B is honest \(r^A_i\) will indeed be random. Then, remember that we also use the seeds \(s^B_i\) that A receives from the OT as a form of commitment to the set of parties \(I^A\) that she has checked during the protocol execution, i.e., in Step 9 we let A send those seeds to B which in turns allows B to reconstruct \(I^B\). We of course need to argue that A cannot lie about her checked set \(I^A\) by, e.g., sending back to B some \(s^B_i\) with \(i \not \in I^A\). It might be tempting to believe that this follows from the security of the OT protocol. However, since B uses the values \(s^B_i\) in the protocol \(\varPi \) we need to “reserve” a sufficiently long chuck of \(s^B_i\), which we call \(w^B_i\), as a “witness” which is only used for the purpose of committing A to the set \(I^A\) and nothing else. Finally, we need to argue for public verifiability and defamation freeness. Public verifiability is obtained by asking A to sign the transcript of the protocol. Then, if B detects any cheating by verifying whether the messages sent by A in the checked executions of \(\varPi \) are consistent with her random tapes, B can output a certificate consisting of A’s signature together with information which allows a judge to reconstruct the random tape \(s^A_j\), where j is the execution in which B claims the cheating happened, i.e., to let the judge reconstruct A’s random tape, B includes the random tape he used when acting as the receiver in the OT protocol. Note that we let B verify for cheating after the execution of \(\varPi \) is completed. The reason for this is that if B aborts as soon as some cheating is detected, B would not receive A’s signature on the protocol transcript. Moreover, it is perfectly safe to run the protocol to the end even if cheating is detected since B has no private input in the protocol.
in step 5 of the protocol, thus, if B is honest \(r^A_i\) will indeed be random. Then, remember that we also use the seeds \(s^B_i\) that A receives from the OT as a form of commitment to the set of parties \(I^A\) that she has checked during the protocol execution, i.e., in Step 9 we let A send those seeds to B which in turns allows B to reconstruct \(I^B\). We of course need to argue that A cannot lie about her checked set \(I^A\) by, e.g., sending back to B some \(s^B_i\) with \(i \not \in I^A\). It might be tempting to believe that this follows from the security of the OT protocol. However, since B uses the values \(s^B_i\) in the protocol \(\varPi \) we need to “reserve” a sufficiently long chuck of \(s^B_i\), which we call \(w^B_i\), as a “witness” which is only used for the purpose of committing A to the set \(I^A\) and nothing else. Finally, we need to argue for public verifiability and defamation freeness. Public verifiability is obtained by asking A to sign the transcript of the protocol. Then, if B detects any cheating by verifying whether the messages sent by A in the checked executions of \(\varPi \) are consistent with her random tapes, B can output a certificate consisting of A’s signature together with information which allows a judge to reconstruct the random tape \(s^A_j\), where j is the execution in which B claims the cheating happened, i.e., to let the judge reconstruct A’s random tape, B includes the random tape he used when acting as the receiver in the OT protocol. Note that we let B verify for cheating after the execution of \(\varPi \) is completed. The reason for this is that if B aborts as soon as some cheating is detected, B would not receive A’s signature on the protocol transcript. Moreover, it is perfectly safe to run the protocol to the end even if cheating is detected since B has no private input in the protocol.
This, together with the transcript of the OT protocol, allows the judge to recompute the output of B in the protocol i.e., the random tape of A and, if we use an OT which satisfies perfect correctness, a corrupt B cannot lie about the output received in the protocol.Footnote 6 Note that, perhaps counterintuitively, the judge does not need to check that the messages sent from the accuser to the accused are correct! This is because whether the messages sent from the accuser to the accused are correct or not has no influence in whether the messages from the accused to the accuser are correct or not according to the protocol specification. In other words, a corrupt party cannot “trick” an honest party into cheating by sending ill-formed messages.
We are now ready for the security analysis.
Judge protocol for our compiler in Fig. 3.
Theorem 1
Let \(\varPi \) be a protocol that implements a two-party functionality \(\mathcal {F} \), which receives no private inputs, with security against passive adversaries. Let \(\varPi _{\mathsf {OT}} ^{(k,k/2-1)}\) be a protocol that implements \(\mathcal {F} _{\mathsf {OT}} ^{(k,k/2-1)}\) with active security and perfect correctness. Then the compiler illustrated in Fig. 3 and 4 implements the two-party functionality \(\mathcal {F} \) with security and public verifiability against covert adversaries with deterrence factor \(\epsilon = \frac{1}{2} - \frac{1}{k}\).
Proof
We will proceed by proving security, public verifiability, and defamation-freeness separately. Without loss of generality we assume that Alice is corrupted by the adversary  . The case for Bob being corrupted is symmetrical. For proving security, we construct a simulator \(\mathcal {S} \) playing the role of Alice in the ideal world and using
. The case for Bob being corrupted is symmetrical. For proving security, we construct a simulator \(\mathcal {S} \) playing the role of Alice in the ideal world and using  as a subroutine as followsFootnote 7:
as a subroutine as followsFootnote 7:
Simulation part A:
-
0.
Generate
 and send
and send 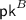 to
to  .
.
-
1.
The simulator picks random seeds \(s^B_i\), for \(i \in [k] \cup \{\mathsf {R}\}\).
-
2.
Do nothing.Footnote 8
-
3.
The simulator uses \(\mathcal {S} _\mathsf {OT}\) to simulate both OT executions. In the one where it acts as a receiver it extracts
 ’s input \((s')^A_1,\ldots , (s')^A_k\). In the one where it acts as the sender it extracts the vector \(I^A\), and sends the corresponding seeds to the adversary.
’s input \((s')^A_1,\ldots , (s')^A_k\). In the one where it acts as the sender it extracts the vector \(I^A\), and sends the corresponding seeds to the adversary. -
4.
For \(i \in [k]\), derive \(u^B_i\) and \(v^B_i\) from seed \(s^B_i\) and send \(v^B_i\) to
 . Receive the \(v^A_i\) from
. Receive the \(v^A_i\) from  .
. -
5.
The simulator \(\mathcal {S} \) engages in k honest executions of \(\varPi \) with
 , where the simulator uses random tape \( r^B_i = u^B_i \oplus v^A_i\) in execution i. Let \(T_{\varPi }\) be the set of transcripts of those executions.
, where the simulator uses random tape \( r^B_i = u^B_i \oplus v^A_i\) in execution i. Let \(T_{\varPi }\) be the set of transcripts of those executions. -
6.
The simulator computes
 and sends it to
and sends it to  . The adversary sends back \(\sigma ^A\). If the adversary’s signature does not verify, then the simulation aborts (similarly, the simulation aborts if at any previous step
. The adversary sends back \(\sigma ^A\). If the adversary’s signature does not verify, then the simulation aborts (similarly, the simulation aborts if at any previous step  stops sending messages or sends messages which are blatantly wrong e.g., they generate an abort in the real world with probability 1).
stops sending messages or sends messages which are blatantly wrong e.g., they generate an abort in the real world with probability 1). -
7.
The simulator uses seeds \((s')^A_i\) to check whether
 behaved correctly during all executions of \(\varPi \) in step 4 and 5 (using the incorrect random tapes \(r^A_i\) constitutes cheating as well). If
behaved correctly during all executions of \(\varPi \) in step 4 and 5 (using the incorrect random tapes \(r^A_i\) constitutes cheating as well). If 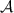 deviated in any of the protocol executions, then the simulator sends \((\mathsf {cheat}, A)\) to the ideal functionality \(\mathcal {F} \), which responds with \(\mathsf {resp} = \{\mathsf {detected}, \mathsf {undetected} \}\). Store index \(j^*\) of the execution in which
deviated in any of the protocol executions, then the simulator sends \((\mathsf {cheat}, A)\) to the ideal functionality \(\mathcal {F} \), which responds with \(\mathsf {resp} = \{\mathsf {detected}, \mathsf {undetected} \}\). Store index \(j^*\) of the execution in which  cheated, along with the exact location \(\mathsf {loc} ^*\) of where cheating happened in that execution itself, and then proceeds to part B if \(\mathsf {flag} =\mathsf {undetected} \).
cheated, along with the exact location \(\mathsf {loc} ^*\) of where cheating happened in that execution itself, and then proceeds to part B if \(\mathsf {flag} =\mathsf {undetected} \). -
8.
If \(\mathsf {flag} = \mathsf {detected} \), the simulator outputs a certificate \(\mathsf {cert}\) in the following way: The simulator rewinds the adversary and this time runs the protocol as an honest party would do, except that it samples \(s^B_{\mathsf {R}}\) under the constraint that \(j^*\in I^B\). The simulator keeps rewinding until it detects cheating again in \((j^*,\mathsf {loc} ^*)\), and outputs a certificate as an honest party would do (this concludes the simulation).
-
9.
If the \(\mathsf {flag} \) was not set: Reveal \((w')^A_i\) for \(i \in I^B\) and receive \((w^*)^B_i\) from the adversary, and checks that they are equal to the \(w^B_i\) derived from \(s^B_i\).
-
10.
If the simulation reaches this stage, then \(\mathcal {S} \) sets \(\mathsf {flag} = \mathsf {all\_good} \), requests output \(y^A\) from \(\mathcal {F} \) and moves to part B.
At this point the simulator \(\mathcal {S} \) rewinds  back to right before step 1 and keeps rewinding
back to right before step 1 and keeps rewinding  until the simulation is successful and
until the simulation is successful and  repeats the same cheating pattern as in part AFootnote 9. In particular the simulator runs the following steps:
repeats the same cheating pattern as in part AFootnote 9. In particular the simulator runs the following steps:
Simulation part B:
-
1.
Do nothing.
-
2.
Do nothing.
-
3.
The simulator uses \(\mathcal {S} _\mathsf {OT}\) to simulate both OT executions. In the one where it acts as a receiver it extracts
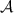 ’s input \((s')^A_1,\ldots , (s')^A_k\). In the one where it acts as the sender it extracts the vector \(I^A\), picks random seeds \(s^B_i\) for all \(i\in I^A\) and sends them to the adversary.
’s input \((s')^A_1,\ldots , (s')^A_k\). In the one where it acts as the sender it extracts the vector \(I^A\), picks random seeds \(s^B_i\) for all \(i\in I^A\) and sends them to the adversary. -
4.
Depending on \(\mathsf {flag} \) do the following:
-
If \(\mathsf {flag} = \mathsf {all\_good} \), then pick a random \(i^* \not \in I^A\) with the same distribution as in the protocol. For all \(i \not \in I^A\) with \(i\ne i^*\) the simulator picks random \(v_i^B\) (while letting the \(w_i^B\) still undefined). It computes the tape \(r^A_{i^*}\) using the simulator for the protocol \(\mathcal {S} _\varPi \), and it computes
 , where the \(u^A_{i^*}\) are derived from the \(s^A_{i^*}\). Send all the the \(v_i^B\) to
, where the \(u^A_{i^*}\) are derived from the \(s^A_{i^*}\). Send all the the \(v_i^B\) to  and receive \(v_i^A\) from
and receive \(v_i^A\) from  .
. -
If \(\mathsf {flag} =\mathsf {undetected} \), then the simulator \(\mathcal {S} \) runs this step as an honest party.
-
-
5.
Depending on \(\mathsf {flag} \) do the following:
-
If \(\mathsf {flag} = \mathsf {all\_good} \), then run all executions of \(\varPi \) honestly (picking random \(u^B_i\) and computing the corresponding random tape \(r^B_i\) to be used in the protocol) except for \(i^*\), which is simulated using \(\mathcal {S} _\varPi \). When \(\mathcal {S} _\varPi \) requests the output, then the simulator provides it with \(y^A\).
-
If \(\mathsf {flag} = \mathsf {undetected} \), then the simulator \(\mathcal {S} \) honestly executes the protocols based on its random seeds.
-
-
6.
The simulator computes
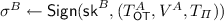 and sends it to
and sends it to  . The adversary sends back \(\sigma ^A\).
. The adversary sends back \(\sigma ^A\). -
7.
Depending on \(\mathsf {flag} \) do the following:
-
If \(\mathsf {flag} = \mathsf {all\_good} \), then the simulator uses all seeds \((s')^A_i\) to check whether
 behaved correctly during the executions of \(\varPi \) in step 4. If
behaved correctly during the executions of \(\varPi \) in step 4. If 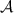 deviated from any of the protocols, then it rewinds back to the beginning of part B, otherwise it terminates the simulation by honestly running the last two steps of the protocol, by choosing a random \(s^B_\mathsf {R}\) and \(I^B\) (consistent with the choice of \(i^*\) in step 5) and sends back the corresponding \((w')^A_i\) derived from \((s')^A_i\) for \(i\in I^B\).
deviated from any of the protocols, then it rewinds back to the beginning of part B, otherwise it terminates the simulation by honestly running the last two steps of the protocol, by choosing a random \(s^B_\mathsf {R}\) and \(I^B\) (consistent with the choice of \(i^*\) in step 5) and sends back the corresponding \((w')^A_i\) derived from \((s')^A_i\) for \(i\in I^B\). -
If \(\mathsf {flag} = \mathsf {undetected} \), then the simulator checks whether
 deviated from any of the protocol executions. If
deviated from any of the protocol executions. If  did not deviate, if it deviated somewhere other than execution \(j^*\) in location \(\mathsf {loc} ^*\), or if \(j^* \not \in I^B\), then rewind back to the beginning of part B. Otherwise, terminate the execution and send output \(\widetilde{y}^B\) of execution \(i^*\) to the ideal functionality \(\mathcal {F} \).
did not deviate, if it deviated somewhere other than execution \(j^*\) in location \(\mathsf {loc} ^*\), or if \(j^* \not \in I^B\), then rewind back to the beginning of part B. Otherwise, terminate the execution and send output \(\widetilde{y}^B\) of execution \(i^*\) to the ideal functionality \(\mathcal {F} \).
To conclude the proof, we show that the real and the simulated view of the adversary is indistinguishable. We defer these hybrids to the full version of the paper.
Public Verifiability. Without loss of generality assume that Alice is corrupt. If cheating occurred, then Alice must have deviated from one of the protocol executions in step 5 of the protocol, i.e., one of the messages in one of the executions that originates from Alice must be inconsistent with the random tape she should be using. If an honest Bob publishes a certificate, then cheating was detected, meaning that Bob obtained Alice’s random tape for the execution in which she cheated. Since the transcripts of the protocol executions are signed by Alice, any party can verify that one message is inconsistent with one of Alice’s random tapes. Importantly, since Alice has no way of knowing whether cheating will be successful or not before sending the signature in step 6, her decision to abort the protocol at any point before that has to be independent of Bob’s choice of \(I^B\).
Defamation-Freeness. Assume that  acting as Alice manages to break the defamation-freeness of the protocol and blames an honest B. We argue that this leads to a forgery to the underlying signature scheme, thus reaching a contradiction with the assumption of the theorem. In particular, for a \(\mathsf {Judge}\) to blame Bob it must hold that in step 5 the judge finds a message from B to A which is not consistent with the next-message function of \(\varPi \) in execution \(j^*\). Since Bob is honest, this means that either the transcript of the protocol \(T^*\) included in the certificate or the random tape \(r^*\) used by the judge to verify B in this step are not the ones that Bob used in the protocol (this of course is true for all \(j\in [k]\) and therefore independent of which execution \(j^*\) is claimed by
acting as Alice manages to break the defamation-freeness of the protocol and blames an honest B. We argue that this leads to a forgery to the underlying signature scheme, thus reaching a contradiction with the assumption of the theorem. In particular, for a \(\mathsf {Judge}\) to blame Bob it must hold that in step 5 the judge finds a message from B to A which is not consistent with the next-message function of \(\varPi \) in execution \(j^*\). Since Bob is honest, this means that either the transcript of the protocol \(T^*\) included in the certificate or the random tape \(r^*\) used by the judge to verify B in this step are not the ones that Bob used in the protocol (this of course is true for all \(j\in [k]\) and therefore independent of which execution \(j^*\) is claimed by  ). Since Bob is honest he will not sign a protocol transcript \(T^*\ne T_\varPi \), e.g., a transcript different than the one in the protocol executed by the honest Bob. Thus, \(r^*\) must be the wrong random tape. From step 4 we know that \(r^*\) is computed as the exclusive OR of a value \(v^*\) included in the certificate and signed by Bob and a value \(u^*\) derived from previous steps in the protocol. Again, since an honest Bob would not have signed the wrong \(v^*\ne v^A_j\) if \(r^*\) is not the real randomness used by Bob in the protocol the it is because of a fault in \(u^*\), which is in turn derived by the seed \(s^*\) received as the \(j^*\)-th output of A in the execution of the OT protocol. Now, if \(s^* \ne s^B_{j^*}\) (the value used as input by Bob in the real protocol execution), this must be because either the OT protocol transcript \(T^A_{OT}\) in the certificate are incorrect or the randomness \(s^*\) included in the certificate is incorrect. Remember that both A’s input and randomness in the OT protocol are derived by \((s^*)^A_{j^*}\) which is included in the certificate. Now it must be that \((s^*)^A_{j^*}\) leads to an input set \(I^*\) such that \(j^*\in I^*\), or the judge would not be able to reconstruct \(s^B_{j^*}\). Then, fixed any input set \(I^*\), the perfect correctness of the OT protocol implies that given the correct protocol transcript \(T^A_{OT}\) there cannot exist any random tape such that the output of A in the protocol is incorrect. Thus, the transcript \(T^A_{OT}\) included in the certificate must be the wrong one. Once again, since Bob would not have signed the wrong transcript this implies that
). Since Bob is honest he will not sign a protocol transcript \(T^*\ne T_\varPi \), e.g., a transcript different than the one in the protocol executed by the honest Bob. Thus, \(r^*\) must be the wrong random tape. From step 4 we know that \(r^*\) is computed as the exclusive OR of a value \(v^*\) included in the certificate and signed by Bob and a value \(u^*\) derived from previous steps in the protocol. Again, since an honest Bob would not have signed the wrong \(v^*\ne v^A_j\) if \(r^*\) is not the real randomness used by Bob in the protocol the it is because of a fault in \(u^*\), which is in turn derived by the seed \(s^*\) received as the \(j^*\)-th output of A in the execution of the OT protocol. Now, if \(s^* \ne s^B_{j^*}\) (the value used as input by Bob in the real protocol execution), this must be because either the OT protocol transcript \(T^A_{OT}\) in the certificate are incorrect or the randomness \(s^*\) included in the certificate is incorrect. Remember that both A’s input and randomness in the OT protocol are derived by \((s^*)^A_{j^*}\) which is included in the certificate. Now it must be that \((s^*)^A_{j^*}\) leads to an input set \(I^*\) such that \(j^*\in I^*\), or the judge would not be able to reconstruct \(s^B_{j^*}\). Then, fixed any input set \(I^*\), the perfect correctness of the OT protocol implies that given the correct protocol transcript \(T^A_{OT}\) there cannot exist any random tape such that the output of A in the protocol is incorrect. Thus, the transcript \(T^A_{OT}\) included in the certificate must be the wrong one. Once again, since Bob would not have signed the wrong transcript this implies that  has managed to forge a signature, thus reaching a contradiction.
has managed to forge a signature, thus reaching a contradiction.
\(\square \)
In Theorem 1 we have assumed that each party checks less than half of the executions, which guarantees that there exists an execution that is not checked by either of the parties, but limits our deterrence factor \(\epsilon \) to be less than 1/2. We can modify our protocol to allow each party to check \(\delta k\) executions for any constant \(1/2 \le \delta < 1\), which allows us to obtain deterrence factors larger than 1/2. The main observation here is that, as long as each party leaves a constant fraction of the executions unchecked, we have a constant probability of ending up with an execution that is not checked by either of the parties. In our modified protocol, we run the protocol from Fig. 3 as before up to including step 10. If there exists no execution that is not checked by either party, i.e., \([k] \setminus (I^A \cup I^B) = \emptyset \), then the parties simply start over the whole protocol run until the condition is satisfied.
Lemma 1
The modified protocol described above runs in expected polynomial time.
Proof
To clarify terminology, we will call one execution of the overall protocol from Fig. 3 an outer execution and the executions of \(\varPi \) within will be called inner executions. Observe that one outer execution runs in polynomial time. Let \(\mathsf {good}\) be the event that the outer execution has an unchecked inner execution and let  be the opposite event. If we can show that \(\Pr [\mathsf {good}] \ge c\), where c is a constant, then we are done, since this means that, in expectation, we need to run the outer protocol 1/c times until the event \(\mathsf {good}\) happens.
be the opposite event. If we can show that \(\Pr [\mathsf {good}] \ge c\), where c is a constant, then we are done, since this means that, in expectation, we need to run the outer protocol 1/c times until the event \(\mathsf {good}\) happens.
Now observe that for any \(\delta k\) inner executions chosen by Alice, Bob would need to choose the remaining \(k - \delta k\) with his \(\delta k\) choices to trigger the  event. We can loosely upper bound the probability of this event by just considering the Bernoulli trial, where we only ask Bob to pick \(k - \delta k\) inner executions (with repetitions) that were not chosen by Alice.
event. We can loosely upper bound the probability of this event by just considering the Bernoulli trial, where we only ask Bob to pick \(k - \delta k\) inner executions (with repetitions) that were not chosen by Alice.

Now since both k and \(\delta \) are constants, this whole expression is also a constant. Since the probability for  is upper bounded by a constant, the event \(\mathsf {good}\) is lower bounded by a constant too.
is upper bounded by a constant, the event \(\mathsf {good}\) is lower bounded by a constant too.
\(\square \)
The calculation above is very loose and just aims to show that the expected number of repetitions is constant. To get a better feeling of how often we have to rerun the protocol for some given deterrence factor, consider for instance \(k = 3\) with \(\epsilon = 2/3\). The probability of the event \(\mathsf {good}\) is the probability of Bob picking the same two executions that Alice picked, that is, the probability is \(2/3 \cdot 1/2 = 1/3\), meaning that we need to repeat the protocol three times in expectation.
4 Efficient Two-Party Computation in the Preprocessing Model
In this section, we consider actively secure two-party protocols in the preprocessing model. Such protocols are composed of an input-independent preprocessing protocol \(\varPi _{\mathsf {OFF}} \) for generating correlated randomness and separate protocol \(\varPi _{\mathsf {ON}} \) for the online phase, which uses the preprocessed correlated randomness to compute some desired function on some given private inputs. The main advantage of such protocols is that the computational “heavy lifting” can be done in the preprocessing, such that the online phase can be executed very efficiently, in particular, much faster than what can be done by a standalone protocol that computes the same functionality without correlated randomness from scratch. One of the most well known protocols in the preprocessing model is the SPDZ [DPSZ12] protocol for computing arbitrary arithmetic circuits.
A natural question to ask is, whether we can use our results from Sect. 3 to construct more efficient protocols in the preprocessing model by relaxing the security guarantees from active to covert. The main idea here is to replace slow preprocessing protocols with active security by faster preprocessing protocols with passive security, which are then used in combination with our compiler from Theorem 1 to generate the correlated randomness. Note, that we do not need to apply our compiler to the online phase, which is already actively secure. That is, we can combine a preprocessing protocol with covert security with an actively secure online phase to obtain an overall protocol which is secure against covert adversaries as we show in the following Lemma.
Lemma 2
Let \((\varPi _{\mathsf {OFF}}, \varPi _{\mathsf {ON}})\) be a protocol implementing \(\mathcal {F} _f\) with active security, where the preprocessing protocol \(\varPi _{\mathsf {OFF}} \) implements \(\mathcal {F} _{\mathsf {OFF}} \) and \(\varPi _{\mathsf {ON}} \) implements \(\mathcal {F} _{\mathsf {ON}} \) with active security respectively. If \(\widetilde{\varPi }_{\mathsf {OFF}} \) implements \(\mathcal {F} _{\mathsf {OFF}} \) with security against covert adversaries (and public verifiability), then \((\widetilde{\varPi }_{\mathsf {OFF}}, \varPi _{\mathsf {ON}})\) implements \(\mathcal {F} _f\) with security against covert adversaries (and public verifiability) with the same deterrence factor as \(\widetilde{\varPi }_{\mathsf {OFF}} \).
Proof
To prove the statement above, we need to construct a simulator \(\mathcal {S} \) that interacts with the (covert version of) ideal functionality \(\mathcal {F} _f\). By assumption, there exists simulators \((\mathcal {S} _{\mathsf {OFF}}, \mathcal {S} _{\mathsf {ON}})\) for \((\varPi _{\mathsf {OFF}}, \varPi _{\mathsf {ON}})\) and simulator \(\widetilde{\mathcal {S}}_{\mathsf {OFF}} \) for \(\widetilde{\varPi }_{\mathsf {OFF}} \). We will use \((\widetilde{\mathcal {S}}_{\mathsf {OFF}}, \mathcal {S} _{\mathsf {ON}})\) to simulate the view of the adversary  . If
. If  attempts to cheat after we finished the preprocessing simulation, then we can simply consider each attempt as an abort, since the online phase is actively secure. If during the preprocessing simulation
attempts to cheat after we finished the preprocessing simulation, then we can simply consider each attempt as an abort, since the online phase is actively secure. If during the preprocessing simulation  attempts to cheat and consequently \(\widetilde{\mathcal {S}}_{\mathsf {OFF}} \) outputs a cheat command, we will forward it to \(\mathcal {F} _f\). If cheating is undetected, then the ideal functionality returns all inputs and finishing the simulation is trivial. If cheating is detected, then we inform \(\widetilde{\mathcal {S}}_{\mathsf {OFF}} \) and finish the simulation accordingly.
attempts to cheat and consequently \(\widetilde{\mathcal {S}}_{\mathsf {OFF}} \) outputs a cheat command, we will forward it to \(\mathcal {F} _f\). If cheating is undetected, then the ideal functionality returns all inputs and finishing the simulation is trivial. If cheating is detected, then we inform \(\widetilde{\mathcal {S}}_{\mathsf {OFF}} \) and finish the simulation accordingly.
Observe that if cheating was detected in the preprocessing, then the simulated view is indistinguishable from a real one by assumption on the security of \(\widetilde{\mathcal {S}}_{\mathsf {OFF}} \). If no cheating happened, then the actively secure and covertly secure versions of \(\mathcal {F} _f\) have identical input/output behaviors and thus the simulated views are also indistinguishable by assumption.
The resulting protocol is also publicly verifiable, since the preprocessing protocol is publicly verifiable, and in the (actively secure) online phase only “blatant cheating” can be performed.
\(\square \)
We now consider the concrete case of SPDZ for two-party computation. In the SPDZ preprocessing, Alice and Bob generate correlated randomness in the form of secret shared multiplication triples over some field \(\mathbb {F}\), i.e. Alice should obtain a set \(\{(a^A_i, b^A_i, c^A_i)\}_{i \in [\ell ]}\) and Bob should obtain \(\{(a^B_i, b^B_i, c^B_i)\}_{i \in [\ell ]}\) such that for all \(i \in [\ell ]\) it holds that
Current actively secure preprocessing protocols for generating such randomness use a combination of checks based on message authentication codes and zero-knowledge proofs. To obtain a passively secure counterpart that we can then plug into our compiler, we simply take one of those existing protocols and remove those checks.
For completeness, we sketch how one such preprocessing protocol could look like. Assume we are given access to a somewhat homomorphic encryption scheme, i.e., a scheme that allows us to compute additions  and a limited number of multiplications
and a limited number of multiplications  . Furthermore, assume that the decryption key
. Furthermore, assume that the decryption key  is shared between Alice and Bob. For \(P \in \{A, B\}\), each party P separately picks random values \(\{a_i^P, b_i^P, r_i^P\}_{i \in [\ell ]}\) and sends
is shared between Alice and Bob. For \(P \in \{A, B\}\), each party P separately picks random values \(\{a_i^P, b_i^P, r_i^P\}_{i \in [\ell ]}\) and sends  to the other party. Each party \(P \in \{A, B\}\) uses the homomorphic properties of the encryption scheme to compute
to the other party. Each party \(P \in \{A, B\}\) uses the homomorphic properties of the encryption scheme to compute  , where \(r_i = r_i^A + r_i^B\), and
, where \(r_i = r_i^A + r_i^B\), and  , where \(c_i = \left( a^A_i + a^B_i\right) \cdot \left( b^A_i + b^B_i\right) \). Both parties jointly decrypt each ciphertext in the set
, where \(c_i = \left( a^A_i + a^B_i\right) \cdot \left( b^A_i + b^B_i\right) \). Both parties jointly decrypt each ciphertext in the set  . Alice computes \(\{c^A_i\}_{i \in [\ell ]}\), where \(c_i^A = (c_i - r_i) + r_i^A\) and Bob sets \(\{c_i^B\}_{i \in [\ell ]} := \{r_i^B\}_{i \in [\ell ]}\). It is easy to see that this protocol outputs correct multiplication triples and securely hides the value of each \(c_i\), since \(r_i\) is a uniformly random string.
. Alice computes \(\{c^A_i\}_{i \in [\ell ]}\), where \(c_i^A = (c_i - r_i) + r_i^A\) and Bob sets \(\{c_i^B\}_{i \in [\ell ]} := \{r_i^B\}_{i \in [\ell ]}\). It is easy to see that this protocol outputs correct multiplication triples and securely hides the value of each \(c_i\), since \(r_i\) is a uniformly random string.
One more detail that we need to consider here is that actively secure preprocessing protocols output correlated randomness along with authentication values. Our preprocessing protocol from above can easily be modified output these authentication values as well. Without going into too much detail, these authentication values are essentially the product of the secret shared multiplication triples and some encrypted key. These multiplications can be performed as above by using the homomorphic properties of the encryption scheme.
Combining the passively secure preprocessing protocol outlined above with our compiler from Theorem 1 results in a covertly secure preprocessing protocol with public verifiability that, for a deterrence factor of 1/3, is roughly 3 times faster than the best known actively secure protocol. Since the total running time of SPDZ is mostly dominated by the running time of the preprocessing protocol, we also obtain an overall improvement in the total running time of SPDZ of roughly the same factor 3.
5 General Compiler for Two-Party Protocols
The first ingredient we need in this section is a two-party protocol \(\widetilde{\varPi }_{\mathsf {SETUP}}\) that realizes \(\mathcal {F} _{\mathsf {SETUP}} ^{(m,t)}\) (Fig. 5) with passive security. Let \(\varPi _{\mathsf {SETUP}} \) be the protocol one obtains by applying our compiler from Theorem 1 to the protocol \(\widetilde{\varPi }_{\mathsf {SETUP}}\).
Given the protocol \(\varPi _{\mathsf {SETUP}} \), we are now ready to present our main compiler in Fig. 6. In the protocol description, we overload notation and identify the i-th virtual party \(\mathbb {V}_{i} ^P\) belonging to real party P with the set containing the random tapes and symmetric encryption keys used by this party in the protocol. This set, together with the public ciphertext containing the party’s input encrypted with its own symmetric encryption key, completely determines the behaviour of that virtual party in the protocol. Let \(f\!\left( x^A, x^B\right) \) be the function Alice and Bob would like to compute on their respective inputs \(x^A\) and \(x^B\). Let \(\varPi \) be a 2m-party protocol that implements a related functionality
where
with security against \(m\,+\,t\) passive corruptions. That is, the ideal functionality \(\mathcal {F} _g\) takes as input an m-out-of-m secret sharing of \(x^A\) and \(x^B\) and computes a 2m-out-of-2m secret sharing of \(f(x^A, x^B)\).
Judge protocol for our two-party protocol in Fig. 6.
Theorem 2
Let f be an arbitrary two-party functionality and let g be the related functionality as defined above. Let \(\varPi \) be a 2m-party protocol that implements the ideal functionality \(\mathcal {F} _g\) with security against \(m+t\) passive corruptions. Let \(\varPi _{\mathsf {SETUP}} \) be the protocol from Fig. 3 realizing ideal functionality \(\mathcal {F} _{\mathsf {SETUP}} \) from Fig. 5 with deterrence factor \(\frac{t}{m}\). Let \(\mathsf {Com} \) be a commitment scheme that realizes \(\mathcal {F} _{\mathsf {Com}} \). Then the compiler illustrated in Fig. 6 and 7 implements the two-party ideal functionality \(\mathcal {F} _f\) with security and public verifiability against covert adversaries with deterrence factor \(\epsilon = t/m\).
Proof
We will proceed by proving security, public verifiability, and defamation-freeness separately. Without loss of generality again we assume that Alice is corrupted by the adversary  . The case for Bob being corrupted is completely symmetrical. For proving security, we construct a simulator \(\mathcal {S} \) playing the role of Alice in the ideal world and using
. The case for Bob being corrupted is completely symmetrical. For proving security, we construct a simulator \(\mathcal {S} \) playing the role of Alice in the ideal world and using  as a subroutine. Let \(\mathcal {S} _\mathsf {SETUP} \) be the simulator corresponding to the ideal functionality \(\mathcal {F} _{\mathsf {SETUP}} \).
as a subroutine. Let \(\mathcal {S} _\mathsf {SETUP} \) be the simulator corresponding to the ideal functionality \(\mathcal {F} _{\mathsf {SETUP}} \).
Simulation:
-
0.
Generate
 and send
and send  to
to  . Like a real party, the simulator aborts in any case of blatant cheating.
. Like a real party, the simulator aborts in any case of blatant cheating.
-
1.
Simulate the functionality \(\mathcal {F} _{\mathsf {SETUP}} \).
-
(a)
In case
 inputs \(\mathsf {cheat} \), the simulator forwards \(\mathsf {cheat} \) to \(\mathcal {F} _f\). If \(\mathcal {F} _f\) outputs \(\mathsf {detected} \), the simulation sets \(\mathsf {flag} =\mathsf {detected} \) and stops.
inputs \(\mathsf {cheat} \), the simulator forwards \(\mathsf {cheat} \) to \(\mathcal {F} _f\). If \(\mathcal {F} _f\) outputs \(\mathsf {detected} \), the simulation sets \(\mathsf {flag} =\mathsf {detected} \) and stops. -
(b)
If \(\mathcal {F} _f\) outputs \(\mathsf {undetected} \), it also provides the simulator with the input \(x^B\) of the honest party. The simulator then sets \(\mathsf {flag} =\mathsf {undetected} \) and allows
 to pick the output \(y^B\) of B in \(\mathcal {F} _{\mathsf {SETUP}} \) and runs the protocol honestly, finally it has to provide \(\mathcal {F} _f\) with the output for B in the ideal world, and he does so by running the protocol as an honest party would do with
to pick the output \(y^B\) of B in \(\mathcal {F} _{\mathsf {SETUP}} \) and runs the protocol honestly, finally it has to provide \(\mathcal {F} _f\) with the output for B in the ideal world, and he does so by running the protocol as an honest party would do with  , and using the output \(z^B\) obtained in this execution.
, and using the output \(z^B\) obtained in this execution. -
(c)
Finally, if
 does not attempt to cheat in \(\mathcal {F} _{\mathsf {SETUP}} \), the simulator picks the output of the corrupt party \(y^A\) in the following way: Pick a random set \(I^A\), and run the simulator \(\mathcal {S} _\varPi \) of the 2m-party protocol \(\varPi \), to produce the random tapes of all the virtual parties belonging to A for all \(i\in [m]\) and of the checked virtual parties belonging to B for \(i\in I^A\).
does not attempt to cheat in \(\mathcal {F} _{\mathsf {SETUP}} \), the simulator picks the output of the corrupt party \(y^A\) in the following way: Pick a random set \(I^A\), and run the simulator \(\mathcal {S} _\varPi \) of the 2m-party protocol \(\varPi \), to produce the random tapes of all the virtual parties belonging to A for all \(i\in [m]\) and of the checked virtual parties belonging to B for \(i\in I^A\).The simulator also picks random keys \(k^A_{(i,j)}\) for \(i,j\in [m]\) and \(k^B_{(i,j)}\) for all \(i,j\in I^A\) at random. Now the simulator can honestly produce commitments \((c^A_i,d^A_i)\leftarrow \mathsf {Com} (\mathbb {V}_{i} ^A)\) for all \(i\in [m]\) and \((c^B_i,d^B_i)\leftarrow \mathsf {Com} (\mathbb {V}_{i} ^B)\) for \(i\in I^A\). Finally, use the simulator \(\mathcal {S} _\mathsf {Com} \) to simulate all commitments \(c^B_i\) with \(i\not \in I^A\).
-
(a)
-
2.
As in the protocol, send the signature \(\sigma ^B_c\) to
 . Receive \(\sigma ^A_c\) (and abort if invalid).
. Receive \(\sigma ^A_c\) (and abort if invalid). -
3.
Do nothing. (see Footnote 8)
-
4.
Receive \(e^A_i,\sigma ^A_i\) for \(i\in [m]\). Compute
 where \(\tilde{x}^B_i\) is uniformly random if \(i\in I^A\) or 0 otherwise.
where \(\tilde{x}^B_i\) is uniformly random if \(i\in I^A\) or 0 otherwise. -
5.
Decrypt
 for all \(i\in [m]\) and reconstruct \(x^A\).
for all \(i\in [m]\) and reconstruct \(x^A\). -
6.
Simulate the execution of the 2m-party protocol \(\varPi \) in the following way: Use the simulator \(\mathcal {S} _\varPi \) to simulate the execution of the unchecked virtual parties belonging to B i.e., \(\mathbb {V}_{i} ^B\) for \(i\not \in I^A\), and execute the checked parties belonging to B as an honest party would do e.g., consistent with the random tapes and keys from step 1c, and inputs \(\tilde{x}^B_i\) as defined in step 4.
In particular, this means that all messages that are sent from the virtual parties belonging to B to the virtual parties belonging to A or to the checked virtual parties belonging to B are generated using the simulator. The former kind are simply sent to
 while the latter kind are first encrypted using the appropriate keys. To simulate the message exchanged between pairs of unchecked parties belonging to B, send encryptions of 0 to
while the latter kind are first encrypted using the appropriate keys. To simulate the message exchanged between pairs of unchecked parties belonging to B, send encryptions of 0 to  . Moreover, if the simulator gets to step 6c, it produces commitments \(\gamma ^B_i\) using the simulator for the commitment \(\mathcal {S} _\mathsf {Com} \) for \(i\in [m]\setminus I^A\), and commits honestly to the shares obtained by the virtual parties for all \(i\in I^A\).
. Moreover, if the simulator gets to step 6c, it produces commitments \(\gamma ^B_i\) using the simulator for the commitment \(\mathcal {S} _\mathsf {Com} \) for \(i\in [m]\setminus I^A\), and commits honestly to the shares obtained by the virtual parties for all \(i\in I^A\).This concludes the description of how the simulator simulates outgoing messages from \(\mathcal {S} \) to
 . We now describe how the simulator reacts to incoming messages from
. We now describe how the simulator reacts to incoming messages from  to \(\mathcal {S} \): the simulator performs the checks in steps 6a–6c of the protocol for all virtual parties belonging to A i.e., \(\forall i\in [m]\). If
to \(\mathcal {S} \): the simulator performs the checks in steps 6a–6c of the protocol for all virtual parties belonging to A i.e., \(\forall i\in [m]\). If  deviated in any of its virtual parties \(i^*\), then the simulator sends \((\mathsf {cheat}, A)\) to the ideal functionality \(\mathcal {F} _f\), which responds with \(\mathsf {resp} = \{\mathsf {detected}, \mathsf {undetected} \}\).
deviated in any of its virtual parties \(i^*\), then the simulator sends \((\mathsf {cheat}, A)\) to the ideal functionality \(\mathcal {F} _f\), which responds with \(\mathsf {resp} = \{\mathsf {detected}, \mathsf {undetected} \}\).
-
(a)
If \(\mathsf {flag} =\mathsf {detected} \), the simulator produces a certificate as an honest party would do (since the simulator knows the output \(y^A\) of the \(\mathcal {F} _{\mathsf {SETUP}} \), the simulator knows the decommitting information for all \(i\in [m]\)).
-
(b)
If \(\mathsf {flag} =\mathsf {undetected} \), the simulator receives the input of the honest party \(x^B\). Now the simulator rewinds
 to step 4 where it now generates the \(\tilde{x}^B_i\)’s as a secret sharing of \(x^B\). The simulator keeps rewinding
to step 4 where it now generates the \(\tilde{x}^B_i\)’s as a secret sharing of \(x^B\). The simulator keeps rewinding  until it again cheats in the same position (e.g., same virtual party and protocol location), and then completes the execution. The simulator reconstructs the output \(z^*\) from this execution and provides it to the ideal functionality \(\mathcal {F} _f\).
until it again cheats in the same position (e.g., same virtual party and protocol location), and then completes the execution. The simulator reconstructs the output \(z^*\) from this execution and provides it to the ideal functionality \(\mathcal {F} _f\).
-
7.
If no cheating was detected, the simulator sets the \(\mathsf {flag} =\mathsf {all\_good} \). Then it computes the
 shares of the output \(z^A_i\) for all \(i\in [m]\) by executing the virtual parties belonging to
shares of the output \(z^A_i\) for all \(i\in [m]\) by executing the virtual parties belonging to  using their random tapes and inputs which have been already extracted in steps 1 and 4 of the simulation. Then the simulator inputs \(x^A\) (which was reconstructed in step 4 of the simulation) to \(\mathcal {F} _f\) and receives the output z. Now the simulator decommits honestly to the commitments \(\gamma ^B_i\) for \(i\in I^A\) but uses the simulator \(\mathcal {S} _\mathsf {Com} \) to produce decommitting information \(\delta ^B_i\) for the commitments \(\gamma ^B_i\) with \(i\not \in I^A\) such that the opened values \(z^B_i\) are uniformly random under the constraint that \(\oplus _{i=1}^m z^B_i = z \oplus _{i=1}^m z^A_i\). This concludes the simulation.
using their random tapes and inputs which have been already extracted in steps 1 and 4 of the simulation. Then the simulator inputs \(x^A\) (which was reconstructed in step 4 of the simulation) to \(\mathcal {F} _f\) and receives the output z. Now the simulator decommits honestly to the commitments \(\gamma ^B_i\) for \(i\in I^A\) but uses the simulator \(\mathcal {S} _\mathsf {Com} \) to produce decommitting information \(\delta ^B_i\) for the commitments \(\gamma ^B_i\) with \(i\not \in I^A\) such that the opened values \(z^B_i\) are uniformly random under the constraint that \(\oplus _{i=1}^m z^B_i = z \oplus _{i=1}^m z^A_i\). This concludes the simulation.
To conclude the proof, we show that the real and the simulated view of the adversary is indistinguishable. We defer these hybrids to the full version of the paper.
Public Verifiability. Without loss of generality assume that Alice is corrupt. Since the setup phase is already publicly-verifiable, we only need to worry about public verifiability in the rest of the protocol. If an honest Bob outputs a certificate it must be because Alice has cheated during step 6 of the protocol i.e., one of the messages is not consistent with the input and random tape for that virtual party. Since Alice signs every outgoing message together with the entire transcript of the protocol execution, as well as her commitments in step 2 of the protocol, the judge can verify whether the message is correct or not.
Defamation-Freeness. Assume that  acting as Alice manages to break the defamation-freeness of the protocol and blames an honest B. We argue that this leads to a forgery to the underlying signature scheme, thus reaching a contradiction with the assumption of the theorem. In particular, for a \(\mathsf {Judge}\) to blame Bob it must hold that in step 7 the judge finds a message from B to A which is not consistent with the next-message function of \(\varPi \) in execution \(j^*\). Consider e.g., step 7a. Since Bob is honest, if the judge blames Bob it must be the case that that either the transcript of the protocol \((T^*,v^*)\) included in the certificate, the random tape \(r^*\) or the input \(x^*\) used by the judge to verify B in this step are not the ones that Bob used in the protocol (this of course is true for all \(j\in [m]\) and therefore independent of which execution \(j^*\) is claimed by
acting as Alice manages to break the defamation-freeness of the protocol and blames an honest B. We argue that this leads to a forgery to the underlying signature scheme, thus reaching a contradiction with the assumption of the theorem. In particular, for a \(\mathsf {Judge}\) to blame Bob it must hold that in step 7 the judge finds a message from B to A which is not consistent with the next-message function of \(\varPi \) in execution \(j^*\). Consider e.g., step 7a. Since Bob is honest, if the judge blames Bob it must be the case that that either the transcript of the protocol \((T^*,v^*)\) included in the certificate, the random tape \(r^*\) or the input \(x^*\) used by the judge to verify B in this step are not the ones that Bob used in the protocol (this of course is true for all \(j\in [m]\) and therefore independent of which execution \(j^*\) is claimed by  ). Since Bob is honest he will not sign a protocol transcript \((T^*,v^*)\ne (T,v)\), e.g., a transcript different than the one in the protocol executed by the honest Bob. Thus, \(x^*\) or \(r^*\) must be the wrong input or random tape. From step 5 we know that \(x^*\) is computed by decrypting some ciphertext \(e^*\) included in \(T^*\) using key \(k^*\). Again, since Bob is honest the signed \(e^*\) must be the correct one from the protocol execution, so the fault must be in \(k^*\). This is derived in step 4 as the opening of some commitment \(c^*\) with decommitting information \(d^*\). As the commitment \(c^*\) was signed this must be the right commitment \(c^B_{j^*}\) that Bob received from the setup functionality. And, since the commitment is binding, the decommitting information \(d^*\) cannot open \(c^*\) to anything else but the view of the virtual party used by Bob in the honest execution of the protocol. The judge can also blame Bob in steps 7b or 7c. The argument for why this is not possible for a PPT
). Since Bob is honest he will not sign a protocol transcript \((T^*,v^*)\ne (T,v)\), e.g., a transcript different than the one in the protocol executed by the honest Bob. Thus, \(x^*\) or \(r^*\) must be the wrong input or random tape. From step 5 we know that \(x^*\) is computed by decrypting some ciphertext \(e^*\) included in \(T^*\) using key \(k^*\). Again, since Bob is honest the signed \(e^*\) must be the correct one from the protocol execution, so the fault must be in \(k^*\). This is derived in step 4 as the opening of some commitment \(c^*\) with decommitting information \(d^*\). As the commitment \(c^*\) was signed this must be the right commitment \(c^B_{j^*}\) that Bob received from the setup functionality. And, since the commitment is binding, the decommitting information \(d^*\) cannot open \(c^*\) to anything else but the view of the virtual party used by Bob in the honest execution of the protocol. The judge can also blame Bob in steps 7b or 7c. The argument for why this is not possible for a PPT  is very similar to the one for the case 7a with few differences: in case 7b we also need to argue that
is very similar to the one for the case 7a with few differences: in case 7b we also need to argue that  cannot blame Bob making the judge use a wrong decryption key \(k^*\). This is however taken care of since the key is part of the view of the virtual party, which is committed (and the commitment is signed by Bob). Similarly, in case 7c,
cannot blame Bob making the judge use a wrong decryption key \(k^*\). This is however taken care of since the key is part of the view of the virtual party, which is committed (and the commitment is signed by Bob). Similarly, in case 7c,  could also blame an innocent Bob by making the judge use the wrong randomness \(u^*\) but, this is also taken care of since the randomness is part of the view of the virtual party, which is committed (and the commitment is signed by Bob).
could also blame an innocent Bob by making the judge use the wrong randomness \(u^*\) but, this is also taken care of since the randomness is part of the view of the virtual party, which is committed (and the commitment is signed by Bob).
6 Compiler for Multiparty Computation
It is natural to ask, whether the compilers described in the previous sections of the paper extend to the multiparty setting. In this section we provide some intuition for how the compiler from Sect. 5 can be extended the multiparty setting with a constant fraction of corruptions. More concretely, we argue that any \((cn^2\,+\,n)\)-party protocol \(\varPi \) with passive security against \(cn^2\,+\,cn\) corruptions, for some \(1/2< c < 1\), can be compiled into a n-party protocol with covert security and public verifiability against cn corruptions.Footnote 10
Assume we have n parties \(\mathrm {P}_{1}, \dots , \mathrm {P}_{n} \) with private inputs \(x^1, \dots , x^n\), who would like to compute \(f(x^1, \dots , x^n)\), and we would like to tolerate cn corruptions, for some \(1/2< c < 1\). Assume that \(\varPi \) implements the following \((cn^2 + n)\)-party functionality, where \(m = cn+1\)
where
The compiler for the multiparty setting is very similar to the compiler for the two-party setting. Each real party \(\mathrm {P}_{i} \) will simulate virtual parties \(\mathbb {V}_{j} ^i\) for \(1 \le j \le cn+1\). All virtual parties will jointly run a passively secure \((cn^2 + n)\)-party protocol. For every pair of real parties \((\mathrm {P}_{i}, \mathrm {P}_{j})\) with \(i\ne j\), we let \(\mathrm {P}_{i} \) check one virtual party of \(\mathrm {P}_{j} \), chosen uniformly at random. Observe that for any honest \(\mathrm {P}_{j} \), the corrupted parties learn at most cn out of the \(m = cn+1\) corresponding virtual parties’ views, thus the adversary will not learn enough shares to reconstruct the input of the honest party \(\mathrm {P}_{i} \). In total, the adversary learn the views of

virtual parties which is exactly the number of passive corruptions that we have assumed are tolerated by the protocol \(\varPi \).
To instantiate the compiler we need a generalized multiparty version of our two-party setup functionality \(\mathcal {F} _{\mathsf {SETUP}} \) from Fig. 5. This generalized functionality, called \(\mathcal {F} _{\mathsf {SETUP}} ^{(n, cn+1)}\), can be found in Fig. 8.
Observe that the multiparty functionality generates symmetric keys for all communication channels, including the ones between virtual parties belonging to different real parties. The reason is that we could have the case, where a virtual party of \(\mathrm {P}_{1} \) sends a message to a virtual party of \(\mathrm {P}_{2} \), which should be checked by \(\mathrm {P}_{3} \). Thus we need to ensure that \(\mathrm {P}_{3} \) can decrypt the message if he is indeed checking the corresponding virtual party. Each real party \(\mathrm {P}_{i} \) secret shares its input \(x^i\) into shares \(x^i_1, \dots , x^i_{cn+1}\), encrypts every share \(x^i_j\) under key \(k^{(i, j)}_{(i, j)}\), and broadcasts the encrypted shares to all real parties. The virtual parties jointly execute the passively secure protocol \(\varPi \). Whenever a virtual party sends a message to any other virtual party, it encrypts the message with the corresponding communication channel key and broadcasts the message among all real parties. Once the computation using \(\varPi \) is complete, each party commits to its output share. Finally all parties open their commitments and compute the desired output.
Security of this construction can be argued in a very similar fashion to the compiler from Sect. 5. The main technical difference between the two proofs lies in the calculation of the deterrence factor. Assume that the adversary misbehaves in some corrupt party \(\mathrm {P}_{i} ^{*}\). This means that the adversary misbehaves in at least one of the \(cn+1\) corresponding virtual parties. Let \(\mathbb {V}_{j} ^i\) be that party. Out of those \(cn+1\) virtual parties, the \((1-c)n\) honest parties each check one uniformly random one. The probability that none of the honest parties check \(\mathbb {V}_{j} ^i\) is
by binomial approximation. Thus we get a deterrence factor \(\epsilon \approx \frac{1-c}{c}\).
Notes
- 1.
In the remainder of the paper we will use the terms “covert security” and “security against covert adversaries” interchangeably to refer to the notion that was defined by Aumann and Lindell. We note, however, that the term “covert security” has also been used to denote a different flavor of secure computation as defined in [vHL05].
- 2.
In general, OT requires the use of public key cryptography. OT extension protocols allow two parties to perform large numbers of OT protocol executions using only a small number of public key operations.
- 3.
- 4.
Observe that in the two-party case active security implies covert security with public verifiability, since every attempt to cheat can simply be interpreted as an abort.
- 5.
If the passively secure protocol has a preprocessing phase of its own, then this would need to be executed after the setup phase of our compiler.
- 6.
Note that Hong et al. [HKK+19] use a similar derandomization trick in their garbled circuit construction, but do not mention the need for a perfectly correct OT, nor formally proves defamation freeness of their protocol. The extra assumption appears to be necessary to achieve this property in their protocol as well, since OT security itself does not imply that the receiver cannot “equivocate” its view by finding a random tape that produces a different output than the one in the real execution.
- 7.
For the sake of clarity, we assume that the adversary
 cheats in at most one location. Our proof easily generalizes to the case where
cheats in at most one location. Our proof easily generalizes to the case where  cheats in arbitrarily many locations at the cost of becoming a little less readable.
cheats in arbitrarily many locations at the cost of becoming a little less readable. - 8.
Some steps are left empty on purpose to keep the numbering of steps consistent with the protocol.
- 9.
- 10.
\(c < 1/2\) is possible, but here we are specifically interested in the dishonest majority setting.
References
Applebaum, B., Brakerski, Z., Tsabary, R.: Perfect secure computation in two rounds. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 152–174. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_6
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A.: Two round information-theoretic MPC with malicious security. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 532–561. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_19
Aumann, Y., Lindell, Y.: Security against covert adversaries: efficient protocols for realistic adversaries. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 137–156. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_8
Asharov, G., Orlandi, C.: Calling out cheaters: covert security with public verifiability. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 681–698. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_41
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols (extended abstract). In: 22nd ACM STOC, pp. 503–513 (1990)
Bracha, G.: An O(log n) expected rounds randomized byzantine generals protocol. J. ACM 34(4), 910–920 (1987)
Cohen, G., et al.: Efficient multiparty protocols via log-depth threshold formulae - (extended abstract). In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 185–202. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_11
Damgård, I., Geisler, M., Nielsen, J.B.: From passive to covert security at low cost. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 128–145. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_9
Damgård, I., Ishai, Y.: Constant-round multiparty computation using a black-box pseudorandom generator. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 378–394. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_23
Damgård, I., Keller, M., Larraia, E., Pastro, V., Scholl, P., Smart, N.P.: Practical covertly secure MPC for dishonest majority – or: breaking the SPDZ limits. In: Crampton, J., Jajodia, S., Mayes, K. (eds.) ESORICS 2013. LNCS, vol. 8134, pp. 1–18. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40203-6_1
Damgård, I., Orlandi, C., Simkin, M.: Yet another compiler for active security or: efficient MPC over arbitrary rings. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 799–829. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_27
Damgård, I., Pastro, V., Smart, N., Zakarias, S.: Multiparty computation from somewhat homomorphic encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 643–662. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_38
Goldreich, O., Kahan, A.: How to construct constant-round zero-knowledge proof systems for NP. J. Cryptol. 9(3), 167–189 (1996). https://doi.org/10.1007/BF00208001
Goyal, V., Mohassel, P., Smith, A.: Efficient two party and multi party computation against covert adversaries. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 289–306. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_17
Hong, C., Katz, J., Kolesnikov, V., Lu, W., Wang, X.: Covert security with public verifiability: faster, leaner, and simpler. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 97–121. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_4
Hazay, C., Lindell, Y.: Efficient Secure Two-Party Protocols - Techniques and Constructions. ISC. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14303-8
Hirt, M., Maurer, U.M.: Player simulation and general adversary structures in perfect multiparty computation. J. Cryptol. 13(1), 31–60 (2000). https://doi.org/10.1007/s001459910003
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: a new representation with applications to round-efficient secure computation. In: 41st FOCS, pp. 294–304 (2000)
Ishai, Y., Kilian, J., Nissim, K., Petrank, E.: Extending oblivious transfers efficiently. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 145–161. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_9
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Zero-knowledge from secure multiparty computation. In: 39th ACM STOC, pp. 21–30 (2007)
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_32
Kolesnikov, V., Malozemoff, A.J.: Public verifiability in the covert model (almost) for free. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 210–235. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_9
Lindell, Y.: How to simulate it - a tutorial on the simulation proof technique. Cryptology ePrint Archive, Report 2016/046 (2016). http://eprint.iacr.org/2016/046
Lindell, Y., Oxman, E., Pinkas, B.: The IPS compiler: optimizations, variants and concrete efficiency. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 259–276. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_15
von Ahn, L., Hopper, N.J., Langford, J.: Covert two-party computation. In: 37th ACM STOC, pp. 513–522 (2005)
Yao, A.C.-C.: Protocols for secure computations (extended abstract). In: 23rd FOCS, pp. 160–164 (1982)
Acknowledgements
This work was supported by the European Research Council (ERC) under the European Unions’s Horizon 2020 research and innovation programme under grant agreement No 669255 (MPCPRO), grant agreement No 803096 (SPEC), Danish Independent Research Council under Grant-ID DFF-6108-00169 (FoCC), and the Concordium Blockchain Research Center.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Damgård, I., Orlandi, C., Simkin, M. (2020). Black-Box Transformations from Passive to Covert Security with Public Verifiability. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12171. Springer, Cham. https://doi.org/10.1007/978-3-030-56880-1_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-56880-1_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56879-5
Online ISBN: 978-3-030-56880-1
eBook Packages: Computer ScienceComputer Science (R0)





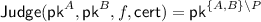 except with negligible probability.
except with negligible probability. , then the probability that
, then the probability that  outputs
outputs  is negligible.
is negligible.



 and send
and send  to
to  .
. ’s input
’s input  . Receive the
. Receive the  .
. , where the simulator uses random tape
, where the simulator uses random tape  and sends it to
and sends it to  . The adversary sends back
. The adversary sends back  stops sending messages or sends messages which are blatantly wrong e.g., they generate an abort in the real world with probability 1).
stops sending messages or sends messages which are blatantly wrong e.g., they generate an abort in the real world with probability 1). behaved correctly during all executions of
behaved correctly during all executions of  deviated in any of the protocol executions, then the simulator sends
deviated in any of the protocol executions, then the simulator sends  cheated, along with the exact location
cheated, along with the exact location 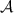 ’s input
’s input  , where the
, where the  and receive
and receive  .
.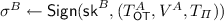 and sends it to
and sends it to  . The adversary sends back
. The adversary sends back  behaved correctly during the executions of
behaved correctly during the executions of  deviated from any of the protocols, then it rewinds back to the beginning of part B, otherwise it terminates the simulation by honestly running the last two steps of the protocol, by choosing a random
deviated from any of the protocols, then it rewinds back to the beginning of part B, otherwise it terminates the simulation by honestly running the last two steps of the protocol, by choosing a random  deviated from any of the protocol executions. If
deviated from any of the protocol executions. If  did not deviate, if it deviated somewhere other than execution
did not deviate, if it deviated somewhere other than execution 


 and send
and send  to
to  . Like a real party, the simulator aborts in any case of blatant cheating.
. Like a real party, the simulator aborts in any case of blatant cheating. inputs
inputs  to pick the output
to pick the output  , and using the output
, and using the output  does not attempt to cheat in
does not attempt to cheat in  . Receive
. Receive  where
where  for all
for all  while the latter kind are first encrypted using the appropriate keys. To simulate the message exchanged between pairs of unchecked parties belonging to B, send encryptions of 0 to
while the latter kind are first encrypted using the appropriate keys. To simulate the message exchanged between pairs of unchecked parties belonging to B, send encryptions of 0 to  . Moreover, if the simulator gets to step
. Moreover, if the simulator gets to step  . We now describe how the simulator reacts to incoming messages from
. We now describe how the simulator reacts to incoming messages from  to
to  deviated in any of its virtual parties
deviated in any of its virtual parties  to step
to step  until it again cheats in the same position (e.g., same virtual party and protocol location), and then completes the execution. The simulator reconstructs the output
until it again cheats in the same position (e.g., same virtual party and protocol location), and then completes the execution. The simulator reconstructs the output  shares of the output
shares of the output  using their random tapes and inputs which have been already extracted in steps
using their random tapes and inputs which have been already extracted in steps 
 cheats in at most one location. Our proof easily generalizes to the case where
cheats in at most one location. Our proof easily generalizes to the case where  cheats in arbitrarily many locations at the cost of becoming a little less readable.
cheats in arbitrarily many locations at the cost of becoming a little less readable.