Optimization of Search Space for Finding Very Short Lattice Vectors

Abstract

Shortest vector problem on lattices (SVP) is a well-known algorithmic combinatorial problem. The hardness of SVP is a foundation for the security of Lattice-based cryptography, which is a promising candidate of the post-quantum cryptographic algorithms. Therefore, many works have focused on the estimation of the hardness of SVP and the construction of efficient algorithms. Recently, a probabilistic approach has been proposed for estimating the hardness, which is based on the randomness assumption. The approach can estimate quite accurately the distribution of very short lattice vectors in a search space. In this paper, a new method is proposed for optimizing a box-type search space in random sampling by this probabilistic approach. It has been known empirically that the tail part of the search space should be more intensively explored for finding very short lattice vectors efficiently. However, it was difficult to adjust the search space quantitatively. On the other hand, our proposed method can find the best search space approximately. Experimental results show that our method is useful when the lattice basis is small or already reduced in advance.

1 Introduction

Shortest vector problem (SVP) on lattices is a combinatorial problem of finding the shortest non-zero lattice vector in a given lattice. SVP is known as one of the most promising candidates in post-quantum cryptography [10]. As the hardness of SVP gives a foundation to the security of the cryptographic system, it has become more important to estimate the hardness. The computational complexity for solving SVP is theoretically estimated in many algorithms such as enumeration [11], sieving [1], the Lenstra-Lenstra-Lovász algorithm (LLL) [12], the block Korkine-Zolotarev algorithm (BKZ) [17], random sampling reduction (RSR) [18], and so on. However, the complexity deeply depends on each specific algorithm so that it is different from the general hardness of SVP. Actually, there are several much more efficient algorithm in practice, for example, [7, 20] and [2]. In order to estimate the general hardness irrespective of the algorithms, it is useful to estimate the number of very short vectors in a search space of a given lattice. The widely-used approach is called the Gaussian heuristic (GH) [6], which assumes that the number of very short vectors in a search space is proportional to the volume of the intersection between a ball with the short diameter and the search space [3, 8]. GH is theoretically based on the theorem by Goldstein and Mayer [9]. However, the GH-based approach is not so efficient in practice because of its complicated estimation. On the other hand, the probabilistic approach has been proposed recently for estimating the number of short vectors [7, 14, 15], which is based on the Schnorr’s randomness assumption (RA) [18]. RA assumes that the residuals in the Gram-Schmidt orthogonalized basis of a given lattice are independently and uniformly distributed. The probabilistic approach can estimate the distribution of the lengths of lattice vectors over the search space. It has been experimentally shown in [14] that the probabilistic approach using the Gram-Charlier A series can estimate the distribution of the lengths of very short lattice vectors over a search space both accurately and quite efficiently.

In this paper, a method is proposed for finding approximately the best search space under the same size by utilizing the probabilistic approach. Such best search space is expected to be useful for both estimating the theoretical complexity and constructing efficient algorithms. The essential assumption is that the mean of the distribution should be minimized in the best search space. This assumption can enable us to calculate the best search space concretely and to estimate the theoretical bound of this optimization.

This paper is organized as follows. Section 2 gives the preliminaries of this work. Section 3 gives a method for finding the best search space under a given lattice basis and a given size of search space. In Sect. 4, the experimental results of the proposed optimization method are described. Lastly, this paper is concluded in Sect. 5.

2 Preliminaries

2.1 Lattices and Shortest Vector Problem

A lattice basis is given as a full-rank $n \times n$ integral matrix $\textit{\textbf{B}} = \{\mathbf {b}_{1}, \ldots , \mathbf {b}_{n}\}$, where each $\mathbf {b}_{i} = \left( b_{ij}\right) \in \mathbb {Z}^{n}$ is called a basis vector. The lattice $L\left( \textit{\textbf{B}}\right)$ is defined as an additive group consisting of $\sum _{i=1}^{n}a_{i}\mathbf {b}_{i}$ for $a_{i} \in \mathbb {Z}$. The Euclidean inner product of $\mathbf {x}$ and $\mathbf {y}$ is denoted by $\langle \mathbf {x},\mathbf {y}\rangle =\mathbf {x}^{T}\mathbf {y}$. The Euclidean norm (namely, the length) of $\mathbf {x}$ is defined as $\left\| \mathbf {x}\right\| =\sqrt{\langle \mathbf {x},\mathbf {x}\rangle }$. The exact SVP is defined as the problem of finding a non-zero integer vector $\mathbf {a} = \left( a_{i}\right)$ so that the length $\ell = \left\| \mathbf {a}^{T}\mathbf {b}\right\|$ is minimized. The approximate version of SVP is also widely used, where we search a very short vector with a sufficiently small length. In other words, we search a non-zero integer vector $\mathbf {a}$ satisfying $\left\| \mathbf {a}^{T}\mathbf {b}\right\| < \hat{\ell }$, where $\hat{\ell }$ is a threshold. The approximate SVP is denoted by SVP hereafter.

The determinant of $\textit{\textbf{B}}$ (denoted by $\mathrm {det}\left( \textit{\textbf{B}}\right)$) is constant even if the current lattice basis is changed. By using $\mathrm {det}\left( \textit{\textbf{B}}\right)$, the length of the shortest lattice vector can be estimated as

$$\begin{aligned} \ell _{\mathrm {GH}}= \frac{\left( \varGamma \left( \frac{n}{2}+1\right) \mathrm {det}\left( \textit{\textbf{B}}\right) \right) ^{\frac{1}{n}}}{\sqrt{\pi }}, \end{aligned}$$

(1)

where $\varGamma$ is the gamma function occurring in the calculation of the volume of an n-dimensional ball [10]. This approximation is called the Gaussian heuristic. Though this heuristic does not hold for any lattice, it holds at least for a random lattice. The threshold $\hat{\ell }$ in SVP can be given as $\left( 1+\epsilon \right) \ell _{\mathrm {GH}}$ where $\epsilon$ is a small positive constant ($\epsilon = 0.05$ in TU Darmstadt SVP challenge [16]).

2.2 Gram-Schmidt Orthogonalization and Search Space

$\mathbf {b}_{i}$ can be orthogonalized to $\mathbf {b}_{i}^{*} =\left( b_{ij}^{*}\right)$ by the Gram-Schmidt orthogonalization:

$$\begin{aligned} \mathbf {b}_{i}^{*} = \mathbf {b}_{i} - \sum _{j=1}^{i-1}\eta _{ji}\mathbf {b}_{j}^{*} \text { and } \eta _{ji} = \frac{\langle \mathbf {b}_{j}^{*},\mathbf {b}_{i}\rangle }{\left\| \mathbf {b}_{j}^{*}\right\| ^{2}}, \end{aligned}$$

(2)

where $\langle \mathbf {b}_{i}^{*},\mathbf {b}_{j}^{*}\rangle =0$ holds for $i \ne j$. Note that $\left\| \mathbf {b}_{i}^{*}\right\|$ is not constrained to be 1. $\textit{\textbf{B}}^{*}=\left( \mathbf {b}_{1}^{*},\ldots ,\mathbf {b}_{n}^{*}\right)$ is called an orthogonalized lattice basis. $\textit{\textbf{B}}^{*}$ can be characterized by a vector $\varvec{\rho } = \left( \rho _{i}\right)$, where $\rho _{i}$ is defined as

$$\begin{aligned} \rho _{i} = \left\| \mathbf {b}_{i}^{*}\right\| ^{2} = \sum _{j=1}^{n}\left( b_{ij}^{*}\right) ^{2}. \end{aligned}$$

(3)

$\varvec{\rho }$ is called the shape of $\textit{\textbf{B}}^{*}$. Any lattice vector $\sum _{i=1}^{n}a_{i}\mathbf {b}_{i}$ ($a_{i} \in \mathbb {Z}$) can be given as $\sum _{i=1}^{n}\zeta _{i}\mathbf {b}_{i}^{*}$. The squared length of this lattice vector is given as

$$\begin{aligned} \ell ^{2} = \sum _{i=1}^{n}\rho _{i}\zeta _{i}^{2}. \end{aligned}$$

(4)

Because each $\zeta _{i} \in \mathbb {R}$ is given as the sum of $\bar{\zeta }_{i}$ ($-\frac{1}{2} \le \bar{\zeta }_{i} < \frac{1}{2}$) and an integer, $\zeta _{i}$ is uniquely determined by a natural number $d_{i}$ satisfying

$$\begin{aligned} -\frac{d_{i}+1}{2} \le \zeta _{i}< -\frac{d_{i}-1}{2} \ \mathrm {or} \ \frac{d_{i}-1}{2} \le \zeta _{i} < \frac{d_{i}}{2}. \end{aligned}$$

(5)

Here, the natural numbers begin with 1. A vector $\mathbf {d} = \left( d_{1},\ldots ,d_{n}\right)$ is called a tag in the same way as in [3]. $\bar{\zeta }_{i}$ is called the residual of $\zeta _{i}$.

It was proved in [7] that any lattice vector is uniquely determined by $\mathbf {d}$, and vice versa. Therefore, a search space of the lattice vectors can be defined as a set of tags (denoted by $\varUpsilon$). In this paper, $\varUpsilon$ is constrained to be an n-ary Cartesian product in the same way as in random sampling [4, 13, 18]: $\varUpsilon = \upsilon _{1} \times \upsilon _{2} \times \cdots \times \upsilon _{n}$. Here, each $\upsilon _{i}$ is a set of natural numbers under a maximum $T_{i}$: $\{1, \ldots , T_{i}\}$. It is called a box-type search space characterized by a natural number vector $\mathbf {T} = \left( T_{i}\right) \in \mathbb {N}^{n}$. The size of a search space is defined as $V\left( \mathbf {T}\right) = \prod _{i=1}^{n}T_{i}$.

2.3 Randomness Assumption and Gram-Charlier a Series

The probabilistic approach is based on the following assumption asserted in [18].

Assumption 1

(Randomness Assumption (RA)). Each residual $\bar{\zeta }_{i}$ is uniformly distributed in $\left[ -\frac{1}{2},\frac{1}{2}\right)$ and is statistically independent of $\bar{\zeta }_{j}$ for $j \ne i$.

Though there are some different definitions of RA, the above one is employed here. Though RA cannot hold rigorously [3], it empirically holds if the index i is not near to n [19]. Regarding a box-type search space, RA can be extended to the assumption that each $\zeta _{i}$ is independently and uniformly distributed in the range $\left[ -\frac{T_{i}}{2},\frac{T_{i}}{2}\right)$. Therefore, the distribution of the squared lengths $\ell ^{2}=\sum \rho _{i}\zeta _{i}$ of the lattice vectors over a box-type search space is uniquely determined by $\mathbf {T}$ and $\mathbf {\rho }$.

The distribution of $\ell ^{2}$ can be approximated by the Gram-Charlier A series [5, 22]. The details of this technique are described in [14, 15]. Here, only the necessary parts for the proposed method are explained. Generally, the cumulative distribution function $\bar{F}\left( x\right)$ of a normalized random variable x (the mean and the variance are 0 and 1, respectively) can be approximated by the following Gram-Charlier A series:

$$\begin{aligned} \bar{F}_{Q}\left( x\right) = \int _{-\infty }^{x}\frac{e^{-\frac{w^2}{2}}}{\sqrt{2\pi }}\mathrm {d}w - \left( \sum _{r=3}^{Q}c_{r}He_{r-1}\left( x\right) \right) \frac{e^{-\frac{x^2}{2}}}{\sqrt{2\pi }}, \end{aligned}$$

(6)

where $He_{r}\left( x\right)$ is the r-th degree Hermite polynomial and $c_{r}$ is a coefficient depending on from the 3rd to the r-th order cumulants of x. It is guaranteed to converge to the true distribution for $Q \rightarrow \infty$ if x is bounded [22]. A general cumulative distribution function $F\left( z\right)$ with non-normalized z (with the mean $\mu$ and the variance $\sigma ^{2}$) is given as

$$\begin{aligned} F_{Q}\left( z\right) = \bar{F}_{Q}\left( \frac{z-\mu }{\sigma }\right) . \end{aligned}$$

(7)

Now, let $\ell ^{2}$ be the random variable z. Then, the r-th order cumulant of $\ell ^{2}$ (denoted by $\kappa _{r}\left( \ell ^{2}\right)$) is given as

$$\begin{aligned} \kappa _{r}\left( \ell ^{2}\right) = \sum _{i=1}^{n}\rho _{i}^{r} \kappa _{r}\left( T_{i}\right) \end{aligned}$$

(8)

due to the homogeneity and the additivity of cumulants. Here, $\kappa _{r}\left( T_{i}\right)$ denotes the r-th order cumulant of $\zeta ^{2}$, where $\zeta$ is uniformly distributed over $\left[ -\frac{T_{i}}{2},\frac{T_{i}}{2}\right)$. $\kappa _{r}\left( T_{i}\right)$ is determined by only $T_{i}$. $\mu$ and $\sigma ^{2}$ correspond to $\kappa _{1}\left( \ell ^{2}\right)$ and $\kappa _{2}\left( \ell ^{2}\right)$, respectively. The normalized cumulants of $\bar{F}\left( \frac{z-\mu }{\sigma }\right)$ are given as

$$\begin{aligned} \bar{\kappa }_{r} = \frac{\kappa _{r}\left( \ell ^{2}\right) }{\sqrt{\kappa _{2}\left( \ell ^{2}\right) }^{r}} \end{aligned}$$

(9)

for $r \ge 3$. Consequently, we can estimate $F_{Q}\left( \ell ^{2}; \mathbf {T}, \mathbf {\rho }\right)$ by $\mathbf {T}$ and $\mathbf {\rho }$. In addition, it is guaranteed in [14] that $F_{Q}\left( \ell ^{2}\right)$ monotonically converges to the true distribution as Q becomes larger.

Note that we can easily calculate $F_{Q}\left( \ell \right)$ (the cumulative distribution of Euclidean lengths of the lattice vectors) from $F_{Q}\left( \ell ^{2}\right)$ (squared Euclidean) and vice versa. $F_{Q}\left( \ell ^{2}\right)$ is employed in this paper.

3 Method and Algorithm

3.1 Purpose

Our purpose is to find the search space including as many very short lattice vectors as possible under the same size K. In the original random sampling [18], the search space $\mathbf {T}$ is given as

$$\begin{aligned} T_{i} = {\left\{ \begin{array}{ll} 1 &{} i \le n - u,\\ 2 &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

(10)

where the size of the space is $2^{u}$. In other words, $d_{i}$ can be switched between 1 and 2 in only the tail u indices (otherwise, $d_{i}$ is fixed to 1). However, it is still unclear whether the employment of the only two choices (1 or 2) is sufficiently efficient or not. In [4, 13], the choices are generalized into $d_{i} \in \{1, 2, \ldots , T_{i}\}$. Nevertheless, it has not been known what search space is best.

3.2 Principle and Assumption

In the principle of the probabilistic approach under RA, the best search space $\hat{\mathbf {T}}$ has the highest probability of generating very short lattice vectors for a current lattice basis (whose shape is $\mathbf {\rho }$), where the size of the search space $V\left( \hat{\mathbf {T}}\right)$ is constrained to be a constant K. By utilizing $F_{Q}\left( \ell ^{2}; \mathbf {T}, \mathbf {\rho }\right)$, it is formalized as follows:

$$\begin{aligned} \hat{\mathbf {T}} = \mathrm {argmax}_{\mathbf {T}}F_{Q}\left( \ell ^{2}; \mathbf {T}, \mathbf {\rho }\right) \mathrm {\ subject \ to \ } V\left( \mathbf {T}\right) = K. \end{aligned}$$

(11)

Unfortunately, it is intractable to estimate $F_{Q}$ over all the possible $\mathbf {T}$. Therefore, the following assumption is introduced.

Assumption 2

(Best Search Assumption (BSA)). When the mean $\mu$ of the distribution $F_{Q}\left( \ell ^{2}; \mathbf {T}, \mathbf {\rho }\right)$ is the lowest, the probability of generating very short lattice vector is the highest. In other words, $\mathbf {T}$ minimizing $\mu$ is the best search space.

This assumption utilizes only the first order cumulant (namely, the mean) and neglects the other cumulants. Thus, the form of the distribution is assumed to be unchanged except for its mean. Therefore, the lowest mean maximizes the expected number of very short vectors. This assumption can be justified at least if $T_{i} \ge 2$ holds for only relatively small $\rho _{i}$. It is because the effects of large $T_{i}$ on the r-th order cumulants are decreased in proportion to $\rho _{i}^{r}$.

3.3 Problem and Algorithm

The mean of $\zeta _{i}^{2}$ over the uniform distributed $\zeta _{i}$ in $\left[ -\frac{T_{i}}{2},\frac{T_{i}}{2}\right)$ is given as

$$\begin{aligned} \mu _{i} = \int _{-\frac{T_{i}}{2}}^{\frac{T_{i}}{2}}\frac{x^{2}}{T_{i}}\mathrm {d}x = \frac{T_{i}^{2}}{12} \end{aligned}$$

(12)

Then, the mean of $F_{Q}\left( \ell ^{2}; \mathbf {T}, \mathbf {\rho }\right)$ is given as

$$\begin{aligned} \mu = \frac{\sum _{i=1}^{n}\rho _{i}T_{i}^2}{12}. \end{aligned}$$

(13)

Under BSA, the best search space $\hat{\mathbf {T}}$ can be estimated by solving the following optimization problem:

$$\begin{aligned} \hat{\mathbf {T}} = \mathrm {argmin}_{\mathbf {T} \in \mathbb {N}^{n}} \sum _{i=1}^{n}\rho _{i}T_{i}^2 \mathrm {\ subject \ to \ } \prod _{i=1}^{n}T_{i} \ge 2^{u}. \end{aligned}$$

(14)

Here, the size of the search space is limited to $2^{u}$ for simplicity. In addition, the constraint is changed to the lower bound because the equality constraint hardly can be satisfied. This is a sort of combinatorial integer problem. This problem is solved by using the two stages.

At the bound stage, the search space of $\mathbf {T}$ is bounded. First, $\rho _{i}$ is sorted in descending order. Then, $\mathbf {T}$ is constrained to be monotonically increasing along the index i. Second, $T_{i} = 2$ is allocated to the smallest u elements of the shape $\varvec{\rho }$ (otherwise, $T_{i} = 1$) in the similar way as in the original random sampling. This allocation is utilized as the baseline. Under the monotonically increasing constraint, the upper bound $U_{i}$ for each $T_{i}$ is given so that the objective function for the candidate $\mathbf {T}$ does not exceed the baseline. Third, the lower bound $L_{i}$ for each $T_{i}$ is given so that the current upper bounds can satisfy $\prod _{i=1}^{n}T_{i} \ge 2^{u}$. Lastly, the upper bounds and the lower bounds are updated alternately until the convergence. The algorithm is described in Algorithm 1. It can be carried out instantly.

At the minimization stage, the minimum of $\sum _{i=1}^{n}\rho _{i}T_{i}^{2}$ is searched within the above bounded space. It can be implemented by a recursive function, which finds the best tail part $\tilde{\mathbf {T}}_{p} = \left( T_{p}, T_{p+1}, \ldots , T_{n}\right)$ minimizing $E = \sum _{i=p}^{n}\rho _{i}T_{i}^{2}$ for the head index p of the current tail part, the preceding $T_{p-1}$, the current lower bound of the size $K_{\mathrm {cur}}$. The details are described in Algorithm 2. This can be regarded as a sort of breadth first search. Though its complexity is exponential, it is not so time consuming in practice.

3.4 Theoretical Lower Bound

Though the best search space can be found by the above algorithm, the theoretical analysis is difficult. Here, a simple lower bound of the effects of the best search space is introduced. By neglecting the integer constraint, the optimization problem is relaxed into

$$\begin{aligned} \hat{\mathbf {T}} = \mathrm {argmin}_{\mathbf {T}} \sum _{i=n-u+1}^{n}\rho _{i}T_{i}^2 \mathrm {\ subject \ to \ } \sum _{i=n-u+1}^{n}\log _{2}\left( T_{i}\right) = u, \end{aligned}$$

(15)

where $T_{i} = 1$ for every $i \le n - u$. This problem can be solved easily by the method of Lagrange multiplier, where the optimum $\hat{T}_{i} (i > n - u + 1)$ is given as

$$\begin{aligned} \hat{T}_{i} = \frac{2\left( \prod _{k=n-u+1}^{n}\rho _{k}\right) ^{\frac{1}{2u}}}{\sqrt{\rho _{i}}}. \end{aligned}$$

(16)

This solution gives a lower bound of the best search space.

4 Experimental Results

Here, it is experimentally investigated whether the best search space in our proposed method is useful in practice or not for the following four lattice bases:

• B100 was originally generated in TU Darmstadt SVP challenge [16] ($n=100$, $\mathrm {seed}=0$) and was roughly reduced by the BKZ algorithm of the fplll package [21] with block size 20.

• B128 was generated in the same way as B100 except for $n = 128$.

• B150 was generated in the same way as B100 except for $n = 150$.

• B128reduced was a reduced basis from B128 (ranked in [16] with the Euclidean norm 2984).

The best search space is compared with the baseline $2^{u}$. The baseline allocates $T_{i} = 2$ to the smallest u elements of the shape $\varvec{\rho }$ in the similar way as in the original random sampling [18].

Fig. 1.

Actual numbers and Gram-Charlier approximation of short lattice vectors from B100 (the bases with $n = 100$) over the baseline ($2^{28}$) and the best search space.

Fig. 2.

Actual numbers and Gram-Charlier approximation of short lattice vectors from B128, B150, and B128reduced over the baseline ($2^{28}$) and the best search space.

Figure 1 shows the results for B100, where the baseline was set to $2^{28}$ (namely, $u = 28$). The actual number of short lattice vectors is displayed by the (cumulative) histograms for the baseline and the best search space. Note that the trivial zeros vector ($d_{i} = 1$ for every i) is removed. Note also that $10^0 = 1$ in vertical axis is the minimum of the actual number. The estimated number using the Gram-Charier approximation ($V\left( \mathbf {T}\right) F_{Q}$) is also displayed by the curves for each space ($Q=150$). Figure 1 shows that the estimated number over the best search space is always larger than that over the baseline. It suggests the validity of BSA. Figure 1 also shows the best search space tends to find more very short lattice vectors actually. The actual number of quite short lattice vectors is fluctuating because it is determined probabilistically. Actually, the shortest lattice vector of the baseline is shorter than that of the best search space. Nevertheless, the actual number over the best space is larger than that over the baseline in almost all lengths. Figure 2 shows the results for B128, B150, and B128reduced. It shows that there is not much difference between the best search space and the baseline for B128 and B150. The actual number seems to be fluctuating irrespective of the search space. On the other hand, the best search space seems to be superior to the baseline for B128reduced. Those results suggest that the best search space is useful for a relatively small lattice basis and a reduced lattice basis.

Fig. 3.

Cumulative bar chart of the frequency of $T_{i}$ in the best search space of the four bases for various u (from 1 to 40): The curves (scaled by the right axis) show the expansion rate $V\left( \hat{\mathbf {T}}\right) /2^{u}$.

Fig. 4.

Mean of the distribution of the squared lengths over the best search space and the baseline for various u (from 1 to 40): The theoretical lower bound without the integer constraint is also shown. The left axis is divided by $\ell _{\mathrm {GH}}^{2}$.

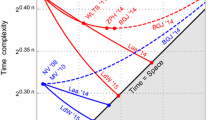
In order to investigate the best search space furthermore, its behavior was observed for changing u from 1 to 40. Figure 3 shows the frequency of each value of $T_{i}$ in the best search space for various u. The results are similar in all the four bases. It shows that the best search space is completely equivalent to the baseline for relatively small u (around $u < 20$). As u is larger, the number of relatively large $T_{i}$ is larger. The maximum of $T_{i}$ was 4. Figure 3 also shows the expansion rate of the size of the best search space in proportion to the baseline $2^{u}$. It shows that the expansion rate is always near to 1. It verifies that the relaxation of the size constraint is useful. Figure 4 shows the mean of the distribution for the best search space and the baseline. Under BSA, as the mean is lower, the number of very short lattice vector is larger. The qualitative results are similar in the four bases. If u is relatively small (around $u < 20$), the mean for the best search space is approximately equal to that for the baseline and the theoretical lower bound. As u is larger, the theoretical lower bound is lower than the baseline. In addition, the mean for the search space is nearer to the theoretical bound for relatively large u (around $u = 40$). These results are consistent with Fig. 3. On the other hand, the quantitative results are different among the four bases. The scale of the left axis (regularized by $\ell _{\mathrm {GH}}^{2}$) is relatively large in B100 and B128reduced. It is small in B128 and B150. These results are consistent with the relatively large fluctuations in B128 and B150 as shown in Fig. 2.

5 Conclusion

In this paper, a new method is proposed, which finds approximately the best search space in the random sampling. This method is based on the probabilistic approach for SVP under RA. The experimental results show that the proposed method is effective for a small lattice basis and a reduced one.

The proposed method is not so time consuming and can be easily implemented in any algorithm including the random sampling. Therefore, the author is planning to utilize this method for accelerating the sampling reduction algorithms such as [20] and solving high-dimensional SVP in [16]. For this purpose, the method should be improved by additional experimental and algorithmic analysis. For example, Algorithms 1 and 2 are expected to be simplified as a linear integer programming with higher performance. For another example, though the size of the search space $V\left( \hat{\mathbf {T}}\right)$ is constrained to be a constant K in this paper, the adaptive tuning of K is promising to accelerate the sampling reduction algorithms.

In addition, the proposed method can give the theoretical lower bound. Now, the author is planning to utilize this bound for estimating the general difficulty of SVP. For this purpose, the validity of BSA should be verified more rigorously. The asymptotic analysis using the Gram-Charlier A series is expected to be crucial to the theoretical verification. The asymptotic convergence has been theoretically proved for a single distribution. On the other hand, BSA is related to the “difference” among multiple distributions. The author is now constructing a more rigorous definition of BSA and is investigating the difference among the distributions theoretically.