Anonymous IBE from Quadratic Residuosity with Fast Encryption

Abstract

We develop two variants of Cocks’ identity-based encryption. One variant has faster encryption, where the most time-consuming part only requires several modular multiplications. The other variant makes the first variant anonymous under suitable complexity assumptions, while its decryption efficiency is about twice lower than the first one. Both the variants have ciphertext expansion twice more extensive than the original Cocks’ identity-based encryption. To alleviate the issue of the second variant’s large ciphertext expansion, we consider using it to construct a public-key encryption with keyword search scheme with a fast encryption algorithm by means of the transform in [1].

A A Public-Key Encryption with Keyword Search Scheme from Quadratic Residuosity

Boneh et al. introduced the notion of public-key encryption with keyword search (PEKS) and gave a proper security model and a construction methodology in [4]. PEKS is a form of “searchable encryption” that performs a keyword search on data encrypted using a public-key system. A promising application of PEKS is that of intelligent email routing. One may consider that mails come through a gateway which tests whether a keyword (e.g., “urgent”) exists in an email. Of course, any other information about the email can not be revealed. A PEKS scheme consists of four $\mathsf {PPT}$ algorithms $\mathsf {\left( KeyGen,PEKS,Trapdoor,Test\right) }$.

• $\mathsf {KeyGen}(1^\kappa )$ The key generation algorithm $\mathsf {KeyGen}$ is a randomized algorithm that takes as input a security parameter $1^\kappa$ and generates a public/private key pair $(\mathsf {pk},\mathsf {sk})$.

• $\mathsf {PEKS}(\mathsf {pk},W)$ Given a public key $\mathsf {pk}$ and a keyword W, $\mathsf {PEKS}$ returns a searchable ciphertext S for W.

• $\mathsf {Trapdoor}(\mathsf {sk},W)$ Given a private key $\mathsf {sk}$ and a keyword W, the trapdoor algorithm $\mathsf {Trapdoor}$ produces a trapdoor $T_W$ for keyword W.

• $\mathsf {Test}(\mathsf {pk},S,T_W)$ Given a public key $\mathsf {pk}$, a searchable ciphertext $S \leftarrow \mathsf {PEKS}\left( \mathsf {pk},W'\right)$ and a trapdoor $T_W \leftarrow \mathsf {Trapdoor}(\mathsf {sk},W)$, the test algorithm $\mathsf {Test}$ returns a bit b with 1 meaning “accept” or “yes” and 0 meaning “reject” or “no”. It is required that $b=1$ when $W=W'$.

In [1], the authors presented a new transform called $\mathsf {new\text {-}ibe\text {-}2\text {-}peks}$ that transforms any $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$-secure and anonymous IBE scheme into a $\mathsf {PEKS}$-$\mathsf {IND}$-$\mathsf {CPA}$-secure and computationally consistent PEKS scheme. The resulting PEKS-encryption algorithm picks and encrypts a random message X and appends X to the ciphertext. We can naturally apply $\mathsf {new\text {-}ibe\text {-}2\text {-}peks}$ to the scheme of Sect. 4 and obtain the following PEKS scheme from quadratic residuosity.

• $\mathsf {KeyGen}(1^\kappa )$ Given a security parameter $\kappa$, $\mathsf {KeyGen}$ defines a parameter k and generates two RSA primes p and q such that and their product $N=pq$. $\mathsf {KeyGen}$ also samples an element $u {\mathop {\leftarrow }\limits ^{\textit{R}}}\mathbb {J}_N \setminus \mathbb {QR}_N$. The public key is $\mathsf {pk} = \{N,k,u,\mathsf {H}\}$ where $\mathsf {H}$ is a publicly available cryptographic hash function mapping an arbitrary binary string to $\mathbb {J}_{N}$. The secret key is $\mathsf {sk} = \{p,q\}$.

• $\mathsf {PEKS}(\mathsf {pk},W)$ Given a public key $\mathsf {pk}$ and a keyword W, $\mathsf {PEKS}$ selects a k-bit message $X=[x_{k-1},x_{k-2}, \ldots , x_0]$ (with $x_i \in \left\{ 0, 1\right\}$) and computes $R=\mathsf {H}(W)$. For each $i = 0,1, \ldots k-1$, it chooses at random two polynomials $f_{i,1},f_{i,2}$ of degree 1 from $\mathbb {Z}_N[x]$, and two bits $\beta _{i,1},\,\beta _{i,2} {\mathop {\leftarrow }\limits ^{\textit{R}}}\left\{ 0, 1\right\}$. Set

  

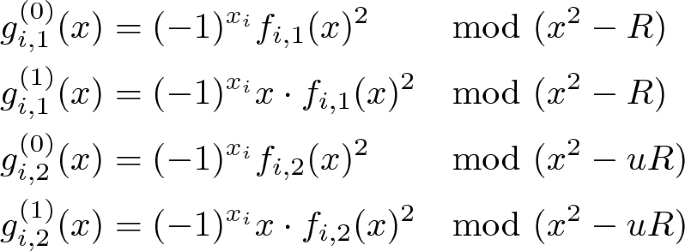
  $\mathsf {PEKS}$ returns the searchable ciphertext

  $$ S=\left( g_{0,1}^{(\beta _{0,1})}(x),g_{0,2}^{(\beta _{0,2})}(x),g_{1,1}^{(\beta _{1,1})}(x),g_{1,2}^{(\beta _{1,2})}(x), \ldots , g_{k-1,1}^{(\beta _{k-1,1})}(x),g_{k-1,2}^{(\beta _{k-1,2})}(x) ,X\right) . $$

• $\mathsf {Trapdoor}(\mathsf {sk},W)$ Given a private key $\mathsf {sk}$ and a keyword W, the trapdoor algorithm $\mathsf {Trapdoor}$ computes $R=\mathsf {H}(W)$. If $R \in \mathbb {QR}_N$, it computes $T_W = R^{1/2} \bmod N$; otherwise it computes $T_W = \left( uR\right) ^{1/2} \bmod N$. $\mathsf {Trapdoor}$ returns $T_W$.

• $\mathsf {Test}(\mathsf {pk},S,T_W)$ Given a public key $\mathsf {pk}$, a searchable ciphertext

  $$\begin{aligned} S=\left( C_{0,1}(x), C_{0,2}(x), C_{1,1}(x), C_{1,2}(x), \ldots , C_{k-1,1}(x), C_{k-1,2}(x), X \right) \end{aligned}$$

  where $C_{i,j}(x)=c_{i,j,0}+c_{i,j,1}x,\forall 0\le i <k,\forall 1\le j \le 2$, and a trapdoor $T_W \leftarrow \mathsf {Trapdoor}(\mathsf {sk},W)$, the test algorithm $\mathsf {Test}$ computes $R=\mathsf {H}(W)$. If $T_W^2 \equiv R \pmod {N}$, $\mathsf {Test}$ computes $\sigma _i=\left( \frac{c_{i,1,0}^2-c_{i,1,1}^2R}{N}\right)$ and sets $h_i(x)=C_{i,1}(x),\forall 0\le i <k$; otherwise it computes $\sigma _i=\left( \frac{c_{i,2,0}^2-c_{i,2,1}^2uR}{N}\right)$ and sets $h_i(x)=C_{i,2}(x),\forall 0\le i <k$. Finally, $\mathsf {Test}$ computes

  $$\begin{aligned} x'_{i}&= {\left\{ \begin{array}{ll} \left( \frac{h_i(T_W)}{N}\right) , &{} \text{ if } \sigma _i=1; \\ \left( \frac{T_Wh_i(T_W)}{N}\right) , &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

  and recovers $X'=[\mathcal {J}_{N}(x'_{k-1}),\mathcal {J}_{N}(x'_{k-2}), \ldots , \mathcal {J}_{N}(x'_0)]$. $\mathsf {Test}$ returns 1 if $X=X'$; and 0 otherwise.

For encrypting a message m with n keywords $W_1,W_2,\ldots , W_n$ with user’s public key $\mathsf {upk}$, Boneh et al. in [4] suggested that the sender computes and sends the ciphertext

$$ C=\left( \mathsf {Enc}\left( \mathsf {upk},m\right) ,\mathsf {PEKS}\left( \mathsf {upk},W_1\right) , \mathsf {PEKS}\left( \mathsf {upk},W_2\right) , \ldots ,\mathsf {PEKS}\left( \mathsf {upk},W_n\right) \right) $$

to a proxy given the trapdoor $T_{W_i}$ for each keyword $W_i$. Then the proxy can test whether m contains some keyword $W_i$, but it learns nothing more about any other information about m.