Abstract
Randomness is typically thought to be essential for zero knowledge protocols. Following this intuition, Goldreich and Oren (Journal of Cryptology 94) proved that auxiliary-input zero knowledge cannot be achieved with a deterministic prover. On the other hand, positive results are only known in the honest-verifier setting, or when the prover is given at least a restricted source of entropy. We prove that removing (or just bounding) the verifier’s auxiliary input, deterministic-prover zero knowledge becomes feasible:
-
Assuming non-interactive witness-indistinguishable proofs and subexponential indistinguishability obfuscation and one-way functions, we construct deterministic-prover zero-knowledge arguments for
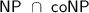 against verifiers with bounded non-uniform auxiliary input.
against verifiers with bounded non-uniform auxiliary input. -
Assuming also keyless hash functions that are collision-resistant against bounded-auxiliary-input quasipolynomial-time attackers, we construct similar arguments for all of
 .
.
Together with the result of Goldreich and Oren, this characterizes when deterministic-prover zero knowledge is feasible. We also demonstrate the necessity of strong assumptions, by showing that deterministic prover zero knowledge arguments for a given language imply witness encryption for that language. We further prove that such arguments can always be collapsed to two messages and be made laconic. These implications rely on a more general connection with the notion of predictable arguments by Faonio, Nielsen, and Venturi (PKC 17).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Goldwasser, Micali, and Rackoff [18] founded the concept of zero-knowledge proofs on two main elements: interaction and randomness. While both interaction and verifier randomness are known to be essential for zero knowledge, the answer as to whether the prover must also be randomized is not as definite. Goldreich and Oren [16] showed that prover randomness is essential in order to achieve auxiliary-input zero-knowledge for non-trivial languages. According to this notion, motivated by composition [15], anything that a verifier can learn from the proof, on top of the auxiliary information z it already possesses, can be efficiently simulated given the same auxiliary information z.
So when is deterministic-prover zero knowledge possible? So far, deterministic prover zero knowledge have only been shown to exist in the honest-verifier setting. Here Faonio, Nielsen, and Venturi [12] proved that any  language \(\mathcal {L}\) that has a witness encryption scheme [13], also has a deterministic-prover honest-verifier (perfect) zero-knowledge argument, or proof, if the language \(\mathcal {L}\) has a hash proof system [10]. A similar result was recently shown by Dahari and Lindell [11]. In the same work, Dahari and Lindell also show a statistically sound honest-verifier zero knowledge protocol with an unbounded honest prover for all of
language \(\mathcal {L}\) that has a witness encryption scheme [13], also has a deterministic-prover honest-verifier (perfect) zero-knowledge argument, or proof, if the language \(\mathcal {L}\) has a hash proof system [10]. A similar result was recently shown by Dahari and Lindell [11]. In the same work, Dahari and Lindell also show a statistically sound honest-verifier zero knowledge protocol with an unbounded honest prover for all of  assuming doubly-enhanced injective one-way functions. In the malicious verifier setting, they give a protocol satisfying a non-standard distributional notion of zero knowledge. In their definition, the prover has access to a pair of witnesses sampled from a distribution, which satisfy a certain entropy guarantee.
assuming doubly-enhanced injective one-way functions. In the malicious verifier setting, they give a protocol satisfying a non-standard distributional notion of zero knowledge. In their definition, the prover has access to a pair of witnesses sampled from a distribution, which satisfy a certain entropy guarantee.
Whether zero knowledge with a truly deterministic prover is possible considering any meaningful form of malicious verifiers remains unknown.
1.1 This Work
We prove that deterministic-prover zero knowledge for non-trivial languages is feasible for the class of malicious verifiers with bounded auxiliary input.
Theorem 1
(Informal). Assuming non-interactive witness-indistinguishable proofs and subexponentially-secure indistinguishability obfuscation and one-way functions, there exist two-message deterministic-prover arguments for  that are zero-knowledge against bounded-auxiliary-input verifiers.Footnote 1
that are zero-knowledge against bounded-auxiliary-input verifiers.Footnote 1
Theorem 2
(Informal). Assuming also keyless hash functions that are collision-resistant against bounded-auxiliary-input quasipolynomial-time attackers, there exist similar arguments for all of  .
.
By zero knowledge against bounded-auxiliary-input verifiers we formally mean that for any polynomial bound b, there exists a corresponding deterministic-prover argument that is zero knowledge against (malicious) verifiers with non-uniform auxiliary input of size at most b. This, in particular, includes the class of uniform verifiers, considered in the original zero-knowledge definition of [18]. We stress that the running time of the verifier may be an arbitrary polynomial, potentially larger than b. Also, indistinguishability of simulated and real proofs holds against non-uniform distinguishers of arbitrary polynomial size. Same goes for soundness, which holds against non-uniform provers of arbitrary polynomial size.
Together with the impossibility result of Goldreich and Oren for unbounded auxiliary input, the above results give a complete picture of when exactly deterministic-prover zero knowledge is feasible. We note that two-message zero knowledge against unbounded auxiliary input is by itself known to be impossible. Our result indeed circumvents this impossibility (for bounded auxiliary input), but this was already known (with a randomized prover) [6].
On the Necessity of Strong Assumptions and Predictable Arguments. To demonstrate the feasibility of deterministic-prover zero knowledge, we rely on hardness assumptions that are arguably strong. We show that this is inherent. Specifically, we show that deterministic prover zero-knowledge arguments for  imply witness encryption for
imply witness encryption for  , which at this point is only known based on strong assumptions, such as indistinguishability obfuscation.
, which at this point is only known based on strong assumptions, such as indistinguishability obfuscation.
The implication to witness encryption, in fact, follows from a more general implication to predictable arguments. Predictable arguments, introduced by Faonio, Nielsen, and Venturi [12], are arguments where the honest verifier’s (private) random coins efficiently determine a unique accepting transcript—in order to convince the verifier, the prover must be consistent with this transcript throughout the entire protocol. We prove that any deterministic-prover zero-knowledge argument against bounded-auxiliary-input verifiers can be turned into a predictable argument. The transformation, in fact, preserves the honest prover algorithm, and in particular also zero knowledge.
Theorem 3
(Informal). Any deterministic-prover zero-knowledge argument against bounded-auxiliary-input verifiers can be made predictable.
We also give a transformation that only requires honest-verifier zero knowledge and works provided that the argument is expressive enough (e.g., for all  or even just
or even just  ). The fact that deterministic-prover zero knowledge arguments imply witness encryption, then follows from [12] where predictable arguments are shown to imply witness encryption.
). The fact that deterministic-prover zero knowledge arguments imply witness encryption, then follows from [12] where predictable arguments are shown to imply witness encryption.
Corollary 1
(of Predictability). Any deterministic-prover zero-knowledge argument against bounded-auxiliary-input verifiers for a language \(\mathcal {L}\) implies a witness encryption scheme for \(\mathcal {L}\).
We use additional known results regarding predictable arguments [12] to deduce similar results for deterministic-prover zero knowledge:
Corollary 2
(of Predictability). Any deterministic-prover zero-knowledge argument against bounded-auxiliary-input verifiers can be reduced to two messages and made laconic.
Here by laconic [12, 17] we mean that the prover sends a single bit and the soundness error is negligibly close to 1/2; or more generally, the prover sends \(\ell \) bit in order to obtain a soundness error negligibly close to \(2^{-\ell }\).
Non-Black-Box Zero-Knowledge Simulation. The zero-knowledge simulator in our constructed arguments makes non-black-box use of the verifier’s code. This is known to be inherent—black-box simulation is impossible in the setting of two (or even three) message zero knowledge against bounded-auxiliary-input verifiers [6, 15].
1.2 Technical Overview
We now give an overview of the main ideas and techniques behind our results.
The Deterministic-Prover Zero-Knowledge Protocol. Our starting point is the protocol against honest verifiers based on witness encryption [12]. In their protocol, the verifier simply sends a witness encryption of a random message u with respect to the statement \(x\in \mathcal {L}\) to be proven, and expects to get u back from the prover. Witness encryption guarantees that a prover that has a corresponding witness w, can obtain u and convince the verifier. However, if the statement is false, namely \(x\notin \mathcal {L}\), u is hidden, and soundness is guaranteed.
While honest verifiers are easy to simulate in this scheme, it is not clear how to simulate malicious verifiers. For this purpose, we aim to add to the protocol a trapdoor way of obtaining u. A simulator that has the code of the verifier should be able to extract the message u. In contrast, a malicious prover who doesn’t have the code (specifically, the verifier’s randomness) should still fail to find u when \(x\notin \mathcal {L}\).
Explainable Verifiers. To explain the idea behind the protocol in its simplest form, let us start by assuming that the first message \(\mathsf {v}\) sent by verifier to the prover is always explainable [7]. That is, there exist honest verifier coins r that explain this message as an honest verifier message  . The difference between this setting and the honest verifier setting is that the explaining coins r may be distributed arbitrarily and also computationally hard to find.
. The difference between this setting and the honest verifier setting is that the explaining coins r may be distributed arbitrarily and also computationally hard to find.
Our basic idea is for the verifier to send the prover yet another witness encryption of u where the witness is basically the malicious verifier code  . Our realization of this idea is inspired by Barak’s uniform simulation technique [1]. Let b be the given bound on the description size of the verifier including its (bounded) auxiliary input hardwired. Then, the honest verifier samples a long random string
. Our realization of this idea is inspired by Barak’s uniform simulation technique [1]. Let b be the given bound on the description size of the verifier including its (bounded) auxiliary input hardwired. Then, the honest verifier samples a long random string  . Then in addition to the witness encryption of u under the statement \(x\in \mathcal {L}\), it sends a witness encryption of u under the statement:
. Then in addition to the witness encryption of u under the statement \(x\in \mathcal {L}\), it sends a witness encryption of u under the statement:
“There exists a program \(\varPi \) of size
(namely short) that outputs R."
To argue that the protocol remains sound, we note that except with negligible probability  over the choice of r, such a short program does not exist. In this case, witness encryption will guarantee that u remains hidden and soundness is preserved. Furthermore, a simulator in possession of the b-size code
over the choice of r, such a short program does not exist. In this case, witness encryption will guarantee that u remains hidden and soundness is preserved. Furthermore, a simulator in possession of the b-size code  of the malicious verifier can now use it to simulate. Specifically, let \(\ell \) be the amount of coins \(r^*\) used by
of the malicious verifier can now use it to simulate. Specifically, let \(\ell \) be the amount of coins \(r^*\) used by  , then the simulator will sample \(r^*\) using a pseudorandom generator that stretches a seed \(s^*\) of length
, then the simulator will sample \(r^*\) using a pseudorandom generator that stretches a seed \(s^*\) of length  to a pseudorandom \(r^*\) of length \(\ell \). Looking at the string R that
to a pseudorandom \(r^*\) of length \(\ell \). Looking at the string R that  outputs, the simulator now possesses a size-
outputs, the simulator now possesses a size- program \(\varPi \) that computes R—the code of
program \(\varPi \) that computes R—the code of  with the seed \(s^*\) hardwired. This in turn leads to valid simulation.
with the seed \(s^*\) hardwired. This in turn leads to valid simulation.
Witness Encryption for Unbounded NP Relations and IO. One thing to notice about the latter protocol is that in fact the existence of program \(\varPi \) that outputs R is not an NP statement, unless we restrict the running time of \(\varPi \) to some specific polynomial. However, while the non-uniform description size (equivalently, auxiliary input size) of the malicious verifier  is a-priori bounded, its running time is not bounded by any specific polynomial.
is a-priori bounded, its running time is not bounded by any specific polynomial.
Accordingly, we need a strong notion of witness encryption for unbounded non-deterministic relations. Specifically, encryption under a statement x should take time polynomial in |x| (and the security parameter), and not depend on the time required to verify a witness for x. In contrast, decrypting with a witness w should take time proportional to the time required to verify w. Such witness encryption schemes directly follow from known indistinguishability obfuscation (IO) schemes for Turing Machines, which are in turn constructed from subexponentially-secure IO for circuits [5, 14, 20].
Malicious Verifiers. Having constructed a protocol against explainable verifiers, we use compilers from the literature to turn it into a protocol against arbitrary verifiers. These compilers use non-interactive witness-indistinguishable proofs (NIWIs) in order to enforce explainable behavior on the verifier’s side. Being non-interactive verifying, these proofs require no randomness from the honest zero-knowledge prover.
The first such compiler [7] works for  and requires no additional hardness assumptions. The second compiler is taken from [3] (where it was used in a different context) and relies in addition on keyless hash functions that are collision resistant against attackers with bounded auxiliary input and quasipolynomial running time, as well as subexponentially secure commitments (which in turn follow from subexponentially secure IO and one-way functions). In the body, we reanalyze these compilers to show that they can be used to enforce robust explainability, which roughly means that the verifier’s messages are almost always explainable on any efficiently samplable distribution on its coins, a property required for our simulation strategy. See more details in Sect. 3.
and requires no additional hardness assumptions. The second compiler is taken from [3] (where it was used in a different context) and relies in addition on keyless hash functions that are collision resistant against attackers with bounded auxiliary input and quasipolynomial running time, as well as subexponentially secure commitments (which in turn follow from subexponentially secure IO and one-way functions). In the body, we reanalyze these compilers to show that they can be used to enforce robust explainability, which roughly means that the verifier’s messages are almost always explainable on any efficiently samplable distribution on its coins, a property required for our simulation strategy. See more details in Sect. 3.
From Deterministic-Prover Zero Knowledge to Predictable Arguments. We now explain how deterministic-prover zero knowledge implies predictable arguments, which in turn imply witness encryption (as well as the additional properties stated in Corollary 2). We start with an oversimplified transformation that captures the main idea, but does not fully work, and then explain how to augment it. This oversimplified transformation, in fact, starts from deterministic-prover honest-verifier zero knowledge.
Let  be our argument, and let \(\mathsf {Sim}\) be the honest-verifier simulator. We consider a new verifier
be our argument, and let \(\mathsf {Sim}\) be the honest-verifier simulator. We consider a new verifier  that works as follows. It applies the simulator \(\mathsf {Sim}(x)\) to obtain simulated randomness \(\tilde{r}\) for the honest verifier along with simulated prover messages \(\tilde{\mathsf{p}}_1,\dots ,\tilde{\mathsf{p}}_k\). The verifier
that works as follows. It applies the simulator \(\mathsf {Sim}(x)\) to obtain simulated randomness \(\tilde{r}\) for the honest verifier along with simulated prover messages \(\tilde{\mathsf{p}}_1,\dots ,\tilde{\mathsf{p}}_k\). The verifier  then certifies that the prover messages lead to an accepting transcript with respect to the verifier coins r. If they do not lead to an accepting transcript,
then certifies that the prover messages lead to an accepting transcript with respect to the verifier coins r. If they do not lead to an accepting transcript,  automatically rejects; otherwise, it interacts with the prover, and rejects the moment it receives a message \(\mathsf{p}_i \ne \tilde{\mathsf{p}}_i\). The described protocol is predictable by construction. Also, since we do not change the honest prover, it is zero knowledge against the same class of verifiers as the original protocol. We now turn to argue that the protocol is complete and sound.
automatically rejects; otherwise, it interacts with the prover, and rejects the moment it receives a message \(\mathsf{p}_i \ne \tilde{\mathsf{p}}_i\). The described protocol is predictable by construction. Also, since we do not change the honest prover, it is zero knowledge against the same class of verifiers as the original protocol. We now turn to argue that the protocol is complete and sound.
To see that the protocol has almost perfect completeness, consider a distinguisher that has the witness w hardwired. Given a transcript \( \mathsf{p}_1,\dots ,\mathsf{p}_k\) and verifier coins r, it can perfectly emulate a conversation between the deterministic prover \(\mathsf {P}(x,w)\) and honest verifier  and check whether the produced prover messages are consistent with the input transcript \( \mathsf{p}_1,\dots ,\mathsf{p}_k\), and that the transcript is accepting. We deduce that with overwhelming probability the simulator produces simulated messages \(\tilde{\mathsf{p}}_1,\dots ,\tilde{\mathsf{p}}_k\), and randomness r, such that the honest prover would produce the same messages, and the transcript will be accepting. To see soundness, notice that if the simulated coins r are pseudorandom and the simulated prover messages \(\tilde{\mathsf{p}}_1,\dots ,\tilde{\mathsf{p}}_k\) are accepting, then by the soundness of the original protocol
and check whether the produced prover messages are consistent with the input transcript \( \mathsf{p}_1,\dots ,\mathsf{p}_k\), and that the transcript is accepting. We deduce that with overwhelming probability the simulator produces simulated messages \(\tilde{\mathsf{p}}_1,\dots ,\tilde{\mathsf{p}}_k\), and randomness r, such that the honest prover would produce the same messages, and the transcript will be accepting. To see soundness, notice that if the simulated coins r are pseudorandom and the simulated prover messages \(\tilde{\mathsf{p}}_1,\dots ,\tilde{\mathsf{p}}_k\) are accepting, then by the soundness of the original protocol  , it should be hard for an efficient prover to produce messages consistent with \(\tilde{\mathsf{p}}_1,\dots ,\tilde{\mathsf{p}}_k\) (or with any accepting transcript).
, it should be hard for an efficient prover to produce messages consistent with \(\tilde{\mathsf{p}}_1,\dots ,\tilde{\mathsf{p}}_k\) (or with any accepting transcript).
Above, when proving soundness we actually made the implicit assumption that the honest verifier simulator \(\mathsf {Sim}(x)\) produces pseudorandom verifier coins, even when given a no instance \(x\notin \mathcal {L}\). Indeed, with respect to random, or pseudorandom, coins, we can argue that it is hard to find accepting transcripts. While this is a natural property, it does not follow directly from honest verifier zero knowledge. To circumvent this difficulty, we slightly augment the above transformation, while relying on zero-knowledge against (not necessarily honest) bounded-auxiliary-input verifiers.
Specifically, the verifier  uses a pseudorandom generator to sample coins r for the honest verifier
uses a pseudorandom generator to sample coins r for the honest verifier  , using a short seed s. It then applies the same procedure as above, except that it runs the simulator
, using a short seed s. It then applies the same procedure as above, except that it runs the simulator  for the deterministic verifier
for the deterministic verifier  that first derives the coins r from the seed s, and then applies
that first derives the coins r from the seed s, and then applies  . By choosing an appropriate pseudorandom generator, we can guarantee that the non-uniform description of
. By choosing an appropriate pseudorandom generator, we can guarantee that the non-uniform description of  is short enough. This transformation guarantees that the simulated coins are pseudorandom, even for a no instance, and allows the above proof to go through. The necessity of zero-knowledge to hold even for verifiers that are not necessarily honest comes from the fact that our description of
is short enough. This transformation guarantees that the simulated coins are pseudorandom, even for a no instance, and allows the above proof to go through. The necessity of zero-knowledge to hold even for verifiers that are not necessarily honest comes from the fact that our description of  deviates from the honest verifier strategy. We give another construction of predictable arguments from deterministic-prover arguments that are only honest-verifier zero knowledge, provided that the arguments supports expressive enough languages. See Sect. A for details.
deviates from the honest verifier strategy. We give another construction of predictable arguments from deterministic-prover arguments that are only honest-verifier zero knowledge, provided that the arguments supports expressive enough languages. See Sect. A for details.
A Word on Two-Message Laconic Arguments. As stated in Corollary 2, we use the implication to predictable arguments to also derive that any deterministic-prover zero knowledge argument for bounded-auxiliary-input verifiers can be made two message and laconic. This corollary is obtained by applying as is general transformations on predictable arguments [12]. The only thing we need to prove is that these transformations preserve zero knowledge. The only hurdle here is that the mentioned transformations involve parallel repetition for the sake of soundness amplification. We observe that (unlike many-round zero knowledge) two-message zero knowledge against bounded-auxiliary-input verifiers is closed under parallel repetition.
On Deterministic Prover Zero-Knowledge Proofs. While our results (in conjunction with prior works) provide a complete picture of deterministic zero-knowledge arguments, our results do not have any bearing on deterministic zero-knowledge proofs, where soundness is required to hold against unbounded provers. Completing the picture for proofs remains an interesting open problem.
2 Definitions
In this work, we will consider \(\mathsf {PPT}\) machines with both, bounded and unbounded non-uniform auxiliary input. For simplicity of notation, rather than considering explicit auxiliary input in our definitions, we consider two basic notions of non-uniformity. The corresponding zero knowledge definition will in particular capture the auxiliary input setting. See Remark 1.
-
1.
non-uniform \(\mathsf {PPT}\): this is the standard notion of non-uniform \(\mathsf {PPT}\) machines. Formally, a non-uniform \(\mathsf {PPT}\)
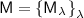 is a family of probabilistic Turing machines (one for each
is a family of probabilistic Turing machines (one for each  ), where there exists a polynomial
), where there exists a polynomial  , such that the description size
, such that the description size  and the running time of
and the running time of  are bounded by
are bounded by  .
. -
2.
b-non-uniform \(\mathsf {PPT}\): These are \(\mathsf {PPT}\) machines with non-uniform description of size
 and arbitrary polynomial running time (possibly larger than
and arbitrary polynomial running time (possibly larger than  ). Formally, a b-non-uniform \(\mathsf {PPT}\)
). Formally, a b-non-uniform \(\mathsf {PPT}\)  is a family of probabilistic Turing machines (one for each
is a family of probabilistic Turing machines (one for each 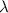 ), where
), where 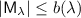 and there exists a polynomial
and there exists a polynomial  , such that the running time of
, such that the running time of  is bounded by
is bounded by  .
.
In both of the above, we often omit from  the subscript
the subscript  when it is clear from the context. If we simply say a \(\mathsf {PPT}\) machine, we mean a uniform one.
when it is clear from the context. If we simply say a \(\mathsf {PPT}\) machine, we mean a uniform one.
Throughout this work, we will talk about computational indistinguishability with respect to non-uniform distinguishers.
Definition 1
(Computational Indistinguishability). Two ensembles \(X=\{X_\alpha \}_{\alpha \in S}\) and \(Y=\{Y_\alpha \}_{\alpha \in S}\) are said to be computationally indistinguishable, denoted by \(X \approx _c Y\), if for every non-uniform \(\mathsf {PPT}\) distinguisher \(\mathcal {D}\), every polynomial  , all sufficiently large
, all sufficiently large  and every
and every 

where the probability are taken over the samples of \(X_\alpha \), \(Y_\alpha \) and coin tosses of \(\mathcal {D}\).
We shall sometimes find it convenient to talk about the stronger notion of statistical indistinguishability, defined below.
Definition 2
(Statistical Indistinguishability). Two ensembles \(X=\{X_\alpha \}_{\alpha \in S}\) and \(Y=\{Y_\alpha \}_{\alpha \in S}\) are said to be statistically indistinguishable, denoted by \({X \approx _s Y}\), if for every polynomial  , all sufficiently large
, all sufficiently large  and every
and every 

where \(\varDelta (X_\alpha ,Y_\alpha )\) corresponds to the statistical distance between \(X_\alpha \) and \(Y_\alpha \).
2.1 Deterministic-Prover Zero Knowledge Against Bounded-Auxiliary-Input Verifiers
We define the notion of deterministic-prover zero-knowledge arguments against verifiers with bounded auxiliary-input (DPZK). We shall denote by \(\mathsf {Out}_A\langle A(a), B(b)\rangle \) the output of party A on execution of the protocol between A with input a, and B with input b. By \(\mathsf {View}_A\langle A(a), B(b)\rangle \), we denote the view of party A consisting of the protocol transcript along with its random tape.
Definition 3
An interactive protocol  between a deterministic polynomial time prover \(\mathsf {P}\) and \(\mathsf {PPT}\) verifier
between a deterministic polynomial time prover \(\mathsf {P}\) and \(\mathsf {PPT}\) verifier  , for a language \(\mathcal {L}\) is a deterministic prover b-bounded-auxiliary-input zero knowledge argument if the following holds.
, for a language \(\mathcal {L}\) is a deterministic prover b-bounded-auxiliary-input zero knowledge argument if the following holds.
-
Completeness: For every \(x \in \mathcal {L}\),
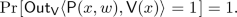
-
Soundness: For any non-uniform \(\mathsf {PPT}\) \(\mathsf {P}^*\), there exists a negligible function
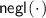 such that for all
such that for all 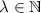 and
and  ,
, 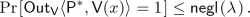
-
Zero Knowledge: There exists a \(\mathsf {PPT}\) simulator \(\mathsf {Sim}\), such that for every b-non-uniform \(\mathsf {PPT}\) verifier
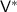 of running time at most
of running time at most  ,
, 
Remark 1
(Universal Simulation). In the above definition, there exists one universal simulator \(\mathsf {Sim}\) that gets the code of the verifier as input. We note that this definition is known [16] to imply the alternative definition of (bounded) auxiliary-input zero knowledge that requires that any for any t-time  there is a \(\mathsf {PPT}\) simulator
there is a \(\mathsf {PPT}\) simulator  such that given (bounded) auxiliary input z,
such that given (bounded) auxiliary input z,  simulates
simulates  .
.
2.2 Indistinguishability Obfuscation (IO)
We now give a definition of indistinguishability obfuscator for Turing Machines, which can be constructed from indistinguishability obfuscators for circuits [5, 14, 20].
Definition 4
(Indistinguishability Obfuscator for Turing Machines). A succinct indistinguishability obfuscator for Turing machines consists of a PPT machine \(\mathsf {iOM}\) that works as follows:
-
\(\mathsf {iOM}\) takes as input the security parameter
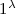 , the Turing machine \(\mathsf {M}\) to obfuscate, an input length n, and time bound t.
, the Turing machine \(\mathsf {M}\) to obfuscate, an input length n, and time bound t. -
\(\mathsf {iOM}\) outputs a Turing machine \(\widetilde{\mathsf {M}}\) which is an obfuscation of \(\mathsf {M}\) corresponding to input length n and time bound t. \(\widetilde{\mathsf {M}}\) takes as input \(x \in \{0,1\}^n\).
The scheme should satisfy the following requirements:
-
Correctness. For all
 , for all
, for all  , for all inputs \(x \in \{0,1\}^n\), time bounds \(t'\) such that \(t' \le t\), let y be the output of \(\mathsf {M}(x)\) after at most t steps, then
, for all inputs \(x \in \{0,1\}^n\), time bounds \(t'\) such that \(t' \le t\), let y be the output of \(\mathsf {M}(x)\) after at most t steps, then 
-
Security. It holds that
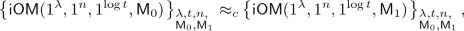
where
 ,
, 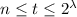 , and \(\mathsf {M}_0, \mathsf {M}_1\) are any pair of machines of the same size such that for any input \(x\in \{0,1\}^n\) both halt after the same number of steps with the same output.
, and \(\mathsf {M}_0, \mathsf {M}_1\) are any pair of machines of the same size such that for any input \(x\in \{0,1\}^n\) both halt after the same number of steps with the same output. -
Efficiency and Succinctness. We require that the running time of \(\mathsf {iOM}\) and the length of its output, namely the obfuscated machine \(\widetilde{\mathsf {M}}\), is
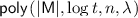 . We also require that the running time \(\tilde{t}_x\) of \(\widetilde{\mathsf {M}}(x)\) is
. We also require that the running time \(\tilde{t}_x\) of \(\widetilde{\mathsf {M}}(x)\) is  , where \(t_x\) is the running time of \(\mathsf {M}(x)\).
, where \(t_x\) is the running time of \(\mathsf {M}(x)\).
2.3 Witness Encryption
The following definition of witness encryption is taken from [13].
Definition 5
A witness encryption scheme for an  language \(\mathcal {L}\), with corresponding witness relation \(R_\mathcal {L}\), consists of the following two polynomial-time algorithms:
language \(\mathcal {L}\), with corresponding witness relation \(R_\mathcal {L}\), consists of the following two polynomial-time algorithms:
-
Encryption. The probabilistic algorithm
 takes as input a security parameter
takes as input a security parameter  , a string \(x \in \{0,1\}^*\), and a message \(m \in \{0,1\}\). It outputs a ciphertext \(\mathsf {ct}\).
, a string \(x \in \{0,1\}^*\), and a message \(m \in \{0,1\}\). It outputs a ciphertext \(\mathsf {ct}\). -
Decryption. The algorithm \(\mathsf {WE}.\mathsf {Dec}(\mathsf {ct},w)\) takes as input a ciphertext \(\mathsf {ct}\), a string \(w \in \{0,1\}^*\). It outputs either a message \(m \in \{0,1\}\).
The above algorithms satisfy the following conditions:
-
Correctness. For any security parameter
 , for any \(m \in \{0,1\}\), and for any \((x,w) \in R_\mathcal {L}\), we have that
, for any \(m \in \{0,1\}\), and for any \((x,w) \in R_\mathcal {L}\), we have that 
-
Security. For any non-uniform \(\mathsf {PPT}\)adversary \(\mathcal {A}\), there exists a negligible function
 such that for any
such that for any 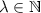 , and any \(x \notin \mathcal {L}\), we have that
, and any \(x \notin \mathcal {L}\), we have that 
We note that the above scheme can be extended to encrypt strings, rather than just bits, by encrypting each bit independently. Witness encryption for all of  can be constructed from IO for circuits [13].
can be constructed from IO for circuits [13].
2.4 Non-interactive Witness Indistinguishability (NIWI)
Definition 6
([2]). A non-interactive witness-indistinguishable proof system \(\mathsf {NIWI}=(\mathsf {NIWI}.\mathsf {Prov},\mathsf {NIWI}.\mathsf {Ver})\) for an  relation \(R_\mathcal {L}\) consists of two polynomial-time algorithms:
relation \(R_\mathcal {L}\) consists of two polynomial-time algorithms:
-
a probabilistic prover
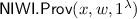 that given an instance x, witness w, and security parameter
that given an instance x, witness w, and security parameter  , produces a proof \(\pi \).
, produces a proof \(\pi \). -
a deterministic verifier \(\mathsf {NIWI}.\mathsf {Ver}(x,\pi )\) that verifies the proof.
We make the following requirements:
-
Completeness for every
 ,
, 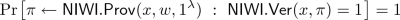
-
Soundness for every \(x \notin \mathcal {L}\) and \(\pi \in \{0,1\}^*\),
$$ \mathsf {NIWI}.\mathsf {Ver}(x,\pi )=0. $$ -
Witness Indistinguishability. It holds that

where
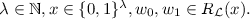
2.5 Collision Resistance Against Bounded Non-uniform Adversaries
We describe here the notion of keyless collision resistance against quasi-polynomial b-non-uniform adversaries, extending the definition in [3].
Syntax. A keyless collision resistance hash function is associated with an input function  and a polynomial time algorithm \(\mathsf {H}\) such that
and a polynomial time algorithm \(\mathsf {H}\) such that  is a deterministic algorithm that takes as input an
is a deterministic algorithm that takes as input an  and outputs a hash
and outputs a hash  .
.
Definition 7
We say that \(\mathsf {H}\) is collision-resistant against quasi-polynomial adversaries if for any b-non-uniform probabilistic  -time \(\mathcal {A}\), there exists a negligible function
-time \(\mathcal {A}\), there exists a negligible function  , such that for any
, such that for any  ,
,

2.6 Non-interactive Commitment Schemes
We define below bit commitment schemes.
Definition 8
(Non-interactive Bit Commitment Schemes). A polynomial time computable function:  is a bit commitment if it satisfies the properties below:
is a bit commitment if it satisfies the properties below:
-
Binding: For any
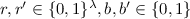 , if \(\mathsf {Com}(b;r)=\mathsf {Com}(b';r')\) then \(b=b'\).
, if \(\mathsf {Com}(b;r)=\mathsf {Com}(b';r')\) then \(b=b'\). -
Computational Hiding: The following holds:

where computational indistinguishability is with respect to arbitrary non-uniform \(\mathsf {PPT}\) distinguisher.
We note that the above scheme can be extended to commit to strings, rather than just bits, by committing to each bit independently. Looking ahead, we require that the underlying string that is committed can be extracted in quasi-polynomial time. Such commitments can be constructed from subexponentiall-secure injective one-way functions (which in turn can be constructed from subexponential IO and one-way functions).
2.7 Explainable Verifiers
We define here the a variant of the notion of explainable verifiers [7] called robustly-explainable verifiers. Roughly speaking, explainable verifiers are ones whose messages almost always lie in the support of the honest verifier messages (or are abort). Robustly-explainable verifiers are such where this occurs when they use random coins sampled from an arbitrary efficient sampler (and not necessarily the uniform distribution).
Definition 9
(Explainable Message). Let  be a two-message protocol. We say that a given message m is explainable with respect to x, if there exist honest verifier coins r such that
be a two-message protocol. We say that a given message m is explainable with respect to x, if there exist honest verifier coins r such that  .
.
Definition 10
(Robustly-Explainable Verifier). Let  be a protocol. A b-non-uniform \(\mathsf {PPT}\) verifier
be a protocol. A b-non-uniform \(\mathsf {PPT}\) verifier  using
using  random coins is robustly-explainable if for any \(\mathsf {PPT}\) sampler R on
random coins is robustly-explainable if for any \(\mathsf {PPT}\) sampler R on  bits, there exists a negligible
bits, there exists a negligible  such that for any
such that for any  and
and  ,
,

2.8 Pseudorandom Generators
Definition 11
(Psedudorandom Generators). A deterministic function  is called a pseudorandom generator (PRG) if:
is called a pseudorandom generator (PRG) if:
-
1.
(efficiency): \(\mathsf {PRG}\) can be computed in polynomial time,
-
2.
(expansion):
 ,
, -
3.
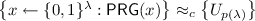 , where
, where  is the uniform distribution over
is the uniform distribution over  bits.
bits.
3 A Deterministic-Prover Zero-Knowledge Protocol
In this section we present our deterministic prover zero knowledge (DPZK) protocol. As explained in the introduction, we start by describing the protocol for robustly-explainable verifiers. We then show how to compile this protocol to one that is secure against malicious verifiers.
3.1 DPZK for Robustly-Explainable Verifiers
We use the following components for the deterministic prover zero knowledge (DPZK) protocol for an  language \(\mathcal {L}\) against b-non-uniform explainable verifiers.
language \(\mathcal {L}\) against b-non-uniform explainable verifiers.
-
A witness encryption scheme
 for language \(\mathcal {L}\).
for language \(\mathcal {L}\). -
An indistinguishability obfuscation (IO) scheme \(\mathsf {iOM}\) for Turing Machines (TM).
Additionally, we will use the machine described below that outputs the hardcoded secret u given as input the description of a “short” Turing machine that outputs a hardcoded public value R.

In what follows, let  ,
,  . The protocol is described in Fig. 1. We prove the properties of the protocol below.
. The protocol is described in Fig. 1. We prove the properties of the protocol below.
Completeness. Completeness follows from the correctness of witness encryption.
Soundness. We now prove that the above protocol is sound against computationally bounded provers.
Proposition 1
Assuming security of the indistinguishability obfuscation scheme and the witness encryption scheme, the protocol is sound.
Proof
We consider a sequence of hybrids transitioning from the real protocol to an ideal protocol where the probability that the prover convinces the verifier of accepting is clearly negligible.
-
\(\mathsf {Hyb}_{0}\): This is the real protocol.
-
\(\mathsf {Hyb}_1\): In this hybrid, we modify the program \(\mathsf {Prog}\) to \(\mathsf {Prog}'\) that always output \(\perp \).
By our choice of parameters and a union bound, the probability that there exists a machine \(\mathsf {M}\in \{0,1\}^\rho \) that outputs R is at most
 . Therefore, except with negligible probability \(\mathsf {Prog}\) and \(\mathsf {Prog}'\) are functionally equivalent. The indistinguishability of \(\mathsf {Hyb}_1\) and \(\mathsf {Hyb}_0\) then follows from the indistinguishability of the IO scheme.
. Therefore, except with negligible probability \(\mathsf {Prog}\) and \(\mathsf {Prog}'\) are functionally equivalent. The indistinguishability of \(\mathsf {Hyb}_1\) and \(\mathsf {Hyb}_0\) then follows from the indistinguishability of the IO scheme. -
\(\mathsf {Hyb}_2\): In this hybrid, we additionally change the ciphertext \(\mathsf {ct}\) of the witness encryption scheme to be the encryption of 0.
Since \(x \notin \mathcal {L}\), the indistinguishability between \(\mathsf {Hyb}_2\) and \(\mathsf {Hyb}_1\) follows from the security of the witness encryption scheme.
It is left to observe that in \(\mathsf {Hyb}_2\) the prover obtains no information about u, and thus convinces the verifier with probability at most  . \(\square \)
. \(\square \)
Zero Knowledge. We prove
Proposition 2
Assuming the existence of pseudorandom generators, the protocol is zero knowledge against b-non-uniform verifiers.
Proof
We describe the simulation strategy below. In what follows  is a b-non-uniform malicious verifier of polynomial running time at most
is a b-non-uniform malicious verifier of polynomial running time at most  . Additionally, let k be the amount of random coins \(r^*\) used by
. Additionally, let k be the amount of random coins \(r^*\) used by  . The simulator \(\mathsf {Sim}\) will use a PRG
. The simulator \(\mathsf {Sim}\) will use a PRG  .
.

-
1.
Construct verifier
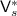 that has the seed s hardwired.
that has the seed s hardwired. 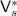 computes \(\mathsf {PRG}(s)\) and uses it as random coins for
computes \(\mathsf {PRG}(s)\) and uses it as random coins for 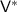 . Additionally,
. Additionally,  truncates
truncates 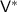 ’s output to R.
’s output to R. -
2.
Initialize
 with random coins \(\mathsf {PRG}(s)\).
with random coins \(\mathsf {PRG}(s)\). -
3.
Given \(\widetilde{\mathsf {Prog}}\) from
 , use the description of
, use the description of  as input to \(\widetilde{\mathsf {Prog}}\) and obtain u.
as input to \(\widetilde{\mathsf {Prog}}\) and obtain u. -
4.
u is then used as the simulated prover message, along with verifier randomness \(\mathsf {PRG}(s)\).
First, consider an execution between the prover and augmented verifier  , and let \(\mathsf {v}\) and \(\mathsf {p}\) denote the verifier and prover messages in such an execution. Then by pseudorandomness of \(\mathsf {PRG}\),
, and let \(\mathsf {v}\) and \(\mathsf {p}\) denote the verifier and prover messages in such an execution. Then by pseudorandomness of \(\mathsf {PRG}\),

Next, by the fact that  is robustly explainable, we know that except with negligible probability, \(\mathsf {v} = (R,\mathsf {ct},\widetilde{\mathsf {Prog}})\) is explainable; namely, has the structure prescribed by the honest verifier algorithm. Noting that
is robustly explainable, we know that except with negligible probability, \(\mathsf {v} = (R,\mathsf {ct},\widetilde{\mathsf {Prog}})\) is explainable; namely, has the structure prescribed by the honest verifier algorithm. Noting that  is a program of length
is a program of length  and running time at most
and running time at most  that outputs R. By the fact that \(\mathsf {v}\) is explainable,
that outputs R. By the fact that \(\mathsf {v}\) is explainable,  . It follows that
. It follows that

and overall

as required. \(\square \)
3.2 From Explainable to Malicious Verifiers
In this section we give generic compilers going from robust-explainable to malicious verifiers. These compilers were constructed in [7] where they were used to enforce explainability and in [3] where they were used in a different context. We prove that these compilers, in fact, enforce robust explainability. The statements, and correspondingly the underlying assumptions, change based on whether we want a DPZK for  , or for all of
, or for all of  . We discuss the two cases separately.
. We discuss the two cases separately.
3.2.1 DPZK for 
We consider languages  , which in turn means that in addition to relation \(R_{\mathcal {L}}\), there is also a
, which in turn means that in addition to relation \(R_{\mathcal {L}}\), there is also a  -relation \(R_{\overline{\mathcal {L}}}\) to certify that a statement \(x \notin \mathcal {L}\).
-relation \(R_{\overline{\mathcal {L}}}\) to certify that a statement \(x \notin \mathcal {L}\).
We use the following primitives in our construction:
-
A two-message deterministic-prover zero-knowledge (DPZK) protocol
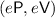 secure against robustly-explainable verifiers. Let the verifier and prover messages be denoted by \(\mathsf {v}\) and \(\mathsf {p}\), respectively.
secure against robustly-explainable verifiers. Let the verifier and prover messages be denoted by \(\mathsf {v}\) and \(\mathsf {p}\), respectively. -
A non-interactive witness indistinguishable proof (NIWI) \((\mathsf {NIWI}.\mathsf {Prov},\mathsf {NIWI}.\mathsf {Ver})\) for the language
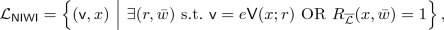
namely, either the verifier’s message is explainable, or the statement is not in the language. Henceforth, we shall refer to the second half of the ‘OR’ statement, that the statement is not in the language, to be the trapdoor statement.
The protocol is presented in Fig. 2.
Completeness. Completeness follows directly from the completeness of the underlying protocol and the NIWI proof.
Zero Knowledge. We show how any b-non-uniform malicious verifier  for the above protocol can be converted to a robustly-explainable \(b+O(1)\)-non-uniform verifier against the original protocol.
for the above protocol can be converted to a robustly-explainable \(b+O(1)\)-non-uniform verifier against the original protocol.
Claim 1
There exist an efficient simulator \(\mathsf {S}\) and a verifier  such that
such that
-
1.
 is a robustly explainable verifier against
is a robustly explainable verifier against  .
. -
2.
 is \((b+O(1))\)-non-uniform and efficiently constructable from
is \((b+O(1))\)-non-uniform and efficiently constructable from  .
. -
3.
For every \(x \in \mathcal {L}\),
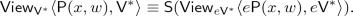
Proof
We construct  .
.

-
1.
Emulates
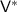 and obtains \((\mathsf {v},\mathsf {wi})\).
and obtains \((\mathsf {v},\mathsf {wi})\). -
2.
If \(\mathsf {wi}\) is not a valid proof for the statement \((\mathsf {v},x)\), send \(e\mathsf {P}\) the message \(\perp \).
-
3.
Else, send \(e\mathsf {P}\) \(\mathsf {v}\), and get \(\mathsf {p}\).
-
4.
Complete emulation of
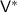 with message \(\mathsf {p}\).
with message \(\mathsf {p}\).

-
1.
Outputs the randomness of the emulated
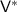 (can be derived from the randomness of
(can be derived from the randomness of 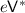 ,
, -
2.
as well as the received prover message \(\mathsf {p}\) (possibly \(\perp \)).
The third property asserted in the claim follows by construction of  and the fact that the prover \(\mathsf {P}\) checks on its own whether the verifier’s proof is accepting. It is left to see that
and the fact that the prover \(\mathsf {P}\) checks on its own whether the verifier’s proof is accepting. It is left to see that  is robustly explainable, \((b+O(1))\)-non-uniform, and efficiently constructable from
is robustly explainable, \((b+O(1))\)-non-uniform, and efficiently constructable from  . Robust explainability follows directly by the (unconditional) soundness of the NIWI—
. Robust explainability follows directly by the (unconditional) soundness of the NIWI— either outputs an explainable message or \(\perp \). \((b+O(1))\)-non-uniformity and efficient construction follow from the fact that
either outputs an explainable message or \(\perp \). \((b+O(1))\)-non-uniformity and efficient construction follow from the fact that  is b-non-uniform and
is b-non-uniform and  uses it as a black box and described by the four code lines above. \(\square \)
uses it as a black box and described by the four code lines above. \(\square \)
Claim 1 directly gives rise to a zero knowledge \(\mathsf {Sim}\) for the protocol  . In what follows, let \(e\mathsf {Sim}\) be the simulator of the underlying DPZK protocol against robustly-explainable verifiers.
. In what follows, let \(e\mathsf {Sim}\) be the simulator of the underlying DPZK protocol against robustly-explainable verifiers.

-
1.
Construct the explainable verifier
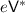 .
. -
2.
Output
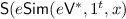 .
.
The validity of the simulator \(\mathsf {Sim}\) follows directly from that of \(e\mathsf {Sim}\) and Claim 1.
Soundness. For soundness, we show that any cheating prover \(\mathsf {P}^*\) breaking the soundness of the above protocol, can be converted into a prover \(e\mathsf {P}^{*}\) that breaks the soundness of the underlying protocol. \(e\mathsf {P}^{*}\) will have the witness \({\bar{w}}\) for \(x \notin \mathcal {L}\) hardwired.

-
1.
Obtain message \(\mathsf {v}\) from
 .
. -
2.
Use \({\bar{w}}\) as the witness to compute the NIWI proof \(\mathsf {wi}\).
-
3.
Emulate \(\mathsf {P}^*\) with \((\mathsf {v},\mathsf {wi})\) and obtain \(\mathsf {p}\).
-
4.
Send \(\mathsf {p}\) to the verifier
 .
.
First note that since  , the statement \(x \notin \mathcal {L}\) has a witness \(\bar{w}\) as required. The only difference in the views of \(\mathsf {P}^{*}\) and its emulated version in \(e\mathsf {P}^{*}\) is in the NIWI proof. From the witness indistinguishability of the NIWI, \(\mathsf {P}^{*}\)’s success probability does not change by more than a negligible amount.
, the statement \(x \notin \mathcal {L}\) has a witness \(\bar{w}\) as required. The only difference in the views of \(\mathsf {P}^{*}\) and its emulated version in \(e\mathsf {P}^{*}\) is in the NIWI proof. From the witness indistinguishability of the NIWI, \(\mathsf {P}^{*}\)’s success probability does not change by more than a negligible amount.
3.2.2 DPZK for All of 
As mentioned to in the introduction, for the case of  , we require stronger primitives. Specifically, we use the following primitives for our construction:
, we require stronger primitives. Specifically, we use the following primitives for our construction:
-
A two round deterministic prover zero knowledge (DPZK) protocol
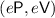 secure against robustly-explainable verifiers. Let the verifier and prover messages be denoted by \(\mathsf {v}\) and \(\mathsf {p}\), respectively.
secure against robustly-explainable verifiers. Let the verifier and prover messages be denoted by \(\mathsf {v}\) and \(\mathsf {p}\), respectively. -
A non-interactive commitment scheme \(\mathsf {Com}\) with perfect binding and computational hiding. Additionally, as mentioned earlier, we require that the plaintext underlying a commitment can be extracted in quasi-polynomial time. Such commitments can be constructed from subexponentiall-secure injective one-way functions (which in turn can be constructed from subexponential IO and one-way functions).
-
A keyless collision-resistant hash function \(\mathsf {H}\) secure against \((b+O(1))\)-non-uniform quasi-polynomial time adversaries.
-
A non-interactive witness-indistinguishable proof (NIWI) \((\mathsf {NIWI}.\mathsf {Prov},\mathsf {NIWI}.\mathsf {Ver})\) for the language

namely, either the verifier’s message is explainable, or the commitment sent by the verifier contains a collision in \(\mathsf {H}\). As before, we shall refer to the second half of the ‘OR’ statement as the trapdoor statement.
The protocol is presented in Fig. 3.
Completeness. Follows directly from the completeness of the underlying protocol and the NIWI.
Zero Knowledge. For zero knowledge, we follow the same strategy as in the previous subsection and show how any b-non-uniform verifier  for the above protocol can be converted into a robustly-explainable \((b+O(1))\)-non-uniform verifier against the original protocol.
for the above protocol can be converted into a robustly-explainable \((b+O(1))\)-non-uniform verifier against the original protocol.
We argue that Claim 1 also holds for this protocol with the exact same \(\mathsf {S}\) and  . The only difference is in the proof of robust explainability of the verifier
. The only difference is in the proof of robust explainability of the verifier  , which is based on complexity leveraging.
, which is based on complexity leveraging.
Robust Explainability of  . Fix some \(\mathsf {PPT}\) sampler R for coins for
. Fix some \(\mathsf {PPT}\) sampler R for coins for  and assume toward contradiction that with noticeable probability it outputs a message \(\mathsf {v}\) that is not explainable when initialized with random coins sampled using R. We show that there exists a \((b+O(1))\)-non-uniform quasi-polynomial time attacker that finds a collision in \(\mathsf {H}\). Recall the
and assume toward contradiction that with noticeable probability it outputs a message \(\mathsf {v}\) that is not explainable when initialized with random coins sampled using R. We show that there exists a \((b+O(1))\)-non-uniform quasi-polynomial time attacker that finds a collision in \(\mathsf {H}\). Recall the  only outputs a non-\(\perp \) message provided that the emulated
only outputs a non-\(\perp \) message provided that the emulated  produces a valid NIWI. By the unconditional soundness of the NIWI, it follows that whenever
produces a valid NIWI. By the unconditional soundness of the NIWI, it follows that whenever  outputs a non-explainable message, it must be that c is a valid commitment to a collision in \(\mathsf {H}\). This collision is then be extracted from the commitment in quasi-polynomial time. Note that the corresponding collision finder can be described by
outputs a non-explainable message, it must be that c is a valid commitment to a collision in \(\mathsf {H}\). This collision is then be extracted from the commitment in quasi-polynomial time. Note that the corresponding collision finder can be described by  and R, which have non-uniform description of size \(b+O(1)\). \(\square \)
and R, which have non-uniform description of size \(b+O(1)\). \(\square \)
Zero knowledge of  now follows from that of
now follows from that of  and the existence of \(\mathsf {S}\) and
and the existence of \(\mathsf {S}\) and  , exactly as in the previous subsection.
, exactly as in the previous subsection.
Soundness. We show that any cheating prover \(\mathsf {P}^*\) breaking the soundness of the above protocol, can be converted into a prover \(e\mathsf {P}^{*}\) that breaks the soundness of the underlying robustly-explainable protocol. The reduction is similar to that in the previous subsection with some required changed. \(e\mathsf {P}^{*}\) will have a collision \((x_1,x_2)\) as (part of the) witness for the trapdoor statement hardwired in its code.

-
1.
Obtain message \(\mathsf {v}\) from
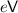 .
. -
2.
Compute \(c=\mathsf {Com}(x_1,x_2;r_\mathsf {Com})\).
-
3.
Use \((x_1,x_2,r_\mathsf {Com})\) as the witness to compute the NIWI proof \(\mathsf {wi}\).
-
4.
Emulate \(\mathsf {P}^*\) with \((\mathsf {v},\mathsf {wi})\) and obtain \(\mathsf {p}\).
-
5.
Send \(\mathsf {p}\) to the verifier
 .
.
The difference in the views of \(\mathsf {P}^{*}\) and its emulated version in \(e\mathsf {P}^{*}\) is the commitment to \((x_1,x_2)\) rather than zero, and in the witness used for the NIWI proof. Using the hiding of the commitment (against non-uniform \(\mathsf {PPT}\) attackers) and the witness indistinguishability of the NIWI, \(\mathsf {P}^{*}\)’s success probability does not change by more than a negligible amount.
Remark 2
We emphasize that for soundness, we require that all the underlying primitives to are secure against non-uniform adversaries since our soundness reduction is non-uniform.
4 Predictable Arguments and DPZK
In this section, we show that any deterministic-prover zero-knowledge (DPZK) argument against bounded-non-uniform verifier can be made predictable. The notion of predictable arguments was introduced in [12], where it is in particular shown to imply witness encryption. In the next section, we address additional properties of DPZK that follow from this connection.
We start by recalling the definition of predictable arguments (PA) [12]. While they also address predictable argument of knowledge, we restrict attention to predictable arguments that are only sound.
Definition 12
(Predictable Argument). A \(\rho \)-round predictable argument is an argument specified by a tuple of algorithms \((\mathsf {Chal},\mathsf {Resp})\) as described below:
-
1.
The verifier
 samples
samples 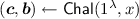 , where
, where 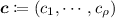 and
and 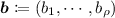 .
. -
2.
For all \(i \in [\rho ]\) in increasing sequence:
-
(a)
 sends \(c_i\) to the \(\mathsf {PA}.\mathsf {P}\);
sends \(c_i\) to the \(\mathsf {PA}.\mathsf {P}\); -
(b)
The prover \(\mathsf {PA}.\mathsf {P}\) computes
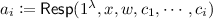 and sends \(a_i\) to
and sends \(a_i\) to 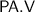 .
. -
(c)
 checks if \(a_i=b_i\), and returns 0 otherwise.
checks if \(a_i=b_i\), and returns 0 otherwise.
-
(a)
-
3.
If all challenges are answered correctly,
 returns 1.
returns 1.
The protocol is required to satisfy:
-
Correctness. There exists a negligible function
 such that for all \(x \in \mathcal {L}\) such that \(R_L(x,w)=1\), we have
such that for all \(x \in \mathcal {L}\) such that \(R_L(x,w)=1\), we have 
-
Soundness. For any non-uniform \(\mathsf {PPT}\) prover \(\mathsf {P}^*\), there exists a negligible function
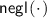 such that for all \(x \notin \mathcal {L}\),
such that for all \(x \notin \mathcal {L}\), 
A deterministic-prover zero-knowledge predictable argument (PA-DPZK) is a deterministic-prover zero-knowledge argument that is also a predictable argument.
We prove the following:
Theorem 4
Let  be a deterministic-prover zero-knowledge argument for \(\mathcal {L}\) against bounded-non-uniform verifiers. There exists a verifier
be a deterministic-prover zero-knowledge argument for \(\mathcal {L}\) against bounded-non-uniform verifiers. There exists a verifier  such that
such that  is a predictable argument.
is a predictable argument.
Note that since we do not change the honest prover \(\mathsf {P}\) it follows that  is also deterministic-prover zero knowledge against the same class of verifiers.
is also deterministic-prover zero knowledge against the same class of verifiers.
Relying on the following result by Faonio, Nielsen, and Venturi,
Theorem 5
([12]). If there exists a Predictable Argument (PA) for a language \(\mathcal {L}\), then there exists a witness encryption scheme for \(\mathcal {L}\).
our theorem holds for all  -non-uniform verifiers, and we deduce
-non-uniform verifiers, and we deduce
Corollary 3
If there exists a deterministic-prover zero-knowledge argument for \(\mathcal {L}\) against  -non-uniform verifiers, then there exists a witness encryption scheme for \(\mathcal {L}\).
-non-uniform verifiers, then there exists a witness encryption scheme for \(\mathcal {L}\).
We now proceed with the proof.
Proof of Theorem 4. Let  be a \(\rho \)-round DPZK argument for \(\mathcal {L}\) against b-non-uniform verifiers, for
be a \(\rho \)-round DPZK argument for \(\mathcal {L}\) against b-non-uniform verifiers, for  . Let
. Let  be a pseudorandom generator, where
be a pseudorandom generator, where  is the amount of coins used by
is the amount of coins used by  . For a given seed
. For a given seed  , we define the deterministic verifier
, we define the deterministic verifier  that derives coins \(r=\mathsf {PRG}(s)\) for
that derives coins \(r=\mathsf {PRG}(s)\) for  then emulates
then emulates  .
.
The transformed verifier  is presented in Fig. 4.
is presented in Fig. 4.
First, note that the protocol satisfies the structural requirement of a predictable argument. We now move to prove completeness and soundness with respect to the new verifier  .
.
Completeness. We show that  is complete based on (a) the completeness of
is complete based on (a) the completeness of  ; (b) zero knowledge of
; (b) zero knowledge of  ; and (c) pseudorandomness of \(\mathsf {PRG}\).
; and (c) pseudorandomness of \(\mathsf {PRG}\).
Fix any statement \(x \in \mathcal {L}\) and corresponding prover witness w. We need to show that in an interaction  rejects with negligible probability. First, by the completeness of
rejects with negligible probability. First, by the completeness of  and the pseudorandomness of \(\mathsf {PRG}\), an interaction
and the pseudorandomness of \(\mathsf {PRG}\), an interaction  is accepting except with negligible probability over the choice of s. Noting that
is accepting except with negligible probability over the choice of s. Noting that  is b-non-uniform, we can invoke zero knowledge, to deduce that the simulated prover messages \(\left\{ \widetilde{\mathsf {p}}_i \right\} _{i=1}^\rho \) make
is b-non-uniform, we can invoke zero knowledge, to deduce that the simulated prover messages \(\left\{ \widetilde{\mathsf {p}}_i \right\} _{i=1}^\rho \) make  accept with overwhelming probability over the choice of s.
accept with overwhelming probability over the choice of s.
We next argue that the deterministic prover \(\mathsf {P}(x,w)\) produces messages \(\left\{ \mathsf {p}_i= \widetilde{\mathsf {p}}_i \right\} _{i=1}^\rho \) with overwhelming probability (over the coins of \(\mathsf {Sim}\) that sampled them). This again follows from zero knowledge. Indeed, we can consider a zero-knowledge distinguisher that has (x, w, s) hardwired, and given messages \({\mathsf {p}}_i\) emulates a conversation of the deterministic \(\mathsf {P}(x,w)\) with  , and outputs “real” if the corresponding prover messages coincide with \({\mathsf {p}}_i\), or “simulated” otherwise. If the simulated messages \(\widetilde{\mathsf {p}}_i\) are inconsistent with the real prover messages \({\mathsf {p}}_i\), the distinguisher will tell them apart.
, and outputs “real” if the corresponding prover messages coincide with \({\mathsf {p}}_i\), or “simulated” otherwise. If the simulated messages \(\widetilde{\mathsf {p}}_i\) are inconsistent with the real prover messages \({\mathsf {p}}_i\), the distinguisher will tell them apart.
Soundness. We show that  is sound based on (a) the pseudorandomness of \(\mathsf {PRG}\); and (b) the soundness of
is sound based on (a) the pseudorandomness of \(\mathsf {PRG}\); and (b) the soundness of  .
.
First, note that by pseudorandomness the protocol  where s is chosen at random is also sound, since otherwise a cheating prover can be directly used to distinguish real verifier coins form pseudorandom ones. Next, note that any cheating prover against
where s is chosen at random is also sound, since otherwise a cheating prover can be directly used to distinguish real verifier coins form pseudorandom ones. Next, note that any cheating prover against  directly implies a cheating prover against
directly implies a cheating prover against  (for a random s) by construction. Indeed,
(for a random s) by construction. Indeed,  emulates
emulates  and accepts only when the prover is consistent with a simulated strategy \(\widetilde{\mathsf {p}}_i\) that convinces
and accepts only when the prover is consistent with a simulated strategy \(\widetilde{\mathsf {p}}_i\) that convinces  .Footnote 2 Soundness follows.
.Footnote 2 Soundness follows.
\(\square \)
5 Round Reduction and Laconicity
Faonio, Nielsen, and Venturi [12] proved that the round complexity of any predictable argument can be collapsed to one (two messages overall) and that any predictable argument can be made laconic—namely, the prover message is a single bit (or more generally \(\ell \) bits to achieve soundness \(\approx 2^{-\ell }\)). In this section, we review their transformations and show that they preserve zero knowledge against bounded-non-uniform verifiers. As a corollary of this and the previous section, we deduce that any deterministic-prover zero knowledge argument against bounded-non-uniform verifiers can be collapsed to one round and made laconic.
5.1 Round Reduction
We start by recalling the round-collapsing transformation from [12]. In what follows, let  be a \(\rho \)-round predictable argument, the following transformation provides a one round predictable argument
be a \(\rho \)-round predictable argument, the following transformation provides a one round predictable argument  with a large soundness error (to be dealt with later on). Roughly, the verifier randomly chooses a “cut-off” point \(i^*\) for the underlying protocol, and sends all the verifier messages up to, and including, the \(i^*\)-th round verifier message to the prover. Being a predictable argument, the verifier is able to do so without requiring the corresponding intermediate prover messages. The prover then iteratively computes the response for each round of the underlying protocol and send over all the prover messages with the verifier accepting if and only if each prover messages corresponds to the predicted prover message.
with a large soundness error (to be dealt with later on). Roughly, the verifier randomly chooses a “cut-off” point \(i^*\) for the underlying protocol, and sends all the verifier messages up to, and including, the \(i^*\)-th round verifier message to the prover. Being a predictable argument, the verifier is able to do so without requiring the corresponding intermediate prover messages. The prover then iteratively computes the response for each round of the underlying protocol and send over all the prover messages with the verifier accepting if and only if each prover messages corresponds to the predicted prover message.
In [12], it is proven that this protocol has soundness error at most  . The protocol is then repeated
. The protocol is then repeated  times to achieve negligible soundness, using a parallel repetition theorem for one round arguments [4].
times to achieve negligible soundness, using a parallel repetition theorem for one round arguments [4].
Proposition 3
The round collapsing transformation preserves zero knowledge against b-non-uniform verifiers.
Proof
We prove the proposition in two steps. First, we show that the transformation in Fig. 5 preserves zero-knowledge. Then we show that two-message zero-knowledge against bounded-non-uniform adversaries is closed under parallel repetition.
To prove the first part, let  be a b-non-uniform verifier. We show the following claim.
be a b-non-uniform verifier. We show the following claim.
Claim 2
There exist an efficient simulator \(\mathsf {S}\) and a verifier  against
against  such that
such that
-
1.
 is \((b+O(1))\)-non-uniform and efficiently constructable from
is \((b+O(1))\)-non-uniform and efficiently constructable from 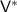 .
. -
2.
For every \(x \in \mathcal {L}\),
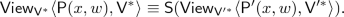
This claim gives rise to a simulator \(\mathsf {Sim}\) for  , which simply invokes \(\mathsf {Sim}'\) of
, which simply invokes \(\mathsf {Sim}'\) of  on
on  and then invokes \(\mathsf {S}\).
and then invokes \(\mathsf {S}\).
Proof of Claim. We construct  .
.

-
1.
Emulates
 and obtains \((\mathsf {v}_1,\dots ,\mathsf {v}_{i^*})\).
and obtains \((\mathsf {v}_1,\dots ,\mathsf {v}_{i^*})\). -
2.
At each round \(i\in [i^*]\), forward \(\mathsf {v}_i\) to \(\mathsf {P}'\).
-
3.
Abort after round \(i^*\).

-
1.
Outputs the randomness of the emulated
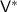 (can be derived from the randomness of
(can be derived from the randomness of  ),
), -
2.
as well as the received prover messages \(\mathsf {p}_1,\dots ,\mathsf {p}_{i^*}\).
The second property asserted in the claim follows by construction of  and the construction of \(\mathsf {P}\) from \(\mathsf {P}'\) in Fig. 5. It is left to see that
and the construction of \(\mathsf {P}\) from \(\mathsf {P}'\) in Fig. 5. It is left to see that  is \((b+O(1))\)-non-uniform and efficiently constructable from
is \((b+O(1))\)-non-uniform and efficiently constructable from  . \((b+O(1))\)-non-uniformity and efficient construction follow from the fact that
. \((b+O(1))\)-non-uniformity and efficient construction follow from the fact that  is b-non-uniform and
is b-non-uniform and  uses it as a black box and described by the three code lines above. \(\square \)
uses it as a black box and described by the three code lines above. \(\square \)
We now prove that closure under parallel repetition.
Claim 3
For any two-message zero knowledge system  against b-non-uniform verifiers and a any polynomial \(\ell \), the \(\ell \)-fold parallel repetition
against b-non-uniform verifiers and a any polynomial \(\ell \), the \(\ell \)-fold parallel repetition  is zero knowledge against
is zero knowledge against  -non-uniform verifiers.
-non-uniform verifiers.
Proof
In what follows, let \(\mathsf {Sim}\) be the simulator for the original argument  , and let
, and let  be any
be any  -non-uniform verifier of polynomial running time
-non-uniform verifier of polynomial running time  . We now describe the simulator \(\mathsf {Sim}_{\otimes \ell }\) for
. We now describe the simulator \(\mathsf {Sim}_{\otimes \ell }\) for  . The simulator will use a pseudorandom generator
. The simulator will use a pseudorandom generator  , where k is the amount of coins used by
, where k is the amount of coins used by  .
.

-
1.
Sample a
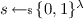 .
. -
2.
For each \(i\in [\ell ]\):
-
(a)
Construct the deterministic verifier
 that first derives coins \(\mathsf {PRG}(s)\), uses them to emulate
that first derives coins \(\mathsf {PRG}(s)\), uses them to emulate  , obtains \({\mathsf {v}}_1,\dots ,{\mathsf {v}}_\ell \), and outputs \({\mathsf {v}}_i\). Let
, obtains \({\mathsf {v}}_1,\dots ,{\mathsf {v}}_\ell \), and outputs \({\mathsf {v}}_i\). Let 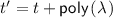 be a bound on its running time.
be a bound on its running time. -
(b)
Sample
 .
.
-
(a)
-
3.
Output \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\ell , \mathsf {PRG}(s)\).
We now prove the validity of \(\mathsf {Sim}_{\otimes \ell }\). First, consider an execution between the prover \(\mathsf {P}(x,w)\) and verifier  , and let \(\mathsf {p}_1,\dots ,\mathsf {p}_\ell \) denote the prover messages in such an execution. Then by pseudorandomness of \(\mathsf {PRG}\),
, and let \(\mathsf {p}_1,\dots ,\mathsf {p}_\ell \) denote the prover messages in such an execution. Then by pseudorandomness of \(\mathsf {PRG}\),

Noting that  is a program of length at most b and running time at most
is a program of length at most b and running time at most  , we can invoke the simulation guarantee
, we can invoke the simulation guarantee  . Specifically, we can deduce that
. Specifically, we can deduce that
This can be shown by a standard hybrid argument and follows from the fact that  and that the distinguisher can have (x, w, s) hardwired in order to simulate any other \({\mathsf {p}}_j\) or \(\widetilde{\mathsf {p}}_i\). Overall
and that the distinguisher can have (x, w, s) hardwired in order to simulate any other \({\mathsf {p}}_j\) or \(\widetilde{\mathsf {p}}_i\). Overall

\(\square \)
This complete the proof of Proposition 3. \(\square \)
5.2 Laconic Prover Messages
As in the previous section, we start by recalling the laconic prover transformation from [12]. In what follows, let  be a one round predictable argument, the following transformation provides a laconic prover predictable argument
be a one round predictable argument, the following transformation provides a laconic prover predictable argument  with a soundness error negligibly close to 1/2, where the prover sends only a single bit (Fig. 6). Roughly, the verifier samples a sufficiently large random string \(\gamma \) and sends it to the prover along with the verifier message. The prover responds with a single bit corresponding to the inner product of \(\gamma \) and its own response to the verifier message, with the verifier accepting if only if the bit matches its own computed inner product of \(\gamma \) with the predicted prover message.
with a soundness error negligibly close to 1/2, where the prover sends only a single bit (Fig. 6). Roughly, the verifier samples a sufficiently large random string \(\gamma \) and sends it to the prover along with the verifier message. The prover responds with a single bit corresponding to the inner product of \(\gamma \) and its own response to the verifier message, with the verifier accepting if only if the bit matches its own computed inner product of \(\gamma \) with the predicted prover message.
In [12], it is proven that this protocol has soundness error at most  . As we have seen in the previous subsection (Claim 3), the soundness can be amplified in a manner that preserves zero knowledge. Specifically, \(\ell \) repetitions yields a protocol with soundness error at most
. As we have seen in the previous subsection (Claim 3), the soundness can be amplified in a manner that preserves zero knowledge. Specifically, \(\ell \) repetitions yields a protocol with soundness error at most  . Therefore, we focus on proving that a single instance of the above transformation preserves zero knowledge.
. Therefore, we focus on proving that a single instance of the above transformation preserves zero knowledge.
Proposition 4
The round collapsing transformation preserves zero knowledge against b-non-uniform verifiers.
Proof
Let  be a b-non-uniform verifier. We show the following claim.
be a b-non-uniform verifier. We show the following claim.
Claim 4
There exist an efficient simulator \(\mathsf {S}\) and a verifier  against
against  such that
such that
-
1.
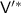 is \((b+O(1))\)-non-uniform and efficiently constructable from
is \((b+O(1))\)-non-uniform and efficiently constructable from  .
. -
2.
For every \(x \in \mathcal {L}\),

This claim gives rise to a simulator \(\mathsf {Sim}\) for  , which simply invokes \(\mathsf {Sim}'\) of
, which simply invokes \(\mathsf {Sim}'\) of  on
on  and then invokes \(\mathsf {S}\).
and then invokes \(\mathsf {S}\).
Proof of Claim. We construct  .
.

-
1.
Emulate
 and obtains \((\mathsf {v},\gamma )\).
and obtains \((\mathsf {v},\gamma )\). -
2.
Forward \(\mathsf {v}\) to \(\mathsf {P}'\).

-
1.
Outputs the randomness of the emulated
 (can be derived from the randomness of
(can be derived from the randomness of  ),
), -
2.
as well as \(\langle \mathsf {p}, \gamma \rangle \), where \(\mathsf {p}\) is the received prover message and \(\gamma \) is derived from the randomness of
 .
.
The proof is similar to that of Claim 2 in the previous subsection. The second property asserted in the claim follows by construction of  and the construction of \(\mathsf {P}\) from \(\mathsf {P}'\). It is left to see that
and the construction of \(\mathsf {P}\) from \(\mathsf {P}'\). It is left to see that  is \((b+O(1))\)-non-uniform and efficiently constructable from
is \((b+O(1))\)-non-uniform and efficiently constructable from  . \((b+O(1))\)-non-uniformity and efficient construction follow from the fact that
. \((b+O(1))\)-non-uniformity and efficient construction follow from the fact that  is b-non-uniform and
is b-non-uniform and  uses it as a black box and described by the two code lines above. \(\square \)
uses it as a black box and described by the two code lines above. \(\square \)
This completes the proof of Proposition 4. \(\square \)
Notes
- 1.
Indistinguishability obfuscation implies non-interactive witness indistinguishable proofs, but with a randomized verifier [8], which is insufficient for our purpose. The verifier can be derandomized under a worst-case Nisan-Wigderson [21] type derandomization assumption [9]. Non-interactive witness indistinguishable proofs with a deterministic verifier are also known from standard assumptions on bilinear maps [19].
- 2.
Here we implicitly rely on the fact that the simulator produces an accepting transcript for the deterministic verifier
 . The deterministic nature of the verifier ensures that the simulator cannot manipulate the verifier’s randomness and therefore must produce an accepting transcript is consistent with
. The deterministic nature of the verifier ensures that the simulator cannot manipulate the verifier’s randomness and therefore must produce an accepting transcript is consistent with  .
. - 3.
Only zero-knowledge against honestly behaving verifiers.
References
Barak, B.: How to go beyond the black-box simulation barrier. In: 42nd FOCS, pp. 106–115. IEEE Computer Society Press (October 2001)
Barak, B., Ong, S.J., Vadhan, S.: Derandomization in cryptography. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 299–315. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_18
Barak, B., Pass, R.: On the possibility of one-message weak zero-knowledge. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 121–132. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_7
Bellare, M., Impagliazzo, R., Naor, M.: Does parallel repetition lower the error in computationally sound protocols? In: 38th FOCS, pp. 374–383. IEEE Computer Society Press (October 1997)
Bitansky, N., et al.: Indistinguishability obfuscation for RAM programs and succinct randomized encodings. SIAM J. Comput. 47(3), 1123–1210 (2018)
Bitansky, N., Canetti, R., Paneth, O., Rosen, A.: On the existence of extractable one-way functions. In: Shmoys, D.B. (ed.) 46th ACM STOC, pp. 505–514. ACM Press (May/June 2014)
Bitansky, N., Khurana, D., Paneth, O.: Weak zero-knowledge beyond the black-box barrier. In: Charikar, M., Cohen, E. (eds.) 51st ACM STOC, pp. 1091–1102. ACM Press (June 2019)
Bitansky, N., Paneth, O.: ZAPs and non-interactive witness indistinguishability from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 401–427. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_16
Bitansky, N., Vaikuntanathan, V.: A note on perfect correctness by derandomization. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 592–606. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_20
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_4
Dahari, H., Lindell, Y.: Deterministic-prover zero-knowledge proofs. Cryptology ePrint Archive, Report 2020/141 (2020). https://eprint.iacr.org/2020/141
Faonio, A., Nielsen, J.B., Venturi, D.: Predictable arguments of knowledge. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10174, pp. 121–150. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54365-8_6
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 467–476. ACM Press (June 2013)
Garg, S., Srinivasan, A.: A simple construction of iO for turing machines. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11240, pp. 425–454. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_16
Goldreich, O., Krawczyk, H.: On the composition of zero-knowledge proof systems. SIAM J. Comput. 25(1), 169–192 (1996)
Goldreich, O., Oren, Y.: Definitions and properties of zero-knowledge proof systems. J. Cryptol. 7(1), 1–32 (1994)
Goldreich, O., Vadhan, S., Wigderson, A.: On interactive proofs with a laconic prover. In: Orejas, F., Spirakis, P.G., van Leeuwen, J. (eds.) ICALP 2001. LNCS, vol. 2076, pp. 334–345. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-48224-5_28
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Groth, J., Ostrovsky, R., Sahai, A.: Non-interactive zaps and new techniques for NIZK. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 97–111. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_6
Koppula, V., Lewko, A.B., Waters, B.: Indistinguishability obfuscation for turing machines with unbounded memory. In: Servedio, R.A., Rubinfeld, R. (eds.) 47th ACM STOC, pp. 419–428. ACM Press (June 2015)
Nisan, N., Wigderson, A.: Hardness vs randomness. J. Comput. Syst. Sci. 49(2), 149–167 (1994)
Acknowledgments
Nir Bitansky is a member of the Check Point Institute of Information Security. Supported by the Alon Young Faculty Fellowship, by Len Blavatnik and the Blavatnik Family foundation, and an ISF grant 18/484.
This work was done in part when Arka Rai Choudhuri was visiting Tel Aviv University and supported by the Check Point Institute of Information Security. He is also supported in part by DARPA/ARL Safeware Grant W911NF-15-C-0213, NSF Grants CNS-1908181, CNS-1414023, CNS-1814919, NSF CAREER 1942789, Samsung Global Research Outreach award, Johns Hopkins University Catalyst award and the Office of Naval Research Grant N00014-19-1-2294.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Predictable Arguments from Honest-Verifier ZK
A Predictable Arguments from Honest-Verifier ZK
In Sect. 4, we showed how to transform any deterministic-prover zero-knowledge (DPZK) protocol into one that is also a predictable argument (PA). In this section, we show that if we start with a weaker notion of deterministic-prover honest verifier zero-knowledge (DP-HVZK)Footnote 3 and the existence of an appropriate hard language, we can transform the DP-HVZK protocol into a predictable argument. One caveat of this transformation is that the languages of the DP-HVZK and PA in our transformation will be related, but not identical. As long as the DP-HVZK we start from is for an expressive enough class of languages (e.g. for  ), we will get a PA for the same class.
), we will get a PA for the same class.
Definition 13
(Hard-on-Average Language). A language \(\mathcal {L}\) is hard-on-average if there exist two \(\mathsf {PPT}\) samplers \(Y_{\mathcal {L}},N_{\mathcal {L}}\) where the support of the first is \(\mathcal {L}\) and of the second is \(\{0,1\}^*\setminus \mathcal {L}\) such that

We establish the following theorem.
Theorem 6
If there exists a deterministic-prover honest-verifier zero-knowledge argument (DP-HVZK) for \(\mathcal {L} \vee \mathcal {L}_\mathsf {hard}\), where \(\mathcal {L}_\mathsf {hard}\) is a hard-on-average language, then there exists a predictable argument (PA) for \(\mathcal {L}\).
By the fact that both  and
and  are closed under OR, we deduce the following corollaries.
are closed under OR, we deduce the following corollaries.
Corollary 4
Assuming DP-HVZK for all of  and hard-on-average languages in
and hard-on-average languages in  , there is a witness encryption scheme for all of
, there is a witness encryption scheme for all of  .
.
Corollary 5
Assuming DP-HVZK for all of  and hard-on-average languages in
and hard-on-average languages in  , there is a witness encryption scheme for all of
, there is a witness encryption scheme for all of  .
.
We note that hard-on-average languages in  are known to follow from one-way functions, and hard-on-average languages in
are known to follow from one-way functions, and hard-on-average languages in  are known to follow from one-way permutations.
are known to follow from one-way permutations.
We now proceed with the proof.
Proof of Theorem 6. To build a predictable argument for \(\mathcal {L}\), we use the following primitives:
-
A hard language \(\mathcal {L}_\mathsf {hard}\) given by samplers \((Y_{\mathcal {L}_\mathsf {hard}},N_{\mathcal {L}_\mathsf {hard}})\).
-
A \(\rho \)-round DP-HVZK protocol
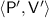 for the language \(\mathcal {L}_{OR}\) defined below, where the verifier
for the language \(\mathcal {L}_{OR}\) defined below, where the verifier 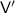 sends messages \(v_i\) in round i, and the prover \(\mathsf {P}'\) sends message \(p_i\) in round i. We denote by \(\mathsf {Sim}'\) the corresponding honest-verifier simulator. The language \(\mathcal {L}_{OR}\) is defined below, $$ \mathcal {L}_{OR} = \left\{ ~ (x,\widetilde{x}) ~\Big \vert ~ \exists (w,\widetilde{w}) \text { s.t. } R_{\mathcal {L}}(x,w)=1 \text { OR } R_{\mathcal {L}_\mathsf {hard}}(\widetilde{x},\widetilde{w})=1 ~\right\} , $$
sends messages \(v_i\) in round i, and the prover \(\mathsf {P}'\) sends message \(p_i\) in round i. We denote by \(\mathsf {Sim}'\) the corresponding honest-verifier simulator. The language \(\mathcal {L}_{OR}\) is defined below, $$ \mathcal {L}_{OR} = \left\{ ~ (x,\widetilde{x}) ~\Big \vert ~ \exists (w,\widetilde{w}) \text { s.t. } R_{\mathcal {L}}(x,w)=1 \text { OR } R_{\mathcal {L}_\mathsf {hard}}(\widetilde{x},\widetilde{w})=1 ~\right\} , $$namely, either the statement x is in \(\mathcal {L}\), or \(\widetilde{x}\) is in \(\mathcal {L}_\mathsf {hard}\).
The transformation is presented in Fig. 7.
Before we proceed with the completeness and soundness, we note that the protocol structure follows that of a predictable argument.
Completeness. We show that  is complete based on the honest verifier zero-knowledge property of
is complete based on the honest verifier zero-knowledge property of  .
.
Fix any \(x \in \mathcal {L}\) and the corresponding witness w, a yes-instance \(\widetilde{x} \in \mathcal {L}_{\mathsf {hard}}\), and let \(x' = (x,\widetilde{x})\). Let \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\rho \) denote the messages and \(\widetilde{r}\) denote the verifier randomness simulated by \(\mathsf {Sim}'(x')\). We argue that the deterministic prover \(\mathsf {P}(x,w)\) produces messages \(\left\{ \mathsf {p}_i= \widetilde{\mathsf {p}}_i \right\} _{i=1}^\rho \) with overwhelming probability (over the coins of \(\mathsf {Sim}'\)). This follows from zero knowledge. Consider a distinguisher that has (x, w) hardwired, and given messages \({\mathsf {p}}_i\) and verifier randomness \(\widetilde{r}\) emulates a conversation of the deterministic \(\mathsf {P}'(x,w)\) with  , and outputs “real” if the corresponding prover messages coincide with \({\mathsf {p}}_i\), or “simulated” otherwise. If the simulated messages \(\widetilde{\mathsf {p}}_i\) are inconsistent with the real prover messages \({\mathsf {p}}_i\), the distinguisher will tell them apart.
, and outputs “real” if the corresponding prover messages coincide with \({\mathsf {p}}_i\), or “simulated” otherwise. If the simulated messages \(\widetilde{\mathsf {p}}_i\) are inconsistent with the real prover messages \({\mathsf {p}}_i\), the distinguisher will tell them apart.
Soundness. We show that  is sound based on the completeness, soundness and zero knowledge of
is sound based on the completeness, soundness and zero knowledge of  , as well as the hardness of \(\mathcal {L}_\mathsf {hard}\).
, as well as the hardness of \(\mathcal {L}_\mathsf {hard}\).
Fix any \(x\notin \mathcal {L}\) and cheating prover \(\mathsf {P}^*\). We prove that \(\mathsf {P}^*\) fails to convince  of accepting, except with negligible probability. We consider several hybrid experiments transitioning from a real interaction to an ideal interaction. We will show that when moving from one hybrid to the next the prover’s chance of convincing the verifier does not decrease by more than a negligible amount. Then we will show that the chance that
of accepting, except with negligible probability. We consider several hybrid experiments transitioning from a real interaction to an ideal interaction. We will show that when moving from one hybrid to the next the prover’s chance of convincing the verifier does not decrease by more than a negligible amount. Then we will show that the chance that  is convinced the final (ideal interaction) hybrid is negligible.
is convinced the final (ideal interaction) hybrid is negligible.
-
\(\mathsf {Hyb}_0\): This is a real interaction between \(\mathsf {P}^*\) and
 .
. -
\(\mathsf {Hyb}_1\): In this hybrid, once
 samples a simulated transcript \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\rho ,\widetilde{r}\)
samples a simulated transcript \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\rho ,\widetilde{r}\) 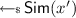 , it emulates an execution of
, it emulates an execution of  with the simulated prover messages and checks whether it is accepting. If it is not,
with the simulated prover messages and checks whether it is accepting. If it is not, 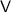 rejects immediately.
rejects immediately.We argue that the probability that \(\mathsf {P}^*\) convinces
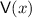 to accept in this hybrid is negligibly close to that in \(\mathsf {Hyb}_0\). For this purpose, we argue that with overwhelming probability \(\mathsf {Sim}(x')\) samples an accepting transcript. This is shown based on completeness and zero knowledge of
to accept in this hybrid is negligibly close to that in \(\mathsf {Hyb}_0\). For this purpose, we argue that with overwhelming probability \(\mathsf {Sim}(x')\) samples an accepting transcript. This is shown based on completeness and zero knowledge of 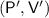 . Specifically, recall that
. Specifically, recall that  samples \(\widetilde{x}\in \mathcal {L}_\mathsf {hard}\) and thus \(x'=(x,\widetilde{x})\in \mathcal {L}_{OR}\). By the completeness of
samples \(\widetilde{x}\in \mathcal {L}_\mathsf {hard}\) and thus \(x'=(x,\widetilde{x})\in \mathcal {L}_{OR}\). By the completeness of 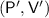 , in an interaction between
, in an interaction between  and \(\mathsf {P}'(x',w')\) where \(w' = (\bot ,\widetilde{w})\) and \(\widetilde{w}\) is a witness for \(\widetilde{x}\), the prover convince
and \(\mathsf {P}'(x',w')\) where \(w' = (\bot ,\widetilde{w})\) and \(\widetilde{w}\) is a witness for \(\widetilde{x}\), the prover convince  with overwhelming probability. It then follows from zero knowledge of
with overwhelming probability. It then follows from zero knowledge of 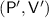 that \(\mathsf {Sim}(x')\) also generates an accepting transcript with overwhelming probability; otherwise, we can non-uniformly fix \(\widetilde{x},\widetilde{w}\) and construct a distinguisher that violates zero knowledge.
that \(\mathsf {Sim}(x')\) also generates an accepting transcript with overwhelming probability; otherwise, we can non-uniformly fix \(\widetilde{x},\widetilde{w}\) and construct a distinguisher that violates zero knowledge. -
\(\mathsf {Hyb}_2\): In this hybrid, the verifier
 does not insist that the prover \(\mathsf {P}^*\) is consistent with the simulated messages \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\rho \). Instead, it emulates
does not insist that the prover \(\mathsf {P}^*\) is consistent with the simulated messages \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\rho \). Instead, it emulates  , and accepts if the messages sent by \(\mathsf {P}^*\) convince
, and accepts if the messages sent by \(\mathsf {P}^*\) convince  .
.The probability that
 accepts in this hybrid is at least as large as the probability it accepts in \(\mathsf {Hyb}_1\). Indeed, any execution that would have been accepted in the previous hybrid \(\mathsf {Hyb}_1\) is in particular an execution in which
accepts in this hybrid is at least as large as the probability it accepts in \(\mathsf {Hyb}_1\). Indeed, any execution that would have been accepted in the previous hybrid \(\mathsf {Hyb}_1\) is in particular an execution in which 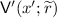 is convinced and thus is also accepted in the current \(\mathsf {Hyb}_2\).
is convinced and thus is also accepted in the current \(\mathsf {Hyb}_2\). -
\(\mathsf {Hyb}_3\): In this hybrid, the verifier
 does not check that the simulated \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\rho ,\widetilde{r}\) make
does not check that the simulated \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\rho ,\widetilde{r}\) make 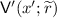 accept. (In particular, the simulated prover messages \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\rho \) are ignored altogether, and only the simulated coins \(\widetilde{r}\) are used).
accept. (In particular, the simulated prover messages \(\widetilde{\mathsf {p}}_1,\dots ,\widetilde{\mathsf {p}}_\rho \) are ignored altogether, and only the simulated coins \(\widetilde{r}\) are used).The probability that
 accepts in this hybrid is at least as large as the probability it accepts in the previous hybrid, as we have only removed a verifier test.
accepts in this hybrid is at least as large as the probability it accepts in the previous hybrid, as we have only removed a verifier test. -
\(\mathsf {Hyb}_4\): In this hybrid, instead of sampling simulated coins \(\widetilde{r}\) using \(\mathsf {Sim}'(x')\),
 samples truly random coins r.
samples truly random coins r.The probability that
 accepts in this hybrids is negligibly close to that in the previous hybrid. This follows from zero knowledge of
accepts in this hybrids is negligibly close to that in the previous hybrid. This follows from zero knowledge of  . Indeed, since \(x'\in \mathcal {L}_{OR}\), the simulated honest verifier coins \(\widetilde{r}\) are pseudorandom.
. Indeed, since \(x'\in \mathcal {L}_{OR}\), the simulated honest verifier coins \(\widetilde{r}\) are pseudorandom. -
\(\mathsf {Hyb}_5\): In this hybrid,
 samples a no-instance \(\widetilde{x} \leftarrow N_{\mathcal {L}_\mathsf {hard}}\) instead of a yes-instance. By the indistinguishability of \(Y_{\mathcal {L}_\mathsf {hard}}\) and \(N_{\mathcal {L}_\mathsf {hard}}\), the probability that \(\mathsf {P}^*\) convinces
samples a no-instance \(\widetilde{x} \leftarrow N_{\mathcal {L}_\mathsf {hard}}\) instead of a yes-instance. By the indistinguishability of \(Y_{\mathcal {L}_\mathsf {hard}}\) and \(N_{\mathcal {L}_\mathsf {hard}}\), the probability that \(\mathsf {P}^*\) convinces  to accept in this hybrid is negligibly close to that in \(\mathsf {Hyb}_4\).
to accept in this hybrid is negligibly close to that in \(\mathsf {Hyb}_4\).
We now argue that the probability that \(\mathsf {P}^*\) convinces  to accept in \(\mathsf {Hyb}_5\) is negligible. Note that in \(\mathsf {Hyb}_5\) it holds that both \(x\notin \mathcal {L}\) and \(\widetilde{x}\notin \mathcal {L}_\mathsf {hard}\) and thus \(x'=(x,\widetilde{x})\notin \mathcal {L}_{OR}\). For \(\mathsf {P}^*\) to convince
to accept in \(\mathsf {Hyb}_5\) is negligible. Note that in \(\mathsf {Hyb}_5\) it holds that both \(x\notin \mathcal {L}\) and \(\widetilde{x}\notin \mathcal {L}_\mathsf {hard}\) and thus \(x'=(x,\widetilde{x})\notin \mathcal {L}_{OR}\). For \(\mathsf {P}^*\) to convince  of accepting in \(\mathsf {Hyb}_5\), it must convince
of accepting in \(\mathsf {Hyb}_5\), it must convince  of accepting, when
of accepting, when  uses truly random coins. By the soundness of
uses truly random coins. By the soundness of  this occurs with negligible probability. Soundness follows. \(\square \)
this occurs with negligible probability. Soundness follows. \(\square \)
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Bitansky, N., Choudhuri, A.R. (2020). Characterizing Deterministic-Prover Zero Knowledge. In: Pass, R., Pietrzak, K. (eds) Theory of Cryptography. TCC 2020. Lecture Notes in Computer Science(), vol 12550. Springer, Cham. https://doi.org/10.1007/978-3-030-64375-1_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-64375-1_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64374-4
Online ISBN: 978-3-030-64375-1
eBook Packages: Computer ScienceComputer Science (R0)


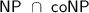 against verifiers with bounded non-uniform auxiliary input.
against verifiers with bounded non-uniform auxiliary input. .
.


 (namely short) that outputs R."
(namely short) that outputs R."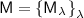 is a family of probabilistic Turing machines (one for each
is a family of probabilistic Turing machines (one for each  ), where there exists a polynomial
), where there exists a polynomial 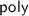 , such that the description size
, such that the description size  and the running time of
and the running time of  are bounded by
are bounded by  .
. and arbitrary polynomial running time (possibly larger than
and arbitrary polynomial running time (possibly larger than 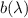 ). Formally, a b-non-uniform
). Formally, a b-non-uniform  is a family of probabilistic Turing machines (one for each
is a family of probabilistic Turing machines (one for each 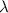 ), where
), where 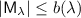 and there exists a polynomial
and there exists a polynomial  , such that the running time of
, such that the running time of  is bounded by
is bounded by  .
.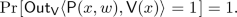
 such that for all
such that for all  and
and  ,
, 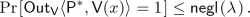
 of running time at most
of running time at most  ,
, 
 , the Turing machine
, the Turing machine  , for all
, for all  , for all inputs
, for all inputs 
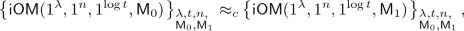
 ,
, 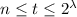 , and
, and 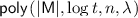 . We also require that the running time
. We also require that the running time  , where
, where  takes as input a security parameter
takes as input a security parameter  , a string
, a string  , for any
, for any 
 such that for any
such that for any 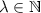 , and any
, and any 
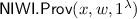 that given an instance x, witness w, and security parameter
that given an instance x, witness w, and security parameter  , produces a proof
, produces a proof  ,
, 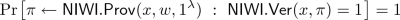

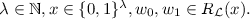
 , if
, if 
 ,
,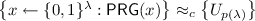 , where
, where  is the uniform distribution over
is the uniform distribution over  bits.
bits. for language
for language 
 . Therefore, except with negligible probability
. Therefore, except with negligible probability  that has the seed s hardwired.
that has the seed s hardwired.  computes
computes  . Additionally,
. Additionally,  truncates
truncates 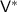 ’s output to R.
’s output to R. with random coins
with random coins  , use the description of
, use the description of  as input to
as input to 
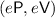 secure against robustly-explainable verifiers. Let the verifier and prover messages be denoted by
secure against robustly-explainable verifiers. Let the verifier and prover messages be denoted by 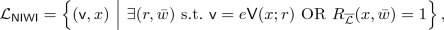

 .
. is a robustly explainable verifier against
is a robustly explainable verifier against  .
. is
is  .
.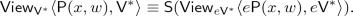
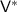 and obtains
and obtains 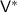 with message
with message 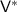 (can be derived from the randomness of
(can be derived from the randomness of 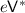 ,
,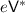 .
.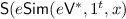 .
. .
. .
.
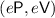 secure against robustly-explainable verifiers. Let the verifier and prover messages be denoted by
secure against robustly-explainable verifiers. Let the verifier and prover messages be denoted by 

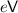 .
. .
. samples
samples 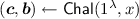 , where
, where 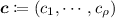 and
and 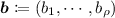 .
. sends
sends 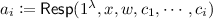 and sends
and sends 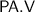 .
. checks if
checks if  returns 1.
returns 1. such that for all
such that for all 
 such that for all
such that for all 


 is
is  .
.
 and obtains
and obtains 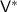 (can be derived from the randomness of
(can be derived from the randomness of  ),
),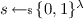 .
. that first derives coins
that first derives coins  , obtains
, obtains 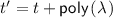 be a bound on its running time.
be a bound on its running time. .
.
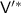 is
is  .
.
 and obtains
and obtains  (can be derived from the randomness of
(can be derived from the randomness of  ),
), .
. . The deterministic nature of the verifier ensures that the simulator cannot manipulate the verifier’s randomness and therefore must produce an accepting transcript is consistent with
. The deterministic nature of the verifier ensures that the simulator cannot manipulate the verifier’s randomness and therefore must produce an accepting transcript is consistent with  .
.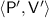 for the language
for the language 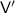 sends messages
sends messages 
 .
. samples a simulated transcript
samples a simulated transcript 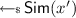 , it emulates an execution of
, it emulates an execution of  with the simulated prover messages and checks whether it is accepting. If it is not,
with the simulated prover messages and checks whether it is accepting. If it is not, 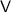 rejects immediately.
rejects immediately.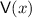 to accept in this hybrid is negligibly close to that in
to accept in this hybrid is negligibly close to that in 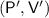 . Specifically, recall that
. Specifically, recall that  samples
samples 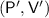 , in an interaction between
, in an interaction between  and
and  with overwhelming probability. It then follows from zero knowledge of
with overwhelming probability. It then follows from zero knowledge of 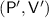 that
that  does not insist that the prover
does not insist that the prover  , and accepts if the messages sent by
, and accepts if the messages sent by  .
. accepts in this hybrid is at least as large as the probability it accepts in
accepts in this hybrid is at least as large as the probability it accepts in 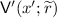 is convinced and thus is also accepted in the current
is convinced and thus is also accepted in the current  does not check that the simulated
does not check that the simulated 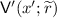 accept. (In particular, the simulated prover messages
accept. (In particular, the simulated prover messages  accepts in this hybrid is at least as large as the probability it accepts in the previous hybrid, as we have only removed a verifier test.
accepts in this hybrid is at least as large as the probability it accepts in the previous hybrid, as we have only removed a verifier test. samples truly random coins r.
samples truly random coins r. accepts in this hybrids is negligibly close to that in the previous hybrid. This follows from zero knowledge of
accepts in this hybrids is negligibly close to that in the previous hybrid. This follows from zero knowledge of  . Indeed, since
. Indeed, since  samples a no-instance
samples a no-instance  to accept in this hybrid is negligibly close to that in
to accept in this hybrid is negligibly close to that in 