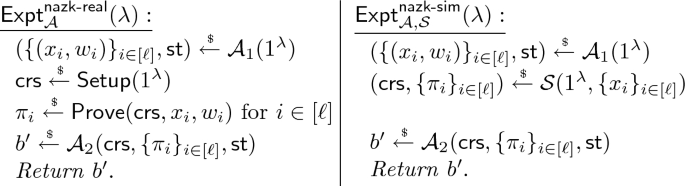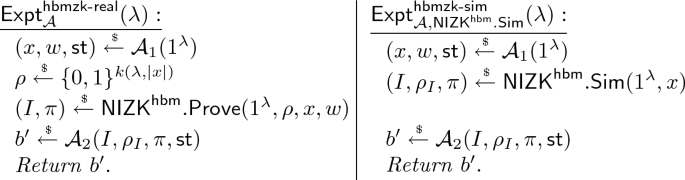NIZK from SNARG

Abstract

We give a construction of a non-interactive zero-knowledge (NIZK) argument for all $\mathsf {NP}$ languages based on a succinct non-interactive argument (SNARG) for all $\mathsf {NP}$ languages and a one-way function. The succinctness requirement for the SNARG is rather mild: We only require that the proof size be $|\pi |=\mathsf {poly}(\lambda )(|x|+|w|)^c$ for some constant $c<1/2$, where |x| is the statement length, |w| is the witness length, and $\lambda$ is the security parameter. Especially, we do not require anything about the efficiency of the verification.

Based on this result, we also give a generic conversion from a SNARG to a zero-knowledge SNARG assuming the existence of CPA secure public-key encryption. For this conversion, we require a SNARG to have efficient verification, i.e., the computational complexity of the verification algorithm is $\mathsf {poly}(\lambda )(|x|+|w|)^{o(1)}$. Before this work, such a conversion was only known if we additionally assume the existence of a NIZK.

Along the way of obtaining our result, we give a generic compiler to upgrade a NIZK for all $\mathsf {NP}$ languages with non-adaptive zero-knowledge to one with adaptive zero-knowledge. Though this can be shown by carefully combining known results, to the best of our knowledge, no explicit proof of this generic conversion has been presented.

1 Introduction

A non-interactive zero-knowledge (NIZK) argument [7] is a non-interactive argument system that enables a prover to convince a verifier of the truth of an NP statement without revealing any information about its witness. Since it is known that a NIZK in the plain model where no setup is needed exists only for trivial languages [32], NIZKs are typically constructed in the common reference string (CRS) model where a trusted party generates a CRS and provides it to both the prover and verifier. In the following, we refer to NIZKs in the CRS model simply as NIZKs. Thus far, NIZKs for all $\mathsf {NP}$ languages have been constructed based on various standard assumptions including factoring [26], pairings [14, 36], and lattices [45]. Besides the theoretical importance on its own, NIZKs have found numerous applications in cryptography including chosen-ciphertext security [23, 43], leakage- and tamper-resilient cryptography [21, 22, 40], advanced types of digital signatures [2, 16, 47], multi-party computation [31], to name a few.

A succinct non-interactive argument (SNARG) is another notion of a non-interactive argument, which satisfies succinctness, i.e., the proof size is (asymptotically) smaller than the statement size and the witness size. Micali [42] gave a construction of SNARGs for all $\mathsf {NP}$ languages in the random oracle model. On the other hand, Gentry and Wichs [29] ruled out a black-box reduction proving the adaptive soundness of a SNARG from any falsifiable assumption in the standard model. Since then, there have been proposed constructions of SNARGs for all $\mathsf {NP}$ languages based on non-falsifiable assumptions on pairings [28, 34, 35], lattices [9, 10]¹, or hash functions [4]. On the application side, SNARGs have natural applications in the context of verifiable computation. They also have been gaining a renewed attention in the context of blockchains (e.g., [3, 8]).²

As mentioned above, there are constructions of NIZKs based on various standard assumptions while there is no known construction of SNARGs based on a standard assumption and there is even a strong impossibility for that. Given this situation, we may think that a SNARG is a stronger primitive than a NIZK. However, it is not known if a SNARG implies a NIZK, and they have been treated as incomparable primitives. For example, Bitansky et al. [4] gave a generic conversion from a SNARG to a zero-knowledge SNARG by additionally assuming the existence of NIZKs. If a SNARG implies a NIZK, we could drop the additional assumption of the NIZK. Besides, since both NIZKs and SNARGs are important and fundamental primitives that have been well-studied, we believe that it is interesting on its own if we find a new relationship between them.

1.1 Our Results

We give a construction of a NIZK for all $\mathsf {NP}$ languages based on a SNARG for all $\mathsf {NP}$ languages and a one-way function (OWF). The succinctness requirement for the SNARG is rather mild: We only require that its proof size be $|\pi |=\mathsf {poly}(\lambda )(|x|+|w|)^c$ for some constant $c<1/2$, where |x| is the statement length, |w| is the witness length, and $\lambda$ is the security parameter. Especially, we do not require anything about the efficiency of the verification.

Based on this result, we also give a generic conversion from a SNARG to a zero-knowledge SNARG assuming the existence of CPA secure public-key encryption. For this conversion, we require a SNARG to have efficient verification, i.e., the computational complexity of the verification algorithm is $\mathsf {poly}(\lambda )(|x|+|w|)^{o(1)}$ (and thus the proof size is also $|\pi |=\mathsf {poly}(\lambda )(|x|+|w|)^{o(1)}$). Before this work, such a conversion was only known if we additionally assume the existence of a NIZK [4].

Along the way of obtaining our result, we give a generic compiler to upgrade a NIZK for all $\mathsf {NP}$ languages with non-adaptive zero-knowledge to one with adaptive zero-knowledge. Though this can be shown by carefully combining known results, to the best of our knowledge, no explicit proof of this generic conversion has been presented.³$^{,}$⁴

We note that we use the adaptive computational soundness as a default notion of soundness for non-interactive arguments in this paper, and our results are proven in this setting. We leave it as an interesting open problem to study if similar implications hold for NIZKs and SNARGs with non-adaptive computational soundness.

To the best of our knowledge, all known constructions of a SNARG in the CRS model satisfies the zero-knowledge property from the beginning. Therefore, we do not obtain a concrete construction of a NIZK from an assumption that was not known to imply NIZKs by using our result. Nonetheless, it is in general important to study generic relationships between different primitives from a theoretical point of view, and we believe that our results contribute to deepening our understanding on the two important and fundamental primitives of NIZKs and SNARGs.

1.2 Technical Overview

In this section, we give an overview of the construction of a NIZK from a SNARG. Once this is done, it is straightforward to obtain a generic conversion from a SNARG to a zero-knowledge SNARG by combining it with the result of [4].

First, we observe that the succinctness of a SNARG implies that a SNARG proof at least “loses” some information about the witness though it may leak some partial information. Based on this observation, our basic idea is to combine a SNARG with a leakage-resilient primitive [1] whose security holds even if a certain fraction of a secret key is leaked. If the SNARG proof size is small enough, then we may be able to use the security of the leakage-resilient primitive to fully hide the witness considering a SNARG proof as a leakage. For example, suppose that we have a leakage-resilient secret-key encryption (LR-SKE) scheme whose semantic security holds as long as the amount of leakage from the secret key is at most a half of the secret key size. Then, a naive (failed) idea to construct a NIZK is to let a NIZK proof consist of an encryption $\mathsf {ct}$ of the witness by the LR-SKE scheme and a SNARG proof proving that there exists a secret key of the LR-SKE scheme that decrypts $\mathsf {ct}$ to a valid witness. Soundness of this construction is easy to reduce to the soundness of the SNARG. In addition, if the SNARG is fully succinct, then we can show that the SNARG proof size is at most a half of the secret key size if we set the secret key size of LR-SKE to be sufficiently large. Then, it seems possible to argue that the information of the witness is completely hidden by the security of LR-SKE. However, there is a flaw in the above idea: The security of a LR-SKE scheme holds only if the leakage does not depend on the challenge ciphertext. On the other hand, in the above construction, the SNARG proof clearly depends on the challenge ciphertext $\mathsf {ct}$, and thus we cannot use the security of a LR-SKE scheme. Though the above naive idea fails, this highlights a potential idea of combining a SNARG with a leakage-resilient primitive to obtain a NIZK. Indeed, we implement this idea by modifying the NIZK construction based on the hidden-bits paradigm [26].

NIZK via the Hidden-Bits Paradigm. First, we recall the construction of a NIZK based on the hidden-bits paradigm [26] following the formalization by Quach, Rothblum, and Wichs [46]. Readers familiar with their formalization can safely skip this paragraph. The construction uses two building blocks: a NIZK in the hidden-bit model (HBM-NIZK) and a hidden-bits generator (HBG).

In an HBM-NIZK, a trusted party picks a random string $\rho \in \{0,1\}^k$ and gives it to the prover. Then a prover, who holds a statement x and a witness w, generates a proof $\pi$ along with a subset $I\subseteq [k]$, which specifies which bits of $\rho$ to be revealed to the verifier. Then, the verifier is given a statement x, a proof $\pi$, a subset I, and a string $\rho _I$ that is the substring of $\rho$ on the positions corresponding to I, and accepts or rejects. We require an HBM-NIZK to satisfy two security requirements: soundness and zero-knowledge. Intuitively, soundness requires that no cheating prover can convince the verifier of a false statement x with non-negligible probability, and the zero-knowledge property requires that the verifier learns nothing beyond that x is a true statement. Feige, Lapidot, and Shamir [26] constructed an HBM-NIZK for all $\mathsf {NP}$ languages that satisfies these security requirements (without relying on any assumption).

An HBG is a primitive introduced in [46], which consists of the following algorithms:

• $\mathsf {HBG}.\mathsf {Setup}(1^\lambda ,1^k)$ generates a CRS $\mathsf {crs}$ where k denotes the length of hidden-bits to be generated.

• $\mathsf {HBG}.\mathsf {GenBits}(\mathsf {crs})$ generates a succinct commitment $\mathsf {com}$ whose length is much shorter than k, “hidden-bits” $r\in \{0,1\}^k$, and a tuple of proofs $\{\pi _i\}_{i\in [k]}$. Intuitively, each $\pi _i$ can be thought of a certificate of the i-th bit of r.

• $\mathsf {HBG}.\mathsf {Verify}(\mathsf {crs},\mathsf {com},i,r_i,\pi _i)$ verifies the proof $\pi _i$ to ensure that the i-th hidden-bit is $r_i$.

We require an HBG to satisfy two security requirements: binding and hiding. The binding property requires that for any fixed commitment $\mathsf {com}$, there exist “committed bits” $r^*\in \{0,1\}^{k}$ and no PPT adversary can generate a proof $\pi _i$ such that $\mathsf {HBG}.\mathsf {Verify}(\mathsf {crs},\mathsf {com},i,\bar{r_i^*},\pi _i)$ accepts, where $\bar{r_i^*}$ denotes the negation of $r_i^*$.⁵ Combined with the succinctness of $\mathsf {com}$, this implies that there should be a “sparse” set $\mathcal {V}^\mathsf {crs}\in \{0,1\}^k$ (dependent on $\mathsf {crs}$) of size much smaller than $2^{k}$ such that no PPT adversary can generate a set of proofs $\{\pi _i\}_{i\in I}$ for bits that are not consistent with any element of $\mathcal {V}^\mathsf {crs}$ even if it can control the value of $\mathsf {com}$. The hiding property requires that for any subset $I \subseteq [k]$, no PPT adversary given $\{(r_i,\pi _i)\}_{i\in I}$ can distinguish $r_{\bar{I}}$ from a fresh random string $r'_{\overline{I}}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^{|I|}$, where $r_{\overline{I}}$ denotes the substring of r on the positions corresponding to $\overline{I}=[k]\setminus I$.

Combining the above two primitives, Quach et al. [46] constructed a NIZK as follows: The setup algorithm generates a CRS $\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}.\mathsf {Setup}(1^\lambda ,1^k)$ of the HBG and a random string $s\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k$ and outputs them as a CRS of the NIZK where $k=\mathsf {poly}(\lambda )$ is a parameter that is set appropriately as explained later. Then the prover generates $(\mathsf {com},r,\{\pi _i\}_{i\in [k]})\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}.\mathsf {GenBits}(\mathsf {crs})$, sets $\rho :=r\oplus s$, runs the prover of the underlying HBM-NIZK w.r.t. the hidden-bits $\rho$ to generate $(I,\pi _\mathsf {hbm})$, and outputs $(I,\pi _\mathsf {hbm}, \mathsf {com}, r_I, \{\pi _i\}_{i\in I})$ as a proof of the NIZK. Then the verifier runs the verification of the underlying HBG to check the validity of $r_I$ and the verification algorithm of the underlying HBM-NIZK under the revealed hidden-bits $\rho _I:=r_I\oplus s_I$.

The security of the above NIZK is argued as follows: For each fixed r, any cheating prover against the above NIZK can be easily converted into a cheating prover against the underlying HBM-NIZK. Moreover, by the binding property of the underlying HBG, the prover has to use r in the subset $\mathcal {V}^\mathsf {crs}$ to pass the verification. Then, by taking the union bound, the success probability of a cheating prover against the above NIZK is at most $|\mathcal {V}^\mathsf {crs}| \ll 2^k$ times larger than that of a cheating prover against the underlying HBM-NIZK. Thus, by setting k to be sufficiently large so that the success probability of a cheating prover against the underlying HBM-NIZK is at most $|\mathcal {V}^\mathsf {crs}|^{-1} \mathsf {negl}(\lambda )$, we can prove the soundness. Intuitively, the zero-knowledge property of the above NIZK is easy to reduce to that of the underlying HBM-NIZK by observing that the hiding property of the underlying HBG ensures that the verifier obtains no information about $r_{\overline{I}}$. We note that this simple reduction works only for non-adaptive zero-knowledge where an adversary declares a challenge statement before seeing a CRS. Roughly speaking, this is because in the definition of the hiding property of a HBG, the subset I is fixed before the CRS is chosen whereas an adversary against adaptive zero-knowledge may choose I depending on the CRS. Quach et al. [46] showed that adaptive zero-knowledge can be also proven assuming that the underlying HBM-NIZK satisfies a stronger notion of zero-knowledge called special zero-knowledge. We omit to explain the details since we will show a generic compiler from non-adaptive to adaptive zero-knowledge.

HBG from a SNARG? Our first attempt is to construct an HBG from a SNARG combined with a leakage-resilient weak pseudorandom function (LR-wPRF) [37]. A (one-bit-output) LR-wPRF is a function family $\mathcal {F}= \{F_K: \{0,1\}^m\rightarrow \{0,1\}\}_{K \in \{0,1\}^{\kappa }}$ such that $(x^*, F_K(x^*))$ for $x^*\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^m$ looks pseudorandom from an adversary that is given an arbitrary polynomial number of input-output pairs $(x, F_K(x))$ for $x\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^m$ and a leakage from K (that does not depend on $x^*$) of at most $\ell$-bit for a certain leakage bound $\ell <\kappa$. Hazay et al. [37] constructed an LR-wPRF for any polynomial $\ell =\mathsf {poly}(\lambda )$ based solely on the existence of a OWF.

Then, our first (failed) attempt for constructing an HBG from a SNARG and an LR-wPRF is as follows:

• $\mathsf {HBG}.\mathsf {Setup}(1^\lambda ,1^k)$ samples $(x_1,\ldots ,x_k)\in \{0,1\}^{m\times k}$ and outputs it as a CRS $\mathsf {crs}$.

• $\mathsf {HBG}.\mathsf {GenBits}(\mathsf {crs})$ randomly picks a key $K\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^{\kappa }$ of the LR-wPRF, and outputs a commitment $\mathsf {com}$ of K by a statistically binding commitment scheme, hidden-bits $r:=(F_K(x_1),\ldots ,F_K(x_k))$, and proofs $\{\pi _i\}_{i\in [k]}$ that are generated by the SNARG to certify r.

• $\mathsf {HBG}.\mathsf {Verify}(\mathsf {crs},\mathsf {com},i,r_i,\pi _i)$ verifies the proof $\pi _i$ by the verification algorithm of the SNARG.

The binding property easily follows from the statistical binding property of the underlying commitment scheme and the soundness of the underlying SNARG. For the hiding property, we would like to rely on the security of the underlying LR-wPRF by viewing the SNARG proofs as a leakage. However, there are the following two problems:

• 1. An adversary against the hiding property can obtain all proofs $\{\pi _i\}_{i\in I}$ corresponding to the subset I whose size may be linear in k. On the other hand, for ensuring the succinctness of the commitment, we have to set $k \gg \kappa$. Thus, the total size of $\{\pi _i\}_{i\in I}$ may be larger than $\kappa$, in which case it is impossible to rely on the security of the LR-wPRF.

• 2. Even if the above problem is resolved, we still cannot apply the security of the LR-wPRF since $\mathsf {com}$ also depends on K and its size must be larger than that of K.

To resolve these issues, our idea is to drop the commitment $\mathsf {com}$ from the output of $\mathsf {HBG}.\mathsf {GenBits}(\mathsf {crs})$, and generate a single SNARG proof $\pi$ that proves that “there exists $K\in \{0,1\}^\kappa$ such that $r_i=F_K(x_i)$ for all $i\in I$” in one-shot instead of generating $\pi _i$ for each $i\in I$ separately. Then, the only leakage of K given to an adversary against the hiding property is the SNARG proof $\pi$, whose size is sublinear in |I| by the succinctness of the SNARG. Thus, it seems possible to apply the security of the LR-wPRF if we set parameters appropriately. However, this idea is not compatible with the syntax of an HBG. This is why we modify the syntax of an HBG to introduce what we call an HBG with subset-dependent proofs (SDP-HBG).

HBG with Subset-Dependent Proofs. Roughly speaking, an SDP-HBG is a (weaker) variant of an HBG with the following modifications:

• 1. A proof is generated depending on a subset I, which specifies positions of bits to be revealed. This is in contrast to the original definition of an HBG where proofs are generated for each position $i \in [k]$. To formalize this, we introduce the proving algorithm separated from the bits generation algorithm.

• 2. The bits generation algorithm does not output a commitment, and we require a relaxed version of the binding property that we call the somewhat binding property as explained later.

More precisely, an SDP-HBG consists of the following algorithms:

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda ,1^k)$ generates a CRS $\mathsf {crs}$.

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}(\mathsf {crs})$ generates “hidden-bits” $r\in \{0,1\}^k$ and a state $\mathsf {st}$.

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}(\mathsf {st},I)$ generates a proof $\pi$ that certifies the sub-string $r_I$.

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Verify}(\mathsf {crs},I,r_I,\pi )$ verifies the proof $\pi$ to ensure that the substring of r on the positions corresponding to the subset I is indeed $r_I$.

We require an SDP-HBG to satisfy the somewhat binding property and the hiding property. The somewhat binding property requires that there exists a “sparse” subset $\mathcal {V}^\mathsf {crs}\in \{0,1\}^k$ (dependent on $\mathsf {crs}$) of size much smaller than $2^{k}$ such that no PPT malicious prover can generate a proof for bits that are not consistent with any element of $\mathcal {V}^\mathsf {crs}$. As mentioned earlier, a similar property easily follows by combining the succinctness of the commitment and the binding property in the original HBG, and this was the essential property to prove soundness in the construction of a NIZK from an HBG. The hiding property is similar to that for an HBG except that an adversary is given a single proof $\pi$ corresponding to the subset I instead of $\{\pi _i\}_{i\in I}$. Namely, it requires that for any subset $I\in [k]$, no PPT adversary given $\{r_i\}_{i\in I}$ and $\pi$ that certifies $\{r_i\}_{i\in I}$ can distinguish $r_{\overline{I}}$ from a fresh random string $r'_{\overline{I}}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^{|I|}$, where $r_{\overline{I}}$ denotes the sub-string of r on the positions corresponding to $\overline{I}=[k]\setminus I$.

To see that an SDP-HBG is a weaker primitive than an HBG, in Sect. 4.2, we formally show that an original HBG indeed implies an SDP-HBG.

SDP-HBG from a SNARG and an LR-wPRF. Next, we construct an SDP-HBG from a SNARG and an LR-wPRF. Since the idea is already explained, we directly give the construction below:

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda ,1^k)$ samples $(x_1,\ldots ,x_k)\in \{0,1\}^{m\times k}$ and outputs it as a CRS $\mathsf {crs}$.

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}(\mathsf {crs})$ randomly picks a key $K\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^{\kappa }$ of the LR-wPRF and outputs hidden-bits $r:=(F_K(x_1),\ldots ,F_K(x_k))$ and a state $\mathsf {st}:=K$.

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}(\mathsf {st},I)$ outputs a SNARG proof $\pi$ that proves that there exists $K\in \{0,1\}^\kappa$ such that $r_i=F_K(x_i)$ for all $i\in I$.

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Verify}(\mathsf {crs},I,r_I,\pi )$ verifies the proof $\pi$ by the verification algorithm of the SNARG.

The somewhat binding property is easy to reduce to the soundness of the underlying SNARG if $\kappa \ll k$. The hiding property is easy to reduce to the security of the underlying LR-PRF if $|\pi | \le \ell$ where $\ell$ is the leakage bound by noting that the proof $\pi$ corresponding to the subset I does not depend on $x_{\overline{I}}$, and thus we can think of $x_{\overline{I}}$ as challenge inputs and $\pi$ as a leakage. Therefore, what remains is to show that we can appropriately set the parameters to satisfy these two inequalities. Here, for simplicity we assume that the SNARG is fully succinct, i.e., $|\pi |=\mathsf {poly}(\lambda )$ independently of the statement/witness size.⁶ Especially, $|\pi |$ can be upper bounded by a polynomial in $\lambda$ that does not depend on k. Then, we first set $\ell =\mathsf {poly}(\lambda )$ so that $|\pi | \le \ell$. According to this choice of $\ell$, $\kappa =\mathsf {poly}(\lambda )$ is determined. Here, we emphasize that $\kappa$ does not depend on k. Thus, for sufficiently large $k=\mathsf {poly}(\lambda )$, we have $\kappa \ll k$ as desired.⁷ The crucial point is that no matter how large k is, this does not affect $|\pi |$ thanks to the full succinctness of the SNARG. We note that we assume nothing about the leakage-rate (i.e., $\ell /\kappa$) of the LR-wPRF, and thus we can use the LR-wPRF based on a OWF in [37], which achieves a relatively poor leakage-rate of $O(\frac{\log \lambda }{\lambda })$. For the case of slightly-succinct SNARGs, a more careful analysis is needed, but we can extend the above proof as long as $|\pi |=\mathsf {poly}(\lambda )(|x|+|w|)^c$ holds for some constant $c<1/2$.

As seen above, the underlying SNARG in fact needs to prove only a statement of an $\mathsf {NP}$ language with a specific form that is dependent on the LR-wPRF (which is in turn based on a OWF). Thus, if the latter is determined beforehand, the SNARG is required to support this particular language (and not all $\mathsf {NP}$ languages).⁸

NIZK from an SDP-HBG. Then, we show that an SDP-HBG suffices for constructing a NIZK. In fact, the construction and security proof are essentially the same as that from an HBG in [46]:

• The setup algorithm generates a CRS $\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda ,1^k)$ of the SDP-HBG and a random string $s\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k$, and outputs them as a CRS of the NIZK;

• The prover generates $(r,\mathsf {st})\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}(\mathsf {crs})$, sets $\rho :=r\oplus s$, runs the prover of the underlying HBM-NIZK w.r.t. the hidden-bits $\rho$ to generate $(I \subseteq [k],\pi _\mathsf {hbm})$, generates $\pi _\mathsf {bgen}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}(\mathsf {st},I)$, and outputs $(I,\pi _\mathsf {hbm}, r_I, \pi _\mathsf {bgen})$ as a proof of the NIZK;

• The verifier runs the verification of the underlying SDP-HBG to check the validity of $r_I$ and the verification of the underlying HBM-NIZK under the revealed hidden-bits $\rho _I:=r_I\oplus s_I$.

It is easy to see that essentially the same proofs as the NIZK from an HBG work for soundness and non-adaptive zero-knowledge. However, it is not clear how to prove the adaptive zero-knowledge for this construction. As mentioned earlier, for the construction of a NIZK from an HBG, Quach et al. [46] proved its adaptive zero-knowledge assuming that the underlying HBM-NIZK satisfies a stronger notion of zero-knowledge called special zero-knowledge. However, their proof does not extend to the proof of adaptive zero-knowledge for the above NIZK from an SDP-HBG even if we rely on the special zero-knowledge for the underlying HBM-NIZK. Roughly speaking, the problem comes from the fact that the SDP-HBG enables us to generate a proof $\pi _\mathsf {bgen}$ corresponding to a subset I only after I is fixed. This is in contrast to an HBG where we can generate $\pi _i$ that certifies the i-th hidden bit for each $i\in [k]$ before I is fixed. Specifically, the proof of adaptive zero-knowledge from an HBG in [46] crucially relies on the fact that if $I \subseteq I^*$, then a set of proofs $\{\pi _i\}_{i\in I}$ can be derived from $\{\pi _i\}_{i\in I^*}$ in a trivial manner. On the other hand, we do not have a similar property in SDP-HBG since it generates a proof for a subset I in one-shot instead of generating a proof in a bit-by-bit manner. Thus, we have to come up with an alternative way to achieve adaptive zero-knowledge.

Non-adaptive to Adaptive Zero-Knowledge. Based on existing works, we give a generic compiler from non-adaptive to adaptive zero-knowledge. First, we observe that we can construct an HBG by combining a commitment, a pseudorandom generator (PRG), and a NIZK in a straightforward manner. We note that essentially the same construction was already mentioned by Dwork and Naor [24] where they constructed a verifiable PRG, which is a similar but slightly different primitive from an HBG. Our crucial observation is that non-adaptive zero-knowledge is sufficient for this construction of an HBG. Then, we can apply the construction of [46] instantiated with the above HBG and an HBM-NIZK with special zero-knowledge to obtain a NIZK with adaptive zero-knowledge.

1.3 Related Work

Known Constructions of NIZKs. Here, we review known constructions of a NIZK for all $\mathsf {NP}$ languages. Below, we just write NIZK to mean NIZK for all $\mathsf {NP}$ languages for simplicity. In this paragraph, we omit a NIZK that is also a SNARG since such schemes are mentioned in the next paragraph. Blum, Feldman, and Micali [7] introduced the concept of NIZK and constructed a NIZK based on the quadratic residuosity assumption. Feige, Lapidot, and Shamir [26] established the hidden-bits paradigm and constructed a NIZK based on trapdoor permutations. The requirements on trapdoor permutations for realizing a NIZK have been revisited and refined in a series of works [15, 30, 33]. Canetti, Halevi, and Katz [14] constructed a NIZK based on pairing by instantiating the hidden-bits paradigm. Groth, Ostrovsky, and Sahai [36] constructed a pairing-based NIZK based on a completely different approach, which yields the first NIZK with perfect zero-knowledge. Sahai and Waters [48] constructed the first NIZK with a deterministic proving algorithm and perfect zero-knowledge based on indistinguishability obfuscation and a OWF. Recently, there has been a line of researches [12, 13, 38] aiming at realizing the Fiat-Shamir transform [27] in the standard model. Peikert and Shiehian [45] constructed a NIZK based on a standard lattice-based assumption following this approach. Very recently, Couteau, Katsumata, and Ursu [20] constructed a NIZK based on a certain exponential hardness assumption on pairing-free groups. We note that it still remains open to construct a NIZK from polynomial hardness assumption on pairing-free groups.

We omit NIZKs in a different model than the CRS model including preprocessing, designated prover, and designated verifier models since our focus in this paper is constructions in the CRS model. We refer to [39, 41] for a survey on NIZKs in these models.

Known Constructions of SNARGs. Here, we review known constructions of a SNARG for all $\mathsf {NP}$ languages. Below, we just write SNARG to mean SNARG for all $\mathsf {NP}$ languages. We note that some of the following constructions are actually a SNARK, which satisfies a stronger notion of soundness called extractability, but we just call them a SNARG since we do not discuss extractability in this paper. Also, other than [18, 42], here we only mention works that do not rely on random oracles. For the recent advances on practical SNARGs (SNARKs) including those in the random oracle model, see, e.g., the recent papers [11, 17, 19, 25] and references therein.

Micali [42] constructed a zero-knowledge SNARG in the random oracle model. Chiesa, Manohar, and Spooner [18] proved that the Micali’s construction is also secure in the quantum random oracle model. Groth [34, 35] and Gennaro, Gentry, Perno, and Raykova [28] proposed zero-knowledge SNARGs in the CRS model based on non-falsifiable assumptions on pairing groups. There are several constructions of (zero-knowledge) SNARGs in the designated-verifier model where verification can be done only by a designated verifier who possesses a secret verification key. These include constructions based on an extractable collision-resistant hash function [4], homomorphism-extractable encryption [5], linear-only encryption [6, 9, 10], etc.

NIZKs/SNARGs and OWFs. Pass and shelat [44] showed that a NIZK for a hard-on-average language implies the existence of (non-uniform) OWFs. On the other hand, Wee [49] gave an evidence that a SNARG for a hard-on-average language is unlikely to imply the existence of OWFs. Therefore, it is considered reasonable to additionally assume the existence of OWFs for constructing a NIZK from a SNARG.

2 Preliminaries

In this section, we review the basic notation and definitions of cryptographic primitives.

Basic Notation. For a natural number $n > 0$, we define $[n] :=\{1, \dots , n\}$. Furthermore, for $I \subseteq [n]$, we define $\overline{I} :=[n] \setminus I$.

For a string x, |x| denotes the bit-length of x. For bits $b, b' \in \{0,1\}$, $(b' {\mathop {=}\limits ^{?}}b)$ is defined to be 1 if $b' = b$ holds and 0 otherwise.

For a set S, |S| denotes its size, and $x \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }S$ denotes sampling x uniformly at random from S. Furthermore, for natural numbers i, k such that $i \in [k]$ and a sequence $z \in S^k$, $z_i$ denotes the i-th entry in z. Also, for $I \subseteq [k]$, we define $z_I :=(z_i)_{i \in I}$, namely the subsequence of z in the positions I.

For a probabilistic (resp. deterministic) algorithm $\mathsf {A}$, $y \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {A}(x)$ (resp. $y \leftarrow \mathsf {A}(x)$) denotes $\mathcal {A}$ on input x outputs y. If we need to specify a randomness r used in $\mathsf {A}$, we write $y \leftarrow \mathsf {A}(x;r)$ (in which case the computation is deterministic). If $\mathcal {O}$ is a function or an algorithm, then $\mathsf {A}^{\mathcal {O}}$ means that $\mathsf {A}$ has oracle access to $\mathcal {O}$.

Throughout the paper, we use $\lambda$ to denote the security parameter, and a “PPT adversary” is a non-uniform PPT adversary (equivalently, a family of polynomial-sized circuits). A function $\epsilon (\lambda )$ with range [0, 1] is said to be negligible if $\epsilon (\lambda ) = \lambda ^{-\omega (1)}$, and $\mathsf {negl}(\lambda )$ denotes an unspecified negligible function of $\lambda$. $\mathsf {poly}(\lambda )$ denotes an unspecified (constant-degree) polynomial of $\lambda$.

2.1 NIZK and SNARG

Here, we define several notions of a non-interactive argument for an $\mathsf {NP}$ language $\mathcal {L}$. Throughout this paper, for an $\mathsf {NP}$ language $\mathcal {L}$, we denote by $\mathcal {R}\subseteq \{0,1\}^* \times \{0,1\}^*$ the corresponding efficiently computable binary relation. For $(x, w) \in \mathcal {R}$, we call x a statement and w a witness.

Definition 2.1

(Non-interactive Arguments). A non-interactive argument for an $\mathsf {NP}$ language $\mathcal {L}$ consists of the three PPT algorithms $(\mathsf {Setup}, \mathsf {Prove}, \mathsf {Verify})$:

• $\mathsf {Setup}(1^\lambda ) \overset{\mathsf {\scriptscriptstyle \$}}{\rightarrow }\mathsf {crs}$: The setup algorithm takes the security parameter $1^\lambda$ as input, and outputs a CRS $\mathsf {crs}$.

• $\mathsf {Prove}(\mathsf {crs}, x, w) \overset{\mathsf {\scriptscriptstyle \$}}{\rightarrow }\pi$: The prover’s algorithm takes a CRS $\mathsf {crs}$, a statement x, and a witness w as input, and outputs a proof $\pi$.

• $\mathsf {Verify}(\mathsf {crs}, x, \pi ) \rightarrow \top ~\text {or}~ \bot$: The verifier’s algorithm takes a CRS $\mathsf {crs}$, a statement x, and a proof $\pi$ as input, and outputs $\top$ to indicate acceptance of the proof or $\bot$ otherwise.

A non-interactive argument must satisfy the following requirements:

• Completeness: For all pairs $(x, w) \in \mathcal {R}$, we have

  $$ \Pr \left[ \mathsf {Verify}(\mathsf {crs}, x, \pi ) = \top : \begin{array}{l} \mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\lambda );\\ \pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Prove}(\mathsf {crs}, x, w) \end{array} \right] = 1. $$

• Soundness: We define the following four variants of soundness.

  • Adaptive Computational Soundness: For all PPT adversaries $\mathcal {A}$, we have

    $$ \Pr \left[ x \not \in \mathcal {L}\wedge \mathsf {Verify}(\mathsf {crs}, x, \pi ) = \top : \begin{array}{l} \mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\lambda );\\ (x, \pi ) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {A}(\mathsf {crs}) \end{array} \right] = \mathsf {negl}(\lambda ). $$

  • Adaptive Statistical Soundness: This is defined similarly to adaptive computational soundness, except that $\mathcal {A}$ can be any computationally unbounded adversary.

  • Non-adaptive Computational (resp. Statistical) Soundness: This is defined similarly to adaptive computational (resp. statistical) soundness, except that $\mathcal {A}$ must declare $x \notin \mathcal {L}$ before it is given $\mathsf {crs}$.

If we only require completeness and soundness as defined above, a non-interactive argument trivially exists for all $\mathsf {NP}$ languages, since a witness itself can be used as a proof. Thus, we consider two other properties that make non-interactive arguments non-trivial. First, we define non-interactive zero-knowledge arguments (NIZKs).

Definition 2.2

(NIZK). A non-interactive argument $(\mathsf {Setup}, \mathsf {Prove}, \mathsf {Verify})$ for an $\mathsf {NP}$ language $\mathcal {L}$ is a non-interactive zero-knowledge argument (NIZK) if it satisfies the following property in addition to completeness and soundness.

• (Computational) Zero-Knowledge: We define the following four variants of zero-knowledge property.

  • Adaptive Multi-theorem Zero-Knowledge: There exists a PPT simulator $\mathcal {S}= (\mathcal {S}_1, \mathcal {S}_2)$ that satisfies the following. For all PPT adversaries $\mathcal {A}$, we have

    $$ \Bigl | \Pr [\mathsf {Expt}_{\mathcal {A}}^{\mathsf {azk}\text {-}\mathsf {real}}(\lambda ) = 1] - \Pr [\mathsf {Expt}_{\mathcal {A},\mathcal {S}}^{\mathsf {azk}\text {-}\mathsf {sim}}(\lambda )=1] \Bigr | = \mathsf {negl}(\lambda ), $$

    where the experiments $\mathsf {Expt}_{\mathcal {A}}^{\mathsf {azk}\text {-}\mathsf {real}}(\lambda )$ and $\mathsf {Expt}_{\mathcal {A},\mathcal {S}}^{\mathsf {azk}\text {-}\mathsf {sim}}(\lambda )$ are defined as follows, and in the experiments, $\mathcal {A}$’s queries (x, w) must satisfy $(x, w) \in \mathcal {R}$.

    

  Though we treat adaptive multi-theorem zero-knowledge as defined above as a default notion of zero-knowledge, we also define weaker notions of zero-knowledge.

  • Adaptive Single-Theorem Zero-Knowledge: This is defined similarly to adaptive multi-theorem zero-knowledge, except that $\mathcal {A}$ is allowed to make only a single query.

  • Non-adaptive Multi-theorem Zero-Knowledge: There exists a PPT simulator $\mathcal {S}$ that satisfies the following. For all PPT adversaries $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ we have

    $$ \Bigl | \Pr [\mathsf {Expt}_{\mathcal {A}}^{\mathsf {nazk}\text {-}\mathsf {real}}(\lambda )=1] - \Pr [\mathsf {Expt}_{\mathcal {A},\mathcal {S}}^{\mathsf {nazk}\text {-}\mathsf {sim}}(\lambda )=1] \Bigr | = \mathsf {negl}(\lambda ), $$

    where the experiments $\mathsf {Expt}_{\mathcal {A}}^{\mathsf {nazk}\text {-}\mathsf {real}}(\lambda )$ and $\mathsf {Expt}_{\mathcal {A},\mathcal {S}}^{\mathsf {nazk}\text {-}\mathsf {sim}}(\lambda )$ are defined below. In the experiments, $\ell$ (the number of statement/witness pairs) is arbitrarily chosen by $\mathcal {A}_1$, and $\mathcal {A}_1$’s output must satisfy $(x_i, w_i) \in \mathcal {R}$ for all $i \in [\ell ]$.

    

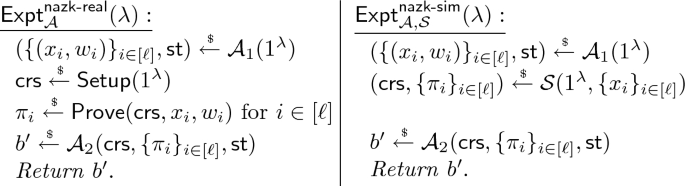
  • Non-adaptive Single-Theorem Zero-Knowledge: This is defined similarly to non-adaptive multi-theorem zero-knowledge, except that $\ell$ must be 1.

It is well-known that a NIZK with adaptive single-theorem zero-knowledge can be generically converted into a NIZK with adaptive multi-theorem zero-knowledge using a PRG [26]. It is easy to see that the same construction works in the non-adaptive setting. Thus, we have the following lemma.

Lemma 2.1

If there exist a OWF and a NIZK for all $\mathsf {NP}$ languages with adaptive (resp. non-adaptive) single-theorem zero-knowledge, then there exists a NIZK for all $\mathsf {NP}$ languages with adaptive (resp. non-adaptive) multi-theorem zero-knowledge. The resulting NIZK satisfies the same notion of soundness (which is either of adaptive/non-adaptive statistical/computational soundness) as the building-block NIZK.

Remark 2.1

Pass and shelat [44] showed that a NIZK for a hard-on-average language implies the existence of a (non-uniform) OWF. Therefore, we can weaken the assumption of the existence of a OWF to the existence of a hard-on-average $\mathsf {NP}$ language. We just assume the existence of a OWF for simplicity. A similar remark also applies to Theorem 3.1 and Lemmas 3.1 and 3.2.

Next, we define SNARGs. The following definition is taken from [29] with a minor modification in the definition of slight succinctness (see Remark 2.2).

Definition 2.3

((Fully/Slightly Succinct) SNARG). A non-interactive argument $(\mathsf {Setup}, \mathsf {Prove}, \mathsf {Verify})$ for an $\mathsf {NP}$ language $\mathcal {L}$ is a fully (resp. $\delta$-slightly) succinct non-interactive argument (SNARG) if it satisfies full (resp. $\delta$-slight) succinctness defined as follows in addition to completeness and soundness.

• Succinctness: We define the following two variants of succinctness.

  • Full Succinctness: For all $(x,w)\in \mathcal {R}$, $\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\lambda )$, and $\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Prove}(\mathsf {crs}, x, w)$, we have $|\pi |=\mathsf {poly}(\lambda )(|x|+|w|)^{o(1)}$.

  • $\underline{\delta \text {-}{} \mathbf{Slight\,Succinctness:}}$ For all $(x,w)\in \mathcal {R}$, $\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\lambda )$, and $\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Prove}(\mathsf {crs}, x, w)$, we have $|\pi |=\mathsf {poly}(\lambda )(|x|+|w|)^{\delta }$.

Remark 2.2

The notion of $\delta$-slight succinctness is meaningful only when $\delta <1$ since otherwise we can use a witness itself as a proof. We note that our definition of $\delta$-slight succinctness for any $\delta <1$ is stronger than slight succinctness defined in [29] where they require $|\pi |=\mathsf {poly}(\lambda )(|x|+|w|)^{\delta }+o(|x|+|w|)$ for some $\delta <1$. Namely, they allow the proof size to grow according to any function dominated by $|x|+|w|$ asymptotically as long as that is independent of the security parameter $\lambda$.

We define an additional property for SNARG.

Definition 2.4

(Efficient Verification of SNARG). A SNARG $(\mathsf {Setup}, \mathsf {Prove}, \mathsf {Verify})$ for an $\mathsf {NP}$ language $\mathcal {L}$ has efficient verification if the following is satisfied.

• Efficient Verification: For all $(x,w)\in \mathcal {R}$, $\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Setup}(1^\lambda )$, and $\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {Prove}(\mathsf {crs}, x, w)$, the running time of $\mathsf {Verify}(\mathsf {crs},x,\pi )$ is $\mathsf {poly}(\lambda )(|x|+|w|)^{o(1)}$.

Remark 2.3

The efficient verification property immediately implies full succinctness.

Remark 2.4

The efficient verification property is usually a default requirement for SNARGs. On the other hand, we do not assume a SNARG to have efficient verification unless otherwise mentioned. This is because efficient verification is not needed for the construction of a NIZK in this paper.

2.2 NIZK in the Hidden-Bits Model

Here, we define a NIZK in the hidden-bits model introduced in [26]. The following definition is taken from [46].

Definition 2.5

(NIZK in the Hidden-Bits Model). Let $\mathcal {L}$ be an $\mathsf {NP}$ language and $\mathcal {R}$ be its associated relation. A non-interactive zero-knowledge proof in the hidden-bits model (HBM-NIZK) for $\mathcal {L}$ consists of the pair of PPT algorithms $(\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Prove}, \mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify})$ and a polynomial $k=k(\lambda , n)$, which specifies the hidden-bits length.

• $\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Prove}(1^\lambda ,\rho , x, w) \overset{\mathsf {\scriptscriptstyle \$}}{\rightarrow }(I, \pi )$: The prover’s algorithm takes the security parameter $1^\lambda$, a string $\rho \in \{0,1\}^{k(\lambda ,n)}$, a statement $x\in \{0,1\}^n$, and a witness w as input, and outputs a subset of indices $I \subseteq [k]$ and a proof $\pi$.

• $\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify}(1^\lambda , I, \rho _I, x,\pi ) \rightarrow \top ~\text {or}~ \bot$: The verifier’s algorithm takes the security parameter $1^\lambda$, a subset $I \subseteq [k]$, a string $\rho _I$, a statement x, and a proof $\pi$ as input, and outputs $\top$ to indicate acceptance of the proof or $\bot$ otherwise.

An HBM-NIZK must satisfy the following requirements.

• Completeness: For all pairs $(x, w) \in \mathcal {R}$, we have

  $$\begin{aligned} \Pr \left[ \begin{array}{r} \mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify}(1^\lambda ,I,\rho _I, x, \pi )\\ = \top \end{array} : \begin{array}{l} \rho \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^{k(\lambda ,|x|)};\\ (I,\pi ) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Prove}(1^\lambda ,\rho , x, w) \end{array} \right] \\ = 1.\quad \end{aligned}$$

• $\underline{\epsilon \text {-}{} \mathbf{Soundness:}}$ For all polynomials $n=n(\lambda )$ and computationally unbounded adversaries $\mathcal {A}$, we have

  $$ \Pr \left[ \begin{array}{l} x \in \{0,1\}^{n}\setminus \mathcal {L}\\ \wedge ~ \mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify}(1^\lambda , I,\rho _I,x, \pi ) = \top \end{array} : \begin{array}{l} \rho \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^{k(\lambda ,n)};\\ (x, I,\pi ) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {A}(\rho ) \end{array} \right] \le \epsilon (\lambda ). $$

• Zero-Knowledge: There exists a PPT simulator $\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Sim}$ that satisfies the following. For all computationally unbounded adversaries $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$, we have

  $$ \Bigl | \Pr [\mathsf {Expt}_{\mathcal {A}}^{\mathsf {hbmzk}\text {-}\mathsf {real}}(\lambda )=1] - \Pr [\mathsf {Expt}_{\mathcal {A},\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Sim}}^{\mathsf {hbmzk}\text {-}\mathsf {sim}}(\lambda )=1] \Bigr | = \mathsf {negl}(\lambda ), $$

  where the experiments $\mathsf {Expt}_{\mathcal {A}}^{\mathsf {hbmzk}\text {-}\mathsf {real}}(\lambda )$ and $\mathsf {Expt}_{\mathcal {A},\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Sim}}^{\mathsf {hbmzk}\text {-}\mathsf {sim}}(\lambda )$ are defined as follows, and $\mathcal {A}_1$’s output must satisfy $(x, w) \in \mathcal {R}$.

  

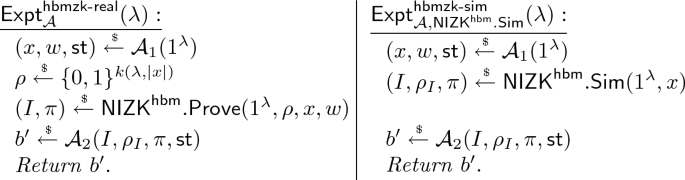
Lemma 2.2

([26]). For any $\mathsf {NP}$ language $\mathcal {L}$, there exists an HBM-NIZK satisfying completeness, $2^{-\varOmega (k)}$-soundness, and zero-knowledge.

Remark 2.5

Though Quach et al. [46] also defined a stronger definition of zero-knowledge called special zero-knowledge, we omit its definition since we do not use it in security proofs given in this version. We note that we use an HBM-NIZK with special zero-knowledge in a proof of Lemma 3.2, which is given in the full version.

2.3 Leakage-Resilient Weak Pseudorandom Function

Here, we review the definition of a leakage-resilient weak pseudorandom function (LR-wPRF) [37]. Though the definition is essentially the same as that in [37], we make it more explicit that we can arbitrarily set the leakage bound $\ell =\ell (\lambda )$ instead of treating $\ell$ as a fixed parameter hardwired in a scheme.⁹ Specifically, we define parameters of an LR-wPRF including the key length, input length, and output length as polynomials of $\lambda$ and $\ell$. This implicitly means that an evaluation of an LR-wPRF also depends on $\ell$ since it is given a key and an input whose length depends on $\ell$.

Definition 2.6

(Leakage-Resilient Weak Pseudorandom Function). Let $\kappa = \kappa (\lambda , \ell )$, $m= m(\lambda ,\ell )$, and $n= n(\lambda ,\ell )$ be polynomials. A leakage-resilient weak pseudorandom function (LR-wPRF) with the key length $\kappa$, input length $m$, and output length $n$, is a family of efficiently computable functions $\mathcal {F}= \{F_K: \{0,1\}^m\rightarrow \{0,1\}^n\}_{K \in \{0,1\}^{\kappa }}$ such that for all polynomials $\ell = \ell (\lambda )$ and PPT adversaries $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$, we have

$$ \Bigl |\Pr [\mathsf {Expt}_{\mathcal {F},\mathcal {A}}^{\mathsf {\mathsf {LRwPRF}}\text {-}\mathsf {0}}(\lambda ,\ell ) = 1] - \Pr [\mathsf {Expt}_{\mathcal {F},\mathcal {A}}^{\mathsf {\mathsf {LRwPRF}}\text {-}\mathsf {1}}(\lambda ,\ell ) = 1] \Bigr | = \mathsf {negl}(\lambda ), $$

where the experiment $\mathsf {Expt}_{\mathcal {F},\mathcal {A}}^{\mathsf {\mathsf {LRwPRF}}\text {-}\mathsf {b}}(\lambda ,\ell )$ (with $b \in \{0,1\}$) is described in Fig. 1.

Fig. 1.

The experiment for defining the leakage-resilience for a wPRF.

Hazay et al. [37] showed how to construct an LR-wPRF from a OWF. Their result can be stated in the following form that is convenient for our purpose.

Theorem 2.1

([37]). If there exists a OWF, then there exists an LR-wPRF with the key length $\kappa =\ell \cdot \mathsf {poly}(\lambda )$, input length $m= \ell \cdot \mathsf {poly}(\lambda )$, and output length $n= 1$.

Remark 2.6

Actually, Hazay et al. showed that we can set $\kappa =O(\ell \lambda /\log \lambda )$, $m=O(\ell \lambda )$, and n to be any polynomial in $\lambda$. We state the theorem in the above form since this is sufficient for our purpose.

3 Non-adaptive to Adaptive Zero-Knowledge for NIZK

In this section, we show the following theorem.

Theorem 3.1

If there exist a OWF and a NIZK for all $\mathsf {NP}$ languages that satisfies adaptive computational (resp. statistical) soundness and non-adaptive single-theorem zero-knowledge, then there exists a NIZK for all $\mathsf {NP}$ languages that satisfies adaptive computational (resp. statistical) soundness and adaptive multi-theorem zero-knowledge.

Remark 3.1

The theorem remains true even if we start from a NIZK with non-adaptive statistical soundness since we can convert it into one with adaptive statistical soundness while preserving the zero-knowledge property by a simple parallel repetition. On the other hand, we do not know whether the theorem remains true if we start from a NIZK with non-adaptive computational soundness.

HBG from Non-adaptive NIZK. First, we show that we can construct an HBG by combining a non-interactive commitment scheme, a PRG, and a NIZK in a straightforward manner.¹⁰ We note that Dwork and Naor [24] already mentioned a similar construction.¹¹ Our crucial observation is that non-adaptive multi-theorem zero-knowledge is sufficient for this purpose. Moreover, as stated in Lemma 2.1, we can generically upgrade non-adaptive single-theorem zero-knowledge to non-adaptive multi-theorem zero-knowledge. Therefore, we obtain the following lemma.

Lemma 3.1

If there exist a OWF and a NIZK for all $\mathsf {NP}$ languages that satisfies adaptive computational (resp. statistical) soundness and non-adaptive single-theorem zero-knowledge, then there exists an HBG that satisfies succinct commitment, computational (resp. statistical) binding, and computational hiding.

Since the construction and security proof are straightforward, we omit them here and give them in the full version.

Adaptive NIZK from HBG. Quach et al. [46] gave a construction of a NIZK with adaptive statistical soundness and adaptive multi-theorem zero-knowledge based on an HBG with statistical binding and computational hiding. It is easy to see that the same construction works for a computationally binding HBG to construct an adaptively computationally sound NIZK. Namely, we have the following lemma.

Lemma 3.2

If there exist a OWF and an HBG that satisfies succinct commitment, computational (resp. statistical) binding, and computational hiding, then there exists a NIZK for all $\mathsf {NP}$ languages that satisfies adaptive computational (resp. statistical) soundness and adaptive multi-theorem zero-knowledge.

Since the construction and proof are essentially the same as those in [46], we omit them here, and give them in the full version.

Theorem 3.1 can be obtained by combining Lemmata 3.1 and 3.2.

4 Hidden-Bits Generator with Subset-Dependent Proofs

In this section, we introduce a weaker variant of an HBG that we call an HBG with subset-dependent proofs (SDP-HBG). We also give a construction of an SDP-HBG from the combination of a SNARG and an LR-wPRF (and thus, from a SNARG and a OWF).

4.1 Definition

Here, we define an SDP-HBG.

Definition 4.1

(SDP-HBG). A hidden-bits generator with subset dependent proofs (SDP-HBG) consists of the four PPT algorithms $(\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}, \mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}, \mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}, \mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Verify})$:

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda ,1^k) \overset{\mathsf {\scriptscriptstyle \$}}{\rightarrow }\mathsf {crs}$: The setup algorithm takes the security parameter $1^\lambda$ and the length parameter $1^k$ as input, and outputs a CRS $\mathsf {crs}$.

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}(\mathsf {crs}) \overset{\mathsf {\scriptscriptstyle \$}}{\rightarrow }(r, \mathsf {st})$: The bits generation algorithm takes a CRS $\mathsf {crs}$ as input, and outputs a string $r\in \{0,1\}^k$ and a state $\mathsf {st}$.

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}(\mathsf {st},I) \overset{\mathsf {\scriptscriptstyle \$}}{\rightarrow }\pi$: The proving algorithm takes a state $\mathsf {st}$ and a subset $I\subseteq [k]$ as input, and outputs a proof $\pi$.

• $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Verify}(\mathsf {crs},I,r_I,\pi ) \rightarrow \top ~\text {or}~ \bot$: The verification algorithm takes a CRS $\mathsf {crs}$, a subset $I\subseteq [k]$, a string $r_I\in \{0,1\}^{|I|}$, and a proof $\pi$ as input, and outputs $\top$ indicating acceptance or $\bot$ otherwise.

We require an SDP-HBG to satisfy the following properties:

• Correctness: For any natural number k and $I\subseteq [k]$, we have

  $$ \Pr \left[ \mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Verify}(\mathsf {crs},I,r_I,\pi )=\top : \begin{array}{l} \mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda ,1^k);\\ (r,\mathsf {st})\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}(\mathsf {crs});\\ \pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}(\mathsf {st},I) \end{array} \right] =1. $$

• Somewhat Computational Binding: There exists a constant $\gamma <1$ such that (1) for any polynomial $k=k(\lambda )$ and $\mathsf {crs}$ generated by $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda , 1^k)$, there exists a subset $\mathcal {V}^{\mathsf {crs}} \subseteq \{0,1\}^{k}$ such that $|\mathcal {V}^{\mathsf {crs}}| \le 2^{k^\gamma \mathsf {poly}(\lambda )}$, and (2) for any PPT adversary $\mathcal {A}$, we have

  $$\begin{aligned} \Pr \left[ \begin{array}{l} r_I \notin \mathcal {V}^{\mathsf {crs}}_I\\ \wedge ~\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Verify}(\mathsf {crs},I,r_I,\pi ) = \top \end{array}: \begin{array}{l} \mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda , 1^k);\\ (I,r_I,\pi )\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {A}(\mathsf {crs}) \end{array} \right] \;\; \\ = \mathsf {negl}(\lambda ), \end{aligned}$$

  where $\mathcal {V}^{\mathsf {crs}}_I :=\{r_I: r\in \mathcal {V}^{\mathsf {crs}}\}$.

• Computational Hiding: For any polynomial $k = k(\lambda )$, $I\subseteq [k]$, and PPT adversary $\mathcal {A}$, we have

  $$ \Bigl | \Pr [\mathcal {A}(\mathsf {crs},I,r_I,\pi ,r_{\overline{I}}) = 1] - \Pr [\mathcal {A}(\mathsf {crs},I,r_I,\pi ,r'_{\overline{I}})=1] \Bigr | = \mathsf {negl}(\lambda ), $$

  where we generate $\mathsf {crs}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda ,1^k)$, $(r,\mathsf {st})\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}(\mathsf {crs})$, $\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}(\mathsf {st},I)$, and $r' \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k$.

An SDP-HBG can be seen as a weaker variant of an ordinary HBG, in the sense that the former can be naturally constructed from the latter. A proof can be found in the full version.

4.2 Construction

Here, we give a construction of an SDP-HBG from a SNARG and a OWF.

Theorem 4.1

If there exist a OWF and a $\delta$-slightly succinct SNARG for all $\mathsf {NP}$ languages for some $\delta < 1/2$ that satisfies adaptive computational soundness, then there exists an SDP-HBG that satisfies somewhat computational binding and computational hiding.

Our construction of an SDP-HBG uses the following ingredients.

• An LR-wPRF $\mathcal {F}= \{F_K: \{0,1\}^m\rightarrow \{0,1\}\}_{K \in \{0,1\}^\kappa }$, built from a OWF via Theorem 2.1, with the key length $\kappa = \kappa (\lambda , \ell ) = \ell \cdot \mathsf {poly}(\lambda )$, input length $m=m(\lambda ,\ell )=\ell \cdot \mathsf {poly}(\lambda )$, and output length 1.

• A $\delta$-slightly succinct SNARG $(\mathsf {SNARG}.\mathsf {Setup},\mathsf {SNARG}.\mathsf {Prove},\mathsf {SNARG}.\mathsf {Verify})$ for some $\delta <1/2$ for the language $\mathcal {L}$ associated with the relation $\mathcal {R}$ defined as follows:

  $$ \Bigl ( (k',\{x_i\}_{i\in [k']},\{r_i\}_{i\in [k']}), ~K \Bigr ) \in \mathcal {R}\quad \Longleftrightarrow \quad r_i = F_K(x_i) ~\text {for all}~ i \in [k']. $$

In our construction of an SDP-HBG, the leakage bound $\ell$ of the underlying LR-wPRF is chosen depending on the length parameter k input to the setup algorithm of the SDP-HBG, so that

• (a) $\kappa \le k^\gamma \cdot \mathsf {poly}(\lambda )$ holds for some constant $\gamma <1$, and

• (b) for any $k'\le k$, $x_i\in \{0,1\}^m$ for $i\in [k']$, $r_i \in \{0,1\}$ for $i\in [k']$, and $K\in \{0,1\}^{\kappa }$, if $\mathsf {crs}_{\mathsf {snarg}}\overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SNARG}.\mathsf {Setup}(1^\lambda )$ and $\pi \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SNARG}.\mathsf {Prove}(\mathsf {crs}_{\mathsf {snarg}},(k',\{x_i\}_{i\in [k']},\{r_i\}_{i\in [k']}), K)$, then we have $|\pi |\le \ell$.

Below we explain how we choose such $\ell$.

Recall that the $\delta$-slight succinctness of the SNARG ensures that the size of a proof $\pi$ generated from a statement/witness pair $(x,w) \in \mathcal {R}$ satisfies $|\pi | \le (|x|+|w|)^\delta \cdot \mathsf {poly}(\lambda )$. In our case, the bit-length of a statement $x = (k', \{x_i\}_{i \in [k']}, \{r_i\}_{i \in [k']})$ is bounded by $\log k + k \cdot (m+ 1) \le k \cdot (m+ 2)=k\ell \cdot \mathsf {poly}(\lambda )$, and the bit-length of a witness $w = K$ is just $\kappa = \ell \cdot \mathsf {poly}(\lambda )$. Hence, the size of a proof $\pi$ generated by $\mathsf {SNARG}.\mathsf {Prove}$ for (x, w) is bounded by

$$ |\pi | \le (k\ell \cdot \mathsf {poly}(\lambda ) + \ell \cdot \mathsf {poly}(\lambda ))^\delta \cdot \mathsf {poly}(\lambda ) \le (k \ell )^\delta \cdot p, $$

for some polynomial $p=\mathsf {poly}(\lambda )$ that is independent of k and $\ell$.

Then we set the leakage bound $\ell = \ell (\lambda ,k)$ as

$$\begin{aligned} \ell :=k^{\frac{\delta }{1-\delta }} \cdot p^{\frac{1}{1-\delta }}. \end{aligned}$$

Since we assume $\delta <1/2$, we have $\frac{\delta }{1-\delta }<1$. Thus the property (a) is satisfied with $\gamma :=\frac{\delta }{1-\delta }$. Furthermore, we have

$$\begin{aligned} |\pi |&\le (k \ell )^\delta \cdot p = k^{\frac{\delta }{1-\delta }} p^{\frac{1}{1-\delta }}=\ell . \end{aligned}$$

Hence, the property (b) is also satisfied, as desired.

Using the above ingredients, our construction of an SDP-HBG $(\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}, \mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}, \mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}, \mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Verify})$ is described in Fig. 2. In the description, $x_I$ is a short hand for $\{x_i\}_{i \in I}$.

Fig. 2.

The construction of an SDP-HBG based on an LR-wPRF and a SNARG.

It is easy to see that the construction satisfies correctness. The security properties of the SDP-HBG are guaranteed by the following theorem.

Theorem 4.2

The above SDP-HBG satisfies somewhat computational binding and computational hiding.

Proof

We start by showing somewhat computational binding, then computational hiding.

Somewhat Computational Binding. For a CRS $\mathsf {crs}= (\mathsf {crs}_{\mathsf {snarg}}, \{x_i\}_{i \in [k]})$ output from $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda ,1^k)$, we define $\mathcal {V}^{\mathsf {crs}} :=\{(F_K(x_1),\ldots ,F_K(x_k)) ~|~ K \in \{0,1\}^{\kappa }\}$. Then, since $|K| = \kappa \le k^{\gamma } \mathsf {poly}(\lambda )$, we have $|\mathcal {V}^{\mathsf {crs}}| \le 2^{k^{\gamma } \mathsf {poly}(\lambda )}$. Furthermore, it is straightforward to see that by the soundness of the underlying SNARG, no PPT adversary can generate a valid proof for $(I, r_I)$ that is inconsistent with any element of $\mathcal {V}$. More specifically, any PPT adversary that given $\mathsf {crs}= (\mathsf {crs}_{\mathsf {snarg}}, \{x_i\}_{i \in [k]})$ outputs a tuple $(I, r_I, \pi )$ satisfying $\mathsf {SNARG}.\mathsf {Verify}(\mathsf {crs}_{\mathsf {snarg}}, (|I|, x_I, r_I), \pi ) = \top$ and $r_I \notin \mathcal {V}^{\mathsf {crs}}_I$, can be straightforwardly turned into a PPT adversary that breaks the adaptive soundness of the underlying SNARG, since $r_I \notin \mathcal {V}^{\mathsf {crs}}_I$ implies $(|I|, x_I, r_I) \notin \mathcal {L}$.

Computational Hiding. It is easy to reduce the computational hiding of our SDP-HBG to the security of the underlying LR-wPRF in which the leakage bound is $\ell$, by noting that the leakage from K is $\pi$ whose size is at most $\ell$. Formally, given any polynomial $k = k(\lambda )$, $I \subseteq [k]$, and PPT adversary $\mathcal {A}$, consider the following PPT adversary $\mathcal {B}= (\mathcal {B}_1, \mathcal {B}_2)$ that attacks the security of the underlying LR-wPRF with the leakage bound $\ell$.

• $\mathcal {B}_1^{F_K(\$), \mathsf {Leak}(\cdot )}(1^\lambda )$: (where $K \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^{\kappa }$) $\mathcal {B}_1$ makes |I| queries to the oracle $F_K(\$)$, and regards the returned values from the oracle as $\{(x_i, r_i = F_K(x_i))\}_{i \in [I]}$. Next, $\mathcal {B}_1$ computes $\mathsf {crs}_{\mathsf {snarg}} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {SNARG}.\mathsf {Setup}(1^\lambda )$, and defines the circuit $f: \{0,1\}^{\kappa } \rightarrow \{0,1\}^{\ell }$ by $f(\cdot ) :=\mathsf {SNARG}.\mathsf {Prove}(\mathsf {crs}_{\mathsf {crs}}, (|I|, x_I, r_I), \cdot )$. Then, $\mathcal {B}_1$ submits $f(\cdot )$ to the oracle $\mathsf {Leak}(\cdot )$, and receives $\pi$. Finally, $\mathcal {B}_1$ sets $\mathsf {st}_{\mathcal {B}}$ as all the information known to $\mathcal {B}_1$, and terminates with output $\mathsf {st}_{\mathcal {B}}$.

• $\mathcal {B}_2^{\mathsf {Chal}(\$)}(\mathsf {st}_{\mathcal {B}})$: $\mathcal {B}_2$ submits $k - |I|$ queries to the challenge oracle $\mathsf {Chal}(\$)$, and regards the returned values from the oracle as $\{(x_i, r_i)\}_{i \in \overline{I}}$. Note that $r_i = F_K(x_i)$ if $b = 0$ and $r_i \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}$ if $b = 1$, where b is $\mathcal {B}$’s challenge bit. Now, $\mathcal {B}_2$ sets $\mathsf {crs}:=(\mathsf {crs}_{\mathsf {snarg}}, \{x_i\}_{i \in [k]})$, and runs $\mathcal {A}(\mathsf {crs}, I, r_I, \pi , r_{\overline{I}})$. When $\mathcal {A}$ terminates with output $b'$, $\mathcal {B}_2$ outputs $b'$ and terminates.

Since $|f(\cdot )| = \ell$, $\mathcal {B}$ complies with the rule of the LR-wPRF security experiment with the leakage bound $\ell$. Furthermore, it is straightforward to see that if $b = 0$, then the pairs $\{(x_i, r_i)\}_{i \in \overline{I}}$ that $\mathcal {B}_2$ receives from the challenge oracle satisfy $F_K(x_i) = r_i$, and $\mathcal {B}$ simulates the computational hiding experiment in the case $r_{\overline{I}}$ is the real randomness generated by $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}(\mathsf {crs})$, perfectly for $\mathcal {A}$. On the other hand, if $b = 1$, then $\{r_i\}_{i \in \overline{I}}$ are random bits, and $\mathcal {B}_2$ simulates the experiment of the opposite case (i.e. $r_{\overline{I}} = \{r_i\}_{i \in \overline{I}}$ is random) perfectly for $\mathcal {A}$. Hence, $\mathcal {B}$’s advantage in breaking the security of the underlying LR-wPRF is exactly the same as $\mathcal {A}$’s advantage in breaking the computational hiding property of our SDP-HBG.    $\square$

5 NIZK from SDP-HBG

In this section, we show the following theorem.

Theorem 5.1

If there exists an SDP-HBG, then there exists a NIZK for all $\mathsf {NP}$ languages that satisfies adaptive computational soundness and non-adaptive single-theorem zero-knowledge.

Combining Theorems 3.1, 4.1 and 5.1, we obtain the following theorem.

Theorem 5.2

If there exist a OWF and a $\delta$-slightly succinct SNARG for all $\mathsf {NP}$ languages for some $\delta <1/2$ that satisfies adaptive computational soundness, then there exists a NIZK for all $\mathsf {NP}$ languages that satisfies adaptive soundness and adaptive multi-theorem zero-knowledge.

In the following, we prove Theorem 5.1. The construction of our NIZK is almost the same as the scheme by Quach, Rothblum, and Wichs [46], except that we use an SDP-HBG instead of an HBG.

Construction. Our NIZK uses the following ingredients:

• An SDP-HBG $(\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup},\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits},\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}, \mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Verify})$.

• An HBM-NIZK $(\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Prove}, \mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify})$ for an $\mathsf {NP}$ language $\mathcal {L}$ with $\epsilon$-soundness.

Let $\gamma < 1$ be the constant regarding the somewhat computational binding of the SDP-HBG, which satisfies $|\mathcal {V}^{\mathsf {crs}_{\mathsf {bgen}}}| \le 2^{k^\gamma \mathsf {poly}(\lambda )}$ for all $\mathsf {crs}_{\mathsf {bgen}}$ generated by $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda , 1^k)$. When we use an HBM-NIZK with the random-string length k, we can make $\epsilon =2^{-\varOmega (k)}$ as stated in Lemma 2.2. Therefore, we can take $k=k(\lambda ) = \mathsf {poly}(\lambda )$ so that $|\mathcal {V}^{\mathsf {crs}}| \cdot \epsilon =\mathsf {negl}(\lambda )$ holds. We fix such k in the following.

Then, our construction of a NIZK for $\mathcal {L}$ is described in Fig. 3.

Fig. 3.

The construction of a NIZK based on an SDP-HBG and an HBM-NIZK.

It is easy to see that the construction satisfies completeness. The security properties of the NIZK is guaranteed by the following theorem.

Theorem 5.3

The above NIZK satisfies adaptive computational soundness and non-adaptive single-theorem zero-knowledge.

Proof

We start by showing soundness, and then zero-knowledge.

Adaptive Computational Soundness. Let $\mathcal {A}$ be any PPT adversary that attacks the adaptive soundness of our NIZK. Let $\mathsf {Win}$ be the event that $\mathcal {A}$ succeeds in breaking the adaptive soundness (i.e. $\mathsf {NIZK}.\mathsf {Verify}(\mathsf {crs},x,\pi ) = \top$ and $x \notin \mathcal {L}$). Suppose $\mathcal {A}$ on input $\mathsf {crs}= (\mathsf {crs}_{\mathsf {bgen}}, s)$ outputs a pair $(x, \pi = (I, \pi _{\mathsf {hbm}}, r_I, \pi _{\mathsf {bgen}}))$. Let $\mathcal {V}^{\mathsf {crs}_{\mathsf {bgen}}} \subseteq \{0,1\}^k$ be the set with which the somewhat computational binding of the underlying SDP-HBG is considered. We have

$$ \Pr [\mathsf {Win}] = \Pr [\mathsf {Win}\wedge r_I \notin \mathcal {V}^{\mathsf {crs}_{\mathsf {bgen}}}_I] + \Pr [ \mathsf {Win}\wedge r_I \in \mathcal {V}^{\mathsf {crs}_{\mathsf {bgen}}}_I]. $$

It is straightforward to see that $\Pr [\mathsf {Win}\wedge r_I \notin \mathcal {V}^{\mathsf {crs}_{\mathsf {bgen}}}_I] = \mathsf {negl}(\lambda )$ holds by the somewhat computational binding of the underlying SDP-HBG.

Hence, it remains to show $P :=\Pr [\mathsf {Win}\wedge r_I \in \mathcal {V}^{\mathsf {crs}_{\mathsf {bgen}}}_I] = \mathsf {negl}(\lambda )$. Fix $\mathsf {crs}^*_{\mathsf {bgen}}$ in the image of $\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda , 1^k)$ and $\mathcal {A}$’s randomness $r^*_{\mathcal {A}}$ that maximize the above probability P. Let $\mathcal {V}^* := \mathcal {V}^{\mathsf {crs}^*_{\mathsf {bgen}}}$. Let $F(\cdot )$ be the function that on input $s \in \{0,1\}^k$, computes $(x, \pi = (I, \pi _{\mathsf {hbm}}, r_I, \pi _{\mathsf {bgen}})) \leftarrow \mathcal {A}(\mathsf {crs}= (\mathsf {crs}^*_{\mathsf {bgen}}, s);r^*_{\mathcal {A}})$, and outputs $(x, I, \pi _{\mathsf {hbm}}, r_I)$. (Looking ahead, F is essentially an adversary against the $\epsilon$-soundness of the underlying HBM-NIZK.) Let $P'$ be the following probability:

$$ P' :=\Pr \left[ \begin{array}{l} \mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify}(I, s_I \oplus r_I, x, \pi _{\mathsf {hbm}}) = \top \\ \wedge ~ r_I \in \mathcal {V}^*_I \wedge x \notin \mathcal {L}\end{array}: \begin{array}{l} s \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k;\\ (x, I, \pi _{\mathsf {hbm}}, r_I) \leftarrow F(s)\end{array} \right] . $$

Fig. 4.

The simulator for showing non-adaptive single-theorem zero-knowledge in the proof of Theorem 5.3.

Clearly, we have $P \le P'$. We also have

$$\begin{aligned}&P' = \sum _{r' \in \mathcal {V}^*} \Pr \left[ \begin{array}{l} \mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify}(I, s_I \oplus r_I, x, \pi _{\mathsf {hbm}}) = \top \\ \wedge ~ r_I = r'_I \wedge x \notin \mathcal {L}\end{array} : \begin{array}{l} s \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k;\\ (x, I,\pi _{\mathsf {hbm}}, r_I) \leftarrow F(s) \end{array} \right] \\&\le |\mathcal {V}^*| \cdot \max _{r^* \in \mathcal {V}^*} \Pr \left[ \begin{array}{l} \mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify}(I, s_I \oplus r_I, x, \pi _{\mathsf {hbm}}) = \top \\ \wedge ~ r_I = r^*_I \wedge x \notin \mathcal {L}\end{array}: \begin{array}{l} s \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k;\\ (x, I, \pi _{\mathsf {hbm}}, r_I) \leftarrow F(s) \end{array} \right] \\&= |\mathcal {V}^*| \cdot \max _{r^* \in \mathcal {V}^*} \Pr \left[ \begin{array}{l} \mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify}(I, \rho _I, x, \pi _{\mathsf {hbm}}) = \top \\ \wedge ~ r_I = r^*_I \wedge x \notin \mathcal {L}\end{array} : \begin{array}{l} \rho \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k;\\ (x, I, \pi _{\mathsf {hbm}}, r_I) \leftarrow F(\rho \oplus r^*) \end{array} \right] \\&\le |\mathcal {V}^*| \cdot \max _{r^* \in \mathcal {V}^*} \Pr \left[ \begin{array}{l} \mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Verify}(I, \rho _I, x, \pi _{\mathsf {hbm}}) = \top \\ \wedge ~ x \notin \mathcal {L}\end{array} : \begin{array}{l} \rho \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k;\\ (x, I, \pi _{\mathsf {hbm}}, r_I) \leftarrow F(\rho \oplus r^*) \end{array} \right] \\&\le |\mathcal {V}^*| \cdot \epsilon (k) = \mathsf {negl}(\lambda ), \end{aligned}$$

where the last inequality uses the $\epsilon$-soundness of the underlying HBM-NIZK which we consider for the adversary $\mathcal {B}(\rho )$ that outputs $F(\rho \oplus r^*)$ other than $r_I$, and the last equality is due to our choice of k. Hence, we have $P = \Pr [\mathsf {Win}\wedge r_I \in \mathcal {V}^{\mathsf {crs}_{\mathsf {bgen}}}_I] = \mathsf {negl}(\lambda )$ as well.

Combined together, we have seen that $\mathcal {A}$’s advantage in breaking the adaptive soundness of our NIZK is negligible. This implies that our NIZK satisfies adaptive soundness.

Non-adaptive Single-Theorem Zero-Knowledge. Let $\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Sim}$ be the simulator that is guaranteed to exist by the zero-knowledge of the underlying HBM-NIZK. Using $\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Sim}$, we first give the description of the simulator $\mathcal {S}$ in Fig. 4 for showing the non-adaptive single-theorem zero-knowledge of our NIZK.

We prove the non-adaptive single-theorem zero-knowledge of the above NIZK via a sequence of games argument using four games, among which the first game $\mathsf {Game}_1$ (resp. the final game $\mathsf {Game}_4$) is exactly the real (resp. simulated) experiment. Let $\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)$ be any PPT adversary that attacks the non-adaptive single-theorem zero-knowledge of the above NIZK. For $j \in [4]$, let $\mathsf {T}_j$ be the event that $\mathcal {A}_2$ finally outputs 1 in $\mathsf {Game}_j$. The description of the games is as follows.

• $\mathsf {Game}_1$: This is exactly the real experiment $\mathsf {Expt}_{\mathcal {A}}^{\mathsf {nazk}\text {-}\mathsf {real}}$. We have $\Pr [\mathsf {T}_1] = \Pr [\mathsf {Expt}_{\mathcal {A}}^{\mathsf {nazk}\text {-}\mathsf {real}}(\lambda )=1]$.

• $\mathsf {Game}_2$: We change the ordering of the steps of $\mathsf {Game}_1$, and furthermore “program” s by first choosing $\rho \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k$ and then setting $s :=\rho \oplus r$, without changing the distribution of $\mathcal {A}$’s view. Specifically, this game proceeds as follows.

  • 1. Run $(x, w, \mathsf {st}_{\mathcal {A}}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {A}_1(1^\lambda )$.

  • 2. Pick $\rho \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k$.

  • 3. Compute $(\pi _{\mathsf {hbm}}, I) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Prove}(\rho , x, w)$.

  • 4. Compute $\mathsf {crs}_{\mathsf {bgen}} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Setup}(1^\lambda , 1^k)$.

  • 5. Compute $(r, \mathsf {st}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {GenBits}(\mathsf {crs}_{\mathsf {bgen}})$.

  • 6. Compute $\pi _{\mathsf {bgen}} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {HBG}^{\mathsf {sdp}}.\mathsf {Prove}(\mathsf {st}, I)$.

  • 7. Set $s_I :=\rho _I \oplus r_I$.

  • 8. Set $s_{\overline{I}} :=\rho _{\overline{I}} \oplus r_{\overline{I}}$.¹²

  • 9. Set $\mathsf {crs}:=(\mathsf {crs}_{\mathsf {bgen}}, s)$ and $\pi :=(I, \pi _{\mathsf {hbm}}, r_I, \pi _{\mathsf {bgen}})$.

  • 10. Run $b' \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathcal {A}_2(\mathsf {crs}, \pi , \mathsf {st}_{\mathcal {A}})$.

  It is easy to see that the distribution of $\mathcal {A}$’s view has not been changed from $\mathsf {Game}_1$. Hence, we have $\Pr [\mathsf {T}_1] = \Pr [\mathsf {T}_2]$.

• $\mathsf {Game}_3$: This game is identical to the previous game, except that the 8th step “$s_{\overline{I}} :=\rho _{\overline{I}} \oplus r_{\overline{I}}$” is replaced with “$s_{\overline{I}} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^{k - |I|}$”.

  It is straightforward to see that $|\Pr [\mathsf {T}_2] - \Pr [\mathsf {T}_3]| = \mathsf {negl}(\lambda )$ holds by the computational hiding of the underlying SDP-HBG.

• $\mathsf {Game}_4$: This game is identical to the previous game, except that $(\rho , \pi _{\mathsf {hbm}}, I)$ is generated as $(\rho _I, \pi _{\mathsf {hbm}}, I) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Sim}(x)$, instead of picking $\rho \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\{0,1\}^k$ and then executing $(\pi _{\mathsf {hbm}}, I) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow }\mathsf {NIZK}^{\mathsf {hbm}}.\mathsf {Prove}(\rho ,x,w)$.

  It is immediate to see that $|\Pr [\mathsf {T}_3] - \Pr [\mathsf {T}_4]| = \mathsf {negl}(\lambda )$ holds by the zero-knowledge of the underlying HBM-NIZK.

  It is also straightforward to see that $\mathsf {Game}_4$ is identical to the simulated experiment $\mathsf {Expt}_{\mathcal {A},\mathcal {S}}^{\mathsf {nazk}\text {-}\mathsf {sim}}$. Hence, we have $\Pr [\mathsf {T}_4] = \Pr [\mathsf {Expt}_{\mathcal {A},\mathcal {S}}^{\mathsf {nazk}\text {-}\mathsf {sim}}(\lambda ) = 1]$.

Combined together, $\mathcal {A}$’s advantage against the non-adaptive single-theorem zero-knowledge can be estimated as follows:

$$\begin{aligned} \Bigl | \Pr [\mathsf {Expt}_{\mathcal {A}}^{\mathsf {nazk}\text {-}\mathsf {real}}(\lambda ) = 1] - \Pr [\mathsf {Expt}_{A,\mathcal {S}}^{\mathsf {nazk}\text {-}\mathsf {sim}}(\lambda ) = 1] \Bigr | = \Bigl | \Pr [\mathsf {T}_1] - \Pr [\mathsf {T}_4] \Bigr |\qquad \quad \\ \le \sum _{j \in [3]} \Bigl | \Pr [\mathsf {T}_j] - \Pr [\mathsf {T}_{j+1}] \Bigr | = \mathsf {negl}(\lambda ). \end{aligned}$$

This proves that our NIZK is non-adaptive single-theorem zero-knowledge.    $\square$

Remark 5.1

(On adaptive zero-knowledge.) One may think that we can prove that the above construction satisfies adaptive single-theorem zero-knowledge by relying on the special zero-knowledge property of the underlying HBM-NIZK, since a similar statement is proven for the construction of a NIZK based on an (ordinary) HBG in [46]. However, we believe that this is not possible. Roughly speaking, the problem comes from the fact that the SDP-HBG enables us to generate a proof $\pi _\mathsf {bgen}$ corresponding to a subset I only after I is fixed. This is in contrast to an HBG where we can generate $\pi _i$ that certifies the i-th hidden bit for each $i\in [k]$ before I is fixed. Specifically, the proof of adaptive zero-knowledge from an HBG in [46] crucially relies on the fact that if $I \subseteq I^*$, then a set of proofs $\{\pi _i\}_{i\in I}$ can be derived from $\{\pi _i\}_{i\in I^*}$ in a trivial manner. On the other hand, we do not have a similar property in SDP-HBG since it generates a proof for a subset I in one-shot instead of generating a proof in a bit-by-bit manner. We note that if SDP-HBG satisfies an adaptive version of computational hiding where an adversary can choose a subset I depending on a CRS $\mathsf {crs}_{\mathsf {bgen}}$, then we can prove the adaptive zero-knowledge of the above scheme relying on special zero-knowledge of HBM-NIZK. However, such an adaptive version of computational hiding cannot be proven by a similar proof to the one in Sect. 4.2 due to the fact that a leakage function cannot depend on a challenge input in the security game of LR-wPRF. Therefore, instead of directly proving that the above scheme satisfies adaptive zero-knowledge, we rely on the generic conversion from non-adaptive to adaptive zero-knowledge as stated in Theorem 3.1.

6 Zero-Knowledge SNARG

In this section, we consider a zero-knowledge SNARG (zkSNARG) which is a SNARG that also satisfies the zero-knowledge property.

Bitansky et al. [4] gave a construction of a zkSNARG in the designated verifier model based on a SNARG (with efficient verification) in the designated verifier model, a NIZK argument of knowledge, and a circuit-private FHE scheme. As noted in [4], if we consider a publicly verifiable SNARG (which is the default notion of a SNARG in this paper), then we need not rely on FHE. Moreover, a NIZK argument of knowledge can be constructed by combining any NIZK and CPA secure PKE. Thus, we obtain the following theorem:

Lemma 6.1

Assume that there exist a fully succinct SNARG for all $\mathsf {NP}$ languages with adaptive computational soundness and efficient verification, a NIZK for all $\mathsf {NP}$ languages with adaptive computational soundness and adaptive multi-theorem zero-knowledge, and a CPA secure PKE scheme. Then, there exists a fully succinct SNARG for all $\mathsf {NP}$ languages with adaptive computational soundness, adaptive multi-theorem zero-knowledge, and efficient verification.

Since this lemma follows from a straightforward extension of existing works, we omit the proof here and give it in the full version.

Combining Lemma 6.1 and Theorem 5.2, we obtain the following theorem.

Theorem 6.1

If there exist a CPA secure PKE scheme and a fully succinct SNARG for all $\mathsf {NP}$ languages with adaptive computational soundness and efficient verification, then there exists a fully succinct SNARG for all $\mathsf {NP}$ languages with adaptive computational soundness, adaptive multi-theorem zero-knowledge, and efficient verification.

Remark 6.1

We cannot prove a similar statement for a SNARG without efficient verification since efficient verification is essential in the construction of a zkSNARG in Lemma 6.1.