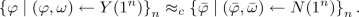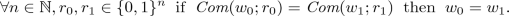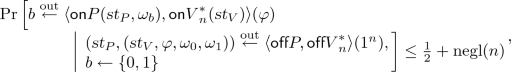Weakly Extractable One-Way Functions

Abstract

A family of one-way functions is extractable if given a random function in the family, an efficient adversary can only output an element in the image of the function if it knows a corresponding preimage. This knowledge extraction guarantee is particularly powerful since it does not require interaction. However, extractable one-way functions (EFs) are subject to a strong barrier: assuming indistinguishability obfuscation, no EF can have a knowledge extractor that works against all polynomial-size non-uniform adversaries. This holds even for non-black-box extractors that use the adversary’s code.

Accordingly, the literature considers either EFs based on non-falsifiable knowledge assumptions, where the extractor is not explicitly given, but it is only assumed to exist, or EFs against a restricted class of adversaries with a bounded non-uniform advice. This falls short of cryptography’s gold standard of security that requires an explicit reduction against non-uniform adversaries of arbitrary polynomial size.

Motivated by this gap, we put forward a new notion of weakly extractable one-way functions (WEFs) that circumvents the known barrier. We then prove that WEFs are inextricably connected to the long standing question of three-message zero knowledge protocols. We show that different flavors of WEFs are sufficient and necessary for three-message zero knowledge to exist. The exact flavor depends on whether the protocol is computational or statistical zero knowledge and whether it is publicly or privately verifiable.

Combined with recent progress on constructing three message zero-knowledge, we derive a new connection between keyless multi-collision resistance and the notion of incompressibility and the feasibility of non-interactive knowledge extraction. Another interesting corollary of our result is that in order to construct three-message zero knowledge arguments, it suffices to construct such arguments where the honest prover strategy is unbounded.

N. Bitansky—Member of the Check Point Institute of Information Security. Supported by the Alon Young Faculty Fellowship, by Len Blavatnik and the Blavatnik Family foundation, by the Blavatnik Interdisciplinary Cyber Research Center at Tel Aviv University, and an ISF grant 484/18.

N. Eizenstadt—Supported by ISF grant 484/18.

O. Paneth—Member of the Check Point Institute of Information Security. Supported by an Azrieli Faculty Fellowship, by Len Blavatnik and the Blavatnik Foundation, by the Blavatnik Interdisciplinary Cyber Research Center at Tel Aviv University, and ISF grant 1789/19.

1 Introduction

An extractable one-way function is a family of functions $\left\{ f_{k}\right\}$ that satisfies two properties: One-wayness: Given an image $y=f_{k}(x)$ for random key $k$ and input $x$, it is hard to find a corresponding pre-image $x'\in f_{k}^{-1}(y)$; and Extraction: Given a random key $k$, it is hard to produce an image $y$ obliviously, without knowing a corresponding preimage $x'$. This is formalized by requiring that for any efficient algorithm $A$ that given $k$ produces an image $y$, there is an efficient extractor $\mathcal {E}$ (that depends on $A$) that given the same key $k$, extracts a preimage $x'$.

While their extraction property is reminiscent of proofs of knowledge [FS89, BG92], EFs are essentially different—they draw their power from the fact that extraction can be done without interaction.

The Good. The non-interactive nature of EFs gives rise to killer applications such as encryption with strong CCA security [Dam91, BP04], three-message zero knowledge [HT98, CD08], and by extending one-wayness to collision-resistance, also succinct non-interactive arguments of knowledge (SNARKs) [BCC+14].

The Bad. Constructing EFs has proven to be an elusive task. A first barrier is that without interaction, traditional black-box extraction techniques, like rewinding, (provably) do not work. Accordingly, extraction must use the code of the adversary in a non-black-box way. Bitansky, Canetti, Paneth, and Rosen [BCPR16], following Goldreich’s intuition [HT98], demonstrated an even stronger barrier that holds for non-black-box extractors. Assuming indistinguishability obfuscation, they show that no efficient extractor can work against all polynomial-size non-uniform adversaries; that is, even when the extractor is given the adversary’s code.

The Ugly. One approach that avoids the above barriers is to simply assume the existence of an extractor for every adversary, without giving an explicit extraction strategy. An EF with such non-explicit extractors follows, for example, from the knowledge of exponent assumption [Dam91]. Such knowledge assumptions translate in applications to security reductions that are, at least in part, non-explicit. Knowledge assumptions are arguably unsatisfying, and in particular are not falsifiable [Nao03].

Another way to circumvent known barriers is to restrict the class of adversaries. Bitansky et al. construct EFs with an explicit extractor against adversaries with bounded non-uniform advice, under standard assumptions.¹ The restriction on the adversaries carries over to applications—they obtain three-message zero-knowledge, but only against verifiers with bounded non-uniformity. This of course falls short of the gold standard in cryptography of security against non-uniform adversaries of arbitrary polynomial size.

Given this state of affairs, we ask:

Is there hope for explicit extraction from general non-uniform adversaries?

1.1 This Work

We put forward a new definition of weakly extractable one-way functions (WEFs) that circumvents the [BCPR16] extraction barrier. We then show that WEFs are deeply connected to three-message zero knowledge protocols, establishing a loose equivalence between the two notions.

The New Definition. Our notion of WEFs is inspired by simulation-based definitions of multi-party computation. We relax the extraction requirement as follows: instead of requiring that the extractor $\mathcal {E}$, given a random key $k$ and the code of the adversary $A$, is able to find a preimage $x'\in f_{k}^{-1}(y)$ for the adversary’s image $y=A(k)$, we allow the extractor to sample a simulated key $\widetilde{k}$ on its own together with an extracted preimage $x'\in f_{\widetilde{k}}^{-1}(y)$ for $y=A(\widetilde{k})$. The simulated key $\widetilde{k}$ must be indistinguishable from a randomly sampled key $k$.

For this relaxation to be meaningful we must also strengthen the one-wayness requirement. Instead of one-wayness for a random key, we require that $f_{k}$ is hard to invert on any key $k$. More generally, we can require hardness for any key from some NP set of valid keys. In this case, we further require that the extractor’s simulated keys be valid and thus extraction cannot simply sample “easy to invert” keys. Rather, just as in standard EFs, the WEF extractor must use the code of the adversary to extract a preimage or it could be used to break one-wayness.

Our main motivation for studying WEFs is that they are weak enough to circumvent the impossibility of [BCPR16] (see the technical overview for more details) yet, appear to capture a natural and meaningful notion of extraction. We confirm this intuition by showing that WEFs are sufficient for one of the central applications of EFs: three-message zero knowledge arguments.

Theorem 1 (Informal)

Assuming WEFs, two-message witness-indistinguishable arguments, and non-interactive commitments, there exist three-message ZK arguments for NP.

The existence of three-message zero knowledge arguments (with negligible soundness error) is one of the central questions in the area. The main barrier to constructing such arguments is that they require non-black box simulation [GK96]. In addition to constructions based on EFs, the only known construction secure against arbitrary polynomial size non-uniform adversaries was given recently by Bitansky, Kalai and Paneth [BKP18] based on keyless multi-collision resistant hash functions (and other, more standard, assumptions). A feature of the WEF-based zero knowledge argument, which [BKP18] protocol lacks, is that it is publicly verifiable. This means that the verifier’s decision can be inferred from the message transcript alone.

A Tighter Connection. We continue to show a tighter connection between the notions of WEF and three-message zero knowledge. We show that a slight generalization of WEF is sufficient as well as necessary for three-message zero knowledge. Our generalization follows Bitansky et al.’s [BCPR16] generalization of EFs, allowing for a more general forms of hardness than one-wayness. They consider a relation $\mathcal {R}_{k}(y,x')$ on images $y=f_{k}(x)$ and solutions $x'$, and replace one-wayness with the hardness of finding solutions. Likewise, the extractor only has to find $x'$ that satisfies the relation $\mathcal {R}_{k}$, rather than a preimage.² We generalize WEFs in an analogous way.

We establish the following equivalence between generalized WEFs (GWEFs) and three-message zero knowledge arguments:

Theorem 2 (Informal)

Assuming two-message witness- indistinguishable and non interactive commitments arguments, GWEFs exist if and only if publicly verifiable three-message zero knowledge arguments exist.

Finally, we ask if there is some natural notion of WEF that corresponds to three-message ZK arguments that are privately verifiable, such as the argument of [BKP18]. Again following [BCPR16], we consider a notion of privately verifiable GWEFs where the hard relation $\mathcal {R}_{k}$ is not publicly verifiable—efficiently testing whether $(f_{k}(x),x')\in \mathcal {R}_{k}$ requires the preimage $x$ (see the technical overview for a more details on privately verifiable GWEFs).

In the privately verifiable settings, we show the following loose equivalence:

Theorem 3 (Informal)

• 1. Assuming privately verifiable GWEFs and secure function evaluation, there exist privately verifiable three-message computational zero-knowledge arguments for NP.

• 2. Assuming privately verifiable three-message statistical zero-knowledge arguments for NP and non-interactive commitments, there exist privately verifiable GWEFs.

Recently, building on [BKP18] and relying on the same assumptions, three-message statistical zero-knowledge arguments were constructed in [BP19]. Thus, as a corollary from Theorem 3 we obtain privately verifiable GWEFs from keyless multi-collision resistant hashing (and other standard assumptions). This connects between the notion of incompressibility, which stands behind keyless multi-collision-resistance and the notion of knowledge extraction. We further note that keyless collision-resistance is a falsifiable assumption, which should be contrasted with the fact that standard EFs all crucially rely on non-falsifiable assumptions such as the knowledge of exponent assumption.

On WEFs Candidates. As mentioned above, the negative result of Bitansky et al. [BCPR16] does not extend to WEFs. Therefore, even assuming indistinguishability obfuscation, existing candidate constructions, such as the one based on the knowledge of exponent assumption, may be weakly extractable. In the current work, however, we do not provide any evidence in support of that. Demonstrating, under standard assumptions, a WEF with an explicit extractor against non-uniform adversaries is left as an open question. We view the privately verifiable GWEFs from keyless multi-collision resistant hashing that follows from Theorem 3 as a first step in this direction.

On Zero Knowledge with an Unbounded Honest Prover. Our GWEF constructions from zero knowledge arguments, in fact, work even if the honest prover is unbounded. Combined with our results in the reverse direction, this has an interesting implication—to obtain three-message zero knowledge arguments with an efficient honest prover, it suffices to obtain such argument with with an unbounded honest prover.

1.2 Technical Overview

We now provide an overview of the main technical ideas behind our results. We start by explaining how the definition of WEFs circumvents the [BCPR16] barrier. We then discuss the equivalence between GWEFs and (publicly verifiable) three-message zero knowledge. Finally, we discuss the case of private verification.

Circumventing the Impossibility. The [BCPR16] impossibility constructs a distribution $\mathcal {A}$ over obfuscated adversaries, and shows that if the extractor works given a random key $k$ and adversary $A$ sampled from $\mathcal {A}$, then it must also work when the adversary $A$ is sampled after the key $k$ from an alternative distribution $\mathcal {A}_k$ over adversaries that have a random image $f_{k}(x)$ hardwired in their code. This argument crucially relies on the fact that the extractor does not control the key $k$.

GWEFs to Publicly Verifiable Zero Knowledge. The construction of publicly verifiable zero knowledge from $\text{ GWEF }$s is mostly similar to previous constructions (e.g., [CD08, BCC+14]). We sketch it here briefly, highlighting the differences. To prove some NP statement $\varphi \in \mathcal {L}$, the protocol follows the Feige-Lapidot-Shamir trapdoor paradigm [FLS90]. The prover sends a random key $k$ for a GWEF, and the verifier responds with a random image $y=f_{k}(x)$. The prover then provides a witness-indistinguishable proof of knowledge that either the statement $\varphi$ is true, or that (a) the chosen key $k$ is valid (and thus hard), and (b) it knows a solution $x'$ for $y$; namely, $(y,x')\in \mathcal {R}_{k}$.

The protocol is publicly verifiable, as it only requires verifying the witness indistinguishable proof, which is publicly verifiable. Soundness follows from the fact that for a valid key $k$ and a random image $f_{k}(x)$, it is hard to find a solution $x'$ satisfying $\mathcal {R}_k$. For zero knowledge, the simulator uses the extractor $\mathcal {E}({V}^*)$ to extract from the verifier a solution $x'$ together with a corresponding simulated key $k$ and an NP certificate for the key’s validity. It then uses $x'$ and the certificate of validity as its witness in the witness-indistinguishable proof. The protocol, as described, implicitly assumes that the malicious verifier’s message $y$ can indeed be explained as an image $y=f_{k}(x)$. We bridge this gap using standard techniques, based on two-message witness-indistinguishability and commitments, for compiling protocols against explainable verifiers to ones against malicious verifiers [BKP19].

Publicly Verifiable Zero Knowledge to GWEFs. The main idea behind the construction of GWEFs from three-message zero knowledge is a natural one—a key $k$ for a function $f_{k}$ consists of the first zero knowledge message $\mathsf {zk}_1$ as well a statement $\varphi \in \mathcal {L}$ for some language $\mathcal {L}$ (to be specified), an image under the function $f_{k}(x)$ is the honest verifier response $y= \mathsf {zk}_2$, when using $x$ as its randomness. The corresponding hard relation $\mathcal {R}_k(y,x')$ accepts as a solution $x'$ any message $\mathsf {zk}_3$ that convinces the verifier. Indeed, given that the zero knowledge is publicly verifiable, this can be tested efficiently.

The set of valid keys (for which the relation is hard) consists of false statements $\varphi \notin \mathcal {L}$. Indeed, finding a solution $x'=\mathsf {zk}_3$ to a random image $y=\mathsf {zk}_2$ under a valid key $k=(\mathsf {zk}_1,\varphi )$, amounts to producing an accepting proof for the false statement $\varphi$, which is computationally hard due to the soundness of the argument.

The extractor $\mathcal {E}(A)$ samples a false $\varphi$ on its own, and runs the zero knowledge simulator $S(\varphi ,V_A)$ on the code of the verifier $V_A$ induced by the adversary $A$ to produce a simulated transcript $(\mathsf {zk}_1,\mathsf {zk}_2,\mathsf {zk}_3)$. It then sets the simulated key to be $(\mathsf {zk}_1,\varphi )$ and the extracted preimage to be $\mathsf {zk}_3$. To argue that the extractor indeed works we have to argue that the simulator produces an accepting transcript. We note that had $\varphi$ been a true statement, then this would have followed from the zero knowledge and completeness of the underlying argument. Indeed, the honest prover necessarily generates accepting transcripts due to completeness, and the simulated transcript must be indistinguishable.

To establish faithful extraction, we choose the language $\mathcal {L}$ so to guarantee indistinguishable distributions over true-statements and false-statements. Since the simulator is efficient, and cannot tell them apart, it will also generate accepting transcripts on false-statements like the one sampled by the extractor. We also require that false-statements are taken from an NP set. The existence of a language $\mathcal {L}$ satisfying these properties follow from non-interactive commitments.

Privately Verifiable GWEFs. We now move to discuss privately verifiable GWEFs and their connection to privately verifiable zero knowledge. Here the hard relation $\mathcal {R}_{k}$ is not publicly verifiable—efficiently testing whether $(f_{k}(x),x')\in \mathcal {R}_{k}$ requires the preimage $x$.

In the setting of privately verifiable GWEF, where testing a solution $x'$ for $y$ requires private information (a preimage), there are two knowledge-related questions: (1) the usual one: must the adversary know a solution for the produced image $y$? but also (2) can it even recognize such a solution? The definition we consider essentially says that if the adversary can generate an image $y$, for which it can verify solutions, then it must also know a solution. If it cannot even verify a solution, we only require that the extractor generates $x'$ that the adversary cannot distinguish from a solution.

Following this intuition, we further relax the previous extraction definition as follows. The extractor $\mathcal {E}$ may sometime fail to extract. However, there is an additional extractor $\widetilde{\mathcal {E}}$ that is guaranteed to always succeed and produce a key $k$ and candidate solution $x'$ that are indistinguishable from those generated by $\mathcal {E}$. The extractor $\widetilde{\mathcal {E}}$ is given the extra freedom to solve invalid keys (indeed invalid keys may be indistinguishable from valid keys, if the NP certificate of validity is hidden). Note that in the publicly verifiable setting, or if the adversary generates images $y$ whose solutions it can recognize, the original extractor $\mathcal {E}$ must indeed always succeed just like the alternative $\widetilde{\mathcal {E}}$ (otherwise, we can tell them apart).

Privately Verifiable GWEFs to Privately Verifiable Zero Knowledge. The construction of privately verifiable zero knowledge from privately verifiable $\text{ GWEF }$s follows the construction of [BCPR16] from privately verifiable GEFs. In a nutshell, in the case of privately verifiable GWEFs, the prover cannot directly prove that it found a solution $x'$, as testing a solution requires the private randomness $x$ used to generate $y=f_{k}(x)$. Instead, the verifier and prover execute a secure function evaluation protocol, which allows to perform this verification in an “encrypted manner”. This results in privately verifiable zero knowledge due to the private state of the verifier in the secure function evaluation protocol.

Soundness of the protocol is argued similarly to [BCPR16]. For zero knowledge, we rely on the relaxed extraction guarantee described above. The simulator uses $\mathcal {E}$ to generate a simulated key $k$ along with an NP certificate of validity, and extracted a solution $x'$. Only in the analysis, we switch to indistinguishably generating the keys using the alternative extractor $\widetilde{\mathcal {E}}$, and use the fact that it successfully extracts.

Privately Verifiable Statistical Zero Knowledge to Privately Verifiable GWEFs. The construction of GWEFs from Privately Verifiable Zero Knowledge is essentially the same as that from publicly verifiable zero knowledge. We address the difference in the analysis, explaining why statistical zero knowledge is needed, and how the alternative extractor relaxation aids the construction.

Recall that in the GWEF construction from publicly verifiable zero knowledge, to prove hardness it is crucial that a valid key corresponds to a false statement $\varphi$. To show that the extractor faithfully extracts, we had to show that the simulator faithfully generates an accepting transcript. We argued that in two steps: (1) the simulator generates accepting transcripts on true statements, and (2) even though the extractor generates false statements, the simulator would still succeed as it cannot tell false statements from true ones.

In the private verification setting, (1) is not clear. Indeed, testing whether a transcript is accepting cannot be done efficiently, and thus computational zero knowledge is insufficient for arguing that the simulator would also generate accepting transcripts. This is where we resort to statistical zero knowledge—indeed, an unbounded distinguisher can generate verifier coins consistent with the transcript and test acceptance. However, the second argument (2) should also be treated with care. The fact that the simulator generates accepting transcripts on true statements does not necessarily mean that it generates such transcripts on false statements. Indeed these are inherently only computational indistinguishable. However, this argument is sufficient for establishing our relaxed extraction guarantee: the alternative extractor $\widetilde{\mathcal {E}}$ simply chooses true statements rather than false statements. Since these are computationally indistinguishable, and the extracted solution $x'$ is efficiently generated from the statement, we are guaranteed that the two extractors are indeed indistinguishable.

1.3 Open Questions

The notions of WEFs and GWEFs suggest a new avenue for dealing with knowledge extraction in the non-interactive settings. We address a few of the open questions that arise.

• Can we use our new notions of extraction to go beyond zero knowledge and obtain results on the round complexity of secure computation? One concrete approach is to construct (G)WEFs with a unique hard property. That is, a GWEFs and a property $\pi$ such that an image $y$ uniquely determines the value $\pi (x')$ for any solution $x'$ but given only $y$ the value $\pi (x')$ is pseudo-random. Indeed, this can be seen as a generalization of WEF that are injective and will lead to extractable commitments in two messages.

• Can we construct any form of collision resistant (G)WEFs? Can these suffice for applications such as succinct non-interactive arguments of knowledge (SNARKs)?

• Is there an implication in the reverse direction from (G)WEF to keyless multi-collision-resistance, or, more generally to some non-trivial notion of incompressibility.

2 Preliminaries

We rely on the following standard computational concepts and notation:

• A PPT is a probabilistic polynomial-time algorithm.

• We follow the standard practice of modeling any efficient adversary strategy as a family of polynomial size circuits. For an adversary $A$ corresponding to a family of polynomial-size circuits $\left\{ A_n\right\} _{n\in \mathbb {N}}$.

• A distinguisher algorithm is one that has a single output bit.

• We say that a function $f:\mathbb {N}\rightarrow \mathbb {R}$ is negligible if for all constants $c > 0$, there exists $N \in \mathbb {N}$ such that for all $n> N$, $f(n) < n^{-c}$. We sometimes denote negligible functions by $\mathrm {negl}$.

• We say that a function $f:\mathbb {N}\rightarrow \mathbb {R}$ is noticeable if there exist constants $c > 0$ and $N\in \mathbb {N}$ such that for all $n>N$, $f(n) \ge n^{-c}$.

• Two ensembles of random variables $\mathcal {X}=\{X_{i}\}_{n\in \mathbb {N}, i \in I_n}$, $\mathcal {Y}=\{Y_{i}\}_{n\in \mathbb {N}, i \in I_n}$ over the same set of indices $I = \bigcup _{n\in \mathbb {N}}I_n$ are said to be computationally indistinguishable, denoted by $\mathcal {X}\approx _{c} \mathcal {Y}$, if for every polynomial-size distinguisher $D=\left\{ D_n\right\} _{n\in \mathbb {N}}$ there exists a negligible function $\mu (\cdot )$ such that for all $n\in \mathbb {N}, i \in I_n$,

  $$\begin{aligned} \mathbb {E} D(X_i) - \mathbb {E} D(Y_i) \le \mu (n). \end{aligned}$$

  The ensembles are statistically indistinguishable if the above holds also for unbounded (rather than polynomial-size distinguishers).

• For a finite set S, denote by $x\leftarrow S$ the process of uniformly sampling $x$ from S.

• For a distribution X, we denote by $x\in X$ the fact that $x$ is in the support of X.

Let $\mathcal {R}=\left\{ (\varphi , \omega )\right\}$ be a relation. Denote by $\mathcal {L}(\mathcal {R})$ the corresponding language:

For any $\varphi$, we denote by $\mathcal {R}(\varphi )$ the set of witnesses corresponding to $\varphi$:

2.1 Hard on Average Relations

We define hard-on-average problems with solved instance and co-instance samplers. Such a hard problem is given by two efficient samplers Y, N and corresponding $\text{ NP }$ relations $\mathcal {R}_Y,\mathcal {R}_N$. Y outputs yes-instances along with a witness and N outputs no-instances along with a witness. The two types of instances are computationally indistinguishable.

Definition 1 (Hard on Average Problem)

A hard-on-average problem consists of $\text{ PPT }$ samplers Y, N supported on $\text{ NP }$ relations $\mathcal {R}_Y,\mathcal {R}_N$. We require

• 1. Disjointness: $\mathcal {L}(\mathcal {R}_Y) \cap \mathcal {L}(\mathcal {R}_N) = \emptyset$.

• 2. Indistinguishability:

  

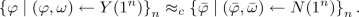
The notion is, in fact, equivalent to non-interactive commitments, but will be useful for presenting our constructions of generalized weakly extractable one-way functions, in a conceptually clear manner. To see this equivalence, we can consider the two $\text{ NP }$ languages corresponding to commitments of 0 and 1, and consider their respective relations. Analogously, we can construct commitments, where committing to 1 is done by sampling from Y, and committing to 0 is done by sampling from N.

2.2 Non-interactive Commitments

Definition 2

(Non-interactive Commitment [Blu81]). A non-interactive commitment scheme consists of a polynomial-time commitment algorithm $\textit{Com}(x;r)$ that given a message $x\in \{0,1\}^*$ and randomness $r\in \{0,1\}^n$ outputs a commitment c. We make the following requirements:

• 1. Perfect Binding: For every security parameter $n\in \mathbb {N}$, and string $c\in \{0,1\}^{*}$ there exists at most a single $x\in \{0,1\}^{*}$ such that c is a commitment to $x$:

  

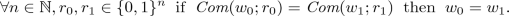
• 2. Computational Hiding: for any sequence $\mathcal {I}=\left\{ n\in \mathbb {N}, w_0, w_1 \in \{0,1\}^{\mathrm {poly}(n)}\right\}$:

  $$\begin{aligned} \left\{ c_0: \begin{array}{c} r\leftarrow \{0,1\}^{n}\\ c_0 \leftarrow \textit{Com}(w_0;r)\end{array}\right\} _{(n,w_0,w_1) \in \mathcal {I}} \approx _c \left\{ c_1: \begin{array}{c} r\leftarrow \{0,1\}^{n}\\ c_1 \leftarrow \textit{Com}(w_1;r)\end{array}\right\} _{(n,w_0,w_1) \in \mathcal {I}}. \end{aligned}$$

Non-interactive commitments can be constructed from any injective one-way function (or a certifiable collection thereof) [Blu81].

2.3 Zero-Knowledge and Witness Indistinguishable Protocols

Throughout, for an interactive protocol between a prover P and verifier V (one of which possibly malicious), we denote by $\langle P(\omega ),V \rangle (\varphi )$ the transcript of an interaction with prover private input $\omega$ (possibly empty), and common input $\varphi$. We denote by $\textit{Acc}/\textit{Rej}\overset{\mathrm {out}}{\leftarrow }\langle P(\omega ),V \rangle (\varphi )$ the output of the (honest) verifier.

Definition 3 (Zero-Knowledge Arguments)

We say that a pair of interactive PPT machines $\langle P{},V{} \rangle$ is a zero-knowledge argument system for a NP relation $\mathcal {R}$ if the following holds:

• 1. Completeness: For every element $\varphi \in \mathcal {L}(\mathcal {R})$, and a witness $\omega \in \mathcal {R}(\varphi )$:

  $$ \underset{}{\Pr } \left[ \textit{Acc}\overset{\mathrm {out}}{\leftarrow }\langle P{(\omega )},V{} \rangle (\varphi )\right] =1. $$

• 2. Soundness: For any family of polynomial-size circuits ${P}^*= \left\{ {P}^*_n\right\} _n$, and every $\varphi \in \{0,1\}^n\setminus \mathcal {L}$:

  $$ \underset{}{\Pr } \left[ \textit{Acc}\overset{\mathrm {out}}{\leftarrow }\langle P{^*_n},V{} \rangle (\varphi )\right] \le \mathrm {negl}(n). $$

• 3. Zero Knowledge: There exists a PPT simulator $S$ such that for any non-uniform family of polynomial-size circuits ${V}^*=\left\{ {V}^*_n\right\} _n$,

  $$ \left\{ \langle P(\omega ),{V}^*_n \rangle (\varphi )\right\} _{\varphi ,\omega } \approx _c \left\{ S({V}^*_n,\varphi )\right\} _{\varphi ,\omega } , $$

  where $(\varphi ,\omega )\in \mathcal {R}$ and $\left| \varphi \right| = n$.

  The argument is statistical zero knowledge if the above indistinguishability is statistical (rather than computational).

The protocol is publicly verifiable is the verifier’s decision can be determined solely from the protocol’s transcript (without the private coins of the verifier).

Definition 4 (Argument of Knowledge)

An argument system $\langle P{},V{} \rangle$ is an argument of knowledge for a relation $\mathcal {R}$ if there exists a PPT extractor $\mathcal {E}$ such that for any non-uniform family of polynomial-size circuits ${P}^*= \left\{ {P}^*_n\right\} _{n\in \mathbb {N}}$, any noticeable function $\varepsilon (n)$, any $n\in \mathbb {N}$, and any $\varphi \in \{0,1\}^n$:

$$\begin{aligned}&\text {if} \qquad \underset{}{\Pr } \left[ \textit{Acc}\overset{\mathrm {out}}{\leftarrow }\langle P{^*_n},V{} \rangle (\varphi )\right] = \varepsilon (n) \\&\text {then } \\&\qquad \begin{array}{l} \underset{}{\Pr } \left[ \begin{array}{l} \omega \leftarrow \mathcal {E}^{{P}^*_n}(1^{1/\varepsilon (n)},\varphi ) \\ \omega \in \mathcal {R}(\varphi ) \end{array} \right] \ge \varepsilon (n) -\mathrm {negl}(n) \end{array} . \end{aligned}$$

2.4 Offline-Online Witness Indistinguishable Arguments

An offline-online interactive argument is a protocol $\langle P{},V{} \rangle$ that can be divided into two phases: an offline phase independent of the proven statement, and an online phase where the statement (and witness) become available and the proof is completed. We define such witness-indistinguishable arguments (and arguments of knowledge). Our formal definition follows that of [BP19]. Below, we consider sub-protocols $\langle \textsf {off}{P},\textsf {off}{V} \rangle (1^n)$ where both prover and verifier may have an output; we denote this by $(O_P,O_V) \overset{\mathrm {out}}{\leftarrow }\langle \textsf {off}P,\textsf {off}V \rangle (1^n)$.

Definition 5 (Offline-Online Witness-Indistinguishable Arguments)

An interactive protocol $\langle P{},V{} \rangle$ is an offline-online witness-indistinguishable argument for an NP relation $\mathcal {R}$ if it consists of two sub-protocols $P=(\textsf {off}P ,\textsf {on}P),V=(\textsf {off}V ,\textsf {on}V)$, that satisfy:

• 1. Completeness: For any $(\varphi ,\omega )\in \mathcal {R}$ where $\left| \varphi \right| =n$:

  

• 2. Adaptive Soundness: For any non-uniform family of polynomial-size circuits ${P}^*=\left\{ \textsf {off}{P}^*_n,\textsf {on}{P}^*_n\right\} _{n}$, and for all $n\in \mathbb {N}$:

  

  where $\varphi \notin \mathcal {L}$ and $\left| \varphi \right| = n$.

• 3. Adaptive Witness-Indistinguishability For any non-uniform family of polynomial size circuits ${V}^*=\left\{ {V}^*_n\right\} _n$, all $n\in \mathbb {N}$:

  

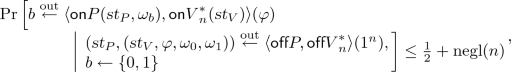
  where $(\varphi ,\omega _0),(\varphi ,\omega _1)\in \mathcal {R}$ and $\left| \varphi \right| = n$.

Definition 6 (Adaptive Argument of Knowledge)

We say that the system is an Adaptive Argument of Knowledge if there exists a PPT extractor $\mathcal {E}$ such that for any non-uniform family of polynomial-size circuits ${P}^*=\left\{ \textsf {off}{P}^*_n,\textsf {on}{P}^*_n\right\} _{n\in \mathbb {N}}$, and for all $n\in \mathbb {N}$:

where $\left| \varphi \right| =n$. This further holds for randomized circuits $\textsf {off}{P}^*,\textsf {on}{P}^*$, provided that the first prover message of $\textsf {off}P$ is deterministic.³

Assuming non-interactive commitments, there exist three-message systems as the one defined above that are adaptive arguments of knowledge, and have two offline (prover and verifier) messages and a single online (prover) message [FLS90].

Two-message systems (that are only sound) are known under a variety of assumptions like trapdoor permutations, or concrete number-theoretic or lattice assumptions (e.g. [DN00, GOS06, KKS18]).

2.5 Secure Function Evaluation

We define two-message secure function evaluation.

Definition 7 (Two-Message Secure Function Evaluation Scheme)

A secure function evaluation scheme consists of three algorithms $(\textit{Enc},\textit{Dec},\textit{Eval})$, where $\textit{Enc},\textit{Eval}$ are probabilistic and $\textit{Dec}$ is deterministic, satisfying:

• 1. Correctness: For any $n\in \mathbb {N}$, $x\in \{0,1\}^{n}$ and circuit C:

  $$ \underset{}{\Pr } \left[ \textit{Dec}_\textit{sk}(\widehat{\textit{ct}})=C(x) \mid (\textit{sk},\textit{ct})\leftarrow \textit{Enc}(x), \widehat{\textit{ct}}\leftarrow \textit{Eval}(\textit{ct},C)\right] = 1 . $$

• 2. Semantic Security:

  $$ \left\{ \textit{ct}\mid (\textit{sk},\textit{ct})\leftarrow \textit{Enc}(w_0)\right\} _{n,w_0,w_1} \approx _c \left\{ \textit{ct}\mid (\textit{sk},\textit{ct})\leftarrow \textit{Enc}(w_1)\right\} _{n,w_0,w_1}, $$

  where $n\in \mathbb {N}, w_0,w_1\in \{0,1\}^n$.

• 3. Circuit Privacy:

  $$ \left\{ \textit{Eval}(\textit{ct},C_0)\right\} _{n,C_0,C_1,\textit{ct}} \approx _c \left\{ \textit{Eval}(\textit{ct},C_1)\right\} _{n, C_0,C_1,\textit{ct}}, $$

  where $n\in \mathbb {N}$, $C_0,C_1\in \{0,1\}^{\mathrm {poly}(n)}$ compute the same function, and $ct\in \{0,1\}^{\ell (n)}$, where $\ell (n)$ is the size of encryptions of messages of length $n$.

Such secure function evaluation schemes are known from a variety of assumptions such as DDH [NP01] and LWE [BD18].

3 Extractable-One Way Functions: A New Definition

In this section, we provide our new definition of extractable one-way functions against adversaries with arbitrary polynomial-size non-uniform advice. We start by recalling the concept of generalized extractable one-way functions (GEF) [BCPR16], which considers general (hard) relations, rather than the specific preimage relation. We then present our new definition of generalized weakly extractable one-way functions (GWEF).

Definition 8

(GEF [BCPR16]). A polynomial-time computable family of functions

$$ \mathcal {F}=\left\{ f_{k}:\{0,1\}^{\ell (n)}\rightarrow \{0,1\}^{\ell '(n)}\mid n\in \mathbb {N}, k\in \{0,1\}^{m(n)}\right\} , $$

associated with an efficient key sampler $K$, is a generalized extractable one-way function with respect to a polynomial-time relation $\mathcal {R}^\mathcal {F}$ if the following holds:

• 1. $\mathcal {R}^\mathcal {F}$-Hardness: For any non-uniform family of polynomial-size circuits $A=\left\{ A_n\right\} _n$ and every $n\in \mathbb {N}$,

  $$\begin{aligned} \underset{}{\Pr } \left[ (f_{k}(x),x')\in \mathcal {R}^\mathcal {F}_{k}\mid k\leftarrow K(1^n), x\leftarrow \{0,1\}^{\ell (n)}, x' \leftarrow A_n(k,f_{k}(x)) \right] \\ \le \mathrm {negl}(n) . \end{aligned}$$

• 2. $\mathcal {R}^\mathcal {F}$-Extractability: There exists a $\text{ PPT }$ extractor $\mathcal {E}$ such that for any non-uniform family of polynomial size circuits $A=\left\{ A_n\right\} _n$ and every $n\in \mathbb {N}$,

  

Definition 9 (Privately Verifiable GEF)

A GEF is (only) privately verifiable if the relation $\mathcal {R}^\mathcal {F}_k$ is not necessarily polynomial-time, but there exists a polynomial-time tester $\mathcal {M}$ such that for any $(k,x,x')$:

$$\begin{aligned} \mathcal {M}(k,x,x')=1 \quad \textit{ iff }\quad (f_{k}(x),x')\in \mathcal {R}^\mathcal {F}_{k}. \end{aligned}$$

On the Amount of Non-uniformity. The definition of [BCPR16] also considers $\text{ PPT }$ adversaries with bounded non-uniform advice. In contrast, the above definition is formulated for non-uniform circuit adversaries of arbitrary polynomial size, which is equivalent to considering $\text{ PPT }$ adversaries with arbitrary polynomial-size non-uniform advice. As discussed in the introduction, while security against such adversaries is the gold standard in cryptography, such extractable functions are shown in [BCPR16] to be impossible assuming indistinguishability obfuscation.

The New Definition for Arbitrary Non-uniformity. The main relaxation we introduce in order to overcome the impossibility is to only require that extraction holds with respect to simulated keys, indistinguishable from real keys. That is, we allow the extractor to also simulate the key, for which it may use the code of the adversary.

Having relaxed extraction, we also strengthen the hardness requirement—we ask that one-wayness holds with respect to any key from a predefined set of valid keys $\mathcal {L}({\mathcal {K}})$, certifiable by an NP relation $\mathcal {K}$, rather than only when the key is chosen at random by the (real) key sampler. (As noted in the introduction, without this strengthening, extraction relative to extractor-simulated keys becomes trivial, assuming trapdoor one-way functions. Indeed, this stronger form of one-wayness will be crucial for the application of three-message zero-knowledge.) We shall require that the simulated keys are also valid and are generated by the extractor along with an NP certificate for their validity.

Definition 10 (GWEF)

An efficiently computable family of functions

$$ \mathcal {F}=\left\{ f_{k}:\{0,1\}^{\ell (n)}\rightarrow \{0,1\}^{\ell '(n)}\mid n\in \mathbb {N}, f_{k}\in \{0,1\}^{m(n)}\right\} , $$

associated with an efficient key sampler $K$ and NP relation $\mathcal {K}$, is a generalized weakly extractable one-way function with respect to a polynomial-time relation $\mathcal {R}^\mathcal {F}$ if the following holds:

• 1. Worst-case $\mathcal {R}^\mathcal {F}$-Hardness: For any non-uniform family of polynomial-size circuits $A=\left\{ A_n\right\} _n$, every $n\in \mathbb {N}$, and every $k\in \mathcal {L}({\mathcal {K}})\cap \{0,1\}^{m(n)}$,

  $$ \underset{}{\Pr } \left[ (f_{k}(x),x')\in \mathcal {R}^\mathcal {F}\mid x\leftarrow \{0,1\}^{\ell (n)}, x' \leftarrow A_n(k,f_{k}(x)) \right] \le \mathrm {negl}(n) . $$

• 2. Weak $\mathcal {R}^\mathcal {F}$-Extractability: There exists a $\text{ PPT }$ extractor $\mathcal {E}$ such that for any non-uniform family of polynomial-size circuits $A=\left\{ A_n\right\} _n$, we have:

  • (a) Extraction: For all $n\in \mathbb {N}$,

    

  • (b) Key Indistinguishability:

    $$\begin{aligned}\left\{ k\mid k\leftarrow K(1^n)\right\} _{n} \approx _c \left\{ k\mid (k,v,x') \leftarrow \mathcal {E}(1^n,A_n)\right\} _{n}. \end{aligned}$$

  • (c) Validity: For all $n\in \mathbb {N}$,

    $$\begin{aligned}\underset{k,v,x' \leftarrow \mathcal {E}(1^n,A_n)}{\Pr } \left[ (k,v) \in \mathcal {K}\right] \ge 1- \mathrm {negl}(n). \end{aligned}$$

Remark 1 (On Validity of Keys)

We note that we do not insist that random keys sampled by $K$ are valid. Indeed, requiring this is typically not useful in settings where keys are not necessarily generated by trusted parties. We note, however, that due to key-indistinguishability, it is possible to add this additional requirement generically, by having the $K(1^n)$ sample using $\mathcal {E}(1^n,C_n)$, for any fixed circuit $C_n$.

3.1 Privately Verifiable GWEF

We now turn to define private-verifiable GWEF. Here we relax the definition even further, allowing that simulated keys generated by the extractor are not necessarily valid. Rather, we require that there exists another extractor $\widetilde{\mathcal {E}}$ that does output valid keys, and such that the key $k$ and extracted $w$ sampled by $\widetilde{\mathcal {E}}$ are indistinguishable from those sampled by $\mathcal {E}$. However, $\widetilde{\mathcal {E}}$, may not necessarily succeed in producing $w$ that satisfies the relation $\mathcal {R}^\mathcal {F}_k$.

We present the definition, and then further discuss the intuition behind it.

Definition 11 (Privately Verifiable GWEF)

A GWEF is (only) privately verifiable if the relation $\mathcal {R}^\mathcal {F}_k$ is not necessarily polynomial-time, but there exists a polynomial-time tester $\mathcal {M}(k,x,w)$ for $(f_{k}(x),w)\in \mathcal {R}^\mathcal {F}_{k}$ as in Definition 9.

In addition, Weak $\mathcal {R}^\mathcal {F}$-Extractability is augmented.

Weak $\mathcal {R}^\mathcal {F}$-Extractability: There exist $\text{ PPT }$ extractors $\mathcal {E},\widetilde{\mathcal {E}}$ such that for any non-uniform family of polynomial size circuits $A=\left\{ A_n\right\} _n$, we have:

• 1. Extraction: For all $n\in \mathbb {N}$,

  

• 2. Key Indistinguishability:

  $$\begin{aligned}\left\{ k\mid k\leftarrow K(1^n)\right\} _{n} \approx _c \left\{ k\mid (k,w) \leftarrow \mathcal {E}(1^n,A_n)\right\} _{n}. \end{aligned}$$

• 3. $\widetilde{\mathcal {E}}$-Validity: For all $n\in \mathbb {N}$,

  $$\begin{aligned}\underset{}{\Pr } \left[ (k,v) \in \mathcal {K}\mid (k,v,w) \leftarrow \widetilde{\mathcal {E}}(1^n,A_n) \right] \ge 1- \mathrm {negl}(n). \end{aligned}$$

• 4. Extractor Indistinguishability:

  $$\begin{aligned} \left\{ k,w\mid (k,w) \leftarrow \mathcal {E}(1^n,A_n)\right\} _{n} \approx _c \left\{ k,w\mid (k,v,w) \leftarrow \widetilde{\mathcal {E}}(1^n,A_n)\right\} _{n}. \end{aligned}$$

More on the Definition. In the setting of privately verifiable GWEF, where testing a solution $w$ for $y$ requires private information (a preimage), there are two knowledge-related questions: (1) the usual one: must the adversary know a solution for the produced image $y$? but also (2) can it even recognize such a solution? The definition we consider essentially says that if the adversary can generate an image $y$, for which it can verify solutions, then it must also know a solution. If it cannot even verify a solution, we only require that the extractor generates $w$ that the adversary cannot distinguish from a solution.

4 From Three-Message ZK to GWEF

In this section, we present our constructions of generalized weakly extractable one-way functions from three-message zero-knowledge arguments.

4.1 Publicly Verifiable GWEF

In this section, we construct publicly verifiable three-message zero-knowledge protocols from GWEF.

Theorem 4

Assuming publicly verifiable three-message zero-knowledge argument system for NP and non-interactive commitments, there exists a GWEF.

Ingredients and Notation:

• $\mathcal {H}= (Y,N,\mathcal {R}_Y,\mathcal {R}_N)$, a hard-on-average problem with solved instances and co-instances. (Recall that such problems follow from non-interactive commitments.)

• $\langle P{},V{} \rangle$, a ZK argument system for $\mathcal {R}_Y$. We denote the protocol’s messages by $\mathsf {zk}_1, \mathsf {zk}_2, \mathsf {zk}_3$.

We now define our GWEF $\mathcal {F}$ with associated key sampler $K$, key-relation $\mathcal {K}$, and hard relation $\mathcal {R}^\mathcal {F}$. These are given in Fig. 1.

Fig. 1.

GWEF

4.1.1 Security Analysis.

We now show that the described function family $\mathcal {F}$ (and associated $K,\mathcal {K},\mathcal {R}^\mathcal {F}$) satisfy the requirements of a $\text{ GWEF }$.

Hardness. We show hardness based on the soundness of the argument system and disjointness property of $\mathcal {H}$.

Proposition 1

$\mathcal {F}$ satisfies $\mathcal {R}^\mathcal {F}$-hardness.

Proof

Assume toward contradiction there exists a family of polynomial-size circuits $A=\left\{ A_n\right\} _n$ and a noticeable function $\varepsilon (n)$, such that for infinitely many $n$, there exists a valid key $k=(\bar{\varphi },\mathsf {zk}_1)\in \mathcal {L}({\mathcal {K}})$, such that

That is, parsing $y= \mathsf {zk}_2, x' = \mathsf {zk}_3$, the transcript $(\mathsf {zk}_1,\mathsf {zk}_2,\mathsf {zk}_3)$ is accepting with respect to statement $\bar{\varphi }$.

We construct a corresponding prover ${P}^*=\left\{ {P}^*_n\right\} _n$ (Fig. 2) that convinces the verifier of accepting the statement $\bar{\varphi }$ with probability $\varepsilon (n)-\mathrm {negl}(n)$. Since $k\in \mathcal {K}$, it holds that $\bar{\varphi }\in \mathcal {L}(\mathcal {R}_N)$. By the disjointness property of $\mathcal {H}$, this means that $\bar{\varphi }\notin \mathcal {L}(\mathcal {R}_Y)$ and thus, ${P}^*$ will violate the soundness of the underlying argument system.

Fig. 2.

ZK malicious prover GWEF

Note that the view of $A_n$ when emulated by ${P}^*_n$ is identical to its view when breaking the hardness of $\mathcal {R}^\mathcal {F}$. Thus ${P}^*_n$ convinces the verifier of accepting the false statement with probability $\varepsilon (n)-\mathrm {negl}(n)$.

Weak Extractability. We now prove weak extractability, based on the zero-knowledge and completeness properties of the argument system and indistinguishability of $\mathcal {H}$.

Proposition 2

$\mathcal {F}$ satisfies weak extractability.

Proof

We start by defining the extractors $\mathcal {E}$, which is described in Fig. 3.

Fig. 3.

GWEF extractor

We prove the three properties—extraction, key-indistinguishability and validity—required by weak extractability (Definition 10). From hereon, fix a family of polynomial size circuits $A= \left\{ A_n\right\} _n$.

Claim (Extraction)

For all $n\in \mathbb {N}$,

Proof

We start by recalling that whenever $y$ is in the image of $f_{k}$, it is the case that $y=\mathsf {zk}_2$, such that $\mathsf {zk}_2$ is the response of the honest verifier to $\mathsf {zk}_1$, using some randomness $r$, where $\mathsf {zk}_1$ is given by the key $k=(\varphi ,\mathsf {zk}_1)$.

Our goal is to show that except with negligible probability, the extractor produces $\mathsf {zk}_3$, such that the simulated transcript $(\mathsf {zk}_1,\mathsf {zk}_2,\mathsf {zk}_3)$ is accepting with respect to statement $\bar{\varphi }$. We show that this follows from the zero-knowledge and completeness of the underlying argument, and the hardness of the language $\mathcal {H}$.

To see this, consider an alternative experiment where $(\varphi ,\omega )$ are sampled from the yes-instances sampler Y. From the ZK guarantee of the simulator, the generated transcript is computationally indistinguishable from the honest interaction. Note that by the (perfect) completeness of the zero-knowledge argument, whenever $A_n(k)$ outputs $y=\mathsf {zk}_2$ in the image of $f_{k}$, the interaction results in an accepting transcript. By the zero-knowledge property, it follows that except with negligible probability, the simulator also generates accepting transcripts whenever $A_n$ outputs $y$ in the image of $f_{k}$.

It is left to note that from the indistinguishability of the hard samplers Y, N, the simulated transcripts of the experiment are indistinguishable from the ones used by the extractor. Therefore they are accepting with the same probability, and thus $\mathcal {E}$ successfully extracts $x'$ such that $(y,x')\in \mathcal {R}^\mathcal {F}_k$, as required.

Claim (Key Indistinguishability)

$$\begin{aligned} \left\{ k\mid k\leftarrow K(1^n)\right\} _{n} \approx _c \left\{ k\mid (k,v,x') \leftarrow \mathcal {E}(1^n,A_n)\right\} _{n}. \end{aligned}$$

Proof

Recall that $k= (\varphi ,\mathsf {zk}_1)$ where the statement $\varphi$ is sampled from $Y(1^n)$ in the key sampler, and from $N(1^n)$ in the simulated case. Consider the hybrid experiment where $\varphi$ is sampled from $Y(1^n)$ in the simulated case. The message $\mathsf {zk}_1$ is then sampled from $S(V_0,\varphi )$, where $V_0$ is the honest verifier with hardwired randomness $0^n$, by the key sampler, and from $S({V}^*,\varphi )$, where ${V}^*$ is the verifier constructed from $A_n$, by the hybrid extractor. Using zero-knowledge guarantee, and the fact that the honest prover’s first message $\mathsf {zk}_1$ is independent of the verifier, we have:

where throughout $\varphi \leftarrow Y(1^n)$.

From the hardness of the samplers, Y-instances are indistinguishable from N- instances, and therefore the simulated transcripts are distinguishable. The extractor indistinguishability follows.

Claim (Validity)

For all $n\in \mathbb {N}$:

$$ \underset{}{\Pr } \left[ (k,v)\in \mathcal {K}\mid (k,v,x')\leftarrow \mathcal {E}(1^n,A_n)\right] \ge 1 -\mathrm {negl}(n). $$

Recall that $\mathcal {E}$ always samples $(\bar{\varphi },\bar{\omega }) \leftarrow N(1^n)$ and sets $k= (\bar{\varphi },\mathsf {zk}_1)$ and $v= \bar{\omega }$. Thus $(k,v)\in \mathcal {K}$ by definition.

4.2 Privately Verifiable GWEF

In this section, we construct privately verifiable GWEF from privately verifiable three-message zero knowledge protocols.

Theorem 5

Assuming privately verifiable three-message statistical zero-knowledge argument system for NP and non-interactive commitments, there exists a privately verifiable GWEF.

Adjustments from GWEF. In this construction we use privately verifiable ZK, rather than publicly verifiable one. Therefore, unlike the previous construction, the verifier’s randomness is required in order to efficiently decide whether the transcript is accepting or not. To overcome it, SZK is needed. This will guarantee that the simulated transcripts are indeed accepting (and are not simply hard to distinguish). Note that the definition of the privately GWEF extractor is relaxed as well, allowing two different extractors. One of which will guarantee extraction, and will use the ZK simulator on true statements, and the other will guarantee validity, and will use false statements. From the hardness of the problem $\mathcal {H}$, both extractors will be indistinguishable, as required.

Ingredients and Notation:

• $\mathcal {H}= (Y,N,\mathcal {R}_Y,\mathcal {R}_N)$, a hard-on-average problem with solved instances and co-instances. (Recall that such problems follow from non-interactive commitments.)

• $\langle P{},V{} \rangle$, an SZK argument system for $\mathcal {R}_Y$. We denote the protocol’s messages by $\mathsf {zk}_1, \mathsf {zk}_2, \mathsf {zk}_3$.

• $\textit{Com}$, a non-interactive string commitment scheme.

We now define our privately verifiable GWEF $\mathcal {F}$ with associated key sampler $K$, key-relation $\mathcal {K}$, hard relation $\mathcal {R}^\mathcal {F}$, and corresponding tester $\mathcal {M}$. These are given in Fig. 4.

Fig. 4.

Privately verifiable GWEF

4.2.1 Security Analysis

We now show that the described function family $\mathcal {F}$ (and associated $K,\mathcal {K},\mathcal {R}^\mathcal {F}, \mathcal {M}$) satisfy the requirements of a $\text{ GWEF }$.

Hardness. We show hardness based on the soundness of the argument system, disjointness property of $\mathcal {H}$, and hiding of the commitment scheme.

Proposition 3

$\mathcal {F}$ satisfies $\mathcal {R}^\mathcal {F}$-hardness.

Proof

Assume toward contradiction there exists a family of polynomial-size circuits $A=\left\{ A_n\right\} _n$ and a noticeable function $\varepsilon (n)$, such that for infinitely many $n$, there exists a valid key $k=(\bar{\varphi },\mathsf {zk}_1)\in \mathcal {L}({\mathcal {K}})$, such that

That is, parsing $y= (\mathsf {zk}_2,c),x= (r,r'), x' = \mathsf {zk}_3$, the verifier $V$ accepts $(\mathsf {zk}_1,\mathsf {zk}_2,\mathsf {zk}_3)$ with respect to statement $\bar{\varphi }$ and verifier randomness $r$.

We construct a corresponding prover ${P}^*=\left\{ {P}^*_n\right\} _n$ (Fig. 5) that convinces the verifier of accepting the statement $\bar{\varphi }$ with probability $\varepsilon (n)-\mathrm {negl}(n)$. Since $k\in \mathcal {K}$, it holds that $\bar{\varphi }\in \mathcal {L}(\mathcal {R}_N)$. By the disjointness property of $\mathcal {H}$, this means that $\bar{\varphi }\notin \mathcal {L}(\mathcal {R}_Y)$ and thus, ${P}^*$ will violate the soundness of the underlying argument system.

Fig. 5.

ZK malicious prover GWEF

We then consider a hybrid experiment in which the prover ${P}^*_{n}$ obtains a commitment c to the verifier’s randomness $r$, rather than simulating the commitment c as a commitment to $0^n$ on its own. By the hiding of the commitment, the prover in this hybrids experiment convinces the verifier of accepting with the same probability as in a real interaction up to a negligible difference $\mathrm {negl}(n)$.

It is left to note that the view of $A_n$ when emulated by ${P}^*_n$ in this hybrid experiment is identical to its view, when breaking the hardness of $\mathcal {R}^\mathcal {F}$. Thus in the hybrids experiment, the verifier is convinces with probability $\varepsilon (n)$.

It follows that in a real interaction ${P}^*_n$ convinces the verifier of accepting the false statement with probability $\varepsilon (n)-\mathrm {negl}(n)$.

Weak Extractability. We now prove weak extractability, based on the statistical zero-knowledge and completeness properties of the argument system, indistinguishability of $\mathcal {H}$, and binding of the commitment $\textit{Com}$.

Proposition 4

$\mathcal {F}$ satisfies weak extractability.

Proof

We start by defining the extractors $\mathcal {E},\widetilde{\mathcal {E}}$. These are described in Fig. 6.

Fig. 6.

GWEF extractors

We now prove the four properties—extraction, key-indistinguishability, $\widetilde{\mathcal {E}}$-validity, and extractor-indistinguishability—required by weak extractability (Definition 11). From hereon, fix a family of polynomial size circuits $A= \left\{ A_n\right\} _n$.

Claim (Extraction)

For all $n\in \mathbb {N}$,

Proof

We start by recalling that whenever $y$ is in the image of $f_{k}$, it is the case that $y=(\mathsf {zk}_2,c)$, such that:

• $\mathsf {zk}_2$ is the response to $\mathsf {zk}_1$ of the honest verifier, using some randomness $r$, where $\mathsf {zk}_1$ is given by $k=(\varphi ,\mathsf {zk}_1)$.

• c is a commitment to the verifier randomness $r$.

Our goal is to show that except with negligible probability, whenever this occurs, the extractor produces $\mathsf {zk}_3$, such that the honest verifier accepts the simulated $(\mathsf {zk}_1,\mathsf {zk}_2,\mathsf {zk}_3)$ with respect to statement $\varphi$ and randomness $r$. We show that this follows from the statistical zero-knowledge and completeness of the underlying argument.

To see this, consider an alternative experiment where $\mathsf {zk}_1,\mathsf {zk}_3$ are generated by the honest zero knowledge prover $P(\varphi )$. Note that by the (perfect) completeness of the zero-knowledge argument, in this experiment, whenever $A_n(k)$, where $k=(\varphi ,\mathsf {zk}_1)$, outputs $y=(\mathsf {zk}_2,c)$ in the image of $f_{k}$, the prover outputs a message $\mathsf {zk}_3$ such that the corresponding transcript $(\mathsf {zk}_1,\mathsf {zk}_2,\mathsf {zk}_3)$ is accepting with respect to the corresponding verifier randomness $r$, which by the binding of $\textit{Com}$ is uniquely defined by the commitment c.

By statistical zero knowledge, it follows that except with negligible probability $\mathrm {negl}(n)$, the simulator also generates accepting transcripts whenever $A_n$ outputs $y$ in the image of $f_{k}$. In this case, $\mathcal {E}$ successfully extracts $x'$ such that $(y,x')\in \mathcal {R}^\mathcal {F}_k$, as required.

Claim (Key Indistinguishability)

$$\begin{aligned}\left\{ k\mid k\leftarrow K(1^n)\right\} _{n} \approx _c \left\{ k\mid (k,x') \leftarrow \mathcal {E}(1^n,A_n)\right\} _{n}. \end{aligned}$$

Proof

Recall that $k= (\varphi ,\mathsf {zk}_1)$ where the statement $\varphi$ is sampled from $Y(1^n)$ in both distributions. The message $\mathsf {zk}_1$ is sampled from $S(V_0,\varphi )$, where $V_0$ is the honest verifier with hardwired randomness $0^n$, by $K$, and from $S({V}^*,\varphi )$, where ${V}^*$ is the verifier constructed from $A_n$, by $\mathcal {E}$.

Using zero-knowledge guarantee, and the fact that the honest prover’s first message $\mathsf {zk}_1$ is independent of the verifier, we have:

where throughout $\varphi \leftarrow Y(1^n)$.

Claim

($\widetilde{\mathcal {E}}$-Validity). For all $n\in \mathbb {N}$:

$$ \underset{}{\Pr } \left[ (k,v)\in \mathcal {K}\mid k,v,x'\leftarrow \widetilde{\mathcal {E}}(1^n,A_n)\right] \ge 1 -\mathrm {negl}(n) . $$

Proof

Recall that $\widetilde{\mathcal {E}}$ always samples $(\bar{\varphi },\bar{\omega }) \leftarrow N(1^n)$ and sets $k= (\bar{\varphi },\mathsf {zk}_1)$ and $v= \bar{\omega }$. Thus $(k,v)\in \mathcal {K}$ by definition with all but negligible probability.

Claim (Extractor Indistinguishability)

Proof

Observe that the extractors $\mathcal {E}$ and $\widetilde{\mathcal {E}}$ generate $(k,x')$ efficiently from $\varphi$ sampled using $Y(1^n)$ and $\bar{\varphi }$ sampled using $N(1^n)$, respectively. Thus, extractor indistinguishability follows from the indistinguishability of Y-instances from N-instances.

5 From GWEF to Three-Message ZK

In this section, we show that GWEF (with additional standard assumptions) are sufficient for constructing three-message zero-knowledge arguments.

5.1 Publicly Verifiable ZK

In this section, we construct publicly verifiable three-message zero-knowledge arguments from $\text{ GWEF }$s. The construction itself is mostly similar to previous constructions (e.g., [CD08, BCC+14]), but requires a new analysis, following the weaker extractability guarantee.

Theorem 6

Assume there exist GWEF, non-interactive commitments, and two-message witness indistinguishable arguments. Then there exists a publicly verifiable three-message ZK argument.

Ingredients and Notation:

• $\mathcal {F}$, a GWEF with associated key sampler $K$, valid key relation $\mathcal {K}$, and a hard relation $\mathcal {R}^\mathcal {F}$.

• $\textit{Com}$, a non-interactive string commitment scheme.

• $\langle (\textsf {off}P,\textsf {on}P), (\textsf {off}V,\textsf {on}V) \rangle$ an offline-online WIAOK system for NP with two offline messages and a single online message. (Recall that such systems follow from non-interactive commitments. We denote its corresponding messages by $\mathsf {wi}_1,\mathsf {wi}_2,\mathsf {wi}_3$)

• $\langle \textsf {on}P', (\textsf {off}V',\textsf {on}V') \rangle$ an offline-online WI system for NP with a single offline (verifier) message and a single online (prover) message. We denote its corresponding messages by $\mathsf {wi}'_1,\mathsf {wi}'_2$

The protocol is described in Fig. 7.

Security Analysis. The security analysis is omitted from this extended abstract and can be found in the full version of the paper.

5.2 Privately Verifiable ZK

In this section, we construct privately verifiable three-message zero-knowledge arguments from privately verifiable $\text{ GWEF }$s. The construction is similar to that of [BCPR16], but requires a new analysis, following the weaker extractability guarantee.

Theorem 7

Assume there exist privately verifiable GWEF and secure function evaluation. Then there exists a privately verifiable three-message ZK argument.

Adjustments from Public Verification. There are two main differences between this construction and the publicly verifiable one. First, as membership in $\mathcal {R}$ can no longer be tested efficiently given only $(y,x')$, it will be done homomorphically over the verifier’s encrypted input. Second, as membership is already tested homomorphically, the validity of the image can be tested in the same circuit, thus sparing the two-message WI used in the public version.

Ingredients and Notation:

• $\mathcal {F}$, a privately verifiable GWEF with associated a key sampler $K$, valid key relation $\mathcal {K}$, hard relation $\mathcal {R}^\mathcal {F}$ and an efficient tester $\mathcal {M}$. We denote by $\mathcal {M}_{k,y,x'}$ the augmented $\mathcal {R}^\mathcal {F}$-tester that on input $x$ returns 1 if either $y\ne f_{k}(x)$ or $\mathcal {M}(k,x,x')=1$.

• $(\textit{Enc},\textit{Dec},\textit{Eval})$, a secure function evaluation scheme.

• $\langle (\textsf {off}P,\textsf {on}P), (\textsf {off}V,\textsf {on}V) \rangle$ an offline-online WIAOK system for NP with two offline messages and a single online message. (Recall that such systems follow from non-interactive commitments, which in turn follow from secure function evaluation [LS19]).

The protocol is described in Fig. 8.

Fig. 7.

Privately verifiable three-message ZK protocol for $\mathcal {R}\in \text{ NP }$

Fig. 8.

Privately verifiable three-message ZK protocol for $\mathcal {R}\in \text{ NP }$

5.2.1 Security Analysis.

The completeness of the protocol follows readily from the completeness and correctness of the underlying primitives. We focus on proving that the protocols is an argument of knowledge and that it is zero knowledge.

Proposition 5 (Argument of Knowledge)

The protocol is an argument of knowledge (and in particular, sound). Specifically, there exists a PPT extractor $\text{ ZK }.\mathcal {E}$ such that for any non-uniform family of polynomial-size circuits ${P}^*= \left\{ {P}^*_n\right\} _{n\in \mathbb {N}}$, any noticeable function $\varepsilon (n)$, any $n\in \mathbb {N}$, and any $\varphi \in \{0,1\}^n$:

$$\begin{aligned}&\text {if} \qquad \underset{}{\Pr } \left[ \textit{Acc}\overset{\mathrm {out}}{\leftarrow }\langle P{^*_n},V{} \rangle (\varphi )\right] = \varepsilon (n) \\&\text {then } \\&\qquad \begin{array}{l} \underset{}{\Pr } \left[ \begin{array}{l} \omega \leftarrow \text{ ZK }.\mathcal {E}^{{P}^*_n}(1^{1/\varepsilon (n)},\varphi ) \\ \omega \in \mathcal {R}(\varphi ) \end{array} \right] \ge \varepsilon (n) -\mathrm {negl}(n) \end{array} . \end{aligned}$$

Proof

We define the extractor $\text{ ZK }.\mathcal {E}$ in Fig. 9.

Fig. 9.

Argument of knowledge extractor for the three-message ZK protocol

We now prove the validity of the extractor. Let ${P}^*= \left\{ {P}^*_n\right\} _{n\in \mathbb {N}}$ be a non-uniform family of polynomial-size circuits, and assume the for every $n$, there exists $\varphi$ such that ${P}^*_n$ convinces the verifier $V$ of accepting $\varphi$ with probability $\varepsilon (n)$. We prove that $\text{ ZK }.\mathcal {E}^{{P}^*_n}(1^{\varepsilon },\varphi )$ outputs $\omega \in \mathcal {R}(\varphi )$ with probability at least $\varepsilon (n)-\mathrm {negl}(n)$.

First note that each execution of $\text{ ZK }.\mathcal {E}$ perfectly emulates an interaction $\langle {P}^*_n,V \rangle (\varphi )$.

Claim

Let $\widehat{\textit{ct}}$ and $\varPsi$ be the evaluated cipher-text and statement induced by the execution of $\text{ ZK }.\mathcal {E}$. Then, with probability at least $\varepsilon (n)-\mathrm {negl}(n)$, the extracted witness $\omega$ satisfies $\varPsi$ and in addition $\textit{Dec}_\textit{sk}(\widehat{\textit{ct}})=1$.

Proof

Since $\text{ ZK }.\mathcal {E}$ perfectly emulates an interaction $\langle {P}^*_n,V \rangle (\varphi )$, the verifier $V$ accepts in the induced interaction with probability $\varepsilon (n)$. Whenever this occurs:

• The WI verifier $(\textsf {off}V,\textsf {on}V)$ accepts.

• It holds that $\textit{Dec}_{\textit{sk}}(\widehat{\textit{ct}})=1$.

Noting that the prover $(\textsf {off}{P}^*_n,\textsf {on}{P}^*_n)$ constructed by $\text{ ZK }.\mathcal {E}$ has a deterministic first message, it follows by the adaptive argument of knowledge guarantee of the WI system that except with negligible probability $\mathrm {negl}(n)$, whenever the WI verifier accepts, $\text{ WI }.\mathcal {E}$ succeeds in extracting a witness for $\varPsi$. The claim follows.

To complete the proof of Proposition 5, and conclude that the extracted $\omega$ is a witness for $\varPsi _1(\varphi ) = (\varphi \in \mathcal {L})$, we prove:

Claim

Except with negligible probability $\mathrm {negl}(n)$, either the extracted witness $\omega$ does not satisfy $\varPsi _2(k,y,\textit{ct},\widehat{\textit{ct}})$ or $\textit{Dec}_{\textit{sk}}(\widehat{\textit{ct}})\ne 1$.

Proof

Assume toward contradiction that for infinitely many $n$, the extracted witness $\omega$ satisfies $\varPsi _2$ and $\textit{Dec}_{\textit{sk}}(\widehat{\textit{ct}})=1$ with probability $\delta (n)$. That is, $\omega = (v,x')$ such that:

• $(k,v)\in \mathcal {K}$, the key is valid.

• $\widehat{\textit{ct}}\in \textit{Eval}(\textit{ct},\mathcal {M}_{k,y,x'})$, the cipher-text $\widehat{\textit{ct}}$ is a homomorphic evaluation of the augmented $\mathcal {R}^\mathcal {F}$-tester $\mathcal {M}_{k,y,x'}$.

The second condition implies that $\mathcal {M}(k,x,x')=1$, and accordingly $(y,x')\in \mathcal {R}^\mathcal {F}_{k}$. Indeed, recalling that $(\textit{ct},\textit{sk}) \in \textit{Enc}(x)$ and that $\textit{Dec}_\textit{sk}(\widehat{\textit{ct}})=1$, this follows from the correctness of the SFE scheme.

We now construct a polynomial-size adversary $A= \left\{ A_n\right\} _n$ that breaks the $\mathcal {R}^\mathcal {F}$-hardness of $\mathcal {F}$ with probability $\delta (n)-\mathrm {negl}(n)$, relative to the valid key $k$ (deterministically defined by the first prover message) (Fig. 10).

Fig. 10.

Adversary for the $\mathcal {R}^\mathcal {F}$ hardness

Claim

For infinitely many $n$,

Proof

To see this we first consider an alternative experiment, where $A_n$ also obtains an SFE encryption $\textit{ct}\leftarrow \textit{Enc}(x)$ of $x$ and uses it in the emulation of $\text{ ZK }.\mathcal {E}$, instead of using $\widetilde{\textit{ct}}$. We argue that in this alternative experiment, $A_n$ outputs $x'$ such that $(f_{k}(x),x')\in \mathcal {R}^\mathcal {F}_{k}$ with the same probability as in the original experiment up to a negligible difference $\mathrm {negl}(n)$.

Indeed, this follows directly from the semantic security of SFE encryptions. Any noticeable difference between the experiments directly leads to a distinguisher between encryptions of $0^{\ell (n)}$ and $x$. (Note that given $x$, we can efficiently test the condition $(f_{k}(x),x')\in \mathcal {R}^\mathcal {F}_{k}$, using $\mathcal {M}(f_{k}(x),x,x')$).

It is left to observe that in this alternative experiment the extractor $\text{ ZK }.\mathcal {E}$ is perfectly emulated, and thus by our assumption on $\text{ ZK }.\mathcal {E}$, $A_n$ it outputs the required $x'$ with probability at least $\delta (n)-\mathrm {negl}(n)$.

This complete the proof of Proposition 5.

Proposition 6 (Zero Knowledge)

The protocol $\langle P{},V{} \rangle$ is zero knowledge.

Proof

We start by describing the simulator $S$ in Fig. 11. In what follows, let $\mathcal {E},\widetilde{\mathcal {E}}$ be the GWEF extractors guaranteed by Definition 11.

Fig. 11.

Simulator for the three-message ZK protocol

We now prove the validity of the simulator $S$, using a sequence of hybrids.

$H_1$: The transcript $(\mathsf {zk}_1,\mathsf {zk}_2,\mathsf {zk}_3)$ is generated by $S$.

$H_2$: Instead of generating $\mathsf {wi}_3$, using the witness $(v,x')$ for $\varPsi _2$, it is generated using a witness $\omega$ for $\varPsi _1 = (\varphi \in \mathcal {L})$. We note that by the $\widetilde{\mathcal {E}}$-validity property of the $\text{ GWEF }$, $v\in \mathcal {K}(k)$ with overwhelming probability. Thus, like $\omega$, $(v,x')$ is also a valid witness for the statement $\varPsi$. By the adaptive witness-indistinguishability of the WI system, this hybrid is computationally indistinguishable from $H_1$.

$H_3$: Instead of generating $k,x'$ using $\widetilde{\mathcal {E}}$, we generate it using $\mathcal {E}$. By the extractor-indistinguishability, this hybrid is computationally indistinguishable from $H_2$.

$H_4$: Instead of generating $\widehat{\textit{ct}}\leftarrow \textit{Eval}(\textit{ct},\mathcal {M}_{k,y,x'})$, we generate $\widehat{\textit{ct}}\leftarrow \textit{Eval}(\textit{ct},\varvec{1})$. By the extraction guarantee of $\mathcal {E}$ we have that the probability that $y$ is in the image of $f_{k}$, but the extractor $\mathcal {E}$ fails to extract $x'\in \mathcal {R}^\mathcal {F}_k(y)$, is negligible. We observe that if it is the case that $y$ is in the image and $x'\in \mathcal {R}^\mathcal {F}_k(y)$, then by definition $\mathcal {M}_{k,y,x'} \equiv \varvec{1}$; indeed, for any preimage $x$ of $y$, it returns 1, since $\mathcal {M}(k,x,x')=1$, and for any $x$ that is not a preimage $\mathcal {M}_{k,y,x'} \equiv \varvec{1}$ returns 1. Furthermore, if $y$ is not in the image then no $x$ is a preimage and again $\mathcal {M}_{k,y,x'}\equiv \varvec{1}$. Since the two circuits are of equal size and compute the same function, the indistinguishability of the two hybrids follows by circuit privacy.

$H_5$: Here the transcript is generated as in a real interaction between $P$ and ${V}^*$. The only difference between this hybrids and the previous ones is that in this hybrid the GWEF key $f_{k}$ is sampled from $K(1^n)$ instead of by $\mathcal {E}$. Indistinguishability of the hybrids follows by the key-indistinguishability property.