Abstract
There has been a large body of work characterizing the round complexity of general-purpose maliciously secure two-party computation (\(\mathsf {2PC}\)) against probabilistic polynomial time adversaries. This is particularly true for zero-knowledge, which is a special case of \(\mathsf {2PC}\). In fact, in the special case of zero knowledge, optimal protocols with unconditional security against one of the two players have also been meticulously studied and constructed.
On the other hand, general-purpose maliciously secure \(\mathsf {2PC}\) with statistical or unconditional security against one of the two participants has remained largely unexplored so far. In this work, we initiate the study of such protocols, which we refer to as \(\mathsf {2PC}\) with one-sided statistical security. We settle the round complexity of \(\mathsf {2PC}\) with one-sided statistical security with respect to black-box simulation by obtaining the following tight results:
-
In a setting where only one party obtains an output, we design \(\mathsf {2PC}\) in 4 rounds with statistical security against receivers and computational security against senders.
-
In a setting where both parties obtain outputs, we design \(\mathsf {2PC}\) in 5 rounds with computational security against the party that obtains output first and statistical security against the party that obtains output last.
Katz and Ostrovsky (CRYPTO 2004) showed that \(\mathsf {2PC}\) with black-box simulation requires at least 4 rounds when one party obtains an output and 5 rounds when both parties obtain outputs, even when only computational security is desired against both parties. Thus in these settings, not only are our results tight, but they also show that statistical security is achievable at no extra cost to round complexity. This still leaves open the question of whether \(\mathsf {2PC}\) can be achieved with black-box simulation in 4 rounds with statistical security against senders and computational security against receivers. Based on a lower bound on computational zero-knowledge proofs due to Katz (TCC 2008), we observe that the answer is negative unless the polynomial hierarchy collapses.
This material is based on work supported in part by DARPA under Contract No. HR001120C0024. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the United States Government or DARPA.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Secure two-party computation allows two mutually distrustful participants to compute jointly on their private data without revealing anything beyond the output of their computation. Protocols that securely compute general functionalities have been constructed under a variety of assumptions, and with a variety of efficiency guarantees.
A fundamental question in the study of secure computation is round complexity. This question has been researched extensively, and even more so for the special case of zero-knowledge.
Zero-Knowledge. Computational zero-knowledge arguments with negligible soundness error can be achieved in 4 messages [19], under the minimal assumption that one-way functions exist [7]. This is tight: for languages outside BPP, with black-box simulation and without any trusted setup, zero-knowledge arguments require at least four messages [24].
For zero-knowledge with black-box simulation, different flavors have been studied depending on the level of soundness and zero knowledge achieved. Either property can be statistical or computational, meaning that it holds against unbounded or computationally bounded adversaries, respectively. Protocols that satisfy both properties statistically, known as statistical zero knowledge proofs, are only possible for languages in \(\mathsf {AM} \cap \mathsf {coAM}\) [1, 20]; however, once either property is relaxed to be computational, protocols for all of \(\mathsf {NP}\) can be constructed assuming the existence of one way functions [11, 25, 26, 40, 41]. Specifically,
-
Statistical Zero-knowledge Arguments for \(\mathsf {NP}\), where soundness is computational and zero-knowledge is statistical, are known to be achievable in 4 rounds with black-box simulation, assuming the existence of collision resistant hash functions [7].
-
Computational Zero-knowledge Proofs for \(\mathsf {NP}\), that satisfy statistical soundness and computational zero-knowledge, are known to be achievable in 5 rounds with black-box simulation, assuming the existence of collision resistant hash functions [24].
Protocols that satisfy statistical security, either against a malicious prover or a malicious verifier, are more secure and therefore can be more desirable than protocols that are only computationally secure on both sides. For instance, statistical zero-knowledge arguments provide an unconditional privacy guarantee – even a verifier that runs an arbitrary amount of post-processing on the proof transcript, does not obtain any information that cannot be simulated efficiently.
Secure Computation of General Functionalities. While tight results for zero-knowledge with black-box simulation with statistical security against one party are known, the state of affairs is significantly lacking in the case of two-party secure computation of general functionalities. Specifically, in the two-party setting, it is natural to ask whether statistical or unconditional security can be achieved, against at least one of the parties.
In a setting where both parties are computationally bounded, Katz and Ostrovsky [33] showed how to securely compute general functionalities with black-box simulation, with only 4 messages of interaction, when one party receives the output, and 5 messages when both parties receive the output. They also demonstrate that this result is tight with respect to black-box simulation. There has been significant progress in the last few years, extending the results of Katz and Ostrovsky to obtain better round optimal secure protocols both in [15, 44] and beyond the two-party setting [3, 6, 10, 13, 14, 23].
Despite all this progress, there are significant gaps in our understanding of the round complexity of \(\mathsf {2PC}\) with one-sided statistical security, i.e. statistical security against one of the participants. While there are known techniques to achieve weaker notions such as super-polynomial simulation with statistical security [12, 31, 43], the (standard) setting of polynomial simulation is not well understood at all.
1.1 Our Results
In this paper, we settle the round complexity of two-party secure computation with black-box simulation and one-sided statistical security. This is the best possible security that can be achieved by any non-trivial two-party protocol in the plain model.
We now describe our results in some detail. First, we consider a setting where only one party receives the output of the computation. Without loss of generality, we call the party that receives the output, the receiver \(\mathsf {R}\), and the other party the sender \(\mathsf {S}\). We obtain a tight characterization with respect to black-box simulation, as follows.
Informal Theorem 1
Assuming polynomial hardness of either DDH or QR or LWE, there exists a 4 round two-party secure computation protocol for general functionalities with black-box simulation, with statistical security against an adversarial receiver and computational security against an adversarial sender.
Next, we recall a result due to Katz [32] who proved that 4 round computational zero-knowledge proofs for \(\mathsf {NP}\) with black-box simulation cannot exist unless the polynomial hierarchy collapses. This helps rule out the existence of a 4 round two-party protocol for secure computation of general functionalities with black-box simulation, with statistical security against an adversarial sender and computational security against an adversarial receiver, unless the polynomial hierarchy collapses. A formal proof of this statement appears in the full version of the paper. We also match this lower bound with the following result.
Informal Theorem 2
Assuming polynomial hardness of either DDH or QR or LWE, there exists a 5 round two-party secure computation protocol for general functionalities with black-box simulation, with statistical security against an adversarial sender and computational security against an adversarial receiver.
We formalize and prove Informal Theorem 1 and Informal Theorem 2 by demonstrating a single 5 round protocol for symmetric functionalities (i.e. functionalities that generate identical output for both parties), where the receiver \(\mathsf {R}\) obtains the output at the end of the \(4^{th}\) round, and the sender \(\mathsf {S}\) obtains the output at the end of the \(5^{th}\) round. This protocol is unconditionally secure against malicious receivers, and computationally secure against malicious senders. Such a protocol can be unconditionally compiled (in a round-preserving way) to work for asymmetric functionalities using the following folklore technique: each participant additionally inputs a random key to the functionality, and the symmetric functionality masks each participant’s output with their respective key.
We prove that our protocol provides statistical security against a malicious receiver \(\mathsf {R}\) and computational security against a malicious sender \(\mathsf {S}\). We observe that Informal Theorem 1 follows from this protocol by simply eliminating the last message from the receiver \(\mathsf {R}\) to the sender \(\mathsf {S}\). Informal Theorem 2 also follows from this protocol by simply renaming the players: that is, we will now call the party \(\mathsf {S}\) in our original protocol, \(\mathsf {R}\); and we will call \(\mathsf {R}\) , \(\mathsf {S}\). The resulting protocol, after renaming parties, is statistically secure against a malicious sender \(\mathsf {S}\) and computationally secure against a malicious receiver \(\mathsf {R}\). Because both parties obtain the output by the end of the \(5^{th}\) round, the (re-named) receiver \(\mathsf {R}\) is guaranteed to obtain the output at the end of round 5.
Together, these results completely characterize the round complexity of secure two-party computation with black-box simulation and statistical security against one participant. Along the way, we develop a toolkit for establishing statistical security that may be useful in other settings.
In the rest of this paper, in protocols where a single party gets the output – we will call the party that obtains an output the receiver, and the other party the sender. In protocols both parties get the output, we call the party that obtains its output first, the receiver and the party that obtains output second, the sender.
2 Our Techniques
We now provide an informal overview of our techniques. Our starting point is the simple case of security against semi-honest adversaries, with statistical security against one party and computational security against the other. A simple way to obtain round-optimal secure computation for general functionalities, in the semi-honest setting, is to rely on Yao’s garbling technique. In this technique, one party, referred to as the garbler, computes a garbled circuit and labels for the evaluation of a circuit. The garbler sends the resulting circuit to the other party, the evaluator, and both parties rely on 2-choose-1 oblivious transfer (OT) to transfer the “right” labels corresponding to the input of the evaluator. The evaluator then executes a public algorithm on the garbled circuit and labels to recover the output of the circuit.
Limitations in the Semi-honest Setting. Even in the semi-honest setting, garbled circuits that provide security against unbounded evaluators are only known for circuits in \(\mathsf {NC}1\). In fact, whether constant round two-party semi-honest protocols secure against unbounded senders and unbounded receivers exist, even in the OT hybrid model, is an important unresolved open problem in information-theoretic cryptography. In the absence of such protocols, the best security we can hope to achieve even in the semi-honest setting, is when at least one party is computationally bounded. As a result, in the malicious setting also, the best we can hope for is security against unbounded senders and bounded receivers, or unbounded receivers and bounded senders.
As discussed in the previous section, we construct a single 5 round protocol for symmetric functionalities (i.e. functionalities that generate identical output for both parties), where the receiver \(\mathsf {R} \) obtains the output at the end of the \(4^{th}\) round, and the sender \(\mathsf {S} \) obtains the output at the end of the \(5^{th}\) roundFootnote 1. We prove that this protocol provides statistical security against an unbounded malicious receiver \(\mathsf {R}^* \) and security against a computationally bounded malicious sender \(\mathsf {S}^* \). For simplicity, we discuss the first 4 rounds of this protocol in more detail: specifically, we discuss a 4 round protocol where \(\mathsf {R} \) obtains the output (and \(\mathsf {S} \) does not), that we prove is secure against an unbounded malicious \(\mathsf {R} ^*\) and computationally bounded malicious \(\mathsf {S} ^*\).
\(\mathsf {R} \) must generate the garbled circuit, and \(\mathsf {S} \) must evaluate it. Garbled circuits form an important component of our protocol. Because garbled circuits for functions outside of \(\mathsf {NC}1\) are insecure against unbounded evaluators, when looking at all efficiently computable functions (which is the focus of this work), our de-facto strategy will be to have a malicious evaluator that is computationally bounded whereas a malicious garbler may be computationally unbounded.
Because we desire statistical security against \(\mathsf {R} ^*\), the receiver \(\mathsf {R} \) must be the entity that generates the garbled circuit, and \(\mathsf {S} \) will evaluate this circuit on labels obtained via a 2-choose-1 oblivious transfer (\({\mathsf {OT}}\)) protocol. Recall that we also require the receiver \(\mathsf {R} \) to obtain the output by the end of round 4. Since \(\mathsf {S} \) is the one evaluating the garbled circuit, this enforces that the garbled circuit must be evaluated by the sender by the end of round 3. In other words, \(\mathsf {R} \) must output the garbled circuit and transfer labels to the sender by round 3.
This requires that labels for the garbled circuit be transferred from \(\mathsf {R} \) to \(\mathsf {S} \) via a 3 round \({\mathsf {OT}}\) protocol, in which \(\mathsf {R} \) is the \({\mathsf {OT}}\) sender and \(\mathsf {S} \) is the \({\mathsf {OT}}\) receiver. Naturally, this oblivious transfer protocol is also required to be statistically secure against malicious \(\mathsf {R}^* \) (who is the \({\mathsf {OT}}\) sender) and computationally secure against malicious \(\mathsf {S}^* \) (who is the \({\mathsf {OT}}\) receiver). Unfortunately, no OT protocols achieving malicious security are known in 3 rounds (in fact, the existence of such protocols with black-box simulation would contradict the lower bound of [33]). The fact that the OT must also be statistically secure against malicious senders complicates matters further. This brings us to our first technical barrier: identifying and using weaker forms of OT to obtain full malicious security.
Reconciling Three Round Oblivious Transfer. Here, it is appropriate to discuss known notions of oblivious transfer that are achievable in three rounds and provide some semblance of malicious security. A popular notion has been game-based security: roughly, this requires that the receiver choice bit be hidden from a malicious sender, and one of the sender messages remain hidden from the receiver. A further strengthening of this notion is security with superpolynomial simulation, commonly called SPS-security. Very roughly, this requires the existence of a superpolynomial simulator that simulates the view of a malicious sender/receiver only given access to the ideal functionality. There are known constructions of SPS-secure OT: in 2 rounds, SPS-secure OT was first constructed by [5] based on two-round game-based OT, which can itself be realized based on a variety of assumptions, including DDH, LWE, QR, and \(N^{th}\)-residuosity [2, 9, 27, 30, 42].
Here, recall that we also desire statistical security against an adversarial sender. Achieving this property requires at least three rounds [31], and [31] obtained 3 round OT with SPS security based on superpolynomial hardness of DDH, LWE, QR, and \(N^{th}\)-residuosity. Even more recently, [28] improved this result to rely only on polynomial hardness of any of the same assumptions. In fact, [28] achieve a notion in between SPS-security and standard security against malicious receivers: their protocol obtains distinguisher-dependent security [18, 29] against malicious receivers. This relaxes the standard notion of malicious security by reversing the order of quantifiers, namely, by allowing the simulator to depend upon the distinguisher that is attempting to distinguish the real and ideal experiments. Importantly, unlike standard security, a distinguisher-dependent OT simulator is not guaranteed to efficiently extract the adversary’s actual input, unless it has access to the distinguisher. On the other hand, we would like to achieve full-fledged malicious security in our \(\mathsf {2PC}\) protocol. This means that our \(\mathsf {2PC}\) simulator must nevertheless find a way to extract the adversary’s input and cannot rely on the OT simulator for this purpose. Looking ahead, we will only rely on the OT protocol to obtain an indistinguishability-based guarantee, and our \(\mathsf {2PC}\) simulator will not use the OT simulator at all. Next, we describe additional components that we add to this protocol to enable full-fledged malicious security.
Immediate Pitfalls of the Current Template. Now as discussed previously, garbled circuits and an appropriate OT protocol do not by themselves guarantee meaningful security against malicious adversaries. A malicious garbler could generate the garbled circuit or labels so as to completely alter the output of an honest evaluator. As such, the sender must be convinced that the garbled circuit and labels that she obtained from the receiver were generated “correctly”, before she evaluates the garbled circuit. In other words, \(\mathsf {R} \) should convince \(\mathsf {S} \), within three rounds, that the garbled circuit and oblivious transfer messages were correctly generated, so that it is “safe” for the sender to evaluate the garbled circuit.
A naïve approach would entail the use of a computational zero-knowledge proof, where \(\mathsf {R} \) proves to \(\mathsf {S} \) that the garbled circuit, labels and OT messages sent by \(\mathsf {R} \) were correctly generated. Unfortunately, computational zero-knowledge proofs are not known to exist in less than 4 rounds of interaction from standard assumptions, even assuming non-black-box simulation. This brings us to our second technical barrier.
We overcome this barrier with the help of a special conditional disclosure of secrets (CDS) protocol, that we will detail towards the end of this overview. This CDS protocol will help us compile protocols that are secure against adversaries that “promise to behave well” (that we will denote as explainable adversaries in line with [8]) into protocols secure against arbitrarily malicious adversaries, while retaining one-sided statistical security. An “explainable” adversary generates messages in the support of the distribution of all honestly generated messages.Footnote 2
In fact, we take a modular approach to building \(\mathsf {2PC}\) with one-sided statistical security against fully malicious adversaries: first, we obtain a protocol secure against explainable adversaries alone, and next, we compile this protocol to one that is secure against arbitrary malicious adversaries. For now, we focus our attention towards achieving simulation-based security against explainable adversaries alone, instead of arbitrary malicious ones. Later, we discuss our CDS-based approach to achieve security against arbitrary malicious adversaries.
Extracting inputs of Explainable Adversaries. Recall that by definition of explainability, for every garbled circuit \(\mathsf {GC}\) and OT message that an explainable \(\mathsf {R}^* \) sends, there exists randomness r and input \(\mathsf {inp} \) such that \(\mathsf {GC}\) is generated as an output of the garbling algorithm for the circuit corresponding to the two-party function f, on input \(\mathsf {inp} \) and with randomness r.
As already discussed, proving security requires establishing the existence of a simulator that interacts with an ideal functionality and with the adversary to output a view that is indistinguishable from the adversary’s view in its interaction with the honest party. Importantly, this simulator must extract the input of a malicious \(\mathsf {R}^* \) or \(\mathsf {S}^* \), and cannot use the 3-round OT for this purpose.
Therefore, to enable extraction from \(\mathsf {R}^* \), we modify the protocol to require the receiver to send a statistically binding extractable commitment (constructed, eg, in [45]) to its input, in parallel with the rest of the protocol. By definition, an explainable \(\mathsf {R}^* \) is guaranteed to send an extractable commitment to the “right” input that is consistent with the garbled circuit, and a simulator \(\mathsf {Sim}^{\mathsf {R}^*}\) will be able to extract \(\mathsf {R}^* \)’s input from the extractable commitment. Such extractable commitments are known to exist in 3 rounds by the work of Prabhakaran et al. [45].
Similarly, in order to enable the extraction of \(\mathsf {S}^* \)’s input, we will modify the protocol to require \(\mathsf {S} \) to send an extractable commitment to its input, in parallel with the rest of the protocol. The simulator \(\mathsf {Sim}^{\mathsf {S}^*}\) will be able to extract the sender’s input from this extractable commitment. Since we require statistical security against \(\mathsf {R} \), the extractable commitment used by \(\mathsf {S} \) should be statistically hiding. A simple modification to the extractable commitments of Prabhakaran et al. [45], replacing statistically binding computationally hiding commitments with statistically hiding computationally binding commitments yields the required extractable commitment in 4 rounds. Unfortunately, this also means that \(\mathsf {Sim}^{\mathsf {S}^*}\) can only send the input of \(\mathsf {S}^* \) and obtain an output from the ideal functionality at the end of the \(4^{th}\) round. However, \(\mathsf {S}^* \) evaluates the garbled circuit and may obtain an output before round 4 even begins, which would allow \(\mathsf {S}^* \) to distinguish the real and ideal executions. Said differently, this would leave \(\mathsf {Sim}^{\mathsf {S}^*}\) with no opportunity to program the output of the ideal functionality in the view of \(\mathsf {S}^* \).
To provide \(\mathsf {Sim}^{\mathsf {S}^*}\) with such an opportunity and overcome this technical barrier, we modify the protocol as follows: instead of garbling the circuit corresponding to the function f, \(\mathsf {R} \) samples the keys \((\mathsf {pk}, \mathsf {sk})\) for a public key encryption scheme, and garbles a circuit that computes \((\mathsf {Enc}_{\mathsf {pk}} \circ f)\). Here \(\mathsf {Enc}_{\mathsf {pk}}\) denotes the encryption algorithm of an IND-CPA secure encryption scheme, and the randomness used for encryption is hardwired by \(\mathsf {R} \) into the circuit. As a result, \(\mathsf {S} \) on evaluating the garbled circuit, obtains a ciphertext that encrypts the output of the function under \(\mathsf {R} \)’s public key. It must then forward this ciphertext to \(\mathsf {R} \), who uses the corresponding secret key to decrypt the ciphertext and recover the output of the functionFootnote 3. This concludes the bare-bones description of our 5-round protocol with security against explainable adversaries.
In addition to proving that this protocol is secure against explainable PPT adversaries, we also establish an additional property, that will come in handy later. We prove that the protocol is robust in the first two rounds: meaning that even an adversary that behaves arbitrarily maliciously (and not necessarily explainably) in the first two rounds can only influence the function output, but not obtain any information about the private input of the other participant.
Simulating Explainable Adversaries. This completes a simplified overview of our protocol with security against explainable adversaries. But there are several subtleties that arise when formalizing the proof of security. We describe our simulators and discuss a few of these subtleties below.
First, we discuss how to build a simulator \(\mathsf {Sim}^{\mathsf {S}^*}\) that simulates the view of a malicious sender \(\mathsf {S}^* \). Recall that \(\mathsf {Sim}^{\mathsf {S}^*}\) must extract the input of a malicious \(\mathsf {S}^* \), query the ideal functionality, and program the resulting output in the view of \(\mathsf {S}^* \). The use of statistically hiding extractable commitments allows \(\mathsf {Sim}^{\mathsf {S}^*}\) to extract \(\mathsf {S}^* \)’s input by the end of the fourth round. Therefore, \(\mathsf {Sim}^{\mathsf {S}^*}\) only obtains an output from the ideal functionality by the end of the fourth round. But \(\mathsf {Sim}^{\mathsf {S}^*}\) must send to \(\mathsf {S}^* \) a garbled circuit in the third round, on behalf of \(\mathsf {R} \), even before learning the output. How should \(\mathsf {Sim}^{\mathsf {S}^*}\) construct this circuit? \(\mathsf {Sim}^{\mathsf {S}^*}\) cannot even invoke the simulator of the garbled circuit because it has not extracted \(\mathsf {S}^* \)’s input at this time. Instead, we have the simulator simply garble a circuit that outputs an encryption of the all zeroes string. Finally, the simulator extracts the input of \(\mathsf {S}^* \) from the fourth round message, and queries the ideal functionality to obtain an output. In the fifth round, it sends this output \(\mathsf {S}^* \) in the clear.
Recall that \(\mathsf {S}^* \) can behave arbitrarily maliciously while generating its OT message, and only provides a proof of correct behaviour in round 4. Therefore, we must use a careful argument to ensure that the result appears indistinguishable to \(\mathsf {S}^* \). The indistinguishability argument heavily relies on the distinguisher-dependent simulation property of the OT protocol. In particular, we build a careful sequence of hybrids where we extract \(\mathsf {S}^* \)’s (who is the OT receiver) input to the OT protocol in a distinguisher-dependent manner, and use the extracted input to replace the actual garbled circuit with a simulated one. Next, we change the output of the garbled circuit from an encryption of the right output to an encryption of the all zeroes string, and finally we replace the simulated garbled circuit with a real circuit that always outputs an encryption of the all zeroes string. All intermediate hybrids in this sequence are distinguisher-dependent. A similar argument also helps prove robustness of our protocol against \(\mathsf {S}^* \) that behaves maliciously in the second round.
Next, we discuss how we simulate the view of an unbounded malicious \(\mathsf {R}^* \). The simulator \(\mathsf {Sim}^{\mathsf {R}^*}\) uses the third round extractable commitment to obtain the input of \(\mathsf {R}^* \), queries the ideal functionality to obtain an output, and in the fourth round message, sends an encryption under the receiver’s public key \(\mathsf {pk} \) of this output. Here, we carefully prove that for any explainable receiver \(\mathsf {R}^* \), the simulated message (encrypting the output generated by the ideal functionality) is indistinguishable from the message generated by an honest sender.
This concludes an overview of how we achieve a protocol with security against explainable adversaries. Next, we discuss techniques to compile any explainable protocol with robustness in the first two rounds, into one that is secure against malicious adversaries. We also discuss a few additional subtleties that come up in this setting.
Security against Malicious Senders via Statistical ZK Arguments. In order to achieve security against arbitrary malicious \(\mathsf {S}^* \), the protocol is further modified to require \(\mathsf {R} \) and \(\mathsf {S} \) to execute a statistical zero-knowledge argument, where \(\mathsf {S} \) proves to \(\mathsf {R} \) that \(\mathsf {S} \) generated its OT messages correctly, and perform the garbled circuit evaluation correctly to obtain the result that it output to \(\mathsf {R} \). Because of a technical condition in the proof, we actually require the SZK argument to be an argument of knowledge. Such arguments of knowledge with delayed-input completeness and soundness, and requiring exactly 4 rounds can be obtained by instantiating the FLS paradigm with statistically hiding extractable commitments. These are executed in parallel with our 4 round explainable protocol described above. With these arguments in place, at the end of the fourth round \(\mathsf {R} \) will decrypt the ciphertext to recover the output only if the verification algorithm applied to the zero-knowledge argument accepts. Otherwise \(\mathsf {R} \) rejects. This helps argue security against malicious \(\mathsf {S}^* \), but we point out one subtlety: the SZK argument can only be verified at the end of round 4, an unwitting receiver could send its round 3 message in response to an arbitrarily maliciously generated round 2 sender message. This is where we invoke the additional robustness property discussed earlier. Next, we discuss the somewhat more complex case of malicious receivers.
Security against Malicious Receivers via Statistical Conditional Disclosure of Secrets. So far, an arbitrary malicious \(\mathsf {R}^* \) could recover additional information about the sender’s input based on the output of evaluation of incorrectly garbled circuits. Ideally, we would like to ensure that \(\mathsf {R}^* \) can obtain the sender’s fourth round message if and only if \(\mathsf {R}^* \) generated its first and third round messages in an “explainable” manner.
As discussed at the beginning of this overview, using zero-knowledge proofs to enable this requires too many rounds: therefore, our next idea is to rely on a two-round conditional disclosure of secrets (CDS) protocol. This will allow \(\mathsf {R}^* \) to recover the message sent by \(\mathsf {S} \) if and only if \(\mathsf {R}^* \) inputs a witness attesting to the fact that its first and third messages were explainable. Notably, the witness input by \(\mathsf {R}^* \) is hidden from \(\mathsf {S} \). Furthermore, when no such witness exists (i.e. when \(\mathsf {R}^* \) does not generate explainable messages), the CDS protocol computationally hides the message of \(\mathsf {S} \)Footnote 4. Clearly, such a protocol can be used to ensure that \(\mathsf {R}^* \) recovers the output of evaluation of the garbled circuit iff it behaved in an explainable fashion, and otherwise obtains no information.
However, because we desire statistical security against \(\mathsf {R}^* \), we need the CDS protocol to provide statistical security against \(\mathsf {R}^* \). Fortunately, a CDS protocol with statistical security can be obtained for the class of relations that are verifiable by \(\mathsf {NC1}\) circuits, by combining two round game-based OT (eg, Naor-Pinkas [42]) with information-theoretic garbled circuits for \(\mathsf {NC1}\). Specifically, the receiver generates OT receiver messages corresponding to each of the bits in his witness, and the sender garbles a circuit that outputs the original sender message if and only if the receiver’s input is a valid witness. We also note that there exists a generic transform [21] that allows verifying (given the randomness and inputs of \(\mathsf {R}^* \)) that \(\mathsf {R}^* \) behaved in an explainable way – in logarithmic depth, or by an \(\mathsf {NC1}\) circuit.
Next, we rely on robustness of the underlying protocol to argue security against a receiver that may have behave arbitrarily maliciously in the first round of the protocol. Finally, to ensure that the receiver sends the correct output to the sender in the fifth round, we require the receiver to send a zero-knowledge proof asserting that it computed this final message explainably. This proof can be obtained in 5 rounds [24], and is executed in parallel with the rest of the protocol.
Another hurdle, and its Resolution. While \(\mathsf {CDS}\) helps keep round complexity low, it leads to another technical barrier when simulating the view of a malicious sender. Specifically, the malicious simulator obtains messages from the underlying simulator of the robust explainable protocol. Because it obtains these messages externally, there is no way for the malicious simulator to recover the sender’s next message encoded within the CDS protocol. At the same time, the simulator needs to necessarily recover this next message in order to generate the final message of the protocol. To get around this issue, we require the statistical ZK argument provided by the simulator to be an argument of knowledge (AoK). As a result, the malicious simulator is able to use the AoK property of the sender’s SZK argument to extract a witness, and we carefully ensure that this witness helps the simulator reconstruct the next message of the sender, and proceed as before.
Concluding Remarks. This completes an overview of our techniques. In summary, we obtain round optimal two-party computation with one-sided statistical security assuming the existence of public key encryption, collision resistant hash functions, and two round statistically sender-private OT. We also note that we depart from existing work by using OT protocols with distinguisher-dependent simulation to achieve an end goal of standard simulation security in a general-purpose two-party computation protocol. We believe that this application to statistically secure \(\mathsf {2PC}\) represents a meaningful new application domain for distinguisher-dependent simulation [29], beyond [16, 17, 29, 34]. In addition, we rely on several other technical tools such as deferred evaluation of garbled circuits, and combining robust protocols with delayed-input proofs - that may be of independent interest.
Open Problems and Future Directions. Our work obtains feasibility results for round optimal two-party secure computation with one-sided statistical security, which is the best possible security that one can hope to achieve in two-party protocols in the plain model. A natural question is whether statistical security can be obtained against at least one of the participants in more general multi-party settings. It is also interesting to understand the minimal assumptions required to obtain \(\mathsf {2PC}\) with one-sided statistical security, in a round optimal manner, following similar investigations on assumptions versus round complexity in ZK with one-sided statistical security, perhaps via highly optimized cut-and-choose techniques. Another interesting question is whether it is possible to achieve one-sided statistically secure protocols that make black-box use of cryptography. Finally, it is also interesting to understand whether 4 rounds are necessary to obtain specialized statistically secure protocols, such as statistical ZAPs, from polynomial hardness assumptions (in light of the fact that recent constructions of statistical ZAPs in less that 4 rounds [4, 28, 37] rely on superpolynomial hardness assumptions).
Roadmap. We refer the reader to Sect. 4 for a detailed description of our protocol against explainable adversaries, and a sketch of the proof of its security; and to Sect. 5 for a description of our protocol against malicious adversaries, and a sketch of the proof of its security.
3 Preliminaries
In the rest of this paper, we will denote the security parameter by \(k \), and we will use \(\mathsf {negl} (\cdot )\) to denote any function that is aymtpotically smaller than the inverse of every polynomial.
3.1 Secure Two-Party Computation
Two Party Computation. A two-party protocol \(\varPi \) is cast by specifying a process that maps pairs of inputs to pairs of outputs (one for each party). We refer to such a process as a functionality and denote it by \(\mathcal {F} = f_n: \{0,1\}^{n} \times \{0,1\}^{n} \rightarrow \{0,1\}^{\mathsf {poly} (n)} \times \{0,1\}^{\mathsf {poly} (n)}\). We restrict ourselves to symmetric functionalities, where for every pair of inputs (x, y), the output is a random variable f(x, y) ranging over pair of strings.
Secure Two Party Computation. In this definition we assume an adversary that corrupts one of the parties. The parties are sender \({\mathsf S} \) and receiver \({\mathsf R} \). Let \(\mathcal {A} \in \{{\mathsf S}, {\mathsf R} \}\) denote a corrupted party and \(\mathcal {H}\in \{{\mathsf S}, {\mathsf R} \}, \mathcal {H} \ne \mathcal {A}\) denote the honest party.
-
Ideal Execution. An ideal execution for the computation of functionality \(\mathcal {F}\) proceeds as:
-
Inputs: \({\mathsf S} \) and \({\mathsf R} \) obtain inputs \(x \in X_n\) and \(y \in Y_n\), respectively.
-
Send inputs to trusted party: \(\mathcal {H}\) sends its input to \(\mathcal {F}\). Moreover, there exists a simulator \(\mathsf {Sim}^{\mathcal {A}}\) that has black box access to \(\mathcal {A}\), that sends input on behalf of \(\mathcal {A}\) to F.
-
Trusted party output to simulator: If \(x \notin X_n\), \(\mathcal {F}\) sets x to some default input in \(X_n\); likewise if \(y \notin Y_n\), \(\mathcal {F}\) sets y equal to some default input in \(Y_n\). Then the trusted party sends f(x, y) to \(\mathsf {Sim}^{\mathcal {A}}\). It waits for a special symbol from \(\mathsf {Sim}^{\mathcal {A}}\), upon receiving which, it sends the output to \(\mathcal {H}\). If it receives \(\bot \) from \(\mathsf {Sim}^{\mathcal {A}}\), it outputs \(\bot \) to \(\mathcal {H}\).
-
Outputs: \(\mathcal {H}\) outputs the value it obtained from \(\mathcal {F}\) and \(\mathcal {A}\) outputs its view. We denote the joint distribution of the output of \(\mathcal {H}\) and the view of \(\mathcal {A}\) by \(\mathsf {IDEAL}_{\mathcal {F}, \mathsf {Sim}, {A}}(x,y,n)\).
We let \(\mathsf {IDEAL}_{\mathcal {F}, \mathsf {Sim}, {\mathcal {A}}}(x,y,n)\) be the joint distribution of the view of the corrupted party and the output of the honest party following an execution in the ideal model as described above.
-
-
Real Execution. In the real world, the two party protocol \(\varPi \) is executed between \({\mathsf S} \) and \({\mathsf R} \). In this case, \(\mathcal {A}\) gets the inputs of the party it has corrupted and sends all the messages on behalf of this party, using an arbitrary polynomial-time strategy. \(\mathcal {H}\) follows the instructions in \(\varPi \). Let \(\mathcal {F}\) be as above and let \(\pi \) be two-party protocol computing \(\mathcal {F}\). Let \(\mathcal {A}\) be a non-uniform probabilistic poly-time machine with auxiliary input z. We let \(\mathsf {REAL}_{\varPi , {\mathcal {A}}}(x,y, n)\) denote the joint distribution the view of corrupted party and the output of the honest party, in the real execution of the protocol.
Definition 1
A protocol \(\varPi \) securely computes \(\mathcal {F}\) with computational security against a party if there exists a PPT simulator \(\mathsf {Sim}\) such that for every non-uniform probabilistic polynomial time adversary \(\mathcal {A}\) corrupting the party,
It securely computes \(\mathcal {F}\) with statistical security against a party if there exists a PPT simulator \(\mathsf {Sim}\) such that for every non-uniform probabilistic polynomial time adversary \(\mathcal {A}\) corrupting the party,
Definition 2 (Explainable transcript)
Let \(\varPi _{{\mathsf S} ^*, {\mathsf R} ^*}\) be a protocol between an arbitrary sender \({\mathsf S} ^*\) and arbitrary receiver \({\mathsf R} ^*\). We say that a transcript T of an execution \(\varPi \) between \({\mathsf S} ^*\) and \({\mathsf R} ^*\) is explainable for \({\mathsf S} ^*\) if there exists an input i and coins r such that T is consistent with the transcript of an execution between \({\mathsf S} _{i,r}\) and \({\mathsf R} ^*\), until the point in T where \({\mathsf S} _{i,r}\) aborts. (Here \({\mathsf S} _{i,r}\) is the honest sender on input i using coins r). Similarly, we say that a transcript T of an execution \(\varPi \) between \({\mathsf S} ^*\) and \({\mathsf R} ^*\) is explainable for \({\mathsf R} ^*\) if there exists an input i coins r such that T is consistent with the transcript of an execution between \({\mathsf R} _{i,r}\) and \({\mathsf S} ^*\), until the point in T that \({\mathsf R} _{i,r}\) aborts. (Here \({\mathsf R} _{i,r}\) is the honest receiver strategy using input i and coins r).
Definition 3 (Explainable sender)
Let \(\varPi _{{\mathsf S} ^*, {\mathsf R} ^*}\) be a protocol between an arbitrary sender \({\mathsf S} ^*\) and arbitrary receiver \({\mathsf R} ^*\). A (possibly probabilistic) sender \({\mathsf S} ^* = \{{\mathsf S} ^*_k \}_{k \in \mathbb {N}}\) is explainable if there exists a negligible \(\mu (\cdot )\) such that for any receiver \({\mathsf R} ^* = \{{\mathsf R} ^*_k \}_{k \in \mathbb {N}}\), and large enough \(k \in \mathbb {N}\),
Definition 4 (Explainable receiver)
Let \(\varPi _{{\mathsf S} ^*, {\mathsf R} ^*}\) be a protocol between an arbitrary sender \({\mathsf S} ^*\) and arbitrary receiver \({\mathsf R} ^*\). A (possibly probabilistic) receiver \({\mathsf R} ^* = \{{\mathsf R} ^*_k \}_{k \in \mathbb {N}}\) is explainable if there exists a negligible \(\mu (\cdot )\) such that for any sender \({\mathsf S} ^* = \{{\mathsf S} ^*_k \}_{k \in \mathbb {N}}\), and large enough \(k \in \mathbb {N}\),
Definition 5 (Robust Explainable Secure Protocol)
We will say that a protocol is secure against explainable adversaries, if Definition 1 holds against explainable adversaries. Furthermore, such a protocol is robust if for every (arbitrarily) malicious \(\mathsf {R} ^*\), the real view of an adversary conditioned on aborting after round 2 is indistinguishable from the adversary’s simulated view, and for every (arbitrarily) malicious \(\mathsf {S} ^*\), the real view of the adversary conditioned on aborting after round 3 is indistinguishable from the adversary’s simulated view.
3.2 Yao’s Garbled Circuits
We will also rely on Yao’s technique for garbling circuits [46]. In the following, we define the notation that we will use, and the security properties of Yao’s garbling scheme.
Definition 6
Let \(p(\cdot )\) denote any fixed polynomial. We will consider a circuit family \(\mathsf {\mathbb {C}: \{0,1\}^k \rightarrow \{0,1\}^{p(k)}}\), that takes an input of size k bits and outputs p(k) bits. Yao’s garbled circuits consist of the following algorithms:
-
\(\mathsf {GARBLE}(1^k, C; r)\) obtains as input a circuit \(C \in \mathbb {C}\) and randomness r, and outputs the garbled circuit \(\mathsf {G_C}\) as well as a set of 2k keys corresponding to setting each of the k input bits to 0 and 1. We will denote this by:
$${(\mathsf {G_C},\{\mathtt {label}_{i,b}\}_{i \in [k], b \in \{0,1\}})\leftarrow \mathsf {GARBLE}(1^{k}, C; r)}.$$ -
\(\mathsf {EVAL}(\mathsf {G_C}, \{\mathtt {label}_{i,x_i}\}_{i \in [k]})\) obtains as input garbled circuit \(\mathsf {G_C}\), and a set of k keys. It generates an output z. We will denote this by
$$z \leftarrow \mathsf {EVAL}(\mathsf {G_C},\{\mathtt {label}_{i,x_i}\}_{i \in [k]}).$$
We require these algorithms to satisfy the following properties:
-
Correctness: For all \(C \in \mathbb {C}, x \in \{0,1\}^k\),
$$\mathop {\Pr }\limits \Bigg [C(x)=z \Bigg | \begin{array}{c} {(\mathsf {G_C},\{\mathtt {label}_{i,b}\}_{i \in [k], b \in \{0,1\}})\leftarrow \mathsf {GARBLE}(1^{k}, C; r)} \\ z \leftarrow \mathsf {EVAL}(G_C,\{\mathtt {label}_{i,x_i}\}_{i \in [k]}) \end{array} \Bigg ] = 1 - \mathsf {negl} (k) $$ -
Security: There exists a PPT simulator \(\mathsf {Sim}\) such that for all non-uniform PPT \({\mathcal {D}} \), and all \(C \in \mathbb {C}, x \in \{0,1\}^k,\)
$$ \Big |\mathop {\Pr }\limits [{\mathcal {D}} (\mathsf {G_C},\{\mathtt {label}_{i,x_i}\}_{i \in [k]}) = 1] - \Pr [{\mathcal {D}} (\mathsf {Sim}(1^{k}, C(x))) = 1] \Big | = \mathsf {negl} (k)$$where
$${(\mathsf {G_C},\{\mathtt {label}_{i,b}\}_{i \in [k], b \in \{0,1\}})\leftarrow \mathsf {GARBLE}(1^{k}, C; r)}.$$
3.3 Extractable Commitments
Definition 7 (Extractable Commitment)
A statistically binding and computationally hiding three round commitment scheme is said to be extractable if there exists a PPT extractor \(\mathsf {Ext}\) such that for any PPT committer \(\mathsf {C}\) and every polynomial \(p(\cdot )\), If
then
where \(\mathsf {R}\) denotes the honest receiver algorithm, d denotes a decommitment string (obtained from \(\mathsf {C}(\mathsf {c}_1,\mathsf {c}_2,\mathsf {c}_3)\) at the start of the decommit phase), and \(\mathsf {R}\) outputs s to be equal to the decommitted value if it accepts the decommitment, and \(\bot \) otherwise.
Three-message computationally hiding extractable commitments can be constructed from non-interactive commitments [45]. We will also consider statistically hiding extractable commitments, that satisfy the same extraction guarantee, except against computationally unbounded committers. These can be obtained in four rounds by substituting non-interactive commitments in the construction of [45] with two round statistically hiding commitments.
3.4 Zero-Knowledge Proofs and Arguments for NP
An n-round delayed-input interactive protocol \(\langle \mathsf {P}, \mathsf {V} \rangle \) for deciding a language L with associated relation \(\mathsf {R_L}\) proceeds in the following manner:
-
At the beginning of the protocol, \(\mathsf {P}\) and \(\mathsf {V}\) receive the size of the instance and execute the first \(n-1\) rounds.
-
At the start of the last round, P receives input \((x,w) \in \mathsf {R_L}\) and \(\mathsf {V}\) receives x. Upon receiving the last round message from \(\mathsf {P}\), \(\mathsf {V}\) outputs 0 or 1.
We will rely on proofs and arguments for NP that satisfy delayed-input completeness, adaptive soundness and adaptive ZK.
Definition 8 (Statistical Zero Knowledge Argument)
Fix any language L. Let \(\mathsf {\langle P, V \rangle }\) denote the execution of a protocol between a PPT prover \({\mathsf P} \) and a (possibly unbounded) verifier \({\mathsf V} \), let \(\mathsf {V}_{\mathsf {out}}\) denote the output of the verifier and let \(\mathsf {View}_\mathcal{A}\langle \mathsf {P, V} \rangle \) denote the transcript together with the state and randomness of a party \(\mathcal{A} \in \{\mathsf {P, V}\}\) at the end of an execution of a protocol. Then we say \(\mathsf {\langle P, V \rangle }\) is zero knowledge proof system for L if the following properties hold:
-
Completeness: For all \(x \in L\),
$$\mathsf {\Pr [V_{out} \langle P, V \rangle }=1] = 1- \mathsf {negl} (k),$$where the probability is over the random coins of \(\mathsf {P}\) and \(\mathsf {V}\).
-
Adaptive Soundness: For all polynomial size \({\mathsf P} ^{*}\) and all \(x \notin L\) sampled by \({\mathsf P} ^{*}\) adaptively depending upon the first \(n-1\) rounds,
$$\Pr [\mathsf {V_{out}} \langle \mathsf {P^{*},V} \rangle =1] = \mathsf {negl} (k)$$ -
Statistical Zero Knowledge: There exists a PPT simulator \(\mathsf {Sim}\) such that for all \(V^{*}\) and all \(x \in L\),
$$\Big |\Pr [{\mathsf V} ^*(\mathsf {View}_{{\mathsf V} ^*}\langle {\mathsf P} (x,w), {\mathsf V} ^* \rangle ) = 1] - \Pr [{\mathsf V} ^*(\mathsf {Sim}^{{\mathsf V} ^{*}}(x)) = 1]\Big | = \mathsf {negl} (k)$$
These can be obtained by a simple modification to delayed-input ZK arguments based on the Lapidot-Shamir [35] technique, by relying on a two round statistically hiding commitent (that can itself be based on any collision-resistant hash functions), instead of a one-round statistically binding one.
Definition 9 (Zero Knowledge Proof)
Fix any language L. Let \(\mathsf {\langle P, V \rangle }\) denote the execution of a protocol between a (possibly unbounded) prover \({\mathsf P} \) and a PPT verifier \({\mathsf V} \), let \(\mathsf {V}_{\mathsf {out}}\) denote the output of the verifier and let \(\mathsf {View}_\mathcal{A}\langle \mathsf {P, V} \rangle \) denote the transcript together with the state and randomness of a party \(\mathcal{A} \in \{\mathsf {P, V}\}\) at the end of an execution of a protocol. Then we say \(\mathsf {\langle P, V \rangle }\) is zero knowledge proof system for L if following properties hold:
-
Completeness: For all \(x \in L\),
$$\mathsf {\Pr [V_{out} \langle P, V \rangle }=1] = 1- \mathsf {negl} (k),$$where the probability is over the random coins of \(\mathsf {P}\) and \(\mathsf {V}\).
-
Adaptive Soundness: For all \({\mathsf P} ^{*}\) and all \(x \notin L\) sampled by \({\mathsf P} ^{*}\) adaptively depending upon the first \(n-1\) rounds,
$$\Pr [\mathsf {V_{out}} \langle \mathsf {P^{*},V} \rangle =1] = \mathsf {negl} (k)$$ -
Computational Zero Knowledge: There exists a PPT simulator \(\mathsf {Sim}\) such that for all polynomial size \(V^{*}\) and all \(x \in L\),
$$\Big |\Pr [{\mathsf V} ^*(\mathsf {View}_{{\mathsf V} ^*}\langle {\mathsf P} (x,w), {\mathsf V} ^* \rangle ) = 1] - \Pr [{\mathsf V} ^*(\mathsf {Sim}^{{\mathsf V} ^{*}}(x)) = 1]\Big | = \mathsf {negl} (k)$$
Such proofs were first constructed by [24], and can be made complete and sound when the instance is chosen by the prover in the last round of the interaction, by relying on the work of [35].
Imported Theorem 1 [24, 35]. Assuming the existence of collision-resistant hash functions, there exist 5 round zero-knowledge proofs for all languages in \(\mathsf {NP}\), satisfying Definition 9.
3.5 Oblivious Transfer (OT)
Oblivious Transfer (OT) is a protocol between two parties, an (unbounded) sender S with messages \((m_0, m_1)\) and a (PPT) receiver R with choice bit b, where R receives output \(m_b\) at the end of protocol. We let \(\langle S(m_0,m_1), R(b) \rangle \) denote execution of the OT protocol with sender input \((m_0,m_1)\) and receiver input b. We will rely on a three round oblivious transfer protocol that satisfies perfect correctness and the following security guarantee:
Definition 10 (Statistically Receiver-Private OT)
We will say that an oblivious transfer protocol is statistically receiver private if it satisfies the following properties.
-
Statistical Receiver Security. For every unbounded \(S^{*}\) and all \((b,b') \in {\{0,1\}}\), the following distributions are statistically indistinguishable:
$$\mathsf {View}_{S^{*}}{\langle S^{*}, R(b) \rangle } \text { and } \mathsf {View}_{S^{*}}{\langle S^{*}, R(b') \rangle }$$ -
Sender Security (Distinguisher-dependent Simulation Under Parallel Composition). For every polynomial \(n = n(k)\), for every efficiently sampleable distribution over messages \(\{\mathcal {M}_{0,i}, \mathcal {M}_{1,i}\}_{i \in [n]}\), there exists a PPT simulator \(\mathsf {Sim}\) such that for every non-uniform PPT receiver \(R^*\) and non-uniform PPT distinguisher \({\mathcal {D}} \),
$$|\Pr [{\mathcal {D}} (\mathsf {View}_{R^*} {\langle S(\{m_{0,i}, m_{1,i}\}_{i \in [n]}), R^{*}\rangle }) = 1] $$$$-\,\Pr [{\mathcal {D}} (\mathsf {Sim}^{R^*, {\mathcal {D}}, \{\mathcal {F}_{\mathsf {OT},i}(m_{0,i}, m_{1,i}, \cdot )\}_{i \in [n]}}) = 1]| = \mathsf {negl} (k)$$where the probability is over the randomness of sampling
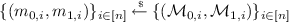 , the randomness of the sender and the simulator, and where \({\mathcal {F}} _{\mathsf {OT}}\) is a single-query ideal OT functionality with \(\{(m_{0,i}, m_{1,i})\}_{i \in [n]}\) hardwired, that on input \(\{b_i\}_{i \in [n]}\) outputs \(\{m_{b_i,i}\}_{i \in [n]}\) and then self-destructs.
, the randomness of the sender and the simulator, and where \({\mathcal {F}} _{\mathsf {OT}}\) is a single-query ideal OT functionality with \(\{(m_{0,i}, m_{1,i})\}_{i \in [n]}\) hardwired, that on input \(\{b_i\}_{i \in [n]}\) outputs \(\{m_{b_i,i}\}_{i \in [n]}\) and then self-destructs.
Imported Theorem 2 [28]. Assuming the existence of any two-round statistical sender-private OT (resp., polynomial hardness of CDH), there exists a three-round statistically receiver-private OT protocol in the plain model satisfying Definition 10.
Here, we note that two-round statistical sender-private OT can in turn be based on the polynomial hardness of DDH [42], QR and \(N^{th}\) residuosity [27, 30] and LWE [9]. We will represent the three messages of an OT protocol satisfying Definition 10 by \({\mathsf {OT}} _{\mathsf {S,1}},{\mathsf {OT}} _{\mathsf {R}}({\cdot }), {\mathsf {OT}} _{\mathsf {S,3}}({\cdot }) \).
3.6 Conditional Disclosure of Secrets
Conditional disclosure of secrets for an \(\mathsf {NP}\) language \(\mathcal {L}\) [2] can be viewed as a two-message analog of witness encryption [22]. That is, the sender holds an instance x and message m and the receiver holds x and a corresponding witness w. If the witness is valid, then the receiver obtains m, whereas if \(x\notin \mathcal {L}\), m remains hidden. We further require that the protocol hides the witness w from the sender.
Definition 11
A conditional disclosure of secrets scheme \((\mathsf {CDS.R},\mathsf {CDS.S},\) \(\mathsf {CDS.D})\) for a language \(\mathcal {L}\in \mathsf {NP}\) satisfies:
-
1.
Correctness: For any \((x,w)\in R_\mathcal {L}\), and message \(m\in \{0,1\} ^*\),
$$ \Pr \Big [\mathsf {CDS.D}_K(c') = m \Big | \begin{array}{c} (c,K) \leftarrow \mathsf {CDS.R}(x,w) \\ c' \leftarrow \mathsf {CDS.S}(x,m,c) \end{array} \Big ]=1 $$ -
2.
Message Indistinguishability: For any \(x \in \{0,1\} ^{k} \setminus \mathcal {L}\), \(c^*\), and two equal-length messages \(m_0,m_1\), the following distributions are statistically indistinguishable:
$$ \mathsf {CDS.S}(x,m_0,c^*) \text { and } \mathsf {CDS.S}(x,m_1,c^*) $$ -
3.
Receiver Simulation: There exists a simulator \(\mathsf {CDS.Sim}\) such that for any polynomial-size distinguisher \({\mathcal {D}} \), there exists a negligible \(\mu \) such that for any \(x \in \mathcal {L}\), \(w\in R_{\mathcal {L}}(x)\) and large enough security parameter \(k \in \mathbb {N}\),
$$\begin{aligned} |\Pr [{\mathcal {D}} (\mathsf {CDS.R}(x,w)) = 1] - \Pr [{\mathcal {D}} (\mathsf {CDS.Sim}(x)) = 1]| = \mu (k) \end{aligned}$$
Instantiations. CDS schemes satisfying Definition 11 for relations that are verifiable in \(\mathsf {NC1}\) can be instantiated by combining information-theoretic Yao’s garbled circuits for \(\mathsf {NC1}\) with any two-message oblivious transfer protocol where the receiver message is computationally hidden from any semi-honest sender, and with (unbounded) simulation security against malicious receivers. Such oblivious transfer schemes are known based on DDH [42], Quadratic (or \(N^{th}\)) Residuosity [27], and LWE [9].
3.7 Low-Depth Proofs
We will describe how any computation that is verifiable by a family of polynomial sized ciruits can be transformed into a proof that is verifiable by a family of circuits in \(\mathsf {NC1}\). Let R be an efficiently computable binary relation. For pairs \((x, w) \in R\) we call x the statement and w the witness. Let L be the language consisting of statements in R.
Definition 12 (Low-Depth Non-Interactive Proofs)
A low-depth non-interactive proof with perfect completeness and soundness for a relation R consists of an (efficient) prover P and a verifier V that satisfy:
-
Perfect Completeness. A proof system is perfectly complete if an honest prover with a valid witness can always convince an honest verifier. For all \((x, w) \in R\) we have
$$\Pr [V(\pi ) = 1 | \pi \leftarrow P(x) ] = 1$$ -
Perfect Soundness. A proof system is perfectly sound if it is infeasible to convince an honest verifier when the statement is false. For all \(x \not \in L\) and all (even unbounded) adversaries \({\mathcal {A}} \) we have
$$Pr[ V (x, \pi ) = 1| \pi \leftarrow {\mathcal {A}} (x)] = 0.$$ -
Low Depth. The verifier V can be implemented in \(\mathsf {NC1}\).
We discuss a very simple construction of a low-depth non-interactive proof, that was outlined in [21]. The prover P executes the NP-verification circuit on the witness and generates the proof as the concatenation (in some specified order) of the bit values assigned to the individual wires of the circuit. The verifier V proceeds by checking consistency of the values assigned to the internal wires of the circuit for each gate. In particular for each gate in the \(\mathsf {NP}\)-verification circuit the verifier checks if the wire vales provided in the proof represent a correct evaluation of the gate. Since the verification corresponding to each gate can be done independent of every other gate and in constant depth, we have that V itself is constant depth.
4 \(\mathsf {2PC}\) with One-Sided Statistical Security Against Explainable Parties
4.1 Construction
As a first step, in Fig. 1, we describe a 5 round protocol with security against explainable adversaries (Definitions 3 and 4). In a nutshell, these adversaries are like malicious adversaries, but with an additional promise: explainable adversaries generate messages that are in the suport of honestly generated messages, except with negligible probability.
Our protocol uses the following building blocks:
-
A 3 round statistically binding and computationally hiding commitment scheme satisfying extractability according to Definition 7, denoted by \(\mathsf {Ecom}\).
-
A 4 round statistically hiding and computationally binding commitment scheme satisfying extractability according to Definition 7, denoted by \(\mathsf {SHEcom}\).
-
A 3 round statistically receiver private oblivious transfer protocol satisfying Definition 10, denoted by \(\mathsf {OT}\).
-
Garbled circuits satisfying Definition 6, with algorithms denoted by \(\mathsf {Garble}, \mathsf {Eval}\).
4.2 Analysis
We demonstrate security of our protocol against explainable adversaries by proving the following theorem.
Theorem 1
Assuming 3 round computationally hiding and 4 round statistically hiding extractable commitments according to Definition 7, garbled circuits satisfying Definition 6 and three round oblivious transfer satisfying Definition 10, there exists a robust 5-round secure two-party computation protocol with black-box simulation against unbounded explainable receivers and PPT explainable senders, where the receiver obtains its output at the end of round 4 and the sender obtains its output at the end of the fifth roundFootnote 5.
We observe that 3 round computationally hiding commitments can be based on any non-interactive commitment scheme [45], which can itself be based on any public-key encryption [36], and 4 round statistically hiding extractable commitments can be based on collision-resistant hash functions. Garbled circuits can be obtained only assuming the existence of one-way functions [46], and three round oblivious transfer satisfying Definition 10 can be based on any statistically sender-private 2 round OT. All of these primitives can be based on the hardness of the Decisional Diffie-Hellman assumption (DDH), or Quadratic Residuosity (QR), or the Learning with Errors assumption (LWE), and we therefore have the following corollary.
Corollary 1
Assuming polynomial hardness of the Decisional Diffie-Hellman assumption (DDH), or Quadratic Residuosity (QR), or the Learning with Errors assumption (LWE), there exists a robust 5-round secure two-party computation protocol with black-box simulation against unbounded explainable receivers and PPT explainable senders, where the receiver obtains its output at the end of round 4 and the sender obtains its output at the end of round 5.
Theorem 1 follows immediately from Lemma 1 that proves security against bounded explainable senders and Lemma 2 that proves security against unbounded explainable receivers.
Lemma 1
Assuming computational hiding of \(\mathsf {Ecom}\), extractability of \(\mathsf {SHEcom}\) according to Definition 7, security of garbled circuits according to Definition 6, and sender security of OT according to Definition 10, the construction in Fig. 1 satisfies robust simulation-based security against explainable PPT senders according to Definition 3.
Proof
We prove that there exists a simulator \(\mathsf {Sim}^{\mathsf {{\mathsf S} ^*}} \) that with black-box access to a computationally bounded explainable sender \(\mathsf {S} ^*\), outputs a simulated view that is indistinguishable from the real view of \(\mathsf {S} ^*\). Our simulator is described in Fig. 2, with differences from the real protocol underlined.
In the full version of the paper, we prove via a sequence of hybrids, that the real and ideal distributions are indistinguishable.
Lemma 2
Assuming statistical hiding of \(\mathsf {SHEcom}\) and extractability of \(\mathsf {Ecom}\) according to Definition 7 and receiver security of OT according to Definition 10, the construction in Fig. 1 satisfies robust statistical simulation security (Definition 1) against explainable unbounded receivers as per Definition 3.
Proof
We prove that there exists a PPT simulator \(\mathsf {Sim}^{\mathsf {\mathsf {R} ^*}} \) that with black-box access to an unbounded explainable sender \(\mathsf {R} ^*\), outputs a simulated view that is statistically indistinguishable from the real view of \(\mathsf {R} ^*\). Our simulator is described in Fig. 3, with changes from the real protocol underlined.
In the full version of the paper, we prove via a sequence of hybrids, that the real and ideal distributions are indistinguishable.
5 From Explainable to Malicious One-Sided Statistical Security
In this section, we describe a compiler that compiles any robust two-party secure computation protocol against explainable adversaries, into one that is secure against arbitrary malicious adversaries. Assuming the hardness of DDH/LWE/QR, the resulting protocol is computationally secure against PPT malicious senders. In addition, we demonstrate that the resulting protocol is secure against unbounded malicious receivers if the underlying robust explainable protocol is secure against unbounded malicious receivers.
5.1 Construction
In Fig. 4, we describe a protocol compiler that compiles any 5 round robust explainable protocol into a fully malicious protocol while preserving round complexity. Our protocol uses the following building blocks:
-
Any robust two-party protocol secure against explainable adversaries from Fig. 1 by \(\varPi _{\mathsf {exp}} \langle \mathsf {S}, \mathsf {R} \rangle \). We denote the messages of this protocol where \(\mathsf {S} \) uses input \(\mathsf {B} \) and randomness \(\mathsf {r}_{\mathsf {S}}\), and \(\mathsf {R} \) uses input \(\mathsf {A} \) and randomness \(\mathsf {r}_{\mathsf {R}}\), by:
$$\big (\tau _{\mathsf {R},1} = \varPi _{\mathsf {exp}, \mathsf {R}, 1}(\mathsf {A};\mathsf {r}_{\mathsf {R}}), \tau _{\mathsf {S},2} = \varPi _{\mathsf {exp}, \mathsf {S}, 2}(\tau _{\mathsf {R},1},\mathsf {B};\mathsf {r}_{\mathsf {S}}), \tau _{\mathsf {R},3} = \varPi _{\mathsf {exp}, \mathsf {R}, 3}(\tau _{\mathsf {S},2},\mathsf {A};\mathsf {r}_{\mathsf {R}}),$$$$\tau _{\mathsf {S},4} = \varPi _{\mathsf {exp}, \mathsf {S}, 4}(\tau _{\mathsf {R},1},\tau _{\mathsf {R},3},\mathsf {B};\mathsf {r}_{\mathsf {S}}), \tau _{\mathsf {R},5} = \varPi _{\mathsf {exp}, \mathsf {R}, 5}(\tau _{\mathsf {S},2},\tau _{\mathsf {S},4},\mathsf {A};\mathsf {r}_{\mathsf {R}}) \big )$$ -
A 4 round delayed-input adaptively sound and adaptively statistical ZK argument of knowledge according to Definition 8, with messages denoted by
$$\mathsf {SZKA}.\mathsf {V}, \mathsf {SZKA}.\mathsf {P}(\cdot ), \mathsf {SZKA}.\mathsf {V}(\cdot ), \mathsf {SZKA}.\mathsf {P}(\cdot , x, w),$$and the output of the verifier denoted by \(\mathsf {SZKA}.\mathsf {out}(\cdot ,x)\).
-
A 5 round delayed-input adaptively sound and adaptively computational ZK proof according to Definition 9, with messages denoted by
$$\mathsf {ZKP}.\mathsf {P},\mathsf {ZKP}.\mathsf {V}(\cdot ), \mathsf {ZKP}.\mathsf {P}(\cdot ), \mathsf {ZKP}.\mathsf {V}(\cdot ), \mathsf {ZKP}.\mathsf {P}(\cdot , x, w),$$and the output of the verifier denoted by \(\mathsf {ZKP}.\mathsf {out}(\cdot ,x)\).
Languages for the CDS protocol, SZK argument and ZK proof are defined as:
where \(\mathsf {R} (\mathsf {A},r_\mathsf {R},\tau _{\mathsf {S},2}))\) denotes that the transcript \((\tau _{\mathsf {R},1},\tau _{\mathsf {R},3})\) is generated using honest receiver strategy with input \(\mathsf {A} \) and randomness \(r_\mathsf {R} \); \(\mathsf {R} (\mathsf {A},r_\mathsf {R},\tau _{\mathsf {S},2},\tau _{\mathsf {S},4}))\) denotes that the transcript \((\tau _{\mathsf {R},1},\tau _{\mathsf {R},3},\tau _{\mathsf {R},5})\) is generated using honest receiver strategy with input \(\mathsf {A} \) and randomness \(r_\mathsf {R} \); and \(\mathsf {S} (\mathsf {B},r_\mathsf {S},\tau _{\mathsf {R},1},\tau _{\mathsf {R},3}))\) denotes that the transcript \((\tau _{\mathsf {S},2},c)\) is generated using honest sender strategy with input \(\mathsf {B} \) and randomness \(r_{\mathsf {S}}\), and \(\mathsf {ldp}\) denotes a low-depth proof.
5.2 Analysis
We demonstrate one-sided statistical security of our protocol against arbitrary malicious adversaries by formally proving the following theorem.
Theorem 2
Assume the existence of four round delayed-input adaptive statistical zero-knowledge arguments of knowledge with adaptive soundness according to Definition 8, five round delayed-input adaptive computational zero-knowledge proofs with adaptive soundness according to Definition 9, and two round statistical \(\mathsf {CDS}\) for \(\mathsf {NP}\) relations verifiable by \(\mathsf {NC}_1\) circuits according to Definition 11. Assume also that there exists a robust two-party secure computation protocol against explainable adversaries according to Definition 5. Then there exists a 5-round secure two-party computation protocol for general functionalities with black-box simulation against unbounded malicious receivers and PPT malicious senders, where the receiver obtains its output at the end of round 4 and the sender obtains its output at the end of round 5.
Here, we note that the required proof systems can be based on two round statistically hiding commitments, which can themselves be based on the hardness of Decisional Diffie-Hellman (DDH), Quadratic Residuosity (QR) or the Learning with Errors (LWE) assumption. Furthermore, the requisite statistical \(\mathsf {CDS}\) for \(\mathsf {NP}\) relations verifiable by \(\mathsf {NC}_1\) circuits can be based on any two round statistically sender private OT, which can itself be based on DDH/QR/LWE. We also make use of a transform due to [21] that converts arbitrary proofs to low depth proofs (Definition 12) verifiable in \(\mathsf {NC}_1\) – this is done to ensure that the \(\mathsf {CDS}\) relation of interest is verifiable in \(\mathsf {NC}_1\). In addition, we observe that the robust two-party secure computation protocol against explainable adversaries constructed in Sect. 4 satisfies Definition 5, and can be instantiated based on DDH/QR/LWE. This results in the following Corollary of Theorem 2.
Corollary 2
Assuming polynomial hardness of the Decisional Diffie-Hellman (DDH) assumption, or Quadratic Residuosity (QR) or Learning with Errors (LWE), there exists a 5-round secure two-party computation protocol with black-box simulation against unbounded malicious receivers and PPT malicious senders, where the receiver obtains its output at the end of round 4 and the sender obtains its output at the end of round 5.
The proof of Theorem 2 follows from Lemma 3 and Lemma 4, that prove security against malicious senders and unbounded malicious receivers respectively. These are formally stated and proved below.
Lemma 3
Assuming \(\mathsf {CDS}\) satisfies receiver simulation according to Definition 11, \(\mathsf {SZKA}\) is adaptively sound according to Definition 8 and \(\mathsf {ZKP}\) satisfies adaptive computational zero-knowledge according to Definition 9, and assuming \(\varPi _{\mathsf {exp}}\) is a robust explainable protocol satisfying the additional property described in Theorem 2, the protocol \(\varPi _{\mathsf {mal}}\langle \mathsf {S}, \mathsf {R} \rangle \) in Fig. 4 is secure against PPT malicious senders according to Definition 1.
Proof
We prove that there exists a simulator \(\mathsf {Sim}^{\mathsf {\mathsf {S} ^*}} \) that with black-box access to a computationally bounded malicious sender \(\mathsf {S} ^*\), outputs a simulated view that is indistinguishable from the real view of \(\mathsf {S} ^*\). Our simulator is in Fig. 5, and the proof is deferred to the full version.
Lemma 4
Assuming \(\mathsf {CDS}\) satisfies statistical message indistinguishability for \(\mathsf {NP}\) relations verifiable by \(\mathsf {NC}_1\) circuits according to Definition 11, assuming \(\mathsf {L}_{\mathsf {CDS}}\) is verifiable in \(\mathsf {NC}_1\), assuming \(\mathsf {ZKP}\) is adaptively sound against unbounded provers according to Definition 9 and \(\mathsf {SZKA}\) satisfies adaptive statistical zero-knowledge according to Definition 8, and assuming \(\varPi _{\mathsf {exp}}\) is robust and statistically secure against unbounded explainable receivers, the protocol \(\varPi _{\mathsf {mal}}\langle \mathsf {S}, \mathsf {R} \rangle \) in Fig. 4 is statistically secure against unbounded malicious receivers according to Definition 1.
Proof
We prove that there exists a simulator \(\mathsf {Sim}^{\mathsf {\mathsf {R} ^*}} \) that with black-box access to a malicious receiver \(\mathsf {R} ^*\), outputs a simulated view that is indistinguishable from the real view of \(\mathsf {R} ^*\). Our simulator is described in Fig. 6, and the proof is deferred to the full version.
Notes
- 1.
We note that this is without loss of generality, since any asymmetric functionality can be unconditionally computed from a symmetric one by having each party input a random value, and using it to mask the output.
- 2.
Importantly, this is different from semi-malicious security [38, 39] where the adversary in addition to generating messages in the support of the distribution of all honestly generated messages, outputs the input and randomness that it used, on a special tape. On the other hand, simulating an explainable adversary is much more challenging: since in this case the adversary does not output any such special tape, and therefore the input and randomness must still be extracted from an explainable adversary by the simulator.
- 3.
Alternatively, \(\mathsf {R} \) could withhold the garbled circuit decoding information, i.e. the correspondence between the output wire labels and the output of the circuit, from \(\mathsf {S} \) until the \(5^{th}\) round. This would achieve the same effect, but leads to a more complex analysis. For simplicity of analysis, we choose to garble an encrypted circuit in our formal presentation.
- 4.
Such protocols have been used previously in the literature, most recently in [8].
- 5.
We point out that Informal Theorem 2 follows from this theorem by exchanging the roles of \(\mathsf {S} \) and \(\mathsf {R} \).
References
Aiello, W., Håstad, J.: Statistical zero-knowledge languages can be recognized in two rounds. J. Comput. Syst. Sci. 42(3), 327–345 (1991)
Aiello, B., Ishai, Y., Reingold, O.: Priced oblivious transfer: how to sell digital goods. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 119–135. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_8
Ananth, P., Choudhuri, A.R., Jain, A.: A new approach to round-optimal secure multiparty computation. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 468–499. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_16
Badrinarayanan, S., Fernando, R., Jain, A., Khurana, D., Sahai, A.: Statistical ZAP arguments. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 642–667. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_22
Badrinarayanan, S., Garg, S., Ishai, Y., Sahai, A., Wadia, A.: Two-message witness indistinguishability and secure computation in the plain model from new assumptions. In: Takagi, T., Peyrin, T. (eds.) Advances in Cryptology - ASIACRYPT 2017–23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, December 3–7, 2017, Proceedings, Part III. pp. 275–303 (2017)
Badrinarayanan, S., Goyal, V., Jain, A., Kalai, Y.T., Khurana, D., Sahai, A.: Promise zero knowledge and its applications to round optimal MPC. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 459–487. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_16
Bellare, M., Jakobsson, M., Yung, M.: Round-optimal zero-knowledge arguments based on any one-way function. In: Advances in Cryptology - EUROCRYPT 1997, Proceeding. pp. 280–305 (1997)
Bitansky, N., Khurana, D., Paneth, O.: Weak zero-knowledge beyond the black-box barrier. In: Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, STOC 2019, pp. 1091–1102, Phoenix, AZ, USA, June 23–26 (2019)
Brakerski, Z., Döttling, N.: Two-message statistically sender-private OT from LWE. In: TCC (2018)
Brakerski, Z., Halevi, S., Polychroniadou, A.: Four round secure computation without setup. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 645–677. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_22
Brassard, G., Chaum, D., Crépeau, C.: Minimum disclosure proofs of knowledge. J. Comput. Syst. Sci. 37(2), 156–189 (1988)
Chongchitmate, W., Ostrovsky, R.: Circuit-private multi-key FHE. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10175, pp. 241–270. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_9
Choudhuri, A.R., Ciampi, M., Goyal, V., Jain, A., Ostrovsky, R.: On round optimal secure multiparty computation from minimal assumptions. IACR Cryptology ePrint Archive 2019, 216 (2019). https://eprint.iacr.org/2019/216
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Delayed-input non-malleable zero knowledge and multi-party coin tossing in four rounds. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 711–742. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_24
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Round-optimal secure two-party computation from trapdoor permutations. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 678–710. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_23
Döttling, N., Garg, S., Goyal, V., Malavolta, G.: Laconic conditional disclosure of secrets and applications. In: 60th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2019, pp. 661–685, Baltimore, Maryland, USA, November 9–12 (2019). https://doi.org/10.1109/FOCS.2019.00046
Döttling, N., Garg, S., Hajiabadi, M., Masny, D., Wichs, D.: Two-round oblivious transfer from CDH or LPN. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12106, pp. 768–797. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45724-2_26
Dwork, C., Naor, M., Reingold, O., Stockmeyer, L.J.: Magic functions. In: 40th Annual Symposium on Foundations of Computer Science, FOCS 1999, pp. 523–534, New York, USA October 17–18 (1999)
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: Proceedings of the 22nd Annual ACM Symposium on Theory of Computing, pp. 416–426, Baltimore, Maryland, USA, May 13–17 (1990)
Fortnow, L.: The complexity of perfect zero-knowledge (extended abstract). In: Proceedings of the 19th Annual ACM Symposium on Theory of Computing, 1987, pp. 204–209, New York, USA (1987)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. SIAM J. Comput. 45(3), 882–929 (2016). https://doi.org/10.1137/14095772X
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: Symposium on Theory of Computing Conference, STOC 2013, pp. 467–476, Palo Alto, CA, USA, June 1–4, (2013). https://doi.org/10.1145/2488608.2488667
Garg, S., Mukherjee, P., Pandey, O., Polychroniadou, A.: The exact round complexity of secure computation. In: EUROCRYPT (2016)
Goldreich, O., Kahan, A.: How to construct constant-round zero-knowledge proof systems for NP. J. Cryptol. 9(3), 167–189 (1996). https://doi.org/10.1007/BF00208001
Goldreich, O., Micali, S., Wigderson, A.: Proofs that yield nothing but their validity for all languages in NP have zero-knowledge proof systems. J. ACM 38, 691–729 (1991)
Haitner, I., Nguyen, M., Ong, S.J., Reingold, O., Vadhan, S.P.: Statistically hiding commitments and statistical zero-knowledge arguments from any one-way function. SIAM J. Comput. 39(3), 1153–1218 (2009)
Halevi, S., Kalai, Y.T.: Smooth projective hashing and two-message oblivious transfer. J. Cryptology 25(1), 158–193 (2012)
Jain, A., Jin, Z., Goyal, V., Malavolta, G.: Statistical zaps and new oblivious transfer protocols, to appear. In: Eurocrypt (2020)
Jain, A., Kalai, Y.T., Khurana, D., Rothblum, R.: Distinguisher-dependent simulation in two rounds and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 158–189. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_6
Kalai, Y.T.: Smooth projective hashing and two-message oblivious transfer. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 78–95. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_5
Kalai, Y.T., Khurana, D., Sahai, A.: Statistical witness indistinguishability (and more) in two messages. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 34–65. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_2
Katz, J.: Which languages have 4-round zero-knowledge proofs? In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 73–88. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_5
Katz, J., Ostrovsky, R.: Round-Optimal secure two-party computation. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 335–354. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_21
Khurana, D.: Round optimal concurrent non-malleability from polynomial hardness. In: Theory of Cryptography - 15th International Conference Proceedings, Part II, TCC 2017, pp. 139–171, Baltimore, MD, USA, November 12–15 (2017). https://doi.org/10.1007/978-3-319-70503-3_5
Lapidot, D., Shamir, A.: Publicly verifiable non-interactive zero-knowledge proofs. In: Advances in Cryptology - CRYPTO 1990, 10th Annual International Cryptology Conference Proceedings. pp. 353–365, Santa Barbara, California, USA, August 11–15 (1990). https://doi.org/10.1007/3-540-38424-3_26
Lombardi, A., Schaeffer, L.: A note on key agreement and non-interactive commitments. IACR Cryptol. ePrint Arch. 2019, 279 (2019). https://eprint.iacr.org/2019/279
Lombardi, A., Vaikuntanathan, V., Wichs, D.: Statistical ZAPR arguments from bilinear maps. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 620–641. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_21
López-Alt, A., Tromer, E., Vaikuntanathan, V.: On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. IACR Cryptol. ePrint Arch. 2013, 94 (2013)
Mukherjee, P., Wichs, D.: Two round multiparty computation via multi-key FHE. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 735–763. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_26
Naor, M.: Bit commitment using pseudorandomness. J. Cryptol. 4(2), 151–158 (1991). https://doi.org/10.1007/BF00196774
Naor, M., Ostrovsky, R., Venkatesan, R., Yung, M.: Perfect zero-knowledge arguments for NP using any one-way permutation. J. Cryptology 11(2), 87–108 (1998)
Naor, M., Pinkas, B.: Efficient oblivious transfer protocols. In: SODA (2001)
Ostrovsky, R., Paskin-Cherniavsky, A., Paskin-Cherniavsky, B.: Maliciously circuit-private FHE. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 536–553. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_30
Ostrovsky, R., Richelson, S., Scafuro, A.: Round-Optimal Black-Box Two-Party Computation. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 339–358. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_17
Prabhakaran, M., Rosen, A., Sahai, A.: Concurrent zero knowledge with logarithmic round-complexity. In: 43rd (FOCS 2002), pp. 366–375, Vancouver, BC, Canada, November 16–19 (2002)
Yao, A.C.: How to generate and exchange secrets (extended abstract). In: 27th Annual Symposium on Foundations of Computer Science, pp. 162–167, Toronto, Canada, October 27–29 (1986)
Acknowledgement
We thank Giulio Malavolta, Akshayaram Srinivasan and the anonymous TCC reviewers for useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Khurana, D., Mughees, M.H. (2020). On Statistical Security in Two-Party Computation. In: Pass, R., Pietrzak, K. (eds) Theory of Cryptography. TCC 2020. Lecture Notes in Computer Science(), vol 12551. Springer, Cham. https://doi.org/10.1007/978-3-030-64378-2_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-64378-2_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64377-5
Online ISBN: 978-3-030-64378-2
eBook Packages: Computer ScienceComputer Science (R0)





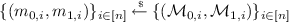 , the randomness of the sender and the simulator, and where
, the randomness of the sender and the simulator, and where 





