On the Complexity of Arithmetic Secret Sharing

Abstract

Since the mid 2000s, asymptotically-good strongly-multiplicative linear (ramp) secret sharing schemes over a fixed finite field have turned out as a central theoretical primitive in numerous constant-communication-rate results in multi-party cryptographic scenarios, and, surprisingly, in two-party cryptography as well.

Known constructions of this most powerful class of arithmetic secret sharing schemes all rely heavily on algebraic geometry (AG), i.e., on dedicated AG codes based on asymptotically good towers of algebraic function fields defined over finite fields. It is a well-known open question since the first (explicit) constructions of such schemes appeared in CRYPTO 2006 whether the use of “heavy machinery” can be avoided here. i.e., the question is whether the mere existence of such schemes can also be proved by “elementary” techniques only (say, from classical algebraic coding theory), even disregarding effective construction. So far, there is no progress.

In this paper we show the theoretical result that, (1) no matter whether this open question has an affirmative answer or not, these schemes can be constructed explicitly by elementary algorithms defined in terms of basic algebraic coding theory. This pertains to all relevant operations associated to such schemes, including, notably, the generation of an instance for a given number of players n, as well as error correction in the presence of corrupt shares. We further show that (2) the algorithms are quasi-linear time (in n); this is (asymptotically) significantly more efficient than the known constructions. That said, the analysis of the mere termination of these algorithms does still rely on algebraic geometry, in the sense that it requires “blackbox application” of suitable existence results for these schemes.

Our method employs a nontrivial, novel adaptation of a classical (and ubiquitous) paradigm from coding theory that enables transformation of existence results on asymptotically good codes into explicit construction of such codes via concatenation, at some constant loss in parameters achieved. In a nutshell, our generating idea is to combine a cascade of explicit but “asymptotically-bad-yet-good-enough schemes” with an asymptotically good one in such a judicious way that the latter can be selected with exponentially small number of players in that of the compound scheme. This opens the door to efficient, elementary exhaustive search.

In order to make this work, we overcome a number of nontrivial technical hurdles. Our main handles include a novel application of the recently introduced notion of Reverse Multiplication-Friendly Embeddings (RMFE) from CRYPTO 2018, as well as a novel application of a natural variant in arithmetic secret sharing from EUROCRYPT 2008.

1 Introduction

Background

This paper deals with linear secret sharing schemes (LSSS for short) defined over a finite field $\mathbb {F}_q$, with the additional property of being strongly-multiplicative [12]. We first briefly recall these (well-known) notions below (for precise definitions, see Sect. 2). We consider LSSS with share-space dimension 1, i.e., each of the n players is assigned a single $\mathbb {F}_q$-element as a share. The dimension of the secret-space or the size of the secret, however, is not restricted, i.e., the secret is generally a vector in $\mathbb {F}_q^k$ (for some given positive integer k) instead of an element of $\mathbb {F}_q$. As a matter of terminology, we speak of an LSSS for $\mathbb {F}_q^k$ over $\mathbb {F}_q$ (on n players).¹

The linearity property means that an $\mathbb {F}_q$-linear combination of “input” sharings, adding shares “player-wise” (similar for scalar multiplication), results in a correct “output” sharing where the corresponding secret is defined by taking the same combination over the secrets of the input sharings. There is t-privacy if the shares of any t out of n players jointly give no information about the secret and there is r-reconstruction if the shares of any r out of n players jointly always determine the secret uniquely, as follows: for each set of r-players, there is an $\mathbb {F}_q$-linear map that, when applied to the vector consisting of their shares, always gives the secret,

An LSSS $\varSigma$ for $\mathbb {F}_q^k$ over $\mathbb {F}_q$ on n players is t-strong-multiplicative² if there is t-privacy ($t\ge 1$) and if “the square of the LSSS” has $(n-t)$-reconstruction. For a vector $(\mathbf{s}_0,s_1,\ldots ,s_n)\in \varSigma$, $(s_1,\ldots ,s_n)\in \mathbb {F}_q^n$ is said to be a full share-vector with secret $\mathbf{s}_0\in \mathbb {F}_q^k$. The latter is equivalent to the statement that, if $\mathbf{x},\mathbf{x}' \in \mathbb {F}_q^n$ are full share-vectors with respective secrets $\mathbf{s}_0,\mathbf{s}_0' \in \mathbb {F}_q^k$, then, for each set A of $n-t$ players, the “player-wise” product $\mathbf{x}_A * \mathbf{x}'_A\in \mathbb {F}_q^{n-t}$ of the respective share-vectors $\mathbf{x}_A,\mathbf{x}'_A$ held by A determines the coordinate-wise product $\mathbf{s}_0*\mathbf{s}'_0\in \mathbb {F}_q^k$ of the secrets uniquely in that, for each such A, there exists an $\mathbb {F}_q$-linear map $\phi ^{(A)}$ such that $\phi ^{(A)}(\mathbf{x}_A * \mathbf{x}'_A)= \mathbf{s}_0*\mathbf{s}_0'$ always holds.³ We may also refer to the t as the adversary-parameter. We note that t-strong-multiplicativity trivially implies $(n-t)$-reconstruction. Also, it implies an effective algorithm for recovering the secret from n shares even if at most t of them are corrupted, by a generalization of the Berlekamp-Welch algorithm (see [13]).

We note that the classical application of these schemes is in information-theoretic multiparty computation (MPC) perfectly secure against an active adversary (in [1] and follow-up work based on Shamir’s secret sharing scheme, abstracted and generalized in [12] for linear secret sharing). Although the Shamir secret sharing scheme satisfies the t-strong-multiplicativity mentioned above, the share size grows with the number of players, i.e., the share size of the Shamir secret sharing scheme on n players is $n\log n$. On the other hand, there does exist secret sharing scheme that the share size does not grow with the number of players. We call it asymptotically good secret sharing scheme.

For an infinite family of such schemes, with $\mathbb {F}_q$ fixed and n tending to infinity, we say it is asymptotically good if $k,t \in \varOmega (n)$. We emphasize that, in this asymptotic context, there is yet another parameter of importance to some (theoretical) applications, namely the density (within the set of positive integers) of the infinite sequence of player-numbers $n_1, n_2,\ldots$ realized by the successive instances. Concretely, we equate this density to $\limsup _{i\rightarrow \infty } n_{i+1}/n_{i}$. If this is bounded by a constant (as is the case for known constructions), i.e., not infinity, then we may as well assume that the family realizes any given player-number n if it is large enough. Briefly, this is by folding the schemes and by slightly generalizing the definitions as follows. For $n\in (n_i, n_{i+1})$ we simply give each player an appropriate constant number of shares in the $n_{i+1}$-st scheme, thereby shrinking the length to its desired magnitude. Effectively, the share-space is now a product over a constant number of copies of $\mathbb {F}_q$, endowed with coordinate-wise multiplication (and-addition). This will affect the adversary parameter t only by a constant multiplicative factor (and will not affect the secret-space dimension k). The definitions are trivially adapted to this situation. Finally, note that if the density equals 1, then there is essentially no such loss.⁴

This asymptotic notion was first considered and realized in [3] in 2006, thereby enabling an “asymptotic version” of the general MPC theorem from [1]. Since 2007, with the advent of the so-called “MPC-in-the-head paradigm” [19], these asymptotically-good schemes have been further exposed as a central theoretical primitive in numerous constant communication-rate results in multi-party cryptographic scenarios, and, surprisingly, in two-party cryptography as well.

As to the construction of these schemes, all known results [3, 5, 9] rely heavily on algebraic geometry, more precisely, on dedicated algebraic geometric codes based on good towers of algebraic function fields defined over finite fields. It is a well-known open question since 2006 whether the use of “heavy machinery” can be avoided here. I.e., the question is whether the mere existence of such schemes can also be proved by “elementary” techniques only (say, from classical algebraic coding theory), even disregarding effective construction. So far, no progress on this question has been reported. For a full account on history, constructions and applications, see [13].

Our Results

In this paper we show the theoretical result that, no matter whether this open question has an affirmative answer or not, these schemes can be constructed explicitly by elementary algorithms defined in terms of basic algebra. This pertains to all relevant operations associated to such schemes: the generation of an instance for a given number of players n, the generation of shares, the computation of the linear maps associated to the strongly-multiplicative property, as well as error correction in the presence of corrupt shares. In fact, we show the algorithms are quasi-linear time (in n). To the best of our knowledge, the asymptotically-good strongly-multiplicative LSSS based on algebraic geometry code has time complexity at least quadratic [22]. The density in our construction is minimal, i.e., it equals 1. As a contrast, the best explicit algebraic geometry codes lead to an strongly-multiplicative LSSS over $\mathbb {F}_q$ with density $\sqrt{q}$. On the other hand, the algebraic geometry code derived from Shimura curve achieves density 1 but is non-constructive.

In spite of the elementary nature of the algorithms, the analysis of their mere termination does currently rely on algebraic geometry, in that it is founded, in part, on “blackbox use” of suitable existence results on asymptotically good schemes. Thus. in particular, there is no paradox here. In some sense, we may conclude that, even though algebraic geometry may be essential to the existence of these schemes (as the state-of-the-art may seem to suggest), it is not essential to their explicit construction.

We do note, however, that the positive adversary rate t/n we achieve is smaller than the optimal rate achieved by known results. Namely, here we achieve rate 1/27 instead of getting arbitrarily close to 1/3. Also, we do not achieve t-uniformity of the shares (i.e., the additional property that, besides t-privacy, the shares of any t players are uniformly random in $\mathbb {F}_q^t$, But, for (almost) all theoretical applications, this does not matter.

Finally, though this is somewhat besides the theoretical point we are making here, our quasi-linear time algorithms may perhaps help to show that some of the theoretical applications enjoy overall quasi-linear time complexity as well. This could be interesting in its own right, but it still remains to be seen.

Overview of Our Method

A naive hope for elementary, effective (Monte-Carlo) construction would be the following. At the core of all known constructions is the observation that it suffices to find linear codes C over $\mathbb {F}_q$ such that each of the codes C, $C^{\bot }$ (its dual) and $C^{*2}$ (its square⁵) is asymptotically-good.⁶ If such codes could be shown to be “sufficiently dense”, then an approach by selecting random codes could potentially work. However, using the theory of quadratic forms over finite fields, it has been shown in [8] that, over a fixed finite field $\mathbb {F}_q$, a random linear code C of length n and dimension $\sqrt{n}+\lambda$, has the property that $C^{*2}=\mathbb {F}_q^n$ with probability exponentially (in $\lambda$) close to 1. Thus, although C and $C^{\bot }$ can be rendered asymptotically good in this way (by Gilbert-Varshamov arguments), the code $C^{*2}$ would be “maximally-bad” almost certainly; the powering operation on codes is very destructive, almost always.

Instead, our method employs a nontrivial, novel adaptation of a classical paradigm from coding theory that enables transformation of existence results on asymptotically good codes into explicit construction of such codes via concatenation, at some constant loss in parameters achieved. In a nutshell, the idea is to combine an effective construction of “asymptotically-bad-yet-good-enough codes” with asymptotically good ones in such a judicious way that the latter can be selected with exponentially small length in that of the compound code. This opens the door to efficient, elementary exhaustive search. That said, the analysis of the time-complexity of these algorithms (in fact, that there exists correct such algorithms at all, even disregarding their actual complexity) continues to rely on algebraic geometry. We note that this complexity is superior to that of previous schemes. On the other hand, the adversary-rate is some small factor below the optimal rate of 1/3 achieved by previous schemes.

The approach taken in this paper is inspired by a classical idea from coding theory, going back to the 1960s [14]: results on the existence of asymptotically good linear codes may be transformed into effective construction of such codes via concatenation, incurring just a constant loss in the parameters achieved.

On a high level, this works as follows. One can take a “sufficiently good” code defined over an extension of the target “base field” as the outer code. This code needs not to be asymptotically good. Viewing the extension field as a vector space over the base field, one then encodes each coordinate to a vector over the base field through an asymptotically good code defined over the base field, the inner code. This compound scheme is linear over the base field and its length is the product of the lengths of the outer and inner codes.

The point is now that, if the outer code has constant rate and relative minimum distance as a function of its length and the degree of the extension grows very slowly with respect to its length, say logarithmically (which could be achieved e.g. with Reed-Solomon codes), then, in order for the compound code to be asymptotically good, it suffices that the inner code has exponentially small length as a function of the length of the outer code. This makes it possible to derandomize the random argument for Gilbert-Varshamov bound so as to find a linear inner code attaining this bound in polynomial time with respect to the length of the outer code [17].⁷ The concatenation idea that reduces the dimension of the searching space also enlightens us to look for a similar result in linear secret sharing scheme with strong multiplication.

In order to make such a paradigm work for us here, we overcome a number of nontrivial obstacles.

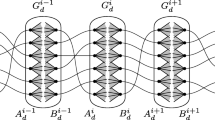
1. How to define a proper and useful concatenation for linear secret sharing schemes with strong multiplication. The purpose of concatenation is to bring down the field size so as to make our exhaustive search run in quasi-linear time. Let $\varSigma _1$ be an LSSS on $n_1$ players for $\mathbb {F}_{Q^m}$ over $\mathbb {F}_Q$ and $\varSigma _2$ be an LSSS on $n_2$ players for $\mathbb {F}_Q$ over $\mathbb {F}_q$ where $\mathbb {F}_Q$ is an extension field of $\mathbb {F}_q$. Let us call $\varSigma _1$ an outer LSSS and $\varSigma _2$ an inner LSSS. The concatenation $\varSigma _1\circ \varSigma _2$ of $\varSigma _1$ with $\varSigma _2$ is an LSSS on $n_1n_2$ players defined as follows: $(s_0,\mathbf{z}_1,\ldots ,\mathbf{z}_{n_1})\in \varSigma _1\circ \varSigma _2\subseteq \mathbb {F}_{Q^m}\times (\mathbb {F}_q^{n_2})^{n_1}$ if $(s_i,\mathbf{z}_i)\in \varSigma _2\subseteq \mathbb {F}_Q\times \mathbb {F}_q^{n_2}$ for $i=1,\ldots ,n_1$ and $(s_0,s_1,\ldots ,s_{n_1})\in \varSigma _1\subseteq \mathbb {F}_{Q^m}\times \mathbb {F}_Q^{n_1}$.⁸ As an analogy to concatenated codes, we show that if $\varSigma _1$ is a $t_1$-strongly-multiplicative LSSS on $n_1$ players and $\varSigma _2$ is a $t_2$-strongly-multiplicative LSSS on $n_2$ players, then $\varSigma _1\circ \varSigma _2$ is a $t_1t_2$-strongly-multiplicative LSSS on $n_1n_2$ players.

2. The exhaustive search space should be small. We first describe what we can achieve for one concatenation. We set our outer LSSS $\varSigma _1$ to be a Shamir secret sharing scheme. The encoding and decoding time of this LSSS is quasi-linear. Since our compound scheme is defined over a constant field, we set $q=O(1)$ and $n_2=\log Q$ in $\varSigma _2$ defined above. Now, the search space has dimension $\log Q$. Since the Shamir secret sharing scheme is asymptotically-bad, the compound scheme $\varSigma _1\circ \varSigma _2$ is not asymptotically-good strongly-multiplicative LSSS unless $\varSigma _2$ is asymptotically-good strongly-multiplicative LSSS. The existence of asymptotically-good strongly-multiplicative LSSS is ensured by algebraic geometry codes. However, to meet our elementary algorithm claim, we have to replace the explicit construction with an exhaustive search algorithm which enumerates every linear subspace. This can only be done in time $\exp (\varOmega (\log ^2 Q))$. Clearly, the search space is not small enough to meet our quasi-linear time claim. We resolve this issue by concatenating twice. Let $\varSigma _1$ be an Shamir secret sharing scheme $\varSigma _1$ on O(Q) players for $\mathbb {F}_{Q^m}$ over $\mathbb {F}_Q$ and $\varSigma _2$ be another Shamir secret sharing scheme on O(q) players for $\mathbb {F}_Q$ over $\mathbb {F}_q$ with $q=O(\log Q)$. The compound scheme $\varSigma :=\varSigma _1\circ \varSigma _2$ is a strongly-multiplicative LSSS for $\mathbb {F}_{Q^m}$ over $\mathbb {F}_q$. Let $\varSigma _3$ be an asymptotically-good strongly-multiplicative LSSS on $O(\log \log Q)$ players for $\mathbb {F}_q$ over $\mathbb {F}_p$ with $p=O(1)$ which is found by an exhaustive search and ensured by algebraic geometry codes. The final scheme $\varSigma \circ \varSigma _3$ turns out to be an asymptotically-good strongly-multiplicative LSSS on $O(Q\log Q \log \log Q)$ players for $\mathbb {F}_{Q^m}$ over $\mathbb {F}_p$ with $p=O(1)$. We can see that this two-rounds concatenation brings down the field size so small that an exhaustive search only runs in time complexity polynomial in $\log Q$.

3. The dimension of secret space should be linear in the number of players. When we overcome the above two obstacles, we already obtain an asymptotically-good strongly-multiplicative LSSS $\varSigma \circ \varSigma _3$ for $\mathbb {F}_{Q^m}$ over $\mathbb {F}_p$ that runs in quasi-linear time. Note that the secret space is still $\mathbb {F}_{Q^m}$. We are not done yet since we claim that our LSSS has secret space $\mathbb {F}_p^k$ with $k=\varOmega (Q)$. We resort to a recent developed tool called reverse multiplication friendly embedding (RMFE) [10] to overcome this obstacle. An RMFE is a pair of maps $(\phi ,\psi )$ with $\phi : \mathbb {F}_q^k\rightarrow \mathbb {F}_{q^m}$ and $\psi : \mathbb {F}_{q^m}\rightarrow \mathbb {F}_q^k$ such that for any $\mathbf{x},\mathbf{y}\in \mathbb {F}_q^k$, $\mathbf{x}*\mathbf{y}=\psi (\phi (\mathbf{x})\cdot \phi (\mathbf{y}))$. This RMFE keeps multiplication property and bring down the field size at a price of constant loss in rate, i.e., the component-wise product of two secrets $\mathbf{x},\mathbf{y}\in \mathbb {F}_q^k$ are mapped to the product of two elements $\phi (\mathbf{x}),\phi (\mathbf{y})\in \mathbb {F}_{q^m}$ with $m=O(k)$. By applying RMFE to our secret space, we are able to obtain an strongly-multiplicative LSSS with a linear-dimensional secret space. The original paper [5] about RMFE does not take quasi-linear time and elementary algorithm into account. To meet quasi-linear time and elementary algorithm claim, we apply above paradigm to our RMFE as well.

4. The last obstacle is the density issue. The density issue affects the performance of LSSS in the following way. Assume that we have a class of LSSSs on the number of players $n_1,\ldots ,$ such that $\liminf _{i\rightarrow \infty } \frac{n_{i+1}}{n_{i}}=\tau$. Then, we have to use the same LSSS on the number of players between $n_i+1$ to $n_{i+1}$. The density issue implies that the LSSS on $n_i+1$ players is only $\frac{1}{\tau }$-fractionally as good as arithmetic secret sharing schemes on $n_{i+1}$. Thus, we prefer LSSS with density 1. We observe that our compound scheme $\varSigma \circ \varSigma _3$ can be made to satisfy density 1 even if $\varSigma _3$ has any constant density larger than 1. This is because $\varSigma$ is a concatenation of two Shamir secret sharing scheme which yields a secret sharing scheme on any desired number of players. By exploiting this property and carefully tuning the length of $\varSigma$ so as to cope with the length of $\varSigma _3$, we manage to produce an LSSS with density 1. It is worth emphasizing that LSSS based on algebraic geometry codes has density either significantly bigger than 1 or density 1 but non-explicit. To see this, let us first take a look at the best constructive algebraic geometry codes derived from Garcia-Stichtenoth function field tower. Unfortunately, the density of these algebraic geometry codes over $\mathbb {F}_q$ is merely $\sqrt{q}$. On the other hand, there does exist families of algebraic geometry codes with density 1, e.g. the Shimura curve. To our best knowledge, none of them is explicit. In conclusion, our strongly-multiplicative LSSS is explicit and has density 1 both of which can not be simultaneously satisfied by previous constructions.

The paper is organized as follows. In Sect. 2, we briefly recall linear secret sharing schemes, then introduce the concatenation of linear secret sharing schemes. In Sect. 3, we present a quasi-linear time elementary algorithm to generate an asymptotically-good strongly-multiplicative linear secret sharing schemes. To convert the secret space from the extension field $\mathbb {F}_{q^m}$ to $\mathbb {F}_q^k$, we resort to reverse multiplication friendly embedding that was recently developed in [10]. In the appendix, we include linear secret sharing from algebraic curves and the decoding of concatenated codes.

2 Linear Secret Sharing Schemes and Concatenation

The relation between linear secret sharing schemes and linear codes has been well understood since the work of [20]. Further details on this relation can be found in [5, 9]. In this section, we briefly introduce strongly-multiplicative LSSS and some related notational convention that will be used throughout this paper.

Denote by [n] the set $\{1,2,\dots ,n\}$ and denote by $2^{[n]}$ the set of all subsets of [n]. Let q be a prime power and denote by $\mathbb {F}_q$ the finite field of q elements. For vectors $\mathbf{u}=(u_0,u_1,\dots ,u_n)$ and $\mathbf{v}=(u_0,v_1,\dots ,v_n)$ in $\mathbb {F}_{q^{k_0}}\times \mathbb {F}_{q^{k_1}}\times \cdots \times \mathbb {F}_{q^{k_n}}$ with integers $k_i\geqslant 1$, we define the Schur product $\mathbf{u}*\mathbf{v}$ to be the componentwise product of $\mathbf{u}$ and $\mathbf{v}$, i.e., $\mathbf{u}*\mathbf{v}=(u_0v_0,u_1v_1,\dots ,u_nv_n)$. The notion Schur product plays a crucial role in multiplicative LSSS. Although the secret space $\mathbb {F}_{q^{k_0}}$ and share spaces $\mathbb {F}_{q^i}$ can be different, both of them are $\mathbb {F}_q$-linear.

For an subset A of $\{0\}\cup [n]$, define the projection $\mathrm {proj}_A(\mathbf{u})$ of $\mathbf{u}$ at A by $(u_i)_{i\in A}$. For an $\mathbb {F}_q$-subspace C of $\mathbb {F}_{q^{k_0}}^s\times \mathbb {F}_{q^{k_1}}\times \cdots \times \mathbb {F}_{q^{k_n}}$, we denote by $C^{*2}$ the $\mathbb {F}_q$-linear span of $\{\mathbf{b}*\mathbf{c}:\; \mathbf{b},\mathbf{c}\in C\}$. Motivated by multiplicative secret sharing schemes, the square codes $C^{*2}$ have been extensively studied [8, 21, 23, 24]. To have a good multiplicative secret sharing scheme from an $\mathbb {F}_q$-linear code C, we require that the square code $C^{*2}$ and its dual code $C^{\perp }$ should have large minimum distance. That means, we need a special class of linear codes so that we can control the dimension and minimum distance of $C^{*2}$. There are some candidates satisfying this requirement, e.g. Reed-Solomon codes and algebraic geometry codes.

For convenience, we require that all-one vector $\mathbf{1}$ belongs to C. If this happens, then C becomes an $\mathbb {F}_q$-linear subspace of $C^{*2}$. C is said to be unitary if C contains the all-one vector $\mathbf{1}$.

Definition 1

A q-ary linear secret sharing scheme on n players with secret space $\mathbb {F}_{q^\ell }^s$, share space $\mathbb {F}_{q^k}$ is an $\mathbb {F}_q$-subspace C of $\mathbb {F}_{q^\ell }^s\times \mathbb {F}_{q^k}^{n}$ such that (i) $\mathrm {proj}_{\{0\}}(C)=\mathbb {F}_{q^\ell }^s$; and (ii) the map $C\rightarrow \mathrm {proj}_{[n]}(C)$; $(\mathbf{c}_0,c_1,c_2,\dots ,c_n)\mapsto (c_1,c_2,\dots ,c_n)$ is a bijection, i.e., for any $\mathbf{c}\in C$, $\mathrm {proj}_{[n]}(\mathbf{c})=\mathbf{0}$ if and only if $\mathbf{c}=\mathbf{0}$. Thus, for a codeword $(\mathbf{c}_0,c_1,c_2,\dots ,c_n)\in C$, the map $\rho$ sending $(c_1,c_2,\dots ,c_n)$ to $\mathbf{c}_0$ is well defined. We call $\rho$ the share-to-secret map. Furthermore, $c_i$ is called the i-th share and $\mathbf{c}_0$ is called the secret.

It can be easily shown that (i) a subset A of [n] is authorized⁹ if $\mathrm {proj}_A(\mathbf{c})=\mathbf{0}$ implies $\mathrm {proj}_{A\cup \{0\}}(\mathbf{c})=\mathbf{0}$; and (ii) a subset B of [n] is unauthorized¹⁰ if for any $\mathbf{c}_0\in \mathrm {proj}_0(C)$, there is a codeword $\mathbf{c}\in C$ such that $\mathrm {proj}_B(\mathbf{c})=\mathbf{0}$ and $\mathrm {proj}_{\{0\}}(\mathbf{c})=\mathbf{c}_0$. The $\mathrm {proj}_A$ plays the same role as the map $\pi _A$ in Definition 1 [5].

Definition 2

Let $C\subseteq \mathbb {F}_{q^\ell }^s\times \mathbb {F}_{q^k}^{n}$ be an LSSS.

• (i) C is said to have r-reconstruction if for any subset A of [n] of size at least r and $\mathbf{c}\in C$, one has that $\mathrm {proj}_A(\mathbf{c})=\mathbf{0}$ if and only if $\mathrm {proj}_{A\cup \{0\}}(\mathbf{c})=\mathbf{0}$ (note that an LSSS on n players always has n-reconstruction).

• (ii) We say that C has t-privacy if for any subset A of [n] of size at most t and $\mathbf{u}\in \mathbb {F}_{q^\ell }^s$, there is a codeword $\mathbf{c}\in C$ such that $\mathrm {proj}_A(\mathbf{c})=\mathbf{0}$ and $\mathrm {proj}_{\{0\}}(\mathbf{c})=\mathbf{u}$.

• (iii) We say that C is a t-strongly multiplicative LSSS if C has t-privacy and $C^{*2}$ has r-reconstruction for any $r\leqslant n-t$ (note that C is 0-strongly multiplicative if and only if $C^{*2}$ is an LSSS). In this case, t is called corruption tolerance of C.

• (iv) Let $\mathcal {C}=\{C_i\}_{i=1}^\infty$ be a family of LSSS. Suppose that each $C_i$ is a $t_i$-strongly multiplicative LSSS on $n_i$ players. If $\lim _{i\rightarrow \infty }n_i=\infty$ and $\lim _{i\rightarrow \infty }\frac{t_i}{n_i}=\tau$, we say that $\mathcal {C}$ is $\tau$-strongly multiplicative.

• (v) Let $\mathcal {C}=\{C_i\}_{i=1}^\infty$ be a family of LSSS. Suppose that each $C_i$ has $n_i$ players. We say $\mathcal {C}$ has density $\theta$ if $\lim _{i\rightarrow \infty }n_i=\infty$ and $\limsup _{i\rightarrow \infty }\frac{n_{i}}{n_{i-1}}\leqslant \theta$.

Lemma 1

Let $C\subseteq \mathbb {F}_{q^\ell }^s\times \mathbb {F}_{q^k}^{n}$ be an LSSS. Then $C^{*2}$ has t-privacy as long as C has t-privacy.

Proof

Let $\mathbf{c}_0\in \mathrm {proj}_0(C^{*2})$. Let B be a subset of [n] of size at most t. Let $\mathbf{c}=\sum \lambda _i\mathbf{b}_i*\mathbf{c}_i\in C^{*2}$ with $\mathrm {proj}_0(\mathbf{c})=\mathbf{c}_0$ for some $\lambda _i\in \mathbb {F}_q$ and $\mathbf{b}_i,\mathbf{c}_i\in C$. Then there exist $\mathbf{u}_i,\mathbf{v}_i\in C$ such that $\mathrm {proj}_B(\mathbf{u}_i)=\mathrm {proj}_B(\mathbf{v}_i)=\mathbf{0}$ and $\mathrm {proj}_0(\mathbf{u}_i)=\mathrm {proj}_0(\mathbf{b}_i)$, $\mathrm {proj}_0(\mathbf{v}_i)=\mathrm {proj}_0(\mathbf{c}_i)$. Put $\mathbf{w}=\sum \lambda _i\mathbf{u}_i*\mathbf{v}_i\in C^{*2}$. Then $\mathrm {proj}_B(\mathbf{w})=\mathbf{0}$ and $\mathrm {proj}_0(\mathbf{w})=\sum \lambda _i\mathrm {proj}_0(\mathbf{u}_i)*\mathrm {proj}_0(\mathbf{v}_i)=\sum \lambda _i\mathrm {proj}_0(\mathbf{b}_i)*\mathrm {proj}_0(\mathbf{c}_i)=\mathbf{c}_0$. The proof is completed.

One of the key ideas of this paper is to exploit concatenation techniques which have been widely used in coding theory. We resort to this concatenation technique to achieve quasi-linear time strongly-multiplicative LSSS. Let us briefly describe the concatenation technique in coding theory. Let $C_0\subseteq \mathbb {F}_q^{n_0}$ be a linear code over $\mathbb {F}_q$ of dimension $k_0$ and let $C_1\subseteq \mathbb {F}_{q^{k_0}}^{n_1}$ be an $\mathbb {F}_{q}$-linear code of dimension $k_1$. Fix an $\mathbb {F}_q$-linear isomorphism $\phi$ from $\mathbb {F}_{q^{k_0}}$ to $C_0$. Then the concatenated code $C=\{(\phi (c_1),\phi (c_2),\dots ,\phi (c_{n_1}):\; (c_1,c_2,\dots ,c_{n_1})\in C_1\}$ is an $\mathbb {F}_q$-linear code of length $n_0n_1$ and dimension $k_1$. There are various purposes in coding theory for concatenation. For instance, one can construct long codes over small field through long codes over large field. As for secret sharing scheme, we can also apply this concatenation technique accordingly with some variation. One can view this technique as re-sharing the share. The formal definition is given below.

Definition 3

Let $C_0$ be a q-ary linear secret sharing scheme on $n_0$ players with secret space $\mathbb {F}_{q^k}$, share space $\mathbb {F}_{q}$. Let $C_1$ be a q-ary linear secret sharing scheme on $n_1$ players with secret space $\mathbb {F}_{q^\ell }$, share space $\mathbb {F}_{q^k}$. Then the concatenated LSSS is a q-ary linear secret sharing scheme on $n_0n_1$ players with secret space $\mathbb {F}_{q^\ell }$, share space given by

$$\begin{aligned} C=\{(c_0,\mathbf{c}_1,\dots ,\mathbf{c}_{n_1})\in \mathbb {F}_{q^\ell }\times (\mathrm {proj}_{[n_0]}(C_0))^{n_1}: (c_0,\rho (\mathbf{c}_1),\dots ,\rho (\mathbf{c}_{n_1}))\in C_1\}, \end{aligned}$$

where $\rho$ is the share-to-secret map for the LSSS $C_0$. Then C is a subset of $\mathbb {F}_{q^\ell }\times \mathbb {F}_q^{n_0n_1}$.

Remark 1

• (i) Let us verify that this concatenated scheme is an LSSS with secret space $\mathbb {F}_{q^\ell }$. Suppose $(c_0,\mathbf{c}_1,\dots ,\mathbf{c}_{n_1})\in C$ with $\mathbf{c}_i=\mathbf{0}$ for all $1\leqslant i\leqslant n_1$. Then we have $\rho (\mathbf{c}_i)=0$. This forces $c_0=0$ as $C_1$ is an LSSS. To prove that $\mathrm {proj}_{\{0\}}(C)=\mathbb {F}_{q^\ell }$, we pick an arbitrary element $c_0\in \mathbb {F}_{q^\ell }$. Then there exists a vector $(c_0,a_1,a_2,\dots ,a_n)\in C_1\subseteq \mathbb {F}_{q^\ell }\times \mathbb {F}_{q^k}^{n_1}$. As $\mathrm {proj}_{\{0\}}(C_0)=\mathbb {F}_{q^k}$, there exists $\mathbf{c}_i\in \mathrm {proj}_{[n_0]}(C_0)$ such that $(a_i,c_i)\in C_0$ for all $1\leqslant i\leqslant n_1$. This implies that $(c_0,\mathbf{c}_1,\dots ,\mathbf{c}_{n_1})\in C$. Hence, $\mathrm {proj}_{\{0\}}(C)=\mathbb {F}_{q^\ell }$.

• (ii) It is clear that the concatenated LSSS is still $\mathbb {F}_q$-linear. The $\mathbb {F}_q$-dimension of C is $\dim (C_1)+n_1(\dim (C_0)-k)$. To see this, each secret $\alpha \in \mathbb {F}_{q^k}$, there are $q^{\dim (C_0)-k}$ possible ways of re-sharing. Thus, for a given a $(n+1)$-tuple $(c_0,c_1,\dots ,c_{n_1})$, there are $q^{n_1(\dim (C_0)-k)}$ ways of re-sharing. Hence, the total number of elements in C is $q^{\dim (C_1)+n_1(\dim (C_0)-k)}$.

Let C be a unitary LSSS and assume that $C^{*2}$ is an LSSS. Let $\rho$ be the share-to-secret map of C. Then $\rho$ can be extended to the share-to-secret map of $C^{*2}$, i.e., the share-to-secret map $\rho '$ of $C^{*2}$ satisfies $\rho '|_C=\rho$.

Definition 4

Let C be a unitary LSSS and $\rho$ be the share-to-secret map of C. We say $\rho$ is multiplicative if $\rho (\mathbf{u}*\mathbf{v})=\rho (\mathbf{u})\rho (\mathbf{v})$ for any $\mathbf{u},\mathbf{v}\in \mathrm {proj}_{[n]}(C)$. C is said to be multiplicative if $C^{*2}$ is an LSSS and $\rho$ is multiplicative.

Remark 2

Whenever we say that the share-to-secret map $\rho$ of a q-ary LSSS C is multiplicative, the conditions that C is unitary and $\rho$ can be extended to the share-to-secret map of $C^{*2}$ are satisfied.

Lemma 2

Let $C_0$ be a q-ary linear secret sharing scheme on $n_0$ players with secret space $\mathbb {F}_{q^k}$, share space $\mathbb {F}_{q}$. Let $C_1$ be a q-ary linear secret sharing scheme on $n_1$ players with secret space $\mathbb {F}_{q^\ell }$, share space $\mathbb {F}_{q^k}$. Let $\rho _i$ be the share-to-secret map of $C_i$ for $i=0,1$. If $C_i$ is multiplicative for $i=0,1$, then

• (i) $C^{*2}$ is an $\mathbb {F}_q$-subspace of the concatenated LSSS $\varSigma$ of $C^{*2}_0$ with $C_1^{*2}$, where C is the concatenated LSSS $C_0$ with $C_1$, i.e., $C=\{(c_0,\mathbf{c}_1,\dots ,\mathbf{c}_{n_1})\in \mathbb {F}_{q^\ell }\times (\mathrm {proj}_{[n_0]}(C_0))^{n_1}:\; (c_0,\rho _0(\mathbf{c}_1),\dots ,\rho _0(\mathbf{c}_{n_1}))\in C_1\}$.

• (ii) C is also multiplicative.

Proof

To prove Part (i), we have to show that $(b_0,\mathbf{b})*(c_0,\mathbf{c})=(b_0c_0,\mathbf{b}*\mathbf{c})\in \varSigma$ for any $(b_0,\mathbf{b}), (c_0,\mathbf{c})\in C$. This is true since

$$\begin{aligned}&(b_0c_0,\rho _0(\mathbf{b}_1*\mathbf{c}_1),\dots ,\rho _0(\mathbf{b}_{n_1}*\mathbf{c}_{n_1}))\\&=(b_0c_0,\rho _0(\mathbf{b}_1)\rho _0(\mathbf{c}_1),\dots ,\rho _0(\mathbf{b}_{n_1})\rho _0(\mathbf{c}_{n_1}))\in C_1^{*2}, \end{aligned}$$

and $(\rho _0(\mathbf{b}_i)\rho _0(\mathbf{c}_i),\mathbf{b}_i*\mathbf{c}_i)\in C_0^{*2}$. We conclude $C^{*2}$ is an $\mathbb {F}_q$-subspace of $\varSigma$.

It remains to check that C is multiplicative. By the definition of share-to-secret map $\rho$ of C, for any $(c_0,\mathbf{c}_1,\dots ,\mathbf{c}_{n_1})\in C$, we have $\rho _1(\rho _0(\mathbf{c}_1),\dots ,\rho _0(\mathbf{c}_{n_1}))=c_0=\rho (\mathbf{c}_1,\dots ,\mathbf{c}_{n_1})$. Then, for any $(b_0,\mathbf{b}),(c_0,\mathbf{c})\in C$ with $\mathbf{b}=(\mathbf{b}_1,\dots ,\mathbf{b}_{n_1})$ and $\mathbf{c}=(\mathbf{c}_1,\dots ,\mathbf{c}_{n_1})$, we have

$$\begin{aligned} \rho (\mathbf{b}*\mathbf{c})= & {} \rho _1(\rho _0(\mathbf{b}_1*\mathbf{c}_1),\dots ,\rho _0(\mathbf{b}_{n_1}*\mathbf{c}_{n_1}))\\= & {} \rho _1(\rho _0(\mathbf{b}_1)\rho _0(\mathbf{c}_1),\dots ,\rho _0(\mathbf{b}_{n_1})\rho _0(\mathbf{c}_{n_1}))\\= & {} \rho _1((\rho _0(\mathbf{b}_1),\dots ,\rho _0(\mathbf{b}_{n_1}))*(\rho _0(\mathbf{c}_1),\dots ,\rho _0(\mathbf{c}_{n_1}))\\= & {} \rho _1(\rho _0(\mathbf{b}_1),\dots ,\rho _0(\mathbf{b}_{n_1}))\rho _1(\rho _0(\mathbf{c}_1),\dots ,\rho _0(\mathbf{c}_{n_1}))=\rho (\mathbf{b})\rho (\mathbf{c}) \end{aligned}$$

This completes the proof.

The above lemma shows that a concatenated LSSS is multiplicative as long as both $C_0$ and $C_1$ are multiplicative. In fact we can further show that this concatenated LSSS is strongly-multiplicative as long as both $C_0$ and $C_1$ are strongly-multiplicative.

Lemma 3

Let $C_0$ be a q-ary LSSS on $n_0$ players with secret space $\mathbb {F}_{q^k}$, share space $\mathbb {F}_{q}$. Let $C_1$ be a q-ary LSSS on $n_1$ players with secret space $\mathbb {F}_{q^\ell }$, share space $\mathbb {F}_{q^k}$. If $C_i$ has $r_i$-reconstruction and $t_i$-privacy for $i=0,1$. Then the concatenated LSSS C defined in Definition 3 has $n_0n_1-(n_0-r_0+1)(n_1-r_1+1)$-reconstruction and has $(t_0+1)t_1$-privacy.

Furthermore, if $C_1^{*2}$ (and $C_0^{*2}$, respectively) has $r'_1$ (and $r'_0$, respectively)-reconstruction and the share-to-secret maps $\rho _i$ of $C_i$ are multiplicative for $i=0,1$, then C is a t-strongly multiplicative LSSS with $t=\min \{(t_0+1)t_1, (n_0-r'_0+1)(n_1-r'_1+1)\}$.

Proof

Given a codeword $\mathbf{c}$ in C, we can write $\mathbf{c}=(c_0,c_{1,1},\ldots ,c_{1,n_0},c_{2,1},$ $\ldots ,c_{2,n_0},\ldots ,c_{n_1,n_0})$ where $\mathbf{c}_i=(c_{i,1},\ldots ,c_{i,n_0})$ is a share-vector of $C_0$. Let S be the collection of indices of C, i.e., $S:=\{0,(1,1),\dots ,(1,n_0),(2,1),\dots ,(2,n_0),\cdots ,$ $(n_1,1),\dots ,(n_1,n_0)\}$. Let A be a subset of $S\setminus \{0\}$ and $A_i=A\cap \{(i,1),\dots ,(i,n_0)\}$ for $i=1,2,,\dots , n_1$. Then A is partitioned into $\cup _{i=1}^nA_i$. Let $B_i=\{j: (i,j)\in A_i\}$. It is clear that $|B_i|=|A_i|$ and $B_i$ is a subset of $[n_0]$. This gives $\sum _{i=1}^{n_1}|B_i|=|A|$.

If $|A|\geqslant n_0n_1-(n_0-r_0+1)(n_1-r_1+1)$, then there exists a subset $I\subseteq [n_1]$ with $|I|\geqslant r_1$ such that $|B_i|\geqslant r_0$ for all $i\in I$. Otherwise, we have $|A|\le n_1(r_0-1)+(n_0-r_0+1)(r_1-1)<n_0n_1-(n_0-r_0+1)(n_1-r_1+1).$ If $\mathbf{c}=(c_0,\mathbf{c}_1,\dots ,\mathbf{c}_{n_1})\in C$ such that $\mathrm {proj}_A(\mathbf{c})=\mathbf{0}$, then $\mathrm {proj}_{B_i}(\mathbf{c}_i)=\mathbf{0}$ for all $i\in I$. As $|B_i|\geqslant r_0$ and $C_0$ has $r_0$-reconstruction, we must have $\rho _0(\mathrm {proj}_{B_i}(\mathbf{c}_i))=0$. Thus, $\mathrm {proj}_I(\rho _0(\mathbf{c}_1),\dots ,\rho _0(\mathbf{c}_{n_1}))=\mathbf{0}$. This implies that $c_0=0$ since $|I|\geqslant r_1$.

Now we consider the case where $|A|\leqslant (t_0+1)t_1$. Let J be the subset of $[n_1]$ such that $|B_j|\geqslant t_0+1$ if and only if $j\in J$. Then $|J|\leqslant t_1$. Let $\alpha \in \mathbb {F}_{q^\ell }$. We choose a vector $\mathbf{c}=(c_0,c_1,\dots ,c_{n_1})\in C_1$ such that $\mathrm {proj}_J(\mathbf{c})=0$ and $\mathrm {proj}_{\{0\}}(\mathbf{c})=\alpha$. For $j\in J$, let $\mathbf{u}_j=\mathbf{0}$. For $j\not \in J$, choose $\mathbf{u}_j\in C_0$ such that $\rho _0(\mathbf{u}_j)=c_j$ and $\mathrm {proj}_{B_j}(\mathbf{u}_j)=\mathbf{0}$. This implies that $\mathbf{u}:=(\alpha ,\mathbf{u}_1,\dots ,\mathbf{u}_{n_1})\in C$ and $\mathrm {proj}_A(\mathbf{u})=0$.

Now, we turn to furthermore part of the claim. The assumption says that $C_1^{*2}$ and $C_0^{*2}$ has $r'_1$ and $r'_0$-reconstruction respectively. By Lemma 2, $C^{*2}$ is an $\mathbb {F}_q$-subspace of the concatenated LSSS $\varSigma$ of $C^{*2}_0$ with $C_1^{*2}$. By the first part of the proof, $\varSigma$ has $(n_0n_1-(n_0-r'_0+1)(n_1-r'_1+1))$-reconstruction and hence $C^{*2}$ also has $(n_0n_1-(n_0-r'_0+1)(n_1-r'_1+1))$-reconstruction. The desired result follows.

Remark 3

To the best of our knowledge, no prior work considered concatenation of two strongly-multiplicative LSSSs. Perhaps the most relevant reference is the multiplication friendly embedding in [5]. Multiplication friendly embedding can be viewed as a multiplicative LSSS without privacy.

3 Quasi-linear Time LSSS with Strong Multiplication

3.1 Secret Space Is the Extension Field $\mathbb {F}_{q^m}$

The parameters of LSSS based on Reed-Solomon codes and algebraic geometry codes can be found in appendix. In general, those codes derived from algebraic curves can be converted into a LSSS with strong multiplication. This becomes the building block of our quasi-linear time LSSS. Our LSSS is obtained via the concatenation of two LSSS, one based on Reed-Solomon codes and another one based on algebraic geometry codes. The following theorem shows that the density of our LSSS can be 1 as long as we pick an asymptotically good algebraic geometry code as an inner code.

Theorem 1

Let q be an even power of a prime. Then for any positive real $\varepsilon \in \left( 0,\frac{1}{2}-\frac{2}{\sqrt{q}-1}\right)$ and $\eta \in (0,\frac{1}{2})$, there exists a family $\mathcal {C}=\{\varGamma _i\}_{i=1}^{\infty }$ of $\tau _q$-strongly multiplicative q-ary LSSS with density 1, each $\varGamma _i$ has $N_i$ players, secret space $\mathbb {F}_{q^{s_i}}$ and quasi-linear time (depending on $\varepsilon$) for share generation and secret reconstruction, where

$$\begin{aligned} \tau _q=\frac{1}{9}(1-2\eta )\left( 1-2\varepsilon -\frac{4}{\sqrt{q}-1}\right) ,\quad \frac{s_i}{N_i}\rightarrow \varepsilon \eta . \end{aligned}$$

Proof

Let $\{C_i\}_{i=1}^\infty$ be the family of q-ary LSSS with the same $\varepsilon$ and $\gamma$ given in Theorem 6. We can set $\gamma =\frac{1}{3}(1+\varepsilon +\frac{2}{\sqrt{q}-1})$. Note that we have $\frac{k_i}{k_{i-1}}\rightarrow \sqrt{q}$ and $\frac{n_i}{n_{i-1}}\rightarrow \sqrt{q}$. Put $t_i=n_i-2\lfloor \gamma n_i\rfloor$, $r_i=\lfloor \gamma n_i\rfloor$ and $\alpha =\frac{1}{\sqrt{q}}$, $\lambda =\frac{1}{3}(1+\eta )$.

Consider $\varSigma _{ij}:=\textsf {RS}_{k_i,R_{ij}}[N_{ij},K_{ij}]_q$ with $N_{ij}=\alpha q^{k_{i-1}}+j$ and $K_{ij}=\lfloor \lambda N_{ij}\rfloor ,$ $R_{ij}=\lfloor \eta N_{ij}\rfloor$ for $j=0, 1,2,\dots ,q^{k_i}-\alpha q^{k_{i-1}}$ and $i\geqslant 2$. Then by Lemma 2, the concatenated LSSS of $C_i$ with $\varSigma _{ij}$ is a q-ary LSSS $\varGamma _{ij}$ on $n_iN_{ij}$ players of secret space $\mathbb {F}_{q^{k_iR_{ij}}}$, share space $\mathbb {F}_q$. By Lemmas 2, 3 and Theorem 6, it has $t_{ij}$-privacy with $t_{ij}=(t_i+1)(K_{ij}-R_{ij}-1)$. Furthermore, $\varGamma _{ij}^{*2}$ has $r_{ij}$-reconstruction with

$$\begin{aligned} r_{ij}=N_{ij}n_i-(N_{ij}-2K_{ij}+1)(n_i-2r_i+1). \end{aligned}$$

where $r_i=\lfloor \gamma n_i\rfloor$. Put $\tau _{ij}=\min \{(t_i+1)(K_{ij}-R_{ij}-1),(N_{ij}-2K_{ij}+1)(n_i-2r_i+1)\}$. Due to the setting of our parameters, $t_i\approx n_i-2r_i$ and $K_{ij}-R_{ij}\approx N_{ij}-2K_{ij}$, we come to the conclusion that

$$\begin{aligned} r_{ij}=(N_{ij}-2K_{ij}+1)(n_i-2r_i+1), \qquad \frac{\tau _{ij}}{N_{\varGamma _{ij}}}=\frac{\tau _{ij}}{n_iN_{ij}}\rightarrow \tau _q. \end{aligned}$$

As the secret space of $\varGamma _{ij}$ is $\mathbb {F}_{q^{k_iR_{ij}}}$ and the number of players is $n_iN_{ij}$, we have $\frac{k_iR_{ij}}{n_iN_{ij}}\rightarrow \eta \varepsilon$.

Now we arrange the order of $\varGamma _{ij}$ in the following way

$$\begin{aligned} \varGamma _{1,0},\varGamma _{2,0},\dots , \varGamma _{2,q^{k_2}-\alpha q^{k_1}},\varGamma _{3,0},\dots , \varGamma _{3,q^{k_3}-\alpha q^{k_2}},\varGamma _{4,0},\dots , \varGamma _{4,q^{k_4}-\alpha q^{k_3}},\dots . \end{aligned}$$

(1)

The number of players $N_{\varGamma _{ij}}$ of $\varGamma _{ij}$ is $n_i(\alpha q^{k_{i-1}}+j)$. Thus we have, (i) for $1\leqslant j\leqslant q^{k_i}-\alpha q^{k_{i-1}}$

$$\begin{aligned} \frac{N_{\varGamma _{i,j}}}{N_{\varGamma _{i,j-1}}}=\frac{n_i(\alpha q^{k_{i-1}}+j)}{n_i(\alpha q^{k_{i-1}}+j-1)}=1+\frac{1}{\alpha q^{k_{i-1}}+j-1}\rightarrow 1, \end{aligned}$$

and (ii) for $i\geqslant 2$

$$\begin{aligned} \frac{N_{\varGamma _{(i+1),0}}}{N_{\varGamma _{i,q^{k_i}-\alpha q^{k_{i-1}}}}}=\frac{n_{i+1} \alpha q^{k_{i}}}{n_{i}q^{k_{i}}}=\frac{\alpha n_{i+1}}{n_{i}}\rightarrow 1. \end{aligned}$$

By abuse of notation, we denote the ith LSSS in (1) by $\varGamma _i$. Let $N_i$ be the number of players of $\varGamma _i$. Then we have $\frac{N_i}{N_{i-1}}\rightarrow 1$ as i tends to $\infty$.

Finally, we analyze time complexity for share generation and secret reconstruction. Note that $N_{ij}\geqslant n_iq^{k_{i-1}}$. As $k_i=\varOmega _\varepsilon (n_i)$, we have $n_i=O_\varepsilon (\log _q N_{ij})$. The share generation consists of encoding of $\varSigma _{ij}$ which is quasi-linear in $q^{k_i}$, and share generation of LSSS in Theorem 6 which is polynomial in $n_i$. Hence, the total time complexity of share generation is quasi-linear in the number of players. As for secret reconstruction, by Lemma 15, a similar analysis shows that the time complexity is also quasi-linear in the number of players. This completes the proof.

Our concatenation idea can greatly reduce the complexity of construction, sharing secret and reconstructing secret by letting this algebraic geometry code to be an inner LSSS. If the number of players of this inner LSSS is small enough, we do not even need an explicit construction of it. In fact, we can brute force all possible generator matrix of algebraic geometry code C such that C, its dual code $C^{\perp }$ and its square code $C^{*2}$ are all asymptotically good. All we have to acknowledge is the existence of such code. This could allow us to present an explicit construction of strongly multiplicative LSSS based on a quasi-linear time searching algorithm without any prior knowledge of algebraic geometry codes.

Theorem 2

Let q be an even power of a prime. Then for any positive real $\varepsilon \in \left( 0, \frac{1}{2}-\frac{2}{\sqrt{q}-1}\right)$, $\lambda \in (0,\frac{1}{2})$ and $\eta \in (0,\frac{1}{2})$, there exists an quasi-linear time elementary algorithm to generate a family $\mathcal {C}$ of $\tau _q$-strongly multiplicative q-ary LSSS on $N_i$ players with density 1, secret space $\mathbb {F}_{q^{s_i}}$ and quasi-linear time (depending on $\varepsilon$) for share generation and secret reconstruction, where

$$\begin{aligned} \tau _q=\frac{1}{27}(1-2\eta )(1-2\lambda )(1-2\varepsilon -\frac{4}{\sqrt{q}-1}),\qquad \frac{s_i}{N_i}\rightarrow \eta \lambda \varepsilon . \end{aligned}$$

Proof

We notice that it takes $q^{O(n^2)}$ times to enumerate generator matrices of all linear codes in $\mathbb {F}_q^n$. For each linear code C, we check its multiplicative property by checking minimum distance, dual distance and the distance of $C^{*2}$. We know the existence of this linear code by algebraic geometry codes given in Sect. 3. This algorithm must find at least one such a code. The question is now reduced to how to make our exhaustive search algorithm run in quasi-linear time. It turns out that if $n=\log \log N$, the running time is then sublinear in N. Moreover, the encoding and reconstructing time is bounded by $\exp (O(n))=O(\log N)$.

To let our exhaustive search to be quasi-linear, we have to concatenate twice instead of once. Theorem 1 says there exists a class of $\frac{1}{9}(1-2\eta )(1-2\varepsilon -\frac{4}{\sqrt{q}-1})$-strongly multiplicative q-ary LSSS $C_i$ on $n_i$ players with secret space $\mathbb {F}_{q^{s_i}}$ and share space $\mathbb {F}_q$ such that $\lim _{i\rightarrow \infty } \frac{n_{i+1}}{n_i}=1$ and $\frac{s_i}{n_i}=\eta \varepsilon$. We use this $C_i$ to be our new inner LSSS. Our outer LSSS is a Shamir secret sharing scheme defined as follows. Let $D_{ij}$ be a Shamir secret sharing scheme on $N_{ij}$ players with secret space $\mathbb {F}_{q^{\lambda N_{ij}s_i}}$ and share space $\mathbb {F}_{q^{s_i}}$ such that $N_{ij}=q^{s_{i-1}}+j$ for $j=1,\ldots ,q^{s_i}-q^{s_{i-1}}$. By Lemma 13, $D_{ij}$ is a class of $(1-2\lambda )$-strongly multiplicative LSSS with density 1. Then by Lemma 2 and Lemma 3, the concatenation $\varSigma _{ij}$ of $D_{ij}$ with $C_i$ yields a $\tau _q N_{ij}n_i$-strongly LSSS on $N_{ij}n_i$ players with secret space $\mathbb {F}_{q^{\lambda N_{ij}s_i}}$ and share space $\mathbb {F}_q$ where $\frac{\lambda N_{ij}s_i}{N_{ij}n_i}=\frac{\lambda s_i}{n_i}=\lambda \eta \varepsilon$. Moreover, $\varSigma _{ij}$ has density 1 as both of the inner LSSS $C_i$ and the outer LSSS $D_{ij}$ have density 1. Note that the inner LSSS in $C_i$ is derived from algebraic geometry code. We want to construct it via exhaustive search instead of exploiting its mathematical structure. By Theorem 1, the number of players in $C_i$ is $O(\log _q s_i)=O(\log _q \log _q N_{ij} )$. Our desired result follows.

Remark 4

• (i) Reducing time complexity via concatenation is not a new technique for coding theorists and it can be dated back to 1966 [14]. They discovered that the concatenation of codes yields a large constructive family of asymptotically good codes. To show the existence of codes with some special property, we usually resort to randomness argument. The concatenation idea allows us to reduce the space of our inner code and make it possible to find it in polynomial time. Different from the traditional randomness argument, our existence argument depends on the result from algebraic geometry codes, i.e., showing the existence of asymptotically-good code C, its dual $C^{\perp }$ and its square code $C^{*2}$. This extra multiplicative property creates some difficulties in finding the desirable codes by concatenating only once. Instead, we concatenate twice so as to further narrowing down the searching space.

• (ii) If we abandon either quasi-linear time construction claim or elementary algorithm claim, we only need to concatenate once. As a result, this concatenated LSSS is $\frac{1}{9}(1-2\lambda )(1-2\varepsilon -\frac{4}{\sqrt{q}-1})$-strongly multiplicative.

3.2 Reverse Multiplication Friendly Embedding

As we have seen, the secret space of LSSS in the previous subsection is an extension field $\mathbb {F}_{q^m}$. In order to convert $\mathbb {F}_{q^m}$ to a secret space $\mathbb {F}_q^k$, we need reverse multiplication friendly embeddings (RMFE for short).

Before introducing RMFEs, let us recall multiplication friendly embedding that have found various applications such as complexity of multiplication in extension fields [4], hitting set construction [18] and concatenation of LSSS [5].

Definition 5

Let q be a power of a prime and let $\mathbb {F}_q$ be a field of q elements, let $k, m\geqslant 1$ be integers. A pair $(\sigma ,\pi )$ is called a $(k,m)_q$-multiplication friendly embedding (MFE for short) if $\sigma :\mathbb {F}_{q^k}\rightarrow \mathbb {F}_q^m$ and $\pi : \mathbb {F}_q^m\rightarrow \mathbb {F}_{q^k}$ are two $\mathbb {F}_q$-linear maps satisfying

$$\begin{aligned} \alpha \beta =\pi (\sigma (\alpha )*\sigma (\beta )) \end{aligned}$$

for all $\alpha ,\beta \in \mathbb {F}_{q^k}$. A multiplication friendly embedding $(\sigma ,\pi )$ is called unitary if $\sigma (1)=\mathbf{1}$.

It is easy to verify that the map $\sigma$ must be injective and $\sigma (\mathbb {F}_{q^k})$ is a q-ary [m, k]-linear code with minimum distance at least k. So far, the only way to construct $(k,m)_q$-multiplication friendly embedding with $m=O(k)$ is via algebraic curves over finite fields [4]. Now we explain how multiplication friendly embeddings are used to concatenate LSSS.

Assume that $C\subset \mathbb {F}_{q^m}\times \mathbb {F}_{q^k}^{n}$ is an LSSS and let $(\sigma ,\pi )$ be a $(k,m)_q$-multiplication friendly embedding. Consider the concatenation:

$$\begin{aligned} \sigma (C)=\{(c_0,\sigma (c_1),\sigma (c_2),\dots ,\sigma (c_n)):\; (c_0,c_1,c_2,\dots ,c_n)\in C\}. \end{aligned}$$

Then $\sigma (C)\subseteq \mathbb {F}_q^{m(n+1)}$.

Lemma 4

Let $(\sigma ,\pi )$ be a unitary multiplication friendly embedding. Then $\sigma (C)$ is a multiplicative LSSS as long as C is a multiplicative LSSS.

Proof

Assume that C is a multiplicative LSSS. If $(c_0,c_1,c_2,\dots ,c_n)\in C$ and $(\sigma (c_1),\dots ,\sigma (c_n))=\mathbf{0}$, then $\sigma (c_i)=\mathbf{0}$ for all $1\leqslant i\leqslant n$. As $\sigma$ is injective, we have $c_i=0$. Hence, $c_0=0$. This means that $\sigma (c_0)=\mathbf{0}$. Thus, $\sigma (C)$ is an LSSS.

Next we show that $\sigma (C)^{*2}$ is an LSSS. Let $(b_0,b_1,b_2,\dots ,b_n),(c_0,c_1,c_2,\dots ,c_n)\in C$ and $\sigma (b_1,b_2,$ $\dots ,b_n)*\sigma (c_1,c_2,\dots ,c_n)=\mathbf{0}$, i.e., $\sigma (b_i)*\sigma (c_i)=\mathbf{0}$ for all $1\leqslant i\leqslant n$. Then we have $0=\pi (\sigma (b_i)*\sigma (c_i))=b_ic_i$. This implies that $b_0c_0=0$ since $C^{*2}$ is an LSSS.

To prove multiplicativity, let $\rho$ and $\rho '$ be the share-to-secret maps of C and $\sigma (C)$, respectively. Let $(b_0,b_1,b_2,\dots ,b_n),(c_0,c_1,c_2,\dots ,c_n)\in C$. Since C is multiplicative,

$$\begin{aligned} \rho ((b_1,b_2,\dots ,b_n)*(c_1,c_2,\dots ,c_n))=b_0c_0. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \rho '(\sigma (b_1,b_2,\dots ,b_n)*\sigma (c_1,c_2,\dots ,c_n))=b_0c_0=\rho '(\sigma (b_1,b_2,\dots ,b_n))\rho '(\sigma (c_1,c_2,\dots ,c_n)).\end{aligned}$$

This completes the proof.

Remark 5

Concatenation of an LSSS via a unitary multiplication friendly embedding does not maintain privacy although it maintains multiplitivity because dual distance of $\sigma (C)$ is destroyed. That is why we introduce our concatenation of LSSS given in this paper to maintains both privacy and multiplitivity as shown in Lemmas 2 and 3.

By applying the concatenation techniques given in this paper, we are able to bring down share size to a constant at a constant fractional loss in privacy and reconstruction (see Lemma 3). However, our secret is still defined over the extension field of the share space. For most applications of multiplicative secret sharing schemes, the share space is a fixed finite field $\mathbb {F}_q$ and the secret space is desirably $\mathbb {F}_q^k$ for some integer $k\geqslant 1$. We make use of reverse multiplication friendly embedding to convert the secret space from the extension field $\mathbb {F}_{q^m}$ to $\mathbb {F}_q^k$ while still maintaining strong multiplitivity.

Let us first give a formal definition of RMFE.

Definition 6

Let q be a power of a prime and let $\mathbb {F}_q$ be a field of q elements, let $k, m\geqslant 1$ be integers. A pair $(\phi ,\psi )$ is called an $(k,m)_q$-reverse multiplication friendly embedding if $\phi :\mathbb {F}_q^k\rightarrow \mathbb {F}_{q^m}$ and $\psi : \mathbb {F}_{q^m}\rightarrow \mathbb {F}_q^k$ are two $\mathbb {F}_q$-linear maps satisfying

$$\begin{aligned} \mathbf{x}*\mathbf{y}=\psi (\phi (\mathbf{x})\cdot \phi (\mathbf{y})) \end{aligned}$$

for all $\mathbf{x},\mathbf{y}\in \mathbb {F}_q^k$.

The definition of RMFE was first proposed in [10]. Thanks to this technique, the authors managed to bring down the amortized complexity of communication complexity from $O(n\log n)$ to O(n) for Shamir-based MPC protocols over any finite field. The key observation is that the classic threshold MPC protocols requires large field to implement the hyper-invertible matrix technique and the threshold secret sharing scheme. Therefore, even faced with MPC protocol over binary field, one has to choose an extension field for its share while the secret is still restricted to the binary field, a subfield of its secret space. This causes another $\varOmega (\log n)$ overhead. In fact, the authors in [10] noticed that such overhead can be amortized away if one can convert the extension field of the secret space into a vector space so that it is possible to implement several multiplication in parallel via RMFE.

In this work, we need RMFE for a different purpose, namely, we convert the extension field $\mathbb {F}_{q^m}$ of the secret space into a vector space $\mathbb {F}_q^k$ via RMFE while maintaining strong multiplicitivity.

Lemma 5

If $(\phi ,\psi )$ is a $(k,m)_q$-RMFE, then $\phi$ is injective and $m\geqslant 2k-1$.

Proof

Let $\mathbf{x},\mathbf{y}\in \mathbb {F}_q^k$ such that $\phi (\mathbf{x})=\phi (\mathbf{y})$. Let $\mathbf{1}\in \mathbb {F}_q^k$ be the all-one vector. Then we have

$$\begin{aligned} \mathbf{x}=\mathbf{1}*\mathbf{x}=\psi (\phi (\mathbf{1})\phi (\mathbf{x}))=\psi (\phi (\mathbf{1})\phi (\mathbf{y}))=\mathbf{1}*\mathbf{y}=\mathbf{y}. \end{aligned}$$

This shows the injectivity of $\phi$.

To show the second claim, let us show that $\psi$ is surjective. For any $\mathbf{x}\in \mathbb {F}_q^k$, we have $\psi (\phi (\mathbf{1})\phi (\mathbf{x}))=\mathbf{1}*\mathbf{x}=\mathbf{x}$. This means that $\psi$ is surjective. Let $\mathbf{u}\in \mathbb {F}_q^k$ be the vector $(1,0,0,\dots ,0)$. Consider the set $A:=\{\mathbf{x}\in \mathbb {F}_q^k:\; \psi (\phi (\mathbf{u})\phi (\mathbf{x}))=\mathbf{0}\}$. As $\psi (\phi (\mathbf{u})\phi (\mathbf{x}))=\mathbf{u}*\mathbf{x}=(x_1,0,0,\dots ,0)$, we have $A=\{(0,\mathbf{c}):\; \mathbf{c}\in \mathbb {F}_q^{k-1}\}$. It is clear that $\phi (\mathbf{u})\phi (A)$ is a subspace of the kernel of $\psi$. As the dimension of $\phi (\mathbf{u})\phi (A)$ is $k-1$, we have that $m=\dim (\ker (\psi ))+\dim (\mathrm {Im}(\psi ))\geqslant \dim (\phi (\mathbf{u})\phi (A))+k=k-1+k=2k-1$.

Though we have the inequality $m\geqslant 2k-1$, it was shown in [10] that, via construction of algebraic function fields, one has $m=O(k)$ with a small hidden constant.

Lemma 6

(see [10]). Let $F/\mathbb {F}_q$ be a function field of genus ${\mathfrak {g}}$ with k distinct rational places $P_1,P_2,\dots ,P_k$. Let G be a divisor of F such that $\mathrm{supp }(G)\cap \{P_1,\dots ,P_k\}=\emptyset$ and $\deg (G)\geqslant 2{\mathfrak {g}}-1+k$. If there is a place R of degree m with $m>2\deg (G)$, then there exists an $(k,m)_q$-RMFE.

Let us briefly recall construction of the RMFE given in Lemma 6. Consider the map

$$\begin{aligned} \pi :\; \mathcal {L}(G)\rightarrow \mathbb {F}_q^k;\quad f\mapsto (f(P_1),\dots ,f(P_k)). \end{aligned}$$

Then $\pi$ is surjective. Thus, we can choose a subspace V of $\mathcal {L}(G)$ of dimension k such that $\pi (V)=\mathbb {F}_q^k$. We write by $\mathbf{c}_f$ the vector $(f(P_1),\dots ,f(P_k))$, and by f(R) the evaluation of f in the higher degree place R, for a function $f\in \mathcal {L}(2G)$. We now define

$$\begin{aligned} \phi :\; \pi (V)=\mathbb {F}_q^k\rightarrow \mathbb {F}_{q^m};\quad \mathbf{c}_f\mapsto f(R)\in \mathbb {F}_{q^m}. \end{aligned}$$

Note that the above $f\in V$ is uniquely determined by $\mathbf{c}_f$. The map $\psi$ can then be defined (see the detail in [10, Lemma 6]). Thus, the time complexity of constructing such a RMFE consists of finding a basis of $\mathcal {L}(G)$ and evaluation of functions of $\mathcal {L}(G)$ at the place R and the rational places $P_1,P_2,\dots ,P_k$.

As the algebraic geometry code associated with this function field tower can not run in quasi-linear time, we need to apply our concatenation idea again so as to give rise to a quasi-linear time RMFE.

Lemma 7

(see [10]). Assume that $(\phi _1,\psi _1)$ is an $(n_1,k_1)_{q^{k_2}}$-RMFE and $(\phi _2,\psi _2)$ is an $(n_2,k_2)_{q}$-RMFE. Then $\phi :\; \mathbb {F}_q^{n_1n_2}\rightarrow \mathbb {F}_{q^{k_1k_2}}$

$$\begin{aligned} (\mathbf{x}_1,\dots ,\mathbf{x}_{n_1})\mapsto (\phi _2(\mathbf{x}_1),\dots ,\phi _2(\mathbf{x}_{n_1}))\in \mathbb {F}_{q^{k_2}}^{n_1}\mapsto \phi _1(\phi _2(\mathbf{x}_1),\dots ,\phi _2(\mathbf{x}_{n_1})) \end{aligned}$$

and $\psi :\; \mathbb {F}_{q^{k_1k_2}}\rightarrow \mathbb {F}_q^{n_1n_2}$

$$\begin{aligned} \alpha \mapsto \psi _1(\alpha )=(\mathbf{u}_1,\dots ,\mathbf{u}_{n_1})\in \mathbb {F}_{q^{k_2}}^{n_1}\mapsto (\psi _2(\mathbf{u}_1),\dots ,\psi _2(\mathbf{u}_{n_1})) \end{aligned}$$

give an $(n_1n_2,k_1k_2)_q$-RMFE.

Lemma 8

The Reed-Solomon code leads to a $(k,r)_q$-RMFE $(\phi ,\psi )$ for all $2\le r\le 2q$ and $k\leqslant r/2$. Furthermore, the pair $(\phi ,\psi )$ can be computed in quasi-linear time.

Proof

Apply the rational function field $\mathbb {F}_q(x)$ to the construction of RMFE given in Lemma 6. Choose an irreducible polynomial R of $\mathbb {F}_q[x]$ of degree r and k distinct elements $\alpha _1,\alpha _2,\dots ,\alpha _k$ of $\mathbb {F}_q$. Then it turns out that the codes are Reed-Solomon codes and hence $(\phi ,\psi )$ can be computed in time $O(k\log ^2 k\log \log k)$ (see [2]).

By applying the Garcia-Stichtenoth tower to the construction of the RMFE given in Lemma 6, we obtain the following result.

Lemma 9

For any integer $a>1$, there exists a family of $(k,a)_q$-RMFEs with $k\rightarrow \infty$ and $\lim _{k\rightarrow \infty }\frac{a}{k}\rightarrow 2+\frac{4}{\sqrt{q}-1}$ that can be computed in time $O(a^3)$.

Lemma 10

For any integers $a>1$ and r with $2r\leqslant q^a$, there exists a family of $(k,ar)_q$-RMFEs with $k\rightarrow \infty$ and $\lim _{k\rightarrow \infty }\frac{ar}{k}=4+\frac{8}{\sqrt{q}-1}$ that can be computed in time $O(a^3+r\log ^2 r\log \log r)$.

Proof

Let $(\phi _1,\psi _1)$ be a $(k_1,r)_{q^a}$-RMFE with $k_1= \lfloor r/2\rfloor$ given in Lemma 8 and let $(\phi _2,\psi _2)$ be a $(k_2,a)_q$-RMFE with $\frac{a}{k_2}\rightarrow 2+\frac{4}{\sqrt{q}-1}$ given in Lemma 9. By Lemma 7, concatenation of these two RMFEs gives an $(k_1k_2,ar)_q$-RMFE $(\phi ,\psi )$ with $\frac{ar}{k_1k_2}\rightarrow 4+\frac{8}{\sqrt{q}-1}$. Moreover, since $(\phi _1,\psi _1)$ is associated with Reed-Solomon codes, it can be computed in time $O(r\log ^2 r\log \log r)$. As $(\phi _2,\psi _2)$ is constructed via the Garcia-Stichtenoth tower, it can be computed in time $O(a^3)$. The overall running time for $(\phi ,\psi )$ is then upper bounded by $O(a^3+r\log ^2 r\log \log r)$.

Recall that we claim that our LSSS is generated by an elementary algorithm. In this sense, This RMFE should also be produced by an elementary algorithm. We again resort to exhaustive search instead of using Garcia-Stichtenoth tower to find this RMFE. As we argue in Theorem 2, we need to concatenate twice instead of once. The first two RMFEs are associated with Reed-Solomon codes and the third one is found by exhaustive search and guaranteed by Lemma 9. The exhaustive search consists of enumerating all linear subspaces $C\subseteq \mathbb {F}_q^{\log \log n}$ and determining the distance, dual distance of C and the distance of its square code $C^{*2}$. The first step takes time $2^{\varOmega (\log \log n)^2}$ and the second step takes time $2^{\varOmega (\log \log n)}$. Therefore, this exhaustive search will find the desired linear subspaces in less than O(n) time. Emulating the proof of Lemma 10 gives the following result.

Lemma 11

There exists an quasi-linear time elementary algorithm to generate a family of $(k_i,m_i)_q$-RMFEs with $k_i\rightarrow \infty$ and $\lim _{i\rightarrow \infty }\frac{m_i}{k_i}=8+\frac{16}{\sqrt{q}-1}$ that can be computed in time $O(m_i\log ^2 m_i\log \log m_i)$.

Given a LSSS $\varSigma$ with secret space $\mathbb {F}_{q^m}$, the following theorem shows how to obtain a LSSS with secret space $\mathbb {F}_q^k$ by applying RMFE to the secret space of $\varSigma$.

Theorem 3

Assume that there is a t-strongly multiplicative linear secret sharing scheme C with secret space $\mathbb {F}_{q^m}$ and share space $\mathbb {F}_q$. If there exists a $(k,m)_q$-RMFE $(\phi ,\psi )$, then there exists a t-strongly multiplicative linear secret sharing scheme $\varSigma$ with secret space $\mathbb {F}_q^k$. Moreover, the time complexity of share generation and secret reconstruction of $\varSigma$ is bounded by that of C and $(\phi ,\psi )$.

Proof

Note that for any $\mathbf{s}\in \mathbb {F}_q^k$, $\phi (\mathbf{s})\in \mathbb {F}_{q^m}$. Let

$$\begin{aligned} C_1=\{(\mathbf{s},c_1,\ldots ,c_n): \mathbf{s}\in \mathbb {F}_q^k,(\phi (\mathbf{s}),c_1,\ldots ,c_n)\in C\} \end{aligned}$$

where $\mathbf{s}$ is the secret and $c_i$ is the i-th share. Let us show that $C_1$ is indeed a LSSS with the secret space $\mathbb {F}_q^k$. If $(\mathbf{s},c_1,\ldots ,c_n)\in C_1$ with $(c_1,\ldots ,c_n)=\mathbf{0}$, then we must have $\phi (\mathbf{s})=0$ since $(\phi (\mathbf{s}),c_1,\ldots ,c_n)\in C$. As $\phi$ is injective, this forces that $\mathbf{s}=\mathbf{0}$. Hence, $C_1$ is a LSSS. To show that the secret space is $\mathbb {F}_q^k$, we choose an arbitrary $\mathbf{s}\in \mathbb {F}_q^k$. Then $\phi (\mathbf{s})\in \mathbb {F}_{q^m}$. As the secret space of C is $\mathbb {F}_{q^m}$, there exists a vector $(c_1,\ldots ,c_n)\in \mathbb {F}_q^n$ such that $(\phi (\mathbf{s}),c_1,\ldots ,c_n)\in C$. Thus, $(\mathbf{s},c_1,\ldots ,c_n)$ belongs to $C_1$.

It is clear that $C_1$ is an $\mathbb {F}_q$-LSSS as $\phi$ is a linear map and C is an $\mathbb {F}_q$-LSSS. We next show that $C_1$ has t-privacy and $C_1^{*2}$ has $(n-t)$-reconstruction. The t-privacy argument follows from the fact that C has t-privacy and $\{(\phi (\mathbf{s}),c_1,\ldots ,c_n)\in C:\mathbf{s}\in \mathbb {F}_q^k\}$ is a subset of C. As C is multiplicative, we can find the secret-to-share map $\rho$ such that for $(b_0,\mathbf{b}),(c_0,\mathbf{c})\in C$ with $\mathbf{b}=(b_1,\dots ,b_{n})$ and $\mathbf{c}=(c_1,\dots ,c_{n})$,

$$\begin{aligned} \rho (\mathbf{b}* \mathbf{c})=\rho (\mathbf{b})\rho (\mathbf{c})=b_0c_0. \end{aligned}$$

For any $(\mathbf{s},c_1,\ldots ,c_n)\in C_1$, we define the share-to-secret map

$$\begin{aligned} \rho _1(c_1,\ldots ,c_n)=\psi \circ \rho (c_1,\ldots ,c_n)= \psi (\phi (\mathbf{s})\cdot \phi (\mathbf {1}))=\mathbf{s}. \end{aligned}$$

The second step is due to the fact that C is unitary. To see that $C_1$ is multiplicative, for any $(\mathbf{x},x_1,\ldots ,x_n)$, $(\mathbf{y},y_1,\ldots ,y_n)\in C_1$, we have

$$\begin{aligned} \rho _1(x_1y_1,\ldots ,x_ny_n)=\psi \circ \rho (x_1y_1,\ldots ,x_ny_n)=\psi (\phi (\mathbf{x})\cdot \phi (\mathbf{y}))=\mathbf{x}*\mathbf{y}. \end{aligned}$$

The last step comes from the definition of RMFE. It remains to prove the $(n-t)$-reconstruction of $C_1^{*2}$. We note that $(\mathbf{s},c_1,\ldots ,c_n)\in C_1^{*2}$ indicates that $(\phi (\mathbf{s}),c_1,\ldots ,c_n)\in C^{*2}$. That means we can reconstruct $\phi (\mathbf{s})$ from any $(n-t)$ shares in $(c_1,\ldots ,c_n)$ due to the $(n-t)$-reconstruction property of $C^{*2}$. The desired result follows as $\mathbf{s}=\psi \circ \phi (\mathbf{s})$.

3.3 Make the Secret Space to Be $\mathbb {F}_q^k$

Putting Theorems 1, 3 and Lemma 10 together leads to our main results.

Theorem 4

Let q be any even power of prime. Then for any positive real $\varepsilon \in (0,\frac{1}{2}-\frac{2}{\sqrt{q}-1})$ and $\eta \in (0,\frac{1}{2})$, there exists a family $\mathcal {C}$ of $\tau _q$-strongly multiplicative q-ary LSSS on $N_i$ players with density 1, secret space $\mathbb {F}_q^{s_i}$ and quasi-linear time for share generation and secret reconstruction, where

$$\begin{aligned} \tau _q=\frac{1}{9}(1-2\eta )\left( 1-2\varepsilon -\frac{4}{\sqrt{q}-1}\right) ,\qquad \frac{s_i}{N_i}\rightarrow \varepsilon \eta \left( \frac{1}{4+\frac{8}{\sqrt{q}-1}}\right) . \end{aligned}$$

Proof

Note that the secret space of $\varGamma _i$ in Theorem 1 is $\mathbb {F}_{q^{k_iR_{ij}}}$. By Lemma 10, there exists a $(s_i,k_iR_{ij})_q$-RMFE $(\phi ,\psi )$ with $\frac{k_iR_{ij}}{s_i}\rightarrow \frac{1}{4+\frac{8}{\sqrt{q}-1}}$ that can be computed in time $O(k_i^3+R_{ij}\log ^2R_{ij}\log \log R_{ij})=O(N_i\log ^2N_i\log \log N_i)$ as $k_i=O(\log R_{ij})$. The desired result follows from Theorem 3.

By emulating the proof of Theorem 2 and referring to RMFE in Lemma 11, we can also obtain a similar result without resorting to the Garcia-Stichtenoth tower at a cost of slightly worse strong multiplicative property.

Theorem 5

(Elementary construction of LSSS with strong multiplicative property). Let q be any even power of prime. Then for any positive real $\varepsilon \in (0,\frac{1}{2}-\frac{2}{\sqrt{q}-1})$ and $\eta \in (0,\frac{1}{2})$, there exists a quasi-linear time elementary algorithm to generate a family $\mathcal {C}$ of $\tau _q$-strongly multiplicative q-ary LSSS on $N_i$ players with density 1, secret space $\mathbb {F}_q^{s_i}$ and quasi-linear time (depending on $\varepsilon$) for share generation and secret reconstruction, where

$$\begin{aligned} \tau _q=\frac{1}{27}(1-2\eta )(1-2\lambda )\left( 1-2\varepsilon -\frac{4}{\sqrt{q}-1}\right) ,\qquad \frac{s_i}{N_i}\rightarrow \frac{\varepsilon \eta \lambda }{8+\frac{16}{\sqrt{q}-1}}. \end{aligned}$$

Appendices

A LSSS from Algebraic Curves

As we have seen, a concatenated LSSS consists of two LSSSs, one used as an inner LSSS and another one used as an outer LSSS. In this section, we provide a construction of LSSS via algebraic function fields. This gives us LSSSs with desired property. Let us briefly recall some background on algebraic function fields. The reader may refer to [27] for the details.

A function field $F/\mathbb {F}_q$ is an algebraic extension of the rational function field $\mathbb {F}_q(x)$, that contains all fractions of polynomials in $\mathbb {F}_q[x]$. Associated to a function field, there is a non-negative integer ${\mathfrak {g}}$ called the genus, and an infinite set of “places” P, each having a degree $\deg P\in \mathbb {N}$. The number of places of a given degree is finite. The places of degree 1 are called rational places. Given a function $f\in F$ and a place P, two things can happen: either f has a pole in P, or f can be evaluated in P and the evaluation f(P) can be seen as an element of the field $\mathbb {F}_{q^{\deg P}}$. If f and g do not have a pole in P then the evaluations satisfy the rules $\lambda (f(P))=(\lambda f)(P)$ (for every $\lambda \in \mathbb {F}_q$), $f(P)+g(P)=(f+g)(P)$ and $f(P)\cdot g(P)=(f\cdot g)(P)$. Note that if P is a rational place (and f does not have a pole in P) then $f(P)\in \mathbb {F}_q$. The functions in F always have the same zeros and poles up to multiplicity (called order). An important fact of the theory of algebraic function fields is as follows: call $N_1(F)$ the number of rational places of F. Then over every finite field $\mathbb {F}_q$, there exists an infinite family of function fields $\{F_n\}$ such that their genus ${\mathfrak {g}}_n$ grow with n and $\lim _{n\rightarrow \infty } N_1(F_n)/{\mathfrak {g}}_n=c_q$ with $c_q\in \mathbb {R}$, $c_q>0$. The largest constant $c_q$ satisfying the property above is called Ihara’s constant A(q) of $\mathbb {F}_q$. It is known that $0<A(q)\le \sqrt{q}-1$ for every finite field $\mathbb {F}_q$. Moreover, $A(q)=\sqrt{q}-1$ for a square q. The result is constructive, since explicit families of function fields attaining these values are known and given in [15, 16].

A divisor G is a formal sum of places, $G=\sum c_P P$, such that $c_P\in \mathbb {Z}$ and $c_P=0$ except for a finite number of P. We call this set of places where $c_P\ne 0$ the support of G, denoted by $\mathrm{supp }(G)$. The degree of G is $\deg G:=\sum c_P \deg P\in \mathbb {Z}$.

The Riemann-Roch space $\mathcal {L}(G)$ is the set of all functions in F with certain prescribed poles and zeros depending on G (together with the zero function). More precisely if $G=\sum c_P P$, every function $f\in \mathcal {L}(G)$ must have a zero of order at least $|c_P|$ in the places P with $c_P<0$, and f can have a pole of order at most $c_P$ in the places with $c_P>0$. The space $\mathcal {L}(G)$ is a vector space over $\mathbb {F}_q$. Its dimension is governed by certain laws (given by the so-called Riemann-Roch theorem). A weaker version of that theorem called Riemann’s theorem states that if $\deg G\ge 2{\mathfrak {g}}-1$ then $\dim \mathcal {L}(G)=\deg (G)-{\mathfrak {g}}+1$. On the other hand, if $\deg G<0$, then $\dim \mathcal {L}(G)=0$.

Lastly, we note that, given $f,g\in \mathcal {L}(G)$, its product $f\cdot g$ is in the space $\mathcal {L}(2G)$.

Lemma 12

Let $F/\mathbb {F}_q$ be a function field of genus ${\mathfrak {g}}$ with $n+1$ distinct rational places ${P_{\infty }},P_1,$ $P_2,\dots ,P_n$. If there is a place ${P_0}$ of degree $k>1$ and $n/2>m\geqslant k+2{\mathfrak {g}}-1$, then there exists a q-ary LSSS C satisfying

• (i) C has $(m+1)$-reconstruction and $(m-k-2{\mathfrak {g}}+1)$-privacy.

• (ii) The share-to-secret map $\rho$ of C is multiplicative.

• (iii) $C^{*2}$ has $(2m+1)$-reconstruction.

Proof

Denote by $F_{P_0}$ the residue class field of place ${P_0}$. Then we know that $F_{P_0}\simeq \mathbb {F}_{q^k}$. For a function f that is regular at $P_0$, we denote by $f({P_0})$ the residue class of f in $F_{P_0}$. Consider the map $\pi :\; f\in \mathcal {L}(G)\mapsto (f({P_0}),f(P_1),\dots ,f(P_n))\in F_{P_0}\times \mathbb {F}_q^n\simeq \mathbb {F}_{q^k}\times \mathbb {F}_q^n$ and define

$$\begin{aligned} C:=\mathrm{Im}(\pi )=\{(f({P_0}),f(P_1),\dots ,f(P_n)):\; f\in \mathcal {L}(m{P_{\infty }})\}\subseteq F_{P_0}\times \mathbb {F}_q^n. \end{aligned}$$

For a subset A of $\{0\}\cup [n]$, we denote by $\pi _A$ the map

$$\begin{aligned} f\in \mathcal {L}(G)\mapsto \mathrm {proj}_A(f({P_0}),f(P_1),\dots ,f(P_n)). \end{aligned}$$

Since the kernel of $\pi _{\{0\}}$ is $\mathcal {L}(m{P_{\infty }}-{P_0})$ and $\dim \mathcal {L}(m{P_{\infty }})-\dim \mathcal {L}(m{P_{\infty }}-{P_0})=k$, $\pi _{\{0\}}$ is surjective. Hence, we have $\mathrm {proj}_0(C)=\mathbb {F}_{q^k}$.

Let A be a subset of [n]. If $|A|\geqslant m+1$ and $\mathrm {proj}_A(f({P_0}),f(P_1),\dots ,f(P_n))=\mathbf{0}$. Then $f\in \mathcal {L}(m{P_{\infty }}-\sum _{i\in A}P_i)$. This implies that $f=0$ as $\deg \left( m{P_{\infty }}-\right. \left. \sum _{i\in A}P_i\right) <0$. Therefore, $f({P_0})=0$.

If $|A|\leqslant m-k-2{\mathfrak {g}}+1$, then $\dim \mathcal {L}\left( m{P_{\infty }}\right) -\dim \mathcal {L}\left( m{P_{\infty }}-\sum _{i\in A}P_i-{P_0}\right) =k+|A|$. This implies that $\pi _{\{0\}\cup A}$ is surjective. Hence, for any $\alpha \in F_{P_0}$, there is a function f such that $\mathrm {proj}_A(f({P_0}),f(P_1),\dots ,f(P_n))=0$ and $f({P_0})=\alpha$.

Next we will prove that the share-to-secret map of C is multiplicative. First, we note that C is unitary as $1\in \mathcal {L}(m{P_{\infty }})$. Consider the $\mathbb {F}_q$-linear space

$$\begin{aligned} \varSigma =\{(f({P_0}),f(P_1),\dots ,f(P_n)):\; f\in \mathcal {L}(2m{P_{\infty }})\}\subseteq F_{P_0}\times \mathbb {F}_q^n. \end{aligned}$$

Then $\varSigma$ contains $C^{*2}$. As $2m+1\leqslant n$, the vector $(f(P_1),\dots ,f(P_n))$ determines the function $f\in \mathcal {L}(2m{P_{\infty }})$ uniquely, and hence $f(P_0)$. Therefore, $\varSigma$ has n-reconstruction. Thus, we can define the share-to-secret map $\rho$: $\rho (f(P_1),\dots ,f(P_n))=f(P_0)$. It is clear that $\rho$ is an extension of the share-to-secret map of C. Furthermore, for any two functions $f,g\in \mathcal {L}(m{P_{\infty }})$, we have $fg\in \mathcal {L}(2m{P_{\infty }})$. Hence, we have

$$\begin{aligned}&\rho ((f(P_1),\dots ,f(P_n))*(g(P_1),\dots ,g(P_n)))=\rho ((fg)(P_1),\dots ,(fg)(P_n))\\&=(fg)(P_0)=f(P_0)g(P_0). \end{aligned}$$

Since $\varSigma$ has $(2m+1)$-reconstruction, so does $C^{*2}$.

1.1 A.1 Construction via Reed-Solomon Codes

Let $\alpha _1,\dots ,\alpha _N\in \mathbb {F}_{q^k}$ be N pairwise distinct nonzero elements. Let $\alpha _0$ be a root of an irreducible polynomial over $\mathbb {F}_{q^k}$ of degree $\ell$. Denote by $\mathbb {F}_{q^k}[x]_{<K}$ the set of polynomials over $\mathbb {F}_{q^k}$ of degree less than K. The Reed-Solomon code is defined by

$$\begin{aligned} \textsf {RS}_{k,\ell }[N,K]_q:=\{(f(\alpha _0),f(\alpha _1),\dots ,f(\alpha _N)):\; f\in \mathbb {F}_{q^k}[x]_{<K}\}\subset \mathbb {F}_{q^{k\ell }}\times \mathbb {F}_{q^k}^N. \end{aligned}$$

Applying Lemma 12 to the rational function fields gives the following result.

Lemma 13

Let $\textsf {RS}_{k,\ell }[N,K]_q$ be the Reed-Solomon code defined above. If $N/2>K-1\geqslant \ell -1$, then it is a $q^k$-ary LSSS on N players with secret space $\mathbb {F}_{q^{k\ell }}$, share space $\mathbb {F}_{q^k}$. Moreover, we have the following properties

• (i) It has K-reconstruction and $(K-\ell )$-privacy.

• (ii) The share-to-secret of $\textsf {RS}_{k,\ell }[N,K]_q$ is multiplicative.

• (iii) $\textsf {RS}_{k,\ell }[N,K]_q^{*2}$ has $(2K-1)$-reconstruction.

• (iv) If $N=\varOmega (q^k)$, then the share generation and secret reconstruction can be computed in time $O(N\log ^2 N\log \log N)$.

Proof

The first three parts follows from Lemma 12 when applying the rational function field $\mathbb {F}_{q^k}(x)$. As the encoding and decoding of a Reed-Solomon code can be run in time $O(N\log ^2 N\log \log N)$ (see [2]), the last claim follows.

1.2 A.2 Garcia-Stichtenoth Tower

In the Garcia-Stichtenoth tower $\{E_i\}$ over $\mathbb {F}_q$, each extension $E_i/E_{i-1}$ has degree $\sqrt{q}$. The detailed result is given below.

Lemma 14

(via Garcia-Stichtenoth tower). Let q be an even power of a prime. Then there exists a family $\{F_i/\mathbb {F}_q\}$ function fields such that

• (i) The number $N(F_i)$ of $\mathbb {F}_q$-rational places is strictly increasing as i increases.

• (ii) $\lim _{i\rightarrow \infty }\frac{N(F_i)}{{\mathfrak {g}}(F_i)}=\sqrt{q}-1$, where ${\mathfrak {g}}(F_i)$ denotes the genus of $F_i$.

• (iii) $\lim _{i\rightarrow \infty }\frac{N(F_i)}{N(F_{i-1})}=\sqrt{q}$.

Furthermore, algebraic-geometry codes of length n based on this family can be encoded and decoded in time $O(n^3\log ^2 q)$ (see [26]).

1.3 A.3 Construction via Garcia-Stichtenoth Tower

By applying the Garcia-Stichtenoth tower given in Lemma 14 and the construction of LSSS given in Lemma 12, we obtain the following result.

Theorem 6

(via Garcia-Stichtenoth tower). Assume q is an even power of a prime. Let $\varepsilon \in \left( 0, \frac{1}{2}-\frac{2}{\sqrt{q}-1}\right)$ and $\gamma \in \left( 0,\frac{1}{2}\right)$ be two reals with $\gamma \geqslant \varepsilon +\frac{2}{\sqrt{q}-1}$. Then there exists a sequence $\{C_i \}$ of q-ary LSSS on $n_i$ players with the secret space $\mathbb {F}_{q^{k_i}}$, the share space $\mathbb {F}_q$ such that

• (i) $\frac{k_i}{k_{i-1}}\rightarrow \sqrt{q}$.

• (ii) $\lim _{i\rightarrow \infty }\frac{k_i}{n_i}=\varepsilon .$

• (iii) $C_i$ has $\lfloor \gamma n_i\rfloor$-reconstruction and $t_i$-privacy satisfying $\frac{t_i}{n_i}\rightarrow \gamma -\frac{2}{\sqrt{q}-1}-\varepsilon$.

• (iv) $C_i^{*2}$ has $2\lfloor \gamma n_i\rfloor$-reconstruction.

• (v) the share-to-secret map $\rho _i$ of $C_i$ is multiplicative.

• (vi) $C_i$ can be constructed and computed in time $O(n_i^3)$.

Proof

Let $\{F_i/\mathbb {F}_q\}$ be the family of the function fields given in Lemma 14. Put $n_i=N(F_i)-1$, $m_i=\lfloor \gamma n_i\rfloor -1$ and $k_i=\lfloor \varepsilon n_i\rfloor$. Then $n_i/2>m_i\geqslant k_i+2{\mathfrak {g}}(F_i)-1$ and

$$\begin{aligned} \frac{k_{i}}{k_{{i-1}}}=\frac{\lfloor \varepsilon n_i\rfloor }{\lfloor \varepsilon n_{i-1}\rfloor }\rightarrow \sqrt{q}. \end{aligned}$$

The desired results on Parts (i)–(v) follow from Lemma 12.

B Decode Concatenated Codes up to Its Unique Decoding Radius

A naive decoding algorithm for concatenated code can not correct errors up to its unique decoding radius. Let us explain why a naive algorithm fails to achieve this goal. Let C be a concatenated code with an inner code $C_1$ and outer code $C_0$. Let $En_0$ and $En_1$ be the encoding algorithm of $C_0$ and $C_1$ respectively. Let $Dec_0$ and $Dec_1$ be the decoding algorithm of $C_0$ and $C_1$ respectively. Given a codeword $\mathbf{c}\in C$, we can write $\mathbf{c}=(\mathbf{c}_1,\ldots ,\mathbf{c}_n)$ with $\mathbf{c}_i\in C_1$. Let $\mathbf{y}=(\mathbf{y}_1,\ldots ,\mathbf{y}_n)$ be a corrupted codeword. The naive decoding algorithm goes as follows: we first decode each substring $\mathbf{y}_i$ by running the unique decoding algorithm $Dec_1(\mathbf{y}_i)$. Let $\mathbf{c}_i=Dec_1(\mathbf{y}_i)$ and $x_i$ be the message encoded to $\mathbf{c}_i$, i.e., $En_1(x_i)=\mathbf{c}_i$. The second step of our decoding algorithm is to decode $(x_1,\ldots ,x_n)$ by running $Dec_0$. Since the decoding algorithm of inner code and outer code can correct errors up to half of its minimum distance, this decoding strategy can correct errors up to one-fourth of its minimum distance.

Forney [14] proposed a randomized algorithm to decoding concatenated code up to its unique decoding radius provided that the decoding algorithms of inner code and outer code are available. The time complexity of this random decoding algorithm is the same as that of the naive decoding algorithm. Let us briefly introduce this algorithm. This randomized algorithm first runs the decoding algorithm of inner code on each $\mathbf{y}_i$ of $\mathbf{y}=(\mathbf{y}_1,\ldots ,\mathbf{y}_n)$, i.e., $\mathbf{c}_i:=Dec_1(\mathbf{y}_i)$. Let $\mathbf{e}_i=\mathbf{c}_i-\mathbf{y}_i$ be the error vector. This randomized algorithm labels coordinate i an erasure error with probability $\frac{2wt(\mathbf{e}_i)}{d}$. Then, we run the erasure and error decoding algorithm of the outer code on $(x_1,\ldots ,x_n)$ with $En_1(x_i)=\mathbf{c}_i$ or $x_i=\perp$. This randomized algorithm can be further derandomized at the cost of $\log n$ factor increase in the time complexity [17] by setting a threshold w such that an erasure error happens when $\frac{2wt(\mathbf{e}_i)}{d}\ge w$. We summarize the result in the following lemma and refer interested readers to Chap. 12 in [17] for details.

Lemma 15

Let C be a concatenated code whose inner code $C_1$ is a linear code of length N and minimum distance D and outer code $C_0$ is a linear code of length n and minimum distance d. Assume that the decoding algorithm of $C_0$ can correct e errors and r erasures with $2e+r\le D-1$ in time $T_0(N)$ and the decoding algorithm of $C_1$ can correct errors up to its unique decoding radius $\frac{d-1}{2}$ in time $T_1(n)$. Then, there exists a deterministic decoding algorithm for C that can correct errors up to its unique decoding radius $\frac{Dd-1}{2}$ and run in time $O((T_1(n)N+T_0(N))n)$.

Remark 6

If we let $n=O(\log N)$, $T_0(N)$ be quasi-linear in N and $T_1(n)$ is a polynomial in n. Then, the total running time is quasi-linear in N and thus quasi-linear in the code length of C. We will see that our concatenated LSSS meets this condition. Thus, we can assume that our concatenated LSSS can be decoded up to its unique decoding radius.