Lower Bounds on the Degree of Block Ciphers

Abstract

Only the method to estimate the upper bound of the algebraic degree on block ciphers is known so far, but it is not useful for the designer to guarantee the security. In this paper we provide meaningful lower bounds on the algebraic degree of modern block ciphers.

1 Introduction

Along with stream ciphers and, more recently, permutation based cryptography, block ciphers are among the most efficient cryptographic primitives. As such block ciphers are one of the cornerstones of our cryptographic landscape today and indeed are used to ensure the security for a large fraction of our daily communication. In a nutshell, a block cipher should be an, efficient to implement, family of permutations that cannot be distinguished from a randomly selected family of permutations without guessing the entire secret key. The community has, in general, a rather good understanding of the security of block ciphers and arguments of their security have become significantly more precise and, using tool-based approaches for many aspects, significantly less error-prone. However, for some of the most basic properties a block cipher should fulfill, good arguments are still missing. One of those properties is the algebraic degree of a permutation, resp. the degree of a family of permutations. For a randomly drawn permutation, the degree is $n-1$ almost certainly. Thus, in order to be indistinguishable from a random permutation, a block cipher should also have degree $n-1$. This observation, and generalisations of it, leads indeed to a class of attacks called integral attacks, introduced already in [10, 14]. Very similar concepts are known as high-order differential attacks [15] and cube-attacks [11].

It is highly desirable to be able to argue that a given block-cipher has degree $n-1$, or in general high degree. However, so far, we only have upper bounds on the degree of our ciphers. Those bounds, see e.g., [15] and in particular [6, 8] are very efficient to compute in most cases and far from trivial. Unfortunately, upper bounds on the degree are not very helpful for a designer of a cipher, as this is not what is needed to argue about the security of a given design. What we actually need, and what has not been achieved so far, is to give meaningful lower bounds on the degree.

Algebraic Degree of Keyed (Vectorial) Functions. Before we describe our results, we will define precisely the degree and discuss how lower and upper bounds have to be understood in order to avoid confusion, see e.g., [9] for more background on Boolean functions. Consider a general set-up of a (parameterized, vectorial) Boolean function

$$\begin{aligned} F_k: \mathbb {F}_2^n \rightarrow \mathbb {F}_2^m \end{aligned}$$

with $k \in \mathbb {F}_2^{\ell }$. Any such function can be uniquely described by its algebraic normal form as

$$\begin{aligned} F_k(x) = \sum _{ u \in \mathbb {F}_2^n} p_u(k) x^u \end{aligned}$$

where $x^u$ is short for $\prod _i x_i^{u_i}$ and $p_u(k)$ are functions

$$\begin{aligned} p_u: \mathbb {F}_2^{\ell } \rightarrow \mathbb {F}_2^m \end{aligned}$$

mapping keys to values in $\mathbb {F}_2^m$. If there is no parameter, i.e., no key, then all $p_u$ degenerate naturally to constants and if, on top, it is not a vectorial Boolean function, i.e., if $m=1$, these constants are just bits, i.e., $p_u \in \mathbb {F}_2$. The definition of (algebraic) degree is the same in all cases and is given as

$$\begin{aligned} \deg (F) := \max _u \{{{\,\mathrm{wt}\,}}(u) \ | \ p_u \ne 0 \}. \end{aligned}$$

Here ${{\,\mathrm{wt}\,}}(u)$ denotes the Hamming weight of u, i.e., the number of 1 and this weight corresponds to the number of variables multiplied in $x^u$.

For clarity, consider the case of a keyed vectorial function. The degree of F is d or higher if there exist a u of Hamming weight d such that $p_u$ is not zero, i.e., not the constant zero function.

A lower bound d on the degree of F implies that there exists at least one key and at least one output bit which is of degree at least d. An upper bound d on the degree of F implies that for all keys all output bits are of degree at most d.

For cryptographic purposes, the degree as defined above is not always satisfactory. An attacker can always pick the weakest spot, e.g., an output bit of lowest degree. A vectorial function of high degree might still have very low degree in one specific output bit or, more general, in a specific linear combination of output bits. This motivates the notion of minimum degree. For this, one considers all non-zero linear combination of output bits $\langle \beta , F \rangle$ and the minimum degree of all those Boolean functions

$$\begin{aligned} {{\,\mathrm{minDeg}\,}}(F)=\min _{\beta \ne 0} \deg ( \langle \beta , F \rangle ) . \end{aligned}$$

A lower bound d on the minimum degree of a function implies that for all component functions $\langle \beta , F \rangle$ there exist a key such that the degree of the component function is at least d. An upper bound d on the minimum degree of a function implies that there exist at least one component function that has degree at most d for all keys.

Table 1. Summary of the number of rounds to get full degree/full minimum degree/appearance of all max-degree monomials. We also label “tight” when they fit with the upper bounds.

Fig. 1.

Algebraic degree and minimum degree on SKINNY64, where UB and LB denote upper bound and lower bound, respectively.

Our Results. In this paper we present – for the first time – non-trivial lower bounds on the degree and minimum degree of various block ciphers with the sole assumption of independent round-keys. More precisely, we assume that after each round a new round key is added to the full state.

We hereby focus in particular on the block ciphers that are used most frequently as building blocks in the ongoing NIST lightweight project¹, namely GIFT-64, SKINNY64, and AES. Furthermore, we investigate PRESENT. Our results are summarized in Table 1. To give a concrete example of our results, consider the block cipher SKINNY64   [4]. We are able to show that 10 and 11 rounds are sufficient to get full, i.e., 63, degree and minimum degree, respectively. Together with the known upper bounds, we get a rather good view on the actual degree development of SKINNY64 with increasing number of rounds (see Fig. 1). Besides the degree and the minimum degree, we also elaborate on the appearance of all n possible monomials of maximal degree, i.e., degree $n-1$. While this is not captured by a natural notion of degree, it does capture large classes of integral attacks. With respect to this criterion, we also show that 13 rounds are enough for SKINNY64.

Technical Contribution. Our results are based on the concept of division property and require a non-negligible, but in all cases we consider, practical computational effort. They can be derived within a few hours on a single PC. All code required for our results will be made publicly available.

The main technical challenge in our work (and many previous works based on division property) is to keep the model solvable and the number of division trails in a reasonable range. For our purpose, we solve this by optimizing the division property of the key, a freedom that was (i) previously not considered and (ii) allows to speed-up our computations significantly.

Previous Works. This paper has strong ties with all the previous works related to division property. Division property is a cryptanalysis technique introduced at EUROCRYPT’15 by Todo [19], which was then further refined in several works [20, 21]. Technically, the papers at EUROCRYPT’20 [12] is the most important previous work for us. We will give a more detailed review of previous works in Sect. 2 when also fixing our notation.

Outline. We present our notation related to the division property in Sect. 2. We try to simplify and clarify some previous definitions and results. We hope that in particular readers without prior knowledge on division property might find it accessible. In Sect. 3 we provide a high-level overview of our results and how they were achieved. As mentioned above, the main technical contribution is the optimization for a suitable division-property for the key, which is explained in Sect. 4. Our applications and the detailed results for the ciphers studied are given in Sect. 5. Being the first paper to derive meaningful lower bounds on ciphers by relying only on independent round-keys, our work leaves many open questions and room for improvements. We elaborate on this in Sect. 6 concluding our work.

Finally we note that all our implementations are available at

https://github.com/LowerBoundsAlgDegree/LowerBoundsAlgDegree.

2 Notation and Preliminaries

Let us start by briefly fixing some basic notation. We denote by $\mathbb {F}_2$ the finite field with two elements, basically a bit, and by $\mathbb {F}_2^n$ the n-dimensional vector space over $\mathbb {F}_2$, i.e., the set of n-bit vectors with the XOR operation as the addition. For $x,y \in \mathbb {F}_2^n$ we denote by $\langle x,y \rangle = \sum _i x_i y_i$ the canonical inner product. For a function $F: \mathbb {F}_2^n \rightarrow \mathbb {F}_2^m$ given as $F(x)=(F^{(1)}(x), \dots , F^{(m)}(x))$ with $F^{(i)}: \mathbb {F}_2^n \rightarrow \mathbb {F}_2$, the $F^{(i)}$ are referred to as the coordinate functions of F and any linear combination $\langle \beta , F(x) \rangle$ of those as a component function of F. We use $+$ to denote all kind of additions (of sets, vectors, polynomials, monomials) as it should be clear from context.

In this section we start by recalling the development of division property since its first introduction by Todo  [18]. The technique has been proven very helpful in many applications and led to a large variety of results. The notion of trails  [22] has been an important technical improvement that itself already has undergone several iterations. We try to simplify notations and at the same time make some previous definitions and results more rigid and precise. The aim is to be self contained and accessible to readers without prior knowledge on division property. Before doing so, we briefly recapture the previous developments.

2.1 Previous Works on Division Properties

This paper has strong ties with all the previous works related to division property and as such, we would like to precisely describe where our work fits and what are the precise relations and differences with the division property. Division property is a cryptanalysis technique introduced at EUROCRYPT’15 by Todo as a technique to study the parity of $x^u$ [19]. This initial variant is by now referred to as the conventional division property (CDP). This was further refined to the bit-based division property (BDP) by Todo and Morii at FSE’16 [21]. The core idea of the division property is to evaluate whether the ANF of a block cipher contains some specific monomials. More precisely, given a monomial m in the plaintext variables, the BDP can essentially allows us to derive one of two possible results: either the ANF of a block cipher does not contain any multiple of the monomial m, or we simply do not know anything (i.e., we cannot prove the existence or non-existence of the monomial or its multiples). Another way to see the BDP is that, for a given set $\mathbb {X}$, it splits the space $\mathbb {F}_2^n$ into two distinct parts, depending on the value of the sum $s_u = \sum _{x \in \mathbb {X}} x^u, u \in \mathbb {F}_2^n$:

• A set $\mathbb {K} \subset \mathbb {F}_2^n$ such that for any $u \in \mathbb {K}$, we do not know the value of $s_u$.

• For the remaining $u \in \mathbb {F}_2^n\setminus \mathbb {K}$, we know that $s_u = 0$.

While this was already powerful enough to find new integral distinguishers (e.g. [18, 20]), the imperfect nature of the division property means that some known integral distinguisher could not be explained using the division property. This was noticed by Todo and Morii in their FSE’16 paper, as a 15-round distinguisher over the block cipher SIMON [3] could not be explained with BDP. They thus extended the concept to three-subset division property (3SDP) to cover this distinguisher. Now, for a given monomial, the 3SDP can give us one of the following:

• The ANF does not contains any multiple of the monomial.

• The ANF contains exactly this monomial.

• We cannot prove neither existence nor non-existence of the monomials.

The term three-subset comes from the fact that we now split $\mathbb {F}_2^n$ into three parts: one where we know that $s_u =0$, one where we know that $s_u = 1$ (aka, the $\mathbb {L}$ set), and the results is unknown for the remaining u’s (aka, the $\mathbb {K}$ set). Again, there is still a loss of information and there are some cases where we do not get any information.

The main reason for this loss of information comes from the fact that previous techniques give results that are independent from the key used, hence the inability to precisely compute (parts of) the ANF. This fact was noticed and exploited at EUROCRYPT’20 by Hao et al. [12], where they introduced the three-subset division property without unknown subset (3SDPwoU). Their idea was to remove the “unknown subset”, splitting $\mathbb {F}_2^n$ into two parts, either $s_u = 0$ or $s_u = 1$, however the implication for this is that we can no longer ignore the key. While they applied this technique to stream ciphers, they mentioned that this technique might be used for block ciphers, but left as an open problem.

It is worth noting that this idea of splitting $\mathbb {F}_2^n$ into two parts where either $s_u = 0$ or $s_u = 1$ has also been studied as another view of the division property by Boura and Canteaut at CRYPTO’16 [7] using the term parity set. However, they did not focus on actual algorithmic aspects. For our results, the focus on algorithmic aspects and in particular the notation of division trails is essential.

To summarize, originating with the division property, many variants such as BDP, 3SDP, and the parity set (which is essentially the same as the 3SDPwoU) have been proposed. After many algorithmic improvements for BDP and 3SDP, nowadays, it enables us to evaluate the most extreme variant, parity set, which allows to decide whether or not a specific monomial appears in the ANF.

2.2 Division Properties and the ANF

Any function $F:\mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ can be uniquely expressed with its algebraic normal form.

$$\begin{aligned} F(x) = \sum _{u} \lambda _u x^u \end{aligned}$$

where $\lambda _u \in \mathbb {F}_2^n$. It is well known that the coefficients can be computed via the identity

$$\begin{aligned} \lambda _u= & {} \sum _{x \preceq u } F(x) \end{aligned}$$

(1)

where $x \preceq u \text{ if } \text{ and } \text{ only } \text{ if } x_i \le u_i \text{ for } \text{ all } i$ where elements of $\mathbb {F}_2$ are seen as integers.

We start by recalling the division property, more accurately the definition of parity set, as given in [7].

Definition 1

(Parity Set). Let $\mathbb {X} \subseteq \mathbb {F}_2^n$ be a set. We define the parity set of $\mathbb {X}$ as

$$\begin{aligned} \mathcal {U}(\mathbb {X}) := \left\{ u \in \mathbb {F}_2^n \ \text{ such } \text{ that } \ \sum _{x \in \mathbb {X}} x^u =1 \right\} \end{aligned}$$

The power of the division property as introduced in [19] is that (i) it is often easier to trace the impact of a function on its parity set than on the set itself and (ii) the evolution of certain parity sets is related to the algebraic normal form of the functions involved.

Defining the addition of two subsets $\mathbb {X}, \mathbb {Y} \subseteq F_2^n$ by

$$\begin{aligned} \mathbb {X} + \mathbb {Y} := (\mathbb {X} \cup \mathbb {Y} ) \setminus (\mathbb {X} \cap \mathbb {Y}) \end{aligned}$$

the set of all subsets of $\mathbb {F}_2^n$ becomes a binary vector space of dimension $2^n$. Note that this addition is isomorphic to adding the binary indicator vectors of the sets. Also note that if an element is contained both in $\mathbb {X}$ and $\mathbb {Y}$ is not contained in the sum.

From this perspective $\mathcal {U}$ is a linear mapping and the division property can be seen as a change of basis. In particular for $\mathbb {X}_i \subset \mathbb {F}_2^n$ it holds that

$$\begin{aligned} \mathcal {U}\left( \sum \mathbb {X}_i \right) = \sum \mathcal {U}\left( \mathbb {X}_i \right) \end{aligned}$$

It was shown in [7] that there is a one to one correspondence between sets and its parity set, that is the mapping

$$\begin{aligned} \mathcal {U} : \mathbb {X} \mapsto \mathcal {U}(\mathbb {X}) \end{aligned}$$

is a bijection and actually its own inverse, i.e.,

$$\begin{aligned} \mathcal {U}(\mathcal {U}(\mathbb {X}) ) =\mathbb {X} . \end{aligned}$$

Those properties follow from the linearity of $\mathcal {U}$ and the following lemma. The proof is added for completeness and to get familiar with the notation.

Lemma 1

Let $\mathcal {U}$ be the mapping defined above and $\ell$ be an element in $\mathbb {F}_2^n$. Then

• 1. $\mathcal {U}(\{\ell \})=\{ u \in \mathbb {F}_2^n \ | \ u \preceq \ell \}$

• 2. $\mathcal {U}(\{ x \in \mathbb {F}_2^n \ | \ x \preceq \ell \})=\{\ell \}$

Proof

For the first property, we note that $x^u=1$ if and only if $u \preceq x$. Thus we get

$$\begin{aligned} \mathcal {U}(\{\ell \})= & {} \left\{ u \in \mathbb {F}_2^n \ \text{ such } \text{ that } \ \sum _{x \in \{\ell \} } x^u =1 \right\} \\= & {} \left\{ u \in \mathbb {F}_2^n \ \text{ such } \text{ that } \ {\ell }^u =1 \right\} \\= & {} \left\{ u \in \mathbb {F}_2^n \ | \ u \preceq \ell \right\} \end{aligned}$$

For the second property, we see that $\sum _{x \in \mathbb {F}_2^n \ | \ x \preceq \ell } x^u = 1$ if and only if $u = \ell$. Let $A_u$ be the number of elements $x \preceq \ell$ such that $x^u =1$ we get

$$\begin{aligned} A_u = | \{ x \preceq \ell \ | \ x^u =1 \} | = | \{ x \preceq \ell \ | \ u \preceq x \} | = | \{ x \in \mathbb {F}_2^n \ | \ u \preceq x \preceq \ell \} | \end{aligned}$$

and it holds that $A_u$ is odd if and only if $\ell =u$, which completes the proof.    $\square$

We next introduce the propagation of the division property and the notion of the division trail. More formally, as our focus is the parity set, its propagation is identical to the propagation of the so-called $\mathbb {L}$ set in 3SDP introduced in   [21]. Moreover, the division trail is identical to the three-subset division trail introduced in [12].

The division property provides the propagation rule for some basic operations, such as XOR or AND, and the propagation has been defined in this context as a bottom-up approach. The propagation rule allows us to evaluate any ciphers without deep knowledge for underlying theory for the division property, and it is one of advantages as a cryptanalytic tool. On the other hand, for a mathematical definition of the propagation, a top-down approach, starting with a general function and deriving the propagation rules as concrete instances, is helpful.

Definition 2

(Propagation). Given $F :\mathbb {F}_2^n \rightarrow \mathbb {F}_2^m$ and $a \in \mathbb {F}_2^n, b \in \mathbb {F}_2^m$ we say that the division property a propagates to the division property b, denoted by

$$\begin{aligned} a \xrightarrow {F} b \end{aligned}$$

if and only if

$$\begin{aligned} b \in \mathcal {U}(F(\mathcal {U}(\{a\}))) \end{aligned}$$

Here the image of a set $\mathbb {X}$ under F is defined as

$$\begin{aligned} F(\mathbb {X}):=\sum _{a \in \mathbb {X}} \{F(a)\}, \end{aligned}$$

that is again using the addition of sets as defined above.

The propagation is defined without specifying each concrete operation in Definition 2. For any application, Definition 2 will never be applied directly. Nevertheless, only using this definition reveals one important property of the propagation very simply. Given $U_1=\mathcal {U}({\mathbb {X}})$, for any function F, $U_2=\mathcal {U}(F({\mathbb {X}}))$ is evaluated as

$$\begin{aligned} U_2= & {} \mathcal {U}(F({\mathbb {X}})) = \sum _{x \in \mathbb {X}} \mathcal {U}(F(\{x\})) = \sum _{a \in \mathcal {U}(\mathbb {X})} \mathcal {U}(F(\mathcal {U}(\{a\}))) = \sum _{ a \in U_1 \atop a \xrightarrow {F} b} \{b\}. \end{aligned}$$

(2)

This shows that our definition fits to the intuitive meaning of propagation: In order to determine $U_2$ after applying the function F, it is enough to consider what happens with individual elements of $U_1$ to start with. Here again, we like to emphasize that the sum in Eq. 2 is modulo two, that is, if an element appears an even number of times on the right side, it actually does not appear in $U_2$. Of course, to evaluate the propagation in real, we need to mention the concrete propagation $a \xrightarrow {F} b$, and we also give the following proposition, which allows to easily deduce the possible propagation given the ANF of a function.

Proposition 1

Let $F : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^m$ be defined as

$$\begin{aligned} F(x_1,\dots ,x_n) = (y_1,\dots ,y_m) = y \end{aligned}$$

where $y_i$ are multivariate polynomials over $\mathbb {F}_2$ in the variables $x_i$. For $a \in \mathbb {F}_2^n$ and $b \in \mathbb {F}_2^m$, it holds that $a {\mathop {\rightarrow }\limits ^{F}} b$ if and only if $y^b$ contains the monomial $x^a$.

Proof

By Definition 2, we have $a {\mathop {\rightarrow }\limits ^{F}} b$ if and only if $b \in \mathcal {U}(F(\mathcal {U}(\{a\})))$. Using Lemma 1, we can see that

$$\begin{aligned} \mathbb {Y} := F(\mathcal {U}(\{a\})) = \{F(x) \ | \ x \preceq a, x \in \mathbb {F}_2^n\}. \end{aligned}$$

Hence $b \in \mathcal {U}(\mathbb {Y})$ exactly means $\sum \limits _{x \preceq a} F^b(x) = 1$. Note that $F^b$ is a Boolean function over the variables $x_1,\dots ,x_n$ whose ANF is exactly $y^b$, that is

$$\begin{aligned} F^b(x) = \sum \limits _{u \in \mathbb {F}_2^n}\lambda _ux^u = y^b. \end{aligned}$$

Using the well known relation between a function and the coefficients of its ANF, having $\sum \limits _{x \preceq a} F^b(x) = 1$ directly gives that $\lambda _a = 1$, i.e., the monomial $x^a$ appears in the ANF of $F^b$, said ANF being exactly $y^b$.    $\square$

We remark that all propagation rules already introduced in  [21] are generated by assigning concrete function to F. We refer the reader to [21] for more details about these propagation rules

Following previous work, we now generalize the definition above to the setting where F is actually given as the composition of many functions

$$\begin{aligned} F= F_R \circ \cdots \circ F_2 \circ F_1 . \end{aligned}$$

Definition 3

(Division Trail). Given $F :\mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ as

$$\begin{aligned} F= F_R \circ \dots \circ F_2 \circ F_1 \end{aligned}$$

and $a_0 \dots a_R \in \mathbb {F}_2^n$ we call $(a_0,\dots , a_R)$ a division trail for the compositions of F into the $F_i$ if and only if

$$\begin{aligned} \forall i \in \{1,\dots ,R\}, a_{i-1} \xrightarrow {F_i} a_i. \end{aligned}$$

We denote such a trail by

$$\begin{aligned} a_0 \xrightarrow {F_1} a_1 \xrightarrow {F_2} \cdots \xrightarrow {F_R} a_R . \end{aligned}$$

Using the same considerations as in Eq. 2, we can now state the main reason of why considering trails is useful.

Theorem 1

Given $F :\mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ as

$$\begin{aligned} F= F_R \circ \cdots \circ F_2 \circ F_1 \end{aligned}$$

and $\mathbb {X}\subseteq \mathbb {F}_2^n$. Then

$$\begin{aligned} \mathcal {U}(F(\mathbb {X})) = \sum _{ a_0,\dots ,a_R \atop a_0 \in \mathcal {U}(\mathbb {X}) , a_0 \xrightarrow {F_1} a_1\xrightarrow {F_2} \cdots \xrightarrow {F_R} a_R } \{a_R\} \end{aligned}$$

The important link between the division property and the ANF is the following observations and is actually a special case of Proposition 1.

Corollary 1

Let $F:\mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be a function with algebraic normal form

$$\begin{aligned} F(x) = \sum _{ u \in \mathbb {F}_2^n} \lambda _u x^u \end{aligned}$$

where $\lambda _u =(\lambda _u^{(1)},\dots ,\lambda _u^{(n)}) \in \mathbb {F}_2^n$. Furthermore, let $\mathbb {X}$ be the set such that $\mathcal {U}({\mathbb {X}})=\{\ell \}$. Then

$$\begin{aligned} \lambda _{\ell }^{(i)} =1 \ \Leftrightarrow e_i \in \mathcal {U}({F(\mathbb {X})}) \end{aligned}$$

Proof

If $\mathcal {U}({\mathbb {X}})=\{\ell \}$, by Lemma 1 we have

$$\begin{aligned} \mathbb {X}=\{ x \in \mathbb {F}_2^n \ | \ x \preceq \ell \} . \end{aligned}$$

Now by Eq. (1) we get

$$\begin{aligned} \lambda _{\ell }^{(i)}= & {} \sum _{x \preceq \ell } F^{(i)}(x) = \sum _{x \in \mathbb {X}} F^{(i)}(x) \\= & {} \sum _{x \in F(\mathbb {X})} x^{e_i} = \left\{ \begin{array}{cc} 1 &{} \text{ if } e_i \in \mathcal {U}({F(\mathbb {X})}) \\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

which concludes the proof.    $\square$

Theorem 1 and Corollary 1 finally result in the following corollary.

Corollary 2

Let $F:\mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be a function with algebraic normal form

$$\begin{aligned} F(x) = \sum _{ u \in \mathbb {F}_2^n} \lambda _u x^u \end{aligned}$$

where $\lambda _u =(\lambda _u^{(1)},\dots ,\lambda _u^{(n)}) \in \mathbb {F}_2^n$ and $F= F_R \circ \dots \circ F_2 \circ F_1$. Then $\lambda _{\ell }^{(i)} =1$ if and only if the number of trails

$$\begin{aligned} \ell \xrightarrow {F_1} a_1 \xrightarrow {F_2} \cdots \xrightarrow {F_R} e_i \end{aligned}$$

is odd.

Proof

Follows immediately from the statements above.    $\square$

This is what is actually solved using SAT solvers and/or mixed integer linear programming techniques. Before going into the details of the algorithmic approach, we explain why the case of a keyed function does not significantly change the perspective in our application in the next section.

3 High-Level Approach

Conceptually, there is no difference between key variables and input variables when it comes to division properties as used here and outlined in the previous section. It is only about splitting the set of variables into two (or potentially more) sets and changing the notation accordingly. Consider a function

$$\begin{aligned} E:\mathbb {F}_2^n \times \mathbb {F}_2^m\rightarrow & {} \mathbb {F}_2^n \\ (x,k)\mapsto & {} E(x,k) \end{aligned}$$

When thinking of E as a block cipher, we usually rephrase this as a family of functions indexed by k, i.e., we consider

$$\begin{aligned} E_k :\mathbb {F}_2^n\rightarrow & {} \mathbb {F}_2^n \\ \text{ where } E_k(x)= & {} E(x,k). \end{aligned}$$

The algebraic normal form (ANF) of E and $E_k$ are not identical, but related. Starting with the ANF of E expressed as

$$\begin{aligned} E(x,k)&= \sum _{u \in \mathbb {F}_2^n, v \in \mathbb {F}_2^m} \lambda _{u,v} x^u k^v, \end{aligned}$$

(3)

we get the ANF of $E_k$ by rearranging terms as

$$\begin{aligned} E_k(x)&= \sum _{u \in \mathbb {F}_2^n} \left( \sum _{ v \in \mathbb {F}_2^m} \lambda _{u,v} k^v \right) x^u = \sum _{u \in \mathbb {F}_2^n} p_u(k) x^u , \end{aligned}$$

where

$$\begin{aligned} p_u(k)=\sum _{ v \in \mathbb {F}_2^m} \lambda _{u,v} k^v \end{aligned}$$

are the key-dependent coefficients of the ANF of function $E_k$.

Note that the degree of E and $E_k$, which we already defined in Sect. 1 are usually different as

$$\begin{aligned} \deg (E)= \max _{u \in \mathbb {F}_2^n, v \in \mathbb {F}_2^m} \{ {{\,\mathrm{wt}\,}}(u) + {{\,\mathrm{wt}\,}}(v) \ | \ \lambda _{u,v} \ne 0 \} \end{aligned}$$

while

$$\begin{aligned} \deg (E_k)= \max _{u \in \mathbb {F}_2^n} \{ {{\,\mathrm{wt}\,}}(u) \ | \ p_u(k) \ne 0 \} . \end{aligned}$$

Here, clearly, we are interested in the later.

In order to lower bound the degree of $E_k$ by some value d, we have to find a vector u of hamming weight d, such that $p_u(k)$ is non-zero. For a given u, there are two basic approaches to do so.

Fixed Key. Conceptually, the easiest way to lower bound the degree of $E_k$ is to simply choose a random key k and, using Corollary 2 for computing one ANF coefficient of large degree. If this is feasible for a random key and the corresponding coefficient is actually 1, the degree must be larger or equal than d. If, however, the corresponding coefficient is zero, nothing can be concluded and one might have to repeat either for a different key or a different coefficient, or both. The advantage of this approach is its conceptual simplicity and that it can take an arbitrary key-scheduling into account. The significant drawback is that this approach becomes quickly impossible in practice. We elaborate on our initial findings using this approach in Sect. 6.

Variable Key. Luckily, we can use another approach. Namely, in order to show that the degree of $E_k$ is at least d, it is sufficient to identify a single $u \in \mathbb {F}_2^n$ of Hamming weight d and an arbitrary $v \in \mathbb {F}_2^m$ such that $\lambda _{u,v} \ne 0$ (see Eq. 3) as this implies $p_u(k) \ne 0$. While this approach might seem more difficult at first glance, computationally it is significantly easier, especially when independent round-keys are assumed.

By definition, the keyed function $E_k$ has degree at least d if for one $u \in \mathbb {F}_2^n$ of weight d and any $v \in \mathbb {F}_2^m$ the coefficient vector

$$\begin{aligned} \lambda _{u,v} =(\lambda _{u,v}^{(1)},\dots ,\lambda _{u,v}^{(n)}) \in \mathbb {F}_2^n. \end{aligned}$$

is non zero. So actually it is enough if, for one such u of weight d, an arbitrary v and any $1 \le i\le n$ it holds that $\lambda _{u,v}^{(i)}=1$.

3.1 Minimum Degree

However, from an attacker perspective it is sufficient if there exists a single output bit of low degree. Thus, a stronger bound on the degree would potentially show that for all i there exist a u of weight d and an arbitrary v such that $\lambda _{u,v}^{(i)}=1$. This would ensure that for each output bit there exists a key such that the degree of this output bit is at least d.

Again, this is not enough, as the attacker could equally look at any linear combination of output bits of her choice. The above result does not imply any bound on the degree of such linear combinations. Indeed, we would like to show that for each linear combination, there exists a key such that the degree of this linear combination is at least d. This is exactly captured in the definition of minimum degree.

Definition 4

The minimum degree of a function $F : \mathbb {F}_2^{n} \rightarrow \mathbb {F}_2^n$ is defined as

$$\begin{aligned} \text{ minDeg }(F)=\min _{\beta \in \mathbb {F}_2^n, \beta \ne 0} \deg \langle \beta , F \rangle \end{aligned}$$

Now, while for the degree it was sufficient to identify a single suitable coefficient $\lambda _{u,v}^{(i)}$ equal to one, things are more intricate here. There are, in principle, $2^n-1$ component functions $\langle \beta , F \rangle$ to be studied. Indeed, considering a single (u, v) pair and the corresponding $\lambda _{u,v}$ coefficient is not sufficient, as choosing any $\beta$ such that $\langle \beta , \lambda _{u,v} \rangle =0$ results in a component function that does not contain the monomial $k^v x^u$ in its ANF. It is this canceling of high degree monomials that has to be excluded for lower bounding the minimum degree.

In order to achieve this it is sufficient (and actually necessary) to find a set

$$\begin{aligned} S= \{ (u_1,v_1),\dots ,(u_t,v_t)\} \end{aligned}$$

of pairs (u, v) of size $t \ge n$ and compute the value of $\lambda _{u,v}^{(i)}$ for all i and all $(u,v) \in S$. This will lead to a binary matrix

$$ M_S(E_k)=\left( \begin{array}{cccc} \lambda _{u_1,v_1}^{(1)} &{} \lambda _{u_2,v_2}^{(1)} &{} \cdots &{} \lambda _{u_t,v_t}^{(1)} \\ \lambda _{u_1,v_1}^{(2)} &{} \lambda _{u_2,v_2}^{(2)} &{} \cdots &{} \lambda _{u_t,v_t}^{(2)} \\ &{} \vdots &{}\\ \lambda _{u_1,v_1}^{(n)} &{} \lambda _{u_2,v_2}^{(n)} &{} \cdots &{} \lambda _{u_t,v_t}^{(n)} \\ \end{array} \right) .$$

What has to be excluded, in order to bound the minimum degree is that columns of this matrix can be combined to the all zero vector, as in this case all monomials $k^{v_i} x^{u_i}$ cancel in the corresponding linear combination. Clearly, this is possible if and only if the columns are linear dependent. This observation is summarized in the following proposition.

Proposition 2

A keyed function $E_k$ has minimum degree at least d if and only if there exist a set S such that the matrix $M_S(E_k)$ has rank n and

$$\begin{aligned} d \le \min _{(u,v) \in S} {{\,\mathrm{wt}\,}}(u) \end{aligned}$$

3.2 Appearance of All High-Degree Monomials

Returning to the attacker perspective, it is clear that bounds on the minimum degree are more meaningful than bounds on the algebraic degree. However, it is also clear that even those are not enough to exclude the existence of integral attacks. In particular, even so the minimum degree of a function is $n-1$, it could be the case that a certain monomial $x^{u}$ of degree $n-1$ never occurs in the ANF of the linear combination $\langle \beta , E_k(x) \rangle$ of output bits. That is, a minimum degree of $n-1$ does not exclude that $\langle \beta , \lambda _{u,v} \rangle =0$ for a fixed u and all v.

In order to ensure that this does not happen we have to show that for each fixed u of weight $n-1$ there exist vectors $v_i$ such that $M_{S_u}(E_k)$ has full rank for

$$\begin{aligned} S_u=\{ (u,v_1),\dots , (u,v_t)\} . \end{aligned}$$

Here, we are (i) more restricted in the choice of the pairs in S as we always have to use the same fixed u and (ii) have to repeat the process n times, once for each u of weight $n-1$.

Interestingly, the appearance of all high-degree monomials excludes a large class of integral distinguishers. Namely, for a cipher where all high-degree monomials appear (for at least one key), there will not be integral distinguisher by fixing bits that work for all keys. This is a consequence of the following observation that separates the pre-whitening key from the remaining round keys.

Proposition 3

Let $E_k:\mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be a cipher with ANF

$$\begin{aligned} E_k(x)= \sum _{u \in \mathbb {F}_2^n} p_u(k) x^u \end{aligned}$$

and consider a version of $E_k$ with an additional pre-whitening key $k_0$, i.e.

$$\begin{aligned} E_{k,k_0}(x):=E_k(x+k_0) \end{aligned}$$

with ANF

$$\begin{aligned} E_{k,k_0}(x) = \sum _{v \in \mathbb {F}_2^n} q_v(k,k_0) x^v \end{aligned}$$

If, for all u of weight $n-1$ the coefficient $p_u(k)$, is non-constant, it follows that $q_v(k,k_0)$ is non-constant for all v of weight less than n.

Proof

We first express $q_v(k,k_0)$ in terms of $p_u$. We get

$$\begin{aligned} E_{k,k_0}(x)= & {} E_k(x+k_0) = \sum _{u \in \mathbb {F}_2^n} p_u(k) \left( x+k_0\right) ^u \\= & {} \sum _{u \in \mathbb {F}_2^n} p_u(k) \left( \sum _{v \preceq u} x^v k_0^{u \oplus v}\right) = \sum _{v \in \mathbb {F}_2^n} \left( \sum _{ u \succeq v} p_u(k) k_0^{u \oplus v} \right) x^v \end{aligned}$$

This shows that

$$\begin{aligned} q_v(k,k_0)= \sum _{ u \succeq v} p_u(k) k_0^{u \oplus v} \end{aligned}$$

Now, for any v of weight at most $n-1$, there exists at least one $u'\succeq v$ of weight $n-1$ in the sum above. By the assumption on $E_k$ it holds that $p_{u'}(k)$ is not constant. Therefore, $q_v$ is not constant as a function in k and $k_0$, which concludes the proof.    $\square$

3.3 The Key Pattern

Computing the values of $\lambda _{u,v}^{(i)}$ is certainly not practical for arbitrary choice of (u, v) and i. There is not a lot of freedom in the choice of u, especially not if we aim at showing the appearance of all high degree monomials. However, there is a huge freedom in the choice of v, that is in the key monomial $k^v$ that we consider.

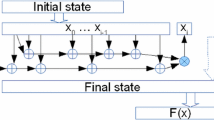
It is exactly the careful selection of suitable v that has a major impact on the actual running time and finally allows us to obtain meaningful results in practical time. It is also here where assuming independent round-keys is needed. Consider that case of a key-alternating block cipher depicted below²

When considering independent round-keys, the key monomial $k^v$ actually consists of

$$\begin{aligned} k^v = k_0^{v^{(0)}} k_1^{v^{(1)}} \dots k_R^{v^{(R)}}. \end{aligned}$$

Here, we can select for each round-key $k_i$ a suitable vector $v^{(i)}$ freely.

Returning to Corollary 2 and the division property, recall that $\lambda _{u,v}^{(i)}=1$ if and only if the number of division trails $(u,v) \rightarrow e_i$ is odd. The vector v and therefore its parts $v=(v^{(0)}, \dots , v^{(R)})$ correspond to (parts of) the input division property. We will refer to v and its parts as the key-pattern. The number of trails, and therefore the computational effort, is highly dependent on this choice. This is the main technical challenge we solve, which is described in the following Sect. 4.

4 How to Search Input/Key/Output Patterns

As we already discussed above, we need to find u (called an input pattern) and $(v_0,\ldots ,v_R)$ (called a key pattern), in which the number of trails from $(u,v_0,\ldots ,v_R)$ to some unit vector $e_i$ (called a output pattern) is odd and, equally important, efficiently computable. To do so, we will mainly rely on the use of automatic tools such as MILP and SAT. We refer the reader to [12] for the modeling in MILP and to [16] for the modeling in SAT (note that this paper shows how to modelize BDP in SAT, but it can easily be adapted in our context).

Once we get such an input/key/output pattern, it is very easy to verify the lower bound of the degree using standard techniques. We simply enumerate all trails and check the parity of the number of trails³.

Therefore, the main problem that we need to solve is how to select suitable input/key/output patterns. In general, we search key patterns whose Hamming weight is as high as possible. The number of trails is highly related to the number of appearances of the same monomial when they are expanded without canceling in each round. Intuitively, we can expect such a high-degree monomial is unlikely to appear many times. Unfortunately, even if the key pattern is chosen with high weight, the number of trails tends to be even or extremely large when these patterns are chosen without care.

Parasite Sub-Trails. To understand the difficulty and our strategy to find proper input/key/output patterns, we introduce an example using SKINNY64.

Fig. 2.

Extraction from the trail of SKINNY64

Assume that we want to guarantee that the lower bound of algebraic degree of R-round SKINNY64 is 63. Given an input/key/output pattern, let us assume that there is a trail that contains the trail shown in Fig. 2 somewhere in the middle as a sub-trail. This sub-trail only focuses on the so-called super S-box involving the 4th anti-diagonal S-boxes in the $(r\,+\,1)$th round and the 1st-column S-boxes in the $(r+2)$th round. A remarkable, and unfortunately very common, fact is that this sub-trail never yields an odd-number of trails because we always have the following two different sub-trails.

$$\begin{aligned} T1 :~&\mathtt {0x76E0} \xrightarrow {SC} \mathtt {0xC420} \xrightarrow {ART(+\mathtt {0x2000})} \mathtt {0xE420} \xrightarrow {MC} \mathtt {0x0E60} \xrightarrow {SC} \mathtt {0x0240} \\ T2 :~&\mathtt {0x76E0} \xrightarrow {SC} \mathtt {0x1420} \xrightarrow {ART(+\mathtt {0x2000})} \mathtt {0x3420} \xrightarrow {MC} \mathtt {0x0360} \xrightarrow {SC} \mathtt {0x0240} \end{aligned}$$

The trail shown in Fig. 2 is T1, and we always have another trail T2. Like this, when the number of sub-trails is even under the fixed input, key, and output pattern of the sub-trail, we call it an inconsistent sub-trail. Moreover, inconsistent sub-trails are independent of other parts of the trail and might occur in several parts of trails simultaneously. Assuming that there are 10 inconsistent sub-trails, the number of the total trails is at least $2^{10}$. In other words, inconsistent sub-trails increase the number of total trails exponentially.

Heuristic Approach. It is therefore important to avoid trails containing inconsistent sub-trails. Instead of getting input/key/output pattern, the goal of the first step in our method is to find a trail, where all sub-trails relating to each super S-box are consistent, i.e., there is no inconsistent sub-trail as long as each super S-box is evaluated independently. Note that this goal is not sufficient for our original goal, and the number of total trails might still be even. Therefore, once we get such a trail, we extract the input/key/output pattern from the found trail, and check the total number of trails with this pattern.

We have several approaches to find such a trail. As we are actually going to search for these patterns and enumerate the number of trails using MILP or SAT solvers, the most straightforward approach is to generate a model to represent the propagation by each super S-box accurately. However, modeling a 16-bit keyed S-box has never been done before. Considering the difficulty to model even an 8-bit S-box, it is unlikely to be a successful path to follow.

Another approach is to use the well-known modeling technique, where the S-box and MixColumns are independently modeled, and exclude inconsistent sub-trail in each super S-box only after detecting them in a trail⁴. This approach is promising, but the higher the number of rounds gets, the less efficient it is as the number of super S-boxes we need to check the consistency increases. Indeed, as far as we tried, this approach is not feasible to find proper patterns for 11-round SKINNY64.

The method that we actually used is a heuristic approach that builds the trail round by round. Let $x_r$, $y_r$, and $z_r$ be an intermediate values for the input of the $(r+1)$th S-box layer, output of the $(r+1)$th S-box layer, and input of the $(r+1)$th MixColumns in each trail, respectively. Our main method consists of the following steps.

• 1. Given $e_i (=y_{R-1})$, determine $(x_{R-2},v_{R-1})$, where the Hamming weight of $x_{R-2}$ and $v_{R-1}$ is as high as possible and the number of trails from $x_{R-2}$ to $e_i$ is odd and small (1 if possible).

• 2. Compute $(x_{R-3}, v_{R-2}, y_{R-2})$, where the Hamming weight of $x_{R-3}$ and $v_{R-2}$ is as high as possible and the number of trails from $x_{R-3}$ to $y_{R-2}$ is odd (1 if possible). Then, check if the number of trails from $x_{R-3}$ to $e_i$ is odd (1 if possible) under $(v_{R-2},v_{R-1})$.

• 3. Repeat the procedure above to $R_{mid}$ rounds. This results in a key pattern $(v_{R_{mid} + 1}, \ldots , v_{R-1})$, where the number of trails from $x_{R_{mid}}$ to $e_i$ is odd and small (again, 1 in the best case).

• 4. Compute $(v_1, \ldots , v_{R_{mid}})$ such that the number of trails from $u(=x_0)$ to $y_{R_{mid}}$ is odd.

• 5. Compute the number of trails satisfying $(u, v_1, \ldots , v_{R-1}) \rightarrow e_i$.

Our method can be regarded as the iteration of the local optimization. As we already discussed in the beginning of this section, we can expect that the number of trails from pattern with high weight is small. The first three steps, called trail extension in our paper, are local optimization in this context from the last round. Note that these steps are neither a deterministic nor an exhaustive methods. In other words, the trail extension is randomly chosen from a set of optimal or semi-optimal choices. Sometimes, there is an unsuccessful trail extension, e.g., it requires too much time to extend the trail after a few rounds or we run into trails that cannot reach the input pattern u. The heuristic and randomized algorithm allows, in case we faces such unsuccessful trail extensions, to simply restart the process from the beginning.

As far as we observe some ciphers, unsuccessful trail extensions happens with higher probability as the trail approaches the first round. Therefore, after some $R_{mid}$ rounds, we change our strategy, and switch to the more standard way of searching for $(u,v_1,\ldots ,v_{R_{mid}})$, e.g., $R_{mid}=5$ or 6 is used in SKINNY64. More formally, we search trails from u to $y_{R_{mid}}$ while excluding inconsistent sub-trails. Note that this is possible now because this trail has to cover less rounds. Once we find such a trail, we extract the key-patterns $(u,v_1,\ldots ,v_{R_{mid}})$ from the trail and check if the number of trails from $(u,v_1,\ldots ,v_{R_{mid}})$ to $y_{R_{mid}}$ is odd. If so, we finally extract the entire input/key/output pattern and verify the number of trails satisfying $(u,v_1,\ldots ,v_{R-1}) \rightarrow e_i$.

Our algorithm is not generic, and it only searches “the most likely spaces” at random. Therefore, it quickly finds the proper pattern only a few minutes sometimes, but sometimes, no pattern is found even if we spend one hour and more.

We like to stress again that, once we find input/key/output patterns whose number of trails is odd, verifying the final number of trails is easy and standard, and for this we refer the reader to the code available at https://github.com/LowerBoundsAlgDegree/LowerBoundsAlgDegree.

How to Compute Minimum-Degree. The minimum degree is more important for cryptographers than the algebraic degree. To guarantee the lower bound of the minimum degree, we need to create patterns whose resulting matrix $M_S(E_k)$ has full rank.

Our method allows us to get the input/key/output pattern, i.e., compute $\lambda _{u,v}^{(i)}$ for the specific tuple (u, v, i). However, to construct this matrix, we need to know all bits of $\lambda _{u,v}$. And, the use of the input/key pattern for different output patterns is out of the original use of our method. Therefore, it might allow significantly many trails that we cannot enumerate them with practical time.

To solve this issue, we first restrict ourselves to use a non-zero key pattern $v_{R-1}$ for the last-but one round during the trail extension. This is motivated by the observation that, usually, a single round function is not enough to mix the full state. Therefore it is obvious that the ANF of some output bits is independent of some key-bits $k_r^{v_{R-1}}$.

Equivalently, many output bits of $\lambda _{u,v}$ are trivially 0, i.e., the number of trails is always 0. Thus, the matrix $M_S(E_k)$ is a block diagonal matrix

$$\begin{aligned} M_S(E_k) = \begin{pmatrix} M_{S_1}(E_k) &{} 0 &{} \cdots &{} 0 \\ 0 &{} M_{S_2}(E_k) &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} M_{S_m}(E_k) \end{pmatrix}. \end{aligned}$$

As such, $M_{S}(E_k)$ has the full rank when $M_{S_i}(E_k)$ has the full rank for all i. This technique allows us to generate input/key/output patterns for the full-rank matrix efficiently.

Even if we use non-zero $v_{R-1}$, we still need to get full-rank block matrices. Luckily, there is an important (algorithmic) improvement that we like to briefly mention here. In many cases, it is not needed to compute the entire set of entries of a matrix $M_S(F)$ to conclude it has full rank. As an example, consider the matrix

$$ M_S(F) = \left( \begin{array}{ccc} 1 &{} 0 &{} *\\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) $$

where $*$ is an undetermined value. Then $M_S(F)$ has full rank, no matter what the value of $*$ actually is. Even so this observation is rather simple, it is often an important ingredient to save computational resources.

How to Compute All High-Degree Monomials. Guaranteeing the appearance of all high-degree monomials is more important for cryptographers than minimum degree. Conceptually, it is not so difficult. We simply use a specific u in the 4th step instead of any u whose Hamming weight is $n-1$ and guarantee the lower bound of the minimum degree. Then, we repeat this procedure for all us with Hamming weight $n-1$.

How to Compute Lower Bounds for Intermediate Rounds. While the most interesting result for cryptographers is to show the full algebraic degree and full minimum degree, it is also interesting to focus on the degree or minimum degree in the intermediate rounds and determine how the lower bounds increase.

In our paper, these lower bounds are computed by using the input/key/output pattern, which is originally generated to guarantee the full degree and minimum degree. For example, when we prove the lower bound of r rounds, we first enumerate all trails on this pattern, and extract $x_{R-r}$ whose number of trails $(x_{R-r}, v_{R-r+1}, \ldots , v_{R-1}) \rightarrow e_i$ is odd. Let $X_{R-r}^{(i)}$ be the set of all extracted values, and a lower bounds of the algebraic degree for r rounds is given by

$$\begin{aligned} \max _i \max _{u \in X_{R-r}^{(i)}} wt(u). \end{aligned}$$

A more involved technique is needed for the minimum degree. We first construct the matrix $M_S(E_k)$ for R rounds, where for non-diagonal elements, we set 0 if there is no trail, and we set $*$ if there is trail. If this matrix has the full rank, we always have the full-rank matrix even when we focus on intermediate rounds. In this case, a lower bounds of the minimum degree for r rounds is given by

$$\begin{aligned} \min _i \max _{u \in X_{R-r}^{(i)}} wt(u). \end{aligned}$$

How to Compute Upper Bounds. While some work has been done previously to find upper bounds on the algebraic degree [6, 8], we want to point out that we can easily compute such upper bounds using our MILP models, and our results in Sect. 5 show that the resulting upper bounds are quite precise, especially for the algebraic degree. Indeed, to prove an upper bound for R rounds and for the i-th coordinate function, we simply generate a model for R rounds, fix the output value of the trail to the unit vector $e_i$ and then simply ask the solver to maximize wt(u). This maximum value thus leads to an upper bound on the degree, since it is the maximum weight that u can have so that there is at least one trail. Then, once we collected an upper bound $ub_i$ for each coordinate function, we easily get an upper bound on the algebraic degree of the vectorial function as $\max _i ub_i.$ To get an upper bound on the minimum degree, recall that the minimum degree is defined as the minimal algebraic degree of any linear combination of all coordinate functions. Thus, in particular, this minimum degree is at most equal to the minimal upper bound we have on each coordinate function, i.e., using the upper bounds on each coordinate function as before, we simply need to compute $\min _i ub_i.$

5 Applications

Clearly, we want to point out that the result about the lower bounds do not depend on how we model our ciphers. That is, the parity of the number of trails must be the same as long as we create the correct model. However the number of trails itself highly depends on the way we model, e.g., the number is 0 for one model but it is 1,000,000 for another model. As enumerating many trails is a time consuming and difficult problem, we have to optimize the model.

For example, we could use only the COPY, XOR and AND operations to describe the propagation through the S-box. However this would lead to more trails than necessary, while directly modeling the propagation using the convex hull method as in [22] significantly reduces the induced number of trails.

We already mentioned earlier that we consider independent round-keys added to the full state. In particular for GIFT and SKINNY, the cipher we study are strictly speaking actually not GIFT and SKINNY. However, we stress that this is a rather natural assumption that is widely used for both design and cryptanalysis of block ciphers.

Fig. 3.

Round function of GIFT-64 using SSB-friendly description

5.1 GIFT

GIFT is a lightweight block cipher published at CHES’17 by Banik et al. [2]. Two variants of this block cipher exists depending on the block length (either 64-bit or 128-bit) and use a 128-bit key in both case. Its round function and the Super S-boxes are depicted in Fig. 3. Note that in the original design, the round key is added only to a part of the state.

Modeling. The round function of GIFT-64 is very simple and only consist of an S-box layer and a bit permutation layer. We give the propagation table of this S-box in Table 2, namely, an x in row u and column v means that $u {\mathop {\rightarrow }\limits ^{S}} v$ where S is the GIFT-64 S-box. For example, the column 0x1 corresponds to the monomials appearing in the ANF of the first output bit of the S-box. We can obtain linear inequalities to modelize this table according to the technique given in [22].

The bit permutation is simply modelized by reordering the variables accordingly.

Table 2. Propagation table for the S-box of GIFT

Algebraic Degree. We applied our algorithm for GIFT-64 and obtained that the algebraic degree of all coordinate functions is maximal (i.e., 63) after 9 rounds. However, we can go even further and prove that 32 of the coordinate functions are of degree 63 after only 8 rounds. As such, the algebraic degree of GIFT-64 as a vectorial function is maximal after only 8 rounds. In Fig. 4 on the left side, we give the lower and upper bounds for the algebraic degree of GIFT-64, and we will give the detailed lower and upper bounds for each coordinate function in the full version of the paper.

Note that we thus have two data-sets: one for 8 rounds and another one for 9 rounds. To get the curve for the lower bounds on algebraic degree, we simply “merged” the data-sets and extracted the best lower bound for each coordinate function and for each number of rounds. Thus this curve shows the best results we were able to get.

While the execution time can widely vary depending on a lot of factors, in practice our algorithm proved to be quite efficient when applied to GIFT-64. Indeed, to prove that each output bit is of maximal degree after 9 rounds as well as computing the lower bounds for a smaller number of rounds, we needed less than one hour on a standard laptop, and about 30 min to find all coordinate functions with algebraic degree 63 after 8 rounds (and again, also computing all lower bounds for less rounds).

Fig. 4.

Algebraic degree and minimum degree for GIFT-64

Minimum Degree. In about one hour of computation on a standard laptop, we were able to show that the minimum degree is maximal after 10 rounds. In Fig. 4 on the right side we show the lower and upper bounds on the minimum degree for each number of rounds from 1 to 10.

All Maximal Degree Monomials. As described in Sect. 3.2 we were able to show that all 63-degree monomials appear after 11 rounds for any linear combination of the output bits. This computation was a bit more expensive than the previous one, yet our results were obtained within about 64 h.

5.2 SKINNY64

SKINNY is a lightweight block cipher published at CRYPTO’16 by Beierle et al. [4]. SKINNY supports two different block lengths (either 64 bits or 128 bits). The round function adopts the so-called AES-like structure, where significantly lightweight S-box and MixColumns are used.

Please refer to Fig. 2 for the figure of the round function of our variant of SKINNY64.

Modeling. We introduce how to create the model to enumerate trails. For the S-box, the method is the same as for GIFT, i.e. using the technique from [22]. Therefore, here, we focus on MixColumns.

Naively, propagation through linear layers would be done with a combination of COPY and XOR propagations as in [12]. However, this leads to more trails that we need to count, which thus increase the overall time needed for our algorithm. Therefore, we use that MixColumns of SKINNY can be seen as the parallel application of several small linear S-boxes, denoted by L-box hereinafter. Formally, MixColumns is the multiplication over $\mathbb {F}_{2^4}$, but equivalently, we can see this operation over $\mathbb {F}_2$, where it is the multiplication with the following block matrix over $\mathbb {F}_2$

$$\begin{pmatrix} I_4 &{} 0 &{} I_4 &{} I_4\\ I_4 &{} 0 &{} 0 &{} 0\\ 0 &{} I_4 &{} I_4 &{} 0\\ I_4 &{} 0 &{} I_4 &{} 0 \end{pmatrix},$$

where $I_4$ is the identity matrix over $\mathbb {F}_2$ of dimension 4. By carefully examining the structure of this matrix, we can actually notice that it can be written as the parallel application of 4 L-boxes, which is defined as

$$ L(x_1,x_2,x_3,x_4) = (x_1 \oplus x_3 \oplus x_4, x_1, x_2 \oplus x_3, x_1 \oplus x_3), $$

Hence, instead of using the COPY and XOR operations, we consider that it is actually the parallel application of this L-box. Thus, the modelization for MixColumns is done in the same way as for S-boxes using the technique from  [22].

Algebraic Degree. Before we discuss the algebraic degree of SKINNY, we introduce a column rotation equivalence. We now focus on SKINNY, where all round keys are independent and XORed with the full state. Then, the impact on the round constant is removed, and each column has the same algebraic normal form with different input. Overall, we remove the last ShiftRows and MixColumns, and the output bit is the output of the last S-box layer. Then, in the context of the division property, once we find a trail $(u,v_0,\ldots ,v_{R}) \rightarrow e_i$, we always have a trail $(u^{\lll 32 \cdot i}, v_0^{\lll 32 \cdot i},\ldots ,v_R^{\lll 32 \cdot i}) \rightarrow e_{i+32 \cdot i})$, where $u^{\lll 32 \cdot i}$ is a value after rotating u by i columns. The column rotation equivalence enables us to see that it is enough to check the first column only.

Table 3. Algebraic degree and minimum degree on SKINNY64

We evaluated the upper bound of the algebraic degree for each coordinate function in the first column. The UB of degree in Table 3 shows the maximum upper bound among upper bounds for 16 coordinate functions, as well as the best lower bounds we managed to compute. The detailed results for the UB and LB of each coordinate function will be given in the full version of the paper.

In 10 rounds, the lower bound is the same as the upper bound. In other words, the full degree in 10 rounds is tight, and we can guarantee the upper bound of the algebraic degree is never less than 63 in 10-round SKINNY under our assumption.

Minimum Degree. The upper bound of the algebraic degree for bits in the 2nd row is 62 in 10 rounds. Therefore, 10 rounds are clearly not enough when we consider the full minimum degree. As we already discussed in Sect. 3.1, we need to construct 64 input/key patterns whose matrix $M_S(E_k)$ has the full rank.

Fig. 5.

Deterministic trail extension for the last MixColumns and S-box

To guarantee the lower bounds of the minimum degree, the method shown in Sect. 4 is used. In SKINNY64, when $v_{R-2}$ is non-zero, the resulting matrix becomes a block diagonal matrix, where each block is $16 \times 16$ matrix. Moreover, thanks to the column rotation equivalence, we always have input/key patterns such that each block matrix is identical. Therefore, only getting one full-rank $16 \times 16$ block matrix is enough to guarantee the lower bound of minimum degree.

Unfortunately, the use of the technique described in Sect. 4 is not sufficient to find patterns efficiently. We use another trick called a deterministic trail extension, where we restrict the trail extension for the last MixColumns and S-box such that it finds key patterns whose matrix is the full rank efficiently. Figure 5 summarizes our restriction, where the cell labeled deep red color must have non-zero value in the trail. We assume that taking the input of each pattern is necessary for the trail to exist. Then, taking Pattern 1 (resp. Pattern 3) implies that $\lambda _{u,v}^{(i)}$ can be 1 only when i indicates bits in the 1st nibble (resp. 3rd nibble). Taking Pattern 2 allows non-zero $\lambda _{u,v}^{(i)}$ for i which indicates bits in the 1st, 2nd, and 4th nibbles. Taking Pattern 4 allows non-zero $\lambda _{u,v}^{(i)}$ for i which indicates bits in the 1st, 3rd, and 4th nibbles. In summary, we can expect the following matrix

$$\begin{aligned} M_{S_1}(E_k) = \begin{pmatrix} A &{} *&{} 0 &{} *\\ 0 &{} B &{} 0 &{} 0 \\ 0 &{} 0 &{} C &{} *\\ 0 &{} *&{} 0 &{} D \end{pmatrix}, \end{aligned}$$

where 0 is $4 \times 4$ zero matrix, and $*$ is an arbitrary $4 \times 4$ matrix. We can notice that this matrix is full rank if A, B, C, and D are full rank.

By using these techniques, we find 16 input/key patterns to provide the lower bound of the minimum degree on SKINNY64 (see ${{\,\mathrm{minDeg}\,}}$ in Table 3). In 11 rounds, the lower bound is the same as the upper bound, thus having full minimum degree in 11 rounds is tight. In other words, we can guarantee the upper bound of the minimum degree is never less than 63 in 11-round SKINNY under our assumption.

All Maximum-Degree Monomials. To guarantee the appearance of all maximum-degree monomials, much more computational power must be spent. The column rotation equivalence allows us to reduce the search space, but it is still 64 times the cost of the minimum degree. After spending almost one week of computations, we can get input/key patterns to prove the appearance of all maximum-degree monomials in 13-round SKINNY64. All input/key patterns are listed in https://github.com/LowerBoundsAlgDegree/LowerBoundsAlgDegree.

Fig. 6.

Round function of PRESENT using SSB-friendly description

5.3 PRESENT

PRESENT is another lightweight block cipher published at CHES’07 [5], with a 64-bit block size and two variants depending on the key-length : either 80 bits or 128 bits. Its round function is very similar to the round function of GIFT and is also built using a 4-bit S-box and a bit permutation, see Fig. 6.

Modeling. As for GIFT-64, the S-box is modelized using the technique from [22] and the bit permutation can easily be modelized by reordering variables.

Algebraic Degree. Using our algorithm, we were able to show that all output bits have an algebraic degree of 63 after 9 rounds in about nine hours, including the lower bounds for a smaller number of rounds. Even better, for 8 rounds, we were able to show that 54 out of all 64 coordinate functions are actually already of degree 63. We give the resulting lower and upper bounds for the algebraic degree of PRESENT on the left side of Fig. 7. As for GIFT-64, these curves were obtained by taking the best bounds over all coordinate functions, and the detailed bounds for each coordinate function will be given in the full version of the paper.

Minimum Degree. Note that while directly using the PRESENT specification would still allow us to get some results for the minimum degree, we found out a way to largely improve the speed of the search for this case. Similarly to SKINNY64, we used a deterministic trail extension for the last S-box layer. We will give the full details about this observation and how we managed it in the full version.

Fig. 7.

Algebraic degree and minimum degree for PRESENT

In short, we change the S-box in the last S-box layer to a linearly equivalent one $S'$ (thus preserving the correctness of our results for the minimum degree) and add additional constraints to help finding “good” key patterns during the search. While these constraints could slightly restrict the search space, in practice it proved to be a very efficient trick to speed up the search and was enough to prove the full minimum degree over 10 rounds. The same trick is used for the all monomial property since it is essentially the same as for the minimum degree, only repeated several time for each possible input monomial. In the end, within about nine hours, we were able to show that the minimum degree is also maximal after 10 rounds using this trick. In Fig. 7 on the right side, we give the lower and upper bounds for the minimum degree over 1 to 10 rounds.

All Maximal Degree Monomials. Showing that all 63-degree monomials appear after 11 rounds for any linear combinations of output bits required quite a bit more computational power, however we were still able to show this result in about 17 days of computation.

5.4 AES

Despite many proposals of lightweight block ciphers, AES stays the most widely-used block cipher. The application to AES of our method is thus of great interest.

However, our method uses automatic tools such as MILP or SAT and such tools are not always powerful for block ciphers using 8-bit S-boxes like AES. As therefore expected, our method also has non-negligible limitation, and it is difficult to prove the full, i.e., 127, lower bound of algebraic degree. Yet, our method can still derive new and non-trivial result regarding the AES.

Modeling. We first construct linear inequalities to model the propagation table for the AES S-box, where we used the modeling technique shown in [1]. While a few dozens of linear inequalities are enough to model 4-bit S-boxes, 3,660 inequalities are required to model the AES S-box. Moreover, the model for MixColumns is also troublesome because the technique using L-boxes like SKINNY is not possible. The only choice is a naive method, i.e., we would rely on the COPY + XOR rules for the division property  [21]. Unfortunately, this method requires 184, which is equal to the weight of the matrix over $\mathbb {F}_2$, temporary variables, and such temporary variables increase the number of trails. In particular, when the weight of the output pattern in MixColumns is large, the number of sub-trails exponentially increases even when we focus on one MixColumns.

Algebraic Degree. Due to the expensive modeling situation, proving full algebraic degree is unlikely to be possible. Nevertheless, this model still allows us to get non-trivial results. We exploit that the number of sub-trails can be restrained to a reasonable size when the weight of the output pattern in MixColumns is small. Namely, we extend the trail such that only such trails are possible.

Fig. 8.

Trail on 5-round AES

Figure 8 shows one trail for 5-round AES. When the input/key/output pattern, shown in red, is fixed, the number of trails is odd. Moreover, we confirmed that the number of trails for reduced-number of rounds is odd, e.g., in 3-round AES, the number of trails $(x_2, v_3, v_4) \rightarrow y_4$ is odd.

This result provides us some interesting and non-trivial results.

On 3-round AES, the input of this trail is 16 values with Hamming weight 7. In other words, the lower bound of the degree is $16 \times 7 = 112$. Considering well-known 3-round integral distinguisher exploits that the monomial with all bits in each byte is missing, this lower bound is tight.

From the 4-round trail, we can use the input, which includes 0xFF. Unfortunately, using many $\texttt {0xFF}$ implies the output of MixColumns with higher Hamming weight, and as we already discussed, the resulting number of trails increases dramatically. While we can have 12 $\texttt {0xFF}$ potentially, we only extend the trail to 4 $\texttt {0xFF}$. Then, the lower bound of the degree is 116 in 4-round AES.

The first column in $x_1$ has $\texttt {0xFFFFFFFF}$. When we use the naive COPY+XOR rules, there are many trails from $\texttt {0xFFFFFFFF}$ to $\texttt {0xFFFFFFFF}$ via MixColumns. However, this trail must be possible and this input (resp. output) cannot propagate to other output (resp. input). Therefore, we bypass only this propagation without using COPY+XOR rule. This technique allows us to construct $x_0$ in Fig. 8. One interesting observation is all diagonal elements take 0xFF, and well-known 4-round integral distinguisher exploits that the monomial with all bits in diagonal elements is missing. Our result shows 5-round AES includes the monomial, where 84 bits are multiplied with the diagonal monomial.

While we can give non-trivial and large enough lower bound for 3-round and 4-round AES, the results are not satisfying. Many open questions are still left, e.g., how to prove the full degree, full minimum degree, the appearance of all high-degree monomials.

6 Conclusion

Cryptographers have so far failed to provide meaningful lower bounds on the degree of block cipher, and in this paper, we (partially) solve this long-lasting problem and give, for the first time, such lower bounds on a selection of block ciphers. Interestingly, we can now observe that the upper bounds are relatively tight in many cases. This was hoped for previously, but not clear at all before our work.

Obviously, there are some limitations and restrictions of our current work that, in our opinion, are good topics for future works. The main restriction is the applicability to other ciphers. For now, all ciphers studied so far needed some adjustment in the procedure to increase the efficiency and derive the results. It would be great if a unified and improved method could avoid those hand made adjustments. This restriction is inherently related to our heuristic search approach for the key-pattern. A better search, potentially based on new insights into how to choose the key-pattern in an optimal way, is an important topic for future research. Moreover, if we focus on the appearance of all maximal degree monomials, we still have a gap between the best integral distinguishers and our results. Thus, either our bounds or the attacks might be improved in the future. Finally, for now, computing good bounds for fixed key variants of the ciphers is not possibly with our ideas so far. This is in particular important for cryptographic permutations where we fail for now to argue about lower bounds for the degree. Only in the case of PRESENT, we were able to compute a non-trivial lower bound on the algebraic degree in the fixed key setting for a few bits for 10 rounds. Here, we counted the number of trails using a #SAT solver⁵  [17]. Especially for other ciphers with a more complicated linear layer like SKINNY, we were not able to show a lower bound on any output bit.